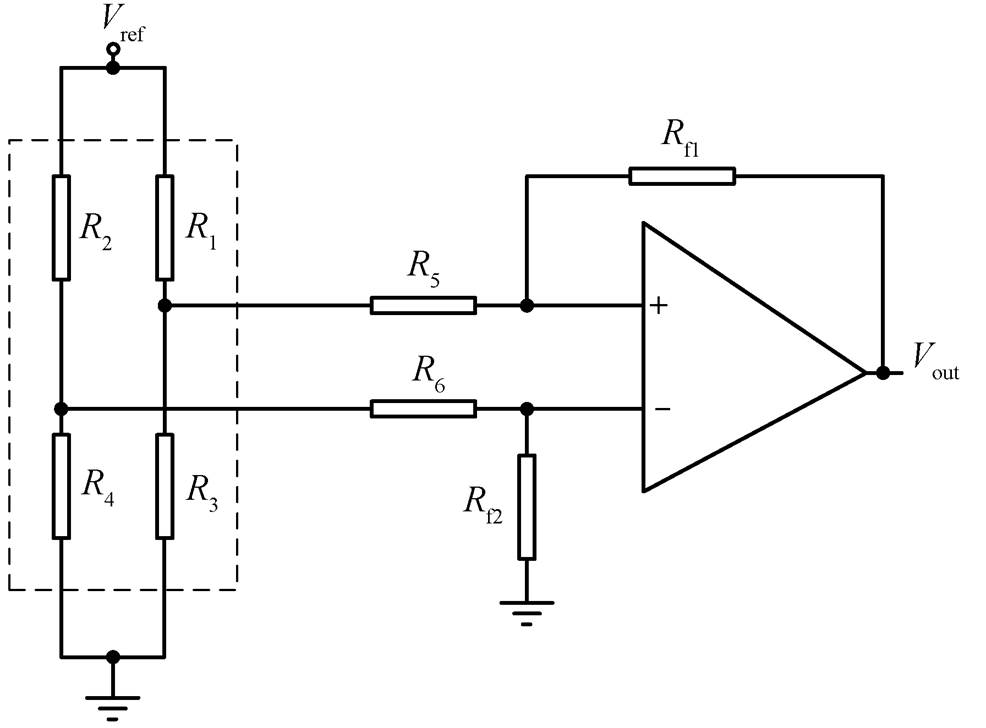
图1 惠斯通电桥式磁阻传感器的典型应用电路
Fig. 1 Equivalent circuit of the magnetometer adopting full Wheatstone-type bridge
摘要 基于惠斯通电桥式磁阻传感器 4 个电阻元件存在温度差异的事实, 提出一个惠斯通电桥式磁阻传感器零位温度漂移的简明准线性模型。在 MATLAB 环境下, 准线性模型的仿真结果与实验结果吻合, 验证了准线性模型的有效性, 为解释惠斯通电桥型磁阻传感器零位温度漂移的原因提供了清晰的思路, 此模型也可应用于其他具有惠斯通电桥结构的传感器。
关键词 惠斯通电桥结构; 磁阻传感器; 零位温度漂移简明模型
惠斯通电桥结构广泛应用于包括磁阻传感器在内的各种传感器。与由相同元件组成的其他任何结构相比, 惠斯通电桥结构可获得更佳的灵敏度和线性度[1−3]。惠斯通电桥式磁阻传感器主要应用于工业自动化、汽车工业、航空工业、仪器仪表和空间科学研究等领域[4−5]。在实际应用前, 需要对传感器的性能进行测试, 特别是涉及微弱磁场测量时[4]。其中, 温度特性是研究的重点。惠斯通电桥式磁阻传感器的温度特性包括灵敏度温度漂移和零位温度漂移。已有研究表明, 惠斯通电桥式磁阻传感器的灵敏度对温度的依赖性很小, 而零位对温度的依赖性较大[5]。零位漂移量的变化由单个元件的电阻变化决定。磁阻元件由金属材料组成, 大多数金属材料的电阻率会受温度影响。因此, 磁阻传感器的零位与温度密切相关[1]。组成惠斯通电桥的 4 个电阻元件在零场下都有一个基本阻值(R), R 在一定温度下会发生变化(变化量为 ΔR)。使 4 个电阻元件具有相同的温度变化量是不可能的, 因此, 实际的磁阻传感器总存在零位温度漂移。
惠斯通电桥式磁阻传感器的零位温度漂移研究对提高其测量精度至关重要。虽然许多传感器手册以定量的方式给出其输出与温度的依赖性关系, 但是, 对其中的物理机理还没有完全了解[4]。与磁通门相比, 磁阻传感器对温度有很高的依赖性, 其漂移量与温度呈近似的线性关系[6−7]。Archer 等[5]和Brown等[6]进行了磁阻传感器的零位温度漂移实验, 结果表明有些传感器的零位温度漂移量随温度的升高而升高, 有些则随温度的升高而降低, 即使具有相同变化趋势的传感器, 其变化斜率也不同。目前还没有研究从理论上解释这一现象。
基于温度引起的 4 个磁阻元件的电阻变化量不可能完全相同这一事实, 本文提出一个简明的模型, 从理论上证明惠斯通电桥式磁阻传感器的零位温度漂移量与温度的依赖关系。
惠斯通电桥结构的磁阻传感器(HMC1001[8])的典型应用等效电路如图 1 所示。表 1 给出图 1 中变量的含义。
图1 惠斯通电桥式磁阻传感器的典型应用电路
Fig. 1 Equivalent circuit of the magnetometer adopting full Wheatstone-type bridge
表1 变量的含义
Table 1 Definitions of variables
变量含义 R1～R4惠斯通电桥结构的磁阻传感器的4个电阻元件 Vref传感器的基准电压 R5～R6运算放大器的输入电阻, 阻值为R Rf1运算放大器的反馈电阻, 阻值为Rf Rf2运算放大器的旁路电阻, 阻值为Rf Vout运算放大器的输出电压
运算放大器的输出电压为
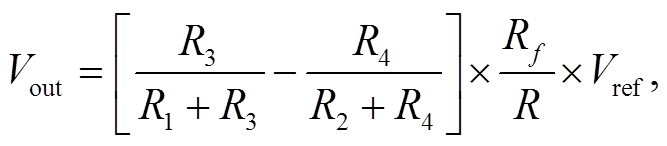(1)考虑到输出电压与周围磁场的正比关系, 输出电压对应的磁场可以表示为
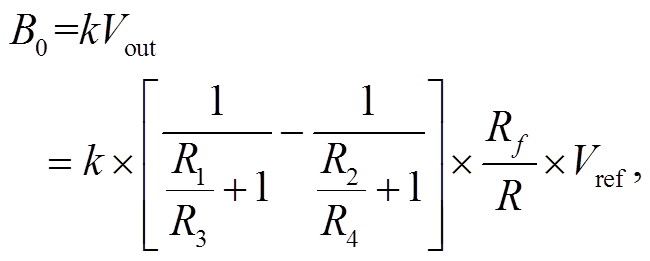(2)
其中, k 为灵敏度, 表示单位电压代表的磁场值。对于一个确定的电路, Rf, R 和 Vref 都是常数。因此, 零位温度漂移量 ΔB0 取决于温度引起的 R1～R4 变化量。
由式(2)可知, 当温度 T 引起的变化量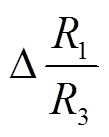
>
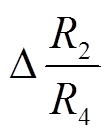时, ΔB0 为负, 即零位温度漂移量随着温度的升高而降低; 当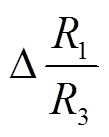<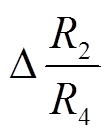时, 零位温度漂移量随着温度的升高而升高。
理论研究表明, 电阻对温度的依赖关系可以采用一级近似[1,9]表示:
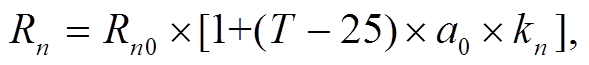(3)其中, n=1, 2, 3, 4; Rn0是参考温度为25°C时的典型电阻值;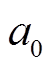 
是理论温度系数, 通常由制造商给出; kn是由温度变化引起的4个电阻元件阻值变化的差异系数。
如式(3)所示, 在没有外部磁场的情况下, 4 个电阻元件 R1, R2, R3 和 R4 的初始电阻分别为 R10, R20, R30 和 R40。在理想情况下, 这 4 个电阻相等, 输出为零。然而, 在实际情况下, 各个电阻的初始电阻Rn0 和温度系数 an0 是不同的, 温度的影响也不同, 可能是由元件结构误差或其他误差而引起[1]。因此, 4 个元件由于温度变化造成的电阻变化差异(kn之间的差异)导致电桥输出不平衡, 引起输出的零位温度出现漂移, 如式(4)所示：
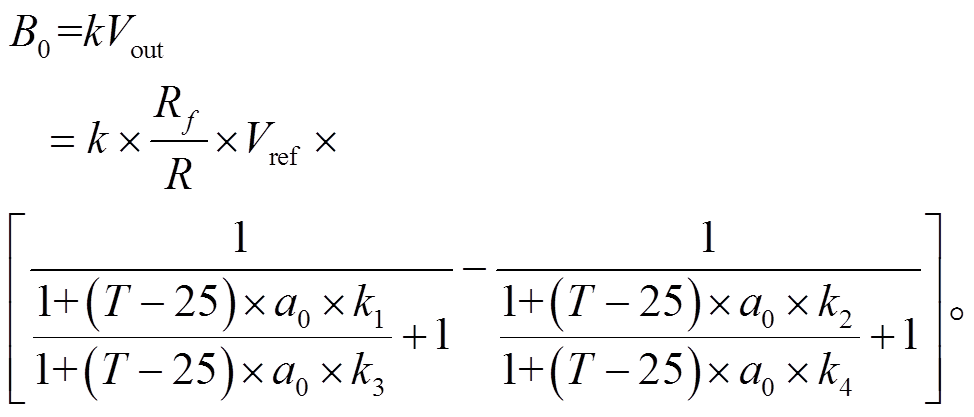(4)利用这一简明准线性模型, 可以通过实验确定磁阻传感器 4 个电阻元件的电阻温度差异系数 kn, 从而可以方便地估计磁阻传感器的零位温度漂移量。另外, 零位温度漂移量与温度的关系曲线的方向和斜率都是可变的, 在实际应用中, 需对每个传感器的零位漂移特性逐个校准。
以常用的磁阻传感器 HMC1001 为例, 在 MAT-LAB 环境下, 对提出的惠斯通桥式磁阻传感器的零位温度漂移准线性模型进行仿真计算。在实际应用中, Rf=390kΩ, R=1kΩ, Vref=2.5V, k=70000nT/V, 4 个元件的典型偏移温度系数为 10−5/℃[8]。将上述参数代入式(4), 可以得到零位漂移量与温度以及 4 个电阻元件的电阻温度差异系数 k1～k4 的关系, 如式(5)所示：
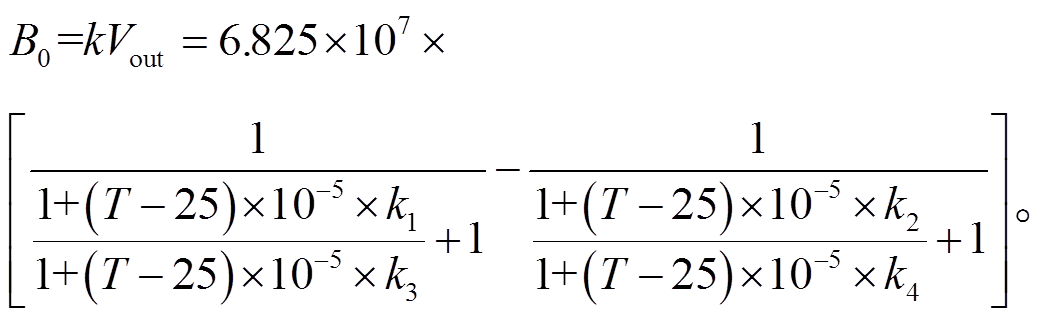(5)假定的温度引起的磁阻传感器的 4 个元件的电阻差异系数为 5%, 即系数 k1～k4 取值范围为 0.95～ 1.05。预设两类具有不同电阻温度差异系数 k1～k4的磁阻传感器, 如表 2 和 3 所示。表 2 是负温度系数的情况, 即零位温度漂移量随着温度的升高而降低。表3 是正温度系数的情况, 即零位温度漂移随着温度的升高而升高。
根据式(5), 可以得到各种情况下磁场传感器的零位温度漂移量随温度的变化曲线, 如图 2 和 3 所示。仿真时, 假设起始温度为−20℃。由图 2 和 3 可知, 仿真计算结果与第 1 节的理论分析相吻合, 并且可以看出, 零位温度漂移量随温度变化的斜率也呈现个体差异。
实验在中国船舶科技集团第 710 研究所国防科技工业弱磁一级计量站进行。为了排除地球磁场和其他外部杂散磁场的干扰, 实验在无磁高低温实验装置中进行。如图 4 所示, 实验装置将地球磁场和外部杂散磁场屏蔽到 nT 量级以下, 磁场传感器HMC1001 附近放置温度传感器, 实时监测传感器的温度。
逐步改变磁场传感器所处的环境温度, 得到零位温度漂移量随温度的变化关系。每个温度点至少停留 30 分钟, 保证传感器与周围环境处于热平衡状态。共有 10 个 HMC1001 磁场传感器参加实验。假定零位温度漂移量的温度起点为−20℃, 对实验数据进行归一化处理。
表2 零位温度漂移量随着温度升高而降低
Table 2 Negative drift offset due to temperature
传感器k1k2k3k4 #11.020.981.010.99 #21.010.960.990.98 #31.041.011.011.04 #41.050.951.010.99 #51.040.970.991.02
表3 零位温度漂移量随着温度升高而升高
Table 3 Positive drift offset due to temperature
传感器k1k2k3k4 #61.031.011.041.00 #70.970.990.990.97 #81.001.011.030.98 #90.981.021.020.98 #100.961.001.010.95
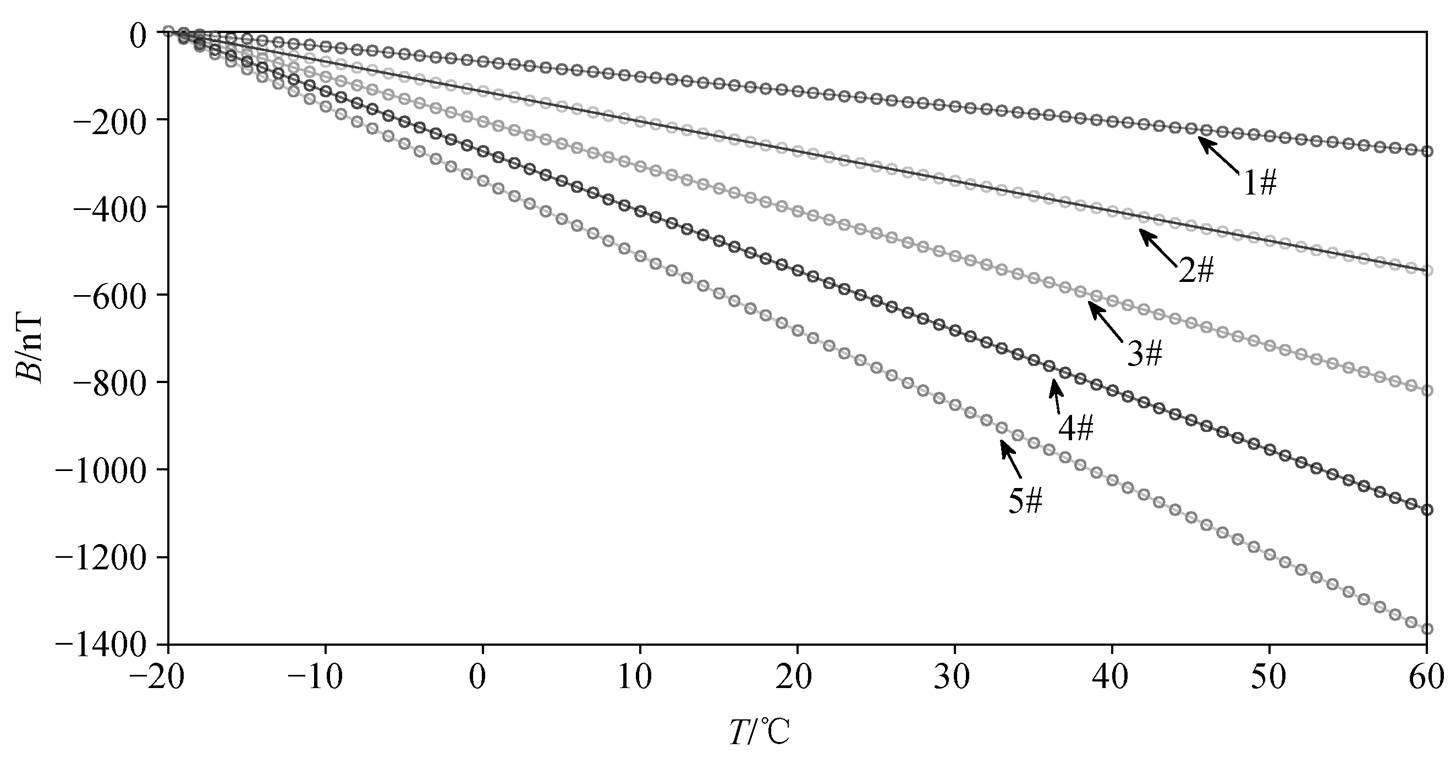
图2 零位温度漂移量为负温度系数的情况
Fig. 2 Calculated temperature drift of offset for negative offset drift
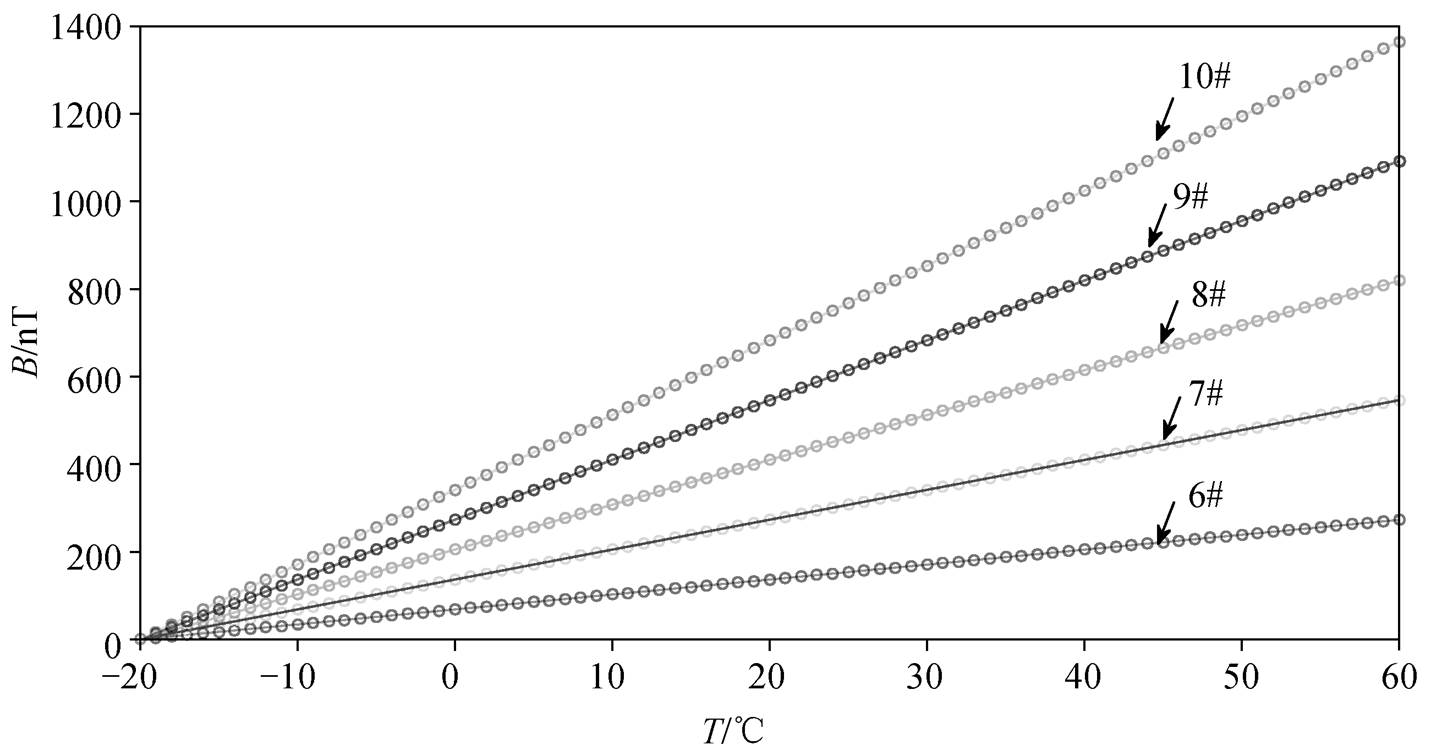
图3 零位温度漂移量为正温度系数的情况
Fig. 3 Calculated temperature drift of offset for positive offset drift
图4 无磁高低温实验装置
Fig. 4 Nonmagnetic high- and low-temperature experimental device
实验结果分为两类。第一类, 有 7 个磁场传感器的零位温度漂移量表现为负温度系数, 即随着温度的升高, 零位温度漂移量降低, 如图 5 所示。采用基于最小二乘法的曲面拟合方法求解式(5), 得到 4 个元件的电阻温度差异系数 k1～k4, 如表 4 所示。求解至少需要 4 个温度数据点, 但更多的数据点可以得到更佳的拟合结果。第二类, 有 3 个磁场传感器的零位温度漂移量表现为正温度系数, 即随着温度的升高, 零位温度漂移量升高, 如图 6 所示。同样采用基于最小二乘法的曲面拟合方法求解式(5), 可得到 4 个元件的电阻温度差异系数 k1～k4, 拟合结果如表 5 所示。
由图 5 和 6 以及表 4 和 5 可以看出, 实验得到的正负温度漂移情况与仿真结果一致, 说明采用简单的一阶近似, 建立的准线性模型与实验结果吻合。
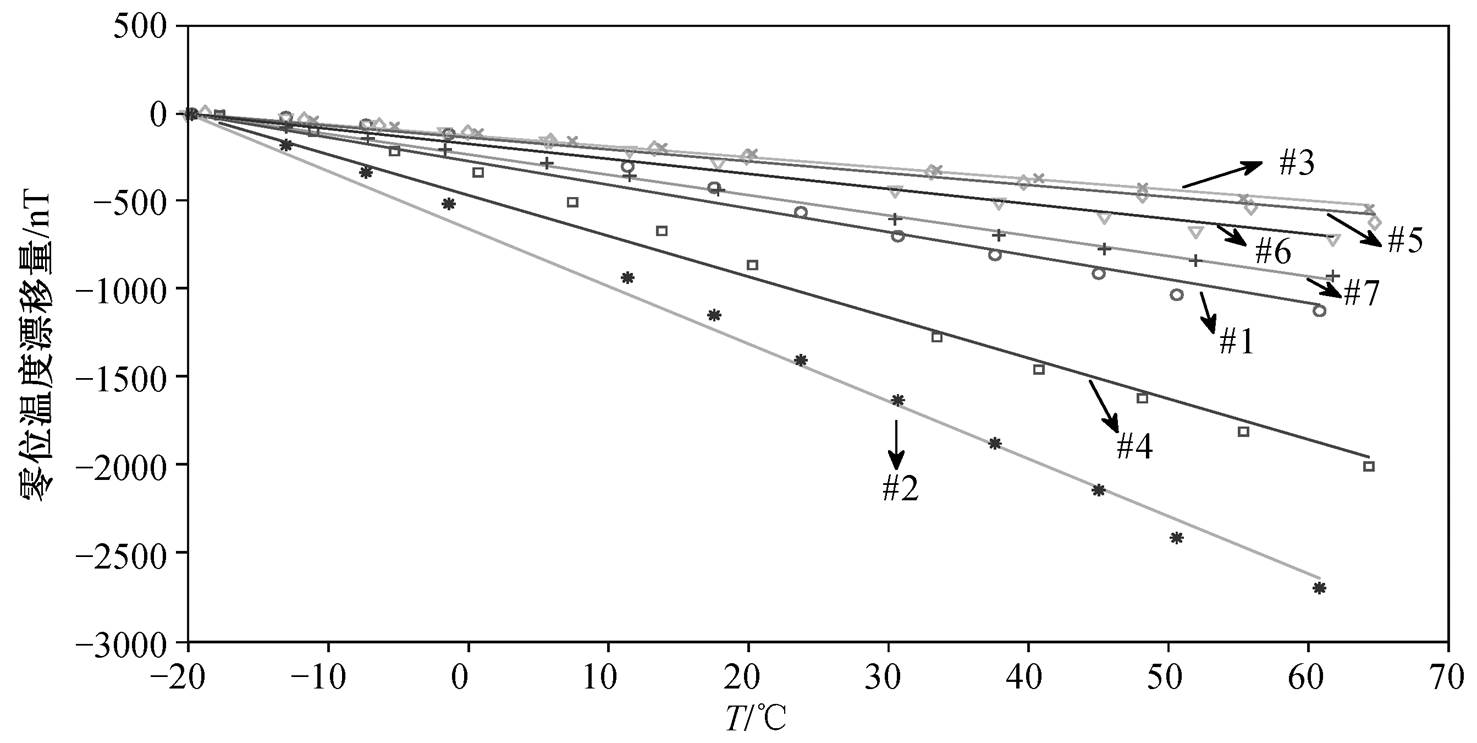
数据点为实验结果, 实线为拟合结果, 下同
图5 7个磁场传感器的零位温度漂移量表现为负温度系数
Fig. 5 Temperature-dependent magnetic field offsets for 7 negative-offset-drift sensors
图6 3个磁场传感器的零位温度漂移量表现为正温度系数
Fig. 6 Temperature-dependent magnetic field offsets for 3 positive-offset-drift sensors
表4 第一类磁场传感器的温度差异系数
Table 4 Estimated resistance divergence coefficient for class 1
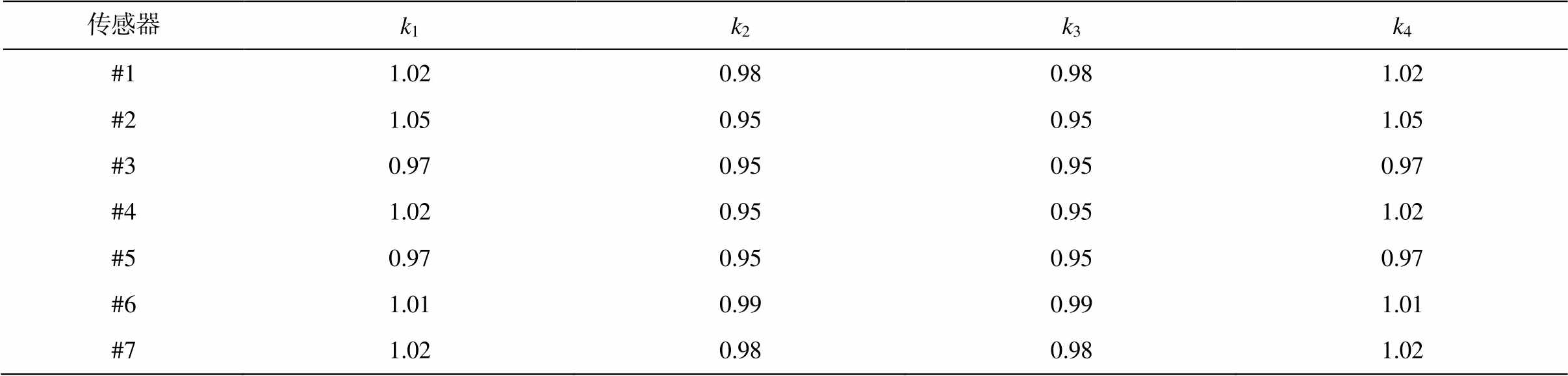
传感器k1k2k3k4 #11.020.980.981.02 #21.050.950.951.05 #30.970.950.950.97 #41.020.950.951.02 #50.970.950.950.97 #61.010.990.991.01 #71.020.980.981.02
表5 第二类磁场传感器的温度差异系数
Table 5 Estimated resistance divergence coefficient for class 2
传感器k1k2k3k4 #80.981.021.020.98 #90.991.011.010.99 #100.991.011.010.99
基于惠斯通电桥式磁阻传感器的 4 个电阻元件存在温度差异的事实, 本文建立描述惠斯通电桥式磁阻传感器零位温度漂移的准线性模型。利用这一准线性模型, 得到惠斯通电桥式磁阻传感器零位与理论温度的依赖关系。在 MATLAB 环境下, 对所提出的准线性模型进行仿真, 计算结果表明, 零位温度漂移量随着温度的升高而升高或降低, 其变化斜率也呈现个体差异。
采用典型的惠斯通电桥式磁阻传感器 HMC 1001, 对提出的准线性模型进行实验验证。虽然准线性模型只包含一阶近似, 但与实验结果吻合较好。准线性模型为解释惠斯通电桥式磁阻传感器的零位温度漂移的原因提供了一个清晰的思路, 有助于理解惠斯通电桥式磁阻传感器产生温度漂移的原因, 更好地拟合和解释实验结果。实验数据与模型的差异可能是由模型只考虑一阶多项式逼近而忽略高阶项。
本文提出的准线性模型不仅适用于磁阻传感器, 也适用于其他惠斯通电桥结构的传感器。
参考文献
[1] Vopalensky M, Platil A. Temperature drift of offset and sensitivity in full-bridge magnetoresistive sen-sors. IEEE Transactions on Magnetics, 2013, 49(1): 136−139
[2] Schulz L, Heinisch P, Richter I. Calibration of off-the-shelf anisotropic magnetoresistance magnetometers. Sensors, 2019, 19(8): 1850−1867
[3] Brown P, Beek T, Carr C, et al. Magnetoresistive magnetometer for space science applications. Mea-surement Science and Technology, 2012, 23(2): 1−11
[4] Nording F, Weber S, Ludwig F, et al. Measurement system for temperature dependent noise characteri-zation of magnetoresistive sensors. Review of Scien-tific Instruments, 2017, 88(3): 035006
[5] Archer M O, Horbury T S, Brown P, et al. The MAGIC of CINEMA: first in-flight science results from a miniaturised anisotropic magnetoresistive mag-netometer. Annales Geophysicae, 2015, 33(6): 725–735
[6] Brown P, Whiteside B J, Beek T J, et al. Space magnetometer based on an anisotropic magnetoresi-stive hybrid sensor. Review of Scientific Instruments, 2014, 85(1): 125117
[7] Fish C, Swenson C, Crowley G, et al. Design, deve-lopment, implementation, and on-orbit perfor-mance of the dynamic ionosphere cubesat experiment mis-sion. Space Science Reviews, 2014, 181(1): 61–120
[8] Honeywell HMC1001 datasheet [EB/OL]. (2008) [2021–01–21]. http://web.cse.ohio-state.edu/siefast/nest/nest_webpage/datasheet/Honeywell%20-%20Magneto meter%20-%20HMC1002.pdf
[9] Counil G, Devolder T, Kim J, et al. Temperature dependences of the resistivity and the ferromagnetic resonance linewidth in permalloy thin films. IEEE Transactions on Magnetics, 2006, 42(10): 3323–3325
Study on Temperature Drift of Offset for Full-Bridge Magneto Resistive Sensors
Abstract A concise quasi-linear model of the temperature offset for full Wheatstone-type bridges magneto resistive sensors is proposed based on the temperature-dependent of resistivity of four elements. In MATLAB environment, the simulation results of quasi-linear model agree well with the experimental results, indicating that the quasi-linear model is simple but efficient for the offset calibration, can explain the causes of the temperature offset for full Wheatstone-type bridges magneto resistive sensors, and can be applied to other sensors with full Wheatstone-type bridges structure.
Key words full Wheatstone-type bridges structure; magneto resistive sensors; concise model of temperature offset
doi: 10.13209/j.0479-8023.2021.028
风云三号03批空间环境监测器分系统磁阻磁强计项目和国家重大科技基础设施(8201701679)资助
收稿日期: 2020-03-30;
修回日期: 2020-10-30