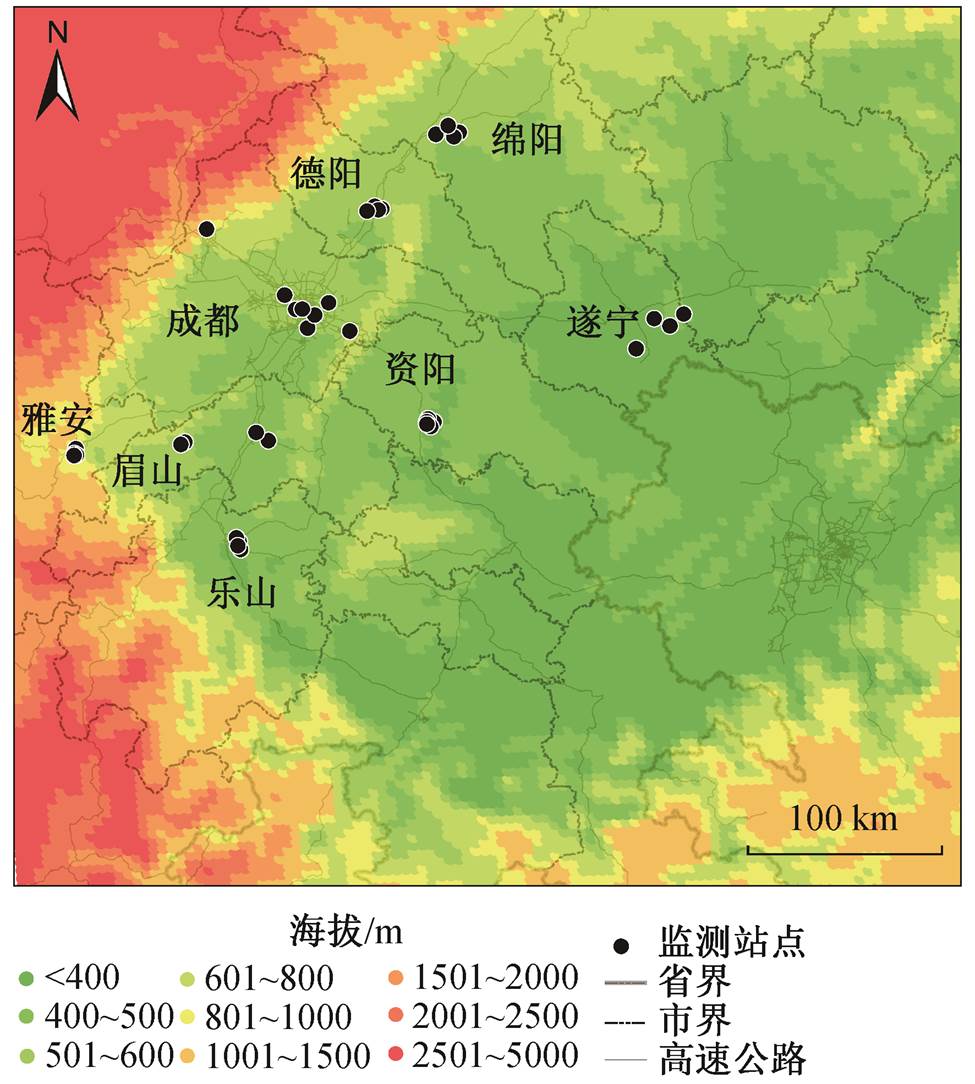
图1 研究区域
Fig. 1 Map of the study area
摘要 提出一种快速构建臭氧生成等浓度曲线的新方法。该方法利用区域空气质量模式进行臭氧前体物的敏感性分析, 基于一阶和二阶敏感性系数构建简化模型, 快速计算前体物不同排放水平对应的臭氧生成浓度。使用该方法, 结合调整的源排放清单, 对 2018 年 8 月成都平原地区进行臭氧回溯模拟并绘制臭氧生成等浓度曲线图。在此基础上, 以成都市为例, 对城市臭氧污染控制提出对策建议。
关键词 臭氧前体物; CMAQ-DDM; 臭氧污染控制
近年来, 中国经济快速增长引发的空气污染问题也越来越多地受到社会关注。自 2013 年国务院发布《大气污染防治行动计划》[1]以来, 全国各地都加强对空气污染的治理, 将大气污染防治作为改善民生的重要着力点。在近几年的大力整治下, 全国大部分地区的空气质量明显改善, 尤其对细颗粒物(空气动力学直径小于 2.5μm 的颗粒物, 即PM2.5)的治理普遍取得显著成效, 细颗粒物浓度逐年降低, 空气质量优良率不断提升[2-4]。然而, 在颗粒物污染明显改善的情况下, 臭氧污染问题日益凸显, 多地臭氧浓度不断上升[5-6], 相当多的城市以臭氧为首要污染物的超标日数逐年增加[7-8], 臭氧成为除PM2.5 外影响我国城市空气质量的又一重要污染物。
近地面大气中的臭氧主要来源于其前体物——氮氧化物(NOx)与挥发性有机物(VOCs)在光照条件下发生的一系列复杂的光化学反应。臭氧浓度水平与前体物之间具有很强的非线性关系[9-12]。当大气中氮氧化物的浓度较高时, 臭氧生成主要与 VOCs浓度的变化密切相关, 即“VOCs 控制”; 反之, 为“NOx 控制”。由于 NOx 与 VOCs 的排放差异以及气象条件的变化, 臭氧的生成控制机制也会发生时空上的转换。有研究表明, 我国不同地区的臭氧生成对 NOx 或 VOCs 的敏感性不同, 如京津唐地区[13]、粤东北地区[14]、珠江三角洲地区[15-17]等主要受VOCs 控制, 因此限制 VOCs 的排放能够有效地控制臭氧污染。罗恢泓等[18]利用 WRF/MODIFIED SMOKE/CMAQ 模式系统, 对上海市 2017 年 8 月 1 —9 日的一次持续性臭氧污染时段进行回溯模拟, 结果表明, 当所受的大尺度环流影响发生变化时, 上海市整体的臭氧生成机制可由 NOx 控制经过渡转变为 VOCs 控制。Li 等[19]利用 MM5-SMOKE-CAMx模式系统, 对珠江三角洲区域 2006 年的臭氧污染状况进行模拟, 发现该区域大部分地区在清晨时受 VOCs 控制, 但在臭氧高值时段(12:00—16:00)转变为受 NOx 控制。这种臭氧生成控制机制在时空上的动态变化使得对臭氧治理的难度大大增加, 直接划分 VOCs 或 NOx 敏感区, 或制定单一的 NOx 或VOCs 减排措施都无法有效地控制臭氧污染。因此, 及时并准确地识别臭氧生成机制的变化特征, 包括获取臭氧生成对前体物源排放变化的敏感性强弱等定量信息, 可以为制定臭氧控制策略提供重要科学依据, 是臭氧污染防治的关键。
基于空气质量模式的敏感性分析方法是进行源排放控制策略研究的重要工具[20]。敏感性系数定量地描述源排放改变与污染物浓度变化之间的关系, 可以很方便地用于追踪和解析特定地点污染物浓度来源的贡献情况。污染源敏感性分析的主要方法包括 BFM (brute-force method)[21]和“去耦合直接法”(decoupled direct 3D method, DDM-3D)[22-23]等。传统的 BFM 通过改变各影响因子(如源排放速率),进行大量空气质量模式的运算, 分析各污染源排放对污染物浓度的影响。但是, 多次重复运行空气质量模式导致 BFM 运算耗时较长, 尤其是臭氧和PM2.5 等二次非线性污染物的浓度计算本身就非常耗费计算资源[24-25]。此外, 对于较小扰动的计算, BFM 也容易产生数值噪声, 严重地影响最终结果的准确性[25]。与 BFM 相比, DDM-3D 计算量减少, 且能够快速、准确地估算由非常小的源排放变化引起的污染物浓度变化。目前, 作为一种有效的敏感性分析工具, DDM-3D 已广泛地应用于各项研究中, 包括排放源对臭氧生成的敏感性分析[26-28]以及将臭氧敏感性分析与臭氧生成等浓度曲线相结合来提供臭氧控制建议等[14-15]。
臭氧生成等浓度(empirical kinetic modeling approach, EKMA)曲线能够直观地反映臭氧生成浓度与其前体物 NOx 和 VOCs 排放量削减之间的非线性关系[29-31], 并且能够评估不同减排比例降低臭氧浓度的有效程度, 广泛用于设计臭氧污染控制的最佳减排途径[15,18,27,32]。EKMA 曲线的绘制需要足够多的情景计算, 以便得到足够密集的、与 VOCs 和NOx 减排情景相对应的臭氧生成浓度数值, 除 BFM外, 还可以采用简化模型(reduced form model, RFM)[22,24,33-34]来实现快速计算。RFM 是基于污染物敏感性系数的泰勒展开, 在避免重复运行完整的空气质量模式、节省大量计算资源的同时, 完整地保留污染物浓度与各影响因子之间的依赖关系, 能够快速有效地对控制措施进行定量评估。
本研究提出一种快速构建臭氧生成等浓度曲线的新方法, 利用 CMAQ-DDM-3D 方法, 针对臭氧前体物进行敏感性分析, 基于敏感性系数构建简化模型, 快速计算 NOx 和 VOCs 不同控制情景的臭氧浓度, 构建臭氧生成等浓度曲线。我们将该方法应用于成都平原地区, 对 2018 年 8 月的臭氧污染情况进行回溯模拟和敏感性系数计算, 并绘制EKMA 曲线图, 并在 EKMA 曲线指导下, 以成都市为例, 提出针对性减排建议, 为臭氧污染防治提供决策支持。
成都平原地区位于四川盆地西部(图 1), 属亚热带季风气候区, 总面积约为 1.881 万 km2, 地势自西北向东南倾斜, 平均海拔 542m 左右[35]。盆地四周环山, 封闭的地形导致该地区常年风速偏低, 不利于污染物的扩散, 尤其在夏季高温季节臭氧污染频发。

图1 研究区域
Fig. 1 Map of the study area
1.2.1臭氧观测数据
空气质量观测数据来源于四川省空气质量监测网络管理平台(http://www.scnewair.cn:3389/smartad min), 包括四川全省共 94 个国控监测站的逐小时和逐日的臭氧以及 NO2 浓度数据。利用成都平原区域内 8 个城市(图 1)以及紧邻的内江市相应国控站点的臭氧观测数据, 剔除城市对照点, 计算分析各城市的臭氧平均浓度, 用于评估城市空气质量。以成都市为例, 2018 年 8 月以臭氧为首要污染物的超标天数共 11 天, 其中 6 日和 15 日的臭氧日最大滑动 8小时平均浓度均超过 200µg/m3, 28 日和 29 日的臭氧日最大滑动 8 小时平均浓度均超过 190µg/m3 (见附录表 1。附录请访问 http://xbna.pku.edu.cn 查看, 下同)。这是一段典型的夏季连续高温时期, 成都地面日最高气温持续保持在 30°C 左右, 云量偏少, 日照强烈, 基本上无降水, 属于有利于臭氧光化学污染的典型气象条件[7,36-37]。
1.2.2模型模拟数据
根据成都平原地区臭氧污染季节分布特征, 选择回溯模拟的时段为 2018 年 7 月 21 日—9 月 2 日, 其中前 10 天为模拟启动时段。采用三层嵌套网格, 水平分辨率分别为 36, 12 和 4km。最外层网格覆盖包括青藏高原在内的所有中国地区以及东南亚和印度次大陆部分地区, 次外层网格覆盖四川省全境以及周边省市部分地区, 有助于为最内层网格提供较好的边界条件。最内层的 4km 网格以成都平原地区为主要区域, 同时覆盖四川盆地所有主要城市(图 1)。
气象模拟数据来自中尺度天气预报模式 WRF[38](weather research and forecast model) 3.6 版本的回溯模拟结果。采用 Lambert 投影坐标, 垂直方向从地面到 50hPa 共分为 35 个 σ 层。主要物理过程分别采用 Kain-Fritsch 积云方案、YSU 边界层参数化方案、NOAH+MOSAIC 陆面模式以及 Lin微物理参数化方案。模拟结果和地面观测数据的对比表明, 模拟气象场的准确性符合进一步进行空气质量模式模拟的要求(见附录表 2)。
空气质量模拟数据来自多尺度化学传输模式CMAQ (community multiscale air quality model,5.0.2 版本)模型。该模型在源排放和气象场等输入数据的驱动下, 对空气污染物(包括气态污染物和气溶胶)在大气中的迁移、转化等物理和化学过程进行模拟, 计算得到污染物的时空分布场[39-40]。CMAQ 模拟选用 SAPRC07tc 气相反应机理[41]以及AERO6 气溶胶模块[42]。
CMAQ 输入使用的源清单来自四川省空气质量数值预报系统的 2017 年基准排放清单, 经初始模拟并与实测数据比对后, 采用 1.2.3 节的源排放清单调整方法, 经迭代调整后作为最终的输入源清单。清单中 NOx 和 VOCs 的人为源主要包括工业源、电厂源、民用源、移动源、生物质燃烧源和溶剂使用源, 其中移动源和工业源在 NOx 和 VOCs 排放中的占比都较高, 溶剂使用源在 VOCs 排放总量中也占有很高的比例。
利用 DDM-3D 计算敏感性系数。DDM-3D 是在 CMAQ 模型中内置的污染物敏感性分析模块, 可以在 CMAQ 模拟污染物浓度的同时, 计算三维空间每一个格点各污染物浓度随时间变化的敏感性系数。污染物敏感性系数反映某一影响因子变化引起的某污染物浓度的时空变化, 从数学的角度看, 它是污染物浓度对某一影响因子的偏导数, 具体方法详见文献[43]。DDM-3D 计算得到的一阶敏感性系数结合二阶敏感性系数描述臭氧生成的复杂的非线性变化。利用 DDM-3D 敏感性系数, 结合反演算法, 可对源清单进行优化调整[44]。利用一阶和二阶敏感性系数, 也可构建简化模型以便快速计算排放量改变条件下的臭氧生成浓度。本研究涉及的针对臭氧的一阶和二阶敏感性系数的定义见表 1 和 2, 包括细分的人为源及天然源的 NOx 和 VOCs 排放的一阶参数、总的 NOx 和 VOCs排放的一阶和二阶参数以及两者之间的交叉二阶参数。表 1 中参数用于调整源排放清单(见 1.2.3 节)及臭氧敏感性分析, 表2 中参数用于绘制 EKMA 曲线(见 1.2.4 节)。
1.2.3源排放清单调整方法
使用基准年清单作为 CMAQ 输入, 模拟成都平原 2018 年 8 月的空气质量状况, 并使用同期观测数据, 对成都、德阳、乐山、眉山、绵阳、遂宁、雅安、资阳及紧邻的内江等 9 个城市的 NO2 和 O3 模拟效果进行评估。根据评估结果, 结合表 1 中一阶敏感性系数对 9 个城市基准年的人为源 NOx 和VOCs 排放量, 采用优化下述目标函数的方法, 求取源排放调整系数:
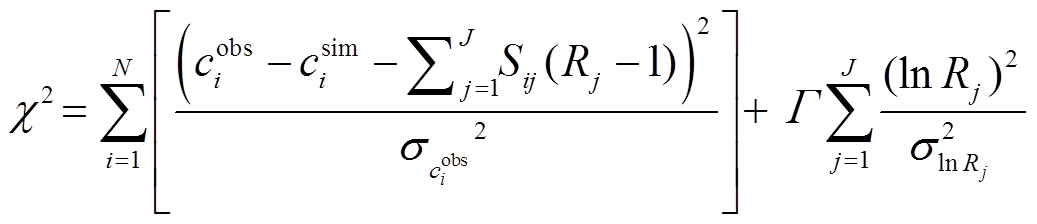 , (1)
, (1)其中, 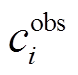 和
和 分别代表第 i 个污染物的观测值和模拟值,
分别代表第 i 个污染物的观测值和模拟值, 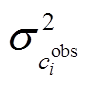 代表第 i 个观测值浓度的不确定性(即观测误差), Sij 是污染物浓度 i 对排放源 j 的敏感性(由 DDM-3D 计算得到), Rj 是针对基准年排放源 j的调整系数,
代表第 i 个观测值浓度的不确定性(即观测误差), Sij 是污染物浓度 i 对排放源 j 的敏感性(由 DDM-3D 计算得到), Rj 是针对基准年排放源 j的调整系数, 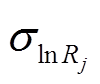 是排放源 j 不确定性的自然对数。目标函数右边第一项是模拟误差, 第二项是调整后的排放相对于基准年(调整前)的差值。引进 Γ 来平衡两项, Γ = N/J, N 是总的观测值个数, J 是排放源的种类。目标函数取上述两项之和, 可以在尽量优化模拟误差的同时, 限制源排放调整系数的过度优化, 确保其具有真实的物理意义。采用 L-BFGC 优化方法[45]计算目标函数 χ2 的最小值, 求得最优化目标函数值对应的一组调整系数 Rj。利用 Rj 对输入源清单进行调整, 并将调整后的清单重新输入模式进行计算, 经过多次迭代调整后[44,46-47]的源清单用于最终的模拟, 并绘制臭氧生成等浓度曲线。
是排放源 j 不确定性的自然对数。目标函数右边第一项是模拟误差, 第二项是调整后的排放相对于基准年(调整前)的差值。引进 Γ 来平衡两项, Γ = N/J, N 是总的观测值个数, J 是排放源的种类。目标函数取上述两项之和, 可以在尽量优化模拟误差的同时, 限制源排放调整系数的过度优化, 确保其具有真实的物理意义。采用 L-BFGC 优化方法[45]计算目标函数 χ2 的最小值, 求得最优化目标函数值对应的一组调整系数 Rj。利用 Rj 对输入源清单进行调整, 并将调整后的清单重新输入模式进行计算, 经过多次迭代调整后[44,46-47]的源清单用于最终的模拟, 并绘制臭氧生成等浓度曲线。
表1 CMAQ-DDM-3D臭氧敏感性计算的DDM参数设置
Table 1 DDM parameters defined in CMAQ-DDM-3D calculation for ozone sensitivity analysis

源分类NOx排放 DDM-3D参数VOCs排放 DDM-3D参数 工业源INIV 电厂源PNPV 民用源RNRV 移动源TNTV 生物质燃烧源FNFV 溶剂使用−SV 天然源BNBV
表2 绘制EKMA曲线的RFM模式的DDM参数
Table 2 DDM parameters used in RFM model for plotting EKMA diagram

代码DDM-3D 参数 EN内层网格 NOx 总排放 EV内层网格 VOCs 总排放 NNNOx 排放二阶 VVVOCs 排放二阶 NVNOx和VOCs 排放交叉二阶
1.2.4臭氧生成等浓度曲线绘制方法
对表 2 中 5 个 DDM-3D 参数分别进行 100%人为源排放(basecase)和 1%人为源排放(1pctcase)条件下的敏感性系数计算, 生成两套 DDM-3D 模拟结果, 并基于这两套结果分别构建人为源 NOx 和VOCs 排放的臭氧生成浓度的 RFM 模式, 计算公式如下:

 (2)
(2)式中 ecase 为 basecase 或 1pctcase 排放水平。基于实测数据计算的相对响应因子 RRF (relative response factor, RRF 为观测值与模拟值的比值), 可以对上一步骤中 RFM 的计算结果进行“修订”, 即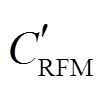 = CRFM·RRF。然后, 对 basecase 和 1pctcase 情形下得到的 RFM 修订结果进行加权平均(使用削减后的排放比例到 100%或 1%的距离进行加权平均), 得到该排放水平对应的预测臭氧浓度。这是利用 DDM-3D 对排放水平进行分段(stepwise)模拟的方法来构筑 RFM 模式的一个简单应用, 据此制作的 EKMA曲线将显著地减少排放削减力度较大(如超过 30%~ 40%)时的误差[48]。最后, 用经加权平均的 RFM 修订结果绘制 EKMA 曲线, 选取间隔足够小(每次差距选为 0.01)的一组 NOx 和 VOCs 排放削减量, 通过RFM 模式计算并“修订”对应的臭氧浓度预测值, 最后加权平均, 在分别以 VOCs 减排量和 NOx 减排量为横、纵轴的平面空间上, 得到足够密集的代表臭氧浓度数值的点, 绘制臭氧生成等浓度曲线, 即EKMA 曲线图。
= CRFM·RRF。然后, 对 basecase 和 1pctcase 情形下得到的 RFM 修订结果进行加权平均(使用削减后的排放比例到 100%或 1%的距离进行加权平均), 得到该排放水平对应的预测臭氧浓度。这是利用 DDM-3D 对排放水平进行分段(stepwise)模拟的方法来构筑 RFM 模式的一个简单应用, 据此制作的 EKMA曲线将显著地减少排放削减力度较大(如超过 30%~ 40%)时的误差[48]。最后, 用经加权平均的 RFM 修订结果绘制 EKMA 曲线, 选取间隔足够小(每次差距选为 0.01)的一组 NOx 和 VOCs 排放削减量, 通过RFM 模式计算并“修订”对应的臭氧浓度预测值, 最后加权平均, 在分别以 VOCs 减排量和 NOx 减排量为横、纵轴的平面空间上, 得到足够密集的代表臭氧浓度数值的点, 绘制臭氧生成等浓度曲线, 即EKMA 曲线图。
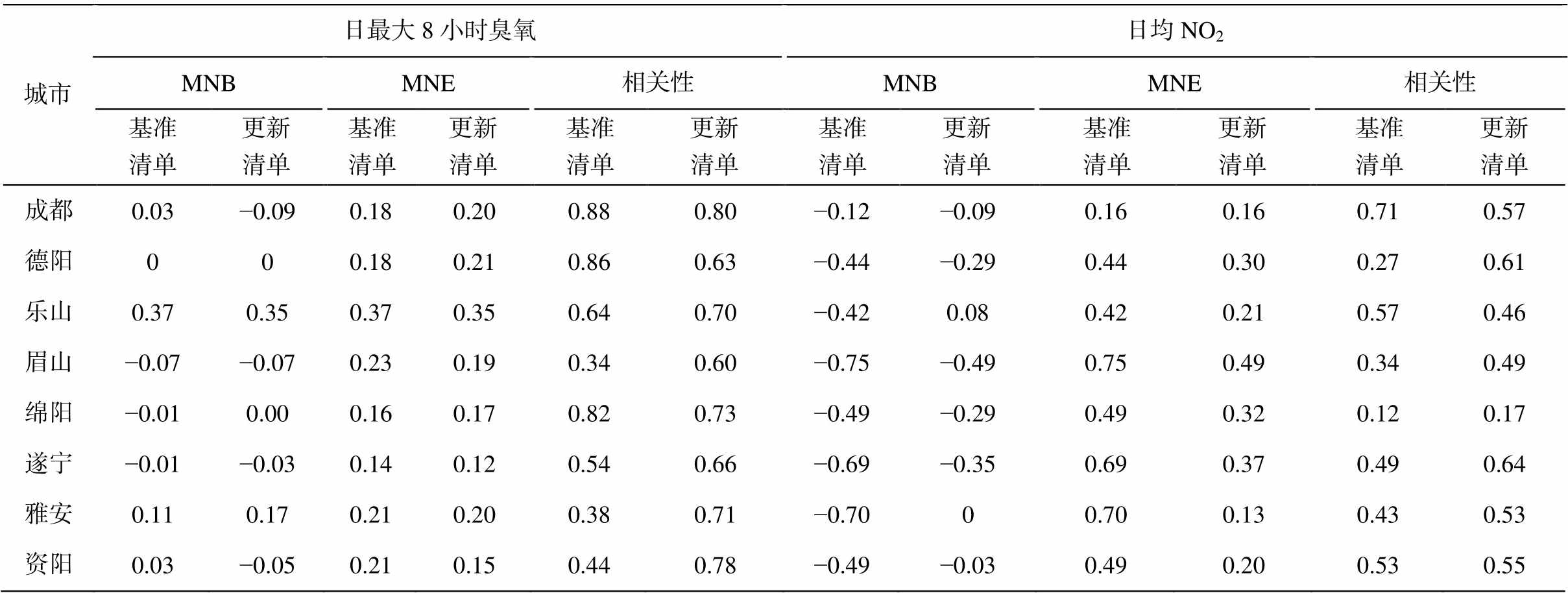
采用 1.2.3 节的方法, 在城市级别上对基准年源清单进行调整, 即对 9 个城市分别求取一组调整系数, 用于调整该城市相关细分源的 NOx 和 VOCs 排放。将调整后的清单重新输入 CMAQ, 经过 3 次迭代计算后, 总模拟误差趋于收敛。利用区域内所有国控站的逐时和逐日观测数据, 对 CMAQ 空气质量模拟最内层网格(4km 网格)的模拟结果进行评估。对比使用基准清单及最后更新清单对成都平原各城市 O3 及 NO2 模拟的评估结果(表 3, 详细结果见附录中表 3 及图 1 和 2)可知, 清单更新后的总体表现显著优于更新前。各城市更新清单后的模拟值与观测值的逐日变化相关性普遍比更新之前提高, 臭氧的相关系数在 0.6~0.8 之间, 平均值约为 0.70, 比基准清单的 0.61 提高 15%; NO2 的相关系数在 0.17~ 0.61 之间, 平均值约为 0.50, 比基准清单的 0.43 提高 16%。各城市臭氧模拟整体评估的平均标准化偏差(mean normalized bias, MNB)和平均标准化误差(mean normalized error, MNE)分别为 3%和 20%, 与基准清单相比, 分别降低约 50%和 5%; NO2 模拟整体评估的 MNB 和 MNE 分别为−18%和 27%, 比基准清单分别降低约 65%和 48%。
更新清单后的模拟效果总体上符合进一步进行控制决策方案制定的相关要求(臭氧模拟的推荐阈值: MNB 在±15%之间, MNE 小于30%)[49]。就成都市而言, 更新清单之后 O3 和 NO2 的模拟值与观测值之间的相关性略有降低, 但在所有城市中仍保持最高值, 具有较好的模拟效果。另外, 模拟结果对成都市实测臭氧浓度高值存在一定程度的低估, 但从整个模拟时段来看, 其 MNB 和 MNE 分别为−9%和 20%, 都在推荐的参考值[50]范围内。成都周边城市中, 除乐山和雅安的臭氧模拟误差稍大外, 其他城市模拟结果都符合推荐标准。
使用更新清单计算的臭氧对各主要贡献源的敏感性系数的空间分布具有显著的差异(见附录中图3)。以 8 月 29 日的臭氧日最大 8 小时平均浓度为例, 当日臭氧高值区主要分布在成都市主城区及西部的郫都区、温江区和双流区西北部等地区。在各细分源类别中, 臭氧对天然源 NOx 的敏感性系数可达 2~ 5µg/m3 的水平, 对天然源 VOCs 的敏感性系数可达到更高的 5~10µg/m3 的水平。工业源 NOx 和 VOCs对成都臭氧高值区有重要影响, 是主要的人为贡献源。其中, 臭氧对工业源 NOx 的敏感性系数在成都主城区的中心地带为−2~2µg/m3 的较低水平, 在成都市其他大部分地区都在 5~20µg/m3的水平。在臭氧的高值区, 工业源 VOCs 对臭氧浓度的影响都在5µg/m3 以上, 最高可达 20µg/m3 以上。移动源 NOx的敏感性系数在成都主城区的中心地带为负值, 表明移动源 NOx 排放量较大, 所体现的滴定作用能够在局地抑制臭氧的生成[18,51]。臭氧浓度对移动源VOCs 的敏感性也很强, 在臭氧高值区普遍大于 10µg/m3。溶剂使用 VOCs 排放对臭氧的影响在成都及周边地区与移动源 VOCs 的影响水平接近。
表3 2018年8月成都平原城市日最大8小时臭氧、日均NO2浓度基准清单和更新清单评估结果
Table 3 Model performance statistics of daily maximum 8-hour average ozone and daily average NO2 concentrations of Chengdu Plain cities in August 2018 simulation using a priori and a posteriori emissions
城市日最大8小时臭氧日均NO2 MNBMNE相关性MNBMNE相关性 基准清单更新清单基准清单更新清单基准清单更新清单基准清单更新清单基准清单更新清单基准清单更新清单 成都0.03−0.090.180.200.880.80−0.12−0.090.160.160.710.57 德阳000.180.210.860.63−0.44−0.290.440.300.270.61 乐山0.370.350.370.350.640.70−0.420.080.420.210.570.46 眉山−0.07−0.070.230.190.340.60−0.75−0.490.750.490.340.49 绵阳−0.010.000.160.170.820.73−0.49−0.290.490.320.120.17 遂宁−0.01−0.030.140.120.540.66−0.69−0.350.690.370.490.64 雅安0.110.170.210.200.380.71−0.7000.700.130.430.53 资阳0.03−0.050.210.150.440.78−0.49−0.030.490.200.530.55
臭氧对前体物排放的敏感性系数也会随气象条件(如湿度和风速)的变化而变化。以成都市为例, 在污染天, 成都市臭氧日最大 8 小时平均浓度对区域内 NOx 和 VOCs 排放都敏感, 特别是对工业源、电厂源和移动源的 NOx, 以及工业源、移动源、溶剂使用的 VOCs 和天然源 VOCs 排放更敏感(图 2), 在制定减排方案时, 应优先考虑控制上述人为源的排放。例如, 8 月 29 日臭氧日最大 8 小时平均浓度(观测值为 194µg/m3)对上述 3 个 NOx 排放的敏感性系数都在 10µg/m3以上, 对上述 3 个人为源 VOCs排放的敏感性系数都在 15µg/m3 以上, 显著高于其他人为源排放 NOx 和 VOCs 的敏感性系数, 并且对所有 VOCs 和 NOx排放的敏感性均为正值。在相对清洁天, 由于气象条件的变化, 成都市臭氧日最大8 小时平均浓度对移动源的 NOx 表现出很高的负值敏感性。以 8 月 30 日为例, 成都市臭氧日最大 8 小时平均浓度对移动源的 NOx 敏感性系数低于−15µg/m3。因此, 在控制移动源时, 需考虑 NOx 的负敏感性作用, 根据实际情况对移动源的 NOx 和 VOC进行更精细化的控制。
臭氧对前体物排放的敏感性系数具有显著的日变化特征(图 3)。在一天当中, 臭氧浓度对 VOCs 源的敏感性系数总是正值, 其数值从日出开始增加, 日落时处于较低水平, 在中午前后(即太阳辐射最强时)达到峰值。臭氧浓度对 NOx 源的敏感性系数在一天中的大部分时间都是负值(即消耗臭氧), 随着日出, 其对臭氧的滴定作用逐渐减弱[52], 且在中午前后敏感性系数变为正值, 并在臭氧 8 小时浓度峰值(一般在下午 4―5 点钟)前后表现出显著的正敏感性, 随后又开始下降, 并在日落前后变为负值(即重新开始消耗臭氧)。从逐时敏感性系数的时间序列(图 3)看, 成都市臭氧对电厂源和工业源的 NOx敏感度相对更高, 高污染天时, 臭氧峰值对移动源NOx 也表现出较强的敏感性(图 3)。
通过绘制逐日的城市站点日最大8小时臭氧平均浓度 EKMA 曲线, 可以快速地研判不同时间、不同污染程度和不同减排目标下城市臭氧控制的最佳减排途径。在 EKMA 曲线图中, 连接代表当前浓度水平的点(100%NOx 和 100%VOCs 排放对应的点)到臭氧浓度标准的 160µg/m3 等浓度线的最短直线(图4 中带箭头黑线指示)即为最佳减排控制路径。例如, 26 日成都市最大 8 小时臭氧浓度对 NOx 更敏感, 可采用 NOx 减排 50%, VOCs 减排 15%的最佳方案将臭氧浓度降低到 160µg/m3(图 4(a)); 31 日成都臭氧对 VOCs 更敏感, 只需将 VOCs 减排 38%即可达标(图 4(d))。其他多数天, 成都臭氧对 NOx 和 VOCs的敏感性较接近, 即对区域内 NOx 和 VOCs 采取接近 1:1 的比例进行减排的效果最佳。例如 28 和 29日, 成都臭氧的最佳减排路径都在对角线附近, 28日对 NOx 和 VOCs 分别减排 48%和 45%效果最佳(图4(b)), 29 日对 NOx 和 VOCs 分别减排 36%左右效果最佳(图 4(c))。
在确定最佳控制路径后, 结合细分源敏感性分析结果, 可制定减排控制情景方案。以成都市 8 月29 日的臭氧达标控制为例, 可利用细分源敏感性系数, 将最佳控制路径揭示的 NOx 和 VOCs 的减排总量细分到主要排放源上, 形成可执行的控制方案(如表 4 所列的两个细分方案)。8 月 29 日成都市最大 8 小时臭氧浓度为 194µg/m3, 需要减排至少 34µg/m3方可达标(160µg/m3)。方案 Q1 和 Q2 采用的都是最佳减排路径, 即 NOx 和 VOCs 总量同时削减 36%。其中, Q1 将总量削减比例应用于所有细分源, 预期臭氧浓度将刚好达标; Q2 则集中削减高敏感性的源(包括工业源的 NOx 和 VOCs、电厂源的 NOx 以及溶剂使用源的 VOCs), 其中部分高敏感性源的削减比例可达 57%以上, 控制难度加大。需要强调的是, 这里使用细分源的一阶敏感性系数的相对比例来设计细分源减排执行方案。由于没有充分考虑不同细分源减排对臭氧生成浓度可能具有的不同的非线性影响, 因此在减排程度较大的情况下, 对各细分源相对减排效果的估算会存在一定程度的误差。对总的减排效果, 是基于所构建的臭氧生成等浓度曲线估算的, 估算误差相对较小。这是因为, 简化模型同时利用 DDM-3D 计算的一阶和二阶敏感性系数来计算臭氧生成浓度, 较充分地考虑了在减排程度较大的情况下臭氧生成浓度的非线性响应特征。另外, 在构建臭氧生成等浓度曲线时, 还同时用到基于 1%和 100%人为源排放的一阶和二阶敏感性系数, 运用权重插值的方法计算得到不同减排比例对应的臭氧生成浓度, 可进一步减少在排放水平变化较大, 但不趋近于零的情形下对臭氧非线性响应特征的预测误差。
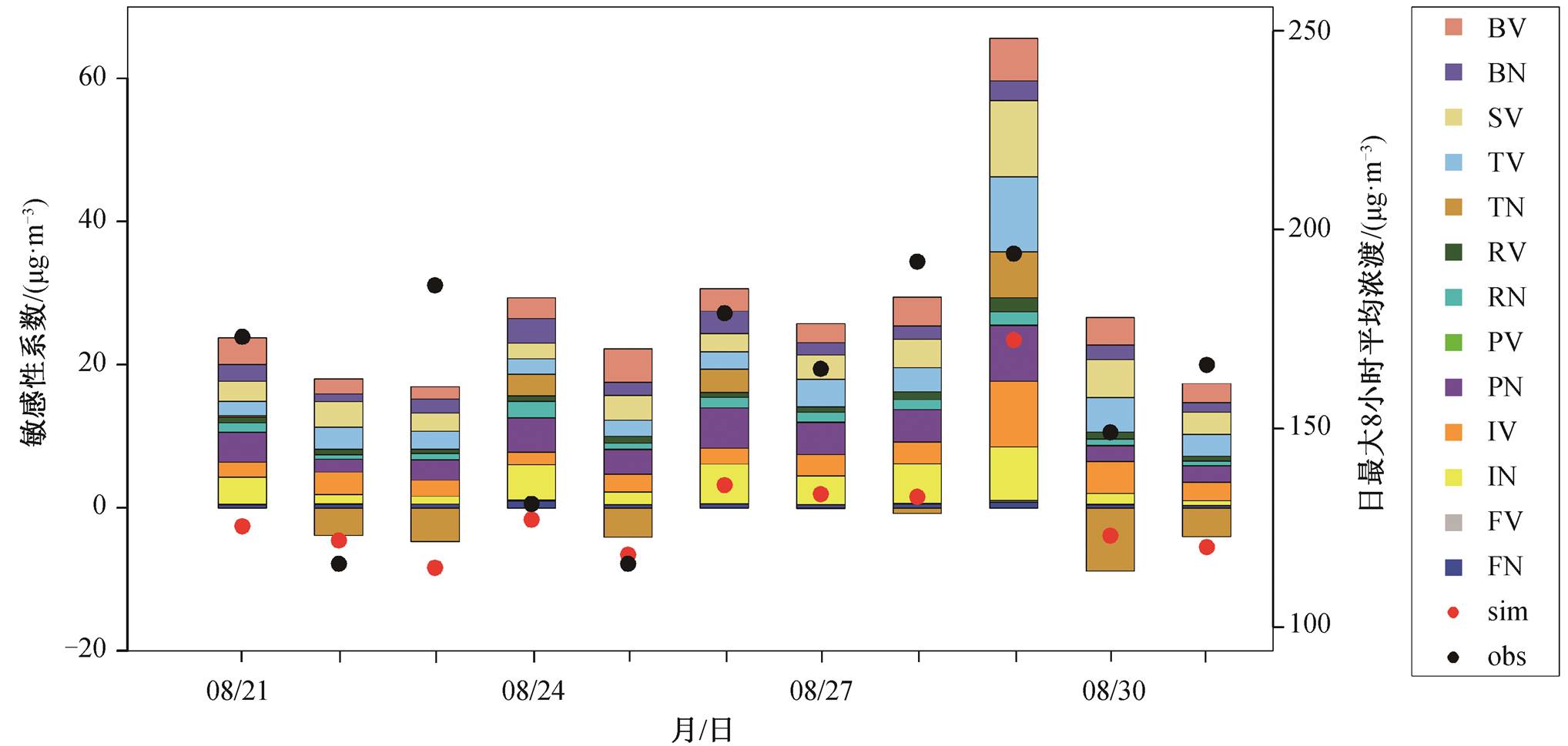
图2 由 CMAQ-DDM-3D 计算的 2018 年 8 月 21—31 日成都市臭氧日最大 8 小时平均浓度对各个DDM源排放参数的敏感性系数与模拟和实测浓度的逐日累积柱状图
Fig. 2 Stacked bars of daily maximum 8-hour average ozone concentration sensitivities to sector emissions calculated by CMAQ-DDM-3D with dots representing observed and simulated daily maximum 8-hour average ozone concentrations of Chengdu City from August 21 to 31, 2018
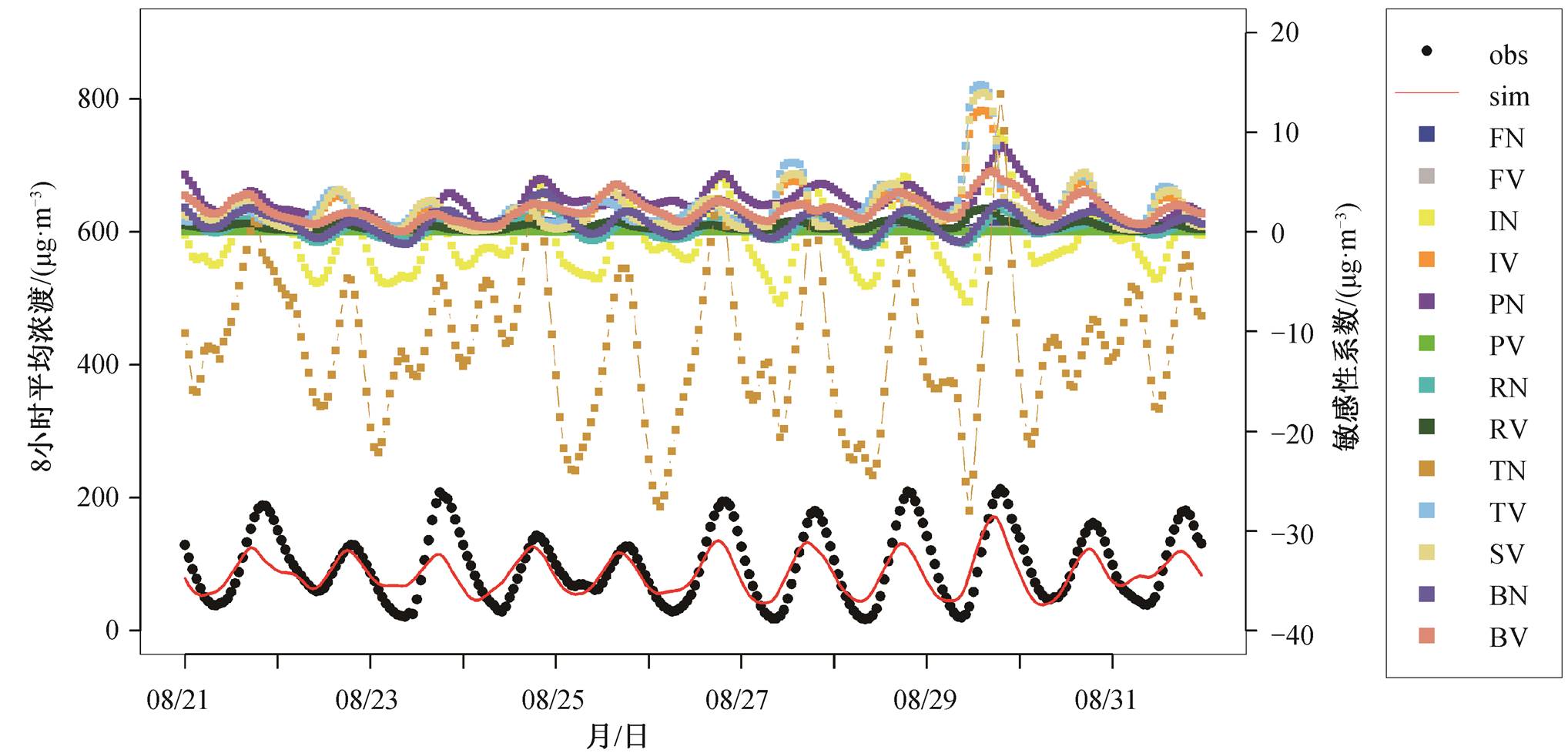
图3 由 CMAQ-DDM-3D 计算的 8 月 21—31 日成都市平均臭氧滑动 8 小时平均浓度对各个 DDM 源排放参数的敏感性系数与模拟和实测浓度的时间序列对比
Fig. 3 Time series of sliding 8-hour average ozone concentration sensitivities to sector emissions calculated by CMAQ-DDM-3D, and observed and simulated sliding 8-hour average ozone concentrations of Chengdu City from August 21 to 31, 2018
在大部分情况下, 成都市的大气臭氧生成对NOx 和 VOCs 排放都敏感, 特别是对工业源的 NOx和 VOCs、电厂源的 NOx 以及移动源和溶剂使用的VOCs 排放最敏感, 削减这些源项的排放能够有效地降低成都市臭氧污染水平。同时, 成都市大气臭氧生成对前体物的敏感性随气象条件变化而改变, 在不利气象条件下, 其对 NOx 排放的敏感度增加, 对上风向较远距离的 NOx 输送尤为敏感, 因此区域协同削减 NOx 排放同样关键。近期, 成都市大气臭氧控制策略应考虑联合削减 NOx 和 VOCs 的排放,
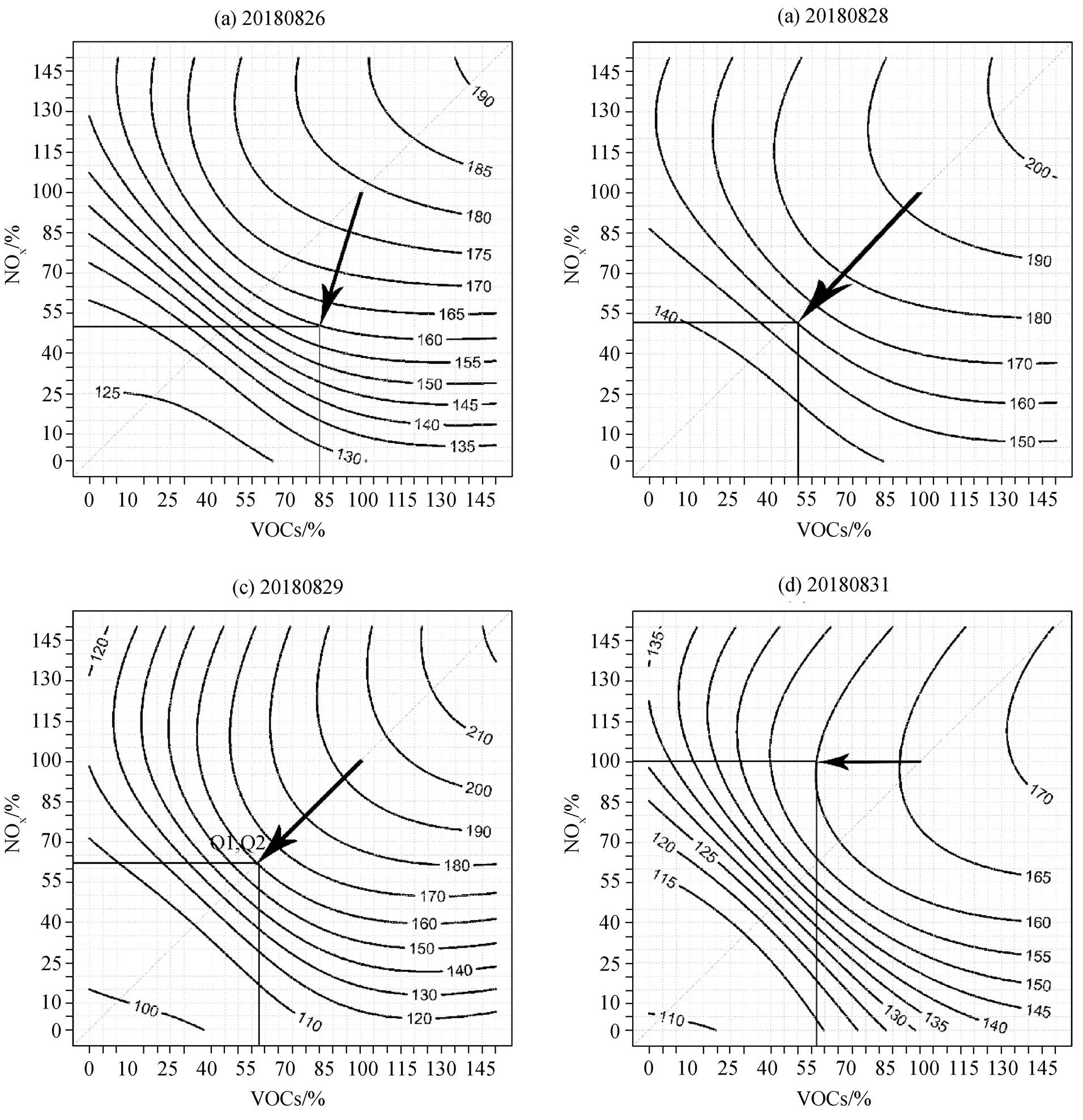
图4 区域内人为源 NOx 和 VOCs 减排对应的 2018 年 8 月成都市典型臭氧污染日日最大 8 小时臭氧平均浓度EKMA曲线
Fig. 4 EKMA diagrams of Chengdu city daily maximum 8-hour average ozone concentration isopleths of selected ozone exceedance days in August 2018
表4 成都市 2018 年 8 月 29 日日最大 8 小时臭氧浓度达标细分源减排情景方案
Table 4 Control strategy scenarios to attain ozone standard in Chengdu on August 29, 2018

减排目标目标比例/%(µg·m−3)(µg·m−3)S人为源/(µg·m−3) FNINPNRNTN和FVIVPVRVTVSV和 34361.4112.5613.033.0910.7940.880.3815.380.083.3117.5317.9154.5995.48 方案/%/%NOx源削减浓度/(µg·m−3)VOCs源削减浓度/(µg·m−3)削减总和/(µg·m−3)预期O3/(µg·m−3) FNINPNRNTN和FVIVPVRVTVSV和 Q136360.50(36)4.52(36)4.69(36)1.11(36)3.88(36)14.720.13(36)5.53(36)0.027(36)1.19(36)6.31(36)6.44(36)19.6534.37159.63 Q236360.42(30)7.15(57)7.42(57)--15.010.11(30)8.76(57)0.043(57)--10.7(60)19.6734.68159.32
说明: 括号内数字为百分比。S表示敏感性系数, R表示减排比例。
并借助盆地内其他地区以 NOx 为重点的协同控制。若单独对 NOx 进行削减, 在早期可能引起某些地区和时段的臭氧浓度升高。因此, 无论是本地源的前体物排放削减还是周边地区的协同控制, 都要联合削减NOx 和 VOCs 排放。需要强调的是, 在达标减排量占当前排放水平比例较高的情况下, 应该将减排任务分解为分阶段达标, 通过工业企业挖潜改造、产业重新布局、调整升级产业结构、优化能源结构以及提高交通运输效率等综合手段, 循序渐进地达到逐年减排目标, 避免冒进式的减排, 同时也可有效地防止排放和污染的短期反弹。
本文提出一种快速构建臭氧生成等浓度曲线的新方法, 结合区域空气质量模式敏感性分析和简化模型, 可快速地计算人为源氮氧化物和可挥发性有机物在不同排放水平时对应的臭氧生成浓度, 高效准确地构建臭氧生成等浓度曲线, 帮助决策部门快速地判断最佳控制路径, 同时结合细分源的臭氧敏感性分析, 可帮助选择和评估最合适的可执行减排控制方案。该方法可为城市和区域空气污染治理的精细化管理提供有力的技术支撑。
本文利用多次迭代调整后的源排放清单, 对成都平原 2018 年 8 月臭氧污染进行回溯模拟, 模拟结果的准确度比清单调整前有显著的提高, 模拟性能指标符合进行空气污染控制决策分析的要求。进一步地, 利用 DDM-3D 敏感性分析技术以及 RFM 简化模型, 绘制成都平原地区各城市平均的逐日臭氧生成等浓度曲线图(EKMA 曲线)。结合 EKMA曲线以及细分源敏感性分析结果, 以成都市 8 月 29 日臭氧达标为例, 制定遵循最佳控制路径的精细化减排方案。研究发现, 重点削减区域内工业源和电厂源的 NOx 以及工业源、移动源和溶剂使用源的 VOCs排放, 可有效地降低成都市臭氧污染水平。成都市臭氧控制应考虑本地联合削减 NOx 和 VOCs 排放, 同时借助周边城市的协同控制。
参考文献
[1] 中国国务院. 大气污染防治行动计划. 北京: 人民出版社, 2013
[2] 姜磊, 周海峰, 赖志柱, 等. 中国城市 PM2.5 时空动态变化特征分析: 2015-2017 年. 环境科学学报, 2018, 38(10): 3816–3825
[3] 刘孟琴, 汤家法, 刘小青, 等. 四川省近 15 年以来PM2.5的时空分布特征及原因分析. 四川环境, 2017, 36(3): 74–81
[4] 杨兴川, 赵文吉, 熊秋林, 等. 2016 年京津冀地区PM2.5时空分布特征及其与气象因素的关系. 生态环境学报, 2017, 26(10): 1747–1754
[5] 孟晓艳, 宫正宇, 张霞, 等. 全国及重点区域臭氧污染现状. 中国环境监测, 2017, 44(4): 17–25
[6] 张倩倩, 张兴赢. 基于卫星和地面观测的 2013 年以来我国臭氧时空分布及变化特征. 环境科学, 2019, 40(3): 1132–1142
[7] 李波兰, 罗彬, 张巍, 等. 四川省臭氧时空分布特征及污染特征分析. 环境科学与技术, 2018, 41(增刊 1): 293–298
[8] 黄小刚, 赵景波. 2016年长三角城市群 O3浓度的时空变化规律. 中国环境科学, 2018, 38(10): 3611–3620
[9] Sillman S. The relation between ozone, NOx and hy-drocarbons in urban and polluted rural environments. Atmospheric Environment, 1999, 33(12): 1821–1845
[10] Solomon P, Cowling E, Hidy G, et al. Comparison of scientific findings from major ozone field studies in North America and Europe. Atmospheric Environment, 2000, 34(12): 1885–1920
[11] Hidy G M. Ozone process insights from field experi-ments part I: overview. Atmospheric Environment, 2000, 34(12/13/14): 2001–2022
[12] Zhang Yuanhang, Su hang, Zhong Liuju, et al. Re-gional ozone pollution and observation-based app-roach for analyzing ozone-precursor relationship du-ring the PRIDE-PRD2004 campaign. Atmospheric En-vironment, 2008, 42(25): 6203–6218
[13] 漏嗣佳, 朱彬, 廖宏. 中国地区臭氧前体物对地面臭氧的影响. 大气科学学报, 2010, 33(4): 451–459
[14] 沈劲, 陈多宏, 蒋斌, 等. 粤东北地区臭氧与前体物关系. 环境科学与技术, 2018, 41(9): 90–95
[15] 梁永贤, 尹魁浩, 胡泳涛, 等. 深圳地区臭氧污染来源的敏感性分析. 中国环境科学, 2014, 34(6): 1390–1396
[16] Cheng Hairong, Guo Hai, Wang Xinming, et al. On the relationship between ozone and its precursors in the Pearl River Delta: application of an observation-based model (OBM). Environmental Science and Pol-lution Research, 2010, 17(3): 547–560
[17] Shao Min, Zhang Yuanhang, Zeng Limin, et al. Ground-level ozone in the Pearl River Delta and the roles of VOC and NOx in its production. Journal of Environmental Management, 2009, 90(1): 512–518
[18] 罗恢泓, 袁自冰, 郑君瑜, 等. 上海夏季臭氧生成机制时空变化特征及其影响因素研究. 环境科学学报, 2019, 39(1): 154–168
[19] Li Ying, Lau A K H, Fung J C H, et al. Importance of NOx control for peak ozone reduction in the Pearl River Delta region. Journal of Geophysical Research: Atmospheres, 2013, 118(16): 9428–9443
[20] Refsgaard J C, van der Sluijs J P, Hojberg A L, et al. Uncertainty in the environmental modelling process-a framework and guidance. Environmental Modelling and Software, 2007, 22(11): 1543–1556
[21] Dunker A M, Morris R E, Pollack A K, et al. Photochemical modeling of the impact of fuels and vehicles on urban ozone using auto/oil program data. Environmental Science and Technology, 1996, 30(3): 787–801
[22] Yang Y J, Wilkinson J G, Russell A G. Fast, direct sensitivity analysis of multidimensional photochemi-cal models. Environmental Science and Technology, 1997, 31(10): 2859–2868
[23] Hakami A, Odman M T, Russell A G, et al. High-order, direct sensitivity analysis of multidimensional air quality models. Environmental Science and Tech-nology, 2003, 37(11): 2442–2452
[24] Zhang W X, Capps S L, Hu Y T, et al. Development of the high-order decoupled direct method in three dimensions for particulate matter: enabling advanced sensitivity analyssi in air quality models. Geoscien-tific Model Development, 2012, 5(2): 355–368
[25] Hakami A, Odman M T, Russell A G. Nonlinearity in atmospheric response: a direct sensitivity analysis approach. Journal of Geophysical Research, 2004, 109 (D15): D15303
[26] Napelenok S L, Cohan D S, Hu Y T, et al. Decoupled direct 3D sensitivity analysis for particulate matter (DDM-3D/PM). Atmospheric Environment, 2006, 40 (32): 6112–6121
[27] Wang Xuesong, Zhang Yuanhang, Hu Yongtao, et al. Decoupled direct sensitivity analysis of regional ozone pollution over the Pearl River Delta during the PRIDE-PRD2004 campaign. Atmospheric Environment, 2011, 45(28): 4941–4949
[28] 王丽涛, 张普, 杨晶, 等. CMAQ-DDM-3D 在细颗粒物(PM2.5)来源计算中的应用. 环境科学学报, 2013, 33(5): 1355–1361
[29] US Environmental Protection Agency. Guideline for use of city-specific EKMA in preparing ozone SIPs. Research Triangle Park: EPA-450/4-80-027, 1981
[30] Kinoslan J R. Ozone precursor relationships from EKMA diagrams. Environmental Science and Tech-nology, 1982, 16(12): 880–883
[31] 李冰, 陈长和, 余金香. 利用 EKMA 曲线制定光化学烟雾污染区域总量控制方案. 高原气象, 1998, 17(2): 111–119
[32] 郝伟华, 王文勇, 张迎春, 等. 成都市臭氧生成敏感性分析及控制策略的制定. 环境科学学报, 2018, 38(10): 3894–3899
[33] Pinder R W, Gilliam R C, Appel K W, et al. Efficient probabilistic estimates of surface ozone concentration using an ensemble of model configurations and direct sensitivity calculations. Environmental Science and Technology, 2009, 43(7): 2388–2393
[34] Zhang W X, Trail M A, Hu Y T, et al. Use of high-order sensitivity analysis and reduced-form modeling to quantify uncertainty in particulate matter simula-tions in the presence of uncertain emissions rates: a case study in Houston. Atmospheric Environment, 2015, 122: 103–113
[35] 四川省测绘地理信息局. 2012四川省地理省情公报[EB/OL]. (2012–12–04) [2020–01–06]. https://www.sc. gov.cn/10462/10464/10465/10574/2012/12/13/10239785.shtml
[36] 徐琨, 刘志红, 何沐全, 等. 成都市夏季近地面臭氧污染气象特征. 中国环境监测, 2018, 34(5): 36–45
[37] 闫静. 盆地气候条件下成都市城区臭氧污染特性研究[D]. 成都: 西南交通大学, 2013
[38] Skamarock W C, Klemp J B, Dudhia J, et al. A description of the advanced research WRF Version 3. NCAR Technology Note: NCAR/TN-475+STR, 2008
[39] Appel W, Napelenok S L, Foley K M, et al. Des-cription and evaluation of the Community Multiscale Air Quality (CAMQ) modeling system version 5.1. Geoscientific Model Development, 2017, 10(4): 1703–1732
[40] Byun D, Schere K L. Review of the governing equa-tions, computational algorithms, and other compo-nents of the Models-3 Community Multiscale AIR Quality (CMAQ) modeling system. Applied Mecha-nics Reviews, 2006, 59(2): 51–77
[41] Hutzell W T, Luecken D J, Appel K W, et al. Inter-preting predictions from the SAPRC07 mechanism based on regional and continential simulations. At-mospheric Environment, 2012: 46: 417–429
[42] Pye H O T, Pouliot G A. Modeling the role of alkanes, polycyclic aromatic hydrocarbons, and their oli-gomers in secondary organic aerosol formation. En-vironmental Science and Technology, 2012, 46(11): 6041–6047
[43] Cohan D S, Hakami A, Hu Y T, et al. Nonlinear re-sponse of ozone to emissions: source apportionment and sensitivity analysis. Environmental Science and Technology, 2005, 39(17): 6739–6748
[44] Streets D G, Canty T, Carmichael G R, et al. Emissions estimation from satellite retrievals: a review of current capability. Atmospheric Environ-ment, 2013, 77: 1011–1042
[45] Liu D C, Nocedal J. On the limited memory BFGS method for large scale optimization. Mathematical Programming, 1989, 45(1/2/3): 503–528
[46] Gilliland A B, Abbitt P J. A sensitivity study of the discrete Kalman filter (DKF) to initial condition dis-crepancies. Journal of Geophysics Research: Atmos-phere, 2001, 106(D16): 17939–17952
[47] Pison I, Menut L, Bergametti G. Inverse modeling of surface NOx anthropogenic emission fluxes in the Paris area during the Air Pollution Over Paris Region (ESQUIF) campaign. Journal of Geophysical Re-search, 2007, 112(D24): D24302
[48] Huang Zhijiong, Hu Yongtao, Zheng Junyu, et al. A new combined stepwise-based high-order decoupled direct and reduced-form method to improve uncer-tainty analyssi in PM2.5 simulations. Environmental Science and Technology, 2017, 51(7): 3852–3859
[49] US Environmental Protection Agency. Guidance on the use of models and other analyasis for demons-trating attainment of air quality goals for ozone, PM2.5 and regional haze. Research Triangle Park: EPA-454/B-07-0002, 1981
[50] Boylan J W, Russell A G. PM and light extinction model performance metrics, goals, and criteria for three-dimensional air quality models. Atmospheric Environment, 2006, 40(26): 4946–4959
[51] Wu Rongrong, Xie Shaodong. Spatial distribution of ozone formation in China derived from emissions of speciated volatile organic compounds. Environmental Science and Technology, 2017, 51(5): 2574–2583
[52] Wang T, Xue L K, Brimblecombe P, et al. Ozone pollution in China: a review of concentrations, me-teorological influences, chemical precursors, and effects. Science of Total Environment, 2016, 575: 1582–1596
Implementing Reduced Form Model to Construct Ozone Isopleths and Its Application
Abstract An efficient approach to construct ozone isopleths was established. It utilizes both first- and second-order sensitivity analysis from a regional air quality model to build a reduced form model (RFM) for calculating ozone concentrations that respond to the different levels of nitrogen oxides (NOx) and volatile organic compounds (VOCs) emissions. The approach was applied to the Chengdu Plain area by simulating the ozone concentration and its sensitivities to anthropogenic emissions for August 2018 with adjusted emissions inventory. Ozone isopleth diagrams were plotted for cities in the area. Under the guidance of ozone isopleths, effective ozone control strategies were further suggested for Chengdu city as an example.
Key words ozone precursors; CMAQ-DDM; surface ozone pollution control
doi: 10.13209/j.0479-8023.2020.120
国家重点研发计划(2018YFC0214004)和四川省科技厅重点研发项目(2018SZ0316)资助
收稿日期: 2020–01–22;
修回日期: 2020–03–13