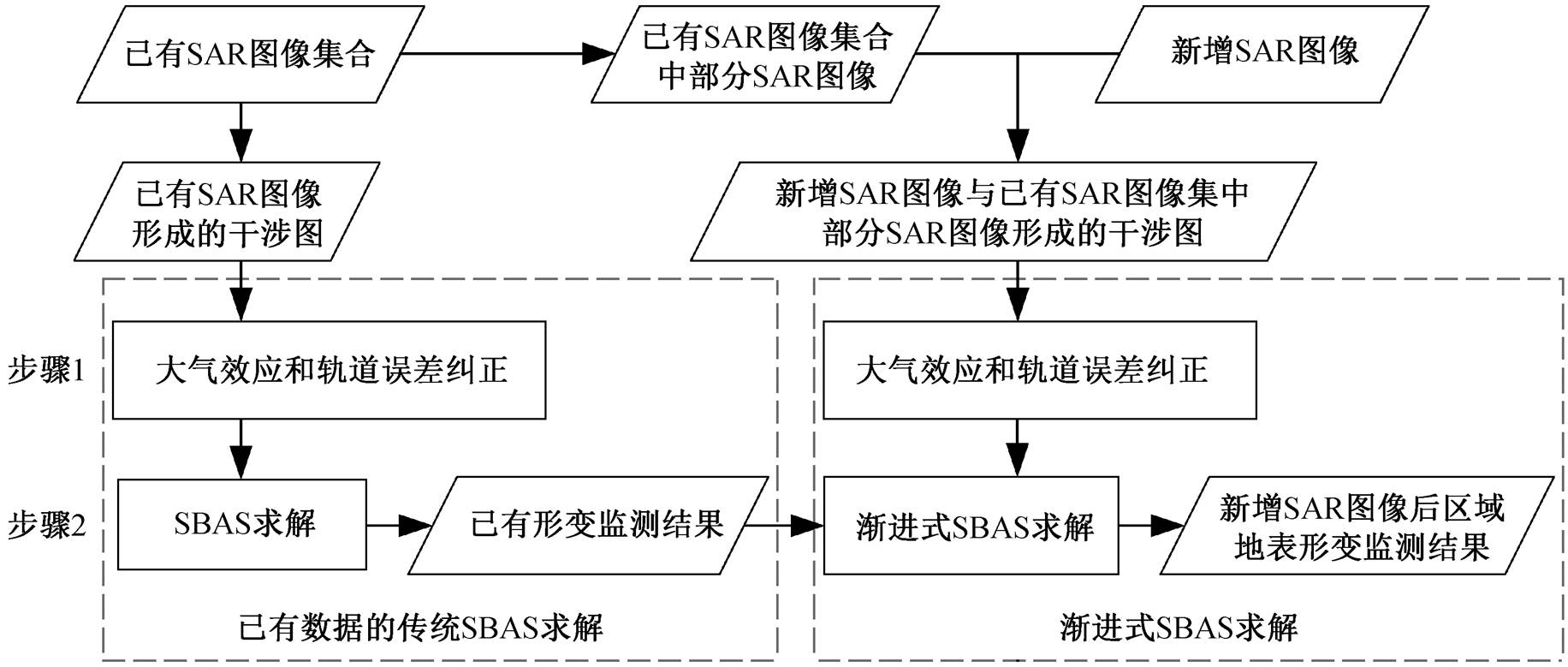
图1 渐进式SBAS方法流程
Fig. 1 Flow chart of a progressive SBAS method
摘要 基于短重访周期 SAR 卫星影像, 对黄河三角洲地表形变进行高效和持续监测的 SBAS-InSAR 时序分析。首先对研究区已有的 SAR 影像集进行干涉处理, 得到干涉图, 并进行大气效应校正和轨道误差去除, 然后利用传统的 SBAS (small baseline subset)方法获取地表形变。在此基础上, 当增加新的 SAR 数据时, 采取渐进式 SBAS 方法处理, 反演新时刻的地表形变。渐进式 SBAS 方法融合序贯平差的思想, 以已有的解算结果为基础, 结合新的观测数据进行增量解算, 可以达到整体解算的效果。相对于传统的 SBAS 方法, 每次增加新影像都要采用重新全部解算的方式, 能够减少冗余运算, 提高计算效率。实验证明, 基于 2018 年 5 月—2016 年 8 月在黄河三角洲地区获取的 Sentinel-1 卫星 SAR 数据, 利用渐进式 SBAS 方法反演的地表形变与地表实测控制点结果相近, 相关系数(R)为 0.82, 且与传统的 SBAS 方法反演得到的地表形变速率差异在 1mm/a内, 解算时间缩短约 40%, 能够持续高效地监测地表形变。
关键词 InSAR时序分析; 小基线集(SBAS); 渐进式SBAS; 序贯平差; 地表形变; 持续监测
雷达差分干涉测量(differential interferometry synthetic aperture radar, D-InSAR)是通过对两景或多景 SAR 影像进行干涉处理, 获取高精度和高空间分辨率微小形变的技术[1-3]。传统的 D-InSAR 技术因时空失相干和大气效应等因素的干扰[4-5], 测量精度受到影响。SBAS (small baseline set, 小基线集)-InSAR 时序分析技术[6-8]通过对时域上一系列差分干涉影像的处理, 能够消除或减弱上述因素的影响, 得到毫米级的沉降速率。目前, SBAS-InSAR已广泛应用于对地面沉降、滑坡和泥石流等灾害的研究中[9-11], 成为长时间缓慢地表形变监测的主流方法之一。
随着测量技术的发展, 以欧洲航天局(European Space Agency, ESA) Sentinel-1 为代表的 SAR 卫星重访周期不断缩短, 可以稳定地获取 SAR 数据, 为InSAR 时序分析提供丰富的数据基础, 也给高效、持续地反演地表形变带来挑战。传统的 SBAS 方法通常是在某区域积累一定量的数据后进行处理, 获得数据积累时间段内的形变监测结果[12-13]; 若新增几景 SAR 影像, 就要“从头开始”, 重复全部的处理流程来获取新时刻的形变结果。随着区域 SAR 数据的增加, 运算的复杂度也快速加大。因此, 这种“从头开始”的处理思想难以满足动态、高效和持续的地表形变监测的需求。
陈继伟[14]将序贯平差思想[15]融合到 InSAR 时序分析中, 并探索在已有的数据集中新增一景 SAR影像后反演新时刻地表沉降量的可能性, 在保证精度的同时, 提高计算效率。Ansari 等[16]提出结合序贯估计的高效 InSAR 时序算法, 采用递归估计和分析数据协方差矩阵, 将数据划分为小数据集, 然后对数据集进行压缩, 避免对整个数据集进行重新处理, 能够极大地提高时间效率。胡俊等[17]研究新增两张或多景 SAR 影像后, 利用结合序贯平差方法的InSAR 时序分析技术反演地表形变的一般性规律, 并用模拟数据验证方法的可行性。
本研究提出渐进式 SBAS 时序分析方法融合序贯平差的思想, 在已有解算结果的基础上, 结合新的观测数据进行增量解算, 便可达到整体解算的效果, 实现对地表形变的高效和持续监测。选取 2015年 5 月— 2016 年 8 月覆盖黄河三角洲地区的 34 景Sentinal-1 卫星 SAR 影像作为实验数据, 开展渐进式SBAS 时序分析。通过与实测控制点数据以及传统SBAS 时序分析方法反演的地表形变对比, 验证渐进式 SBAS 方法反演地表形变的可靠性和在时间效率上的优越性。
如图 1 所示, 渐进式 SBAS 方法分为两个阶段。阶段 1: 已有 SAR 数据的传统 SBAS 方法求解; 阶段 2: 新增 SAR 数据后的渐进式 SBAS 方法求解。阶段 1 和 2 各自包含两个步骤, 其中步骤 1 是干涉图的大气效应校正[18]和轨道误差去除[19], 两个阶段的步骤 1 相似, 仅处理的干涉图不相同。阶段 1 的SBAS 求解(步骤 2)为已有 SAR 数据对应的地表形变量解算, 为阶段 2 的渐进式 SBAS 求解(步骤 2)提供数据基础, 使得阶段 2 通过增量结算获得新时刻的地表形变, 同时更新已有的地表形变量。

图1 渐进式SBAS方法流程
Fig. 1 Flow chart of a progressive SBAS method
卫星对同一区域连续观测, 在 t0–tN 时间内获得N+1 景 SAR 影像, 在给定时间基线阈值 tc 和空间基线阈值 bc 后, 得到 M 张干涉图。将经过大气效应校正和轨道误差去除的差分干涉图作为观测值, 地表形变量作为待求值进行 SBAS 求解, 得到的观测方程为
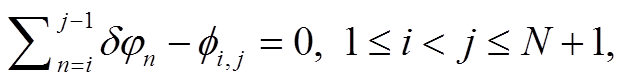 (1)
(1)式中, 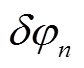 为第 n 景到第 n+1 景 SAR 影像的相位变化量, 反映的物理量为相邻时间的地表形变量;
为第 n 景到第 n+1 景 SAR 影像的相位变化量, 反映的物理量为相邻时间的地表形变量;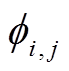 为 ti 和 tj 时刻 SAR 影像形成的干涉图中与地表形变有关的相位值, 可以从干涉图中直接获取。
为 ti 和 tj 时刻 SAR 影像形成的干涉图中与地表形变有关的相位值, 可以从干涉图中直接获取。
该区域新增加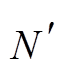 景 SAR 影像, 对应的时间段为
景 SAR 影像, 对应的时间段为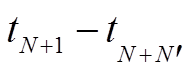 , 在相同的时间和空间基线约束下, 增加
, 在相同的时间和空间基线约束下, 增加![]() 张干涉图, 其中一些干涉图通过对已有数据集中较新时刻(
张干涉图, 其中一些干涉图通过对已有数据集中较新时刻(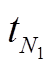 时刻以后)的 SAR 数据与新增 SAR数据做干涉处理获得。同理, 有如下观测方程:
时刻以后)的 SAR 数据与新增 SAR数据做干涉处理获得。同理, 有如下观测方程:
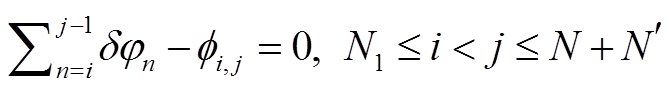 。 (2)
。 (2)将式(1)和(2)整理成如下矩阵形式:
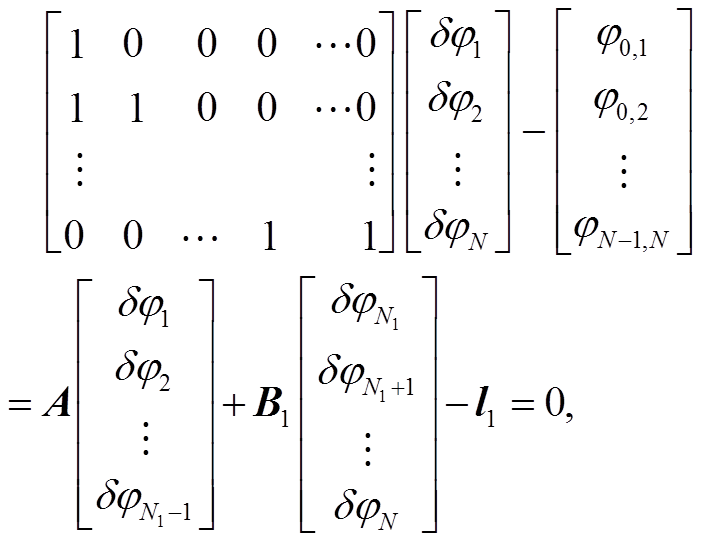 (3)
(3)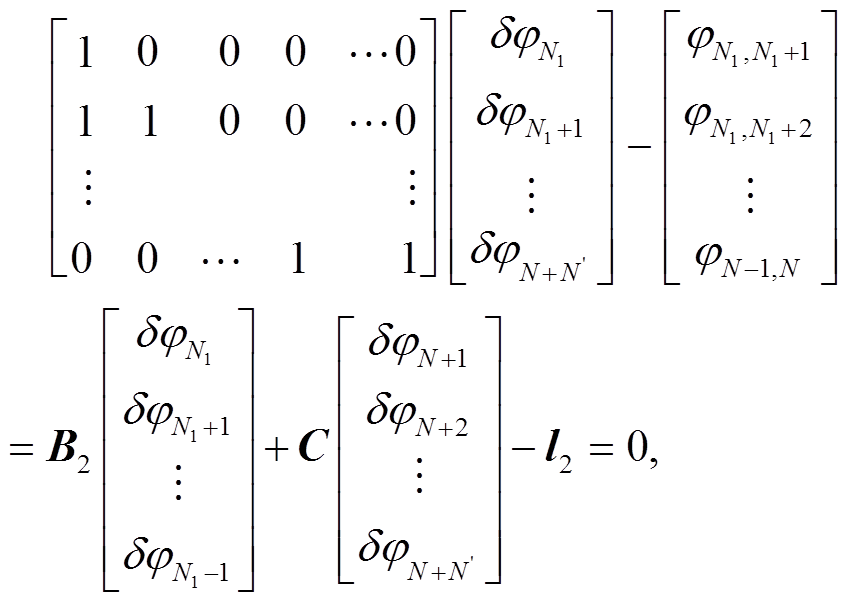 (4)
(4)
亦即
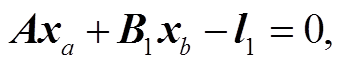 (5)
(5)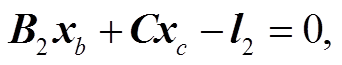 (6)
(6)
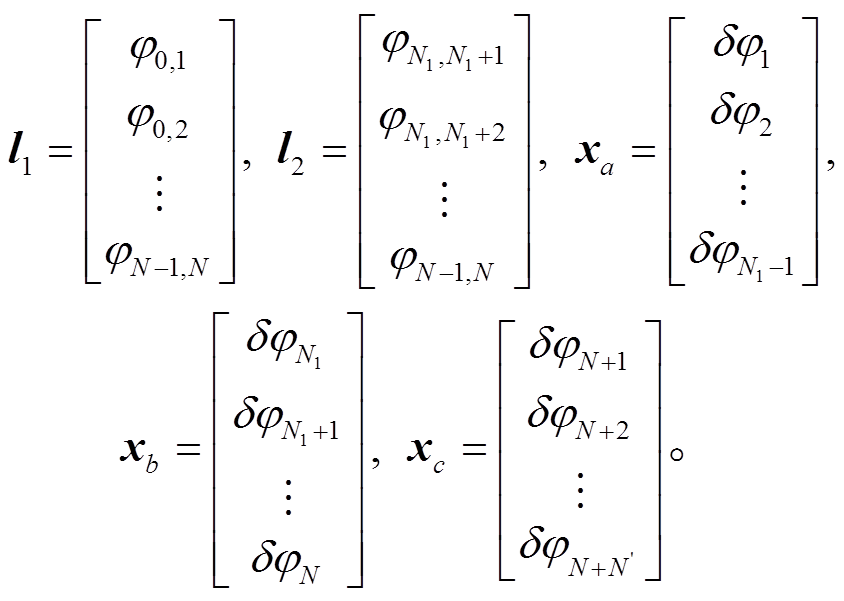 (7)
(7)式(3)~(6)中, A, B1, B2 和 C 是由 0 和 1 构成的系数矩阵, l1, l2 为干涉图中与地表形变相关的相位, xa, xb 和 xc 分别代表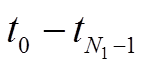 ,
, 时刻对应的地表形变量。
时刻对应的地表形变量。
如果把已有数据和新增数据的解算视为两次平差过程, 则式(5)和(6)与平差测量中的序贯平差方法在形式上一致, 分别对应序贯平差的第一次和第二次平差过程, 这样就把序贯平差的思想引入新增数据的地表形变解算中。对于 xa 和 xb, 已经有通过传统 SBAS 方法求解得到的初始化结果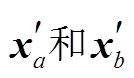 , 则
, 则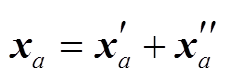 ,
, , 其中
, 其中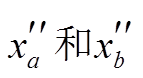 表示对已求得变量
表示对已求得变量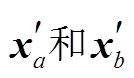 的修正。各个时刻观测获得的 SAR 影像相互独立, 权矩阵为单位矩阵, 结合序贯平差知 识[20]可求解得到
的修正。各个时刻观测获得的 SAR 影像相互独立, 权矩阵为单位矩阵, 结合序贯平差知 识[20]可求解得到
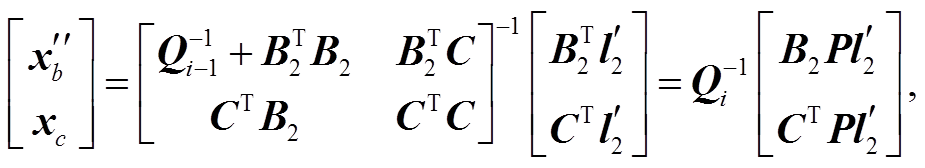 (8)
(8)式中,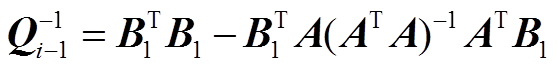 , 是传统 SBAS 方法求解过程中保存的协方差矩阵。另有
, 是传统 SBAS 方法求解过程中保存的协方差矩阵。另有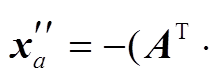
 , 由此得到在新增
, 由此得到在新增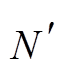 景 SAR 影像之后, 在
景 SAR 影像之后, 在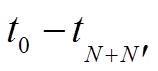 时间段的地表沉降量变化:
时间段的地表沉降量变化:
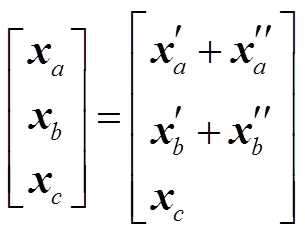 。 (9)
。 (9)为了验证渐进式 SBAS 方法反演地表形变的精度和时间效率, 选择实验区内包含一定量数据的SAR 数据集, 分别用渐进式 SBAS 方法和传统SBAS 方法处理, 进行 3 个方面的对比: 1)对比渐进式 SBAS 方法反演的地表形变结果与实测控制点测量结果; 2)对比两种方法的反演结果; 3)统计两种方法反演地表形变所需时间。
选取山东半岛东营市境内黄河三角洲为研究区。如图 2 所示, 该区域是以垦利县宁海为顶点, 向东展开的扇形区域[21], 受地质构造及人类活动的影响, 存在明显的地面持续沉降。已采取多种手段对该区域的地面沉降进行监测, 以传统的水准测量[22]和 GPS 监测[23]为主。
选取 34 景 Sentinel-1 卫星 SAR 数据, 影像的时间跨度为 2015 年 5 月 19 日—2016 年 8 月 29 日。采用覆盖实验区 30m 分辨率的 SRTM (shuttle radar topography mission) DEM 作为参考高程数据, 辅助去除地形相位。同时获取东营市双王城水库 2015年 9 月底首测和 2016 年 8 月复测的 16 个控制点, 用于对比验证。
2.3.1 干涉网络设计及干涉处理
以 2015 年 11 月 15 日的图像作为主图像, 时间基线阈值为 72 天, 空间基线阈值为 100m, 得到 115组干涉影像对, 构建时空基线网络(图 3)。用基于地理位置的方法进行配准, 在重采样后, 用 GMTSAR软件进行干涉处理。结合外部 DEM 去除地形相位, 并进行相位解缠, 最后得到去除大气效应和轨道误差的干涉图。此外, 为了抑制干涉图噪声, 进行多视处理(方位向 4 视, 距离向 12 视)。
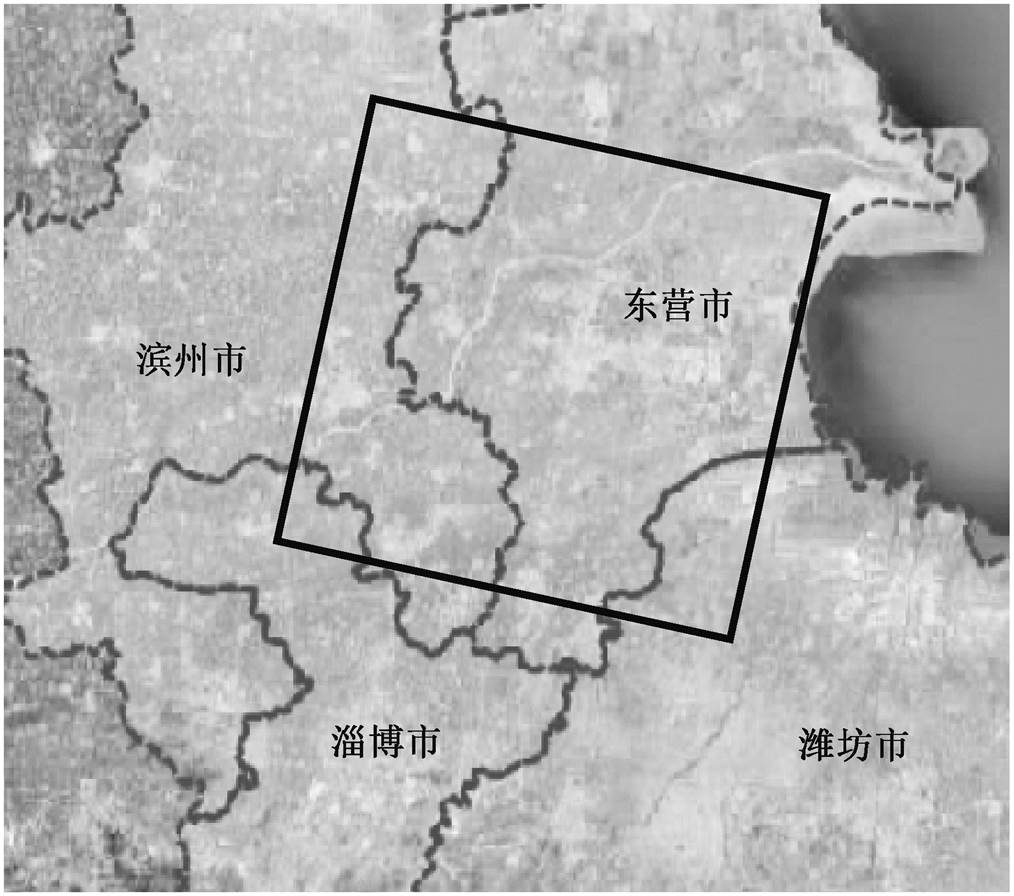
图2 研究区地理位置
Fig. 2 Geographical location of the study area
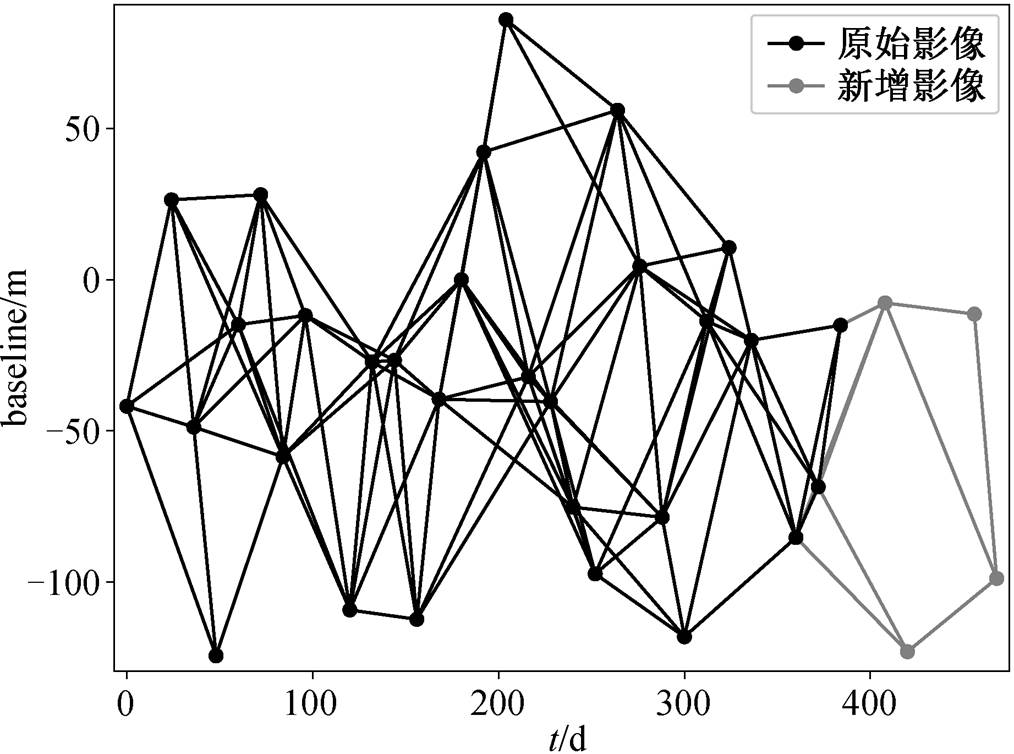
图3 干涉对的时空基线网络
Fig. 3 Spatio-temporal baseline network of interference pairs
2.3.2 渐进式SBAS和传统SBAS处理
已有 SAR 数据的传统 SBAS 处理(图 4): 2015年 5 月 19 日―2016 年 6 月 6 日共 30 景图像, 生成的106 对干涉对(图 3 中时空基线网络黑色部分)作为已有SAR 数据集, 反演已有 SAR 数据的对应的地表形变量。
新增 SAR 数据的传统 SBAS 方法处理(图 4): 在 2015 年 5 月 19 日―2016 年 6 月 6 日共 30 景 SAR影像的基础上, 新增 1~4 景 SAR 影像后, 利用传统SBAS 方法, 对 2015 年 5 月 19 日―2016 年 8 月 29 日所有 SAR 影像重新整体解算, 获取新时刻对应的地表形变量。
新增 SAR 数据后渐进式 SBAS 方法处理(图 4):以第一部分传统 SBAS 方法的产生中间结果为基础(虚线框, 不再处理), 使用 2015 年 6 月 30 日―2016年 8 月 29 日时间段内 1–4 景 SAR 影像(实线框), 结合渐进式 SBAS 方法进行增量处理, 反演新增影像对应时刻的地表形变量。
图 5 为两种方法反演得到的黄河三角洲地区2015 年 5 月 19 日—2016 年 8 月 29 日沿视线方向的形变速率场, 可以看出, 该区域存在大范围的地表形变, 空间分布不均匀, 东营市、滨州市和广饶县等主要城镇存在不同程度的沉降, 区域东部存在明显的沉降漏斗(图 5 中蓝-紫色区域)。
选取双王城水库 2015 年 9 月底首测, 2016 年 8月复测的 16 个控制点(图 6)作为验证数据, 其高程坐标由二等水准测量获得。InSAR 测量结果为 LOS方向, 地面控制点获得的是水平和高程的形变。为了统一形变测量方向, 将控制点形变量投影至 LOS方向。

图4 新增影像后渐进式SBAS和传统SBAS获取新时刻地表形变的实验设计
Fig. 4 Experimental design of the progressive SBAS and the traditional SBAS method for obtaining surface deformation when new images are added
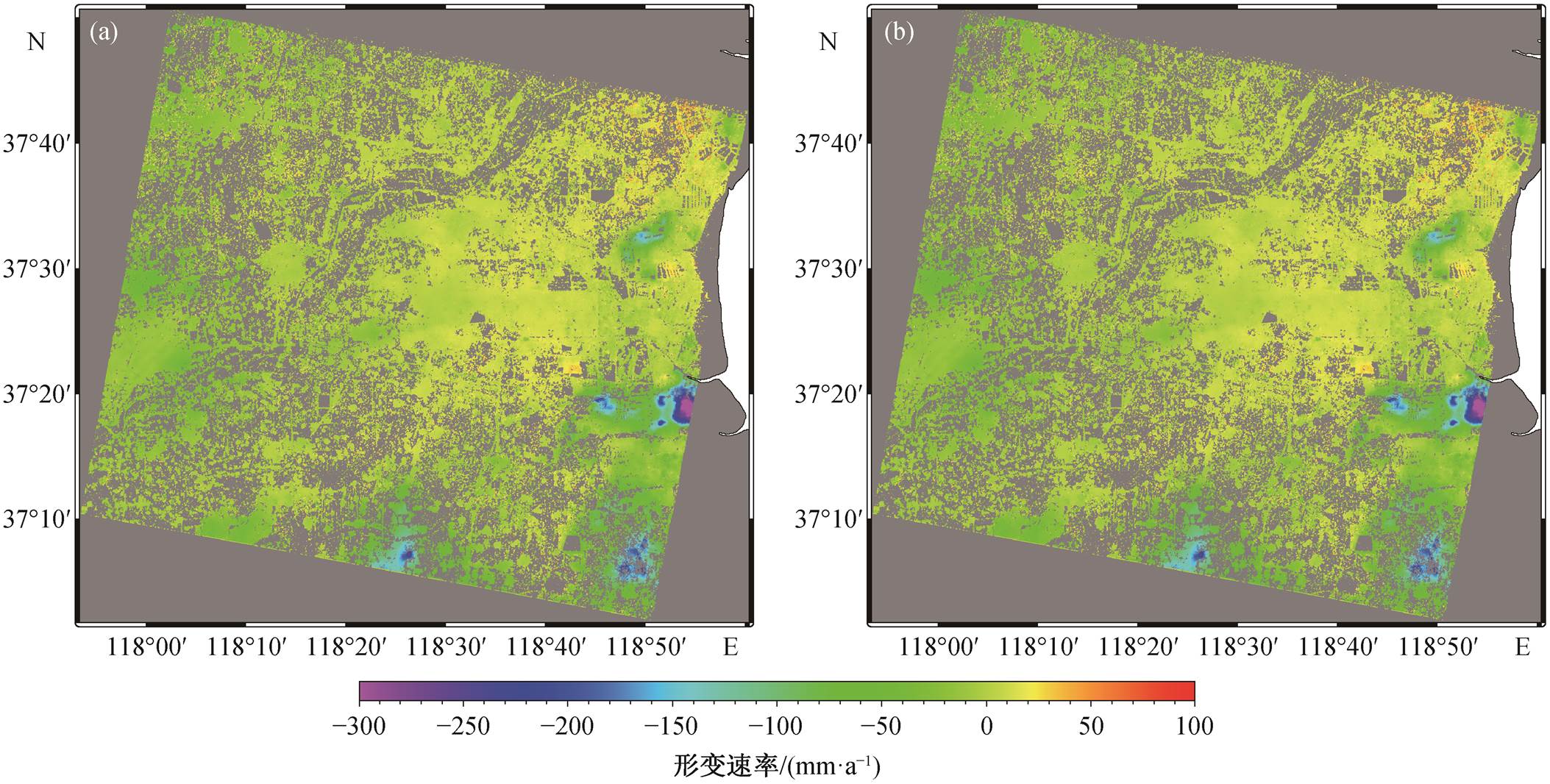
(a)传统SBAS; (b)渐进式SBAS
图5 黄河三角洲地区形变速率场(2015年5月19日—2016年8月29日)
Fig. 5 Deformation rate field in the Yellow River Delta (from May 19, 2015 to August 29, 2016)
用渐进式 SBAS 得到的形变速率与地面测量获得的形变速率的相关系数(R)为 0.82, 差值绝对值最大为 8.6mm/a, 最小为 0.48mm/a。两种方法得到的结果显示水库东西两侧形变规律有较高的一致性, 形变速率虽然有差异, 但处在同一个数量级(图 7)。
对两种方法反演得到的整个研究区形变速率(2015 年 5 月 19 日— 2016 年 8 月 29 日)进行差值运算, 结果如图 8(a)所示。对形变速率的差值进行统计, 结果如下: 绝大多数差值<0.3mm/a, 平均值为0.08mm/a, 标准差为 0.168mm/a, 两种方法反演得出的地表形变速率差异极小。
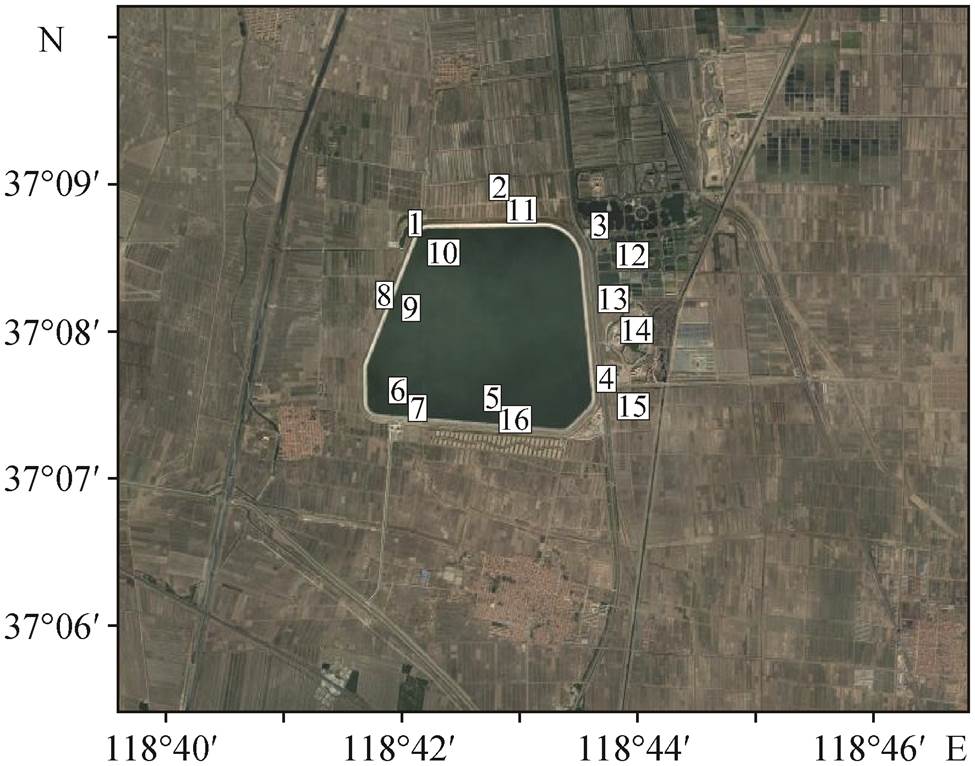
图6 地面控制点分布
Fig. 6 Distribution of ground control points
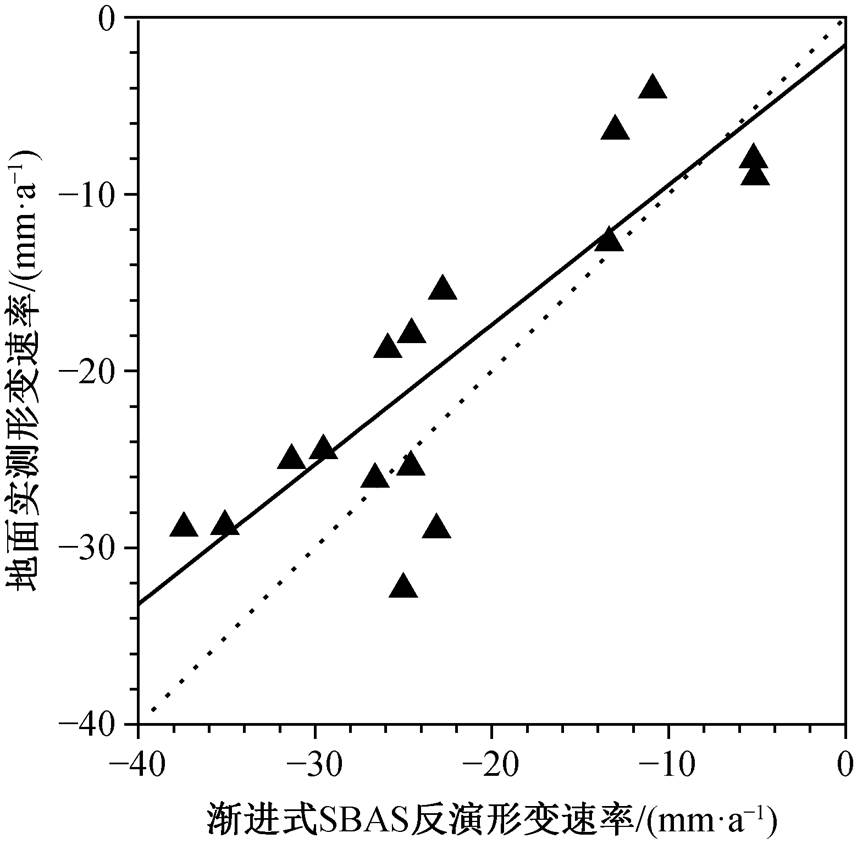
图7 渐进式SBAS反演形变速率与地面实测形变速率对比
Fig. 7 Comparison of deformation rate inversion by the progressive SBAS method and ground-based mea-sured deformation rate
选取研究区东部和南部沉降漏斗区, 更详细地比较两种方法反演典型区域地表形变的差异, 结果如图 8(b)和(c)所示。在沉降漏斗附近, 两种方法解算出的累积地表形变量几乎相同, 绝大多数差值接近 0, 只有极小的区域存在差值为 4~8mm 的异常点(可能是系统误差导致), 与沉降漏斗几百毫米的沉降量相比, 可以忽略不计。上述结果说明, 即使在沉降漏斗附近, 两种方法的反演结果也十分接近。
进一步地, 在研究区东部、南部和东南部严重沉降区域(见图 5), 随机选取 4 个特征点位, 对比两种方法反演的沿视线方向形变量, 结果如图 9 所示。总体而言, 所选特征点位的累计形变量差异在 1.5 mm 以内, 与累积形变量相比, 这样的差异显得微小, 可见两种方法反演的累计形变量基本上相同; 在像元层次上, 两种方法反演的地表形变也几乎相同。
渐进式 SBAS 方法是为适应动态增加的 SAR 数据的时序处理而提出的, 每次新增观测数据, 都可获得该数据成像时刻的累计形变量。将新增 2~3 景SAR 影像时渐进式 SBAS 反演的累计形变量与传统SBAS 方法进行对比, 结果见图 10。总体而言, 两种方法反演地表累计形变量的差异均值和标准差均很小, 在 1mm 以内, 说明渐进式 SBAS 在处理连续的动态的 SAR 数据时, 仍与传统 SBAS 方法保持极高的一致性。
传统 SBAS 和渐进式 SBAS 是按照相同的规则选择高相干点, 所以两种方法处理的高相干点个数K 相等。为了将问题简化, 我们以其中任意一个高相干点为例, 分析大气效应和轨道误差纠正(步骤1)以及形变量求解(步骤 2)的时间复杂度。
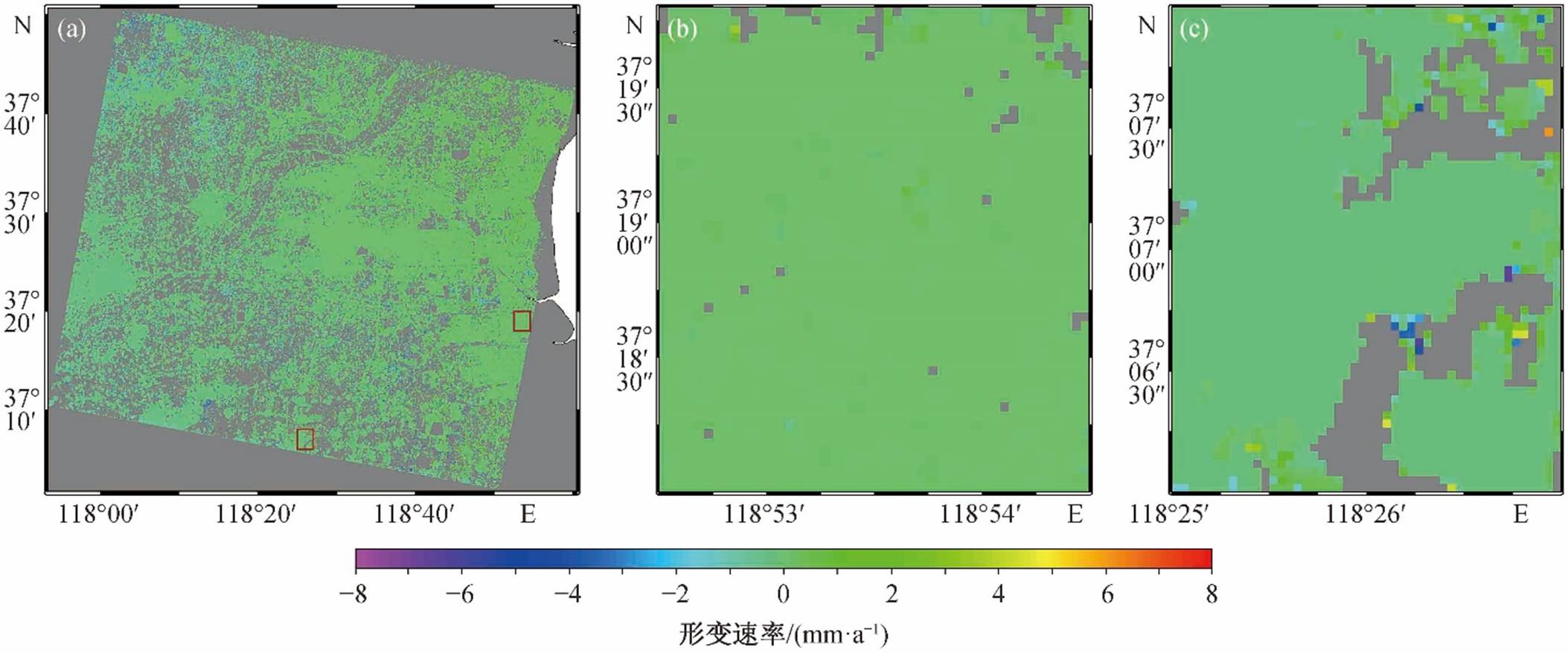
(a)整个研究区; (b)东部沉降漏斗; (c)南部沉降漏斗
图8 渐进式SBAS与传统SBAS反演的地表形变速率差值
Fig. 8 Difference between the deformation rate calculated from the progressive SBAS and the traditional SBAS
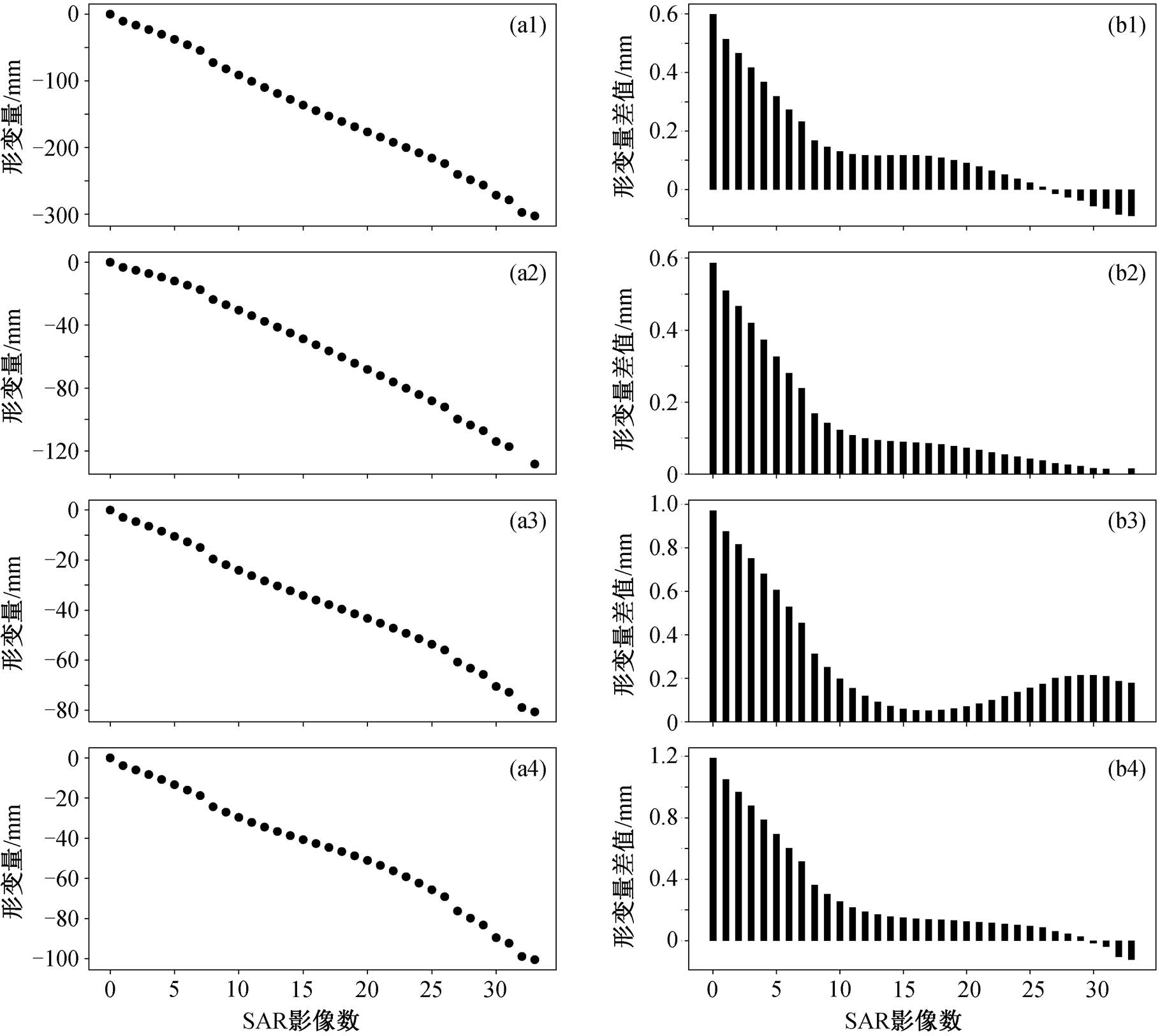
(a1)~(a4) 传统SBAS; (b1)~(b4) 两种方法的差值
图9 渐进式SBAS与传统SBAS方法反演累计形变量对比
Fig. 9 Comparison of the cumulative deformation variables calculated by the progressive SBAS and the traditional SBAS
假定实验数据集合由 N 景 SAR 影像构成的已有 SAR 数据集和 N′景 SAR 影像构成的新增 SAR 数据集组成, 在相同的时空基线约束下, 分别形成 M和 M′张干涉图。对于单个高相干点, 新增 N′景SAR 影像后, 传统 SBAS 在步骤 1 需要对(M+M′)张干涉图进行大气效应和轨道误差纠正, 渐进式SBAS 则只需对新增 SAR 数据和部分已有 SAR 数据形成的 M′张干涉图进行大气效应和轨道误差纠正。每次新增 SAR 数据, 传统 SBAS 都避不开对已有 SAR 数据集的处理, 因此比渐进式 SBAS 效率低很多。两种方法处理问题的规模与干涉图的个数有关, 时间复杂度为 O(K(M+M'))和 O(KM')。从理论上讲, 当新增 SAR 影像数不多时, 已有 SAR 数据形成的干涉图 M 数量远大于新增 SAR 数据与部分已有 SAR 数据形成的干涉图 M′, 因此渐进式 SBAS 比传统 SBAS 效率高很多。在形变量求解阶段(步骤 2), 传统 SBAS 需要求解(N+N')景 SAR 数据对应的地表形变, 存在大量对已有 N 景 SAR 数据集对应的地表形变的重复运算, 冗余度高, 渐进式 SBAS 则只针对新增的 N′景 SAR 数据对应的地表形变求解, 并更新已有的 N景 SAR 数据对应的地表形变, 计算的复杂度大大降低。从 1.2 节的介绍可知, 形变量的求解主要涉及线性方程组(式(5)和(6))的最小二乘法计算。线性方程组求解的复杂度与待求解未知数个数有关, 两种方法待求解的未知数个数分别为(N+N')和 N', 时间复杂度分别为 O(K(N+N')3)和 O(KN'3)。
在配置相同的计算机上分别运行渐进式 SBAS与传统 SBAS, 计算机配置为 Intel Core i5 CPU (2.8GHz), 4G 内存。针对每次新增的 SAR 图像, 分别记录大气效应和轨道误差纠正以及形变量求解所需的时间。
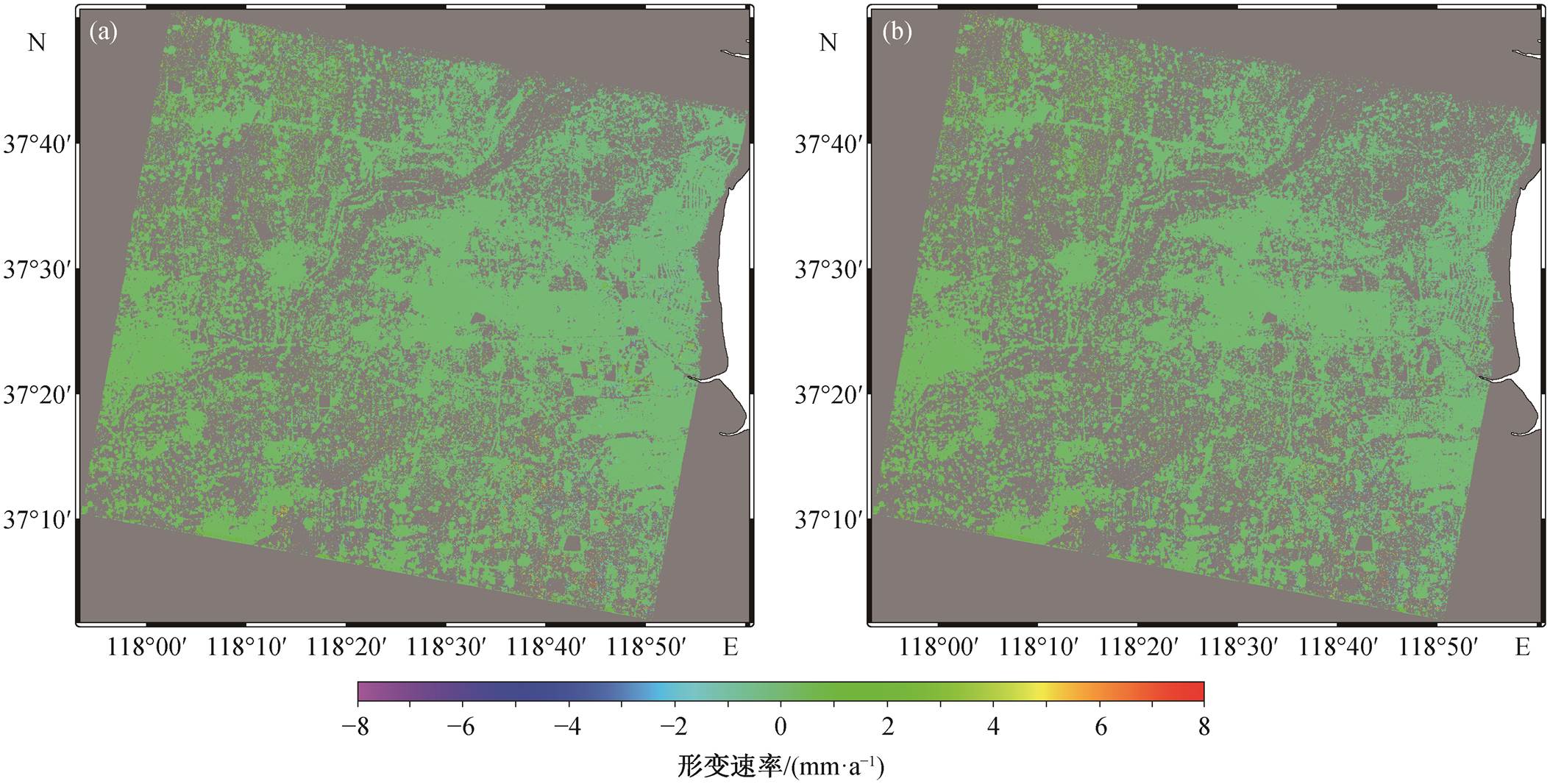
图10 新增2~3景SAR影像时渐进式SBAS (a)与传统SBAS (b)反演累计形变量的差值
Fig. 10 Cumulative deformation difference between the progressive SBAS (a) and the traditional SBAS (b) when 2–3 SAR images are added
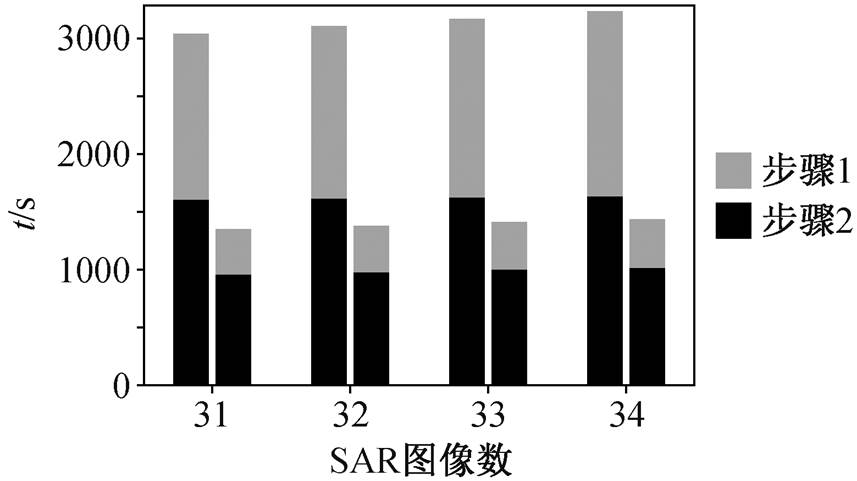
相邻柱子中, 左侧为传统SBAS, 右侧为渐进式SBAS
图11 渐进式SBAS与传统SBAS运行时间对比
Fig. 11 Comparison of running time between the progressive SBAS and the traditional SBAS
图 11 比较在 30 景 SAR 影像的基础上, 新增 1~ 4 景 SAR 影像后两种方法反演地表形变所需时间。在步骤 1, 传统 SBAS 所需时间是渐进式 SBAS 的 3~ 5 倍, 原因是渐进式 SBAS 只处理新增的干涉图, 而传统 SBAS 对所有干涉图都进行处理, 因此渐进式SBAS 能大大地减少运行的时间, 与前面的理论分析可以较好地相互验证。在形变量求解阶段, 虽然从理论上讲渐进式 SBAS 的时间效率应该比传统SBAS 高很多, 但统计结果表明两者在前期(新增 1~ 2 景 SAR 图像时)的运行时间差异并不大, 原因主要是在解算形变结果时, 渐进式 SBAS 一方面要引入和使用已有数据的传统 SBAS 求解阶段保留的协方差矩阵, 另一方面还要对已有数据反演的地表形变结果进行修正, 此外还有干涉相位相关文件的读入与保存, 故不能像前两个阶段那样明显地减少运行时间。但是, 随着 SAR 图像增加, 渐进式 SBAS 的时间效率相对于传统 SBAS 仍得到较大的提升, 在增加第 4 景 SAR 图像时, 其形变求解时间是传统 SBAS 的 64.7%。
总体而言, 在 30 景 SAR 影像的基础上新增加1~4 景 SAR 影像时, 传统 SBAS 的运行时间随着SAR 图像增加呈现线性增加趋势, 与传统 SBAS 相比, 渐进式 SBAS 的时间效率不断提高。因此, 处理动态增加的 SAR 数据时, 渐进式 SBAS 的时间效率更高。
本文以 Sentinel-1 卫星 SAR 影像作为实验数据, 使用渐进式 SBAS 方法, 获得黄河三角洲地区地表形变信息。通过对比传统 SBAS 方法的处理结果与地面实测控制点数据, 验证了渐进式 SBAS 方法的可靠性。结合理论分析和定量统计, 证明了渐进式SBAS 方法在时间上的高效性。
使用双王城水库地面实测控制点数据, 对渐进式 SBAS 方法反演地表形变结果进行验证, 两者形变规律一致, 说明渐进式 SBAS 方法反演地表形变的精度是可靠的。
渐进式 SBAS 与传统 SBAS 方法反演得到的地表形变速率差值在 1mm/a 以内, 累计形变量差值在1.5mm 以内, 得到的形变监测结果基本上相同。
与传统 SBAS 方法相比, 针对随时间动态增加的数据, 渐进式 SBAS 方法具有更高的时间效率, 适用于地表形变的连续、动态和高效监测。
参考文献
[1] Massonnet D, Rossi M, Carmona C, et al. The dis-placement field of the Landers earthquake mapped by radar interferometry. Nature, 1993, 364: 138‒142
[2] Massonnet D, Thatcher W, Vadon H. Detection of postseismic fault-zone collapse following the Landers earthquake. Nature, 1996, 382: 612‒616
[3] Zebker H A, Rosen P. On the derivation of coseismic displacement fields using differential radar interfero-metry: the Landers earthquake. Geosci Remote Sens Symp, 1994, 32(5): A206‒A207
[4] 董玉森, Ge Linlin, Chang Hsingchun, 等. 基于差分雷达干涉测量的矿区地面沉降监测研究. 武汉大学学报(信息科学版), 2007, 32(10): 888‒891
[5] Zebker H A, Villasenor J. Decorrelation in interfero-metric radar echoes. IEEE Transactions on Geosci-ence and Remote Sensing, 1992, 30(5): 950‒959
[6] Berardino P, Fornaro G, Lanari R, et al. A new algo-rithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2375‒2383
[7] Hooper A, Zebker H, Segall P, et al. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophy-sical Research Letters, 2004, 31(23): 1‒5
[8] Hooper A, Segall P, Zebker H. Persistent scatterer inteferometric synthetic aperture radar for crustal deformation analysis, with application to Vlocan Alcedo, Galapagos. Journal of Geophysical Research, 2007, 112 (B7): Doi: 10. 1029/2006JB004763
[9] 陈继伟, 曾琪明, 焦健, 等. Sentinel-1A卫星TOPS模式数据的SBAS时序分析方法——以黄河三角洲地区为例. 国土资源遥感, 2017, 29(4): 82‒87
[10] 张金芝, 黄海军, 毕海波, 等. SBAS时序分析技术监测现代黄河三角洲地面沉降. 武汉大学学报(信息科学版), 2016, 41(2): 242‒248
[11] 李珊珊, 李志伟, 胡俊, 等. SBAS-InSAR技术监测青藏高原季节性冻土形变. 地球物理学报, 2013, 56(5): 1476‒1486
[12] Casu F, Manzo M, Lanari R. A quantitative assess-ment of the SBAS algorithm performance for surface deformation retrieval from D-InSAR data. Remote Sensing of Environment, 2006, 102(3): 195‒210
[13] 杨成生, 刘媛媛, 敖萌. 基于SBAS时序分析的大同地面沉降与地下水活动研究. 国土资源遥感, 2015, 27(1): 127‒132
[14] 陈继伟. TOPS模式SAR数据的渐进式SBAS时序分析方法[D]. 北京: 北京大学, 2017
[15] 曾安敏, 杨元喜, 欧阳桂崇. 附加约束条件的序贯平差. 武汉大学学报(信息科学版), 2008, 33(2): 183‒186
[16] Ansari H, de Zan F, Bamler R. Sequential estimator: toward efficient InSAR time series analysis. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(10): 5637‒5652
[17] 胡俊, 刘计洪, 李志伟, 等. 一种基于序贯平差的InSAR地表形变监测方法[P]. 中国 109061641A, 2018‒12‒21
[18] Jolivet R, Grandin R, Lasserre C, et al. Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data. Geophysical Research Letters, 2011, 38(17): Doi: 10.1029/2011GL048757
[19] Cavalié O, Lasserre O, Doin M P, et al. Measurement of interseismic strain across the Haiyuan fault (Gansu, China), by InSAR. Earth and Planetary Science Let-ters, 2008, 275(3): 246‒257
[20] 隋立芬, 刘雁雨, 王威. 自适应序贯平差及其应用. 武汉大学学报(信息科学版), 2007, 32(1): 51‒54
[21] 叶青超. 黄河三角洲的地貌结构及发育模式. 地理学报, 1982, 37(4): 349‒363
[22] 宋波, 王德生, 王锦丽. 东营地面沉降监测. 地矿测绘, 2004, 20(1): 34‒36
[23] 毛继军, 孟黎, 苏艳红, 等. 基于GPS的东营市地面沉降监测研究. 工程勘察, 2014, 42(10): 56‒59
InSAR Time Series Analysis Technique Combined with Sequential Adjustment Method for Monitoring of Surface Deformation
Abstract Based on the SAR satellite imagery with short revisit periods, this paper proposes a novel SBAS-InSAR time series analysis technique for efficient and continuous monitoring of surface deformation in the study area. First, standard interferometric processing is carryed out with the existing SAR image set in the study area to obtain the interference map. Thenthe atmospheric and orbital errors are removed, and the traditional SBAS (small baseline subset) method is used to obtain the surface deformation. On this basis, when a new SAR image is added, the progressive SBAS is adopted to invert the surface deformation at the new moment. The progressive SBAS method integrates the idea of sequential adjustment based on the obtained results derived from existing data set, and combines the newly acquired data to implement incremental calculations, finally achieves the equivalent effect of overall processing. Compared with the traditional SBAS method which needs to resolve all the calculations every time when a new image is added, the progressive SBAS method can reduce redundant operations and improve computing efficiency. The experiment proves that based on the Sentinel-1 satellite SAR data acquired in the Yellow River Delta from May 2018 to August 2016, the surface deformations retrieved by the progressive SBAS method are almost the same as the results of the measured ground level. The correlation coefficient (R) is 0.82, and the difference between the ground deformation rate and the traditional SBAS method is within 1 mm/a. The solution time is shortened by about 40%, and the ground deformation can be efficiently and continuously monitored.
Key words InSAR time series analysis; small baseline set (SBAS); progressive SBAS; sequential adjustment; surface deformation; continuous monitoring
doi: 10.13209/j.0479-8023.2021.002
国家自然科学基金(41571337)资助
收稿日期: 2020–02–24;
修回日期: 2020–05–28