摘要 为了揭示胰岛炎症导致 2 型糖尿病发生发展的机制, 建立胰岛 β 细胞和巨噬细胞相互作用的数学模型, 包括 IL-1β 的产生和巨噬细胞的浸润过程, 研究高浓度葡萄糖和游离脂肪酸对 IL-1β 的共同作用, 揭示胰岛炎症在 2 型糖尿病进程中的动力学机理。通过对模型中动力学参数的敏感性分析, 提出针对不同患病情况的可能的优化治疗策略。
关键词 2 型糖尿病; 胰岛炎症; 动力学模型; 巨噬细胞浸润; IL-1β
2 型糖尿病(type 2 diabetes, T2D)是一种由于胰岛素抵抗和/或胰岛素分泌不足, 导致代谢紊乱、血糖持续升高的慢性疾病。糖毒性和脂毒性等因素会诱发胰岛慢性炎症反应[1], 持续和过度的胰岛炎症反应是加速 T2D 进程的重要因素之一。
胰腺是人体第二大腺体, 由内分泌腺和外分泌腺组成。胰腺的内分泌腺为胰岛, 胰岛是分散在胰腺中的不规则细胞团。胰岛细胞主要分为 α 细胞、β 细胞、δ 细胞和 PP 细胞等。其中 β 细胞占细胞总数的 75%, α细胞占 20%, 其他细胞占 5%[2]。β 细胞分泌的胰岛素作为机体唯一的降血糖激素, 与 α 细胞分泌的胰高血糖素一起共同调节机体血糖, 维持血糖平衡。
在胰岛炎症过程中, 胰岛 β 细胞分泌炎症因子IL-1β 以及趋化因子 CCL2 和 CCL3 等, 导致巨噬细胞浸润活化, 巨噬细胞又分泌大量炎症因子(如 IL-1β、IL-6、IL-8 和 TNF-α 等[3]), 加重胰岛 β 细胞损伤。其中, IL-1β 对多种炎症因子起调节作用, 是引起炎症反应的关键因子。在巨噬细胞和胰岛 β 细胞中, IL-1β 通过 NF-![]() B 等通路, 促使细胞分泌更多的IL-1β, 高浓度的 IL-1β 可影响胰岛素分泌[4], 引起胰岛 β 细胞凋亡[5], 最终加速 T2D 的发生和发展[6]。胰岛炎症是胰岛
B 等通路, 促使细胞分泌更多的IL-1β, 高浓度的 IL-1β 可影响胰岛素分泌[4], 引起胰岛 β 细胞凋亡[5], 最终加速 T2D 的发生和发展[6]。胰岛炎症是胰岛![]() 细胞功能受损的主要原因之一, IL-1β 已成为胰岛炎症治疗的重要靶标。通过降低胰岛和外周组织的炎症反应, 改善胰岛 β 细胞功能, 是治疗 2 型糖尿病的一种新途径。
细胞功能受损的主要原因之一, IL-1β 已成为胰岛炎症治疗的重要靶标。通过降低胰岛和外周组织的炎症反应, 改善胰岛 β 细胞功能, 是治疗 2 型糖尿病的一种新途径。
T2D 动物模型的胰岛中一般都存在炎症反应, GK 大鼠是一种常用的自发性 T2D 动物模型。Hou 等[7]通过 RNA 测序和蛋白组学检测, 分析 GK 大鼠胰岛中各细胞因子在 4~24 周内的表达水平, 发现GK 大鼠胰岛中炎症因子 IL-1β 的表达分为两个阶段:早期的低表达阶段和后期的爆发阶段。4~8 周, IL-1β 表达水平处于低态, 8 周后突然跃迁到高态, 并且巨噬细胞的大量浸润也发生在 8 周之后。
基于上述研究背景, 本文构建高浓度葡萄糖和游离脂肪酸(free fatty acid, FFA)刺激下, 胰岛 β 细胞群与巨噬细胞群之间的相互作用模型, 从动力学角度研究胰岛炎症促进 T2D 发生和发展的作用机制。通过参数敏感性分析, 我们还提出 T2D 治疗过程的给药策略。
在高浓度葡萄糖或高浓度 FFA 条件下, 胰岛中胰岛 β 细胞和巨噬细胞将产生 IL-1β, 其简化的调控过程如图 1(a)所示。高浓度的葡萄糖和 FFA 可以激活胰岛 β 细胞产生炎症小体(inflammasome), 活化caspase1, 将无活性的 IL-1β 前体(pro-IL-1β)转化为成熟的 IL-1β [8]。IL-1β 与 IL-1R1 受体结合, 会激活转录因子 NFκB, 该过程被 IL-1β 受体拮抗剂(IL-1RA)抑制。FFA 也可以通过 TLR 通路激活 NF κB。NFκB 不仅促进 pro-IL-1β 和 NLRP3 的转录, 还促进大量趋化因子 CCL2, CCL3 和 CXCL8 等的转录, 进而招募巨噬细胞[9]。同时, 在高糖高脂的刺激下, 巨噬细胞也通过类似胰岛 β 细胞的信号通路, 生成更多的 IL-1β。这种正反馈会引起更多的巨噬细胞浸润[10], 导致 β 细胞淀粉样蛋白多肽的沉积和凋亡, 胰岛素分泌功能受损, 最终加速 T2D 的发展。
从图 1(a)可以看出, 调控网络中存在多个正反馈回路(红色箭头), 其中炎症因子 IL-1β 参与两个正反馈回路: IL-1β→NFΚB→IL-1β 回路和 NLRP3→ IL-1β→NFΚB→NLRP3 回路, 持续的高浓度 IL-1β 会引起胰岛 β 细胞分泌功能受损。巨噬细胞的浸润也存在一条正反馈回路, 即趋化因子→巨噬细胞→趋化因子。因此, 我们构建单个胰岛中β 细胞与巨噬细胞相互作用的常微分方程动力学模型, 主要研究 IL-1β 的活性, 判断胰岛炎症的程度和 β细胞分泌功能的受损情况。
简化起见, 我们假设胰岛细胞数量固定不变, 不讨论 IL-1β 使 β 细胞受损的情况, 同时忽略胰岛 β 细胞和巨噬细胞内生物大分子与细胞间质中细胞因子的空间浓度差异以及血流对细胞因子的稀释, 假定 β细胞和巨噬细胞产生的 IL-1β 立即全部分泌到细胞质基质中。胰岛内葡萄糖和 FFA 的浓度分别用[glucose]和[FFA]来表示, 作为参数, 不随时间变化。模型中胰岛 β 细胞和巨噬细胞中的变量包括: [NLRP3]和[inf], 分别表示 NLRP3 和炎症小体的浓度; [pro-caspase1]和[caspase1], 分别表示caspase1 前体和 caspase1 的浓度; [pro-IL-1β]和[IL-1β], 分别表示 IL-1β 前体和 IL-1β 的浓度; [IL-1βIL-1R1]和[IL-1RA·IL-1R1], 分别表示 IL1β 和 IL-1RA与受体 IL-1R1 结合的复合物; [NFκB], 表示转录因子 NFκB的活性; [m], 表示单个胰岛中巨噬细胞的个数。
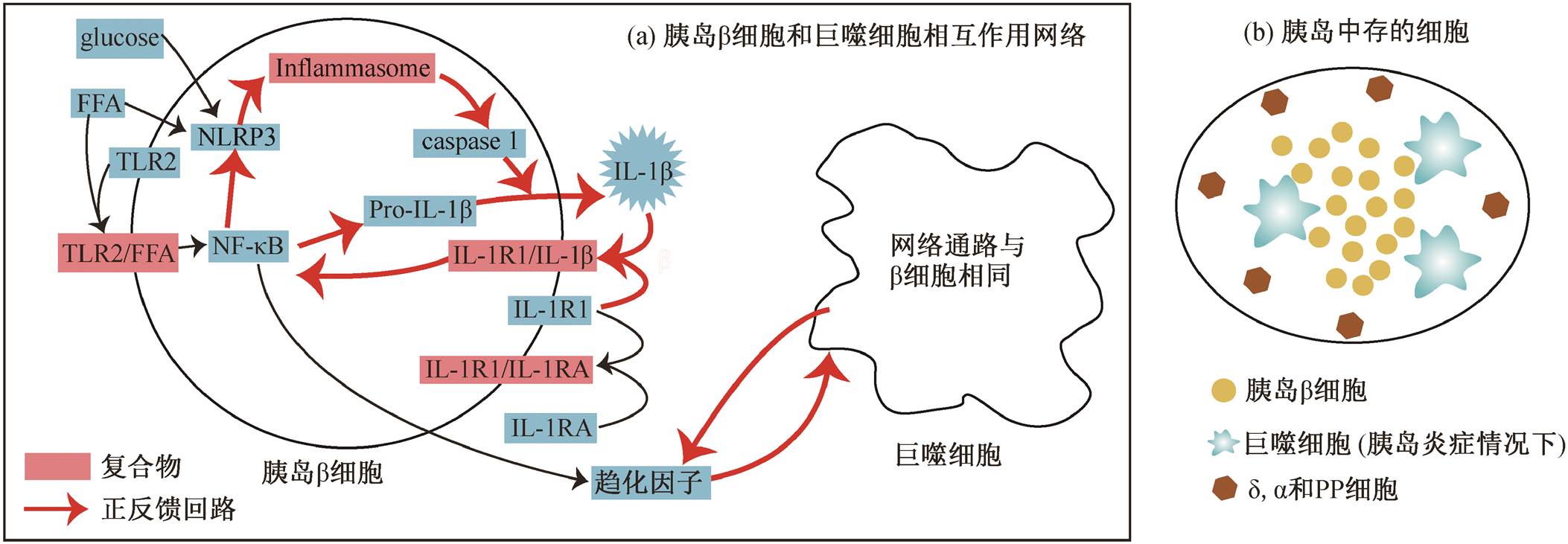
图1 葡萄糖和FFA诱导的胰岛炎症模型网络图
Fig. 1 Schematic regulatory network of inflammation in islets induced by glucose and FFA
如图 1(b)所示, 胰岛中存在胰岛 α 细胞、β 细胞、δ 细胞和PP 细胞等, 在炎症情况下, 还存在巨噬细胞浸润。巨噬细胞的浸润会导致胰岛炎症的加重, 因此巨噬细胞的数量和体积是本模型中非常重要的参数, 假设单个胰岛的体积为 V, 在单个胰岛中存在 nβ 个 β 细胞和 M 个巨噬细胞, 单个 β 细胞的体积为 vβ, 单个巨噬细胞的体积为 vM, 单个胰岛中β 细胞的总体积为 vβ=nβÍvβ, 巨噬细胞的总体积为VMф= MÍvM, 其他胰岛 α 细胞、δ 细胞和 PP 细胞的总体积为 V0。
针对单个胰岛中 IL-β 产生以及巨噬细胞的浸润过程, 我们构建以下胰岛 β 细胞和巨噬细胞相互作用的动力学模型。模型包括 3 个部分, 共 10 个方程, 其中含 10 个 ka 类型参数, 表征激活速率; 7 个kd 类型参数, 表征降解速率; 2 个 kb 类型参数, 表征复合物解离速率; 6 个 KM 类型参数, 表征米氏(或类米氏)常数。
模型的第一部分。在胰岛 β 细胞和巨噬细胞中, 由 FFA 和葡萄糖作为上游信号, 激活 IL-1β 的过程如下:
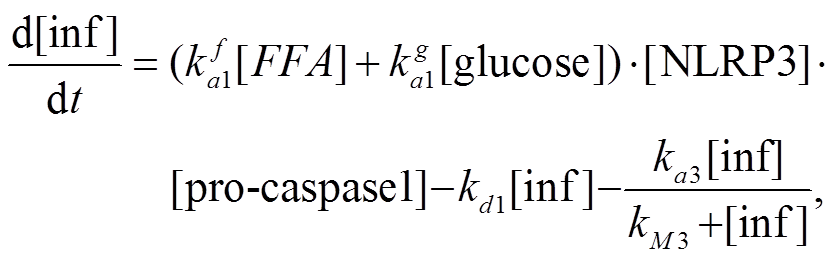 (1)
(1) (2)
(2)
 (3)
(3)
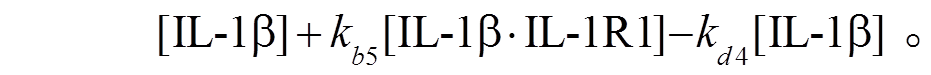 (4)
(4)炎症小体是由 NLRP3, pro-caspase1 和 ASC 形成的复合物。我们假设 ASC 浓度固定, 因此未引入该参数。式(1)中第 3 项用米氏方程描述炎症小体在酶的催化下生成 caspase1 的速率, 并假设酶的浓度固定, 故也未引入该参数。β 细胞内, 在 caspase1的催化下, pro-IL-1β 转化为 IL-1β 的速率为
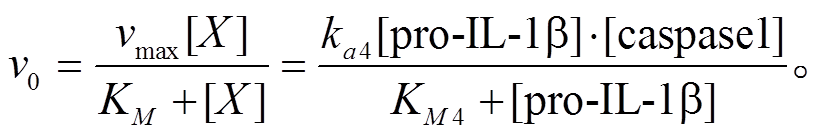
然而, IL-1R1 与分泌到细胞外的 IL-1β 结合, 因此需推导细胞间质中 IL-1β 的浓度。在单个胰岛中, IL-1β 均由胰岛 β 细胞和巨噬细胞分泌到细胞间质中, 因此在 dt 时间内, β 细胞和巨噬细胞中增加的IL- 1β 分子数等于细胞外增加的 IL-1β 分子数, 即 dNext= dNβ+dNMφ。考虑到细胞间质中 IL-1β 的浓度, 因此在上式两边除以细胞间质液体积 V-Vβ-VMφ-V0。
以 β 细胞分泌 IL-1β 过程为例, 得到由 β 细胞分泌到细胞间质的 IL-1β 的浓度为
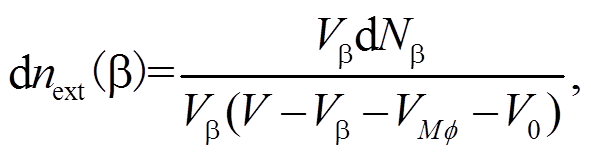
其中, 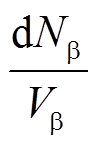 就是 β 细胞内 IL-1β 增加的浓度, 可以用生成项
就是 β 细胞内 IL-1β 增加的浓度, 可以用生成项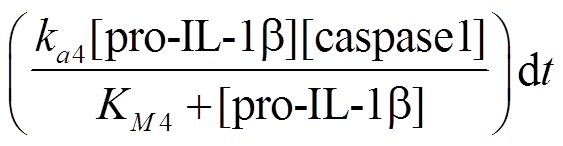 来表示。
来表示。
由于巨噬细胞也通过相同的通路产生 IL-1β, 巨噬细胞内 IL-1β 增加的浓度 dnMφ 与胰岛 β 细胞内 IL-1β 增加的浓度 dnβ 相等, 因此细胞间 IL-1β的生成速率为
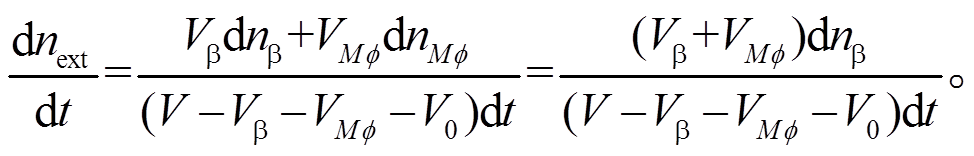
在 IL-1β 的扩散和降解以及 IL-1β 与 IL-1R1 的结合和解离过程中, 细胞间质中 IL-1β 的变化速率如式(4)所示。
模型的第二部分。在胰岛 β 细胞和巨噬细胞中, IL-1β 通过激活 NFκB 产生更多的 IL-1β, 过程如式(5)~(9)所示。其中, IL-1R1 总量为 I=[IL-1βIL-1R1]+ [IL-1R1IL-1RA]+[IL-1R1]。
 (5)
(5) (6)
(6)
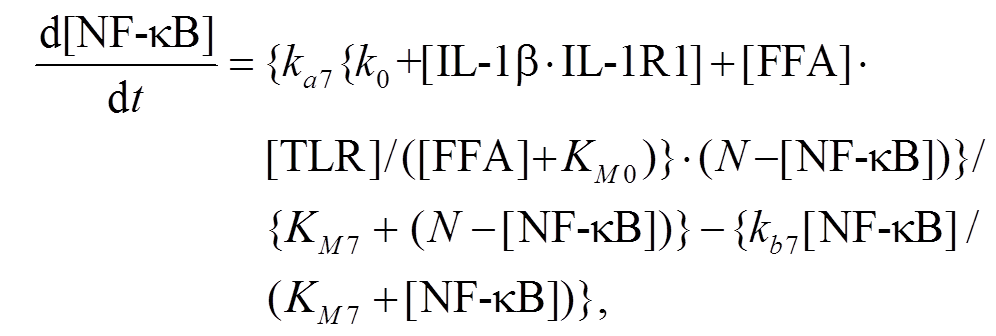 (7)
(7) (8)
(8)
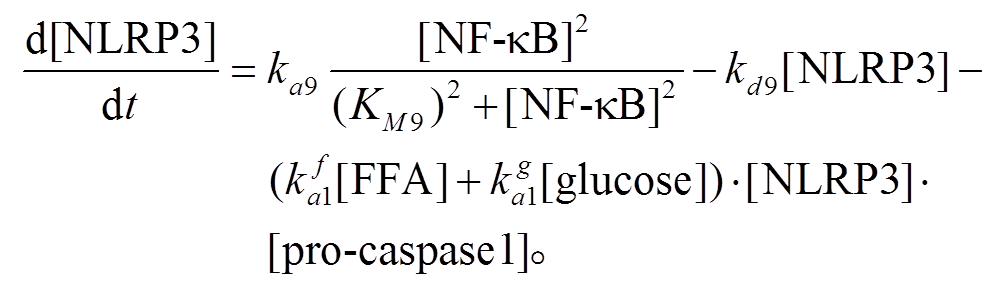 (9)
(9)式(7)描述的化学反应方程式为
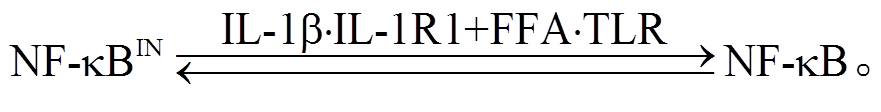
由于 NFκB 的激活非常复杂, 且与磷酸化反应有关, 因此我们用米氏方程来表示 NFκB 的激活和抑制过程。NFκB 的激活信号与[IL-1IL-1R1]以及FFATLR2 有关, 我们把激活 NFκB 的酶浓度简单地假设为
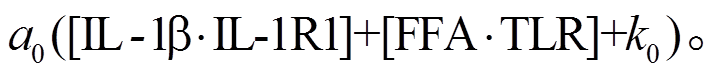
根据米氏方程, NFκB 的激活速率为
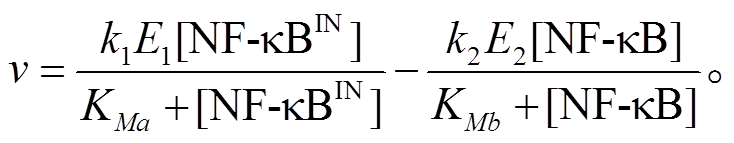
假设 NFκB 总量保持不变, 即
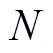 , 则上式中E1表示为
, 则上式中E1表示为

令 ka7=k1a0,kb7=k1E,KM7=KMa=KMb,进一步假设FFA 与 TLR 受体结合过程可迅速达到平衡状态, 即

且TLR总量保持不变, 即[FFATLR]+[TLR]=T, 则
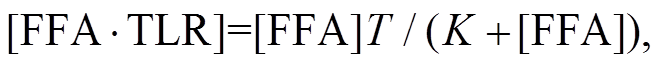
其中, 解离常数 。
。
将上述参数整理带入 NFκB 的激活速率表达式, 即得到式(7)。式(8)和(9)的第一项分别描述 pro-IL-1 和 NLRP3 在转录因子 NFκB 的作用下发生转录翻译的速率, 可用希尔函数表示为
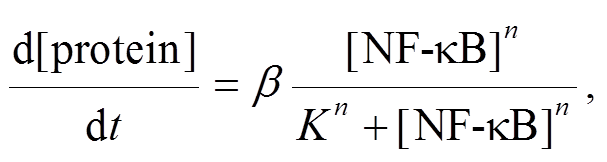
这里取希尔函数 n=2, 即得到式(8)和(9)的第一项。
模型的第三部分描述胰岛 β 细胞和巨噬细胞中 NFκB产生的趋化因子能够招募更多的巨噬细胞。胰岛 β细胞内和巨噬细胞内趋化因子生成速率均用希尔函数表示:

由于趋化因子也会被分泌到细胞间质中, 因此细胞间质中趋化因子生成速率也表示为

假设胰岛中浸润的巨噬细胞都是促炎型巨噬细胞, 且招募的巨噬细胞平均个数与细胞间趋化因子浓度成正比, 则有

令 ka10=αÍβ, 再考虑到细胞的凋亡和扩散, 则胰岛中巨噬细胞变化率可由式(10)表示。
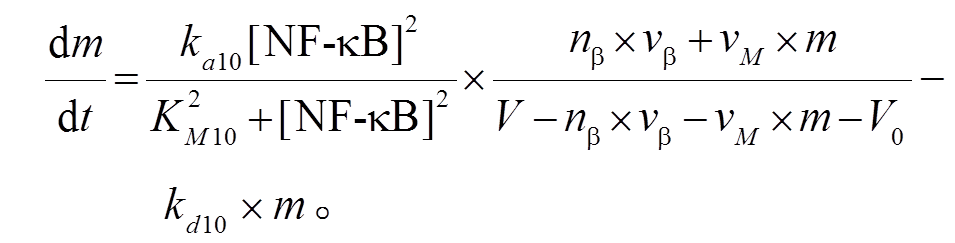 (10)
(10)为了模拟在葡萄糖和 FFA 刺激下胰岛中 IL-1β的激活情况, 动力学模型中各个变量的初值均设为0。根据文献[2]、2 型糖尿病人各炎症因子的测量数据[11]以及 2 型糖尿病人中巨噬细胞的浸润情况[12], 我们在生化反应合理的范围内选择反应速率参数, 如表 1 所示。
我们模拟高浓度葡萄糖和较低浓度脂肪(假设[glucose]=20 mmol/L, [FFA]=0.05 mmol/L)刺激下胰岛中巨噬细胞数量和 IL-1β 浓度随时间的变化, 结果如图 2(a)所示。随着时间的推移, 胰岛组织中浸润的巨噬细胞数量逐渐增加, 在某一时刻发生跳变, 并演化至稳态, 随后 IL-1β 浓度也发生跳变。
表1 动力学参数的选取
Table 1 Selected simulation parameters

参数参数意义参数值 N/(nmolL-1)NFκB总量6 IA/ (nmolL-1)IL1β受体拮抗剂浓度15 T/(nmolL-1)Toll样受体总浓度1 I/(nmolL-1)IL1β受体总浓度5 k0/(nmolL-1)NFκB自激活速率0.04 K/(mmolL-1)FFA与TLR2解离常数3000 /(L2mmol-2s-1)葡萄糖激活炎症小体速率80000 /(L2mmol-2s-1)FFA激活炎症小体速率800000 kd1/(s-1)炎症小体降解速率0.06 ka2/(nmolL-1s-1)Pro-caspase产生速率1 kd2/(s-1)Pro-caspase降解速率0.5 ka3/(nmolL-1s-1)caspase1的生成速率1 KM3/(nmolL-1)caspase1酶促反应米氏常数5 kd3/(s-1)caspase1的降解速率0.01 ka4/(s-1)IL1β生成速率0.0011 KM4/(nmolL-1)IL1β酶促反应米氏常数4 kd4/(s-1)IL1β降解速率0.04 ka5/(Lnmol-1s-1)IL1β与IL-1R1结合速率0.03 kb5/(s-1)IL1β与IL-1R1解离速率0.004 ka6/(Lnmol-1s-1)IL-1RA与IL-1R1结合速率0.16 kb6/(s-1)IL-1RA与IL-1R1解离速率1 ka7/(s-1)NFκB激活速率0.9 KM7/(nmolL-1)NFκB类米氏常数10 kb7/(nmolL-1s-1)NFκB失活速率0.2 ka8/(nmolL-1s-1)ProIL1β转录速率1 KM8/(nmolL-1)ProIL1β类米氏常数5 kd8/(s-1)ProIL1β降解速率1 ka9/(nmolL-1s-1)NLRP3转录速率50 KM9/(nmolL-1)NLRP3类米氏常数5 kd9/(s-1)NLRP3降解速率11 ka10/(cells-1)巨噬细胞浸润的速率5 KM10/(nmolL-1)巨噬细胞浸润的类似米氏常数1 kd10/(s-1)巨噬细胞的凋亡和扩散速率1 nβ/cell胰岛β细胞数目20 vM/(μm3)单个巨噬细胞体积20000* vβ/(μm3)单个胰岛β细胞体积4000* V/(μm3)单个胰岛体积393000* V0/(μm3)胰岛α和δ细胞总体积33000*
注: *表示巨噬细胞半径为 17 μm, 胰岛 β 细胞半径为 10 μm, 胰岛半径为45 μm, 胰岛 α (或δ)细胞、PP细胞半径为11μm。
胰岛组织中单个胰岛浸润的巨噬细胞数量以及IL-1β 浓度在不同浓度葡萄糖(假设[FFA]=0.05 mmol/L)中的稳态结果如图 2(b)和(c)所示。可以看出, 当系统处于低巨噬细胞数量的初态时, 随着葡萄糖浓度逐渐增大, 巨噬细胞数量逐渐增加, 当葡萄糖浓度增至 11.1mmol/L 时, 单个胰岛中巨噬细胞的平均数量由 0.8 个跃迁到 3.3 个。当巨噬细胞达到 3.0 个以上时, 胰岛处于炎症状态。模型中, 因为巨噬细胞的浸润过程存在双稳态和磁滞回线效应, 如果通过降低血糖的方式来减少胰岛巨噬细胞的浸润, 则需要将血糖浓度降到低于 0.7mmol/L, 而这在生理上无法实现。

(a)高糖刺激下, IL-1β 稳态浓度和巨噬细胞浸润数量的时序变化; (b)单个胰岛中, 浸润的巨噬细胞平均个数对葡萄糖浓度的响应; (c)有或无巨噬细胞时, IL-1β稳态浓度随葡萄糖浓度的变化
图2 胰岛中炎症因子 IL-1β 和浸润的巨噬细胞的动力学分析
Fig. 2 Dynamical analysis of IL-1β and infiltrated macrophages in the islet
Richardson 等[12]比较 545 个 T2D 患者和非糖尿病患者胰岛中巨噬细胞的分布情况, 发现非糖尿病患者胰腺病理切片中每个胰岛平均有 0.52±0.08个巨噬细胞浸润, T2D 患者每个胰岛平均有 1.34± 0.18 个巨噬细胞浸润, 且 T2D 患者单个胰岛中巨噬细胞浸润超过 3 个的比例为 20.6%±4.1%。我们的模拟结果与 Richardson 等[12]的实验结果相符合。
为了进一步分析巨噬细胞对胰岛炎症的影响, 我们讨论在不同的巨噬细胞浸润情况下, 胰岛中IL-1β 稳态浓度对葡萄糖的响应, 如图 2(c)所示。可以发现, 无论胰岛中有无巨噬细胞浸润, 随着葡萄糖浓度增加, 胰岛中 IL-1β 的稳定性都发生改变, 从单稳低态经过双稳区, 最后变为单稳高态。
当胰岛中没有巨噬细胞的浸润时, 模拟结果表明, 当系统的初态为 IL-1β 浓度处于低态时, 随着葡萄糖浓度逐渐增大, IL-1β 浓度仍然处于低态(小于 2 pmol/L); 当葡萄糖浓度增加到 17.1mmol/L 时, IL-1β 的浓度跃迁到高态 (40pmol/L), 此时我们认为胰岛处于炎症状态, 定义该葡萄糖浓度为激活 IL-1β的阈值点。当胰岛炎症中 IL-1β 浓度处于高态 (40pmol/L)时, 如果通过降低血糖的方式使IL-1β 浓度由高态跃迁到低态(小于 2pmol/L), 则需要将血糖浓度降至低于 3.5mmol/L, 我们定义该葡萄糖浓度为抑制 IL-1β 的阈值点。
当胰岛处于巨噬细胞浸润的初态时, 随着葡萄糖浓度逐渐增大, IL-1β 浓度仍然处于低态(小于 2 pmol/L), 当葡萄糖浓度超过 11.1mmol/L 的阈值水平后, IL-1β 被激活并跃迁到高态(108pmol/L)。如果通过降低血糖的方式来使胰岛炎症中 IL-1β 浓度由高态降至低态, 则需要将血糖浓度降到低于 0.7mmol/L。当胰岛中存在巨噬细胞浸润时, IL-1β 激活和抑制的阈值点均减小, 并且, 当 IL-1β 激活时, 其浓度是巨噬细胞未浸润时的 2 倍以上。由此可以推断, 当巨噬细胞未浸润时, 需更高浓度的葡萄糖才能激活 IL-1β。据此可以推断, Hou 等[7]实验中的GK 大鼠 4~8 周时, IL-1β 浓度未激活的原因是巨噬细胞未浸润胰岛组织。8 周之后 GK 大鼠中 IL-1β 激活, 是由于巨噬细胞浸润导致较低浓度的葡萄糖就将诱导产生胰岛炎症。
巨噬细胞的浸润对胰岛炎症是一种恶化作用。当存在巨噬细胞浸润时, 网络中的正反馈强度更大, 不仅存在胰岛 β 细胞的 IL-1β 自激活过程, 还存在胰岛 β 细胞对巨噬细胞的招募以及巨噬细胞的自激活过程。我们希望通过使趋化因子失活来抑制巨噬细胞浸润, 从而控制胰岛炎症。
前面取 FFA 浓度为定值 0.05mmol/L 来分析胰岛中 IL-1β 稳态浓度对葡萄糖浓度的响应, 但在实际情况中, 葡萄糖和 FFA 浓度都是变量。图 3(a)给出当 FFA 浓度取 3 个不同的定值(0.05, 0.3 和 0.5mmol/L)时, IL-1β 稳态浓度与葡萄糖浓度的关系。可以看出, 当 FFA 浓度增大时, 系统由可逆双稳态(FFA=0.05mmol/L)变为不可逆双稳态(FFA=0.3, 0.5mmol/L)。当 FFA 浓度较大时, IL-1β 对葡萄糖的响应为不可逆双稳态, 这样 IL-1β 一旦激活, 即使血糖降低到零, IL-1β 仍然处于高态。
当葡萄糖浓度取 3 个不同的定值(0.5, 3 和 5 mmol/L)时, IL-1β 稳态浓度对 FFA 的响应关系如图3(b)所示。可以看出, 当葡萄糖浓度较大时, IL-1β对 FFA 的响应也为不可逆双稳。
葡萄糖-FFA 的相图如图 3(c)所示, 据此分析系统处于可逆双稳态时, 参数葡萄糖和 FFA 选取的区间。若固定 FFA 浓度小于 0.12mmol/L, IL-1β 浓度相对于葡萄糖浓度的变化为可逆双稳(紫色虚线); 若固定 FFA 浓度处于 0.12~1.14mmol/L 之间, IL-1β浓度相对于葡萄糖浓度的变化为不可逆双稳(绿色虚线)。同理, 若固定葡萄糖浓度小于 1.16 mmol/L, IL-1β 浓度相对于 FFA 浓度的变化为可逆双稳; 若固定葡萄糖浓度处于 1.16~11.8mmol/L 之间, IL-1β 浓度相对于 FFA 浓度的变化为不可逆双稳。在治疗胰岛炎症和 T2D 时, 若系统处于不可逆双稳态, 就不能通过只降低血糖浓度或只降低FFA 浓度使 IL-1β 活性降低, 而需先降低 FFA 浓度, 使系统变为可逆双稳态, 再降低血糖浓度, 才有可能治愈胰岛炎症。根据图 3(c)中红线和黑线的负斜率可以推断, FFA 和葡萄糖通过协同作用活化 IL-1β, 并且1.14mmol/L FFA 即可独自激活 IL-1β, 而葡萄糖独自激活 IL-1β 的阈值为 11.8mmol/L, 因此 FFA 对IL-1β 的作用更强。这也解释了为何肥胖的人更容易患糖尿病, 且肥胖的 T2D 患者机体炎症水平相对更高。
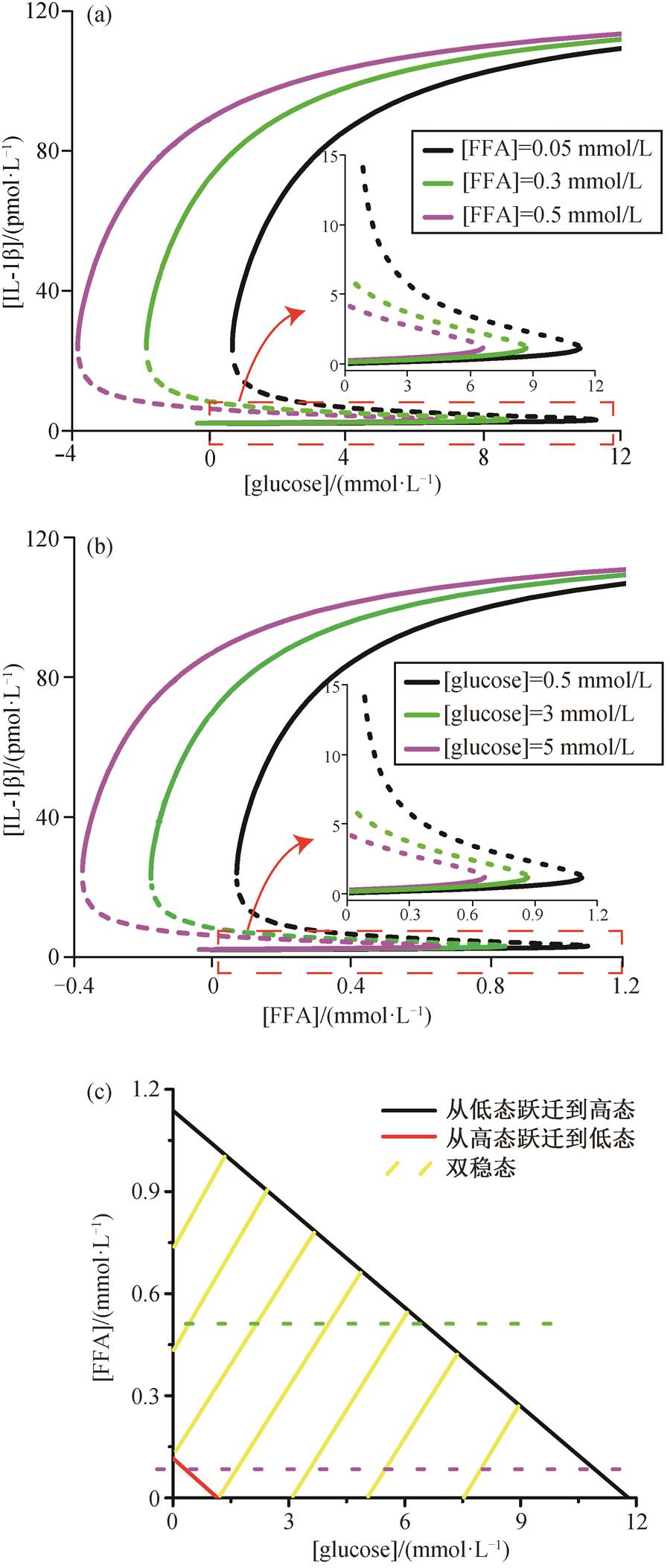
图3 IL-1β激活过程中IL-1β稳定性随FFA或葡萄糖的变化
Fig. 3 Stability of IL-1βvarying with FFA or glucose in the process of IL-1β activation
对 T2D 患者使用免疫治疗, 可有效地缓解胰岛炎症, 增强胰岛素敏感性, 促进胰岛素分泌[13-16]。针对系统中任意一种分子用药, 都可以改变 T2D 病人的动力学参数, 但由于与炎症系统相关的动力学参数比较复杂, 因此需要对模型的动力学参数进行单参数敏感性分析, 以此推断对哪一种分子用药更加有效。
在我们的模型中, 动力学参数不同会造成激活IL-1β 活性所需要的葡萄糖浓度的阈值(记为 T1)和IL-1β 活性被抑制时的葡萄糖浓度的阈值(记为 T2)不同。我们对动力参数进行单参数敏感性分析, 即仅改变一个参数, 固定其他参数, 研究对哪个信号通路用药能更有效地增大 T1 和 T2, 从而提高 IL-1β激活和抑制时葡萄糖浓度的阈值。
根据敏感性系数的定义[17], 为衡量模型中参数P的敏感程度, 我们定义 cost(P)为

其中, Xα(P0)表示当所有参数均为表 1 中所示时, IL-1β 激活的阈值(T1)和 IL-1β 抑制时的阈值(T2)的大小; Xa (P)表示当其他参数保持不变, 参数 P=P0+ 0.1P0 (即参数 P 增加 10%)时, T1 或 T2 的大小; cost (P)可以表征 T1 或 T2 对参数 P 的敏感性。由此得到全参数敏感性谱, 如表 2 所示。
cost(P)越大, 系统对动力学参数 P 越敏感, 针对该参数用药越有效。根据表 2, T1 的敏感动力学参数为 kb7 (NFκB 失活速率)和 ka7 (NFκB 激活速率), T2 的敏感动力学参数为 V, V0, nβ, vβ 和 vM (胰岛体积, 胰岛中 α、δ 细胞和 PP 细胞总体积, 胰岛 β 细胞个数和单个细胞体积以及胰岛中巨噬细胞体积)。因为胰岛中各细胞的体积不可更改, 我们只讨论 kb7和 ka7 这两个动力学参数涉及的过程:
 。
。增加 kb7, T1 和 T2 均增大, 即 IL-1β 激活和抑制的阈值更大, 此时胰岛炎症和 T2D 更容易预防和治疗。ka7 减小, T1 和 T2 也增大, 因此降低 ka7 也可有效地预防和治疗胰岛炎症和 T2D。这两个敏感的动力学参数都与 NFκB 的激活有关。NFκB 激活会增强网络的正反馈强度, 易诱发胰岛炎症, 加重 T2D, 因此针对阻断 NFκB 的信号通路特异性地用药来增大kb7, 减小 ka7, 抑制 NFκB 的激活, 有利于预防和治疗胰岛炎症和 T2D。
目前临床使用的免疫治疗的用药包括以下几种。1)水杨酸: 可抑制 NFκB 的激活。使用水杨酸后, 胰岛素分泌增多, 胰岛素敏感性增强, 系统炎症得到减缓[13]。在我们的模型中, 增加水杨酸, 相当于增加动力学参数 kb7。2)TNF 拮抗剂: 可抑制NFκB 的上游信号分子。使用 TNF 拮抗剂后, 血糖和脂连素下降, 胰岛素分泌增加, 可以减小患 T2D的风险[14]。在我们的模型中, 增加TNF拮抗剂, 相当于减小动力学参数 ka7。3)阿那白滞素: IL-1β 受体拮抗剂。使用阿那白滞素后, 可以减缓系统炎症, 促进胰岛素分泌, 降低血糖[15]。在我们的模型中, 增加阿那白滞素, 相当于增加动力学参数 IA。4)卡那单抗: IL-1β 特异性抗体。使用卡那单抗后, 胰岛素分泌增强, 系统炎症得到减缓[16]。在我们的模型中, 增加卡那单抗, 相当于增加动力学参数 kd4。从临床用药的角度推断, 针对胰岛炎症用药, 抑制NFκB 的激活可以成为胰岛炎症和 T2D 治疗的一个重要方向。
表2 动力学参数敏感程度
Table 2 Cost of T1 and T2 when the parameters change

参数T1对参数的敏感性/%T2对参数的敏感性/%药物 kb75310 水杨酸 ka7166.6TNF拮抗剂 KM81110 N1123 k0100.14 V8.5127 V08.5127 KM96.25.9 nβ3.792 vβ3.792 kd42.56.3卡那单抗 kb52.56.3 kd32.56.3 KM42.45.3 kd82.45.3 I2.36.6 ka51.74.5 ka41.74.5 ka81.74.5 IA1.43.6阿那白滞素 KM71.40.04 ka21.34.1 ka91.12.6 kd91.13.1 kd21.13.1 0.92.6 ka60.82.2 kb60.61.7 KM100.20.5 ka100.220 vM0.272 kd100.217 ka30.10.4 KM30.10.4 kd10.10.4 K0.00020.000002 T0.00020.000002 0.00020.000002
根据单参数敏感性分析, kb7 和 ka7 是最敏感的动力学参数, 并且当FFA浓度大于 0.12mmol/L 时, IL-1β 存在不可逆双稳。一旦存在不可逆双稳, 胰岛炎症的治愈将会变得极其困难。为了研究敏感参数对 IL-1β 稳定性的影响, 我们假设胰岛中 FFA 的浓度为 0.1mmol/L。首先给出在不同kb7 取值下, 系统达到稳态时 IL-1β 浓度与葡萄糖浓度的关系(图4(a))。当 kb7 从小到大变化时, 系统的稳定性发生改变, 从单稳态(kb7=0.07nM/s)变成不可逆双稳态(kb7=0.15nM/s), 再到可逆双稳态(kb7=0.2nM/s)。当 kb7 取值较小时, IL-1β 对葡萄糖的响应存在不可逆双稳, IL-1β 一旦激活, 就无法通过降低血糖浓度来治愈胰岛炎症。图 4(b)给出系统处于双稳态的区域, 当 kb7 取值在 0.11~0.18 之间时, 系统存在不可逆双稳态; 小于 0.11 时, 系统处于单稳态; 取值大于 0.18 时, 系统处于可逆双稳态。值得注意的是, 虽然 kb7很小时, 系统处于单稳态, 但葡萄糖浓度为零时, IL-1β 浓度为 47pmol/L, 此时, 不能通过降低血糖使IL-1β 浓度降到低态。因此我们不能通过减小 kb7 使系统稳定性由双稳态变为单稳态的方式来治愈胰岛炎症和治疗 T2D。当 kb7<0.18 时, 推荐采用水杨酸等药物增加 kb7, 使系统由单稳态或不可逆双稳态转变为可逆双稳态, 再通过降低血糖浓度来治愈胰岛炎症。当 kb7>0.18 时, 系统处于可逆双稳态, 此时视情况而定, 可以直接降低血糖使 IL-1β表达水平降到低态, 也可先增大 kb7, 提高系统中血糖的阈值, 再降低血糖, 使 IL-1β 失活来治愈胰岛炎症和治疗 T2D。

(b)和(d)中, 红色和黑色边界代表系统从低态跃迁到高态的阈值, 黑色边界和红色边界之间为双稳区(绿色区域为不可逆双稳区, 黄斜线区域为可逆双稳区)
图4 IL-1β 激活过程中 IL-1β 稳定性随动力学参数kb7和ka7的变化
Fig. 4 Stability of IL-1β varying with kb7or ka7in the process of IL-1β activation
图 4(c)和(d)展示不同 ka7 取值条件下系统达到稳态时 IL-1β 浓度与葡萄糖浓度的关系。当 ka7 取值在0.99~1.58 之间时, 系统存在不可逆双稳态; 大于1.58 时, 系统处于单稳态; 取值小于 0.99 时, 系统处于可逆双稳态(图 4(d))。同样地, 当系统处于单稳态, 葡萄糖浓度降低到零时, IL-1β 浓度并不为零。因此, 当 ka7>0.99 时, 推荐使用 TNF 拮抗剂等药物来减小 ka7,使系统转变为可逆双稳态, 再通过降低血糖浓度来治愈胰岛炎症。当 ka7<0.99 时, 根据情况, 可以直接降低血糖, 也可先减小 ka7, 再降低血糖来治愈胰岛炎症和治疗T2D。
本文针对 T2D 患者慢性炎症过程中正反馈引起的细胞因子激活的不可逆过程进行定量研究, 揭示了炎症过程中可能的动力学机制。针对胰岛中IL-1β 的产生过程, 构建胰岛 β 细胞和巨噬细胞相互作用简化网络, 并建立非线性常微分动力学模型。通过分析巨噬细胞对 IL-1β 激活过程的影响, 揭示巨噬细胞恶化胰岛炎症的机理。本文分析了葡萄糖和 FFA 对系统稳定性的影响, 当葡萄糖 (FFA)浓度超过阈值时, 胰岛中 IL-1β 对 FFA 的响应存在不可逆双稳。针对该模型, 使用单参数敏感性分析, 指出敏感参数为 NF-κB 失活速率 kb7 和 NF-κB 激活速率 ka7, 并提出临床上可通过抑制 NF-κB 的活性来预防和治疗胰岛炎症。针对 kb7 或 ka7 的不同取值, 通过模拟发现 ka7 较大和 ka7 较小时能导致不可逆现象发生, 并提出系统存在可逆双稳或不可逆双稳时的不同治疗策略。近期, 我们在大鼠和转基因小鼠实验中完成了部分理论的实验验证, 结果证实巨噬细胞与胰岛炎症进程相关[18]。
本文模型忽略了生理和病理过程中某些正负反馈通路, 数学模型也进行了简化和近似。例如, 没有讨论 IL-1β 导致 β 细胞凋亡, 胰岛素分泌减少的后续影响。未来工作中, 我们希望构建更复杂的模型来模拟不同病人的实际情况, 定性或半定量地反映 2 型糖尿病炎症过程中的发病机理, 为优化治疗方案提供参考。
参考文献
[1] Jiang H Y, Wek S A, McGrath B C, et al. Phosphory-lation of the α subunit of eukaryotic initiation factor 2 is required for activation of NF-κB in response to diverse cellular stresses. Molecular & Cellular Bio-logy, 2003, 23(16): 5651–5663
[2] 胡国潢. 实用临床胰腺外科学. 北京: 科学技术文献出版社, 2016: 28
[3] Westwell-Roper C Y, Ehses J A, Verchere C B. Resi-dent macrophages mediate islet amyloid polypeptide-induced islet IL-1β production and β-cell dysfunction. Diabetes, 2014, 63(5): 1698–1711
[4] Park Y J, Warnock G L, Ao Z, et al. Dual role of interleukin-1β in islet amyloid formation and its β-cell toxicity: implications for type 2 diabetes and islet transplantation. Diabetes Obes Metab, 2017, 19(5): 682–694
[5] Maedler K, Sergeev P, Ris F et al. Glucose-induced β cell production of IL-1β contributes to glucotoxicity in human pancreatic islets. J Clin Invest, 2002, 110 (6): 851–860
[6] Cavelti-Weder C, Babians-Brunner A, Keller, C et al. Effects of gevokizumab on glycemia and inflamma-tory markers in type 2 diabetes. Diabetes Care, 2012, 35(8): 1654–1662
[7] Hou J, Li Z, Zhong W, et al. Temporal transcriptomic and proteomic landscapes of deteriorating pancreatic islets in type 2 diabetic rats. Diabetes, 2017, 66(8): 2188–2200
[8] Zhou R, Tardivel A, Thorens B, et al. Thioredoxin-interacting protein links oxidative stress to inflamma-some activation. Nature Immunology, 2010, 11(2): 136–140
[9] Donath M Y, Böni-schnetzler M, Ellingsgaard H, et al. Islet inflammation impairs the pancreatic β-cell in type 2 diabetes. Physiology, 2009, 24 (6): 325–331
[10] Ehses J A, Meier D T, Wueest S, et al. Toll-like receptor 2-deficient mice are protected from insulin resistance and beta cell dysfunction induced by a high-fat diet. Diabetologia, 2010, 53(8): 1795–1806
[11] Tong H V, Luu N K, Son H A, et al. Adiponectin and pro-inflammatory cytokines are modulated in Vietna-mese patients with type 2 diabetes mellitus. J Dia-betes Investig, 2017, 8(3): 295–305
[12] Richardson S J, Willcox A, Bone A J, et al. Islet-associated macrophages in type 2 diabetes. Diabeto-logia, 2009, 52(8): 1686–1688
[13] Fleischman A, Shoelson S E, Bernier R, et al. Salsa-late improves glycemia and inflammatory parameters in obese young adults. Diabetes Care, 2008, 31(2): 289–294
[14] Dominguez H, Storgaard H, Rask-Madsen C, et al. Metabolic and vascular effects of tumor necrosis factor-α blockade with etanercept in obese patients with type 2 diabetes. J Vasc Res, 2005, 42: 517–525
[15] Larsen C M, Faulenbach M, Vaag A, et al. Interleukin-1-receptor antagonist in type 2 diabetes mellitus. N Engl J Med, 2007, 356: 1517–1526
[16] Cavelti-Weder C, Babians-Brunner A, Keller C, et al. Effects of gevokizumab on glycemia and inflamma-tory markers in type 2 diabetes. Diabetes Care, 2012, 35(8): 1654–1662
[17] Zi Z. Sensitivity analysis approaches applied to systems biology model. IET Syst Biol, 2011, 5(6): 336–346
[18] 雷蕾, 林智立, 王琳琳, 等. 2 型糖尿病发病过程中胰岛炎症的动力学机理. 科学通报, 65(35): 4139–4148
Dynamics Model of Type 2 Diabetes with Inflammation in Islets and Treatment Strategies
Abstract In order to reveal the pathogenesis of type 2 diabetes caused by inflammation in islets, this paper established the mathematical model of interaction between β cell and macrophage, including the process of IL-1β production and macrophage infiltration in islets. The combined effects of glucose and free fatty acid on IL-1β was analyzed to reveal the dynamic mechanism of islet inflammation in the progression of type 2 diabetes. By analyzing this model’s sensitivity to parameters variation, the feasible optimal treatment strategies was given to different type 2 diabetes patients.
Key words type 2 diabetes; islets inflammation; dynamic model; macrophage infiltration; IL-1β
doi: 10.13209/j.0479-8023.2020.038
科技部重大科学研究计划(MSTC2015CB910300)资助
收稿日期: 2020-02-06;
修回日期: 2020-04-11