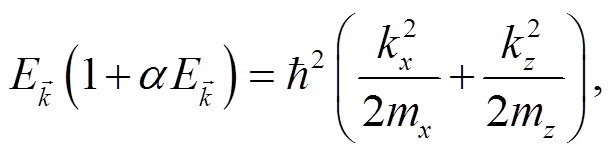(1)摘要 采用基于有效质量近似的多子带、多能谷系综蒙特卡洛方法, 考虑纳米尺度 MOSFET 沟道二维电子气中实际存在的多种散射机制, 模拟 InGaAs 肖特基源漏 MOSFET。结果显示, 在稳态下, 散射虽然改变了InGaAs 肖特基源漏 MOSFET 沟道中沟道电势、电子浓度和速度的分布, 但对 InGaAs 肖特基源漏 MOSFET 的输出特性和转移特性影响较小; 而在施加阶跃漏端电压时, 散射的存在增加了过冲电流的峰值和转换时间, 降低了器件的截止频率。
关键词 InGaAs; 肖特基源漏MOSFET; 系综蒙特卡洛
肖特基源漏利用金属或金属硅化物形成的肖特基结替代重掺杂 PN 结作为 MOSFET 的源漏, 具有串联电阻低、工艺简单等优点[1–3]。与 Si 或 Ge 等IV 族半导体材料相比, InGaAs 等 III-V 族半导体材料可以提供更高的饱和速度和迁移率[4–7]。这些特点使得 InGaAs 肖特基源漏 MOSFET[8–10]成为高速集成电路技术可能的选择方案。
在纳米尺度下, 准弹道输运和量子尺寸效应使得传统的基于漂移扩散的模拟方法不再适用, 而完全基于量子力学的非平衡格林函数等模拟方法运算量过大, 难以应对多种散射效应等问题。多子带系综蒙特卡洛方法[11–12]是将泊松–薛定谔耦合求解静电特性与蒙特卡洛求解玻尔兹曼输运方程相结合的一种半导体器件模拟方法, 可以很好地考虑量子效应、多种散射机制乃至准弹道输运, 具有较高的准确性和可以接受的计算时间, 广泛地应用于纳米尺度半导体器件的模拟[13–14]。
本文采用多子带系综蒙特卡洛方法, 对纳米尺度 InGaAs 肖特基源漏 MOSFET 的输运特性进行模拟, 研究散射机制对肖特基晶体管稳态、瞬态和高频特性的影响。
肖特基 MOSFET 器件结构如图 1 所示。其中沟道材料为 In0.53Ga0.47As, 栅介质材料为 HfO2, 等效氧化层厚度为 1nm, 沟道厚度 Tch=10nm, 沟道长度Lg=20nm/60nm, Spacer 区长度 Lsp=5nm。整个沟道未掺杂, 肖特基势垒高度为 0.2eV。沟道方向为(100)方向, 图示截面为<001>截面。表 1 给出由InAs 和 GaAs 插值得到的 In0.53Ga0.47As 有效质量[15]。采用自洽的泊松方程和薛定谔方程对器件的静电特性进行模拟; 基于自洽求解泊松方程和薛定谔方程的结果, 采用多子带系综蒙特卡洛方法模拟半导体器件的电学特性。
考虑 InGaAs Γ 谷和 L 谷中各 3 条子带, 因此采用非抛物线近似的能带结构:
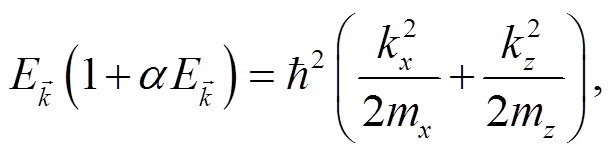(1)其中, α 是相应能谷的非抛物性因子,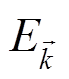 
是电子的动能, mx, mz, kx 和 kz 是相应能谷在 x 和 z 方向有效质量以及电子波矢。
在图 1 所示的坐标系中求解泊松方程:
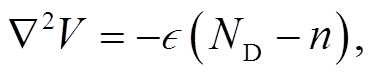(2)其中, 取x方向为载流子输运方向, y方向为垂直于沟道受量子约束的方向, z 方向规定为宽度方向, 不受量子约束; ϵ 为沟道材料的介电常数; V 代表电势; ND 代表半导体器件中电离施主浓度, 在本文模拟的器件中沟道未掺杂为 0; n 代表器件中电子浓度, 可以根据电子波函数计算, 公式为
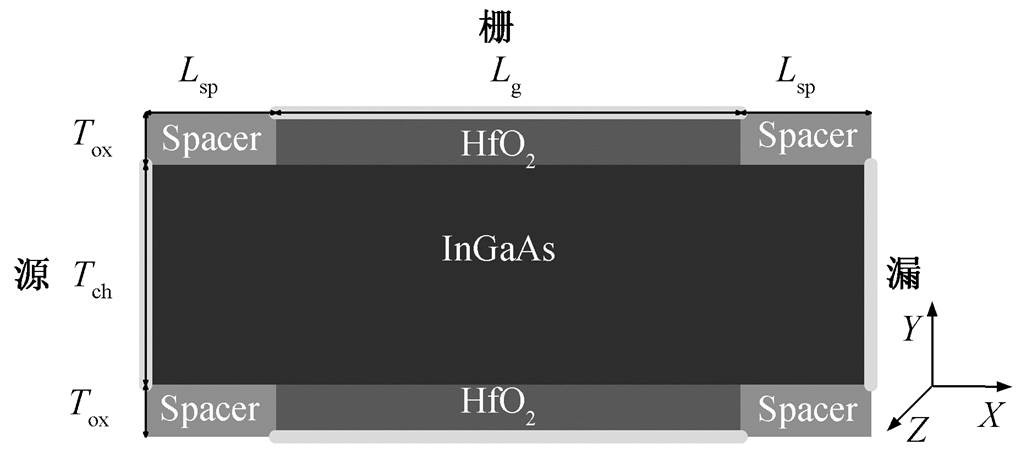
图1 肖特基源漏双栅MOSFET
Fig. 1 Schottky source/drain double gate MOSFET
表1 不同能谷的有效质量及非抛物性因子[15]
Table 1 Effective mass and non-parabolicity of InGaAs[15]
能谷ml/m0mt/m0α/eV−1 Γ0.0460.0461 L1.900.0750.5
(3)其中, 下角标 i 按照一定的粒子–网格耦合方法遍历位于网格 x 中的粒子, wi 是粒子 i 的权重, ψx(y)是网格 x 处粒子 i 所处子带的归一化波函数, dx 是 x 处网格的宽度, Ty=Tch+2×Tox 是整个沟道的厚度。
在固定的横坐标为 x 处, 沿 y 方向的薛定谔方程为
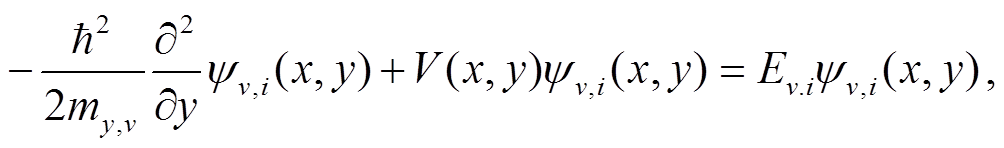(4)其中,my,v为能谷 v 中载流子在 y 方向上的有效质量, 
Vv,i(x, y)和Ev,i(x)分别为在能谷 v 中第 i 条子带位于 x处的波函数与特征能量。由于量子约束的作用, 载流子在约束方向(即 y 方向)上的能量不再连续, 因此在原本连续的能谷中分裂出子带。图 2 展示在不同漏压 Vds 下, 沟道电子第一子带随 x 坐标的变化。
式(2)和(4)相互耦合, 由此可以得到在量子约束情况下的器件中的子带、波函数和器件中电势的分布。子带和波函数用来计算不同区域电子的散射率, 电势分布决定电子在器件中运动的加速度。结合蒙特卡洛方法求解波尔兹曼方程模拟载流子的输运过程, 从而实现器件电学特性的模拟。
基于泊松–薛定谔方程自洽求解到的子带 Ev,j (x)和波函数 ψv,j(x, y), 可以求得当电子在 x 附近时的散射率 γ(x)。多子带系综蒙特卡洛模拟考虑的散射机制包括非极性声学声子散射(AP)、非极性光学声子散射(OP)、极性光学声子散射(POP)、表面粗糙散射(SR)和合金无序散射(AD)。
对于能谷 v 内从子带 i 到子带 j 的准弹性谷内非极性声学声子散射, 散射率[16–18]为
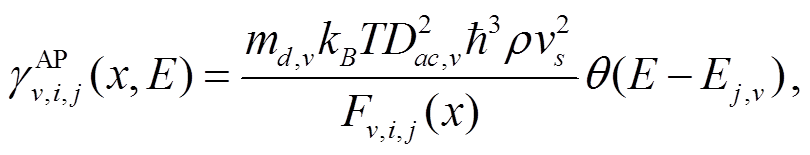(5)其中, Dac,v 是能谷 v 中的等效声学形变势因子, md,v是能谷 v 的态密度有效质量, ρ 是密度, vs 是声速, kB是玻尔兹曼常数, T 是晶格温度, θ(E)是阶跃函数, Fv,i,j(x)是 x 处从初态 i 到终态 j 的形貌因子, 计算公式如下:
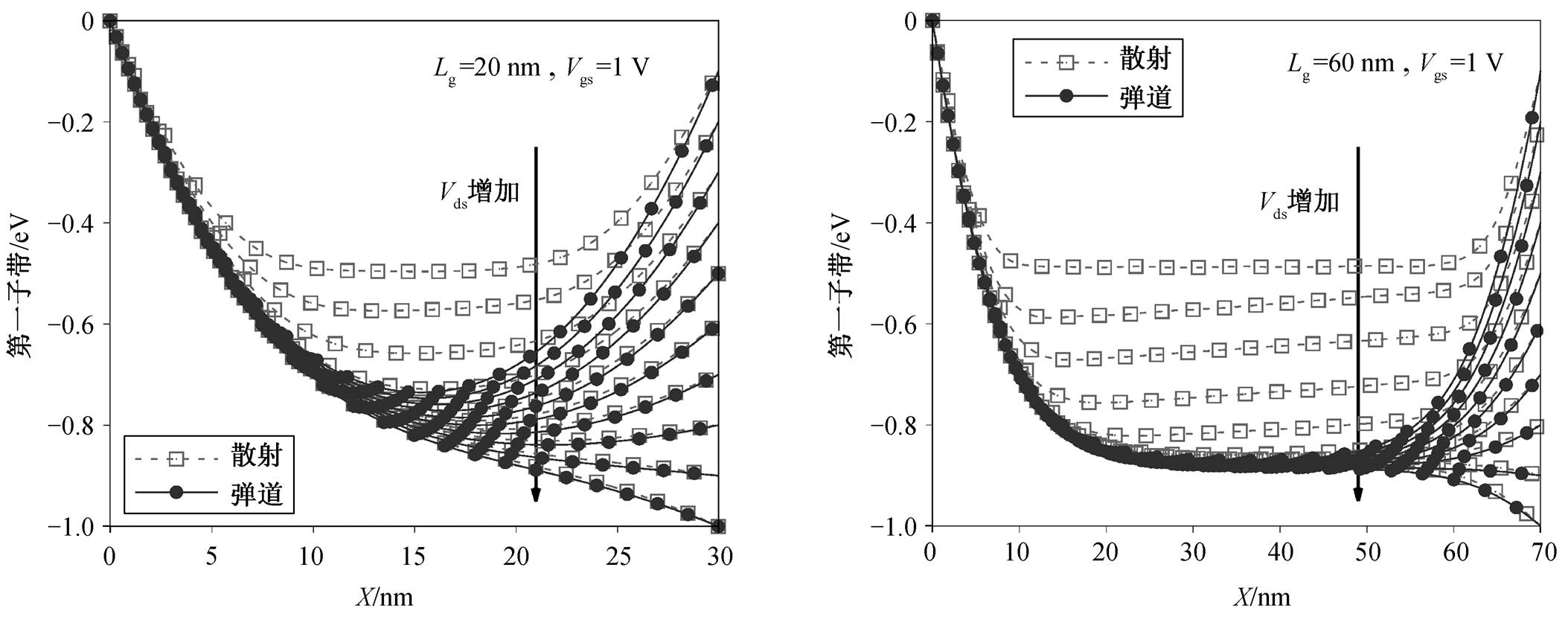
图2 沟道电子第一子带随x坐标的变化
Fig. 2 First sub-band of channel electron at varying x positions
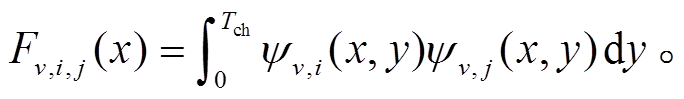(6)对于从能谷 vi 的子带 i 到能谷 vf的子带 j 的非极性光学声子散射, 散射率[16–18]计算公式为
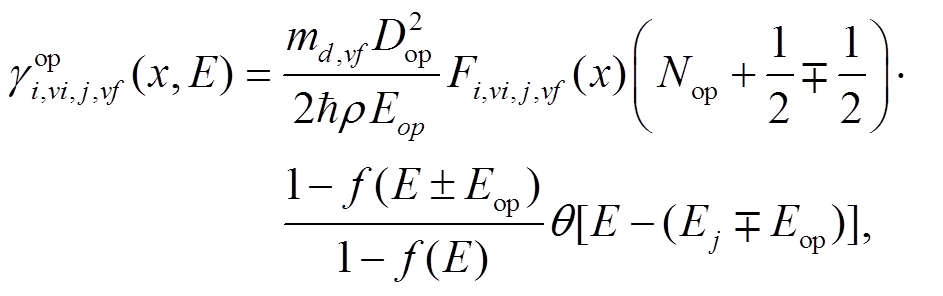(7)
其中, Dop, Dop 和Nop 分别为形变势、光学声子能量和占据数, f (E)是费米狄拉克分布函数。在 InGaAs等 III-V 化合物半导体中, 考虑 Γ 与 L 谷间以及 L 谷间的非极性光学散射。
对于 InGaAs 等 III-V 化合物半导体, 考虑能谷v 中从子带 i 到子带 j 的极性光学散射, 散射率[16,18–19]计算公式为
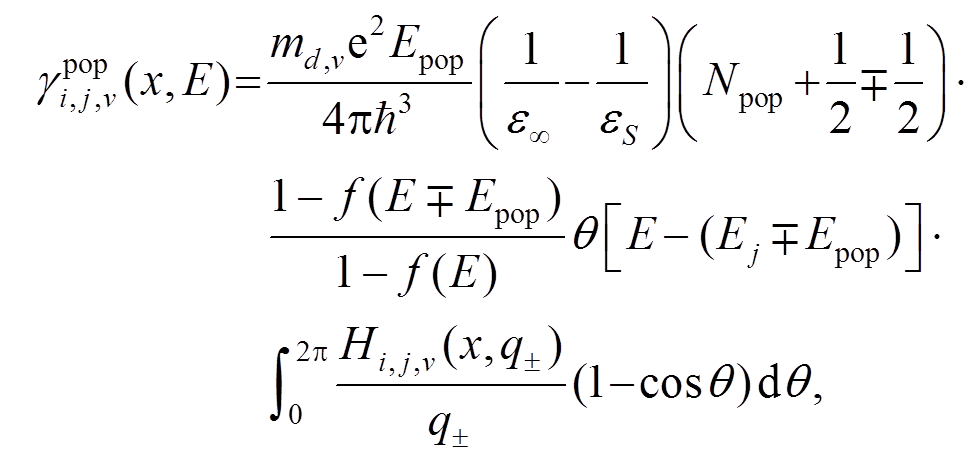(8)其中, Epop 和 Npop 是极性光学声子能量和占据数, ϵ∞和 ϵS 分别为高频和静态介电常数, q 是初态和终态电子波矢的差值。Hi,j,v(x, q)由下式给出:
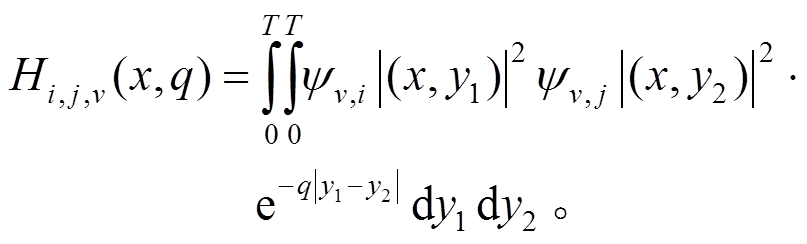(9)
表面粗糙(SR)散射的矩阵元正比于界面粗糙的谱密度。能谷 v 内子带 i 到子带 j 的散射矩阵元[20–21]计算公式为
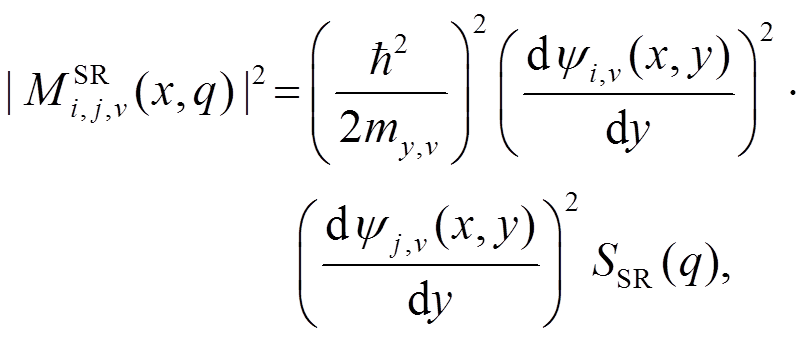(10)其中, my,v 是能谷 v 中的限域有效质量, S(q)是界面粗糙谱密度, 假设为下式[16]:
(11)
其中Δ和 L 是界面粗糙的幅度和关联长度。只考虑谷内 SR 散射, 能谷 v 中从子带 i 到子带 j 的 SR 散射率计算公式为
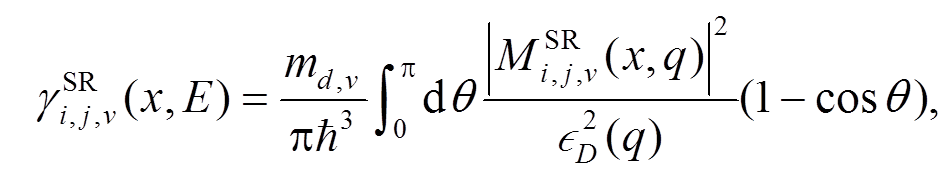(12)其中, M 是 SR 散射矩阵元, ϵD 是为计入静电屏蔽的静态界电函数, 近似为 1。
合金无序散射由多元化合物中带边的涨落引起, 对于能谷 v 子带 i 的合金无序散射, 散射率[16–18]计算公式为
(13)其中, x1=0.53, a 是 InGaAs 的晶格常数, V0 是合金散射势。
InGaAs 的散射率参数如表 2 所示。图 3 给出InGaAs 半导体材料散射率与电子能量的关系, 可以看出, 表面粗糙散射是这类 III-V 半导体材料中的主要散射机制, 特别是在电子能量较低时。
金属注入半导体的隧穿电流可以通过下式来计算:
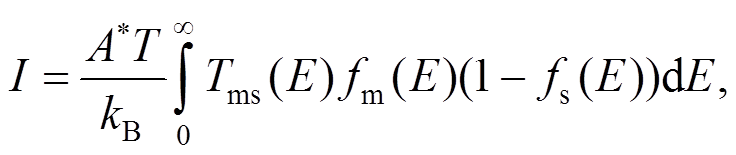(14)其中, A*是有效理查德孙常数; fm 和fs分别为金属和半导体的费米分布函数; Tms 为透射系数, 对于场发射电流, 由 WKB 近似给出[23]:
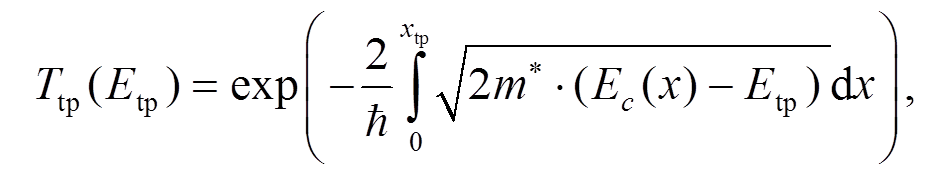(15)
表2 InGaAs的散射参数[15,22]
Table 2 Scattering parameters of InGaAs[15,22]
散射机制参数 声学非极性Dac,Γ =5.42 eV, Dac,L=9.0 eV vs =4253 m/s, ρ=5506 kg/m3 光学非极性Eop,Γ-L=19.9 meV, Dop,Γ-L=5.43×108 eV/cm Eop,L-L=21.9 meV, Dop,L-L=6.16×108 eV/cm 光学极性Epop=33 meV, ϵ∞=13.9, ϵs =11.6 合金无序a=5.858, V0=1.6 eV 表面粗糙Δ=1.76 nm, L=2 nm
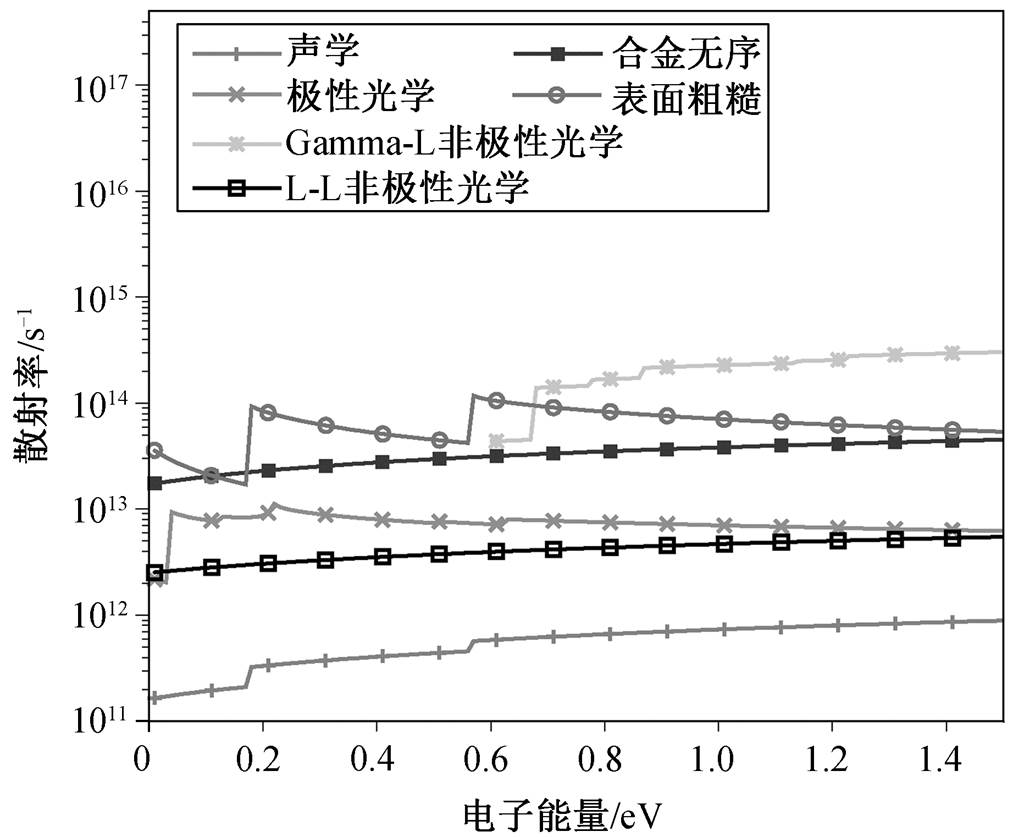
图3 InGaAs的散射率
Fig. 3 Scattering rate of InGaAs
其中, m*是电子的隧穿有效质量, Ec(x)是子带的能量, Etp是发生隧穿的电子的能量, xtp 是发生隧穿后电子的位置, 满足 Ec(xtp)=Etp。对于热发射电流, 透射系数为1。
利用建立的多子带系综蒙特卡洛模拟程序, 模拟不同栅长的纳米尺度 InGaAs 肖特基源漏 MOS-FET 的直流和瞬态特性, 分析不同工作模式下散射的影响。
图 4 给出不同栅长的 InGaAs 肖特基源漏 MOS-FET 在弹道和有散射情况下的输出与转移特性曲线。由图 4(a)可见, 在较低的源漏偏压下, 散射对Ids 的影响显著; 而在高源漏偏压下, 散射的存在对漏端电流几乎没有影响。仿真器件的 Ids 没有显示出随栅长减小而增加, 这是由于更长的栅具有对源端隧穿势垒更强的控制能力。用考虑散射时的 Ids与无散射时的 Ids 的比值 Ids,scattering/Ids,ballistic表示器件的弹道因子。图 5 为不同栅长的 InGaAs 肖特基源漏 MOSFET 弹道因子随 Vds 的变化。可以看出, 弹道因子随 Vds 的增大而增大, 在 Vds=0.6V 以上时, 器件的弹道因子接近 1。
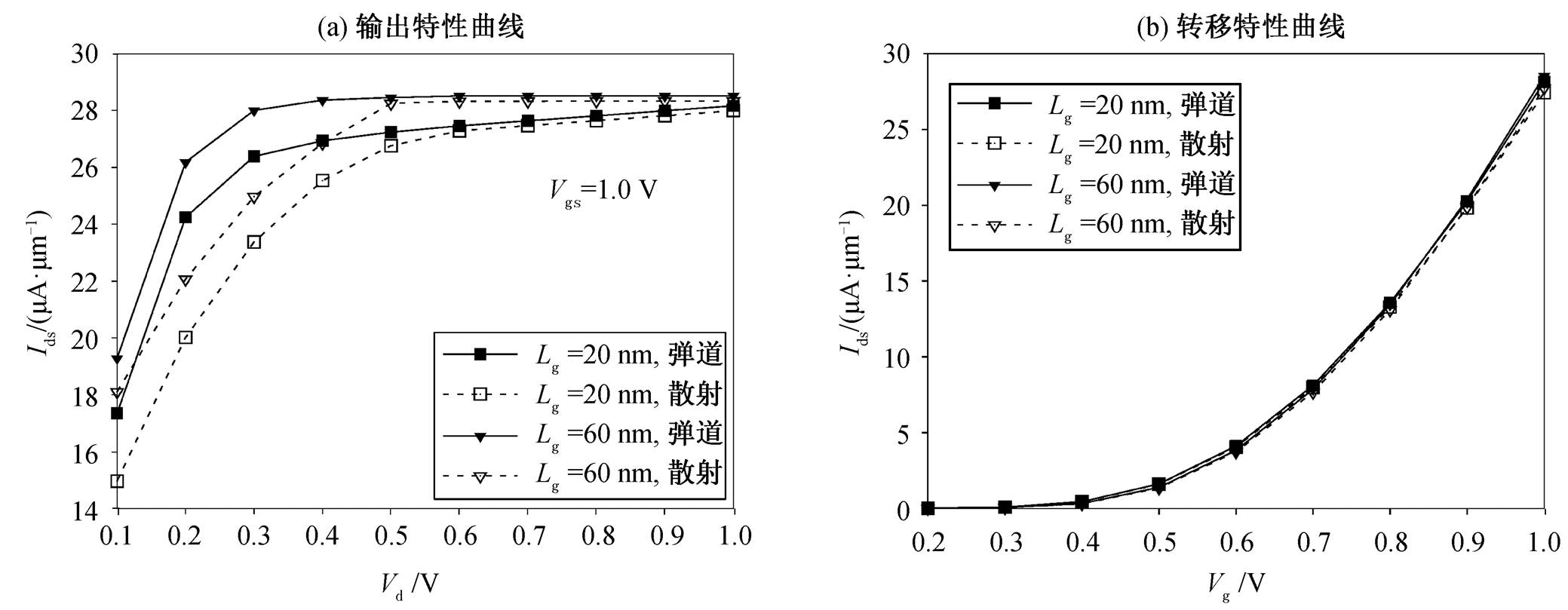
图4 肖特基晶体管的输出特性曲线和转移特性曲线
Fig. 4 Output and transfer characteristics of Schottky barrier MOSFET
图 6 给出不同沟长时, 高(1.0V)、低(0.2V) Vds下器件中沟道中央电势分布和载流子平均漂移速度的分布。可以看出, 散射明显地减小了沟道中电子的平均漂移速度。在高 Vds 下, 无论是 20nm 的器件还是 60nm 的器件, 尽管散射使电子平均漂移速度减小, 但源端势垒并没有因为散射的存在而发生较大的变化, 源端隧穿注入基本上不变, 器件具有接近 1 的弹道因子。在低 Vds 下, 器件中电子平均漂移速小, 电子浓度高, 散射造成的电子漂移速度和浓度分布的改变造成源端肖特基势垒展宽, 特别是在栅长为 20nm, 栅对沟道的控制比 60nm 更弱时。因此, 在Vds=0.2V时, 器件的弹道因子较低。
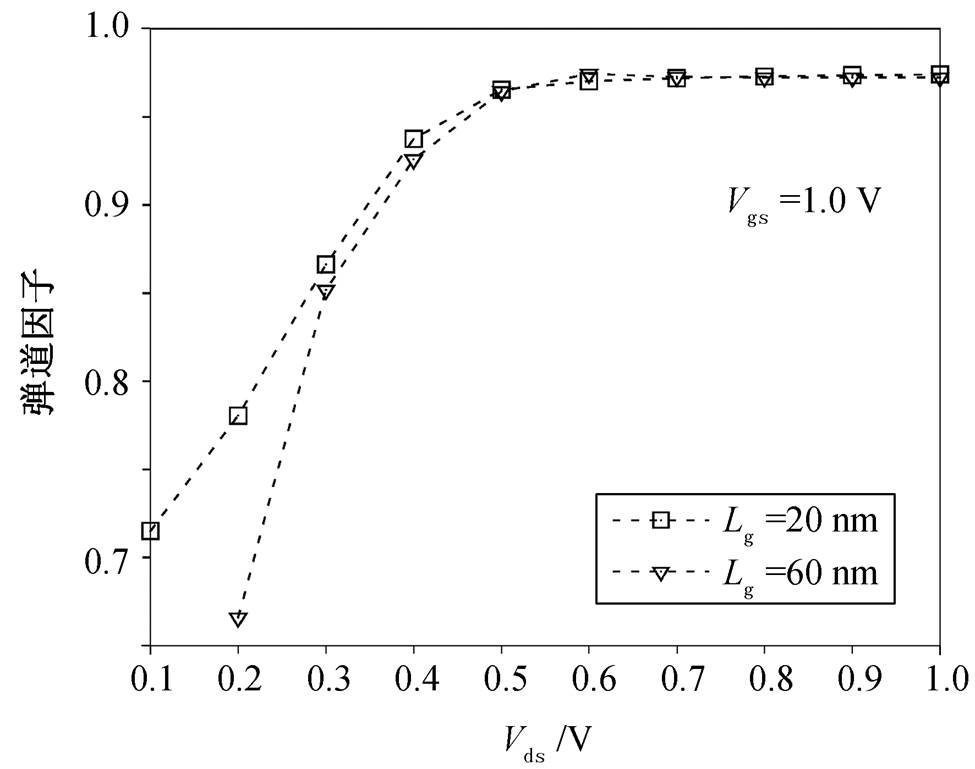
图5 不同Vds下肖特基晶体管的弹道因子
Fig. 5 Ballistic ratio of Schottky barrier MOSFET under varying Vds
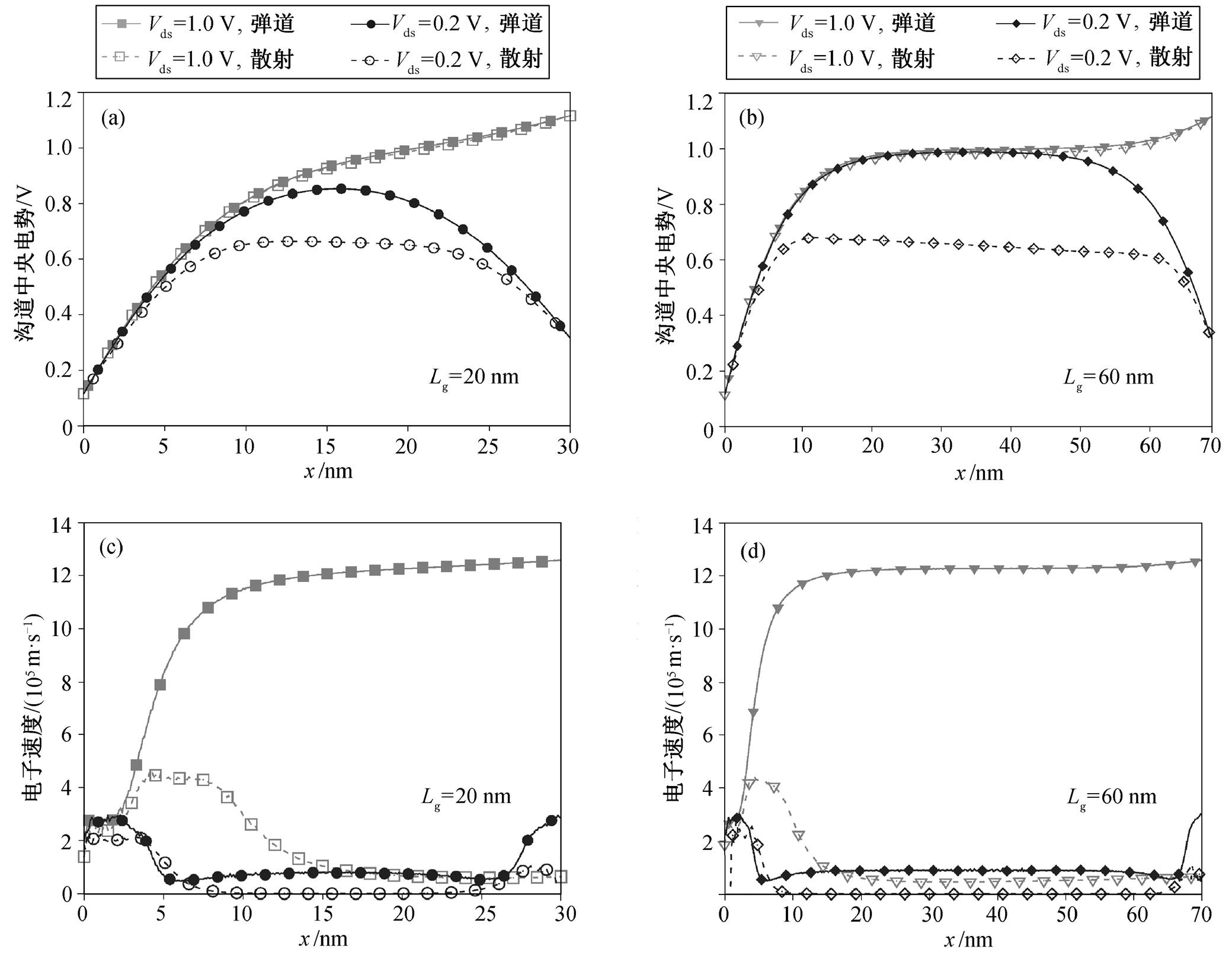
图6 肖特基晶体管的沟道中央电势分布和平均漂移速度分布
Fig. 6 Electric potential at middle-channel and electron velocity of Schottky MOSFET
图 7 给出 InGaAs 肖特基势垒场效应晶体管中不同能谷和子带电子占总电子数目的比例。InGaAs中 Γ 谷和 L 谷带底的差距 E 约为 0.45eV。当 Vds 较小(Vds<0.5V)时, 沟道中的电子主要为 Γ 谷电子, 散射对电子漂移速度的影响主要表现为电子动能和速度方向的改变; 当 Vds 超过 ΔE 较多(Vds=1V)时, 由于较强 Γ-L 非极性光学散射带来的谷间转移, 沟道中 L 谷电子增多, L 谷电子有更大的有效质量和较小的平均漂移速度, 这是高 Vds 时沟道电子速度下降的主要原因。
图 8 给出在栅电压维持在 1V, 漏端电压由 0.2 V 突变到 0.4~1.0V 时, InGaAs 肖特基源漏 MOSFET源端和漏端电流以及沟道总电荷随时间的变化。低漏压下, 沟道中载流子浓度比高漏压下更大, 漏端施加由低到高的突变电压时, 沟道电子被突然加速, 造成短时间内漏端电流的过冲; 源端电流主要由金属到半导体注入的电流组成, 因而不会表现出短时间内电流的过冲。图 9 给出不同沟长和 Vds 下, 漏端过冲电流的峰值和漏端电流在达到过冲峰值后, 重新恢复到高漏压下稳定电流的 10%范围内(即达到稳定电压的 110%)需要的时间。可以看出, 突变后的漏端电压越强, 过冲电流的峰值越高, 上升时间和恢复时间也越短。散射的存在显著地增大了过冲电流峰值和恢复时间, 是由于低 Vds 下散射显著地增加了沟道电子数目, 而高 Vds 下沟道电子数目基本上相同, 因此存在散射时, 更多的电子需要从漏端飞出, 以便重新达到稳定状态。
根据蒙特卡洛模拟得到的电子平均渡越时间τT, 可以计算得到器件的截止频率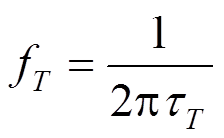
。图10(a)给出仿真器件的截止频率。可以看出, 模拟器件的截止频率在有散射时可以达到 100GHz 量级, 无散射时可达 1THz量级。图 10(b)给出 20nm/60nm 沟长时, 有散射时与无散射时截止频率的比值。可以看出, 沟长较长时, 散射会造成更大的截止频率降低。
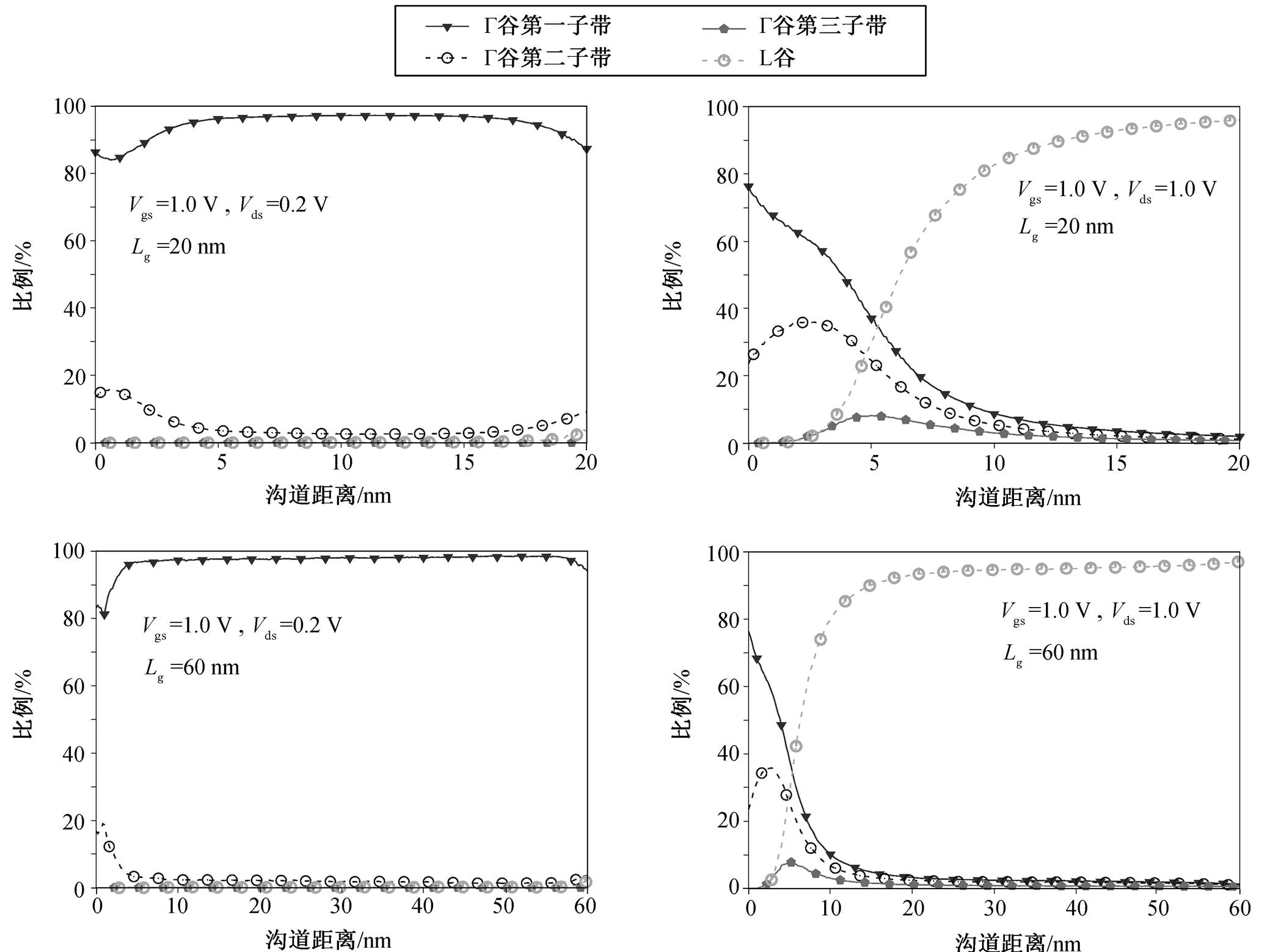
图7 20/60nm 肖特基晶体管在 Vds =0.2/1.0V 时不同能谷和子带电子的百分比
Fig. 7 Percentage of each valley and sub-band of 20/60 nm Schottky barrier MOSFET under Vds=0.2/1.0 V
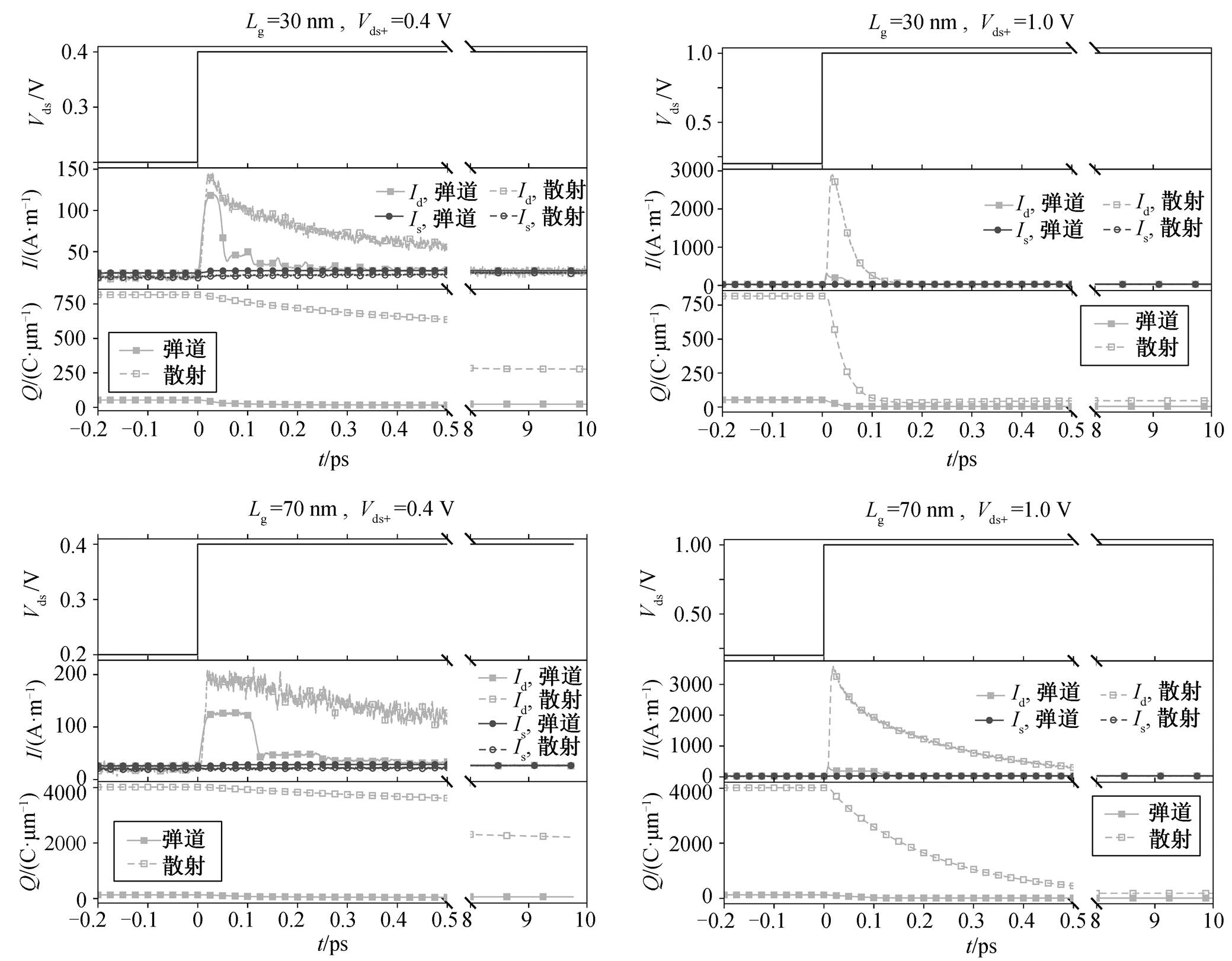
图8 漏极施加突变电压, 肖特基晶体管沟道电荷、漏端电流和源端电流的变化
Fig. 8 Response of Schottky MOSFET’s channel charge, drain current and source current with drain step voltages
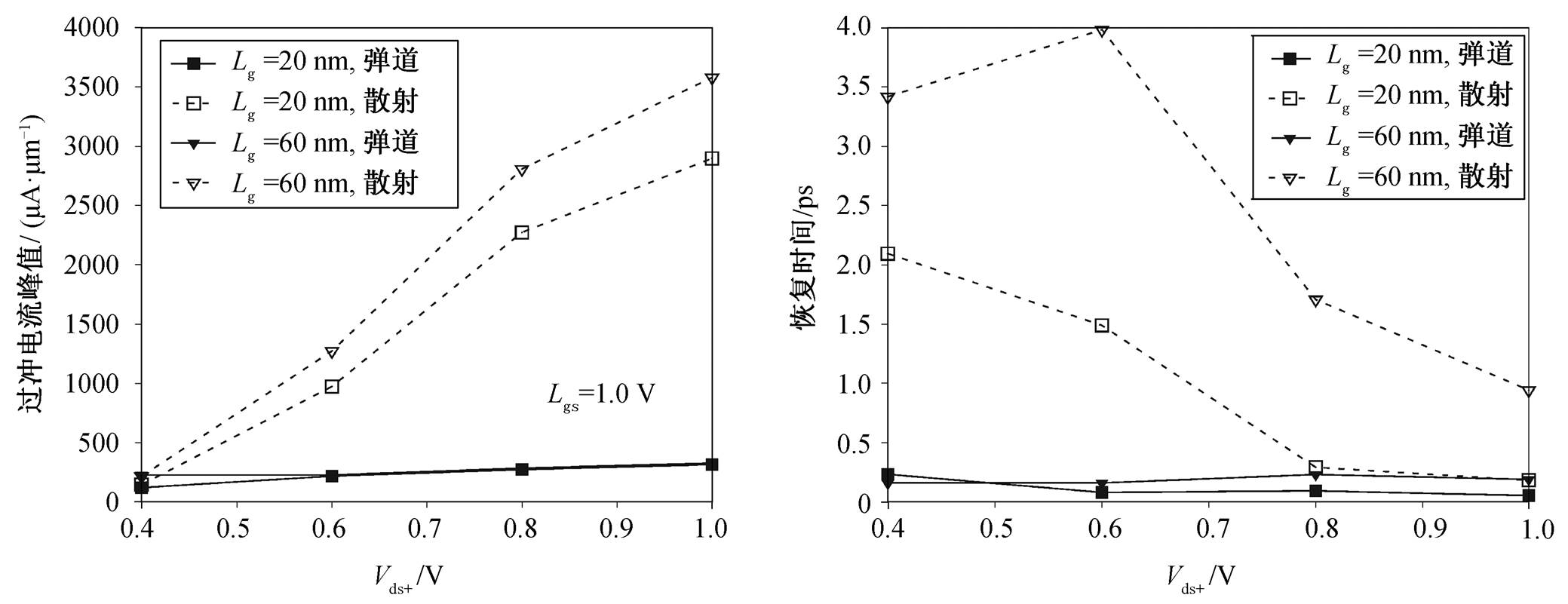
图9 过冲电流峰值和恢复时间随沟长和偏置电压的变化
Fig. 9 Peak overshot current and recover time at different channel lengths and drain step voltages
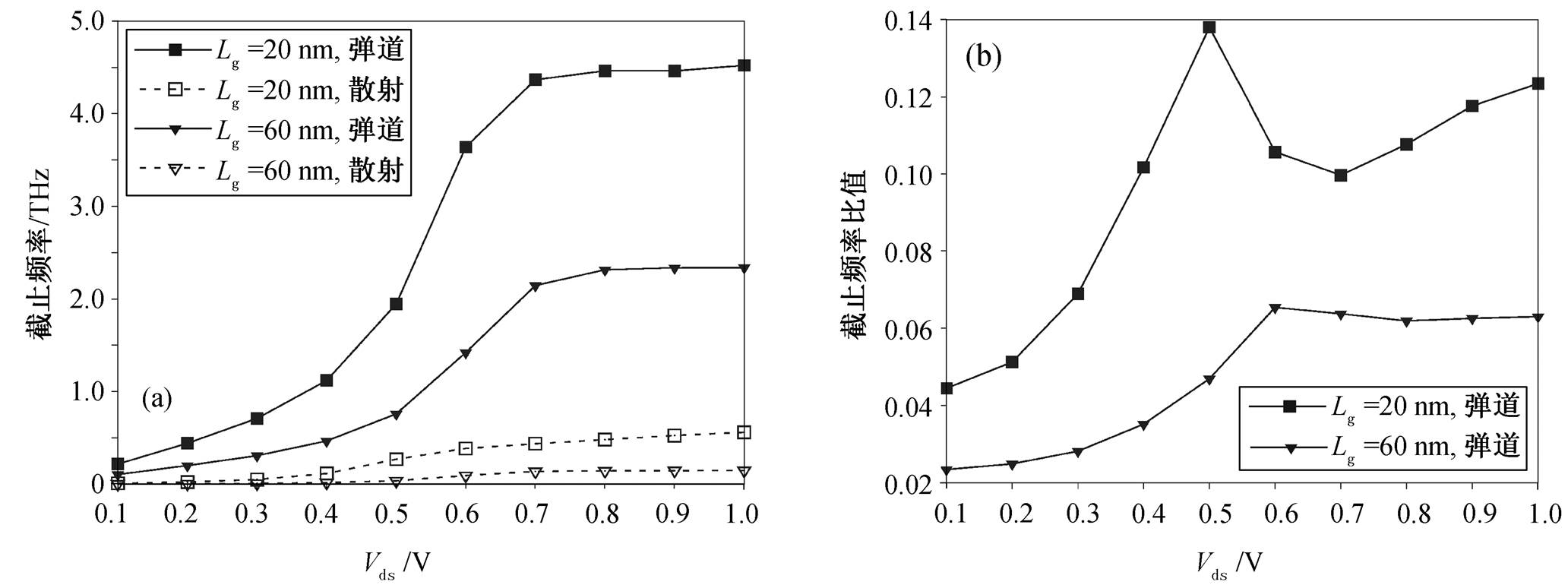
图10 截止频率随沟长和漏端电压的变化(a)以及有散射时截止频率占无散射时截止频率的比值(b)
Fig. 10 Cutoff frequency at different channel lengths and drain step voltages (a) and the ratio of scattering cutoff frequency vs. ballistic cutoff frequency (b)
本研究采用多子带系综蒙特卡洛方法, 对InGaAs 肖特基源漏 MOSFET 进行模拟, 研究不同栅长时 InGaAS 肖特基源漏 MOSFET 稳态下的输运特性和转移特性, 分析瞬态下沟道电子和源、漏端电流对外加阶跃电压的响应、器件的截止频率以及散射对 InGaAs 肖特基源漏 MOSFET 特性的影响。结果显示, InGaAs 肖特基源漏 MOSFET 可以在 THz频率下工作; 散射对 InGaAs 肖特基源漏 MOSFET输出特性和转移特性影响较小, 但是会增加器件对漏端阶跃电压的响应时间, 减小器件的截止频率。本文模拟结果将有助于优化设计 InGaAs 肖特基源漏MOSFET。
参考文献
[1] Bashir F, Alharbi A G, Loan S A. Electrostatically doped DSL Schottky barrier MOSFET on SOI for low power applications. IEEE Journal of the Electron Devices Society, 2017, 6: 19–25
[2] Kumar P, Bhowmick B. Scaling of dopant segrega-tion Schottky barrier using metal strip buried oxide MOSFET and its comparison with conventional de-vice. Silicon, 2018, 10(3): 811–820
[3] Prakash A, Ilatikhameneh H, Wu P, et al. Under-standing contact gating in Schottky barrier transistors from 2D channels. Scientific Reports, 2017, 7(1): no. 12596
[4] del Alamo J A, Antoniadis D A, Lin J, et al. III- V MOSFETs for future CMOS // 2015 IEEE Com-pound Semiconductor Integrated Circuit Symposium (CSICS). New Orleans, 2015: 1–4
[5] Svensson J, Dey A W, Jacobsson D, et al. III-V nanowire complementary metal-oxide semiconductor transistors monolithically integrated on Si. Nano Letters, 2015, 15(12): 7898–7904
[6] Schmid H, Cutaia D, Gooth J, et al. Monolithic integration of multiple III-V semiconductors on Si for MOSFETs and TFETs // 2016 IEEE International Electron Devices Meeting (IEDM). San Francisco, 2016: 3–6
[7] Chelliah C R J, Swaminathan R. Current trends in changing the channel in MOSFETs by III-V semicon-ducting nanostructures. Nanotechnology Reviews, 2017, 6(6): 613–623
[8] Zhao X, Heidelberger C, Fitzgerald E A, et al. Sub-10-nm-diameter InGaAs vertical nanowire MOSFETs: Ni Versus Mo contacts. IEEE Transactions on Elec-tron Devices, 2018, 65(9): 3762–3768
[9] Schwarz M, Calvet L E, Snyder J P, et al. On the physical behavior of cryogenic IV and III-V Schottky barrier MOSFET devices. IEEE Transactions on Electron Devices, 2017, 64(9): 3808–3815
[10] Ahangari Z. Impact of indium mole fraction on the quantum transport of ultra-scaled InxGa1–xAs double-gate Schottky MOSFET: tight-binding approach. Ap-plied Physics A, 2016, 122(2): no. 69
[11] Du Gang, Liu Xiaoyan, Xia Zhiliang, et al. Monte Carlo simulation of p-and n-channel GOI MOSFETs by solving the quantum Boltzmann equation. IEEE Transactions on Electron Devices, 2005, 52(10): 2258–2264
[12] Du Gang, Liu Xiaoyan, Han Ruqi. Quantum Boltz-mann equation solved by Monte Carlo method for nano-scale semiconductor devices simulation. Chinese Physics, 2006, 15(1): 177–181
[13] Zeng Lang, Liu Xiaoyan, Zhao Yuning, et al. A computational study of dopant-segregated Schottky barrier MOSFETs. IEEE Transactions on Nanotech-nology, 2009, 9(1): 108–113
[14] Zeng Lang, Liu Xiaoyan Liu, Du Gang, et al. A Monte Carlo study of ambipolar Schottky Barrier MOSFETs // 2009 13th International Workshop on Computa-tional Electronics. Beijing, 2009: 1–4
[15] 俄罗斯科学院 Ioffe 物理技术研究所. New semi-conductor materials. Biology systems. Characteris-tics and properties [EB/OL]. (1999) [2020–10–08]. http://www.ioffe.ru/SVA/NSM/
[16] Esseni D, Palestri P, Selmi L. Nanoscale MOS transistors: semi-classical transport and applications. Cambridge: Cambridge University Press, 2011
[17] Esseni D, Abramo A, Selmi L, et al. Physically based modeling of low field electron mobility in ultrathin single-and double-gate SOI n-MOSFETs. IEEE Tran-sactions on Electron Devices, 2003, 50(12): 2445–2455
[18] Poljak M, Jovanovic V, Grgec D, et al. Assessment of electron mobility in ultrathin-body InGaAs-on-insulator MOSFETs using physics-based modeling. IEEE Transactions on Electron Devices, 2012, 59(6): 1636–1643
[19] Ferry D K, Goodnick S M, Bird J. Transport in nano-structures. Cambridge: Cambridge University Press, 2009
[20] Esseni D, Abramo A. Modeling of electron mobility degradation by remote Coulomb scattering in ultrathin oxide MOSFETs. IEEE Transactions on Electron De-vices, 2003, 50(7): 1665–1674
[21] Jin S, Fischetti M V, Tang T W. Modeling of surface-roughness scattering in ultrathin-body SOI MOSFETs. IEEE Transactions on Electron Devices, 2007, 54(9): 2191–2203
[22] Mateos J, González T, Pardo D, et al. Improved Monte Carlo algorithm for the simulation of/spl delta/-doped AlInAs/GaInAs HEMTs. IEEE Transac-tions on Electron Devices, 2000, 47(1): 250–253
[23] Sun L, Liu X Y, Liu M, et al. Monte Carlo simulation of Schottky contact with direct tunnelling model. Semiconductor science and technology, 2003, 18(6): 576–581
Multi-subband Ensemble Monte Carlo Simulation of InGaAs Schottky Barrier MOSFETs
Abstract With the help of a multi-subband, multi-valley ensemble Monte Carlo simulator, which takes into account of multiple scattering mechanisms present in nano-scale MOSFET channel’s two-dimensional electron gas, InGaAs Schottky barrier MOSFET is simulated. The results show that under steady state, although scattering alters its carrier density, velocity and electric potential distribution, Schottky barrier MOSFET’s output and transfer characteristic is merely impacted by scattering. When a step voltage is applied to the device’s drain contact, scattering increases the device’s peak over-shoot current and transition time. Besides, scattering also reduces the cut-off frequency, especially for short channel device.
Key words InGaAs; Schottky barrier MOSFET; ensemble Monte Carlo
doi: 10.13209/j.0479-8023.2020.106
国家自然科学基金(61674008)资助
收稿日期: 2019–11–27;
修回日期: 2020–06–28