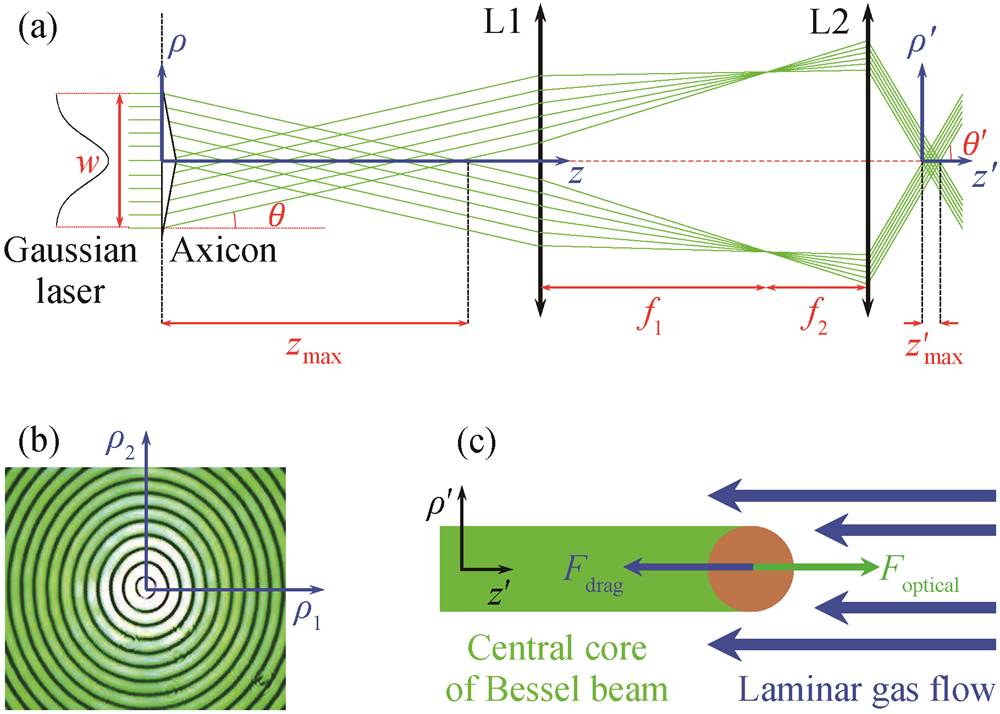
图 1 贝塞尔光的形成光路(a)、贝塞尔光垂直于光轴的形态(b)以及颗粒物在贝塞尔光镊中的受力(c)
Fig. 1 Formation light path of Bessel beam (a), pattern of Bessel beam perpendicular to the optical axis (b) and forces exerted on the particle levitated by the Bessel beam optical tweezer (c)
摘要 搭建贝塞尔光镊颗粒物观测系统。通过圆锥透镜产生贝塞尔光, 利用贝塞尔光施加的光压力和反向气流施加的阻力, 稳定地悬浮气溶胶颗粒物。结合弹性光散射信号, 实现对气溶胶单颗粒粒径和折射率的测量。该系统还可用于研究不同环境条件下气溶胶的吸湿性、挥发性以及折射率等物理化学性质。
关键词 贝塞尔光; 光镊; 气溶胶单颗粒
对单个气溶胶颗粒的测量可以将气溶胶块体性质与颗粒个体联系起来[1], 减少块体测量中尺度和化学成分的复杂性, 更精确地探讨与气溶胶相关的问题。目前, 对气溶胶单颗粒的采样分析有基底承载测量[2‒4]和悬浮测量[5‒7]等方法, 其中悬浮测量法更具优势: 一方面, 样品被悬浮, 不与任何界面接触, 避免机械损伤; 另一方面, 处于悬浮状态的样品更接近气溶胶颗粒在环境中的实际状态, 可以更真实地再现气溶胶颗粒在环境中经历的过程。
根据悬浮的原理不同, 悬浮测量分为光悬浮(光镊)[5]、声悬浮[6]和电悬浮[7]等方法。光镊法可以稳定地悬浮粒径约 0.5μm 到约 10μm 的颗粒物, 该粒径尺度与实际环境中积聚模态及粗模态颗粒物一致。另外, 光镊可以对颗粒物进行精细的微操作。这些特点使得光镊成为研究气溶胶颗粒的一种有效手段, 广泛应用于气溶胶表面张力和黏度[8‒9]、气溶胶光学性质[10‒11]、水汽分子界面吸附[12‒13]、气溶胶热力学和吸湿性[14‒15]、异相化学和气溶胶老化[16‒17]、气溶胶玻璃态和无定形态[18‒19]以及颗粒物入肺[20]等方面的研究。
根据原理不同, 目前用于大气科学研究的光镊技术分为高斯光镊[14]和贝塞尔光镊[21]。高斯光镊技术成熟较早, 已商品化, 主要用于研究粗模态颗粒物[1]。相比之下, 贝塞尔光镊技术成熟较晚[22]。Arlt 等[23] 2001 年首次在液相环境中利用贝塞尔光捕获直径为 1μm 和 5μm 的小球, 并操纵被捕获小球以 5~10m/s 的速度移动。他们将激光经透镜组准直扩束后送入圆锥透镜, 产生贝塞尔光, 再经透镜组调整后, 照射在盛有小球的溶液中。2002 年, Garces-Chavez 等[24]使用同样的设计, 利用贝塞尔光自重构的性质, 实现在两个相距约 3mm 的样品平面上同时捕获微粒。
上述设计不能在气相环境中捕获颗粒物。并且, 相比于对被捕获颗粒物进行观测, 更侧重对颗粒物进行微操作, 因此在气溶胶研究中的作用十分有限。贝塞尔光施加在颗粒物上的光压力无法让颗粒物受力平衡, 要在气相中稳定地悬浮颗粒物, 需要引入其他外力。2006 年, Summers 等[25]改进 Arlt等[23]的设计, 在贝塞尔光传播方向引入反向的气体稳定层流。这种巧妙的设计既让颗粒物因同时受到方向相反的光压力和气流阻力而保持平衡, 又为颗粒物提供气相环境, 使贝塞尔光镊可以在气相中捕获颗粒物。此外, Carruthers 等[26] 2010 年发明利用两束反向的贝塞尔光来平衡颗粒物的方法, 也在气相中成功地悬浮颗粒物。
实现在气相中稳定悬浮颗粒物后, 就要对颗粒物进行测量。2009 年, Meresman 等[27]利用 CCD 相机(Charge Coupled Device Camera), 观测到颗粒物的散射光强分布, 借助米散射理论[28], 从散射光强分布反演颗粒物的粒径, 首次实现对贝塞尔光镊悬浮颗粒物的测量。2013 年, Walkers 等[11]将衰荡腔与贝塞尔光镊结合, 实现对单颗粒消光截面的测量, 并根据米散射理论[28], 从散射光强反演得到粒径。反演粒径时, 需要预先确定颗粒物的折射率。2015年之前, 对折射率的处理要么是用给定值, 要么是将折射率参数化成相对湿度的函数, 这些处理方法都需要已知颗粒物的化学组分。2015 年, Cotterell等[29]基于最大皮尔森相关的思想编写算法, 直接从散射光强同时得到粒径和折射率。实际环境中气溶胶颗粒物成分复杂, 这种不需要已知颗粒物的化学组分或相对湿度, 就能得到粒径和折射率的方法在气溶胶研究中具有现实意义。
目前贝塞尔光镊的应用场景比高斯光镊少, 主要应用在气溶胶热动力学(如吸湿性和挥发性[30)、气溶胶光学(如气溶胶消光效率[29]和折射率参数化[31])方面, 应进一步拓展贝塞尔光镊的应用范围。贝塞尔光镊可以悬浮的颗粒物粒径接近积聚模态, 积聚模态气溶胶在实际大气中对环境及辐射都有重要影响, 因此利用贝塞尔光镊表征颗粒物具有实际意义。鉴于我国目前还没有贝塞尔光镊相关技术, 我们自主搭建贝塞尔光镊系统, 实现对气溶胶单颗粒的捕捉和测量。
如图 1(a)所示, 激光(Gaussian laser)沿 z 轴正方向传播, 垂直于 z 轴的平面为横截面。激光在横截面的光强分布为二维高斯分布, 中心强, 周围弱。激光通过圆锥透镜 Axicon 后, 波矢方向改变的角度为 θ, 形成贝塞尔光[22]。圆锥透镜是一种特殊的透镜, 形态为圆锥体, 圆锥体的轴与 z 轴一致, 与 z 轴正交的平面在图 1(a)中记为平面r和平面r′, 在图1(b)中记为平面r1r2。贝塞尔光在 zmax 区域内可被观测到, 它的横截面由中心的亮核与一系列围绕中心亮核的同心圆环构成(图 1(b)), 每个圆环上的光功率与中心亮核相同[32]。随着光束的传播, 贝塞尔光横截面的形态会发生变化, 在靠近圆锥透镜的某个位置为一个中心亮核和一个圆环(图 2(a))。随着远离圆锥透镜, 圆环数目增加。当与圆锥透镜的距离足够远时, 形如图 1(b)的结构消失(图 2(t))。在一定的距离内, 中心亮核的形态不发生变化, 即中心亮核在一定的距离内保持“准无衍射”, 这段距离称为传播距离[33], 在图 1(a)中标记为 zmax 和 z′max。当中心亮核内有颗粒物时, 中心亮核的光场将对颗粒物施加光压力[34], 在图 1(c)中用 Foptical 表示。当中心亮核的尺寸与颗粒物尺寸相当时, 光压力大到不可忽略。气溶胶颗粒尺寸为 μm 级, 可将凸透镜组中心亮核的尺寸缩小到 μm 级(如图 1(a)所示)。凸透镜 L1 和 L2 相距 f1+f2, f1 和 f2 分别是凸透镜 L1 和 L2的焦距, f1>f2, 这样的透镜组配置称为望远镜。在z′max 区域内将产生新的贝塞尔光, 中心亮核尺寸缩小f1/f2倍。
悬浮颗粒物, 要求其受力平衡。仅有贝塞尔光中心光核(Central core of Bessel beam)施加的光压力不能使颗粒物平衡, 需要引入其他外力。本文参考Summers 等[25]和 Preston 等[34]的方案, 如图 1(c)所示, 颗粒物处于 z′max 区域时, 受到贝塞尔光施加的正 z 方向的光压力。引入沿负 z 方向流动的气体层流(Laminar gas flow), 对颗粒物施加负 z 方向的斯托克斯阻力, 在图 1(c)中用 Fdrag 表示。适当地调整光强和气流流速, 当 Foptical=Fdrag 时, 颗粒物受力平衡, 被稳定地悬浮。
本研究搭建的贝塞尔光镊测量系统如图 3(a)所示, 图 3(b)展示实景。采用 532nm 激光作为光源, 激光依次经平面镜 M1 和 M2 反射后, 照射在凸透镜 L1 上。平面镜 M1 和 M2 的作用为准直经过凸透镜 L1 和 L2 的激光, 通过调整平面镜 M1 和 M2 的位置或仰角, 使激光依次经过凸透镜 L1 和 L2 的中心。凸透镜 L1 和 L2 组成一望远镜, 焦距分别为 f1= 75mm, f2=150mm, 相距f1+f2=225mm, 其作用是扩大激光横截面宽度 w (扩大倍数为 f2/f1=2), 进而增加贝塞尔光的传播距离zmax[35]:

图 1 贝塞尔光的形成光路(a)、贝塞尔光垂直于光轴的形态(b)以及颗粒物在贝塞尔光镊中的受力(c)
Fig. 1 Formation light path of Bessel beam (a), pattern of Bessel beam perpendicular to the optical axis (b) and forces exerted on the particle levitated by the Bessel beam optical tweezer (c)
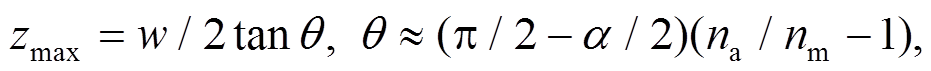
其中, na 和 nm 分别是圆锥透镜和介质的折射率, 本文中介质为空气; α 是圆锥透镜 Axicon 的顶角, 本文中 α = 178°。
激光经过扩束后, 依次经过平面镜 M3 和 M4反射, 照射在圆锥透镜 Axicon 上。平面镜 M3 和M4 的作用是准直经过 Axicon 的激光, 使激光沿着圆锥透镜的轴传播。本文使用的圆锥透镜 Axicon的顶角为 178°。
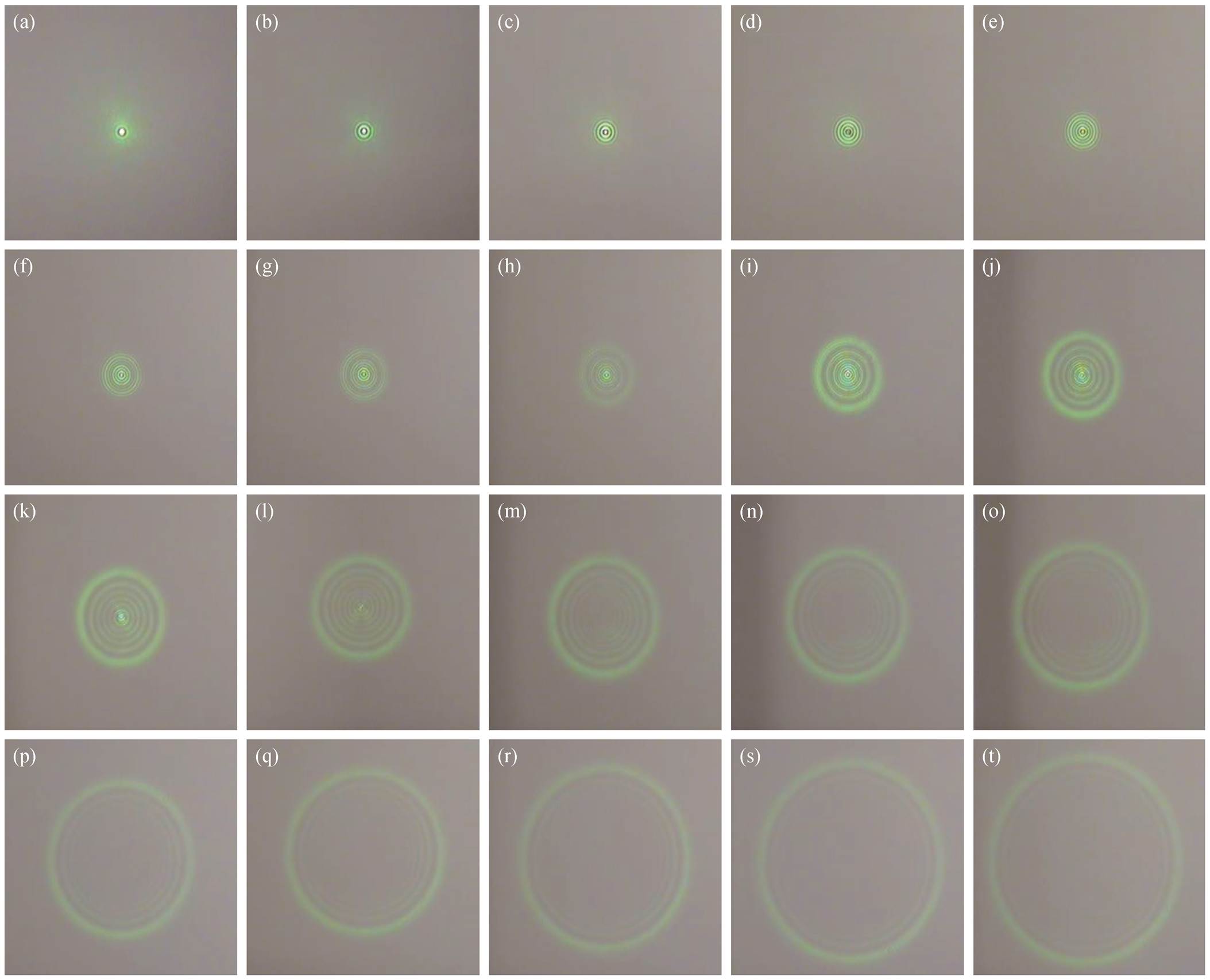
从(a)到(t), 依次远离圆锥透镜
图2 贝塞尔光横截面形态沿光轴的变化
Fig. 2 Variation of patterns of Bessel beam along the optical axis
激光经过圆锥透镜 Axicon 后, 在 Axicon 与凸透镜 L3 之间形成贝塞尔光。贝塞尔光的尺寸可用贝塞尔光中心亮核的半径 rB=2.4048/ksinθ [35]衡量, 其中 k 为波矢。当贝塞尔光用来捕获颗粒物时, 要求 rB 在微米级, 本文的圆锥透镜 Axicon 产生的贝塞尔光尺寸过大, 不能满足要求, 于是利用两个凸透镜 L3 和 L4 组成的望远镜来缩小 rB。贝塞尔光经过平面镜 M5 和 M6 反射后, 进入凸透镜 L3 和 L4 组成的望远镜中。平面镜 M5 和 M6 的作用是使光场中心可以分别经过凸透镜 L3 和 L4 的中心。凸透镜L3 和 L4 的焦距分别为 f3=300mm, f4=50.8mm, 相距f3+f4=350.8mm, rB 被缩小为原来的 f4/f3=1/5.9。新的贝塞尔光在凸透镜 L4 上方的样品池(Sample Cell)中形成, 用于捕获微粒。
平面镜 M7 的作用是改变光路, 使新生成的贝塞尔光竖直向上, 方便观测颗粒物。凸透镜 L4 与样品池之间有一透明载玻片, 用来防止气溶胶样品污染凸透镜 L4。样品池是颗粒物被悬浮的地方, 是两端连通的中空结构, 用于引导并保持层流, 是捕获颗粒物的关键部位。为了保持层流, 国外的样品池常为长方体结构, 如 1cm × 1cm × 10cm [26]。本文的样品池为圆柱体结构, 长 10cm, 横截面直径为 1cm。与长方体相比, 光滑的圆柱体结构没有直角, 更有利于层流的保持。
在样品池的另一端通入气流, 本文实验中为氮气(N2)。具有一定流量的氮气被分成两条支路, 分别经过流量控制器 1 和 2 (图 3(a)中 Flowmeter1 和Flowmeter2)。经过 Flowmeter1 的气流不经过水浸润, 始终保持干燥, 称为“干气”; 经过 Flowmeter2的气流经过水浸润, 含有一定量的水汽, 称为“湿气”。可以通过两个流量控制器分别控制“湿气”与“干气”的比例, 再将两路气流混合, 从而调节进入样品池中气流的相对湿度。
样品池的另一个上游是超声雾化器(图 3(a)中Nebulizer), 用来将样品溶液雾化, 产生一定量的多分散气溶胶颗粒。雾化产生的颗粒物顺着气路被氮气引入样品池, 在其中受到方向相反的两个力(贝塞尔光施加的竖直向上的光压力和气流施加的竖直向下的斯托克斯阻力)的作用, 颗粒物的重力可忽略。当颗粒物到达光压力与气流阻力平衡的位置时, 就被稳定地悬浮。
对样品池环境的监测通过温湿探头实现。国外使用单一探头, 将其置于样品池内, 位于颗粒物的下游[30]。使用单一探头可能导致测量偏差, 将其置于样品池内也可能对颗粒物所处的环境造成扰动。为了避免这些问题, 本研究在样品池外靠近样品池的上游和下游分别放置温‒湿探头(图 3(a)中 T/RH probe1 和 T/RH probe2), 颗粒物附近的温‒湿度可由两者插值得到, 探测结果比单一探头更可靠。
当气溶胶颗粒物被稳定地悬浮后, 可以通过CCD 相机对其进行观察。如图 3(a)所示, CCD 相机前应当加上足够的消光片, 防止因颗粒物散射光过强而损伤相机, 也可加上适当的透镜组来调整相机接收的视场。适当地调整 CCD 前的透镜组后, 可以通过 CCD 相机看到如图 4(a)所示明暗相间的颗粒物散射光强度分布, 其中心左侧为气溶胶前向散射的光, 右侧为后向散射的光。贝塞尔光具有自重构的性质[24], 当其遇到一个颗粒物时, 在颗粒后部一段距离处又会形成新的贝塞尔光。这段距离约为Dpk/2kz, 其中 Dp 是颗粒物的直径, kz 是波矢 k 在光轴上的投影。贝塞尔光的自重构性使得同时捕获多个颗粒物成为可能[21], 图 4(b)显示利用本文搭建系统同时捕获的 5 个颗粒物组成的微粒链。这种微粒链不稳定, 一般最后只会剩下一个微粒。
本文利用凸透镜组收集散射光。由于凸透镜的直径有限, 无法收集 0°~180°的所有散射光, 收集到的散射角范围与凸透镜的直径以及凸透镜到被悬浮颗粒物之间的距离有关。如图 3(a)所示, 被悬浮颗粒物在凸透镜上的投影应位于凸透镜的中心, 凸透镜的直径为 d, 颗粒物与凸透镜的距离为 x, 则收集到的散射光角度范围为
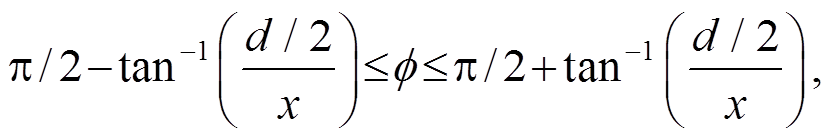
每个角度对应的散射光强 Iobs(ϕ)的相对大小可由图4(a)沿 y 方向平均得到, 本文收集到的散射角度范围为约 70°到约 110°。经过 y 方向平均后, 图 4(a)中颗粒物的散射光强度 Iobs(ϕ)如图 5 中五角星所示, 散射由强变弱的部分为 70°~74°, 79°~83°, 88°~93°和 99°~106°, 分别对应图 5 中区域I, III, V 和 VII; 由弱变强的部分为 75°~78°, 84°~87°, 94°~98°和107°~110°, 分别对应图 5 中区域 II, IV, VI 和 VIII。
根据前面得到的 Iobs(ϕ), 可以反演得到气溶胶颗粒的粒径 Dp 和复折射率 m, 反演的过程本质上是寻找最优解的过程。不同于 Cotterell 等[29]利用最大皮尔森相关的思想寻找最优解, 本文通过“分段匹配散射强度趋势”来确定最优解。本文实验中悬浮的颗粒物为硫酸铵与水的混合物, 硫酸铵的复折射率为 1.52, 水的复折射率为 1.33, 因此被悬浮颗粒的折射率在 1.33~1.52 之间。基于 Carruthers 等[36]的工作, 可以假定被悬浮颗粒的粒径在 1~4μm 之间。假定被悬浮颗粒物是均匀内混合的球形, 被颗粒物散射的光无偏振, 则根据米散射理论[28], 可由此计算不同粒径(Dp)、不同复折射率(m)的颗粒物在不同散射方向ϕ的散射强度IMie(Dp, m, ϕ), 1 μm<Dp<4μm, 1.33<m<1.52。IMie(Dp, m, ϕ)相当于查算表, 在遍历 Dp 和 m 后, 如果可以找到一个 Dp*和一个 m*, 使得Iobs(ϕ)与IMie(Dp*, m*, ϕ)最相近, 则认为Dp*和m*分别为被悬浮颗粒的粒径和复折射率。
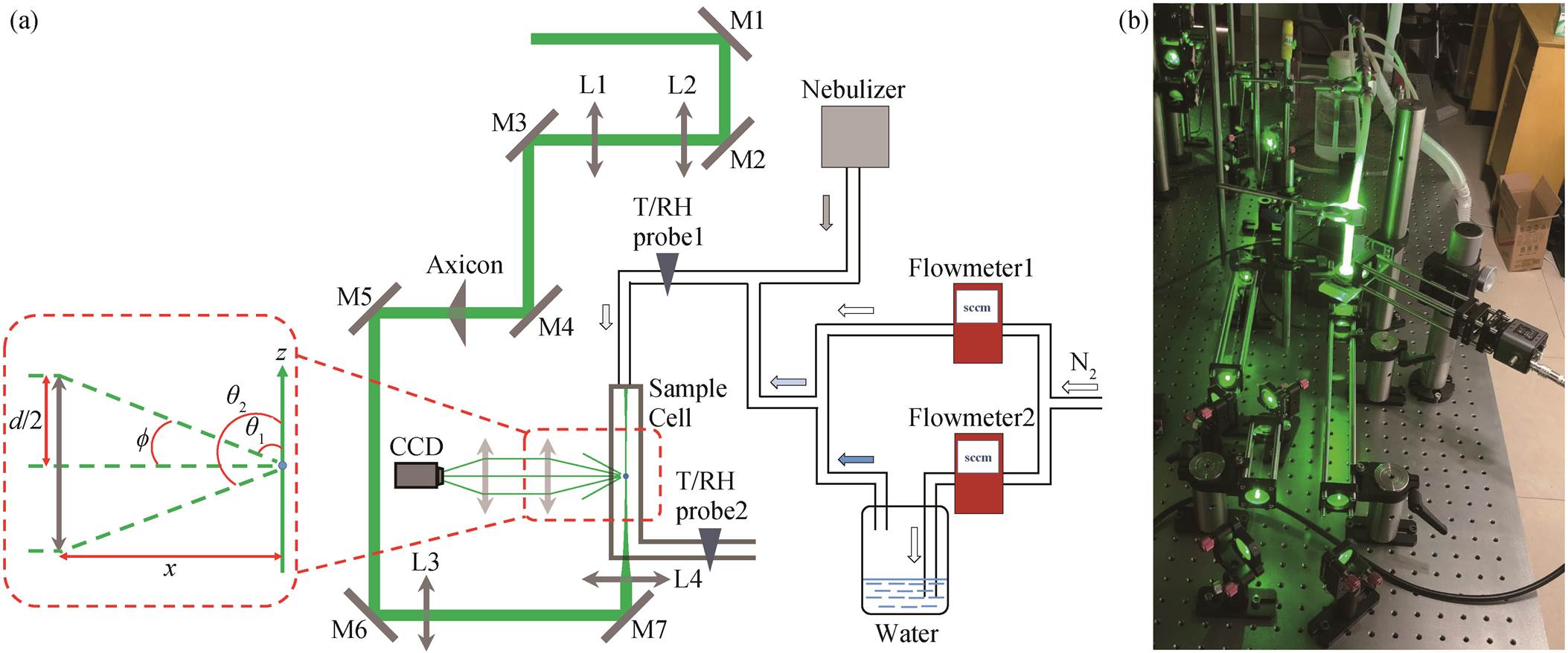
图3 贝塞尔光镊示意图(a)和实景(b)
Fig. 3 Schematic diagram (a) and photo of Bessel beam optical tweezer (b)
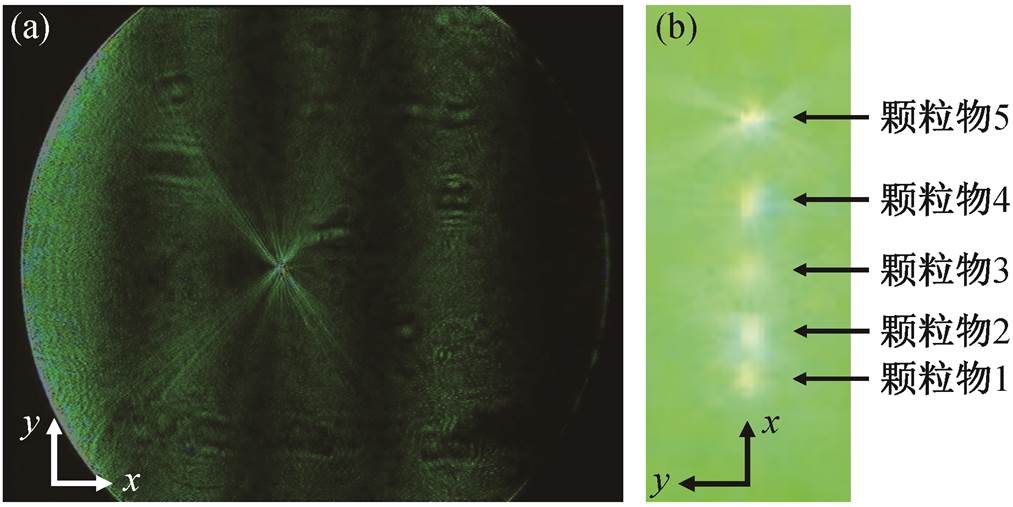
图 4 利用 CCD 相机看到的被悬浮颗粒物的散射光强度分布(a)和同时捕获的 5 个颗粒物(b)
Fig. 4 Scattering pattern of single levitated particle (a) and 5 simultaneously levitated particles (b)
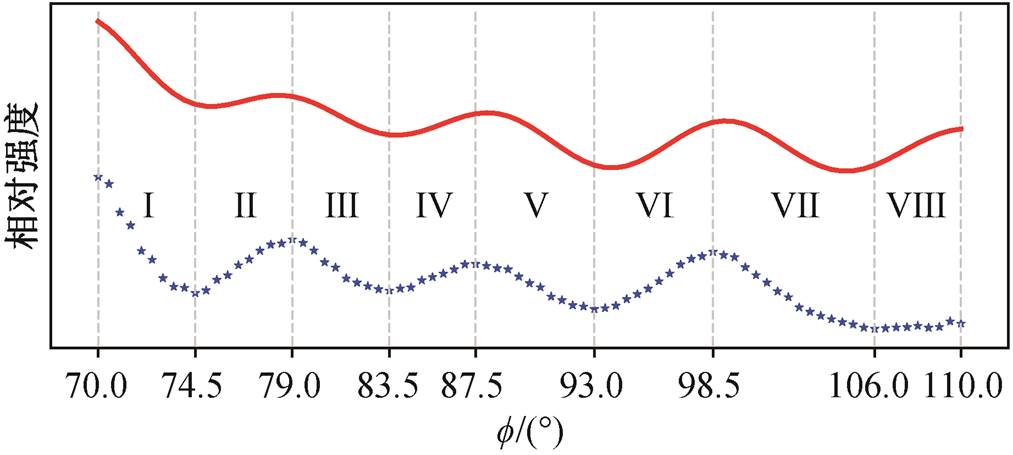
蓝色五角星为图 4(a)中散射强度随角度的变化, 红色曲线为米散射理论给出的散射强度随角度的变化
图5 被悬浮颗粒物散射光随角度的变化
Fig. 5 Angular variation of the scattering light by the levitated particle
在查算表IMie(Dp, m, ϕ)中找到与观测散射光强Iobs(ϕ)相近的最优米散射光强 IMie(Dp*, m*, ϕ)的思路如下所述。考虑到凸透镜的边缘对散射光强接收的影响, 在图 5 的 8 个区域中, 优先找到 90°附近区域III, IV, V 和 VI 中与 Iobs(ϕ)趋势一致的 IMie(Dp, m, ϕ), 即 IMie(Dp, m, ϕ)和Iobs(ϕ)在区域 III, IV, V 和 VI 都是先减小, 再增加, 再减小, 再增加。如果满足要求的(Dp, m)只有 1 组, 则这组(Dp, m)就定为被悬浮颗粒的粒径和折射率(Dp*, m*); 如果这时满足要求的(Dp, m)大于 1 组, 则再增加区域限定条件; 如果没有满足要求的(Dp, m), 则逐个减小区域限定条件。本文案例中满足要求的(Dp, m)大于 1 组, 故增加区域限定条件, 直到满足区域限定条件的(Dp, m)只有1 组为止。最终, 当区域限定条件增加到区域 I, II, III, VI, V 和 VI, 共 6 个区域时, 满足要求的(Dp, m)只剩下 1 组, (Dp, m) = (2660 nm, 1.38)(如图5中红色曲线所示), 此时观测得到的 Iobs(ϕ)与 IMie(Dp, m, ϕ)在区域 I, II, III, VI, V 和 VI 具有相同的变化趋势, 可认为图 4(a)中被悬浮颗粒物的粒径为 2660nm, 折射率为1.38。
本文利用“贝塞尔光‒反向气流”方法搭建贝塞尔光镊测量系统, 成功地捕获并稳定地悬浮气溶胶单颗粒。利用贝塞尔光自重构的性质, 成功地同时悬浮多颗粒组成的颗粒链。通过透镜组和 CCD 相机, 拍摄到颗粒物明暗相间的散射强度分布, 并借助米散射理论反演得到颗粒物的粒径和折射率。与国外学者用最大相关法确定最优解[29]的不同之处在于, 本文反演方法利用分段匹配散射强度变化趋势的方式确定最优解, 最终得到的粒径在贝塞尔光镊可以悬浮的粒径范围[36]内。
虽然在搭建的系统中安装了温湿探头, 但本文并没有使用。在大流量(比如约 1L/min)下, 温室探头对湿度的变化能够及时地响应, 但本文实验中流量相对较小(约 0.1L/min), 温湿探头响应缓慢, 不能实时地记录样品池的湿度变化。将来解决这个问题之后, 会得到较准确的温度和相对湿度数据, 配合同步测量得到的粒径和折射率数据, 我们将有针对性地开展吸湿性测量实验。
参考文献
[1] Wills J B, Knox K J, Reid J P. Optical control and characterisation of aerosol. Chemical Physics Letters, 2009, 481(4): 153‒165
[2] Pant A, Parsons M T, Bertram A K. Crystallization of aqueous ammonium sulfate particles internally mixed with soot and kaolinite, crystallization relative humi-dities and nucleation rates. Journal of Physical Che-mistry A, 2006, 110(28): 8701‒8709
[3] Murray B J, Broadley S L, Wilson T W, et al. Hetero-geneous freezing of water droplets containing kao-linite particles. Atmospheric Chemistry & Physics & Discussions, 2011, 11(9): 4191‒4207
[4] Li K K, Wang F, Zeng G, et al. Probing the time scale for bulk equilibration and mass transport of water in amorphous inorganic aerosol. Journal of Physical Chemistry B, 2011, 115(49): 14397
[5] Reid J P. Particle levitation and laboratory scattering. Journal of Quantitative Spectroscopy & Radiative Transfer, 2009, 110(14): 1293‒1306
[6] Davis E J. A history of single aerosol particle levi-tation. Aerosol Science and Technology, 1997, 26(3): 212‒254
[7] Al Zaitone B A, Tropea C. Evaporation of pure liquid droplets: comparison of droplet evaporation in an acoustic field versus glass-filament. Chemical Engi-neering Science, 2011, 66(17): 3914‒3921
[8] Power R M, Reid J P. Probing the micro-rheological properties of aerosol particles using optical tweezers. Reports on Progress in Physics Physical Society, 2014, 77(7): 074601
[9] Power R M, Simpson S H, Reid J P, et al. The transition from liquid to solid-like behaviour in ul-trahigh viscosity aerosol particles. Chemical Science, 2013, 4(6): 2597‒2604
[10] Mason B J, Walker J S, Reid J P, et al. Deviations from plane-wave mie scattering and precise retrieval of refractive index for a single spherical particle in an optical cavity. Journal of Physical Chemistry A, 2014, 118(11): 2083‒2088
[11] Walker J S, Carruthers A E, Orr-Ewing A J, et al. Measurements of light extinction by single aerosol particles. Journal of Physical Chemistry Letters, 2013, 4(10): 1748‒1752
[12] Davies J F, Miles R E H, Haddrell A E, et al. Temperature dependence of the vapor pressure and evaporation coefficient of supercooled water. Journal of Geophysical Research Atmospheres, 2015, 119(18): 10931‒10940
[13] Davies J F, Miles R E H, Haddrell A E, et al. Influence of organic films on the evaporation and condensation of water in aerosol. Proceedings of the National Academy of Sciences of the United States of America, 2013, 110(22): 8807‒8812
[14] Cai C, Stewart D J, Preston T C, et al. A new app-roach to determine vapour pressures and hygroscopi-cities of aqueous aerosols containing semi-volatile organic compounds. Physical Chemistry Chemical Physics, 2014, 16(7): 3162‒3172
[15] Lienhard D M, Bones D L, Zuend A, et al. Measure-ments of thermodynamic and optical properties of se-lected aqueous organic and organic–inorganic mix-tures of atmospheric relevance. Journal of Physical Chemistry A, 2012, 116(40): 9954‒9968
[16] Dennis-Smither B J, Marshall F H, Miles R E H, et al. Volatility and oxidative aging of aqueous maleic acid aerosol droplets and the dependence on relative hu-midity. Journal of Physical Chemistry A, 2014, 118 (30): 5680‒5691
[17] Dennis-Smither B J, Miles R E H, Reid J P. Oxidative aging of mixed oleic acid/sodium chloride aerosol particles. Journal of Geophysical Research Atmos-pheres, 2012, 117(D20): 1‒13
[18] Lu J W, Rickards A M J, Walker J S, et al. Timescales of water transport in viscous aerosol: measurements on sub-micron particles and dependence on condi-tioning history. Physical Chemistry Chemical Physics, 2014, 16(21): 9819‒9830
[19] Bones D L, Reid J P, Lienhard D M, et al. Comparing the mechanism of water condensation and evaporation in glassy aerosol. Proceedings of the National Aca-demy of Sciences of the United States of America, 2012, 109(29): 11613‒11618
[20] Haddrell A E, Davies J F, Miles R E H, et al. Dy-namics of aerosol size during inhalation: hygroscopic growth of commercial nebulizer formulations. Interna-tional Journal of Pharmaceutics, 2014, 463(1): 50‒61
[21] Carruthers A E, Reid J P, Orr-Ewing A J. Longitudinal optical trapping and sizing of aerosol droplets. Optics Express, 2010, 18(13): 14238‒14244
[22] Mcgloin D, Dholakia K. Bessel beams: diffraction in a new light. Contemporary Physics, 2005, 46(1): 15‒ 28
[23] Arlt J, Garces-Chavez V, Sibbett W, et al. Optical micromanipulation using a Bessel light beam. Opt Commun, 2001, 197(4/5/6): 239‒245
[24] Garces-Chavez V, McGloin D, Melville H, et al. Simultaneous micromanipulation in multiple planes using a self-reconstructing light beam. Nature, 2002, 419: 145‒147
[25] Summers M D, Reid J P, McGloin D. Optical guiding of aerosol droplets. Optics Express, 2006, 14(14): 6373‒6380
[26] Carruthers A E, Orrewing A J, Reid J P. Optical trapping and sizing of aerosol droplets using counter-propagating Bessel beams. 2010, 7762(1): 77610V‒ 77620V
[27] Meresman H, Wills J B, Summers M, et al. Manipula-tion and characterisation of accumulation and coarse mode aerosol particles using a Bessel beam trap. Physical Chemistry Chemical Physics, 2009, 11(47): 11333‒11339
[28] Bohren C F, Huffman D R. Absorption and scattering by a sphere. Weinheim: John Wiley & Sons, 2007
[29] Cotterell M I, Mason B J, Preston T C, et al. Optical extinction efficiency measurements on fine and ac-cumulation mode aerosol using single particle cavity ring-down spectroscopy. Physical Chemistry Chemical Physics, 2015, 17(24): 15843‒15856
[30] Cotterell M I, Mason B J, Carruthers A E, et al. Measurements of the evaporation and hygroscopic response of single fine-mode aerosol particles using a Bessel beam optical trap. Physical Chemistry Chemi-cal Physics, 2014, 16(5): 2118‒2128
[31] Cotterell M I, Willoughby R E, Bzdek B R, et al. A complete parameterisation of the relative humidity and wavelength dependence of the refractive index of hygroscopic inorganic aerosol particles. Atmospheric Chemistry & Physics, 2017, 17(16): 1‒27
[32] Durnin J, Miceli J J, Eberly J H. Comparison of Bessel and Gaussian beams. Optics Letters, 1988, 13(2): 79‒80
[33] Mason B J, Cotterell M I, Preston T C, et al. Direct measurements of the optical cross sections and re-fractive indices of individual volatile and hygroscopic aerosol particles. Journal of Physical Chemistry A, 2015, 119(22): 5701‒5713
[34] Preston T C, Mason B J, Reid J P, et al. Size-dependent position of a single aerosol droplet in a Bessel beam trap. Journal of Optics, 2014, 16(2): 25702‒25712
[35] Jezek J, Cizmar T, Nedela V, et al. Formation of long and thin polymer fiber using nondiffracting beam. Optics Express, 2006, 14(19): 8506‒8515
[36] Carruthers A E, Walker J S, Casey A, et al. Selection and characterization of aerosol particle size using a bessel beam optical trap for single particle analysis. Physical Chemistry Chemical Physics, 2012, 14(19): 6741‒6748
Design of Bessel Beam Optical Tweezers for Single Particle Study
Abstract Bessel beam optical tweezer is built for particle measurement. An axicon is used to generate Bessel beam. The trapped single aerosol particle is stably levitated by optical force exerted by Bessel beam and drag force exerted by the counter gas flow. In combination with light signal scattered by the levitated aerosol particle, the diameter and the refractive index can be measured. Physicochemical properties of aerosol, such as hygroscopicity, volatility, and the refractive index, could be studied under different environmental conditions with this system.
Key words Bessel beam; optical tweezers; single aerosol particle
doi: 10.13209/j.0479-8023.2020.090
国家自然科学基金(41590872)和中国博士后科学基金(2017M620505)资助
收稿日期: 2019‒12‒30;
修回日期: 2020‒03‒16