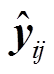 :
: 摘要 针对高斯牛顿(Gauss-Newton, GN)方法求解光束法平差模型时对初值准确度要求高、应用场景受限的问题, 提出基于拟牛顿法 BFGS (Broyden-Fletcher-Goldfarb-Shanno)修正的高斯牛顿算法——BFGS-GN 法。当高斯牛顿法的信息矩阵失去正定性后, 使用 BFGS 算法对法方程进行补充修正, 可从根本上消除高斯牛顿方法对初值敏感的数学缺陷。在数据集上的实验结果表明, BFGS-GN 算法对不同类型的初值具有鲁棒性, 在初值较好的情况下, 所提方法与高斯牛顿法具有相同的精度和迭代效率; 在初值较差的情况下, 高斯牛顿方法因发散而失效, BFGS-GN 算法仍可以收敛到较高的精度。
关键词 光束法平差; 高斯牛顿; BFGS 算法; 初值鲁棒
光束法平差(bundle adjustment, BA)是三维重建和视觉 SLAM (simultaneous localization and mapp-ing)的核心技术, 主要应用于相机位姿和路标点的后端优化。获得相机内参矩阵、外参矩阵、影像特征点和空间 3D 物点坐标初值后, 可以使用 BA 模型对以上参数进行整体优化, 消除误差, 并获得精确的视觉信息[1]。
在视觉重建中, BA 模型的目标是获得更加精确的相机位姿和空间路标点。围绕这一目标, 针对光束法平差的研究分为以下几个方向。
1)使用其他质量更高的传感器获得更高质量的初值。Zhang 等[2]着眼于使用标靶来获得精度更高的初值, 以保证优化过程中的问题收敛, 但在提高初值精度时, 往往需要精度更高的采集设备和更多的人工预处理。
2)建立包含更多约束内容的光束法平差模型。Dabeer 等[3]在 BA 模型中融合路标点特征和车道线特征来优化自动驾驶车辆的姿态信息。Yang 等[4] 提出点面 BA 模型来处理纹理缺乏场景中机器人的状态优化问题。Wu 等[5]利用计算机并行计算方式, 通过使用多核 CPU 和 GPU 进行算法加速。Zhao 等[6]用影像间的视差角等角度信息代替直角坐标, 降低雅克比矩阵(Jacobian matrix)的稀疏性。
3)借助深度学习方法求解 BA 问题。这种方法往往需要基于数据特征进行精巧的设计来增强训练过程的收敛性, 且参数估计部分仍然采用传统方法, 通用性不强。如 Tang 等[7]设计 BA-Net, 通过学习到的量度特征来衡量重投影误差、优化场景深度和相机运动。
4)直接研究 BA 模型的数值优化解。这是更加基础性的研究方向, 其目标是以各种质量的传感器采集的数据为基础, 提高求解方法的准确度和可拓展性。本文详细介绍此方向的研究。
光束法平差模型的本质是非线性最小二乘求解问题, 通过多次迭代, 使 3D 路标点的重投影误差最小。在数值优化问题的诸多解法中, 牛顿法因具备二阶收敛速度而得到广泛的应用, 但在迭代求解的过程中, 牛顿法因计算复杂度过高而无法应用在数据量较大的 BA 模型求解中。这种情况下, 高斯牛顿方法通过忽略牛顿方法中产生的高阶导数, 极大地降低计算复杂度, 因此普遍应用于工程问题中。但是, 在忽略高阶项的同时也为高斯牛顿带来问题: 当输入模型的初始值偏离真值较远时, 此方法极易发散, 无法满足收敛要求。
LM (Levenberg-Marquardt)方法[8]通过为高斯牛顿增加阻尼项来实现问题可解, 但由于阻尼的具体数值是通过不断尝试得到的, 因此很难获得精准的下降方向, 并导致迭代中的下降速度较慢。CG (Conjugate Gradient)方法[9]则是在高斯牛顿方法的数学模型基础上, 使用共轭梯度的方式求解方程, 但由于信息矩阵的条件数较大, 会影响矩阵的收敛速度。CGBA 方法[10]通过分解雅克比矩阵, 能够降低矩阵的条件数, 提高收敛速度, 但基于共轭梯度方式的解算方法通常无法收敛到更高精度的局部最小点。
BFGS (Broyden-Fletcher-Goldfarb-Shanno)方法[11]是一种常见的拟牛顿方法, 具有良好的正定保持特性, 因此是数值优化领域常用的优化方法。sBFGS-BA 是利用 BFGS 的正定保持特性提出的一种新解算方法[12], 但每步迭代都需计算海森矩阵(Hessian matrix)的高阶信息, 无法实现实时运行。本文通过分析高斯牛顿方法对初值敏感的原因发现, 在解算过程中, 是由于近似海森矩阵失去正定特点, 才导致下降方向无法求解。本文引入 BFGS 方法迭代求解目标方程的高阶导信息, 更加精准的表现求解目标中的海森矩阵, 在增加少量可控计算量的基础上, 可以极大地提高方法的鲁棒性。在较差初值的情况下, 本文方法也可以获得较好的下降方向, 从根本上解决基于高斯牛顿方法的光束法平差方法对初值敏感的问题。
光束法平差是摄影测量和计算机视觉中的黄金定律, 其本质是关于相机姿态(ci)与三维点(pj)的最小二乘优化问题。相机姿态包含平移矩阵 Ri 和旋转矩阵 Ti。通过三角化方法, 可以利用一对同名点获得一个空间中的三维路标点。在优化阶段, 需要把空间中的三维点通过相机模型重投影到影像上, 形成坐标点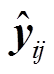 :
:
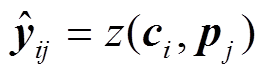 ,(1)
,(1)其中, 函数 z(x)是把空间中的三维点投影成二维像点的投影方程。此时, 可以为所有观测到的图像特征点 yij 和图像坐标空间中的预测点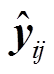 构建重投影误差方程:
构建重投影误差方程:
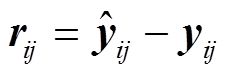 。(2)
。(2)
可以将 BA 问题描述为
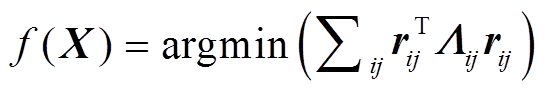 ,(3)
,(3)其中, X 是所有未知参数的集合; Λij 是一个协方差矩阵, 使用同一个传感器进行观测时, 我们认为误差之间是相互独立的, 故通常将Λij 作为一个对角阵存在, 实际中通常取单位矩阵。通过对目标方程的解算, 可以获得最终优化的结果。
牛顿法是求解无约束优化问题最早的算法之一, 主要思路是使用迭代点处的一阶导数和二阶导数对目标方程进行近似, 然后将二次模型的极小点作为新的迭代点, 不断重复, 达到满足的精度为止。对式(3)进行二阶泰勒展开:
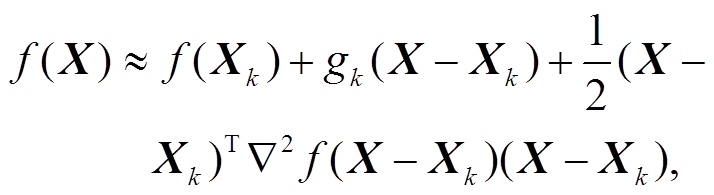 (4)
(4)其中, 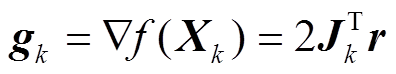 , 这里 Jk 表示雅克比矩阵(Jacobian matrix), 即观测方程对未知参数X的一阶偏导矩阵。取X=Xk+1, 则式(4)可改写为
, 这里 Jk 表示雅克比矩阵(Jacobian matrix), 即观测方程对未知参数X的一阶偏导矩阵。取X=Xk+1, 则式(4)可改写为
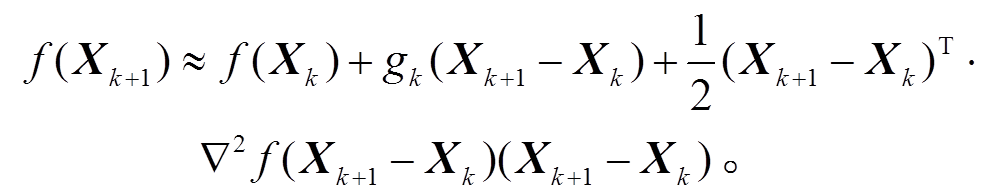 (5)
(5)
为了获得最小值点, 对式(5)右边求导, 并令一阶导数为零。此时求解出来的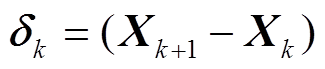 就是两次迭代之间的下降方向:
就是两次迭代之间的下降方向:
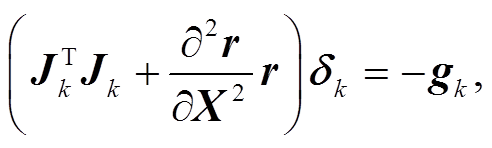 (6)
(6)式(6)中的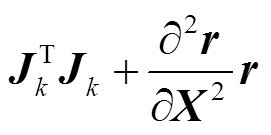 就是观测方程的海森矩阵, 本文中把海森矩阵的前一部分
就是观测方程的海森矩阵, 本文中把海森矩阵的前一部分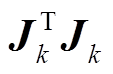 称为低阶导数矩阵, 后一部分
称为低阶导数矩阵, 后一部分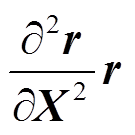 称为高阶导数矩阵。
称为高阶导数矩阵。
牛顿法具有不低于二阶的收敛速度, 但是, 当遇到 BA 问题时, 求解海森矩阵工作量巨大, 同时不能保证目标函数的海森矩阵在每个迭代点处都保持正定。为了利用牛顿法的优势, 避免不足, 出现高斯牛顿方法等 BA 解法。在高斯牛顿方法中, 忽略式(6)中的高阶导数矩阵, 使用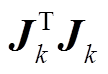 来代替海森矩阵求解方程的下降方向:
来代替海森矩阵求解方程的下降方向:
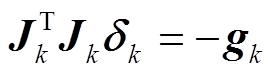 。(7)
。(7)可以看出, 在迭代求解过程中, 缺少高阶导数信息的高斯牛顿算法必须满足 Hessian 矩阵正定的条件, 并且要求式(7)中雅克比矩阵必须是列满秩矩阵, 否则算法失效。Jacobian 矩阵是相机参数与观测的三维特征点之间的一种表示方式, 随输入参数的变化而变化[13]。因此, 对 Jacobian 矩阵的要求就转化成对观测初值的要求, 当初值不好时, 优化问题通常无法求解, 这就是高斯牛顿方法容易发散的根本原因。
针对高斯牛顿法存在的问题, 我们结合 BFGS算法进行修正, 继而提出更加鲁棒的 BA 模型解算方法。
BFGS 是一种常用的拟牛顿方法, 如式(8)所示:
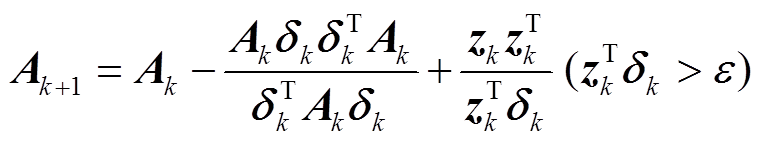 ,(8)
,(8)其中, Ak+1 是 Ak 的下一次迭代,在本文中,二者均是对称矩阵, δk=Xk+1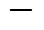 Xk是两次迭代之间的残差向量, ε 是一个小的正量, 我们将其设置为 1×10–6。此外, Zk是雅克比矩阵的差:
Xk是两次迭代之间的残差向量, ε 是一个小的正量, 我们将其设置为 1×10–6。此外, Zk是雅克比矩阵的差:
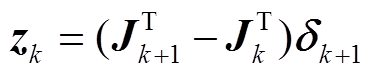 。(9)
。(9)
可将 BFGS 公式可简记为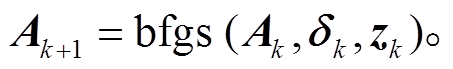 由于该方法通过秩 2 修正, 因此在迭代求解过程中, 对于输入的正定矩阵, 在一定的条件下, 仍能保持正定性。下面是 BFGS 正定保持特性的证明过程。
由于该方法通过秩 2 修正, 因此在迭代求解过程中, 对于输入的正定矩阵, 在一定的条件下, 仍能保持正定性。下面是 BFGS 正定保持特性的证明过程。
当 Ak 是正定矩阵且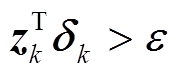 , 则对于任意非零的 x
, 则对于任意非零的 x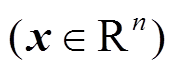 , 可根据式(8)得到
, 可根据式(8)得到
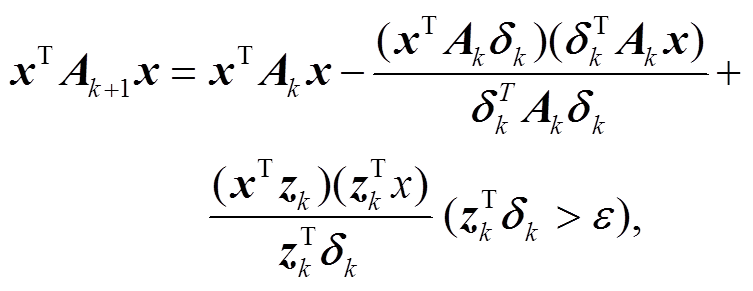 (10)
(10)由于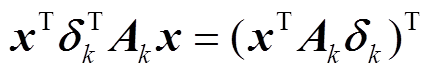 ,
,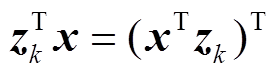 , 则式(10)可简化为
, 则式(10)可简化为
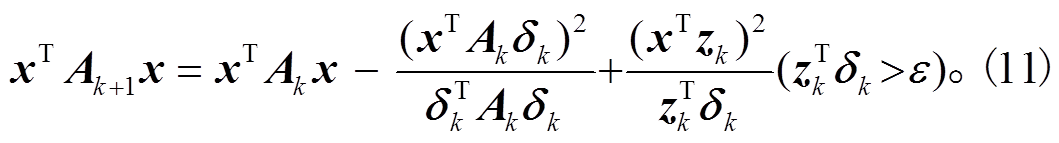
由于 Ak是正定矩阵, 利用 Cuchy-Schwarz 公式进行分解可得
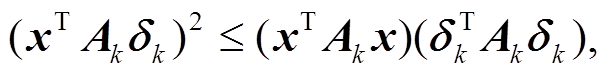 (12)
(12)其中, 等号成立的条件是存在非零实数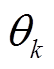 , 使得
, 使得 。式(11)可转换为
。式(11)可转换为
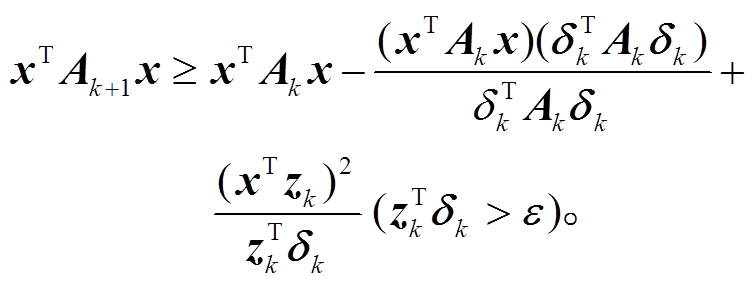 (13)
(13)
因此, 在式(12)等号成立时, 有
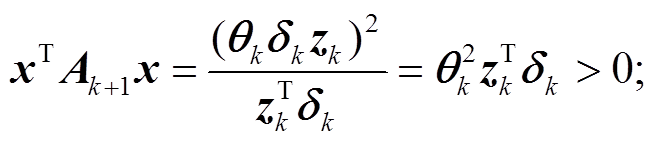 (14)
(14)在式(12)等号不成立并严格小于时, 有
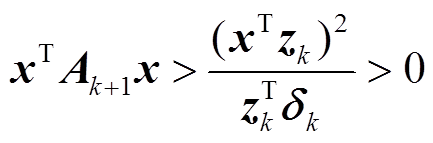 。(15)
。(15)
上述过程证明了 BFGS 方法在 Ak 是正定矩阵且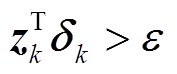 条件下的正定保持特性, 这个性质可用来改善高斯牛顿方法的缺陷。
条件下的正定保持特性, 这个性质可用来改善高斯牛顿方法的缺陷。
当高斯牛顿方法中的近似海森矩阵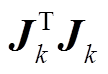 不再正定时, 将引起迭代过程的发散, 因此对高斯牛顿方法进行修正的目标是保证海森矩阵在迭代的过程中始终保持正定。
不再正定时, 将引起迭代过程的发散, 因此对高斯牛顿方法进行修正的目标是保证海森矩阵在迭代的过程中始终保持正定。
在第一次迭代开始时, BFGS-GN 算法首先对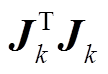 进行正定性判断, 如果该矩阵正定, 则执行式(7); 如果矩阵失去正定性, 则对近似海森矩阵进行修正。
进行正定性判断, 如果该矩阵正定, 则执行式(7); 如果矩阵失去正定性, 则对近似海森矩阵进行修正。
对于第一次迭代的修正方法是: 在开始求解矩阵时, 增加阻尼项I0:
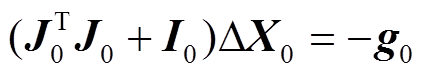 , (16)
, (16)其中, 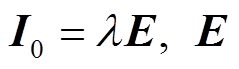 为同阶的单位矩阵,
为同阶的单位矩阵, ![]() 是一个小量, 实验中取
是一个小量, 实验中取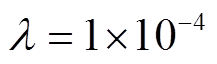 。
。
当完成第 k 次迭代后, 对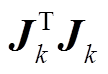 进行正定性判断, 对不正定的
进行正定性判断, 对不正定的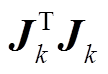 矩阵进行修正。本文利用对称正定矩阵的 Cholesky 分解来进行正定矩阵的判断。在迭代过程中, 若矩阵对称正定, 则存在一个对角元为正数的下三角矩阵; 若矩阵不满足, 则无法实现分解, 表明
矩阵进行修正。本文利用对称正定矩阵的 Cholesky 分解来进行正定矩阵的判断。在迭代过程中, 若矩阵对称正定, 则存在一个对角元为正数的下三角矩阵; 若矩阵不满足, 则无法实现分解, 表明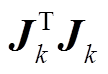 已失去正定性。矩阵失去正定性是由于式(6)中高阶导数信息被忽略导致, 因此使用BFGS 方法来恢复迭代中式(6)的高阶导数信息。
已失去正定性。矩阵失去正定性是由于式(6)中高阶导数信息被忽略导致, 因此使用BFGS 方法来恢复迭代中式(6)的高阶导数信息。
修正时先对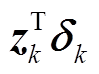 进行判断, 然后使用
进行判断, 然后使用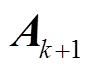 或
或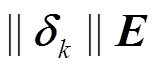 对高斯牛顿的近似海森矩阵进行修正, 使其在迭代过程中始终保持正定, 从而实现对任意情况的初值的解算。
对高斯牛顿的近似海森矩阵进行修正, 使其在迭代过程中始终保持正定, 从而实现对任意情况的初值的解算。
如果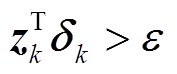 , 则
, 则
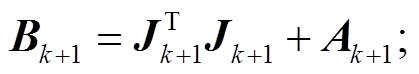 (17)
(17)如果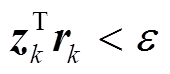 , 则
, 则
 (18)
(18)
式(17)和(18)中, Bk+1是新得到的海森矩阵, ||.||表示L2 范数距离。
修正后的通用形式的矩阵可以定义如下:
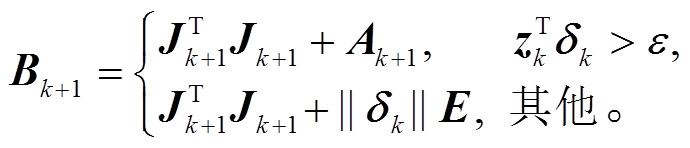 (19)
(19)式(19)得到的 Bk+1 是一个精确的矩阵, 可以更好地模拟Hessian矩阵, Ak+1 是一个稠密矩阵, 通过式(8)获得。基于BFGS修正的GN算法如下。
算法 BFGS-GN
已知: 相机位姿、路标点和特征点
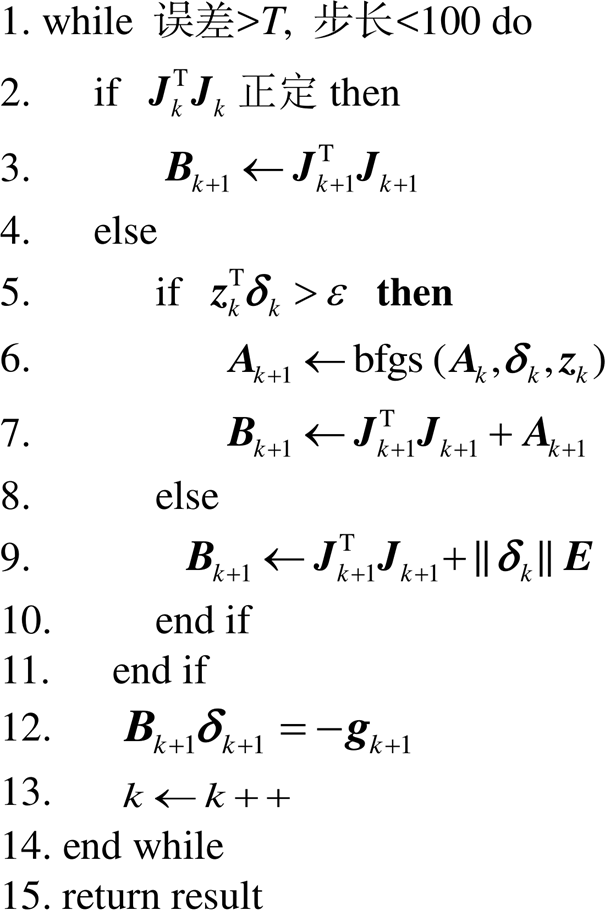
由于 BA 问题涉及的矩阵维数大、计算复杂度高, 会给稠密矩阵 Ak+1 的求解带来困难。然而, 低阶导数矩阵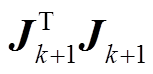 具有稀疏性, 其结构如图 1 所示, 黑色方块表示矩阵在该方块内有数值, 其余无色的区域表示矩阵在该处数值为0。
具有稀疏性, 其结构如图 1 所示, 黑色方块表示矩阵在该方块内有数值, 其余无色的区域表示矩阵在该处数值为0。
本文借助 Hessian 矩阵的低阶导数矩阵建立一个滤波器, 稀疏化高阶导数矩阵 Ak+1。当低阶导数矩阵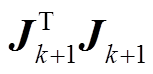 中(i, j)位置的元素为零时, 滤波器中具有相同位置的元素也被设置为零。滤波矩阵 Fi,j可以表示如下:
中(i, j)位置的元素为零时, 滤波器中具有相同位置的元素也被设置为零。滤波矩阵 Fi,j可以表示如下:

图1 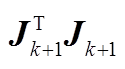 矩阵的稀疏性
矩阵的稀疏性
Fig. 1 Sparsity of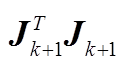 matrix
matrix
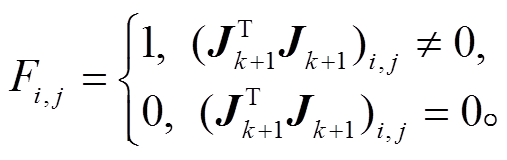 (20)
(20)我们将非零元素分为两类: 对角元素和非对角元素。若将它们都保留在增益矩阵Ak+1 中, 可以获得更好的实验结果。因此, 通过滤波器的Hadamard乘法, 可以得到Ak+1 的稀疏矩阵, 记为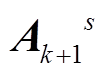 :
:
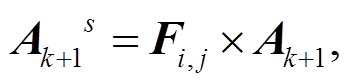 (21)
(21)
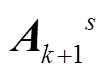 具有与
具有与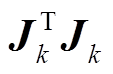 矩阵相同的稀疏结构。
矩阵相同的稀疏结构。
使用稀疏化的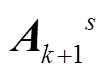 矩阵替代式(19)中的 Ak+1, 在求解下降方向后, 可以顺利地对光束法平差问题进行解算:
矩阵替代式(19)中的 Ak+1, 在求解下降方向后, 可以顺利地对光束法平差问题进行解算:
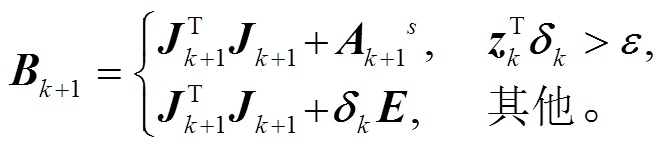 (22)
(22)
为了验证本文提出的 BFGS-GN 方法的有效性, 使用 4 个数据集进行实验, 将实验结果与传统的高斯牛顿解算方法进行比较①代码地址: https://github.com/shzhao/BFGS-GN。。为了确保公平性, 两个算法在同样的计算平台及软件环境下编写和运行: MATLAB-2016b 和华硕 3.4 GHz Windows 系统, 对参数进行同样的初始化操作。采用同样的标准进行限制: 最大迭代次数 100 次。
测试 4 个数据集由高质量摄像机拍摄的近景及航空摄影测量图像组成。表 1 列出数据集的整体参数, 包含数据类型、图像大小、影像张数、投影点数量和 3D 点的个数等信息。第 1 个数据集是使用Cannon 相机在 350m 的高度拍摄的 63 幅野外图像, 产生 4961 个 3D 点和 23150 个投影点。第 2 个数据集是将专业的光度测量摄像机 DMC 安装在 1000m米高的机载结构上, 拍摄的 90 幅航拍图像和 37705个投影。第 3 个数据集是近景数据集, 图像来自公共机器人数据集合, 其中的 51652 个投影使用开源软件 L2SIFT 提取。第 4 个数据集是从无人机(UAV)平台上采集的 468 幅分辨率为 5616×3744 的大学校园图像。
提取高质量的图像投影点后, 使用基于相对姿态估计的算法, 计算两个相邻摄像机之间的相对姿态。在获得两个相邻摄像机的所有相对姿态后, 通过将相对姿态转换为第一摄像头坐标的方式, 将本地坐标参考系中的相机姿态初始化。然后, 通过交点算法实现 3D 点的初始化。将每个数据集整理为 4 个 txt 文件, 分别是相机的内参文件、每张影像的位姿信息、每张影像的特征点文件和特征点对应的空间路标点文件。最后, 将摄像机姿态和路标点位置输入基于高斯牛顿法的光束法平差方法和基于 BFGS 修正的高斯牛顿方法中。统一使用优化参数计算得到的预测点和真实点间的均方误差(MSE)来衡量算法的准确性。
实验结果分为两种情况。如图 2 所示, 对于数据集 DunHuan 和 Village, 高斯牛顿方法(GN)和本文提出的基于 BFGS 修正的高斯牛顿方法(BFGS-GN)具有相同的收敛精度和收敛速度。本文方法在中间迭代点处下降更快速(图 2(a)), 图 2(b)中两种方法取得相同的收敛效果。说明在数据集初值较好的情况下, 两种方法均能很好地模拟真实 Hessian 矩阵, 达到较好的收敛效果。
如图 3 所示, 对于数据集 Magala 和 College, 使用高斯牛顿方法优化相机姿态和 3D 点坐标时, 迭代过程经过振荡后, 最终的结果出现发散。BFGS-GN 方法仍然可以将数据优化到较高的精度。从图3 可以看出, 高斯牛顿方法出现发散的原因在于, 数据集的初始值距离真实值较远, 所以高斯牛顿方法中的近似 Hessian 矩阵不能很好地表示真实的Hessian 矩阵, 并且在优化的过程中失去正定性。BFGS-GN 方法通过对高斯牛顿的目标方程进行修正, 可以更加准确地逼近真实 Hessian 矩阵, 并且始终有能力使矩阵在迭代过程中保持正定特性。对于Malaga 数据集, BFGS-GN 方法可以收敛到 0.512; 对于 College 数据集, 仅需 7 步就能使 MSE 收敛到0.352。
表1 测试数据集的整体参数
Table 1 Overall parameters of the test datasets

数据集数据类型图像大小影像/张投影点/个3D路标点/个 DunHuan航空5616×374463 231504961 Village航空 7680×1382490 377056231 Malaga近景 1024×768170 516528805 College航空 5616×3744468 660318258

图2 Dunhuan 和 Village 数据集收敛情况
Fig. 2 Situation of convergence on Dunhuan and Village datasets

图3 Magala 和 College数据集收敛情况
Fig. 3 Situation of convergence on Magala and College datasets
测试数据集的初始误差、迭代次数和最终收敛精度如表 2 所示, 其中的第 3 和第 4 列分别表示使用初始未知参数计算的均方误差和使用最优参数计算的收敛后的均方误差, 以像素作为统一的单位。此外, 我们还记录了迭代次数。
从整体上看, 与基于高斯牛顿的光束法平差方法相比, 对于初值较好的数据, BFGS-GN 方法具有不弱于高斯牛顿的迭代效率和收敛精度。对于拥有较差初值的数据, BFGS-GN 方法可以顺利地收敛, 解决了基于高斯牛顿的光束法平差方法因对初值敏感而应用场景受限的问题。
表2 高斯牛顿和BFGS-GN优化的收敛结果
Table 2 Convergent results using Gauss-Newton and BFGS-GN solutions
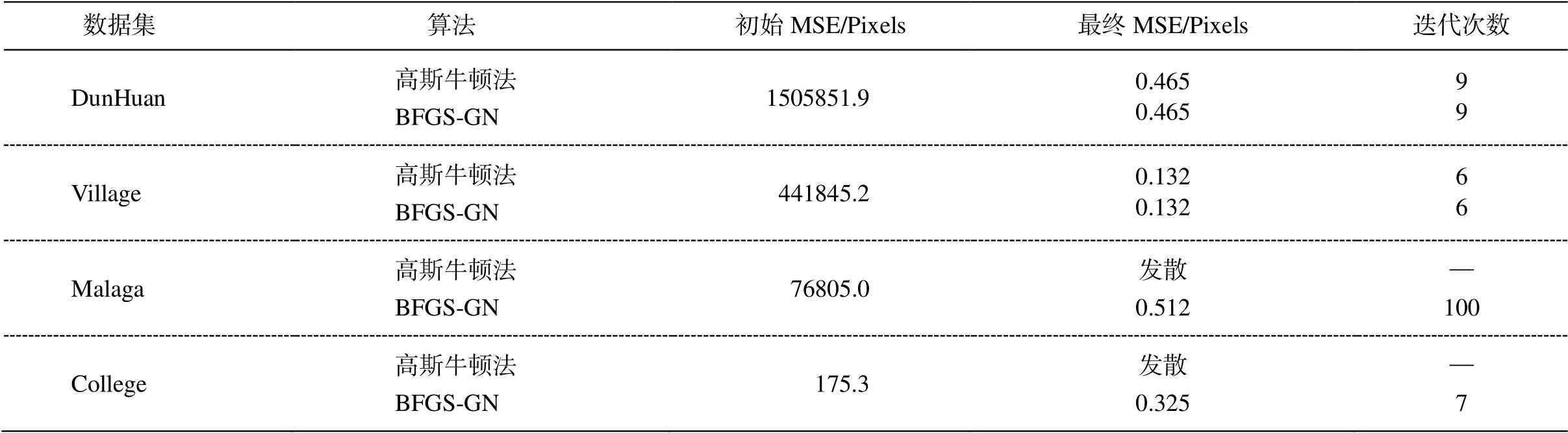
数据集 算法初始MSE/Pixels最终MSE/Pixels迭代次数 DunHuan高斯牛顿法BFGS-GN1505851.90.4650.46599 Village高斯牛顿法BFGS-GN441845.20.1320.13266 Malaga高斯牛顿法BFGS-GN76805.0发散0.512—100 College高斯牛顿法BFGS-GN175.3发散0.325—7
高斯牛顿法是光束法平差中的重要方法, 因收敛精度高和超线性收敛速度而得到广泛应用。但是, 高斯牛顿法由于理论上的缺陷, 使得其对相机姿态和空间路标点的初始值具有较高要求, 当初始值远离真值时, 算法极容易发散, 丧失优化功能。本文通过对高斯牛顿方法初值敏感原因进行探索, 提出基于 BFGS 算法修正的高斯牛顿方法(BFGS-GN 方法)。在每次迭代前, BFGS-GN 方法会对高斯牛顿信息矩阵的正定性进行判断, 在不满足正定规则时, 对高斯牛顿的目标方程进行修正。
实验结果表明, 对于高斯牛顿法不能实现收敛的数据集, BFGS-GN 算法可以正常地收敛, 并获得较高收敛精度; 对于高斯牛顿法可以收敛的数据集, BFGS-GN 算法同样可以获得相同的精度和迭代效率。因此, 本文提出的方法可以很好地解决高斯牛顿方法对于初值敏感的问题, 在保证收敛精度的前提下, 可以增加算法的鲁棒性, 有效地拓展应用场景。
参考文献
[1] Yan Lei, Chen Rui, Sun Huabo, et al. A novel bundle adjustment method with additional ground control point constraint. Remote Sensing Letters, 2017, 8(1): 68–77
[2] Zhang Chunsen, Zhu Shihuan, Zang Yufu, et al. GPS-supported bundle adjustment method of UAV by con-sidering exposure delay. Acta Geodaetica et Cartogra-phica Sinica, 2017, 46(5): 565–572
[3] Dabeer O, Gowaikar R, Grzechnik S K, et al. An end-to-end system for crowdsourced 3D maps for autono-mous vehicles: the mapping component // IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Vancouver, 2017: 634–641
[4] Yang S C, Song Y, Kaess M, et al. Pop-up SLAM: semantic monocular plane SLAM for low-texture environments // IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Daejeon, 2016: 1222–1229
[5] Wu Changchang, Agarwal S, Curless B, et al. Mul-ticore bundle adjustment // The 24th IEEE Confe-rence on Computer Vision and Pattern Recognition (CVPR). Providence, RI, 2011: 3057–3064
[6] Zhao Liang, Huang Shoudong, Sun Yanbiao, et al. ParallaxBA: bundle adjustment using parallax angle feature parametrization. The International Journal of Robotics Research, 2015, 34(4/5): 493–516
[7] Tang Chengzhou, Tan Ping. BA-Net: dense bundle adjustment networks [EB/OL]. (2019–08–25) [2019–12–01]. https://arxiv.org/abs/1806.04807
[8] Madsen K, Tingle O, Nielsen H B, et al. Methods for non-linear least squares problems. 2nd ed. Lyngb: Technical University of Denmark, 2004
[9] Hager W W, Zhang H. A survey of nonlinear con-jugate gradient methods. Pacific Journal of Optimi-zation, 2006, 2(1): 35–58
[10] Byröd M, Astrom K. Conjugate gradient bundle ad-justment // European Conference on Computer Vision. Heraklion, 2010: 114–127
[11] Zhou Weijun, Chen Xiaojun. Global convergence of a new hybrid Gauss-Newton structured BFGS method for nonlinear least squares problems. Siam Journal on Optimization, 2010, 20(5): 2422–2441
[12] Li Yanyan, Fan Shiyue, Sun Yanbiao, et al. Bundle adjustment method using sparse BFGS solution. Remote Sensing Letters, 2018, 9(8): 789–798
[13] 高翔, 张涛. 视觉 SLAM 十四讲: 从理论到实践. 北京: 电子工业出版社, 2017: 248–253
A BFGS-Corrected Gauss-Newton Solver for Bundle Adjustment
Abstract Aiming at the problem that the Gauss-Newton (GN) method is sensitive to the initial information matrixin the Bundle Adjustment (BA) model, which leads to limited application scenarios, the paper proposes a novel method BFGS-GN using BFGS (Broyden-Fletcher-Goldfarb-Shanno) algorithm to improve the traditional Gauss-Newton method. When the information matrix of the Gauss-Newton method loses positive definiteness, BFGS algorithm can be used to modify the normal equations, which fundamentally eliminates the mathematical defect that the Gauss-Newton method is sensitive to initial values. Experimental results demonstrate that proposed method is robust to different types of initials. The same accuracy and the number of iterations as GN can be obtained when the initial values are good. As for bad inputs, GN-based BA method cannot work but BFGS-GN can converge to a minimum.
Key words bundle adjustment; Gauss-Newton;BFGS algorithm;initial value robustness
doi: 10.13209/j.0479-8023.2020.098
国家重点研发计划(2018YFE0203801)资助
收稿日期: 2019-12–10;
修回日期: 2020–02–04