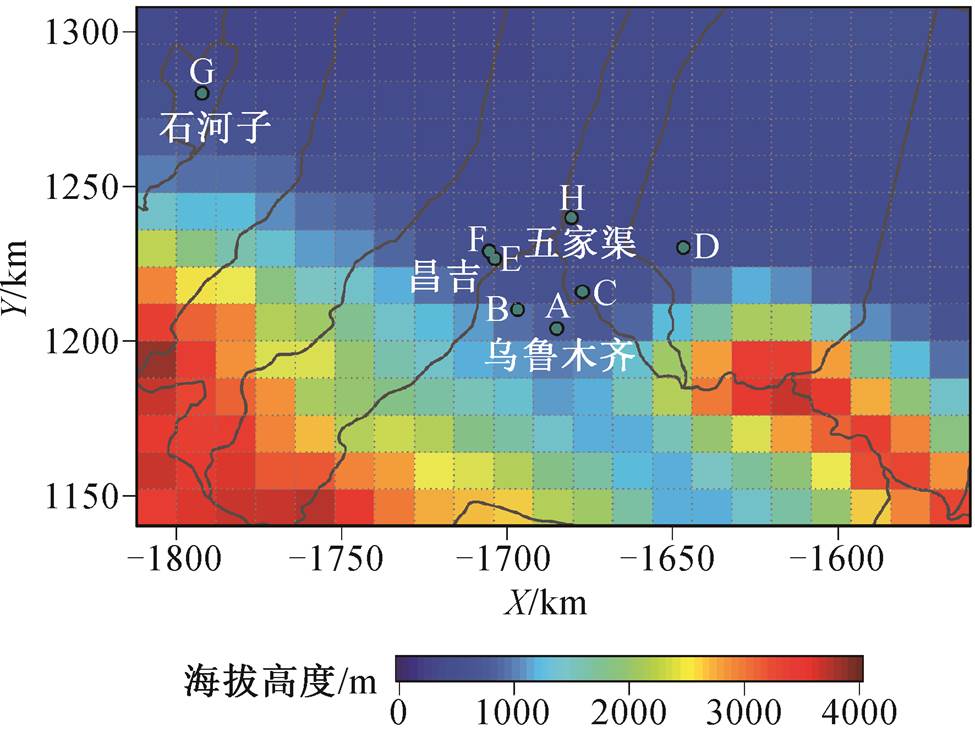
绿色圆点代表空气质量监测站点, 虚线方格代表预报的网格点
图1 研究区域
Fig. 1 Map of the study area
摘要 开展基于空气质量数值模式 CMAQ(社区多尺度空气质量模型)预报结果的后校正算法研究。利用集合深度学习方法, 对 CMAQ 的 PM2.5 (细颗粒物)原始预报结果进行误差订正, 以期提高预报准确率。该方法集合了深度神经网络模型、随机森林模型、梯度提升模型和广义线性模型 4 种机器学习模型, 在每一个模型中结合原始的气象预报、空气质量预报和土地利用类型等多源数据作为辅助变量, 对 PM2.5 预报浓度进行校正, 最后求取 4 个模型的集合结果。将该方法应用于订正新疆乌(鲁木齐)昌(吉)石(河子)城市群的 CMAQ 预报结果, 利用 2018 年的独立样本进行评估, 订正预报结果的准确性显著提升, 站点 5 天预报的决定系数 R2 为0.41~0.60, 比原始预报提高 60%~160%, 均方根误差 RMSE 降低 40% 左右; 交叉验证的站点预报 R2 同样提升 50%~80%, RMSE 下降 30% 左右。该订正方法的计算效率高, 可以部署于业务化预报平台, 进行可靠的运行。
关键词 客观订正; 多源数据; 机器学习; 集合预报
细颗粒物(PM2.5)是近年来中国大多数城市的主要空气污染物, 是城市秋冬季节空气质量的重要表征指标。2016 年全国年平均 PM2.5 浓度为 47μg/m3, 超过 34%的城市 PM2.5 浓度超过国家二级环境空气质量标准(NAQQS)(GB3095—2012) 35μg/m3, 人口稠密地区的污染水平更是远超这一标准[1]。例如京津冀地区, 2016 年的 PM2.5 浓度年均值为 71μg/m3, 是国家二级标准的两倍, 对居民健康造成极为不利的影响[2]。通过空气质量预报向政府生态环境部门以及其他行政和公共机构提供空气污染预警, 一方面可以有效地帮助公众及时采取保护措施来规避风险(如戴口罩、留在室内等), 还可以为政府实施动态管理措施, 限制预警期间空气污染物排放[3]提供必要的信息。
预测未来空气质量的方法主要有两类: 经验统计模型和确定性机理模型。经验方法通常采用关联预测变量和解释变量的统计模型, 从理论上讲, 只要有足够丰富的观测数据, 即可用来训练统计模型进行预测, 很容易业务化运行。然而, 统计模型难以预测较长期和较大空间尺度的空气质量, 尤其是监测站点稀疏的地区。同时, 统计模型无法预测污染物细分成分等没有观测的变量, 也很难提供排放控制的有用信息[4]。基于机理的方法通常采用大气化学传输模型来克服统计模型的上述缺点。例如, 社区多尺度空气质量模型(Community Multi-scale Air Quality model, CMAQ)可以在更长的提前期内进行预测, 且预测的污染物成分种类丰富, 预报的准确度也相对稳定, 还可以在一定程度上提供动态管理需要的辅助信息[5]。大气化学传输模型以详细的空气污染物排放清单和气象预报场作为输入, 通过在空间和时间上求解一系列数学方程来模拟大气中物理和化学演化过程, 从而模拟和预报空气污染物在大气中迁移、转化和沉降的全过程。基于CMAQ 的区域空气质量预报系统已在世界范围内广泛建立, 很多基于 CMAQ 的预报系统能够提供业务化的实时空气质量预报[6]。然而, 由于排放清单和气象预报的不确定性以及空气质量模型中不完善的物理和化学机制, 这种空气质量预报方法存在显著的误差[7]。
提高确定性机理模型预测性能的一种方法是利用基于统计模型的后校正技术, 对原始预测进行客观订正[8]。从本质说, 后校正技术是偏差校正技术, 利用确定性模型的历史误差来纠正当前的模型预测结果。最简单的偏差校正技术是移动平均法或线性模型, 它直接将前一时间段的平均预测偏差应用于当前模型来预测或滚动训练线性模型[9]。卡尔曼滤波器也用于从模型的历史性能评估中获得未来的偏差[8]。另外一种偏差校正方法是利用相似性来订正误差, 首先将历史的预测结果聚类成相似的分组, 然后从历史相似预报结果与实测的对比来获取当前预测偏差的估计值[10-11]。该方法考虑了不同分组之间预报误差的显著区别, 这些区别可能来源于不同的天气类型和排放规律引起的污染水平的差别。基于相似性的方法, 可以进一步与卡尔曼滤波器及其他统计方法相结合, 用以确定同一分组相似预报结果的集合偏差[12]。
本文利用一种新的集合深度学习方法, 对数值模式预报结果[10]进行订正, 并将其应用于数值模式预报误差通常较大的新疆乌(鲁木齐)昌(吉)石(河子)城市群地区。乌昌石城市群位于新疆准噶尔盆地南缘, 是中天山北坡经济带的重要组成部分, 人口稠密, 聚集新疆 40%以上的城镇人口, 经济发达, 创造全疆约 40%的生产总值。同时, 受污染物排放过量以及地形和气象条件的影响[13-15], 当地环境质量日趋严峻, 尤其是冬天采暖季, 受燃煤污染物的排放及逆温层、静稳天气等不利条件的影响, 污染问题尤为突出。此外, 乌昌石城市群各城市间污染物相互传输, 各城市互为污染贡献源, 区域型大气污染特征日渐突显[16]。本研究针对乌昌石城市群这个具有特殊污染气象条件的地区, 探索快速提高空气质量预报准确性的有效途径, 研究结果可推广到其他类似地区, 以期提升各地环境保护部门对空气污染事件的预报和预警能力。
选取乌昌石城市群的乌鲁木齐、五家渠、昌吉和石河子 4 个城市为研究区(图 1), 南北方向包括 14个格点(南北宽 172km), 东西方向包括 21 个格点(东西长 352km), 共 294 个格点。由图 1 可以看出, 乌昌石城市群区域受南部天山山脉对空气对流阻隔的影响, 同时本地的工业和生活污染物排放较为集中, 导致该区域的空气污染较为严重。
PM2.5 观测数据来自中国环境监测总站统一建立和管理的全国空气质量监测网络。该监测网络涵盖全国 1493 个监测站, 提供逐小时的 PM2.5 监测数据, 在中东部和东北地区分布较均匀, 但在新疆分布较为稀疏。在乌昌石城市群区域, 监测站主要分布在城区。本研究选取该地区具有较长监测历史的 8 个站点, 位置如图 1 所示。

绿色圆点代表空气质量监测站点, 虚线方格代表预报的网格点
图1 研究区域
Fig. 1 Map of the study area
气象模拟数据来自 WRF 模型的预报结果, 采用 GFS 预报产品进行驱动。气象模拟网格在研究区域的水平分辨率为 36km。本研究使用的气象模拟数据包括近地面气温、湿度、风速以及边界层高度等, 并利用 12km 分辨率的数字高程数据(DEM)作为解释变量。原始预报数据分辨率较低, 引入较高分辨率的 DEM 数据可以起到空间降尺度的作用, 同时可以提高预报订正的效果。
空气质量预报数据来源于 WRF 模拟气象场驱动的 CMAQ 模型的业务化预报系统, 该系统逐日生产未来 5 天(120 小时)的空气质量预报, 包括 PM2.5浓度预报产品[17]。该系统使用的 CMAQ 模型版本为 v5.0.1[5], 采用的预报模拟网格与气象模拟网格的设置一致。
集合深度学习方法可以有效地利用多个不同机器学习模型的优势, 取得更好的模拟效果。在气象环境数据分析领域, 该方法已应用于多源数据融合的研究中, 成功地开发出具有较高准确度的地面分析格点数据集, 如全国尺度的 PM2.5 和能见度数据集[17-18]。本研究将该方法延展形成后校正方法, 用于校正数值模式的 PM2.5 浓度预报结果。
本研究中后校正方法分为两部分: 基于包含空气质量监测站点格点的空气质量预报后校正、不包含空气质量监测站点格点的误差订正。因此, 该方法可对整个研究区域内的模型预报结果进行订正, 从而提升预报准确率。该方法模型如下:
Cmos =f(Ccmaqe, V1, V2, …, Vn)+δf , (1)
单一机器学习模型 f 将原始的空气质量预报Ccmaq 和其他辅助解释变量V1~Vn作为输入, 辅助变量包括空气质量预报同时刻的气象变量(如气温、风速和相对湿度)预报值以及数字高程(DEM)数据等。这些变量对细颗粒物浓度都有显著影响[19-20], 因此与质量预报误差之间也有较强的相关性, 可用于帮助订正空气质量预报结果 Cmos, 并降低模型残差δf。
本研究使用的模型 f 为集合深度学习模型, 如式(2)所示:
fensemble = fmeta(Cfuse,DNN, Cfuse,RF, Cfuse,GBM, Cfuse,GLM) + δe, (2)
集合深度学习模型是基于堆栈(stacking)原理, 利用元学习器 fmeta, 把不同的机器学习模型整合到一起, 形成一个集合深度学习方法 fensemble, 使其有较小的残差 δe。Cfuse,DNN, Cfuse,RF, Cfuse,GBM 和 Cfuse,GLM 分别为深度神经网络(Deep Neural Network, DNN)、随机森林模型(Random Forest, RF)、梯度提升模型(Gradient Boosting Machine, GBM)和广义线性模型(General Linear Model, GLM)。将这 4 个模型作为主学习器, 训练与模拟过程如图 2 所示。深度神经网络模型具有对复杂非线性关系的拟合能力, 预测结果无偏, 但存在过拟合的可能性[21]。随机森林模型和梯度提升模型都是包含多种弱分类器的集合模型, 区别是前者使用引导聚集算法(bootstrap aggre-gating), 也称装袋算法(bagging)[22], 后者使用提升算法(boosting)[23], 这两种方法在选择数量合适的决策树时都可避免过拟合现象。广义线性模型通过概率分布函数来实现对非线性过程的模拟, 不会出现明显的过拟合, 效果稳定, 但模拟的误差较大。具体来讲, 将深度神经网络模型设计为一个 3 层的全连接神经网络模型, 以双曲正切函数 Tanh 为激活函数, 以 Sigmoid 函数为输出层函数; 随机森林算法和梯度提升模型均使用 100 棵分类树, 激活函数也为双曲正切函数 Tanh; 广义线性模型使用的联系函数则为高斯函数。
为了整合上述 4 个学习器, 我们采用广义线性模型 GLM 为元学习器。GLM 模型的变量权重系数结构清晰且效果稳定, 可对每个主学习器的权重有清晰的识别, 同时能够模拟非线性响应关系。与主学习器的训练方法不同, 元学习器先将 M 条训练数据随机采样分为 N 个批次, 然后将其中的 N-1 个批次循环输入模型, 并对剩余的 1 个批次做模拟。如此循环 N 次, 得到每个主学习器与所有 M条训练数据对应的模拟值, 然后用 4 个初估数据和观测值训练 GLM 模型[24]。本研究中 N 为 10[10,24]。
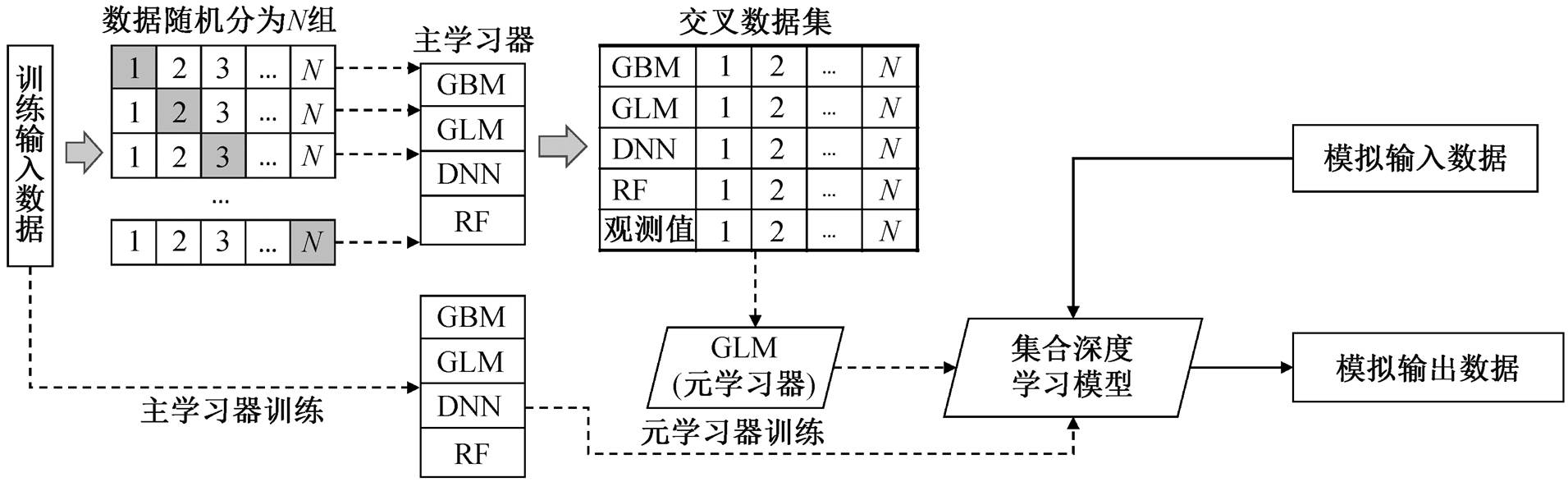
图2 集合深度学习模型训练与模拟过程
Fig. 2 Fitting and prediction processes by the ensemble deep learning framework
集合深度学习模型利用监测数据和预报变量以及与辅助变量匹配的数据集进行训练。从理论上讲, 这些数据反映包含空气质量监测站点的格点单元上的预报误差信息, 如果将其应用于订正其他不包含监测站点的格点预报结果, 则需要进行新的处理, 并可能在一定程度上引入新的误差。因为其本质是对以上两步得到的订正误差的空间外推, 其表现依赖于预报误差结构的空间连续性和稳定性。这里可采用两种订正方法, 第一种是利用所有的(邻近的)站点数据, 训练一个整体的模型, 并将该模型应用到研究区域内所有站点; 第二种是将每个站点的订正误差估计值插值到研究区域内所有站点上。考虑到研究区域的站点分布较为集中, 采用插值方法会在较远的站点上产生较大的偏差, 因此本研究采用整体数据训练模型, 并应用于整体区域的方法来完成在区域空间的预报误差订正。
利用 2015—2017 年共 3 年的数据作为模型的训练数据, 以 2018 年的数据作为独立的测试评估数据集。评估的模型包括梯度提升模型、广义线性模型、随机森林模型、深度神经网络模型和集合深度学习模型, 使用的评估指标为决定系数 R2 和均方根误差 RMSE。同时, 我们还利用交叉验证的方法, 对模型在空间上的外推适用性进行验证。具体做法是, 每次保留一个站点的数据作为评估数据, 用其余 7 个站点的数据训练模型, 将得到的模型应用在评估数据上, 得到一个评估结果。重复该步骤 8 次, 使得每个站点均被作为一次评估站点, 由此得到的结果可以表征模型在空间预报订正上的性能。
首先对 2018 年 CMAQ 模型的原始预报结果进行评估和分析。由图 3 可以看出, 原始的 CMAQ 预报在乌昌石城市群呈现明显的整体低估, 尤其是在监测浓度较高的情况下, 这种低估更明显。空气质量预报在各个站点的误差较为一致(图 4), 其中模型预报结果在位于乌鲁木齐的 B 站点表现最差, 平均预报误差约为−25μg/m3, 预报误差的上下四分位数分别为−15μg/m3 和−70μg/m3。模型预报结果在位于昌吉的 D 站点表现最好, 其平均预报误差接近0μg/m3, 且预报误差较为集中地分布在零值附近。其余站点 CMAQ 模型预报的表现类似, 平均预报误差约为−10μg/m3。
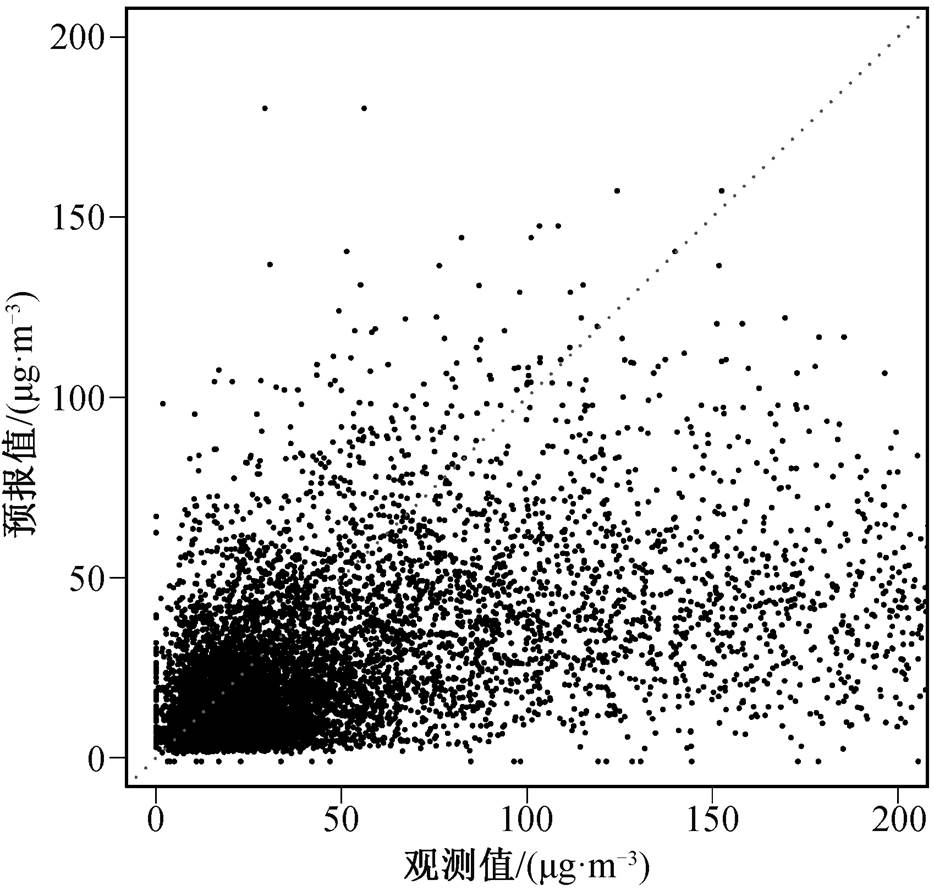
图3 乌昌石城市群8个站点的观测值与第 1 天预报值
Fig. 3 Observed PM2.5 concentrations at the 8 selected moni-tors versus the 1-day CMAQ forecasts in 2018
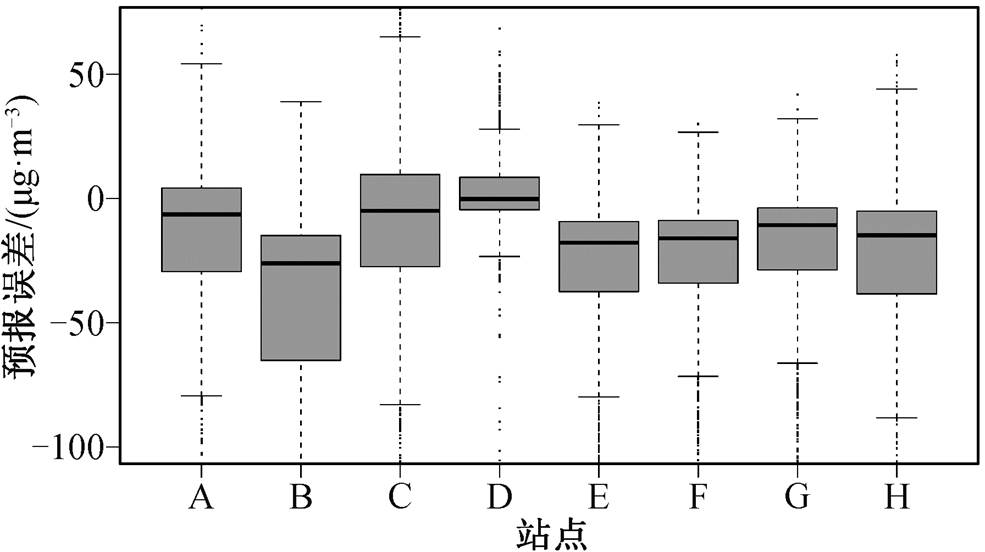
图4 乌昌石城市群8个站点的第1天预报误差
Fig.4 Prediction bias of 1-day CMAQ forecasts against observed PM2.5 concentrations at the 8 selected monitors
原始预报的 R2 和 RMSE 值在第 1~5 天的预报期内较为稳定, R2 稳定在 0.25 左右, RMSE 稳定在 43μg/m3, 原始预报并没有随着预报提前天数的增加而明显地降低, 但整体上表现较差(图 5(a))。其中, 第 1 天预报是每一个预报周期对未来第一天的预报值, 第 2~5 天的预报依此类推。通过比较不同深度模型订正效果的 R2 和 RMSE 值, 可以看出集合深度学习模型的表现最好, 即更明显地改善了原始的预报效果(图 5(b))。虽然所有模型订正结果的 R2 和RMSE 值都明显地改善, 但也出现随着预报提前天数的增加而订正效果下降的趋势。对第 1 天预报的订正效果都是最好的, 经过订正的预报结果 R2 值均显著增加, 表现最好的集合深度学习模型的后校正效果为 0.6, 同时 RMSE 也降至 23.9μg/m3。在第 2~ 5 天的后校正预报中, 集合深度学习模型仍然表现最好, R2 值分别为 0.49, 0.47, 0.43 和 0.41, 比原始预报值分别提升 103%, 85%, 75%和 57%。用误差指标 RMSE 进行评价, 集合深度学习模型的表现也是最好的, RMSE 值在未来 5 天的预报表现分别是23.9, 27.9, 29.8, 31.4 和 32.6μg/m3, 都低于原始预报的 43μg/m3, 显著地提升了预报准确性。
值得注意的是, 在 4 个集合成员模型中, 结构较为简单的广义线性模型和梯度提升模型的误差较低, 而结构较为复杂的深度神经网络模型表现最差。原因可能与乌昌石城市群地区站点 CMAQ 预报误差的结构较为简单有关, 深度神经网络模型适合模拟较为复杂的数据关联。随机森林模型具有最好的表现, 对于集合模型的表现有较为主要的贡献, 该结果与 Lyu 等[17]对全国 PM2.5 数据融合研究的发现较为一致。误差订正是在有监测站点的网格单元中进行, 由于这些站点主要分布在城市地区, 这些网格单元的订正后的预报误差也比较相似。
本文采用交叉验证的方法, 评估订正方法在空间扩展方面的表现。在这一步骤中, 训练数据不包含站点数据。订正后的结果中, R2 的提升没有第一阶段显著, 评估结果的 R2 值对 5 天预报的结果分别为 0.45, 0.43, 0.42, 0.4 和 0.38, 与站点上的模型订正效果相比有所降低, 但对未来 5 天预报效果的增加幅度仍然分别达到 83%, 77%, 63%, 64%和 51% (图6(a))。相应地, RMSE 也明显地下降, 从原始 5 天预报的约 43μg/m3 降至约 30μg/m3, 下降幅度约为 30% (图 6(b))。同样地, 集合深度学习模型仍然表现最好, 在各个集合成员模型中, 随机森林模型的表现最好, 两者订正结果的 R2 和 RMSE 值都比较接近。
通过分析乌昌石城市群地区 2018 年 1 月 7 日的一个典型污染过程案例预报结果的空间分布(图 7), 可以看出经过集合深度学习模型客观订正之后的PM2.5 浓度预报结果比原始的 CMAQ 预报浓度有明显的增加, 并与观测结果更加接近。与此同时, 由于使用了空间分辨率更高的 DEM 海拔高度数据, 订正结果具有更高的空间分辨率。
本文提出一种基于集合深度学习的后校正方法, 用于订正原始 CMAQ 模型的 PM2.5 浓度预报结果。该方法集合了 4 种流行的机器学习统计模型, 包括随机森林模型、广义线性模型、梯度提升模型和深度神经网络模型。使用该方法对乌昌石城市群地区2018 年 CMAQ 的 PM2.5 预报结果进行订正, 订正结果的准确性明显地提升, 站点预报的 R2平均增加约 80%, RMSE 平均降低 35%左右; 交叉验证预报的 R2 也显著地提升 65%左右, RMSE 下降 30%左右。该方法可用于订正 CMAQ 的空间预报结果, 并可提高 CMAQ 预报的空间分辨率。

图5 5天的原始预报与后校正预报的R2(a)和RMSE (b) (站点预报)
Fig. 5 The R2 values (a) and RMSE values (b) by raw CMAQ and post-corrected forecasts (at monitors)
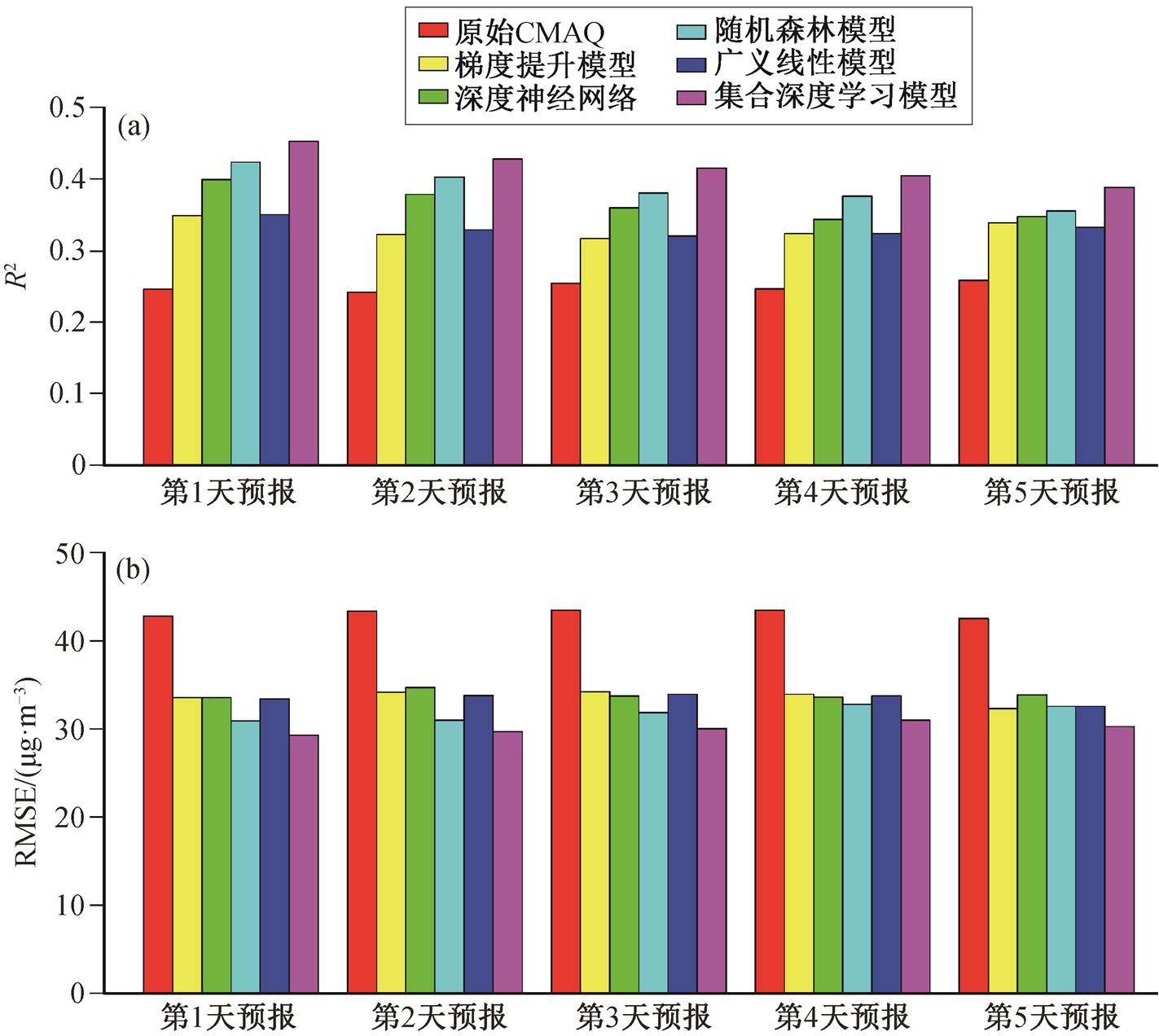
图6 5天的原始预报与后校正预报的R2(a)和RMSE (b) (非站点预报)
Fig. 6 R2 values (a) and RMSE values (b) by raw CMAQ and post-corrected forecasts (at non-monitor locations)
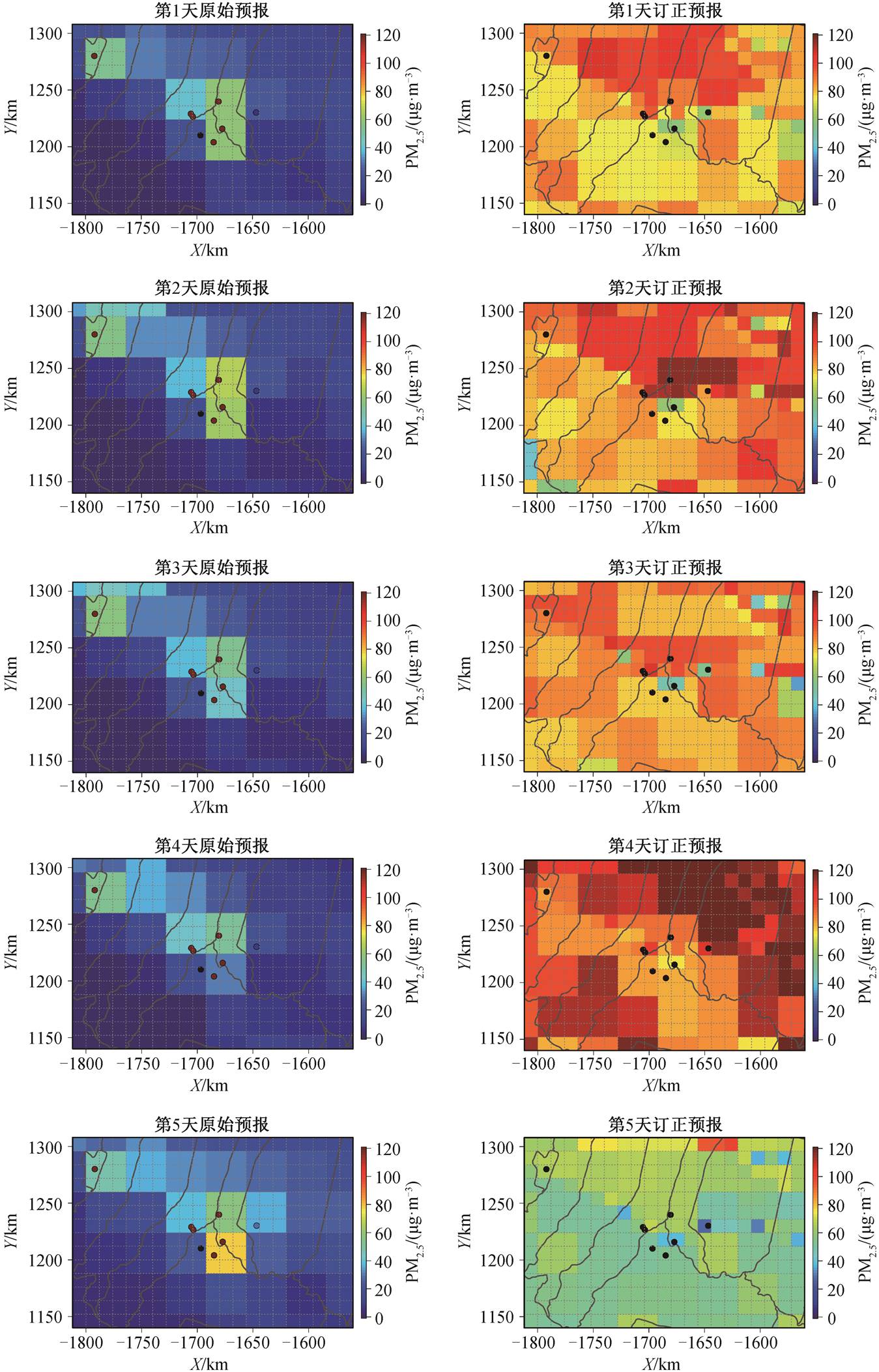
图7 2018年1月7日未来5天原始预报与集合深度学习模型后校正预报PM2.5浓度的空间分布
Fig. 7 Spatial distribution of PM2.5 concentrations of raw CMAQ and post-corrected forecasts on Jan. 7, 2018
参考文献
[1] Xue Tao, Zheng Yixuan, Geng Guannan, et al. Fusing observational, satellite remote sensing and air quality model simulated data to estimate spatiotemporal va-riations of PM2.5 exposure in China. Remote Sensing, 2017, 9(3): 221
[2] Fang Die, Wang Qingeng, Li Huiming, et al. Morta-lity effects assessment of ambient PM2.5 pollution in the 74 leading cities of China. Science of The Total Environment, 2016, 569/570: 1545-1552
[3] Hu Y, Odman M T, Chang M E, et al. Operational forecasting of source impacts for dynamic air quality management. Atmospheric Environment, 2015, 116: 320-322
[4] Zhang Y, Bocquet M, Mallet V, et al. Real-time air quality forecasting, part II: state of the science, cur-rent research needs, and future prospects. Atmos-pheric Environment, 2012, 60: 656-676
[5] Byun D, Schere K L. Review of the governing equations, computational algorithms, and other com-ponents of the Models-3 Community Multiscale Air Quality (CMAQ) modeling system. Applied Mecha-nics Reviews, 2006, 59(2): 51-77
[6] Mckeen S, Grell G, Peckham S, et al. An evaluation of real-time air quality forecasts and their urban emissions over eastern Texas during the summer of 2006 Second Texas Air Quality Study field study. Journal of Geophysical Research Atmospheres, 2009, 114: D00F11
[7] Binkowski F S, Roselle S J. Models-3 Community Multiscale Air Quality (CMAQ) model aerosol com-ponent 1. Model description. Journal of Geophysical Research Atmospheres, 2003, 108(D6): 4183
[8] Djalalova I, Delle M L, Wilczak J. PM2.5 analog forecast and Kalman filter post-processing for the Community Multiscale Air Quality (CMAQ) model. Atmospheric Environment, 2015, 119: 431-442
[9] 王茜, 吴剑斌, 林燕芬. CMAQ 模式及其修正技术在上海市 PM2.5 预报中的应用检验. 环境科学学报, 2015, 35(6): 1651-1656
[10] Lyu Baolei, Zhang Yuzhong, Hu Yongtao. Improving PM2.5 air quality model forecasts in China using a bias-correction framework. Atmosphere, 2017, 8: 147
[11] Delle M L, Nipen T, Liu Y, et al. Kalman filter and analog schemes to postprocess numerical weather predictions. Monthly Weather Review, 2011, 139(11): 3554-3570
[12] Junk C, Delle M L, Alessandrini S. Analog-based ensemble model output statistics. Monthly Weather Review, 2015, 143(7): 2909-2917
[13] 吴彦, 王健, 刘晖, 等. 乌鲁木齐大气污染物的空间分布及地面风场效应. 中国沙漠, 2008, 28(5): 986-991
[14] 蔡仁, 李霞, 赵克明, 等. 乌鲁木齐大气污染特征及气象条件的影响. 环境科学与技术, 2014(增刊1): 40-48
[15] 刘艳, 粟志峰, 彭倩芳, 等. 石河子市空气污染成因及防治对策. 干旱环境监测, 2002, 16(4): 230-233
[16] 冯刚, 孜比布拉, 司马义, 等. 乌鲁木齐城市群内部大气污染特征及趋势对比. 环境工程, 2016, 34 (8): 79-83
[17] Lyu Baolei, Hu Yongtao, Zhang Wenxian, et al. Fusion method combining ground-level observations with chemical transport model predictions using an ensemble deep learning framework: application in China to estimate spatiotemporally-resolved PM2.5 exposure fields in 2014-2017. Environmental Science & Technology, 2019, 53(13): 7306-7315
[18] 吕宝磊, 胡泳涛, 李林, 等. 利用集合深度学习方法融合多源数据开发全国能见度网格数据. 气象科技进展, 2018, 8(6): 79-84
[19] Yang Yiru, Liu Xingang, Qu Yu, et al. Formation mechanism of continuous extreme haze episodes in the megacity Beijing, China, in January 2013. Atmos-pheric Research, 2015, 155: 192-203
[20] Wang Mengya, Cao Chunxiang, Li Guoshuai, et al. Analysis of a severe prolonged regional haze episode in the Yangtze River Delta, China. Atmospheric Environment, 2015, 102: 112-121
[21] Schmidhuber J. Deep learning in neural networks: an overview. Neural Networks, 2015, 61: 85-117
[22] Svetnik V, Liaw A, Tong C, et al. Random forest: a classification and regression tool for compound clas-sification and QSAR modeling. Journal of Chemical Information & Computer Sciences, 2003, 43(6): 1947- 1958
[23] Ridgeway G. Generalized boosted models: a guide to the GBM package [EB/OL]. (2006-04-15) [2019-08-24]. http://www.saedsayad.com/docs/gbm2.pdf
[24] Laan V D, Polley M J, Hubbard E C, et al. Super learner. Statistical Applications in Genetics & Mole-cular Biology, 2007, 6(1): Article25
Improving Air Quality Forecast Accuracy in Urumqi-Changji-Shihezi Region Using an Ensemble Deep Learning Approach
Abstract A post-correction framework based on raw forecasts from the numerical air quality model CMAQ is implemented in the Urumqi-Changji-Shihezi region of Xinjiang Autonomous Region to achieve better forecasting performance of PM2.5. An ensemble deep learning method is used to correct the error of original forecasts of CMAQ. The method integrates four machine learning models: deep neural network model, random forest model, gradient boosting model and generalized linear model. In each model, the original meteorological forecasts, air quality forecasts and land use types are used as input data. With the independent evaluation data in 2018, the accuracy of the “bias-corrected” forecasts is significantly improved. The R2 values of the 5-day forecast is 0.41-0.60, which are improved from the original forecasts by 60%-160%, while the RMSE values are reduced by ~40%. As for the cross evaluation, the R2 values of post-corrected results increase by 50%-80%, while RMSE values are reduced by ~30%. The post-correction method is computationally efficient and can be deployed operationally for reliable daily forecasting.
Key words objective correction; multi-source data; machine learning; ensemble forecast
doi: 10.13209/j.0479-8023.2020.070
收稿日期: 2019-09-11;
修回日期: 2019-10-12
矮马科技自主研发项目(研字2016-003)和华云集团科技项目(hHYKJXM-201803)资助