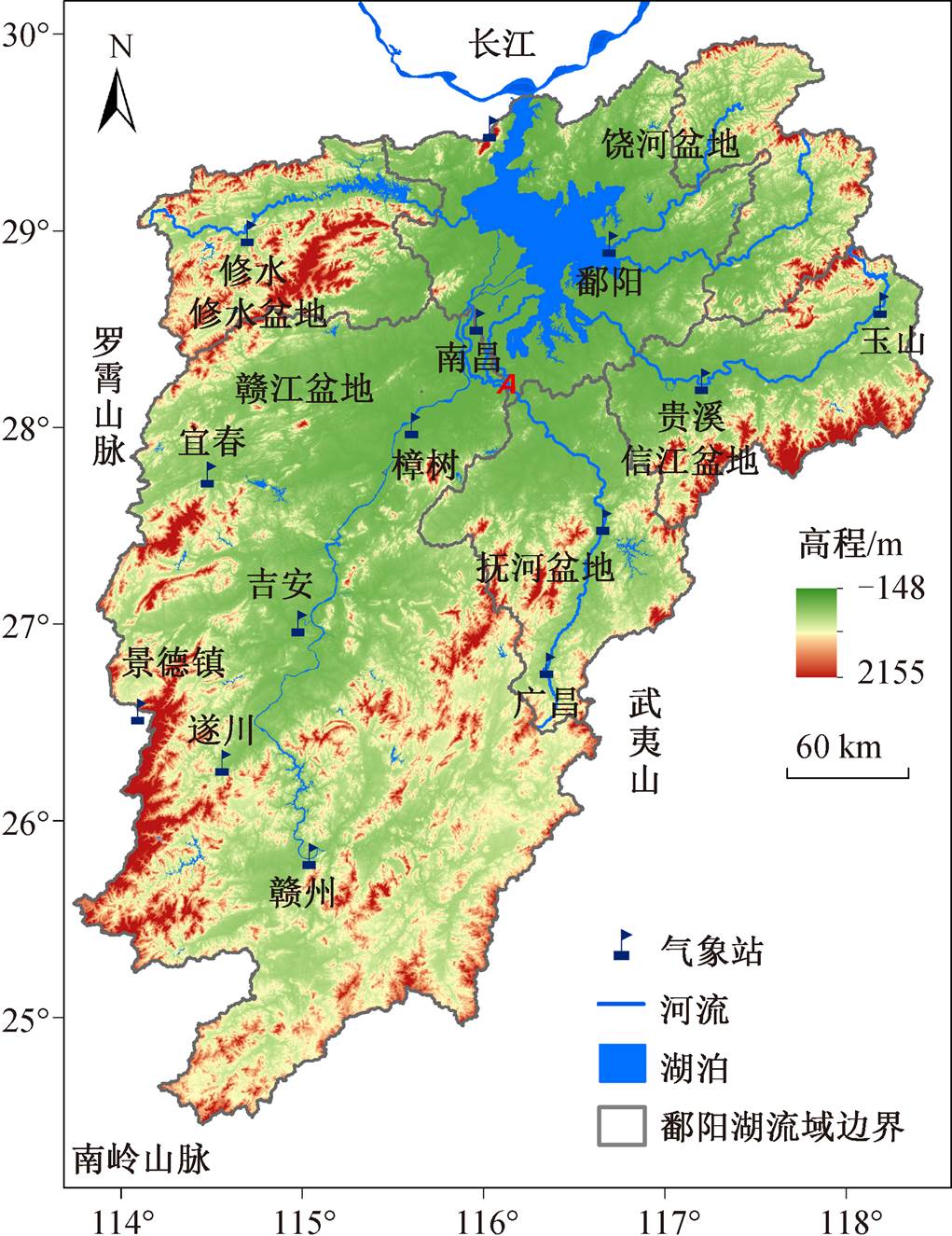
图1 鄱阳湖流域[21]
Fig. 1 Poyang Lake Basin[21]
摘要 为了降低单一模式的不确定性和传统模式集合在时间和空间上分布的不均匀性, 建立时空分布式的CMIP5 气候多模式集合。利用改进的遗传算法, 从时间和空间尺度优化 CMIP5 全球气候数据多模式集合, 并采用 Taylor 图评估其模拟性能。实验结果表明, 基于时空分布式的多模式集合优于单一模式和等权集合。
关键词 多模式集合; 优化; 遗传算法; 时空分布; CMIP5
气候变化是当今国际社会普遍关注的全球性问题[1], 全球气候模式(global climate model, GCM)数据是气候模拟和预估气候未来变化的重要工具[2]。其中, CMIP5 模式是迄今为止时间最长且内容最全的气候变化模式资料库, 广泛应用于气温[3]、降水[4]、径流[5]以及海温变化[6]等模拟能力评估和预估。CMIP5 模拟的是简化的真实的气候系统, 会造成结果的不确定性[7]。为克服单一模式模拟精度有限、空间和时间上分布不均等问题, 学者们提出多模式集合。Kharin 等[8]和 Kang 等[9]提出等权集合方案(EE), 但未考虑集合成员间的不确定性差异, 而是赋予所有成员相同的权重。由于动力气候模式具有系统误差, Peng 等[10]和 Ke 等[11]提出先消除模式的系统误差, 再等权集合的方法(Cali-EE)。因不同集合成员的预测能力不同, Krishnamurti 等[12]提出基于多元线性回归分析, 赋予集合成员不同权重的多模式集合方法(MLR)。以上3种基于经典统计学的多模式集合方案主要用于确定性预测。近几年出现适用于概率密度函数预测的版本[13-14]。Coelho等[15]、Luo 等[16]和 Li 等[17]提出基于贝叶斯(Bayes)统计学的集合方案。Raftery 等[18]使用贝叶斯模式平均(BMA)方法校正预测集合。Zhu 等[19]利用优化多模式集合, 预测北纬地区的叶面积指数分布趋势。但是, 这些方法未考虑不同模式预测能力在时间和空间的差异。
本文利用改进的遗传算法, 从时间和空间尺度优化 CMIP5 全球气候数据多模式集合, 采用 Taylor图[20]评估其模拟性能。
本文以江西省北部的鄱阳湖流域(图 1)为研究对象。鄱阳湖是我国最大的淡水湖, 随着气候变化和人类活动的加剧, 流域的气候水文过程和生态环境发生明显的变化, 尤其是近年来流域极端气候事件趋于引发洪涝干旱频繁发生。因此, 分析流域降水时空变化规律对保障地区资源环境和经济社会协调发展具有重要的现实意义[22]。
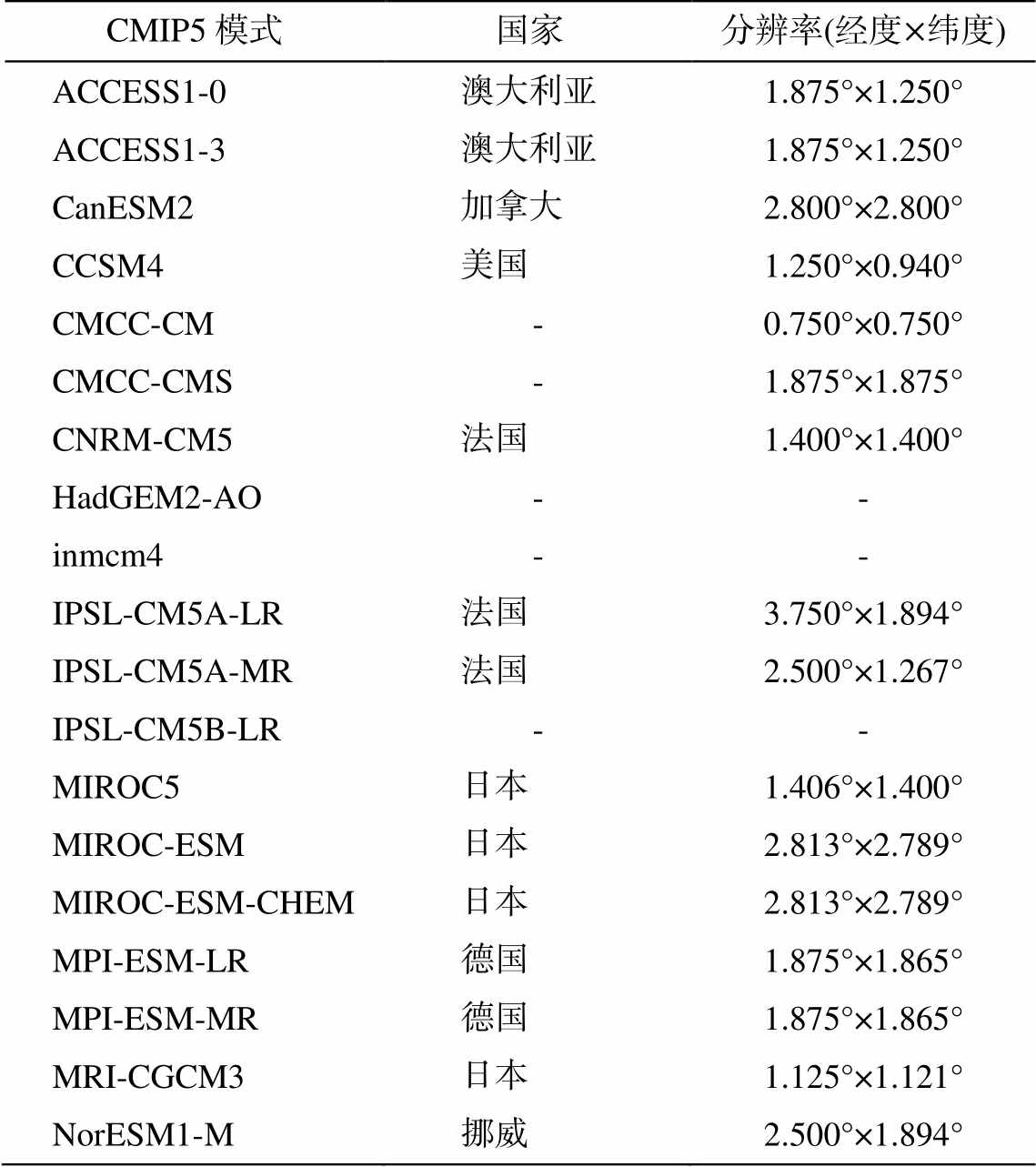
本文使用的数据包括模式数据和实测降水数据。模式数据采用 CMIP5 中 19 个全球气候模式集成资料, 空间分辨率如表 1 所示。采用自然领域法, 将其插值为同一空间分辨率的格点化模式数据, 时间尺度为 1961—2005 年。实测降水数据来自中国气象科学数据共享服务网(http://cdc.cma.gov.cn/)的中国气象格网数据, 空间分辨率为 0.5°×0.5°, 获取方法为对实测气象站点数据进行薄盘样条插值, 并考虑经度、纬度和高程, 插值后的格点化降水资料有较好的精度, 可以作为模式模拟结果的验证数据[23]。
图1 鄱阳湖流域[21]
Fig. 1 Poyang Lake Basin[21]
我们考虑求解如下带约束的函数优化问题:
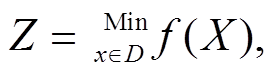
使其满足不等式
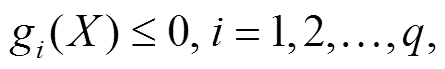
其中
f(X)为目标函数, 记D中的m个数的点为
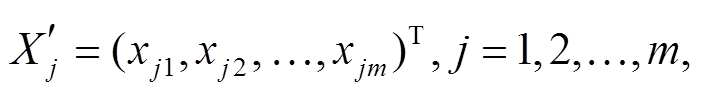
记它们所张成的子空间为
表1 本文采用的19个CMIP5模式数据
Table 1 19 CMIP5 models used in this study
CMIP5模式 国家分辨率(经度纬度) ACCESS1-0澳大利亚1.875°×1.250° ACCESS1-3澳大利亚1.875°×1.250° CanESM2加拿大2.800°×2.800° CCSM4美国1.250°×0.940° CMCC-CM-0.750°×0.750° CMCC-CMS-1.875°×1.875° CNRM-CM5法国1.400°×1.400° HadGEM2-AO-- inmcm4-- IPSL-CM5A-LR法国3.750°×1.894° IPSL-CM5A-MR法国2.500°×1.267° IPSL-CM5B-LR-- MIROC5日本1.406°×1.400° MIROC-ESM日本2.813°×2.789° MIROC-ESM-CHEM日本2.813°×2.789° MPI-ESM-LR德国1.875°×1.865° MPI-ESM-MR德国1.875°×1.865° MRI-CGCM3日本1.125°×1.121° NorESM1-M挪威2.500°×1.894°
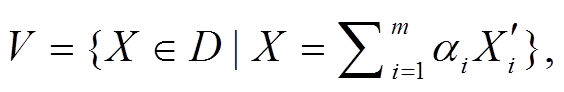
其中, ai满足
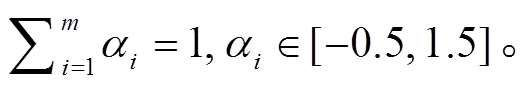
记
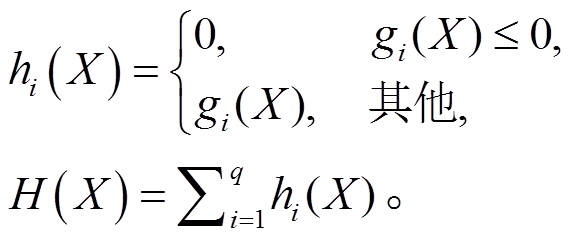
定义逻辑函数
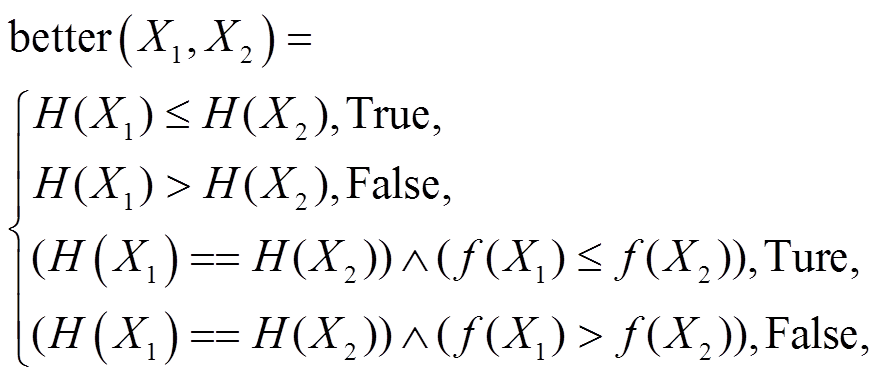
better(X1, X2 )==Ture表示X1优于X2。
传统的遗传算法如图 2 所示。当 M 个个体张成子空间时, 若 M >15, 则遗传算法的生成效率几乎为 0[21](图 3)。但是, 在多模式集合优化研究中,M 的数值远大于 15。本文提出改进的遗传算法(IGA), 解决了上述问题(图 3)。IGA 算法流程如图 4 所示。
Taylor 图[20]适合评估复杂模型的多个指标或相对指标。我们利用 Taylor 图对一组模式与观测结果的匹配程度进行直观的分析, 评估 19 个 CMIP5 气候模式在鄱阳湖流域的模拟能力(图 5)。两种模式之间的相似性通过其相关性、中心化均方根误差及其变化幅度(用标准差表示)来量化。
假设两个场的空间相关系数为 R, 模拟场的标准差为 σf, 观测场的标准差为 σr, 均方根误差为 E, 中心化均方根误差为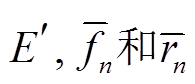
分别表示第像素 n 的模拟值和观测值, 
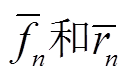分别表示模拟和观测数据的平均值, 则
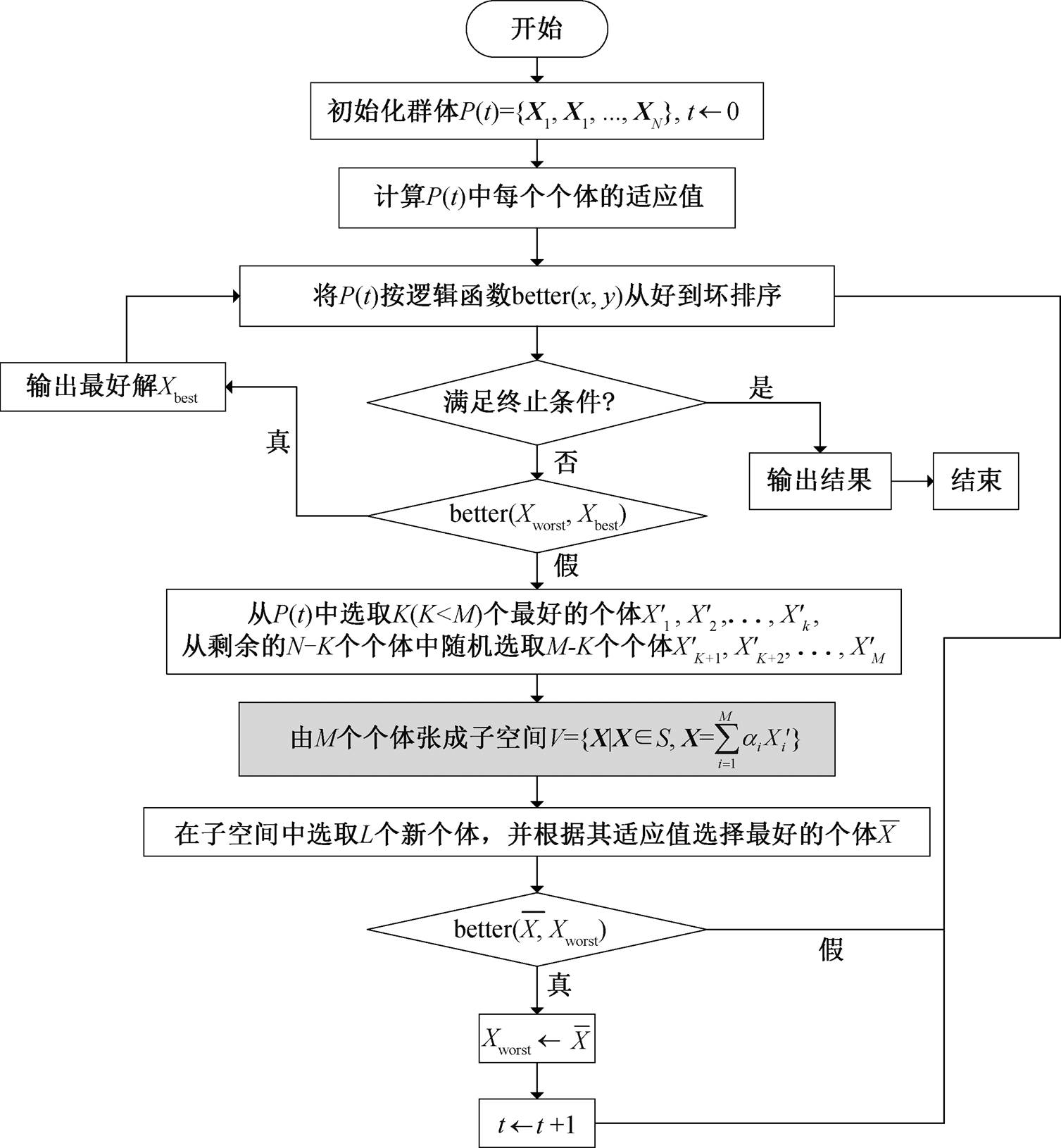
图2 遗传算法流程图(GA)
Fig. 2 Flow chart of Genetic Algorithm (GA)
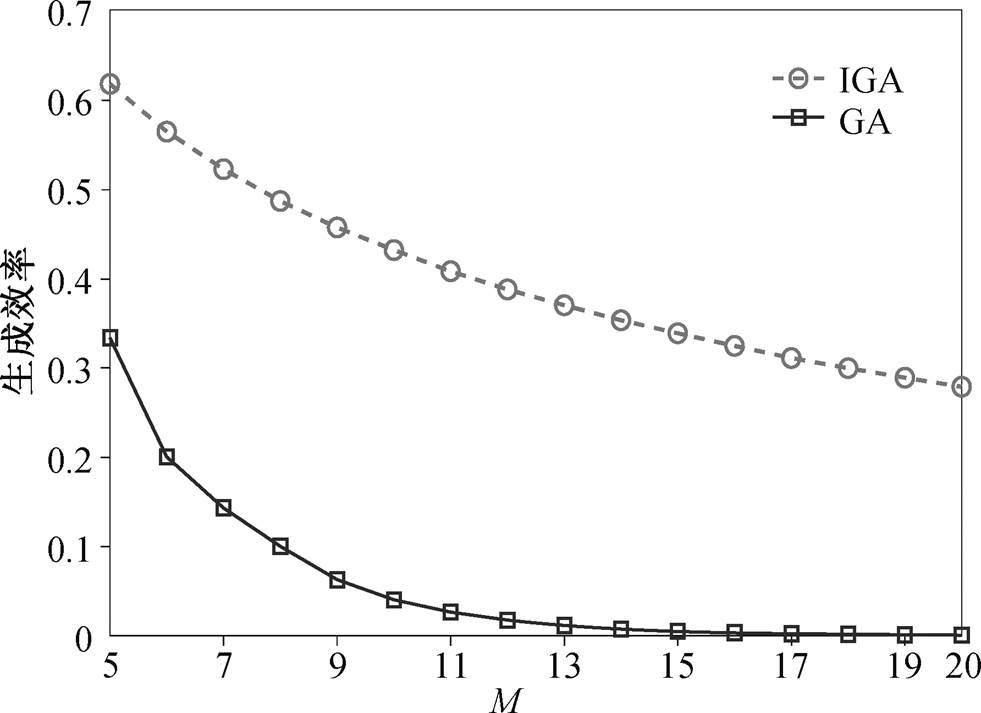
图3 GA和IGA的生成效率随个体数量 M的变化
Fig. 3 Efficiency of GA & IGA with incensement of M value
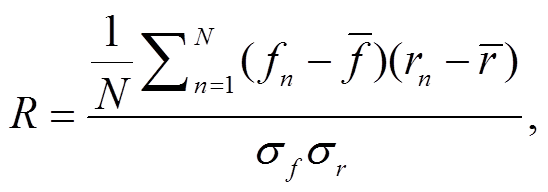
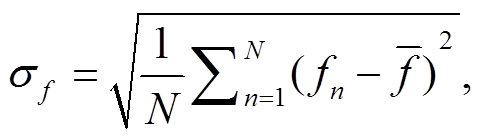
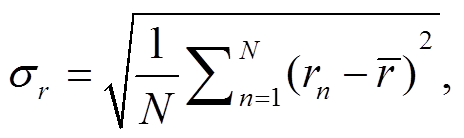
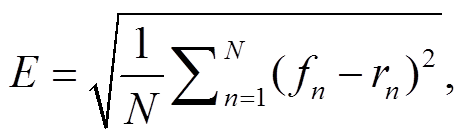
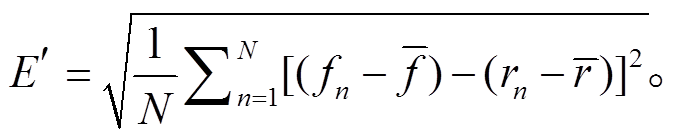
上述统计量遵循关系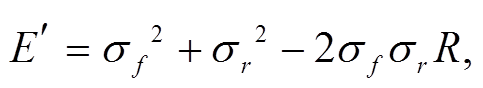
当 R 值越大, 
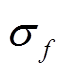与
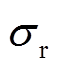越接近时,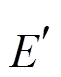 
值越小, 模拟值越靠近观测值, 模式的模拟精度越高[24]。因此,本文将
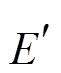作为 IGA 算法的评价函数
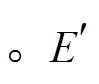引导算法的演化方向, 演化结束后, 模拟值与观测值的
理论上达到最小, 模拟精度最高。
单一的 CMIP5 气候模式在模拟某一区域的月累积降雨量时, 会受到区域分布特征(如地势地貌、经纬度和土地利用类型等)、季节及月份的影响, 而这些因素对多模式集合结果的影响也存在差异。因此, 本文基于 IGA 算法, 构建 4 种多模式集合的优化算法: 集总式算法(Lumped Algorithm, LA)、时间分布式算法(Tempo-distributed Algorithm, TA)、空间分布式算法(Spatially-distributed Algorithm, SA)和时空分布式算法(Tempo-Spatially Distributed Algorithm, TSA)。
图4 改进遗传算法(IGA)
Fig. 4 Flow chart of improved GA (IGA)
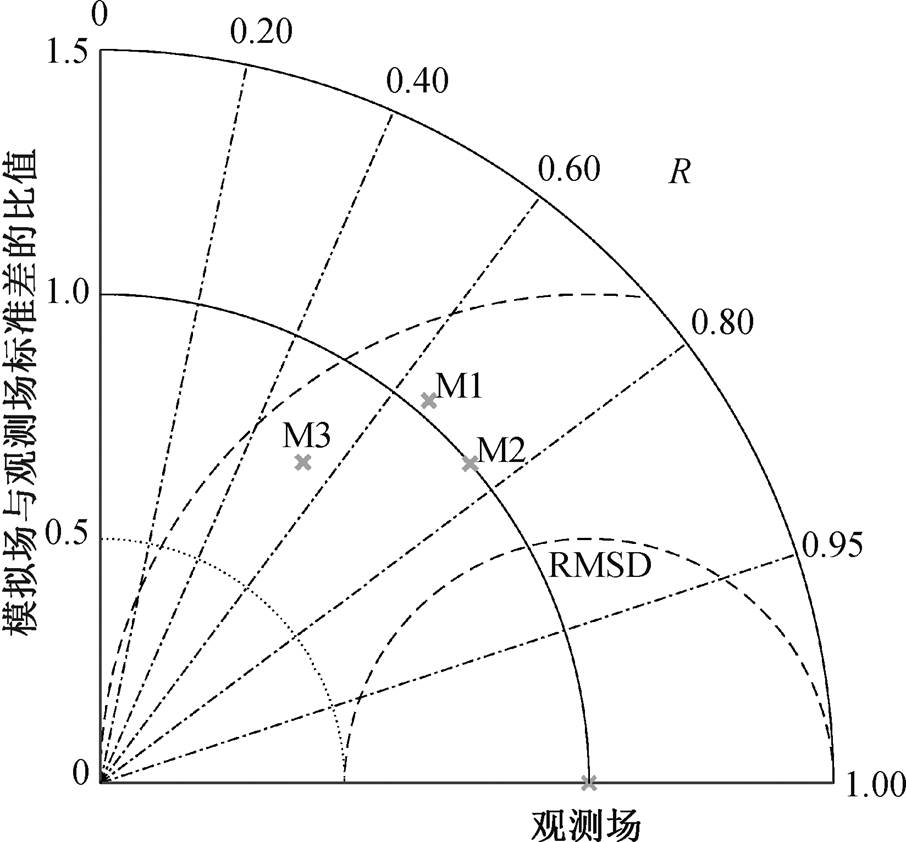
M1, M2 和 M3 分别表示 3 个模型, 其位置表示模型的模拟值与观测结果的匹配程度
图5 样本泰勒图[20]
Fig. 5 Sample Taylor diagram[20]
2.3.1 集总式算法(LA)
LA 算法不考虑模式在时空上的模拟精度差异, 只考虑模式本身的性能, 即为每一个模式分配一个权重ωj, 通过 IGA 优化得到最优权重向量 Wi:
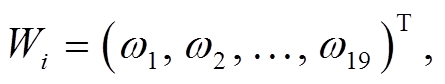
其中,
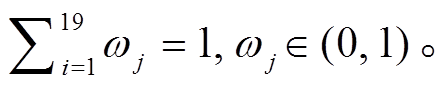
LA算法流程如图 6 所示。
LA 算法的输入数据为 10800 张影像(10260 张模拟影像和 540 张观测影像), 影像大小为 25pixels ×20pixels。输出数据为最优权重向量 Wi=(ω1, ω2,…, ω19)T。Wi 为 10260 张模拟影像的公共权重向量, ωj 为 540 张影像的公共权重, 如图 7 所示。540 张观测影像由 1961 年 1 月至 2005 年 12 月的实测气象站点数据插值后得到。
2.3.2 时间分布式算法(TA)
TA 算法除考虑模式本身的性能外, 还考虑模式在时间尺度上模拟性能的差异性, 其中时间尺度分为季度尺度和月份尺度。在季度尺度上, 为每个模式分配 4 个权重, 每个权重对应春(2 至 4 月)、夏(5 至 7 月)、秋(8 至 10 月)和冬(11 月至 1 月) 4 个季度, 最后得到 19×4=76 个权重值。在月份尺度上, 为每个模式分配 12 个权重, 每个权重对应一个月份, 最后得到 19×12=228 个权重值。本文只从季度尺度来进行分析。
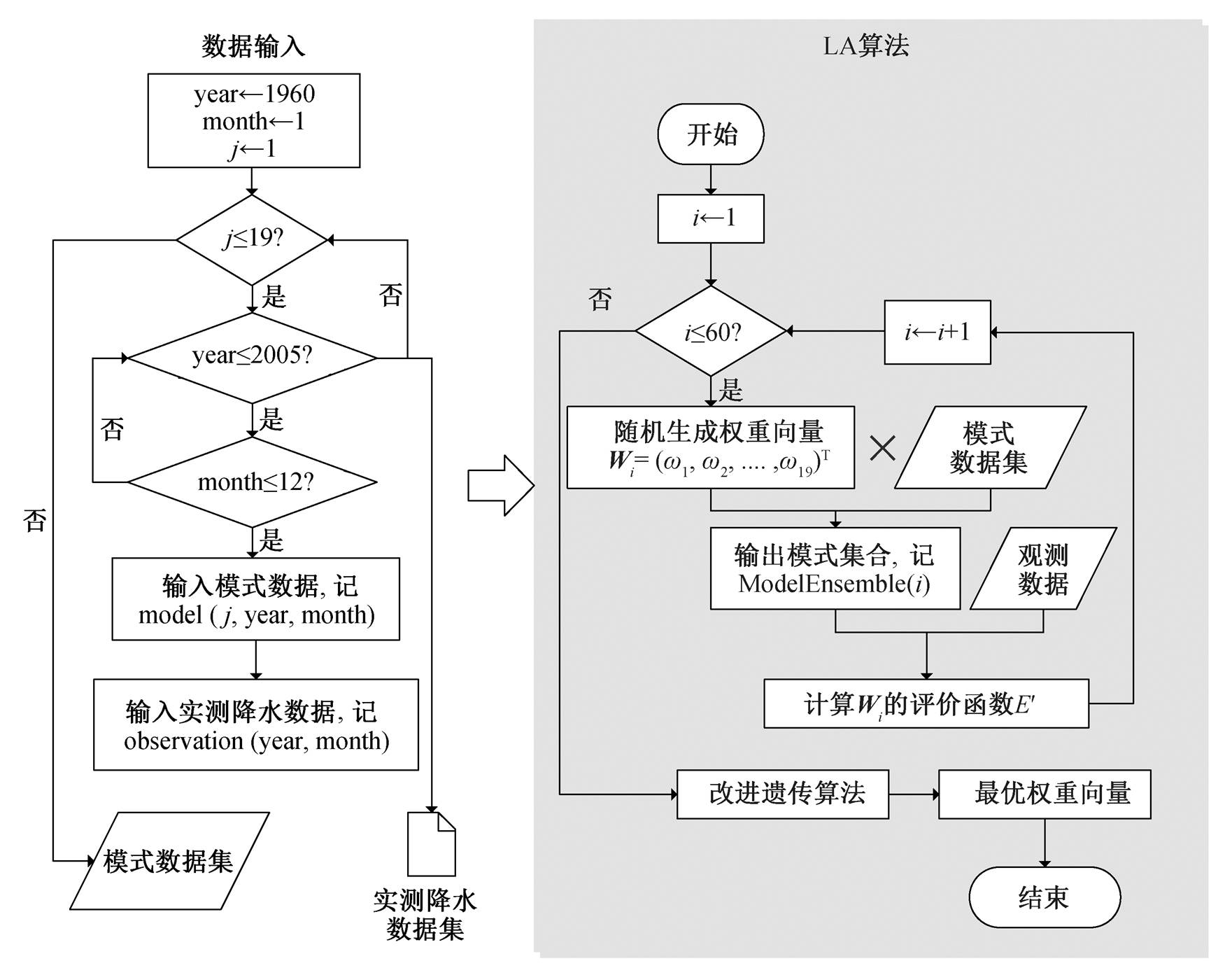
图6 集总式算法流程(LA)
Fig. 6 Flow chart of Lumped Algorithm (LA)
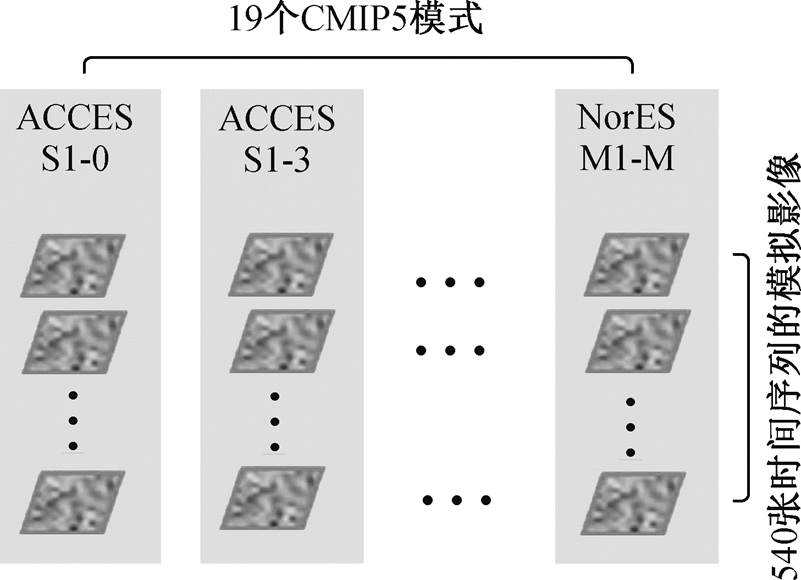
图7 LA算法在模式尺度上的权重分配
Fig. 7 Weight assignment of LA algorithm on model scale
TA 算法与 LA 算法相似, 区别是 LA 算法优化的是权重向量 Wi=(ω1, ω2, …, ω19), 而 TA 算法优化的是权重矩阵(W1, W2, W3, W4)T, 下角标 1 表示春季, 2 表示夏季, 3 表示秋季, 4 表示冬季。
在 19 个模式中, 每个模式都可模拟得到从 1961 年 1 月至 2005 年 12 月的 540 张月累积降雨量影像。前 135 张影像表示 1961—2005 年的春季, 第 136~ 270 张影像表示 1961—2005 年的夏季, 第 271~405张影像表示 1961—2005 年的秋季, 第 406~540 张影像表示 1961—2005 年的冬季。
TA 算法在模式尺度上的权重分配见图 8。
2.3.3 空间分布式算法(SA)
SA 算法除考虑模式本身的性能外, 还考虑模式在空间尺度上模拟性能的差异性, 为每个模式分配 500 个权重(影像大小为 25pixels×20pixels), 每个权重对应一个相同空间位置的像素(即同名像素), 最后得到 19×500=9500 个权重值。SA算法与 TA 算法优化的都是权重矩阵, 但 TA 算法优化的权重矩阵是(W1, W2, W3, W4)T, SA算法优化的权重矩阵是(W1, W2, …, W500)T, 下角标i表示格网编号, i与像素行列号的关系为
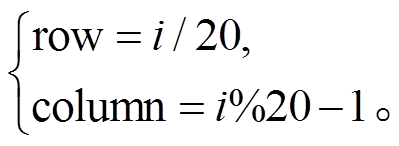
SA 算法中权重矩阵的每一个要素 Wi (i=1,…, 500)在模式尺度上的权重分配与图 7 类似, 只是图 7 中每个格网表示一张影像, 但 SA 算法中的每个格网表示该影像中的第 i 个像素。
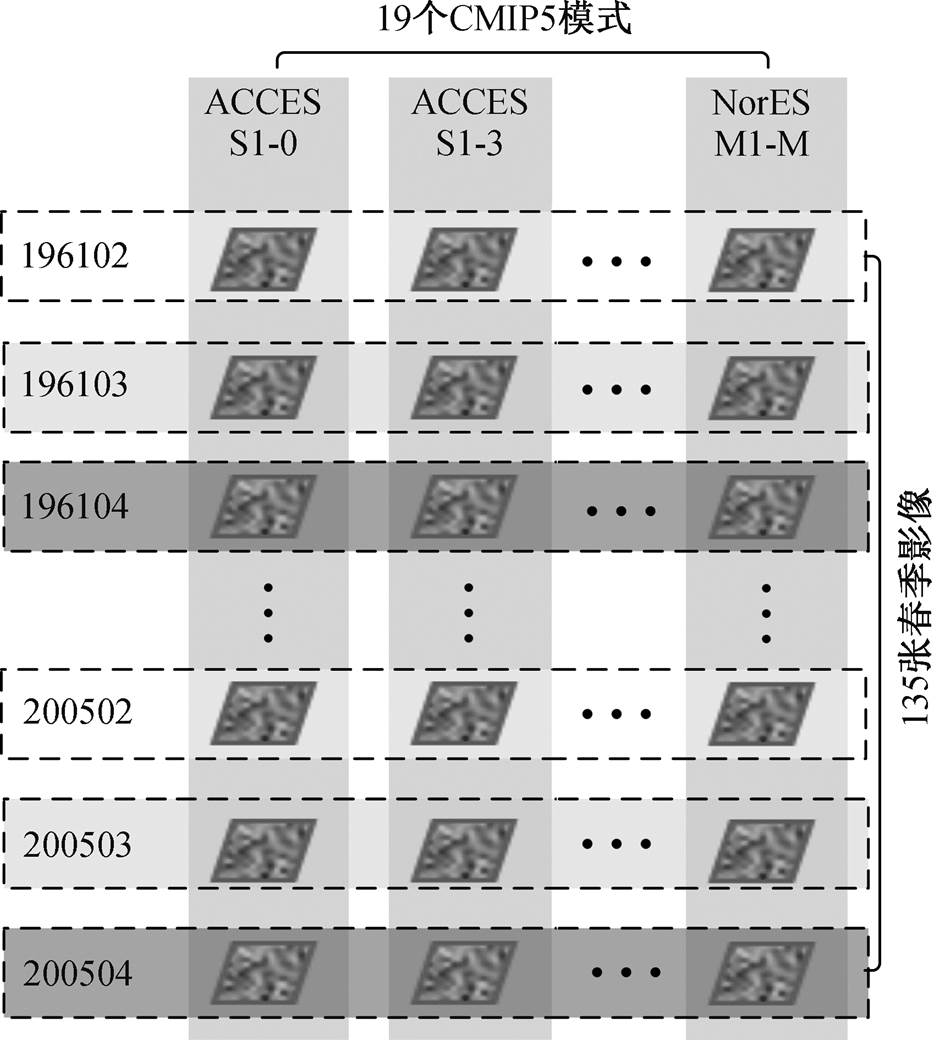
图8 TA算法在时间尺度上的权重分配
Fig. 8 Weight assignment of TA algorithm on time scale
2.3.4 时空分布式算法(TSA)
TSA 算法不仅考虑模式本身的性能, 还考虑模式在时间和空间尺度上模拟性能的差异性。结合TA 和 SA 算法, TSA 算法优化的权重矩阵为
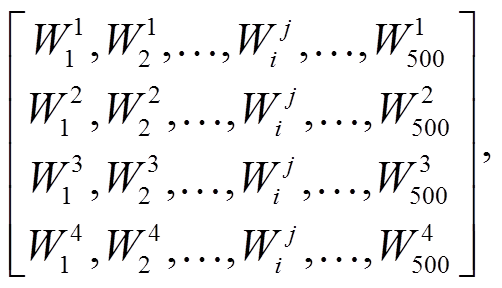
其中, 下角标 i 表示格网编号, 上角标 j 表示季度(j=1 表示春季, j=2 表示夏季, j=3 表示秋季, j=4 表示冬季)。该权重矩阵中的每个元素
是一个向量, 且满足约束“向量中的所有元素之和为 1”, 即
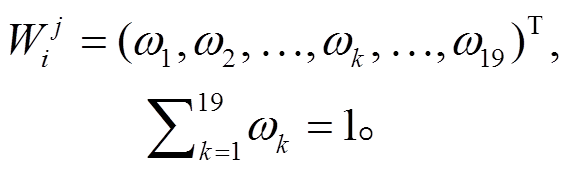
此外, 权重矩阵也满足约束“每一行之和等于1, 每一列之和等于1”, 即
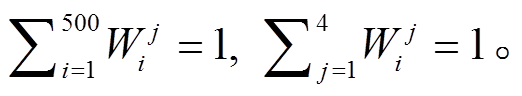
TSA 算法中权重矩阵的每一列向量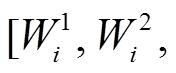
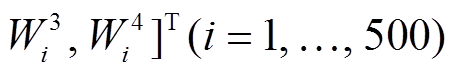的权重分配与图 8 类似, 只是图 8 中每个格网表示一张影像, 但 TSA 算法中的每个格网表示该影像中的第 i 个像素。例如, TSA中
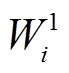向量为 1961—2005 年的 2—4 月(春季)影像的第 i 个像素的权重向量。
一般认为, 单一模式的精度越高, 其在集合模式中的权重越大, 为了分析两者的关系, 首先分析19 个 CMIP5 单一模式的权重在 LA 算法中的演化规律(图 9(a)~(c)), 图 9(d)为 LA 算法的收敛曲线。图10 不仅说明 CMIP5 单一模式在 LA 模式集合中的权重, 还列出不同单一模式的精度。
由图 9(d)可以看出, LA 模式集合的精度在IGA 演化中逐渐变高(E'减小, R 增大), 我们将第20000 代的最优个体作为最终的模式集合。图 9(a)中, 当 MIROC_ESM_CHEM 模式的权重在 LA 算法演化到 20000 代时, 占比由 15%增至 30%。图 10 也清楚地表明 MIROC_ESM_CHEM 模式的精度最高, 在 LA 模式集合中占比也最高。这说明该模式是一个很好的模式, 且在模式集合中有较大的主导作用。图 9(b)中, 当 LA 算法演化到 20000 代时, IPSL-CM5A-MR, CMCC-CMS 和 CNRM-CM5 模式在 LA集合中逐渐消失, 其他模式在 LA 集合的占比也减小 1%~6%, 这些模式对 LA 集合的构建影响很小。图 9(c)中, 当 LA 算法演化到 20000 代时, MIROC-ESM, MPI-ESM-LR 和 inmcm4 模式在 LA集合的占比增加约 3%, 这 3 个模式对 LA 集合的构建虽不起主导作用, 但影响较大。
图 10 中, 精度用 1/E' 表示, E' 越小, 精度越高。可以看出, MIROC5 模式的精度很低, 但它在LA 模式集合中约占 6%。IPSL_CM5B_LR 的精度高于 MIROCS 模式, 但它在 LA 模式的构建中逐渐消失。这说明 CMIP5 单一模式的精度并不能决定模式集合的精度。
图 11 为本文提出的 4 种多模式集合算法 LA, TA, SA, TSA 以及 CMIP5 模式的月降雨量模拟精度评价结果。可以看出, LA 模拟不同月份累积降雨量的精度皆高于 CMIP5 模式。TA 和 SA 的精度皆高于 LA 。除 5 月和 6 月 SA 的精度高于 TA 外, 其余月份两个模式的精度相近。TSA 的精度最高。
图 12 为 Cali-EE, LA, TA, SA, TSA 和 CMIP5 模式的精度评价结果。模式与观测场的距离为模式的中心化均方根误差 E'与观测场标准差的比值。模式愈接近红色线(半径为 1), 标准差愈接近观测场。模式的弧度越接近 π/2, 与观测场的相关系数越大。模式愈接近观测场, 其中心化均方根误差 E'越小。综上所述, 精度高的模式集合需满足: 1)模式与观测场的相关系数大; 2)模式的标准差接近观测场的标准差; 3)模式与观测场的中心化均方根误差小。
5 个集合模式和 19 个单一 CMIP5 模式在图 12的位置表明, 集合模式的 3 个量化指标都优于单一CMIP5 模式, 即集合模式的精度比 CMIP5 模式高。5 个集合模式的精度指标见表 2。图 12 和表 2 表明本文提出的 4 种算法的精度皆高于 Cali-EE[11]。在这 4 种算法中, 同时考虑了模式精度在时间和空间上差异性的 TSA 算法模拟精度最高。
LA 算法未考虑模式在时间和空间上的模拟精度差异, 只考虑不同模式在鄱阳湖流域对降雨的整体模拟能力的差异性, 因此 LA 的模拟精度低于 TA, SA 和 TSA。但是, LA 只需优化 19 个权重, 计算速度较快。TA 算法除考虑模式本身的性能外, 还考虑大气环流的季节性变化对降雨量的影响, 因此 TA 的模拟精度优于 LA。SA 算法除考虑模式本身的性能外, 还考虑到鄱阳湖流域地形多样, 下垫面复杂, 因此 SA 的模拟性能优于 LA。TSA 算法同时考虑了模式在时间和空间尺度上模拟性能的差异性, 因此模拟精度最高, 但该模式集合需要优化的权重数太多, 计算速度较慢。
本文利用改进遗传算法构建 4 种多模式集合的优化算法: 集总式、时间分布式、空间分布式和时空分布式集合。以鄱阳湖流域为研究对象, 将 19个 CMIP5 气候模式数据和一个观测数据作为算法的输入数据, 经过改进遗传算法演化得到优化权重, 并利用 Taylor 图对构建的模式集合进行精度评价。结果表明, 本文构建的 4 种模式集合的模拟精度都优于等权集合和单一模式, 且时空分布式集合的模拟精度最高。本文研究结果对气候模式的应用研究具有借鉴意义。但是, 本研究只利用统计学的方法评估气候模式的精度, 没有从降雨量的时空分布特征上进行评估。此外, 关于 CMIP5 气候模式类型和数量的选择策略也是多模式集合中一个重要的研究方向。
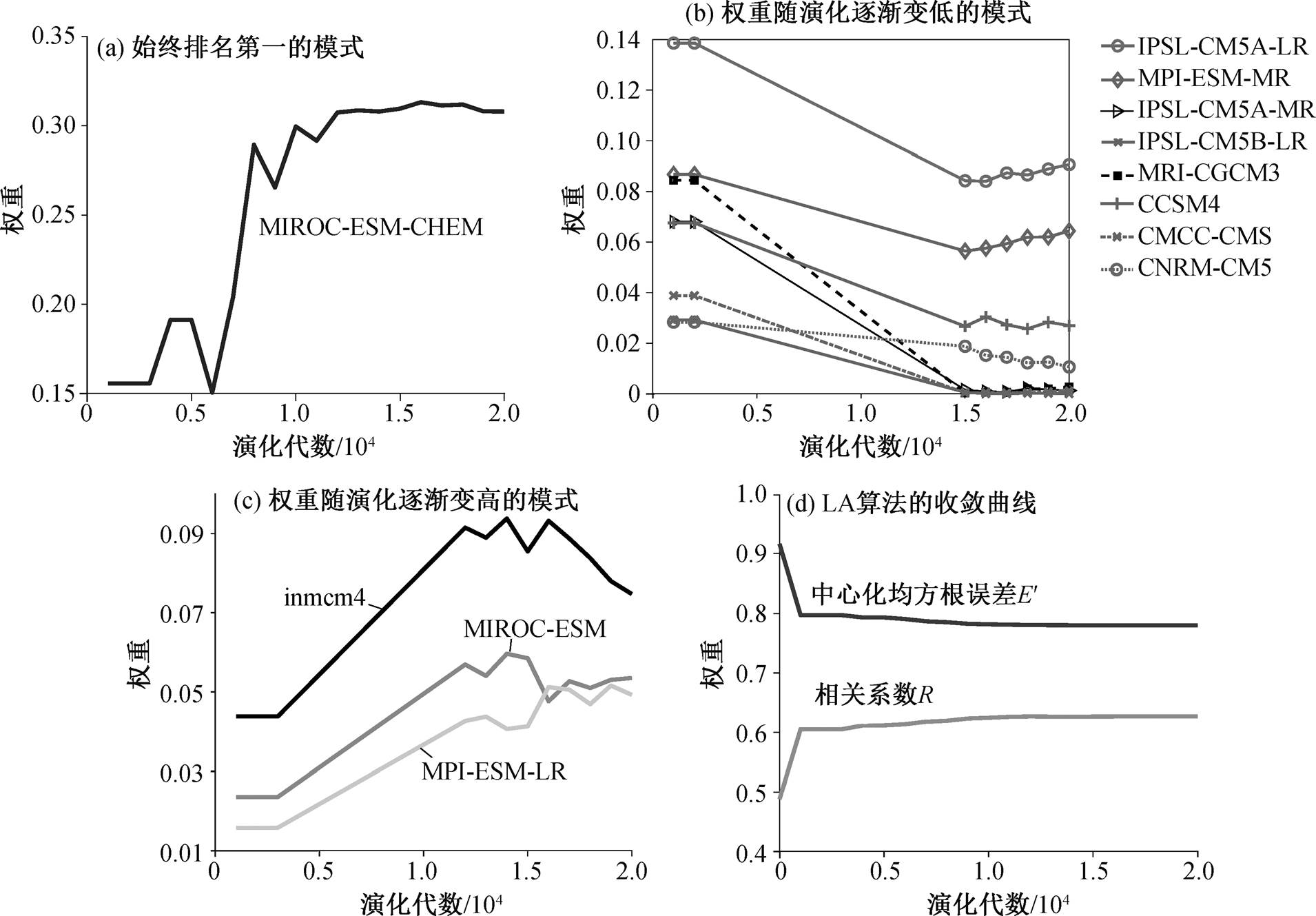
图9 CMIP5单一模式在LA模式集合中的权重变化
Fig. 9 Weight change of CMIP 5 models with LA evolution
图10 CMIP5单一模式的模拟精度以及在LA模式集合中的权重
Fig. 10 Accuracy of CMIP5 models and their weight in LA model ensemble
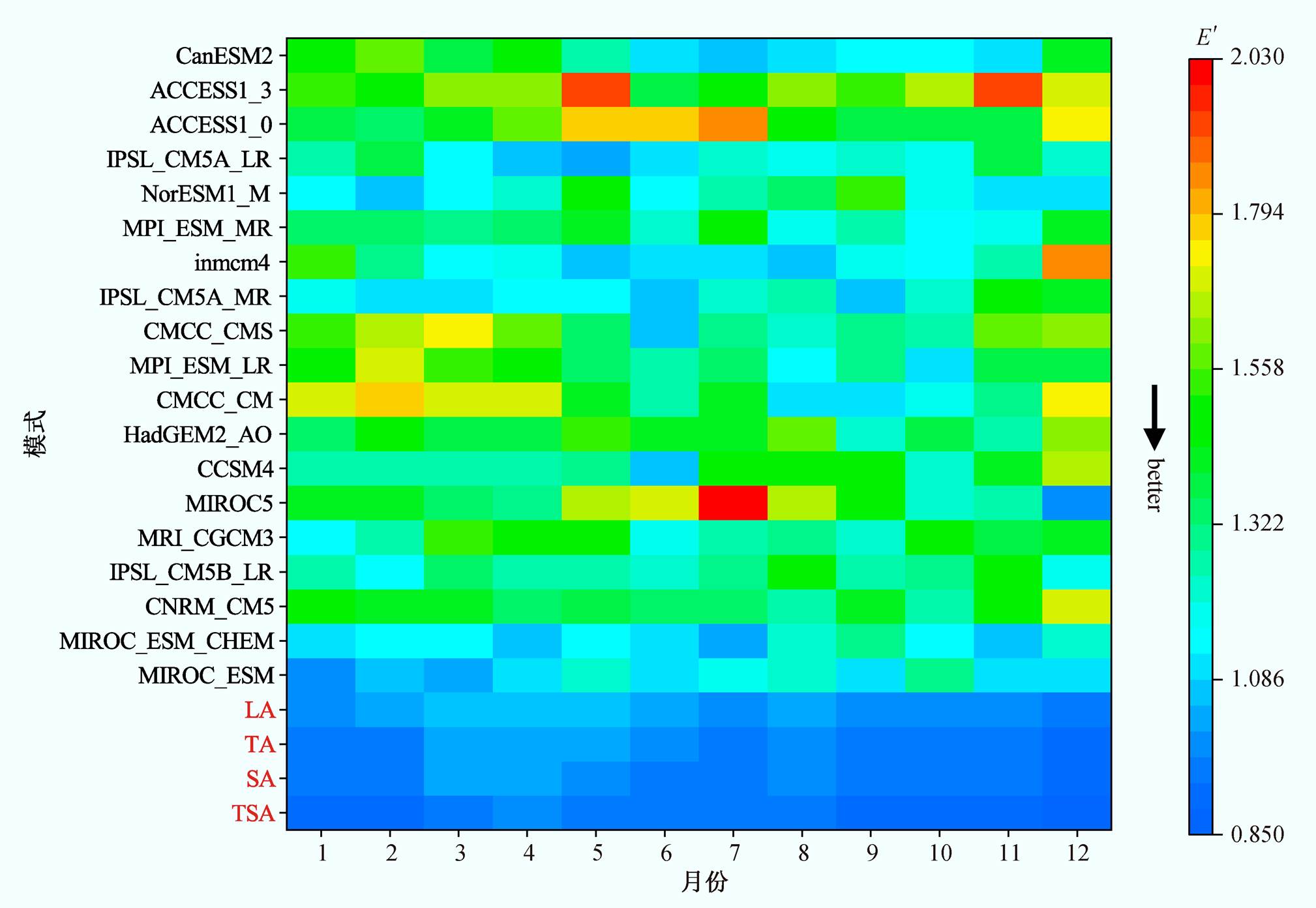
图11 LA, TA, SA, TSA和CMIP5模式的月降雨量模拟精度评价
Fig. 11 Monthly accuracy assessment of LA, TA, SA, TSA and CMIP5 models
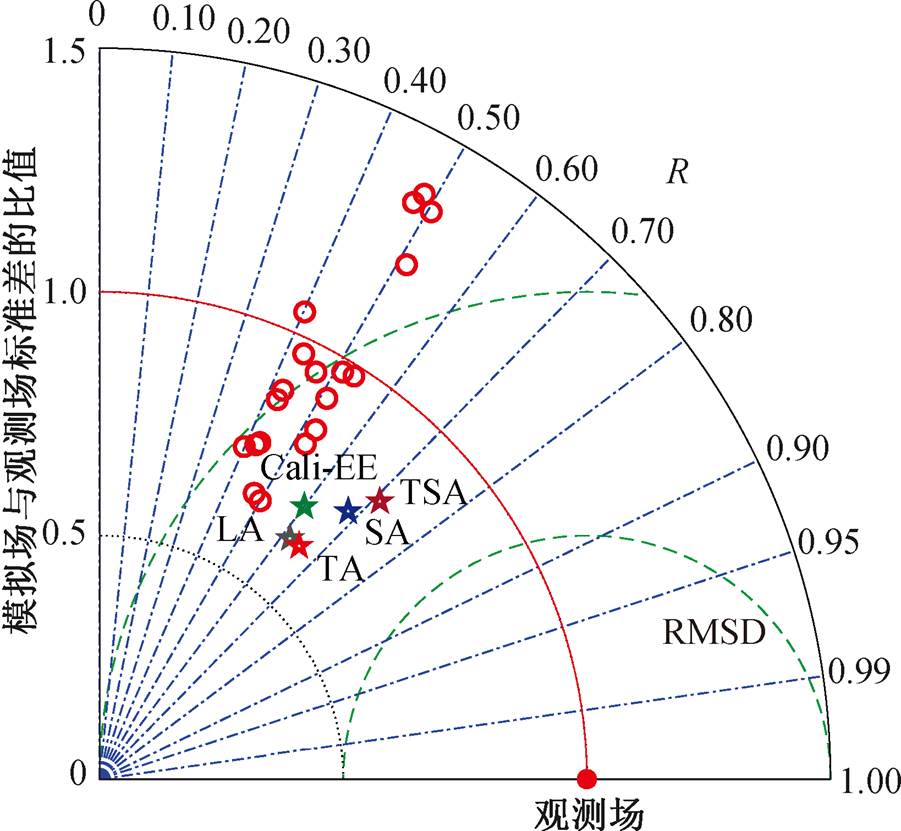
红色空心圆表示单一模式(CMIP5)
图12 Cali-EE, LA, TA, SA, TSA和CMIP5模式的精度评价
Fig. 12 Accuracy assessment of Cali-EE, LA, TA, SA, TSA and CMIP5 models
表2 5种模式集合的精度对比
Table 2 Accuracy comparison of five model ensembles
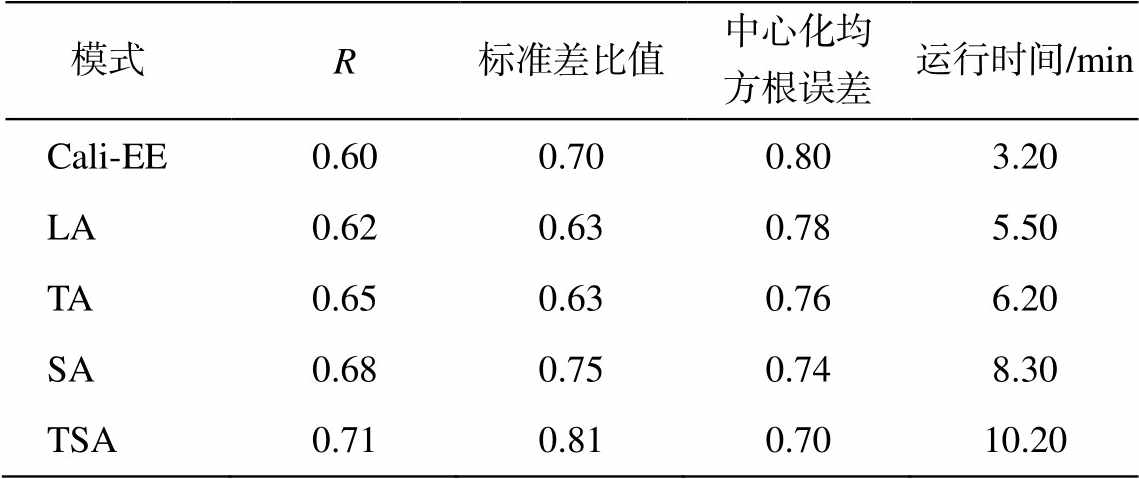
模式R标准差比值中心化均方根误差运行时间/min Cali-EE0.600.700.803.20 LA0.620.630.785.50 TA0.650.630.766.20 SA0.680.750.748.30 TSA0.710.810.7010.20
参考文献
[1] 郭靖. 气候变化对流域水循环和水资源影响的研究[D]. 武汉: 武汉大学, 2010
[2] 纪潇潇. PRECIS 对东亚气候的模拟能力评估和情景分析[D]. 北京: 中国农业科学院, 2015
[3] 魏萌, 乔方利. CMIP5 气候模式模拟的 1850—2014年全球温度变化的集合经验模态分解. 中国科学: 地球科学, 2016, 46(12): 1675-1688
[4] 陈晓晨, 徐影, 许崇海, 等. CMIP5全球气候模式对中国地区降水模拟能力的评估. 气候变化研究进展, 2014, 10(3): 217-225
[5] 杨广. 气候模式中北太平洋海洋环流经向输运对比研究[D]. 杭州: 浙江大学, 2017
[6] 孙. 气候模式对北太平洋海温变率主导模态的评估及其预估[D]. 兰州: 兰州大学, 2013
[7] 李芳. 基于多模式集合方案的中国东部夏季降水概率季度预测. 气象学报, 2012, 70(2): 183-191
[8] Kharin V V, Zwiers F W. Climate predictions with multimodel ensembles. Journal of Climate, 2002, 15 (7): 793-799
[9] Kang I S, Yoo J H. Examination of multi-model ensemble seasonal prediction methods using a simple climate system. Climate dynamics, 2006, 26(2/3): 285-294
[10] Peng P, Kumar A, van den Dool H, et al. An analysis of multimodel ensemble predictions for seasonal climate anomalies. Journal of Geophysical Research: Atmospheres, 2002, 107(D23): 18-1-18-12
[11] Ke Z, Zhang P, Dong W, et al. A new way to improve seasonal prediction by diagnosing and correcting the intermodel systematic errors. Monthly Weather Re-view, 2009, 137(6): 1898-1907
[12] Krishnamurti T N, Kishtawal C M, LaRow T E, et al. Improved weather and seasonal climate forecasts from multimodel superensemble. Science, 1999, 285: 1548- 1550
[13] Gneiting T, Raftery A E, Westveld III A H, et al. Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estima-tion. Monthly Weather Review, 2005, 133(5): 1098-1118
[14] Weigel A P, Liniger M A, Appenzeller C. Seasonal ensemble forecasts: are recalibrated single models better than multimodels?. Monthly Weather Review, 2009, 137(4): 1460-1479
[15] Coelho C A S, Pezzulli S, Balmaseda M, et al. Fore-cast calibration and combination: a simple Bayesian approach for ENSO. Journal of Climate, 2004, 17(7): 1504-1516
[16] Luo L, Wood E F, Pan M. Bayesian merging of multi-ple climate model forecasts for seasonal hydrological predictions. Journal of Geophysical Research: Atmos-pheres, 2007, 112(D10): D10102
[17] Li Fang, Zeng Qingcun, Li Chaofan. A Bayesian scheme for probabilistic multi-model ensemble pre-diction of summer rainfall over the Yangtze River Valley. Atmospheric and Oceanic Science Letters, 2009, 2(5): 314-319
[18] Raftery A E, Gneiting T, Balabdaoui F, et al. Using Bayesian model averaging to calibrate forecast ensem-bles. Monthly Weather Review, 2005, 133(5): 1155-1174
[19] Zhu Z, Piao S, Lian X, et al. Attribution of seasonal leaf area index trends in the northern latitudes with “optimally” integrated ecosystem models. Global Change Biology, 2017, 23(11): 4798-4813
[20] Taylor K E. Summarizing multiple aspects of model performance in a single diagram. Journal of Geophy-sical Research: Atmospheres, 2001, 106(D7): 7183-7192
[21] 左正康, 吴志健, 孙逸渊, 等. 利用经验概率密度曲线加快精英多父体杂交算法中系数向量的生成. 武汉大学学报(工学版), 2020, 53(8): 728-733
[22] 原立峰, 杨桂山, 李恒鹏, 等. 近 50 年来鄱阳湖流域降雨多时间尺度变化规律研究. 长江流域资源与环境, 2014, 23(3): 434-440
[23] Zhang L, Lu J, Chen X, et al. Stream flow simulation and verification in ungauged zones by coupling hydrological and hydrodynamic models: a case study of the Poyang Lake ungauged zone. Hydrology and Earth System Sciences, 2017, 21(11): 5847-5860
[24] 田芝平, 姜大膀. 不同分辨率 CCSM4 对东亚和中国气候模拟能力分析. 大气科学, 2013, 37(1): 171-186
CMIP5 Climate Multi-model Ensemble Optimization Based on Spatial-Temporal Distribution
Abstract The multi-mode ensemble based on spatiotemporal distribution is constructed to reduce the uncertainty of a single-model and the non-uniform distribution of the traditional model ensembles. The improved genetic algorithm is employed to optimize the multi-model ensemble of CMIP5 global climate data from temporal and spatial scales, and Taylor diagram is used to evaluate its simulation performance. The experimental results show that the multi-mode ensemble based on spatiotemporal distribution is superior to the traditional equal weight multi-mode ensemble scheme.
Key words multi-mode ensemble; optimization; genetic algorithm; spatial-temporal distribution; CMIP5
doi: 10.13209/j.0479-8023.2020.057
收稿日期: 2019-09-08;
修回日期: 2019-12-20
国家重点研发计划项目(2018YFC1506506)、武汉市应用基础前沿专项(2019020701011502)、湖北省自然科学基金(2019CFB736)、江西省重点研发计划(20201BBG71002)和测绘遥感信息工程国家重点实验室专项科研经费资助