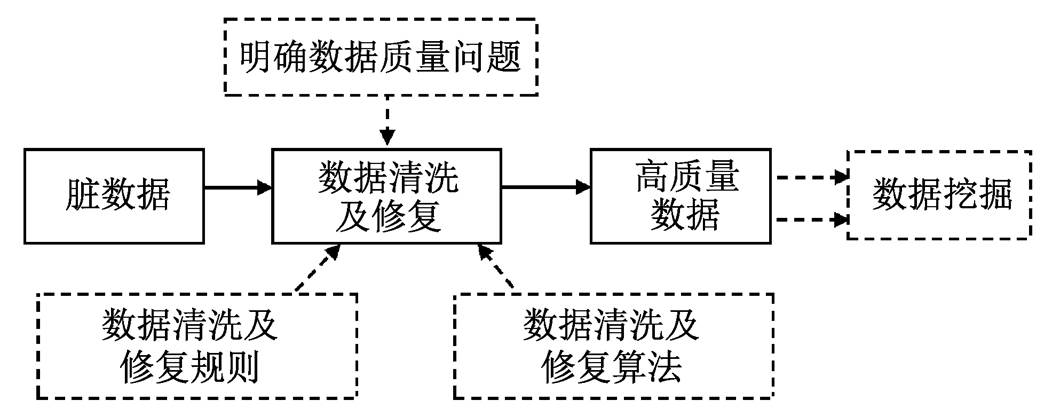
图1 数据清洗及修复流程
Fig. 1 Flow chart of data cleaning and repairing
摘要 针对民用建筑“四节一环保”原始数据中存在的数据质量问题, 使用多种方法实现数据清洗与数据修复。数据清洗方面, 重点关注单栋建筑能耗数据中存在的相似重复记录及异常记录。其中, 识别异常记录采用 3σ 准则、DBSCAN 聚类算法及箱线图内限 3 种方法。数据修复方面, 重点关注缺失值的填补及基于模型的数据修正。其中, 缺失值的填充使用简单填充、线性回归模型和基于用户的协同过滤推荐算法, 并以平均绝对误差为评估指标进行对比。基于多元线性回归、主成分回归、偏最小二乘回归、岭回归及 Lasso 回归 5 种模型, 拟合建筑运行能耗与各解释变量间的关系, 对上海市建筑运行能耗相关数据进行数据修复。结果显示, 单栋建筑能耗数据适合采用箱线图内限来识别异常记录, 并使用中位数填补缺失数据; 上海市建筑运行能耗相关数据中, 岭回归模型的拟合情况最好。
关键词 四节一环保; 数据清洗; 数据修复; DBSCAN聚类算法; 基于用户的协同过滤推荐算法; 岭回归
民用建筑“四节一环保”大数据及数据获取机制构建项目从大规模实际采集数据出发, 结合我国新型城镇化建设需求与绿色建筑及建筑工业化领域的科技需求, 旨在定量地给出我国民用建筑在节能、节水、节地、节材和环保(简称“四节一环保”)等方面的实际状况, 从而实现我国民用建筑基础数据持续更新与共享应用, 推动我国绿色建筑及其工业化实现规模化、高效益和可持续发展。由于采集来源的多样、数据获取软硬件的潜在故障以及数据采集人员的人为因素, 导致通过不同渠道获取的民用建筑“四节一环保”大数据存在缺失、错误和噪声等多方面问题, 对后续处理与分析产生严重影响, 故需厘清“四节一环保”原始数据中存在的数据质量问题, 并进行数据清洗及修复。
在大数据环境下, 很多领域(如数字化文献服务、互联网、金融审计和电子政务等)都涉及数据清洗。人们希望系统中的数据准确且有效, 进而从海量数据中挖掘出有价值的信息或知识, 为决策者提供参考。现实情况中, 由于数据录入错误、指标定义或表示方法不同的数据源合并等原因, 原始数据中掺杂着不完整、不准确和重复的“脏数据(dirty data)”[1]。此时, 需要对源数据进行清洗及修复, 流程如图 1 所示。首先明确数据中存在的质量问题, 其次结合相关技术, 针对性地采用不同清洗及修复规则或算法, 通过删除或修正不符合要求的数据, 将脏数据转化为可用于数据挖掘的高质量数据, 从而提高后续分析的效率和准确性。
数据中存在的质量问题可能出现在单数据源或多数据源下的模式层或实例层, 根据问题的来源, 将数据质量问题进行分类[2-3], 结果如图 2 所示。比如在数据集中, 针对同一现实实体, 可能存在多条不完全相同的记录, 这些记录称为相似重复记录。基于数据的唯一性原则, 需要检测出数据集中存在的相似重复记录, 并对多余记录进行删除。通常采用排序及合并的方式消除相似重复记录, 即先将数据集中的记录按某种顺序排序, 再通过比较近邻记录是否相似来判断是否存在重复记录[4], 最后将重复记录合并, 使得对于一个现实实体, 只存在唯一一条记录与之对应。异常点为样本集中数值与其余观测值相差过大的个别样本(也称为离群点), 对异常记录的识别通常结合描述性统计、箱线图、3σ准则、格拉布斯检验法[5]和 Generalized ESD 检验[6]等较为简单直观的工具和方法。此外, 还有一些较为复杂的异常点检测算法, 如基于模型的异常点检测方法 RobustScaler[7]、基于密度的异常点检测算法局部异常因子算法[8]以及 DBSCAN (density-based spatial clustering of applications with noise)聚类算法[9]等, 孤立森林算法[10]和 One-Class 支持向量机算法[11]也可用于异常点检测。
图1 数据清洗及修复流程
Fig. 1 Flow chart of data cleaning and repairing
推荐系统(recommendation system, RS)[12]常应用于电子商务、数字化图书馆、教育、电影推荐、音乐或视频点播等领域。例如, Netflix 推荐系统结合 PVR 以及 Top-N 等算法,为用户提供个性化推荐, 具有重要的商业价值; Vialardi 等[13]结合数据挖掘技巧, 提出一种推荐系统帮助学生选择课程; Zheng等[14]提出一种名为 WSRec 的网页服务推荐系统, 主要基于一种混合协同过滤算法进行网页服务选择和推荐。协同过滤(collaborative filtering, CF)是推荐系统中的一种常用算法, 关键步骤为识别相似用户, 并推荐相似用户喜欢的物品[15]。Koohi 等[16]提出的基于用户的协同过滤加入模糊 C-均值聚类的方法, 并在数据集MovieLens 上比较不同的聚类算法。张锋等[17]采用BP 神经网络预测用户对物品的评分, 缓解了数据集中存在的极端稀疏性问题, 从而提高协同过滤推荐系统的推荐质量。考虑到建筑间的相似性, 本文采用基于用户(user-based)的协同过滤推荐算法进行缺失值填充, 并与其他方法的填充结果进行对比。此外, 在具有变化趋势的数据序列中常利用模型拟合数据, 并进行可视化分析及预测。针对数据量较小的数据集, 本文通过模型拟合对数据进行分析及修复。
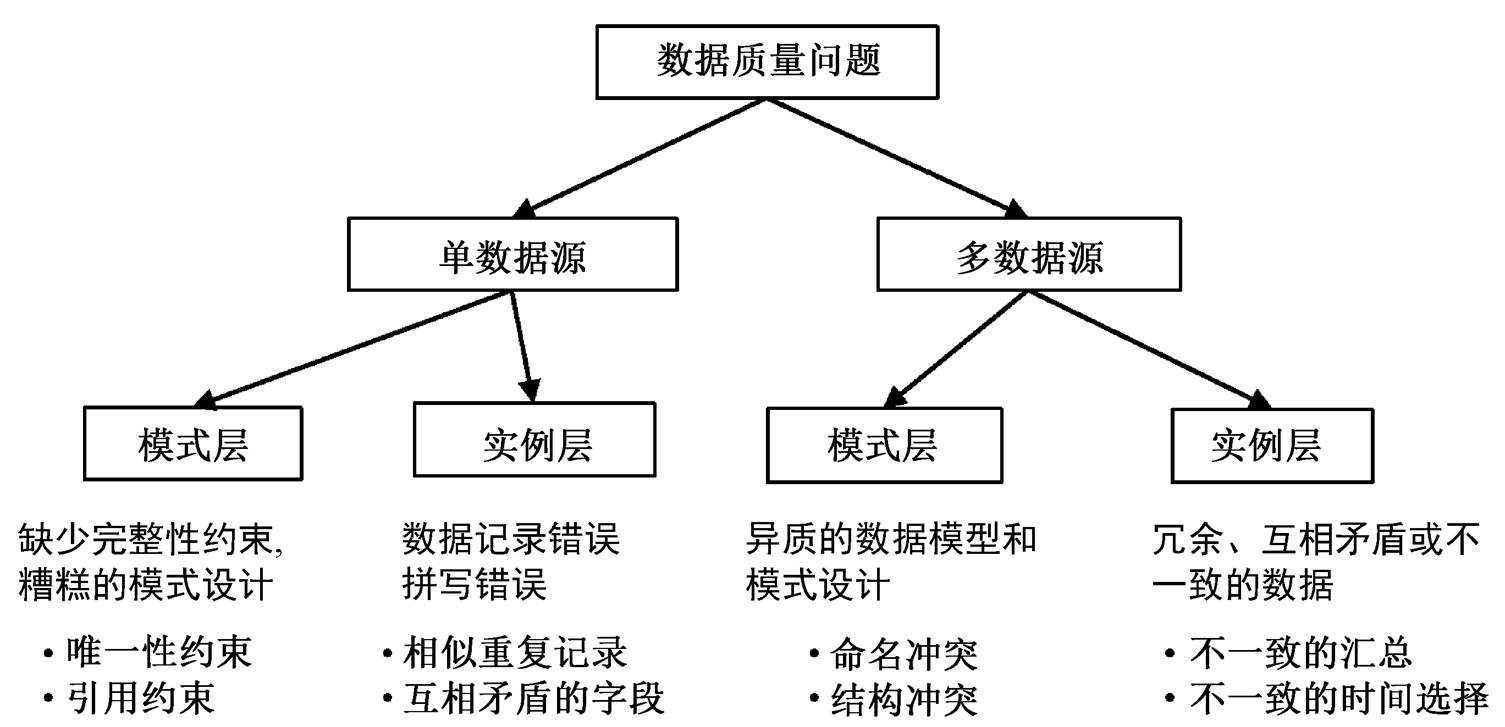
图2 数据质量问题分类
Fig. 2 Classification of data quality issues
本文旨在根据多源多渠道采集的民用建筑“四节一环保”大数据的数据质量现状, 厘清原始数据中存在的数据质量问题, 研究并设计“四节一环保”大数据的数据清洗算法和修复算法。针对民用建筑“四节一环保”大数据中存在的不一致、不精确、不完整等问题, 本文通过剔除相似重复记录、识别异常记录和填补缺失记录等方式进行数据清洗及修复, 以提高数据质量。
民用建筑“四节一环保”大数据来自全国各省市自治区, 数据类型丰富, 能够反映我国各地区建筑业发展水平及民用建筑能耗情况。从数据类型来看, 包括普通数据、流数据、混合数据、结构化数据和非结构化数据等。从领域来看, 不仅包括能源类数据, 还包括人口、资源环境和经济社会数据等其他类别数据。从具体指标来看, 包括新建竣工建筑总量和既有建筑拆除量等建筑规模相关数据, 建材使用量和建筑生产过程能源消耗量等建材生产消耗相关数据, 既有建筑运行能耗状况和各类不同功能建筑分项用能状况等建筑运行消耗相关数据[18]。
根据数据质量问题的分类(图 2), 民用建筑“四节一环保”原始数据中存在的数据质量问题主要出现在实例层, 包括单数据源下的数据记录错误(拼写错误、相似重复记录和互相矛盾的字段等)和多数据源下的冗余、互相矛盾或不一致等。本文结合国际数据管理协会提出的数据质量的 6 个维度(完整性、唯一性、及时性、有效性、准确性和一致性), 对民用建筑“四节一环保”原始数据进行数据质量评估。
根据数据来源, 需进行清洗与修复的“四节一环保”数据大体上可分为来自统计报表的数据和监测数据两类。统计数据的异常主要为缺失、错误和不一致; 监测数据可作为时间序列处理, 其异常主要为缺失和错误, 此外还应提取设备故障信息。
本文数据来自住房和城乡建设部提供的吉林、江苏、河南三省各地区单栋建筑能耗数据及上海建筑科学研究院提供的上海市建筑运行能耗相关数据。数据类型主要为数字型和文本型, 均属于结构化数据。数据集中存在大量异常记录, 表 1 展示2015—2017 年单栋建筑能耗数据缺失情况, 表 2 为存在的相似重复记录示例(对应于同一栋建筑的多条记录)。
数据清洗过程中的重点为相似重复记录检测及异常记录识别。本文采用 3σ 准则、DBSCAN 聚类算法及箱线图内限, 对异常记录进行识别。
1.2.1 3σ 准则
当数据集服从正态分布时, 适合采用 3σ 准则进行异常点的检测与剔除。根据 3σ 准则, 若 X~N (μ, σ2), 则 X 落入以其均值 μ 为中心, 3 倍标准差 σ 为半径的区间内的概率为
表1 能耗数据缺失情况
Table 1 Missing rate of energy consumption data
年份原始记录电煤炭天然气液态石油气人工煤气 缺失记录缺失率/%缺失记录缺失率/%缺失记录缺失率/%缺失记录缺失率/%缺失记录缺失率/% 20151399420 0.141353996.75934466.771358597.081376198.34 201647108 0.17453796.3300.00469899.754710100.00 201732180 0.00320099.44285888.81314497.70319999.41
表2 2012年相似重复记录示例
Table 2 Example of approximately duplicated records in 2012
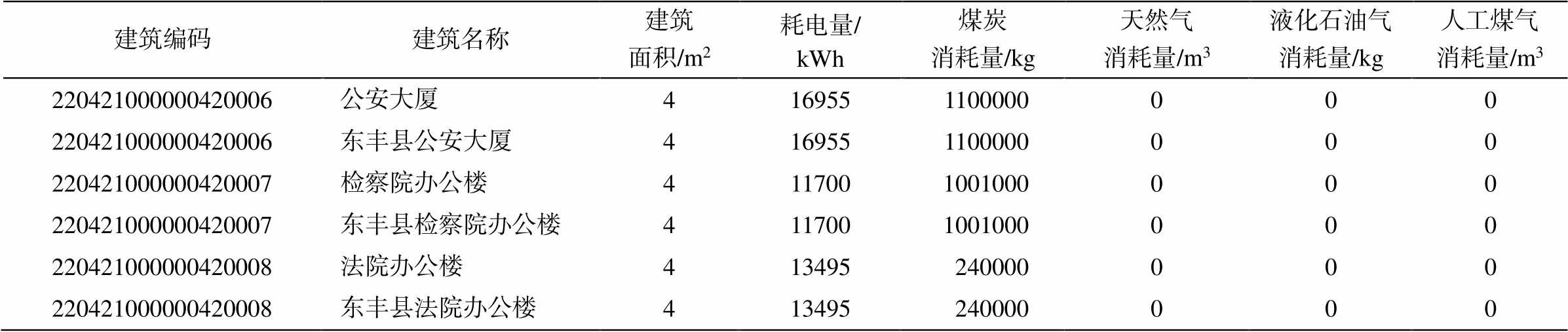
建筑编码建筑名称建筑面积/m2耗电量/ kWh煤炭消耗量/kg天然气消耗量/m3液化石油气消耗量/kg人工煤气消耗量/m3 220421000000420006公安大厦4169551100000000 220421000000420006东丰县公安大厦4169551100000000 220421000000420007检察院办公楼4117001001000000 220421000000420007东丰县检察院办公楼4117001001000000 220421000000420008法院办公楼413495240000000 220421000000420008东丰县法院办公楼413495240000000
P(|X－μ|≤3σ)=0.9973。 (1)
将距离均值超过 3 倍标准差的值标记为异常值。
1.2.2 DBSCAN聚类算法
DBSCAN 是一种基于密度的聚类算法, 可用于异常点检测。DBSCAN 算法定义某对象的密度为该对象指定距离 d 内对象的个数。描述样本集紧密程度的关键参数为(ε, MinPts), 其中 ε 表示以样本点p 为邻域中心对应的领域半径, MinPts 表示样本点p以ε为半径的邻域中包含样本个数的最小值。
记样本集为 D=(x1, x2, …, xm), 相关概念定义如下。
定义 1[9] ε 邻域。样本点 xi∈D 的 ε 邻域记为Nε(xi), 指与样本点xi的距离不超过 ε 的子样本集, 即 Nε(xi)={xj∈D|dist(xi, xj)≤ε}。本文dist(xi, xj)表示样本点 xi 与 xj 的欧氏距离, n 维样本空间下的具体表示为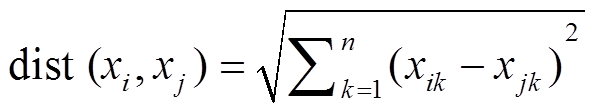
。
定义 2[9] 核心对象。样本点 xj∈D, 若其 ε 邻域 Nε(xj)中至少包含 MinPts 个样本, 即||Nε(xj)||≥MinPts, 则 xj 为核心对象。这里||∙||表示集合的势, 对于有限集合, 是指集合中元素的个数。
定义 3[9] 密度直达。样本点 xi, xj∈D, 若满足
1) xi∈Nε(xj), 2) ||Nε(xj)||≥MinPts, 则称xi由xj密度直达。
定义 4[9] 密度可达。若存在样本序列 P1=xi, P2,…,Pn=xj, 满足 Pi 可由 Pi+1 密度直达, 则称 xi 由 xj密度可达。
定义 5[9] 密度相连。样本点 xi, xj∈D, 若存在核心对象 xk, 使得 xi 和 xj 均由 xk 密度可达, 则称 xi与xj密度相连。
DBSCAN 聚类算法将聚类簇理解为密度相连的数据点组成的最大集合, 并可形成任意形状的聚类, 算法流程[9]如下。
输入: 样本集 D=(x1, x2, …, xm), 邻域半径 ε, 给定点成为核心对象在邻域内最小需包含样本点数MinPts。
1)初始化核心对象集合 T=∅, 聚类簇个数 k=0, 未访问样本集合 P=D, 聚类簇集合 C=∅。
2)对于样本集中的元素, 以下述方法更新核心对象集合 T: 以一种合适的距离度量(本文选择欧氏距离), 确定任意样本点 xi∈D 的 ε 邻域 Nε(xi); 若xi 的 ε 邻域 Nε(xi)中至少包含 MinPts 个样本, 即||Nε(xj)||≥MinPts, 则将样本点 xi 加入核心对象集合, 即 T=T∪{xi}。
3)若核心对象集合 T=∅, 则算法结束, 返回聚类簇集合 C, 否则转入步骤 4。
4)从核心对象集合 T 中随机选择一个核心对象 o, 初始化 P_old 为未访问样本集合 P, 初始化一个队列 Q, 并加入该核心对象 o, 即 Q=Q∪{o}, 并将o从未访问样本集合 P 中移除。
5)若队列 Q 非空, 从队列 Q 中选择第一个元素记为 q (显然, 初次循环时 q 为核心对象 o), 计算 q的 ε 邻域Nq, 若 q 为核心对象, 则将其密度直达的样本点加入队列 Q, 并将这些样本点从未访问集合 P 中移除, 最后将 q 从队列 Q 中移除。重复操作直到队列 Q 为空, 转入步骤 6。
6)当队列 Q=∅时, 将当前聚类簇 Ck 更新为P_old 与 P 的差集, 将 Ck 加入聚类簇集合 C, 将聚类簇个数 k 加 1, 并在核心对象集合 T 中将 Ck 中的元素移除, 转入步骤3。
输出: 聚类簇集合C={C1, C2,…,Ck}。
DBSCAN 算法中, 异常点为低密度区域的对象, 即将不属于任何聚类簇的数据点标记为异常点。
1.2.3 箱线图内限
箱线图的优点在于不受异常值的影响, 能够准确稳定地描绘数据的离散分布情况, 有利于数据的清洗, 如图 3 所示。我们利用箱线图的内限对异常值进行检测与剔除。
数据集上四分位数(Q3)与下四分位数(Q1)的差值称为四分位距(IQR), 内限的计算公式如下:
上限 = Q3 + 1.5·IQR, (2)
下限 = Q1-1.5·IQR。 (3)
异常点的识别标准为将处于区间段[下限, 上限]之外的点标记为异常点。
数据修复的重点为缺失值填补及结合模型预测值实现数据修正。缺失值填充的方法包括: 1)简单填充; 2)利用线性回归模型填充; 3)利用基于用户的协同过滤推荐算法填充。考虑到原始数据中存在多重共线性, 本文建立多种模型拟合数据并进行数据修正。
1.3.1 基于用户的协同过滤推荐算法
协同过滤模型的数据支撑为若干用户及物品的数据, 以用户对物品的评分为元素构成的效应矩阵一般为稀疏矩阵, 只有部分位置的数值是非零的, 需用少量已知数据来预测效应矩阵中的空缺值, 并找到可能为最高评分的物品推荐给用户。
基于用户的协同过滤推荐算法的一个关键步骤是确定近邻用户, 需采用合适的相似性度量方法来判断用户间是否相似。常用的相似性度量方法有欧氏距离、余弦相似性、Jaccard 公式和皮尔逊相关系数等。利用基于用户的协同过滤推荐算法填补空缺值的过程分为以下 3 个步骤。
1)用户信息的表达。将单栋建筑作为用户, 选取若干能够反映单栋建筑能耗情况且数据相对准确和完整的特征作为属性, 将以这些属性作为分量形成的向量称为用户属性向量。
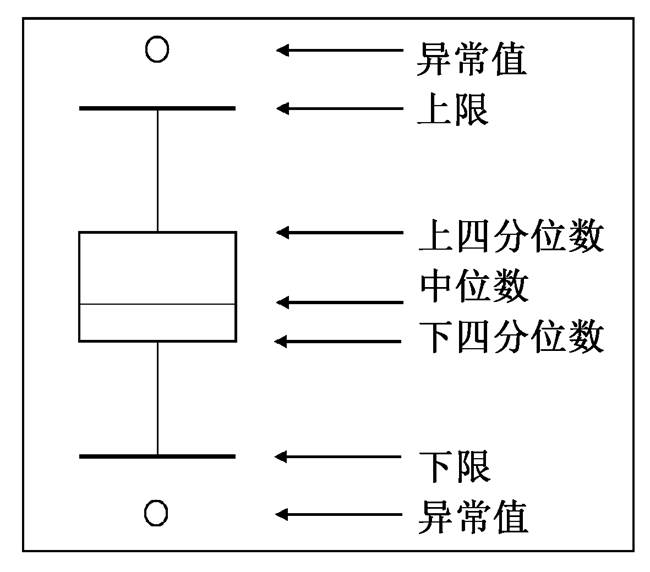
图3 箱线图
Fig. 3 Boxplot
2)近邻用户的生成。选择一种合适的距离度量方法, 计算用户间的相似度。对某一用户而言, 将其与其他所有用户的相似度由高到低排列, 将排名靠前的若干用户作为该用户的近邻用户。
3)推荐的生成。利用近邻用户的对应指标值, 对用户的缺失指标值进行填充。
1.3.2 模型拟合
使用多元线性回归模型拟合数据时, 假定条件之一为各个解释变量之间不存在线性关系, 即任意一个解释变量不能由其他解释变量线性表出, 否则称模型中存在多重共线性。严重的多重共线性会影响回归模型, 进行单变量间相关性检验或多元相关性分析是判断变量间是否存在多重共线性的基本方法, 也可以借助方差膨胀系数[19]等工具进行检验。
常用于处理多重共线性的方法包括删除或改变部分次要解释变量、差分法、逐步回归、主成分分析(principal components analysis, PCA)[20]、偏最小二乘回归(partial least squares regression, PLSR)[21]、Lasso 回归[22]和岭回归(ridge regression)[23]等。主成分分析是将一组可能存在相关性的变量转换为一组线性无关的新变量(称为主成分), 使得主成分间的方差尽可能大且相互独立, 从而在尽量使数据信息损失少的原则下, 将数据降维并得以简化。偏最小二乘回归方法是对最小二乘方法的扩展, 该方法结合了主成分分析及典型相关分析的思想, 适合处理多对多的线性回归问题。此外, 考虑到共线性会导致模型参数的估计值变得很大, Lasso 回归和岭回归模型在最小二乘法目标函数的基础上加上一个对参数的正则化项, 用以防止过拟合, 不同之处在于正则化项分别采用L1范数和L2范数。
拟合上海市建筑运行能耗相关数据, 可以发现得到的多元线性回归模型中存在多重共线性。为了提高模型的可解释性及预测准确度, 本文建立多种模型, 并对比模型拟合结果。
结合“四节一环保”数据特点, 对单栋建筑能耗数据的清洗过程如下: 首先进行相似重复记录的检测与合并; 再删除电力指标为 0 的整条记录及能耗指标全为 0 的整条记录; 然后分别用各能耗量除以建筑面积, 得到各建筑的平均能耗量; 最后尝试利用 3σ 准则、DBSCAN 聚类算法或箱线图内限删除异常记录。以 2015 年单栋建筑能耗数据集为例, 数据清洗步骤如下。
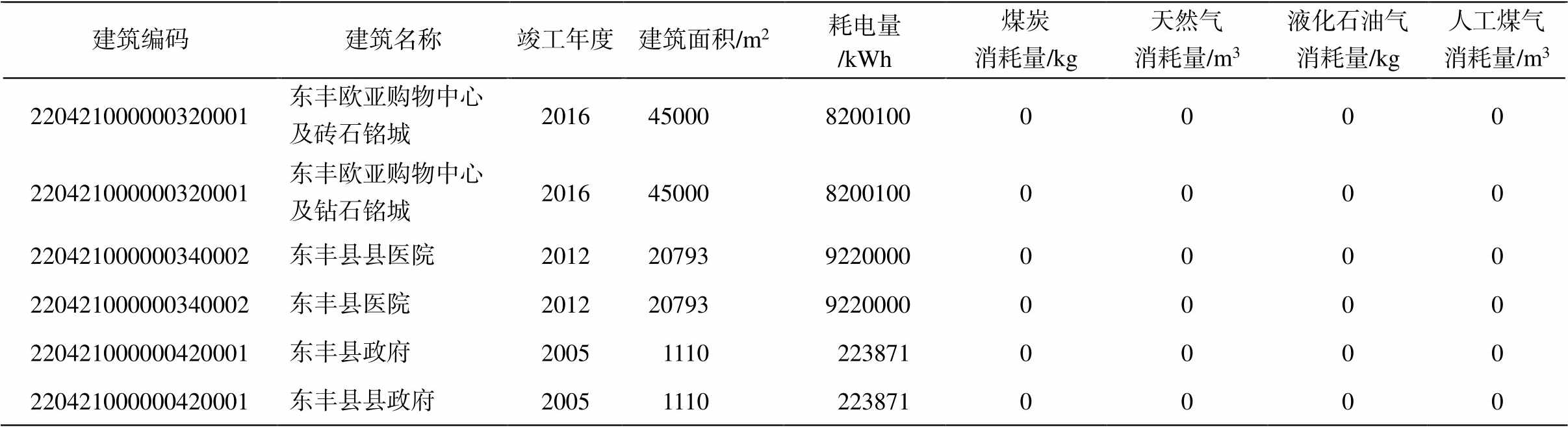
1)相似重复记录的检测与合并。
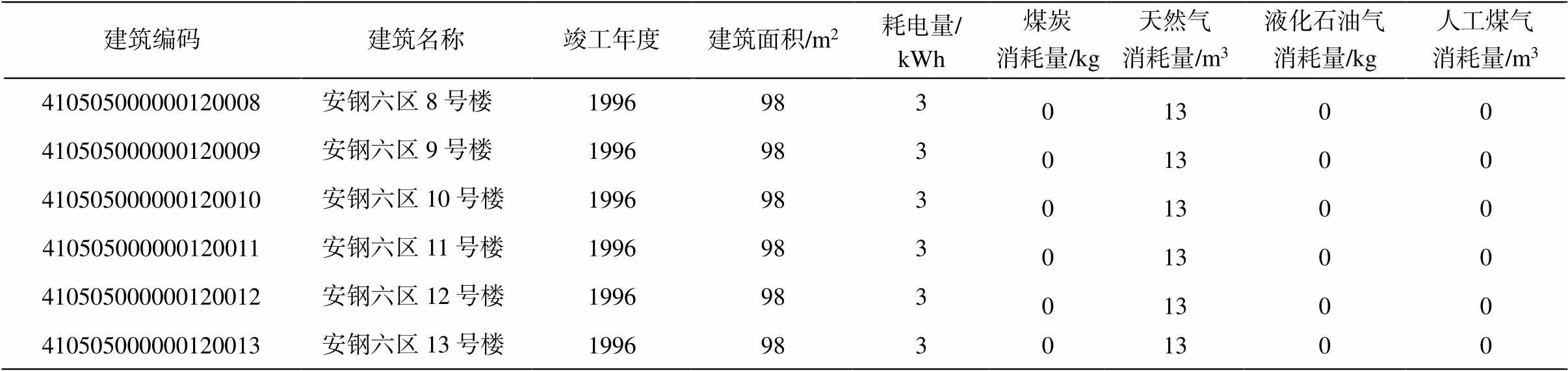
基于数据的唯一性原则, 需检测数据集中是否存在相似重复记录, 并将识别出的相似重复记录删除或合并。表 3 中的重复记录为对应于同一实体的多条记录, 处理方式为只保留第一条记录, 将其余重复记录整条删除。表 4 中的重复记录对应于不同实体但能耗情况完全相同, 对建筑能耗分析无意义, 属于数据采集过程中的误填和误报, 因此只保留第一条记录, 将其余重复记录整条删除。
2)删除能耗指标全为 0 的记录及电力指标为 0的记录。
对于能耗指标全为 0 的记录, 考虑到其对分析建筑能耗情况无意义, 做删除整条记录处理。由于建筑编码、建筑名称、竣工年度、建筑类型、建筑面积和 id 这 6 个基本指标中不存在缺失值, 故保留至少有 7 个非 NaN 数据的行, 即 5 个能耗指标里至少有 1 个非空, 否则将整条记录删除。
部分建筑(例如商场、酒店、教育局等)的耗电为 0, 不符合实际情况。考虑到电力数据相对较多, 删除少数记录对分析总体情况影响不大, 因此对电力指标为 0 的整条记录做删除处理。
3)引入新指标平均能耗量。
引入平均能耗量的原因如下: ①直接以能耗量为指标进行数据清洗时, 会把能耗量指标值较大的记录标记为异常记录, 但能耗量高可能是由于建筑面积较大, 不一定为异常值, 而用平均能耗量为指标进行异常值检测与剔除更为合理; ②以平均能耗量为指标进行缺失值填补, 并乘以建筑面积, 得到能耗量的填充值, 这种方法得到的结果更具多样性, 尤其对于缺失率较高的能耗量指标。平均能耗量的计算公式为
平均能耗量=能耗量/建筑面积, (4)
其中, 能耗量包括电、煤炭、天然气、液化石油气和人工煤气。
将 2015 年单栋建筑能耗数据集经过以上 1~3步处理后的数据集记为 Ω1, 后续异常值检测与剔除均在此数据集上进行。
4)识别并剔除异常记录。
方法 1: 3σ准则。利用 3σ 准则的前提是数据服从正态分布, 故先进行正态性检验。以数据集 Ω1中平均耗电量为例, 借助假设检验的思想, 对原始数据及正态变换后的数据进行 K-S 检验, 尝试的正态变换包括对数变换、平方根变换、倒数变换和平方根反正旋变换等。输出结果显示正态性均不显著, 因此该数据集不适合用 3σ 准则识别异常记录。
表3 对应于同一实体的多条记录
Table 3 Multiple records corresponding to the same entity
建筑编码建筑名称竣工年度建筑面积/m2耗电量 /kWh煤炭消耗量/kg 天然气消耗量/m3液化石油气消耗量/kg 人工煤气消耗量/m3 220421000000320001东丰欧亚购物中心及砖石铭城20164500082001000000 220421000000320001东丰欧亚购物中心及钻石铭城20164500082001000000 220421000000340002东丰县县医院20122079392200000000 220421000000340002东丰县医院20122079392200000000 220421000000420001东丰县政府200511102238710000 220421000000420001东丰县县政府200511102238710000
表4 误填和误报的记录
Table 4 Records of misfilling and misreporting
建筑编码建筑名称竣工年度建筑面积/m2耗电量/ kWh煤炭消耗量/kg天然气消耗量/m3液化石油气消耗量/kg人工煤气消耗量/m3 410505000000120008安钢六区8号楼199698301300 410505000000120009安钢六区9号楼199698301300 410505000000120010安钢六区10号楼199698301300 410505000000120011安钢六区11号楼199698301300 410505000000120012安钢六区12号楼199698301300 410505000000120013安钢六区13号楼199698301300
方法 2: DBSCAN 聚类算法。首先检查数据集中每个数据点的 ε 邻域, 若点 p 的 ε 邻域中包含数据点的数量多于 MinPts, 则创建一个以 p 为核心对象的簇; 其次迭代地将这些核心对象密度直达的数据点加入聚类簇, 重复操作, 当不再有数据点加入当前聚类簇时, 完成当前聚类簇的生成; 当不再有新的数据点加入任何聚类簇时, 算法结束。
以数据集 Ω1 中各建筑耗天然气量为例, 原始记录进行相似重复记录的检测与合并、删除能耗指标全为 0 的记录等初步清洗后, 聚类结果见图 4, 共有 7 个聚类簇。结合基于密度的异常点的定义, 可将不属于任何聚类簇的数据作为异常点处理。
DBSCAN 算法的优势在于不需要提前输入要生成的聚类簇个数, 能快速地将密度足够大的相邻区域连接并生成聚类簇, 从而有效处理异常数据。
方法 3: 箱线图内限。分别做数据集 Ω1 中各平均能耗量指标(平均耗电量、平均耗煤炭量、平均耗天然气量、平均耗液化石油气量和平均耗人工煤气量)对应子集的箱线图。如图 5 所示, 以平均耗人工煤气量指标为例, 将落在箱线图内限外的记录标记为异常记录(为使图像简洁清晰, 未显示重叠记录的指标值), 之后将各指标对应的异常记录(id 值)取并集, 并删除所有异常记录。
箱线图内限的优势在于可以直观明了地识别数据集中的异常值。箱线图利用四分位数和四分位距判断异常值, 由于四分位数具有一定的耐抗性, 多达 25%的数据可以取任意值而不会大幅度地扰动四分位数, 所以异常值不会严重影响箱线图的形状, 识别结果比较客观。
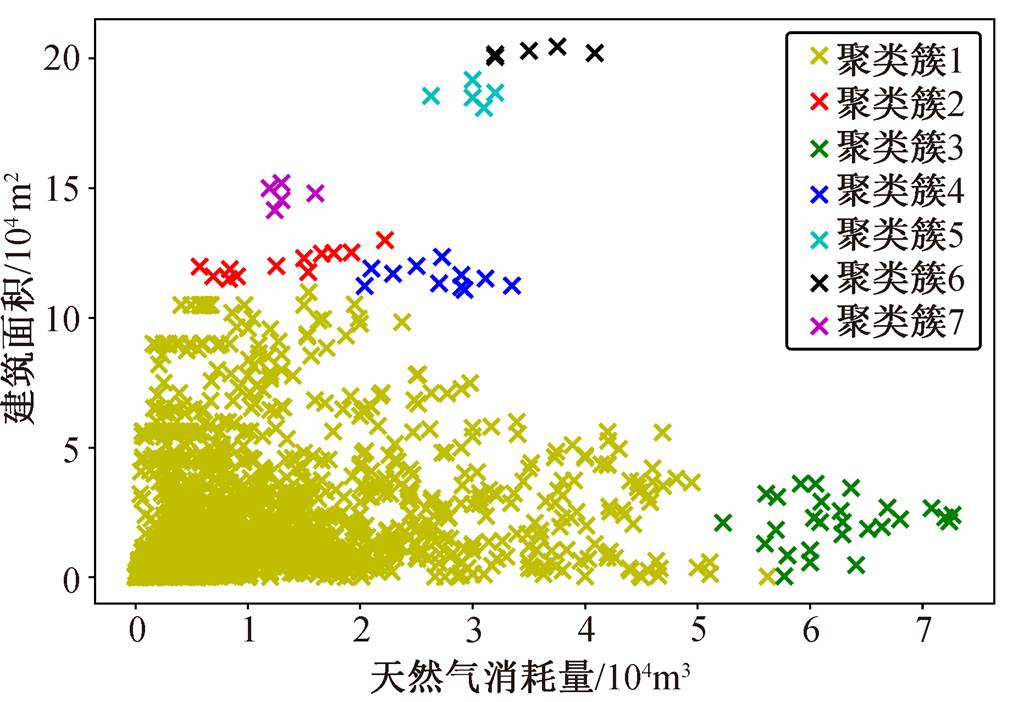
图4 DBSCAN算法聚类结果
Fig. 4 Output of the DBSCAN clustering algorithm
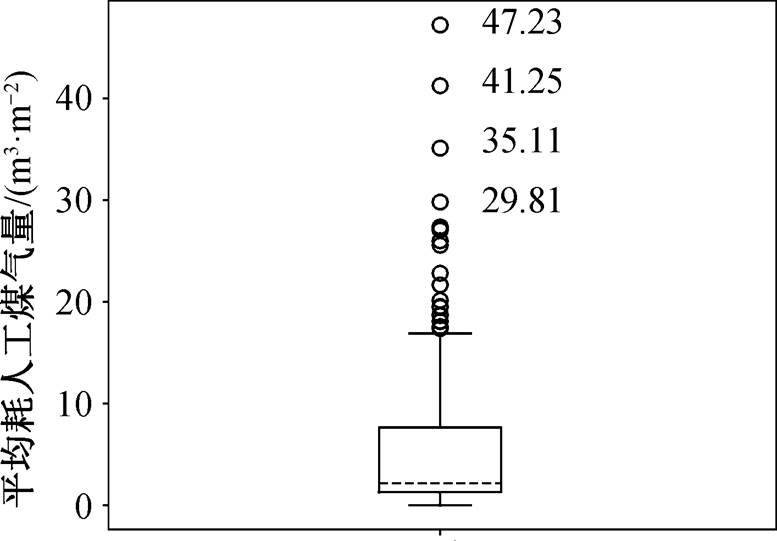
图5 箱线图示例
Fig. 5 An example of boxplot
本节将在不同数据集中采用不同数据修复方法, 在单栋建筑能耗数据中填补缺失数据; 建立模型拟合上海地区建筑运行能耗相关数据, 评估模型并实现数据修正。
2.2.1 填补缺失数据
对住房和城乡建设部提供的单栋建筑能耗数据的修复主要为填补空缺数据, 具体步骤如下: 首先采用不同修复方法, 填充若干平均能耗量指标; 然后令平均能耗量乘建筑面积为各建筑能耗量指标的填充值。
方法 1: 简单填充。填补空缺值的简单方法为以数据集中的数据填充, 如前(后)非缺失值、平均值、中位数和众数等。以 2015 年单栋建筑能耗数据为例, 以填充天然气能耗量指标为目标。将清洗后数据集中的记录按照平均耗电量从小到大的顺序排列, 遍历数据集中平均耗天然气量缺失的记录, 用前(后)平均耗天然气量非缺失值填充; 或计算与该栋建筑相同建筑类型的子集中平均耗天然气量的均值(中位数, 众数), 作为该栋建筑平均耗天然气量指标的填充值。
方法 2: 线性回归模型。假定建筑能耗量之间存在相关关系, 可建立指标间的回归模型, 并将模型预测值作为缺失记录的填充值。如假定单栋建筑平均耗天然气量与平均耗电量成正比, 拟合出变量间的线性回归模型。针对平均耗天然气量缺失的记录, 将平均耗电量代入模型, 得到的模型预测值即为平均耗天然气量的估计值。图 6 为前 50 条记录的拟合情况, 可以看出由于单栋建筑平均能耗量波动较大, 使用线性拟合得到的曲线过于平滑。
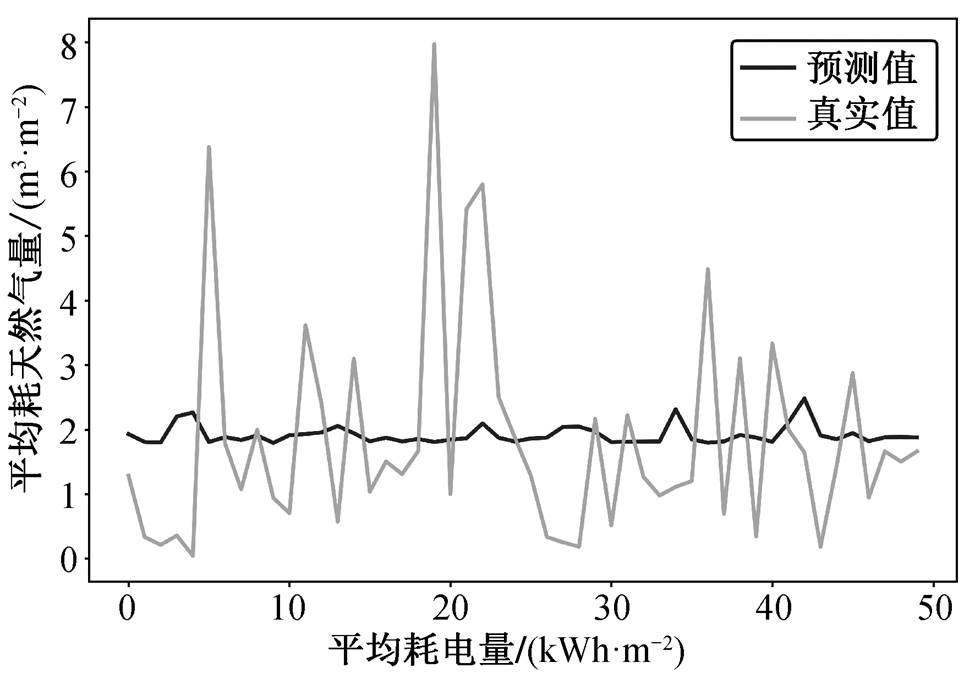
图6 平均耗天然气量拟合结果
Fig. 6 Fitting result of the average natural-gas consumption
方法 3: 基于用户的协同过滤推荐算法。以2015 年单栋建筑能耗数据为例, 以填充天然气能耗量指标为目标。选择竣工年度及平均耗电量作为属性变量, 选择欧氏距离作为相似性度量, 计算不同建筑间的相似度。针对某栋建筑的空缺值, 将其他建筑按相似度由高到低的顺序排列, 并以前 20栋建筑(相似度最高的 20 栋建筑)的平均耗天然气量指标数据的均值作为该建筑平均耗天然气量指标的填充值。将填充后的各建筑的平均耗天然气量指标数据分别乘以其建筑面积, 得到各建筑的天然气能耗量指标的填充值。
2.2.2 基于模型的数据修复
以上海地区建筑运行能耗相关数据为例, 由于该数据集中为年度数据, 数据量较小, 且不存在相似重复记录, 不适合用上所述方法进行数据清洗及修复, 所以采用模型拟合的方式。选择 1995 年后的数据, 并结合变量间相关性选择解释变量进行模型拟合。表 5 列出保留的变量名称及符号, 其中 Xi (i=1, …,8)代表解释变量, 
代表被解释变量。
为消除量纲的影响, 建立模型前, 先对数据集进行标准化处理。采用 Z-score 标准化方法, 标准化公式为
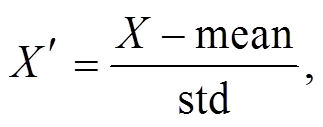(5)其中 mean 和 std 分别表示数据的均值和标准差。随机划分训练集和测试集, 训练集占比为 0.8。下面建立模型来拟合标准化后的数据。
模型1: 多元线性回归。
通过作散点图可以发现, 各解释变量 Xi 与被解释变量 Y 呈线性关系。以第三产业年能耗与上海建筑运行能耗的关系为例, 结果如图 7 所示。其中实线为最佳拟合直线，阴影部分为 95%的置信带。
表5 变量名称及符号
Table 5 Variable names and symbols
变量名称符号 常住人口总量/万人X1 人均生活用能/kg标准煤X2 万元能源消费总量/万吨标准煤X3 第三产业年能耗/万吨标准煤X4 人均地区生产总值/(元·人-1)X5 第三产业产值/亿元X6 居民消费水平/元X7 年末全社会房屋竣工面积/104m3X8 上海建筑运行能耗/万吨标准煤Y
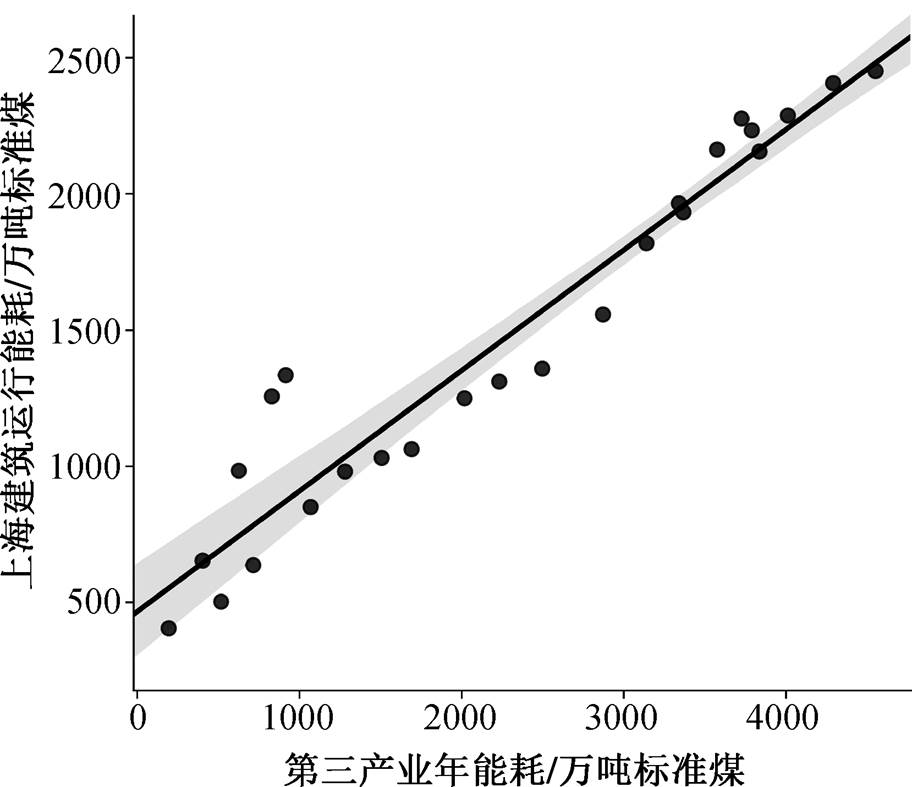
图7 第三产业年能耗与上海建筑运行能耗关系
Fig. 7 Scatter diagram of annual energy consumptionof the tertiary industry and energy consumption of buildings in Shanghai
通过计算可知各解释变量 Xi 与被解释变量 Y的相关系数较高, 大部分相关系数达到 90%以上, 因此考虑以线性模型拟合, 建模结果如下:
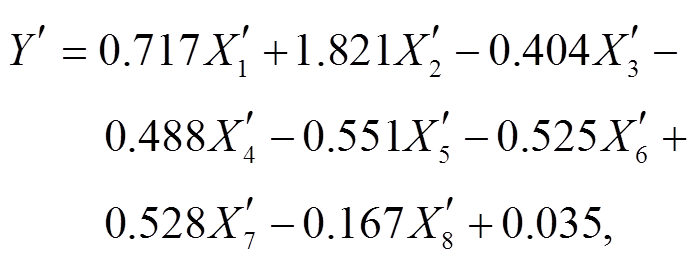(6)其中,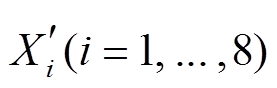
为标准化后的解释变量, 此规定也适用于本节其他公式。
模型 2: 主成分回归(principal components reg-ression, PCR)。
回归模型中多重共线性的直观表现为某一个解释变量与其他解释变量间存在线性关系。由于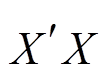
的行列式非常接近 0, 因此推断解释变量间存在多重共线性。
主成分分析的结果显示第一主成分占 96.4%的方差比例。保留第一主成分及第二主成分, 记为FinalData1, 并建立与被解释变量拟合的模型。将每条测试集数据乘以特征向量对应的分量, 得到FinalData2, 输出其模型预测值, 并与测试集真实值对比。输出结果显示第一主成分与各标准化后的解释变量的关系如下:
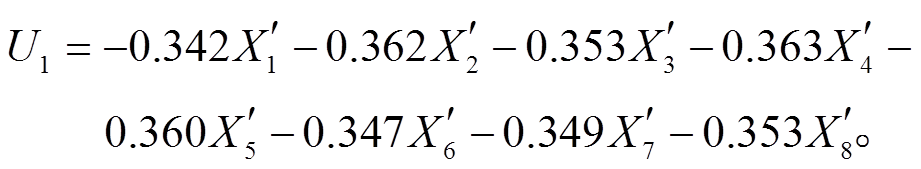(7)以第一主成分和第二主成分为新的解释变量, 得到的模型表达式为
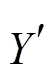= -0.330U1+0.103U2+0.002。 (8)
模型3: 偏最小二乘回归。
与 PCR 类似, PLSR 要在原始解释变量中构建线性组合, 不同之处在于 PCR 仅使用原始解释变量构建主成分, 而 PLSR 要结合被解释变量。使用网格搜索的方法确定模型最优参数, 得到的模型表达式为
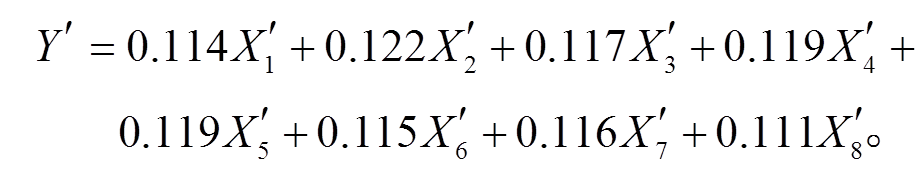(9)模型4: 岭回归。
岭回归中正则化项的参数 λ 称为岭回归参数, 岭迹图可以反映岭回归的参数估计结果与岭回归参数 λ 的关系。首先结合岭迹图选取合适的岭回归参数 λ, 选择各回归系数对应的岭迹稳定地趋于 0, 且不存在明显异常的回归系数时对应的参数。建立岭回归模型, 本文 λ 取 0.15, 建模结果如下:
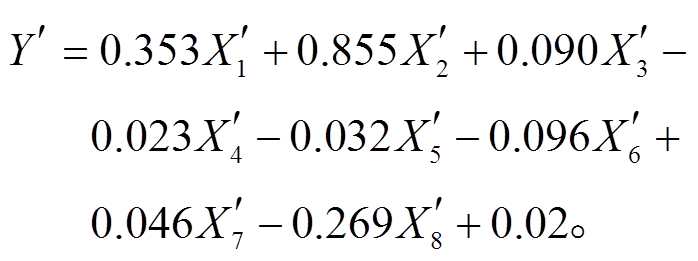(10)模型5: Lasso回归。
Lasso 回归本质上与岭回归类似, 都通过约束参数来防止过拟合。此外, Lasso 回归可以将作用不显著的解释变量(特征)系数训练为 0, 从这一角度来看也有特征筛选的作用。选取最优参数后得到的模型表达式为
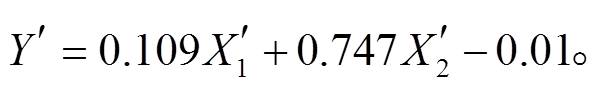(11)表 6 为用 DBSCAN 聚类算法剔除异常记录后保留记录的示例, 其中部分平均耗天然气量指标值过高的记录本应被删除, 但由于达到 DBSCAN 聚类算法的密度要求而被保留。表 7 展示利用箱线图内限删除异常记录后保留的部分记录, 其平均耗天然气量指标值在合理范围内。故针对当前数据集, 本文采用箱线图内限进行异常记录的检测。
将利用箱线图内限识别并剔除异常记录的方法应用于 2016—2017 年单栋建筑能耗数据, 数据清洗情况及数据保留率如图 8 所示。结果显示, 单栋建筑能耗数据清洗后, 数据保留率为 80%~92%。
在数据集 Ω1 识别并剔除异常记录后得到的新数据集(Ω2)中划分训练集和测试集, 设定测试集规模为 30。本节将对比简单填充、线性回归模型和基于用户的协同过滤推荐算法在数据集 Ω2 中的填充结果。
表6 DBSCAN聚类算法保留结果
Table 6 Remaining records of DBSCAN clustering algorithm
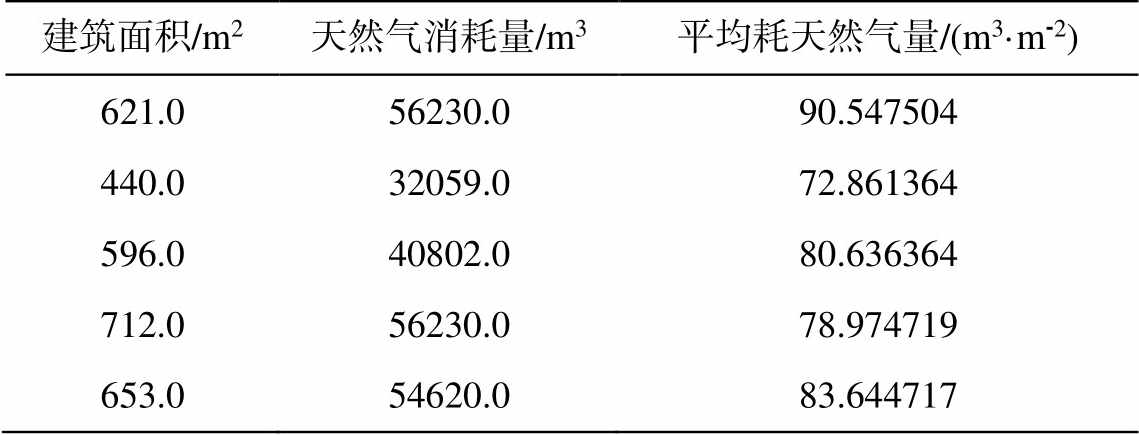
建筑面积/m2天然气消耗量/m3平均耗天然气量/(m3·m-2) 621.056230.090.547504 440.032059.072.861364 596.040802.080.636364 712.056230.078.974719 653.054620.083.644717
表7 箱线图保留结果
Table 7 Remaining records of boxplot
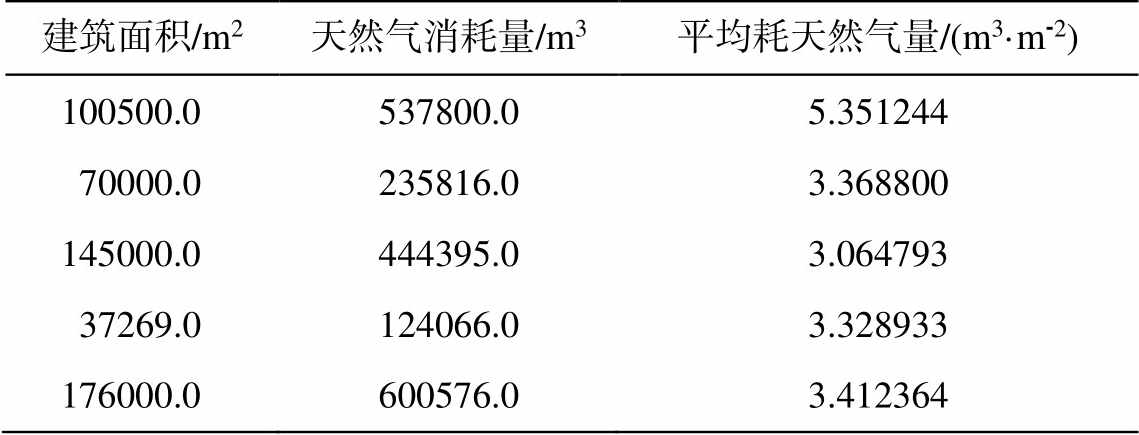
建筑面积/m2天然气消耗量/m3平均耗天然气量/(m3·m-2) 100500.0537800.05.351244 70000.0235816.03.368800 145000.0444395.03.064793 37269.0124066.03.328933 176000.0600576.03.412364
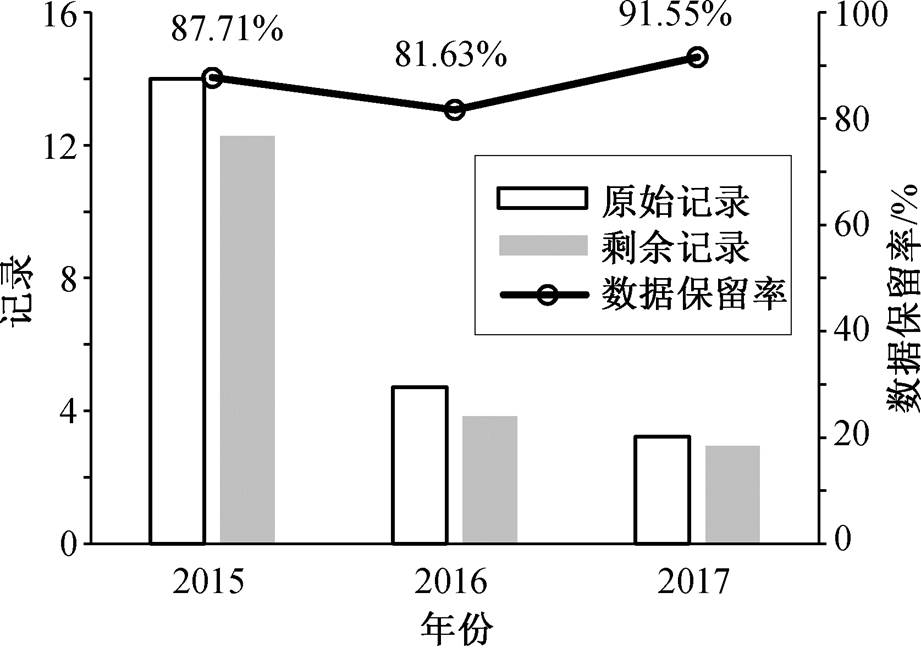
图8 数据保留率
Fig. 8 Retention rate of data
平均绝对误差(MAE)是常用的评估指标, 令指标的真实值 y(i)与填充值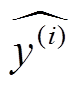
的差值的绝对值为偏差, 并将各记录的偏差求平均, 得到平均绝对误差:
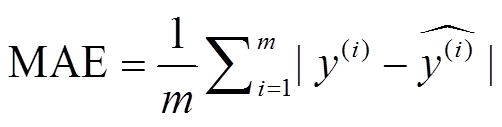。 (12)表 8 为单栋建筑平均耗天然气指标的填充结果对比, 同理可进行其他能耗量指标的填充结果评估。可以看出, 用相同建筑类型的建筑群的平均耗天然气量指标的中位数进行填充的结果与真实值最接近, 原因为能耗量指标间不存在显著的相关关系, 中位数具有一定的抗干扰性, 在某种程度上反映出该指标的经验水平。
将多元线性回归、主成分回归、偏最小二乘回归、岭回归及 Lasso 回归 5 种模型, 应用于上海地区建筑运行能耗相关数据, 选择拟合情况最好的模型, 并进行数据修正。
一般通过比较模型预测值与真实值的差来评估模型的质量。常用的模型评估指标有平均绝对误差、均方误差、均方根误差(RMSE)、精确率及召回率等。本文选择均方根误差作为模型评估指标, 计算公式如下:
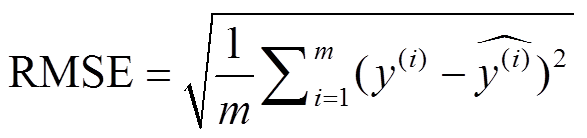。 (13)事实上, 求得测试集中模型预测值与被解释变量标准化后的真实值的均方根误差后, 将其乘以原数据集被解释变量的标准差, 即为标准化还原后预测值与真实值的均方根误差(realRMSE), 结果如表9所示。
结合数据集特点及模型评估结果, 本文认为偏最小二乘回归及岭回归模型拟合情况较好, 所以将岭回归模型应用于整个数据集, 得到的预测值还原后为被解释变量的修正值, 表 10 展示 1995—2000年数据的修正情况。
表8 填充结果对比
Table 8 Comparisons of filling values
填充方法MAE 以前一条非缺失值填充1.29 以各建筑类型均值填充0.96 以各建筑类型中位数填充0.83 用线性回归模型预测值填充1.18 用user-based CF填充1.11
表9 标准化还原后预测值与真实值的均方根误差
Table 9 RealRMSE between predicted value after standardizal reduction and true value
模型realRMSE 多元线性回归211.14 主成分回归170.07 偏最小二乘回归159.92 岭回归156.06 Lasso回归196.46
表10 数据修正情况
Table 10 Data correction
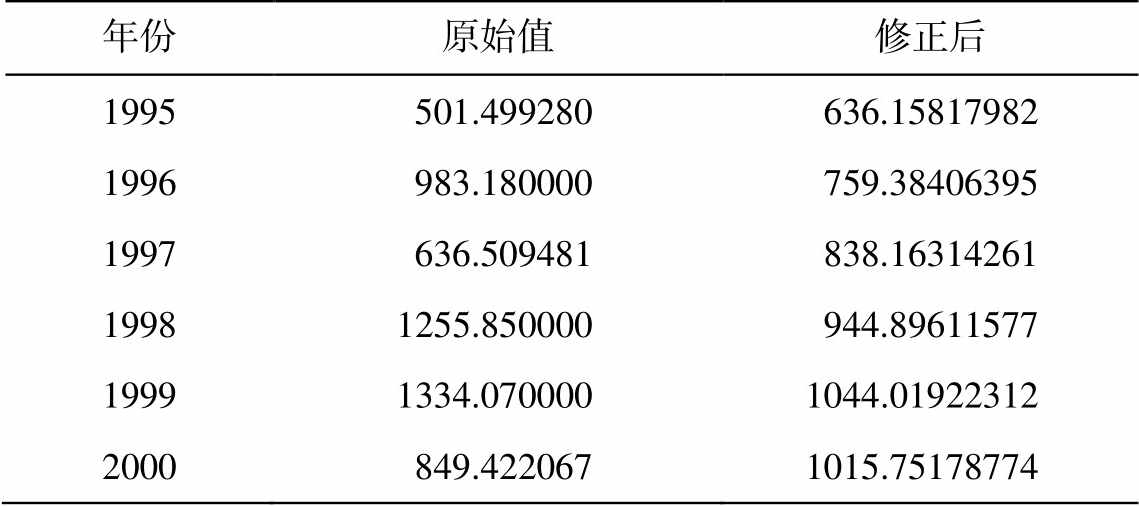
年份原始值修正后 1995501.499280636.15817982 1996983.180000759.38406395 1997636.509481838.16314261 19981255.850000944.89611577 19991334.0700001044.01922312 2000849.4220671015.75178774
本文结合民用建筑“四节一环保”大数据的数据特点及存在的数据质量问题, 使用多种方法对单栋建筑能耗数据集进行清洗及修复, 清洗后的数据保留率为 80%~92%。通过对多种方法进行对比, 发现针对单栋建筑的某能耗量指标, 最适合的填充方法为: 计算相同建筑类型的建筑群的平均能耗量指标的中位数, 将该中位数乘以建筑面积作为该建筑能耗量指标的填充值。此外针对上海地区建筑运行能耗相关数据, 本文建立多种模型进行数据修复, 评估结果显示偏最小二乘回归及岭回归模型的拟合情况较好, 并用岭回归模型预测值对 1995—2000年建筑运行能耗指标数据进行修正。
在单栋建筑能耗数据集中，指标类型较为单一, 缺少能够反映各建筑能源消耗能力及建筑性能等方面的指标, 因此在实现基于用户的协同过滤推荐算法时, 用来识别近邻用户的指标仅有竣工年度及平均耗电量，造成缺失值填充效果不理想。故在后续工作中，应关注缺失率非常高的指标, 例如2015 年单栋建筑能耗数据中煤炭消耗量指标的缺失率高达 96.75%。此外，若有关部门能提供更为完整和全面的指标数据, 缺失值填充等方面的数据修复将进一步完善并得到更为准确的结果。
在大数据环境下, 为了从海量数据中挖掘有用信息, 提高数据分析的效率和准确性, 在数据挖掘前进行清洗与修复具有重要的意义和价值。针对行业数据的清洗与修复, 不仅需要机器学习中相关的工具和技术, 还应结合领域背景及专家知识, 进而提高结果的合理性和有效性。
参考文献
[1] 封富君, 姚俊萍, 李新社, 等. 大数据环境下的数据清洗框架研究. 软件, 2017, 38(12): 193-196
[2] Erhard R, Hong H D. Data cleaning: problems and current approaches. IEEE Data Engineering Bulletin, 2000, 23(4): 3-13
[3] 郭志懋, 周傲英. 数据质量和数据清洗研究综述. 软件学报, 2002, 13(11): 2076-2082
[4] 刘喜文, 郑昌兴, 王文龙, 等. 构建数据仓库过程中的数据清洗研究. 图书与情报, 2013, 5: 22-28
[5] 杨金艳, 江曾杰, 陈伟. 稳健统计与格拉布斯准则在能力验证结果分析中的应用. 计量学报, 2018, 39(6): 112-117
[6] André R M. The Detection of outliers in nondestruc-tive integrations with the generalized extreme studen-tized deviate test. Publications of the Astronomical Society of the Pacific, 2015, 127: 258-265
[7] 张新荣. 基于鲁棒尺度的统计建模数据中异常点去除算法的研究及应用. 计算机应用研究, 2010, 27 (9): 3319-3321
[8] Breunig M M, Kriegel H P, Ng R T, et al. LOF: identifying density-based local outliers // Proceedings of 2000 ACM SIGMOD International Conference on Management of Data. New York, 2000: 93-104
[9] Ester M, Kriegel H P, Sander J, et al. A Density-based algorithm for discovering clusters in large spatial databases with noise // International Conference on Knowledge Discovery & Data Mining. Portland, 1996: 226-231
[10] 余翔, 陈国洪, 李霆, 等. 基于孤立森林算法的用电数据异常检测研究. 信息技术, 2018, 42(12): 96-100
[11] Zhang Y, Meratnia N, Havinga P J M. Adaptive and online one-class support vector machine-based outlier detection techniques for wireless sensor networks// 23rd International Conference on Advanced Informa-tion Networking and Applications Workshops, Brad-ford, 2009: 990-995
[12] Goldberg D, Nichols D, Oki B M, et al. Using colla-borative filtering to weave an information tapestry. Communications of the ACM, 1992, 35(12): 61-70
[13] Vialardi C, Braver J, Shaftr L, et al. Recommendation in higher education using data mining techniques. International Working Group on Educational Data Mining, 2009, 84(2): 326-336
[14] Zheng Z, Ma H, Lyu M R, et al. WSRec: a colla-borative filtering based web service recommender system // 2009 IEEE International Conference on Web Services. Los Angeles, 2009: 437-444
[15] Herlocker J L, Konstan J A, Terveen L G, et al. Evaluating collaborative filtering recommender sys-tems. ACM Transactions on Information Systems, 2004, 22(1): 5-53
[16] Koohi H, KianiK. User based collaborative filtering using fuzzy C-means. Measurement, 2016, 91: 134-139
[17] 张锋, 常会友. 使用 BP 神经网络缓解协同过滤推荐算法的稀疏性问题. 计算机研究与发展, 2006, 43 (4): 667-672
[18] 李兆坚, 江亿. 我国广义建筑能耗状况的分析与思考. 建筑学报, 2006(7): 30-33
[19] 郑家亨. 统计大辞典. 北京: 中国统计出版社, 1995
[20] Garg A, Tai K. Comparison of statistical and machine learning methods in modelling of data with multico-llinearity. International Journal of Modelling, Identi-fication and Control, 2013, 18(4): 295-312
[21] Yanxu L, Jian P, Yanglin W. Application of partial least squares regression in detecting the important landscape indicators determining urban land surface temperature variation. Landscape Ecology, 2018, 33: 1133-1145
[22] Algamal Z Y, Lee M H. Adjusted adaptive lasso in high-dimensional poisson regression model. Modern Applied Science, 2015, 9(4): 170-179
[23] Assaf G A, Tsionas M, Tasiopoulos A. Diagnosing and correcting the effects of multicollinearity: Bayesian implications of ridge regression. Tourism Manage-ment, 2019, 71: 1-8
Research on Cleaning and Repairing Methods of Civil Building Dataon Resources Saving and Environment Protection
Abstract Aiming at the data quality issues existing in the original civil building data on resources saving and environment protection, various methods are used to achieve data cleaning and data repairing. In terms of data cleaning, the authors focus on the approximately duplicated records and abnormal records in the energy consumption data of single building. In particular, the methods for identifying abnormal records include the empirical rule, the DBSCAN clustering algorithm, and inner fence of boxplot. In terms of data repairing, the authors focus on completing missing values and using the models to achieve data correction. In particular, the missing values are filled in these ways: existing values in the datasets, the predicted values of the linear regression model, and the output of the user-based collaborative filtering recommendation algorithm. The average absolute error is used as an evaluation index to compare these filling results. While repairing the building energy consumption data from Shanghai, multiple linear regression, principal component regression, partial least squares regression, ridge regression and Lasso regression are used to fit the correlation between building energy consumption and explanatory variables. The results show that for the energy consumption data of single building, it’s suitable to use the inner fence of boxplot to identify abnormal records, and use the median to complete missing values. For the building energy consumption data from Shanghai, the ridge regression model fits best.
Key words resources saving and environment protection; data cleaning; data repairing; DBSCAN clustering algorithm; user-based collaborative filtering; ridge regression
doi: 10.13209/j.0479-8023.2020.019
收稿日期: 2019‒08‒13;
修回日期: 2019‒11‒07
国家重点研发计划(2018YFC0704300)和国家自然科学基金(11901359)资助