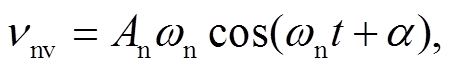(1)摘要为了研究接触界面振动对摩擦的影响, 自主设计实验装置, 以在振动台上匀速滑动的滑块为对象, 采用理论与实验相结合的方法, 分析法向振动和切向振动引起界面切向运动减摩的机理。实验结果表明, 振动台的法向振动和切向振动经常同时存在。当界面振动, 且滑块与振动台之间的切向相对速度方向不变时, 滑块受到的平均滑动摩擦力与无振动时相同, 没有减摩作用;当滑块与振动台之间切向相对速度的方向发生周期性变化或存在 stick-slip (黏滑)时,与无振动时相比, 滑块的平均滑动摩擦力有明显的减摩作用。根据Coulomb 摩擦定律建立动力学模型进行仿真, 仿真结果与实验结果非常吻合, 说明在界面运动为已知的条件下, Coulomb 摩擦模型能够反映界面间的摩擦作用。实验和仿真结果表明, 当法向振动和切向振动同时存在时, 振动引起的界面切向相对运动造成摩擦力方向的周期性变化或 stick-slip 是减摩的主要原因。
关键词法向振动; 切向振动; 相对速度; 摩擦; 减摩
摩擦在很多情况下能够引起振动[1-3], 振动反过来也会影响摩擦[4-5]。在工程中, 有时振动对摩擦的影响会产生有利的结果, 而有时也会产生有害的结果。
摩擦是非光滑多体系统动力学研究中的重要内容之一[6-8], 对摩擦的研究不仅仅局限于宏观尺度[9-10], 随着研究的深入, 微观摩擦学也取得长足的进步[11-15]。但是, 关于振动对摩擦影响的研究比较少。
振动可以减少界面接触摩擦力[16-18]。在宏观尺度, Fridman 等[19]首次对声波振动与静摩擦力的关系开展实验研究, 发现超声引起的振动能够把静摩擦减小至几乎为零。在微观尺度, Carpick[20]利用原子力显微镜证明, 在纳米尺度, 振动对摩擦有降低作用, 当原子力显微镜的探针振动时, 探针与样品表面之间的摩擦力明显小于无振时的摩擦力。
根据振动方向的不同, 学者们分别研究了垂直于界面的法向振动和平行于界面的切向振动对摩擦的影响, 结果表明振动会引起摩擦力降低。
对于法向振动对摩擦的影响, 有研究者认为法向振动能够引起界面之间法向接触面积或接触时间的减少, 导致界面摩擦力的降低[21-23]。但是, 上述研究未获得法向振动时界面间接触面积或接触时间减少的实验数据。并且, 仿真结果与实验结果多是定性地表征法向振动减摩的原因, 没有比较精确的定量对比。因此, 法向振动降低界面摩擦力的机理尚未完全厘清。
切向振动对摩擦的影响分为两类。一类是振动方向平行物体相对运动方向的切向振动对摩擦的影响[24-26]。Gutowski 等[27-28]和 Littmann 等[29]认为, 切向振动速度(幅值)小于滑动速度时, 切向振动不会引起界面摩擦力的降低, 只有当切向振动速度(幅值)大于滑动速度时, 振动引起界面之间摩擦力方向的周期性变化, 才会导致摩擦力的降低。另一类是振动方向垂直于相对运动方向的切向振动对摩擦的影响。此类振动也能引起摩擦力的降低, 但减摩效果远远小于前一类切向振动[30]。上述研究仅关注切向振动对摩擦的影响, 对实验中切向振动是否引起法向振动以及伴随切向振动的法向振动对摩擦是否有影响未予关注。
法向振动台在产生法向振动的同时, 会产生一定幅度的切向振动, 同样, 切向振动台在切向振动时, 也会产生一定幅度的法向振动[31]。我们曾尝试多个振动台, 此现象几乎无法避免, 说明在法向振动减摩的研究中, 法向振动和切向振动常常同时存在。但是, 已有的实验和理论研究仅关注单一的法向振动对摩擦的影响, 没有考虑同时存在的切向振动情况。
本文以法向振动对摩擦的影响为出发点, 并考虑与法向振动同时存在的切向振动对界面摩擦的影响, 分析法向振动和切向振动同时存在时, 对界面滑动摩擦力的影响机理。
我们自主设计的实验装置如图 1 所示。利用信号发生器, 给振动台输入不同频率和振幅的法向正弦振动信号, 在此信号的激励下, 振动台产生法向振动, 同时也产生一定幅度的切向振动。因此, 为了更准确地找到振动影响摩擦力的原因, 我们设置 3 台激光测振仪, 分别测量滑块和振动台运动的绝对速度: 激光测振仪 1 测量振动台的法向振动速度; 激光测振仪 2 测量滑块在滑动方向上的滑动速度; 激光测振仪 3 测量振动台在滑动方向上的切向振动速度。
振动台法向输入的是正弦振动信号, 因此法向振动速度可以表示为
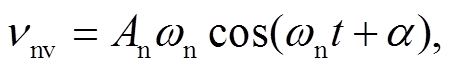(1)其中, νnν为振动台法向振动速度, An为振动台法向振幅, ωn为法向振动频率, α为法向振动初始相位。
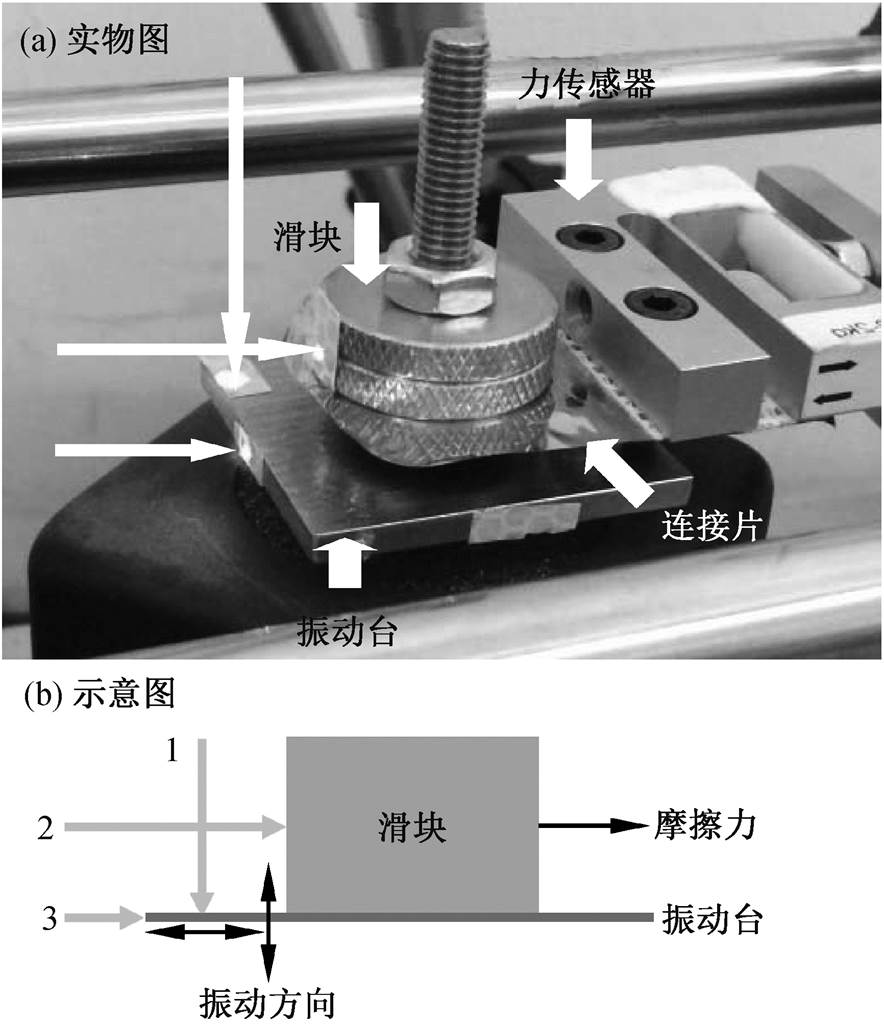
1, 2, 3 分别表示 3 台激光测振仪的激光照射在实验装置上的测试点。测试点 1 测量振动台法向振动速度, 测试点 2 测量滑块在滑动方向上的滑动速度, 测试点 3 测量振动台在滑动方向上的切向振动速度
图1 实验装置实物和示意图
Fig. 1 Photo and schematic diagram of experimental devices
设νnνmax为激光测振仪1测得的振动台法向最大振动速度的平均值, 根据An=νnνmax/ωn,可以计算出振动台的法向振幅An。
通过滑块与力传感器之间的连接片, 水平拉力机匀速拉动滑块在振动台上滑动。在振动状态下, 界面之间的实际摩擦力很难直接测得, 而滑块在振动台上的平均速度不变, 因此水平拉力机上的力传感器采集的拉力平均值等于滑块与振动台之间的平均摩擦力, 所以实验过程中测量了拉力机对滑块的切向拉力。
在实验中, 振动台和滑块的材质均为不锈钢。用温湿度计记录实验环境的温湿度, 所有实验在湿度约为40%, 温度约为26℃的条件下完成。
本文基于Coulomb摩擦定律建立滑块滑动的动力学模型, 同时考虑法向振动和切向振动, 以滑块为研究对象进行受力分析(图2)。
根据牛顿第二定律, 滑块的法向动力学方程为
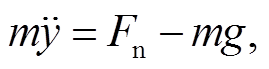(2)其中, y为滑块的法向位移。振动台在法向上为正弦振动,在整个实验过程中, 滑块与振动台在法向上不发生脱离, 则y可表达为
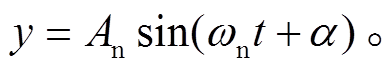(3)
为了保证滑块不脱离振动台, 在实验过程中保持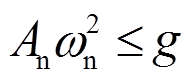
。
由式(2)和(3)可得
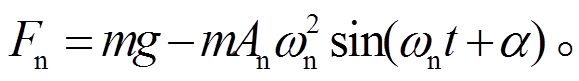(4)根据Coulomb摩擦模型, 界面摩擦力为
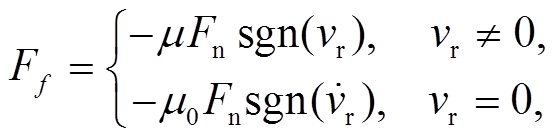(5)
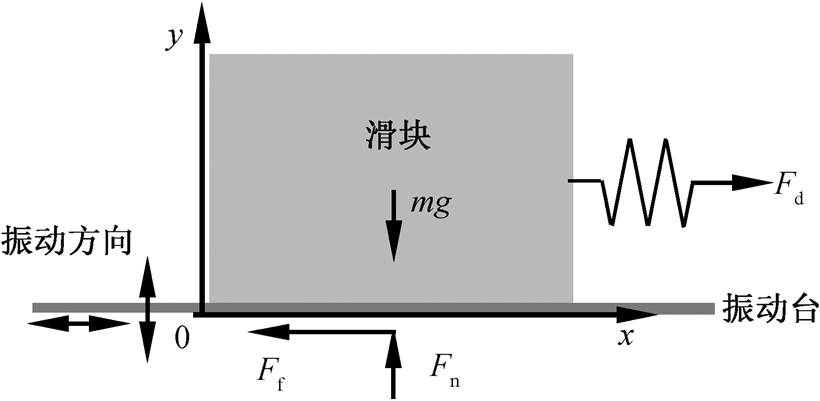
m为滑块的质量, mg为滑块的重力, Fn 为振动台对滑块的法向支持力, Fd为拉力机对滑块的水平拉力, Ff 为滑块与振动台之间的实际摩擦力
图2 滑块的受力分析示意图
Fig. 2 Force analysis diagram of slider
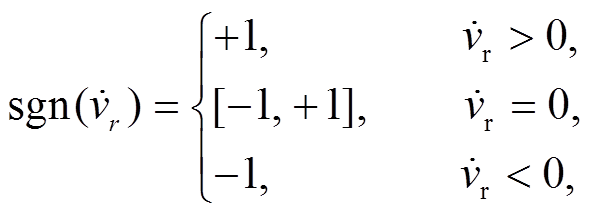
其中, μ为滑块与振动台之间滑动摩擦系数, μ0为滑块与振动台之间的静摩擦系数,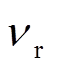
为滑块与振动台之间在滑动方向上的切向相对速度, 并且,
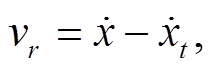(6)
其中,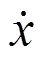 
为滑块在滑动方向的切向滑动速度, 
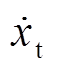为振动台在滑动方向的切向振动速度, 且
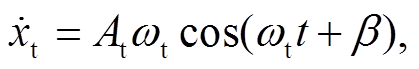(7)其中, At为振动台切向振幅, ωt为振动台的切向振动频率, 由于切向振动是法向振动引起的受迫振动, 因此ωt与ωn相等, β为振动台切向振动的初相位。
滑块的切向动力学方程为
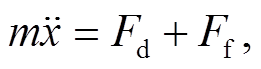(8)式中,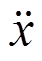 
为滑块在滑动方向上的切向滑动加速度。
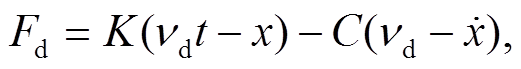(9)
式中, K 为在拉力传感器与滑块之间起连接作用的弹片的弹性系数, C 为弹片的黏性系数(本模型中 C始终为 0), vd为拉力机拉动滑块的速度。
由式(5)可知, 当法向振动和切向振动同时存在时, 滑块与振动台之间的实际摩擦力 Ff 不仅与 Fn相关, 而且与滑块与振动台之间的切向相对速度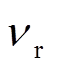相关。
在实验阶段, 通过调整输入的振动信号, 改变振动台的振幅和振动频率, 测量界面摩擦力和 3 个绝对速度: 振动台的法向振动速度、滑块和振动台分别在滑动方向上的切向速度。在仿真阶段, 滑块的质量 m、无振时滑动摩擦系数 μ、无振时静摩擦系数 μ0、振动频率 ωn、弹性系数 K、拉力机的拉动速度 vd、振动台的法向和切向振动速度等都设为已知参数, 并且均在实验中实测获得。
在振动频率为 50Hz 条件下, 给振动台输入法向振动信号。输入信号的电压值越大, 激光测振仪1 测得的振动台的法向振动速度越大, 计算出的法向振幅 An 也越大。此时, 拉力机的水平拉动速度为2×10−3m/s, 在法向的振幅分别为 0.003×10−3, 0.012×10−3, 0.015×10−3 和 0.029×10−3m 条件下, 用拉力传感器测量不同法向振幅条件下的 Fd, 并计算出平均拉力 Fdave (滑块与振动台之间滑动摩擦力的平均值), 结果如图3所示。
可以看出, 在滑块开始完全滑动后, 当 An=0.003×10−3m 时,与无振时的相比, 切向拉力 Fd 没有降低, 随着法向振幅的增加, Fdave 逐渐减小。可见增加法向振动的振幅可以降低界面之间的的滑动摩擦力。
测量在滑动方向上的两个绝对速度——滑块的切向滑动速度和振动台切向振动速度, 结果如图４所示。可以看出, 随着法向振幅的增加, 振动台的切向振动速度也逐渐增加。当 An=0.003×10−3m 时, 滑动摩擦力没有降低(图 3), 此时振动台和滑块的切向速度未发生重合或交叉现象(图 ４(a)), 即振动台和滑块的切向相对速度方向没有发生改变, 也没出现 stick-slip 现象。当 An 为 0.012×10−3, 0.015×10−3 和 0.029×10−3 m 时, 界面之间的滑动摩擦力明显降低, 此时振动台和滑块的切向速度发生重合或交叉(图 4(b)~(d)), 即振动台和滑块的切向相对速度发生方向改变或出现stick-slip现象。
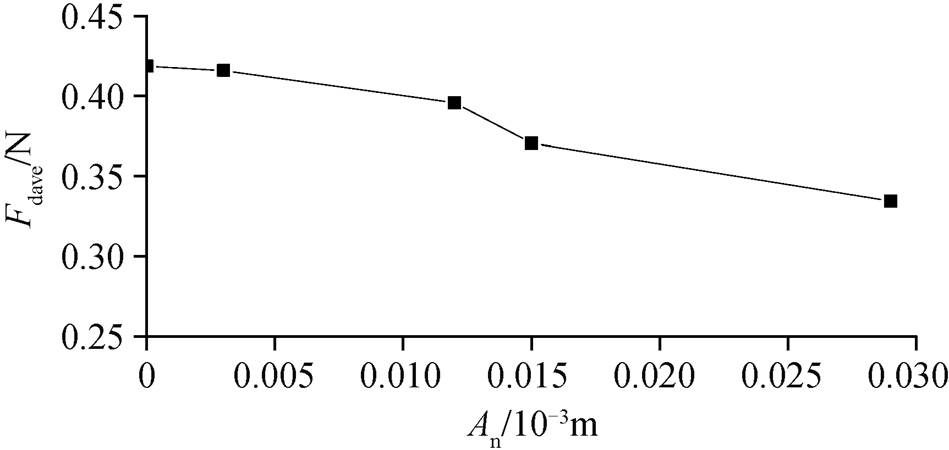
图3 50 Hz振动条件下切向拉力Fd的变化
Fig. 3 Change of tangential driving force Fd at 50 Hz
由图 3 和 4 可知, 只有当滑块和振动台的切向相对速度发生方向改变或出现 stick-slip 现象时, 振动才能起到降低界面之间滑动摩擦力的作用。
我们还测量了更多振动条件下界面摩擦力的变化, 计算振动时滑块在滑动阶段受到切向拉力的平均值(即振动时滑动摩擦力的平均值 Fdave)与无振动时滑块在滑动阶段受到切向拉力的平均值(即无振时滑动摩擦力的平均值 F0ave)的比值 Fdave/F0ave, 该比值可以清晰地反映平均摩擦力减小的程度, 实验结果如图 5 所示。可以看出, 当振动台法向振幅较小时,与无振时滑动摩擦力相比, 界面之间滑动摩擦力没有降低; 随着法向振幅的增加, 滑动摩擦力降低效果越来越明显。
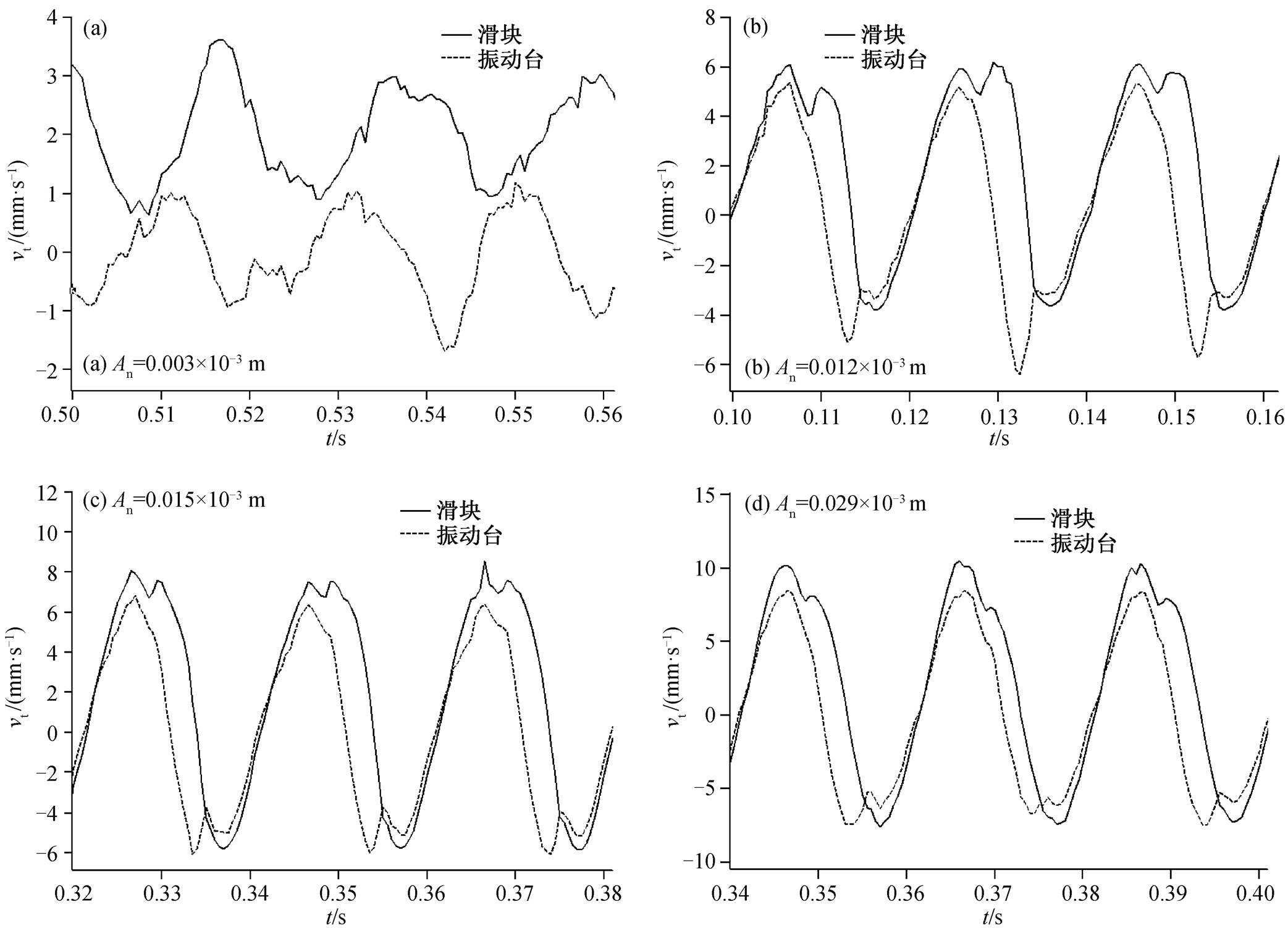
图4 50 Hz振动条件下, 滑块的切向滑动速度和振动台的切向振动速度
Fig. 4 Sliding velocity of slider and the tangential vibration velocity of vibrator at 50 Hz
我们对图 5 中每一个试验点的滑块切向滑动速度和振动台切向振动速度分别进行对比。试验点 2和 3 的法向振幅分别为 0.00179×10−3 和 0.0234×10−3m, 试验点 4 和 5 的法向振幅分别为 0.0000467×10−3和 0.0001876×10−3m。可以发现在试验点 2和 4, 滑动摩擦力未降低, 在试验点 3 和 5, 滑动摩擦力有明显的降低。在试验点 2, 3, 4 和 5, 滑块的切向滑动速度和振动台的切向振动速度如图 6 所示。
由图 6 (a)和(c)可知, 在试验点 2 和 4, 滑块与振动台的切向速度之间没有重合或交叉; 由图 6 (b)和(d)可知, 在试验点 3 和 5, 振动台和滑块的切向速度出现重合和交叉现象。对图 5 中其他试验点滑块和振动台的切向速度也分别进行对比, 发现与图5 有相同的规律。
实验结果表明, 当法向振动和切向振动同时存在时, 在滑块与振动台的切向相对速度方向不变且未发生 stick-slip 条件下, 滑动摩擦力没有降低; 当滑块与振动台的切向相对速度方向发生改变或发生 stick-slip 时, 振动对界面之间的滑动摩擦力明显降低。
根据建立的力学模型进行数值仿真, 计算拉力机对滑块的水平拉力 Fd, 再计算 Fdave/F0ave, 并与实验结果进行对比。
仿真模型中设定的已知参数均按实测数据输入。其中 m=0.2286kg, ωn=50Hz 或 100Hz, K=2837, vd=0.002m/s。仿真过程中设 μ=μ0=0.1852。
代入模型的振动台切向和法向振动速度由激光测振仪测得。以图 5(a)中试验点 1 为例, 振动台法向和切向振动速度的输入如图 7 所示, 可见代入的仿真数据与实验数据一致。滑动摩擦力减摩效果的仿真和实验结果如图 8 所示。
由图 8 可知, 仿真结果与实验结果基本上吻合, 能够反映实验过程中的实际情况, 因此, 可根据以Coulomb摩擦为基础建立的力学模型分析实验中振动影响摩擦的机理。
针对式(2), 设滑块开始滑动时的时间为 t0, 滑动结束的时间为t, 且
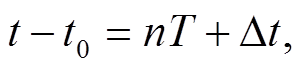(10)式中, n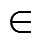
N, T 为一个振动周期, 
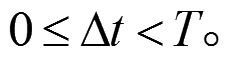在滑动过程中, 对滑块的法向加速度在时间段 t−t0−Δt=nT上积分:
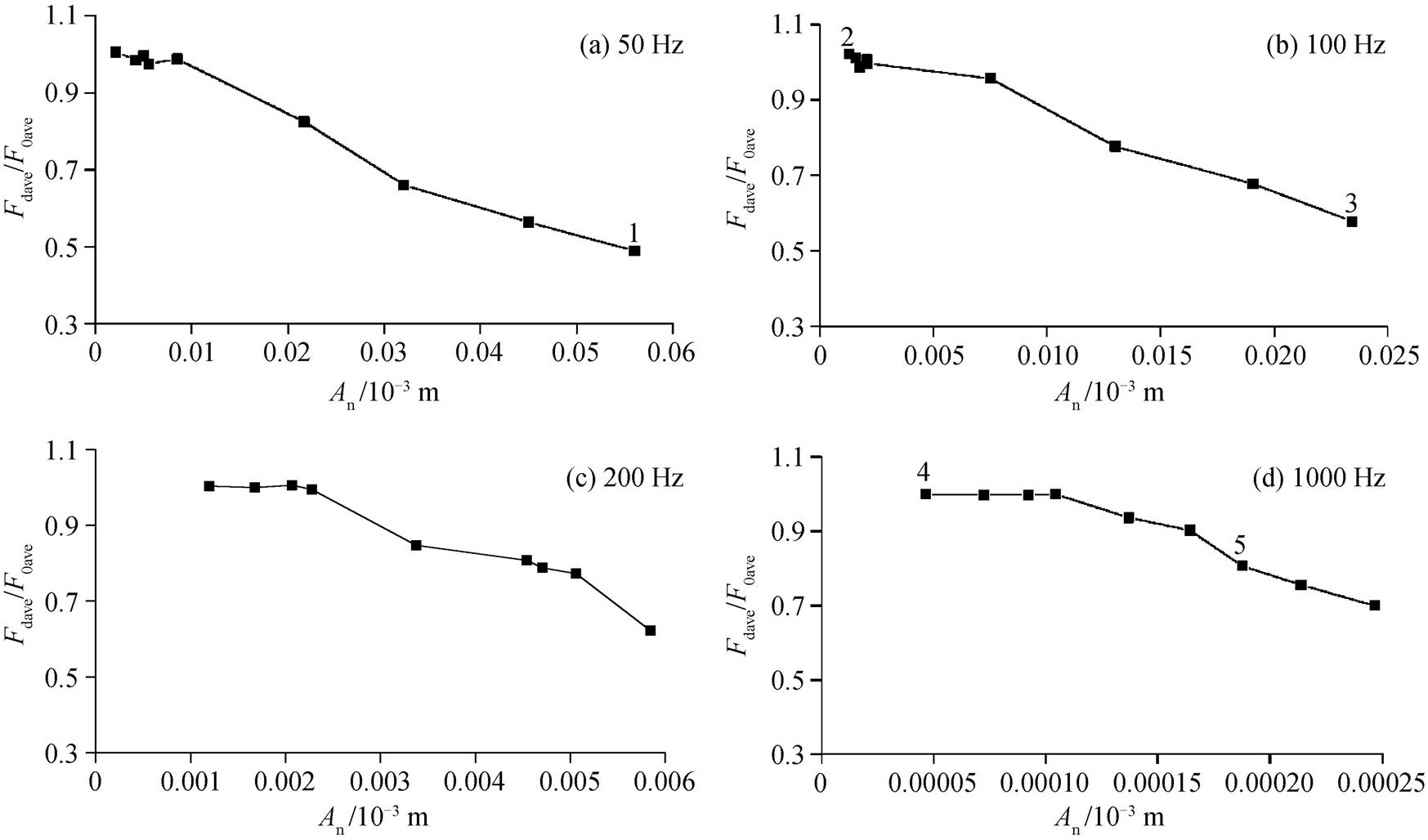
拉力机的水平拉动速度为2×10−3m/s; 1, 2, 3, 4, 5分别代表５个试验点
图5 平均摩擦力减少比例Fdave/F0ave与法向振幅 An 的关系
Fig. 5 Relation between the proportion of average friction reduction Fdave/F0ave and normal amplitude An
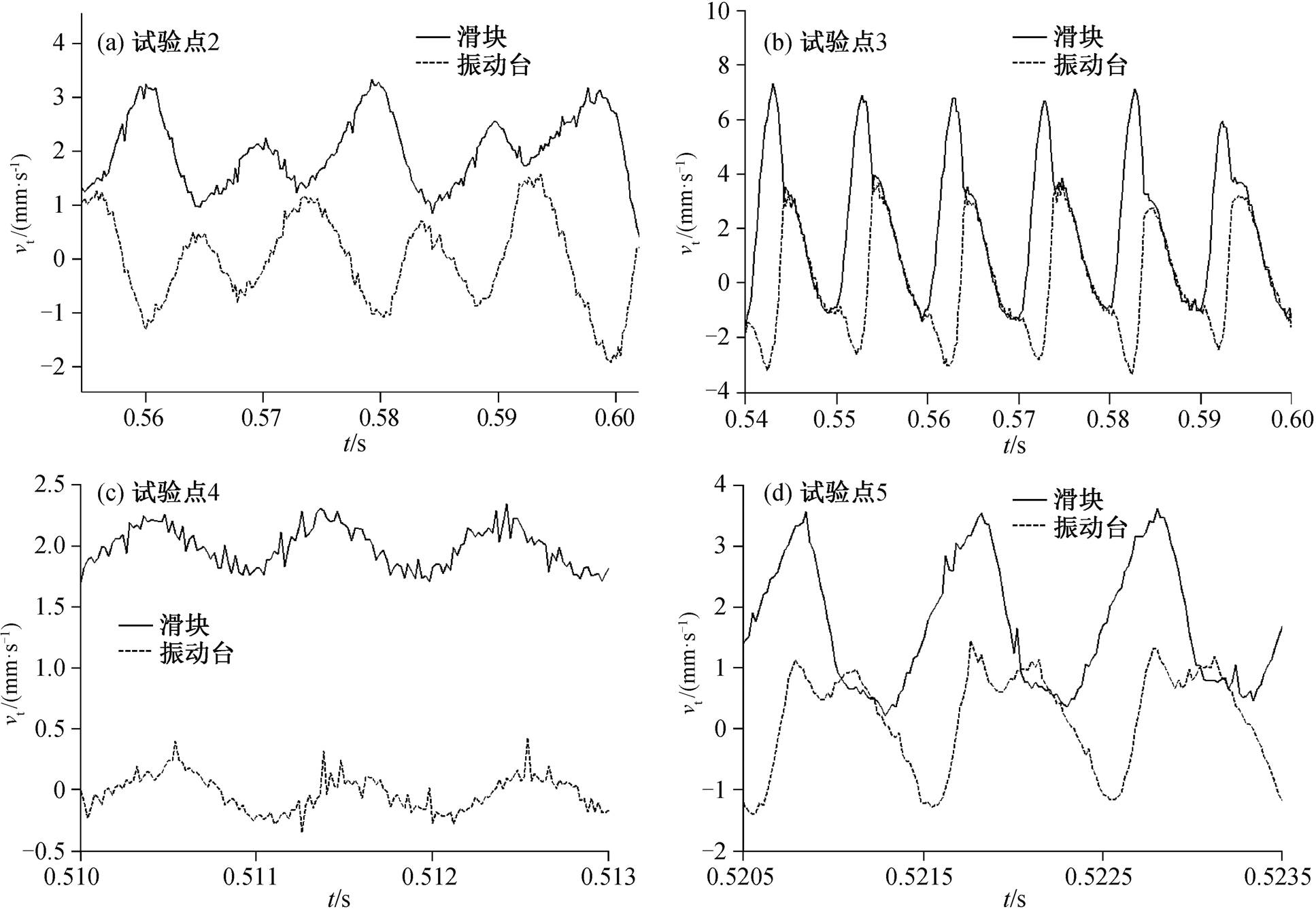
图6 滑块的切向滑动速度与振动台的切向振动速度
Fig. 6 Sliding velocity of slider and the tangential vibration velocity of vibrator
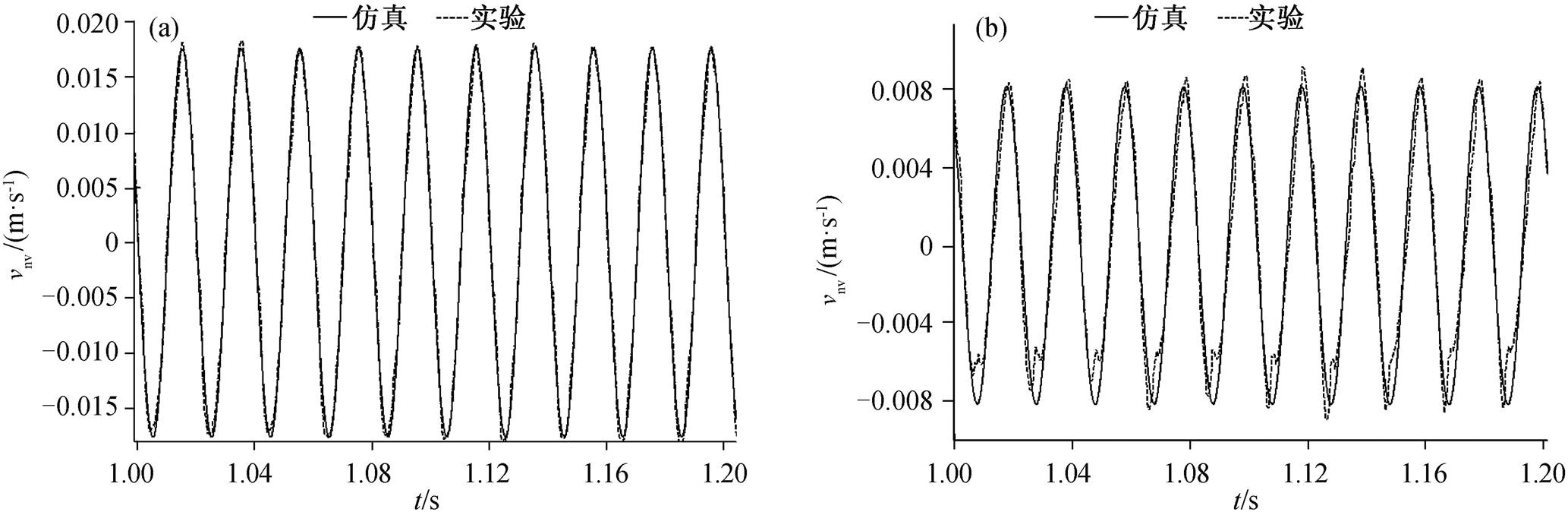
图7 在试验点1, 振动速度的仿真输入与实验数据
Fig. 7 Comparison of simulation data and experimental data of vibration velocity at test point 1
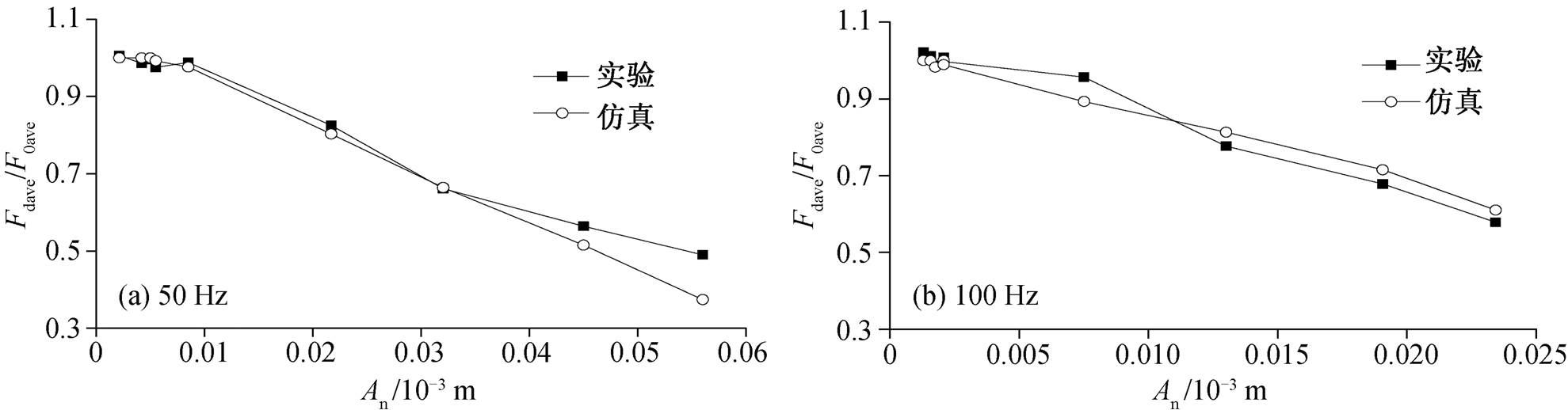
图8 滑动摩擦力减摩的实验与仿真结果
Fig. 8 Comparison of simulation data and experimental data about sliding friction reduction
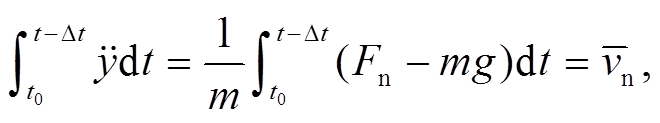(11)其中,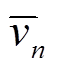 
为滑块在法向上的平均速度。在 nT 的时间范围内, 在法向上滑块始终在平衡位置附近做振动, 所以滑块法向的平均速度为0。
在时间段 t0 到 t 内对滑块的法向加速度做积分:
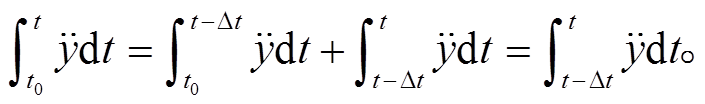(12)如果界面的摩擦始终满足 Coulomb 摩擦定律, 并且滑块与台面之间切向始终为滑动, 则可以根据Coulomb摩擦模型计算滑动摩擦力的平均值。根据式(2)和(12)可得
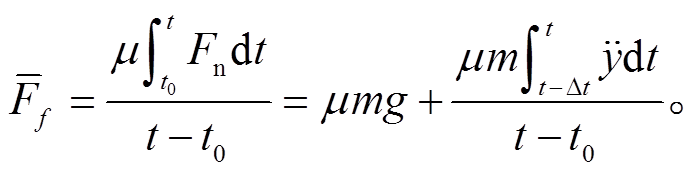(13)
由式(13)可知, 由于 Δt
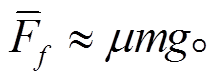(14)由式(14)可知, 当滑块与振动台的切向相对速度方向不变, 且未发生 stick-slip 现象时,μ 的大小和方向均不发生变化, 滑动摩擦力的平均值无变化(恒为 μmg); 当滑块与振动台的切向相对速度方向发生改变或出现 stick-slip 时, μ 的方向或大小会发生变化, μ 的变化将导致在 t 到 t0 时间段内平均滑动摩擦力降低。
综上所述, 当法向振动和切向振动同时存在, 且只有界面之间的切向相对速度方向发生变化或产生 stick-slip 时, 振动才能起到减小摩擦力的作用, 该结论与实验结果一致。
为了研究接触界面振动对滑动摩擦力的影响, 本文通过自主搭建实验装置, 在不同的振动条件下进行实验。以 Coulomb 摩擦模型为基础, 利用牛顿第二定律, 建立能同时反映法向和切向振动对摩擦力影响的力学模型并进行数值仿真, 仿真结果与实验结果基本上吻合。
通过对实验和仿真结果的分析, 可以明确振动降低摩擦力的原因: 在法向振动和切向振动同时存在的条件下,随着振动幅值的增加, 当滑块与振动台的切向相对速度方向发生改变或发生 stick-slip 现象时, 界面之间滑动摩擦力的大小或方向发生变化, 导致界面摩擦力的求和值降低, 进而使得界面之间平均摩擦力降低; 当滑块与振动台的切向相对速度方向不变, 且未发生 stick-slip 现象时,摩擦力的大小和方向不变, 此时摩擦力不会降低。
本文研究结果表明, 当法向和切向振动同时存在时, 振动使得界面的切向相对运动发生变化, 而切向相对运动变化引起的摩擦力方向的周期性改变或者 stick-slip 是振动导致摩擦力降低的主要原因。
参考文献
[1] Lacerra G, Bartolomeo M D, Milana S, et al. Valida-tion of a new frictional law for simulating friction-induced vibrations of rough surfaces. Tribology In-ternational, 2018, 121: 468-480
[2] Sinou J J, Lenoir D, Besset S, et al. Dataset of vibrational and acoustic measurements for squeal analysis from the laboratory brake setup friction-induced vibration and noise at Ecole Centrale de Lyon (FIVE@ECL). Date in Brief, 2018, 21: 639-643
[3] Mercier A, Jezequel L, Besset S, et al. Nonlinear analysis of the friction-induced vibrations of a rotor-stator system. Journal of Sound and Vibration, 2018, 443: 483-501
[4] Yang Chunliang, Wu Chuansong, Shi Lei. Analysis of friction reduction effect due to ultrasonic vibration exerted in friction stir welding. Journal of Manufac-turing Processes, 2018, 35: 118-126
[5] 卢浩宇, 谷丰收, 王铁, 等. 超声振动对内燃机缸套摩擦润滑状态的影响. 科学技术与工程, 2017, 17(34): 67-72
[6] Pfeiffer F. On non-smooth dynamics. Mechanica, 2008, 43: 533-554
[7] 王晓军, 吕敬, 王琪. 含摩擦滑移铰平面多刚体系统动力学的数值算法. 力学学报, 2019, 51(1): 209-217
[8] 唐斌斌, 张艳龙, 崇富权, 等. 含间隙及摩擦的振动系统动力学分析. 机械科学与技术, 2017, 36(9): 1362-1366
[9] Flores P, Leine R, Glocker C. Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach. Multibody System Dynamics, 2010, 23: 165-190
[10] 刘更, 南咪咪, 刘岚, 等. 摩擦对齿轮振动噪声影响的研究进展. 振动与冲击, 2018, 37(4): 35-48
[11] Oded Ben-David, Shmuel M R, Jay F. Slip-stick and the evolution of frictional strength. Nature, 2010, 463: 76-79
[12] Li Qunyang, Tullis T E, Goldsby D, et al. Frictional ageing from interfacial bonding and the origins of rate and state friction. Nature, 2011, 480: 233-236
[13] Braun O M. Bridging the gap between the atomic-scale and macroscopic modeling of friction. Tribol Lett, 2010, 39: 283-293
[14] 周诗杰, 阿达依·谢尔亚孜旦. 摩擦副表面微观动压效应集成、传递及影响的研究. 机械工程学报, 2018, 54(21): 120-126
[15] Persson B N J. Contact mechanics for randomly rough surfaces. Surface Science Reports, 2006, 61(4): 201-227
[16] Holl H J, Meindlhumer M, Simader V, et al. Ex-perimental investigation of friction reduction: by superimposed vibrations. Materialstody: Proceedings, 2018, 5(13): 26615-26621
[17] Vanossi, Manini A, Urbakh N, et al. Colloquium: modeling friction: from nanoscale to mesoscale. Re-views of Modern Physics, 2013, 85(2): 529-551
[18] Jeon S, Thomas T, Yehuda B. Effect of normal vibration on friction in the atomic force microscopy experiment. Applied Physics Letters, 2006, 88(22): 214102
[19] Fridman H D, Levesque P. Reduction of static friction by sonic vibrations. Journal of Applied Physics, 1959, 30(10): 1572-1575
[20] Carpick R W. Controlling Friction. Science. 2006, 313: 184-185
[21] Godfrey D. Vibration reduces metal to metal contact and causes an apparent reduction in friction. ASLE Transactions, 1967, 10: 183-192
[22] 程光明, 曾平, 邱晓阳, 等．超声振动减摩现象的研究. 压电与声光, 1998, 20(5): 322-325
[23] 黄明军, 周铁英, 巫庆华. 超声波振动对摩擦力的影响. 声学学报, 2000, 25(2): 115-119
[24] Popov V L, Starcevic J, Filippov A E. Influence of Ultrasonic in-plane oscillations on static and sliding friction and intrinsic length scale of dry friction processes. Tribology Letters, 2010, 39: 25-30
[25] Tsai C C, Tseng C H. The effect of friction reduction in the presence of in-plane vibrations. Archive of Applied Mechanics, 2006, 75(2): 164-176
[26] Leus M, Gutowski P. Analysis of longitudinal tan-gential contact vibration effect on friction force using Coulomb and Dahl models. Journal of Theoretical and Applied Mechanics, 2008, 46(1): 171-184
[27] Gutowski P, Leus M. The effect of longitudinal tangential vibrations on friction and driving forces in sliding motion. Tribology International, 2012, 55: 108-118
[28] Gutowski P, Leus M. Computational model for fric-tion force estimation in sliding motion at transverse tangential vibrations of elastic contact support. Tribo-logy International, 2015, 90: 455-462
[29] Littmann W, Stork H, Wallaschek J. Sliding friction in the presence of ultrasonic oscillations: superposition of longitudinal oscillations. Archive of Applied Me-chanics, 2001, 71: 549-554
[30] Kumar V C, Hutchings I M. Reduction of the sliding friction of metals by the application of longitudinal or transverse ultrasonic vibration. Tribology Interna-tional, 2004, 37(10): 833-840
[31] 樊雪松,苏文,王晓耕, 等. 电动振动台水平滑台正交方向响应分析及加强台面的设计. 航天器环境工程,2006, 32(2): 90-93
Effect of Interface Tangential Relative Motion Caused by Vibration on Friction
Abstract In order to study the effect of vibration on friction at contact interface, an experimental device was designed. The slider sliding at uniform speed on the vibrator was taken as the object. The mechanism of friction reduction caused by normal vibration and tangential vibration at interface was analyzed by means of experiment and theory. The experimental results show that normal vibration and tangential vibration often exist simul-taneously. When the interface vibrates and the direction of the tangential relative velocity between the slider and the vibrator remains constant, the average sliding friction force of the slider is the same as that without vibration, and there is no friction reduction effect. When the interface vibrates and the tangential relative velocity direction changes periodically or stick-slip, there is an obvious friction reduction effect compared with that without vibration. Coulomb’s friction law was used to establish a dynamic model for simulation, and the simulation results are in good agreement with the experimental results, indicating that Coulomb’s friction model could reflect the friction between interfaces under the condition of known interface motion. The experimental and theoretical results show that the main reason for friction reduction is the periodic change of friction direction between interfaces or stick-slip caused by the tangential relative motion due to the vibration, when normal vibration and tangential vibration exist at the same time.
Key words normal vibration; tangential vibration; relative velocity; friction; friction reduction
doi: 10.13209/j.0479-8023.2020.056
收稿日期: 2019-10-09;
修回日期: 2019-12-23
国家自然科学基金(11572017)资助