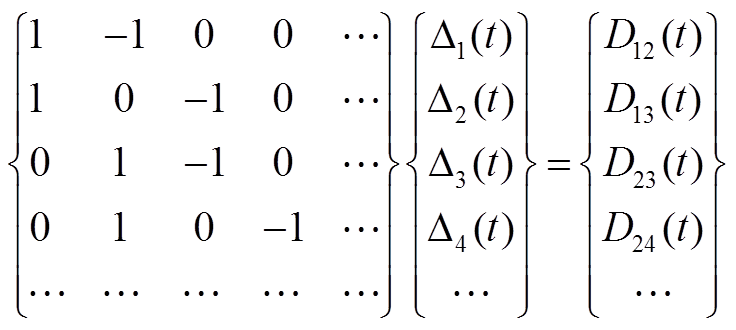。 (3)摘要 利用地震观测台阵中相邻台站间背景噪声互相关函数随时间的偏移的特性, 考虑参考互相关函数、噪声源变化、反演方法和数据误差的影响, 给出基于背景噪声互相关函数的密集台阵时钟偏差分析及其误差评价方法。对盐源短周期地震观测密集台阵的单台时钟偏差分析结果表明, 基于背景噪声互相关函数的时钟偏差分析方法可以给出连续的单台时钟偏差, 并能够筛选出有明显时钟偏差的台站及偏差出现的时段。该台阵的 209 个台站中, 有 17 个台站在观测期内出现大于 1s 的时钟偏差, 可能与仪器数据采集装置的硬件或软件故障有关。
关键词 地震观测密集台阵; 背景噪声互相关函数; 时钟偏差分析; 噪声源分布
地震波形的数据质量评估是使用地震数据进行科学研究的必要前提。随着地震观测密集台阵(简称密集台阵)数据处理和应用技术(简称台阵技术)的快速发展, 已有大量密集台阵数据应用于高精度地下结构成像和地震定位等对波形记录的时间准确性要求很高的研究中。具备准确和统一的时间轴, 是应用大规模密集台阵数据进行深度科学研究的前提之一。
现今的地震仪大多使用数据采集器自动连接全球导航系统(GPS)进行授时, GPS 信号断开时则使用传感器内部时钟进行授时。在仪器运转正常且 GPS信号连接稳定时, 系统的时间精度可以达到 50ns, 能够保证数据授时的精度。授时系统在两种情况下可能产生较大的偏差: 1)GPS 信号连接失败, 导致数据采集系统只能使用传感器内部时钟, 此时记录的波形可能产生连续的时间漂移, 直至 GPS 信号重新连接成功[1‒2]; 2)由于采集或授时系统的硬件或软件出现故障, 数据采集系统的时间可能会出现较大的变化[3‒4]。无论哪种情况产生的时间偏差, 数据使用者都无法获得准确的时间校正信息。
在无法获知准确时间信息的情况下, 可以通过记录的波形数据对台站时钟进行简单的分析。利用波形的时钟偏差分析方法主要有两类。1)通过地震震相在各台站的到时, 估计台站的时钟偏差。例如, Anchieta 等[5]利用海底地震仪与临近海岛上的陆地宽频带地震仪的 P 波到时差, 估计海底地震仪的时钟偏差。此类方法依赖于地震震相的清晰度和出现频率, 因此仅适用于地震频发区域, 对于地震稀少的地区, 不能保证时钟的不间断校正。2)利用台站间的相干噪声信号, 检测时钟偏差。此类方法可用于检测小孔径台阵、海底台阵及区域台网中的台站时钟偏差。例如, Stehly 等[3]利用地球微震频带噪声信号(5~10s 和 10~20s), 对固定台站的时间偏差进行连续检测; Sens-Schönfelder[1]利用两个小孔径火山监测台阵的每日互相关函数相对于全时段叠加互相关函数的偏移量, 给出每个检波器的单台时间日变化, 并指出该台阵的时间漂移主要由 GPS 授时失败期间的内部时钟漂移产生; Xia 等[4]利用几内亚湾的 26s 固定噪声源信号, 分析全球范围的台网时钟偏差; 王俊等[6]对江苏省的固定台网进行连续的时钟分析, 并进行时钟偏差的误差分析。
随着台阵技术的进一步发展, 人们开始尝试布设密集的短时观测台阵(台间距数十米至数公里, 观测周期十几天至数月), 利用噪声中的高频成分, 提取高频(5s 以下)面波乃至体波数据, 以期研究局部小尺度浅层地壳乃至近地表的精细结构[7‒10]。相对于中长周期台阵, 短周期密集台阵具有台间距小、总台站数大和总观测时间短等特点, 数据对时间精度要求较高, 因此需要一种能够同时检测观测时段内所有台站时间精度的快速检测方法。
本文采用类似 Sens-Schönfelder[1]提出的基于台阵间噪声互相关函数的单台时间偏差分析方法, 针对短周期密集观测台阵的特点, 给出适用于它的台阵时间偏差分析方法, 并对盐源短周期地震观测密集台阵(简称盐源台阵)进行时间偏差分析, 探讨参考互相关函数计算误差、矩阵优化方案、数据读取误差及噪声源方向改变等因素对分析结果产生的影响, 最终给出盐源台阵所有台站的时钟偏差以及偏差的误差估计。
在理想状态下, 噪声源均匀地分布, 两个台站之间的背景噪声互相关函数代表两台站间的经验格林函数, 与两台站间的路径结构有关, 不随时间变化[11‒12]。以下因素可能会导致互相关函数的变化: 1)台站间路径结构发生变化; 2)某个台站的时钟出现偏差, 或数据采集器出现相位偏差; 3)噪声源分布发生变化。
可将某一时段内台站间互相关函数相对于参考互相关函数的时间偏差δt用如下式[3]表达:
δt= φ(t)+ D(t)+ ε(t), (1)
其中, φ(t)代表路径结构变化导致的时间偏差, D(t)代表由台站时钟偏差或相位误差导致的时间偏差, ε(t)表示由噪声源分布变化产生的时间偏差。短周期密集台阵的观测时间通常小于 3 个月, 可以认为观测期内台站间的路径结构几乎不随时间变化, 因此相对于 δt, φ(t)可以忽略不计。此时, 台阵中任意两台站 i 与 j 间的时钟(或相位)偏差可以表示为
Dij(t) = ∆i(t) – ∆j(t) = δtij – εij(t), (2)
其中, ∆i(t)表示第 i 个台站的单台时钟偏差, εij(t)表征由于噪声源分布的变化在两台站间产生的时间偏移。若噪声源在空间分布均匀, 或空间分布虽不均匀但随时间变化不大时, 相对于 δt, ε(t)的影响可忽略, 此时 δt 几乎全部由两个台站各自的单台时间偏差贡献。若噪声源的优势方向在一段时间内发生明显的改变, 则 ε(t)的影响不可忽略, 需要想办法予以修正。使用较长观测时间(1 个月以上)的互相关函数叠加, 可以改善噪声源的分布情况, 进而减少ε(t)的影响, 这种做法多应用于对长时间观测的固定台站进行的时钟偏差分析中[2‒3,6], 但会在一定程度上降低计算结果的时间分辨率。本文利用密集观测台阵的特性, 拟合噪声源变化在不同方向的台站间产生的时间变化, 并加以去除, 尽可能地减小噪声源分布变化的影响, 同时保证计算结果的时间分辨率。
对于整个台阵中的共 M 个台站, 通过台阵中所有 K 个台站对互相关函数的时间偏移量(式(2)), 构建求解单台时钟偏差的线性方程组:
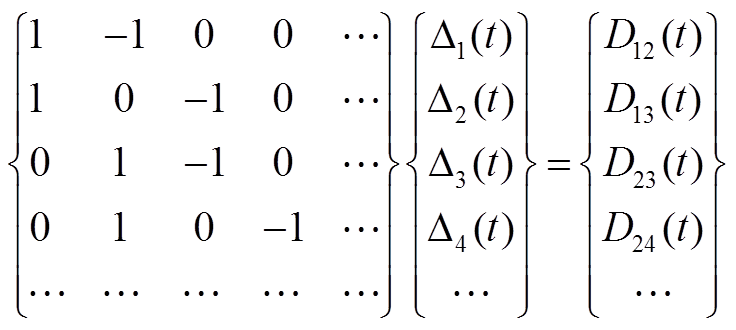。 (3)式(3)中, 线性方程组的系数矩阵为不满秩矩阵, 需要至少选择台阵中的某一个台站 p, 认为它的时钟相对准确, 即∆p(t)=0, 此时式(3)化为典型的超定方程组求解问题, 可以通过最小二乘法求得数据误差最小化的稳定解。
台站对的选择取决于密集台阵的布设方式。距离越近的台站, 互相关函数受介质及噪声源分布变化的影响越小, 也就越能精确地计算台站时间偏差对互相关函数的影响[1]。每个台站应拥有足够的能与之组成台站对的台站, 同时, 为了更精确地去除噪声源变化对时间偏差估计的影响, 台站对应在各个方向上较均匀地分布, 或者有较明显的优势方向。
利用背景噪声分析时钟偏差时, 计算互相关函数的频率范围取决于台站间的距离及台阵布设区域背景噪声场的强度和稳定性。本文通过计算所有台站的单台噪声功率谱密度(power spectrum density, PSD)[13]来考察台阵的背景噪声强度在不同频带的稳定性, 选择强度大且变化幅度小的频带进行互相关计算。除单台背景噪声强度外, 还可根据单日互相关函数与观测期内叠加互相关函数之间的波形相似度来选择互相关频带, 相似度高说明噪声源稳定, 相似度过低则说明单日的噪声源与观测期内的叠加噪声源有较大差别, 不适宜进行时钟偏差分析。实际操作时, 选择的互相关频带应满足如下条件: 利用该频带进行计算时, 台阵中每个台站对都有 90%以上的单日互相关函数与叠加互相关数的波形互相关系数大于0.9。
首先按照 Sens-Schönfelder[1]的方法, 计算台阵中每个台站对每天的互相关函数相对于参考互相关函数的时间偏移量, 操作步骤如下。
1)获取台站对参考互相关函数: 将每个台站对观测期内所有互相关函数叠加, 在 0.1~0.5Hz 频带内做零相移带通滤波, 截取−30~30s 范围内的波形作为该台站对的初步参考互相关函数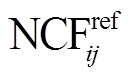
。
2)将每日互相关函数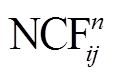
做滤波及截取处理后, 与参考互相关函数做时间域互相关计算, 求出最大相关系数及对应的时间偏移量, 即得到该日期的互相关函数相对时间偏移量
。
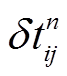3)利用步骤 2 求得的时间偏移量, 对每日互相关函数进行时间修正, 并利用修正后的每日互相关函数, 重复步骤 1, 得到修正的参考互相关函数。
4)重复步骤 2, 得到相对于修正参考互相关函数的时间偏移量。
5)重复步骤 3 和 4, 得到最终的互相关函数相对时间偏差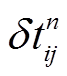及参考互相关函数。
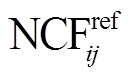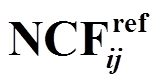的时间偏差修正对于短时观测的台阵, 利用观测期内互相关函数叠加计算求得的参考互相关函数有时不能代表真正的“正确时间”[2]。若存在贯穿观测期的明显时钟或相位偏差, 则简单叠加后的参考互相关函数不能代表台站的“正确”时钟, 此时需要对这类情况进行修正。
本文利用台站对参考互相关函数极值位置偏离零时刻点的时间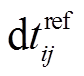
来完成参考时刻的修正。由于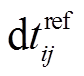受噪声源的方位分布影响, 因此不同方位角的台站对偏移量不同。由于密集台阵的台站对方位角有明显的聚类特性, 因此对台阵内所有台站对的方位角进行聚束分析, 将台站对按方向分组。首先计算每组内所有台站对的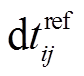, 并计算其平均值
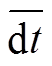和标准差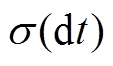
。接下来, 去掉超出
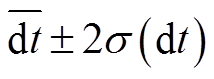的数据, 再次计算其平均值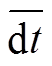与标准差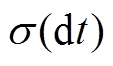。此时, 若某台站对的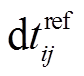满足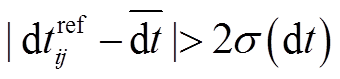
, 则认为此台站对的参考互相关函数相对于“正确时钟”存在不可忽视的偏差。此时, 用参考互相关函数相对于该组台站对偏移量平均值的偏差来代表计算参考互相关函数的时间修正量, 即
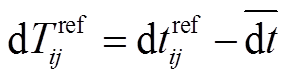。台站对每日时钟相对于“正确时间”的偏移量应为相对时间偏移量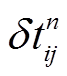与参考互相关函数的时间修正量
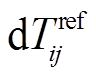之和, 我们称其为台站对的绝对时间偏移量, 即
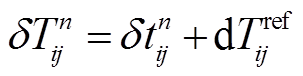, (4)引入绝对时间偏移量后, 式(2)改写为
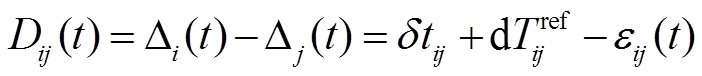。 (5)
利用背景噪声互相关函数进行时钟偏差分析的一个必要条件是背景噪声源均匀分布, 或在观测期内的分布情况没有明显变化。若噪声源分布不均匀且分布方式发生改变, 噪声互相关函数会在时间轴上产生小幅的移动。对于较低频带内距离较近的两个台站, 噪声源分布变化的影响类似传播方向改变的平面波在台站处产生的到时变化, 此时台站对互相关函数相对其参考互相关函数的时间变化量与噪声源的分布以及台站对连线的方位角有关。对密集台阵而言, 台阵内存在大量方位角及台间距相似的台站对, 这些相似的台站对对噪声源改变应该有相似的响应, 可以利用这一特性来估算噪声源改变在台站间互相关函数上产生的时间响应 εij(t)。在盐源台阵每个方位角相似的台站对组I中, 我们将每天组内台站对相对时间偏移量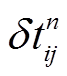的平均值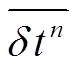
作为该组内所有台站对的噪声源时间响应
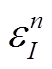。此时, 式(5)可改写为
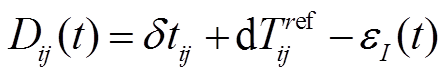。 (6)进行参考互相关函数修正和噪声源响应修正后, 得到各个台站对的时钟偏差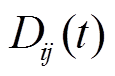
, 继而可以利用式(3)的线性方程组来计算台阵每一天的单台时钟偏差
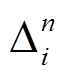。由于式(3)中的系数矩阵永远为不满秩矩阵, 因此在求解线性反演问题前, 要先对矩阵进行优化。本文选择的优化方案为: 选出一个台站作为参考台站, 设定其单台时钟偏差为零, 此时线性方程组变为典型的超定方程组, 可以利用最小二乘法[14]求出稳定解。选取的参考台站 k 应满足以下条件: 1)台站在观测期内数据没有间断; 2)与之相关的所有台站对的参考互相关函数没有明显偏离“正确时间”, 即与参考台站相关的参考互相关函数的极值偏移量
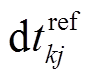均小于整个台阵 dtref 标准差的一半; 3)台站的时钟变化最小, 即与参考台站相关的所有台站对时钟偏差 Dij(t)的标准差最小。
单台时钟偏差分析结果的误差由两部分组成: 1)线性方程组求解过程中引入的误差; 2)数据误差造成的结果误差, 即台站对时钟偏差 Dij(t)的误差对单台时钟偏差的影响。在线性方程组的求解过程中, 参考台站的选取可能对最终的反演结果造成影响。为确定此影响的程度, 我们放宽台站选择的第3 个条件, 选取满足 σ(Dkj(t))
本文中反演数据(即各个台站对的时钟偏差Dij (t))的误差估计由 3 个部分组成:
errD=errdata+errref+errsrc, (7)
其中, errdata为台站对相对时间偏移量δtij 的测量误差, 由获取δtij 时的互相关系数的置信区间决定(互相关系数大于最大值 95%的宽度即为该次测量的测量误差); errref为参考互相关函数修正过程中引入的误差, 仅存在于进行过参考互相关函数修正的台站对中, 其取值为该台站对所属的方位角组内所有未进行参考互相关函数修正的“正常”台站对的极值偏移量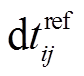的标准差σ(dtnormal)的两倍。errsrc为噪声源分布修正相关的误差, 每个台站对的errsrc为其所属方位角组内台站对的相对时间偏移量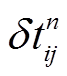的标准差σ(δt)的两倍。
本文使用自举法估计数据误差对单台时间偏差反演结果的影响。在每个台站对的时钟偏差Dij(t)中加入随机误差N(0, σ), 随机误差的标准差取每个台站对数据误差的一半。我们进行100次加入随机误差的线性反演, 并且计算所有反演结果的标准差σerr。最终, 单台时间偏差反演结果的误差由数据误差和反演过程误差组成, 即
ERR∆=2(σsta+σerr)。 (8)
作为本文应用示例的短周期密集台阵数据来自由中国地质科学院和中国地震局地球物理勘探中心布设于中国西南部盐源盆地及其周边山区的短周期密集台阵, 台站总数为209个, 以约2km的台间距密集地布设于约40km×60km的菱形区域内(图1)。台阵使用的仪器全部为EPS-2型短周期三分量地震仪, 频带宽度为0.2~150Hz, 采样频率为200 Hz。台阵观测时间为2017年6月4日至2017年7月10日, 单台最长观测时间为36天, 最短18天。
本文采用Bensen等[15]的背景噪声处理方法, 对背景噪声记录数据进行预处理。首先, 将台站原始记录的采样频率降至50Hz, 并对每天记录完整度大于80%的数据进行去均值和去趋势处理, 再进行去除仪器响应的操作。然后, 对每个长度为1天的数据, 取每段长20分钟、移动步长10分钟的小时窗, 在每个时窗中使用剪切阈值法进行时间域归一化处理, 并在0.05~10Hz频率范围内进行谱白化处理。最后, 对台站间所有长度为20分钟的时窗数据进行频率域互相关计算, 并叠加成为两台站间的单日噪声互相关函数。
盐源台阵最小台站间距为2km, 本文选取台间距5km以内的681个台站对(方位分布见图2)参与台站时钟偏差分析的计算。除台阵边缘的台站以及少量分布不均匀的台站外, 大部分台站可以与距离最近的8个台站进行互相关计算。统计时, 按照台阵分布特点, 台站对的反方位角BAZ∈[0°, 170°]时, 台站对的方向θ=BAZ; BAZ∈[170°, 350°]时, 互相关波形相对于时间零点对称分布后, θ=BAZ− 180°; BAZ∈[350°, 360°]时, θ=BAZ−360°。所有台站对共有4个明显的优势连线方向。
盐源台阵的单台背景噪声强度如图3(a)所示。可以看出, 台阵的单日PSD在频率大于1Hz时变化幅度较大, 可达40dB, 而频率小于1Hz时整体强度较稳定。因此, 从能量的角度考虑, 应选择1 Hz以下的低频带背景噪声来进行互相关计算。图3(b)给出在3个不同的频带范围(1~2, 0.5~1和0.1~ 0.5Hz), 盐源台阵中684个台间距5km以内的台站对的每日互相关函数与观测期内叠加互相关函数之间的相关系数。可以看到, 在0.1~0.5Hz频带内, 互相关函数相似度非常高, 大部分互相关系数均大于0.9; 0.5~1Hz频带内的互相关系数则在0.3~0.9之间, 峰值互相关系数为0.75; 1~2Hz频带内的互相关函数相似度很低, 相关系数峰值仅为 0.3左右。上述结果说明, 盐源台阵的相干噪声场在0.5Hz以上的高频带非常不稳定。为了在最大程度上保证通过背景噪声互相关函数计算得出的时间偏差的准确性, 我们选取0.1~0.5Hz作为背景噪声互相关计算的频带范围。
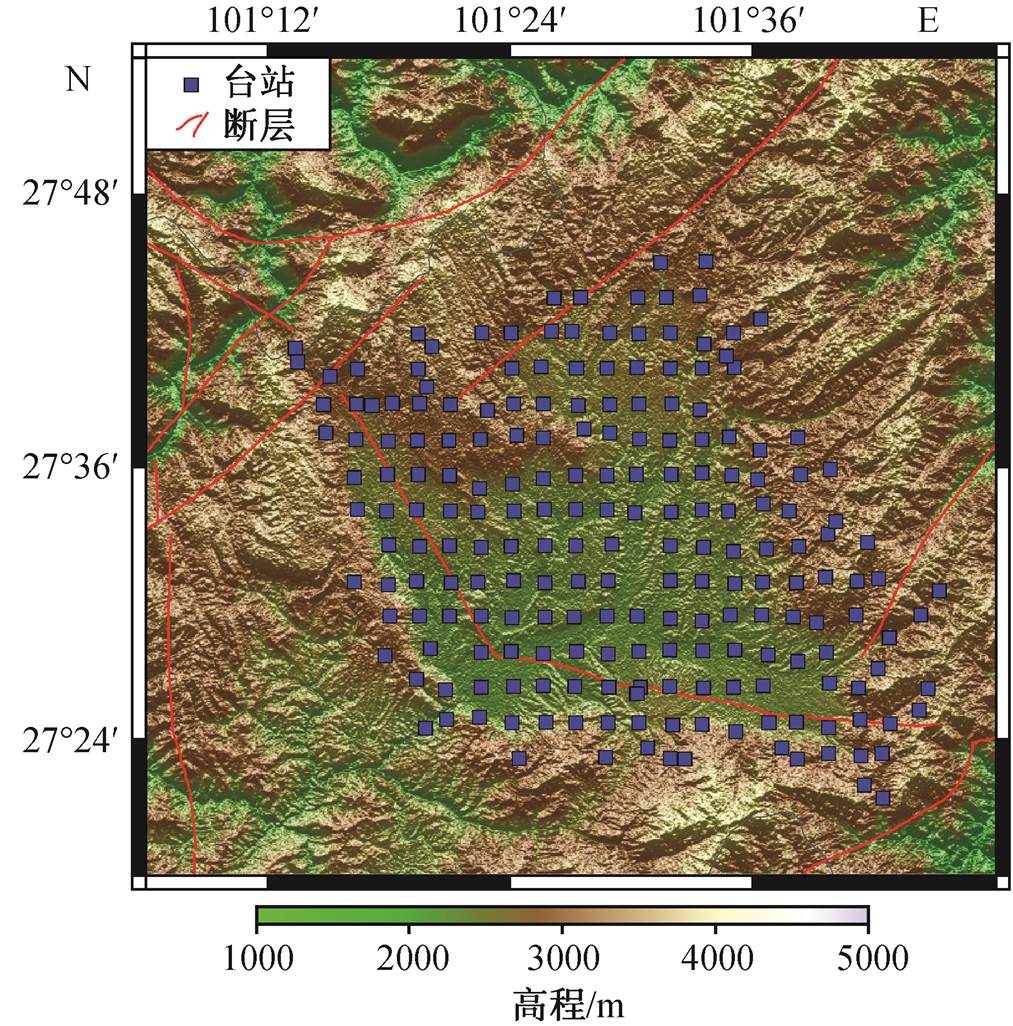
图1 盐源台阵分布
Fig. 1 Spatial distribution of Yanyuan Array
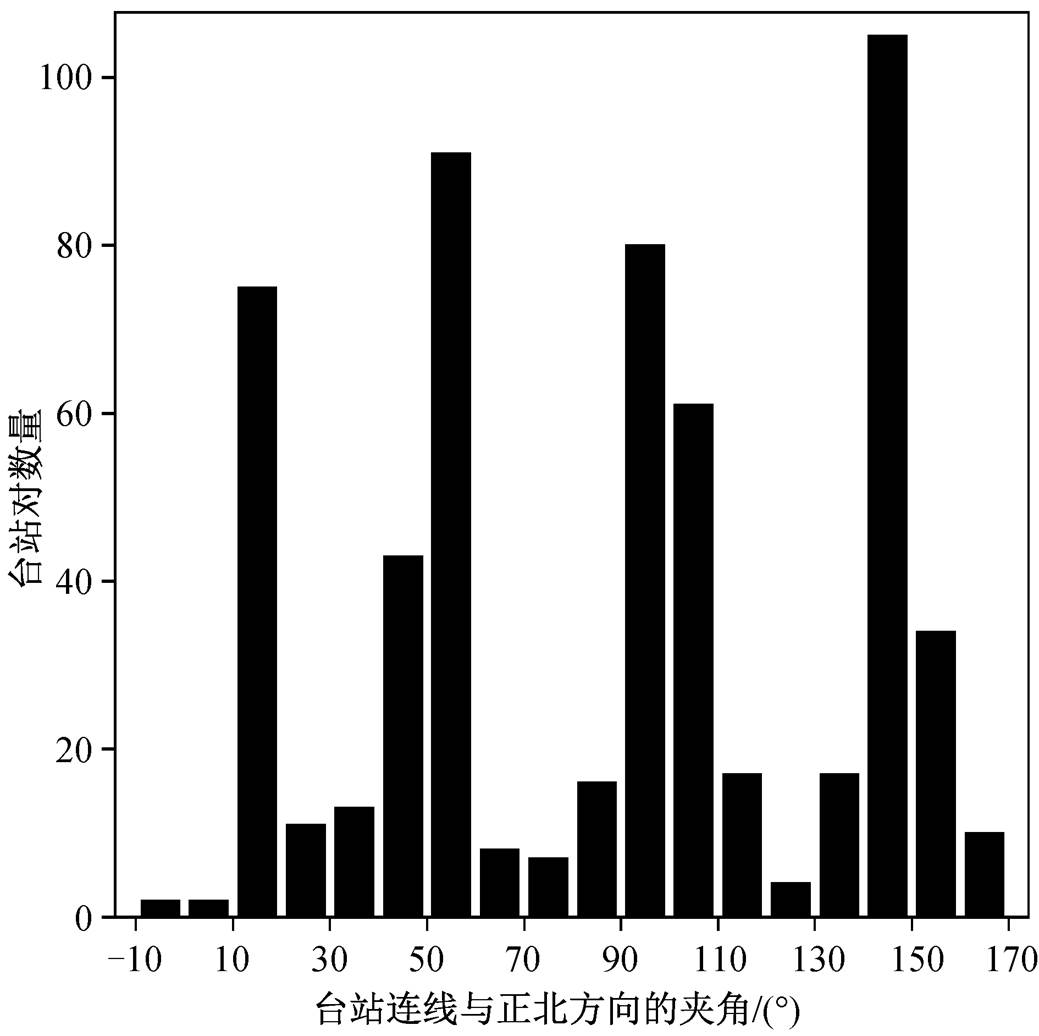
图2 本文使用的台站对方位角分布
Fig. 2 Path azimuth of all station pairs used in this study
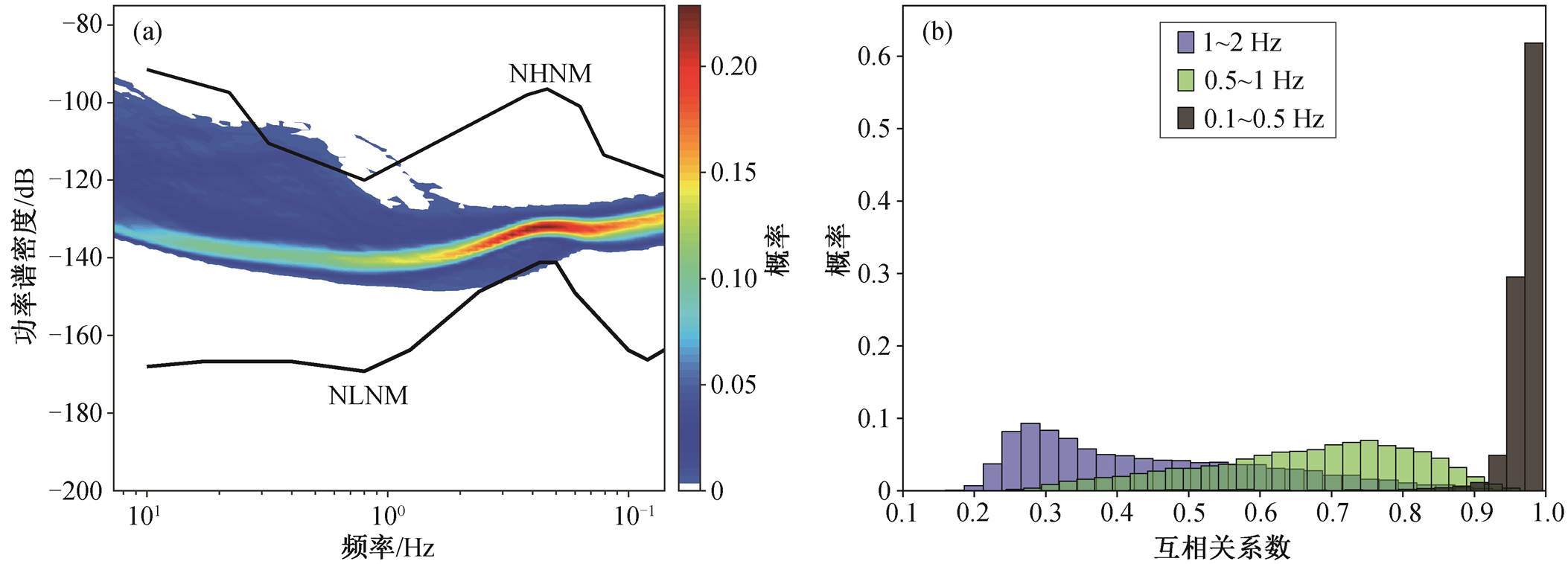
(a)所有台站的单日 PSD 概率密度分布, NHNM 为地球噪声模型中的全球高噪声水平线, NLNM 为低噪声水平线; (b)台站对的每日互相关函数与全时段叠加互相关函数的波形互相关系数在不同频带的概率分布
图3 盐源台阵背景噪声互相关计算的频带选取
Fig. 3 Noise frequency band picked for computing the NCFs of Yanyuan Array
图4展示两个不同台站对原始记录的每日互相关函数、初始参考互相关函数、修正每日互相关函数、修正参考互相关函数及其对应的互相关系数。可以看到, 时钟可能出现偏移的台站对1329-1361, 修正后的参考互相关函数形态发生改变, 对应的每日互相关函数与参考互相关函数的相关系数也大幅度提升。另一个台站对1501-1533, 第26天起数据出现明显错误, 互相关系数大幅度下降。在后续计算过程中, 我们只保留互相关系数大于0.5的数据。
本文对盐源台阵的台站对参考互相关函数进行时间偏差修正。图5(a)展示该台阵中一个台站1377与其周围8个台站的参考互相关函数。8个台站对中, 有6个台站对的参考互相关函数的振幅极大值位置在时间轴(横轴)的零点位置附近, 偏离零点的最大值仅为0.26s, 符合我们对较小台间距(5km以内)及较低频带范围(0.1~0.5Hz)条件下参考互相关函数形态的预期。但是, 存在两个异常的台站对(1377-1411, 1377-1345), 其参考互相关函数的极值位置偏离零点 2s 以上, 远大于其余台站对, 可以断定这两个台站对的参考互相关函数出现明显偏差, 台站对中的某个台站可能在整个观测期内都存在明显的时钟或相位偏差, 此时参考互相关函数的时间轴已不能代表台站对的“正确”时钟。
图5还展示台阵中681个台站对的相对时间偏移量(图5(b)和(c))以及绝对时间偏移量(图 5(d))。为了绘图方便, 图5(b)中统一将台站对中编号较小的台站作为源台站, 用起点在源台站处的射线代表台站对的极值偏移量, 射线长度代表该台站对极值偏移量的绝对值, 当台站间极值偏移量大于0时, 射线方向与台站对连线方向一致, 反之则与台站对连线方向相反。在盐源台阵中, 共有107个台站对存在绝对时间偏移量较大的情况, 说明在盐源台阵的时钟偏差分析过程中, 参考互相关函数的偏差修正是必要的。
图6展示2017年6月12日相对时间偏移量随台站对方位的分布、去除噪声源响应的相对时间偏移量以及修正噪声源前后单台时钟偏差的反演结果, 可以看到噪声源分布的优势方向发生明显的改变, 东南方向的台站对产生最大的时间偏移, 偏移量超过0.3s。这类噪声源响应会使由式(3)得出的单台时间偏差结果产生非常明显的系统性偏差。经过噪声源响应修正后, 大部分台站对的相对时间偏移量大幅度减小, 反演结果中的系统性偏差也得到修正。位于东南角的部分西北‒东南方向台站对, 经过噪声源响应修正后仍残留少量偏差, 说明此处可能存在一些较明显的局部噪声变化。
盐源台阵的时钟偏差反演结果的误差如图 7 所示。由式(8)可知, 反演误差由反演求解造成的误差和数据造成的误差两个部分组成。反演求解造成的误差主要来源于参考台站的选择。本研究选取满足σ(Dkj(t))<0.02 (即台站对时钟偏差的标准差小于采样间隔)的台站作为参考台站, 盐源台阵中满足此要求的参考台站共有 23 个。我们选取这 23 个台站中任意一个作为参考台站, 获得不同的反演结果, 并计算结果的标准差 σsta (图 7(a))。可以看出, 除第一天因参与计算的台站较少而使得反演结果的标准差较大外, 其余时间改变参考台站后的反演结果标准差均小于 0.03s, 说明变换参考台站对反演结果的影响很小。
按照 1.6 节的方法, 计算数据误差造成的反演结果标准差 σerr, 结果如图 7(b)所示。可以看出, 由数据误差造成的反演结果标准差整体上小于 0.1s, 仅部分台站和部分日期达到 0.2s 左右。台阵边缘的台站、参考互相关函数有异常的台站以及噪声源异常的台站数据误差较大, 由其引起的反演标准差也较大。台阵的单台时钟偏差反演的最终误差如图7(c)~(d)所示。可以看出, 反演结果的误差在大部分台站的大部分时间内都小于 0.1s, 台阵边缘台站的总体误差较大, 单台误差平均值达到 0.2s 以上。在观测期内, 6 月 5 日和 7 月 3 日所有台站的反演误差均较大, 可能是由观测开始阶段和结束阶段参与计算的台站数量较少导致。台阵右下角处台站的总体误差较大, 可能与局部噪音源变化强烈(图 6(b))有关。综上所述, 时间偏差结果的准确度受台站在台阵中的位置、参与计算的台站数量以及背景噪声分布稳定性等因素的综合影响。
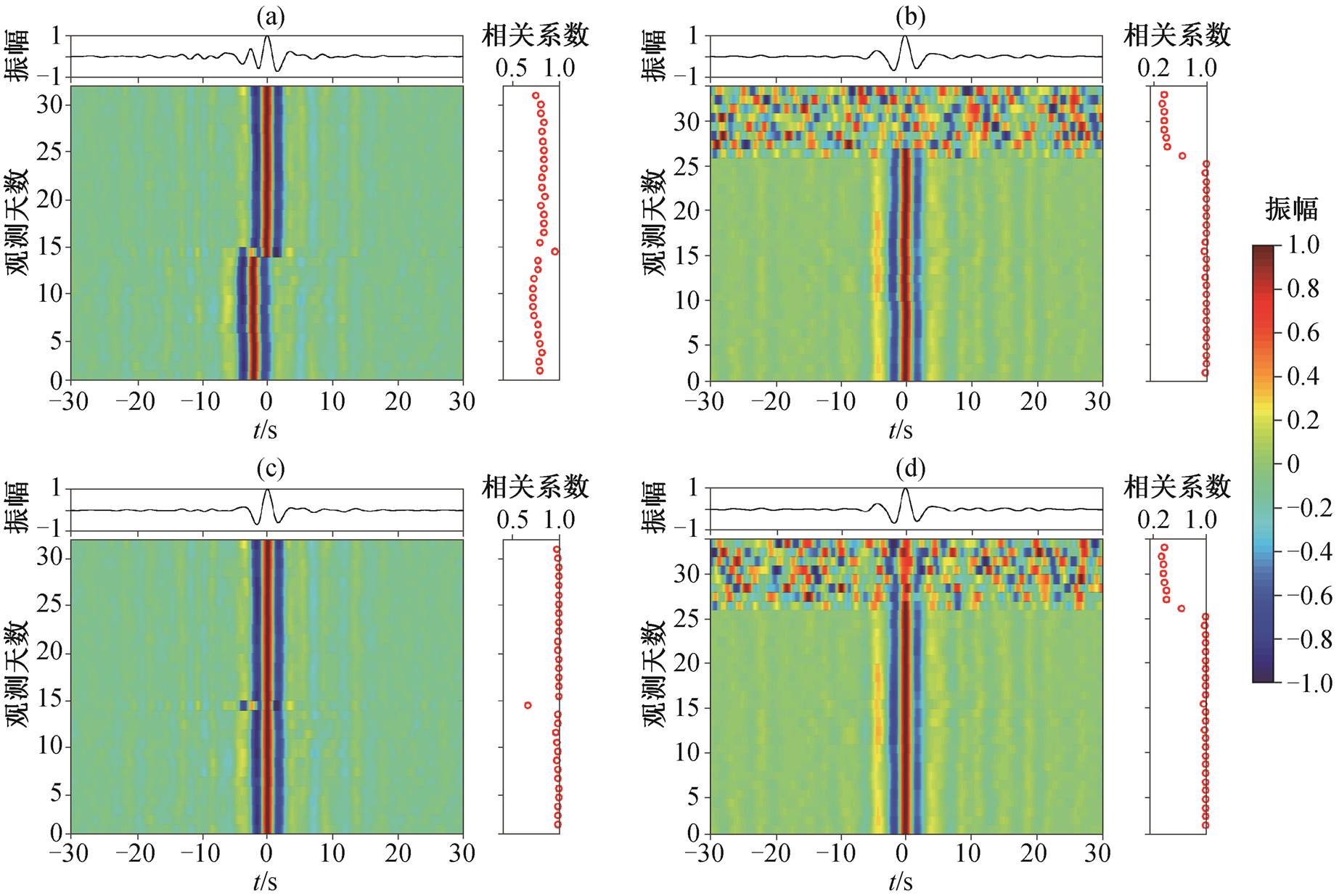
(a)和(c) 台站对1329-1361, (b)和(d) 台站对1501-1533; (a)和(b) 时间偏移修正前, (c)和(d) 时间偏移修正后
图4 不同台站对的每日互相关函数、参考互相关函数及互相关系数变化
Fig. 4 Daily NCF, reference NCF and the correlation coefficients of certain station pairs
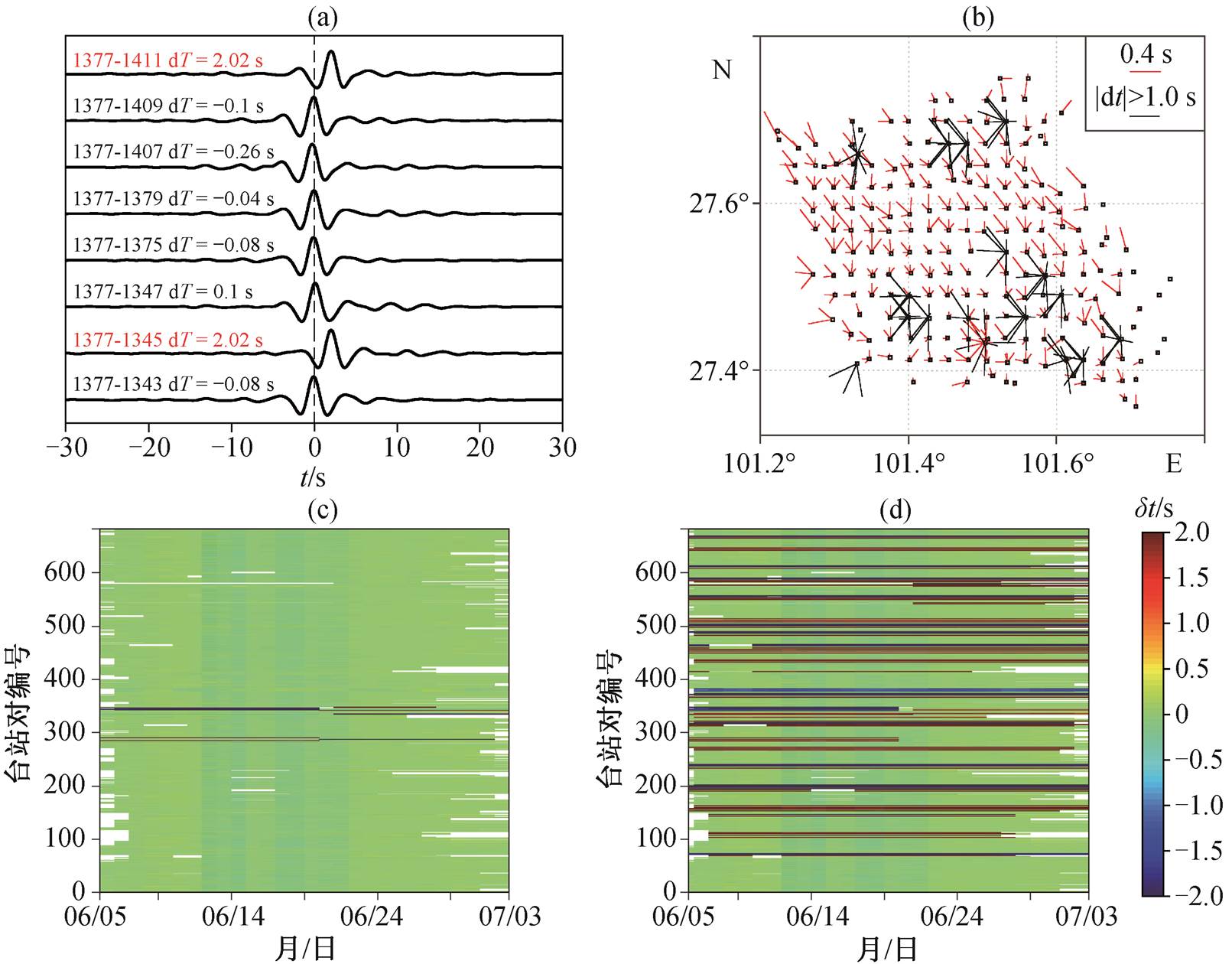
(a)台站 1377 与周围 8 个台站的参考互相关函数; (b)台阵中所有台站对的极值偏移量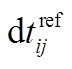
分布; (c)所有台站对每一天的相对时间偏差
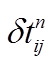; (d)所有台站对的绝对时间偏差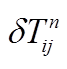
图5 利用绝对时间偏移量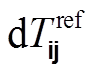
对参考互相关函数进行修正
Fig. 5 Correction of reference NCF using absolute time shift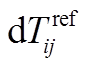 
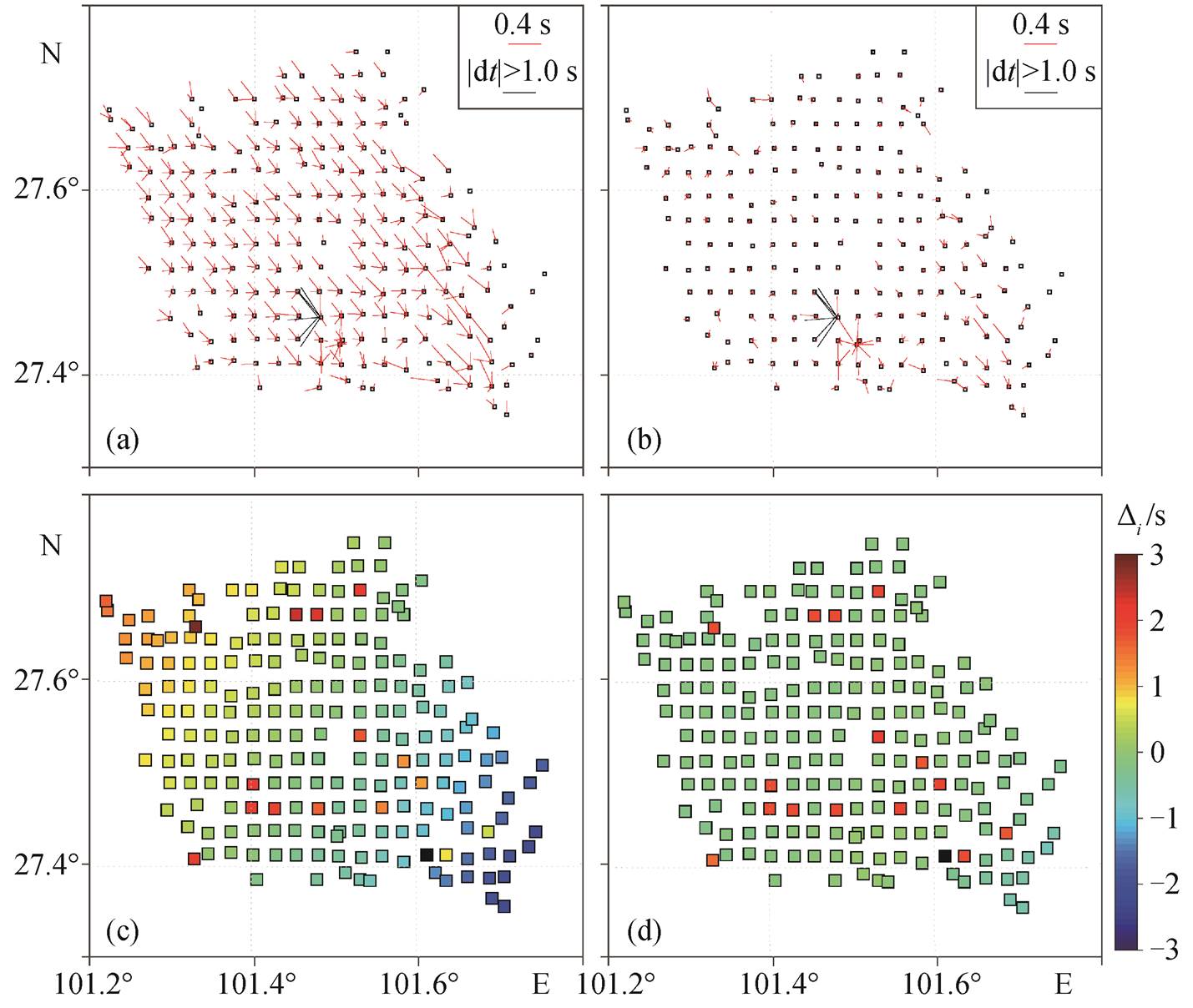
(a)台站对的相对时间偏差δtij; (b)噪声源修正后的相对时间偏移量δtij －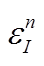
; (c)未进行噪声源修正的单台时钟偏差反演结果; (d)噪声源修正后的单台时钟偏差反演结果
图6 噪声源分布改变对单台时钟偏差分析正确性的影响(2017年6月12日)
Fig. 6 Influence of variable noise source on the correctness of single station clock shift analysis (June 12, 2017)
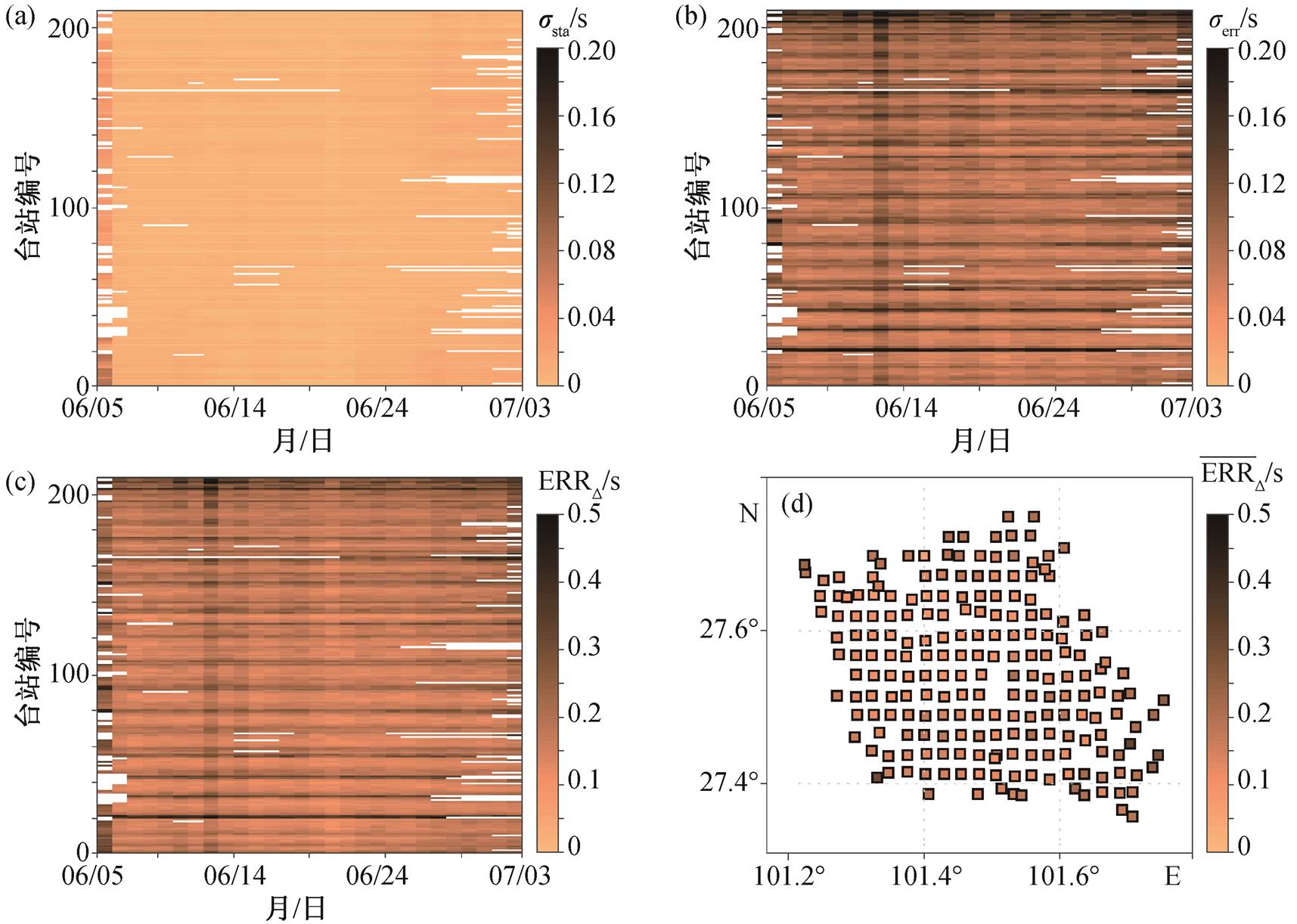
(a)变换参考台站时反演结果的标准差 σsta; (b)数据误差造成的反演结果标准差 σerr; (c)所有台站观测期内的单台时钟偏差分析误差ERR∆; (d)观测期内平均单台时钟偏差分析误差的空间分布
图7 单台时钟偏差反演结果的误差估计
Fig. 7 Error estimate of single station clock shift analysis
盐源台阵的单台时间偏差反演结果及其误差分析结果如图 8 所示。盐源台阵的 209 个台站中, 有17 个台站出现比较明显的时钟偏差, 其中有 15 个台站的时间始终比正常时间提前 2s 以上, 有 1 个台站(1349)的时间始终比正常时间提前 1s 以上, 还有一个台站(1329)在 2017 年 6 月 5—19 日的时间比正常提前 2 s 左右, 自 6 月 20 日起, 时间回到零点附近的正常范围。所有时钟偏差均为跃变式, 可能与数据采集器内的软件或硬件故障有关, 具体原因有待对仪器进行检测后核实。盐源台阵中未出现类似 Sens-Schönfelder[1]和 Gouédard 等[2]的研究中出现单台时钟偏差随时间线性增加或减少的情况, 可能说明盐源台阵的台站未出现数据采集器在一段时间内无法连接 GPS 的情况, 也可能表明台阵使用的仪器内部时钟比较稳定, 没有明显的漂移。
我们利用台阵观测期内一个较大的极远震的 P波数据测试本文方法的准确性。该地震的震中位于危地马拉西岸(13.717°N, 90.972°W), 震源深度为28km, 震级为 Mw6.8, 距离台阵中心的震中距为135°, 台阵中记录到清晰的 PKP 震相。PKP 震相是近似垂直地入射台阵, 可以在最大程度上减少路径差异对地震信号到时的影响。我们利用盐源台阵以及台阵附近一个固定台站(盐源台)接收的该地震波形, 利用临近台站间的波形互相关函数, 求出台站间的到时差, 并设定固定台的到时为 0, 求出台阵中各个台站的到时差。本文对该地震的 PKP 波到时数据进行方位角校正后, 计算盐源台阵中各台站与盐源固定台之间的 PKP 波到时差, 估算台阵中各台站的时钟偏差, 结果如图9 所示。
从图 9 可以看到, 由地震信号求得的时钟偏差与噪声互相关方法求得的时钟偏差的差别在±0.2s之间, 大部分台站的偏差小于 0.1s, 说明本文提出的利用噪声进行单台时钟偏差分析的方法是有效的。两种方法产生差异的可能原因主要有以下 3 个方面: 1)地震数据方法中, 由路径结构造成的干扰, 不同台站下方速度结构的差异会造成到时的小幅差异; 2)噪声互相关方法中, 反演算法及噪声源分布造成的干扰; 3)两种方法代表的意义有所差别, 地震数据求得的时钟偏差是瞬时偏差, 噪声互相关方法求得的时间偏差是一天时钟偏差的平均值。
我们注意到, 2017 年 6 月 12 日的单台时钟偏差分析结果中仍存在一定程度的系统性偏移(图 6(d)), 台阵东南角的台站时钟的整体偏差大于台阵内其他区域的台站, 说明在这一天, 即使是方位角相近的台站对, 时间偏移量仍有一定程度的差别, 仅使用不同方位角的平均值, 不能完全去除由噪声源变化引起的互相关函数时间偏移。这种现象出现的一个可能原因是, 这一天的主要噪声源来自离台阵较近的地方, 甚至台阵内部, 因此其对台阵中不同位置台站对的影响不尽相同。我们查阅当地的小地震记录, 未发现台阵东南角周边在 6 月 12 日有任何地震记录, 此处台站的原始波形记录中的确存在一些疑似事件记录, 推测可能与当地的矿井采集等人为事件有关。同时, 这一天结果的整体误差也比其他时间偏大, 其原因主要有两方面: 1)这一天的噪声源变化较剧烈, 根据式(6)计算得出的数据误差中噪声源对应的数据误差 errsrc 较大; 2)因受台阵布局形态影响, 台阵的东南角的台站分布不均, 此处参与反演计算的台站对数量不足, 台站连线的方位角分布也与台阵的其他位置有差别, 在进行单台时间偏差反演计算时, 较少的台站对会放大数据误差对结果的影响, 我们需要后续更深入的研究来确认这一天噪声源的具体情况及其对台阵噪声互相关函数的影响方式。
介质波速的变化也会引起噪声互相关函数的时间延迟, 但这种影响极其微弱。例如, 地震引起的同震效应会引起介质波速的变化, 由噪声测得的波速相对变化量一般小于 0.1%[16]。Pei 等[17]通过体波成像方法, 发现在较小的断裂带范围内, 大地震后地震波的波速可比震前下降 4%。固体潮、降水和大气压的变化也会影响介质的波速, 但波速的变化量在 0.1%左右, 远小于地震的同震变化[18]。并且, 与波速变化监测常用的尾波信号相比, 直达波对介质的波速变化敏感度不高。在盐源台阵观测期间, 观测区域没有大震发生, 介质的波速发生较强变化的可能性小。在我们选用的 0.1~0.5Hz 频带内, 研究区的面波速度约为 2.5km/s。以波速的相对变化为 1%来计算, 在 5km 台站间距上能够引起的走时变化约为 0.02s, 不足以造成本文检测到的时钟偏差。实际介质的波速变化远达不到 1%, 因此在短时间内检测仪器钟差时, 介质波速的微弱变化可以忽略。
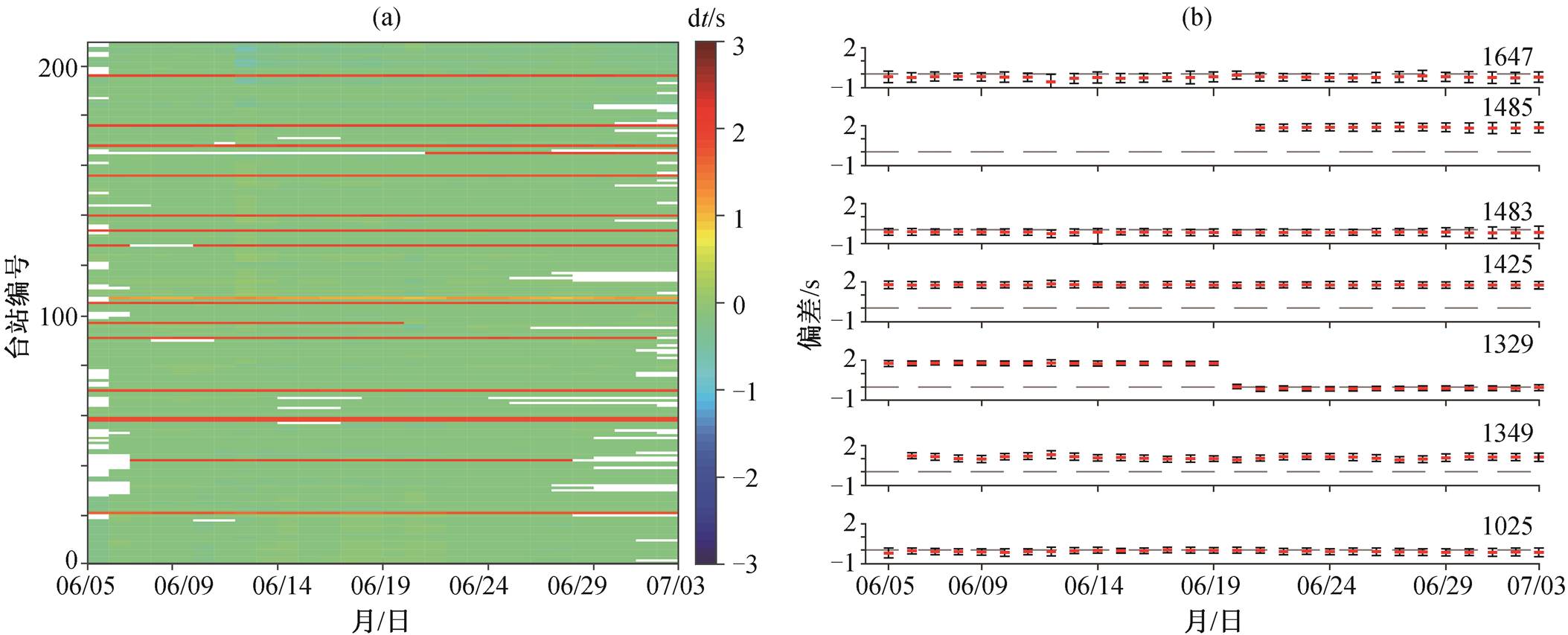
(a)所有台站的单台时钟偏差分析结果; (b)部分台站的单台时钟分析结果及误差, 红色线段代表单台时钟偏差反演结果, 黑色线段代表相应的误差
图8 盐源台阵单台时钟偏差反演结果
Fig. 8 Single station clock shift analysis of Yanyuan Array
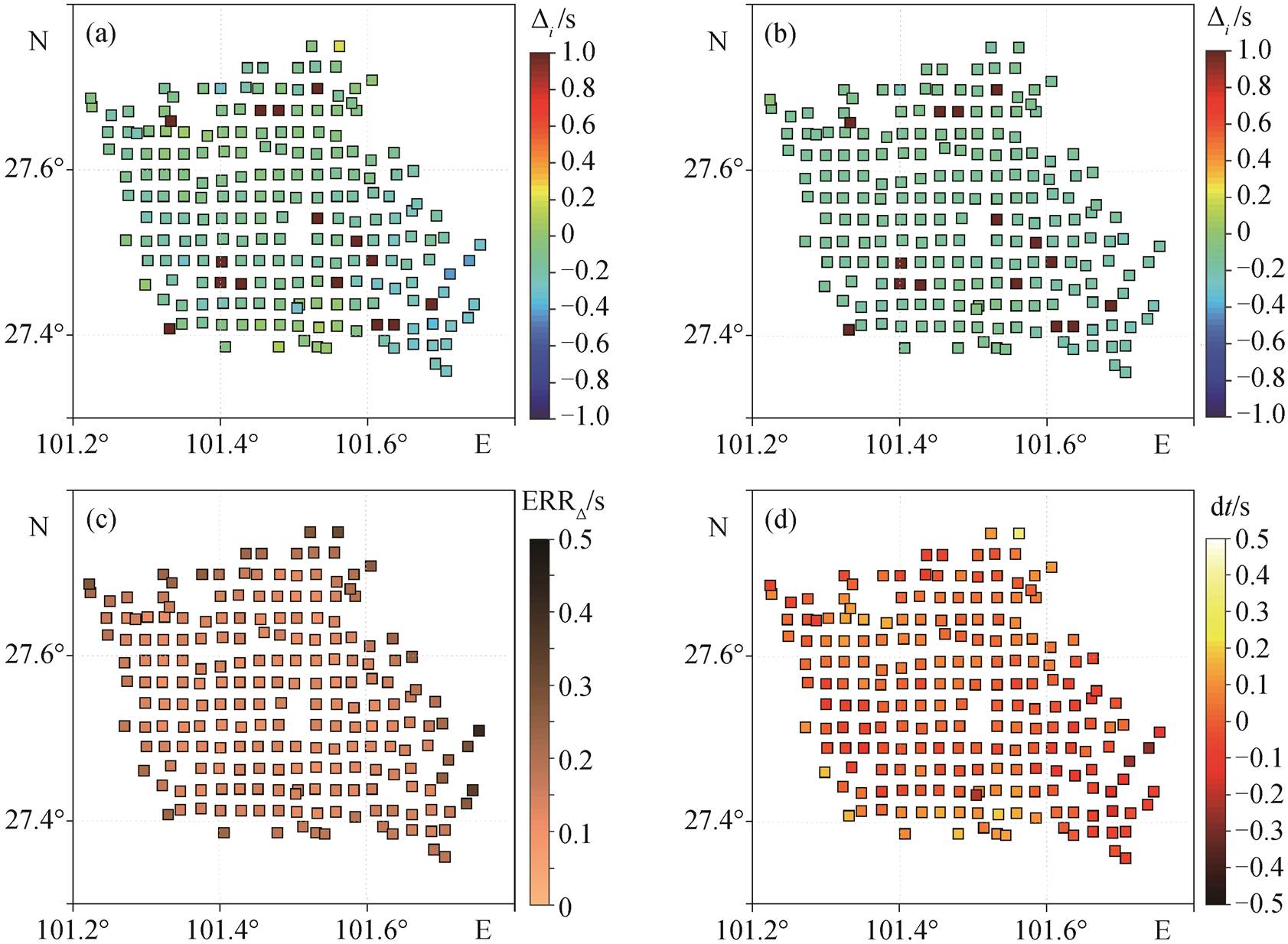
图9 地震数据(a)与噪声数据(b)求得的单台时钟偏差、地震数据方法的误差(c)以及两种结果的对比(d)
Fig. 9 Single station clock shift result from earthquake data (a), ambient noise data (b), error estimates of earthquake data (c) and comparison between the two sets of data (d)
本文提出一种利用短周期地震观测密集台阵中相邻台站间的背景噪声互相关函数进行台阵时钟偏差分析的方法, 针对短周期密集台阵的特性, 修正了参考互相关函数误差及噪声源变化对时钟偏差分析结果的影响, 讨论了数据拾取误差、反演优化方案、参考互相关函数修正以及噪声源变化对结果的影响。通过在盐源台阵的应用, 证明本文提出的方法可以较快速、准确地给出密集台阵全观测期内的连续时钟偏差, 为密集台阵数据的后续应用提供可靠的依据。
对盐源台阵的时钟偏差分析结果显示, 209 个台站中, 有 17 个台站在观测期内出现较明显的跃变式钟差, 可能与仪器数据采集装置的软件或硬件故障有关。在利用台阵数据进行涉及时间的研究(如震相到时拾取、速度结构反演等)时, 应特别注意去除时钟偏差明显的台站数据, 或利用时钟偏差分析结果进行相应的修正。
参考文献
[1] Sens-Schönfelder C. Synchronizing seismic networks with ambient noise. Geophys J Int, 2008, 174: 966–970
[2] Gouédard P, Seher T, McGuire J J, et al. Correction of ocean-bottom seismometer instrumental clock errors using ambient seismic noise. Bull Seismol Soc Am, 2014, 104(3): 1276–1288
[3] Stehly L, Campillo M, Shapiro N M. Traveltime measurements from noise correlations: stability and detection of instrumental time-shifts. Geophys J Int, 2007, 171: 223–230
[4] Xia Y J, Ni S D, Zeng X F, et al. Synchronizing intercontinental seismic networks using the 26 s per-sistent localized microseismic source. Bull Seismol Soc Am, 2015, 105(4): 2101–2108
[5] Anchieta M C, Wolfe C J, Pavlis G L, et al. Seis-micity around the Hawaiian islands recorded by the PLUME seismometer networks: insight into faulting near Maui, Molokai, and Oahu. Bull Seismol Soc Am, 2011, 101: 1742–1758
[6] 王俊, 郑定昌, 詹小艳, 等. 基于背景噪声互相关格林函数的单台时间误差估计. 地震学报, 2013, 35(6): 888–901
[7] Huang Y, Yao H J, Huang B, et al. Phase velocity variation at periods of 0.5–3 seconds in the Taipei basin of Taiwan from correlation of ambient seismic noise. Bull Seismol Soc Am, 2010, 100: 2250–2263
[8] Li C, Yao H J, Fang H J, et al. 3D near-surface shear-wave velocity structure from ambient-noise tomogra-phy and borehole data in the Hefei urban area, China. Seismological Research Letters, 2016, 87(4): 882–892
[9] Lin F C, Li D, Clayton R W, et al. High-resolution 3D shallow crustal structure in Long Beach, California: application of ambient noise tomography on a dense seismic array. Geophysics, 2013, 78: Q45–Q56
[10] Picozzi M, Parolai S, Bindi D, et al. Characterization of shallow geology by high-frequency seismic noise tomography. Geophys J Int, 2009, 176(1): 164–174
[11] Weaver R L, Lobkis O I. On the emergence of the green’s function in the correlations of a diffuse field. J Acoust Soc Am, 2001, 109: 435–439
[12] Shapiro N M, Campillo M. Emergence of broadband Rayleigh waves from correlations of the ambient noise. Geophys Res Lett, 2004, 31: L07614
[13] McNamara D E, Buland R P. Ambient noise levels in the continental united states. Bull Seismol Soc Am, 2004, 94(4): 1517–1527
[14] Paige C C, Saunders M A. LSQR: an algorithm for sparse linear equations and sparse least squares. ACM Transactions on Mathematical Software, 1982, 8(1): 43–71
[15] Bensen G D, Ritzowoller M H, Barmin M P, et al. Processing seismic ambient noise data to obtain re-liable broad-band surface wave dispersion measure-ments. Geophys J Int, 2007, 169: 1239–1260
[16] Brenguier F, Campillo M, Hadziioannou C, et al. Postseismic relaxation along the San Andreas fault at parkfield from continuous seismological observations. Science, 2008, 321: 1478–1481
[17] Pei S P, Niu F L, Ben-Zion Y, et al. Seismic velocity reduction and accelerated recovery due to earthquakes on the Longmenshan fault. Nature Geoscience, 2019, 12(4): 387–392
[18] Wang B S, Zhu P, Chen Y, et al. Continuous sub-surface velocity measurement with coda wave inter-ferometry. J Geophys Res, 2008, 113: B12313
A Synchronizing Method for Dense Seismic Array Based on Ambient Noise Correlation Function
Abstract This paper develops a NCF-based array synchronizing and error-estimation method employing the daily time shift of NCFs between nearby stations to estimate the stability of the timing system of a short-term but densely deployed seismic array. The error related to the reference NCF, the temporal change of ambient noise field, the data error and the optimization method in inversion are all estimated and correspondingly corrected based on the characteristics of a dense seismic array. The proposed method could effectively calculate the daily clock shift of a seismic array and pick out the time period of stations with obvious clock error. As an example, among the 209 stations of Yanyuan Seismic Array, it is found that 17 stations have obvious clock error with time shift over 1 s. These clock errors might be caused by the hardware or software problems related to the data acquisition system.
Key words dense seismic array; ambient noise cross-correlation function; clock error analysis; noise source distribution
doi: 10.13209/j.0479-8023.2020.043
国家重点研发计划(2018YFC1503200)和中国地震局地球物理研究所中央级公益性科研院所基本科研业务费专项(DQJB18B26)资助
收稿日期: 2019‒06‒24;
修回日期: 2019‒09‒23