表1 理论模型参数
Table 1 Parameters of theoretical model
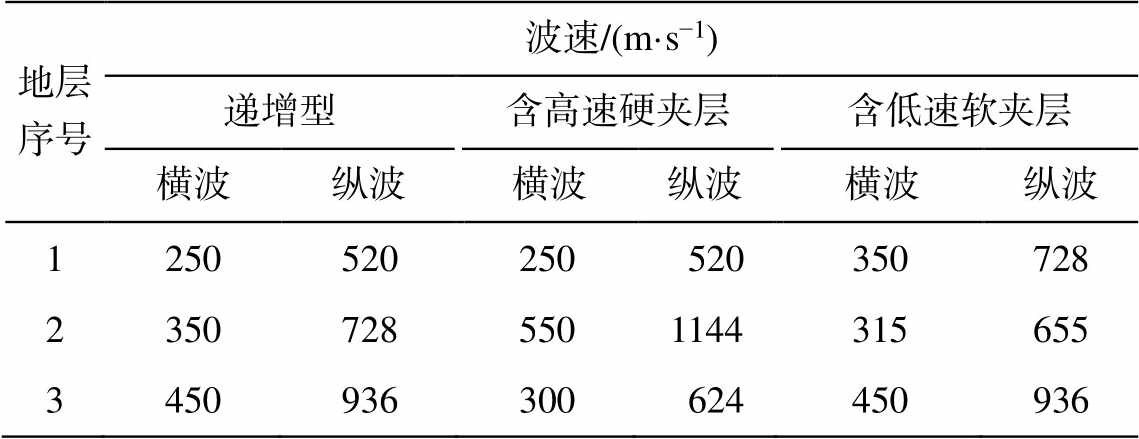
地层序号波速/(m·s−1) 递增型含高速硬夹层含低速软夹层 横波纵波横波纵波横波纵波 1250520250 520350728 23507285501144315655 3450936300 624450936
摘要 为了提高近地表瑞雷波频散曲线反演的效率和精度, 引入快速标量传递算法来计算瑞雷波频散曲线正演理论值。通过对比加入线性约束条件前后遗传算法(GA)与模拟退火法(SA)在反演瑞雷波频散曲线中的表现, 提出将计算速度快的蒙特卡洛法(MC)作为辅助手段来快速识别地层类型, 然后在 GA 和 SA 中加入线性约束条件来提高收敛速度, 并将 GA 得到的反演结果作为 SA 的初始状态, 同时适当地缩小搜索范围, 通过联合反演来克服 GA 的早熟问题。用上述方法计算和验证三层地层模型、含噪声数据以及工区实际模型, 结果表明该方法高效、准确、稳定性强, 有很强的全局寻优能力, 并具有一定的抗噪能力。
关键词 浅地表; 瑞雷波; 频散曲线; 快速标量传递法; 非线性反演
瑞雷面波具有能量强、振幅衰减弱、高信噪比及在层状介质中有频散特性等特点[1]。近年来, 随着高精度地震数据采集技术的发展, 因瑞雷波勘探在地球物理探测和工程勘探中的优越性而被用于获取浅地表、岩石圈或地幔的横波速度结构信 息[2‒6]。瑞雷波勘探主要包括野外数据采集[7]、频散曲线提取[8‒10]和频散曲线反演[11‒14] 3 个步骤。其中, 瑞雷波频散曲线的提取是获取观测数据的重要一步, 在变换域发展出多种方法, 主要有 F-K 变换法[15‒17]、相移法[18]、拉东变换法[8]、S 变换[1]、小波变换[19]以及在多模态面波频散曲线提取中效果显著的矢量波数变换法(vector wavenumber transform method, VWTM)[20]。不同频率的一系列面波可以有相同的相速度, 相同频率下相速度最小者为基阶面波, 其次为一阶、二阶等高阶面波[21]。在面波勘探研究领域, 无论是基阶面波反演, 还是多模态高阶面波的反演, 对于高效的频散曲线正演计算方法的探究以及对反演优化算法的选择和改进都具有重要的意义。各向同性水平层状均匀介质的瑞雷波频散曲线正演方法主要有 Haskell 算法[22]、Knopoff-Schwab 算法[23]、δ 矩阵与 Abo-Zena 算法[24]、快速标量传递算法与快速矢量传递算法[25‒27]以及广义反射‒透射系数法[26]等, 其中快速标量传递算法通过将传递矩阵中的元素表示成没有量纲的实数, 可以提高计算速度, 广义反射‒透射系数法则在高频厚层介质情况下的计算结果更加准确。
反演方法分为局部线性化反演方法和非线性反演方法[28], 局部线性化反演方法包括最小二乘法[29]、自适应阻尼最小二乘法[30]和 Occam 算法[31]。由于此类方法采用泰勒级数展开, 近似地将瑞雷波方程线性化, 并用扰动法计算雅克比矩阵, 因此难免在计算过程中带来误差。瑞雷波频散曲线反演具有高度非线性、多参数和多极值的特点[32], 要求线性化反演方法有较好的初始模型。传统的非线性反演方法包括蒙特卡洛法(Monte Carlo, MC)[33‒34]、遗传算法(genetic algorithm, GA)[35‒37]和模拟退火法(simulated annealing, SA)[38‒40], 具有全局搜索能力, 但收敛速度慢、精度较低, 容易出现早熟收敛的现象。此外, 模式识别算法[41]、粒子群算法[42]、差分化算法[43]、萤火虫和蝙蝠智能算法[44]及相关的改进算法[45]也应用到面波频散曲线的反演中。
针对传统反演方法中的问题, 解决方法分为 3个方向: 1)对瑞雷波频散曲线反演问题中目标函数的改进[46]; 2)对算法的优化(如快速退火算法[47‒48]、杰出个体保护[49]以及自适应交叉变异运算[50])和在遗传算法的基础上加入线性约束[51‒52]都可以在一定程度上解决早熟收敛的问题, 加快收敛速度, 但方法的单一性在一定程度上带来结果的不准确性; 3)采用联合反演方法, 充分利用各个方法的特点, 取长补短(比如 SA 与 GA 相结合的 SAGA 联合反演方法[53‒54]、线性反演方法与非线性反演方法相结合的自适应 GA 与阻尼最小二乘法(damped least squares, DLS)联合反演算法[55]以及瑞雷波与垂直电测深数据联合反演[56]), 但多种反演方法的同时应用难免牺牲计算速度, 影响数据处理的效率。
为了提高反演效率和精度, 本文引入计算效率较高的快速标量传递算法来正演理论频散曲线, 考察 MC 识别地层类型的可能性, 为后续在启发式蒙特卡洛法中加入线性约束条件提供依据, 并基于三层递增型地层模型, 分析线性约束条件在 SA 和GA 中的作用。利用先验信息[57]或者计算速度快的MC 多次反演辅助识别出地层类型后, 在 GA 和 SA中加入相应的线性约束条件, 提高收敛速度, 之后将 GA 得到的反演结果作为 SA 的初始状态, 以线性约束下 GA 的反演结果为参考, 适当缩小搜索范围, 进行联合反演, 克服 GA 的早熟和 SA 搜索效率低的缺陷, 压制多解性, 达到同时提高正、反演计算效率和结果准确性的目的, 并通过对三层地层模型、含噪声数据和工区实际模型的计算, 证实方法的有效性。
近地表一般为风化层、砂砾岩、沙漠、戈壁和黄土等, 其共同特点是横波速度较慢, 地震记录中面波十分发育。本研究基于前人的研究结果[31‒33], 并根据近地表实际情况, 设计较为常见的递增型、含高速硬夹层以及含低速软夹层 3 种三层水平均匀各向同性地层模型(表 1), 设定地层密度均为 1.9 g/cm3, 第一层和第二层的厚度均为 5 m, 第三层为无限厚度介质。
快速标量传递算法[25‒27]是在 Abo-Zena 算法[24]和 Menke 算法[58]的基础上改进的一种快速正演瑞雷波频散曲线的算法, 其基本思想是重新定义Menke算法中的E矢量, 将原本形式复杂、带有复数运算及有量纲运算的传递矩阵 F 分解为 3 个形式简单的五阶矩阵的乘积形式, 各矩阵中有些元素为零, 某些元素在矩阵乘法运算中可以消去, 从而改进为标量运算和无量纲运算, 可以大大地提高计算速度[59], 具体方法如下。
表1 理论模型参数
Table 1 Parameters of theoretical model

地层序号波速/(m·s−1) 递增型含高速硬夹层含低速软夹层 横波纵波横波纵波横波纵波 1250520250 520350728 23507285501144315655 3450936300 624450936
重新定义Menke65B9法的E矢量:
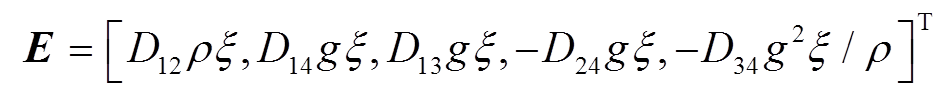 , (1)
, (1)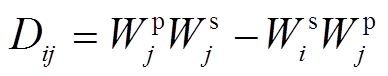 , 其中 Wp 和 Ws 分别为每层介质上界面的纵、横波位移应力矢量; ρ 为密度, g = c2/
, 其中 Wp 和 Ws 分别为每层介质上界面的纵、横波位移应力矢量; ρ 为密度, g = c2/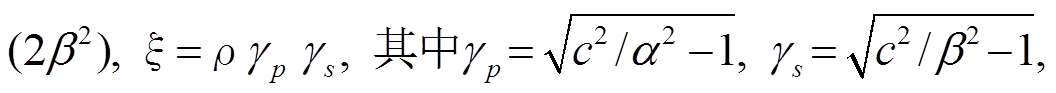
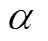 和
和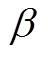 分别为各层介质的纵、横波速度, c为瑞雷波相速度。根据上传关系, E(i)=F(i)E(i+1), 将传递矩阵F表示为
分别为各层介质的纵、横波速度, c为瑞雷波相速度。根据上传关系, E(i)=F(i)E(i+1), 将传递矩阵F表示为
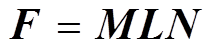 , (2)
, (2)
其中,
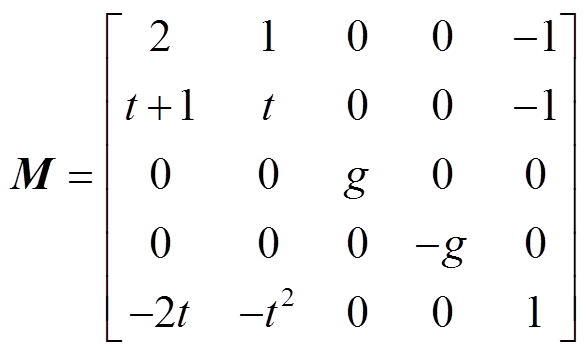 , (3)
, (3)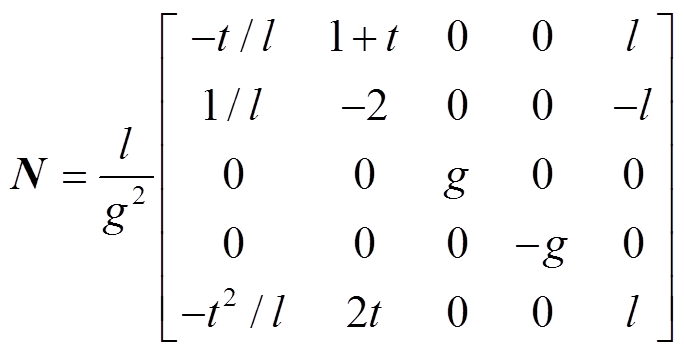 , (4)
, (4)
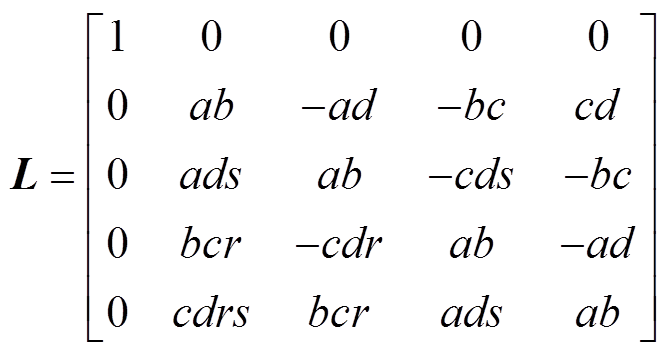 , (5)
, (5)
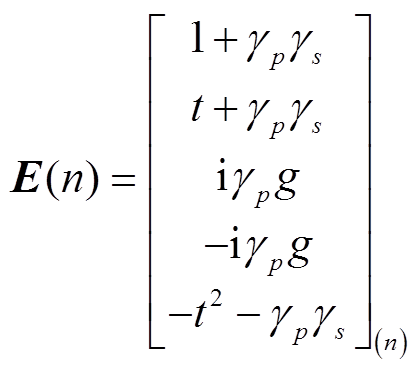 , (6)
, (6)其中, 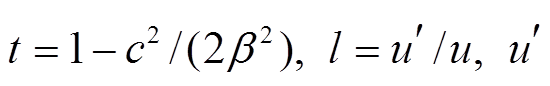 和 u 分别为第 i +1层和第 i 层的拉梅常数; r=
和 u 分别为第 i +1层和第 i 层的拉梅常数; r=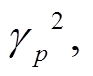 s=
s=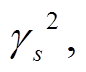 p=γpkh,q=γskh, a=cosp, b=cosq, c=sinp/γp, d=sinq/γs。计算过程中, 可由第n层上界面的矢量E(n)经过上传关系 E(i)=F(i)E(i+1)得到自由表面的 E 矢量 E(1), 从而得到频散方程:
p=γpkh,q=γskh, a=cosp, b=cosq, c=sinp/γp, d=sinq/γs。计算过程中, 可由第n层上界面的矢量E(n)经过上传关系 E(i)=F(i)E(i+1)得到自由表面的 E 矢量 E(1), 从而得到频散方程:
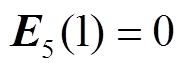 , (7)
, (7)
其中, N 矩阵的系数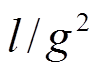 恒为正, 计算根的时候可以不考虑, 而 M, N 和 L 中的元素均为无量纲实数。这样, E 矢量的上传形式就变为标量传递的形式。经过矩阵乘法运算, 其值为0的元素可以直接消去, 得到以下快速标量传递算法。
恒为正, 计算根的时候可以不考虑, 而 M, N 和 L 中的元素均为无量纲实数。这样, E 矢量的上传形式就变为标量传递的形式。经过矩阵乘法运算, 其值为0的元素可以直接消去, 得到以下快速标量传递算法。
首先计算初始值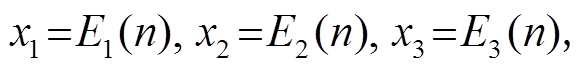 x4=E4(n), x5=E5(n), 然后从第 i 层到第 i−1 层逐层传递:
x4=E4(n), x5=E5(n), 然后从第 i 层到第 i−1 层逐层传递:
1)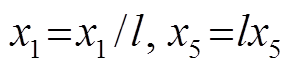 ;
;
2)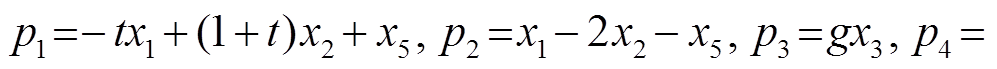
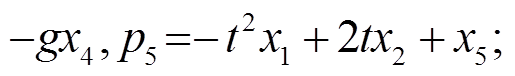
3)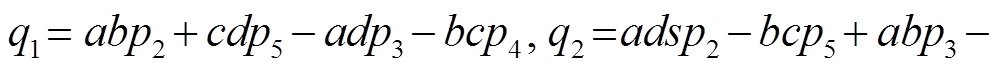
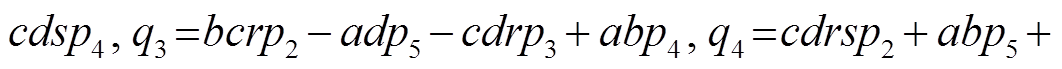
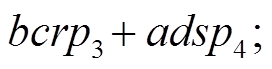
4)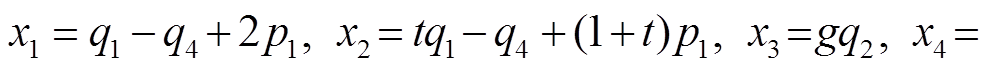
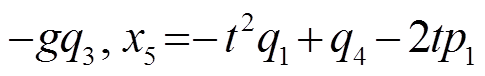 。
。
最终计算至自由表面, 使得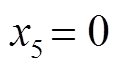 , 即为使式(7)成立的频散方程。
, 即为使式(7)成立的频散方程。
基于以上快速标量传递算法, 采用二分法计算正演理论频散曲线: 1)固定频率的数值, 对面波相速度给定某一扫描区间和搜索步长, 使面波相速度从扫描区间自下而上取值; 2)搜索有根区间, 利用快速标量传递算法计算相邻相速度值对应的频散方程值, 只要找到一个有根区间, 就调用二分法的求根子函数求得零点值, 其对应的相速度值就是该频率下的瑞雷波频散曲线值; 3)最后, 改变频率的数值, 重复第 2 步, 得到不同频率数值下对应的使得频散方程成立的面波相速度值。
图 1 为采用快速标量传递算法正演的表 1 中 3种地层的理论频散曲线, 在 100Hz 以内可见 3 种模式的瑞雷波频散曲线, 且不同类型地层模型的频散曲线形态有较明显的区别。正演计算是反演工作的基础, 由于高阶模式瑞雷波的反演方法与基阶模式的瑞雷波反演方法基本上相同, 因此本文只反演基阶模式的瑞雷波频散曲线(灰色曲线)。
瑞雷波频散方程的非线性隐式形式可以用式(8)[55]表示:
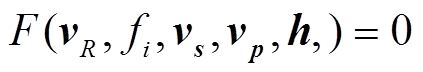 , i=1, 2, …, N, (8)
, i=1, 2, …, N, (8)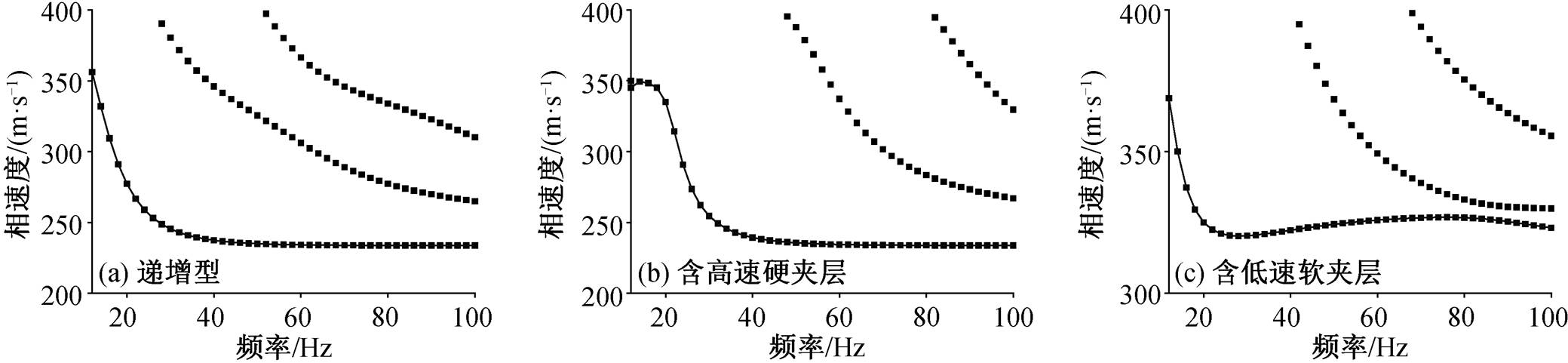
图1 快速标量传递法正演结果
Fig. 1 Forward result of scalar-transfer algorithm
其中, fi 是瑞雷波观测数据的第 i 个频率, 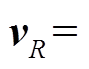
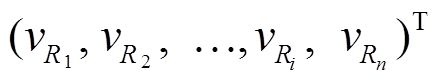 ,
, 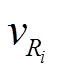 是 fi对应的相速度,
是 fi对应的相速度, 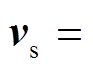
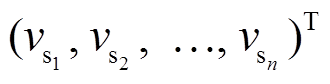 为横波速度向量,
为横波速度向量, 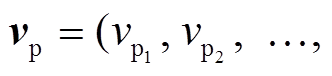
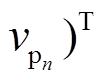 为纵波速度向量, h=(h1, h2, …, hn)T为地层厚度向量, ρ=(ρ1, ρ2,…, ρn)为对应的地层密度向量, N为观测值数目。由于瑞雷波相速度对横波速度和厚度的敏感性较强, 对其他参数的敏感性较弱, 故反演参数可以缩减为 vs 和 h 两组[22], 记为m={vs, h}。
为纵波速度向量, h=(h1, h2, …, hn)T为地层厚度向量, ρ=(ρ1, ρ2,…, ρn)为对应的地层密度向量, N为观测值数目。由于瑞雷波相速度对横波速度和厚度的敏感性较强, 对其他参数的敏感性较弱, 故反演参数可以缩减为 vs 和 h 两组[22], 记为m={vs, h}。
常规非线性反演方法包括蒙特卡洛法(MC)、遗传算法(GA)和模拟退火法(SA)等, 其中 MC 是所有非线性反演算法的鼻祖, GA 和 SA 则是一种启发式的蒙特卡洛法。瑞雷波频散曲线反演的目标函数定义为观测数据与相速度值的均方差(RMS), 即
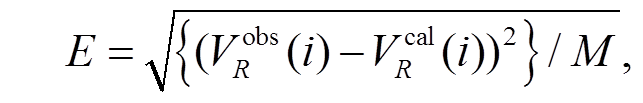 i =1, 2, …, M, (9)
i =1, 2, …, M, (9)式中, 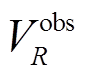 为瑞雷波相速度观测数据,
为瑞雷波相速度观测数据, 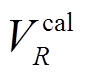 为通过快速标量传递算法正演得到的相速度理论值, M为观测数据的数目。
为通过快速标量传递算法正演得到的相速度理论值, M为观测数据的数目。
传统的蒙特卡洛法又称尝试法或穷举法, 该方法根据给出的参数约束范围, 在范围内随机产生一个初始模型 m0, 通过正演计算目标函数值, 对初始模型 m0, 加入一个随机扰动得到 m1, 保证 m1 的模型空间在给出的约束范围之内; 再次通过正演计算目标函数值, 如果 m1 对应的目标函数值小于 m0 对应的目标函数值, 则新模型被接收, 否则被排斥, 进行下一轮的迭代, 直至达到搜索次数上限或目标函数值小于预设值。即迭代中止条件为
 , (10)
, (10)其中, K为当前迭代次数, Kmax 为预先设定的最大迭代次数, E(K)为第 K 次迭代的目标函数值, 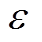 为预先设定的拟合误差阈值。
为预先设定的拟合误差阈值。
由于没有其他判定法则和复杂的搜索方式, 因此计算机产生随机数的速度很快, 从而使 MC 的计算效率很高, 使用起来更加便捷。本文测试 MC 在宽泛的搜索范围下识别地层类型的能力, 设定厚度的搜索范围为 4.00~6.25m, 递增型和含低速软夹层地层横波速度的搜索范围为 200~500m/s, 含高速硬夹层地层横波速度的搜索范围为 200~600m/s。
从 MC 的收敛过程、反演横波速度剖面和频散曲线的拟合情况(图 2)可以看出, 递增型和含高速软夹层地层模型在 510 次左右的时候停止更新, 最终频散曲线拟合的均方差分别为 3.3781 和 5.3584, 含低速软夹层地层模型的最终拟合方差为 1.9972, 反演结果总体上能够反映地层模型的速度变化特征, 识别出地层类型。在先验信息不充分的情况下, 可以利用 MC 多次反演, 得到具有统计意义的地层类型判定结果, 以此作为高效识别地层类型的辅助方法, 为后续在启发式蒙特卡洛法中加入线性约束条件提供依据。
完成地层类型识别后, 对横波速度加入相应的线性约束条件。以递增型地层模型为例, 线性约束条件应为
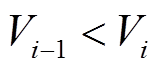 , i=1, 2, 3, (11)
, i=1, 2, 3, (11)其中, Vi为第 i 层的横波速度。下面比较在 SA 与GA 中加入线性约束条件对收敛过程及反演结果的影响。
2.2.1 SA 的基本原理及线性约束条件的加入
SA 是一种启发式蒙特卡洛算法, 源于统计热力学。它模拟物质退火时内部结构的变化过程: 物质先在高温下融化, 然后逐渐冷却。基本思想是: 生成一系列参数向量来模拟粒子的热运动, 通过缓慢地减小一个模拟温度的控制参数, 使模拟的热系统最终冷却结晶, 达到系统能量最小值。
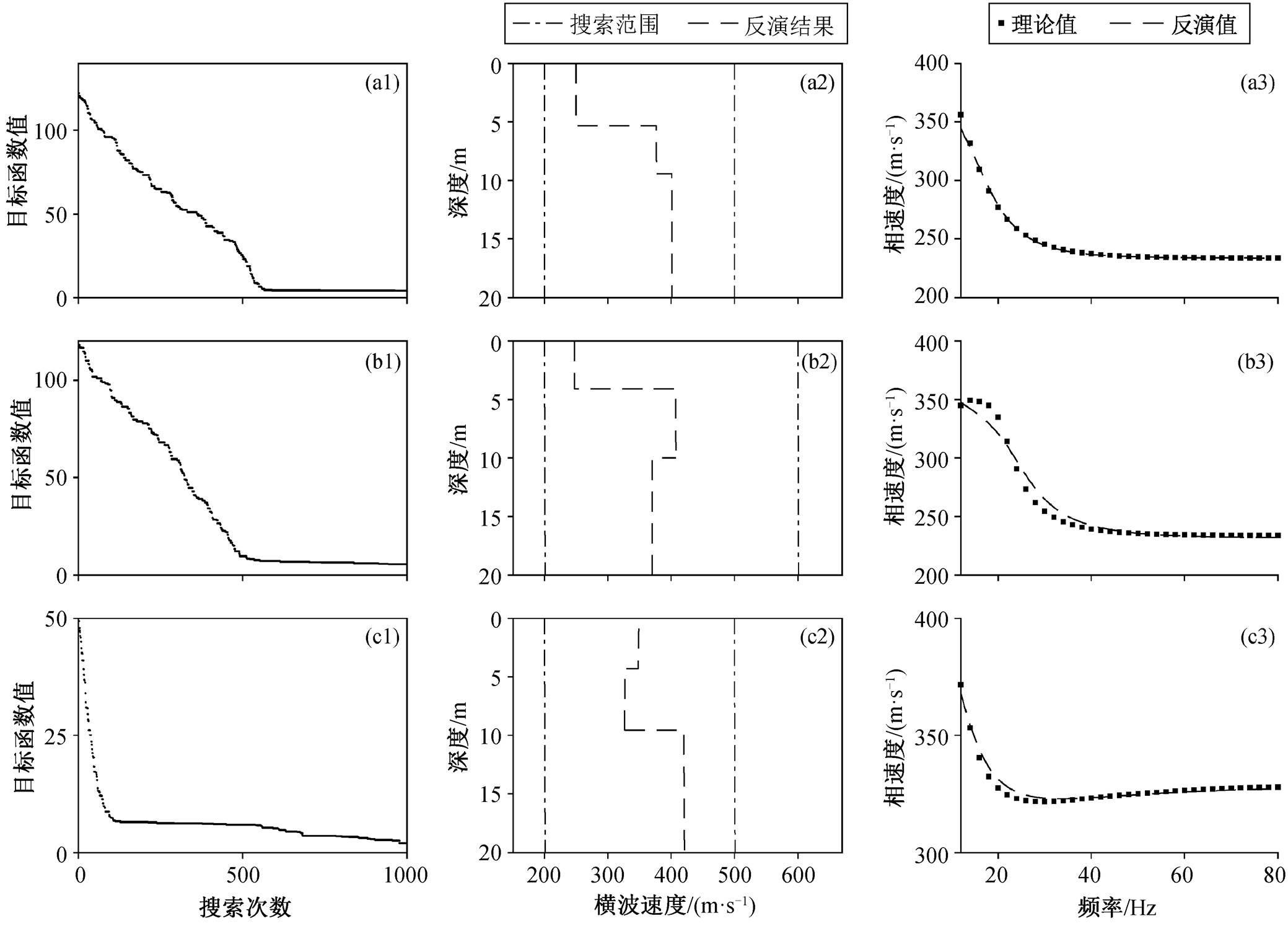
(a1)~(c1)分别为递增型、含高速硬夹层和含低速软夹层地层模型的MC搜索过程; (a2)~(c2)分别为3种地层模型的MC识别结果; (a3)~(c3)分别为3种地层模型的频散曲线拟合情况
图2 MC识别地层类型
Fig. 2 Recognition of formation types by MC
利用 SA 反演瑞雷波频散曲线的过程分为以下步骤。
1)在给定的约束范围内, 随机产生一个初始模型 m0, 或事先给定一个初始模型。设定系统的初始温度 T0、温度变化率 a、最大迭代次数 Kmax 以及拟合误差阀值ε等参数, 初次迭代开始时取 k=1。
2)对初始模型 m0, 加入一个随机扰动, 得到m1, 保证 m1 的模型空间在给出的约束范围之内。根据模型值参数, 分别计算目标函数值 E0 和 E1, 并求出两次目标函数的差值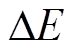 , 同时在小于 1 的范围内随机产生一个概率数b。
, 同时在小于 1 的范围内随机产生一个概率数b。
3)根据 Metropolis 接受准则, 采用下式进行判断:
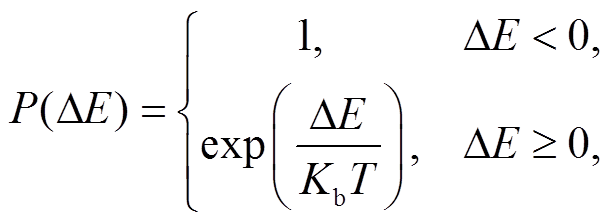 (12)
(12)其中, P为状态跃迁的概率, Kb 为 Boltzmann 常数。根据式(12)计算得到的概率值进行判定, 然后进行下一步的计算。如果 P=1 或 P>b, 则接受新模型, 否则保持原来的模型。
4)采用双曲下降型退火机制 TK=T0ak 进行迭代, 每迭代一次, k 值加 1。迭代中止条件同 MC, 重复步骤 2 和步骤 3。
计算过程中, 设置初始温度为 5°, 温度变化率为 0.96。因为已判定为递增型地层, 为了测试 SA的全局寻优能力, 给定一个远离全局最优的递增型地层初始模型: 横波速度从上至下依次为 300, 310和 420m/s, 初始厚度值从上至下依次为 4.5 和 5.5m, 第三层为半无限空间的介质。由于在实际工作中, 通常会结合先验信息给出合理的约束范围, 在利用 MC 识别出地层类型后, 结合测井信息, 搜索范围可按类给出, 因此本试验中将所有待反演参数的约束范围设定为理论值的 0.8~1.25 倍。加入线性约束条件指在每次退火之前, 即在进行 Metropolis接受准则判断之前, 先对加入随机扰动的新模型进行筛选, 符合线性约束条件的新模型进入下一步的操作。
在相同搜索次数下, 未加入线性约束条件的SA 最终拟合均方差为 9.8018, 加入线性约束条件的 SA 最终拟合均方差为 3.4640。从线性约束下反演所得参数值与理论值对比(表 2)来看, SA 的结果整体上好于常规 SA 方法, 收敛过程(图 3)也表明, 加入线性约束的 SA 收敛过程更加连续稳定, 在 200次搜索后依然保持较快的向全局最优解收敛速度, 能够获得更加精确的结果。反演结果也说明, SA 虽然具有全局搜索能力, 但当初始状态不在全局最优解附近时, 收敛至全局最优解将变得非常困难, 显示其搜索效率的低下。除第一层的反演速度与理论值基本上吻合外, 其他两层反演的速度和厚度都相差较远, 目标函数收敛于距初始模型较近的局部最优解附近, 意味着跳出至距初始模型值更远的全局最优解将花费大量的时间。
2.2.2 GA 的基本原理及线性约束条件的加入
GA 是一种模拟生物进化的自然选择和遗传过程, 依据适者生存原则建立的仿生式蒙特卡洛法, 利用 GA 反演瑞雷波频散曲线的过程包括编码、初始种群的生成、选择、交叉和变异 5 个部分。
1)编码。采用二进制编码, 将反演参数组 m转换生成 0 和 1 字符, 每一个参数对应一串预设固定长度的二进制编码, 一个参数组编码连接起来形成一条染色体。
2)初始种群的生成。按照二进制编码格式, 通过随机函数产生具有一定群体规模的初始种群, 其中每一条染色体为一个个体。利用正演方法, 计算每个个体对应的目标函数值 E(mi)(mi 指第 i 个个体, i=1, 2, …, N, N为群体规模), 并将目标函数转换为适应度函数f :
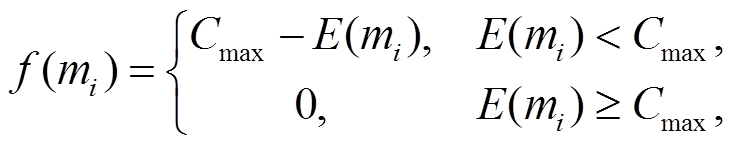 (13)
(13)其中, f(mi)为个体 mi 的适应度, Cmax 是一个大于目标函数最大值的较大整数。
3)选择。将选择概率 P(mi)作为标准, 选出优良个体作为父本繁殖下一代。P(mi)的计算公式为
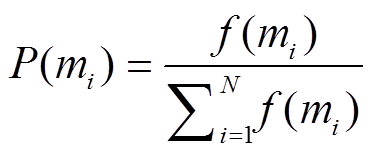 。 (14)
。 (14)然后, 利用计算得到的选择概率, 采用经典轮盘赌的方式, 循环选择父本, 生成新的群体。在 0 与 1之间生成随机数 b, 若 P(m1)+ P(m2)+…+ P(mi–1)<b <P(m1)+P(m2)+…+P(mi), 则个体 mi 被保留。个体的适应值越大, 目标函数值越小, 个体被选中的几率也越大。通过这样选择, 优良个体被保留, 并遗传至下一代, 劣质个体被淘汰。
表2 SA 搜索范围及加入线性约束条件前后的反演结果
Table 2 Search scope and inverted results of SA before and after adding linear constraints

地层序号理论模型搜索范围反演结果(未加线性约束)反演结果(加线性约束) 横波速度/(m·s−1)厚度/m横波速度/(m·s−1)厚度/m横波速度/(m·s−1)厚度/m横波速度/(m·s−1)厚度/m 12505200~3124~6.25257.684.37247.874.18 23505280~4384~6.25291.494.18311.094.23 3450‒360~562‒411.44‒423.50‒
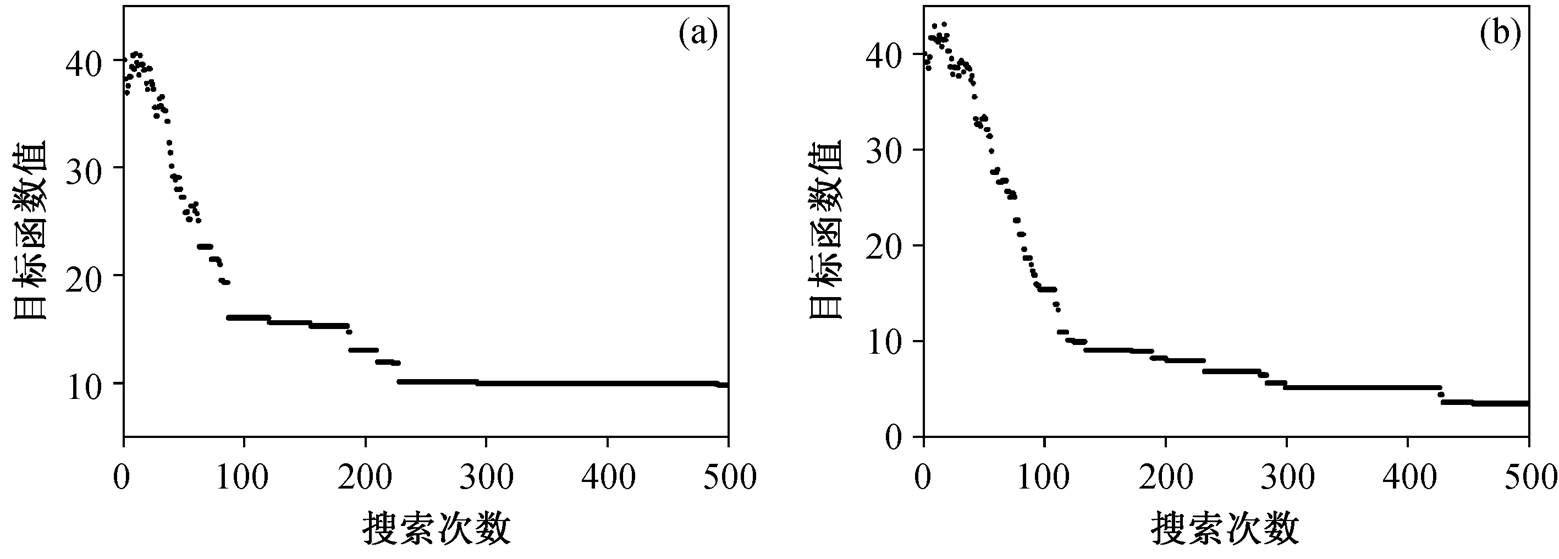
图3 加入线性约束条件前(a)、后(b) SA 的收敛过程
Fig. 3 Convergence process of SA before (a) and after (b) adding linear constraints
4)交叉。对选择产生的新群体进行随机性的两两配对, 对部分配对的个体, 利用一定的概率, 在参数编码的低位进行基因互换(染色体对应编码互换), 目的是在优良个体周围进行随机优化。
5)变异。为了维持种群的多样性, 让群体进化到后期依然保持获得优良基因的能力, 利用一定的变异概率, 对个体参数编码进行反转。交叉和变异过程见图 4, 其中虚线部分为交叉后从其他个体获得的序列。
6)循环选择、交叉、变异过程, 直至达到中止条件。
根据文献[60], 需要对参数给予适当的设置。计算过程中, 设置二进制编码长度为 7, 群体规模为 32, 交叉概率为 0.6, 变异概率为 0.02, 搜索次数为 200, 搜索范围和中止条件同 SA。在 GA 中加入线性约束条件的操作方法: 在每一次迭代过程中, 完成选择、交叉、变异的过程之后, 对群体中的优良个体进行筛选, 满足线性约束条件的个体进入下一代。
经典 GA 最终拟合均方差为 1.3312, 加入线性约束条件的最终拟合均方差为 0.5492。整体上, GA的反演结果已经较为接近理论值(表 3), 加入线性约束后的 GA 得到更加精准的结果, 尤其第三层介质横波速度的反演结果明显优于经典 GA, 但第二层介质的横波速度反演结果仍不太理想。从收敛过程(图 5)来看, 加入线性约束的 GA 有明显的改善, 其收敛过程更加稳定连续, 在迭代搜索 60 次后进入早熟状态, 而经典 GA 仅在反演初期有较好的收敛速度, 后续收敛速度明显变慢, 提前进入早熟收敛状态。
第 2 节的计算结果表明, 线性约束条件可以使SA 和 GA 具有更快的收敛速度和更精确的收敛结果。GA 搜索效率很高, 但后期容易因群体多样性的降低而进入早熟状态。SA 搜索面广, 既可以向目标函数增大的方向进行搜索, 也可以向目标函数减小的方向进行寻找, 但搜索效率低下。
在针对瑞雷波频散曲线的前期反演中, 加入线性约束的 GA 反演结果已经收敛于靠近全局极小值的某一个局部最小值, 因此可以用加入线性约束条件的 GA 反演结果作为 SA 的初始状态进行联合反演。其中, SA 也加入线性约束条件, 相当于让 GA帮助 SA 找到一种能量较低的平衡态, 再利用 SA 在这种状态下跳出局部最小值的突出能力, 达到收敛至全局最优的目的。
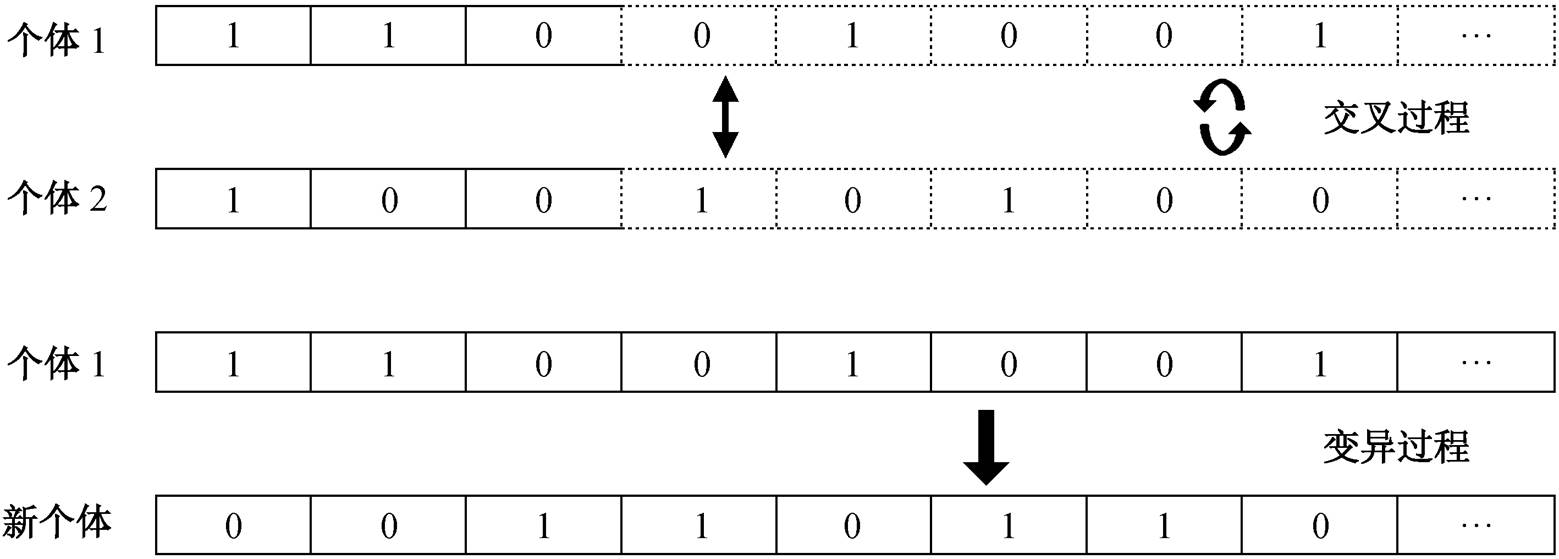
图4 GA 中的交叉和变异过程
Fig. 4 Crossing and mutation processes in GA
表3 GA搜索范围及加入线性约束条件前后的反演结果
Table 3 Search scope and inverted results of GA before and after adding linear constraints

地层序号理论模型搜索范围反演结果(未加线性约束)反演结果(加线性约束) 横波速度/(m·s−1)厚度/m横波速度/(m·s−1)厚度/m横波速度/(m·s−1)厚度/m横波速度/(m·s−1)厚度/m 12505200~3124~6.25248.945.12250.725.21 23505280~4384~6.25363.354.85365.845.19 3450‒360~562‒434.76‒447.48‒
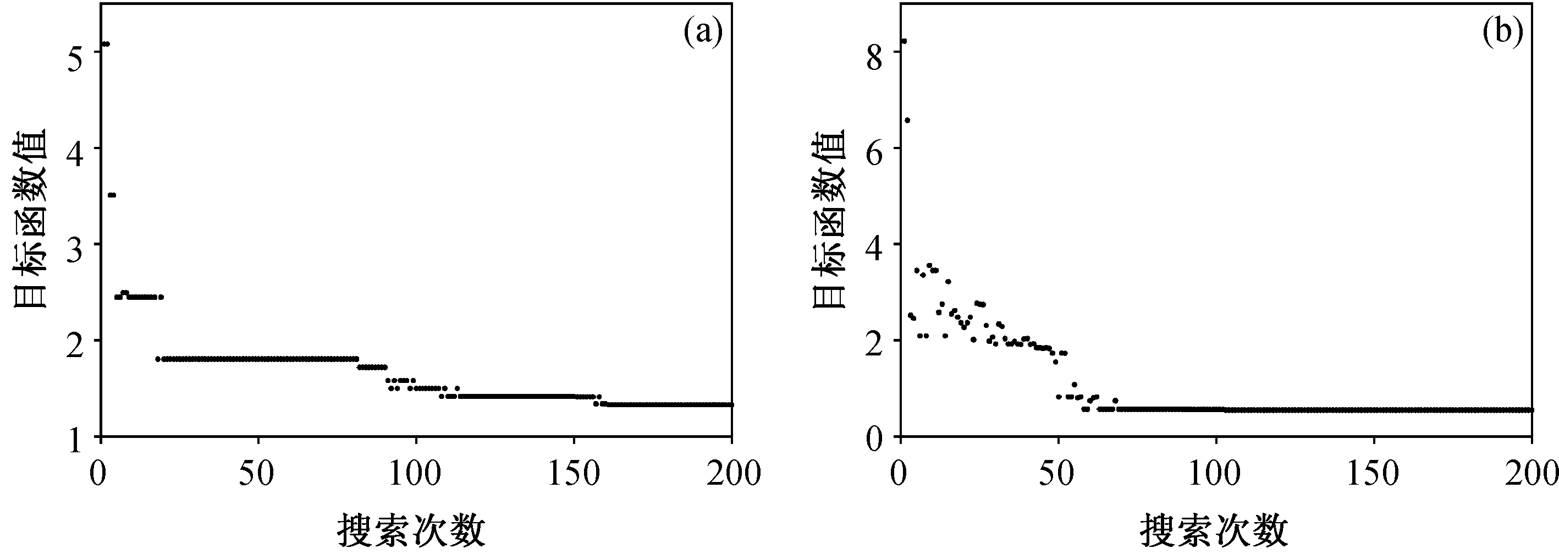
图5 加入线性约束条件前(a)后(b) GA的收敛过程
Fig. 5 Convergence process of GA before (a) and after (b) adding linear constraints
该方法的流程如图 6 所示: 先利用 MC 或者先验信息, 快速地识别地层类型后, 在 SA 和 GA 中加入相应的线性约束条件, 给予合理的约束范围, 先进行 GA 搜索, 进入早熟状态后, 用 GA 反演的结果作为 SA 的初始状态。由于 GA 结果已经靠近全局极小值, 因此可以以 GA 反演结果为参考, 适当地缩小搜索范围, 进行 SA 搜索, 直至达到中止条件。
在加入线性约束条件的 GA 反演结果基础上, 将搜索范围适当地缩小, 从理论值的 0.8~1.25 倍调整为 GA 反演结果的 0.9~1.1 倍, 以 GA 反演结果作为 SA 的初至状态, 设置初始温度为 5°, 温度变化率为 0.96, 在 GA 的反演结果附近进行SA搜索。
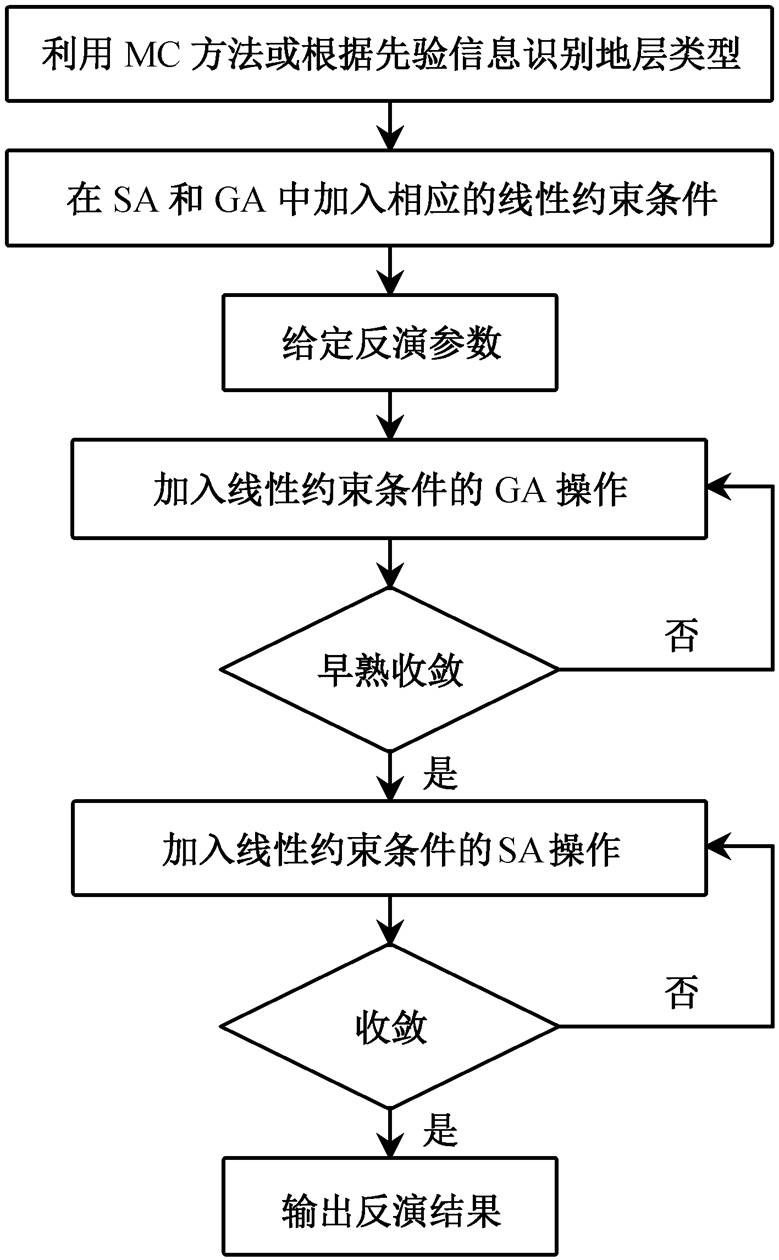
图6 联合反演方法流程
Fig. 6 Flow chart of joint inversion method
经过联合反演, 频散曲线的最终拟合误差为0.0929, 计算得到第一层至第三层的横波速度依次为 249.95, 250.92 和 448.85 m/s, 第一层和第二层的厚度分别为 5.01 和 5.00 m。收敛过程(图 7)显示, 在GA 进入早熟状态的情况下, SA 能够以此为起点, 在反演初期迅速跳出局部最小值的限制, 最终收敛至靠近全局最优解的位置, 频散曲线拟合度很高。反演得到的数值结果和横波速度剖面图(图 8)表明, 联合反演得到的横波速度和地层厚度与理论值几乎完全吻合, 证明该方法对于瑞雷波频散曲线非线性反演问题具有很强的全局寻优能力。
图 9 对比线性约束下的联合反演、未加入线性约束的 SA、加入线性约束的 SA、未入线性约束的GA 和加入线性约束的 GA 拟合的频散曲线, 可以看出, SA 方法受初始状态影响, 拟合效果不太理想, 而 GA 和联合反演方法拟合的频散曲线均能与观测数据较好地吻合, 从侧面反映出瑞雷波反演问题的多解性。
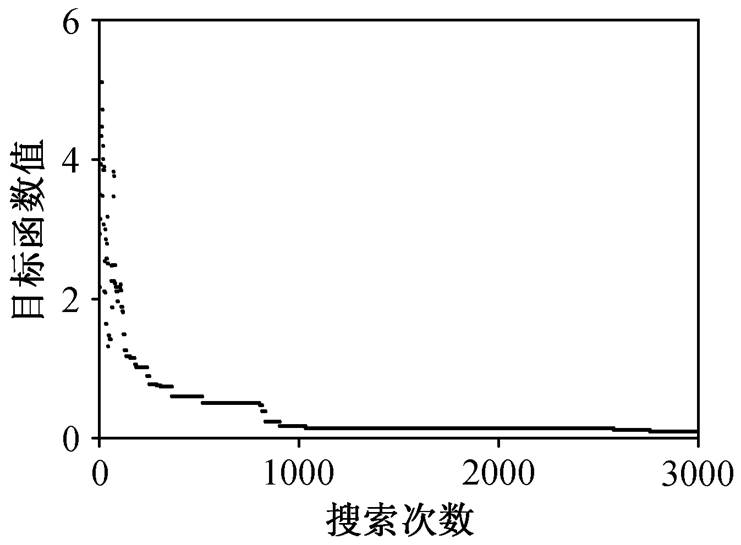
图7 联合反演中的SA搜索过程
Fig. 7 SA search process in joint inversion
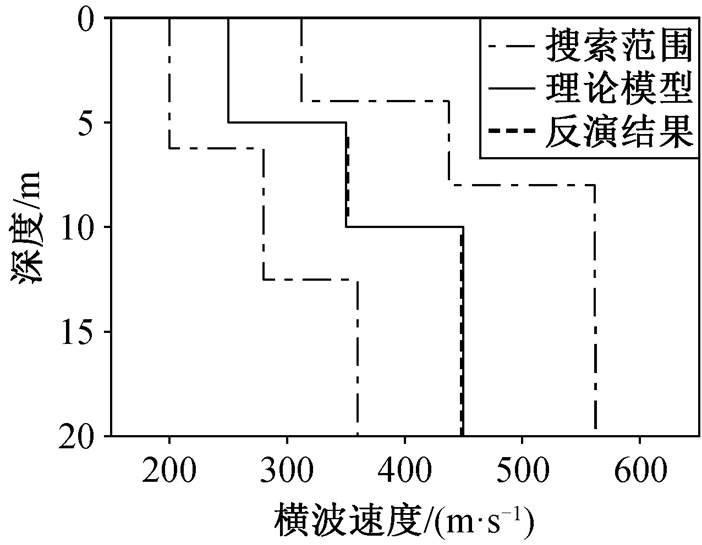
图8 联合反演得到的速度剖面
Fig. 8 Velocity profile obtained by joint inversion
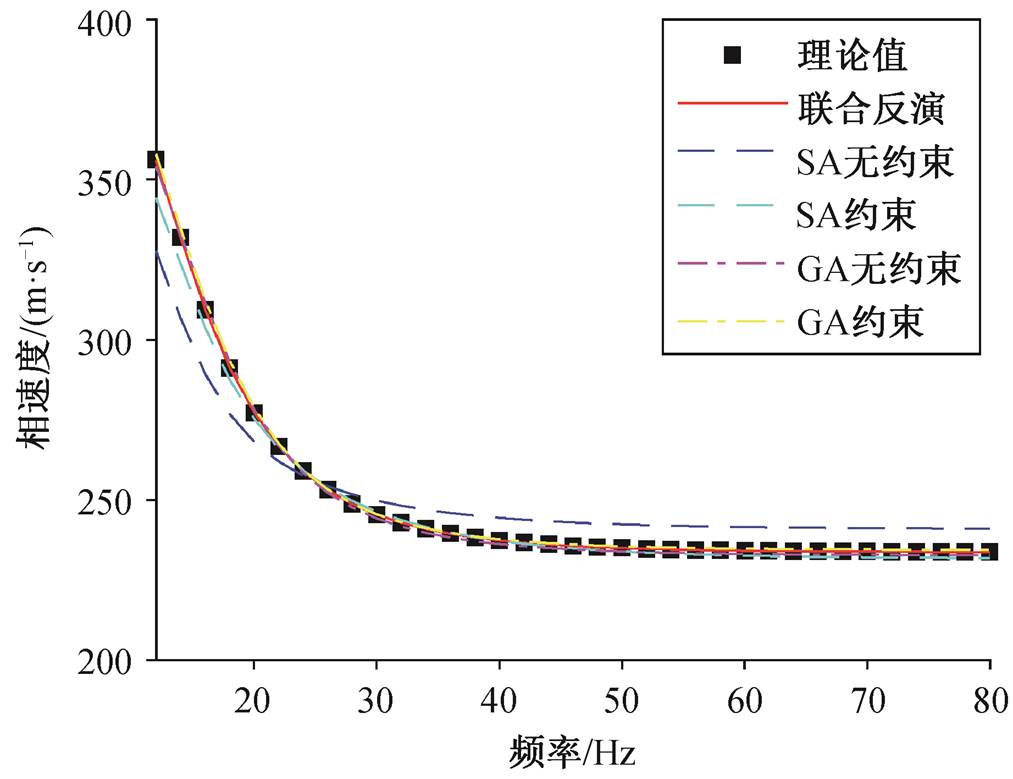
图9 频散曲线拟合结果对比
Fig. 9 Comparison of fitting results of dispersion curve
定义各参数反演结果的相对误差:
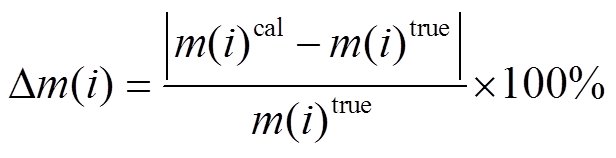 , i=1, 2, …, 5, (15)
, i=1, 2, …, 5, (15)其中, 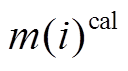 为反演结果的第 i 个参数值,
为反演结果的第 i 个参数值, 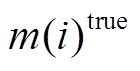 为理论模型的第 i 个参数值。通过相对误差, 可以更准确地评价反演结果。
为理论模型的第 i 个参数值。通过相对误差, 可以更准确地评价反演结果。
以递增型地层模型为例, 加入线性约束的反演方法能得到比经典方法更贴近理论值的速度剖面, 且相对误差(表 4)减小, 说明线性约束可在一定程度上压制多解性, 提高结果的准确性。GA 对面波频散曲线有较好的反演效果, 最小误差为 0.29%, 但最大误差仍然达到 4.53%。因此, 单纯使用 GA进行反演, 结果中可能出现个别参数反演误差过大的现象, 影响整体精度, 不能满足实际工作的要求, 无法作为最终结果使用, 但可以作为基础供二次反演参考。联合反演结果的最大误差仅 0.2%, 最小误差约为 0, 且速度剖面图(图 10)中显示出极高的吻合度, 进一步证明该方法的有效性。
采用加入线性约束的联合反演算法, 计算另外两类地层模型的线性约束条件。含高速硬夹层地层模型的线性约束条件为
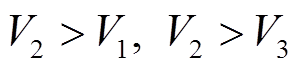 , (16)
, (16)含低速软夹层地层模型的线性约束条件为
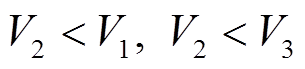 。 (17)
。 (17)
利用 MC 判定出地层类型后, 将约束范围设定为适用于对应地层类型的数值进行反演。计算得到含高速硬夹层模型和含低速软夹层模型频散曲线的最终拟合误差分别为 0.3236 和 0.0685; 含高速硬夹层地层第一层至第三层的横波速度依次为 249.68, 552.01 和 296.91m/s, 第一层和第二层的厚度分别为 4.98 和 4.97m; 含低速软夹层地层第一层至第三层的横波速度依次为 350.08, 315.12 和 450.2m/s, 第一层和第二层的厚度分别为 4.98 和 5.04m。图11 显示, 频散曲线和反演得到的速度剖面几乎都与理论值完全吻合, 各参数的相对误差在 1%以内, 表明该方法对不同类型地层的模型均有较好的反演效果。
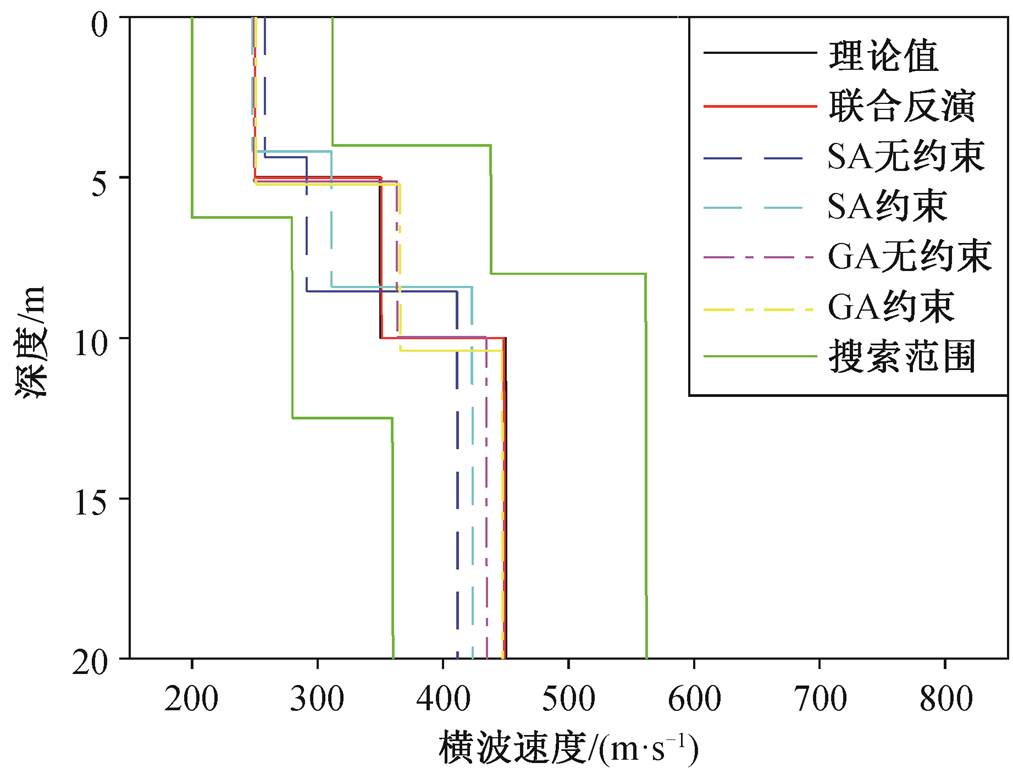
图10 反演结果对比
Fig. 10 Comparison of inversion results
表4 不同方法反演结果的相对误差(%)
Table 4 Relative error comparison of inversion results by different methods (%)

地层序号SASA (线性约束)GAGA (线性约束)联合反演 横波速度厚度横波速度厚度横波速度厚度横波速度厚度横波速度厚度 1 3.07 12.6 0.85 16.40.422.400.294.20.020.20 216.72 16.411.12 15.43.813.004.533.80.260.00 38.57 ‒5.89 ‒3.39‒0.56‒0.26‒
在瑞雷波勘探的反演过程中, 将频散曲线提取的瑞雷波相速度值作为观测数据, 其主要噪声来源于提取方法的局限性和地震记录的信噪比。选择直接在理论频散曲线(观测数据)上加噪声, 叠加了提取方法和原始地震记录带来的噪声。为了检验本文方法的抗噪能力, 在 3 种地层模型的瑞雷波频散曲线观测数据中加入 10%的随机噪声, 搜索范围与对应的无噪声模型相同。设置 MC 搜索次数为 2000, SA 初始温度为 5°, 温度变化率为 0.96, GA 编码长度为 7, 群体规模为 32, 交叉概率为 0.6, 变异概率为 0.02, GA 搜索次数为 100。早熟收敛后进入 SA操作, 设置 SA 搜索次数为 2000, 用线性约束 GA 与SA联合反演方法进行计算。
采用上述加线性约束联合反演方法, 含噪声递增型、含噪声含高速硬夹层和含噪声低速软夹层地层模型频散曲线的最终拟合均方差分别为 3.6935, 3.6384 和 3.1181。计算结果表明, 对含噪声数据, MC 均能很好地识别地层类型。含噪声递增型地层模型反演结果的最大误差为 2.60%(第二层厚度), 最小误差为 0.22%(第一层横波速度); 含噪声含高速硬夹层地层模型反演结果的最大误差为 3.38% (第三层横波速度), 最小误差为 0.33%(第一层横波速度); 含噪声含低速软夹层地层模型反演结果最大误差为 7.10%(第一层厚度), 最小误差为 0.21%(第一层横波速度)。结合速度剖面、频散曲线的吻合程度(图 12), 说明横波速度参数反演结果整体上好于厚度参数反演结果, 浅层的反演结果略好于深层的反演结果, 递增型地层反演效果最佳, 虽然与无噪声数据的反演结果相比精度均有所下降, 但速度曲线吻合得很好, 表明反演结果与理论值相差很小, 精度可以满足实际工作要求, 可见该方法具有一定的抗噪能力。
某工区某井的调查结果如下: 浅地表低速带厚度为80 m, 从上至下依次为松散黄土层、黄土层和黄土夹沙层, 对应的纵波速度分别为 419, 765 和976m/s, 横波速度约为 201, 368 和 469m/s, 第一层和第二层的厚度分别为 8.1 和 36.4m, 各层的密度约为 1.6, 1.79 和 2.22g/cm3。
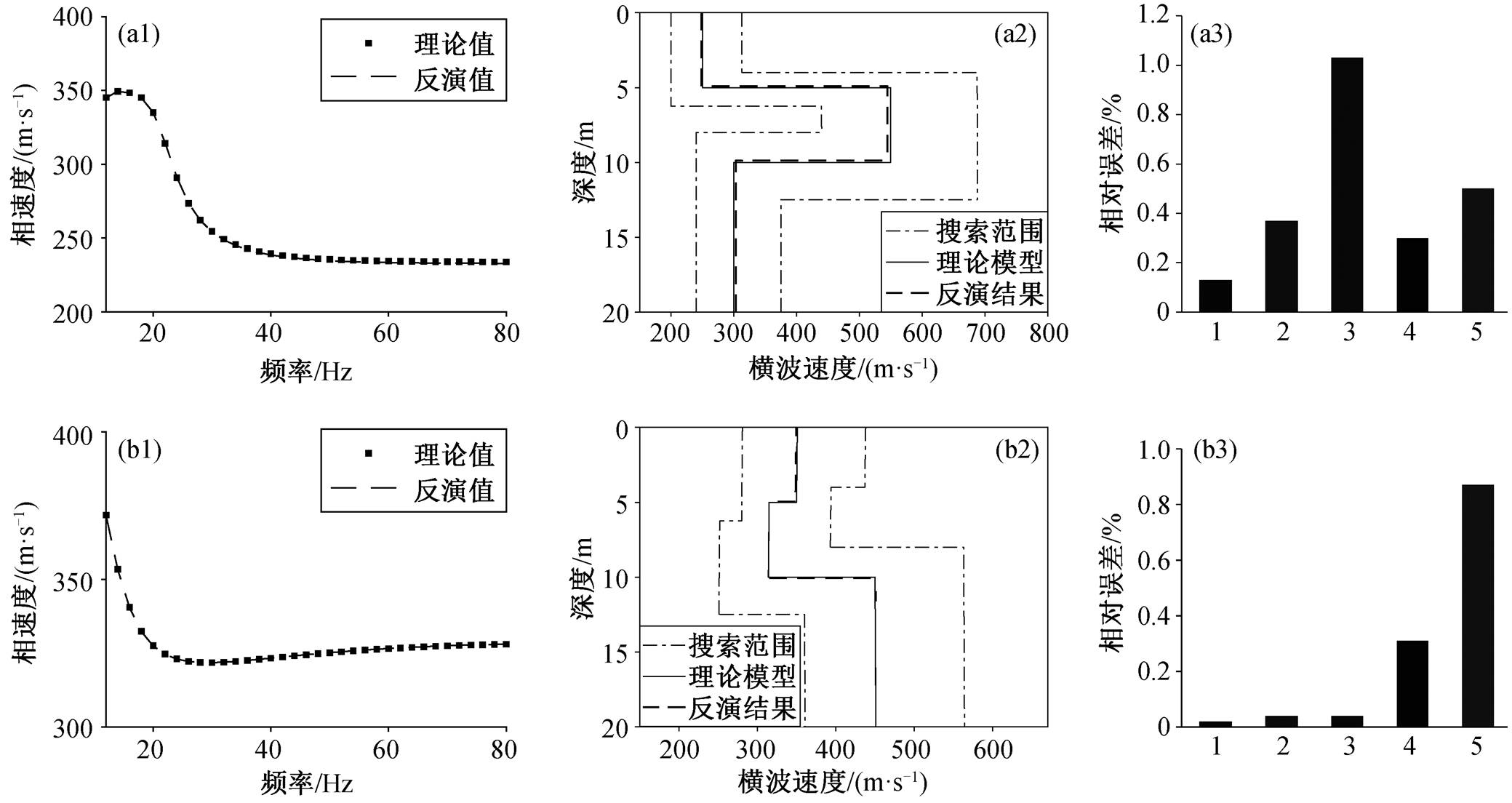
(a1)~(a3)含高速硬夹层; (b1)~(b3)含低速软夹层。(a1)和(b1)频散曲线拟合情况; (a2)和(b2)地层模型反演结果; (a3)和(b3)地层反演结果相对误差, 横轴上 1 为第一层横波速度, 2 为第二层横波速度, 3 为第三层横波速度, 4 为第一层厚度, 5 为第二层厚度
图11 含高速硬夹层和含低速软夹层地层模型反演结果
Fig. 11 Inversion results of the stratum with high-speed hard interlayer and stratum with low-speed soft interlayer
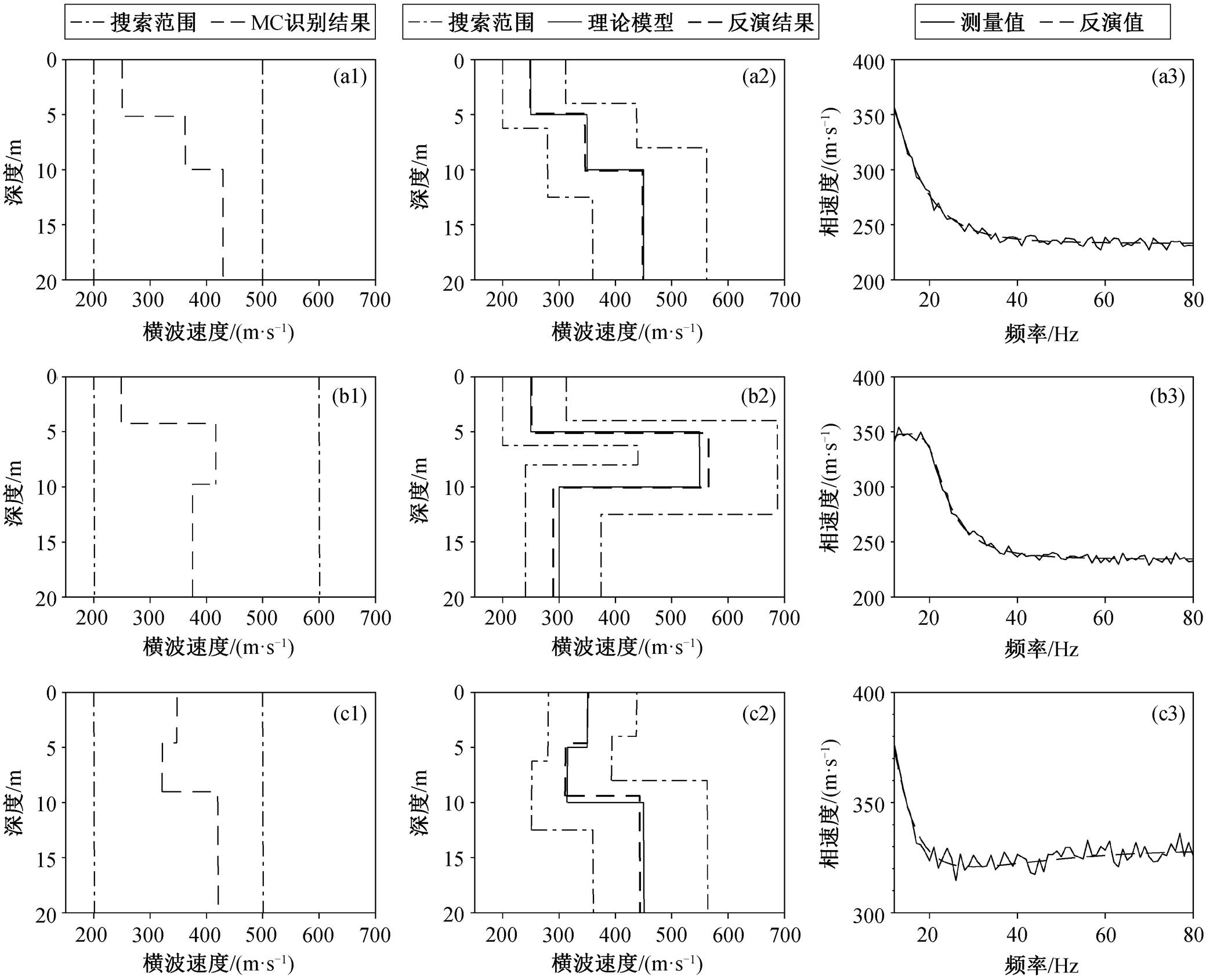
(a1)~(a3) 递增型; (b1)~(b3) 含高速硬夹层; (c1)~(c3)含低速软夹层。(a1)~(c1) MC识别结果; (a2)~(c2) 地层模型反演结果; (a3)~(c3) 频散曲线拟合情况
图12 不同地层类型模型的含噪声数据反演结果
Fig. 12 Inversion results of noisy data for different stratigraphic type models
将该地区的实际模型近似为一维层状模型, 采用高精度有限差分法[61‒62], 对该模型进行全波场正演模拟。雷克子波主频为 20Hz, 子波宽度为 0.1s, 差分网格大小 dx=dz=2m, 网格数为 202×202, 吸收层厚度为 100m, 采样间隔为 0.2ms。上表面设置为自由边界条件, 设置两侧为 PML (perfect match layer)吸收边界条件, 在自由表面进行激发和接收,接收时间为 1.2s。用最小偏移距 30m, 道间距 1m抽取 96 道垂直 V 分量记录。图 13 显示, 模拟地震记录中面波能量最强, 直达波次之, 同相轴清晰可见。与体波勘探不同, 面波记录在面波勘探中不再作为干扰信号被去除, 而是作为有效信息被保留。
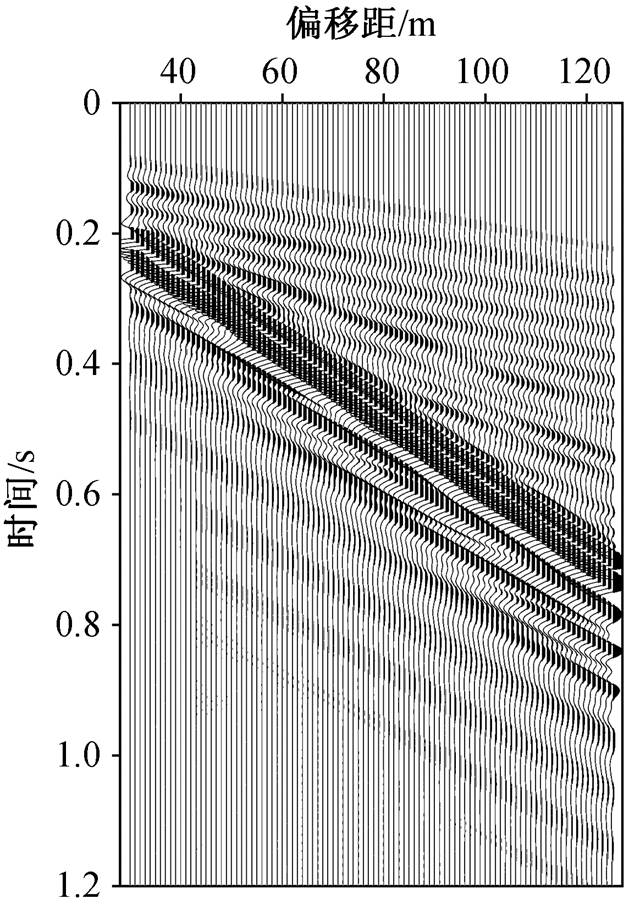
图13 垂直 V 分量记录
Fig. 13 Recording of vertical V component
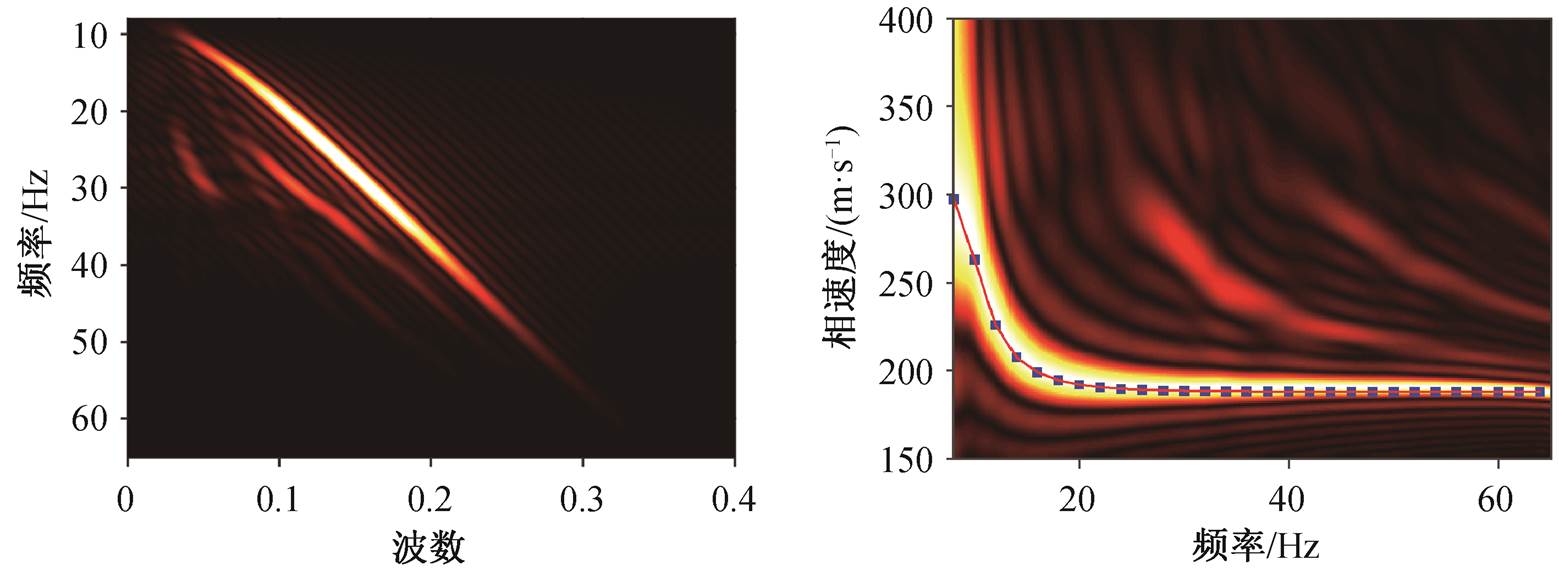
图14 频率‒波数谱(左)和频率‒相速度谱(右)
Fig. 14 Frequency-wavenumber spectrum (left) and frequency-phase velocity spectrum (right)
获取垂直V分量地震记录后, 选取适当的频率和相速度搜索范围, 采用 F-K 法计算其频率相速度谱。归一化后的 F-K 域能量谱和 F-V 域能量谱见图 14, 可见求得的频率波数谱和频率相速度谱均连续且清晰, 以基阶频散曲线能量为最强, 高阶频散曲线能量相对较弱。将每一频率值对应能量最强的相速度值连成曲线, 获得频散曲线观测数据。
设置第一层至第三层的横波速度搜索范围分别为161~251, 294~460和375~586 m/s, 第一层和第二层的厚度搜索范围分别为 6~10 和 29~46m。利用上述联合反演方法进行反演, 瑞雷波频散曲线最终拟合均方差为 0.1479。计算得到第一层至第三层的横波速度依次为 200.92, 364.96 和 455.84m/s, 第一层和第二层的厚度分别为 8.07 和 34.92m。反演结果的最小相对误差为 0.04% (第一层横波速度), 最大相对误差为 4.07% (第二层厚度), 其中第一层的横波速度和厚度以及第二层的横波速度反演结果相对误差均在 1%以内。频散曲线(图 15)的吻合度非常高, 数值计算结果和速度剖面图(图 16)都表明, 该方法对较浅层参数的反演结果非常好, 但由于面波勘探问题的多解性较强, 较深层的反演结果略差于浅层。虽然无法完全避免多解性的出现, 但整体上可以较好地还原该地区的近地表横波速度结构, 进一步证明该方法的有效性和实际应用价值。
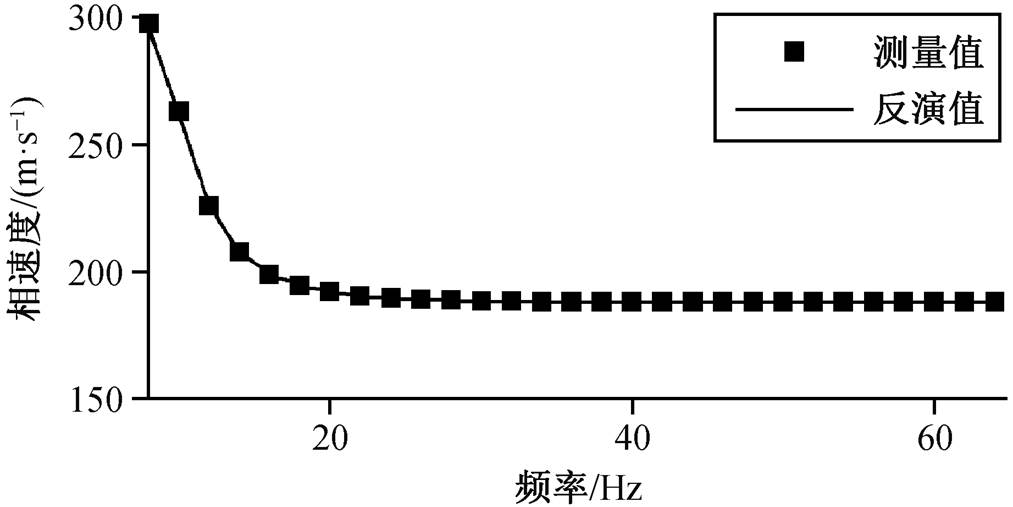
图15 观测数据和联合反演拟合的频散曲线
Fig. 15 Observation data and dispersion curve fitted by joint inversion
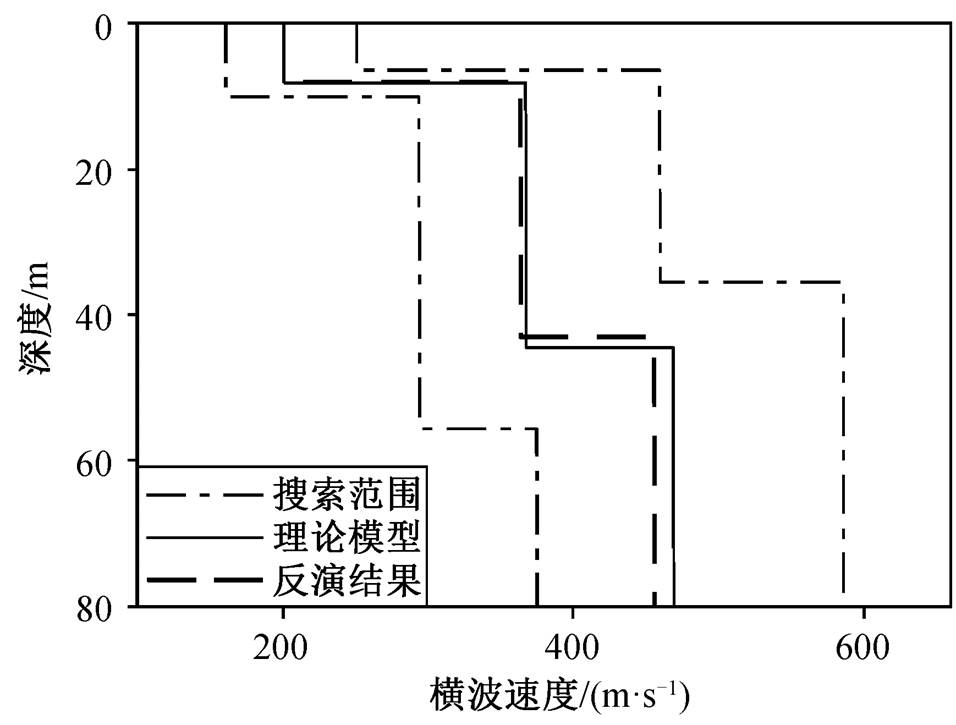
图16 实际模型联合反演结果
Fig. 16 Joint inversion results of real model
本文构建常见的近地表三层地层模型, 引入快速标量传递法进行频散曲线的正演计算, 考察 MC在宽泛约束条件下识别地层类型的能力。基于三层递增型地层模型, 对比加入线性约束条件前后 SA与 GA 瑞雷波频散曲线的反演效果。识别出地层类型之后, 在 SA 和 GA 中加入线性约束条件, 将 GA的反演结果作为 SA 搜索的初始状态, 进行联合反演, 并通过对三层地层模型、含噪声模型和工区实际模型的正演模拟与反演计算, 得到以下结论。
1)在先验信息不足的情况下, 可以利用 MC 计算速度快的特点, 在宽泛约束条件下, 辅助识别地层类型, 为后续加入线性约束条件提供依据。
2)线性约束条件的加入可以使得 SA 和 GA 的收敛过程更加稳定和快速, 并在一定程度上提高反演的精度, 使 GA 的早熟收敛滞后发生。
3)虽然 SA 具有较强的全局搜索能力, 但搜索效率低下, 如果给定的初始状态较差, SA 收敛至全局最优解的速度将十分缓慢。GA 的搜索效率很高, 对瑞雷波频散曲线的反演能够取得较好的效果, 但早熟收敛的情况依然存在。
4)在快速标量传递法正演瑞雷波频散曲线的基础上, 采用加入线性约束条件的 GA 与 SA 进行联合反演, 使得反演速度从正演和反演两方面得到提升, 并且计算结果显示该方法既能克服 GA 的早熟收敛, 也能利用 SA 搜索面广的特点而跳出局部极小值, 压制多解性, 具有很强的全局寻优能力, 能够得到与理论值相对误差较小的解, 并具有一定的抗噪能力。
5)本文提出的方法属于概率性算法的一种, 通常情况下均能收敛到理论值附近, 但在多次计算过程中会有一定的几率出现异常解。如有此类情况发生, 需要进行辨别和剔除。
参考文献
[1] 马见青, 李庆春, 樊金生, 等. 基于 S 变换的瑞利面波频散分析. 地球科学与环境学报, 2010, 32(3): 319‒323
[2] 胡家富, 段永康, 胡毅力, 等. 利用 Rayleigh 波反演浅土层的剪切波速度结构. 地球物理学报, 1999, 42(3): 393‒400
[3] 黄忠贤, 李红谊, 胥颐. 中国西部及邻区岩石圈 S波速度结构面波层析成像. 地球物理学报, 2014, 57(12): 3994‒4004
[4] Strobbia C L, Emam A E, Al-Genai J, et al. Rayleigh wave inversion for the near-surface characterization of shallow targets in a heavy oil field in Kuwait. First Break, 2010, 28(5): 103‒109
[5] Xia Jianghai. Estimation of near-surface shear-wave velocities and quality factors using multichannel ana-lysis of surface-wave methods. Journal of Applied Geophysics, 2014, 103: 140‒151
[6] Socco L V, Foti S, Boiero D. Surface-wave analysis for building near-surface velocity models — estab-lished approaches and new perspectives. Geophysics, 2010, 75(5): 75A83‒75A102
[7] Zhang S X, Chan L S, Xia J. The selection of field acquisition parameters for dispersion images from multichannel surface wave data. Pure and Applied Geophysics, 2004, 161(1): 185‒201
[8] Luo Y, Xia J, Miller R D, et al. Rayleigh-wave dis-persive energy imaging using a high-resolution linear radon transform. Pure and Applied Geophysics, 2008, 165(5): 903‒922
[9] 王季. 基于 F-K 变换的井下多道瑞利波频散曲线提取. 煤田地质与勘探, 2012, 40(2): 75‒77
[10] 金聪, 杨文海, 罗登贵, 等. 面波频散曲线提取方法对比分析. 地球物理学进展, 2016, 31(6): 2735‒2742
[11] Lu L, Wang C, Zhang B. Inversion of multimode Rayleigh waves in the presence of a low-velocity layer: numerical and laboratory study. Geophysical Journal of the Royal Astronomical Society, 2007, 168(3): 1235‒1246
[12] 杨雅慧, 曲杉, 陈裕华, 等. 基于面波频散曲线反演方法综论// 2014年中国地球科学联合学术年会——专题 14: 地下介质结构及其变化的地震面波、背景噪声及尾波研究论文集. 北京: 中国地球物理学会, 2014: 762
[13] 罗银河, 夏江海, 刘江平, 等. 基阶与高阶瑞利波联合反演研究. 地球物理学报, 2008, 51(1): 242‒249
[14] Zhang S, Chan L. Possible effects of misidentified mode number on Rayleigh wave inversion. Journal of Applied Geophysics, 2003, 53(1): 17‒29
[15] 李欣欣, 李庆春. 利用改进的 F-K 变换法提取瑞雷波的频散曲线. 地球物理学进展, 2017, 32(1): 197‒203
[16] Shen H, Chen C, Yan Y, et al. Multiple-transient surface wave phase velocity analysis in expanded f-k domain and its application. Journal of Seismic Exp-loration, 2016, 25: 299‒319
[17] Shen C, Wang A, Wang L, et al. Resolution equiva-lence of dispersion-imaging methods for noise-free high-frequency surface-wave data. Journal of Applied Geophysics, 2015, 122: 167‒171
[18] Zhang S X, Chan L S. Possible effects of misi-dentified mode number on Rayleigh wave inversion. Journal of Applied Geophysics, 2003, 53(1): 17‒29
[19] 房曰荣, 沈斐敏. 小波分析应用于瑞雷波频散曲线提取研究. 地震工程与工程振动, 2014, 34(5): 21‒27
[20] 杨振涛, 陈晓非, 潘磊, 等. 基于矢量波数变换法(VWTM)的多道 Rayleigh 波分析方法. 地球物理学报, 2019, 62(1): 298‒305
[21] Gao L, Xia J, Pan Y, et al. Reason and condition for mode kissing in MASW method. Pure and Applied Geophysics, 2016, 173(5): 1627‒1638
[22] Haskell N A. The dispersion of surface waves on multilayered media. Bulletin of the seismological So-ciety of America, 1953, 43(1): 17‒34
[23] Schwab F A, Knopoff L. Fast surface wave and free mode computations. Methods in Computational Phy-sics Advances in Research & Applications, 1972, 11: 87‒180
[24] Anas A Z. Dispersion function computations for un-limited frequency values. Geophysical Journal Inter-national, 1979, 58(1): 91‒105
[25] 凡友华, 肖柏勋, 刘家琦. 层状介质中轴对称柱面瑞利面波频散函数的计算. 地震工程与工程振动, 2001, 21(3): 1‒5
[26] 凡友华, 刘家琦. 层状介质中瑞雷面波的频散研究. 哈尔滨工业大学学报, 2001, 33(5): 577‒581
[27] 凡友华, 刘家琦, 肖柏勋. 计算瑞利波频散曲线的快速矢量传递算法. 湖南大学学报(自然科学版), 2002, 29(5): 25‒30
[28] Xia J, Miller R D, Park C B. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves. Geophysics, 1999, 64(3): 691‒700
[29] Lu L, Wang C, Zhang B. Inversion of multimode Rayleigh waves in the presence of a low-velocity layer: numerical and laboratory study. Geophysical Journal of the Royal Astronomical Society, 2010, 168(3): 1235‒1246
[30] 宋先海, 肖柏勋, 黄荣荣, 等. 用等厚薄层权重自适应迭代阻尼最小二乘法反演瑞雷波频散曲线. 物探与化探, 2003, 16(4): 212‒216
[31] Constable S C, Parker R L, Constable C G. Occam’s inversion: a practical algorithm for generating smooth models from electromagnetic sounding data. Geophy-sics, 1987, 52(3): 289‒300
[32] Moro G D, Pipan M, Gabrielli P. Rayleigh wave dis-persion curve inversion via genetic algorithms and marginal posterior probability density estimation. Journal of Applied Geophysics, 2007, 61(1): 39‒55
[33] Maraschini M, Foti S. A Monte Carlo multimodal in-version of surface waves. Geophysical Journal Inter-national, 2010, 182(3): 1557‒1566
[34] Yamanaka H, Chimoto K. Variability of shallow soil amplification from surface-wave inversion using the Markov-chain Monte Carlo method. Soil Dynamics and Earthquake Engineering, 2018, 107: 141‒151
[35] 石耀霖, 金文. 面波频散反演地球内部构造的遗传算法. 地球物理学报, 1995, 38(2): 189‒198
[36] Tokeshi K, Harutoonian P, Leo C J, et al. Use of sur-face waves for geotechnical engineering applications in Western Sydney. Advances in Geosciences, 2013, 35: 37‒44
[37] Yamanaka H, Ishida H. Application of genetic algori-thm to an inversion of surface-wave dispersion data. Bulletin of the Seismological Society of America, 2003, 86(2): 436‒444
[38] Martínez M D, Lana X, Badal J, et al. Simulated an-nealing in 3-D seismic modelling and elastic structure of the mediterranean basin. Physics & Chemistry of the Earth Part A Solid Earth & Geodesy, 1999, 24 (3): 253‒260
[39] Martínez M D, Lana X, Olarte J, et al. Inversion of Rayleigh wave phase and group velocities by simu-lated annealing. Physics of the Earth & Planetary In-teriors, 2000, 122(1): 3‒17
[40] Beaty K S, Schmitt D R, Sacchi M. Simulated an-nealing inversion of multimode Rayleigh wave dis-persion curves for geological structure. Geophysical Journal International, 2002, 151(2): 622‒631
[41] Song X, Gu H, Zhang X, et al. Pattern search al-gorithms for nonlinear inversion of high-frequency Rayleigh-wave dispersion curves. Computers and Geosciences, 2008, 34(6): 611‒624
[42] Song X, Tang L I, Xiaochun L V, et al. Application of particle swarm optimization to interpret Rayleigh wave dispersion curves. Journal of Applied Geophy-sics, 2012, 84(9): 1‒13
[43] Kranjcic D, Stumberger G. Differential evolution-based identification of the nonlinear Kaplan turbine model. IEEE Transactions on Energy Conversion, 2014, 29(1): 178‒187
[44] 蔡伟, 宋先海, 袁士川, 等. 基于萤火虫和蝙蝠群智能算法的瑞雷波频散曲线反演. 地球物理学报, 2018, 61(6): 2409‒2420
[45] 于东凯, 宋先海, 江东威, 等. 改进蜂群算法及其在面波频散曲线反演中的应用. 地球物理学报, 2018, 61(4): 1482‒1495
[46] 蔡伟, 宋先海, 袁士川, 等. 新的瑞雷波多模式频散曲线反演目标函数. 地球科学, 2017, 42(9): 1608‒1622
[47] 姚姚. 地球物理非线性反演模拟退火法的改进. 地球物理学报, 1995, 38(5): 643‒650
[48] 王山山, 李灿平, 李青仁, 等. 快速模拟退火地震反演. 地球物理学报, 1995, 38(增刊1): 123‒124
[49] 陈华根, 李丽华, 许惠平, 等. 改进的非常快速模拟退火算法. 同济大学学报(自然科学版), 2006, 34(8): 1121‒1125
[50] 毛承英. 基于改进遗传算法的瑞雷波频散曲线反演[D]. 长沙: 中南大学, 2010: 30‒44
[51] 闫月锋, 孙成禹. 瑞雷波频散曲线反演的线性约束问题研究//2014 年中国地球科学联合学术年会——专题 19: 地震波传播与成像论文集. 北京: 中国地球物理学会, 2014: 1167
[52] 闫月锋. 石油勘探中地震面波的非线性反演方法研究[D]. 青岛: 中国石油大学(华东), 2016: 57‒61
[53] 崔建文. 一种改进的全局优化算法及其在面波频散曲线反演中的应用. 地球物理学报, 2004, 47(3): 521‒527
[54] Iglesias A, Atienza V M C, Shapiro N M, et al. Crustal structure of south-central Mexico estimated from the inversion of surface-wave dispersion curves using genetic and simulated annealing algorithms. Geophysical International, 2013, 40(3): 181‒190
[55] 雷宇航. 自适应GA与DLS联合反演瑞雷波频散曲线方法研究[D]. 西安: 西安石油大学, 2018: 30‒62
[56] Senkaya M, Karslı H. Joint inversion of Rayleigh-wave dispersion data and vertical electric sounding data: synthetic tests on characteristic sub-surface mo-dels. Geophysical Prospecting, 2016, 64(1): 228‒246
[57] Calderon-Macias C, Luke B. Improved parameteriza-tion to invert Rayleigh-wave data for shallow profiles containing stiff inclusions. Geophysics, 2007, 72(1): U1‒U10
[58] Menke W. Comment on ‘Dispersion function compu-tations for unlimited frequency values’ by Anas Abo-Zena. Geophysical Journal of the Royal Astronomi-cal Society, 1979, 59(2): 315‒323
[59] 张晓阳, 郭珍, 唐拓, 等. 基于快速标量传递算法的频散曲线正演模拟. 价值工程, 2015, 34(33): 130‒132
[60] 李杰, 杨婧, 陈宣华. 面波频散曲线遗传算法反演的程序设计. 地球物理学进展, 2013, 28(5): 2693‒2700
[61] 刘建宙. 有限差分法在瑞雷波波场正演模拟中的应用[D]. 北京: 中国地质大学(北京), 2014: 19‒45
[62] Connolly D P, Giannopoulos A, Forde M C. A higher order perfectly matched layer formulation for finite-difference time-domain seismic wave modeling. Geo-physics, 2015, 80(1): T1‒T16
Inversion Research of Rayleigh Wave Dispersion Curve Based on Fast Scalar Transfer Algorithm
Abstract In order to improve the efficiency and accuracy of the inversion of Rayleigh wave dispersion curves near the surface, fast scalar transfer algorithm which has the characteristics of high computational efficiency is introduced to calculate the forward theoretical value of Rayleigh wave dispersion curve. The performances of genetic algorithm (GA), simulated annealing algorithm (SA) in the inversion of Rayleigh wave dispersion curves before and after adding linear constraints are compared. On this basis, linear constraints are added to GA and SA to improve the speed of convergence, and Monte Carlo method (MC) with fast computing speed is used to identify the types of formation as a supplementary means. Then the inversion results obtained by GA are taken as the initial state of SA as well as narrowing search scope appropriately, and this kind of joint inversion is carried out to overcome the premature problem of GA. Using the above method to calculate the three-layer model, noise-containing data and actual model of the work area. The results show that the method above is efficient, accurate and stable, and it has strong ability of global optimization and anti-noise ability to a certain extent.
Key words shallow surface; Rayleigh wave; dispersion curve; fast scalar transfer algorithm; nonlinear inversion
doi: 10.13209/j.0479-8023.2020.020
国家科技重大专项(2016ZX05004003)和国家自然科学基金(41674122)资助
收稿日期: 2019‒05‒10;
修回日期: 2019‒06‒30