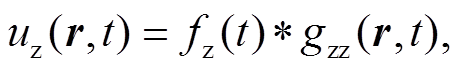(1)摘要 基于瞬态多道面波分析法(MASW)的数据采集方式, 对矢量波数变换法(VWTM)、相移法和高分辨率拉东变换法 3 种瑞雷波频散成像方法进行对比分析。首先, 采用合成地震数据对比 3 种方法的成像效果, 发现 VWTM 在成像精度和成像质量方面都有很大的优势, 成像分辨率高, 与理论频散曲线拟合准确, 高阶模式成像效果突出, 且抗噪能力也优于另两种方法。然后, 采用实际多道瞬态面波数据进行对比分析, 发现与相移法和拉东变换法相比, VWTM 在瑞雷波基阶模式成像精度和高阶模式成像质量方面仍具有优势。采用遗传算法对比基阶与高阶频散曲线反演结果, 发现含有高阶模式的多模式频散曲线联合反演的多解性明显降低, 反演结果精度更高, 也更稳定。在实际瞬态瑞雷波勘探实践中, VWTM 能够高质量地提取多模式瑞雷波频散特征, 可为多模式面波频散联合反演提供可靠的基础数据。研究结果表明, 将 VWTM 法与有效的反演方法相结合, 可以极大地提高瑞雷波浅地层探测能力和探测精度。
关键词 瑞雷波; 矢量波数变换法(VWTM); 多道面波分析法(MASW); 高阶频散曲线; 遗传算法
利用瑞雷波频散特性的勘探方法是一种重要的近地表地球物理勘探方法, 其中的瞬态多道面波分析(multichannel analysis of surface waves, MASW) 方法[1]在过去的 20 年中广泛地应用于工程地球物理勘探领域。目前, 从多道面波记录中获取频散曲线的常见方法有 f-k 法[2]、τ-p 变换法[3]、相移法(shift phase)[1]和拉东变换法(Radon transform)[4‒6]等。f-k法方法简单, 易于实现, 但需要满足空间域与时间域采样间隔相等的条件, 且对总道数要求较高, 如果波场记录中存在坏道, 会对结果产生较大的影响, 使横向分辨率大大降低, 从而降低提取频散曲线的精度[7]。τ-p 变换法和线性拉东变换法均将数据沿一系列直线进行叠加, 高阶模式成像质量较好, 但基阶模式频散曲线在低频段成像效果较差, 容易出现假频现象和端点效应[7‒8]。相移法是先将各道地震数据进行傅里叶变换, 然后在空间域进行积分, 在不同频率下进行速度扫描, 对基阶模式的成像效果较好, 但对高阶模式的成像分辨率不高[8‒9]。
综上所述, 现有利用瑞雷波频散特性的勘探方法对低频部分和高阶模式的成像均具有局限性。随着工程勘查对探测精度要求的不断提高, 对面波勘探也提出更多的要求。研究发现, 高阶面波在地层结构反演分析中起着关键作用[9‒14]。若能在频散能量图中有效地提高高阶模式的成像质量, 将极大地提高面波反演的精度和稳定性。因此, 本研究分析空间格林函数的矢量波数变换法(vector wavenumber transformation method, VWTM)(在噪声成像中也称为频率‒贝塞尔变换法(frequency-Bessel transform method, F-J)[15]的成像能力, 并与相移法及高分辨率线性拉东变换法进行对比。在采集道数不变的情况下, VWTM能提高瑞雷波高阶模式的成像质量和抗噪能力; 通过 VWTM 提取瑞雷波频散曲线进行多模式联合反演, 可明显提高瑞雷波的探测精度。
在水平半无限空间模型中, 震源为原点, 在柱坐标中, 地表观测点r观测到的瑞雷波可表示为
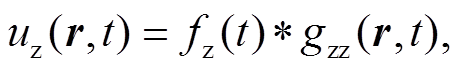(1)其中,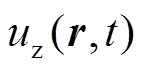 
为地震波的垂直分量, fz(t)为震源时间函数, 
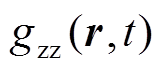为观测点与震源间垂直分量的格林函数[9]。将式(1)变换到频率域, 可以得到
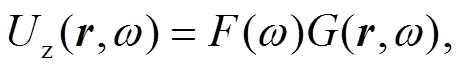(2)
其中,ω表示频率。根据水平层状介质中地震波传播理论[15‒16], 地表观测点与震源间的格林函数在频率域的计算公式可以表示为
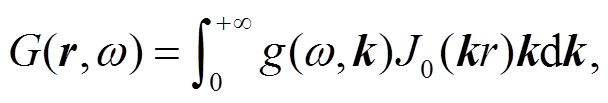(3)其中, g 是格林核函数, J0 是第一类零阶贝塞尔函数。对 G(r,ω)进行矢量波数变换[9,15], 得到
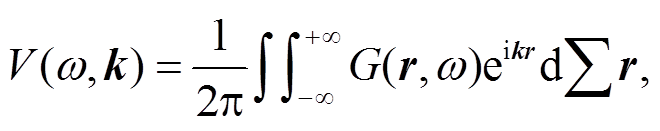(4)
其中, k表示波数。当空间为水平层状介质时, r=|r|, 其矢量波数变换结果仅依赖波数矢量的模k (k=|k|), 与波数矢量的方向无关, 此时式(4)可表示为
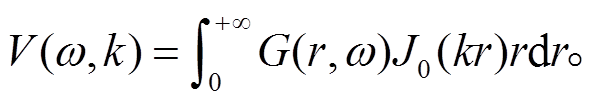(5)将式(3)代入式(5), 可得式(6)[9]:
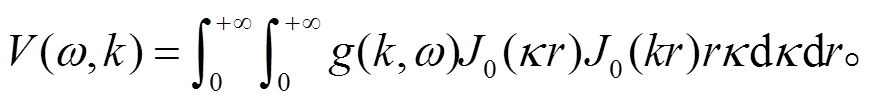(6)
根据贝塞尔函数的正交性:
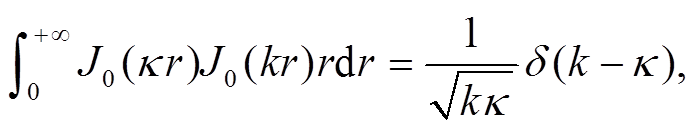(7)将式(7)代入式(6), 则式(6)可以简化为
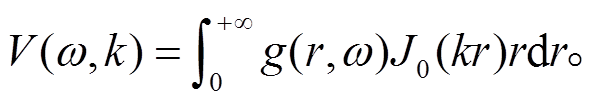(8)
将式(2)代入式(8), 可得
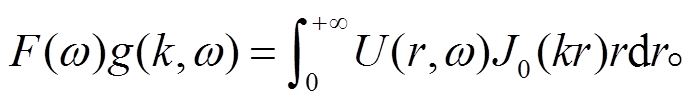(9)式(8)中, 格林函数 g 的核函数值与确定面波频散特性的久期函数值成反比[16]:
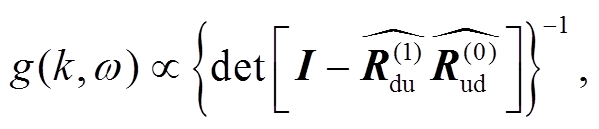(10)
其中, R 是广义反射系数矩阵; 下角标 d 代表向下(down), u 代表向上(up); 上角标 0 代表自由表面, 1代表第一层。当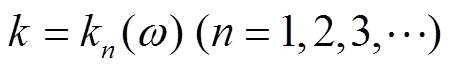
时, 久期函数为零, 即
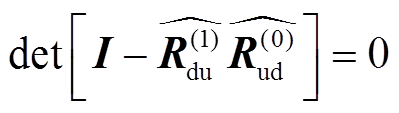, 因此核函数 g(ω, k)的值趋于无穷大[16‒18]。矢量波数变换法正是利用这一性质, 在频散能量图中对频散曲线进行成像[9]。
为了测试 VWTM 的成像能力, 首先采用离散波数法[17‒18], 模拟垂直于地面单力点源产生的地震波场, 然后采用 3 种方法(VWTM、相移法和高分辨率线性拉东变换法)进行成像, 并与广义反射‒透射系数方法[19‒20]得到的理论频散曲线进行叠加对比。
本研究采用含低速层的 4 层水平层状模型, 地层模型参数见表 1。合成地震数据的震源时间函数采用雷克子波近似, 中心频率为 10Hz, 延迟为 0.2 s。震源和检波器呈线性排列, 道间距为 1m, 最小偏移距为 10m, 数据长度为 2s, 采样间隔为 1ms, 合成 84 道地震数据(图 1)。分别采用 24 和 84 道地震数据, 应用 VWTM、相移法和高分辨率线性拉东变换法[5]进行计算, 得到频散能量图, 再与理论频散曲线叠加, 对比其成像效果(图2)。
表1 水平层状地层模型参数[9]
Table 1 Parameters of the horizontally layered stratum model[9]
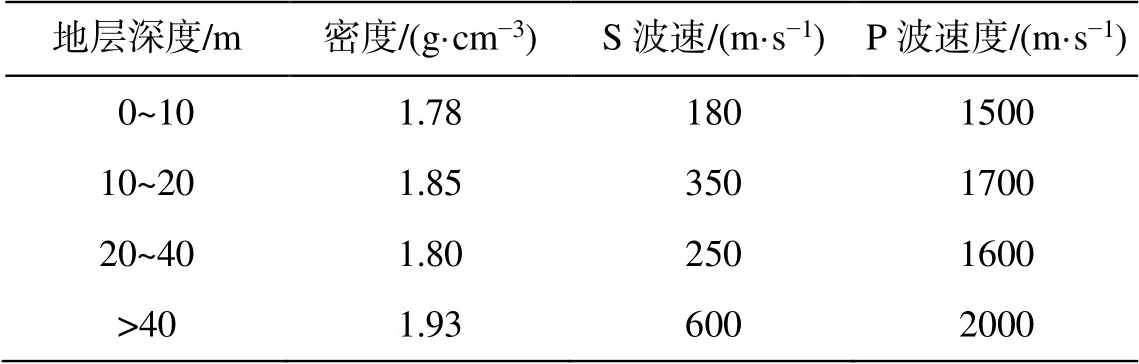
地层深度/m密度/(g·cm−3)S波速/(m·s−1)P波速度/(m·s−1) 0~101.781801500 10~201.853501700 20~401.802501600 >401.936002000
通过对比成像结果发现, 当参与处理的地震道数增加(即排列增长)时, 3 种方法的频散能量图在低频区域的成像质量都明显提高, 表明瑞雷波勘探深度和精度会随着台站数量和排列长度的增加而提高。图 2 显示, 相移法的整体分辨率较低, 尤其是高阶面波的成像分辨率明显弱于其他两种方法; 当只有 24 道地震数据参与成像时效果非常差, 10Hz以下的部分几乎完全不能识别, 随着地震道数增加, 基阶模式成像质量明显提高, 但高阶模式成像质量仍较差。高分辨率线性拉东变换法成像分辨率较高, 尤其在地震道数较少时, 也能得到分辨率较高的频散图像, 但与理论频散曲线对比出现一定的偏差(图 2); 随着地震道数增加, 拉东变换法整体成像效果有所提高, 但在小于 5Hz 区域基阶模式成像与理论频散曲线出现较大偏差。与前两种方法相比, VWTM 的成像质量具有明显优势, 尤其在 4~30Hz频率范围内基阶和高阶模式的成像质量和精度都明显优于其他两种方法; 虽然地震道数较少时不如高分辨率线性拉东变换法的分辨率高, 但地震道数增加后分辨率明显提高, 成像精度明显优于其他两种方法。因此, VWTM 在高阶模式的成像质量和基阶模式的成像精度方面具有巨大的优势。
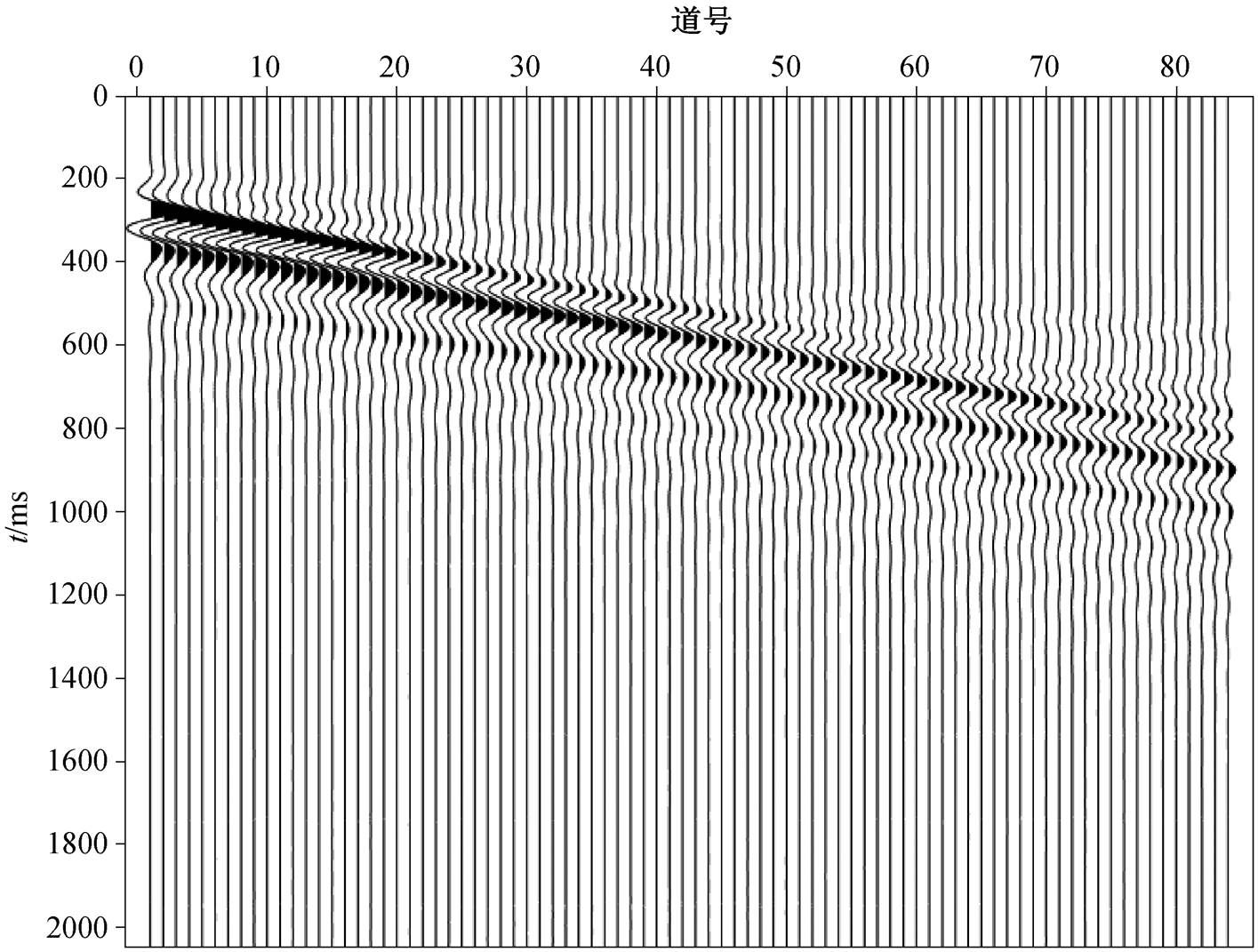
图1 84道地震记录
Fig. 1 Seismic record of 84 channels
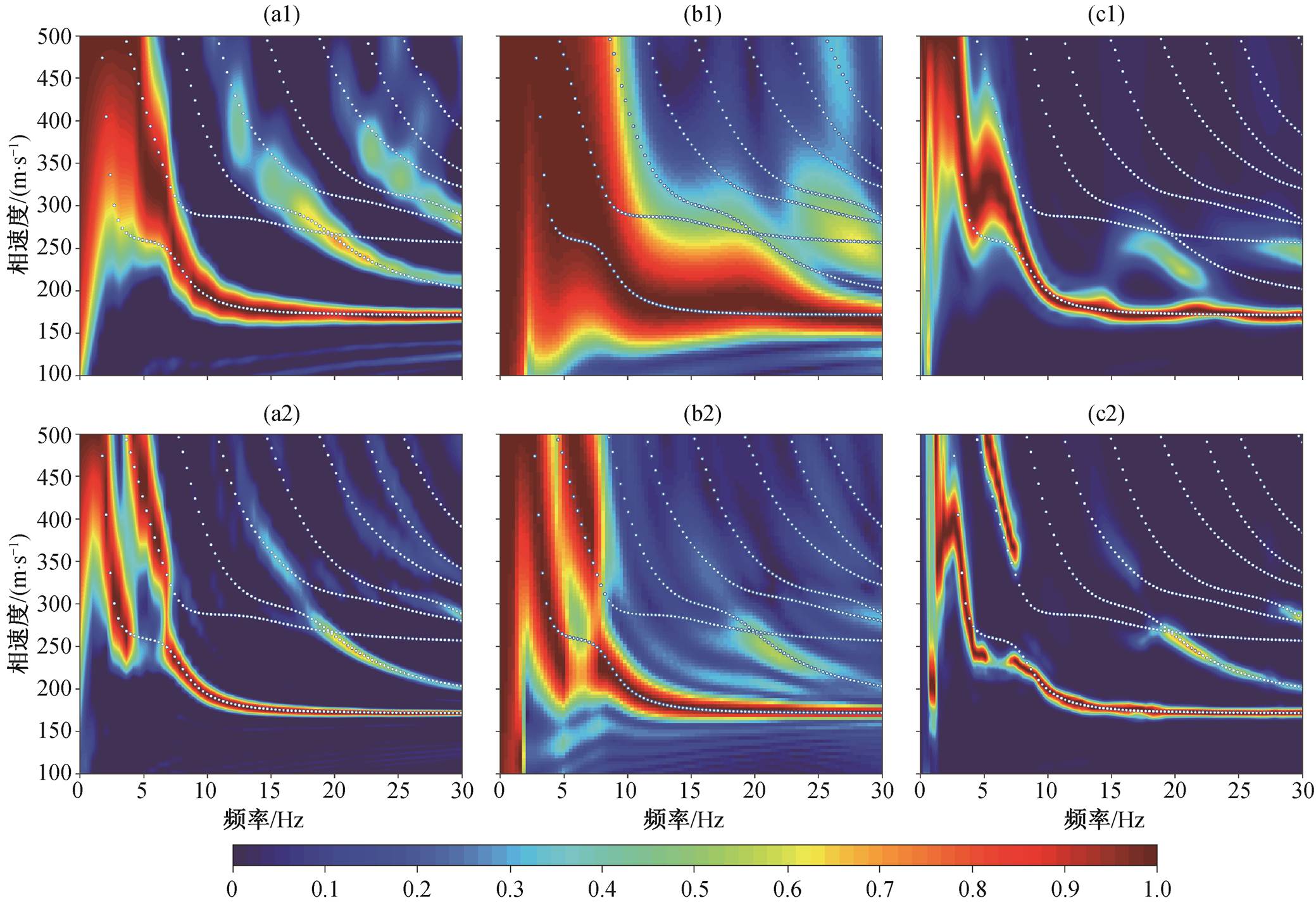
(a1~c1) 1~24道数据, (a2~c2) 1~84道数据; (a1~a2) VWTM, (b1~b2)相移法, (c1~c2)拉东变换法。白色点线为理论频散曲线
图2 无噪声合成数据频散能量图
Fig. 2 Dispersion energy diagrams of synthetic data without noise
为分析成像方法的抗噪能力, 我们模拟随机坏道, 每道加入均值为 0, 标准差为 1 的随机干扰, 噪声水平为原始数据中每道振幅最大值平均值的 20% (图 3), 并随机将各道的噪声水平放大 1 倍、缩小50%或不变。分别采用 24 道和 84 道地震数据, 应用 VWTM、相移法和高分辨率线性拉东变换法进行计算, 得到频散能量图(图4)。
从图 4 看出, 在处理含有噪声的数据时, 相移法成像质量明显降低, 基阶模式成像质量相对稳定, 但高频部分(>21Hz)很难有效地成像, 且高阶模式无法成像; 高分辨率拉东变换法受干扰影响较大, 尤其当参与计算的地震道数较少时, 在高频频率区域(>23Hz)和低频区域(<5Hz), 基阶模式成像与理论频散曲线存在较大的偏差, 且高阶模式成像精度大大降低; VWTM 仍然是受干扰影响最小的方法, 即使在 24 道数据的情况下, 基阶和高阶模式仍能高质量地成像, 且精度高, 仅在高频部分(>25Hz)的成像受到干扰。
遗传算法是一种借鉴生物界遗传机制和自然选择的高效并行、随机全局优化搜索算法, 通过模拟自然进化的过程来搜索最优解, 只计算正演和适应性函数, 可以避免矩阵求逆和偏导数计算而可能产生的数值不稳定或精度丢失等问题。该方法 1975 年由 Holland[21]提出, 现已广泛推广并成功地应用于多个领域, 也是常用的瑞雷波频散曲线反演方法。
作为一种搜索寻优技术, 遗传算法从问题参数编码出发, 并按照一定的操作规则(如选择、交叉和变异等)初始化种群, 然后按照一定的标准更新群体, 实现一代遗传; 如此反复迭代, 逐步逼近问题的解。因为面波频散曲线反演是一种高度非线性、多维度的复杂问题, 因此本文的反演研究采用遗传算法的实数编码遗传算法来进行问题的求解, 相对于二进制编码, 这种编码更适合求解大规模复杂函数优化问题, 且求解精度高, 算法运行快, 结果更稳定[22]。早期的遗传算法中使用的交叉和变异算子是固定不变的, 本研究采用自适应的交叉和变异算子, 以便灵活地应对面波频散曲线反演问题。自适应的交叉和变异算子的概率计算公式为
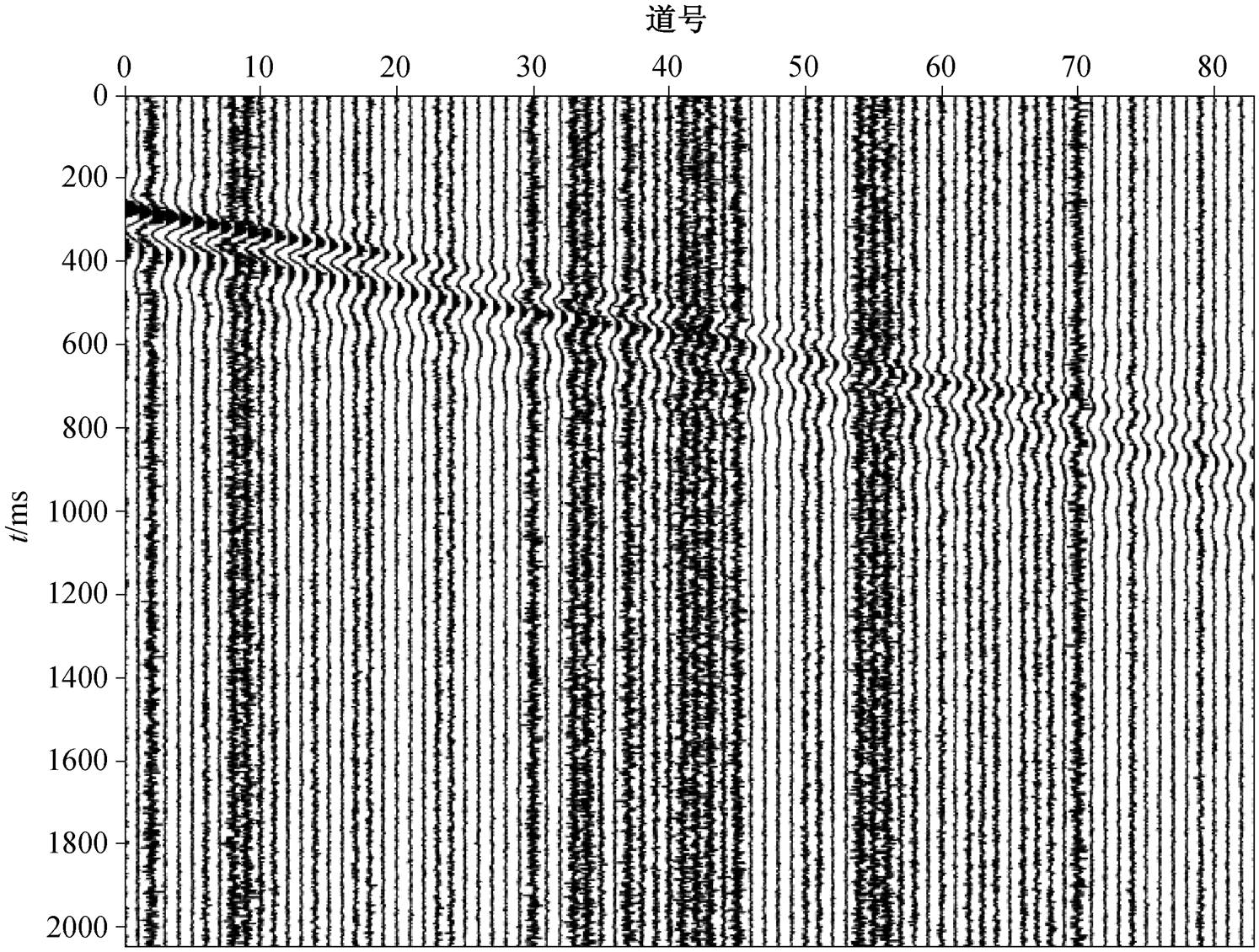
图3 合成数据加入随机坏道干扰
Fig. 3 Synthetic data with interference of random bad channel
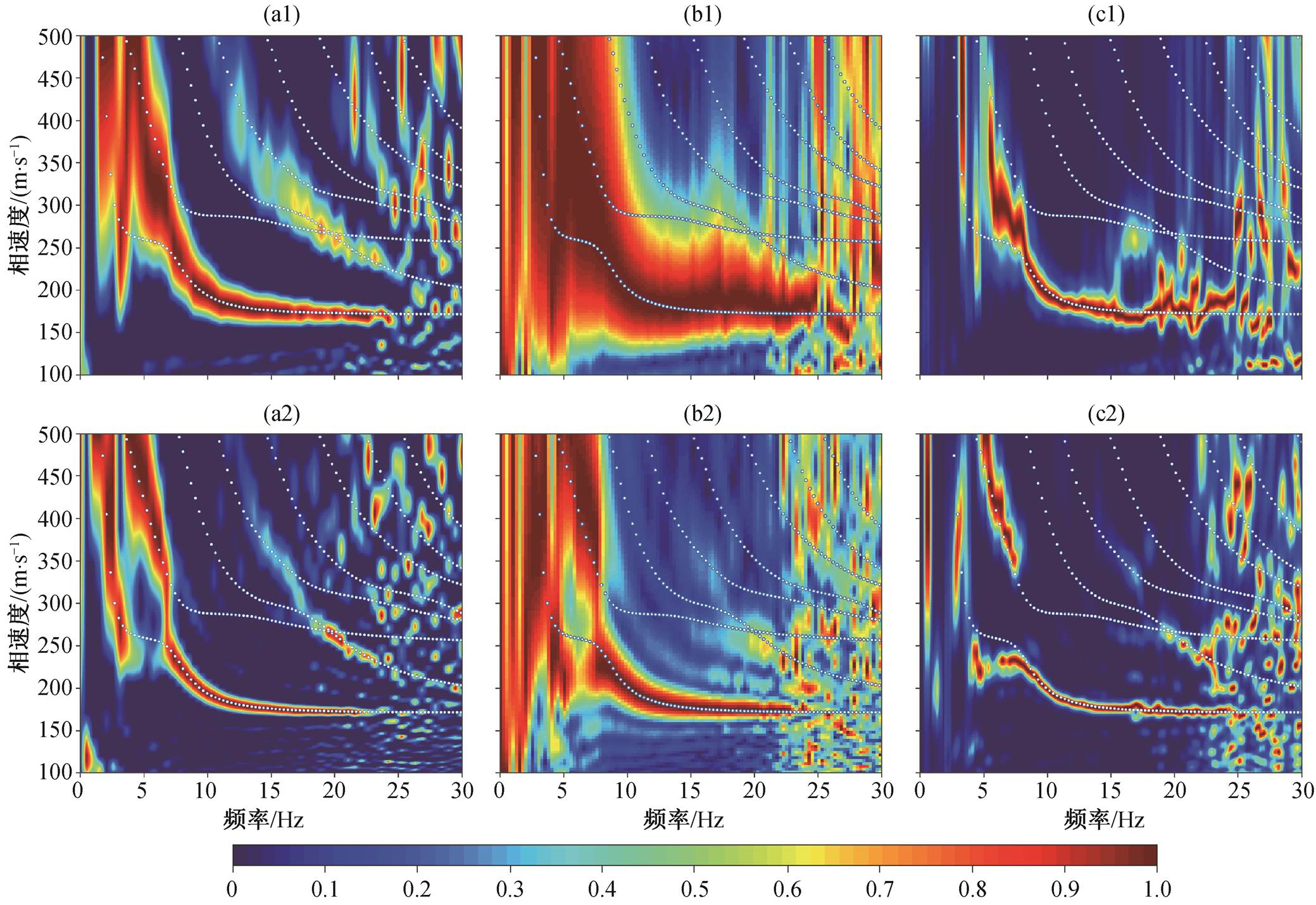
(a1~c1) 1~24道数据, (a2~c2) 1~84道数据; (a1~a2) VWTM, (b1~b2)相移法, (c1~c2)拉东变换法。白色点线为理论频散曲线
图4 随机坏道干扰数据频散能量图
Fig. 4 Dispersion energy diagrams with interference of random bad channel
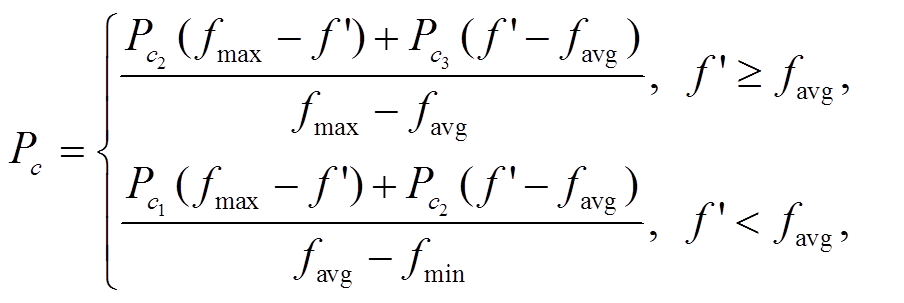(12)
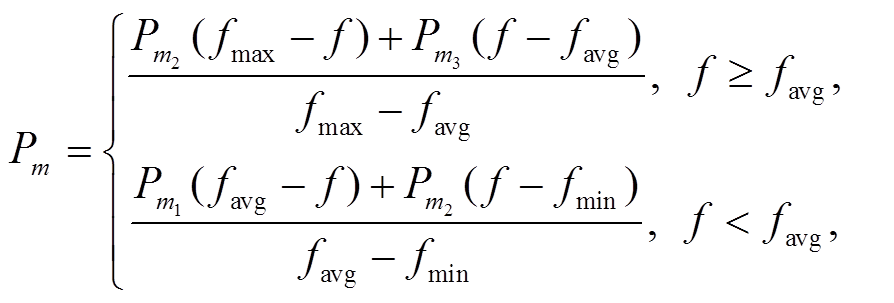(13)
其中,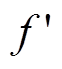 
表示要交叉的两个个体中较大的适应度值, f是要变异个体的适应度值, fmax, fmin和favg分别表示当前种群中适应度的最大值、最小值和平均值, 且满足
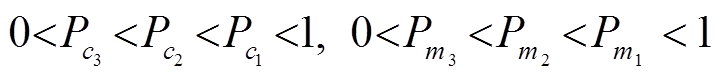。图5 为 Pc 和 Pm 随个体适应度进行自适应调整的示意图, 可以看到个体适应度越低, 交叉或变异的概率越大, 反之亦然。通过自适应调整, 将个体的适应度与种群的平均适应度进行对比, 使优秀个体在种群进化中有效地保留, 劣势个体的变异能力增强, 从而加快种群向好的方向发展。采用式(12)和(13)中的自适应交叉算子和变异算子进行计算, 还可以保证适应度高的个体仍然有机会进行交叉和变异, 在进化后期, 较好的个体依然可以得到改善。
选取 84 道数据, 采用 VWTM 得到的频散能量图(图 2(a2)), 提取频散曲线, 分别用不同的模式进行反演, 并与 4 层理论模型进行对比。
3.2.1 仅用基阶模式进行反演
从图 6(a)可以看出, 仅采用基阶模式反演得到的基阶频散曲线与实测基阶频散点在高频部分能够很好地吻合, 但在低频区域(<5Hz)与理论频散曲线和实测频散点之间仍有一定程度的误差。
图 6(b)为 10 次反演的结果(每次反演迭代 50次, 目标函数均趋于收敛), 得到 1~3 层的层厚标准差分别为 0.18, 1.43 和 2.92 m, 1~4 层的横波速度标准差分别为 0.50, 15.01, 30.09 和 47.72 m/s。可以看到, 仅采用基阶模式反演, 虽然频散曲线趋于拟合, 但多次反演的结果仍具有较大的不稳定性。
3.2.2 多模式联合反演
从图 7(a)看出, 对所有实测频散点进行多模式联合反演得到的理论频散曲线与实测频散点能够很好地吻合。图 7(b)为采用 10 次反演的结果(每次反演迭代 50 次, 目标函数均趋于收敛), 得到 1~3 层的层厚标准差分别为 0.07, 0.91, 1.72 m, 1~4 层的横波速度标准差分别为 0.18, 6.19, 10.71 和 29.28m/s。可以看到, 加入高阶模式的约束后, 反演得到的频散曲线不仅能很好地拟合, 而且反演精度和稳定性都比仅采用基阶模式反演有很大程度的提高。
如前所述, 采用合成数据 VWTM 可以精确地提取瑞雷波高阶模式频散曲线, 随后采用遗传算法多模式联合可以高精度地反演地层结构。为了研究VWTM 对实际数据的适用性, 我们在常州北郊长江滩涂地区进行线性排列瞬态瑞雷波的采集。采集数据的道间距为 1m, 最小偏移距为 10m, 数据长度为 1s, 采样频率为 1000Hz, 24 道采集, 如图 8 所示。分别应用 VWTM、相移法和高分辨率线性拉东变换法进行处理, 对比 3 种方法对实际数据的成像效果, 如图 9 所示。从图中可以看到, VWTM 的成像质量明显优于其他两种方法, 尤其高阶模式的成像优势明显, 分辨率高; 相移法的整体分辨率都很低, 低频区域(<10Hz)的边界效应严重, 高阶面波成像不理想; 高分辨率线性拉东变换法保持很高的分辨率, 但低频区域(<5Hz)的效果很差, 误差明显, 且难以分辨不同模式的高阶面波。
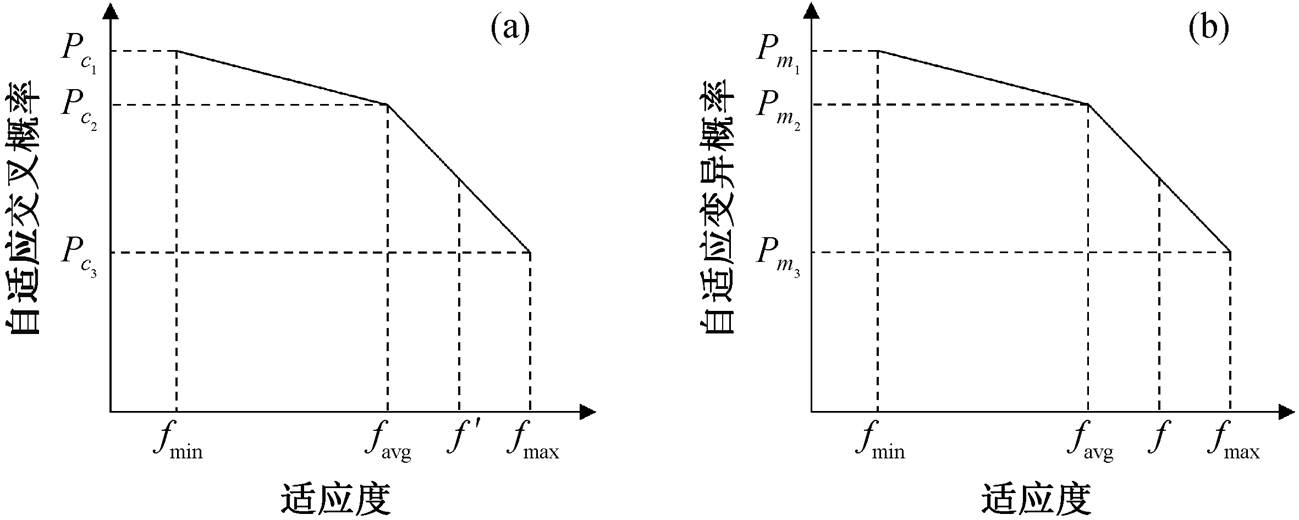
图5 自适应交叉概率(a)和自适应变异概率(b)[23]
Fig. 5 Adaptive crossover probability (a) and adaptive mutation probability (b)[23]
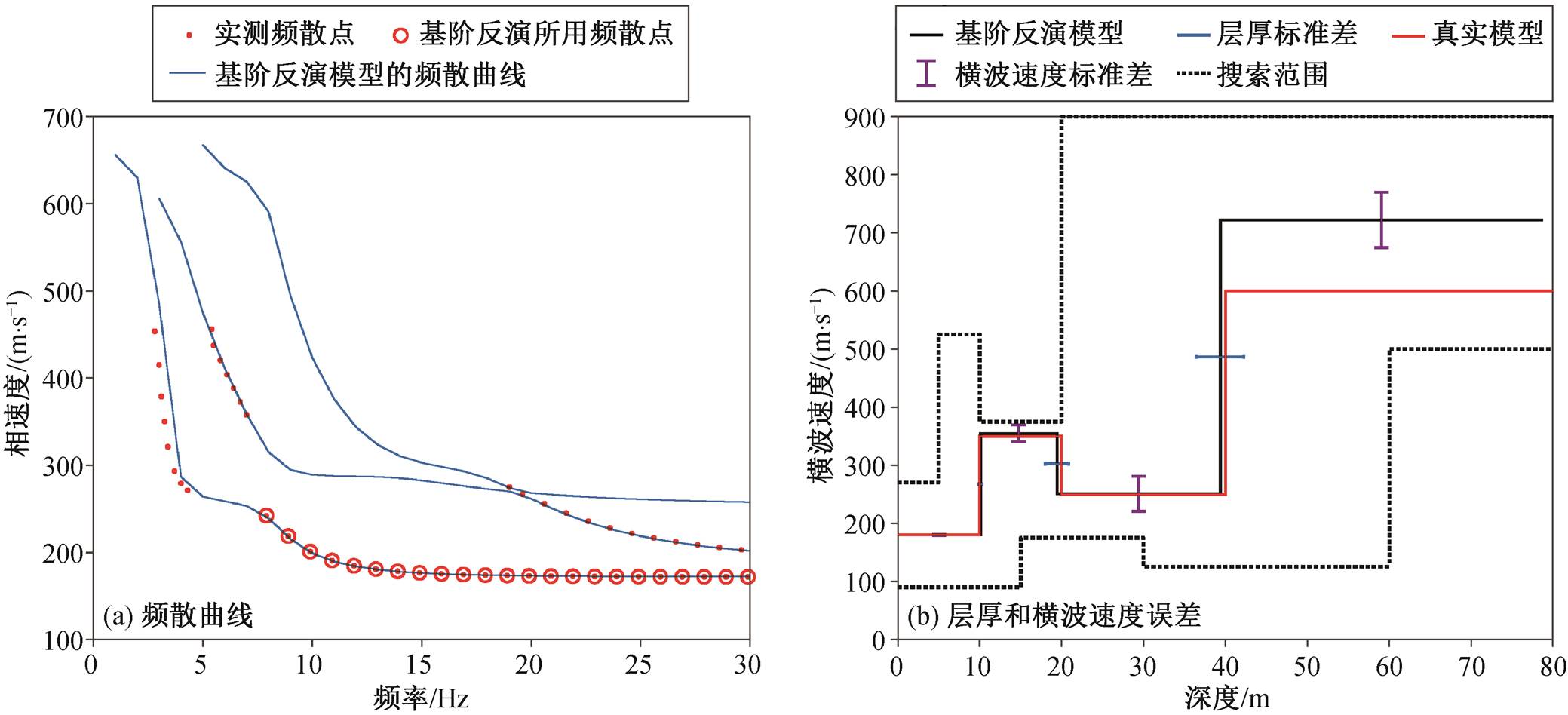
图6 仅用基阶模式的反演结果
Fig. 6 Inversion with only fundamental mode
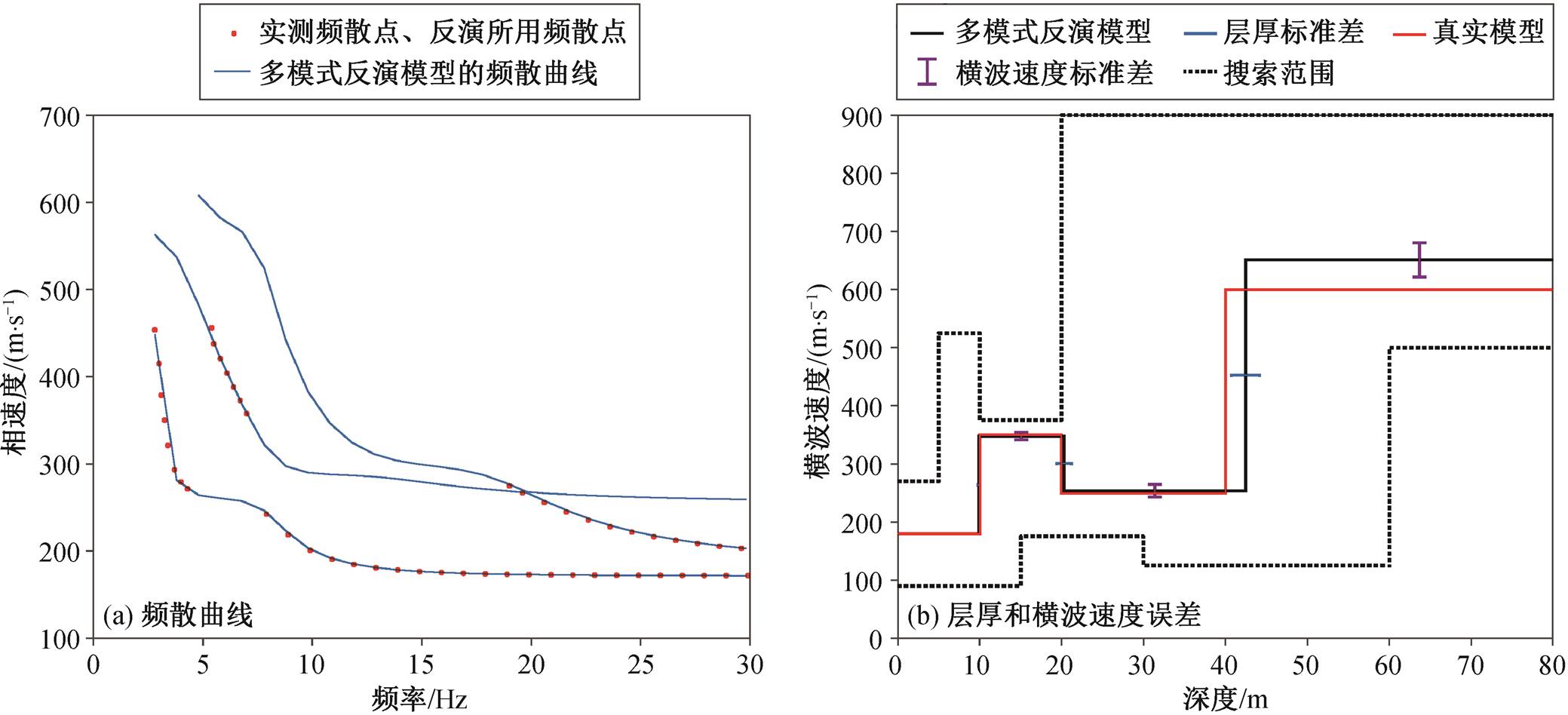
图7 多模式反演结果
Fig. 7 Multi-modes inversion
选取图 9(a)中 VWTM 提取多模式频散曲线的结果, 根据搜集到的地质资料建立一个 7 层初始模型进行反演。通过提取频散能量图中的能量极值点获得频散点, 并对频散点进行遗传算法多模式反演, 结果如图 10 所示。反演得到的频散曲线与实测频散点基本上吻合, 地层结构为速度递增正常沉积地层。该结果与实际勘察资料相符。
本文将一种新的多道面波分析方法——矢量波数变换法(VWTM)与传统相移法以及高分辨率线性拉东变换法对合成数据和实际数据进行成像对比分析, 发现 VWTM 在成像精度和成像质量方面都有巨大的优势, 尤其是 VWTM 的高阶模式成像能力和抗噪能力明显优于其他两种方法; 在实际瑞雷波探测中, 采集道数不是很多的情况下, VWTM 仍能保证高阶模式成像的分辨率。因此, VWTM 能为实际地层多模式联合反演提供更为丰富的频散信息。
图8 常州郊区瞬态瑞雷波实验数据
Fig. 8 Transient Rayleigh wave data from Changzhou suburb
在得到多模式频散曲线的基础上, 本文采用改进的实数编码自适应遗传算法对基阶、高阶频散曲线进行反演对比, 发现对含有高阶模式的频散信息进行联合反演时多解性明显降低, 反演结果精度更高, 也更稳定。在实际瞬态瑞雷波勘探中, VWTM能够有效地高质量地提取多模式瑞雷波频散特征, 为基阶与高阶面波频散联合反演提供可靠的数据基础。VWTM 结合有效的反演方法, 可以极大地提高近地表地层结构的探测精度, 尤其在城市工程勘察中具有巨大的应用潜力。
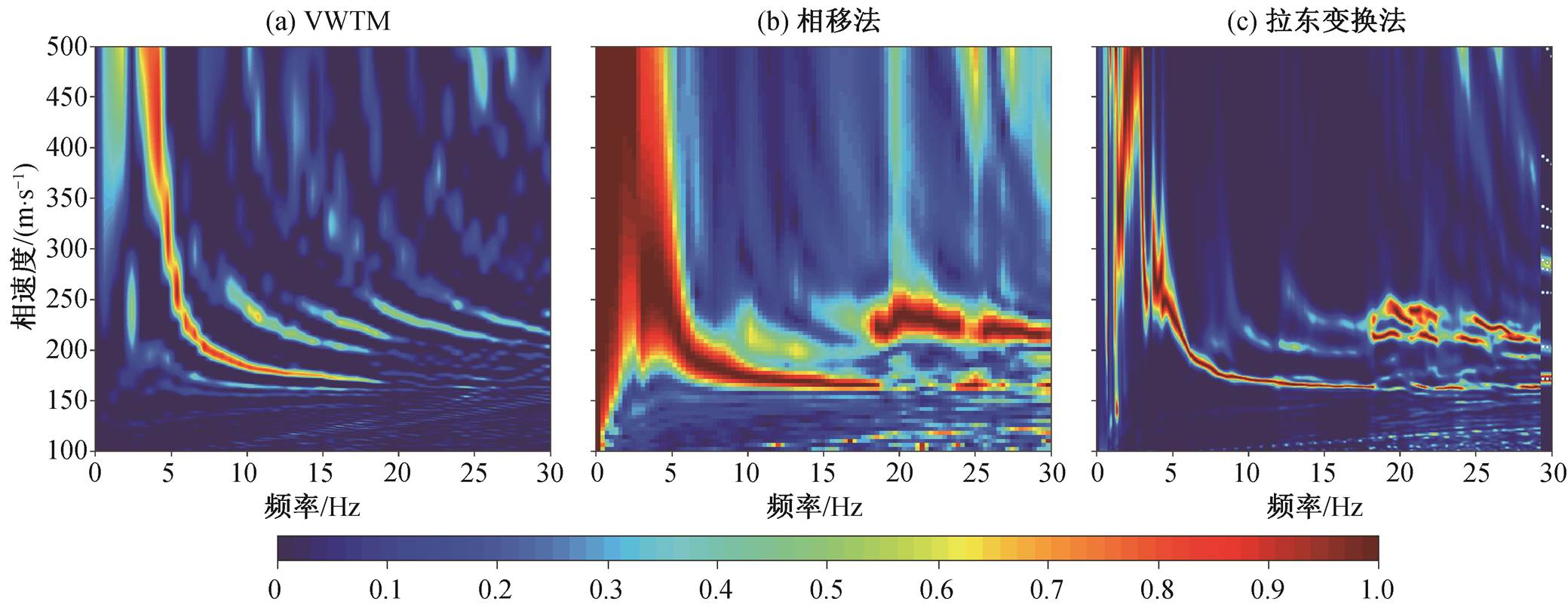
图9 实验数据频散能量图
Fig. 9 Dispersion energy diagrams of Rayleigh wave data from Changzhou suburb
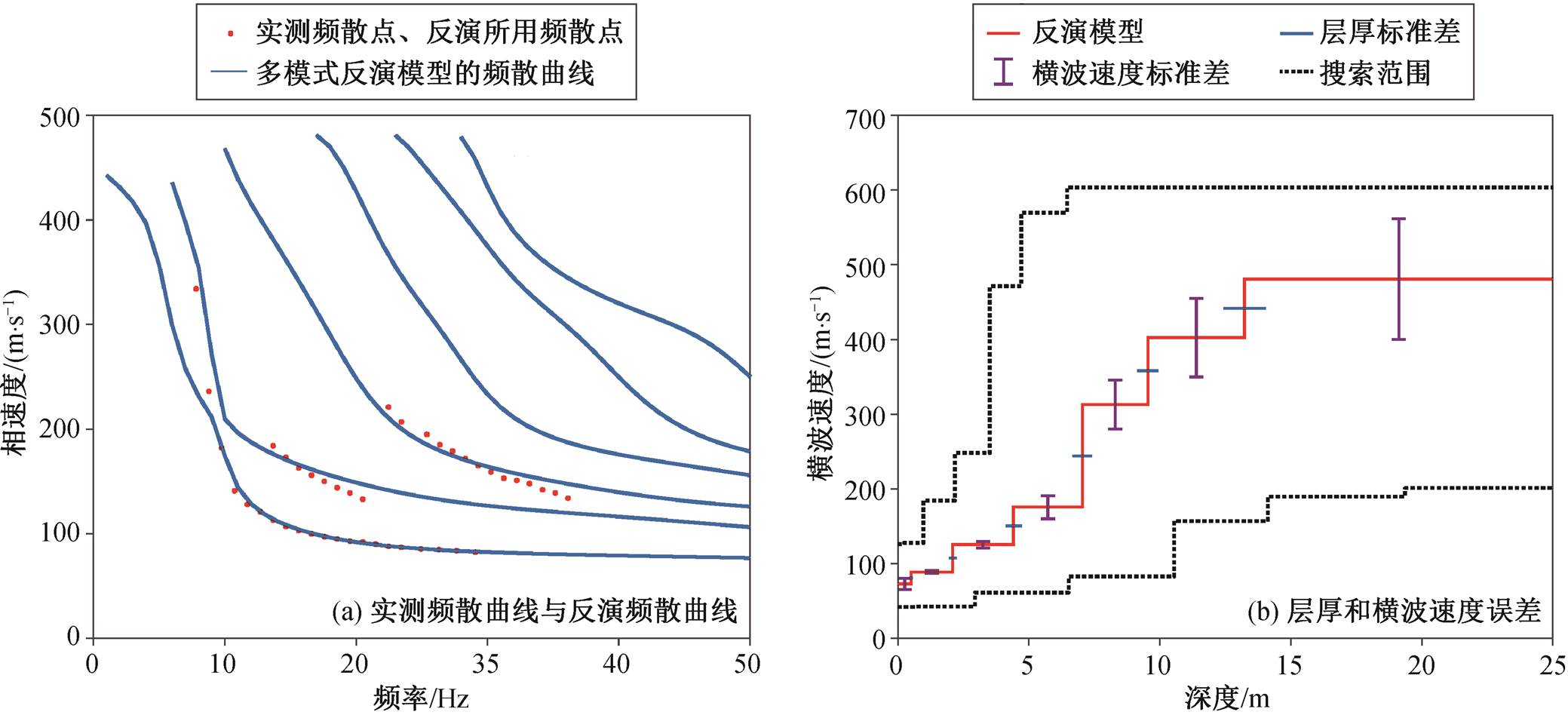
图10 实际瞬态瑞雷波实验数据反演结果
Fig. 10 Inversion of Rayleigh wave data from Changzhou suburb
VWTM 是基于检波器与震源之间的格林函数进行频率‒波数域贝塞尔变换, 所以检波器可以任意排列, 为了与其他方法进行比较, 本文仅采用线性观测进行对比分析。本研究基于水平层状介质模型, 将震源近似为雷克子波, 对实际情况做了近似处理。然而, 实际地下结构非常复杂，震源时间函数也不是简单的雷克子波。因此, 本文的 VWTM方法仍有较大的改善空间。
参考文献
[1] Park C B, Miller R D, Xia J. Multichannel analysis of surface waves. Geophysics, 1999, 64(3): 800‒808
[2] Capon J. High-resolution frequency-wavenumber spec-trum analysis. Proceedings of the IEEE, 2005, 57(8): 1408‒1418
[3] Mcmechan G A, Yedlin M J. Analysis of dispersive by wave field transformation. Geophyscis, 1981, 6(46): 869‒874
[4] 余钦, 范沈操, 牛滨华. Radon 变换的 MATLAB 实现. 物探化探计算技术, 2000, 22(4): 345‒350
[5] Luo Y, Xia J, Miller R D, et al. Rayleigh-wave mode separation by high-resolution linear Radon transform. Geophysical Journal International, 2009, 179(1): 254‒ 264
[6] 潘东明, 胡明顺, 崔若飞, 等. 基于拉东变换的瑞雷面波频散分析与应用. 地球物理学报, 2010, 53 (11): 2760‒2766
[7] 卢建旗. 多道面波分析方法及其应用研究[D]. 北京: 中国地震局工程力学研究所, 2013
[8] 邵广周, 李庆春. 联合应用 τ-p 变换法和相移法提取面波频散曲线. 石油地球物理勘探, 2010, 45(6): 836‒840
[9] 杨振涛, 陈晓非, 潘磊, 等. 基于矢量波数变换法(VWTM)的多道 Rayleigh 波分析方法. 地球物理学报, 2019, 62(1): 298‒305
[10] Zhang B X, Lu L Y, Bao G S. A study on zigzag dis-persion curves in Rayleigh wave exploration. Chinese Journal of Geophysics, 2002, 45(2): 265‒276
[11] 张碧星, 鲁来玉, 鲍光淑. 瑞利波勘探中“之”字形频散曲线研究. 地球物理学报, 2002, 45(2): 263‒ 274
[12] 凡友华. 考虑高阶模的 Rayleigh 波勘探应用研究[D]. 北京: 北京大学, 2003
[13] Pan L, Chen X, Wang J, et al. Sensitivity analiysis of dispersion curves of Rayleigh waves with fundamen-tal and higher modes. Geophyscial Journal Interna-tional, 2019, 216(2): 1276‒1303
[14] Xia J, Miller R D, Park C B, et al. Inversion of high frequency surface waves with fundamental and higher modes. Journal of Applied Geophysics, 2003, 52(1): 45‒57
[15] Wang J, Wu G, Chen X. Frequency-Bessel transform method for effective imaging of higher-mode Ray-leigh dispersion curves from ambient seismic noise data. Journal of Geophysical Research Solid Earth, 2019, 124(4): 3708‒3723
[16] Chen X. Seismogram synthesis in multi-layered half-space partⅠ. theoretical formulations. Earthquake Research in China, 1999, 13(2): 53‒78
[17] Zhang H M, Chen X F, Chang S. An efficient numeri-cal method for computing synthetic seismograms for a layered half-space with sources and receivers at close or same depths. Pure & Applied Geophysics, 2003, 160(3/4): 467‒486
[18] 王建楠. 背景噪音提取高阶频散曲线的矢量波数变换方法[D]. 合肥: 中国科学技术大学, 2017
[19] Chen X. A systematic and efficient method of compu-ting normal modes for multilayered half-space. Geo-physical Journal International, 1993, 115(2): 391‒409
[20] 何耀锋, 陈蔚天, 陈晓非. 利用广义反射‒透射系数方法求解含低速层水平层状介质模型中面波频散曲线问题. 地球物理学报, 2006, 49(4): 1074‒1081
[21] Holland J H. Adaptation in natural and artificial sys-tems. Ann Arbor, 1975, 6(2): 126‒137
[22] 周永华. 实数编码遗传算法杂交算子组合研究[D]. 广州: 华南理工大学, 2003
[23] 毛承英. 基于改进遗传算法的瑞雷波频散曲线反演[D]. 长沙: 中南大学, 2010
Application Research of Active Source Rayleigh Wave Multi-Mode Extraction Method Based on Vector Wavenumber Transformation Method in Near Surface Stratigraphic Structure Detection
Abstract Based on the array of the transient multi-channel analysis of surface waves (MASW), Rayleigh wave dispersion imaging methods including vector wavenumber transformation method (VWTM), phase shift, and high-resolution linear Radon transform are used to carry out comparative analysis. First, the dispersion imaging results of synthetic data are compared to analyze the quality of the three methods. The VWTM is found superior to the other two in terms of resolution, accuracy of higher modes, fitting degree with theoretical dispersion curves and anti-noise property. In the actual Rayleigh wave detection, the VWTM can still has advantages in foundamental mode imaging accuracy and higher order modes imaging quality. Then the genetic algorithm is employed to invert the dispersion curves of fundamental mode and higher modes. The result is more accurate and stable when higher modes are combined in the inversion, it also performs much better in reducing non-uniqueness of inversion. The research shows that the VWTM can extract multi-mode characteristics of Rayleigh wave dispersion effectively and with high quality in field prospecting, which provides a reliable data foundation for joint inversion of multi-mode of Rayleigh wave dispersion curves. In conclusion, the VWTM combined with effective inversion method can remarkably improve the accuracy of near surface stratigraphic structure detection and has great potential in enhancing Rayleigh wave exploration capability.
Key words Rayleigh wave; vector wavenumber transformation method (VWTM); multi-channel analysis of surface waves (MASW); higher-mode dispersion curves; genetic algorithm
doi: 10.13209/j.0479-8023.2020.021
国家重点研发计划(2018YFC0603600)和国家自然科学基金(41974047)资助
收稿日期: 2019‒05‒12;
修回日期: 2019‒06‒29