摘要 以北京市为例, 利用 2015—2018 年空气质量监测站台资料, 通过 BP 神经网络、LSTM 网络及 CNN-LSTM 混合模型等多种模型, 分析时间精度和空间信息对 PM2.5 浓度预报的影响。结果表明, 神经网络模型的效果普遍比多元线性回归模型好; 增加输入数据的时间精度能显著地提高 PM2.5 浓度日均值预报的准确率; 当输入数据的时间精度从一天提高到 6 小时后, LSTM 模型的平均绝对误差从 27.39μg/m3 降至 20.59μg/m3, 这种效果的提升在显著变好和显著变差的天气情况下更明显; 华北地区 PM2.5 浓度分布有明显的时空特征, 第一空间模态为同增同减, 第二空间模态为南北反向; 北京市 PM2.5 浓度与内蒙古、河北及天津等地区前一天的 PM2.5 相关。利用 CNN-LSTM 混合模型学习华北地区 PM2.5 的时空信息, 能进一步提高北京市 PM2.5 浓度的预报水平, 使得误差降低至 17.36 μg/m3。
关键词 神经网络; PM2.5预报; 时间精度; 空间特征
空气污染物组成复杂, 来源多样, 其中细颗粒物(PM2.5)的危害尤为严重。这些细颗粒物体积小, 重量轻, 能在空气中停留更长的时间, 通过呼吸道进入人体, 引发各种疾病[1‒2]。PopeⅢ等[3]的研究表明, 长期环境中 PM2.5 平均浓度每升高 10μg/m3, 会造成 4%~8%的心肺疾病死亡风险。空气中过量的 PM2.5 还会引发灰霾天气, 降低大气能见度, 影响人类的生产和生活。还有研究表明, PM2.5 和灰霾天气对天气过程甚至全球气候有重要影响[4‒6]。因此, 研究 PM2.5 的时空分布特征和预报方法具有重要意义, 并可为政府决策提供科学支持。
目前对 PM2.5 的预报主要有统计模型、模式模拟(化学传输模型)和深度学习模型等方法。Fuller等[7]通过 NOx, PM2.5 与 PM10的统计关系, 构建预报伦敦污染物浓度的经验模型, 为其他城市和地区PM2.5 的预报提供了思路。Baker 等[8]构造一个非线性回归模型来预报单来源的 PM2.5 浓度。Sun 等[9]对隐马尔可夫模型(HMM)进行优化, 显著地降低北加州 PM2.5 浓度的误报率。Saide 等[10]优化 WRF-Chem模式, 提升预报城市 PM2.5 浓度的稳定性。化学传输模型主要考虑化学物质的来源和传输过程, 对PM2.5 的预报不够直接, 且计算过程复杂[11], 深度学习方法给 PM2.5 预报带来新的探索空间。Zhou 等[11]利用集合经验模态分解(ensemble empirical mode decomposition, EEMD)和广义递归神经网络(general regression neural network, GRNN)的深度学习模型, 对西安 PM2.5 做了较好的预报。Liu 等[12]利用自组织长短期记忆(long short-term memory, LSTM)网络, 探索 PM2.5 预报的更多可能性。Huang 等[13]构造一维卷积和 LSTM 的叠加模型, 利用 PM2.5 浓度、风速和累计降水量来预报 PM2.5, 获得比单一 LSTM模型更好的效果。
PM2.5 的预报模型近年来不断更新, 目前对PM2.5 的预报能力还有很大的提升空间。尤其是新兴的深度学习模型, 前人的研究集中在对神经网络模型的构造和改进上, 忽略了 PM2.5 在时间上的强自相关性以及局地排放和区域输送的影响。考虑到PM2.5 浓度变化的物理特征, 本文以北京市 PM2.5 日均浓度预报为出发点, 从两个方面对深度学习方法进行探究: 1)前期 PM2.5 输入数据的时间精度对PM2.5 预报能力的影响; 2)空间 PM2.5 浓度信息对单点预报能力的影响。通过多组常见神经网络模型的对比, 结合对物理机制的分析, 进一步开发深度学习在 PM2.5 预报上的应用潜力。
本文选取的空气质量数据为 2015 年 1 月 2 日至2018 年 12 月 21 日逐小时 PM2.5 浓度数据, 来自中国环境监测总站的全国城市空气质量实时发布平台(http://beijingair.sinaapp.com), 其中北京市 PM2.5 浓度值来自该平台中北京市 12 个观测站的平均值。为了探究临近区域的 PM2.5 信息对北京市 PM2.5 预报的作用, 选取该平台华北地区(105°—125°E, 32°—43°N) 143 个空气质量测站的同时段逐小时 PM2.5数据。由于该区域测站空间分布不均, 部分站点存在较严重的缺测情况, 因此对 PM2.5 数据进行克里金插值(original Kriging)格点化处理, 空间分辨率为 0.75°×0.75°。
多元线性回归(multiple linear regression, MLR)方法用于研究一个因变量与多个自变量之间的关系, 能够很好地解释和预测因变量。本文选择多元线性回归作为不同模型对照的基准, 所有在神经网络中作为输入的变量在其中表示为一个自变量。
虽然 PM2.5 浓度与相对湿度和风速等气象因素以及 SO2 和 NOx 等污染物浓度具有相关性, 但不是线性相关。因此, 具有较强非线性拟合能力的神经网络在PM2.5浓度预报上有更好的表现[11,13‒14]。BP神经网络是基于误差反向传播算法(error back pro-pagation, BP)的多层感知器, 第一层为输入层, 中间为隐含层, 最后是输出层, 每一层的每个神经元与下一层的所有神经元连接, 形成全连接的网络结构, 这种网络也叫全连接神经网络(fully-connected neural networks, FC)。经过各种参数调整和尝试, 本文中的 BP 神经网络采用 3 个隐含层的全连接神经网络, 其中第一层神经元为 1000 个, 第二层神经元为 500 个, 第三层神经元为 20 个, 神经网络的激活函数为 ReLu 函数。
作为一个连续变化的时间序列, PM2.5 序列中后一时刻的信息与前面时刻紧密相关, 此时利用递归神经网络(RNN)就能将上一时刻的信息连接到当前时刻的学习过程中, 从而达到更好的拟合和预测效果。LSTM (long short-term memory)网络是在传统RNN 基础上改进的深度学习网络, 由 Hochreiter 等[15]于 1997 年提出。它能够连接更长时间间隔的信息, 常常可以达到比传统 RNN (如 Vanilla RNN)更好的效果。
本研究中 LSTM 模型采用双层 LSTM 的结构, 第一层神经元结点数为 1000, 第二层神经元结点数为 500, 每层之后添加一个全连接层(FC 层), 其神经元个数分别为 20 和 1。为了与 BP 神经网络进行比较, 激活函数和神经元结点个数基本上与 BP 模型一致。
为了探究临近区域信息对单点 PM2.5 预报的影响, 本文构造三维卷积与 LSTM 的混合预报模型。将区域 PM2.5 的时间序列看做三维图像, 首先利用卷积神经网络(convolutional neural network, CNN)提取信息, 然后将提取出的信息转化为与时间对应的向量, 再利用 LSTM 网络进行单点 PM2.5 预报。
模型结构如图 1 所示, 其中批标准化(batch normalization, BN)可以加速模型收敛, 池化(Max Pooling)层通过降采样, 将固定区域内的最大值提取出来代表该区域信息, 从而降低数据维度, 减少计算消耗, 参数设置如下。
卷积层: 卷积核大小为 3×3, 第一层三维卷积(Conv3D)的卷积核数目为 100, 第二层 Conv3D 的卷积核数目为 50, 第三层 Conv3D 的卷积核数目为 5。
池化层: 第一层 Max Pooling 的池化区域大小为 3×3×3, 第二层池化区域的大小为 2×3×3。
LSTM 层: 第一层 LSTM 的神经元数目为 100, 第二层 LSTM 的神经元数目为 50。
FC 层: 神经元数目为 50。
激活函数: sigmoid函数。
本文中所有神经网络模型均选择 RMSPROP 作为优化器, 初始学习率为 0.001, 迭代次数为 64, 批次大小为 32。
为了直观地评价不同模型对 PM2.5 浓度的拟合和预报能力, 选取绝对平均误差(MAE)、均方根误差(RMSE)、IA (index of agreement)和 MAPE (mean absolute percentage error)作为评价指标, 计算公式如下:
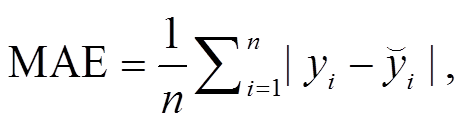
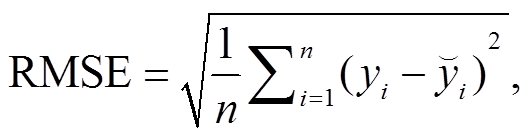
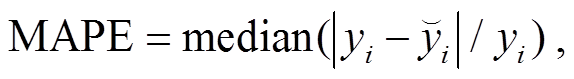
其中, n 表示样本数, y 代表观测数据值,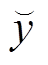
代表预报数据值, 
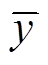是观测数据的均值。本文中的模型均以MAE (μg/m3)作为损失函数来训练神经网络。
图 2(a)是 2015—2018 年北京市 PM2.5 浓度日变化序列。可以看出, PM2.5 浓度夏季最低, 冬、春两季较高, 与徐敬等[16]的研究结果一致。从图 2(b)可以看出, PM2.5 浓度日变化的自相关性较强, 即PM2.5 浓度的日均值与前期 PM2.5 浓度值密切相关。根据李梓铭等[17]的研究, 北京城区 PM2.5 浓度存在显著的“星期效应”, 即存在一周左右的显著周期, 因此本文中 PM2.5 的预报选用前 6 天的数据作为输入数据, 用于捕捉天气尺度的 PM2.5 浓度变化。后期的实验结果表明, 使用前期 1~14 天不同的天数来预报 PM2.5, 得到的结果相差不大, MAE 大约相差2μg/m3。若仅使用前一天的日均值数据, 则 PM2.5浓度的预报能力相对较差。本文的实验结论在使用1~14 天不同天数预报的情况下都成立。
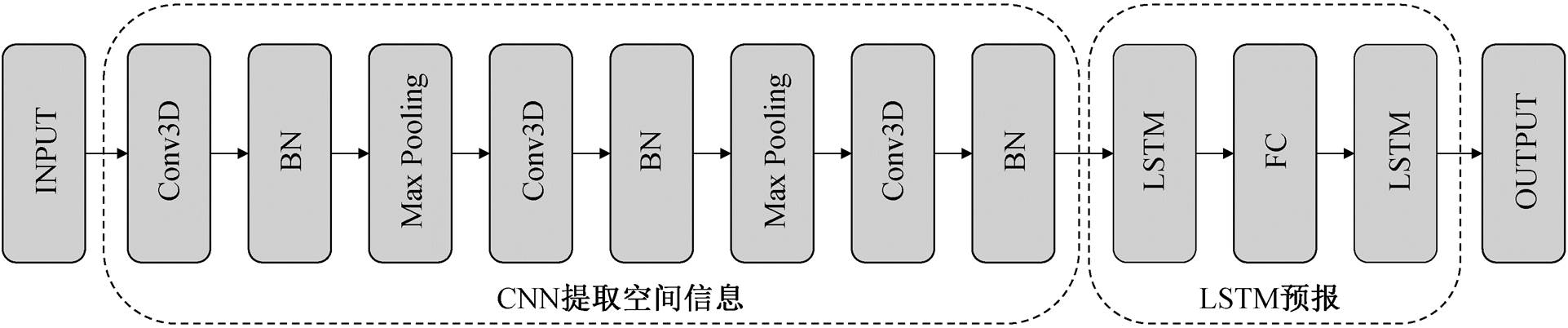
图1 CNN-LSTM混合模型的结构
Fig. 1 Structure of CNN-LSTM hybrid model
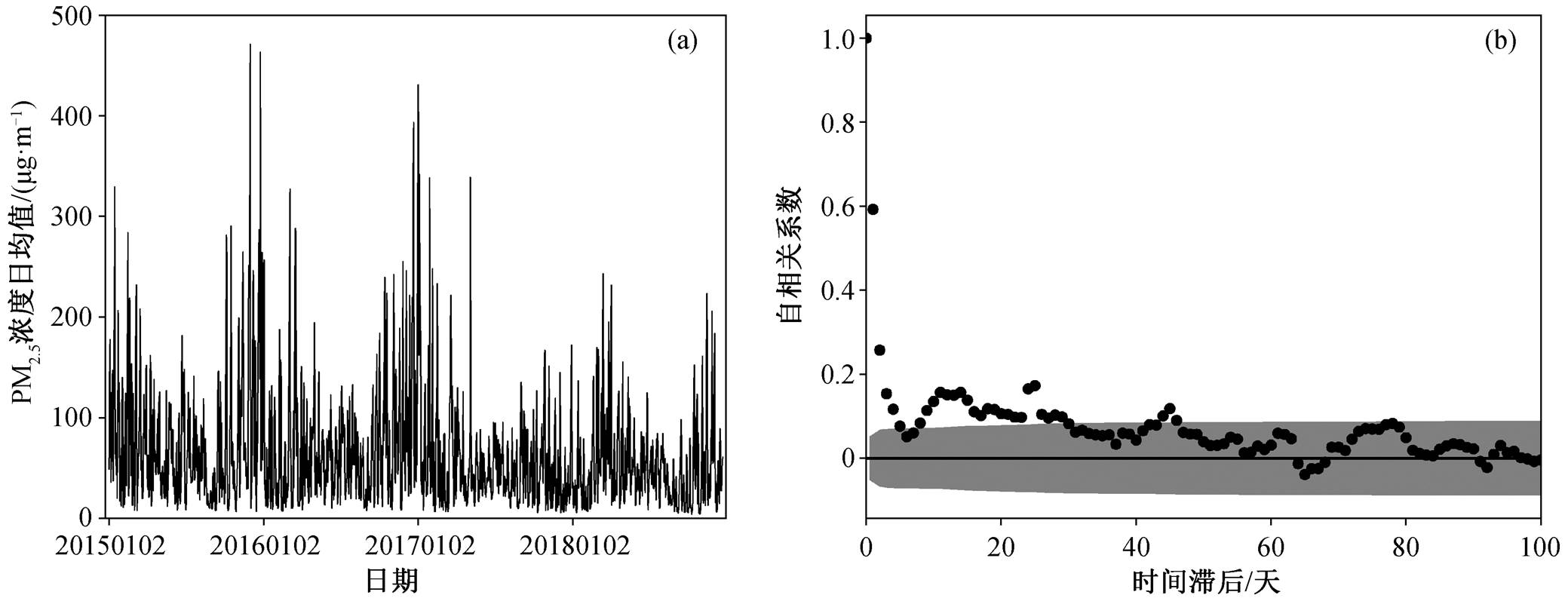
阴影表示95%置信区间, 置信边界的标准差由Bartlett公式[18]计算
图2 北京市PM2.5浓度日均值时间序列(a)及时间滞后自相关系数(b)
Fig. 2 Time series of daily average PM2.5 concentration in Beijing (a) and time-lagged autocorrelation coefficient diagram (b)
首先, 利用北京市 PM2.5 浓度日均值数据进行不同模型间的横向比较, 利用前 6 天的日均值数据预报第 7 天的 PM2.5 日均值。模型中统一采用前 3年的数据(201501~201712)作为训练集, 最后一年的数据(201801~201812)作为测试集, 训练数据中的30%作为验证集, 得到的结果如图 3 所示。多元线性回归得到的 MAE, RMSE 和 MAPE 值都较高, IA值较低, 体现出比神经网络模型更差的拟合和预报能力。LSTM 模型的表现相对更好。尽管 3 种模型的结果存在一定的差距, 但这种差距不明显, 主要是由训练和测试数据集较小以及 PM2.5 浓度日均值较强的自相关性引起的。
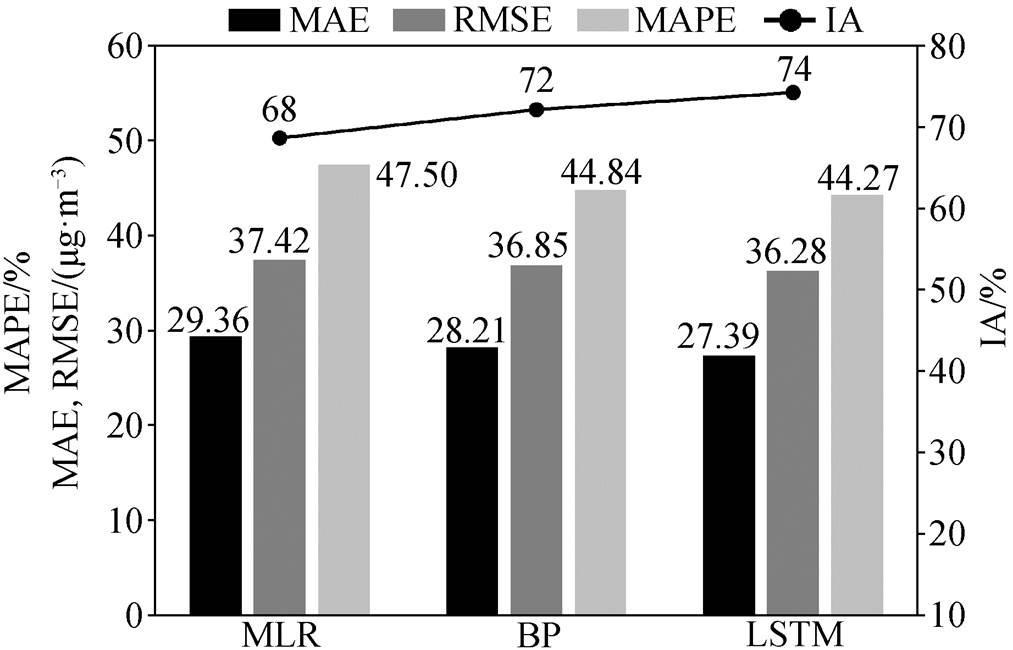
图3 以PM2.5浓度日均值作为输入数据的评估指标比较
Fig. 3 Comparison of evaluation metrics using daily average PM2.5 concentration as input data
PM2.5 浓度的变化存在多个周期叠加的现象, 提升输入数据的精度不仅能反映更短周期的变化, 还能提供短时间内 PM2.5 浓度变化的信息。为此, 将输入数据由原来的 6 天 PM2.5 浓度日均值更换为 6天的 6 小时 PM2.5 浓度平均值, 依然预报第 7 天的PM2.5 浓度日均值, 结果如图 4 所示。与输入数据为日均值的预报结果相比, 无论是多元线性回归, BP神经网络, 还是 LSTM 模型, 对 PM2.5 浓度的预报准确率都明显地提高。LSTM 模型明显优于其他两个模型, 其 MAE 和 RMSE 值更低, 拟合能力更强。
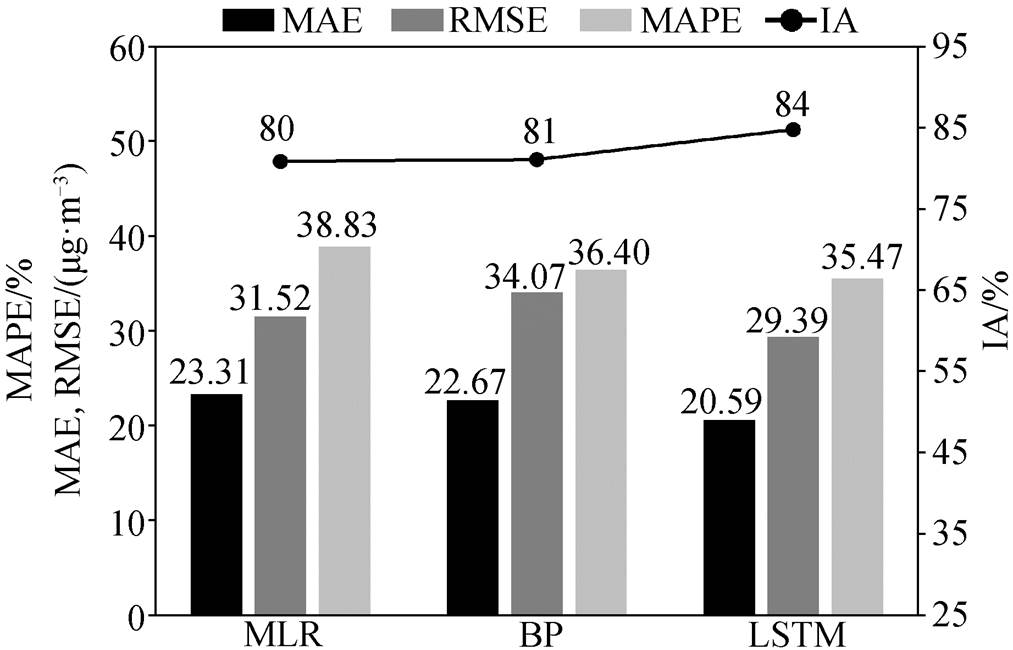
图4 以 6 小时 PM2.5 浓度平均值作为输入数据的评估指标比较
Fig. 4 Comparison of evaluation metrics using 6-hourly average PM2.5 concentration as input data
为了分析高时间精度的数据是如何影响 PM2.5预报的, 我们对训练集中的 PM2.5 浓度逐小时数据进行小波分析, 结果见图 5。可以看出, PM2.5 时间序列有 16 小时至 256 小时(10 天)的显著周期。尽管日均值的数据能够反映 48 小时以上周期的变化, 但不含 48 小时以下的周期, 尤其是 24 小时(日变化)及以下周期的信息, 而这些信息是 PM2.5 浓度变化周期的重要部分。根据赵晨曦等[19]的研究, PM2.5 浓度日变化呈双峰式, 峰值相差约为 10 小时。因此, 提高时间精度能增加 PM2.5 浓度的日变化信息, 对未来 PM2.5 浓度日均值的预报有重要影响。我们的实验结果表明, 如果输入数据的时间精度从日平均提高到 12 小时平均, 就能够显著地提高原模型的预报能力。
除包含更多的 PM2.5 浓度短周期信息外, 提高时间精度还能更好地捕捉前期 PM2.5 浓度的显著变化, 从而提升预报能力。为了进一步说明这个问题, 我们比较日均值 LSTM 模型和 6 小时平均值 LSTM模型对 PM2.5 浓度当天相对于前一天增量的预报能力, 得到图 6 的结果。无论是对显著变好的天气(增量小于−25μg/m3), 还是对显著变坏的天气(增量大于 25μg/m3), 日均值模型预报的增量都在−25~25μg/m3范围内波动, 即日均值模型往往只利用前一天的观测值进行预报, 没有捕捉到空气质量显著变化的信息。6 小时平均值模型对显著变好天气和显著变坏天气的预报有明显更好的效果, 当 PM2.5 浓度明显降低时, 预报值同样显著地降低; 当 PM2.5浓度明显升高时, 预报值也有同样的变化趋势, 观测增量‒预报增量基本上沿y=x对角线分布。
为了更好地阐释 6 小时平均值 LSTM 模型对变好天气和变差天气更强预报能力的现实意义, 根据中华人民共和国国家环境保护标准, 将本文测试集中 PM2.5 浓度划分为优(0~35μg/m3)、良(36~75μg/m3)、轻度污染(76~115μg/m3)、中度污染(116~ 150μg/m3)和重度污染(150μg/m3以上) 5 个等级。图 7 是 PM2.5 浓度不同增量下各污染等级的占比情况, 可以看出, 增量<−25μg/m3 时几乎全部是优良天气, 增量>25μg/m3时大部分是污染天气。对全部数据而言, 这两者组成约 1/4 的优良天气和大部分污染天气。6 小时平均值模型对这两种情况有更好的预报能力, 说明该模型部分地提升了对优良天气的预报能力, 显著地提升了对污染天气的预报能力。鉴于公众对污染天气的关注, 该模型刚好满足PM2.5 浓度预报的现实需求。图 8 对比不同 PM2.5 浓度等级下日均值 LSTM 模型和 6 小时平均值 LSTM 模型的 MAE, 清晰地表明 6 小时平均值模型在优、中度污染和重度污染这 3 个 PM2.5 浓度等级下预报能力的提高。
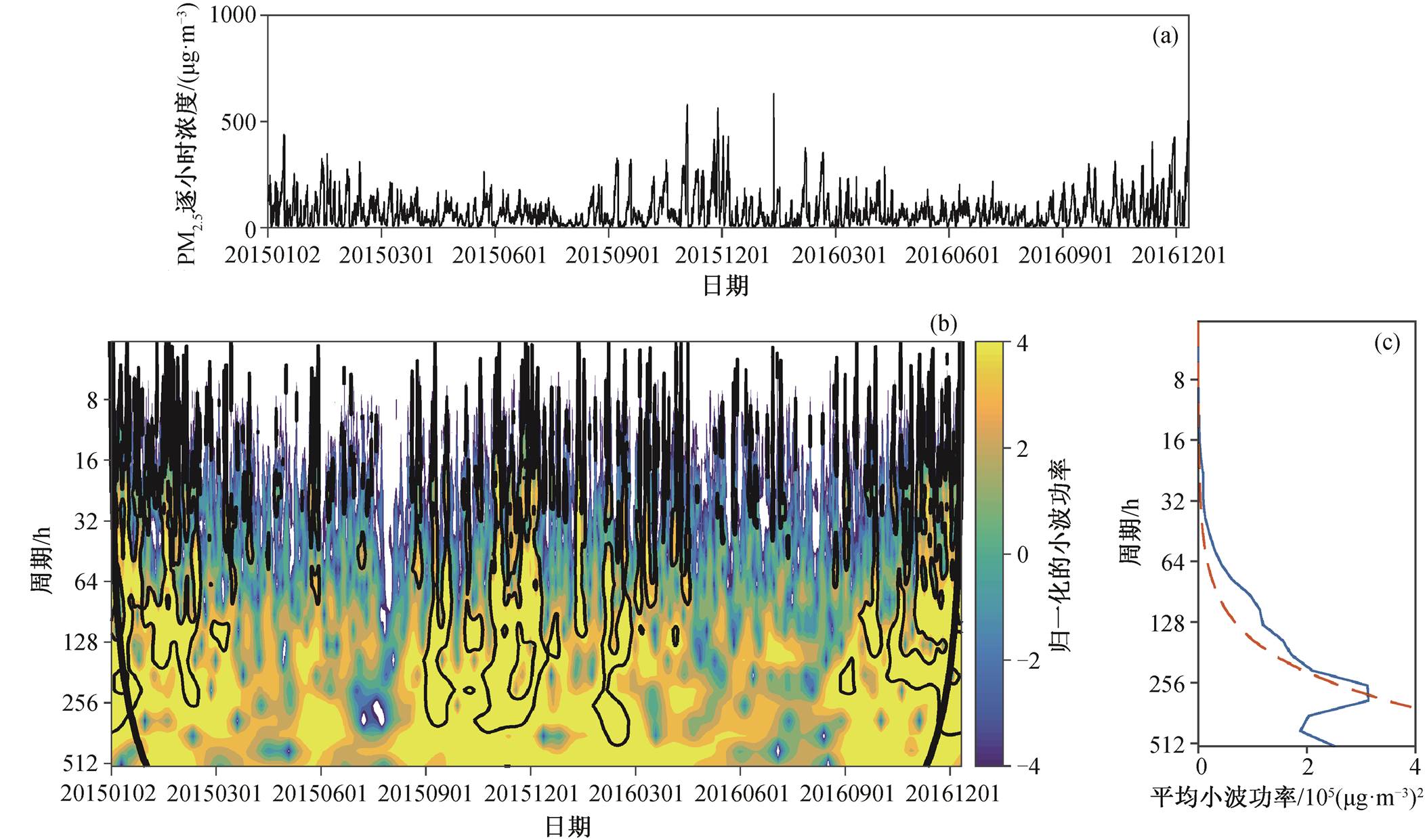
(a)训练集 PM2.5浓度逐小时时间序列; (b)小波功率谱, 黑色等值线包围的区域表示通过 95%显著性检验; (c)平均小波功率谱, 红色虚线以上部分表示通过 95%显著性检验。置信区间的检验方式为卡方检验
图5 训练集(201501~201612)上PM2.5逐小时浓度的小波功率谱
Fig. 5 Morlet wavelet power spectrum of hourly average PM2.5 concentration on training set (201501‒201612)
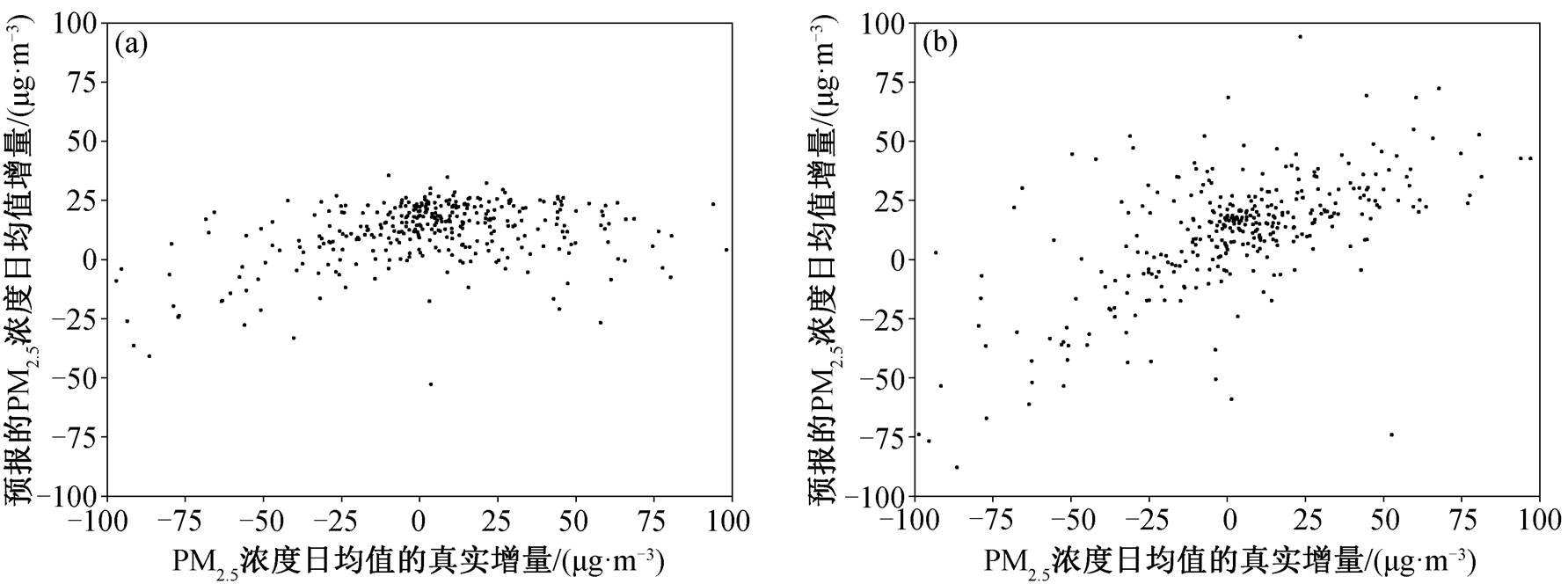
图6 日均值 LSTM 模型(a)和 6 小时平均值 LSTM 模型(b)预报结果散点图
Fig. 6 Scatter plot of LSTM model results using daily average input (a) and 6-hourly average input (b)
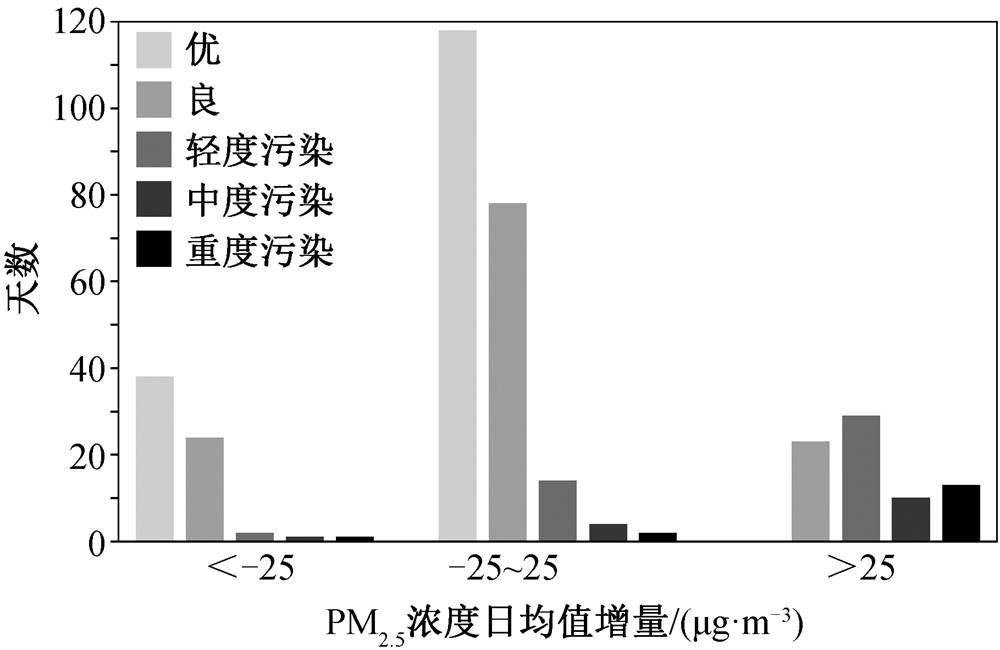
图7 不同增量下各污染等级天数分布
Fig. 7 Distribution of days of different pollution levels at different increments
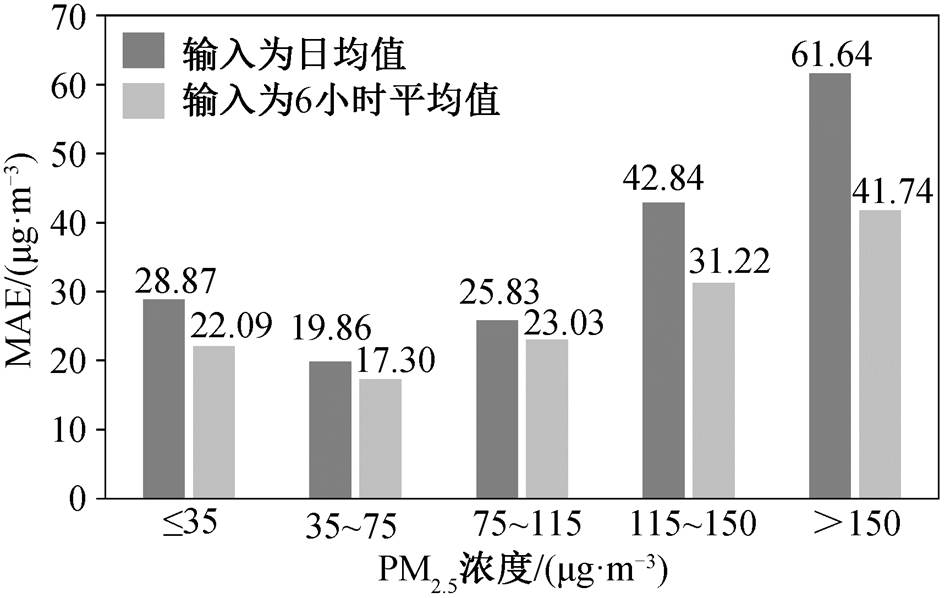
图8 不同 PM2.5 浓度等级下日均值 LSTM 模型和6 小时平均值 LSTM 模型的比较
Fig. 8 Comparison of LSTM model using daily average input and LSTM model using 6-hourly average input at different PM2.5 pollution levels
为了研究空间 PM2.5 浓度信息对单点 PM2.5 浓度预报的影响, 选取华北地区为研究对象, 将站点浓度进行克里金插值后, 对训练集和验证集(2015—2017 年数据)在该区域进行经验正交函数(em-pirical orthogonal functions, EOF)分析, 结果见图9。可以看到, 华北地区 PM2.5 浓度分布的主要模态为同增同减模态, 其解释方差为 50.2%。通过 PC1序列的变化可以看到 PM2.5 浓度明显的季节变化: 冬季一致增多, 夏季一致减少。PM2.5 浓度的第二模态则是南北反向变化的模态, 其解释方差为 9%。从 PC2 序列中可以看到, PM2.5 在冬季常常呈现北少南多的模态, 但是这种南北反向分布没有明显的季节变化。姚雪峰等[20]发现, 我国 PM2.5 浓度时空分布的第一模态(同增同减模态)主要受平均排放场和环流场以及大地形的影响, 而第二模态(南北反向分布模态)主要与冷空气活动影响, 与污染物输送有关。
既然在空间上邻近区域之间的 PM2.5 浓度相互影响, 那么空间 PM2.5 浓度信息对单点 PM2.5 浓度预报有何影响呢？为解答这个疑问, 我们利用 CNN-LSTM 模型学习空间信息, 并进行单点预报。为了便于比较, 模型输入为华北地区前 6 天每 6 小时PM2.5 浓度平均值, 预报数据仍然是北京市 PM2.5 浓度日均值。表 1 对比 6 小时平均值 LSTM 模型与 6小时平均值 CNN-LSTM 模型预报结果, 从可以看到, 前面表现最好的 6 小时平均值 LSTM 模型在各个指标上都差于 CNN-LSTM 模型, 说明提取空间PM2.5 浓度信息对单站 PM2.5 浓度的预报有明显的改善作用。为了进一步比较 CNN-LSTM 模型与 LSTM模型的预报效果, 同样对比各个 PM2.5 浓度等级的MAE。从图 10 可看出, 与 LSTM 模型相比, CNN-LSTM 模型显著地提升了优和重度污染 PM2.5 浓度等级下的预报能力, 对其他天气情况下的预报能力没有提升。
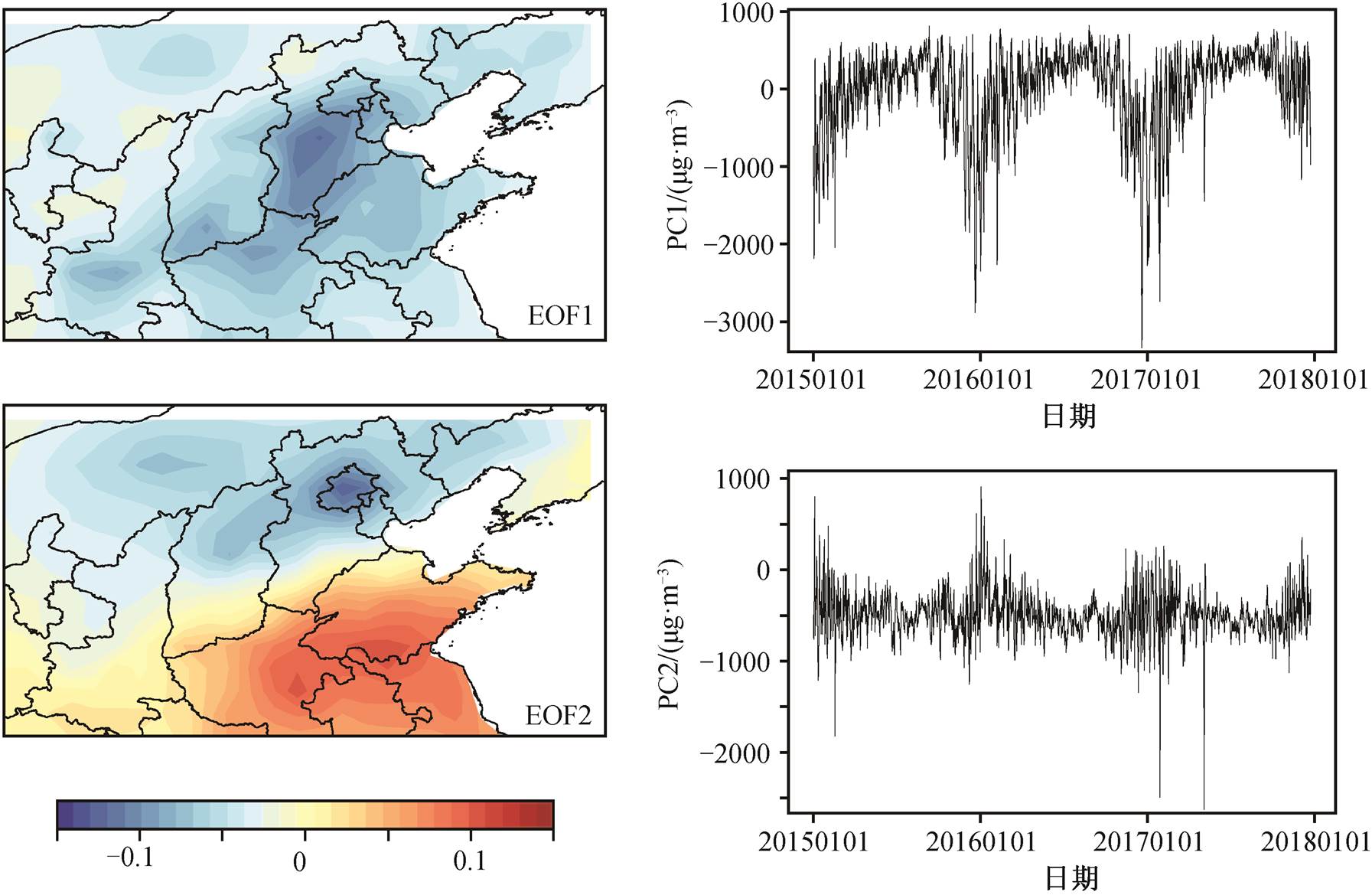
上行为第一模态, 下行为第二模态; 左列为PM2.5浓度的空间分布, 右列为对应的主成分
图9 华北地区 PM2.5 浓度的 EOF 分析结果
Fig. 9 Result of EOF analysis of PM2.5 concentration in North China
那么, 增加空间 PM2.5 浓度信息为何能提升优和重度污染时的预报效果呢?为了理解 CNN-LSTM模型预报效果更好的物理机制, 选择测试集中北京市 PM2.5 浓度日均值分别为低(优)、中(良、轻度污染)、高(中度和重度污染)的时刻, 对应每一个类别, 对它们做北京市 PM2.5 浓度与周边区域 PM2.5 浓度的时间滞后相关性分析, 得到的结果如图 11 所示。
表1 6 小时平均值 LSTM 模型与 CNN-LSTM 模型比较
Table 1 Comparison of LSTM model and CNN-LSTM model results when using 6-hourly average data as input
模型MAE/(μg·m−3)MAPE/%RMSE/(μg·m−3)IA/% LSTM20.5935.4729.3984.78 CNN+LSTM17.3631.6624.5490.68
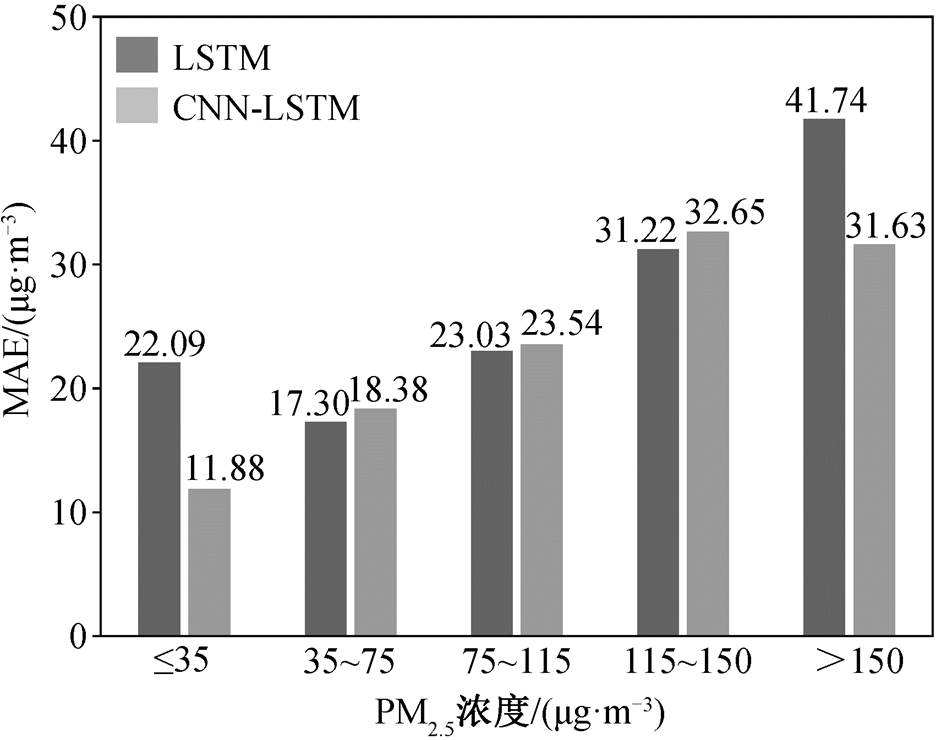
图10 不同 PM2.5 浓度等级下 LSTM 模型与 CNN-LSTM模型的比较
Fig. 10 Comparison of LSTM model and CNN-LSTM model at different PM2.5 pollution levels
当北京市 PM2.5 浓度日均值较低时, 与前 6 小时北京西北部地区的 PM2.5 浓度有相对强的相关性, 与前 12 小时更远的西北地区有相关性, 说明此时PM2.5 浓度的低值很可能是由北风造成。这种情况的典型例子是冬季冷空气南下对北京市 PM2.5 的清除过程[20]。研究表明, 包括 PM2.5 在内的污染物浓度与风速明显负相关[19, 21‒23], CNN-LSTM 模型可能就是捕捉到强北风天气下 PM2.5 浓度的空间变化过程, 从而提升对优良天气的预报能力。然而, 前 24小时的相关性在整个区域非常弱, 从侧面验证了提高时间精度可以捕捉更多的信息, 从而提高预报能力。
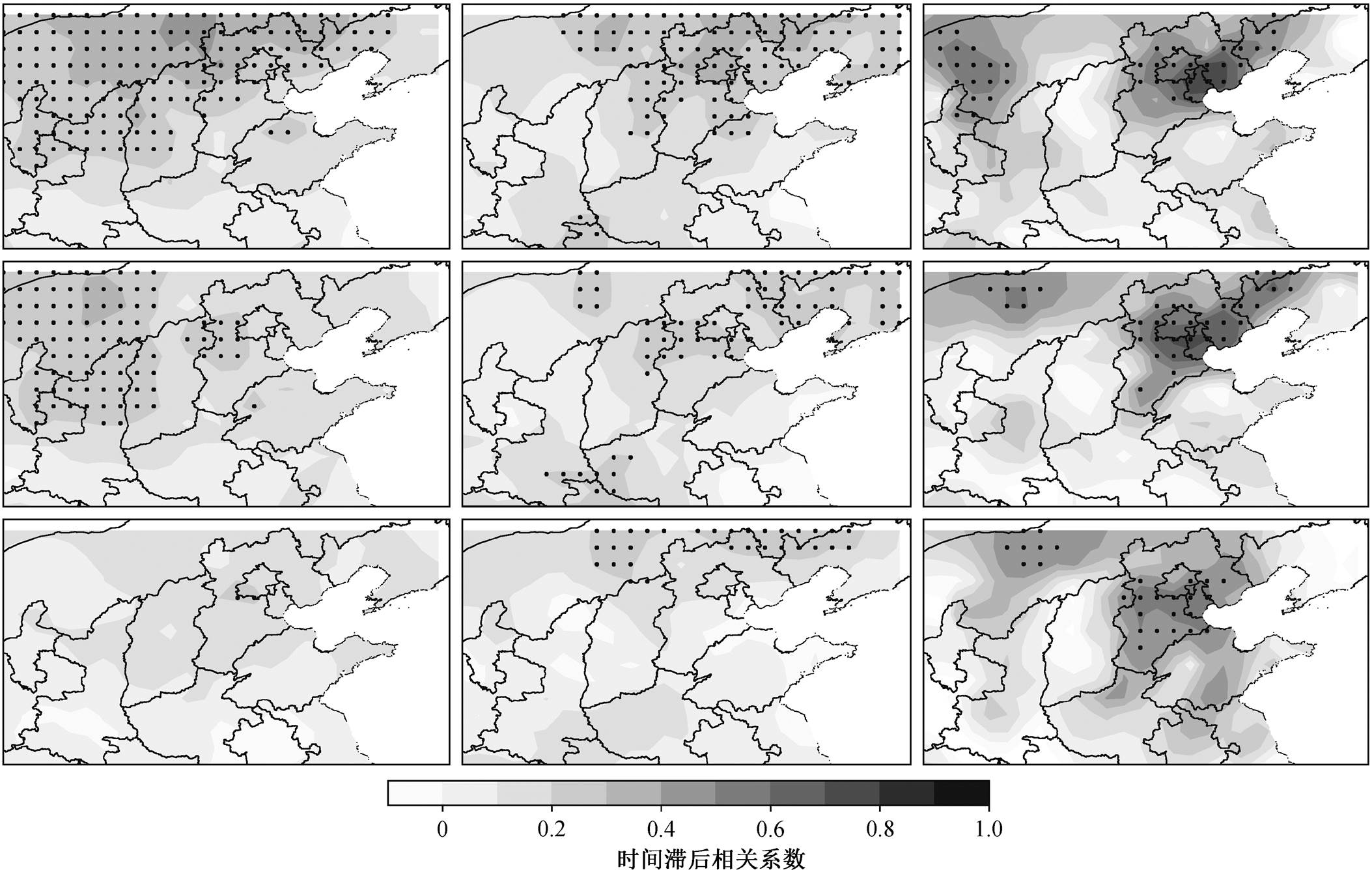
左、中、右列分别为北京市 PM2.5 浓度日均值低、中、高时的时间滞后相关系数空间分布, 上、中、下行分别为北京市PM2.5浓度与前 6, 12 和 24 小时周边区域PM2.5浓度的相关性, 黑色点区表示相关性通过 99%显著性检验。显著性检验由 T检验和 P值进行计算
图11 北京市 PM2.5 浓度与华北地区其他区域 PM2.5 浓度的时间滞后相关性
Fig. 11 Time-lagged correlation coefficient between PM2.5 in Beijing and other areas in North China
当北京市 PM2.5 浓度日均值较高时, 与前 6 小时的天津地区及河北东北部地区(唐山等地)有强的相关性, 与前 12 小时和前 24 小时的天津地区及河北中南部地区(廊坊等地)有显著的相关性。风场等气象条件不仅影响大范围内的 PM2.5 输送, 还影响局地 PM2.5 的累积和扩散[24]。因此, 上述空间相关性可能是由南风的 PM2.5 输送导致, 也可能是由天气系统的移动导致, 如冬季弱冷空气导致的污染物累积[20]。无论是哪种原因, 这种高度相关性能够通过 CNN-LSTM 模型挖掘出来, 从而提升对重度污染天气的预报能力。
对于北京市中等 PM2.5 浓度的情况, 北京市与周边地区的时间滞后相关性很差, 主要表现为显著的自相关。这种情况下, 前期的空间信息不会给北京市 PM2.5 浓度的预报带来额外的影响, 因此 CNN-LSTM 模型对北京市中等 PM2.5 浓度的预报效果并没有更好。
本文利用深度学习方法, 分析提高输入数据的时间精度和增加空间 PM2.5 浓度信息对北京市 PM2.5浓度日均值预报的影响, 并对这种影响可能的物理机制进行初步的分析, 得到以下结论。
1)对北京市 PM2.5 浓度日均值的预报, 神经网络模型普遍比多元线性回归模型效果好, LSTM 模型表现最佳。
2)与输入数据为 PM2.5 浓度日均值相比, 采用PM2.5 浓度 6 小时平均值作为输入数据能显著地提高 PM2.5 浓度日均值预报水平。原因主要是高精度的时间数据包含 24 小时以下周期的信息, 使得模型能更好地学习临近时刻 PM2.5 的显著增减变化, 从而提高对显著变好和显著变差天气的预报能力。
3)华北地区 PM2.5 浓度的时空分布有明显的特征: 第一模态为同增同减, 其时间序列体现 PM2.5浓度冬高夏低的季节变化; 第二模态为南北反向。
4)利用华北地区 PM2.5 浓度信息作为输入, 采用 CNN-LSTM 混合模型, 能够提升北京市 PM2.5 浓度日均值的预报水平, 且主要提高优和重度污染PM2.5 浓度等级下的预报效果。优和重度污染 PM2.5浓度等级下, 北京市 PM2.5 浓度与周边地区 PM2.5 浓度有较强的时间滞后相关性, CNN-LSTM 模型可以通过提取这种相关特征来提升预报能力。
最后, 将本文结果与前人的工作进行对比。由于地区、数据和模型构建等方面的不同, 对比结果仅作为参考。陈宁等[25]也考虑到空间因素对 PM2.5浓度预报的影响, 建立了北京市多基站协同训练的神经网络模型来预报 PM2.5 浓度, 并加入交通和土地等信息, 模型最终的 MAE 为 28.309μg/m3。刘杰等[26]增加神经网络模型的输入因子, 包括气象要素、其他污染物浓度和周期因素, 模型最终的 MAE为 27.6μg/m3 (BP)和 26.2μg/m3 (支持向量机)。Zhou等[11]利用 EEMD-GRNN 模型预报西安 PM2.5 浓度日均值的 MAE 为 19.80μg/m3。当然, 临近预报(如逐小时预报)会有更好的结果, 如 Huang 等[13]用一维卷积与 LSTM 的混合模型来预报北京市逐小时PM2.5 浓度的 MAE 为 14.63μg/m3。此外, 对污染物较少地区的 PM2.5 浓度预报也会更加准确。本文CNN-LSTM 模型最终的 MAE 为 17.36μg/m3, 这在PM2.5浓度日均值预报中比较有竞争力。
总之, 本文提出的提高时间精度和增加空间信息的方法, 可以明显地提高北京市 PM2.5 浓度日均值的预报能力, 预报水平相对于前人也有一定程度的提升。本文仅利用几个典型的统计和深度学习模型进行初步的探讨, 在未来的研究中需要采用更合理的模型来提升PM2.5浓度的预报能力。
参考文献
[1] He K, Yang F, Ma Y, et al. The characteristics of PM2.5 in Beijing, China. Atmospheric Environment, 2001, 35(29): 4959‒4970
[2] 杨新兴, 冯丽华, 尉鹏. 大气颗粒物 PM2.5 及其危害. 前沿科学, 2012, 6(1): 22‒31
[3] Pope Ⅲ C A, Burnett R T, Thun M J, et al. Lung cancer, cardiopulmonary mortality, and long-term ex-posure to fine particulate air pollution. JAMA, 2002, 287(9): 1132‒1141
[4] Sun Y, Zhuang G, Tang A, et al. Chemical character-istics of PM2.5 and PM10 in haze-fog episodes in Bei-jing. Environmental Science & Technology, 2006, 40 (10): 3148‒3155
[5] World Health Organization. Air Pollution, Climate and Health [EB/OL]. (2016‒02) [2019‒03‒24]. https:// www.who.int/sustainable-develoPMent/AirPollution_ Climate_Health_Factsheet.pdf
[6] Menon S, Hansen J, Nazarenko L, et al. Climate effects of black carbon aerosols in China and India. Science, 2002, 297: 2250‒2253
[7] Fuller G W, Carslaw D C, Lodge H W. An empirical approach for the prediction of daily mean PM10 con-centrations. Atmospheric Environment, 2002, 36(9): 1431‒1441
[8] Baker K R, Foley K M. A nonlinear regression model estimating single source concentrations of primary and secondarily formed PM2.5. Atmospheric Environ-ment, 2011, 45(22): 3758‒3767
[9] Sun W, Zhang H, Palazoglu A, et al. Prediction of 24-hour-average PM2.5 concentrations using a hidden Markov model with different emission distributions in Northern California. Science of the Total Environment, 2013, 443: 93‒103
[10] Saide P E, Carmichael G R, Spak S N, et al. Fore-casting urbanPM10 and PM2.5 pollution episodes in very stable nocturnal conditions and complex terrain using WRF-Chem CO tracer model. Atmospheric En-vironment, 2011, 45(16): 2769‒2780
[11] Zhou Q, Jiang H, Wang J, et al. A hybrid model for PM2.5 forecasting based on ensemble empirical mode decomposition and a general regression neural net-work. Science of the Total Environment, 2014, 496: 264‒274
[12] Liu X, Liu Q, Zou Y, et al. A self-organizing LSTM-based approach to PM2.5 forecast // International Con-ference on Cloud Computing and Security. Cham: Springer, 2018: 683‒693
[13] Huang C J, Kuo P H. A deep CNN-LSTM model for particulate matter (PM2.5) forecasting in smart cities. Sensors, 2018, 18(7): doi: 10.3390/s18072220
[14] Chaloulakou A, Grivas G, Spyrellis N. Neural net-work and multiple regression models forPM10 predic-tion in Athens: a comparative assessment. Journal of the Air & Waste Management Association, 2003, 53 (10): 1183‒1190
[15] Hochreiter S, Schmidhuber J. Long short-term me-mory. Neural Computation, 1997, 9(8): 1735‒1780
[16] 徐敬, 丁国安, 颜鹏, 等. 北京地区 PM2.5 的成分特征及来源分析. 应用气象学报, 2007, 18(5): 645‒654
[17] 李梓铭, 孙兆彬, 邵勰, 等. 北京城区 PM2.5 不同时间尺度周期性研究. 中国环境科学, 2017, 37(2): 407‒415
[18] Bartlett M S. On the theoretical specification and sampling properties of autocorrelated time-series. Supplement to the Journal of the Royal Statistical Society, 1946, 8(1): 27‒41
[19] 赵晨曦, 王云琦, 王玉杰, 等. 北京地区冬春 PM2.5和 PM10 污染水平时空分布及其与气象条件的关系. 环境科学, 2014, 35(2): 418‒427
[20] 姚雪峰, 葛宝珠, 郑海涛, 等. 基于多元数据分析的我国 PM2.5 浓度及其主控因子的时空分布特征研究. 气候与环境研究, 2018, 23(5): 596‒606
[21] Chen Y, Schleicher N, Fricker M, et al. Long-term variation of black carbon and PM2.5 in Beijing, China with respect to meteorological conditions and govern-mental measures. Environmental Pollution, 2016, 212: 269‒278
[22] Huang F, Li X, Wang C, et al. PM2.5 spatiotemporal variations and the relationship with meteorological factors during 2013‒2014 in Beijing, China. PloS One, 2015, 10(11): e0141642
[23] 张朝能, 王梦华, 胡振丹, 等. 昆明市 PM2.5 浓度时空变化特征及其与气象条件的关系. 云南大学学报(自然科学版), 2016, 38(1): 90‒98
[24] Li X, Zhang Q, Zhang Y, et al. Source contributions of urban PM2.5 in the Beijing-Tianjin-Hebei region: changes between 2006 and 2013 and relative impacts of emissions and meteorology. Atmospheric Environ-ment, 2015, 123: 229‒239
[25] 陈宁, 毛善君, 李德龙, 等. 多基站协同训练神经网络的 PM2.5 预测模型. 测绘科学, 2018, 43(7): 87‒ 93
[26] 刘杰, 杨鹏, 吕文生, 等. 基于气象因素的 PM2.5 质量浓度预测模型. 山东大学学报(工学版), 2014, 45(6): 76‒83
Impacts of Temporal Resolution and Spatial Information on Neural-Network-Based PM2.5 Prediction Model
Abstract Taking Beijing as an example and using the data of air quality monitoring stations from 2015 to 2018, the impacts of temporal resolution and spatial information on the PM2.5 concentration prediction were analyzed by a BP neural network, an LSTM network, and a CNN-LSTM hybrid model. The results show that neural network models are generally better than the multi-linear regression model. Increasing the temporal resolution of the input data can significantly improve the accuracy of the predicted daily average PM2.5 concentration. When the temporal resolution of the input data increases from one day to 6 hours, the mean absolute error of the LSTM model reduces from 27.39 μg/m3 to 20.59 μg/m3. This improvement is more obvious when the weather is significantly getting better or getting worse. The distribution of PM2.5 concentration in North China has distinct spatial and temporal characteristics. The first spatial mode is a uniformly increasing or decreasing mode, and the second one is a north/south dipole mode. The analysis shows that the concentration of PM2.5 in Beijing is related to the PM2.5 in Inner Mongolia, Hebei, and Tianjin of the previous day. The CNN-LSTM hybrid model, trained with the spatial-temporal information of PM2.5 in North China, can further improve the predictability of PM2.5 in Beijing. It further reduces the mean absolute error to 17.36 μg/m3.
Key words neural networks; PM2.5 prediction; temporal resolution; spatial characteristics
doi: 10.13209/j.0479-8023.2020.012
国家自然科学基金(41476008)和广西壮族自治区特聘专家专项经费(2018B08)资助
收稿日期: 2019‒05‒08;
修回日期: 2019‒08‒10