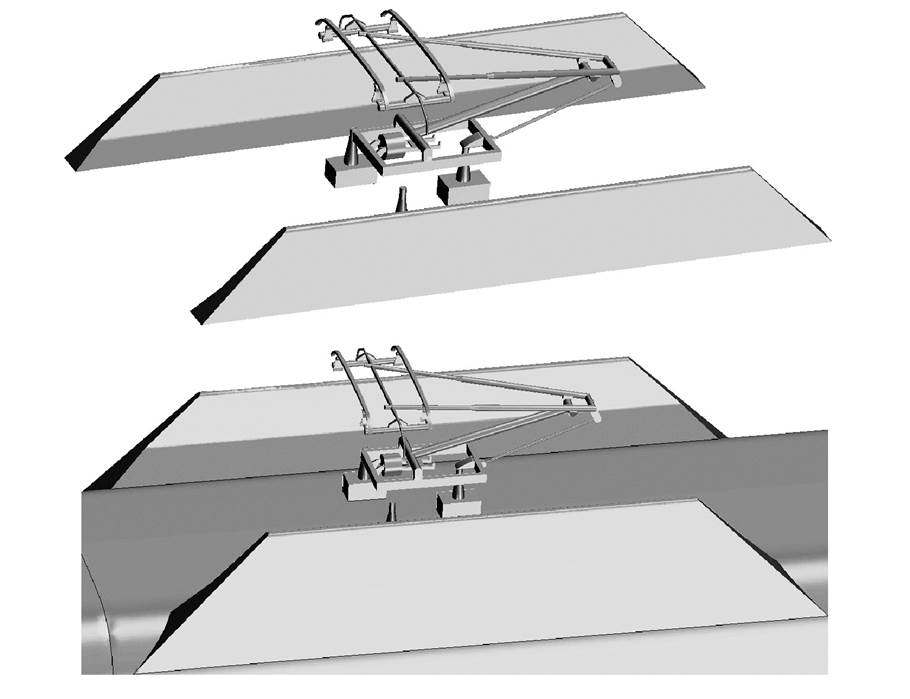
图1 受电弓不同安装情形
Fig. 1 Different installation scenarios of pantograph
摘要 以某高速列车受电弓为研究对象, 探讨其在 350km/h 速度下的气动噪声特性。采用延迟脱体涡模拟(DDES)和声学有限元(FEM)相结合的方法, 分析带导流罩受电弓在升起和下降状态下, 近场和远场气动噪声空间分布规律和频谱特性, 研究流场计算时不同建模方式对诱发噪声幅值和指向性的影响以及壁板的反射和散射作用对噪声频谱特性的影响。结果表明: 1)在本文选取的受电弓外形和开口方向下, 降弓和导流罩诱发噪声略大于升弓和导流罩诱发噪声; 2)导流罩在低于 300Hz 的低频区诱发噪声比例较大, 而受电弓在 300Hz后诱发噪声影响较大; 导流罩诱发噪声在升弓情形时所占比例相对较大; 3)在指向性上, 导流罩诱发噪声在受电弓前部贡献较大, 受电弓诱发噪声在后部区域贡献较大; 在列车正上方区域, 弓体诱发噪声大于导流罩诱发噪声, 是主要的气动噪声源。
关键词 高速列车; 受电弓; 气动噪声; 脱体涡模拟; 声学有限元
随着高速列车速度的提高, 很多低速时可以忽略的问题变得不容忽视, 高速列车气动噪声问题更加突出。张曙光[1]的研究表明, 当高速列车运行速度超过 250 km/h时, 气动噪声超过牵引噪声和轮轨噪声, 占据主导位置, 并与列车运行速度的六次方成正比。因此, 需要更好地了解气动噪声特性, 缓解气动噪声问题。
国内外学者对高速列车室外气动噪声进行了数值仿真和相关实验研究。在数值方法上, 分为直接法和混合法。直接法通常采用直接数值模拟(direct numerical simulation, DNS)、大涡模拟(large-eddy simulation, LES)或者分离涡模拟(detached eddy simulation, DES), 流场和声场的计算同时进行。由于声压与流场中的动压相比非常小, 所以一般采用高阶精度、低耗散和低色散的离散格式, 以便保证解的精度。然而, 高速列车的形状相当复杂, 直接法会带来庞大的计算成本。对于混合方法, 近场声源和远场声传播分别求解, 采用 LES, DES 或其他湍流模型求解波动压力, 利用声学方法(包括Ffowcs Williams&Hawkings (FW-H)、声学边界元(boundary element, BEM)以及声学有限元(finite element, FEM)等)对压力波动进行分析, 求解声传播问题。混合计算方法节约计算成本, 效率较高, 在实际工程中应用广泛。
相关学者采用混合方法对高速列车气动噪声进行研究。孙振旭等[2]分别采用非线性声学求解方法和 FW-H 方程, 计算简化 CRH3 型高速列车近场与远场气动噪声特性, 并对关键部位噪声水平进行综合评估, 表明头部和尾部是主要噪声源, 列车结构上有凹槽的粗糙区域和车体连接区也是造成空气动力噪声的主要原因。Xiao 等[3]采用参数化建模方法, 基于遗传算法构造 Kriging模型等优化技术, 降低简化 CRH3 的气动噪声, 采用非定常不可压缩分析方法, 得到列车表面的脉动压力, 应用 FW-H 声学模型对列车表面远场噪声进行预测, 发现优化列车外形可以降低气动噪声。通过同样的噪声求解方法, 刘加利等[4]研究简化高速列车头部气动噪声源和远场噪声频谱特征, 证明优化列车头部和车体的形状可以大大降低空气动力噪声。除对简化列车外形气动噪声的研究, 朱剑月等[5]和孙艳军等[6]考虑转向架和受电弓等复杂车体结构对噪声影响, 发现高速列车气动噪声源主要为受电弓、转向架及车头和车尾。King[7]采用偶极子点声源描述受电弓漩涡脱离导致的气动噪声, 发现受电弓远场气动噪声与车速的对数为近似的线性关系。Takaishi 等[8–9]利用延迟脱体涡模拟和涡声理论, 数值模拟转向架和受电弓表面的偶极子噪声源分布。Yoshiki 等[10]利用格子 Boltzmann 方法对受电弓气动噪声进行计算, 结果与风洞试验结果吻合较好。在实验分析方面, Kitagawa 等[11]和 Nagakura 等[12]的实验表明, 受电弓和转向架产生气动噪声是高速列车路边噪声的主要来源。Noger 等[13]通过风洞实验, 发现受电弓背部垂直面是重要的噪声源区域。Iwamoto 等[14]结合理论研究和现场试验结果, 提出降低受电弓气动噪声的方法。Zhang 等[15]采用 CFD/FW-H 声学模拟与边界元法相结合的方法, 对受电弓的气动噪声进行分析, 发现受电弓顶部区域为主要的气动噪声源, 而不是底部区域, 还发现受电弓开口方向与运动方向相反时产生的噪声比开口方向与运动方向相同时低 3.4 dBA。
目前, 对于高速列车气动噪声的研究集中于两个方面: 1)气动噪声源确认, 定性认识不同噪声源对于高速列车气动噪声的影响; 2)对不包含受电弓、转向架和导流罩等复杂结构的简化车型进行整体气动噪声分析, 探究车体头尾部位及车厢连接方式对气动噪声的影响。对于受电弓和转向架等极易引发气动噪声的复杂部位产生的噪声特性探究有待进一步深入。在流场计算方面, 以往学者对受电弓气动噪声的分析并未考虑车身对受电弓噪声的影响, 仅对独立受电弓做流场分析, 得到声学方程求解的边界条件求解噪声; 另外, 在计算受电弓噪声辐射方面, 极少考虑车身和导流罩等壁面结构对于声波的反射和散射作用。
本文建立包含受电弓及所在车身的声学有限元模型, 结合脱体涡模拟和声学有限元方法, 对带受电弓的高速列车气动噪声源进行数值计算。流场计算中考虑车体对受电弓流场的影响, 声场计算中考虑车身和导流罩壁面对噪声的反射和散射作用。本文探究流场计算建模方式和声场计算壁面作用对噪声的影响, 并对不同受电弓系统的频谱特性和分布规律进行分析, 旨在为高速列车受电弓系统的气动特性和噪声特性的合理分析提供参考。
由于受电弓区域流场受列车车身流场的影响, 且车身对流场及气动噪声的影响情况不明确, 为了选用更合适的流场计算模型来做进一步的噪声分析, 本文首先以升弓情形为例, 建立不同流场计算模型。本文建模时忽略转向架和风挡的影响, 图 1分别为独立受电弓模型和带受电弓的三编组列车模型, 对于带受电弓的三编组列车模型, 保留受电弓主要气动特性影响部件, 包括绝缘子、基座、下臂杆、推杆、上臂杆和双滑板。
在计算高速列车噪声时, 常用声源和声学基本方程相结合的混合计算方法。声源计算中运用最多的是 LES 和 DES。LES 直接模拟大尺度脉动涡, 小尺度涡对大尺度涡运动的影响通过亚格子尺度模型来模拟[16]。DES 将 RANS 和 LES 相结合进行求解, 边界层内流动特性由 RANS 求解, 分离区流动特性由 LES 求解[17]。二者求解流场控制方程的机理不同, 对计算域网格、时间步长和计算资源的要求也不相同。与直接法相比, 混合方法的计算量明显减小, 但声源计算因采用 LES 方法, 计算量依然庞大。在流场计算中, 当网格量相当时, LES 比 DES的计算时长要长, DES 对壁面边界层内尺度和强度较大的湍流脉动模拟精度与 LES 相当[18]。本文的瞬态流场计算中, 采用经过发展的延迟脱体涡模拟(DDES)进行气动力计算。远场噪声求解采用声学有限元方法。在声学求解阶段, 截取带受电弓的中间车部分做声学网格, 将近场 CFD 瞬态模拟获取的列车物面边界脉动压力时间历程转换到频域, 构成声学方程求解边界条件, 进一步求解远场噪声。
声场计算采用 FEM 方法, 目的在于更加真实地模拟实际的气动噪声, 能够对工程中的气动噪声做更全面的预测。可以考虑结构的反射和散射, 计算流体载荷作用引起的结构辐射噪声(流固耦合噪声)以及材料的吸声特性等[19–20]。

图1 受电弓不同安装情形
Fig. 1 Different installation scenarios of pantograph
分离涡模拟方法由 Spalart 等[21]提出, 将 LES方法与 SA 模型相结合, 通过对当地网格尺度与壁面距离进行对比, 对两种方法自动切换。Strelets[22]借鉴 Spalart 等的思想, 将 DES 方法引入 SST 模型, 对当地网格尺度与湍流长度尺度进行对比, 实现求解。2006 年, Spalart 等[23]借鉴 Menter[24] 的 SST 模型构造思想, 采用“延迟 LES 函数”发展出 SST-DDES方法。SST-DDES控制方程[24]可写为
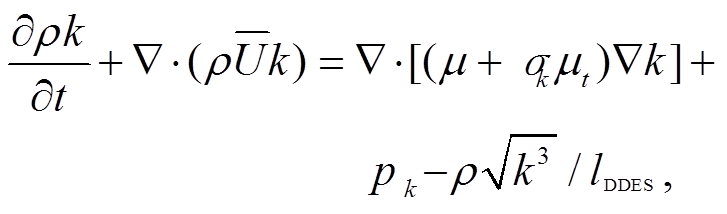 (1)
(1)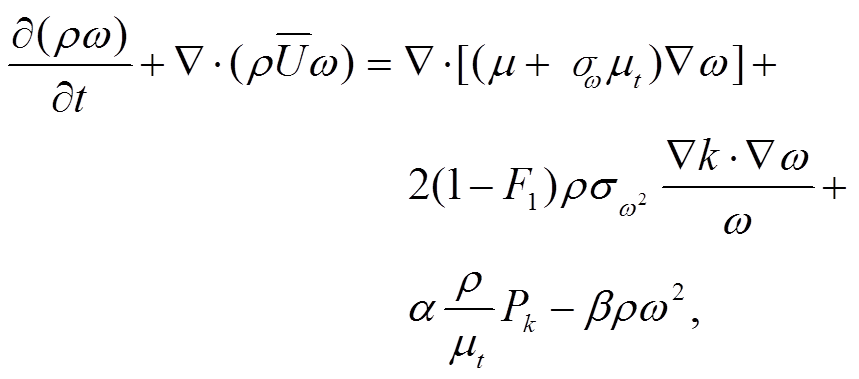 (2)
(2)
其中, k是湍动能,  是速度,
是速度, 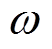 是耗散比率, v是运动粘度, t 是时间,
是耗散比率, v是运动粘度, t 是时间, 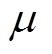 是黏性系数,
是黏性系数, 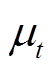 是湍流黏度系数, pk是湍流产生项, lDDES为 DDES 长度尺度, S是应变率张量大小。F1和F2表示 SST 混合函数:
是湍流黏度系数, pk是湍流产生项, lDDES为 DDES 长度尺度, S是应变率张量大小。F1和F2表示 SST 混合函数:
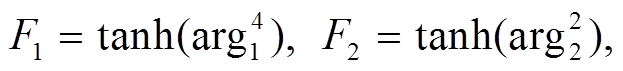
 (3)
(3)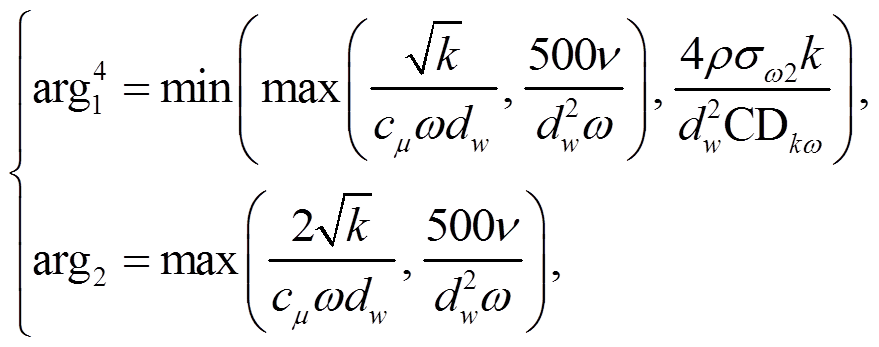 (4)
(4)
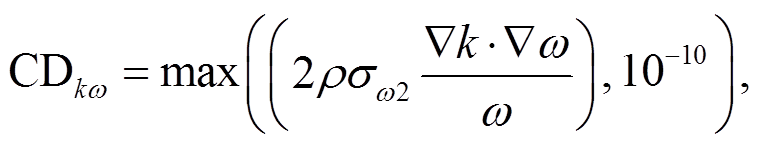 (5)
(5)
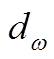 是到最近壁面的距离, DDES尺度为
是到最近壁面的距离, DDES尺度为
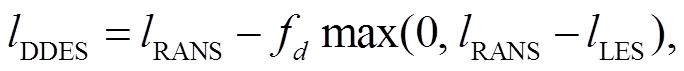 (6)
(6)
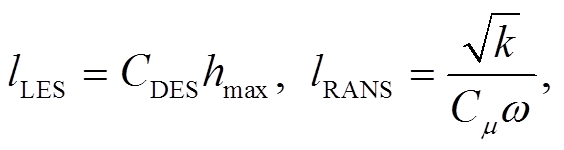 (7)
(7)
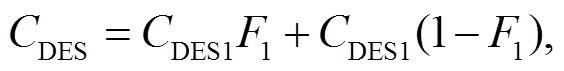 (8)
(8)hmax是单元的最大边长, fd是经验函数, 常用的表达式为
 (9)
(9)
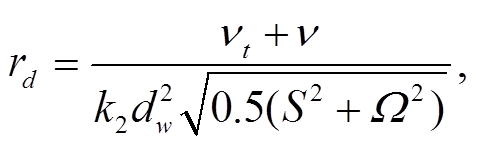 (10)
(10) 是涡量张量值。模型中常数的数值为
是涡量张量值。模型中常数的数值为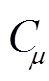 =0.09, k=0.41, a1=0.31, CDES1=0.78, CDES2=0.61, CD1=20, CD2=3。
=0.09, k=0.41, a1=0.31, CDES1=0.78, CDES2=0.61, CD1=20, CD2=3。
有限元和边界元方法[25]均可用于声场辐射分析, 且均可考虑障碍物对声波的反射和散射作用。有限元法的基本思想是在连续体域内划分单元, 而声学边界元法(BEM)只在定义域的边界上划分单元, 进行离散, 使积分方程成为只含边界节点未知量的代数方程组。目前, 较多学者在外场气动噪声的计算中使用声学边界元方法[15,26–27]。与有限元法相比, 声学边界元法具有使分析问题降维、单元个数少和数据准备简单等优点, 便于处理无限域和半无限域问题。但是, 由于边界元法建立的求解代数方程组的系数阵是非对称满阵, 对求解规模产生较大的限制。在处理高速列车气动噪声辐射问题时, 如果考虑车身板块的反射作用, 对车身部分也必须制作声学网格, 则声学边界元方程求解矩阵变得非常庞大, 导致无法计算。采用声学有限元方法, 基于 virtual lab 声学计算模块中的 FEMO (FEM Adaptive Order solver)算法, 可以利用相对较粗的网格达到计算精度, 提高计算效率。
对于声学有限元法, 声场压力满足 Hemholtz方程:
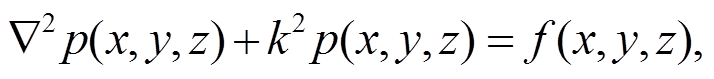 (11)
(11)其中, p(x, y, z)为声场压力, k为波数。针对噪声的处理主要采用Fourier变换分析, 压力波的振幅平方表示为
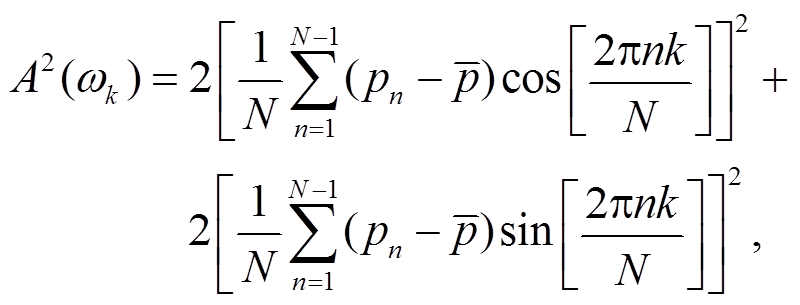
 (12)
(12)
其中, Pn 为数据集, 此处为第n步的脉动压力, n= 0, …, N–1。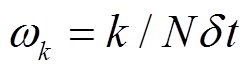 ,
, 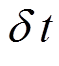 为时间步长。声压级(sound pressure level)定义为
为时间步长。声压级(sound pressure level)定义为
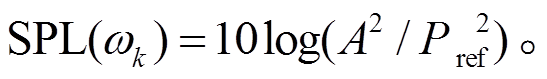 (13)
(13)其中,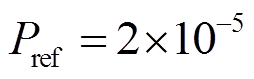 Pa。
Pa。
图 2 为两类模型流场计算网格, 计算域足够大以便消除边界对计算结果的影响。以车体高度H=3.55m 为基准, 对于独立受电弓模型, 计算域尺寸为 10H×5H×2.5H; 对于带受电弓三节车模型, 计算域尺寸为50H×20H×10H。
均采用 Trimmer 网格划分方法, 网格布局如图3 所示, 首层厚度为 0.05mm, 网格增长率为 1.2, 边界层为 10, 受电弓表面网格尺寸不超过 10 mm, 受电弓和导流罩表面网格量约为 60 万, 对受电弓所在区域及后部做加密处理。
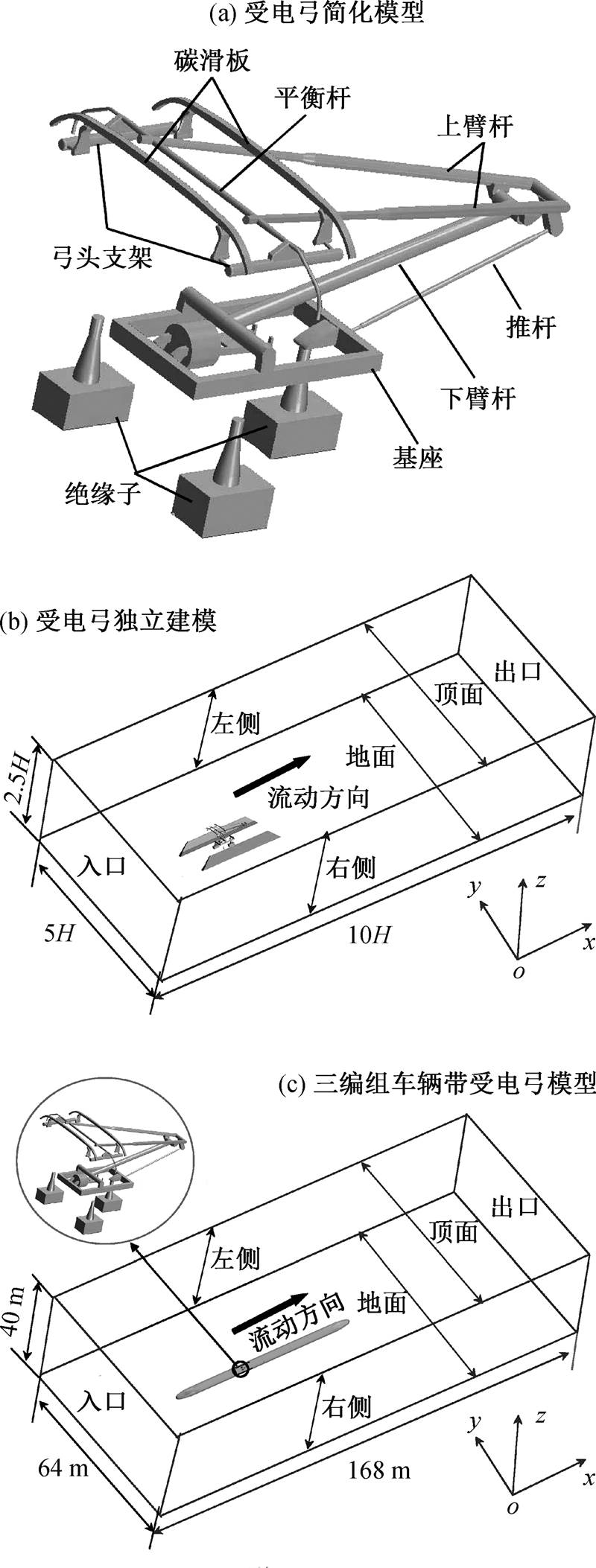
图2 几何模型及流场计算模型
Fig. 2 Simplified model of pantograph and computational domain for flow field

图3 流场计算网格布置
Fig. 3 Distribution of spatial meshes
独立受电弓模型网格总量约为 800 万, 带受电弓的三节车模型网格总量约为 3200 万。流场计算物理时间步长设为 10–4s, 内迭代 20 步, 在大部分计算域内 CFL(CFL=uΔt/Δx)小于 1, 以确保在每个时间步内计算收敛。计算的边界条件如下: 1)列车车体表面为固定壁面, 无滑移, 无穿透条件; 2)远场由特征线方法给出, 给定来流速度(即负的列车速度); 3)地面为移动壁面、无滑移、无穿透条件, 速度同来流速度。本文仅考虑偶极子声源噪声, 事实上, 其空间有复杂的涡旋结构(即四极子声源), 也会对噪声产生影响, 但本文中列车运行速度为 350km/h, 马赫数较低, 产生的噪声占比不大, 分析时可以忽略其影响。计算偶极子声源产生的远场噪声时, 需要保存噪声面的时变数据; 计算带导流罩受电弓诱发噪声时, 将受电弓和导流罩均视为声源面。
选取如图 4 所示的监测点, 以弓本身中心点为参考(x=0), 远离车体, 垂直向外测区域, 每隔 5m取一个监测点, 如图中 y1~y6 所示, 分别表示 y=5m至 y=30m; 在距离轨道中心 25m 远, 3.5m 高的水平线上, 每隔 5m 取一个监测点, 如图中 x1~x5 所示, 其中, x2 与 y5 重合。
由于受电弓上很多结构都可与圆柱类比, 本文通过圆柱绕流算例, 验证 FEM 声学方程求解方法的有效性。验证模型为直径 D=10mm 的圆柱, 展向长度为 πD, 来流速度 U0=72m/s, 雷诺数 Red= 4.8×104(以圆柱直径 D 为特征长度, 来流速度为特征速度)。外场距圆心 15D, 采用 trimmer 网格划分方法, 首层厚度为 0.0035mm, 网格增长率为 1.1, 圆柱表面网格尺寸为 0.25mm, 计算模型网格总量约为 600 万。计算边界条件(即压力远场边界条件)如图 5 所示, 其中 U0=72 m/s, 垂直圆柱延伸方向的前后平面为周期性边界条件。计算马赫数为 0.21, 流场计算采用延迟脱体涡模拟(DDES)湍流模型, 压力和速度耦合求解采用 Simple 算法, 离散得到的代数方程使用 Guass-Seidel 迭代求解。选用声学有限元法求解远场噪声, 为了与实验值进行比较, 远场噪声需要通过 Kato 方程[28]修正, 原因是实验中圆柱展长较大, 数值模拟时为节约计算资源展长长度较小, 噪声监测点位置为圆柱正上方 185D。
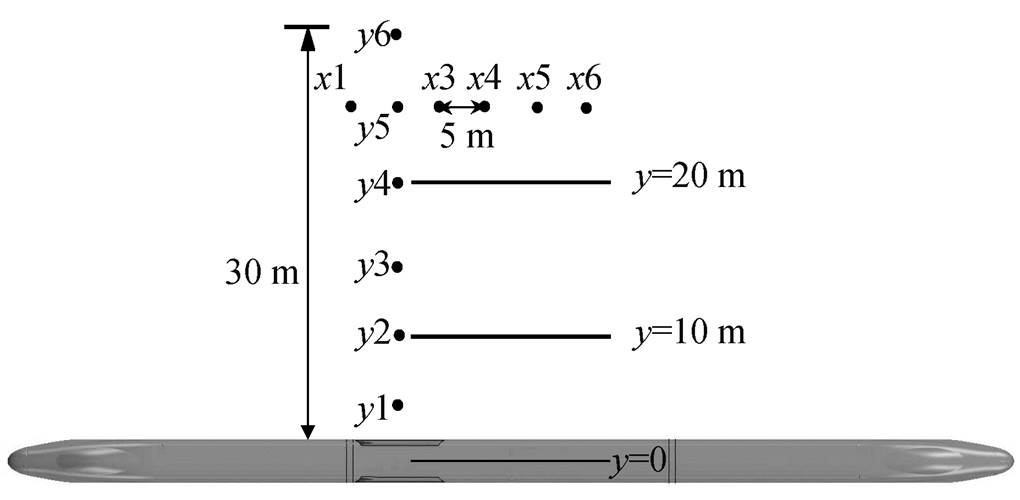
图4 噪声监测面及监测点
Fig. 4 Monitoring surface and point of the noise

图5 圆柱扰流计算几何模型及网格
Fig. 5 Calculation geometry model and grid of cylinder turbulence
图 6 显示圆柱下游背风侧漩涡的产生、发展以及脱离情况。沿流动下游方向, 各漩涡的起始位置交替变化。可以看出, 背风侧涡主要是由圆柱壁面流经的气流在离开背风侧壁面时形成, 涡系在产生、发展和脱落过程中产生噪声。图 7 为远场监测点的声压级图谱, 可以看到 FEM 计算所得涡脱落频率对应的斯特劳哈尔数 St 与实验值[29]和其他数值计算结果[30–31]基本上吻合, 说明在本算例中采用 FEM 对单圆柱远场噪声求解是有效的。
为了对流场计算选用的 DDES 模型和声场数值模拟选用的 FEM 方法进行验证, 本文增加双圆柱流场模拟, 将下游圆柱表面的压力系数和监测点噪声值与测量结果和其他文献进行对比。计算模型如图 8 所示, 圆柱直径 D 为 0.05715m, 圆柱之间的间隔距离 L 为 3.7D, 展向长度为 3D。采用 trimmer 网格划分方法, 第一层厚度为 0.001mm, 壁面法向生增长率为 1.2, 柱面网格尺寸为 1mm, 网格总量约为 850 万。边界条件为均匀速度入口 44m/s, 压力出口以大气压力为参考压力, 其他平行面为对称边界条件。流场及声场计算方法与单圆柱计算相同。图 9(a)显示圆柱下游背风涡的产生、发展和分离情况。本文选取下游圆柱表面 θ=45°(从上游开始测量, 顺时针方向为正)的压力系数均方根值(Cprms)与美国宇航局兰利研究中心在消声风洞的静流动设施(QFF)上得到的测量结果[32]和文献[33]中部分结果进行比较, 结果如图 9(b)所示。可以看出, 本文在流场计算中选用的 DDES 数值计算方法, 结果基本上满足计算精度。以第一个圆柱中心为坐标参考原点, 监测 X-Y 平面内位于(9.11D, 32.49D) 处的噪声,并与文献[32–33]的计算和试验结果相比较, 如图 10所示。可以发现, FEM声学计算方法对较为复杂的双圆柱扰流噪声计算是有效并合理的。
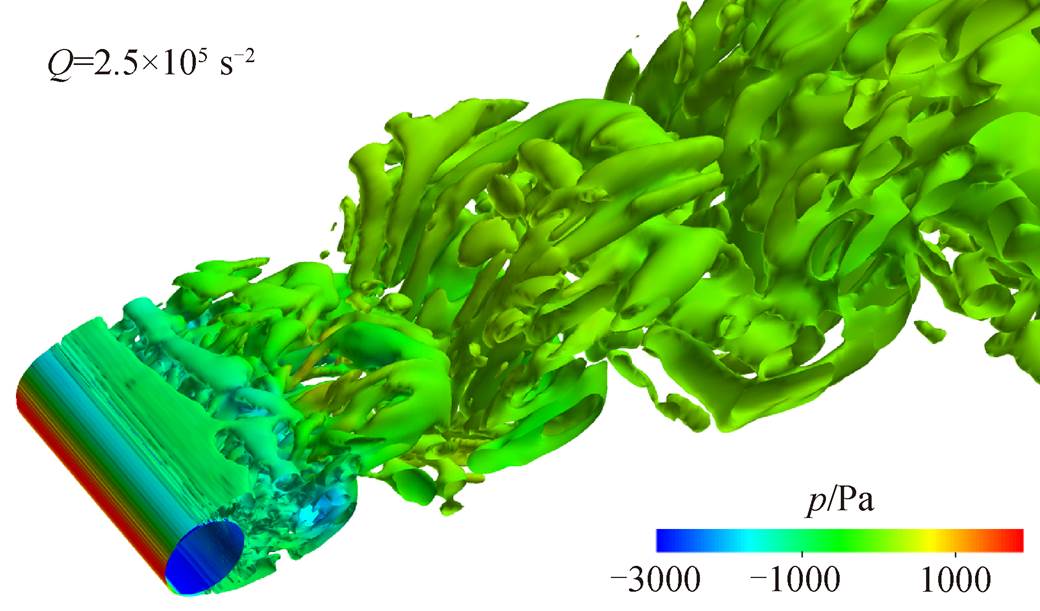
图6 圆柱周围涡量图
Fig. 6 Iso-surface of the instantaneous normalized Q-criterion of cylinder
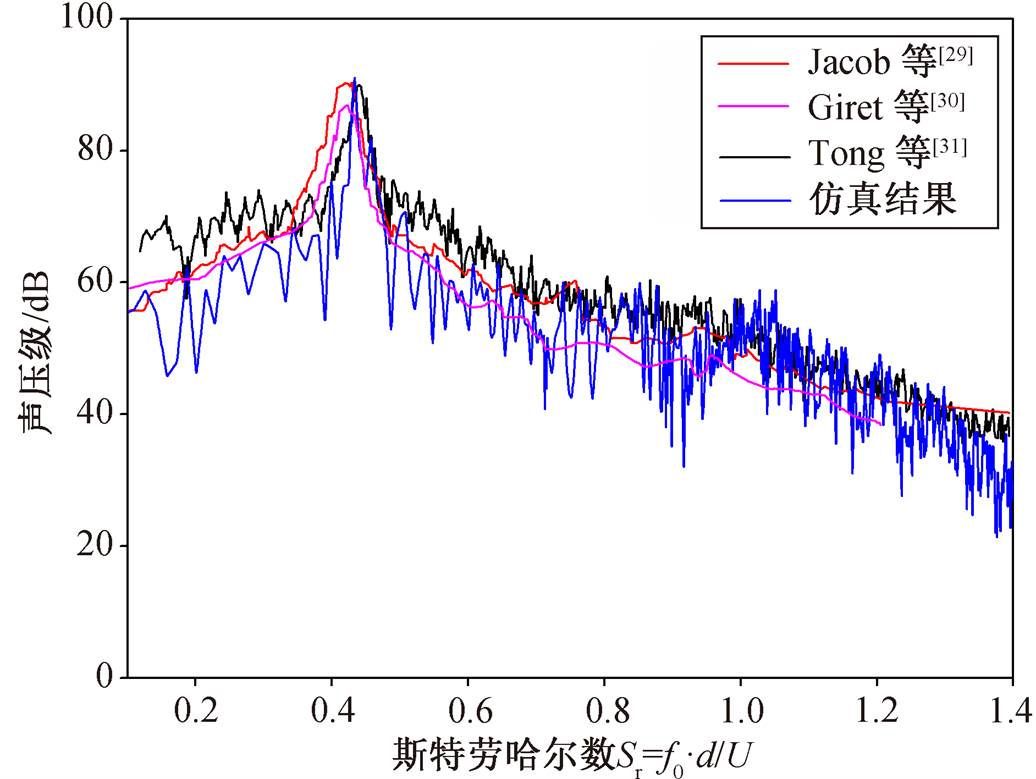
图7 圆柱正上方185D处噪声经Kato理论修正后的结果
Fig. 7 Results of noise at 185D above the cylinder corrected by Kato theory
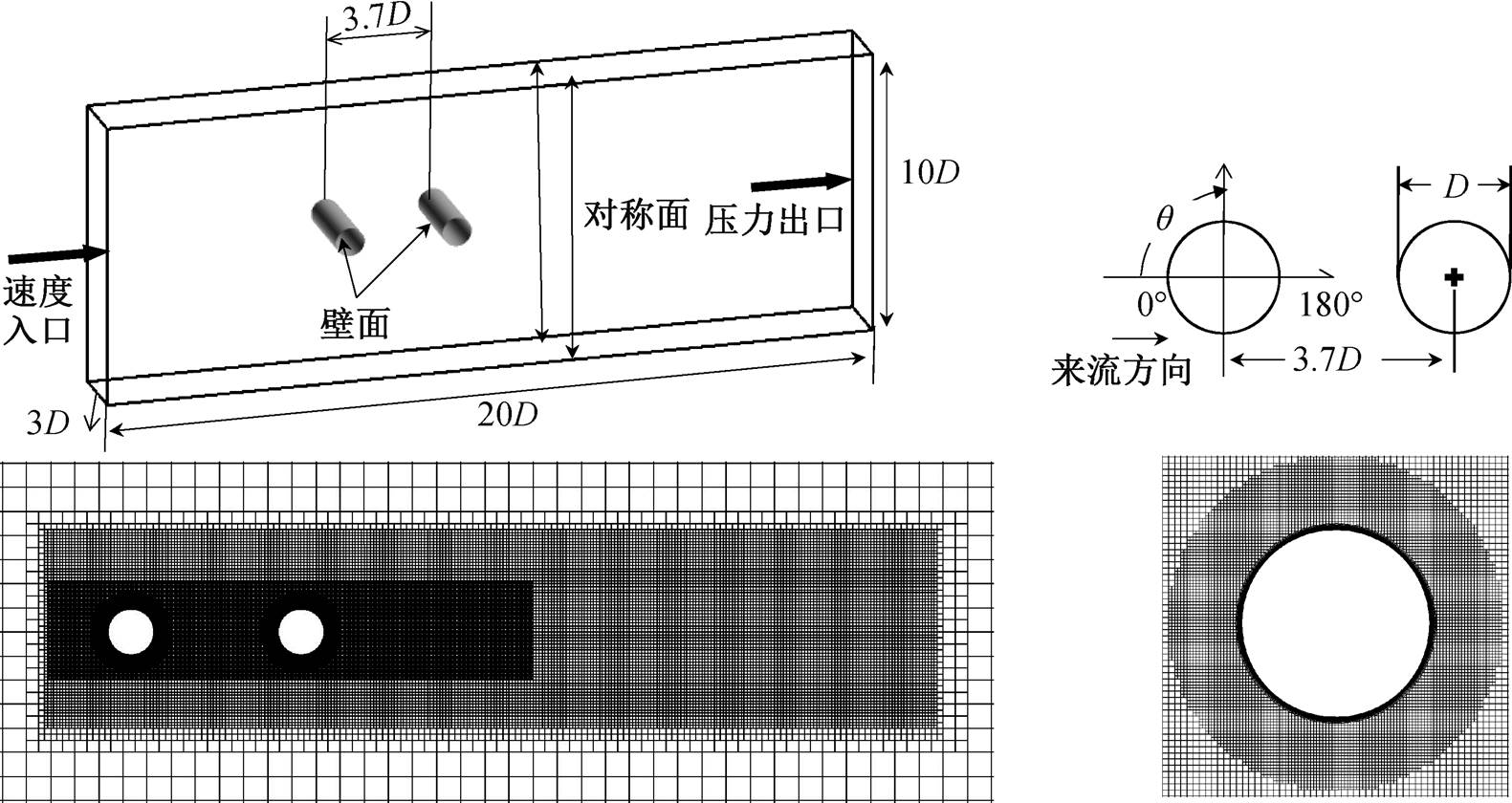
图8 双圆柱扰流计算外场及网格分布
Fig. 8 Geometry and computational domain for flow field.
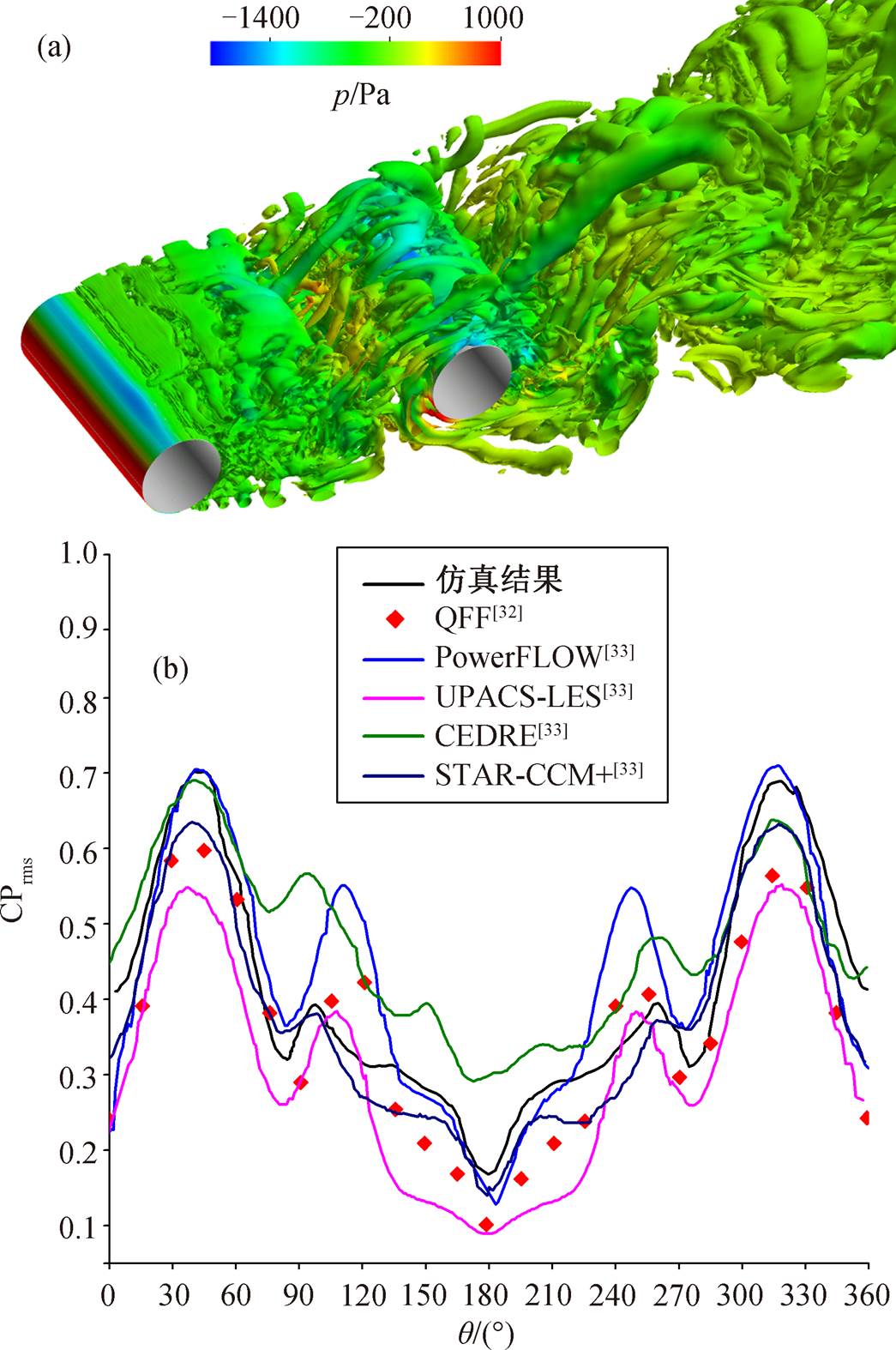
图9 双圆柱扰流等 Q图(Q=10000)(a)和下游圆柱表面压力系数均方根值(Cprms) (b)
Fig. 9 Instantaneous iso-surface normalized Q-criterion (Q = 10000) (a) and the root-mean-square on the cylinder downstream surface (b)
3.1.1 建模方式对流场的影响
受电弓表面压力的分布情况与脉动压力相关。先对受电弓表面压力分布情况进行分析, 如图 11所示。两类建模方式均在受电弓迎风面速度滞止, 形成高压区, 在背风面呈负压状态。在基座和导流罩与车体连接处, 两类建模方式的压力分布有所差异, 主要是因为将弓体安装于三编组车体上, 随气流向后运动, 边界层增厚导致的。
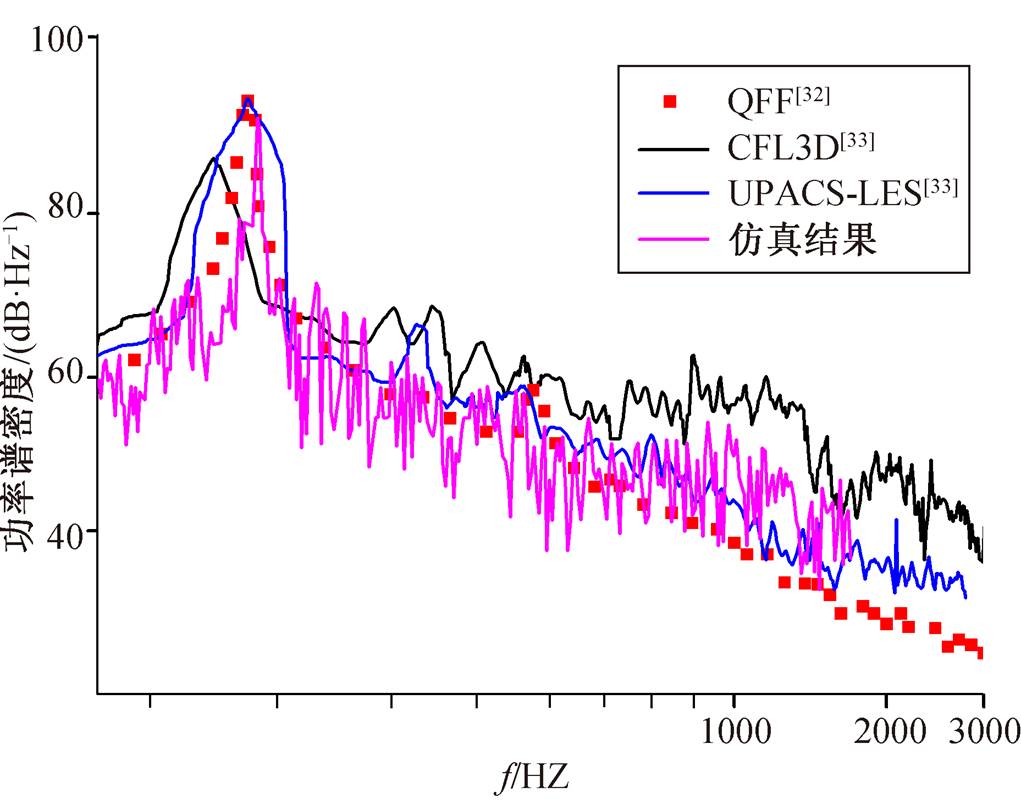
图10 远场监测点位于(9.11D, 32.49D)处的噪声
Fig. 10 Results of noise located at (9.11D, 32.49D)

图11 受电弓及周围区域压力云图
Fig. 11 Pressure contours on the symmetry plane
从图 12 和 13 所示的受电弓对称面涡量图和等Q 图可以看到, 单独受电弓模型和带受电弓三辆编组模型流动特性的共同点在于, 都在构件表面存在流动分离, 受电弓尾流区都有如下流动特性: 1)各杆件下游旋涡脱落, 脱落涡相互干扰, 出现非常明显的不同尺度的发卡涡; 2)强干扰形成强湍流, 气流湍化程度较高, 形成重要气动噪声源; 3)受电弓各个部件以及导流罩诱发的涡相互作用, 相互影响, 形成复杂的尾流结构。两类建模情况在受电弓及后方诱发涡旋的不同点在于, 将弓体安装于三编组车体上, 随气流向后运动, 边界层增厚, 下方 3 个绝缘子被边界层包裹, 基座后方的旋涡强度被削减, 同时, 由于来流在与前方车体的接触中得到缓冲, 使得冲撞到弓头和基座等之后, 进一步诱发的涡旋强度也有所减弱。在单独受电弓模型中, 来流与弓体直接相撞, 在弓头、基座和绝缘子后方均可看到更大强度的涡旋。声波的产生与流体中的涡旋、势流以及涡旋之间的相互作用密切相关。两类建模方式导致受电弓后方涡旋有不同的特性, 涡旋产生与脱落的相互作用使弓体和导流罩表面压力发生变化, 产生脉动压力, 进一步诱发受电弓气动噪声, 导致噪声结果有差异。

图12 受电弓及周围区域在对称面上的涡量图
Fig. 12 Instantaneous vortices on the symmetry plane
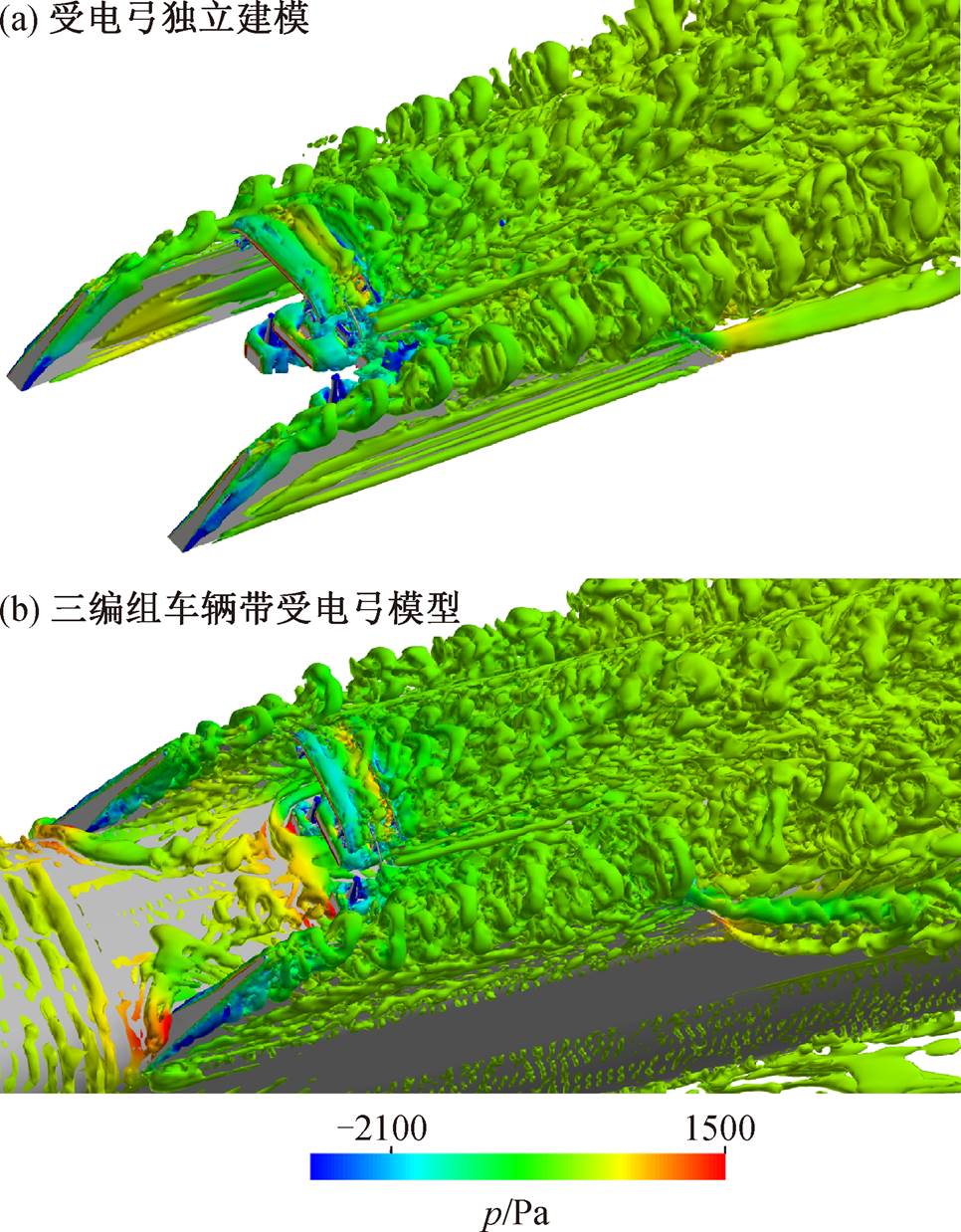
图13 受电弓及周围区域等 Q (Q=100)图
Fig. 13 Iso-surface of the instantaneous normalized Q-criterion (Q=100)
3.1.2 建模方式对声源和远场噪声的影响
为进一步探索不同建模方式对声源和声传播的影响, 本文基于 LMS virtual lab acoustic 计算模块对噪声求解。图 14 为不同建模情况受电弓表面声源, 可以看到, 沿来流方向, 两类情形均在受电弓前缘声源较弱, 后缘声源较强。这是因为前缘始终与来流急剧相撞, 形成迎风滞止区域, 压力脉动较小; 由于前缘脱落涡在后缘发生碰撞, 导致后缘压力脉动瞬时变化剧烈, 压力脉动更大。在不同频率下, 两类建模情况表面声源的声压级幅值都随频率升高而降低, 1000Hz 时声源声压级比 200Hz 时约小 12dB。当频率较低时, 结构表面的声源声压级呈大面积块状分布, 随频率升高, 声源分布趋于均匀。在不同频率下, 受电弓表面气动噪声源的主要位置会有差异, 但都集中在绝缘子、基座背风端、上下臂杆与推杆连接处以及双滑板下游等位置。同时, 两类建模情况的表面声源幅值和远场幅值结果有差异: 单独对受电弓建模时, 表面声源幅值偏大, 相同频率下, 最大幅值约比三编组车辆建模时高 3.6dB, 两类情况对应的最小幅值差异更明显, 原因与上节两类建模方式对流场特性的影响一致。受电弓独立建模时, 来流直接与弓体冲撞, 诱发涡的强度和体积都更大, 导致更大强度的压力脉动, 进一步诱发较大噪声幅值。三辆组编情况下, 来流首先与车头发生碰撞, 气流沿车体摩擦向后, 边界层逐渐变厚, 到达受电弓区, 来流得到缓冲, 与单独建模情况相比, 冲击到受电弓后压力变化较为均匀, 脉动压力反而减弱, 噪声幅值减小。
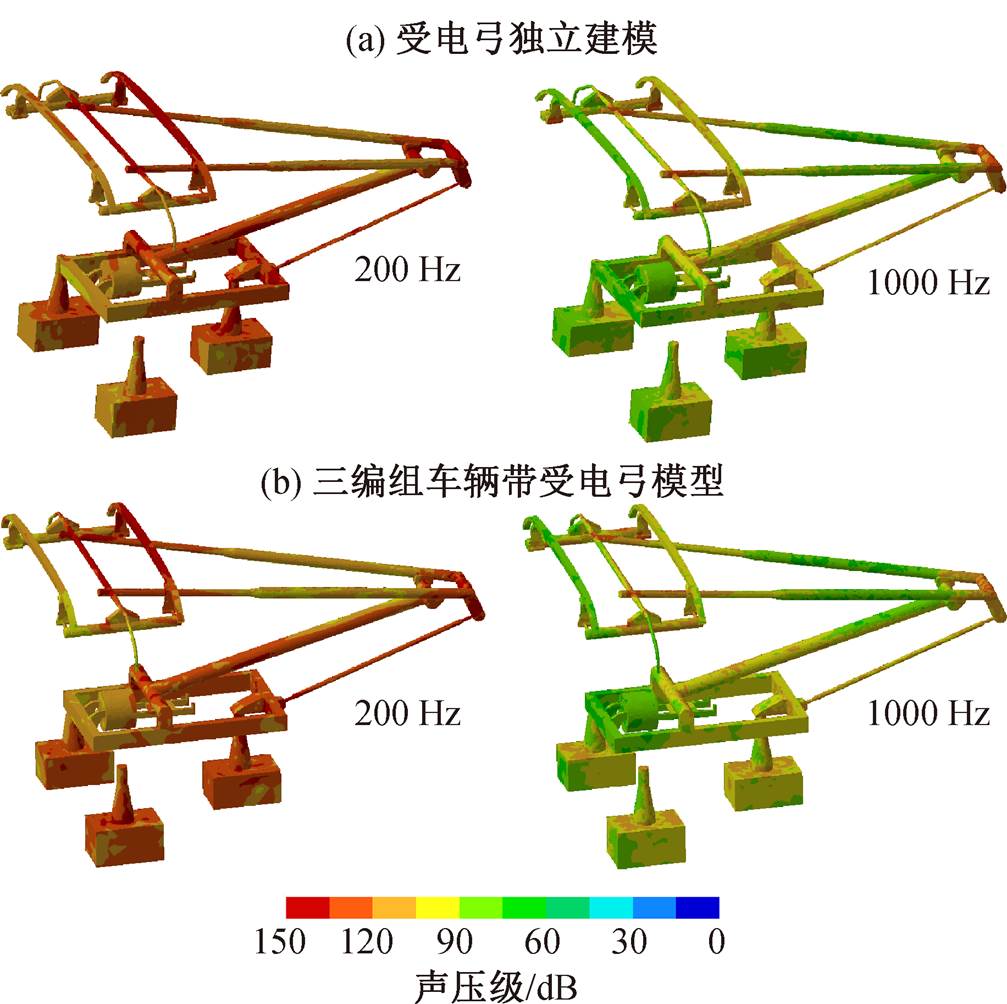
图14 不同建模情况下受电弓表面不同频率噪声源
Fig. 14 Noise sources at different frequencies of the pantograph
图 15 为X-Z半平面方向上的噪声分布, 监测点距离受电弓上取为坐标中心点的距离为 7.5m, 半平面上选取的 32 个监测点邻近间隔角度为 5°, 声源为受电弓和导流罩。此结果未考虑壁面的反射和散射作用。可以看到, 单弓建模所得 X-Z 方向上的噪声幅值高于三编组带受电弓建模所得, 在最大幅值区位置上, 两类建模方式都集中于 75°左右, 但三编组带受电弓建模诱发噪声在其后方 35°左右区域噪声幅值也明显较大。
建模方式的不同使得受电弓后方涡的产生和发展情况以及涡强度不同, 进一步导致受电弓表面压力脉动强度的变化不同, 最终反映在噪声幅值和指向性上有所差异。通过对比不同流场建模方式造成的声源和声传播情况的差异, 本文的流场计算最终选取车辆三编组带受电弓模型。
通过三辆编组带受电弓模型, 对带导流罩受电弓远场气动噪声的辐射特性及衰减特性进行分析, 探究车身及导流罩板块的声波散射和反射作用对噪声特性的影响, 进一步对远场噪声分析中是否考虑车身及导流罩板块影响进行研究。选取距轨道中心y=10m, y=20m的处平面为声场接收面(30m×10m)。图 16(a)为声场计算不考虑壁面反射噪声空间分布结果; 16(b)为考虑壁面反射分布的结果。远场接收面在不同频率时的空间分布可以定性地反映噪声辐射变化。通过对远场噪声是否考虑车身及导流罩板块影响两种情形的分析, 可以看到如下共性特征: 1)10m远处噪声整体上大于 20m 处, 随距离增加, 噪声减弱; 2)随频率升, 高声场接收面上噪声幅值快速降低; 3)低频时噪声呈块状分布, 高频时分布较均匀。两类分析方法的差异体现在以下两方面: 1)考虑壁面作用时(尤其在低频段), 以 200Hz为例, 远场噪声空间分布比不考虑璧面作用时整体偏大, 原因是低频段噪声声波较长, 壁面的反射或散射作用更明显, 弓体处诱发的噪声声波通过车身和导流罩的反射, 或散射后继续传播, 并可以绕射通过导流罩, 辐射到远场区域, 增大低频噪声; 2)在较高频段 1000Hz 情况下, 与不考虑壁面作用时相比, 噪声声压级空间分布幅值, 整体上反而较小, 原因可能是较高频段声波波长较短, 难以发生绕射, 而导流罩对受电弓诱发的高频噪声起到阻挡作用, 导致远场噪声空间分布减弱。
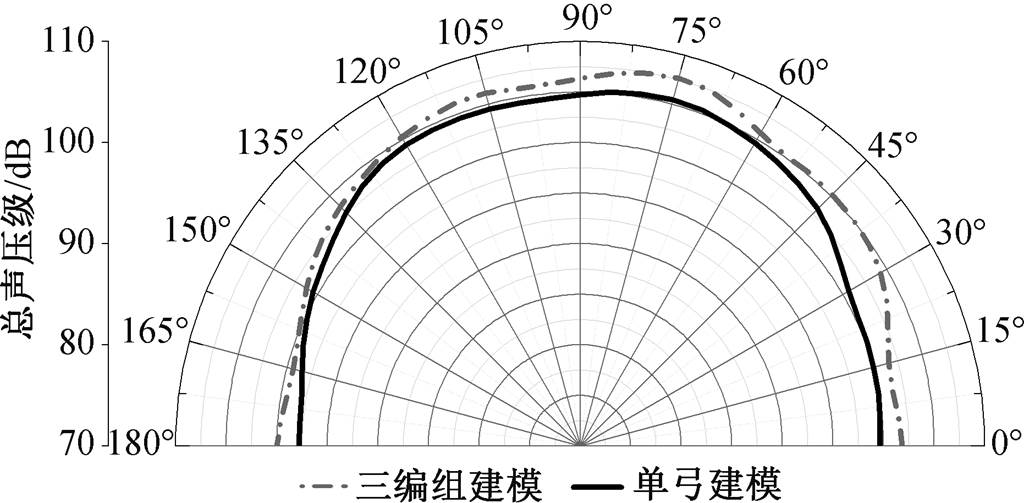
图15 不同建模情况下X-Z方向的噪声幅值和指向性
Fig. 15 Noise amplitude and directivity in X-Z direction induced by pantograph under different modeling conditions
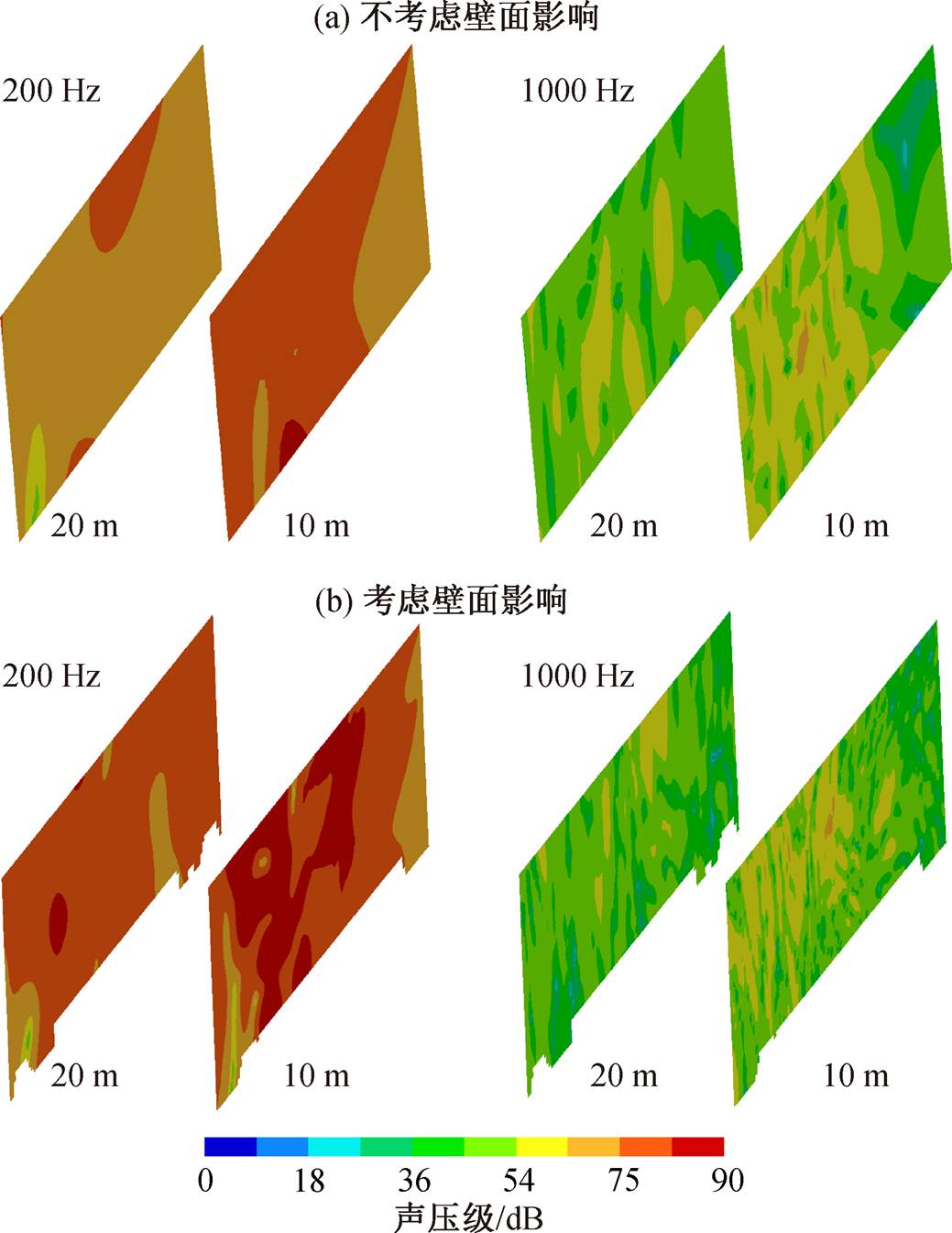
图16 噪声空间分布结果
Fig. 16 Spatial distribution of far-field noise
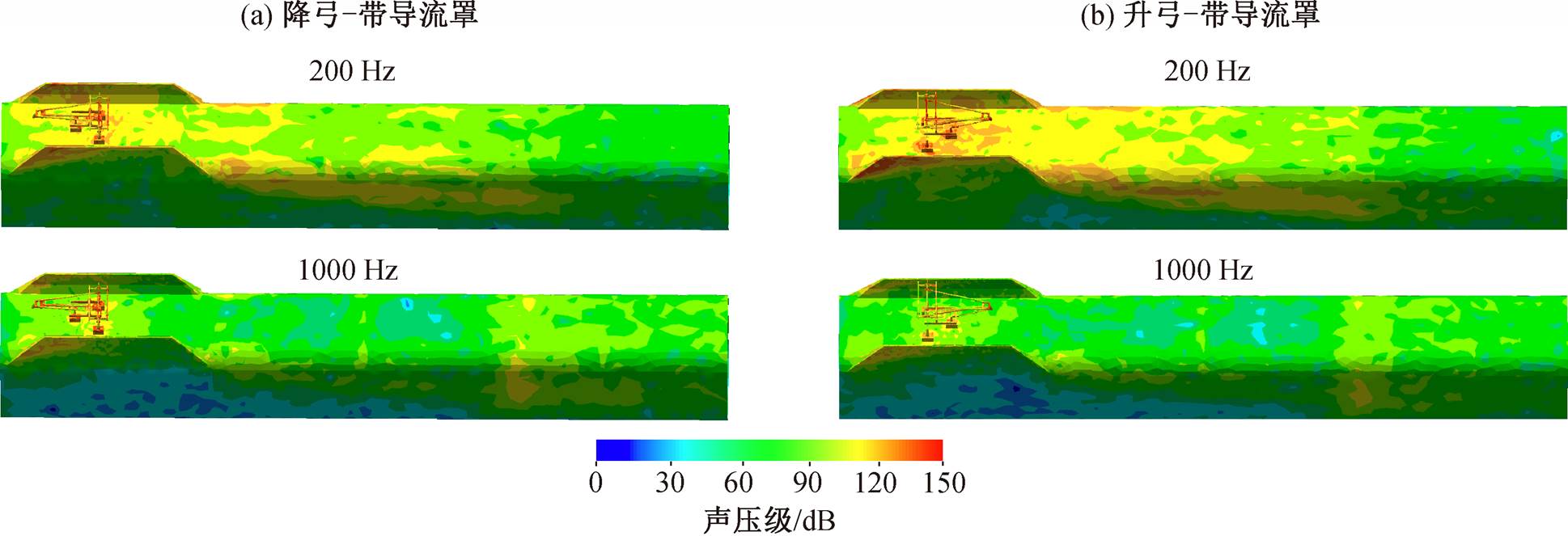
图17 中间车带导流罩受电弓表面在200和1000Hz时的声源分布
Fig. 17 Noise sources of the pantograph with dome in middle car at 200 and 1000 Hz
综上所述, 可知流场计算不同建模方式对噪声幅值和指向性特性产生影响, 是否考虑壁面作用会对噪声的空间分布产生影响。本文在噪声分析中, 流场计算均考虑车身影响(即流场建模), 声场计算考虑车体及导流罩的反射及散射作用影响。
对带导流罩受电弓下降状态下的近场和远场气动噪声空间分布规律和频谱特性进行分析, 并与升弓情形进行对比, 探究受电弓在实际服役时最常见两种状态下噪声特性的差异。流场计算采用带受电弓三编组模型, 考虑壁面反射和绕射作用。
3.3.1 气动噪声源
选取 200Hz 和 1000Hz,对声源的分布特性定性比较。如图 17 所示, 将车体表面脉动压力转换到频域, 发现表面噪声源集中在导流罩和受电弓附近及后方区域, 导流罩两侧及下部车身部位噪声源的数值较低。虽然导流罩是一个噪声源, 但对受电弓产生噪声有一定的阻挡作用, 使受电弓区域的流场产生变化, 使弓体产生的涡旋结构等对车体两侧作用有所减弱, 但导流罩的影响需要进一步分析。
分析降弓状态时的表面声源, 如图 18 所示, 可以看到, 与升弓情形相似, 沿流速方向, 与来流急剧相撞的迎风区声源较弱, 后缘声源较强, 也是因为前缘相撞区压力脉动较小, 而后缘由于前缘脱落涡在后缘发生碰撞, 导致后缘压力脉动瞬时变化剧烈, 压力脉动更大。随频率增加, 表面声源声压级幅值逐渐降低, 1000Hz 时声源声压级比 200Hz 时低约 18dB。表面气动噪声源主要位置仍然几乎集中在绝缘子、上下臂杆与推杆的连接后缘、基座以及双滑板后缘位置。
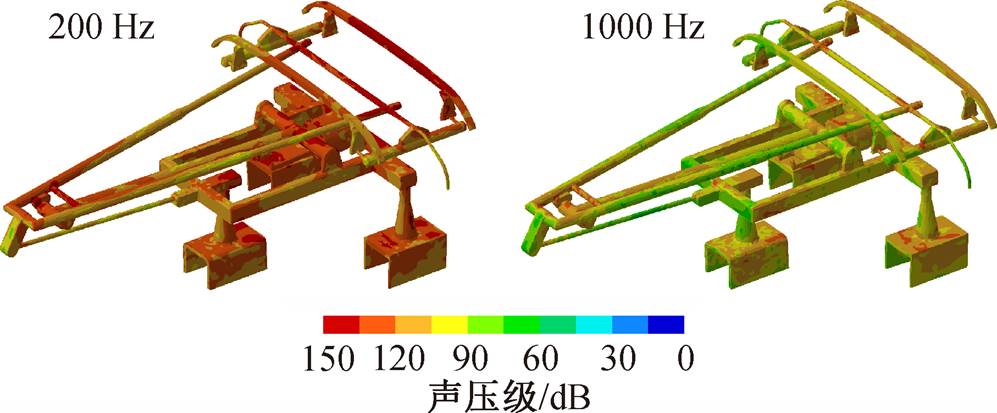
图18 受电弓下降状态时表面不同频率的噪声源
Fig. 18 Noise sources at different frequencies of the down-pantograph
3.3.2 气动噪声辐射及衰减特性
为了探究导流罩和弓体各自对整个受电弓体系噪声的影响, 在降弓状态下, 将降弓单独作为声源诱发的远场噪声与降弓+导流罩共同作为声源进行对比, 选取距轨道中心 y=10m, y=20m 处平面为声场接收面(30m ×10m)。通过远场接收面不同频率下的噪声空间分布, 可以定性地反映噪声辐射变化。图 19 和 20 分别为仅将弓体作为声源面以及将弓体和导流罩共同作为声源面时的空间分布, 可以看出, 两类情形诱发的噪声在低频段差异明显, 与仅将弓作为声源面相比, 弓和导流罩共同作为声源面产生的噪声幅值更大, 原因是导流罩和弓体均为重要的噪声源, 在不考虑导流罩作为声源的情况下, 噪声空间分布幅值偏小。在 1000Hz 的较高频区域,两类声源面诱发噪声的差距不明显, 可能是因为导流罩诱发噪声在低频段有较大的贡献, 但在高频段贡献相对较小, 导致高频时整体分布差异不明显。该结果只能定性地反映声场分布变化, 在不同频率下, 声场接收面上的噪声分布及幅值会有差异, 还需要对频谱特性等进行进一步的分析确认。
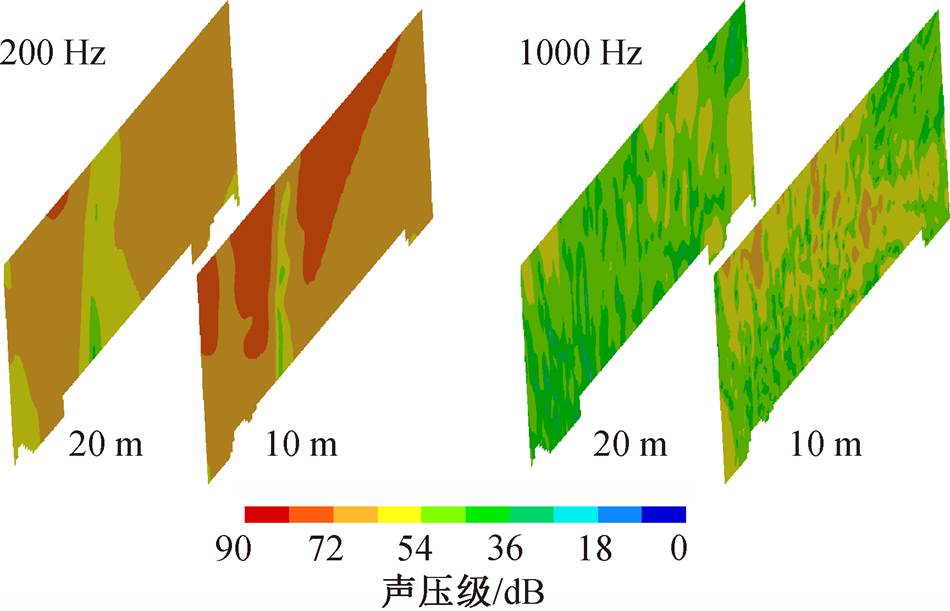
图19 仅将降弓本身作为声源面, 不同频率时距离轨道中心10和20 m处的噪声空间分布
Fig. 19 Spatial distribution of far-field noise at 200 Hz and 1000 Hz (y = 10 m, y = 20 m) when only using the down-pantograph itself as noise source
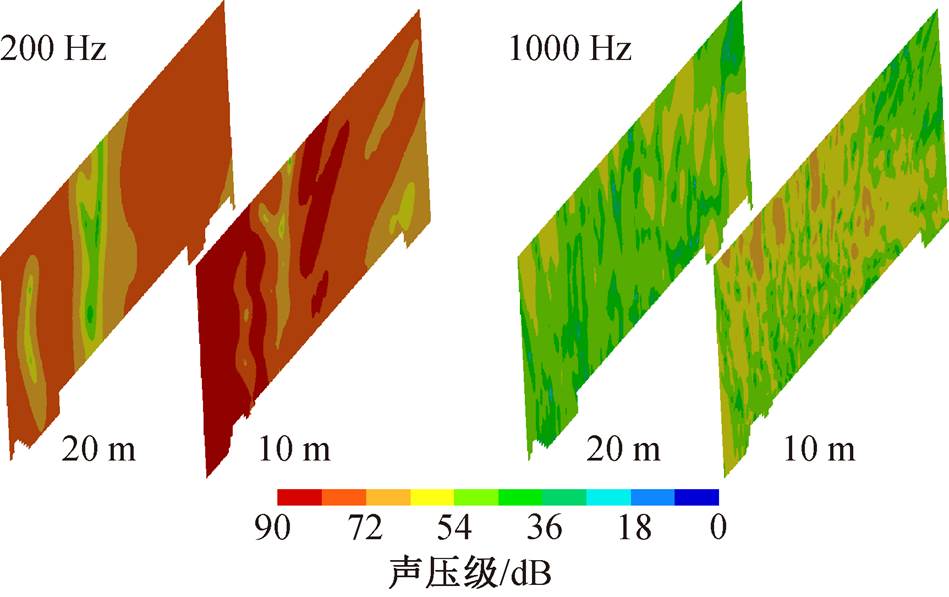
图20 降弓和导流罩共同作为声源面时, 不同频率时距离轨道中心10和20 m处的噪声空间分布
Fig. 20 Spatial distribution of far-field noise at 200 and 1000 Hz (y = 10 m, y = 20 m) when using the down-pantograph with dome as noise sources
图 21(a)给出以受电弓为中心, y=5m, z=3.5m和y=25m, z=3.5m 处受电弓为降弓时诱发的远场噪声。可以看到, 同等情形下:1)随着与轨道中心距离的增加, 监测点声压幅值下降; 2)仅将弓作为声源面, 无论弓上升还是下降状态, 在 300Hz 以上, 弓和导流罩共同诱发噪声明显大于仅将弓作为声源面诱发噪声, 但在 300Hz 以上, 弓诱发的噪声几乎与弓和导流罩共同作为声源诱发噪声持平, 部分频率点超过二者共同诱发噪声, 因此可以推断, 在高于 300Hz 的较高频段, 受电弓诱发噪声影响较大, 在低于 300Hz 的低频区域, 导流罩诱发噪声也有较大影响, 该结论与前面的定性分析结论一致; 3)如图 21(b)所示, 将弓和导流罩同时作为声源面,可以发现, 低于 300Hz 时, 降弓和导流罩诱发噪声较高, 300Hz 以上, 升弓和导流罩诱发噪声略高。原因是降弓弓体较为集中, 且处于导流罩包围区域内, 弓后方诱发的涡在半封闭空间内破碎减缓, 较大的涡产生较低频噪声, 绕射性较好, 对低频噪声贡献较明显, 升弓时弓头高度超过导流罩, 导流罩对弓诱发的中高频噪声阻挡作用减弱, 而 300Hz 以上噪声主要由弓引起, 故在较高频时噪声贡献凸显。
以受电弓中心位置为参考, y=5, 10, 15, 20, 25, 30m 处的总声压级, 在升、降弓下的 3 类声源(即弓、导流罩和弓+导流罩)诱发噪声的分布情况如图22 所示。可以看出: 1)在该受电弓外形和开口方向, 降弓诱发噪声大于升弓; 2)降弓+导流罩诱发噪声大于升弓+导流罩诱发噪声; 3)降弓情形下, 在距离声源较近的范围, 约 y≤10m 内, 导流罩诱发噪声较大, 随着距离增加, 弓诱发噪声逐渐大于导流罩诱发噪声, 而升弓情形下, 导流罩诱发的噪声为 1~2 dB, 整体大于弓诱发噪声。将受电弓和导流罩共同诱发的远场噪声与轨道中心距离进行拟合, 诱发噪声与距离之间的关系对于升弓基本上满足多项式OASPL(dB)=a–b·ln(x+c), 拟合曲线可写为 OASPL (dB)=108–10 ln(x–2.5)。
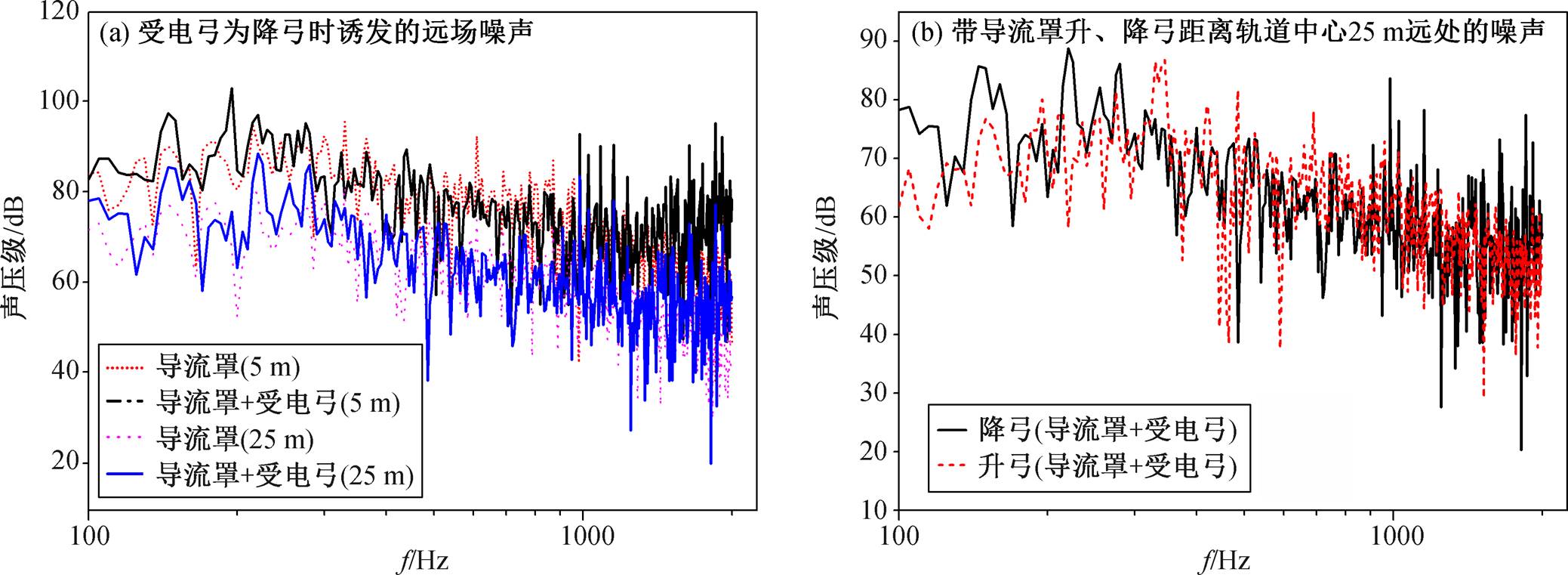
图21 远场监测点噪声对比
Fig. 21 Noise at far field monitoring points
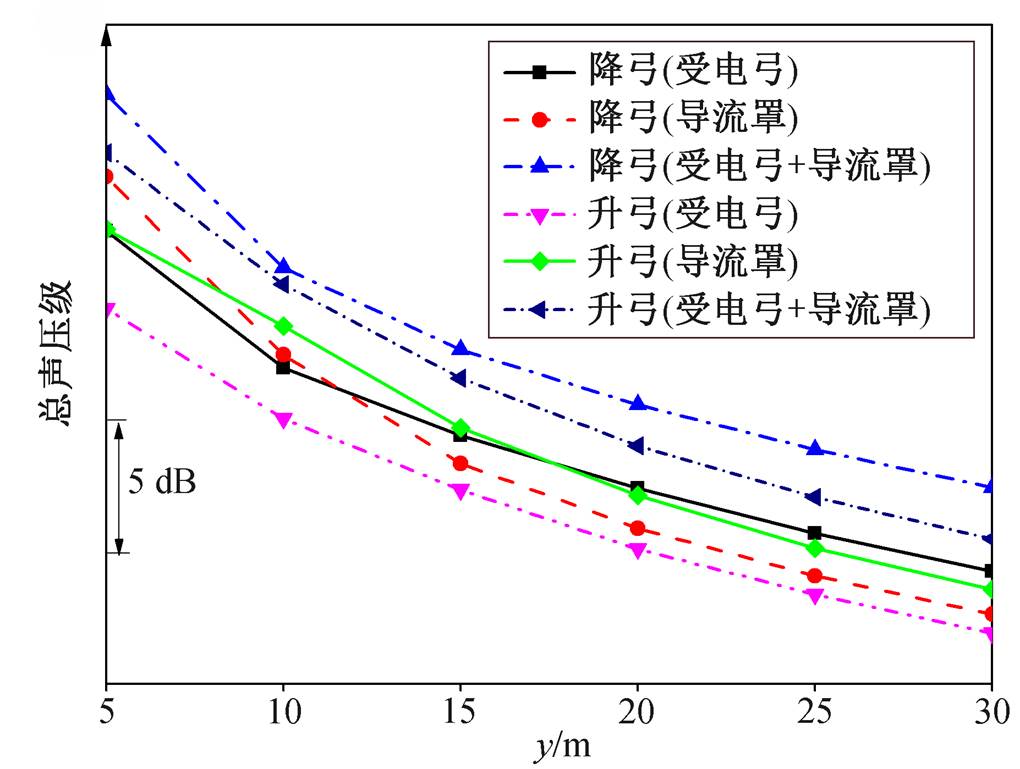
图22 以受电弓中心位置为参考, 垂直于车体向外, 距离轨道中心不同垂直距离处总声压级
Fig. 22 Total sound pressure level at different vertical distan-ces away from the car referring to the central position of the pantograph of different noise sources
图 23 为在 y=25m, z=3.5m处,沿车体运动方向, 每隔 5m 取一个监测点(图 4 中 x1~x5), 不同监测点的噪声, 两图纵轴总声压级幅值取值范围相同。可以看出: 降弓时, 弓诱发噪声在大多数点上大于导流罩诱发值; 升弓时, 导流罩诱发噪声整体上大于弓诱发值。个别点会有反转, 可能是由导流罩或弓体对声波造成的反射和绕射等引起。
3.3.3 气动噪声指向性
根据 ISO3095–2013 标准[34], 远场监测点位于距离中心点 7.5 或 25m 处, 高度为 1.2 或 3.5m, 本文选取 7.5m 半径, 每隔 5°取一个监测点, 探究受电弓的噪声指向性。在受电弓上升和下降两种状态的X-Y 全水平面、Y-Z 上半平面以及 X-Z 上半平面方向上的噪声大小见图 24。在 X-Y 平面, 在受电弓前测区域(180o), 导流罩对噪声影响更大, 在后侧区域(0o)受电弓噪声影响较大; 在 Y-Z 平面, 基本上对称分布, 在靠近车身两侧区域, 导流罩噪声贡献较大, 其他角度受电弓产生噪声贡献较大。在 X-Z 平面, 整体上受电弓对总噪声的贡献较大。
本文对 350km/h 运行速度下某型高速列车受电弓诱发气动噪声的特性进行研究。首先分析受电弓流场不同建模方式对噪声的影响, 并对车体及导流罩的壁面作用对声场的影响进行分析, 发现受电弓独立建模时, 整体噪声水平偏大, 指向性也不同于将受电弓置于车体同步建模所得结果; 考虑壁面作用后, 诱发噪声在低频上明显偏大。为了得到较精细的噪声指向性和频谱特性, 本文在流场计算中采用三编组带受电弓模型, 并在声场计算中考虑壁面作用, 对带导流罩的受电弓在升起和下降状态下的近场和远场气动噪声频谱特性和分布规律进行研究。结果表明: 1)在本文选取的受电弓外形和开口方向, 降弓和导流罩诱发噪声略大于升弓和导流罩时诱发噪声; 2)导流罩在低于 300Hz 的低频区诱发噪声比例较大, 受电弓诱发噪声在 300Hz 以上影响较大; 3)诱发噪声的指向性方面, 在水平面内, 受电弓前部导流罩对产生噪声贡献更大, 后部受电弓贡献较大, 在列车正上方区域, 受电弓诱发噪声大于导流罩诱发噪声, 是主要的气动噪声源, 总体来说, 导流罩诱发的噪声在水平面上大于其包围的受电弓诱发噪声, 在列车正上方区域受电弓诱发噪声大于导流罩诱发量, 二者皆为重要的气动噪声源。
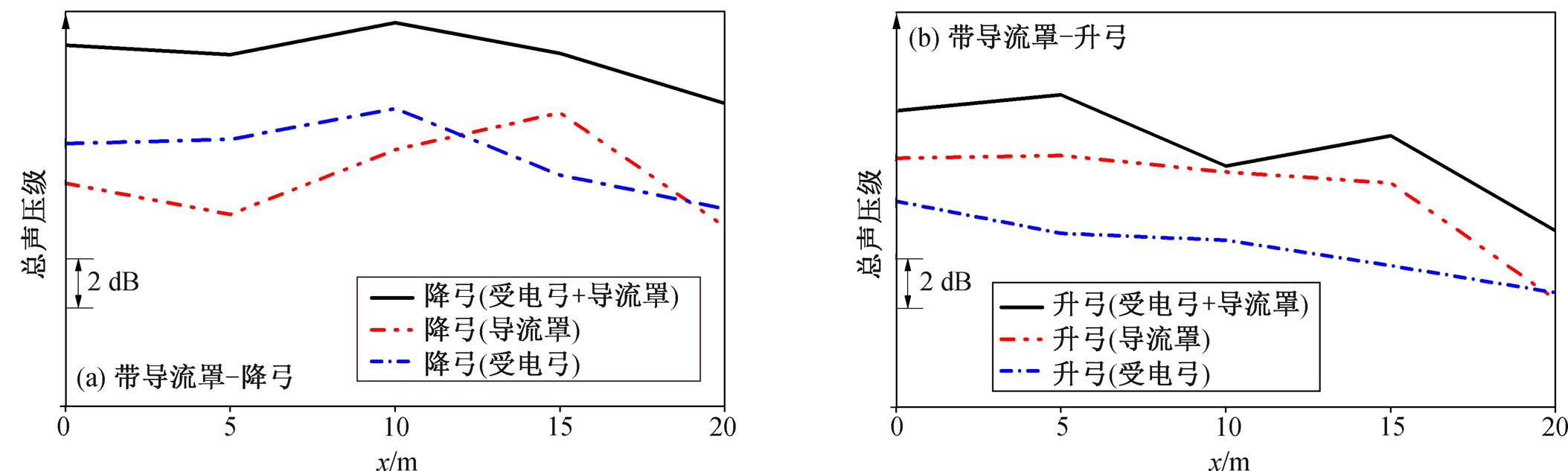
图23 沿车体运动方向受电弓升起或下降状态时不同监测点处的总声压级对比
Fig. 23 Comparison of total sound pressure level at different monitoring points along the moving direction

图24 受电弓诱发噪声在不同平面指向性
Fig. 24 Directivity of the noise induced by different noise sources in different planes
参考文献
[1] 张曙光. 350km/h 高速列车噪声机理、声源识别及控. 中国铁道科学, 2009, 30(1): 86–90
[2] 孙振旭, 宋婧婧, 安亦然.CRH3 型高速列车气动噪声数值模拟研究. 北京大学学报(自然科学版), 2012, 48(5): 701–711
[3] Xiao Y G, Yang Q, Sun L, et al.Longitudinal type-line optimization of high-speed train for low aerody-matic noise. Journal of Central South University, 2014, 21(6): 2494–2500
[4] 刘加利, 张继业, 张卫华.高速列车车头的气动噪声数值分析. 铁道学报, 2011(9): 19–26
[5] 朱剑月, 景建辉.高速列车气动噪声的研究与控制. 国外铁道车辆, 2011, 48(5): 1–8
[6] 孙艳军, 夏娟, 梅元贵.高速列车气动噪声及减噪措施介绍. 铁道机车车辆, 2009, 29(3): 25–28
[7] King W F. A precise of development in the aeroacous-tics of tast trains. Journal of Sound and Vibration, 1996, 193(1): 349–358
[8] Takaishi T, Ikeda M.Method of evaluating dipole sound source in a finite computational domain. Railway Technical Research Institute, 2004, 116(3): 1427–1435
[9] Takaishi T, Sagawa A, Nagakura, et al. Numerical analysis of dipole sound source around high speed trains. Railway Technical Research Institute, 2002, 111(6): 2601–2608
[10] Yoshiki K, Yusuke W, Fumio M, et al. Numerical simulation of aerodynamic noise from high-speed pantographs using Lattice Boltzmann method// The International Symposium on Speed-up, Safety and Service Technology for Railway and Maglev Systems. Seoul,2012: 1–9
[11] Kitagawa T, Nagakura K. Aerodynamic noise gene-rated by shinkansen cars. Journal of Sound and Vibration, 2000, 231(3): 913–924
[12] Nagakura K. Localization of aerodynamic noise sources of shinkansen train. Journal of Sound and Vibration, 2006,293(3): 547–556
[13] Noger C, Patrat J C, Peube J, et al. Aeroacoustical study of the TGV Pantograph reasearch. Journal of Sound and Vibration, 2000, 231(3): 563–575
[14] Iwamoto K,Higashi A. Some consideration toward reducing aerodynamic noise pantograph.Japanese Railway Engineering, 1993, 122(2): 1–4
[15] Zhang Yadong, Zhang Jiye, Li Tian, et al. Investi-gation of the aeroacoustic behavior and aerodynamic noise of a high-speed train pantograph. Technological Sciences, 2017, 60: 561–575
[16] Claus W, Thomas H, Pierre S. Large-eddy simulation for acoustics. Cambridge: Cambridge University Press, 2007
[17] Spalart P R. Detached-eddy simulation // Friedrich R, Rodi W. Advances in LES of Complex Flows. Mu-nich, 2002: 235–237
[18] 付建, 王永生, 靳栓宝, 等. LES和DES在流体动力噪声预报中的适用性分析. 华中科技大学学报(自然科学版), 2015, 43(2): 66–70
[19] 詹福良, 徐俊伟. Virtual. Lab Acoustics 声学仿真计算从入门到精通. 西安: 西北工业大学出版社, 2013
[20] Desmet W, Sas P. Introduction to numerical acoustics. Mammal Review, 2015, 35(2): 3–9
[21] Spalart P R, Jou W H, Strelets M, et al. Comments on the feasibility of LES for wings and on a hybrid RANS/LES approac // Proceedings of 1st AFOSR International Conference on DNS/LES, Advances in DNS/LES. Columbus: Greyden Press,1997: 137–147
[22] Strelets M. Detached eddy simulation of massively separated flows // 39th Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2001: 1–18
[23] Spalart P R, Deck S, Shur M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theoretical and Computational Fluid Dynamics, 2006, 20(3): 181–195
[24] Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA, 1994, 32 (8): 1598–1605
[25] Marburg S, Nolte B, Computational acoustics of noise propagation in fluids finite and boundary element methods. Berlin: Springer-Verlag, 2008: 1–34
[26] Zhang Y, Zhang J, Li T, et al. Research on aero-dynamic noise reduction for high-speed trains. Shock and Vibration, 2016: 6031893
[27] Shi L, Zhang C C, Wang J, et al. Numerical analysis of aerodynamic noise of a high-speed pantograph // Proceedings of Fourth International Conference on Digital Manufacturing and Automation. Qingdao, 2013: 837–841
[28] Kato C, Iida A, Takano Y, et al. Numerical prediction of aerodynamic noise radiated from low Mach number turbulent wake // 31st Aerospace Sciences Meeting & Exhibit. Ibaraki, 1993: 0145
[29] Jacob MC, Boudet J, Casalino D, et al. A rod-airfoil experiment as benchmark for broadband noise. Model Theor Comput Fluid Dyn, 2005, 19:171–196
[30] Giret JC, Sengissen A, Moreau S, et al. Prediction of the sound generated by a rod-airfoil configuration using a compressible unstructured LES solver and a FW-H analogy // 18th AIAA/CEAS Aeroacoustics Conference. Colorado Springs, 2012: 1–18
[31] Tong F, Qiao W Y, Chen W J, et al. Broadband noise prediction using large eddy simulation and a fre-quency domain method. Applied Acoustics, 2017, 117: 94–105
[32] Neuhart D, Jenkins L, Choudhari M, et al. Measure-ments of the flowfield interaction between tandem cylinders // 15th AIAA/CEAS Aeroacoustics Confe-rence. Miami, 2009: 1–18
[33] Lockard D P. Summary of the tandem cylinder solutions from the benchmark problems for airframe noise computations // Workshop49th AIAA Aero-space Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Orlando, 2011: 1–22
[34] ISO 3095–2013. Acoustics — Railway application —measurement of noise emitted by railbound vehicles [S]. Bristol: BSI, 2013
Analysis of Aerodynamic Noise Characteristics of Pantograph in High Speed Train
Abstract The delayed detached eddy simulation (DDES) coupled with the acoustic finite element method (FEM) is applied to analyze aerodynamic noise characteristics of a high-speed train with a pantograph. Numerical results are presented in terms of spectrum characteristics and distributions of aerodynamic noise in near and far fields in the case of pantograph with demo in up and down situations. The influence of different modeling methods on the flow field of the pantograph is considered, and the effects of scattering and reflection of sound waves from the body and shroud panels on aerodynamic noise results are also took into account. The following interesting phenomena are drawn. 1) Under the pantograph shape and selected opening direction, the noise induced by down-pantograph with dome is higher than that induced by up-pantograph with dome. 2) The noise induced by the dome has a large proportion of noise in the low frequency region below 300 Hz,while the noise induced by the pantograph has a greater influence after 300 Hz. Using the dome as the sound source face, the noise is larger in the case of up-pantograph. 3) About the directivity of the induced noise, in the horizontal plane, the front of the pantograph, the dome contributes more to the noise, and in the rear of the pantograph, the pantograph contributes more. In the upper part of the train, the noise induced by the pantograph itself is greater than the noise induced by the dome, becoming the main source of aerodynamic noise in this case.
Key words high-speed train; pantograph; aerodynamic noise; delayed detached eddy simulation; acoustic finite element method
doi: 10.13209/j.0479-8023.2020.014
收稿日期: 2019-04-19;
修回日期: 2019-06-03