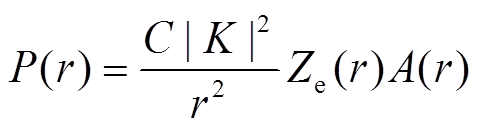 , (1)
, (1)摘要 针对星载雷达陆面衰减订正存在的困难, 提出相似廓线订正方法。利用洋面雷达测得的雷达等效反射率因子廓线(简称降水廓线) Zm 和经表面参考技术(SRT)订正后的降水廓线Ze建立相似廓线库, 通过匹配雷达在洋面和陆面测得的降水廓线, 对陆面降水廓线的地表路径积分总衰减(PIAs)进行估值。借助 2018 年 GPM-CO 2A-Ku 数据产品中洋面降水资料进行检验, 结果表明相似廓线法与 SRT 技术的订正结果具有较好的一致性, 对于容许相对偏差 40%的相似廓线库, 匹配成功的降水廓线中, 两种方法的 PIAs 相对偏差小于 40%的廓线比例依次为对流云降水 88.8%, 无亮带层状云降水 98.9%, 含亮带层状云降水 98.9%, 显示该方法有效。借助 2014—2018 年 GPM-CO 2A-Ku 数据产品中陆面降水资料进行对比, 结果表明相似廓线法的陆面应用效果与洋面差异较大, 与陆面 SRT 技术应用效果差的结论相一致。
关键词 GPM-CO DPR; 相似廓线法; 路径积分总衰减
降水是地气系统能量与水分循环的关键性驱动因素。同时, 降水与气候异常和自然灾害(台风、山洪等)紧密相关, 对人民生命财产安全有重要影响。降水时空变化大, 难以准确地测量。陆面降水测量主要依靠雨量计和地基天气雷达, 但其时空分辨率有限。同时, 获得占地球 70%左右的海洋高质量降水数据非常困难。为实现全球尺度的降水测量, 卫星降水测量近年来得到长足发展。1997 年发射的热带测雨卫星 TRMM, 搭载主动测雨雷达 PR, 获得约 18 年的高质量热带降水数据[1]。为克服TRMM 卫星观测范围小, 观测数据精度不高, 无法捕捉弱降雨过程和降雪过程等缺点, 美国和日本等国联合实施全球降水观测(global precipitation mea-surement, GPM)计划。GPM 由 GPM 核心卫星(GPM core observatory, GPM-CO)和卫星群组成。GPM 核心卫星由美国和日本联合开发, 卫星群由多国共同参与, 对降水的精确测量由安装在 GPM-CO 上的双频降水雷达(dual-frequency precipitation radar, DPR)完成。GPM 将降水测量的时间分辨率提高到 3 小时, 且 GPM-CO 轨道倾角提升到 65°, 可以覆盖全球绝大部分地区。这些降水观测数据将有助于改进数值天气预报模式、气候模式和流域水文模型等。
GPM-CO 首次携带双频降水雷达(DPR), 其频率分别为 13.6GHz(Ku 波段)和 35.5GHz(Ka 波段)[2], 能获得独立于背景(下垫面)辐射特性的降水估计, 因此可得到比微波辐射计精度更高的降水估计, 用来为微波辐射计降水反演算法定标。GPM-CODPR进行降水探测时, 雷达回波会受到降水区域的衰减作用, 造成回波面积减少。同时, 雷达观测的反射率因子小于实际雷达反射率因子。为了准确地反演降水参数, 须进行衰减订正。在对 GPM-CO DPR数据进行衰减订正时, 用到的方法有 HB 方法[13]和基于表面参考技术 SRT(surface reference technique)的方法。HB 方法在中大雨时易产生过量订正或不稳定[3], 需要雷达测量数据和 k-Ze 关系系数“无误差”, 在实际应用中难以满足, 使其应用受限。SRT 技术可以在雷达波束远距离端为 HB 方法提供一个衰减总量估计, 有效地解决过量订正问题, 在洋面上应用效果较好。洋面标准化雷达截面 NRCS(norma-lized radar cross section)与微波频率、风速和入射角等有关[4‒6], 相对稳定, 但陆面的下垫面复杂多变, SRT 技术的基本假设(降水前与降水时的NRCS保持不变)难以满足, 应用受限。衰减订正的基础是HB 方法, 关键是对 PIAs 估值, 避免出现过量订正和不稳定。
上述方案不能较好地解决陆面 PIAs 的估值问题。为此, 本文提出相似廓线法, 利用洋面 SRT 技术应用可靠的降水廓线, 对陆面降水廓线的 PIAs进行估值, 从而实现陆面降水廓线的衰减订正。
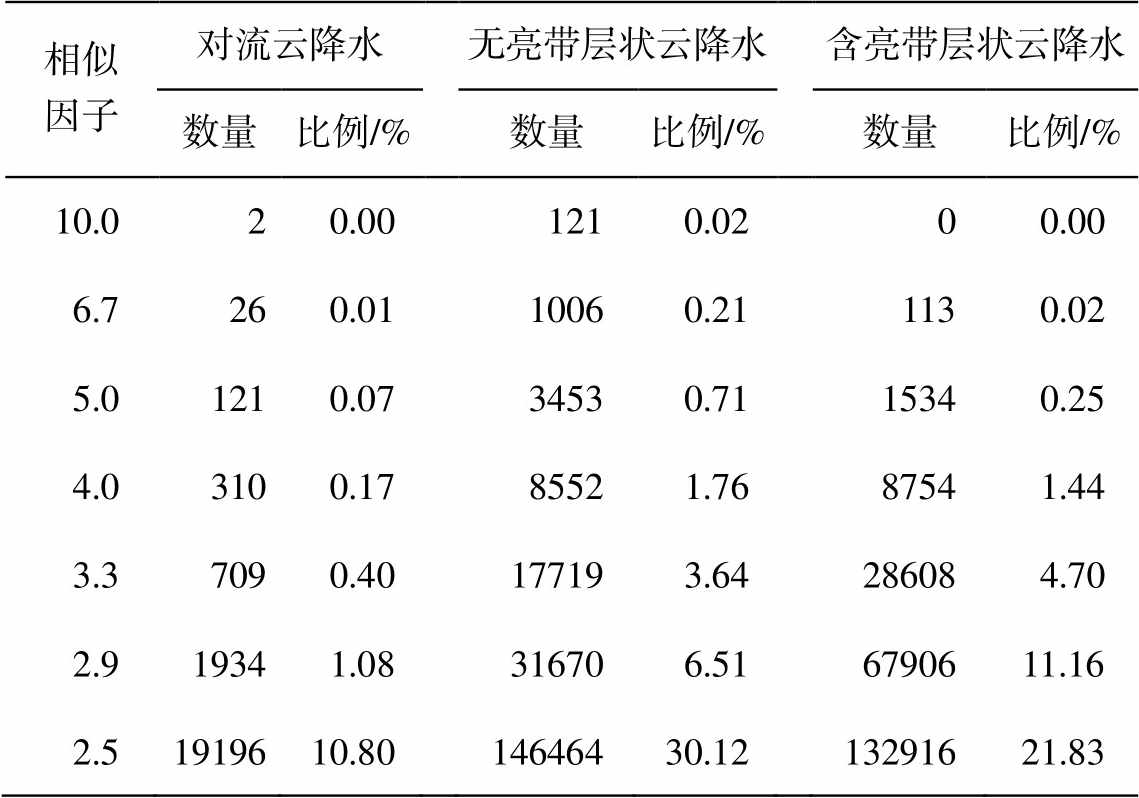
假设雷达天线发射的波束充塞系数为 1, 则气象雷达方程表达如下:
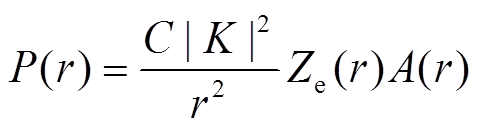 , (1)
, (1)式中, P(r)是接收功率; r是目标与雷达之间的距离; C是雷达常数; K=(m2-1)/(m2+2), 其中m为水滴的复折射指数;Ze(r)为距离r处的雷达等效反射率因子值;A(r)是衰减因子, 即雷达与距离r之间雨区的双程衰减, 表示为
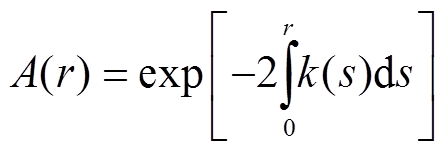 , (2)
, (2)
其中k(s)是衰减系数。
等效雷达反射率因子的测量值 Zm(r)与真值Ze(r)之间存在如下关系:
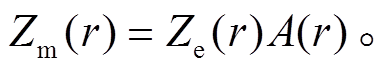 (3)
(3)雷达回波衰减订正, 就是由雷达回波强度的测量值Zm计算得到真值Ze的一个估计值。
Hitschfeld 等[3]提出衰减订正 HB 算法。假设存在关系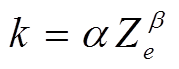 (α和β为常数)和下边界条件Ze(0) =Zm(0), 通过求解式(3), 可得衰减因子[3]:
(α和β为常数)和下边界条件Ze(0) =Zm(0), 通过求解式(3), 可得衰减因子[3]:
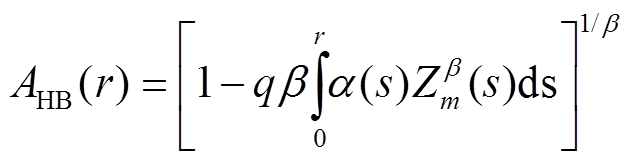 , (4)
, (4)式中, q=0.2ln(10), 则距离为r处的路径积分总衰减PIAs(r)表达式为
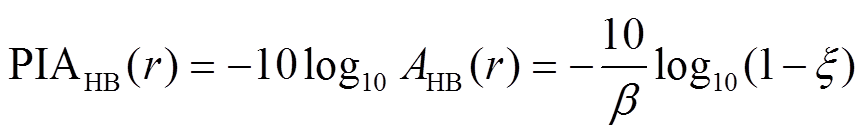 , (5)
, (5)
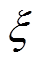 的表达式为
的表达式为
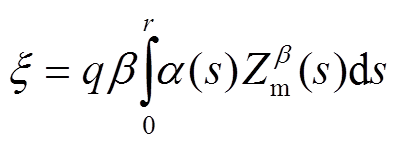 。 (6)
。 (6)
当目标与雷达的距离在[0, r]区间内, 降水强度不大且Zm已知时, 可以得到精确的衰减订正。当r等于雷达与地表之间距离时, 即可得到地表路径积分总衰减量PIAsHB。Meneghini[7]讨论了这一解析订正法与迭代法[8]之间的关系: 在收敛的情况下, 迭代法的极限值与HB解析订正结果相同, 当雷达观测资料和 k-Ze 关系系数“无误差”时, 两种方法对衰减都有较好的订正能力; 随着衰减量增加, 解析订正结果的稳定性变差, 造成过量订正或不稳定; 在衰减量较大时, 这些误差的作用被放大, 因而加剧订正结果的不稳定。王振会等[9]认为 k-Ze 关系系数误差对订正效果的影响是非线性的, 即 k-Ze 关系系数误差较小时, 订正误差较小; 当k-Ze 关系系数误差较大时, 订正误差随k-Ze 关系系数误差增大而迅速变大。因此, 解析法的应用受到限制。对于机载或星载雷达, 远端地表面可能获得无降雨衰减和有降雨衰减的NRCS, 为HB订正提供积分上边界条件, 避免过量订正和结果不稳定。在此背景下, Meneghini等[5]、Iguchi等[10]和Yang等[11]提出SRT技术, 并进行大量的机载雷达测试。
SRT技术的基本假设是, 地表NRCS在有降水与无降水时相同。利用降水前后测得的地表NRCS的差异得到PIAs, 记为PIAsSRT:
PIAsSRT =σ0 (NR) − σ0(R), (7)
其中,σ0(R)是有降水时的NRCS,σ0(NR)为无降水时的NRCS, 单位均为dB。在实际应用中, σ0(NR)无法测量, 只能近似地估值, 则有
式中, <σ0(NR)>是对 σ0(NR)的估值,
洋面地表 NRCS 主要取决于雨强、雷达入射角和风速, SRT 技术应用效果较好。陆面地表 NRCS受地表植被、表面粗糙度、土壤含水量和雷达入射角等多种因素影响, 尤其在降雨过程中, 地表含水量随降雨进程发生改变, 使降雨前后地表 NRCS 发生改变, SRT 技术的基本假设难以满足, 应用受限。赵文中等[12]指出, 自然环境中一些因素(如土壤中水分含量以及地表植被和农作物状况)的变化直接影响地表 NRCS。Komukai 等[13]分析陆面(亚马孙热带雨林和撒哈拉沙漠)Ku 波段的地表 NRCS 与入射角、植被指数(NDVI)、地表粗糙度及土壤含水量的关系, 发现无明显的相关性, 因此, 引入其他因子来改善 SRT 技术在陆面的应用尚处于探索阶段。
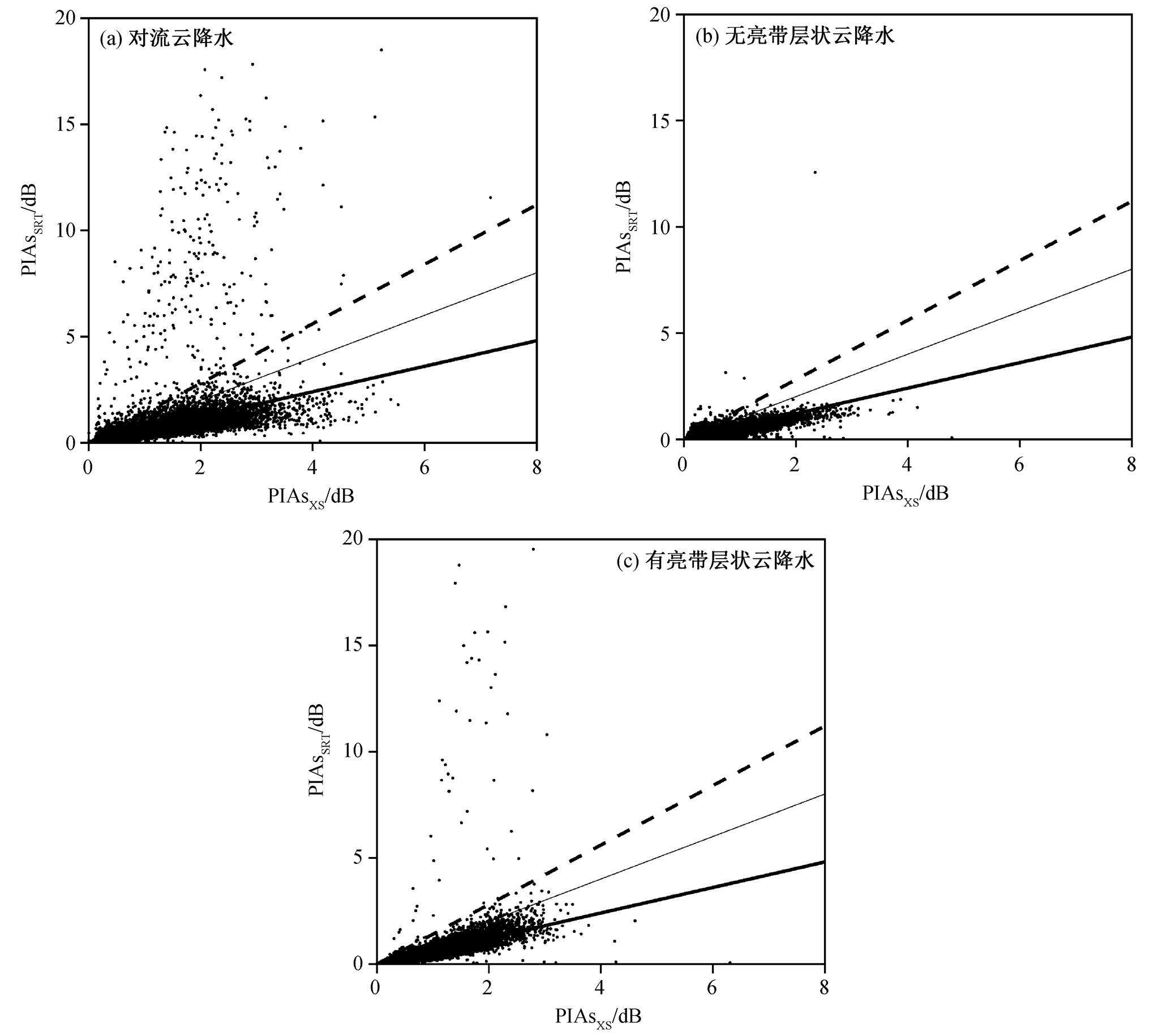
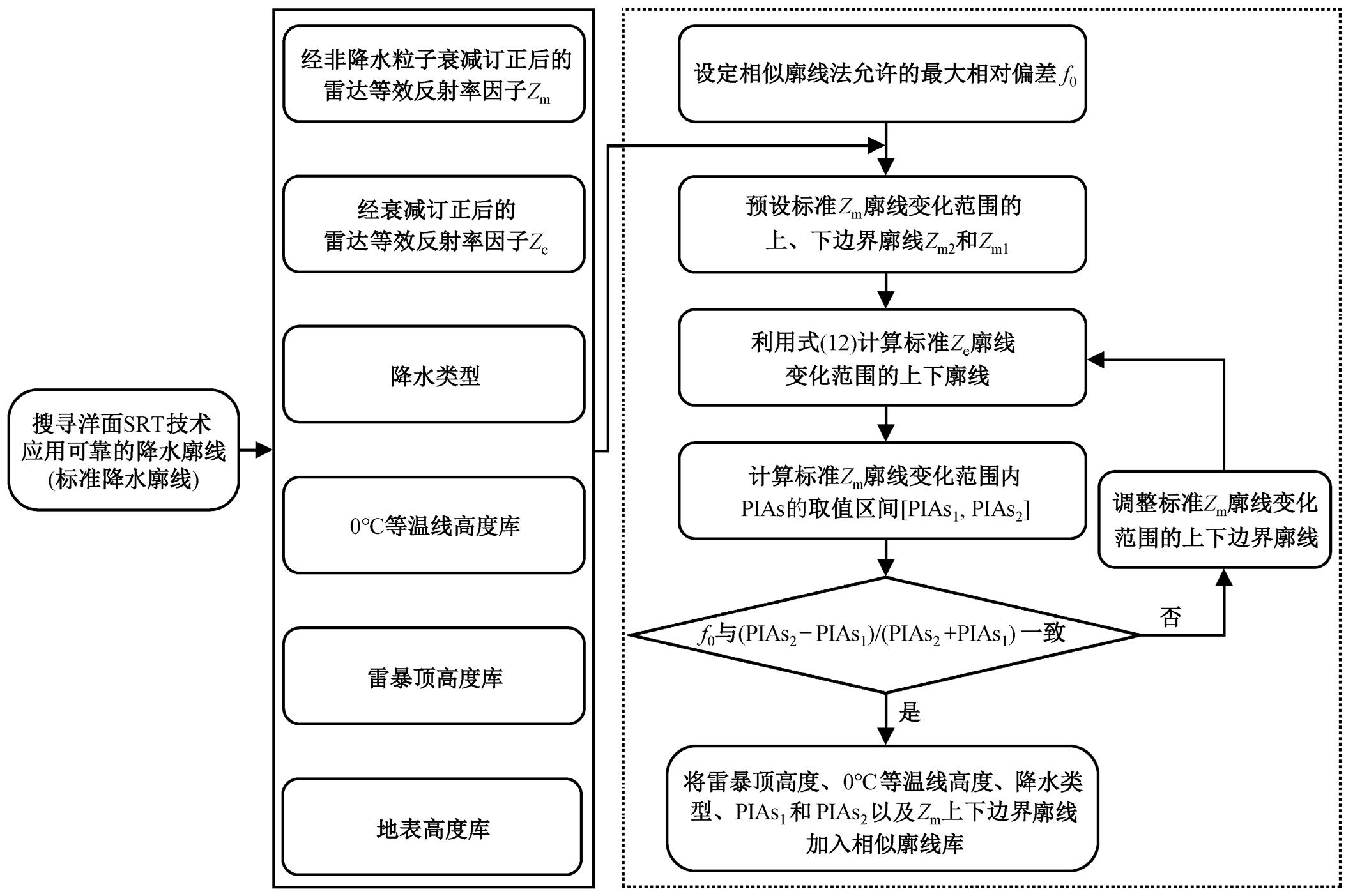
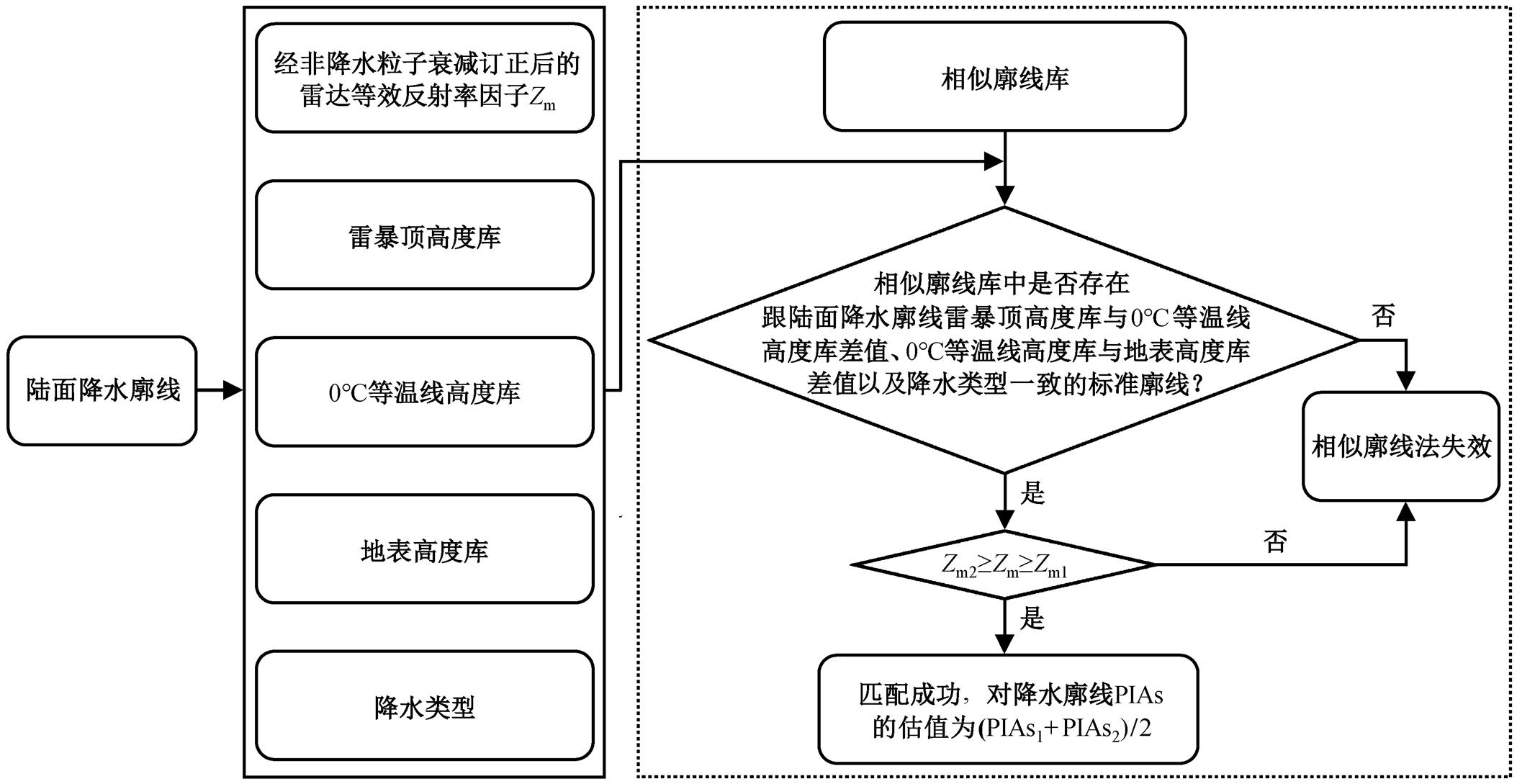
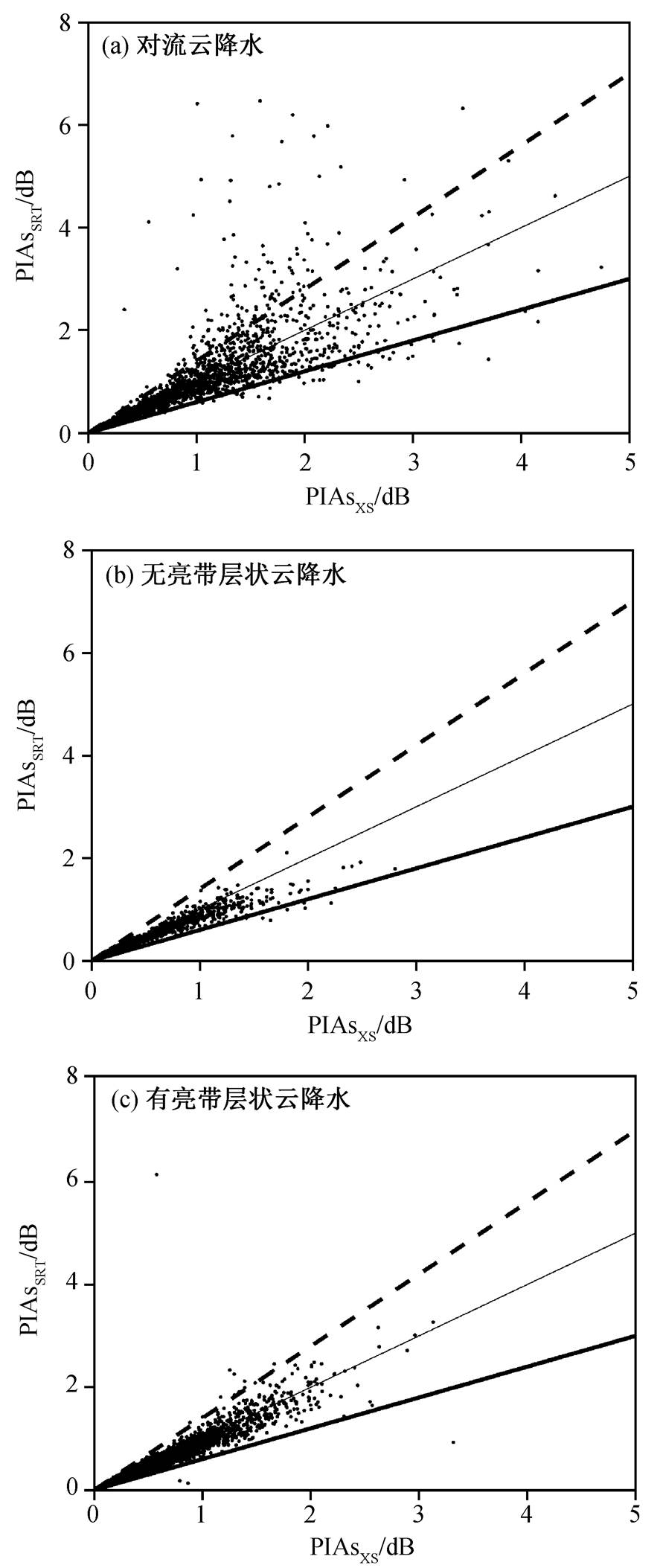
GPM 数据产品使用 6 种不同的方法估计 PIAs值, 并在此基础上定义可靠性因子 reliab factor(简称 rel), 用于反映 SRT 技术的应用质量[14‒16]。当 rel>3 时, 表示 SRT 技术可靠; 当 1 利用美国国家航空航天局(National Aeronautics and Space Administration, NASA)官网GPM L2第7版本 2017 年标准产品 2A.GPM.Ku.V7, 统计不同下垫面(陆地和海洋)不同降水类型(对流云降水、无亮带层状云降水和含亮带层状云降水) SRT 技术应用的可靠性, 结果如表 1 和 2 所示。洋面 SRT 技术应用的可靠性明显高于陆面: 在洋面, 有 1/4 的降水廓线获得可靠的PIAs估计, 而陆面只有 10%。 降水时, 植被和土壤等被雨水打湿, 与无雨天相比, 陆面 NRCS 发生改变, 通过对比有雨与无雨时的 NRCS 不能得到雨区的路径总衰减量 PIAs, 陆面 SRT 技术应用受限, 效果较差。为避免使用降水时的 NRCS, 本文提出相似廓线法, 探索陆面降水廓线估值的新途径。 表1 洋面SRT技术可靠性统计 Table 1 Reliability statistics of the SRT over ocean 降水类型总数可靠不确定不可靠 数量比例/%数量比例/%数量比例/% 含亮带层状云降水2866499969534.786965424.3011730040.92 无亮带层状云降水97616018768019.2324029024.6254819056.16 对流性降水38240613163034.428582622.4416495043.13 总数164521541900525.4739577024.0683044050.48 表2 陆面SRT技术可靠性统计 Table 2 Reliability statistics of the SRT over land 降水类型总数可靠不确定不可靠 数量比例/%数量比例/%数量比例/% 含亮带层状云降水 4150281 413482 9.96 94330522.73 279349467.31 无亮带层状云降水12122687 946018 7.80273677922.58 843989069.62 对流性降水 3743938 73941119.75 87249223.30 213203556.95 总数20016906209891110.49455257622.741336541967.77 由式(5)可知, 降水廓线的PIAs取决于降水滴谱的k-Ze 关系和Zm 廓线, 如果洋面与陆面降水廓线Zm 和k-Ze 关系相同, 则PIAs相同, 借助洋面上降水廓线的衰减订正, 可对陆面Zm 廓线的PIAs进行估值, 从而为HB方法提供路径总积分衰减量。这样, 陆面衰减订正问题就转化为寻找与陆面有相同k-Ze 关系和Zm 廓线的问题。 然而, 洋面与陆面Zm 廓线和k-Ze关系完全相同的几率太低, 为了提高匹配成功率, 可对洋面Zm廓线设定一定的变化区间[Zm1,Zm2], 只要陆面Zm廓线落在洋面Zm 廓线设定的区间内, 就视为匹配成功。洋面Zm 廓线变化区间称为相似区间, 相似区间内的所有廓线称为陆面Zm 廓线的相似廓线。 根据设定的Zm 廓线的变化区间[Zm1,Zm2], 计算Ze廓线的变化区间[Ze1, Ze2], 从而确定相似廓线Zm 的PIAs变化区间[PIAs1, PIAs2], 取中值(PIAs1+ PIAs2)/2作为陆面PIAs的估值。 定义相似因子为(PIAs1+PIAs2)/(PIAs1−PIAs2), 则[PIAs1, PIAs2]区间范围越小, 中值越大, 相似因子越大, 估值的精度越高。相似因子的倒数(PIAs2− PIAs1)/(PIAs1+PIAs2)为估值的最大相对偏差f0。相似廓线法就是利用洋面相似廓线Ze, Zm和k-Ze关系, 对陆面Zm廓线进行PIAs估值。相似廓线法是对SRT技术的一种补充。 在相似廓线法的实际应用中, 首先要设定容许的相对偏差f0, 确定每条洋面Zm廓线的相似区间和PIAs的变化范围, 建立相似廓线库, 然后将陆面降水廓线与相似廓线库匹配, 对PIAs进行估值, 为HB方法提供上边界条件, 最后利用HB方法完成降水廓线的衰减订正。 如图1所示, 建立相似廓线库的流程如下: 提取洋面经大气、云和水汽等非降水粒子衰减订正, 且SRT技术应用可靠的雷达测量的等效反射率因子 Zm、经降水粒子衰减订正后的雷达等效反射率因子 Ze、雷暴顶高度库、地表高度库、降水类型和0℃等温线高度; 设定容许的相对偏差f0; 预设Zm相似廓线的上、下边界廓线Zm2 和Zm1; 计算标准Ze 廓线变化范围的上、下边界廓线Ze2 和Ze1; 利用k-Ze关系计算标准Zm廓线变化范围内PIAs的取值区间[PIAs1, PIAs2]; 若(PIAs2−PIAs1)/(PIAs1+PIAs2)与相似廓线法允许的最大相对偏差不一致, 则调整Zm相似廓线的上、下边界廓线Zm2和Zm1, 直至(PIAs2−PIAs1)/(PIAs1+PIAs2)与f0一致; 将雷暴顶高度库、0℃等温线高度库、地表高度库、降水类型、PIAs1和PIAs2以及Zm的上、下边界廓线加入相似廓线库。 如图2所示, 陆面降水廓线与相似廓线库匹配的流程如下: 提取经大气、云和水汽等非降水粒子衰减订正后陆面雷达测量的等效反射率因子Zm、雷暴顶高度库、降水类型、0℃等温线高度库和地表高度库; 搜寻相似廓线库中跟陆面降水廓线雷暴顶高度库与 0℃等温线高度库差值、0℃等温线高度库与地表高度库差值以及降水类型一致的标准廓线, 若陆面Zm 廓线满足Zm2³Zm³Zm1, 则匹配成功, 取(PIAs1+PIAs2)/2作为陆面Zm 廓线PIAs的值, 如匹配不成功, 则相似廓线法对此廓线失效。 相似廓线法的关键是确定在Zm相似廓线变化范围内PIAs的分布范围, 即确定相似廓线Ze变化范围的边界。 对于洋面上的一条相似廓线Zm (简称标准廓线), 在其相似区间内, 任一邻近廓线Zm'在第r库处与相似廓线Zm的差值记为 其中, 由式(10)可得 由式(11)可知, 对于给定的标准廓线, ∆Ze(r)的值取决于∆A(r)和∆Zm(r), 逐库由近至远(相对于雷达)计算标准Ze 廓线的上、下边界廓线Ze2 和Ze1; 根据 k-Ze 关系确定标准Zm 廓线变化范围内PIAs的分布范围[PIAs1, PIAs2]。 由式(11)可知, ∆Ze(r)是∆A(r), ∆Zm(r), A(r)和Ze(r)的函数。对于给定的标准廓线, Ze 和 Zm 已知, 认为衰减订正准确, 利用 Ze 廓线与 Zm 廓线的差值(单位: dB)确定 PIA 廓线, 进而确定衰减因子 A 廓线; 利用 k-Ze 关系以及已求得的 Ze2, Ze1 和 A 廓线确定∆A(r)廓线。 图1 相似廓线法中相似廓线库的建立流程 Fig. 1 Flowchart of the database using similar profile method 图2 相似廓线法中陆面降水廓线的匹配流程 Fig. 2 Matching flowchart of the rainfall over land using similar profile method 应用相似廓线法对 PIAs 估值时, 陆面降水廓线是在相似廓线变化的一定范围内匹配, 将相似廓线变化范围内 PIAs 取值区间[PIAs1, PIAs2]的中值(PIAs1+PIAs2)/2 作为陆面降水廓线 PIAs 的估值, 由此产生的最大相对偏差为 f0, 这种取值方法在实际应用中会有一定的误差。 数据源自 NASA 官网 GPM L2 第 7 版本标准产品 2A.GPM.Ku.V7, 选取时段为 2014 年 3 月至 2018年 9 月。选取 2014—2017 年洋面 SRT 应用可靠的降水廓线为标准廓线, 建立相似因子分别为 10, 6.7, 5.0, 4.0, 3.3, 2.9 和 2.5 的相似廓线库。选取 2018 年洋面 SRT 应用可靠的降水廓线为检验样本, 视标准PIAsSRT 为真值, 同时应用相似廓线法估计检验样本的PIAsXS, 由此检验相似廓线法的应用效果。 不同相似因子的相似廓线库中不同降水类型匹配成功的降水廓线条数及匹配成功比例如表 3 所示, 其中参加检验的对流云降水廓线为 43569 条, 无亮带层状云降水廓线为 49566 条, 含亮带层状云降水廓线为 132318 条。下面以相似因子为 2.5 的相似廓线库为例进行分析。 表3 SRT技术应用可靠的洋面降水廓线中不同降水类型匹配成功的廓线条数及匹配成功率 Table 3 Percentages and amount of the successfully matched profiles over sea using SRT reliably 相似因子对流云降水无亮带层状云降水含亮带层状云降水 数量比例/%数量比例/%数量比例/% 10.0 70.02 66 0.13 0 0.00 6.7 430.10 459 0.93 15 0.01 5.0 1510.35 1367 2.76 180 0.14 4.0 2960.68 3129 6.31 959 0.72 3.3 5421.24 551511.13 3005 2.27 2.911342.60 839516.94 7461 5.64 2.524555.631165223.511571111.87 图 3 为针对 SRT 技术应用可靠的洋面降水廓线, 分别应用相似廓线法对 PIAs 估值(PIAsXS)和应用 SRT 技术对 PIAs 估值 PIAsSRT 的散点图。对流云降水(图 3(a))中, 相似廓线法结果超出预设容许相对精度的廓线条数较多, 即超出粗实线与虚线间区域的散点数目多, 并且低估问题较为突出(相对于PIAsSRT)。无亮带层状云降水(图 3(b))和有亮带层状云降水(图 3(c))中, 相似廓线法结果超出预设容许相对精度的廓线条数较少, 即超出粗实线与虚线间区域的散点数目少。3 种降水类型的无偏线性拟合系数分别为: 对流云降水 0.9989, 无亮带层状云降水 0.8605, 含亮带层状云降水 0.9398, 两种 PIAs 估值结果较为一致。 粗实线: y=0.6x; 虚线: y=1.4x; 细实线: y=x 图3 SRT技术应用可靠的洋面降水廓线中PIAsxs与PIAsSRT的散点图 Fig. 3 Scatterplot of the path attenuations as estimated by the surface reference technique and the similar profile method of the rainfall over sea using SRT reliably 表 4 显示, SRT 技术应用可靠洋面降水廓线中PIAsSRT 与 PIAsxs 的相对偏差(RE=|PIAsxs−PIAsSRT|/ PIAsxs)小于 40%的分布比例分别为: 对流云降水88.8%, 无亮带层状云降水 98.9%, 含亮带层状云降水 98.9%。平均 96.8%的匹配成功廓线 PIAs 估值达到预设目标, 表明该方法在洋面的应用效果很好。 虽然建库时设定的容许相对偏差达到 40%(相似因子为 2.5), 匹配的成功率依然不高, 对流云降水匹配成功率为 5.63%, 无亮带层状云降水成功率为 23.51%, 含亮带层状云降水成功率为 11.87%。 数据源自 NASA 官网 GPM L2 第 7 版本标准产品 2A.GPM.Ku.V7, 时段为 2014 年 3 月至 2018 年 9月。选取 2014—2017 年洋面 SRT 应用可靠的降水廓线为标准廓线, 建立相似因子分别为 10, 6.7, 5.0, 4.0, 3.3, 2.9 和 2.5 相似廓线库。检验样本选取2014—2018 年陆面降水廓线, 通过第 3 节的检验, 说明相似廓线法应用于洋面降水廓线 PIAs 的估值是可行的, 平均 96.8%的洋面降水廓线 PIAs 在预设的容许相对偏差范围内。由于相似廓线法不受下垫面性质影响, 因此将其应用于陆面降水廓线, 应取得与洋面降水廓线相似的效果。 不同相似廓线库中不同降水类型匹配成功的降水廓线条数及匹配成功比例如表 5 所示, 其中参加检验的陆面降水廓线中有对流云降水廓线 177712条, 无亮带层状云降水廓线 486268 条, 含亮带层状云降水廓线 608763 条。下面以相似因子为 2.5 的相似廓线库为例进行分析。 图 4 为针对陆面降水廓线, 分别应用相似廓线法对 PIAs 估值(PIAsxs)和 SRT 技术对 PIAs 估值(PIAsSRT)的散点图。3 种类型降水中, 相似廓线法结果超出预设相对偏差的廓线条数较多(超出粗实线与粗虚线之间间区域的散点数目多), PIAsSRT 与PIAsxs的差异较大。 从表 6 可以看出, 陆面降水廓线中, PIAsSRT 与PIAsxs 的相对偏差(RE=|PIAsxs−PIAsSRT|/PIAsxs)小于40%的分布比例依次为对流云降水 15.6%, 无亮带层状云降水 10.9%, 含亮带层状云降水 2.6%, PIAsxs与 PIAsSRT 差异较大, 平均 7.5%的匹配样本相对偏差在设定的相对偏差范围内, 两种 PIAs 估值方法的结果差别较大。 综上所述, PIAsxs 与PIAsSRT 的差异较大: 对流云降水中, 15.6%的降水廓线PIAs估值的相对偏差小于40%; 无亮带层状云降水中, 10.9%的降水廓线PIA估值的相对偏差小于40%; 含量带层状降水中, 2.6%的降水廓线PIAs估值的相对偏差小于40%。这与洋面检验结果有较大的差别, 与陆面SRT技术应用效果较差的结论相一致。 本文提出相似廓线法, 探索陆面降水廓线路径积分总衰减 PIAs 估值的新途径。该方法利用 SRT技术在洋面应用中可靠的降水廓线, 建立相似廓线库, 对陆面降水廓线 PIAs 进行估值。通过匹配陆面与洋面的降水廓线, 有效地回避 SRT 技术在陆面应用中降水前后 NRCS 保持不变的基本假设, 是对SRT 技术的一种补充。 相似廓线法在洋面衰减订正的应用检验表明, PIAsxs 与 PIAsSRT 的一致性较好, 相似廓线法对降水廓线 PIAs 估值取得不错的效果, 含亮带层状云降水和无亮带层状云降水的应用效果好于对流云。平均96.8%的匹配样本相对偏差都在设定的范围内。 表4 SRT技术应用可靠的洋面降水廓线中PIAsxs与PIAsSRT的相对偏差统计 Table 4 Statistics of the relative error between PIAsSRT and PIAsxs of the rainfall over sea using SRT reliably 降水类型比例/% 0 粗实线: y=0.6x; 虚线: y=1.4x; 细实线: y=x 图4 陆面降水廓线中PIAsxs与PIAsSRT的散点图 Fig. 4 Scatterplot of the path attenuations as estimated by the surface reference technique and the similar profile method over land 表5 陆面不同降水类型匹配成功的廓线条数及匹配成功率 Table 5 Percentages and amount of the successfully matched profiles over land 相似因子对流云降水无亮带层状云降水含亮带层状云降水 数量比例/%数量比例/%数量比例/% 10.0 2 0.00 121 0.02 0 0.00 6.7 26 0.01 1006 0.21 113 0.02 5.0 121 0.07 3453 0.71 1534 0.25 4.0 310 0.17 8552 1.76 8754 1.44 3.3 709 0.40 17719 3.64 28608 4.70 2.9 1934 1.08 31670 6.51 6790611.16 2.51919610.8014646430.1213291621.83 相似廓线法在陆面衰减订正的应用对比表明, PIAsxs 与 PIAsSRT 存在明显差异。平均 7.5%的匹配样本相对偏差在设定的范围内。由于缺少陆面PIAs 真值, 具体的应用效果有待进一步研究。 相似廓线法的基本假设是匹配廓线的 k-Ze 关系相同, 即相同降雨类型的 k-Ze 关系一致。在实际应用中, 标准廓线的 k-Ze 关系与匹配成功降水廓线的k-Ze 关系存在一定的偏差, 导致相似廓线法的误差, 但避免了 HB 方法的不稳定性。 表6 陆面降水廓线中PIAsxs与PIAsSRT的相对偏差统计 Table 6 Statistics of the relative error between PIAsxs and PIAsSRT of the rainfall over land 降水类型比例/% 0 相似廓线法在实际应用中匹配成功率较低, 平均为 21.92%, 其中最大成功率(30.12%)为陆面无亮带层状云降水, 最小成功率(5.63%)为洋面对流云降水, 这是相似廓线法的局限性所致。相似廓线法的基础是相似廓线库, 需要足够多的洋面观测资料, 才能选取足够多的标准廓线。可以通过两种方法来提高匹配成功率, 一是提高容许相对偏差, 降低匹配条件; 二是增加建立相似廓线库标准廓线的数目, 建立一个高效的有充分代表性的相似廓线库。 参考文献 [1] Braun S A. Tropical rainfall measuring mission senior review proposal 2011 [EB/OL]. (2011‒09‒01) [2019‒ 02‒15]. https://pmm.nasa.gov/sites/default/files/docu ment_files/TRMMSenRevProp_v1.2.pdf [2] Tapiador F J, Turk F J, Peterson W, et al. Global pre-cipitation measurement: methods, datasets and appli-cations. Atmospheric Research, 2012, 104: 70‒ 97 [3] Hitschfeld W, Bordan J. Errors inherent in the radar measurement of rainfall at attenuating wavelengths. J Meteor, 1954, 11: 58–67 [4] Jones J A, Iguchi T, Okamoto K, et al. A hybrid surface reference technique and its application to the TRMM precipitation radar. Journal of Atmospheric and Oceanic Technology, 2004, 21: 1645‒1658 [5] Meneghini R, Eckerman J, Atlas D. Determination of rain ratefrom a spaceborne radar using measurements of total attenuation. IEEE Trans Geosci Remote Sens, 1983, 21: 34–43 [6] liven L F, Giovanangeli J P. An experimental study of microwave scattering from rain- and wind roughened seas. International Journal of Remote Sensing, 1993, 14: 855–869 [7] Meneghini R. Rain rate estimates for an attenuating radar. Radio Sci, 1978, 13: 459‒470 [8] Hildebrand P H. Iterative correction for attenuation of 5 cm radar in rain. Journal of Applied Meteorology, 1978, 17(4): 508‒514 [9] 王振会, 张培昌. 天气雷达回波衰减订正算法的研究(Ⅱ):数值模拟与个例实验. 高原气象, 2001, 20(2): 115‒120 [10] Iguchi T, Meneghini R. Intercomparisons of single-frequency methods for retrieving a vertical profile from airborne or spaceborne radar data. Atmos Ocea-nic Technol, 1994, 11: 1507–1516 [11] Yang Z, Tang S, Wu J. An experimental study of rain effects on fine structures of wind waves. J Phys Oceanogr, 1997, 27: 419–430 [12] 赵文中, 赵柏林, 杜金林. 地物微波反射率的研究[D]. 北京: 北京大学, 1981 [13] Komukai J, Okamoto K, Shige S, et al. Analysis of surface normalized radar cross section for the impro-vement of the TRMM precipitation radar algorithm part II: over the land. Journal of The Remote Sen- sing Society of Japan, 2010, 30(4): 234‒274 [14] PPS. Precipitation processing system global precipi-tation measurement [EB/OL]. (2016‒03) [2019‒02‒13]. https://pmm.nasa.gov/resources/documents/algorithm-information [15] Meneghini R, Iguchi T, Kozu T, et al. Use of the surface reference technique for path attenuation estimates from the SRT. American Meterological Society, 2000, 12: 2053‒2070 [16] Iguchi T, Seto S, Meneghini R. GPM/DPR level-2 algorithm theoretical basis document [EB/OL]. (2017‒08‒01) [2019‒02‒10]. https://pmm.nasa.gov/ sites/default/files/document_files/ATBD_DPR_201708_whole_1.pdf Application of Similar Profile Method in Attenuation Correction of Single-Frequency Satellite-Borne Radar over Land Abstract In view of the difficulty in estimating the path-integrated attenuation(PIA) of rain attenuation over land using GPM-CO Ku data, we propose similar profile method. Using the radar profiles of rainfall over sea and the SRT-corrected radar profiles of rainfall, the profiles database is established with a certain precision to estimate the PIA over land by means of matching profiles over land with those in the database. Applications of the method to measurements for 2018 from the DPR of Ku band suggest that it performs well over the ocean.With 40% margin of error, the percentage of successful applications for convective rain is 88.8%, and it is 98.9% for both stratiform rain with and in the absence of a detectable bright band. In terms of rainfall from 2014 to 2018 over land, the result of using the similarity profile method is different from the rainfall over ocean,which is consistent with the poor performance of the SRT-corrected mothed over land. Key words GPM-CO DPR; similar profile method; path-integrated attenuation (PIA) 国家重点研究发展计划(2017YFC0209602)和国家自然科学基金(41475016)资助 doi: 10.13209/j.0479-8023.2019.118 收稿日期: 2019‒03‒03; 修回日期: 2019‒04‒022 相似廓线法
2.1 相似廓线法的基本思路


2.2 相似廓线法的应用流程
2.3 相似廓线PIAs边界的确定
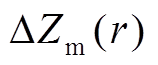 :
: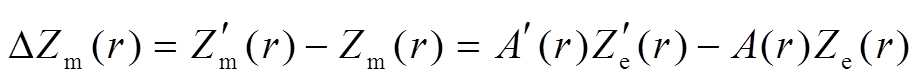 , (9)
, (9)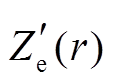 为邻近廓线第r库的雷达反射率因子,
为邻近廓线第r库的雷达反射率因子,  为邻近廓线第r库的衰减因子。记
为邻近廓线第r库的衰减因子。记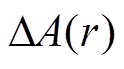 =
= 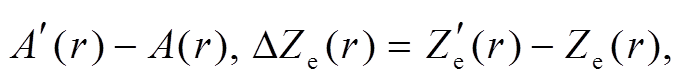 则式(9)变形为
则式(9)变形为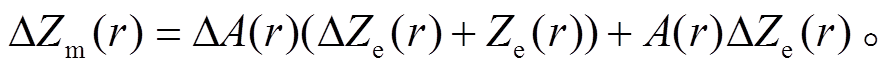 (10)
(10)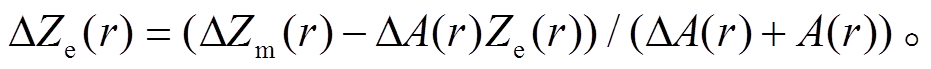 (11)
(11)2.4 衰减因子 A 和∆A 廓线的确定
2.5 影响相似廓线法的因子
3 相似廓线法在洋面衰减订正的应用效果检验
3.1 数据及研究方案
3.2 应用效果

4 相似廓线法在陆面衰减订正的应用效果评估
4.1 数据及研究方案
4.2 应用效果
5 结论