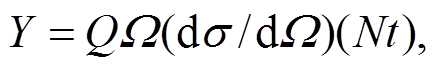 (1)
(1)摘要 为了达成高精度离子束分析, 深入分析立体角的计算误差。以包含束斑大小的面对面立体角为基准, 计算点对面立体角和近似立体角在不同离子束分析实验几何参数下的精度。基于北京大学 4.5MV 静电加速器离子束分析工作, 探讨束流流强分布和截面分布对立体角的影响。最后给出近似立体角精度好于 1%的几何估算条件, 并举例证明高精度立体角的实现依赖于精确的机械加工。
关键词 面对面立体角; 束流流强分布; 核反应截面; 高精度; 离子束分析
离子束分析是通过测量载能离子与物质相互作用的产物而得到表层及近表层物质的元素种类、含量和分布的一类分析方法。离子束分析灵敏度高, 大部分可以进行无损分析, 所以广泛应用于物理学和材料学的基础研究以及微电子、功能材料、能源材料、生物及医学材料、考古、环境、艺术品和文物鉴定等多个领域, 甚至在有些研究中有不可替代的作用[1]。随着各领域研究的不断深入, 研究对象更加精细化和微观化, 对离子束分析(ion beam analysis, IBA)精度也提出更高的要求。Reichart 等[2]通过高精度的离子束分析来确定氢在化学气相沉积(chemical vapor deposition, CVD)金刚石中晶界处的聚集行为, 而之前的离子束分析方法没有足够的精度来判断氢在 CVD 金刚石中的分布状况。当前, 国际上先进的 IBA 实验室离子束分析得到的元素含量数据精度可以达到好于 1%的水平[3–4], 如德国材料研究与测试机构(Institute for Materials Research and Testing, BAM)、比利时参考材料和测量机构(Institute for Reference Materials and Measurements, IRMM)和英国萨里大学离子束分析中心(University of Surrey Ion Beam Centre, SIBC)等。国内的 IBA 误差在 5%左右[5–6]。北京大学核物理与核技术国家重点实验室正在对现有的IBA 平台进行升级改造, 力求使其分析精度达到国际先进水平。作为此工作的一部分, 本文探讨 IBA 中一个重要的参数——探测立体角的误差问题。
IBA 基于式(1)分析均匀薄膜样品的元素含量。在分析厚样品元素含量的深度分布时, 解谱过程把样品视为多层薄样品来处理, 因此式(1)是 IBA 中最基本的公式。在束斑面积和探测器所张的立体角都很小时, 探测器记录到的被探测粒子产额为
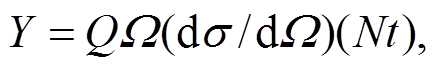 (1)
(1)其中, Y是探测到的相互作用产物产额, Q是入射粒子数, 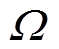 为探测器对束流入射点所张的立体角,
为探测器对束流入射点所张的立体角, 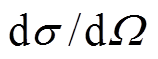 是相互作用微分截面, (Nt)为靶原子面密度。如果(Nt)是待测量的物理量, 由式(1)可知, 在不使用相对测量法的情况下, 解谱得到的误差直接受制于Y, Q,
是相互作用微分截面, (Nt)为靶原子面密度。如果(Nt)是待测量的物理量, 由式(1)可知, 在不使用相对测量法的情况下, 解谱得到的误差直接受制于Y, Q,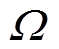 和
和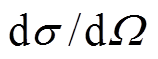 的测量误差。其中, Y 的相对误差
的测量误差。其中, Y 的相对误差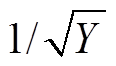 可以通过增加计数的方式来减小。为了得到高精度的结果, 通常采用相对测量法消去 Q,
可以通过增加计数的方式来减小。为了得到高精度的结果, 通常采用相对测量法消去 Q,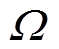 和
和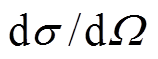 等测量量, 从而减小误差。在同样的技术手段下, 消除越多的测量量, 实验结果的精度越高。若采用多探测通道, 并进行多种分析方法的耦合测量, 探测立体角
等测量量, 从而减小误差。在同样的技术手段下, 消除越多的测量量, 实验结果的精度越高。若采用多探测通道, 并进行多种分析方法的耦合测量, 探测立体角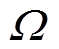 将是一个不能消去的参量。
将是一个不能消去的参量。
Q 通常由法拉第筒和束流积分仪来测量, 在载能离子粒子束为 nA 量级的情况下, 束流积分仪测量的相对误差为千分之几的量级[7]。将束流积分仪与法拉第筒相结合, 在离子束分析中对入射粒子束 Q 测量的相对误差可小于1%[8]。
对于相互作用截面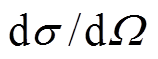 , 除部分有精确的理论公式外, 其余
, 除部分有精确的理论公式外, 其余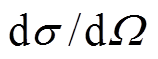 的误差来自测量
的误差来自测量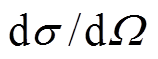 的实验。离子束分析常用的截面数据来自IBANDL。IBANDL 是离子束专用数据库, 提供实验系下的截面数据, 内嵌 Sigmacalc[9]通过结合大量的实验数据和理论核结构模型来评估部分截面数据, 但未提供误差。在进行高精度分析时, 应考察数据库提供的
的实验。离子束分析常用的截面数据来自IBANDL。IBANDL 是离子束专用数据库, 提供实验系下的截面数据, 内嵌 Sigmacalc[9]通过结合大量的实验数据和理论核结构模型来评估部分截面数据, 但未提供误差。在进行高精度分析时, 应考察数据库提供的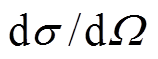 数据的误差以及
数据的误差以及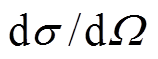 的测量误差, 即探测系统误差、加速器束流误差、标样制样误差、几何条件误差和解谱误差等。
的测量误差, 即探测系统误差、加速器束流误差、标样制样误差、几何条件误差和解谱误差等。
立体角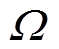 与 IBA 实验的几何设置相关, 大量的文献通过数值计算[10–13]或蒙特卡洛计算[14–15]给出不同几何设置的立体角计算方式。由于实验中束斑面积不可能是理想点, 所以探测器对束斑所张的立体角会偏离几何学定义的立体角(面对面立体角)。本文主要讨论 IBA 实验中使用的
与 IBA 实验的几何设置相关, 大量的文献通过数值计算[10–13]或蒙特卡洛计算[14–15]给出不同几何设置的立体角计算方式。由于实验中束斑面积不可能是理想点, 所以探测器对束斑所张的立体角会偏离几何学定义的立体角(面对面立体角)。本文主要讨论 IBA 实验中使用的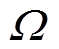 的近似表达及其成立条件, 并针对北京大学 4.5MV 静电加速器离子束分析靶室设置及 3He(D,p)4He 微分截面测量实验[16–18]的条件, 通过数值积分计算面对面立体角, 分析束流强弱分布和微分截面角分布对面对面立体角的影响。
的近似表达及其成立条件, 并针对北京大学 4.5MV 静电加速器离子束分析靶室设置及 3He(D,p)4He 微分截面测量实验[16–18]的条件, 通过数值积分计算面对面立体角, 分析束流强弱分布和微分截面角分布对面对面立体角的影响。
如图 1 所示, 以被观测点为球心, 构造一个球面, 任意物体投影到该球面上的投影面积与球半径平方之比, 即为该物体相对于该被观测点的立体角, 其大小等于在以观测点为球心的单位球面上投影的面积:
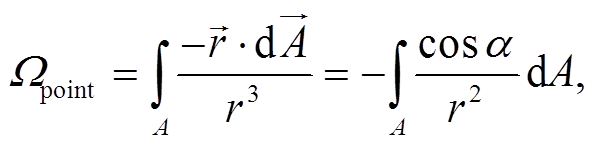 (2)
(2)其中, 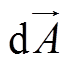 为探测器的微分面积向量,
为探测器的微分面积向量, 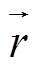 为束斑指向
为束斑指向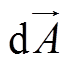 的长度向量, a 为
的长度向量, a 为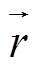 与
与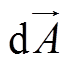 的夹角。
的夹角。
IBA 中的立体角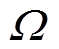 指探测器接收面对束斑所张的立体角。当束斑可近似为一个点时, 可用式(2)计算立体角, 得到的立体角点对面立体角。
指探测器接收面对束斑所张的立体角。当束斑可近似为一个点时, 可用式(2)计算立体角, 得到的立体角点对面立体角。
在离子束分析中, 截面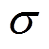 的物理意义为单个入射粒子与单个靶核发生核反应的概率, 为面积量纲。在一般实验几何条件下, 束斑并不是一个很好的几何点, 而是具有一定的面积 S。假设束流通量 f在束斑内是均匀的, 有 Q=fS, 则探测器接收到的反应离子产额为
的物理意义为单个入射粒子与单个靶核发生核反应的概率, 为面积量纲。在一般实验几何条件下, 束斑并不是一个很好的几何点, 而是具有一定的面积 S。假设束流通量 f在束斑内是均匀的, 有 Q=fS, 则探测器接收到的反应离子产额为
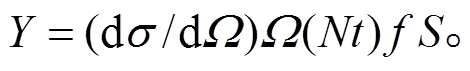 (3)
(3)当束斑的面积不可忽略时, 探测器接收到的产额可以用对束斑面积S的积分得到:
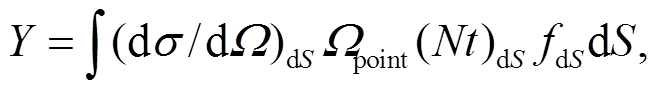 (4)
(4)
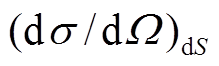 ,
, 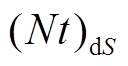 和
和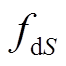 分别为 dS 处的微分截面、靶原子面密度和束流通量。当
分别为 dS 处的微分截面、靶原子面密度和束流通量。当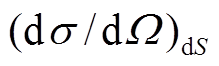 ,
,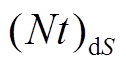 和
和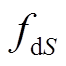 在 S 上可近似为定值时, 可将
在 S 上可近似为定值时, 可将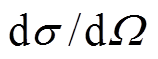 ,
,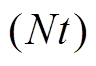 和 f提到积分号外:
和 f提到积分号外: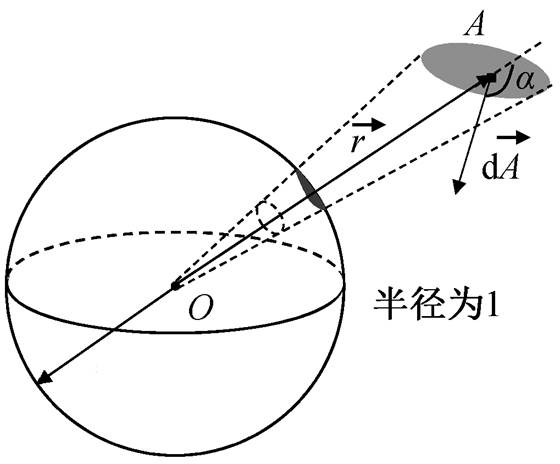
O为束斑, A为探测器
图1 几何学立体角示意图
Fig. 1 Schematic for solid angle in geometry
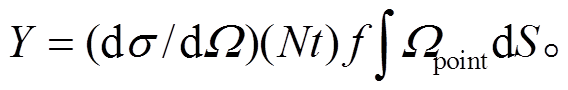 (5)
(5)将式(5)与式(3)对比, 可得到包含束斑面积的立体角![]() (面对面立体角):
(面对面立体角):
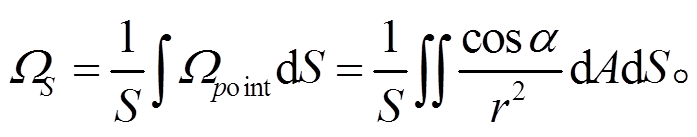 (6)
(6)
图 2 为离子束分析中常用的 IBM 几何设置, 即束流方向、探测器法线和束斑法线在一个平面内。其中, A 为探测器光阑面积, S 为束斑面积, d 为二者中心之间的距离, 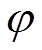 为出射角, 束流入射方向在束斑平面和探测器光阑平面分别以束斑对称中心和探测器光阑对称中心建立两个直角坐标系, z和z¢轴分别为两平面的法线方向。
为出射角, 束流入射方向在束斑平面和探测器光阑平面分别以束斑对称中心和探测器光阑对称中心建立两个直角坐标系, z和z¢轴分别为两平面的法线方向。
通过坐标变换, 可得在 x¢y¢z¢坐标系下, 面对面立体角的计算公式为
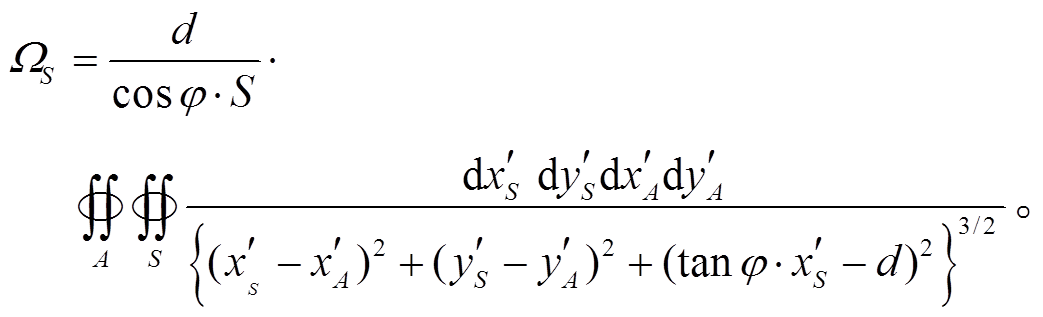 (7)
(7)当![]() ,
,![]() 和
和![]() 在 S 上不能近似为定值(已提到产额公式积分号外)时, 可将其折叠包含到立体角内, 则有以下包含截面修正的面对面立体角
在 S 上不能近似为定值(已提到产额公式积分号外)时, 可将其折叠包含到立体角内, 则有以下包含截面修正的面对面立体角![]() , 包含靶原子面密度修正的立体角
, 包含靶原子面密度修正的立体角![]() 和包含束流通量修正的面对面立体角
和包含束流通量修正的面对面立体角![]() :
:
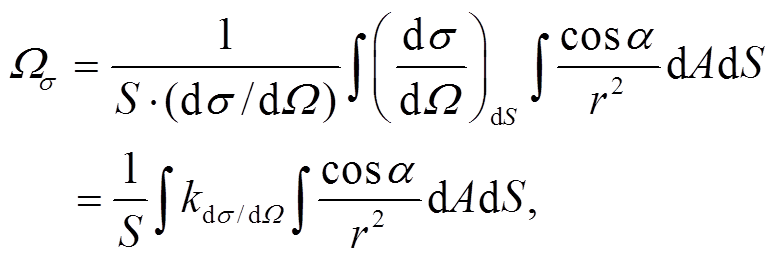 (8)
(8)
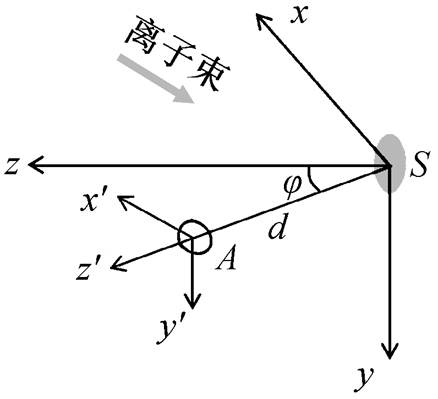
图2 常用IBA平台立体角示意图
Fig. 2 Solid angle schematic for normal IBA platform
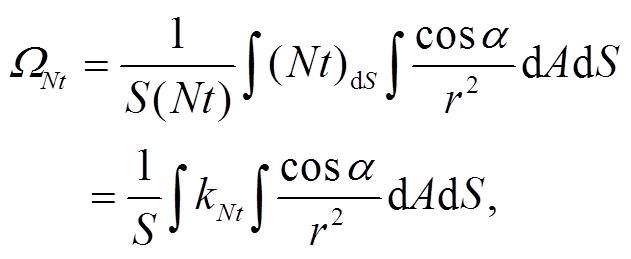 (9)
(9)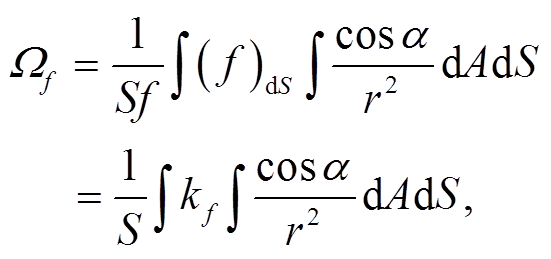 (10)
(10)
![]() ,
,![]() 和
和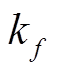 分别为
分别为![]() ,
, ![]() 和
和![]() 在束斑面积 S 上的分布。利用式(8)~(10), 可评估并计算由于将近似值
在束斑面积 S 上的分布。利用式(8)~(10), 可评估并计算由于将近似值 ,
,![]() 和 f 引入到立体角的偏差。
和 f 引入到立体角的偏差。
利用 Simpson1/3 法则[19]进行数值积分, 通过设置截断误差和增加迭代次数, 可得到任意精度的各种立体角的值。这些立体角积分计算的收敛性很好。图 3 展示面对面立体角计算值的迭代收敛过程, 迭代 2 次误差即达 0.001msr, 相对误差好于0.02%。
在实际离子束分析中, 常使用立体角的近似公式![]() 和点对面立体角代替真实的面对面立体角:
和点对面立体角代替真实的面对面立体角:
 (11)
(11)为了衡量![]() 与点对面立体角对面对面立体角的近似程度, 我们采用图 2 的实验几何条件设置, 计算
与点对面立体角对面对面立体角的近似程度, 我们采用图 2 的实验几何条件设置, 计算![]() ,
, 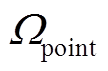 和
和![]() , 定义探测器光阑半径为 RA, 束斑半径为RS, 则
, 定义探测器光阑半径为 RA, 束斑半径为RS, 则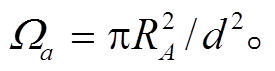
规定![]() 对
对![]() 的近似为
的近似为
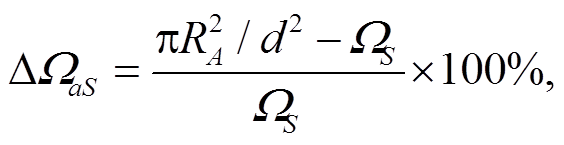
![]() 的绝对值越小, 表明
的绝对值越小, 表明![]() 越接近
越接近![]() , 近似越好。
, 近似越好。
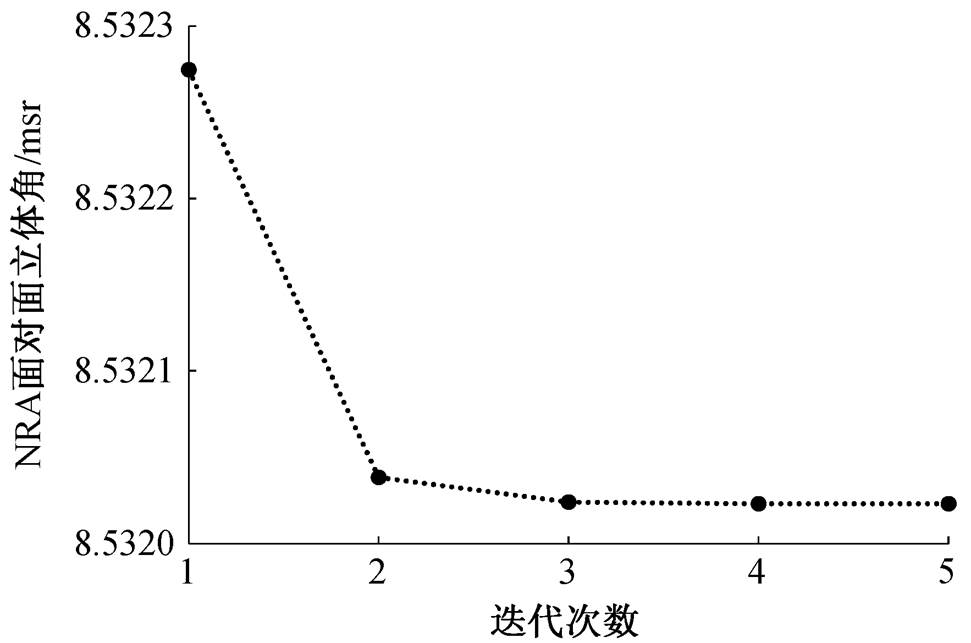
图3 Simpson 1/3法则数值积分面对面立体角计算值随迭代次数的变化
Fig. 3 Face to face solid angle calculated by Simpson 1/3 method vs. increasing times of Simpson iteration
![]() 对
对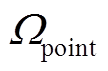 的近似为
的近似为
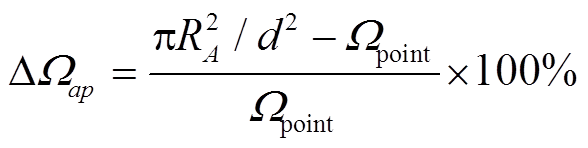 。
。
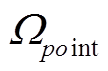 对
对![]() 的近似为
的近似为
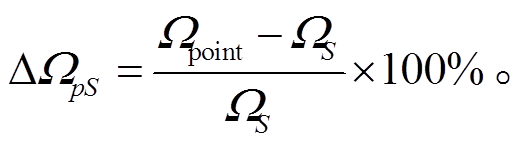
由此可得到
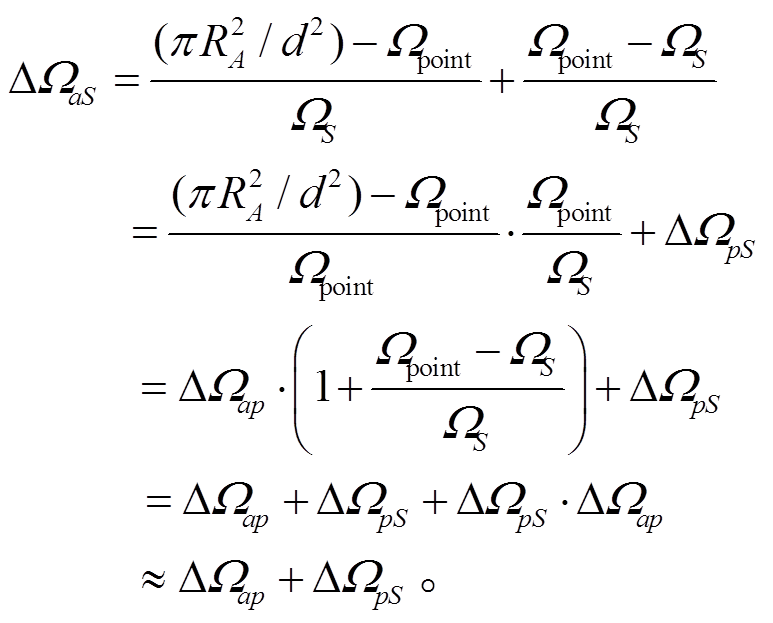 (12)
(12)
在图 2 的几何设置条件下, 点对面立体角可通过式(2)积分得到
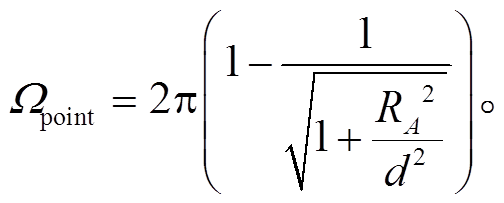 (13)
(13)由式(13)可以看出, 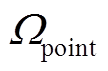 只与
只与![]() 有关。结合
有关。结合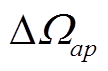 的定义式, 得知
的定义式, 得知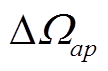 也只与
也只与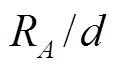 有关。
有关。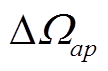 随
随![]() 变化的曲线如图4所示。
变化的曲线如图4所示。
若要求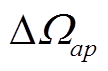 小于1%, 则需要
小于1%, 则需要
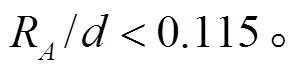 (14)
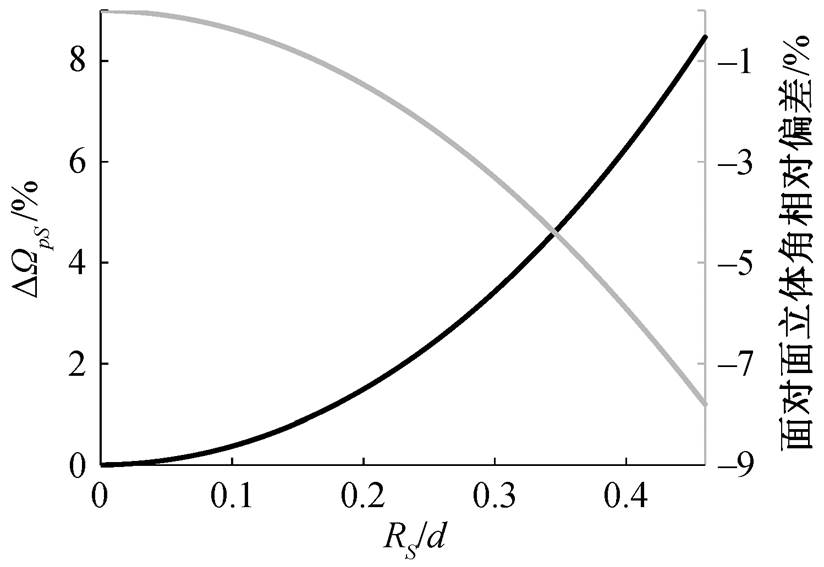
(14)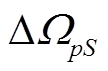 代表点对面立体角和面对面立体角的相对偏差。点对面立体角与面对面立体角的差别在于对束斑大小的考虑, 而与探测器光阑大小无关, 因此只与 RS / d 有关。图 5 为
代表点对面立体角和面对面立体角的相对偏差。点对面立体角与面对面立体角的差别在于对束斑大小的考虑, 而与探测器光阑大小无关, 因此只与 RS / d 有关。图 5 为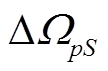 随 RS / d 的变化曲线。
随 RS / d 的变化曲线。
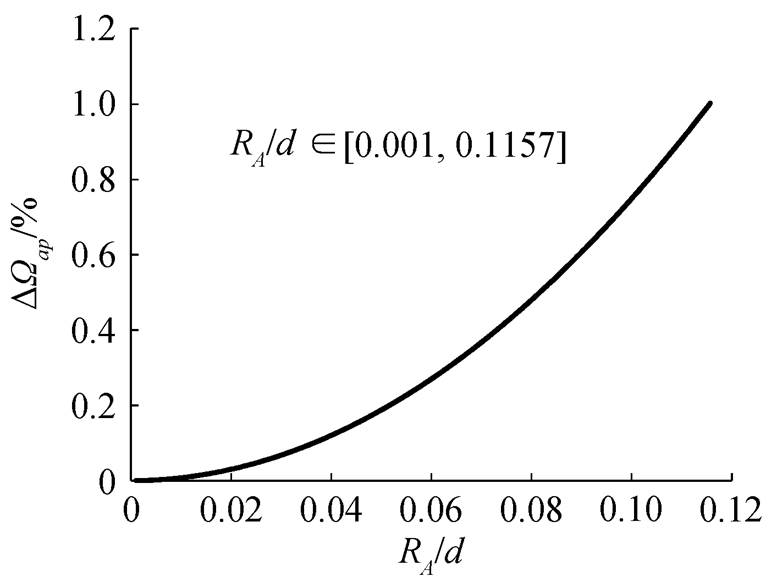
图4 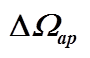 随
随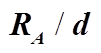 变化关系曲线
变化关系曲线
Fig. 4 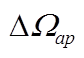 with respect to
with respect to 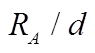
参考点为RS/d=0的点对面立体角, 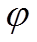 =153°, RS/d
=153°, RS/d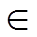 [0, 0.460]
[0, 0.460]
图5 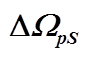 和面对面立体角相对偏差
和面对面立体角相对偏差
Fig. 5 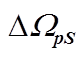 and the percentage deviation of face to face solid angle relative to the value with RS/d
and the percentage deviation of face to face solid angle relative to the value with RS/d
根据图 5, 可以得到相对偏差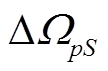 小于 1%的条件为
小于 1%的条件为
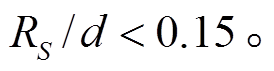 (15)
(15)当探测距离和探测器接收面积都固定时, 增加束斑面积, 则面对面立体角的变化如图 5 所示。若束斑半径变化明显(如当 d=80mm 时, RS从 0 增至 15 mm), 面对面立体角会有 1%以上的变化。束斑越大, 探测距离越小, 面对面立体角随束斑半径的变化越大, 若加速器状态差, 则束斑面积不稳定, 小束斑远距离探测比大束斑近距离带来的立体角的变化小。
由于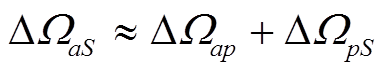 , 综合
, 综合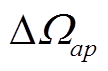 和
和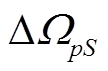 的规律,
的规律, ![]() 好于1%的条件为
好于1%的条件为
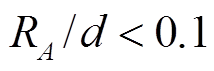 且
且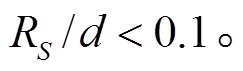 (16)
(16)由式(7), 出射角 对立体角也有影响。图 6 为北京大学 4.5MV 静电加速器离子束分析靶室 RBS路立体角随出射角的变化曲线(RS=3.16, RA=1, d=77.1, φ=153°)。可以看出, 角度误差为 1°, 引入
对立体角也有影响。图 6 为北京大学 4.5MV 静电加速器离子束分析靶室 RBS路立体角随出射角的变化曲线(RS=3.16, RA=1, d=77.1, φ=153°)。可以看出, 角度误差为 1°, 引入
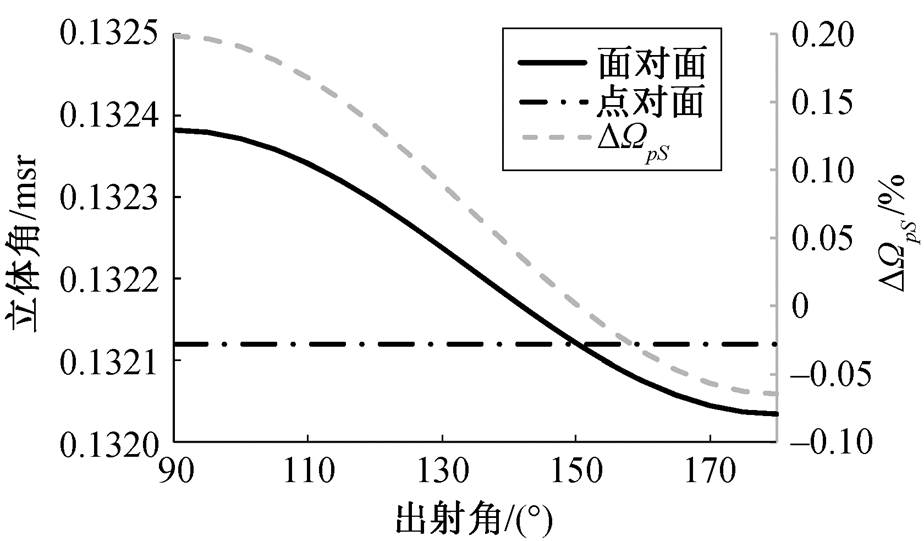
图6 RBS路立体角及 随出射角的变化曲线
随出射角的变化曲线
Fig. 6 Solid angle and 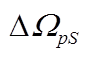 for RBS with respect to ejected angle
for RBS with respect to ejected angle
立体角的误差小于 0.05%, 故可以忽略。
利用立体角的近似公式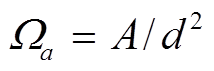 , 可得立体角的相对误差公式为
, 可得立体角的相对误差公式为
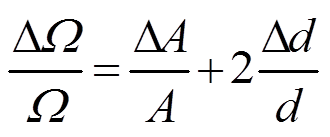 。 (17)
。 (17)在测量时, 若束斑中心与探测器光阑的距离 d 有1%的测量偏差, 则会造成立体角值 2%的系统误差, 这一系统误差可以通过相对测量法实验消除; 若实验平台的几何重复性不好, 距离 d 本身有 1%的误差(比如更换样品前后导致的 d 涨落), 则会造成实际立体角 2%的误差, 进而导致实验精度下降。由此可见, 高精度离子束分析需要精确的测量手段和稳定的实验平台。
下面通过两个例子来说明立体角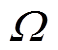 近似方案的选择。
近似方案的选择。
图 7 为北京大学 4.5MV 静电加速器离子束分析靶室示意图。束流通过 2mm×5mm 的长方形光阑进入靶室, 电荷空间效应会带来约千分之一的束斑面积变化, 束斑面积取决于束流光阑面积。
在测量 3He(D,p)4He 实验室系下 135°核反应微分截面时, 利用 135°出射角方向的金硅面垒探测器探测 NRA 产生的质子产额, 利用 153°出射角方向的金硅面垒探测器探测 RBS 的 3He 产额, 实验原理式如下:
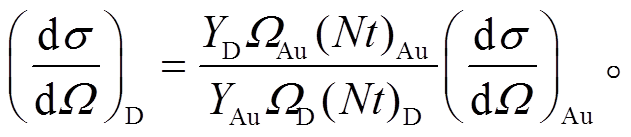 (18)
(18)NRA 探测器前采用抛物线形光阑, 核反应微分截面角分布在光阑范围内有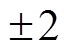 %的涨落。RBS 探测器前采用直径为 1mm 的圆孔光阑, RBS 微分截面角分布在光阑范围内有
%的涨落。RBS 探测器前采用直径为 1mm 的圆孔光阑, RBS 微分截面角分布在光阑范围内有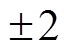 %的涨落。两个探测器光阑中心与束斑中心的距离均为 77.1mm。束流通量在x方向约为半高全宽为束流光阑宽度的高斯分布。
%的涨落。两个探测器光阑中心与束斑中心的距离均为 77.1mm。束流通量在x方向约为半高全宽为束流光阑宽度的高斯分布。
RBS 和 NRA 两路探测系统的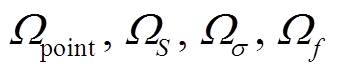 和
和![]() 如表 1 所示。可以看出, 对于本文的实验几何设置, 采用近似值
如表 1 所示。可以看出, 对于本文的实验几何设置, 采用近似值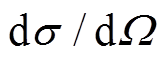 和 f 导致的立体角偏差, 在 0.3%的误差以下可忽略不计。
和 f 导致的立体角偏差, 在 0.3%的误差以下可忽略不计。
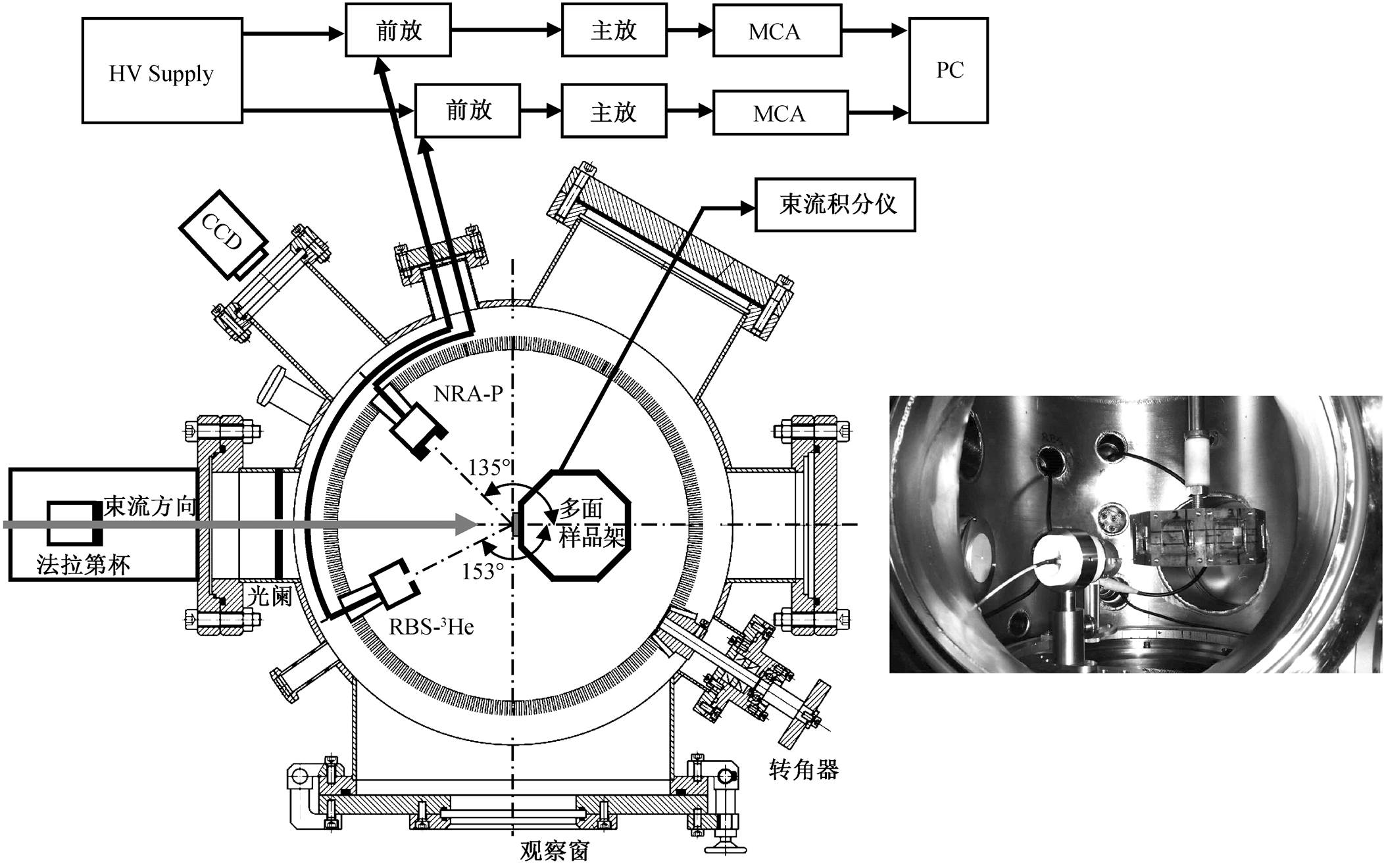
图7 核反应分析实验终端的装置示意图[17]
Fig. 7 Demonstration for nuclear reaction analysis platform[17]
表1 立体角计算结果(msr)
Table 1 different solid angles (msr)

立体角RBS路NRA路 0.1321248.57949 0.1321198.52612 0.1321108.53202 0.1324448.53202 0.1321088.53091
说明: 标注数据误差小于数据最低位数; *为束流通量呈半高全宽为5 mm的高斯分布。
NRA 路 RA / d=4.03 / 77.1 且RS / d=3.16 / 77.1, 满足式(16)。根据表 1 计算得到, 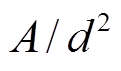 与面对面立体角相差 0.55%。RBS 路RA / d=0.5 / 77.1 且 RS / d= 3.16 / 77.1, 满足式(16),
与面对面立体角相差 0.55%。RBS 路RA / d=0.5 / 77.1 且 RS / d= 3.16 / 77.1, 满足式(16), 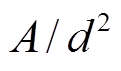 与面对面立体角相差0.01%。
与面对面立体角相差0.01%。
北京大学 4.5MV 静电加速器离子束分析靶室的束流光阑误差不超过 1mm, 由电荷空间效应带来的束斑面积变化不超过千分之一, 根据图 5, 由束斑尺度变化引入立体角的误差可以忽略。
根据图 6, RBS 路由出射角误差引入立体角的误差可忽略不计。NRA 路的计算结果与 RBS 路类似, 由出射角误差引入立体角的误差同样可以忽略不计。
综上所述, 针对北京大学 4.5MV 静电加速器离子束靶室的几何布置, 且假设束流到达光阑前流强分布的 FWHM 等于光阑宽, 核反应截面分布涨落![]() 2%, 束流光阑测量误差和出射角测量误差引入立体角的误差可忽略不计。所以, 可以利用
2%, 束流光阑测量误差和出射角测量误差引入立体角的误差可忽略不计。所以, 可以利用![]() 来近似面对面立体角, 其精度好于 1%。立体角的主要误差来自探测器光阑面积 A 和探测距离 d 的测量误差, 根据式(17), 对于孔径为
来近似面对面立体角, 其精度好于 1%。立体角的主要误差来自探测器光阑面积 A 和探测距离 d 的测量误差, 根据式(17), 对于孔径为![]() 的圆形探测器光阑, 有
的圆形探测器光阑, 有
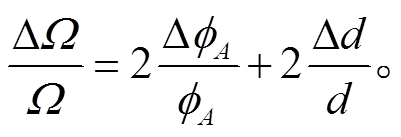 (19)
(19)普通游标卡尺精度为 0.01mm, RBS 路![]() 为 1mm, 立体角测量误差大于 2%。因此, 加工探测器光阑应采用激光打孔的方式, 绝对精度在 0.001mm 以下。同时保证探测距离 d 的测量相对误差在 0.4%以下, 可得到测量精度好于 1%的立体角。
为 1mm, 立体角测量误差大于 2%。因此, 加工探测器光阑应采用激光打孔的方式, 绝对精度在 0.001mm 以下。同时保证探测距离 d 的测量相对误差在 0.4%以下, 可得到测量精度好于 1%的立体角。
粒子激发 X 射线荧光分析(particle induced X-ray emission, PIXE)是 IBA 的一种手段, 常用于分析大气污染成分以及文物和艺术品的元素分布等, 被分析物品有时不能放置在真空靶室内, 离子束通过铍窗被引到大气中进行实验。由于大气对离子的阻止和对光子的吸收, 需要被分析物品尽量靠近铍窗, 探测器也需尽可能靠近样品, 通常探测距离只有几厘米。
文献[20]报道卢浮宫佛罗伦萨加速器实验室对油画《圣母玛利亚和亚恩温德》的外束 PIXE 分析结果, 文中没有给出详细的探测几何信息, 但提到束流采用 1mm 的光阑(约等于束斑尺度)以及两路硅锂探测器, 其中一路有非常大的立体角。在这种情况下, 探测器尺寸与探测距离接近, ![]()
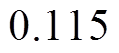 , 因此解谱时不能使用
, 因此解谱时不能使用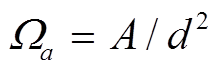 , 否则会带来较大误差。
, 否则会带来较大误差。
在高精度离子束分析中, 根据精度要求和几何条件, 有时需要考虑面对面立体角![]() 、包含截面修正的面对面立体角
、包含截面修正的面对面立体角![]() 、包含面密度修正的立体角
、包含面密度修正的立体角![]() 和包含束流通量修正的面对面立体角
和包含束流通量修正的面对面立体角![]() 。
。
利用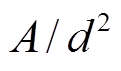 近似立体角(误差好于 1%)需满足:
近似立体角(误差好于 1%)需满足: ![]() <0.1 且
<0.1 且![]() <0.1。利用点对面立体角近似立体角(误差好于 1%)需满足
<0.1。利用点对面立体角近似立体角(误差好于 1%)需满足![]() <0.15。当探测器与靶上束斑很近时(如外束 PIXE 分析), 则不能使用
<0.15。当探测器与靶上束斑很近时(如外束 PIXE 分析), 则不能使用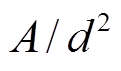 近似立体角。
近似立体角。
北京大学 4.5MV 静电加速器离子束靶室立体角的主要误差来自对实验几何的测量误差。在当前的实验几何设置, 探测器光阑采用激光打孔技术, 且保证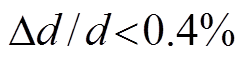 的情况下, 立体角的精度将好于1%, 可以进行高精度离子束分析。
的情况下, 立体角的精度将好于1%, 可以进行高精度离子束分析。
参考文献
[1] Jeynes C, Webb R P, Lohstroh A. Ion beam analysis: a century of exploiting the electronic and nuclear structure of the atom for materials characterisation. Reviews of Accelerator Science and Technology, 2011, 4: 41–82
[2] Reichart P, Datzmann G, Hauptner A, et al. Three-dimensional hydrogen microscopy in diamond. Sci-ence, 2004, 306: 1537–1540
[3] Jeynes C, Barradas N P, Szilágyi E. Accurate deter-mination of quantity of material in thin films by Rutherford backscattering spectrometry. Analytical Chemistry, 2012, 84: 6061–6069
[4] Ecker K H, Wätjen U, Berger A, et al. RBS, SY-XRF, INAA and ICP-IDMS of antimony implanted in silicon — a multi-method approach to characterize and certify a reference material. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2002, 188: 120–125
[5] Gao J, Bao L, Huang H, et al. ERDA, RBS, TEM and SEM characterization of microstructural evolution in helium-implanted Hastelloy N alloy. Nuclear Instru-ments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2017, 399: 62–68
[6] 夏川东, 刘慢天, 朱敬军, 等. 一个PIXE-RBS离子束分析系统的刻度. 核技术, 2017, 40(8): 31–36
[7] 马瑞刚, 崔保群, 马鹰俊, 等. 束流积分仪的研制 //中国物理学会. 第十三届高功率粒子束暨第八届全国高压加速器学术交流会论文集. 贵阳, 2012: 127–130
[8] Colaux J L, Jeynes C, Heasman K C, et al. Certified ion implantation fluence by high accuracy RBS. Ana-lyst, 2015, 140: 3251–3261
[9] Gurbich A F. SigmaCalc recent development and present status of the evaluated cross-sections for IBA. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2016, 371: 27–32
[10] Conway J T. Geometric efficiency for a parallel-surface source and detector system with at least one axisymmetric surface. Nuclear Instruments and Me-thods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2007, 583: 382–393
[11] Gardner R P, Verghese K. On the solid angle sub-tended by a circular disc. Nuclear Instruments and Methods, 1971, 93: 163–167
[12] Gotoh H, Yagi H. Solid angle subtended by a rectan-gular slit. Nuclear Instruments and Methods, 1971, 96: 485–486
[13] Obložinsky P, Ribanský I. The solid angle subtended at a disk source by a non-parallel disk detector. Nuc-lear Instruments and Methods, 1971, 94: 187–188
[14] Carchon R, Van Camp E, Knuyt G, et al. A general solid angle calculation by a Monte Carlo method. Nuclear Instruments and Methods, 1975, 128: 195–199
[15] Wielopolski L. The Monte Carlo calculation of the average solid angle subtended by a right circular cylinder from distributed sources. Nuclear Instru-ments and Methods, 1977, 143: 577–581
[16] 肖璇, 颜莎, 朱吉鹏, 等. 基于北京大学 4.5MV 静电加速器的氘分布多能点 NRA 方法. 北京大学学报(自然科学版), 2016, 52(4): 767–775
[17] 高原, 朱吉鹏, 秦利青, 等. 北京大学 4.5MV 静电加速器核反应分析系统. 原子能科学技术, 2019, 53(5): 906–912
[18] Zhu J P, Xiao X, Yan S, et al. Measurement of differential cross section of D(3He, p)4He from 0.8 MeV to 3.6 MeV. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2017, 412: 81–85
[19] Pozrikidis C. Numerical computation in science and engineering, New York: Oxford University Press, 1998: 530–533
[20] Grassi N, Migliori A, Mandò P A, et al. Differential PIXE measurements for the stratigraphic analysis of the painting Madonna dei fusi by Leonardo da Vinci. X-ray Spectrometry, 2010, 34: 306–309
Determination and Influence of Solid Angle in High Accuracy Analysis
Abstract In order to achieve high accuracy IBA (ion beam analysis), the calculation error of solid angle were discussed meticulously. The accuracies of face to point solid angle and approximate solid angle were calculated, based on face to face solid angle which contained area of beam spot. Based on 4.5 MV electrostatic accelerator ion beam target chamber of Peking University, solid angle influenced by distributions of cross-section and beam intensity was determined. A geometry-condition estimation for accuracy of approximate solid angle better than 1% was given and verified by two examples. For fatherly achievement of high-accuracy solid angle, accurate machining such as laser processing is required.
Key words face-to-face solid angle; beam intensity distribution; nuclear reaction cross-section; high accuracy; ion beam analysis (IBA)
doi: 10.13209/j.0479-8023.2020.009
国家磁约束核聚变研究计划专项(2013GB109004)和国家重点基础研究发展计划(2010CB832902)资助
收稿日期: 2019–03–14;
修回日期: 2019–04–23