
图1 将主动学习应用于 PUL 方法的流程
Fig. 1 Flowchart of active learning applied to PUL method
摘要 针对单类分类方法中只用正类训练样本导致训练样本数量和质量的选择直接影响分类结果精度的问题, 以正类和未标记样本学习(PUL)为例, 研究如何利用主动学习选择训练样本, 以求改善单类分类的精度。首先用随机选取的训练样本进行 PUL 分类, 直到获得稳定的分类精度, 然后利用主动学习选择和增加最有用(informative)的正类或负类样本, 用于 PUL 分类。结果表明, 当利用足够多的随机选取的正类样本得到稳定的分类精度后, 利用主动学习选择和增加正类样本可以提高分类精度; 利用主动学习的同时加入正类和负类样本, 可以得到比只加入正类样本更高的分类精度; 将利用主动学习得到的正类样本经相似性筛选后得到的正类样本, 分类精度与直接利用主动学习选择的样本相似, 但达到同样精度时需要更少的样本。因此, 利用主动学习选择和增加样本可以有效地改善单类分类的精度。
关键词 单类分类; 主动学习; 正类和未标记样本学习(PUL)
单类分类(one-class classification)是一种从遥感图像提取特定地物类别的方法[1]。与经典的多类分类(multi-class classification)不同, 单类分类只需要选择感兴趣的类别或目标类别(正类)样本进行训练, 不需要不感兴趣类别或非目标类别(负类)的样本, 可以使用户只关注感兴趣的地物类别[2]。单类分类方法已广泛应用于目标提取[3]和地表变化提取[4]等领域。
现有的研究中提出一些单类分类方法, 比如支持向量数据描述(SVDD)[5]、单类支持向量机(OCS-VM)[6]和混合高斯模型(Mixture of Gaussians)[7]。这些方法通常只利用正类的训练样本, 其数量和质量直接影响分类结果的精度, 因此探索训练样本选择和优化的有效方法具有重要意义。
正类和未标记样本学习(positive and unlabeled learning, PUL)是近年提出的一种单类分类方法, 它利用正类样本和未标记样本进行训练, 在遥感图像分类中得到良好的分类效果[8]。
主动学习[9]是一种通过用户交互选取和优化训练样本的机器学习方法, 广泛应用于多类分类中。利用主动学习选择优化和训练样本, 可以得到更具代表性的训练样本。近年来, 主动学习被用于单类分类中正类样本的优化和选取。Furlani 等[10]将主动学习与 SVDD 方法相结合, 利用 Landsat-5 数据提取火烧迹地。Mack 等[11]利用改进的有偏支持向量机(Biased-SVM, BSVM)优化训练样本的选择, 通过主动学习剔除随机样本集中的负类样本。Barnabé-Lortie 等[12]将主动学习应用到马氏距离分类器、KNN 及 OCSVM 等多种单类分类中。
现有的利用主动学习改善单类分类精度的研究存在以下问题: 1)初始阶段利用少量随机选取的正类样本, 然后利用主动学习逐渐增加样本, 不断提高精度, 以求达到利用较少的训练样本达到与利用更多的随机选取样本的分类相似或同样的精度[9], 然而, 由于初始样本不够充足, 最终的分类精度可能不够高; 2)一般只利用正类样本, 经用户确定的负类样本(不属于正类的样本)未被利用, 忽略了负类样本对分类的可能的改进作用; 3)直接利用主动学习得到的正类样本间可能具有一定的相似性, 因此这些正类样本可能包含重复和冗余的信息, 在样本集中加入冗余的样本对分类精度的改善作用不大, 但现有的研究中没有对由主动学习得到的具有相似性的正类样本进一步筛选。
本文以 PUL 方法为例, 研究如何有效地利用主动学习选择和优化样本, 以求提高单类分类的精度, 并回答以下问题: 1)当随机选取(或人工选取)的正类样本足够多时, 利用主动学习增加正类样本能否进一步提高单类分类精度; 2)在利用主动学习选择并增加正类样本的同时, 加入经用户确认的负类样本, 能否改进单类分类的精度; 3)在利用主动学习选择正类样本过程中, 通过比较所选取样本间的相似性, 去掉冗余和重复的正类样本, 利用经筛选后的正类样本能否进一步提高单类分类精度。
正类和未标记样本学习(PUL)[13]是一种半监督的单类分类算法, 它利用正类样本和未标记样本训练分类器。首先利用正类和未标记样本, 估计一个未知样本被标记的概率, 然后估计该样本为正类的概率, 最后利用调整后的阈值生成未知样本的类别属性(即属于正类或负类)。PUL 的基本原理如下。
<x, y, s>为一个训练样本, x 代表样本, y 代表样本类别, 若 y=1, 则 x 为正类, 若 y=−1, 则 x 为负类; s 代表样本 x 是否被标记, 若 s=1, 则 x 被标记, 若s=0, 则 x 未被标记。PUL 的目标是估计样本 x 被分为正类的概率 f(x), 并且得到类别属性。假设 g(x)代表样本 x 被标记的概率, Elkan 等[13]证明, 当完全随机选择正类和未标记类样本时, 一个正类样本被标记的概率是一个常数 c, 因此, f(x)与 g(x)存在如下关系:
f(x)= g(x)/c。
这样, 如果能估计出 c 值, 就可以得到 f(x)。Elkan等[13]提出一种估算常量 c 的方法, 即 c 为一个确定的集合中所有样本 g(x)的平均值。现有的研究中采用各种方法估计 g(x), 比如 Elkan 等[13]使用支持向量机(SVM), Li等[8]则采用反向传播神经网络。
主动学习是一种通过交互询问用户(专家)对最不确定或最有信息量(informative)的样本进行标记(类别属性)的机器学习方法[9]。选择最有信息量的样本策略通常包括: 1)选择能够对确定最优参数更有用的样本; 2)选择被拒绝率最高的样本。
基于样本池的方法是一种最常见的主动学习方法[14]。该方法假设有一个样本池, 即候选训练样本(未标记样本池)。基于样本池的主动学习具有 4 个要素: 初始训练样本、分类器(学习引擎)、主动学习函数(或询问函数)和未标记样本池。可以将基于样本池的方法视为一个不停地从样本池中选择样本的循环, 在循环之初通过随机选取得到初始训练样本。由这些初始样本建立一个分类模型, 使用主动学习函数从未标记样本池中选择一个或多个最有信息量的样本, 并询问用户是否对这些样本进行标记(即是否为正类)。如果一个样本被用户标记为正类, 则这个样本被加入训练样本中, 并用于更新分类模型, 直到满足一个特定的停止准则后停止循环。
本文中, 用于 PUL 分类的初始训练样本包括标记样本(正类样本)和未标记样本两类。随机抽取一部分样本作为正类样本, 即初始的训练样本, 从没有被标记为正类样本的样本中随机选择未标记类样本[13]。
本文采用支持向量机(SVM)估算 PUL 算法中的g(x)。由于 g(x)函数要求的输入量是概率值, 本文采用 Platt[15]的方法, 将 SVM 的输出距离值转化为后验概率值, 根据后验概率的大小选择最有信息量或最不确定的样本。后验概率越接近 0.5, 样本越不确定[16]。
用户根据后验概率接近 0.5 的顺序标记一个或几个样本, 并将这些新选出来的标记样本(正类)加入训练样本, 并加入正类样本集, 形成更新后的训练样本。这些更新后的训练样本用于 PUL 分类, 得到更新后的分类结果。
分类器以主动学习的方式不断地对更新的样本进行训练, 最终达到指定的停止准则时迭代停止。在主动学习的研究中, 停止准则通常是在新加入的样本不能进一步提高性能时迭待停止[17]。本文使用 Kappa 系数作为精度判别标准, 当新加入的样本使 Kappa 系数不能进一步提高时, 主动学习停止, 得到最终分类图像。
本文利用主动学习选取训练样本方法的流程如图 1 所示。

图1 将主动学习应用于 PUL 方法的流程
Fig. 1 Flowchart of active learning applied to PUL method
2.2.1 利用主动学习增加更多的正类样本
现有的利用主动学习改进分类精度的方法是先选择一个小的正类样本, 利用主动学习来选择和增加正类样本。本文的方法则是在足够多随机样本的基础上, 利用主动学习继续增加正类样本。先利用随机方式选取足够多的正类样本进行 PUL 分类, 得到稳定的分类精度, 即当随机选取的正类样本增加时, 分类精度不再提高。在此基础上, 利用主动学习选取并增加更多的正类样本, 进行 PUL 分类, 观察PUL 分类精度是否随着正类样本数的增加而提高。
2.2.2 主动学习中负类样本的加入
现有的主动学习与单类分类结合的研究只加入正类样本来改进单类分类, 主动学习过程中经用户确定的负类样本则没有被利用[10,12]。本文将这些确定的负类样本加入未标记样本中, 参与分类过程。具体地, 将主动学习过程中经用户确定不属于正类的样本加入未标记样本中, 用于估计 PUL 分类中的g(x), 可以使估计结果更准确。
2.2.3 主动学习样本的进一步筛选
考虑到利用主动学习选择的正类样本与已有的正类样本(随机或通过主动学习选择的)之间可能存在一定程度的相似性, 本文不是将由主动学习选择的正类样本直接加入正类样本集中, 而是通过比较由主动学习选择的正类样本与已有正类样本的相似性, 决定是否将这个被选择的样本加入正类样本中。具体流程如下: 在主动学习过程中, 如果一个样本被确定属于正类, 则先比较该样本与已有正类样本的相似性, 如果相似, 则不将该样本加入正类样本集中; 如果不相似, 则该样本被选中并加入正类样本集中, 用于后续的 PUL 分类。
本文采用欧氏距离作为样本相似性的度量指标。首先计算一个被主动学习确定为正类的样本与训练集中每个正类样本间的欧氏距离, 并计算所有欧氏距离的最小值。如果该样本与现有正类样本的最小欧氏距离小于设定的阈值, 则表明该样本与现有正类样本相似, 不将该样本加入样本集中; 如果该样本与现有正类样本的最小欧氏距离大于指定的阈值, 则将该样本加入正类训练样本集。
本文利用单类分类方法, 通过两时相 SPOT 图像提取洪水淹没区, 用以评价利用主动学习选择样本对 PUL 分类精度的改进效果。研究区位于英国Gloucester, 该地区于 2000 年 11 月发生一次洪水事件, 导致 Severn 河两岸的农田和村庄被淹没。如图2 所示, 两时相 SPOT 图像分别采集于 1999 年 9 月(洪水前)和 2000 年 11 月(洪水后)。SPOT 图像包含3 个波段(近红外、红、绿), 空间分辨率为 20m。对两个日期的 SPOT 图像进行配准, 并生成一个 6 个波段的两时相图像。使用的 SPOT 图像大小是 2304像元×843 像元。
首先, 需要确定正类样本与未标记样本的数量比。现有研究中采用的比值从 2[18]到 5[13]不等。本文尝试 1~5 的比值, 发现分类精度总体上并不随之变化。本文中, 初始的正类样本与未标记类样本比设为 4。
第二个需要确定的参数是正类样本的数量。本文比较了利用 10~500 个正类样本的分类精度, 以便确定合适的正类样本数量(图 3)。
与 PUL 分类相关的第三个参数是用于估计 g(x)的 SVM 使用的核函数 RBF 核的宽度 σ, 使用网格搜索法确定 σ 的最优参数值为 3.5。在比较正类样本的相似性时, 需要设置欧氏距离的最小值阈值。若阈值选取过大, 通过筛选的样本较少, 无法有效地改善训练样本; 若阈值选取过小, 则达不到筛选效果。通过比较, 确定该阈值为 5。
为了减少随机选择的初始训练样本对分类精度的影响, 最终以不同个数的正类样本作为初始训练样本的分类精度是由 10 次不同初始训练样本(数量相同)得到的分类精度的平均值。对于每次分类训练, 检验样本共 1942272 个。
3.2.1 在足够的初始样本条件下的主动学习
首先采用不同数量的随机选取的正类样本进行PUL 分类, 观察分类精度随正类样本数量变化的情况。从图 3 可以看出, PUL 分类的 Kappa 系数随着随机选取的正类样本数量增加而增大, 当正类训练样本数量超过 200 时, Kappa 系数稳定在 75%~76%之间, 不再提高。
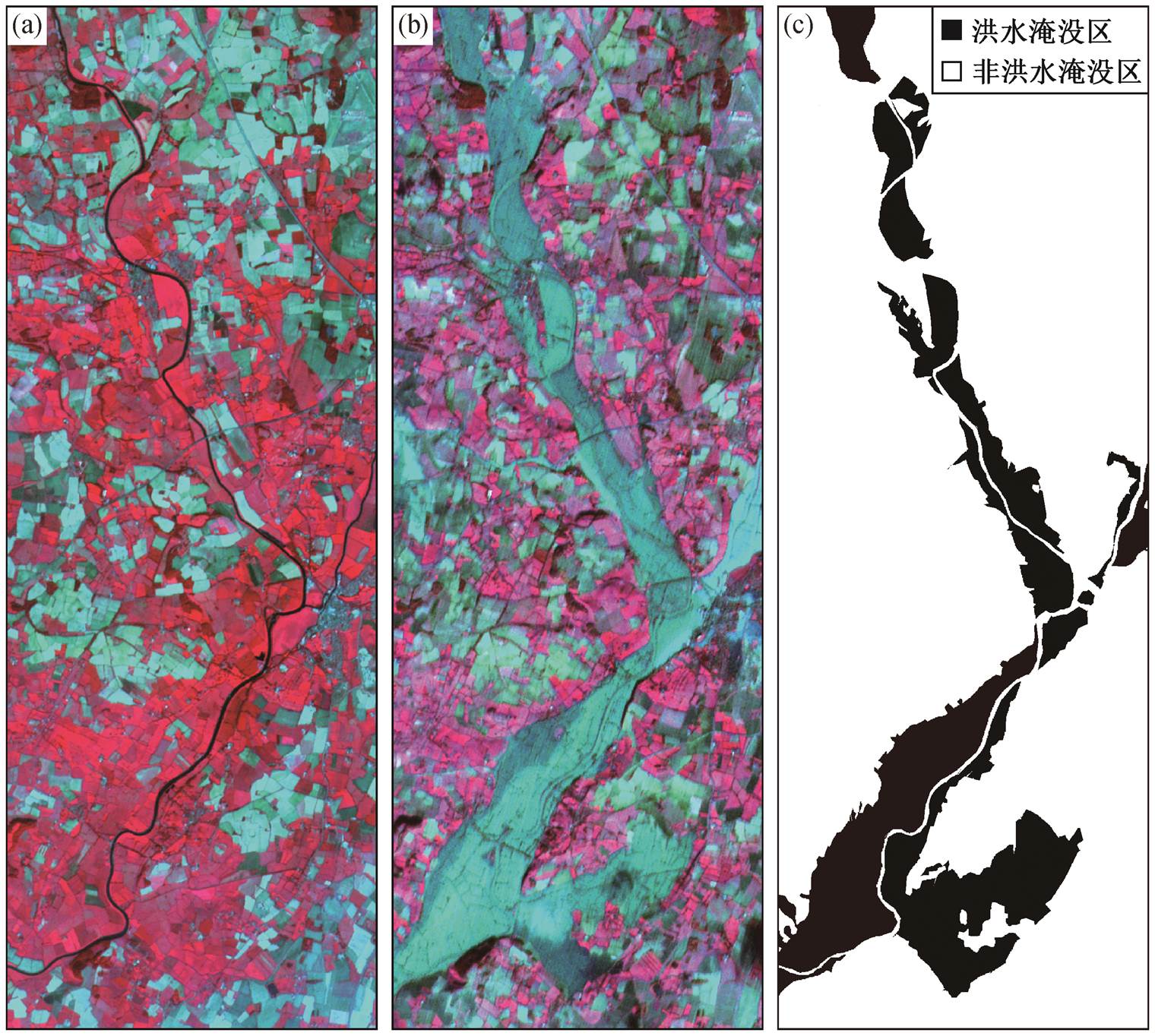
(a)研究区洪水前的 SPOT 假彩色图像; (b)研究区洪水后的 SPOT 假彩色图像(近红外、红、绿波段分别对应为R, G, B三通道假彩色合成); (c)参考图(黑色区域为洪水淹没区, 白色区域为非洪水淹没区)
图2 研究区洪水前后的 SPOT 假彩图像和参考图
Fig. 2 SPOT false color images of the study area collected before and after flood event and the reference data
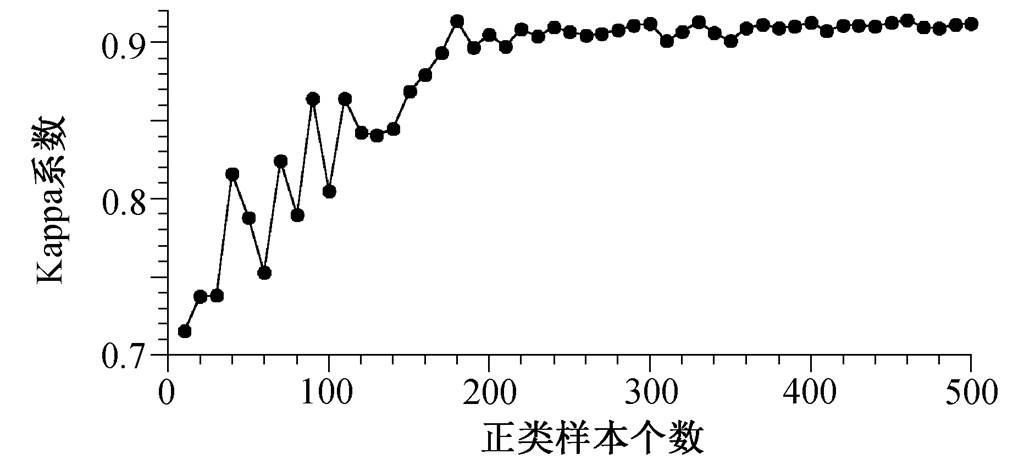
图3 采用不同数量的随机选择的正类训练样本 PUL 分类的 Kappa 系数
Fig. 3 Kappa coefficients of PUL classification with increasing number of positive training samples generated randomly
表 1 显示使用随机选择的正类样本以及通过主动学习选择和增加正类样本得到的 PUL 分类精度, 包括总体精度、Kappa 系数以及淹没区(目标类)的生产者精度(PA)和用户精度(UA)。生产者精度和用户精度反映目标类分类精度的两个方面, 生产者精度越高, 漏分率(omission error, OE)越低, 即 PA+ OE=100%; 用户精度越高, 错分率(commission error, CE)越低, 即 UA+CE=100%。从表 1 可以看出, 尽管使用足够多的随机选择的正类样本(200 个)进行PUL 分类得到较高的总体精度和 Kappa 系数(93.6%和 75.4%), 但利用主动学习进一步增加正类样本数量, 可以得到更高的 PUL 分类精度和 Kappa 系数。例如, 当使用 230 个正类样本(其中 30 个为通过主动学习增加的样本)时, PUL 分类的 Kappa 系数比只用随机选取正类样本提高 6.1%。洪水淹没区的生产者精度显著提高(从 72.9%提高到 83.5%), 用户精度略有下降(从 88.0%下降到 85.2%)。
图 4 显示分别用随机选取的样本和利用主动学习选择的样本进行 PUL 分类的结果, 可以看出, 多数洪水淹没区被正确分类。分别将图 4(a)与图4(b)、图 4(a)与图 4(c)进行比较可以看出, 随着利用主动学习加入更多正类样本, 淹没区被错分为非洪水淹没区的面积显著减小。从局部放大图(图 4(d)~ (f))看出, 当用主动学习分别加入 12 个正类和 30 个正类样本后, 洪水淹没区被错分为非洪水淹没区的面积在每次加入样本后都不同程度地减小, 代表漏分率降低。同样可以观察到, 在利用主动学习加入样本的过程中, 非洪水淹没区被错分为淹没区的面积变化不大, 即错分率变化不大。图 4 的分类结果与表1的分类精度结果相一致。
3.2.2 利用主动学习加入负类样本的 PUL 分类
从表 2 看出, 加入正类和负类样本分类结果的总体精度(95.3%)和 Kappa 系数(83.5%)略高于只加入正类样本的分类结果。从目标类(淹没区)分类结果的精度来看, 与只加入正类样本相比, 加入正类和负类样本使得用户精度显著上升, 生产者精度基本上不变。
从图 5 可以看出, 与只加入正类样本相比, 同时加入正类样本和负类样本(未标记类样本集)的分类结果中, 非淹没区被错分为淹没区的面积明显减小, 代表错分情况变少; 淹没区被错分为非淹没区的面积基本上不变, 代表漏分情况基本上一致。图5 的分类结果与表 2 的分类精度结果相一致。
3.2.3 利用主动学习选取并经筛选的正类样本的PUL分类
从表 3 可以看出, 是否对正类样本进行筛选, 对 PUL 分类精度的影响不明显, 利用筛选前后正类样本的 PUL 分类总体精度分别为 94.4%和 94.5%, Kappa 系数分别为 81.1%和 81.3%。表 3 也显示, 通过对主动学习选择的正类样本进行筛选, 加入更少的样本(15 个)就可以得到与利用更多的不经筛选的正类样本(35 个)相同的分类精度, 体现对由主动学习选取的正类样本进行进一步筛选的意义。
比较图 6 可以看出, 直接利用主动学习选取的正类样本和经进一步筛选后的正类样本进行 PUL分类, 虽然使用的样本个数不同, 但正确分类的区域面积基本上相同。利用经过筛选的正类样本进行PUL 分类, 非淹没区被误分为淹没区的面积较少, 表明经过样本筛选后错分率较低; 淹没区域被误分为非洪水淹没区的面积较大, 表明经过样本筛选后漏分率较高, 但总体上区别不大。图 6 的分类结果与表3的分类精度结果相一致。
表1 利用随机选取和通过主动学习加入的不同数量正类样本的分类精度
Table 1 Accuracies of PUL classification with positive training samples collected randomly and added by using active learning

样本选取方法正类样本个数淹没区总体精度/%Kappa/% PA/%UA/% 随机选取20072.988.093.675.4 随机选取和主动学习212 (200+12)78.186.794.279.7 230 (200+30)83.585.294.681.5
说明: 212(200+12)表示用200个正类样本和12个主动学习加入的样本训练, 230.(200+30)表示用200个正类样本和30个主动学习加入的样本训练, 两种情况下都使用800个未标记样本。
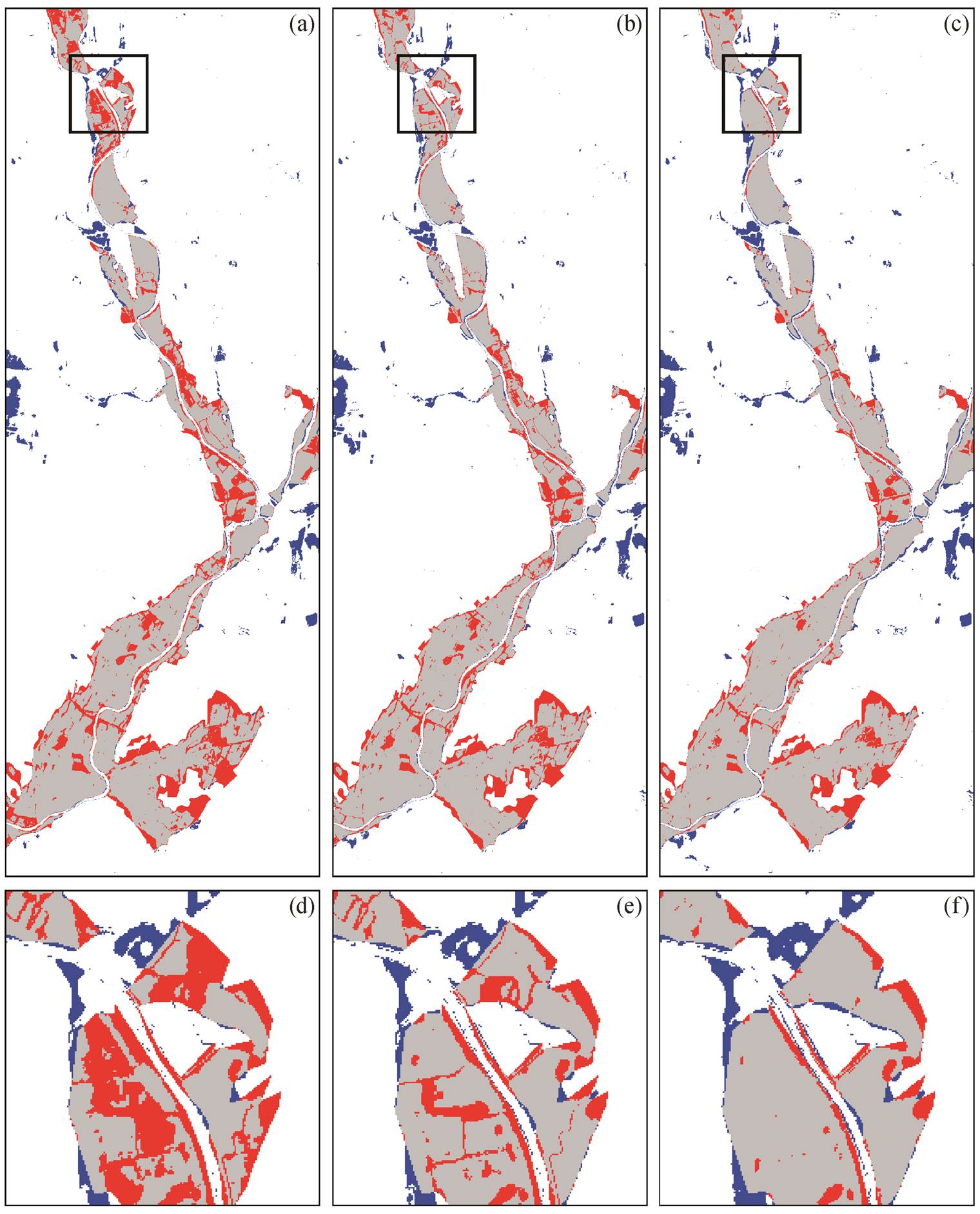
(a)和(d)随机选择 200 个正类样本的分类结果; (b)和(e) 200 个随机选择和 12 个主动学习选择的正类样本(共 212 个)的分类结果; (c)和(f)200 个随机选择和 30 个主动学习选择的正类样本(共 230 个)的分类结果。均使用 800 个未标记样本。灰色为被正确分类的洪水淹没区, 白色为被正确分类的非洪水淹没区, 红色为洪水淹没区被误分为非洪水淹没区, 蓝色为非洪水淹没区被误分为洪水淹没区, 下同
图4 使用不同数量的正类样本得到的分类结果
Fig. 4 PUL classification results using different numbers of positive samples
表2 利用主动学习只加入正类和同时加入正类和负类样本的PUL分类精度
Table 2 Accuracies of PUL classification using positive samples alone and both positive and negative samples added by active learning

样本选取方法样本个数淹没区总体精度/%Kappa/% PA/%UA/% 仅加入正类样本235 (200+35)87.0182.4094.587.3 加入正类和负类样本375 (200+43+132)86.7685.9595.383.5
说明: 235(200+35)表示用 200 个随机选取的正类样本和 35 个主动学习加入的正类样本, 375(200+43+132)表示用 200 个随机选取的正类样本和用主动学习加入 43 个正类样本、132 个负类样本, 两种情况下都使用800个未标记样本。
表3 利用主动学习选取和经进一步筛选的正类样本的PUL分类精度
Table 3 Accuracies of PUL classification using positive samples directly added by active learning and further refined based on similarity

样本选取方法正类样本个数淹没区总体精度/%Kappa/% PA/%UA/% 未经过筛选235 (200+35)88.9080.5894.481.1 经过筛选215 (200+15)83.7385.6894.881.6
说明: 235(200+35)表示用200个正类样本和35个主动学习加入的样本训练, 215(200+15)表示用200个正类样本和15个主动学习加入的样本训练, 训练过程均使用800个未标记类样本。
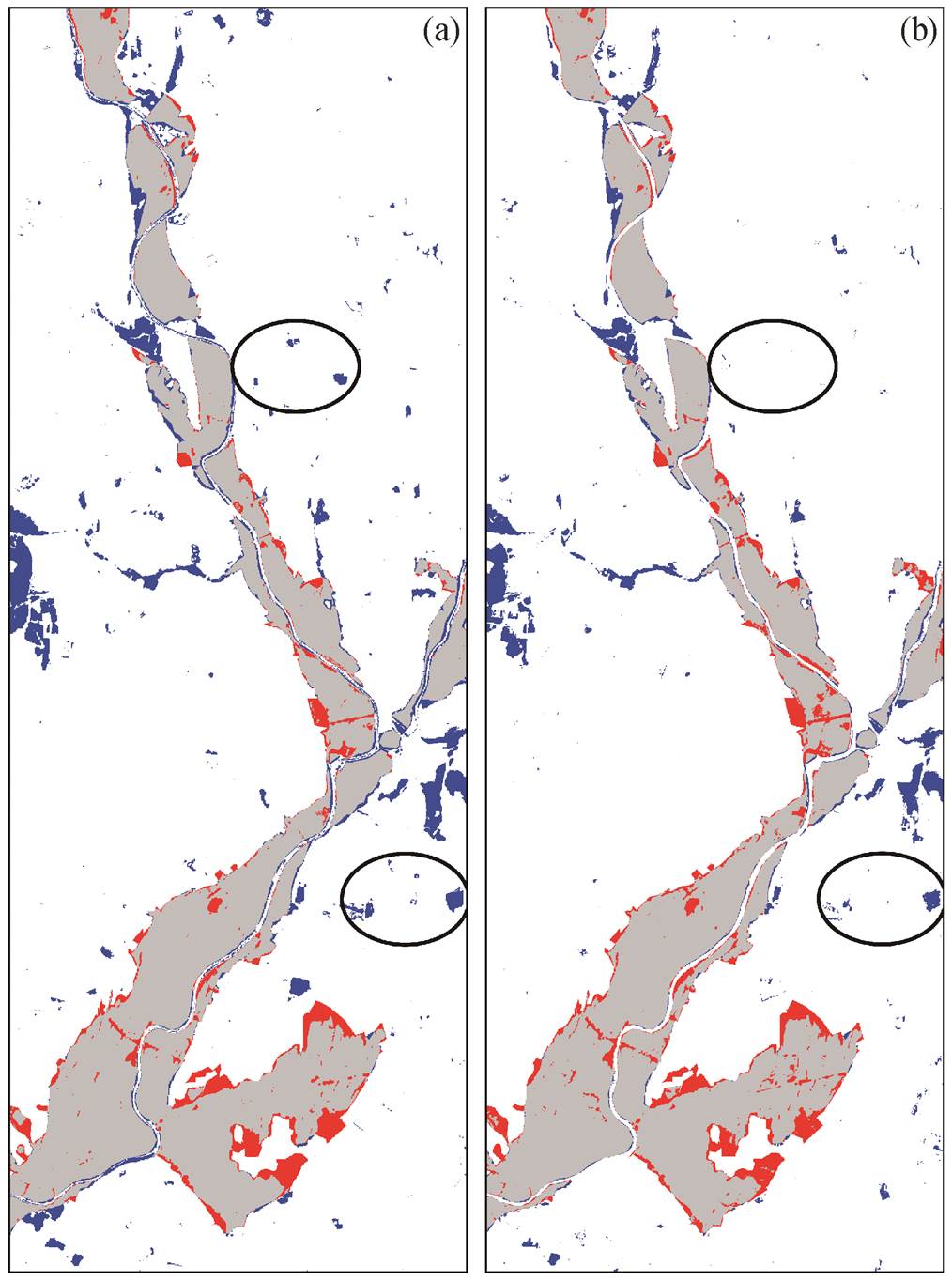
(a)仅利用主动学习加入正类样本; (b)利用主动学习加入正类样本和负类样本。训练过程均使用 800 个未标记类样本。椭圆中区域为非洪水淹没区被误分洪水淹没区, 下同
图5 使用主动学习加入不同样本的PUL分类结果
Fig. 5 PUL classification results using training samples selected by different methods
为了进一步分析利用主动学习选取和加入正类样本对 PUL 分类结果的影响, 将不同情况下得到的正类样本进行比较。图 7 显示随机选择的正类样本、利用主动学习选择以及经进一步筛选的正类样本的光谱曲线, 可以看出, 随机选取的正类样本间存在显著的相似性(图 7(a)), 而利用主动学习选取的正类样本间的相似性显著减弱, 每个样本较为独立, 样本间的差异性和样本的多样性显著增加。利用相似性对由主动学习得到的样本做进一步筛选后的正类样本间相似性进一步减弱, 每个样本更加独立, 样本间的差异性和样本的多样性进一步增加。因此, 利用主动学习选取和增加样本, 可以进一步提高 PUL 分类精度; 进一步筛选正类样本, 可以利用较少的样本达到较高的分类精度。
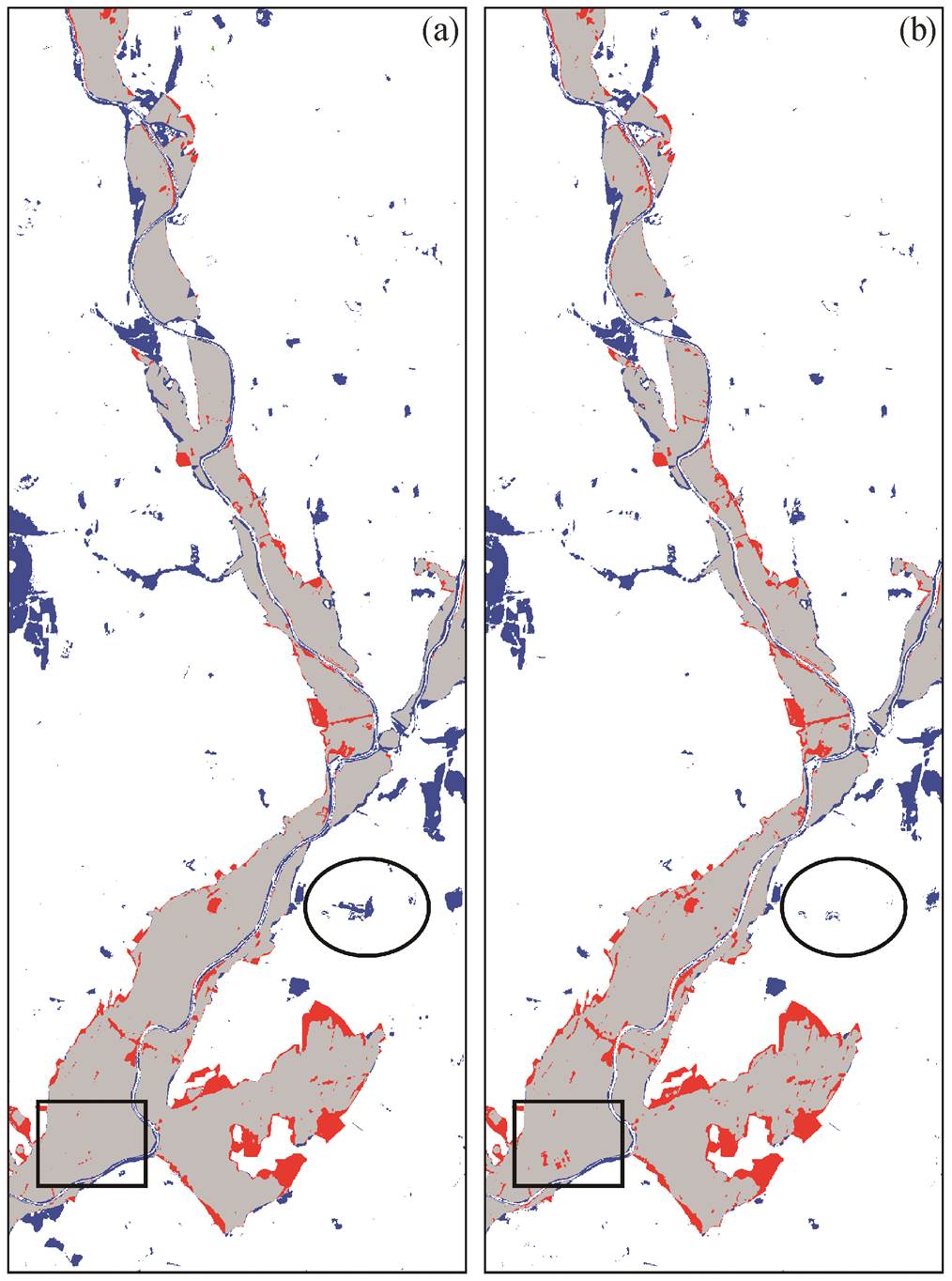
(a)利用主动学习得到的未经过筛选的正类样本; (b)利用主动学习得到的经过筛选的正类样本。矩形中区域为洪水淹没区被误分为非洪水淹没区
图6 不同主动学习策略选择的正类样本PUL分类结果
Fig. 6 PUL classification results using positive samples selected by different methods
本文以 PUL 分类方法为例, 利用主动学习选取和增加训练样本, 以求改善单类分类方法的精度1。结果表明, 当随机加入足够多的正类样本进行单类分类并得到稳定的分类精度时, 利用主动学习选取和增加正类样本可进一步改善分类精度; 利用主动学习同时加入正类和负类样本进行单类分类, 可得到比只加入正类样本更高的分类精度; 利用对主动学习得到的正类样本筛选后得到的正类样本进行PUL 分类, 尽管与直接利用主动学习选择的样本分类精度相似, 但只需要更少的正类样本。因此, 利用主动学习选择和增加样本是改进 PUL 单类分类精度的有效方法。
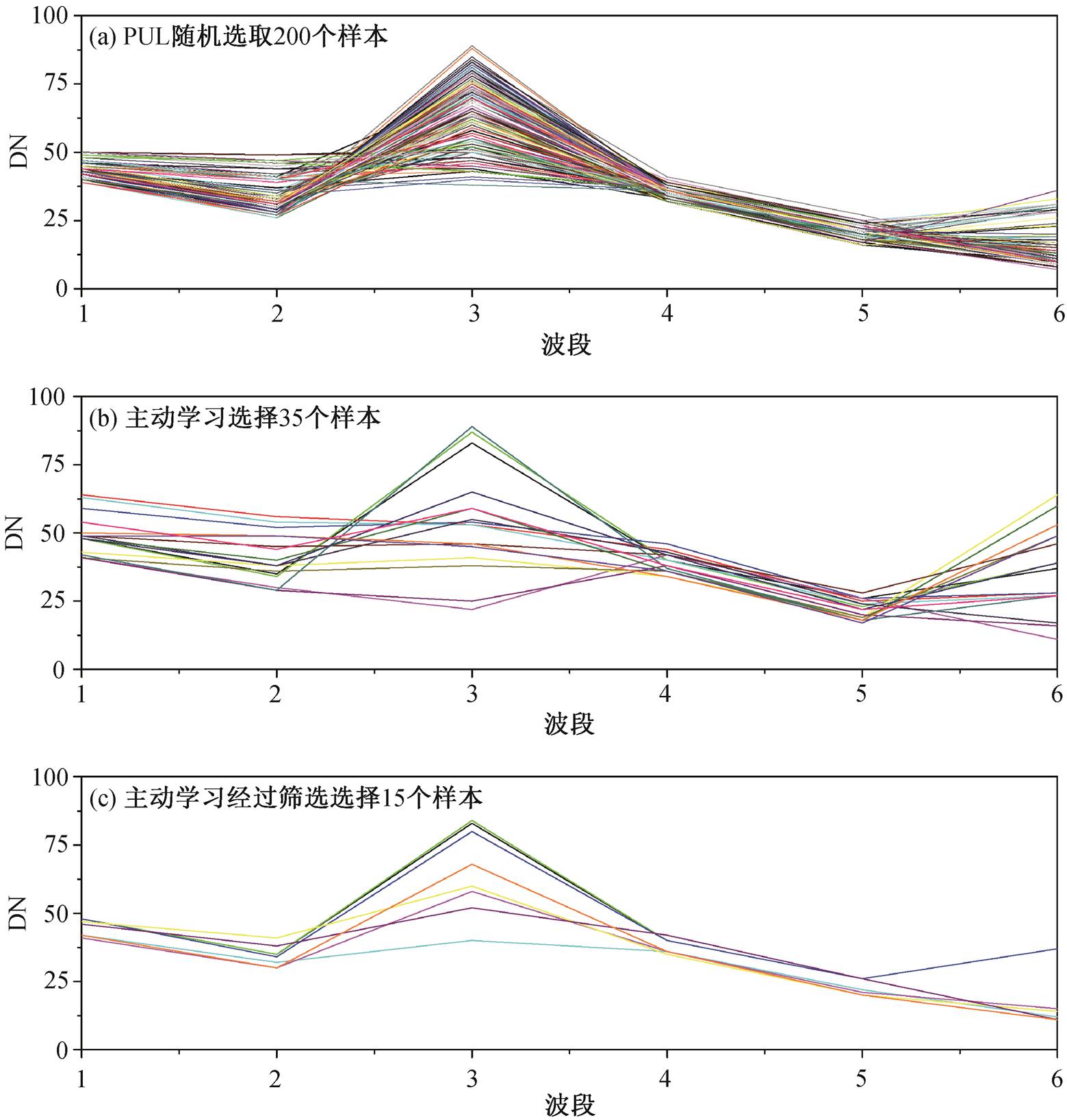
图7 不同方式选择的正类样本的光谱特征
Fig. 7 Spectral signatures of positive samples collected by different ways
参考文献
[1] Khan S S, Madden M G. A survey of recent trends in one class classification // Artificial Intelligence and Cognitive Science — Irish Conference. Dublin, 2009: 188‒197
[2] Sanchez-Hernandez C, Boyd D S, Foody G M. One-class classification for mapping a specific land-cover class: SVDD classification of Fenland. IEEE Transac-tions on Geoscience & Remote Sensing, 2007, 45(4): 1061‒1073
[3] Gambardella A, Giacinto G, Migliaccio M, et al. One-class classification for oil spill detection. Pattern Ana-lysis & Applications, 2010, 13(3): 349‒366
[4] Li P J, Xu H Q. Land-cover change detection using one-class support vector machine. Photogrammetric Engineering & Remote Sensing, 2010, 76(3): 255‒263
[5] Tax D M J, Duin R P W. Data domain description using support vectors // Proceedings of European Symposium on Artificial Neural Networks. Bruges, 1999: 251‒256
[6] Hu X F, Weng Q H. Estimating impervious surfaces from medium spatial resolution imagery using the self-organizing map and multi-layer perceptron neural networks. Remote Sensing of Environment, 2009, 113 (10): 2089‒2102
[7] Ilonen J, Paalanen P, Kamarainen J K, et al. Gaussian mixture pdf in one-class classification: computing and utilizing confidence values // International Conferen-ce on Pattern Recognition. Hong Kong: IEEE, 2006: 595
[8] Li W K, Guo Q H, Elkan C. A positive and unlabeled learning algorithm for one-class classification of remote-sensing data. IEEE Transactions on Geosci-ence and Remote Sensing, 2011, 49(2): 717‒725
[9] Krishnakumar A. Active learning literature survey [R]. Santa Cruz: University of California, 2007
[10] Furlani M, Tuia D, Muñoz-Marí J, et al. Discovering single classes in remote sensing images with active learning // 2012 IEEE International Geoscience and Remote Sensing Symposium. Munich, 2012: 7341‒ 7344
[11] Mack B, Roscher R, Stenzel S, et al. Mapping raised bogs with an iterative one-class classification approach. ISPRS Journal of Photogrammetry & Remote Sen-sing, 2016, 120: 53‒64
[12] Barnabé-Lortie V, Bellinger C, Japkowicz N. Active learning for one-class classification // 2015 IEEE 14th International Conference on Machine Learning and Applications. Miami, 2015: 390‒395
[13] Elkan C, Noto K. Learning classifiers from only positive and unlabeled data // ACM SIGKDD Interna-tional Conference on Knowledge Discovery and Data Mining. Las Vegas, 2008: 213‒220
[14] Wang S, Wang J J, Gao X H, et al. Pool-based active learning based on incremental decision tree // 2010 International Conference on Machine Learning and Cybernetics. Qingdao, 2010: 274‒278
[15] Platt J. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Advances in Large Margin Classifiers, 1999, 10(3): 61‒74
[16] Lewis D D, Gale W A. A sequential algorithm for training text classifiers // Proceedings of International Acm-Sigir Conference on Research and Development in Information Retrieval. London, 1994: 3‒12
[17] Vlachos A. A stopping criterion for active learning. Computer Speech & Language, 2008, 22(3): 295‒312
[18] Song B, Li P, Li J, et al. One-class classification of remote sensing images using kernel sparse represen-tation. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2016, 9(4): 1‒11
Improving One-Class Classification of Remote Sensing Data by Using Active Learning: A Case Study of Positive and Unlabeled Learning
Abstract To address the problem that quality and quantity of training samples directly affect accuracy of one-class classification (OCC) methods, this paper investigates the use of active learning in selection of training samples of target class (positive samples) for improving the performance of OCC, by taking positive and unlabeled learning (PUL) as an example. PUL is first trained with sufficient training samples selected randomly until a stable accuracy is reached. Most informative positive and negative training samples collected by using active learning strategy are then added in PUL classification. The experimental results show that after sufficient samples are used for classification, the use of positive samples selected by using active learning still outperformed that using sufficient positive samples selected randomly. PUL classification by adding both positive and negative samples outperformed that by adding positive samples only. Furthermore, PUL classification using positive samples after removal of redundant positive samples from those directly selected by active learning obtains accuracy comparable to that using more positive samples directly selected by active learning, whereas less samples are needed in the case that redundant samples are removed. This study demonstrates that selecting and adding samples by active learning provides a more effective way of improving accuracy for OCC.
Key words one-class classification; active learning; positive and unlabeled learning (PUL)
doi: 10.13209/j.0479-8023.2019.035
国家自然科学基金(41371329)资助
收稿日期: 2019‒01‒24;
修回日期: 2019‒05‒06