动态图上的最短路径距离并行算法
韩硕 邹磊†
北京大学计算机科学技术研究所, 北京 100080; †通信作者, E-mail: zoulei@pku.edu.cn
摘要 设计动态图上最短路径距离查询的并行计算框架。通过构建增量图的方法, 实现一个批次内的多个查询在不同数据图版本的多线程并发执行。对于每个查询, 使用双向宽度优先搜索算法来减少搜索空间, 并提出搜索过程中扩展方向的决策函数。利用 BSR 对数据图邻接表进行编码, 结合 SIMD 指令和图顶点重标号算法, 进一步提升数据级并行度。在真实图数据集下的大量实验验证了所提方法的高效性。
关键词 动态图; 最短路径距离; 增量图; 线程级并行; 数据级并行; 双向宽度优先搜索; SIMD
近年来, 图模型得到广泛的关注和应用, 例如社交网络、道路运输网络、化学分子结构、语义网和知识图谱等。最短路径查询是图计算领域一个重要的基础问题。早期的研究主要聚焦于解决静态图上的单点对最短路径(single-pair shortest path)、单源最短路径(single-source shortest path)和全局最短路径(all-pairs shortest path)等问题。随着网络信息的爆炸式增长, 图的规模不断扩大, 同时, 图数据从静态向动态转变。以社交网络为例, 用户之间的关联实时变化, 每秒钟都有关注和取消关注等操作, 也有新用户的创建和老用户的注销。反映在图模型上, 就是边和顶点的增加和删除。图的动态变化实时影响图的拓扑结构, 影响顶点之间最短路径距离, 即在不同时刻, 起点和终点相同的两个最短路径查询的结果有可能不同。
动态图(dynamic graph)指图的拓扑结构随时间变化而不断更新的数据模型。更新操作可以是顶点或边的增加、删除以及顶点或边上权值的改变等。动态图算法需要实时地维护更新操作, 并快速地回答一些查询, 例如任意两个顶点之间是否可达[1–2]以及最短路径[3–5]等。如果仅支持增加或删除操作中的其中一种, 则称为半动态(semi-dynamic)算法[3];如果两者皆能支持, 则称为全动态(full-dynamic)算法[4–6]。已有的最短路径全动态算法[4–5]通过维护索引的方式来进行动态更新和查询操作, 其应用场景是更新操作较少、查询操作较频繁的情况。由于更新操作需要实时地调整索引结构, 所以时间开销较大, 而维护索引结构带来的收益是对查询操作能够快速地做出响应, 即在查询执行过程中利用索引快速地找到顶点之间的最短路径。这些工作按照时序串行地进行更新或查询操作, 当图的拓扑结构变化频繁时, 其性能难以达到实时需求。随着处理器多核技术和分布式系统的发展, 研究人员逐渐意识到并行计算对性能的提升作用。
本文从另一个角度, 尝试解决全动态的最短路径查询问题, 主要思路是通过并行计算来分摊查询操作的计算开销。对于更新操作, 则在数据图上直接执行, 避免了因维护索引结构带来的昂贵时间开销。
本文提出一种增量图(delta graph)结构和基于增量图的动态图上查询并行执行框架。使用增量图来维护一段时间窗口内数据图的不同历史版本, 可以高效地支持该时间窗口内所有最短路径距离查询在线程级的并发执行。对于每个查询, 采用双向宽度优先搜索的算法来减少搜索空间。此外, 本文采用 BSR [6]来存储数据图的邻接表, 并在预处理阶段对数据图顶点重新标号。在查询执行过程中, BSR编码的邻接表能够有效地结合 SIMD 指令, 提高算法在数据级的并行度。本文方法结合了线程级并行(thread-level parallelism)和数据级并行(data-level parallelism)技术, 可以有效地解决动态图上的最短路径距离查询任务。
1 问题定义
为方便描述, 我们将图的更新操作仅定义在边集合上, 即每个更新操作为增加或删除一条有向边, 并且每个更新操作带有时间信息。我们认为存在一个全局不变的顶点集合, 每个顶点具有唯一的编号。当一个增边操作中涉及新的顶点时, 该顶点开始拥有相应的邻接边, 删边操作则可能导致涉及的顶点变为孤立顶点。在实现过程中, 所有顶点的增删操作均可转化为对边的增删操作, 图的查询操作则为查询当前时刻下两个顶点的有向最短路径的距离。动态图的更新和查询操作按照时序依次到来, 我们将其划分为一个个时间窗口片段, 每个时间窗口内部的更新和查询操作为一个批次, 集中处理。
我们将初始数据图形式化地表示为 G0=(V, E0), 其中.V是全局顶点集合, E0是初始的有向边集合, 假设图中的边不带权重。第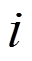 个批次内的图更新操作记为集合
个批次内的图更新操作记为集合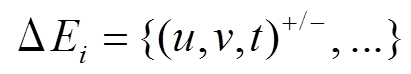 , 三元组(u, v, t)+/–表示在 t 时刻增加或删除一条从顶点 u 到顶点 v 的有向边。可以将更新操作集合 Ei 自然地分为增边集合
, 三元组(u, v, t)+/–表示在 t 时刻增加或删除一条从顶点 u 到顶点 v 的有向边。可以将更新操作集合 Ei 自然地分为增边集合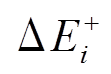 和删边集合
和删边集合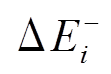 。此外, 我们允许在同一批次内或不同批次间对同一条边的反复增删操作。图查询操作记为集合
。此外, 我们允许在同一批次内或不同批次间对同一条边的反复增删操作。图查询操作记为集合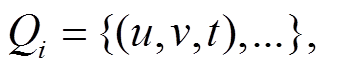 三元组
三元组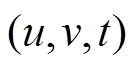 表示在 t 时刻查询从顶点 u 到顶点v 的最短路径长度。对于 t 时刻的查询, 我们认为 t时刻之前的图更新操作均已完成, t 时刻之后的操作均未开始, 即查询
表示在 t 时刻查询从顶点 u 到顶点v 的最短路径长度。对于 t 时刻的查询, 我们认为 t时刻之前的图更新操作均已完成, t 时刻之后的操作均未开始, 即查询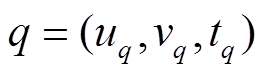 作用于图版本
作用于图版本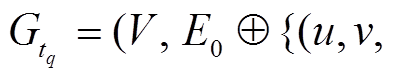
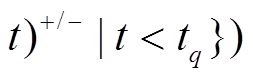 。第 i 个批次后, 数据图更新为
。第 i 个批次后, 数据图更新为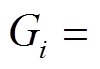
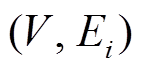 。其中
。其中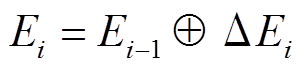 , 符号
, 符号 表示将更新操作集合
表示将更新操作集合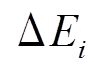 按照时间次序作用于边集合
按照时间次序作用于边集合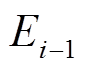 。
。
对于每一个批次到来的更新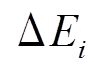 和查询
和查询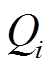 , 我们希望正确且快速地回答
, 我们希望正确且快速地回答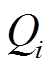 中每个最短路径查询, 并将
中每个最短路径查询, 并将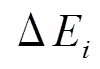 更新至数据图, 从而得到最新版本的
更新至数据图, 从而得到最新版本的 。
。
2 算法框架
对于每个批次, 我们按照以下步骤进行处理。
步骤 1 读入更新操作集合△Ei和查询集合Qi。
步骤2 根据上一个批次处理结束时的数据图版本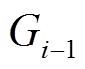 和当前批次的更新
和当前批次的更新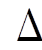 Ei, 建立增量图
Ei, 建立增量图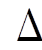 Gi。
Gi。
步骤3 在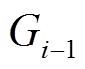 上执行该批次的所有删边操作
上执行该批次的所有删边操作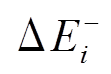 , 得到
, 得到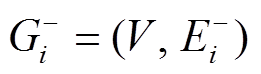 , 其中
, 其中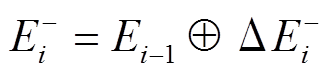 。显然, 对于该批次内的所有查询
。显然, 对于该批次内的所有查询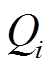 , 图版本
, 图版本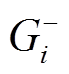 中的所有有向边
中的所有有向边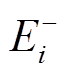 都可以“安全”地经过, 因此称
都可以“安全”地经过, 因此称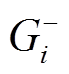 为批次
为批次 的数据图安全版本。
的数据图安全版本。
步骤4 在安全版本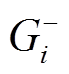 和增量图
和增量图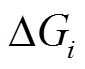 上, 并发地执行查询集合
上, 并发地执行查询集合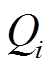 中的最短路径查询。
中的最短路径查询。
步骤5 按照时序输出查询结果。
步骤6 识别增边操作集合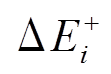 中, 最终应当添加到
中, 最终应当添加到 的边集合
的边集合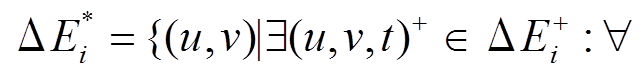
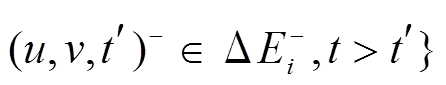 。即, 对于任意一条增边
。即, 对于任意一条增边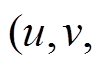
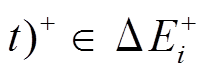 , 我们将边
, 我们将边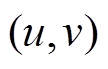 添加至
添加至 , 当且仅当其满足: 1)
, 当且仅当其满足: 1) 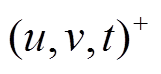 仅出现在增边集合
仅出现在增边集合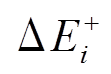 中; 或者2)虽然
中; 或者2)虽然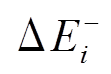 中出现对应的一个或多个删边操作
中出现对应的一个或多个删边操作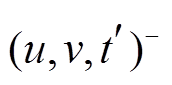 , 但增边操作的
, 但增边操作的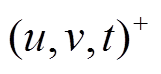 时间标记是最新的(
时间标记是最新的( )。然后, 将最终增边集合
)。然后, 将最终增边集合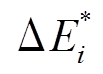 合并至安全版本
合并至安全版本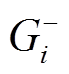 , 从而得到第 i 批次的图版本
, 从而得到第 i 批次的图版本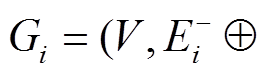
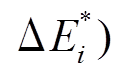 。容易证明:
。容易证明: 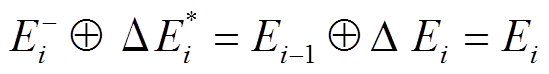 , 因此从安全版本
, 因此从安全版本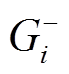 合并最终增边集合
合并最终增边集合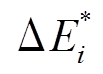 得到的最新图版本
得到的最新图版本 的正确性能够保证。
的正确性能够保证。
图 1 展示算法框架的一个具体例子。图 1(a)和(b)分别为当前批次读入的更新操作集合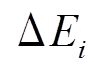 和查询集合
和查询集合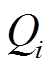 , 图 1(h)为上一个批次处理结束时的数据图版本
, 图 1(h)为上一个批次处理结束时的数据图版本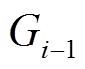 。在步骤中, 2 根据
。在步骤中, 2 根据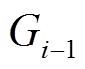 和
和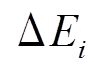 建立图1(f)增量图
建立图1(f)增量图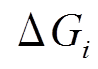 。在步骤 3 中, 图 1(c)删边集合
。在步骤 3 中, 图 1(c)删边集合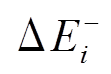 包含两个删边操作
包含两个删边操作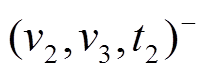 和
和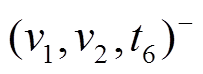 , 相应地, 在图 1(h)数据图版本
, 相应地, 在图 1(h)数据图版本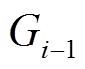 中删除有向边
中删除有向边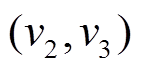 和
和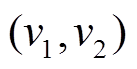 , 得到图 1(i)中安全版本
, 得到图 1(i)中安全版本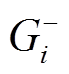 。图 1(g)为查询在
。图 1(g)为查询在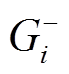 和
和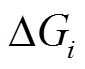 上的执行过程。对于查询
上的执行过程。对于查询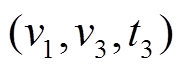 , 以
, 以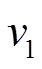 为起点开始搜索, 在
为起点开始搜索, 在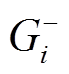 中
中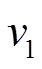 没有出边, 但
没有出边, 但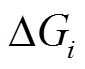 中有出边
中有出边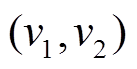 , 通过分析边
, 通过分析边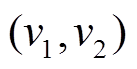 的增删操作时序序列
的增删操作时序序列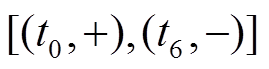 , 可知在查询时刻
, 可知在查询时刻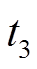 前最近的一次操作是增边
前最近的一次操作是增边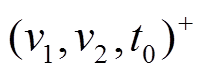 , 因此在
, 因此在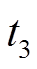 时, 边
时, 边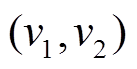 是可经过的。然后, 从
是可经过的。然后, 从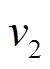 进一步搜索, 发现
进一步搜索, 发现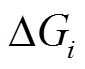 中有出边
中有出边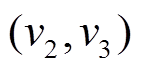 , 通过分析边
, 通过分析边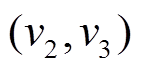 的增删操作时序序列
的增删操作时序序列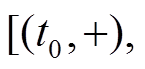
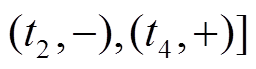 , 可知在
, 可知在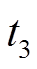 前最近的一次操作是删边
前最近的一次操作是删边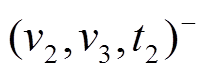 , 因此在
, 因此在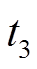 时, 边
时, 边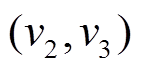 是不可经过的。但是, 在
是不可经过的。但是, 在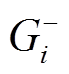 中
中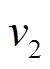 有出边
有出边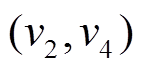 , 可以直接安全地到达
, 可以直接安全地到达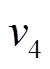 , 然后从
, 然后从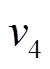 经过
经过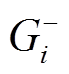 中的边
中的边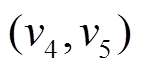 到达
到达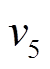 。类似地, 分析
。类似地, 分析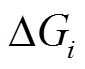 中边
中边 的时序序列, 可知边
的时序序列, 可知边 在
在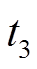 时刻可经过, 最终到达
时刻可经过, 最终到达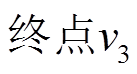 , 因而最短距离为4。
, 因而最短距离为4。
对于查询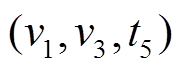 , 按照上述相同的执行逻辑, 发现在
, 按照上述相同的执行逻辑, 发现在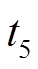 时刻
时刻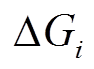 中的边
中的边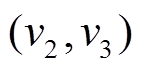 是可经过的, 因而
是可经过的, 因而 时刻
时刻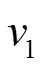 到
到 的最短距离缩短为 2。在执行过程中, 两个查询对
的最短距离缩短为 2。在执行过程中, 两个查询对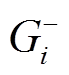 和
和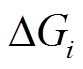 只读不写, 因此不存在数据冲突, 可以使用多线程并发地执行。查询执行结束并按照查询时序输出结果后, 需要将数据图更新至最新版本
只读不写, 因此不存在数据冲突, 可以使用多线程并发地执行。查询执行结束并按照查询时序输出结果后, 需要将数据图更新至最新版本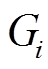 。在步骤 6 中, 计算最终增边集合: 对于
。在步骤 6 中, 计算最终增边集合: 对于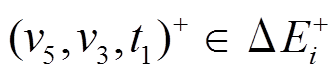 , 满足条件 1, 则该操作仅出现在增边集合
, 满足条件 1, 则该操作仅出现在增边集合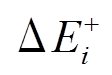 中; 对于
中; 对于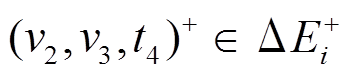 , 满足条件 2, 即虽然存在对应的删边操作
, 满足条件 2, 即虽然存在对应的删边操作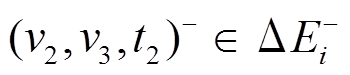 , 但
, 但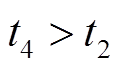 , 所以增边操作是最新的, 从而得到
, 所以增边操作是最新的, 从而得到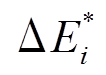
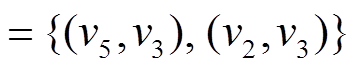 , 如图 1(e)所示。最终, 将
, 如图 1(e)所示。最终, 将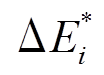 的两条边添加至图 1 (i)中安全图版本
的两条边添加至图 1 (i)中安全图版本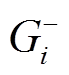 上, 得到图 1 (j)中最新数据图版本
上, 得到图 1 (j)中最新数据图版本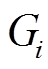 , 该批次的处理流程结束。
, 该批次的处理流程结束。
关于步骤 3 和 6 中的更新操作, 在实现中直接对数据图的 BSR 邻接表进行修改, 单条边增删操作的时间复杂度可以达到 , 因此一个批次的所有更新操作的时间复杂度为
, 因此一个批次的所有更新操作的时间复杂度为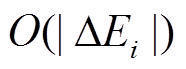 。算法的瓶颈在于查询执行的时间开销, 即步骤4。单个查询执行的时间开销为运行一次双向宽度优先搜索的复杂度, 最坏情况为
。算法的瓶颈在于查询执行的时间开销, 即步骤4。单个查询执行的时间开销为运行一次双向宽度优先搜索的复杂度, 最坏情况为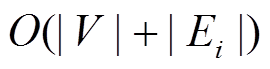 , 因此一个批次的总查询开销为
, 因此一个批次的总查询开销为 。由于图搜索算法的时间复杂度难以从理论上做进一步的改进, 所以我们尝试在不同层级上提高查询的并行度来优化查询执行效率。
。由于图搜索算法的时间复杂度难以从理论上做进一步的改进, 所以我们尝试在不同层级上提高查询的并行度来优化查询执行效率。
3 增量图(delta graph)
对于查询集合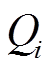 中的每个最短路径查询
中的每个最短路径查询
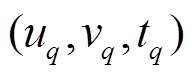 , 需要查询的数据图版本为
, 需要查询的数据图版本为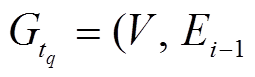
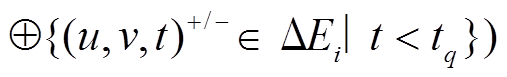 。为每个查询操作单独生成一个
。为每个查询操作单独生成一个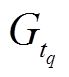 的代价显然是无法接受的。一种直接的策略是按照时序依次执行所有的更新和查询操作, 此时
的代价显然是无法接受的。一种直接的策略是按照时序依次执行所有的更新和查询操作, 此时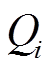 中的各个查询之间为串行执行, 查询执行效率较低。针对当前批次的更新操作集合
中的各个查询之间为串行执行, 查询执行效率较低。针对当前批次的更新操作集合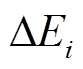 , 我们构建增量图
, 我们构建增量图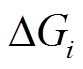 来暂存
来暂存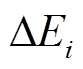 中的所有更新操作, 即增量地记录
中的所有更新操作, 即增量地记录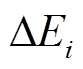 中不同时刻的图版本。在查询执行过程中, 分别考虑记录在安全图版本
中不同时刻的图版本。在查询执行过程中, 分别考虑记录在安全图版本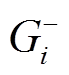 和增量图
和增量图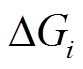 中的边是否可以经过, 从而实现不同查询之间在相应的图版本上的多线程并发执行。
中的边是否可以经过, 从而实现不同查询之间在相应的图版本上的多线程并发执行。
形式化地, 对于增量图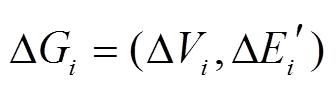 , 顶点集合
, 顶点集合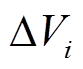 只需要保存在更新操作集合
只需要保存在更新操作集合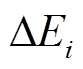 中的增删边涉及的顶点, 即
中的增删边涉及的顶点, 即
增删边集合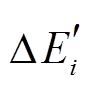 需要在
需要在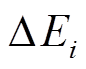 中的增删边操作基础上, 增加每条增删边在上一个数据图版本
中的增删边操作基础上, 增加每条增删边在上一个数据图版本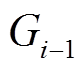 中的状态, 即
中的状态, 即
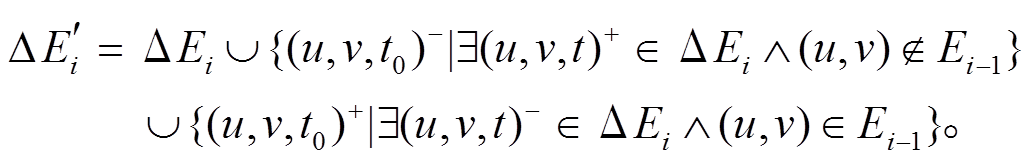
详细地, 对于增边操作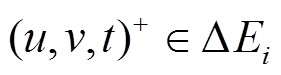 , 若该边未出现在
, 若该边未出现在 中, 则向
中, 则向 增加一个额外的删边操作
增加一个额外的删边操作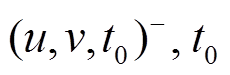 设置为小于
设置为小于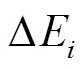 中所有操作的时间标记, 用来表示边
中所有操作的时间标记, 用来表示边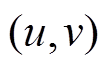 在该批次更新操作发生前是不存在的; 相应地, 对于删边操作
在该批次更新操作发生前是不存在的; 相应地, 对于删边操作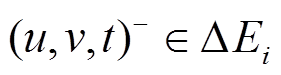 , 若该边已出现在
, 若该边已出现在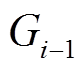 中, 则向
中, 则向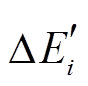 增加一个额外的增边操作(u, v, t0)+, 表示该边在该批次前是存在的。通常, 一个批次内的更新操作数目远小于数据图的规模, 因而增量图的规模也远小于数据图, 即
增加一个额外的增边操作(u, v, t0)+, 表示该边在该批次前是存在的。通常, 一个批次内的更新操作数目远小于数据图的规模, 因而增量图的规模也远小于数据图, 即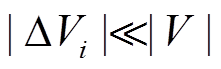 且
且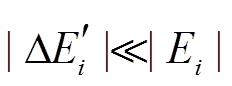 。
。
我们采用邻接表的形式来保存增量图 。对于每个顶点
。对于每个顶点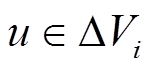 , 将其所有的邻接边增删操作保存在两个列表中, 即将
, 将其所有的邻接边增删操作保存在两个列表中, 即将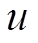 作为起点的有向边的增删操作
作为起点的有向边的增删操作 保存在出边表
保存在出边表 中,
中, 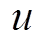 作为终点的有向边的增删操作
作为终点的有向边的增删操作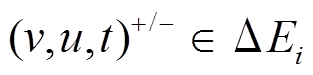 保存在入边表
保存在入边表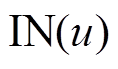 中。边表中的每个数据项都由两部分组成, 例如, 在出边表
中。边表中的每个数据项都由两部分组成, 例如, 在出边表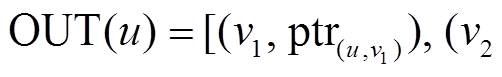 ,
,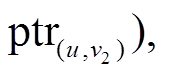 …]中, “v1, v2,…”表示有向边的终点, “
…]中, “v1, v2,…”表示有向边的终点, “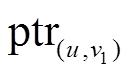 ,
, ”为指针, 分别指向每条有向边的增删操作时序序列, 形式为
”为指针, 分别指向每条有向边的增删操作时序序列, 形式为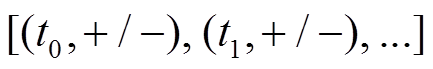 , 其中每项表示该有向边在时刻
, 其中每项表示该有向边在时刻 被增加或删除, 并且按照时序从小到大进行排列, 即
被增加或删除, 并且按照时序从小到大进行排列, 即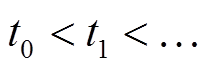 。
。
以图 1 为例, 图 1(a)中以顶点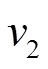 为起点的有向边增删操作为
为起点的有向边增删操作为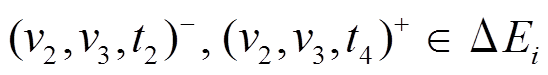 , 即对边
, 即对边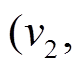
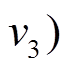 进行先删后增的操作, 并且, 边
进行先删后增的操作, 并且, 边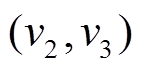 在图 1(h) (前一个批次版本
在图 1(h) (前一个批次版本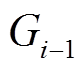 )中是存在的, 因此向
)中是存在的, 因此向 增加
增加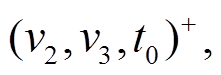 得到图 1(f)增量图
得到图 1(f)增量图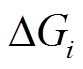 中边
中边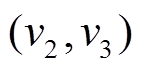 的增删操作时序序列
的增删操作时序序列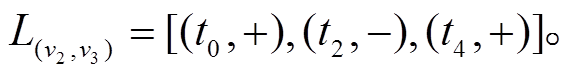 以
以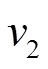 为起点的有向边增删操作仅涉及边
为起点的有向边增删操作仅涉及边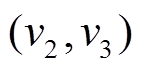 , 因此在
, 因此在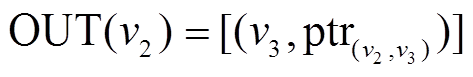 , 指针
, 指针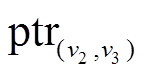 指向
指向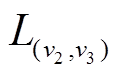 中。对称地, 个边表
中。对称地, 个边表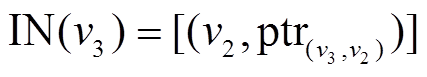 中的
中的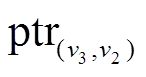 同样指向
同样指向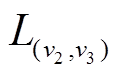 , 即每个增删操作时序序列同时被起点顶点的出边表和终点顶点的入边表中的指针所指向。类似地, 可以得到
, 即每个增删操作时序序列同时被起点顶点的出边表和终点顶点的入边表中的指针所指向。类似地, 可以得到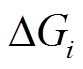 中边
中边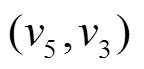 和
和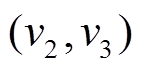 的增删操作时序序列以及相对应顶点的出边表和入边表。
的增删操作时序序列以及相对应顶点的出边表和入边表。
通过构建增量图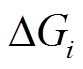 , 查询集合
, 查询集合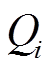 中多个在不同时刻的查询可以完美地进行多线程并发执行。
中多个在不同时刻的查询可以完美地进行多线程并发执行。
4 最短路径查询
对于每一个查询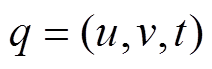 , 由于数据图中所有边都是无权重的, 所以可以使用宽度优先搜索算法(breadth-first search, BFS), 计算从
, 由于数据图中所有边都是无权重的, 所以可以使用宽度优先搜索算法(breadth-first search, BFS), 计算从 到
到 的最短路径距离, 其时间复杂度是线性的, 即
的最短路径距离, 其时间复杂度是线性的, 即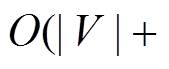
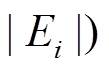 。首先, 在实现过程中, 我们使用双向搜索的策略来减少查询的实际搜索空间。其次, 采用 BSR编码方案[6]来存储数据图的邻接表。基于 BSR 编码, 提出使用 SIMD 指令的搜索优化策略, 从而提高数据块内部的数据并行度。此外, 在离线阶段, 通过对数据图的顶点进行重标号, 一方面从优化BSR 编码紧密性的角度, 进一步提高数据并行度, 另一方面从优化空间局部性的角度, 提高缓存(cache)命中率, 从而进一步提升查询性能。
。首先, 在实现过程中, 我们使用双向搜索的策略来减少查询的实际搜索空间。其次, 采用 BSR编码方案[6]来存储数据图的邻接表。基于 BSR 编码, 提出使用 SIMD 指令的搜索优化策略, 从而提高数据块内部的数据并行度。此外, 在离线阶段, 通过对数据图的顶点进行重标号, 一方面从优化BSR 编码紧密性的角度, 进一步提高数据并行度, 另一方面从优化空间局部性的角度, 提高缓存(cache)命中率, 从而进一步提升查询性能。
对于数据图带有边权的情况, 采用双向 Dijkstra算法[7]来计算最短路径, 时间复杂度则为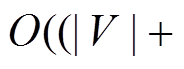
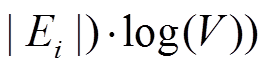 , 类似地可以采用本文提出的优化策略对该算法进行加速。
, 类似地可以采用本文提出的优化策略对该算法进行加速。
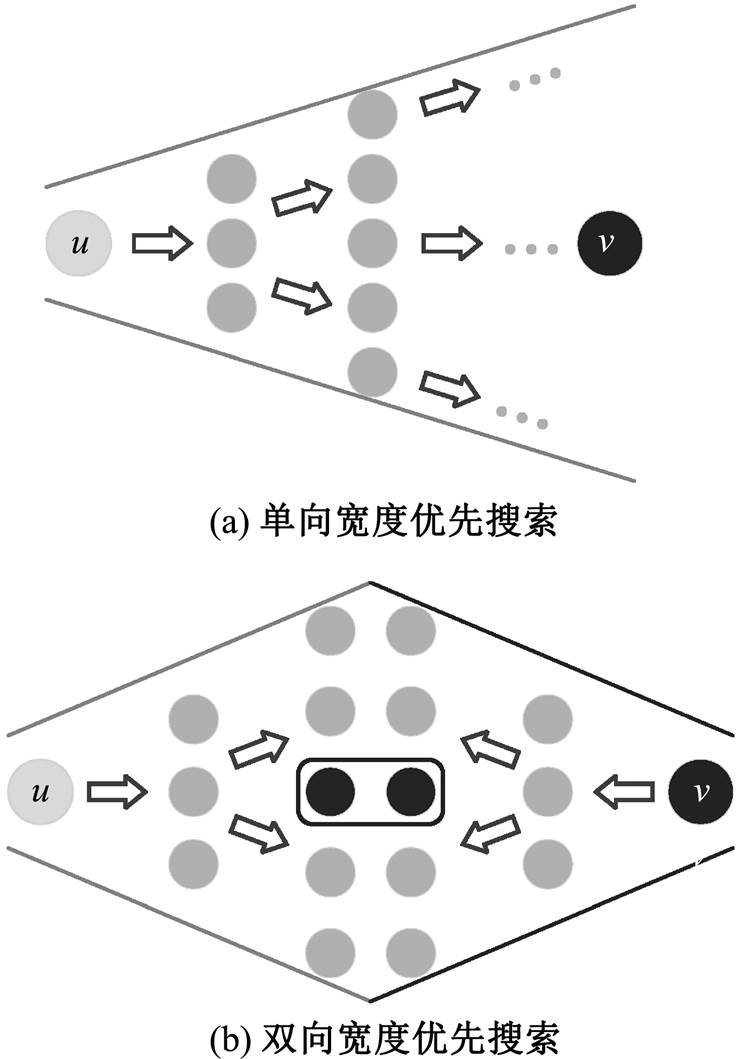
4.1 双向宽度优先搜索
通常意义上, 宽度优先搜索算法是从起点一端开始搜索, 一层层地向外扩展未访问过的顶点, 直到终点被第一次访问时结束, 此时扩展的层数即为最短路径长度。这种搜索方式称为单向宽度优先搜索。双向宽度优先搜索(bidirectional, BFS)则分别从起点和终点两侧扩展顶点, 直到两侧访问过的顶点发生重合时结束, 此时两侧扩展的层数之和为最短路径长度。图 2 展示单向和双向宽度优先搜索的过程; 单向搜索以起点作为根节点, 构建一棵搜索树, 直到终点成为当前搜索树的叶子节点为止; 双向搜索分别以起点和终点为根节点, 构建两棵搜索树, 直到两棵树产生交集。从图 2(a)可以看出, 当搜索层数增加时, 树的宽度相应地变大, 访问过的节点总数增加。假设搜索树的平均扇出为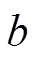 , 起点到终点的距离为
, 起点到终点的距离为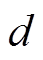 , 则图 2(a)中单向搜索树的节点数为
, 则图 2(a)中单向搜索树的节点数为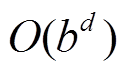 , 图 2(b)中两棵搜索树的节点数之和为
, 图 2(b)中两棵搜索树的节点数之和为
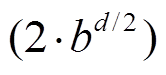 。与单向搜索相比, 双向搜索的搜索空间代价通常更小。
。与单向搜索相比, 双向搜索的搜索空间代价通常更小。
4.1.1算法流程
算法 1 描述使用双向搜索策略计算最短路径距离的算法过程。搜索过程中维护 3 个集合: Vis为长度为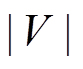 的数组, 记录以
的数组, 记录以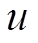 和
和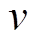 为起始, 所访问过的顶点集合。Vis 数组中的元素有 3 种取值, Vis[y]==0表示顶点
为起始, 所访问过的顶点集合。Vis 数组中的元素有 3 种取值, Vis[y]==0表示顶点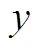 未被任何一棵搜索树访问过; Vis[y]== Left表示顶点 y 已被左侧搜索树访问过; Vis[y]== Right 表示顶点 y 已被右侧搜索树访问过。LQ 和RQ 为两个队列, 分别存储当前待扩展的顶点, 即搜索树中当前的叶子节点集合。初始时将起点
未被任何一棵搜索树访问过; Vis[y]== Left表示顶点 y 已被左侧搜索树访问过; Vis[y]== Right 表示顶点 y 已被右侧搜索树访问过。LQ 和RQ 为两个队列, 分别存储当前待扩展的顶点, 即搜索树中当前的叶子节点集合。初始时将起点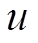 和终点 v 分别放入 LQ 和 RQ , 相应地
和终点 v 分别放入 LQ 和 RQ , 相应地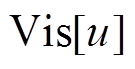 的值赋为Left, Vis[v]的值赋为Right, 其他顶点在Vis数组中的值初始化为
的值赋为Left, Vis[v]的值赋为Right, 其他顶点在Vis数组中的值初始化为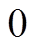 。
。
算法1 双向宽度优先搜索算法
Input:安全图版本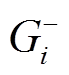 , 增量图
, 增量图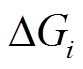 , 查询
, 查询
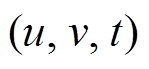
Output:t时刻从u到v的最短路径距离

在每一轮迭代中, 队列 NewQ 用于暂存当前扩展方向的下一层待扩展顶点, 变量 distance 记录两个方向上累计的扩展层数。通过函数 DecideDirection (LQ, RQ)来确定本轮的扩展方向。以扩展左侧搜索树为例: 依次枚举队列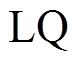 中的每个待扩展顶点
中的每个待扩展顶点 , 分别在安全图和增量图的边集中(即
, 分别在安全图和增量图的边集中(即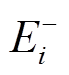 和
和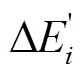 )访问当前时刻
)访问当前时刻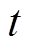 经过的邻接边
经过的邻接边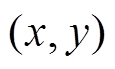 。若邻接顶点
。若邻接顶点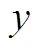 仍未被访问过, 那么将其在 Vis 数组中的状态更新为被左侧搜索树访问过, 并放入下一层待扩展队列NewQ 中。若顶点 y 已被右侧搜素树访问过, 说明此时左右两侧第一次连通, 即两棵搜索树产生交集, 最短路径距离即为当前的累积扩展层数 distance, 可以直接返回结果。当本轮所有顶点已扩展完毕, 将待扩展队列 LQ 更新为 NewQ。
仍未被访问过, 那么将其在 Vis 数组中的状态更新为被左侧搜索树访问过, 并放入下一层待扩展队列NewQ 中。若顶点 y 已被右侧搜素树访问过, 说明此时左右两侧第一次连通, 即两棵搜索树产生交集, 最短路径距离即为当前的累积扩展层数 distance, 可以直接返回结果。当本轮所有顶点已扩展完毕, 将待扩展队列 LQ 更新为 NewQ。
4.1.2 确定扩展方向
在每一轮迭代中, 由函数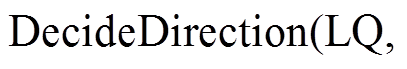
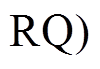 决定本轮的扩展方向, 即确定是扩展队列LQ 还是扩展
决定本轮的扩展方向, 即确定是扩展队列LQ 还是扩展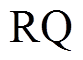 。考虑扩展方向的动机在于尽可能地降低搜索空间。由于从
。考虑扩展方向的动机在于尽可能地降低搜索空间。由于从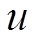 到
到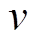 的最短路径距离
的最短路径距离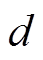 是确定的, 即左右两棵搜索树的总层数为定值, 所以我们优先选择扩展开销较小的一侧进行扩展。一种简单的估算扩展开销的指标为待扩展队列的大小, 即
是确定的, 即左右两棵搜索树的总层数为定值, 所以我们优先选择扩展开销较小的一侧进行扩展。一种简单的估算扩展开销的指标为待扩展队列的大小, 即
在每一轮中选择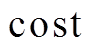 较小的队列进行扩展, 从而尽量保持
较小的队列进行扩展, 从而尽量保持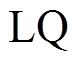 和
和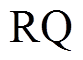 的长度平衡。这种估算扩展开销的方法的计算代价很低, 能够在
的长度平衡。这种估算扩展开销的方法的计算代价很低, 能够在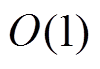 时间得到队列的长度。但是, 这种方法对于扩展开销的估算不够准确。
时间得到队列的长度。但是, 这种方法对于扩展开销的估算不够准确。
在扩展过程中, 需要遍历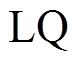 或
或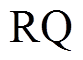 中的每个顶点的邻接边, 得到新的待扩展队列
中的每个顶点的邻接边, 得到新的待扩展队列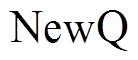 。所以, 更准确的估算方式应为扩展过程中所遍历邻接边的数量。注意到, 需要遍历的邻接边来自两个部分, 即安全图版本的边集合
。所以, 更准确的估算方式应为扩展过程中所遍历邻接边的数量。注意到, 需要遍历的邻接边来自两个部分, 即安全图版本的边集合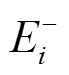 和增量图中带有增删操作时序序列的边集合
和增量图中带有增删操作时序序列的边集合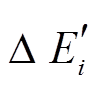 。对来自
。对来自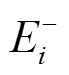 的邻接边无需判断, 可以直接经过; 对来自
的邻接边无需判断, 可以直接经过; 对来自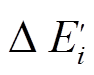 中的边, 需要判断, 在当前查询的时刻
中的边, 需要判断, 在当前查询的时刻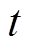 能否经过。判断方式为在该边的增删操作时序序列
能否经过。判断方式为在该边的增删操作时序序列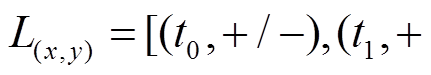
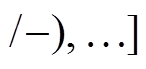 中找到时间标记小于
中找到时间标记小于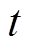 且最新的增删操作
且最新的增删操作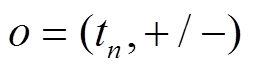 , 即满足
, 即满足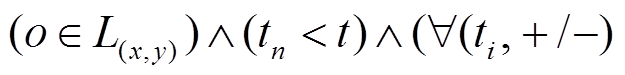
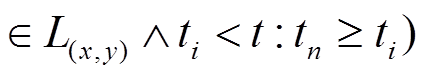 。若
。若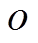 为增边操作, 则在时刻
为增边操作, 则在时刻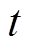 可经过, 否则不可经过。由于增删操作时序序列均是有序的, 并且绝大多数序列的长度较小(意味着对同一条有向边在一个批次内进行反复增删操作的次数不多), 所以可以直接顺序遍历, 找到最新操作
可经过, 否则不可经过。由于增删操作时序序列均是有序的, 并且绝大多数序列的长度较小(意味着对同一条有向边在一个批次内进行反复增删操作的次数不多), 所以可以直接顺序遍历, 找到最新操作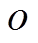 。一次顺序遍历的期望查找次数为
。一次顺序遍历的期望查找次数为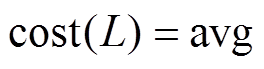
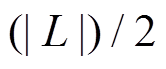 , 其中
, 其中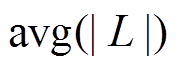 表示
表示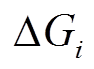 中所有增删操作时序序列长度的平均值。对于时序序列长度较大的情况, 可以采用二分查找, 则
中所有增删操作时序序列长度的平均值。对于时序序列长度较大的情况, 可以采用二分查找, 则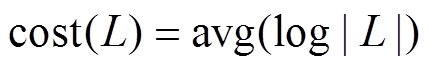 。
。
综上, 我们提出更为精确地估算扩展开销的计算方式: 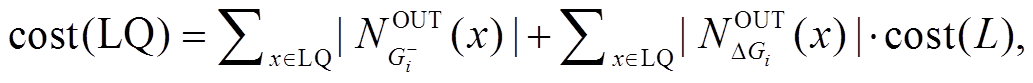 其中,
其中, 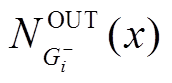 和
和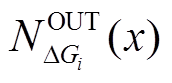 分别表示顶点
分别表示顶点 在安全图
在安全图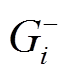 和增量图
和增量图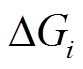 中的邻接边出边集合。相应地,
中的邻接边出边集合。相应地, 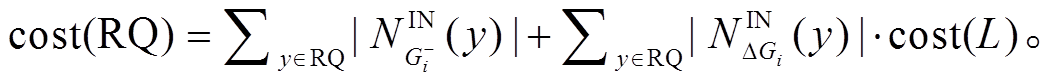
这种精确估算方法的在线计算代价为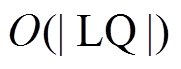 和
和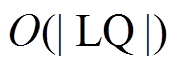 , 而
, 而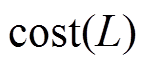 可以在步骤 1 中读入更新操作集合
可以在步骤 1 中读入更新操作集合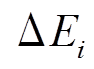 时提前计算好。
时提前计算好。
我们将上述两种估算扩展开销的方法分别称为简单估算和精确估算。尽管后者更为准确, 但其计算代价更高。当数据图中不同顶点之间的邻接边集合大小差异较大(如符合 power-law 分布的社交网络图, 大多数顶点的邻接边较少, 只有极少数顶点的邻接边极多), 使用精确估算法够有效地降低搜索空间。这是因为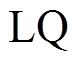 或
或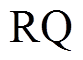 中的待扩展顶点如果包含邻接边极多的少量顶点, 会导致简单估算的结果不准确, 而精确估算可以很好地应对这种情况。当不同顶点之间的邻接边集合大小差异较小时(如公路网络图, 每个顶点表示一个路口, 其邻接边即衔接公路的数量较小), 即便使用简单估算, 带来的相对误差也很小, 精确估算则会由于计算代价相对较高而导致实际性能不如简单估算。第 5.2 节中, 在不同图数据集测试的实验结果也印证了上述现象, 因此两种估算方法各有优势。
中的待扩展顶点如果包含邻接边极多的少量顶点, 会导致简单估算的结果不准确, 而精确估算可以很好地应对这种情况。当不同顶点之间的邻接边集合大小差异较小时(如公路网络图, 每个顶点表示一个路口, 其邻接边即衔接公路的数量较小), 即便使用简单估算, 带来的相对误差也很小, 精确估算则会由于计算代价相对较高而导致实际性能不如简单估算。第 5.2 节中, 在不同图数据集测试的实验结果也印证了上述现象, 因此两种估算方法各有优势。
4.2 提高数据级并行度
我们使用 BSR 编码方案来存储数据图的邻接表, 并利用 CPU 的 SIMD 指令来提高单个查询的数据级并行度。数据并行是指在一条指令内同时并行地处理多个操作数。
单指令多数据流(single instruction multiple data, SIMD)允许一条指令同时对多个数据进行运算, 通过提高数据级并行度来提高程序的运行效率。绝大多数现代 CPU 都支持 SIMD 指令集。在 CPU 架构上, SIMD 指令对应着更宽的 SIMD 寄存器。例如支持 SSE 指令集的 CPU 具有 128-bit 位宽的 SIMD 寄存器, 因而可以支持 16 个 8-bit 操作数, 或 8 个 16-bit 操作数, 或 4 个 32-bit 操作数, 或 2 个 64-bit 操作数, 同时执行相同的指令; 进一步地, 支持 AVX/ AVX2 指令集的 CPU 具有 256-bit 位宽的SIMD 寄存器, 支持 AVX-512 指令集的 CPU 具有 512-bit 位宽的 SIMD 寄存器。SIMD 指令集的设计初衷是为了加速多媒体应用等数据密集型运算, 尤其适用于加速大量的矢量和矩阵运算操作。近年来, 也有一些相关工作借助 SIMD 指令集来优化加速数据库系统中的一些核心操作[8–11]。主流的 C/C++语言编译器(如GCC (GNU Compiler Collection), ICC (Intel C++ Compiler)和 MSVC (Microsoft Visual C++ Compiler))均支持通过编译器内联函数(intrinsics)的方式方便地使用 SIMD 指令, 无需在代码中嵌入汇编代码。
文献[8–11]专注于 SIMD 指令带来的数据级并行。简单地讲, 假设每个数据元素由一个 32 比特整数表示, 以及一个 SIMD 寄存器的位宽为 128 比特, 则一条 SIMD 指令可以同时处理 4 个数据元素。这意味着与不使用 SIMD 的算法相比, 最多可达到 4倍的加速比。这一性能优化完全是由 SIMD 指令带来的, 即算法的并行度取决于 SIMD 指令能够同时处理的数据元素个数。为了突破这一限制, Han 等[6]提出用户 BSR (base and state representation)对集合进行编码, 其基本思路是, 在一个整数内部表示多个数据元素, 使 SIMD 指令能够处理比其本身更多的数据元素。首先, 用位图(bitmap)表示邻接表, 即若顶点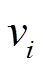 出现在该邻接表中, 就把其对应位图中的第 i 位设置为 1, 否则设置为 0。然后, 将位图切分成大小相等的数据片, 每个数据片的长度为 w。这样, 每个数据片可以直接由两部分表示: 基址域(base)和数据域(state)。基址域记录该划分后的数据片对应原位图的位置, 计算方式为该数据片内的任意数据元素的标号除以 w; 数据域记录该数据片本身的位图状态。图 3 为使用 BSR 对数据图中顶点
出现在该邻接表中, 就把其对应位图中的第 i 位设置为 1, 否则设置为 0。然后, 将位图切分成大小相等的数据片, 每个数据片的长度为 w。这样, 每个数据片可以直接由两部分表示: 基址域(base)和数据域(state)。基址域记录该划分后的数据片对应原位图的位置, 计算方式为该数据片内的任意数据元素的标号除以 w; 数据域记录该数据片本身的位图状态。图 3 为使用 BSR 对数据图中顶点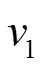 的出边邻接表进行编码。在图 3 中, 设
的出边邻接表进行编码。在图 3 中, 设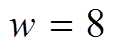 , 则邻居顶点
, 则邻居顶点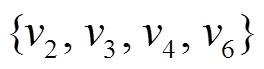 被划分在同一个数据片中, 其基址域为 0, 其他邻居顶点
被划分在同一个数据片中, 其基址域为 0, 其他邻居顶点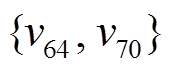 被划分到另一个数据片中, 其基址域为 8。在实现过程中,
被划分到另一个数据片中, 其基址域为 8。在实现过程中, 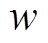 一般设为 128, 256 或 12, 即与 SIMD 寄存器的位宽相 一致。
一般设为 128, 256 或 12, 即与 SIMD 寄存器的位宽相 一致。
双向宽度优先搜索算法的瓶颈在于, 在每一轮迭代的扩展过程中, 对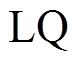 或
或 中每个顶点的邻接边进行遍历。由于数据图规模远大于增量图, 即
中每个顶点的邻接边进行遍历。由于数据图规模远大于增量图, 即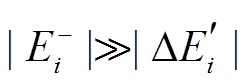 , 因此主要的性能开销在于遍历
, 因此主要的性能开销在于遍历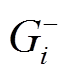 中的邻接边。使用 BSR 对数据图的邻接表进行编码存储后, 遍历邻接边的过程可以利用 SIMD 指令进行数据并发。详细地, 我们把算法 1 中用于记录已访问顶点的
中的邻接边。使用 BSR 对数据图的邻接表进行编码存储后, 遍历邻接边的过程可以利用 SIMD 指令进行数据并发。详细地, 我们把算法 1 中用于记录已访问顶点的 数组改用两个长度为
数组改用两个长度为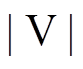 比特的位图(即
比特的位图(即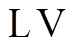 和
和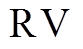 )分别表示。
)分别表示。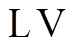 (或
(或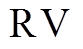 )中的第
)中的第 位记录标号为
位记录标号为 的顶点是否已被左侧搜索树(或右侧搜索树)访问过。数据图邻接表的 BSR 形式为
的顶点是否已被左侧搜索树(或右侧搜索树)访问过。数据图邻接表的 BSR 形式为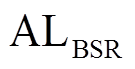
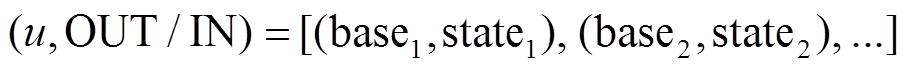 , 即顶点
, 即顶点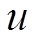 的 BSR 邻接表中的每项由基址域
的 BSR 邻接表中的每项由基址域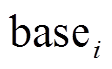 和数据域
和数据域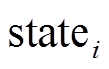 组成, 参数
组成, 参数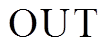 和
和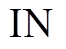 分别表示有向图的出边和入边邻接表。在不产生歧义的前提下, 我们省略参数
分别表示有向图的出边和入边邻接表。在不产生歧义的前提下, 我们省略参数 。在扩展过程中, 以扩展左侧搜索树为例, 枚举
。在扩展过程中, 以扩展左侧搜索树为例, 枚举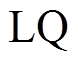 中每个顶点
中每个顶点 的 BSR 出边邻接表
的 BSR 出边邻接表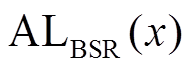 中的一项
中的一项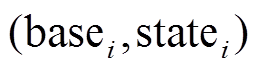 , 按照
, 按照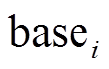 在位图LV中找到位置对应的数据片statej, 然后使用SIMD指令执行两数据片的按位减差操作, 即
在位图LV中找到位置对应的数据片statej, 然后使用SIMD指令执行两数据片的按位减差操作, 即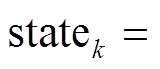
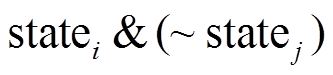 。数据片
。数据片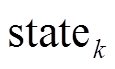 表示在
表示在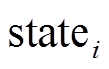 但不在
但不在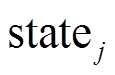 中的数据元素, 即与顶点
中的数据元素, 即与顶点 邻接但未访问的顶点集合, 将其添加到
邻接但未访问的顶点集合, 将其添加到 中。数据片
中。数据片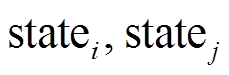 和
和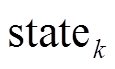 内部能够表示多个顶点, 因此每一次枚举都同时对多个顶点进行运算, 实现数据级并行。
内部能够表示多个顶点, 因此每一次枚举都同时对多个顶点进行运算, 实现数据级并行。
记数据图邻接表的原始存储形式为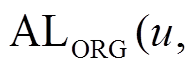
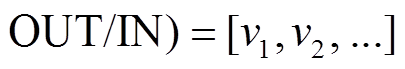 , 在算法 1 第 10 行, 对
, 在算法 1 第 10 行, 对 的数据图邻接表进行遍历需要
的数据图邻接表进行遍历需要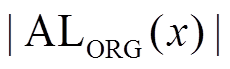 次迭代, 而使用 BSR 和 SIMD 指令优化后的算法, 则需要
次迭代, 而使用 BSR 和 SIMD 指令优化后的算法, 则需要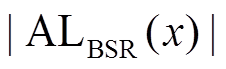 次迭代, 且满足
次迭代, 且满足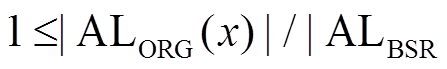
 。记
。记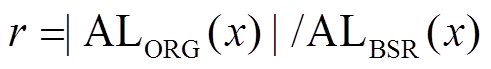 , 量化优化后算法对于原算法在扩展过程的加速比。
, 量化优化后算法对于原算法在扩展过程的加速比。
4.3 数据图顶点重标号
数据图的顶点编号是影响查询性能的一个重要因素。通常情况下, 我们将图中的顶点采用连续的整数进行编号, 这些顶点编号决定顶点和边在存储时的位置分布。数据图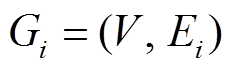 的邻接表存储由2|V|个有序列表组成, 每个顶点拥有其出边列表和入边列表, 每个列表以编号从小到大的顺序记录该顶点的出边或入边连向的邻居顶点。将数据图的邻接表使用 BSR 进行编码时, 不同的顶点编号会改变使用 BSR 邻接表的长度(即
的邻接表存储由2|V|个有序列表组成, 每个顶点拥有其出边列表和入边列表, 每个列表以编号从小到大的顺序记录该顶点的出边或入边连向的邻居顶点。将数据图的邻接表使用 BSR 进行编码时, 不同的顶点编号会改变使用 BSR 邻接表的长度(即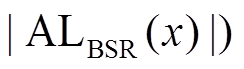 , 进而影响双向宽度优先搜索算法中扩展过程的总迭代次数。Han 等[6]将图顶点重标号问题形式化地定义为数据图的 BSR 邻接表长度之和最小化问题, 即 MIN
, 进而影响双向宽度优先搜索算法中扩展过程的总迭代次数。Han 等[6]将图顶点重标号问题形式化地定义为数据图的 BSR 邻接表长度之和最小化问题, 即 MIN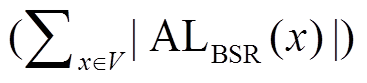 , 证明该问题是强 NP 完全问题, 并提出时间复杂度为
, 证明该问题是强 NP 完全问题, 并提出时间复杂度为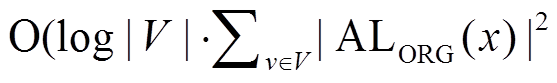 的近似算法GRO。
的近似算法GRO。
在我们使用 BSR 和 SIMD 优化的算法中, 扩展过程的加速比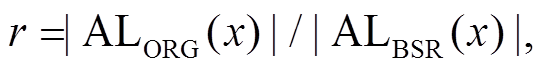 其中的
其中的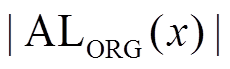 为定值。我们希望在顶点重标号过程中尽可能地减小
为定值。我们希望在顶点重标号过程中尽可能地减小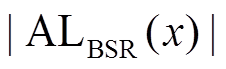 , 从而提高加速比
, 从而提高加速比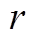 。BSR 邻接表中每个数据片表示的顶点数量越多, 则BSR邻接表越紧凑, 算法扩展过程的迭代次数越少。这一目标与 GRO 算法的目标一致。因此, 我们使用GRO 算法, 在预处理阶段对初始数据图
。BSR 邻接表中每个数据片表示的顶点数量越多, 则BSR邻接表越紧凑, 算法扩展过程的迭代次数越少。这一目标与 GRO 算法的目标一致。因此, 我们使用GRO 算法, 在预处理阶段对初始数据图 的顶点集合进行重标号。经过足够多的批次更新, 最新版本的数据图
的顶点集合进行重标号。经过足够多的批次更新, 最新版本的数据图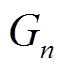 与初始数据图
与初始数据图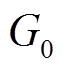 的拓扑结构可能发生较大改变, 当满足
的拓扑结构可能发生较大改变, 当满足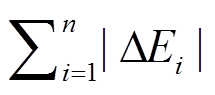
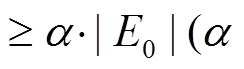 为阈值系数)时, 重新运行 GRO 算法, 再一次对顶点集合重标号。
为阈值系数)时, 重新运行 GRO 算法, 再一次对顶点集合重标号。
Wei 等[12]发现, 通过对顶点进行重标号, 能够有效地改善图遍历算法中对邻接表访问的空间局部性, 从而提高 CPU 缓存(cache)的命中率, 提升算法的运行效率。对于在时间上频繁共同访问的顶点, Wei 等[12]提出的 Gorder 算法可以将它们的编号尽可能地靠近, 导致这些顶点在存储空间上的临近, 从而提高它们处在同一个缓存行(cache line)的概率, 最终提高 CPU 缓存效率。Han 等[6]证实了这一点, 并指出 GRO 算法在缓存效率上与 Gorder 算法接近。
5 实验评估
5.1 实验环境
我们使用来自 SNAP[13]的 4 个真实的图数据集作为初始数据图, 每个批次的更新和查询操作为随机生成, 在随机生成过程中偏向于选中对不同时刻查询结果有影响的更新操作。对于每次生成的一个随机更新操作, 当执行该更新操作后, 如果后续的最短路径距离查询结果随之发生变化, 我们就以较大的概率将该更新操作加入测试集中。这一测试数据生成策略是为了在动态图的最短路径距离查询执行过程中, 尽可能地经过更新操作所涉及的边, 从而对基于增量图的双向宽度优先搜索算法的有效性进行验证。图数据集的信息如表1所示。
表1 图数据集统计信息
Table 1 Statistics of graph datasets

数据集批数 Twitter813061768149850~1502~78 DBLP317080104986612500~1000100~400 LiveJournal399796234681189101000~10000200~5000 RoadCA1965206276660724100~100050~500
测试机为小型 Linux 服务器, 内存为 128G, 配有两个Intel Xeon E5-2640V3@2.6-GHz 处理器, 每颗处理器拥有 8 核, 通过超线程技术, 每核可支持 2线程并发, 因此最多可支持32线程并发执行, 支持SSE 和 AVX/AVX2指令集, 即 SIMD 寄存器位宽为256 比特。实验代码用 C++语言实现, 使用 Intel TBB[14]线程库, 编译环境为 GCC v4.8.7, 已开源[15]。
5.2 单查询性能测试
首先比较单向宽度优先搜索、双向宽度优先搜索和双向搜索时使用不同的扩展方向决策对单个查询性能的影响。测试结果如图 4 所示, 其中 Naive BFS 表示单向宽度优先搜索算法, Bidirectional BFS +Alternate 表示双向宽度优先搜索并采用两棵搜索树轮流扩展的策略, Bidirectional BFS+ Simple 表示双向搜索并采用简单估算的扩展策略, Bidirectional BFS+Precise 表示双向搜索并采用精确估算。实验数据表明, 双向搜索的性能明显优于单向搜索。在Twitter, DBLP 和 LiveJournal 数据集上, 使用精确估算的扩展方向决策的加速比最高, 说明精确估算对搜索空间的降低程度最大。在RoadCA 数据集上简单估算的加速比高于精确估算, 是因为 RoadCA 中不同顶点之间的邻接边数量差异很小, 即便使用简单估算, 带来的相对误差也很小, 而精确估算会引入过多的计算开销。
5.3 线程级并行测试
在安全版本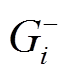 和增量图
和增量图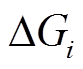 上, 我们测试了使用多线程并发执行查询的性能。数据图邻接表采用原始存储的形式, 每个查询运行双向宽度优先搜索算法, 对于数据集 Twitter, DBLP 和 LiveJournal 采用精确估算的扩展方向决策, 对数据集 RoadCA 则采用简单估算。测试结果如图 5 所示, 可以看出, 随着线程数增加, 运行时间成比例缩短, 加速比提升。在 Twitter 数据集上的加速效果略差于其他 3个数据集, 主要原因是该数据集部分批次的查询操作数量
上, 我们测试了使用多线程并发执行查询的性能。数据图邻接表采用原始存储的形式, 每个查询运行双向宽度优先搜索算法, 对于数据集 Twitter, DBLP 和 LiveJournal 采用精确估算的扩展方向决策, 对数据集 RoadCA 则采用简单估算。测试结果如图 5 所示, 可以看出, 随着线程数增加, 运行时间成比例缩短, 加速比提升。在 Twitter 数据集上的加速效果略差于其他 3个数据集, 主要原因是该数据集部分批次的查询操作数量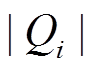 较少, 导致部分线程在执行查询过程中空闲。
较少, 导致部分线程在执行查询过程中空闲。
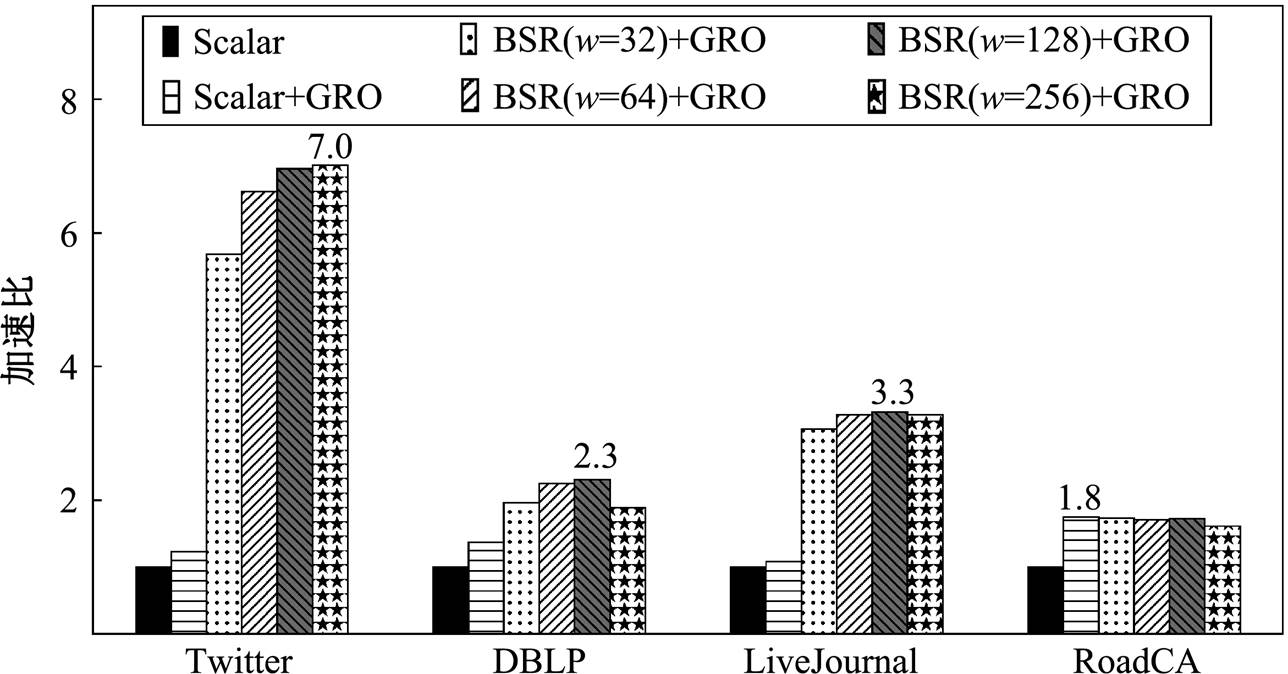
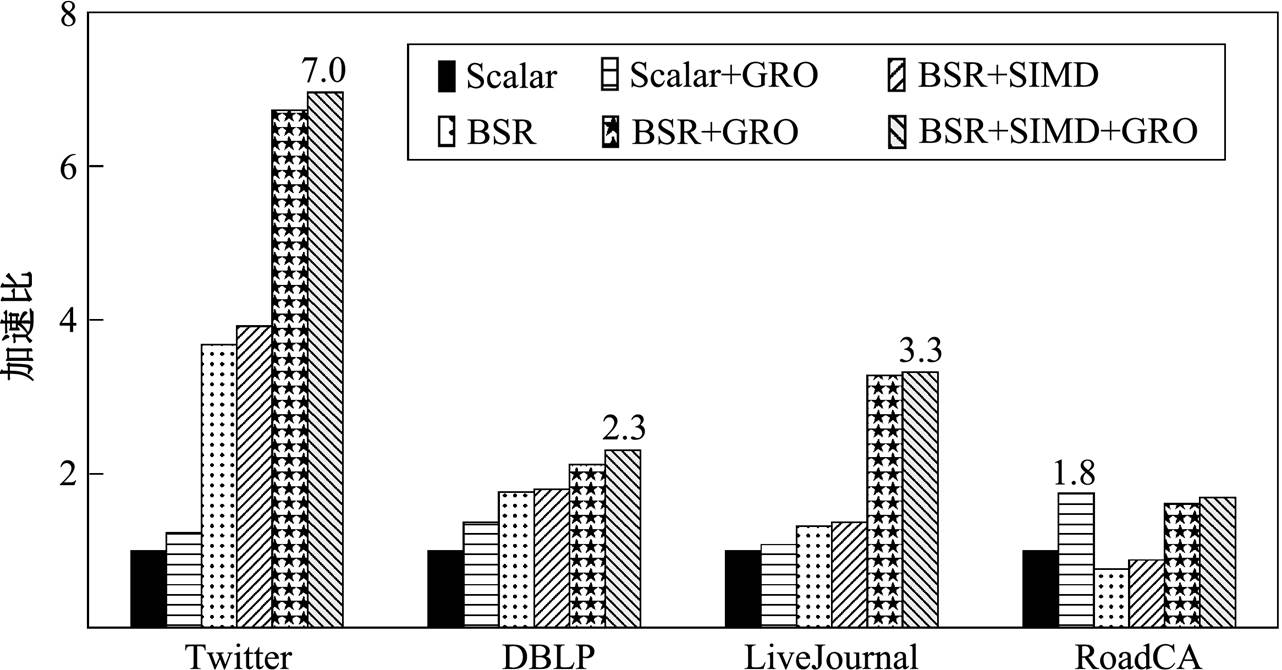
5.4 数据级并行测试
我们分别测试使用 BSR 编码邻接表、SIMD 指令以及采用数据图顶点重标号对数据级并行的优化效果, 结果如图 6 所示。将线程数统一设置为 16, 均采用双向宽度优先搜索算法, 对数据集 Twitter, DBLP 和 LiveJournal 采用精确估算的扩展方向决策, 对数据集 RoadCA 则采用简单估算。Scalar 表示邻接表为原始存储形式, 不使用 SIMD 指令, 使用原始顶点编号, 作为测试基准(加速比为 1.0); +GRO 表示在预处理阶段使用 GRO 算法对数据图顶点进行重标号; +BSR 表示邻接表使用 BSR 编码; +SIMD表示在 BSR 邻接表上使用 SIMD 指令进行计算。实验中数据片长度 设置为 128, GRO算法重新运行的阈值比例系数
设置为 128, GRO算法重新运行的阈值比例系数 设置为0.65。
设置为0.65。
实验数据表明, 当仅使用 GRO 重标号时(Scalar +GRO), 在 4 个数据集上均取得一定的加速效果(1.2~1.8), 这是由于优化了空间局部性, 从而提升缓存效率导致的。当仅使用 BSR 编码邻接表时(BSR), 在 Twitter, DBLP 和 LiveJournal 数据集上性能得到不同程度的提升, 在数据集 RoadCA 上的性能反而下降, 这是因为 RoadCA 中每个顶点的邻接边数量都不多, 即使采用 BSR 编码, 每个数据片内部包含的顶点数量也很少, 因而对数据并行度的提升不多, 但由于引入对基址域匹配等的额外计算开销, 使得整体的性能变差。当使用 BSR 编码和SIMD 指令时(BSR+SIMD), 比仅使用 BSR 编码(BSR)的性能均略有提升, 说明 SIMD 指令能够在BSR 编码的基础上提高数据级并行度, 但效果有限。同时用 BSR 编码和 GRO 重标号时(BSR+ GRO), 比仅使用 BSR编码(BSR)的性能提升幅度较大, 说明 GRO 重标号对 BSR 编码邻接表的紧凑程度改善很明显。当所有的措施同时使用时(BSR+ SIMD+GRO), 性能最优。唯一的例外是 RoadCA, 说明当图较为稀疏且不同顶点间邻接顶点数量差异较小时, BSR 编码和 SIMD 优化是无效的, 甚至有可能带来性能损失。
5.5 参数设置对性能的影响
我们分别测试使用 BSR 编码邻接表时, 数据片长度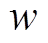 的不同设置对算法性能的影响, 以及 GRO算法重新运行的阈值比例系数
的不同设置对算法性能的影响, 以及 GRO算法重新运行的阈值比例系数 对算法在线阶段整体性能的影响。实验中, 首先将数据片长度
对算法在线阶段整体性能的影响。实验中, 首先将数据片长度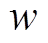 分别设置为
分别设置为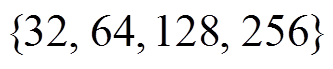 。当
。当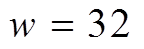 或
或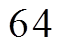 时, 无需使用 SIMD 指令; 当
时, 无需使用 SIMD 指令; 当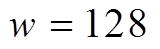 或
或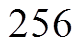 时, 分别使用位宽为 128 比特的 SSE 指令集以及位宽为 256 比特的 AVX/AVX2 指令集。然后, 在
时, 分别使用位宽为 128 比特的 SSE 指令集以及位宽为 256 比特的 AVX/AVX2 指令集。然后, 在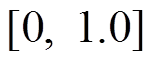 之间以0.05 的间隔选取阈值比例系数 α。在调节 α 的过程中, 相应地生成数量为
之间以0.05 的间隔选取阈值比例系数 α。在调节 α 的过程中, 相应地生成数量为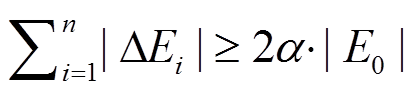 的增删 操作。
的增删 操作。
图 7 展示不同数据片长度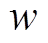 对算法的性能影响。在前 3 个数据集上, 使用 SIMD 指令
对算法的性能影响。在前 3 个数据集上, 使用 SIMD 指令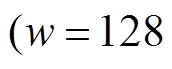 或
或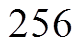 )的加速比明显优于不使用 SIMD 指令
)的加速比明显优于不使用 SIMD 指令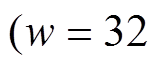 或 64)。整体上随着 w 的增大, 性能提升。但是,
或 64)。整体上随着 w 的增大, 性能提升。但是, 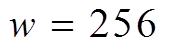 时的性能略差于
时的性能略差于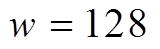 时, 主要原因是
时, 主要原因是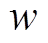 增大导致 BSR 数据域内元素稀疏, 造成由 BSR 编码带来的数据级并行度不足。在 RoadCA 数据集上的测试结果进一步说明了这一点, 因为在每个顶点的BSR 邻接表中, 每个数据域表示的邻接顶点数量上限不会超过该顶点的邻接边数量, 而在 RoadCA中, 绝大部分顶点的邻接边数量在 2~4 之间, 因此随着
增大导致 BSR 数据域内元素稀疏, 造成由 BSR 编码带来的数据级并行度不足。在 RoadCA 数据集上的测试结果进一步说明了这一点, 因为在每个顶点的BSR 邻接表中, 每个数据域表示的邻接顶点数量上限不会超过该顶点的邻接边数量, 而在 RoadCA中, 绝大部分顶点的邻接边数量在 2~4 之间, 因此随着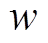 的增大, 数据域变得稀疏, 内部绝大部分比特位为零, 从而导致性能下降。
的增大, 数据域变得稀疏, 内部绝大部分比特位为零, 从而导致性能下降。
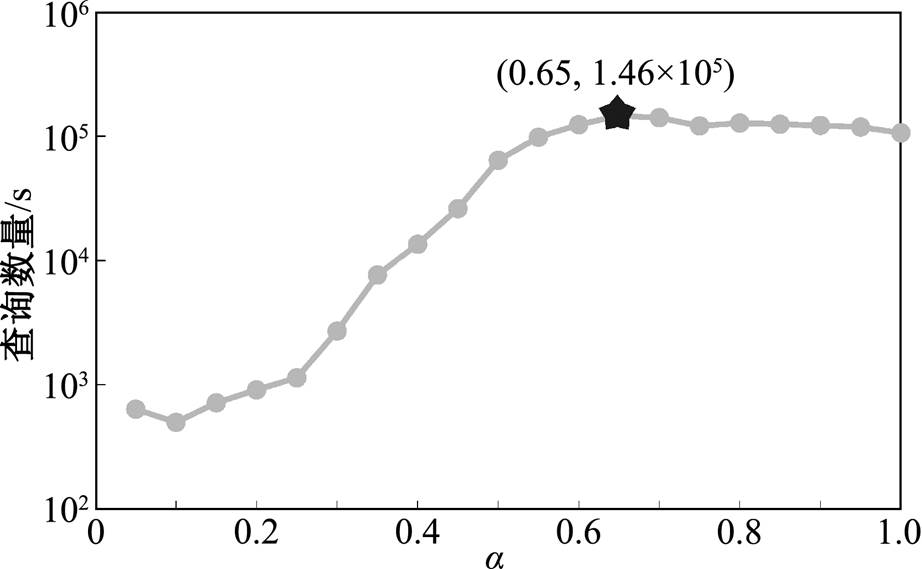
图 8 展示 GRO 算法重新运行的阈值比例系数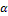 对算法整体性能的影响。纵坐标为每秒处理的平均查询数量, 即总查询数量与算法总运行时间之比, 总运行时间包括 GRO 算法的运行时间。随着
对算法整体性能的影响。纵坐标为每秒处理的平均查询数量, 即总查询数量与算法总运行时间之比, 总运行时间包括 GRO 算法的运行时间。随着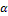 增大, 在线阶段 GRO 算法的重启频率降低, 由GRO 本身带来的运行时间减少, 但数据图的拓扑结构与重启 GRO 时相比发生了较大的改变, BSR带来的数据并行度降低。因此, 需要选取合适的
增大, 在线阶段 GRO 算法的重启频率降低, 由GRO 本身带来的运行时间减少, 但数据图的拓扑结构与重启 GRO 时相比发生了较大的改变, BSR带来的数据并行度降低。因此, 需要选取合适的 在两方面进行折衷。实验结果表明, 当
在两方面进行折衷。实验结果表明, 当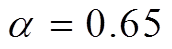 左右时, 算法的整体性能最佳。
左右时, 算法的整体性能最佳。
6 结论
本文提出一种在动态图上并发执行查询操作的计算框架。通过构建增量图的方法, 支持在不同时刻对不同图版本的最短路查询在线程级别并发执行。实验结果表明, 当查询负载充足时, 由多核处理器带来的线程级并行计算能力能够被充分地利用。进一步地, 本文讨论了双向宽度优先搜索中决策扩展方向的多种估算方法, 在不同的图数据特征下, 采用不同的估算方法可以尽可能地提升搜索效率。对于单个查询的执行过程, 通过使用 BSR 编码邻接表和 SIMD 指令来实现一条指令内处理多个数据元素, 可以减少双向宽度优先搜索算法扩展过程中的迭代次数, 提升数据级并行度。通过在预处理阶段对图顶点进行重标号, 有效地优化了 BSR 编码效率, 并提升缓存命中率。因此, 本文从线程级并行和数据级并行两个角度对动态图的最短路径查询问题进行显著的性能优化, 在不同的真实图数据集上取得 1.8~7.2 倍的加速比。
参考文献
[1] Bramandia R, Choi B, Ng W K. Incremental mainte-nance of 2-hop labeling of large graphs. TKDE, 2010, 22(5): 682–698
[2] Zhu A D, Lin W, Wang S, et al. Reachability queries on large dynamic graphs: a total order approach // SIGMOD. Snowbird, 2014: 1323–1334
[3] Franciosa P G, Frigioni D, Giaccio R. Semi-dynamic shortest paths and breadth-first search in digraphs // STACS. Berlin, 1997: 33–46
[4] Frigioni D, Marchetti-Spaccamela A, Nanni U. Fully dynamic algorithms for maintaining shortest paths trees. Journal of Algorithms, 2000, 34(2): 251–281
[5] Roditty L, Zwick U. A fully dynamic reachability algorithm for directed graphs with an almost linear update time. SIAM Journal on Computing, 2016, 45 (3): 712–733
[6] Han S, Zou L, Yu J X. Speeding up set intersections in graph algorithms using SIMD instructions // SIGMOD. Houston, 2018: 1587–1602
[7] Goldberg A V. Point-to-point shortest path algorithms with preprocessing // SOFSEM. Berlin, 2007: 88–102
[8] Zhou J, Kenneth A R. Implementing database opera-tions using SIMD instructions // SIGMOD. Madison, 2002: 145–156
[9] Willhalm T, Popovici N, Boshmaf Y, et al. SIMD-scan: ultra fast in-memory table scan using on-chip vector processing units // VLDB. Lyon, 2009: 385–394
[10] Feng Z, Lo E, Kao B, et al. Byteslice: pushing the envelop of main memory data processing with a new storage layout // SIGMOD. Melbourne, 2015: 31–46
[11] Xu W, Feng Z, Lo E. Fast multi-column sorting in main-memory column-stores // SIGMOD. San Fran-cisco, 2016: 1263–1278
[12] Wei H, Yu X J, Lu C, et al. Speedup graph processing by graph ordering // SIGMOD. San Francisco, 2016: 1813–1828
[13] Leskovec J, Krevl A. SNAP datasets: Stanford large network dataset collection [EB/OL]. (2014–06–30) [2019–01–09]. http://snap.stanford.edu/data
[14] Reinders J. Intel thread building blocks [EB/OL]. (2018–12–03)[2019–01–09].https://www.threading buildingblocks.org
[15] Han S. Source code of implementation details [EB/ OL]. (2016–09–16) [2019–01–09]. https://github.com/ Caesar11/SIGMOD-Progra mming-Contest-2016
A Parallel Algorithm to Answer Shortest Distance on Dynamic Graph
HAN Shuo, ZOU Lei†
Institute of Computer Science and Technology of Peking University, Beijing 100080; † Corresponding author, E-mail: zoulei@pku.edu.cn
Abstract The paper presents a parallel algorithm framework to answer shortest distance queries on dynamic graphs. Based on maintaining a delta graph, multiple queries within a batch are executed in parallel over different versions of data graph by multi-threading. For each query, bidirectional breath-first search (BFS) is utilized to reduce search space. During the search process, an exploration direction decision-making function is proposed. Furthermore, adjacency-lists of data graph are encoded by BSR layout, combined with SIMD instructions and graph reordering algorithm, higher degree of data-level parallelism is achieved. Extensive experiments on real graph datasets confirm the superior efficiency of the proposed solution.
Key words dynamic graph; shortest distance; delta graph; thread-level parallelism; data-level parallelism;bidirectional bidirectional breath-first search (BFS); SIMD
doi: 10.13209/j.0479-8023.2019.113
收稿日期: 2019–01–11;
修回日期: 2019–03–27
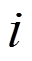 个批次内的图更新操作记为集合
个批次内的图更新操作记为集合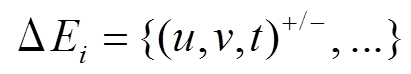 , 三元组(u, v, t)+/–表示在 t 时刻增加或删除一条从顶点 u 到顶点 v 的有向边。可以将更新操作集合 Ei 自然地分为增边集合
, 三元组(u, v, t)+/–表示在 t 时刻增加或删除一条从顶点 u 到顶点 v 的有向边。可以将更新操作集合 Ei 自然地分为增边集合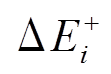 和删边集合
和删边集合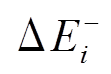 。此外, 我们允许在同一批次内或不同批次间对同一条边的反复增删操作。图查询操作记为集合
。此外, 我们允许在同一批次内或不同批次间对同一条边的反复增删操作。图查询操作记为集合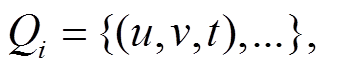 三元组
三元组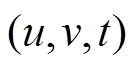 表示在 t 时刻查询从顶点 u 到顶点v 的最短路径长度。对于 t 时刻的查询, 我们认为 t时刻之前的图更新操作均已完成, t 时刻之后的操作均未开始, 即查询
表示在 t 时刻查询从顶点 u 到顶点v 的最短路径长度。对于 t 时刻的查询, 我们认为 t时刻之前的图更新操作均已完成, t 时刻之后的操作均未开始, 即查询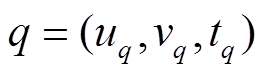 作用于图版本
作用于图版本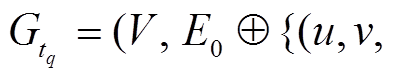
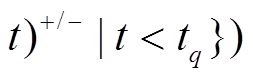 。第 i 个批次后, 数据图更新为
。第 i 个批次后, 数据图更新为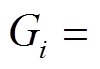
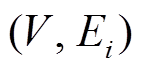 。其中
。其中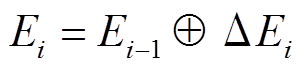 , 符号
, 符号 表示将更新操作集合
表示将更新操作集合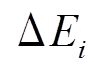 按照时间次序作用于边集合
按照时间次序作用于边集合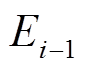 。
。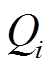 , 我们希望正确且快速地回答
, 我们希望正确且快速地回答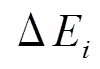 更新至数据图, 从而得到最新版本的
更新至数据图, 从而得到最新版本的 。
。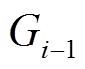 和当前批次的更新
和当前批次的更新 E
E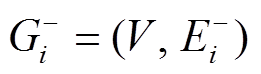 , 其中
, 其中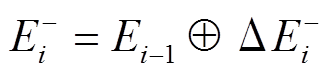 。显然, 对于该批次内的所有查询
。显然, 对于该批次内的所有查询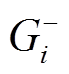 中的所有有向边
中的所有有向边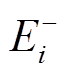 都可以“安全”地经过, 因此称
都可以“安全”地经过, 因此称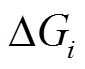 上, 并发地执行查询集合
上, 并发地执行查询集合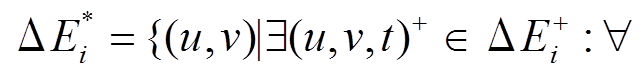
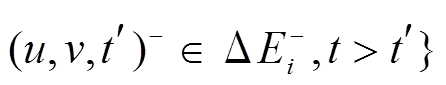 。即, 对于任意一条增边
。即, 对于任意一条增边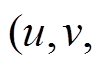
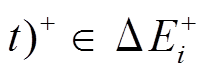 , 我们将边
, 我们将边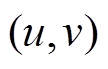 添加至
添加至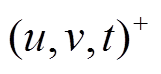 仅出现在增边集合
仅出现在增边集合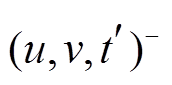 , 但增边操作的
, 但增边操作的 )。然后, 将最终增边集合
)。然后, 将最终增边集合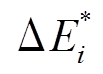 合并至安全版本
合并至安全版本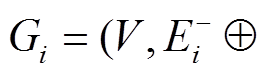
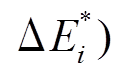 。容易证明:
。容易证明: 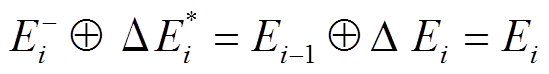 , 因此从安全版本
, 因此从安全版本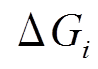 。在步骤 3 中, 图 1(c)删边集合
。在步骤 3 中, 图 1(c)删边集合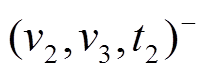 和
和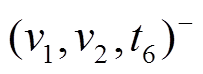 , 相应地, 在图 1(h)数据图版本
, 相应地, 在图 1(h)数据图版本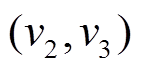 和
和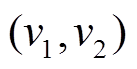 , 得到图 1(i)中安全版本
, 得到图 1(i)中安全版本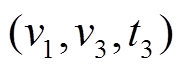 , 以
, 以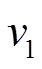 为起点开始搜索, 在
为起点开始搜索, 在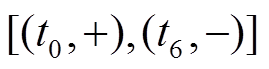 , 可知在查询时刻
, 可知在查询时刻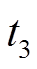 前最近的一次操作是增边
前最近的一次操作是增边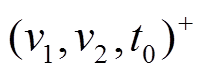 , 因此在
, 因此在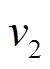 进一步搜索, 发现
进一步搜索, 发现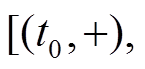
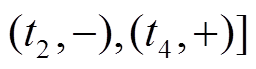 , 可知在
, 可知在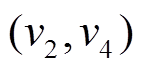 , 可以直接安全地到达
, 可以直接安全地到达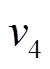 , 然后从
, 然后从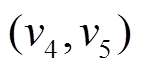 到达
到达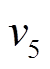 。类似地, 分析
。类似地, 分析 的时序序列, 可知边
的时序序列, 可知边 , 因而最短距离为4。
, 因而最短距离为4。
 , 按照上述相同的执行逻辑, 发现在
, 按照上述相同的执行逻辑, 发现在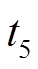 时刻
时刻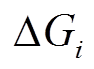 中的边
中的边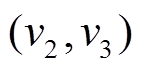 是可经过的, 因而
是可经过的, 因而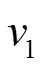 到
到 的最短距离缩短为 2。在执行过程中, 两个查询对
的最短距离缩短为 2。在执行过程中, 两个查询对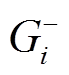 和
和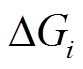 只读不写, 因此不存在数据冲突, 可以使用多线程并发地执行。查询执行结束并按照查询时序输出结果后, 需要将数据图更新至最新版本
只读不写, 因此不存在数据冲突, 可以使用多线程并发地执行。查询执行结束并按照查询时序输出结果后, 需要将数据图更新至最新版本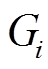 。在步骤 6 中, 计算最终增边集合: 对于
。在步骤 6 中, 计算最终增边集合: 对于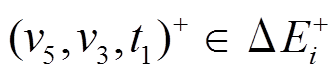 , 满足条件 1, 则该操作仅出现在增边集合
, 满足条件 1, 则该操作仅出现在增边集合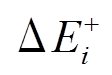 中; 对于
中; 对于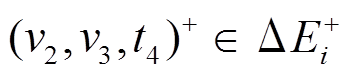 , 满足条件 2, 即虽然存在对应的删边操作
, 满足条件 2, 即虽然存在对应的删边操作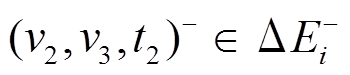 , 但
, 但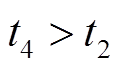 , 所以增边操作是最新的, 从而得到
, 所以增边操作是最新的, 从而得到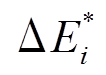
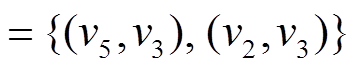 , 如图 1(e)所示。最终, 将
, 如图 1(e)所示。最终, 将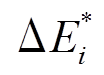 的两条边添加至图 1 (i)中安全图版本
的两条边添加至图 1 (i)中安全图版本 , 因此一个批次的所有更新操作的时间复杂度为
, 因此一个批次的所有更新操作的时间复杂度为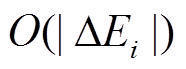 。算法的瓶颈在于查询执行的时间开销, 即步骤4。单个查询执行的时间开销为运行一次双向宽度优先搜索的复杂度, 最坏情况为
。算法的瓶颈在于查询执行的时间开销, 即步骤4。单个查询执行的时间开销为运行一次双向宽度优先搜索的复杂度, 最坏情况为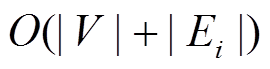 , 因此一个批次的总查询开销为
, 因此一个批次的总查询开销为 。由于图搜索算法的时间复杂度难以从理论上做进一步的改进, 所以我们尝试在不同层级上提高查询的并行度来优化查询执行效率。
。由于图搜索算法的时间复杂度难以从理论上做进一步的改进, 所以我们尝试在不同层级上提高查询的并行度来优化查询执行效率。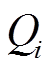 中的每个最短路径查询
中的每个最短路径查询
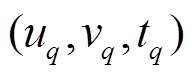 , 需要查询的数据图版本为
, 需要查询的数据图版本为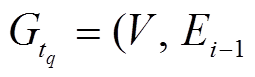
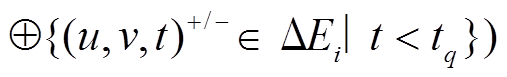 。为每个查询操作单独生成一个
。为每个查询操作单独生成一个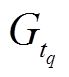 的代价显然是无法接受的。一种直接的策略是按照时序依次执行所有的更新和查询操作, 此时
的代价显然是无法接受的。一种直接的策略是按照时序依次执行所有的更新和查询操作, 此时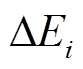 , 我们构建增量图
, 我们构建增量图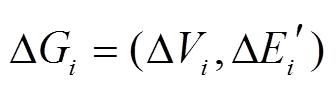 , 顶点集合
, 顶点集合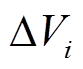 只需要保存在更新操作集合
只需要保存在更新操作集合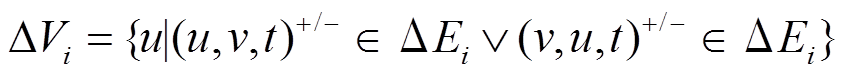 。
。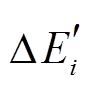 需要在
需要在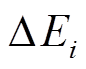 中的增删边操作基础上, 增加每条增删边在上一个数据图版本
中的增删边操作基础上, 增加每条增删边在上一个数据图版本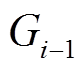 中的状态, 即
中的状态, 即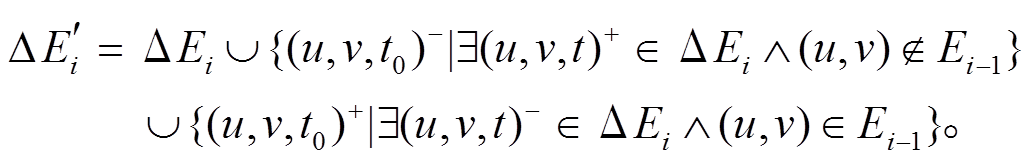
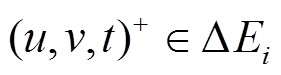 , 若该边未出现在
, 若该边未出现在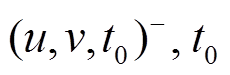 设置为小于
设置为小于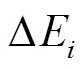 中所有操作的时间标记, 用来表示边
中所有操作的时间标记, 用来表示边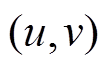 在该批次更新操作发生前是不存在的; 相应地, 对于删边操作
在该批次更新操作发生前是不存在的; 相应地, 对于删边操作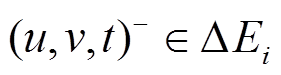 , 若该边已出现在
, 若该边已出现在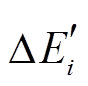 增加一个额外的增边操作(u, v, t
增加一个额外的增边操作(u, v, t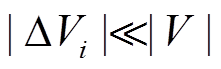 且
且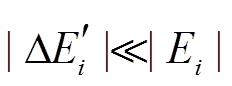 。
。 。对于每个顶点
。对于每个顶点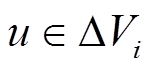 , 将其所有的邻接边增删操作保存在两个列表中, 即将
, 将其所有的邻接边增删操作保存在两个列表中, 即将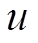 作为起点的有向边的增删操作
作为起点的有向边的增删操作 保存在出边表
保存在出边表 中,
中, 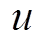 作为终点的有向边的增删操作
作为终点的有向边的增删操作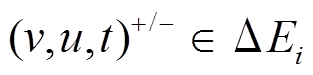 保存在入边表
保存在入边表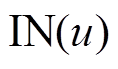 中。边表中的每个数据项都由两部分组成, 例如, 在出边表
中。边表中的每个数据项都由两部分组成, 例如, 在出边表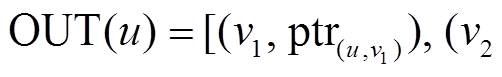 ,
,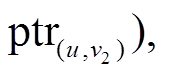 …]中, “v
…]中, “v ”为指针, 分别指向每条有向边的增删操作时序序列, 形式为
”为指针, 分别指向每条有向边的增删操作时序序列, 形式为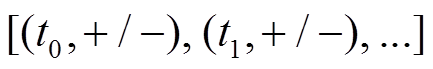 , 其中每项表示该有向边在时刻
, 其中每项表示该有向边在时刻 被增加或删除, 并且按照时序从小到大进行排列, 即
被增加或删除, 并且按照时序从小到大进行排列, 即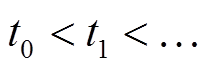 。
。 为起点的有向边增删操作为
为起点的有向边增删操作为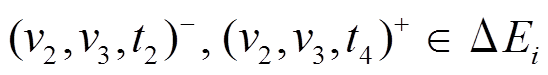 , 即对边
, 即对边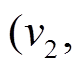
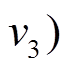 进行先删后增的操作, 并且, 边
进行先删后增的操作, 并且, 边 增加
增加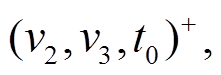 得到图 1(f)增量图
得到图 1(f)增量图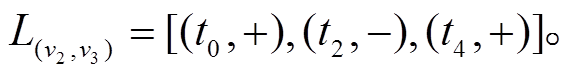 以
以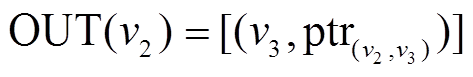 , 指针
, 指针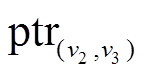 指向
指向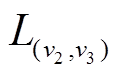 中。对称地, 个边表
中。对称地, 个边表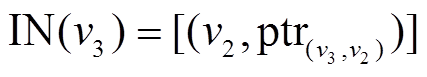 中的
中的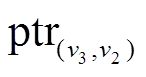 同样指向
同样指向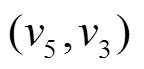 和
和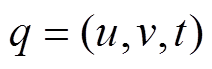 , 由于数据图中所有边都是无权重的, 所以可以使用宽度优先搜索算法(breadth-first search, BFS), 计算从
, 由于数据图中所有边都是无权重的, 所以可以使用宽度优先搜索算法(breadth-first search, BFS), 计算从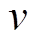 的最短路径距离, 其时间复杂度是线性的, 即
的最短路径距离, 其时间复杂度是线性的, 即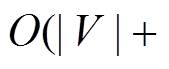
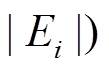 。首先, 在实现过程中, 我们使用双向搜索的策略来减少查询的实际搜索空间。其次, 采用 BSR编码方案
。首先, 在实现过程中, 我们使用双向搜索的策略来减少查询的实际搜索空间。其次, 采用 BSR编码方案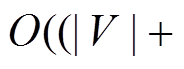
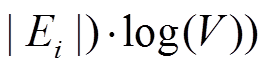 , 类似地可以采用本文提出的优化策略对该算法进行加速。
, 类似地可以采用本文提出的优化策略对该算法进行加速。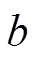 , 起点到终点的距离为
, 起点到终点的距离为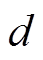 , 则图 2(a)中单向搜索树的节点数为
, 则图 2(a)中单向搜索树的节点数为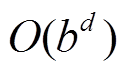 , 图 2(b)中两棵搜索树的节点数之和为
, 图 2(b)中两棵搜索树的节点数之和为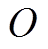
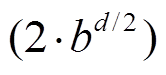 。与单向搜索相比, 双向搜索的搜索空间代价通常更小。
。与单向搜索相比, 双向搜索的搜索空间代价通常更小。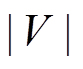 的数组, 记录以
的数组, 记录以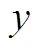 未被任何一棵搜索树访问过; Vis[y]== Left表示顶点 y 已被左侧搜索树访问过; Vis[y]== Right 表示顶点 y 已被右侧搜索树访问过。LQ 和RQ 为两个队列, 分别存储当前待扩展的顶点, 即搜索树中当前的叶子节点集合。初始时将起点
未被任何一棵搜索树访问过; Vis[y]== Left表示顶点 y 已被左侧搜索树访问过; Vis[y]== Right 表示顶点 y 已被右侧搜索树访问过。LQ 和RQ 为两个队列, 分别存储当前待扩展的顶点, 即搜索树中当前的叶子节点集合。初始时将起点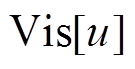 的值赋为Left, Vis[v]的值赋为Right, 其他顶点在Vis数组中的值初始化为
的值赋为Left, Vis[v]的值赋为Right, 其他顶点在Vis数组中的值初始化为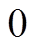 。
。
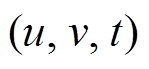

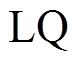 中的每个待扩展顶点
中的每个待扩展顶点 , 分别在安全图和增量图的边集中(即
, 分别在安全图和增量图的边集中(即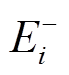 和
和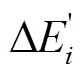 )访问当前时刻
)访问当前时刻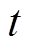 经过的邻接边
经过的邻接边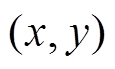 。若邻接顶点
。若邻接顶点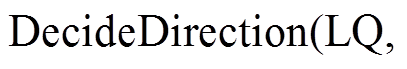
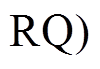 决定本轮的扩展方向, 即确定是扩展队列LQ 还是扩展
决定本轮的扩展方向, 即确定是扩展队列LQ 还是扩展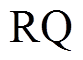 。考虑扩展方向的动机在于尽可能地降低搜索空间。由于从
。考虑扩展方向的动机在于尽可能地降低搜索空间。由于从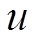 到
到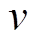 的最短路径距离
的最短路径距离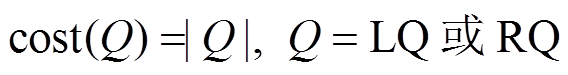 。
。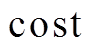 较小的队列进行扩展, 从而尽量保持
较小的队列进行扩展, 从而尽量保持 时间得到队列的长度。但是, 这种方法对于扩展开销的估算不够准确。
时间得到队列的长度。但是, 这种方法对于扩展开销的估算不够准确。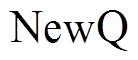 。所以, 更准确的估算方式应为扩展过程中所遍历邻接边的数量。注意到, 需要遍历的邻接边来自两个部分, 即安全图版本的边集合
。所以, 更准确的估算方式应为扩展过程中所遍历邻接边的数量。注意到, 需要遍历的邻接边来自两个部分, 即安全图版本的边集合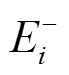 和增量图中带有增删操作时序序列的边集合
和增量图中带有增删操作时序序列的边集合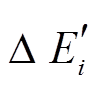 。对来自
。对来自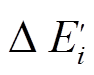 中的边, 需要判断, 在当前查询的时刻
中的边, 需要判断, 在当前查询的时刻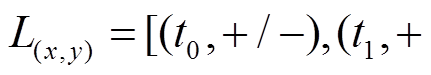
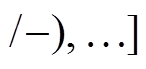 中找到时间标记小于
中找到时间标记小于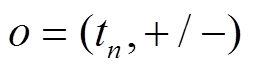 , 即满足
, 即满足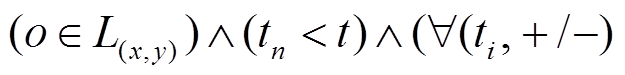
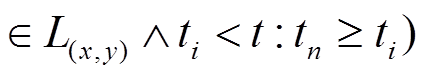 。若
。若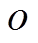 为增边操作, 则在时刻
为增边操作, 则在时刻
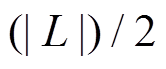 , 其中
, 其中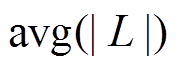 表示
表示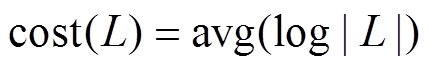 。
。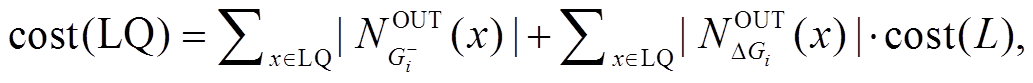 其中,
其中, 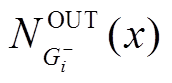 和
和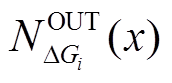 分别表示顶点
分别表示顶点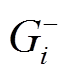 和增量图
和增量图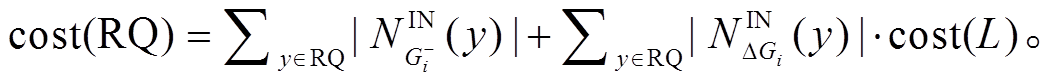
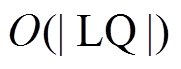 和
和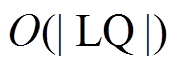 , 而
, 而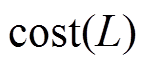 可以在步骤 1 中读入更新操作集合
可以在步骤 1 中读入更新操作集合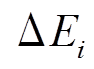 时提前计算好。
时提前计算好。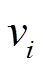 出现在该邻接表中, 就把其对应位图中的第 i 位设置为 1, 否则设置为 0。然后, 将位图切分成大小相等的数据片, 每个数据片的长度为 w。这样, 每个数据片可以直接由两部分表示: 基址域(base)和数据域(state)。基址域记录该划分后的数据片对应原位图的位置, 计算方式为该数据片内的任意数据元素的标号除以 w; 数据域记录该数据片本身的位图状态。图 3 为使用 BSR 对数据图中顶点
出现在该邻接表中, 就把其对应位图中的第 i 位设置为 1, 否则设置为 0。然后, 将位图切分成大小相等的数据片, 每个数据片的长度为 w。这样, 每个数据片可以直接由两部分表示: 基址域(base)和数据域(state)。基址域记录该划分后的数据片对应原位图的位置, 计算方式为该数据片内的任意数据元素的标号除以 w; 数据域记录该数据片本身的位图状态。图 3 为使用 BSR 对数据图中顶点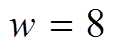 , 则邻居顶点
, 则邻居顶点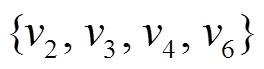 被划分在同一个数据片中, 其基址域为 0, 其他邻居顶点
被划分在同一个数据片中, 其基址域为 0, 其他邻居顶点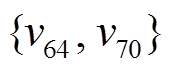 被划分到另一个数据片中, 其基址域为 8。在实现过程中,
被划分到另一个数据片中, 其基址域为 8。在实现过程中, 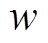 一般设为 128, 256 或 12, 即与 SIMD 寄存器的位宽相 一致。
一般设为 128, 256 或 12, 即与 SIMD 寄存器的位宽相 一致。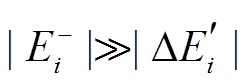 , 因此主要的性能开销在于遍历
, 因此主要的性能开销在于遍历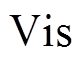 数组改用两个长度为
数组改用两个长度为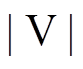 比特的位图(即
比特的位图(即 和
和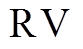 )分别表示。
)分别表示。 位记录标号为
位记录标号为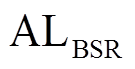
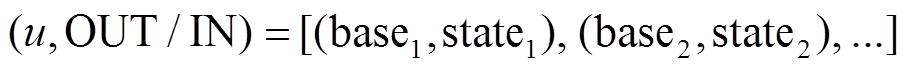 , 即顶点
, 即顶点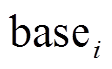 和数据域
和数据域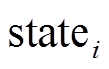 组成, 参数
组成, 参数 和
和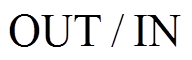 。在扩展过程中, 以扩展左侧搜索树为例, 枚举
。在扩展过程中, 以扩展左侧搜索树为例, 枚举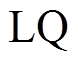 中每个顶点
中每个顶点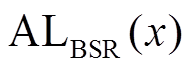 中的一项
中的一项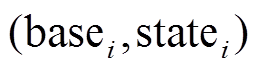 , 按照
, 按照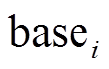 在位图LV中找到位置对应的数据片state
在位图LV中找到位置对应的数据片state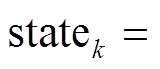
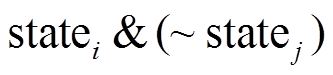 。数据片
。数据片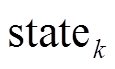 表示在
表示在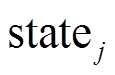 中的数据元素, 即与顶点
中的数据元素, 即与顶点 中。数据片
中。数据片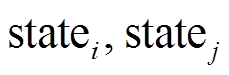 和
和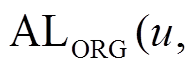
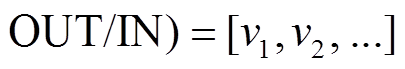 , 在算法 1 第 10 行, 对
, 在算法 1 第 10 行, 对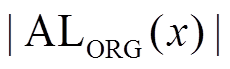 次迭代, 而使用 BSR 和 SIMD 指令优化后的算法, 则需要
次迭代, 而使用 BSR 和 SIMD 指令优化后的算法, 则需要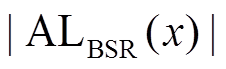 次迭代, 且满足
次迭代, 且满足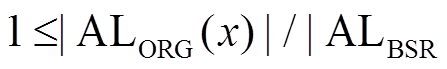
 。记
。记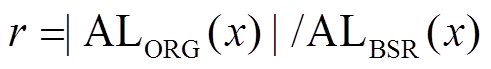 , 量化优化后算法对于原算法在扩展过程的加速比。
, 量化优化后算法对于原算法在扩展过程的加速比。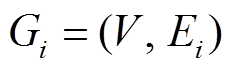 的邻接表存储由2|V|个有序列表组成, 每个顶点拥有其出边列表和入边列表, 每个列表以编号从小到大的顺序记录该顶点的出边或入边连向的邻居顶点。将数据图的邻接表使用 BSR 进行编码时, 不同的顶点编号会改变使用 BSR 邻接表的长度(即
的邻接表存储由2|V|个有序列表组成, 每个顶点拥有其出边列表和入边列表, 每个列表以编号从小到大的顺序记录该顶点的出边或入边连向的邻居顶点。将数据图的邻接表使用 BSR 进行编码时, 不同的顶点编号会改变使用 BSR 邻接表的长度(即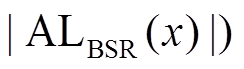 , 进而影响双向宽度优先搜索算法中扩展过程的总迭代次数。Han 等
, 进而影响双向宽度优先搜索算法中扩展过程的总迭代次数。Han 等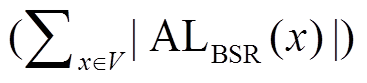 , 证明该问题是强 NP 完全问题, 并提出时间复杂度为
, 证明该问题是强 NP 完全问题, 并提出时间复杂度为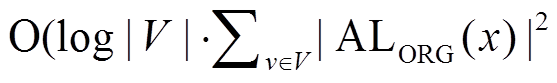 的近似算法GRO。
的近似算法GRO。
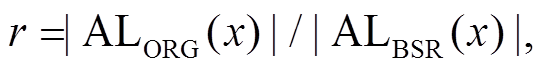 其中的
其中的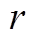 。BSR 邻接表中每个数据片表示的顶点数量越多, 则BSR邻接表越紧凑, 算法扩展过程的迭代次数越少。这一目标与 GRO 算法的目标一致。因此, 我们使用GRO 算法, 在预处理阶段对初始数据图
。BSR 邻接表中每个数据片表示的顶点数量越多, 则BSR邻接表越紧凑, 算法扩展过程的迭代次数越少。这一目标与 GRO 算法的目标一致。因此, 我们使用GRO 算法, 在预处理阶段对初始数据图 的顶点集合进行重标号。经过足够多的批次更新, 最新版本的数据图
的顶点集合进行重标号。经过足够多的批次更新, 最新版本的数据图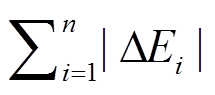
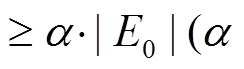 为阈值系数)时, 重新运行 GRO 算法, 再一次对顶点集合重标号。
为阈值系数)时, 重新运行 GRO 算法, 再一次对顶点集合重标号。
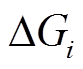 上, 我们测试了使用多线程并发执行查询的性能。数据图邻接表采用原始存储的形式, 每个查询运行双向宽度优先搜索算法, 对于数据集 Twitter, DBLP 和 LiveJournal 采用精确估算的扩展方向决策, 对数据集 RoadCA 则采用简单估算。测试结果如图 5 所示, 可以看出, 随着线程数增加, 运行时间成比例缩短, 加速比提升。在 Twitter 数据集上的加速效果略差于其他 3个数据集, 主要原因是该数据集部分批次的查询操作数量
上, 我们测试了使用多线程并发执行查询的性能。数据图邻接表采用原始存储的形式, 每个查询运行双向宽度优先搜索算法, 对于数据集 Twitter, DBLP 和 LiveJournal 采用精确估算的扩展方向决策, 对数据集 RoadCA 则采用简单估算。测试结果如图 5 所示, 可以看出, 随着线程数增加, 运行时间成比例缩短, 加速比提升。在 Twitter 数据集上的加速效果略差于其他 3个数据集, 主要原因是该数据集部分批次的查询操作数量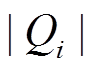 较少, 导致部分线程在执行查询过程中空闲。
较少, 导致部分线程在执行查询过程中空闲。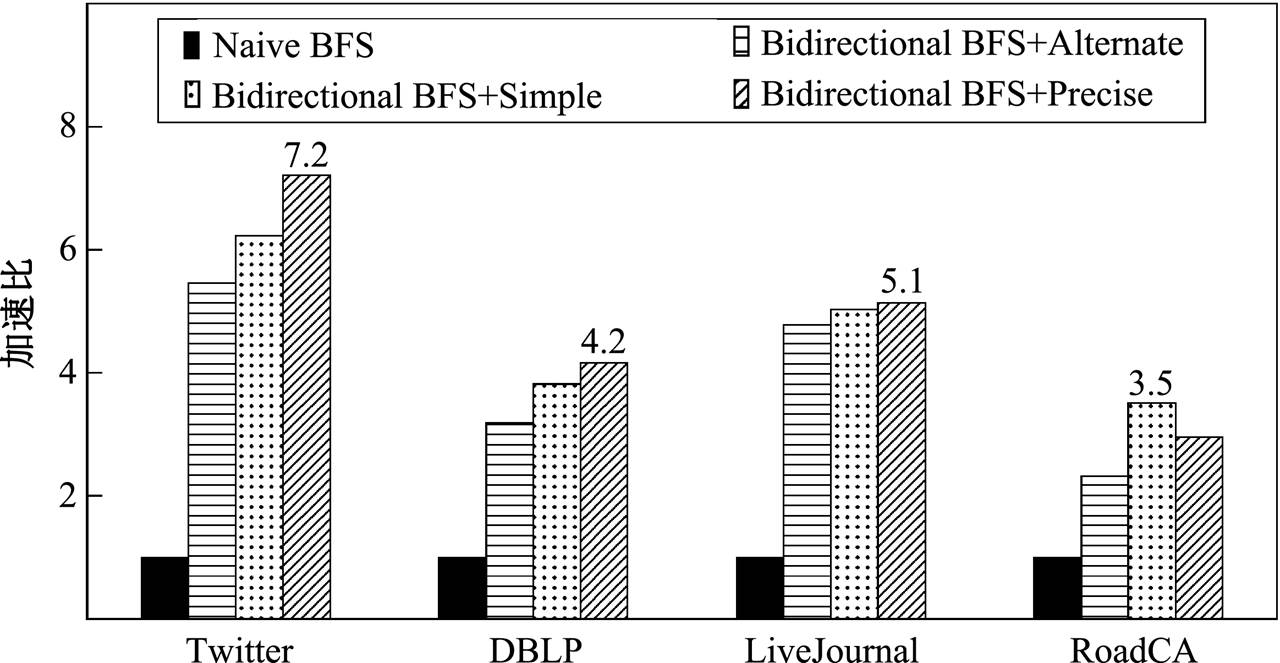
 设置为0.65。
设置为0.65。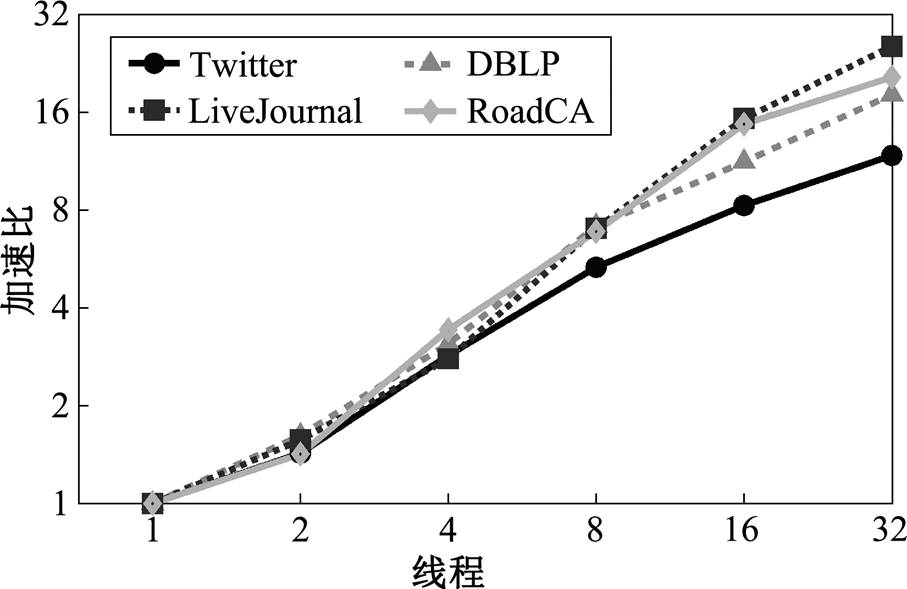
 的不同设置对算法性能的影响, 以及 GRO算法重新运行的阈值比例系数
的不同设置对算法性能的影响, 以及 GRO算法重新运行的阈值比例系数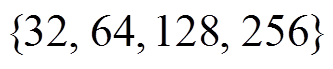 。当
。当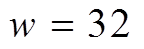 或
或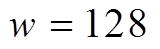 或
或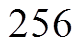 时, 分别使用位宽为 128 比特的 SSE 指令集以及位宽为 256 比特的 AVX/AVX2 指令集。然后, 在
时, 分别使用位宽为 128 比特的 SSE 指令集以及位宽为 256 比特的 AVX/AVX2 指令集。然后, 在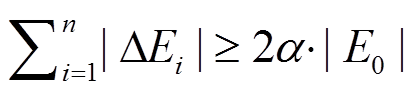 的增删 操作。
的增删 操作。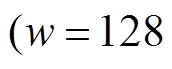 或
或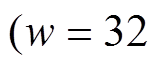 或 64)。整体上随着 w 的增大, 性能提升。但是,
或 64)。整体上随着 w 的增大, 性能提升。但是, 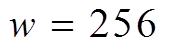 时的性能略差于
时的性能略差于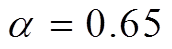 左右时, 算法的整体性能最佳。
左右时, 算法的整体性能最佳。