(1)摘要 前列腺癌是男性常见的恶性肿瘤。临床上常用的干扰雄激素的治疗药物是阿比特龙, 但长期高剂量的阿比特龙治疗常导致患者前列腺肿瘤细胞进化至药物抵抗。为了揭示前列腺癌发展的动力学机制, 本文引入给药剂量因素, 建立二变量的肿瘤演化定量模型。通过分析固定给药和适应性给药策略的动力学性质, 并绘制势能景观图, 从动力学角度展示适应性给药策略的优势, 揭示高剂量药物导致体系演化为不可逆药物抵抗状态的动力学机理。此外还构建治疗策略的评分体系, 以便优化治疗策略。
关键词 前列腺癌; 阿比特龙; 药物抵抗; 动力学模型; 策略优化
前列腺癌是男性最常见的恶性肿瘤之一, 其发病率和死亡率在全球范围内位居前五位[1]。目前临床上采用根治性前列腺切除术、雄激素剥夺治疗以及外放射治疗等多种方法联合治疗前列腺癌。当前列腺癌患者的睾酮达到去势水平, 但血清中前列腺特异性抗原(prostate specific antigen, PSA)持续升高且超过标准值或影像学检查出现病灶转移的情况时, 即认为疾病发展至去势抵抗性前列腺癌[2]。该阶段, 单纯采用雄激素剥夺疗法已无法控制病情发展。研究证实, 肿瘤内合成睾酮的酶过度表达和肿瘤细胞雄激素受体(AR)信号过度活化是导致抵抗性产生的主要原因[3]。该阶段的治疗方案会在雄激素剥夺治疗的基础上联用雄激素抑制剂, 以期达到控制疾病进展的目的。阿比特龙是去势抵抗性前列腺癌治疗的一线常用治疗药物[4], 它通过阻断 CYP17A1表达的 17α-羟化酶和 17, 20-裂解酶来干扰雄激素的合成。
根据阿比特龙是否作用于细胞、细胞是否产生睾酮以及细胞是否依赖睾酮生长, 将肿瘤细胞分为三类。1)Tp 细胞: 产生睾酮, 并可在阿比特龙作用下, 通过阻断 CYP17A1 表达的 17α-羟化酶和 17, 20-裂解酶抑制睾酮的产生; 2)T+细胞: 睾酮依赖性细胞; 3)T–细胞: 睾酮非依赖性细胞[5]。目前临床常用的阿比特龙治疗方案为固定最大耐受剂量给药和节拍性给药, 但最终都会因 T–细胞过度增殖而产生耐药性。为了避免这种情况, Zhang 等[5]发展一套适应性给药方案: 根据PSA 的浓度决定给药边界(PSA+)和停药边界(PSA–), 采用适应性给药方案, 使对药物敏感的 T+肿瘤细胞增殖, 从而竞争性抑制耐药表型的肿瘤细胞, 达到控制去势抵抗性前列腺癌病情进展的目的。2018年, Cunningham 等[6]进一步建立三变量进化动力学模型。
本文构建简化的二变量模型, 其优势在于能够进行更清晰的动力学分析, 从而揭示不同给药策略的动力学机制。
前列腺癌是一个有着大量的组分和复杂的相互作用, 并包含非线性作用的复杂开放系统。为了揭示其恶化的机制并寻求最佳的治疗策略, 我们基于Cunningham 等[6]的三变量模型, 构建二变量并考虑药物剂量的模型。模型变量为 T+细胞和 T–细胞, 其中, T+细胞为睾酮依赖性细胞, 有较高的环境容量和增殖速率, 受阿比特龙抑制; T–细胞不依赖睾酮, 并对阿比特龙抵抗。
由于 Lotka-Volterra(LV)竞争性方程[7]有参数简洁、含义明确的特点, 我们通过 LV 方程来描述 T+细胞与 T–细胞的相互竞争关系, 并将药物剂量加入模型:
(1)其中,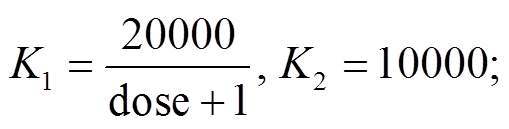
[T+]代表 T+细胞的密度; [T–]代表T–细胞的密度; r1 和r2 代表 T+和 T–细胞的增殖速率; K1 和 K2 是 T+和 T–细胞的环境承载量; a1 和 a2 是细胞间的相互作用常数, a1 代表 T–细胞对 T+细胞环境承载量的影响, a2 代表 T+细胞对 T–细胞环境承载量的影响。药物的剂量 dose 会影响T+细胞的环境承载量, 由于 T–细胞不依赖睾酮, 所以环境承载量恒定为 10000, 此处的变量、时间和参数的单位均为任意单位(A.U.)。我们将(r1, r2)设置成(0.35, 0.67)[5], (a1, a2)的取值与病人的特性相关, 这里假设 a1 和 a2 介于0~1 之间。
此外, 作为特异性的前列腺癌首选标志物, 血清中前列腺特异性抗原的浓度 PSA 对肿瘤进展和适应性给药方案的选择有很大的参考意义。由于临床上还没有确定肿瘤细胞数量与 PSA 含量的定量关系, 我们假设 PSA 与 T+和 T–细胞的总数呈线性关系, PSA 降解速率为 0.5, 表示为
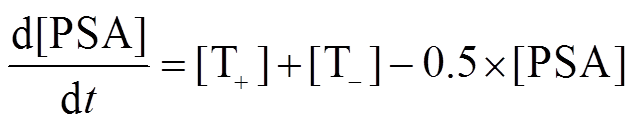。 (2)基于前列腺癌相关的实验研究和部分临床治疗数据[5,8–9], 我们估计模型中的时间单位大约为 7.2 h。文献[10]中给出 PSA 的半衰期为 0.50±0.39 d, 约为 12.0±4.7 h。我们的模型中假设 PSA 降解速率为 0.5, 即 PSA 半衰期为 ln2/0.07≈ 20.2 h, 与实验结果基本相符。
我们利用非线性动力学方法(包括渐进态分析和零解线分析等), 对前列腺肿瘤系统的给药动力学[11]进行研究, 并揭示高剂量药物导致体系演化至药物抵抗的前列腺癌的动力学机理。
图 1 展示 3 种不同剂量药物(dose=0, 1, 10)作用下, T+和 T–细胞相互作用网络和模型(图 1(a))以及演化动力学行为, 模拟实验中病人的细胞间相互竞争参数为 a=(0.5, 0.2)。图 1(b)给出初态[T+]为 4000, [T–]为 100 的病人发病过程的相图和时序图, 在一段时间后, 病人的肿瘤系统演化至 A 点的稳态。通过稳定性分析和零解线分析, 可以知道系统具有 4个不动点: A 点是稳定不动点, B 和 C 是鞍点, D是不稳定不动点。进一步地, 针对演化到稳态的病人, 我们模拟给药后的动力学变化。图 1(c)中, 当 t<500时, 给药剂量为 1, t>500 时停药。我们发现, 低剂量的药物能够使总的细胞密度明显降低, 并在撤药之后还能回到原先的稳定点; 并且低剂量的阿比特龙, 使[T+]的零解线左移, 同时稳定点 A 也沿 d[T–]/dt=0 产生左移, 到达新的稳定点 A'。给予剂量为10 的药物之后(图 1(d)), [T+]的零解线进一步左移, 使原先的稳定点对应的[T+]小于零, 所以系统最终会演化至 B 处的鞍点。在停药之后, 由于系统处于鞍点, 将不能回到原先的稳定点, 此时系统中全部细胞均为 T–细胞, 此时产生药物抵抗[12], 导致药物失效。我们把系统稳态刚好变为B 点的药物剂量称为最大可逆剂量, 细胞相互竞争参数为(0.5, 0.2)的病人的最大可逆剂量为 3。需要注意的是, 系统在(0, 0)点处存在一个不稳定的不动点, 因为我们的简化模型中药物只影响 T+细胞的负载, 当考虑其他的治疗方案(例如直接杀伤 T+和 T–细胞的免疫治疗)时,就会导致(0, 0)附近出现其他的吸引点, 使其有治疗意义。
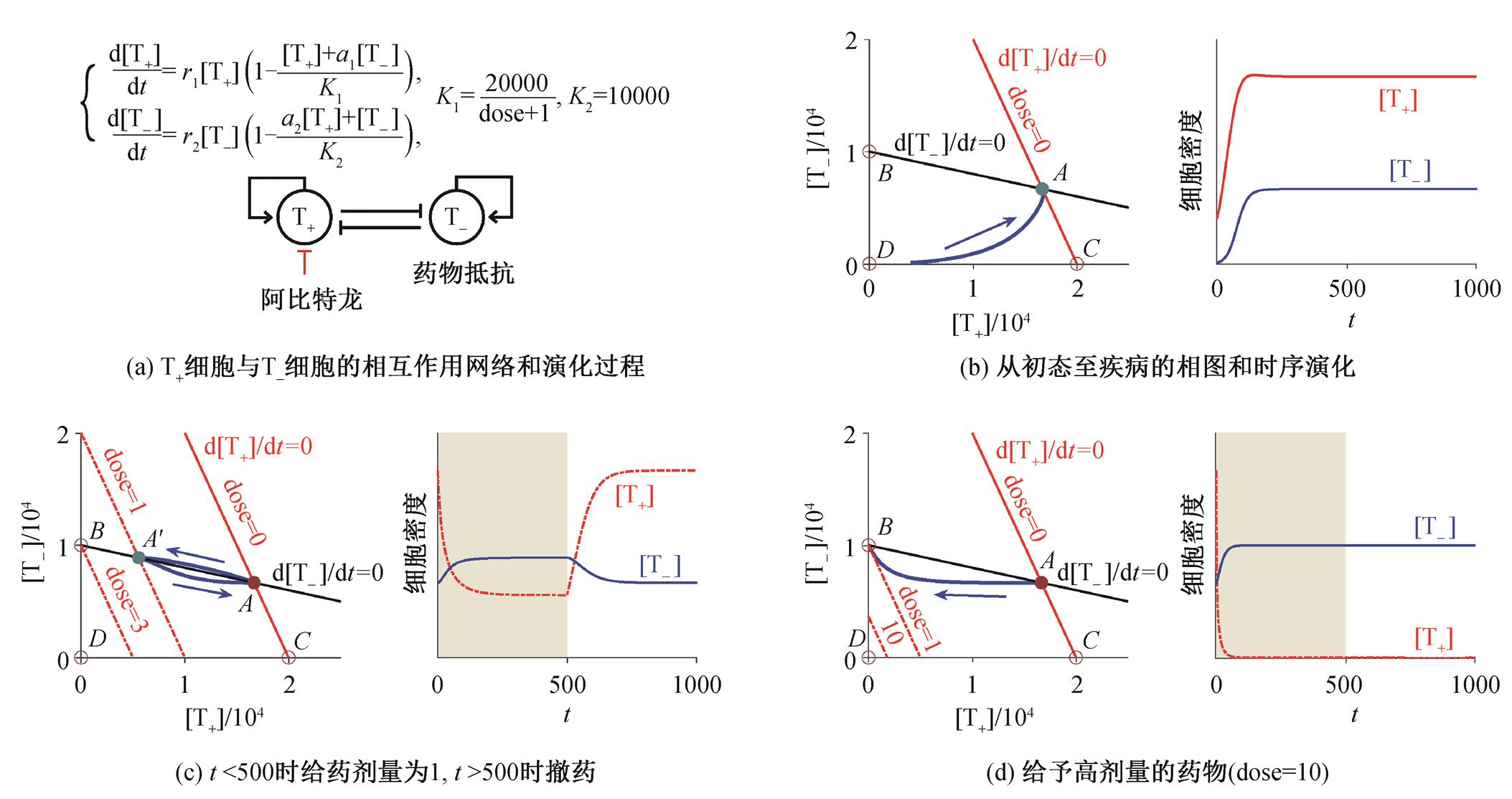
图1 不同剂量药物下, 前列腺肿瘤细胞中T+细胞与T–细胞的相互作用网络和演化动力学
Fig. 1 Interaction networks and kinetics between T+ and T– cells in prostate tumor cells at different doses
图 2(a)为固定剂量给药方案中给药剂量 dose 与T–细胞密度的分岔图。我们发现在阿比特龙剂量较低时, 系统存在一个稳定点和一个鞍点(即图 1(b)中的稳定点 A 和鞍点 B), 不同初始态的病人会演化到稳定点。当给药剂量过高时, 原先的鞍点与稳定点合并, 导致系统只存在一个不动点。由于[T+]=0 处的鞍点位置并不随药物剂量而改变, 鞍点恒定为([T+]=0, [T–]=10000)。当使用高剂量的药物治疗并停药之后, 系统将沿着虚线退化至原鞍点位置, 说明高剂量的给药策略会使系统演化到([T+]=0, [T–] =10000)，该过程不可逆。在该点, 前列腺癌中全部为 T–细胞, 并且对药物抵抗。
通过动力学方法, 根据稳定点的位置, 也可对病人进行大致的分类。当 a 发生变化时, 系统的零解线在一定范围内转动。如图 2(b)所示, 随着 a1 的变化, [T+]的零解线以(K1, 0)为中心转动, a2 的变化会导致[T–]的零解线以(0, K2)为中心转动, 两线交点为稳定不动点。我们按稳定点的位置对病人进行分类, 当 1>a2>0.5 时, 稳定点落在 A 区(阴影部分代表[T+]和[T–]的可能取值区间), 此时系统不动点为(K1, 0)处的鞍点, 如图 2(c)所示。当给药时, 系统将沿着[T–]=0 的直线运动, 这类病人天生不会对药物产生抵抗, 并且在药物作用下会稳定在(0, 0)处的不动点, 达到治愈的效果。稳定点位于 B 区的病人, 当给药剂量过高时, 就会进化至药物抵抗。
鉴于上面的分析, 高剂量的阿比特龙能够使前列腺癌从渐进态演化到不可逆稳态, 产生药物抵抗, 从而导致对阿比特龙失效。通过分析适应性给药的治疗方案, 发现适应性给药能有效地解决药物剂量过高带来的负面影响。如图 3(a)所示, 根据 PSA 占最大值的比例决定给药和撤药的时刻, PSA+代表开始给药时的 PSA 值, PSA –代表撤药时的 PSA 值。当 PSA 高于 0.9 时加入阿比特龙, 当 PSA 低于 0.5 时停药。从相图中可以发现, 给药时[T+]的零解线左移, 稳定不动点向左移动, 停药时零解线回到原先的位置。由 PSA 决定的给药策略能够使系统轨迹在达到鞍点之前返回, 从而在保证治疗效果的同时, 避免系统进化至药物抵抗; 由时间决定的给药策略则无法保证在系统达到鞍点之前停药。需要注意的是, 当 PSA 停药的边界过低时(图 3(b)), 也会导致不可逆效应的发生, 使系统演化至药物抵抗。
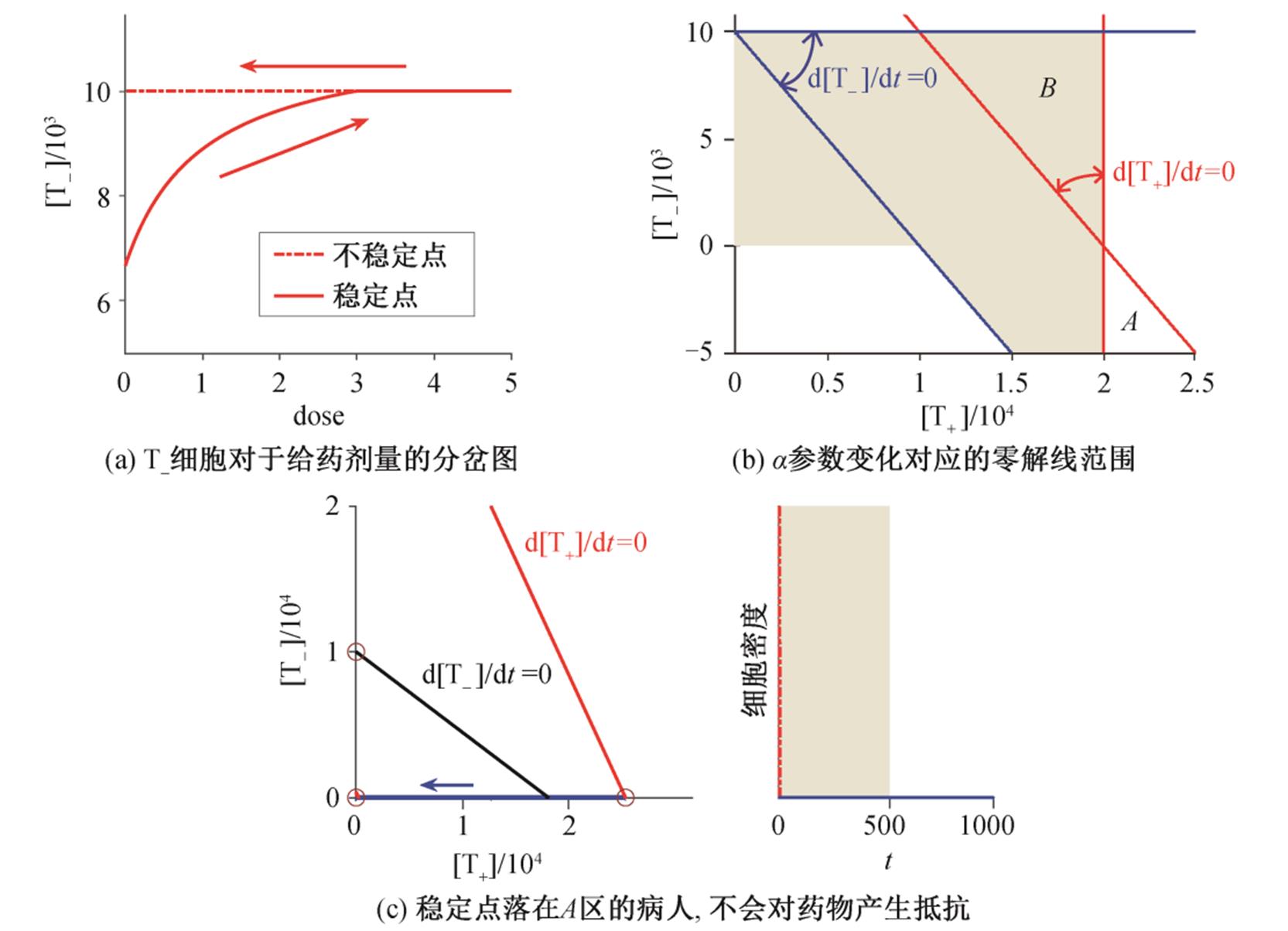
图2 肿瘤细胞的演化动力学及分析
Fig. 2 Evolutionary dynamics and analysis of prostate cancer
图3 适应性给药的动力学分析
Fig. 3 Kinetic analysis of adaptive drug administration
为了直观地揭示蛋白质结构和基因调控网络动力学性质, 研究人员发展了能量景观图方法[13–16]。我们使用蒙特卡洛的方法, 计算噪声扰动下稳态的平稳分布, 势能表达式为
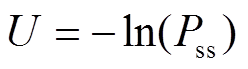, (3)式中, U代表势能, Pss代表平稳分布。图4为固定剂量给药的方式(阿比特龙浓度为0, 1和10)下的势能图。对固定剂量给药方式而言, 系统会向势能最低的点运动。在剂量为 0 时, 系统的稳态会趋向于 A点, 当给予浓度为 1 的阿比特龙时, 系统会从 A 掉落至 B 点。此时, 系统的状态是可逆的, 停药后, 系统将会回到 A 点。当给药剂量超过一定剂量时(例如 dose=10, 图 4(c)), 系统会运动至 C 点, 此时停药系统将趋向于运动至 C 处的鞍点, 当系统演化足够长时间之后, 稳定至 C 点, 从而产生不可逆现象。适应性给药能够避免高剂量带来的不可逆效应, 其机理就是在轨迹渐进运动至 C 点之前撤药, 此时轨迹会趋向于势能更低的 A 点, 使轨迹在 A 点与 C 点之间反复运动, 从而避免高剂量带来的药物抵抗效应。
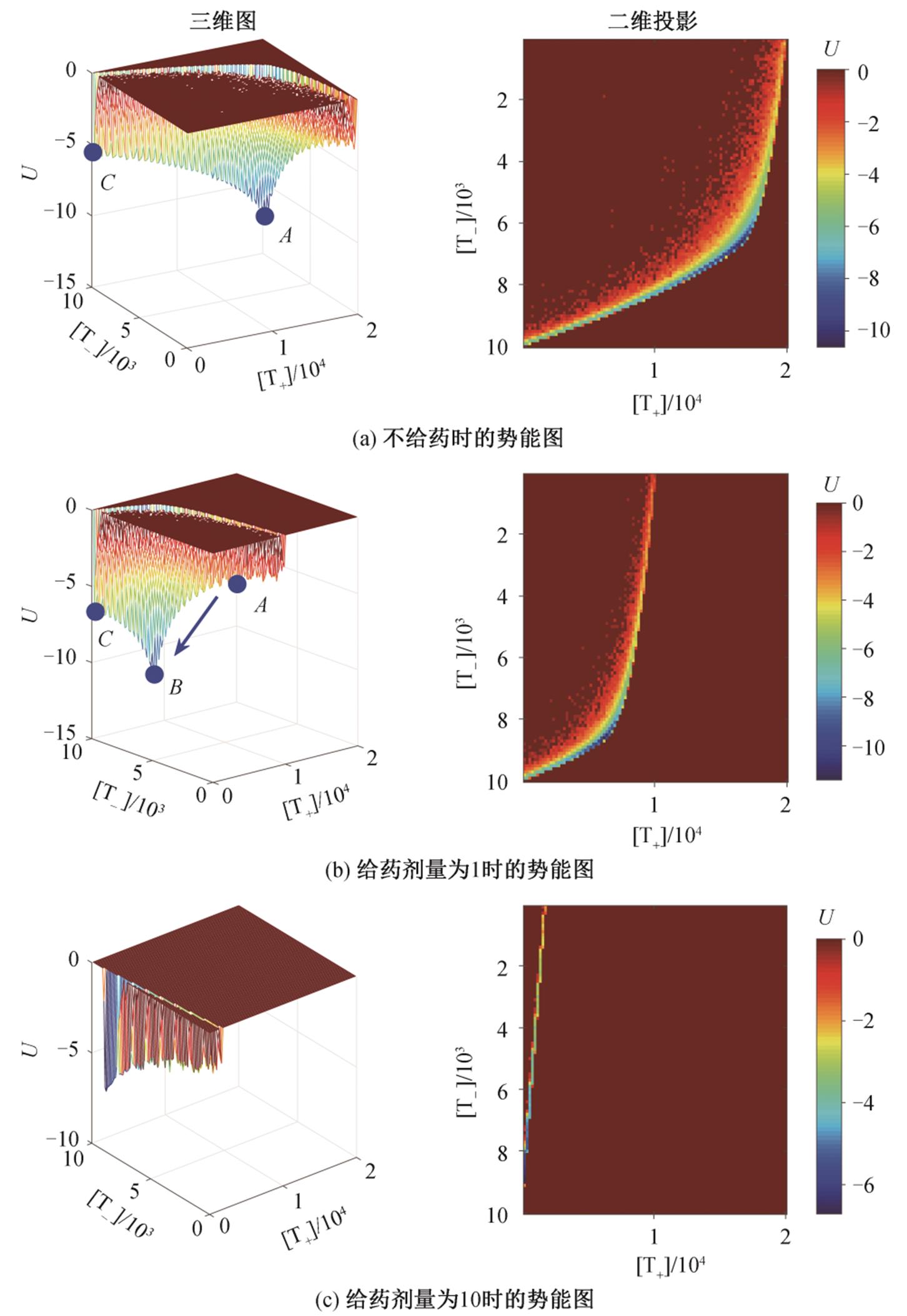
图4 系统在不同浓度药物作用下的势能景观图
Fig. 4 Potential landscape of the system with different doses of drugs
在我们的简化模型中, 如果病人的 T+细胞与 T– 细胞相互竞争系数 a 不同, 会造成病情不同的分类和演化。实际上, 病人的参数可能更为复杂多样, 如何针对特定病人选择最优的治疗策略尤为重要[6]。
为了讨论治疗的效果, 我们参照文献[5], 考虑4 个指标: 1)T–细胞达到最大值 5%的时间 T0.05, 表示何时出现药物抵抗的趋势, T0.05 值越大, 评分越高; 2)T–细胞达到最大值 90%的时间 T0.9, 表示快要出现药物抵抗的时间, T0.9值越大, 评分越高; 3)所用药物的相对剂量(total dose, TD), TD=剂量×给药时间/总时间, 由于阿比特龙价格昂贵, 故 TD 值越小, 评分越高; 4)平均的 PSA 值(average PSA, AP), PSA 间接反映细胞总数, AP 值越小, 评分越高。TMax 代表模拟总时长, 4 项的权重如下: T0.05 占 15%, T0.9 占 35%, TD 占30%, AP 占 20%。总分为 100 分,评分表达式为
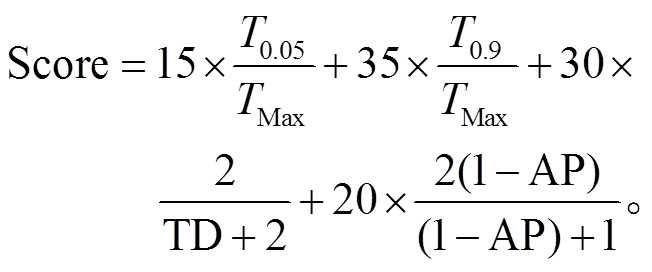(4)图 5(a)给出 a=(0.5, 0.2)的病人药物剂量为 4时, 采用适应性治疗方案取得的评分。通过计算评分, 可以对比固定剂量给药和适应性给药策略的优劣, 例如, 图 5(b)对比在不同剂量下两种给药方式的评分。当剂量较高时, 固定剂量给药评分较低; 由于可以选择给药边界(PSA+)和撤药边界(PSA–), 适应性给药评分在较大范围内波动。如果在高剂量下通过寻找合适的给药和撤药边界, 适应性给药的评分可以远高于固定剂量给药。图 5(c)给出高剂量下不同的给药和撤药边界组合对评分的影响, 可以看到存在一个狭小的区间能获得较高的评分。我们希望通过这种方法对病情进行分析, 并制定最合适的适应性给药方法。
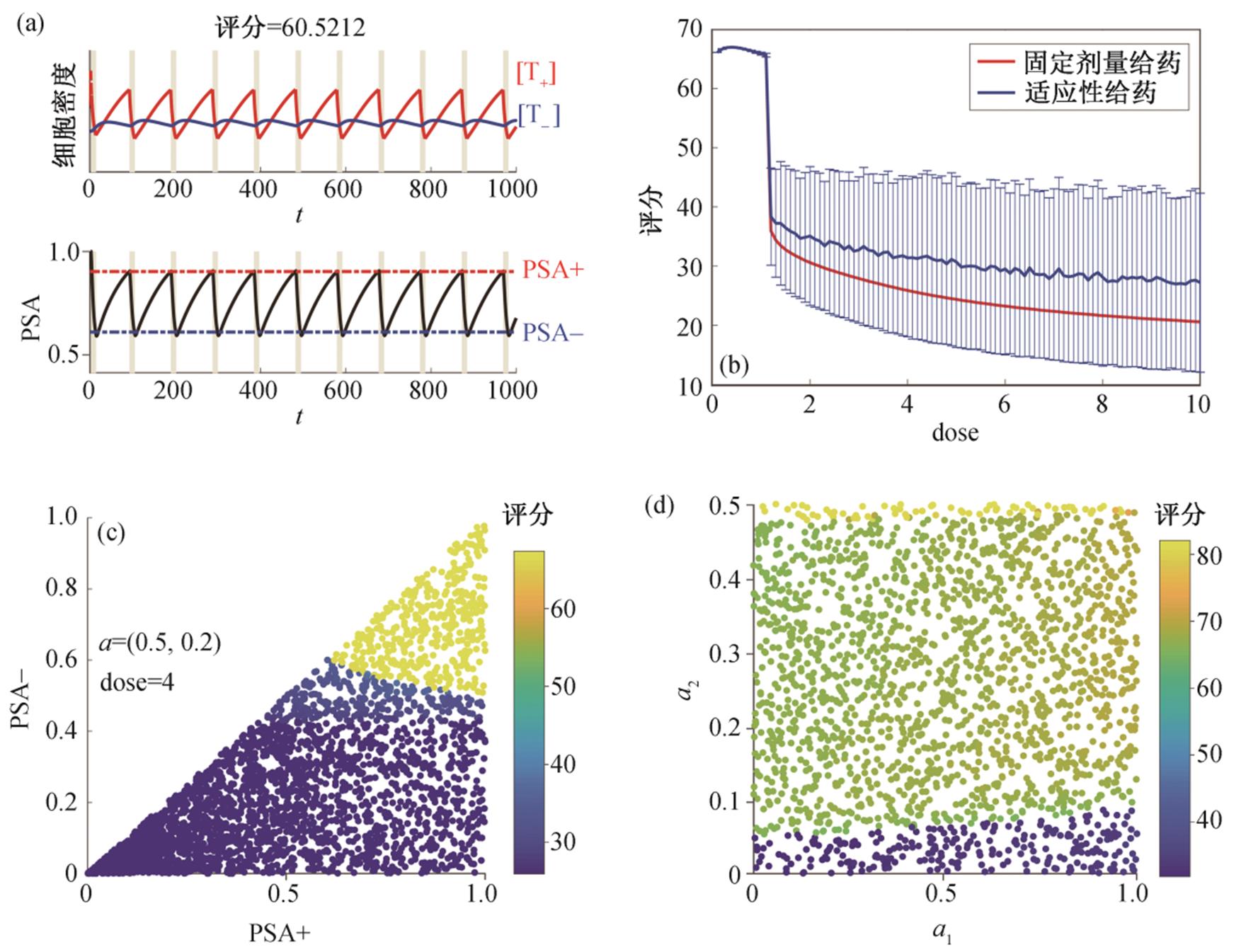
(a)a=(0.5, 0.2)的病人采用适应性治疗方案取得的评分; (b)固定剂量给药与适应性给药的评分对比。红线代表固定剂量给药, 蓝线代表适应性给药, 其误差是由给药边界与停药边界的不同取值所造成; (c)不同的给药撤药组合下获得的评分; (d)10000种适应性治疗方案的评分, 并找到最佳的评分
图5 特定病人固定剂量与适应性剂量给药的评分
Fig. 5 Scoring of fixed and adaptive dosing methods for specific patients
对于不同的病人(不同的 a1, a2 组合), 我们对每个人生成 10000 种适应性治疗方案, 并进行打分, 获得其最佳评分, 如图 5(d)所示。病人获得的评分与 a2 参数有很大的相关性, 对 a1 则不敏感。这是因为 a2 代表 T+细胞对 T–环境承载量的影响, T–细胞的数量决定是否会产生药物抵抗, 故较为敏感。当a2>0.07 时, 病人能够获得较好的治疗效果; 当 a2> 0.5 时(图 2), 病人的细胞会演化至 T–细胞为 0 的状态, 能够通过用药痊愈; 当 a2<0.07 时, 推荐采用其他的治疗策略。我们希望在临床上能够通过实验手段获得病人的准确参数, 并籍此模拟推断其最佳治疗策略。
本文基于 Cunningham 等[6]的三变量模型, 构建简化的双变量前列腺癌 T+与 T–细胞相互作用模型。针对不同的用药策略, 双变量模型可以方便地进行动力学分析, 直观地揭示其机理。针对固定剂量给药的过程, 我们使用零解线分析方法和渐进态分析方法, 发现高剂量药物能够导致不可逆的药物抵抗状态。当不给药时, 系统可能存在一个稳定点、两个鞍点和一个不稳定点; 较低的固定剂量会使系统运动到新的稳定点; 当固定剂量超过最大可逆剂量时, 系统至稳态时会运动至鞍点, 导致不可逆现象的发生。当采用适应性给药策略时(即根据 PSA 的大小确定给药和撤药边界), 可以在系统渐进至[T+] =0 处的鞍点之前撤药, 从而避免系统出现不可逆现象, 同时保证治疗效果。
本文的双变量前列腺癌模型也存在不足之处, 由于药物只影响 T+细胞的负载, 所以 T+细胞与 T–细胞都被清除的(0, 0)点是不稳定的不动点。如果进一步考虑其他药物治疗因素(例如通过抑制微管聚合来抑制细胞分裂的化疗药物多西他赛[17]), 可以清除肿瘤细胞, 导致(0, 0)点变为稳定的不动点或在附近出现新的吸引点。
此外, 本文还分析了适应性给药策略能够避免系统达到药物抵抗状态的原因, 并绘制系统的势能景观图, 构建治疗策略的评分体系。通过固定剂量给药和适应性给药的优劣, 并分析不同参数组合的病人能够获得的最佳评分, 我们发现参数 a2(表征T+对 T–的环境承载量的影响)对评分的影响很大。在临床上, 针对不同参数的病人, 可以进一步构建更加复杂并符合实际情况的模型, 确定最佳的治疗方案[18]。希望本研究能够给前列腺癌的临床用药提供理论框架, 并给予一定的指导。
参考文献
[1]Pernar C H, Ebot E M, Wilson K M, et al. The epidemiology of prostate cancer. Cold Spring Harb Perspect Med, 2018, 8(12): 1–3
[2]Saad F, Chi K N, Finelli A, et al. The 2015 CUA-CUOG Guidelines for the management of castration-resistant prostate cancer (CRPC). Can Urol Assoc J, 2015, 9(3/4): 90–96
[3]Ang J E, Olmos D, De Bono J S. CYP17 blockade by abiraterone: further evidence for frequent continued hormone-dependence in castration-resistant prostate cancer. Br J Cancer, 2009, 100(5): 671–675
[4]Carroll P H, Mohler J L. NCCN guidelines updates: prostate cancer and prostate cancer early detection. J Natl Compr Canc Netw, 2018, 16(5S): 620–623
[5]Zhang J, Cunningham J J, Brown J S, et al. Integ-rating evolutionary dynamics into treatment of metas-tatic castrate-resistant prostate cancer. Nat Commun, 2017, 8(1): 1816
[6]Cunningham J J, Brown J S, Gatenby R A, et al. Optimal control to develop therapeutic strategies for metastatic castrate resistant prostate cancer. J Theor Biol, 2018, 459: 67–78
[7]Takeuchi Y. Diffusion-mediated persistence in two-species competition Lotka-Volterra model. Math Biosci, 1989, 95(1): 65–83
[8]Wf B, Gl A, J G. Does PSA reduction after antibiotic therapy permits postpone prostate biopsy in asympto-matic men with PSA levels between 4 and 10 ng/mL?. Int Braz J Urol, 2015, 41(2): 329–336
[9]Barrabes S, Llop E, Ferrer-Batalle M, et al. Analysis of urinary PSA glycosylation is not indicative of high-risk prostate cancer. Clin Chim Acta, 2017, 470: 97–102
[10]Haab F, Meulemans A, Boccon-Gibod L, et al. Clea-rance of serum PSA after open surgery for benign prostatic hypertrophy, radical cystectomy, and radical prostatectomy. Prostate, 1995, 26(6): 334–338
[11]Ma W, Trusina A, El-Samad H, et al. Defining net-work topologies that can achieve biochemical adap-tation. Cell, 2009, 138(4): 760–773
[12]Meads M B, Gatenby R A, Dalton W S. Environment-mediated drug resistance: a major contributor to mini-mal residual disease. Nat Rev, 2009, 9(9): 665–674
[13]Frauenfelder H, Sligar S G, Wolynes P G. The energy landscapes and motions of proteins. Science, 1991, 254: 1598–1603
[14]Wang J, Xu L, Wang E. Potential landscape and flux framework of nonequilibrium networks: robustness, dissipation, and coherence of biochemical oscillations. Proc Natl Acad Sci USA, 2008, 105(34): 12271–12276
[15]Lv C, Li X, Li F, et al. Energy landscape reveals that the budding yeast cell cycle is a robust and adaptive multi-stage process. PLoS Comput Biol, 2015, 11: e1004156
[16]Lv C, Li X, Li F, et al. Constructing the energy landscape for genetic switching system driven by intrinsic noise. PLoS ONE, 2014, 9: e88167
[17]Mohr L, Carceles-Cordon M, Woo J, et al. Generation of prostate cancer cell models of resistance to the anti-mitotic agent docetaxel. J Vis Exp, 2017: no.127
[18]Chen C, Baumann WT, Xing J, et al. Mathematical models of the transitions between endocrine therapy responsive and resistant states in breast cancer. J R Soc Interface, 2014, 11(96): 20140206
Evolutionary Dynamics Model of Prostate Cancer and Optimization of Treatment Strategies
Abstract Prostate cancer is one of the most common malignant tumors in men. Abiraterone is commonly used in clinical treatment, but it often causes patients to evolve to drug resistance prostate cancer. In order to reveal the dynamic mechanism of prostate cancer development, this paper established a two-variable quantitative model of tumor evolution and introduced dose factors. By analyzing the dynamic properties of fixed and adaptive dosing treatment therapy and plotting the potential energy landscape figure, we revealed the advantages of adaptive dosing method from the perspective of dynamics and the mechanism that high doses of Abiraterone could lead to an irreversible state of drug resistant. In addition, the treatment score system was designed for the strategies, compared the two drug delivery methods and optimized the treatment strategies.
Key words prostate cancer; Abiraterone; drug resistant; dynamic method; optimization strategy
doi: 10.13209/j.0479-8023.2019.115
国家自然科学基金(91130005, 11174011)资助
收稿日期: 2019–05–09;
修回日期: 2019–06–04