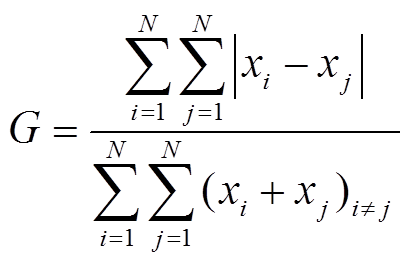 , (1)
, (1)摘要 构造组间相对不均衡指数, 用来描述一个地理系统相对于另一个地理系统发展的不平衡关系, 或一个系统内部的一个指标相对于另一个指标的不均衡关系。首先改变常规组内不均衡指数(即基于 Lorenz 曲线的Gini 系数)的数学表达式, 然后利用新的表达式, 将组内不均衡指数推广到组间不均衡指数表达式。在应用过程中, 两种不均衡指数可以集成到同一个逻辑框架。以京津冀、长江三角洲和珠江三角洲的城市体系为实证对象, 借助新的公式计算组内和组间不均衡指数, 揭示城市系统的时空演化特征。
关键词 Gini系数; 不均衡指数; 京津冀; 长江三角洲; 珠江三角洲; 城市体系
地理系统有两个显著的性质, 一是空间差异性, 二是空间依存性。空间差异性的相关概念是空间异质性, 空间依存性则反映地理现象的空间关联[1-2]。前者也称为区域差异性, 是地理学的传统主题; 后者涉及地理空间的长程作用, 与地理学第一定律有关[3]。地理学家基于空间依存性, 发展了空间自相关[4-5]和空间相互作用理论[4,6-7]; 基于空间差异性, 发展了局部空间自相关测度[1]和空间加权回归[8]等分析方法。然而, 在很多情况下, 地理研究仅仅需要简单的度量指数, 用来描述空间依存性或者区域差异性。空间依存性可以采用 Moran 指数之类的空间统计学测度, 空间差异性则采用不均衡指数、最邻近指数和基于空间熵的冗余指数等方法度量。区域差异性与地域不均衡性有关, 但又存在区别[9]。尽管如此, 在空间测度方面, 区域差异和空间不平衡可以采用类似的指数来描述其特征。一个简单的测度就是从 Gini 系数衍生出的不均衡指数[10-13]。这个不均衡指数反映样本内平均绝对差异, 可以将其视为组内不均衡指数。在许多情况下, 需要考察的不是样本内(组内)的差异或均衡, 而是样本间(组间)的相对差异或均衡, 此时可以借助 Theil 指数之类的交叉熵来描述[14]。交叉熵主要用于反映相同区域内同一批要素不同指标之间的相对差异, 不能描述要素数目不同的任意两个区域之间的相对差异[15]。
本文的目的在于构建简单的组间相对不均衡指数, 用来反映不同区域或不同地理要素的比较差异。首先改变基于 Gini 系数的组内不均衡指数的数学表达, 然后通过类比, 将组内绝对不均衡指数推广到组间相对不均衡指数。以京津冀地区、长江三角洲和珠江三角洲 3 个区域的城市体系为例, 借助人口规模测度和灯光总数测度, 说明新测度公式的应用方法和效果。作为补充和对比, 在描述组间相对差异的同时, 也给出组内绝对差异的计算结果, 并纳入综合分析过程。
假定一个区域存在 N 个地理要素, 采用变量 x度量其规模或发展水平, 基于 Gini 系数的思想和矩阵表达形式, 常规的区域发展不均衡指数可以表示为如下形式:
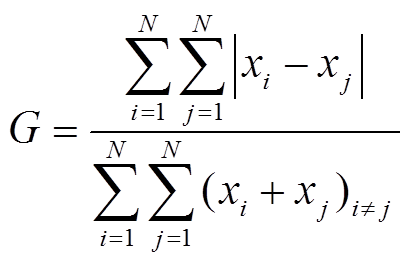 , (1)
, (1)其中, G 为单变量或单区域不均衡指数, 数值介于0~1 之间, i, j=1, 2, 3, …, N。式(1)与文献[10-12]中的表达形式稍有不同, 但等价。i≠ j 表示对分母而言, 不考虑矩阵对角线的元素。如果将对角线元素纳入计算, 则式(1)应转换为如下形式:
 (2)
(2)
其中 N/(N-1)相当于矫正系数, 能够保证 0≤G≤1。式(1)和(2)给出相同的计算结果。
理论上, G 相当于 Gini 系数的替代指数, 用于描述基于同一测度同一个区域的平均差异性, 称为组内不均衡指数。如果描述一个区域的城市规模差异、GDP 分布差异和人均收入差异, 且不考虑无尺度分布的影响, 则可以采用式(1)或(2)来度量[13]。但是, 如果希望借助某个测度描述区域间或不同城市体系之间的相对差异(如京津冀城市体系相对于长三角城市体系的人口分布差异), 或描述同一个区域或城市体系内两种不同地理变量之间相对差异(如京津冀城市体系内人口相对于 GDP 的差异), 则上述公式失效。
基于新的数学表达式, 易将组内不均衡指数推广到组间不均衡指数。为了度量区域间或者测度间的相对差异, 将式(1)推广到二区域或者二变量分析, 得到如下表达:
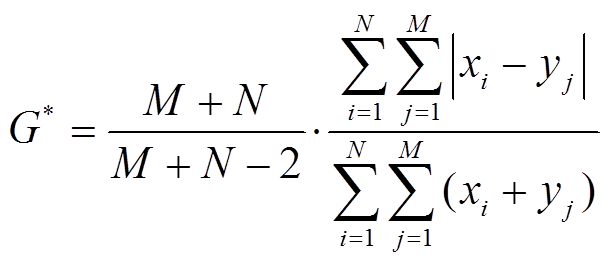 , (3)
, (3)其中, G*为不同区域同一类变量反映的组间不均衡指数(或双区域不均衡指数), 其数值介于 0 ~ 1 之间; x 为一个区域的不同地理元素的某种测度(如不同城市的 GDP); y 为另一个区域的不同地理元素的某种测度(如不同城市的 GDP); i=1, 2, 3, …, N, j=1, 2, 3, …, M。对式(3)的分母而言, 不能忽略矩阵对角线的元素, 因此需要用系数(M+N)/( M+N- 2)将指数值校正到 0 和 1 之间, 否则最终计算结果大于等于0 但小于 1, 数据上限不明确。
有时候, 需要描述的不是不同区域的同一类变量反映的相对不均衡性, 而是同一个区域内不同测度之间表现的不均衡性。令 M=N, 对式(3)稍作做修改, 可得到这样一种指数:
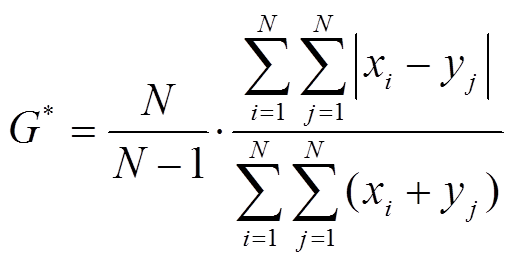 , (4)
, (4)其中, G*为同一区域不同变量之间的相对不均衡指数(或双变量不均衡指数), 其数值介于 0~1 之间; x为一个区域的不同地理元素的某种测度(如不同城市的人口); y 为同一个区域的不同地理元素的另一种测度(如不同城市的 GDP)。x 和 y 都是归一化的变量, 即各个数值除以其总和。当 yj 被 xj 代替时, 式(4)返回到式(2), 表明组间不均衡指数是组内不均衡指数的特例。
将基于常规 Gini 系数的组内不均衡指数与本文提出的组间不均衡指数集成到同一个测度框架, 进行综合差异分析。以京津冀地区、长江三角洲(长三角)和珠江三角洲(珠三角)为研究区, 以城市体系为实证对象, 计算区域发展的组内和组间不均衡指数, 进行简明的时空演化分析。采用 3 个度量指标: 1)市区人口(不包括市辖县人口); 2)市辖区人口(包括区人口和所辖县人口); 3)夜晚灯光总量。3个变量彼此之间高度相关。因此, 3 个变量不代表不同的方向, 只代表不同的测度或者视角。人口总量采用 2000 年第 5 次人口普查数据和 2010 年第 6 次人口普查数据。灯光总量也取 2000 年和2010 年的数据。作为一种新的指数和分析方法的案例说明, 数据的现势性不是首要的条件, 可靠性和代表性更为关键。
在实际操作中, 可以将式(1)~(3)集成到同一个运算过程, 计算方法如下。
第一步, 整理数据。将数据纵向排列, 得到 xi, 将同一组的不同数据或不同组数据横向排列, 得到 xj 或yj。
第二步, 计算两两差值的绝对值。针对式(1)~ (3)中的分子部分, 计算 xi - xj 或 xi - yj 的绝对值, 然后求和。
第三步, 计算两两数值之和。针对式(1)~(3)的分母, 计算 xi+xj 或 xi+yj。根据公式的形式决定是否保留对角线的数值, 然后求和。
第四步, 计算不均衡指数。借助式(1)~(3), 同时计算组内不均衡指数和组间不均衡指数。
计算过程和结果包括 3 个方面: 1)利用新的公式(式(1)或(2))计算组内不均衡指数(表 1); 2)利用式(3), 基于相同的指标计算不同区域的组间不均衡指数(表 1); 3)针对相同的区域, 计算不同指标之间的组间不均衡指数(表 2)。为此, 变量需要归一化, 计算公式为式(4)。
上述 3 个测度反映的空间尺度范围不一样。市辖区人口和灯光总量反映较大的尺度范围, 包括市区和辖县, 而市区人口反映的地区范围相对较小, 不包括县域。
通过从 2000 年到 2010 年的演变, 分析 3 个城市体系差异性的变化特征。从表 1 可以看出: 1)京津冀和长三角城市体系的内部绝对差异上升(G 值增大), 珠三角城市体系的内部差异下降(G 值减小), 相对关系方面只有市区人口差异上升, 灯光总量和辖区人口差异下降; 2)京津冀相对于长三角, 灯光总量差异下降, 市辖区和市区人口差异上升; 3)京津冀和长三角相对于珠三角, 灯光总量和辖区人口差异下降, 市区人口差异上升。
表 2 是矩阵形式的表达, 可以反映测度内部绝对差异和测度之间相对差异的时空变化。可以看到, 京津冀和长三角城市体系 3 个测度反映的自身绝对差异以及测度之间的相对差异均在上升, 珠三角情况则相反, 测度自身绝对差异和测度之间的相对差异下降。
表1 京津冀、长三角和珠三角城市体系的不均衡指数(2000 和 2010年)
Table 1 Values of inequality indexes of the urban systems in Beijing-Tianjin-Hebei region,Yangtze River Delta, and Pear River Delta (in 2000 and 2010)
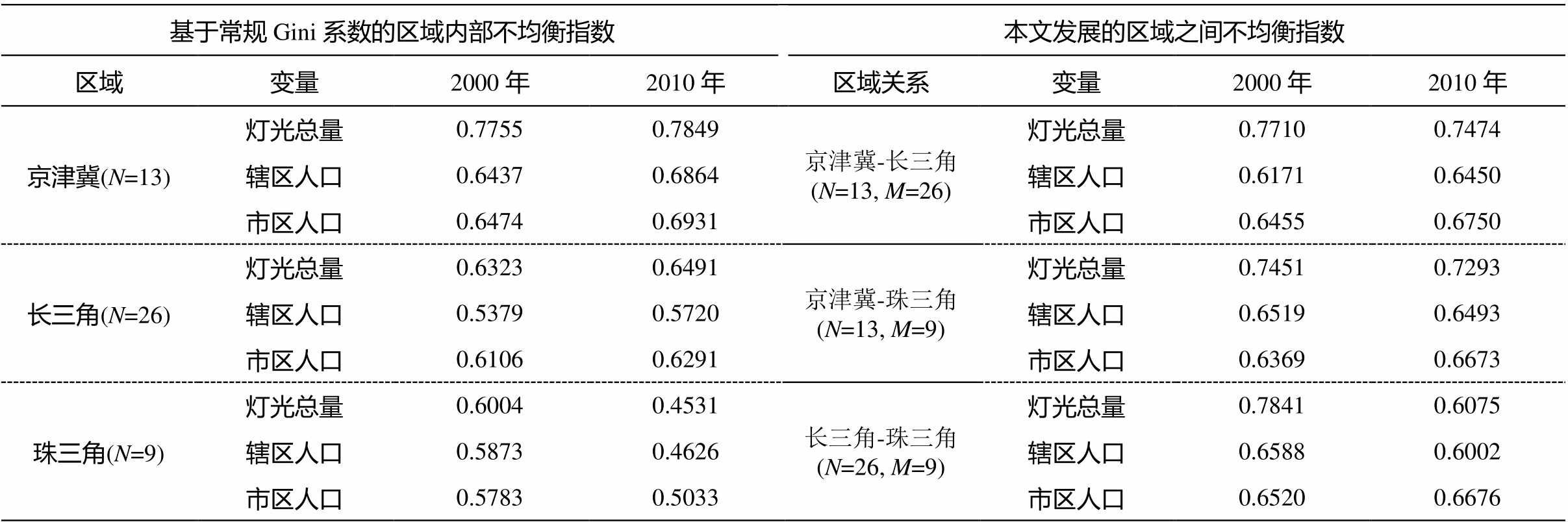
基于常规Gini系数的区域内部不均衡指数本文发展的区域之间不均衡指数 区域变量2000年2010年区域关系变量2000年2010年 京津冀(N=13)灯光总量0.77550.7849京津冀-长三角(N=13, M=26)灯光总量0.77100.7474 辖区人口0.64370.6864辖区人口0.61710.6450 市区人口0.64740.6931市区人口0.64550.6750 长三角(N=26)灯光总量0.63230.6491京津冀-珠三角(N=13, M=9)灯光总量0.74510.7293 辖区人口0.53790.5720辖区人口0.65190.6493 市区人口0.61060.6291市区人口0.63690.6673 珠三角(N=9)灯光总量0.60040.4531长三角-珠三角(N=26, M=9)灯光总量0.78410.6075 辖区人口0.58730.4626辖区人口0.65880.6002 市区人口0.57830.5033市区人口0.65200.6676
说明: 由于关系的对称性, 要素总数M与N为相对表示: 一个总数视为M, 另一个就是N, 反之亦然。
表2 三个城市体系灯光总量、辖区人口和市区人口的不均衡指数的矩阵表示(2000 和 2010年)
Table 2 Matrixes of inequality indexes of total urban lighting, urban population, and population in municipal district of three urban systems (in 2000 and 2010)
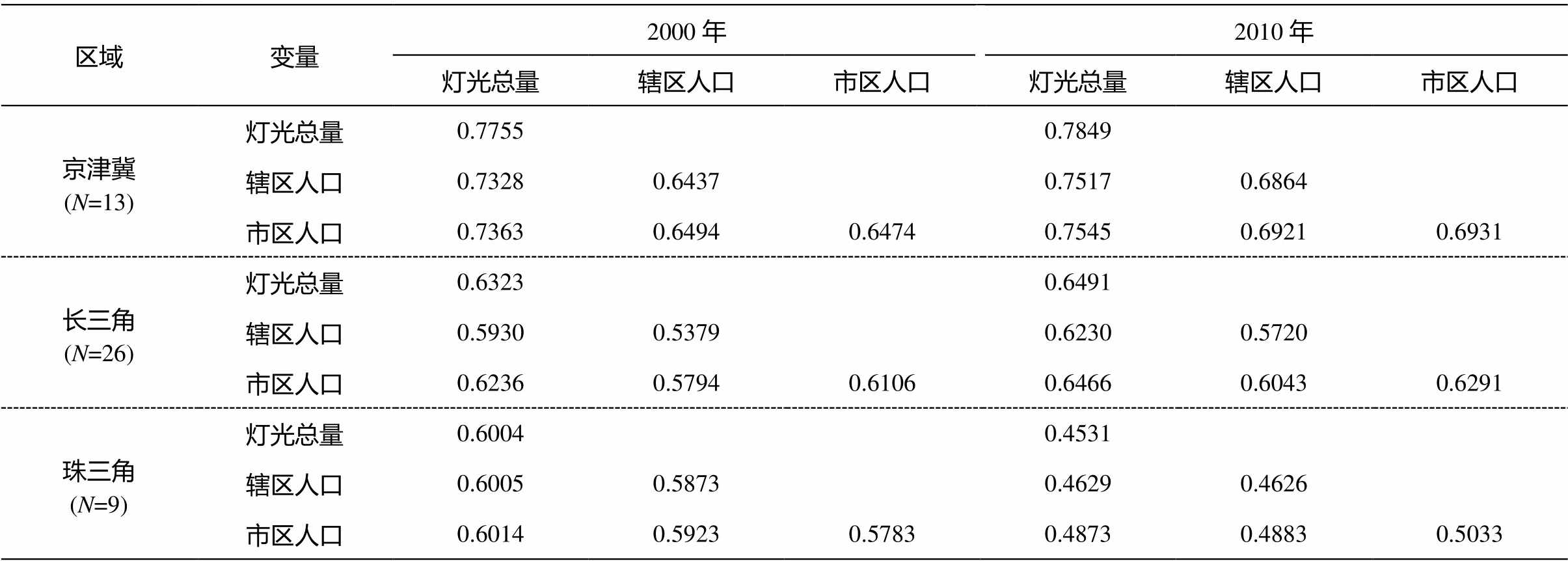
区域变量2000年2010年 灯光总量辖区人口市区人口灯光总量辖区人口市区人口 京津冀(N=13)灯光总量0.77550.7849 辖区人口0.73280.64370.75170.6864 市区人口0.73630.64940.64740.75450.69210.6931 长三角(N=26)灯光总量0.63230.6491 辖区人口0.59300.53790.62300.5720 市区人口0.62360.57940.61060.64660.60430.6291 珠三角(N=9)灯光总量0.60040.4531 辖区人口0.60050.58730.46290.4626 市区人口0.60140.59230.57830.48730.48830.5033
说明: 对角线元素为基于常规Gini系数的组内不均衡指数值, 对角线以外元素为组间不均衡指数值, 下同。
仿照表 2, 将表 1 重新组合为矩阵形式, 得到表3。表 3 从另一个角度反映 3 个城市体系的差异性演变: 1)从灯光总量来看, 京津冀和长三角内部的差异略有上升, 而珠三角内部以及三个城市体系之间的相对差异下降; 2)从辖区人口来看, 京津冀和长三角内部的绝对差异以及京津冀与长三角之间的相对差异略有上升, 珠三角内部以及珠三角与京津冀、长三角之间的相对差异下降; 3)从市区人口来看, 珠三角的内部差异下降, 京津冀、长三角的内部差异以及 3 个体系之间的相对差异上升。
综上所述, 可以将 3 个城市体系从 2000 年到2010 年的差异性变化概括为两个方面的特征: 1) 测度反映地区差异变化的共性, 无论灯光总量、辖区人口、市区人口的绝对差异, 还是彼此间的相对差异, 京津冀和长三角城市体系均上升, 而珠三角则普遍下降; 2)尺度反映地区之间相对差异变化的共性, 较小尺度(如市区范围内)的相对差异普遍上升, 而较大尺度(市辖区范围)的差异有所下降。
表3 京津冀、长三角和珠三角城市体系的不均衡指数矩阵表示(2000 和 2010年)
Table 3 Matrixes of inequality indexes of the urban systems in Beijing-Tianjin-Hebei region, Yangtze River Delta,and Pear River Delta (in 2000 and 2010)
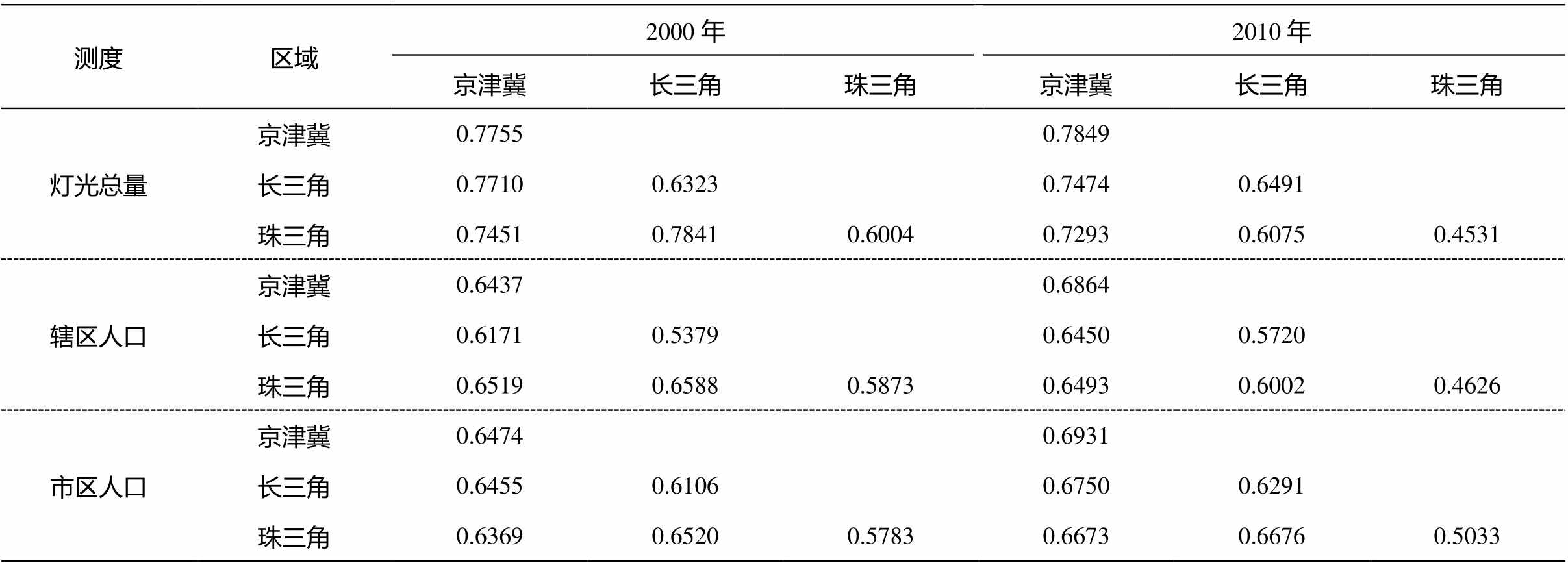
测度区域2000年2010年 京津冀长三角珠三角京津冀长三角珠三角 灯光总量京津冀0.77550.7849 长三角0.77100.63230.74740.6491 珠三角0.74510.78410.60040.72930.60750.4531 辖区人口京津冀0.64370.6864 长三角0.61710.53790.64500.5720 珠三角0.65190.65880.58730.64930.60020.4626 市区人口京津冀0.64740.6931 长三角0.64550.61060.67500.6291 珠三角0.63690.65200.57830.66730.66760.5033
表4 基于广义Gini系数的组间不均衡指数与基于常规Gini系数的组内不均衡指数的比较
Table 4 Comparisons between the between-groups inequality index based on generalized Gini coefficient and the within-groups inequality index based on conventional Gini coefficient

项目组内不均衡指数组间不均衡指数 测度基础常规Gini系数(学界常用)广义Gini系数(本文发展) 计算公式式(1)和(2)式(3)和(4) 计算结果矩阵对角线数值矩阵对角线以外数值 地理意义区域内同一测度反映的同一要素集合的不均衡区域内不同测度反映的同一要素集合的相对不均衡; 区域间同一同测度反映的不同要素集合的相对不均衡
说明: 式(1)等价于式(2), 根据文献中的常用公式变换得到; 式(2)是式(3)和(4)的特例。
常规的不均衡指数属于组内不均衡指数, 本文的目的在于构建组间不均衡指数。上述结果表明, 组间不均衡指数简单实用: 既可以基于同一测度描述不同区域之间的不同地理要素集合的相对差异, 也可以基不同测度描述同一个区域相同要素集合的相对差异(表 4)。实际上, 组间不均衡指数包含组内不均衡指数, 后者是前者的特例。为了描述一个系统中要素规模分布的差异性, 统计学家基于Lorenz 曲线定义了 Gini 系数。理论上, Gini 系数很难测算, 实际应用中常以组内不均衡指数[13]代替。在文献[10-12]中, 不均衡指数采用如下公式估算:
 , (5)
, (5)式中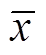 为xi平均值。
为xi平均值。
可以证明, 式(5)与(1)等价, 式(1)是由式(5)变换得出。基于观测数据从大到小的排序, 式(5)可转换为如下集中化指数[16-17]表示:
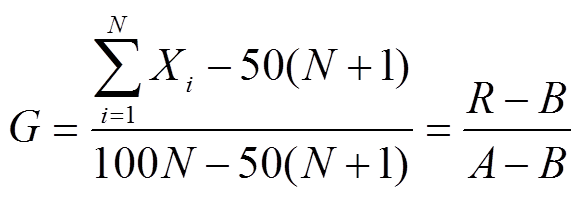 , (6)
, (6)式中, Xi 为 xi 的累积百分比, A 为绝对集中的累积分布之和, B 为绝对均匀的累积分布之和, R 为实际累积分布之和。任何测度方法都有其优势, 也有其局限性。不均衡指数有效性的前提是描述对象的规模分布具有特征尺度, 即平均值、标准差和协方差有效[13]。如果将一个区域的 N 个地理要素从小到大排列(xi+1 ≥xi), 编号为 i=1, 2, 3, …, N, 则式(1)可以表示为
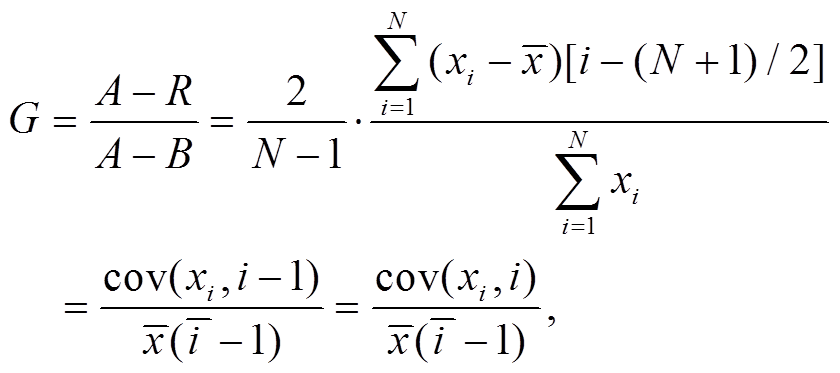 (7)
(7)
这里, 序号i的平均值为(N+1)/2, i -1 的平均值等于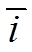 -1, 即(N-1)/2,
-1, 即(N-1)/2, 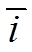 表示序号的算术平均值。进一步地, 如果将序号归一化, 即取 k=(i -1)/(N -1), 则 k的平均值为
表示序号的算术平均值。进一步地, 如果将序号归一化, 即取 k=(i -1)/(N -1), 则 k的平均值为![]() =1/2, 从而式(5)可以简化为
=1/2, 从而式(5)可以简化为
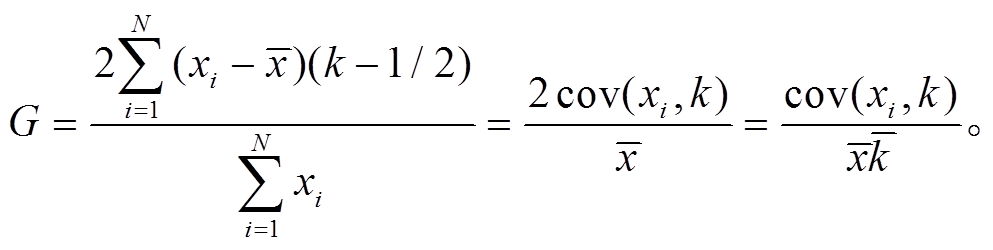 (8)
(8)这表示不均衡指数的统计意义为从小到大排列的序列 xi 与减去 1 之后归一化的序号 k 之间的协方差除以 k 和 xi 的平均值之积。如果序列服从幂律分布(如满足 Pareto 分布或服从 Zipf 定律), 则平均值不可靠, 计算结果的置信度低[8]。类推可知, 如果组内不均衡指数不可靠, 则组间不均衡指数也不可靠。
本文提出的组间不均衡指数定义及其度量方法, 此前未见报道。一个好的测度或指数应该具有明确的边界值或者临界值[15]。如同组内不均衡指数一样, 组间不均衡指数具有确定的下限和上限, 即 0 和 1, 此为边界值。组间不均衡指数的缺点在于没有反映属性变异的临界值。本研究的不足之处在于, 未对案例数据背后隐含的概率分布做无尺度分析, 因此, 不能保证案例分析的严格有效性。尽管如此, 作为一种测度方法的发展, 本研究为具有特征尺度的分布提供了简明、实用的组间不均衡度量方法。
组间不均衡指数是组内不均衡指数的一种推广, 而组内不均衡指数是基于 Lorenz 曲线的 Gini系数的一种近似表达。组间不均衡指数公式可以将组内不均衡指数公式作为特例兼容, 并纳入计算过程。因此, 组间不均衡指数可以理解为组间相对Gini 系数。根据数学推理和实证分析, 可以得出如下结论。
1)组间不均衡指数可以用于度量两个区域地理要素分布的相对差异性。计算过程不要求两个系统的要素数目对等。不均衡指数的数值越小, 两个系统的要素分布相对越均衡, 否则相对差异性越大。
2)组间不均衡指数可以用于度量同一个区域地理要素不同指标分布的相对差异性。不同指标反映地理要素的不同侧面。由于不同指标的量纲通常不同, 因此计算不同测度的组间不均衡指数前需将变量归一化。
3)不均衡指数有效的前提是地理要素分布具有特征尺度。就规模分布而言, 所谓有特征尺度, 就是具有有效的平均值。如果系统要素存在空间关联, 则一般服从幂律分布, 从而平均值不再有效, 不均衡指数的应用效果也会随之降低。
致谢 京津冀城市夜灯数据由博士研究生龙玉清处理, 在此表示感谢。
参考文献
[1]Anselin L. The Moran scatterplot as an ESDA tool to assess local instability in spatial association // Fischer M, Scholten H J, Unwin D. Spatial Analytical Per-spectives on GIS. London: Taylor & Francis, 1996: 111-125
[2]Goodchild M F. GIScience, geography, form, and pro-cess. Annals of the Association of American Geo-graphers, 2004, 94(4): 709-714
[3]陈彦光. 空间相互作用模型的形式、量纲和局域性问题探讨. 北京大学学报(自然科学版), 2009, 45(2): 333-338
[4]Haggett P, Cliff A D, Frey A. Locational analysis in human geography. London: Edward Arnold, 1977
[5]Chen Y G. New approaches for calculating Moran’s index of spatial autocorrelation. PLoS ONE, 2013, 8(7): e68336
[6]Wilson A G. Entropy in urban and regional modelling: retrospect and prospect. Geographical Analysis, 2010, 42(4): 364-394
[7]Chen Y G. The distance-decay function of geogra-phical gravity model: power law or exponential law?. Chaos, Solitons & Fractals, 2015, 77: 174-189
[8]Fotheringham A S, Brunsdon C, Charlton M. Geogra-phically weighted regression: the analysis of spatially varying relationships. Chichester: John Wiley & Sons, 2002
[9]胡兆量, 陈彦光, 刘涛. 经济地理面貌变化三特征. 经济地理, 2018, 38(10): 1-4
[10]Sen A. On economic inequality. 2nd ed. Oxford: Oxford University Press, 1977
[11]Dixon P M, Weiner J, Mitchell-Olds T, et al. Boot-strapping the Gini coefficient of inequality. Ecology, 1987, 68: 1548-1551
[12]Damgaard C, Weiner J. Describing inequality in plant size or fecundity. Ecology, 2000, 81: 1139-1142
[13]陈彦光.基于Euler公式的无尺度分布Gini系数估计公式. 北京大学学报(自然科学版), 2018, 54(6): 1283-1289
[14]Theil H. Economies and information theory. Amster-dam: North Holland, 1967
[15]陈彦光. 城市和区域产业发展分析的增长商测度. 人文地理, 2017, 32(4): 86-94
[16]林炳耀. 计量地理学概论. 北京: 高等教育出版社, 1985
[17]周一星. 城市地理学. 北京: 商务印书馆, 1995
Inequality Indexes for Measuring Between-Groups Mean Difference of Size and Spatial Distributions
Abstract A set of new inequality indexes are constructed to measure the relative unbalanced difference between regions or groups of elements in a geographical systems. Firstly, the within-group inequality index, namely, the Gini coefficient based on the Lorenz curve, is transformed into a new mathematical expression. Then, based on the new formula, the within-group index is generalized to between-group inequality index. Technically, the two types of inequality indexes can be integrated into the same logic framework. As an example, the new formulae are applied to three systems of cities in China, including Beijing-Tianjin-Hebei region, Yangtze River Delta, and Pearl River Delta. The results display a spatio-temporal evolution patterns of relative mean differences within and between these urban systems.
Key words Gini coefficient; inequality index; Beijing-Tianjin-Hebei; Yangtze River Delta; Pearl River Delta;urban system
doi: 10.13209/j.0479-8023.2019.107
国家自然科学基金(41590843,41671167)资助
收稿日期: 2018-12-12;
修回日期: 2019-02-28