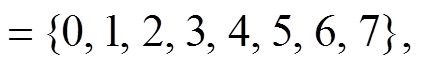如图 1 所示。摘要 目前可以应用于三角形网格的链码方法只有顶点链, 而它对角相邻情况的表达存在缺陷, 针对此问题, 提出 3 种链码方法, 并进行特性分析和性能比较。首先将 Freeman 链码扩展应用到三角形网格, 根据两种不同的三角形单元, 分别设计对应的 12 方向 Freeman 链码编码规则; 然后, 基于外轮廓前进相对方向的变化, 提出相对方向链码; 最后, 通过区分边界网格在外轮廓上的边数和内部网格数的不同组合, 得到边角组合链码。通过实验比较 3 种链码的表达能力和压缩率, 结果表明, 3 种链码方法均能克服顶点链的缺陷, 准确完备地实现三角形网格形状的边界表达。其中, 边角组合链码的综合性能最高, 平均码数为 1, 压缩率可达 0.75。
关键词 三角形网格; Freeman链码; 边角组合链码; 压缩率
链码是通过一定的编码方式对几何形状的边界进行顺序表达的方法。1961 年 Freeman[1]最早提出链码方法, 即 Freeman 四方向和八方向链码, 之后还出现顶点链码(vertex chain code, VCC)[2]、直角三方向链码(orthogonal three-direction chain code, 3OT)[3-4]和无符号曼哈顿链码(unsigned manhattan chain code, UMCC)[5]等多种方法。目前, 链码广泛应用于计算机视觉[6-7]、模式识别[8-9]、数字图像处理[10-11]和地理信息系统[12]等各个领域。
最简单的链码是跟踪目标边界, 并给每两个相邻像素的连线一个方向值, 这就是 Freeman 链码的基本思想。根据边界表达所采用的网格邻域不同, 可分为 4 方向和 8 方向两种链码, 分别需要 4 个和 8个码值进行表达, 记为∑(F4)={0,1,2,3}, ∑(F8)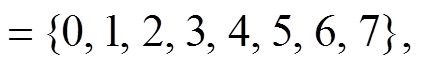 如图 1 所示。
通过依次记录形状轮廓上共顶点的边界网格数进行边界表达, 这是 VCC 的实现方法。对于正方形网格, VCC 只需要“1”, “2”, “3”这 3 个码值即可完成边界描述, 分别对应边界网格的凸角转向、水平或垂直方向前进以及凹角转向, 如图 2 所示。类似地, VCC 可表示为∑(VCC)={1, 2, 3}。
此外, VCC 还可用于六边形网格和三角形网格的形状边界表达, 这是目前唯一能够直接应用于非四边形网格的链码方法。例如, 对于三角形网格, 其轮廓上共顶点的边界网格数最多为 5 个, 因此可以用“1”~“5”这 5 个码值进行表达, 如图 3 所示。
3OT 与 VCC 有相似之处, 二者均由形状外轮廓上边界网格顶点的某个特性出发。不同的是, 3OT分别用“0”, “1”, “2”这 3 个码值表达无方向变化、方向向前改变以及向后回转 3 个相对变化的直角方向,即∑(3OT)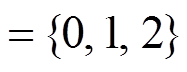
, 如图 4 所示。
UMCC 于 2016 年提出, 该链码只使用“0”和“1”两个码值记录边界网格中心连线沿 x 和 y 方向的前进, 并且利用 3 组“00”开头的标识码, 分别表示两个方向上的单调性变化情况, 表示为∑(UMCC)= {0, 1}。
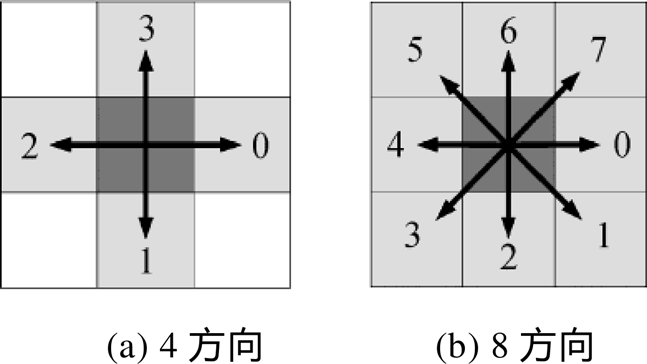
深色表示当前边界网格, 浅色为可能的下一个边界网格
图1 Freeman的4方向和8方向链码
Fig. 1 4-direction and 8-direction Freeman chain code
图2 顶点链码
Fig. 2 Vertex chain code
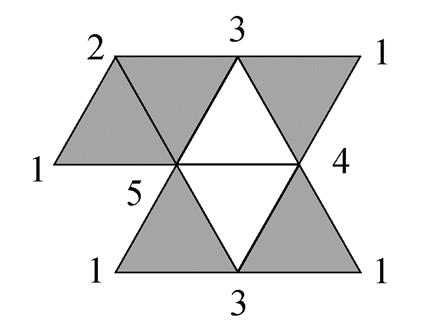
图3 三角形网格顶点链示例
Fig. 3 Example of VCC for triangular grid
图4 直角三方向链码
Fig. 4 Orthogonal three-direction chain code
除 VCC 外, 其他 3 种链码均只考虑四边形网格一种情况。对于连续图像的离散化, 还可以按照三角形或六边形进行采样。这 3 种模式均有固定的规格, 并且能够无缝地覆盖 2D 平面。刘志坤等[13]证明, 规则正三角形网格(简称三角形网格)在有效覆盖面积和覆盖效率两项指标上均优于正四边形, 更适用于 2D 和 3D 的几何表达。但是, 目前还没有针对三角形网格链码的研究报道。
VCC 能够表达三角形网格边界, 但对一些特殊情况的处理存在缺陷。例如, 图 5 展示 3 种不同的角相邻情况,VCC 在斜线网格 3 个顶点上的码值均为“211”, 无法对这 3 种情况进行有效的区分。3OT将形状轮廓的前进方向分为 3 个相对变化的直角方向, 并加以分别表达。然而, 沿三角形网格外轮廓, 并不是简单的直角转折或回转方向, 因此该方法无法直接应用到三角形网格中。UMCC 记录相邻网格中心连线沿边界前进时在 x 和 y 方向上的单调性变化, 但三角形网格的边角关系复杂, 存在 3 种角相邻和 9 种边相邻关系, 导致在笛卡尔坐标系下有多组相同的单调性变化情况, 无法通过“0”和“1”直接进行区分标识。如果增加标识码, 会使编码复杂, 造成过多冗余, 同样也不适用于三角形网格链码。在原有链码方法中, 只有 Freeman 链码可以较好地扩展应用到三角形网格。
本文研究能够应用于三角形网格, 并准确完备地表达形状边界的链码方法及其特性。首先, 分析现有的四边形网格链码方法在三角形网格中的适用性, 并通过扩展, 得到 12 方向的 Freeman 链码。然后, 分别基于轮廓前进的相对方向变化和外轮廓上边界网格的边数与夹角特性, 提出两种新的三角形网格链码方法。在此基础上, 分析 3 种链码方法的几何特性, 并通过实验比较各链码的表达能力和压缩率。
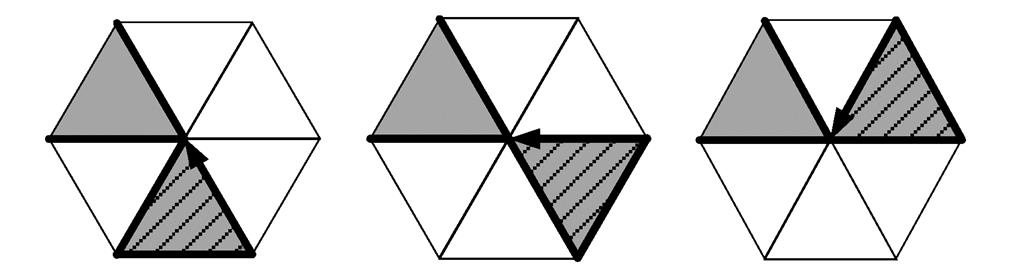
图5 三角形网格中的角相邻情况
Fig. 5 Angle adjacent cases in triangular grids
与四边形网格相比, 三角形网格的单元结构和特性更复杂, 主要体现在两方面: 1) 三角形单元方位不唯一, 根据其在笛卡尔坐标系中的方位, 可分别称为正三角和倒三角单元(图 6); 2) 邻接关系更多样, 存在 3 种边相邻及 9 种角相邻的情况。
Freeman 链码的编码原理是基于相邻边界网格中心连线的绝对方向, 因此适用于三角形网格。通过增加码值, 将 Freeman 链码扩展到三角形网格。结合三角形网格的方位关系和邻接关系, 应用于三角形网格的 Freeman 链码需要 12 个码值, 并分两种情况进行编码。
首先, 对于正三角单元, 从其右侧边相邻的网格起, 沿逆时针方向分别赋予码值“0”~“9”以及“A”和“B”, 如图 6(a)所示。其中, “0”, “4”, “8”对应 3 个边相邻网格, “1”~“3”, “5”~“7”和“9”~“B”分别对应共顶点的三组角相邻网格。
然后, 将倒三角网格单元及其邻域网格视为由正三角网格上下翻转得到, 据此可直接得到倒三角网格的编码结果。这相当于由当前单元右侧边相邻的网格开始, 按顺时针方向依次赋予码值, 如图 6 (b)所示。按这种方式, 无论是在正三角单元还是倒三角单元, 与当前网格边相邻的网格码值均为“0”, “4”和“8”, 其余角相邻网格码值也相同, 因此可较好地保证正三角与倒三角单元编码的一致性。
由于三角形网格邻域内在 0°和 180°方向的网格均不唯一, 如“0”与“B”以及“4”与“5”均为同一方向, 仅根据当前网格与下一网格中心连线的绝对方向无法区分, 需要利用相邻网格距离进行判断。
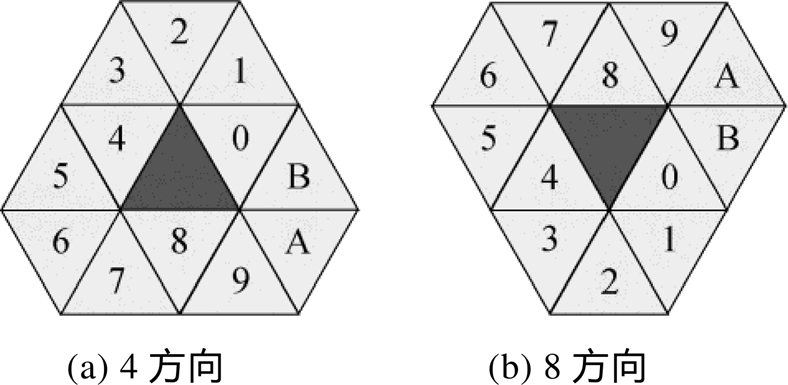
图6两种三角单元的F12编码规则
Fig. 6 Encoding rules of F12 for two triangular units
综上所述, 三角形网格的 12 方向 Freeman 链码可以用∑(F12)={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B}来表示。确定起始网格后, 依次对其他边界网格赋予唯一对应的码值, 每个码需要 4bit 存储空间。图 7 给出利用 F12 按逆时针方向对三角形网格形状边界的编码示例。
多边形网格的邻接关系决定其可能的轮廓前进方向。四边形网格上每个顶点由 4 个 90°角共有, 因此经过该点的轮廓前进方向共 3 种: 向前(0°), 向左(逆时针 90°)或向右(顺时针 90°)。相比之下, 三角形网格每个顶点由 6 个三角形的 60°角共有, 前进方向分为 5 种, 包括与当前方向相比无变化以及相对当前方向分别偏转±60°和±120°(向左为正, 向右为负), 如图 8 中虚线箭头所示。
因此, 三角形网格边界由轮廓前进的 5 个相对变化方向决定, 分别将边界轮廓相对方向偏转 0°, 60°, −60°, 120°和−120°这 5 种情况赋予码值“0”~ “4”, 依次记录形状外轮廓线在各顶点处的前进相对方向变化, 即可完成对边界的表达。我们称这种链码方法为相对方向链码(relative direction chain code, RDCC),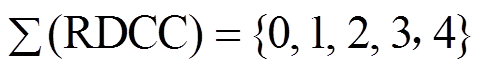
。
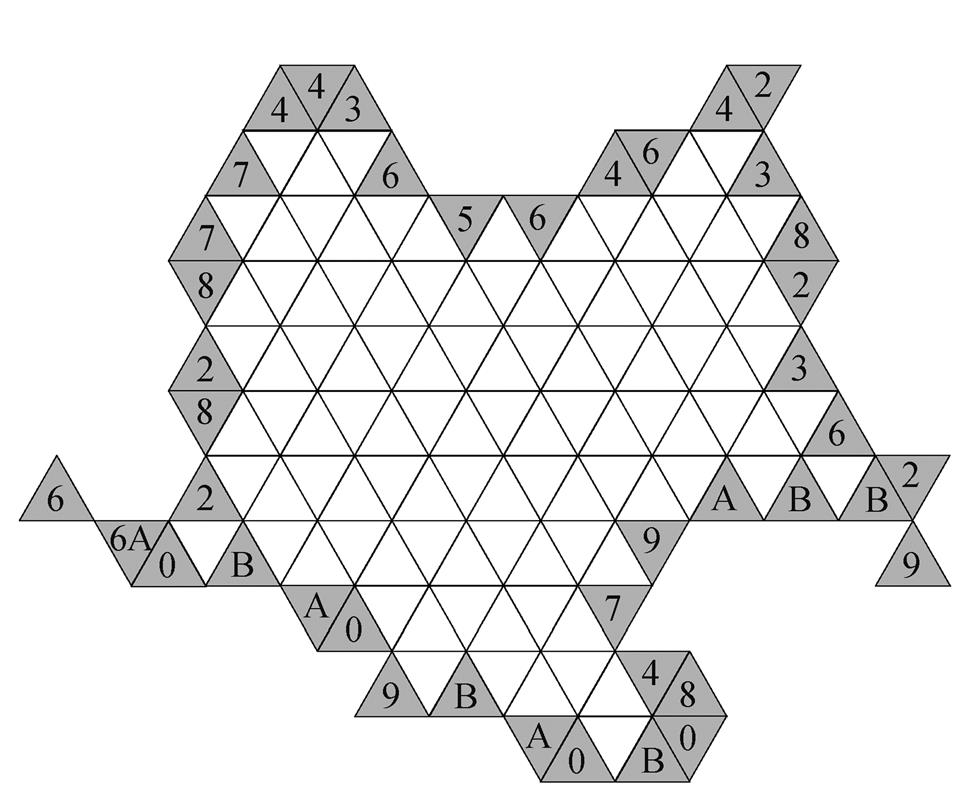
图7 12方向Freeman链码示例
Fig. 7 Example of F12 chain code
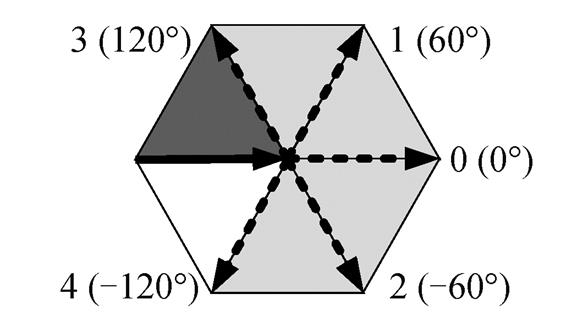
图8 三角形网格轮廓前进相对方向
Fig. 8 Relative move directions of triangular grid contour
由于 RDCC 记录的是外轮廓每个顶点处的相对方向变化, 因此总码数与形状外轮廓上的顶点数相同, 平均每个码占据 3bit 存储空间。用 RDCC 对图7中的形状边界进行编码, 结果如图 9 所示。
与 VCC 相似, RDCC 也通过依次记录形状外轮廓各顶点处的某种特性来完成边界表达, 然而, RDCC 可避免 VCC 在特殊情况下的编码缺陷。如图 9 左侧和右侧的两种角相邻情况, 由于两种情况在外轮廓上的相对前进方向不同, 得到的编码结果也不同。因此, RDCC 比 VCC 更加完备和准确。
形状的外轮廓由各边界网格在外轮廓上的边组成, 因此可以通过统计边界网格在外轮廓上的边数, 实现形状边界的表达。对于三角形网格, 各边界网格在外轮廓上的边数可能为 1, 2 或 3。由于三角形网格边角关系复杂, 存在边数相同但轮廓前进方向不同的情况, 需要进一步区分。
根据边界网格在外轮廓上的边数不同, 分以下两种情况进行讨论。
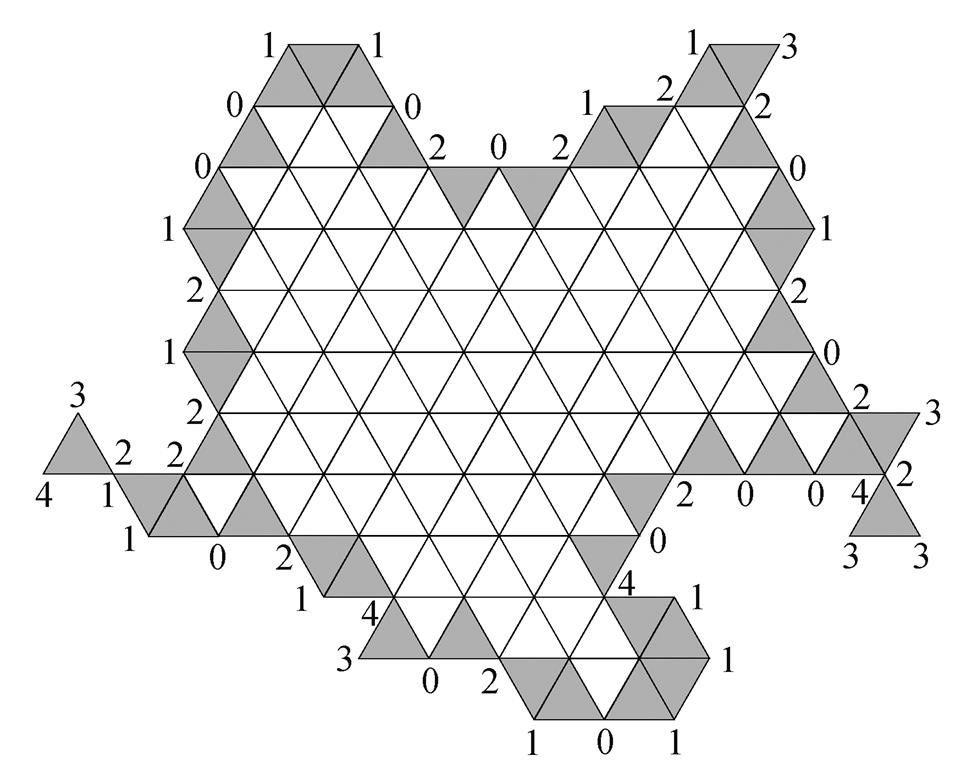
图9 相对方向链码示例
Fig. 9 Examples of RDCC
1)边数为 1 或 2 时。此时分别对应 4 种不同的轮廓前进方向, 如图 10 所示。通过观察可以发现, 对不同的轮廓前进方向, 可以通过相邻边界网格之间的夹角进行区分。不同夹角的直接体现是相邻边界网格共顶点的形状内非边界网格数不同, 即图 10 中的阴影部分, 将其定义为内部网格, 取值范围为 0~3。由于三角形边界网格的外轮廓边数(1~2)与内部网格数(0~3)存在 8 种组合, 因此每种组合可分别由 1 个码值表示, 每个码占用 3bit 存储空间。因此, 8 种情况依次由“0”~“7”这 8 个码值表示。
2)边数为 3 时。此时对应 3 种轮廓前进方向, 即图 5 所示的 3 种角相邻情况。这 3 种情况在实际应用中出现的概率较小, 因此可考虑用冗余的码值组合进行替换, 如图 11 所示。
注意到码值组合“44”表示两个三角形网格的自闭合, 但这种情况实际上并不存在(图 12)。因此, 可将其作为边数为 3 时的区分码, 分别将图 5 中的 3 种角相邻情况用“441”, “442”和“443”这 3 个组合表达。
综上所述, 将基于外轮廓边数与夹角的链码方法称为边角链码(edge angle chain code, EACC),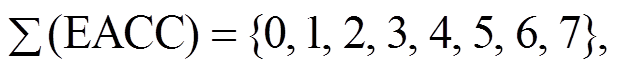 
其中每个码值占 3 bit 存储空间。图 13 展示利用 EACC 的编码结果, 左右两个角相邻网格由不同的码值组合表示, 从而实现有效的区分。
链码的主要几何特性包括可检测直线段、与起始点无关性、旋转不变性和翻转不变性等。不同的三角形链码, 几何特性也有所区别。下面分别对F12, RDCC, VCC 和 EACC 这 4 种三角形网格链码方法的几何特性进行分析与比较。
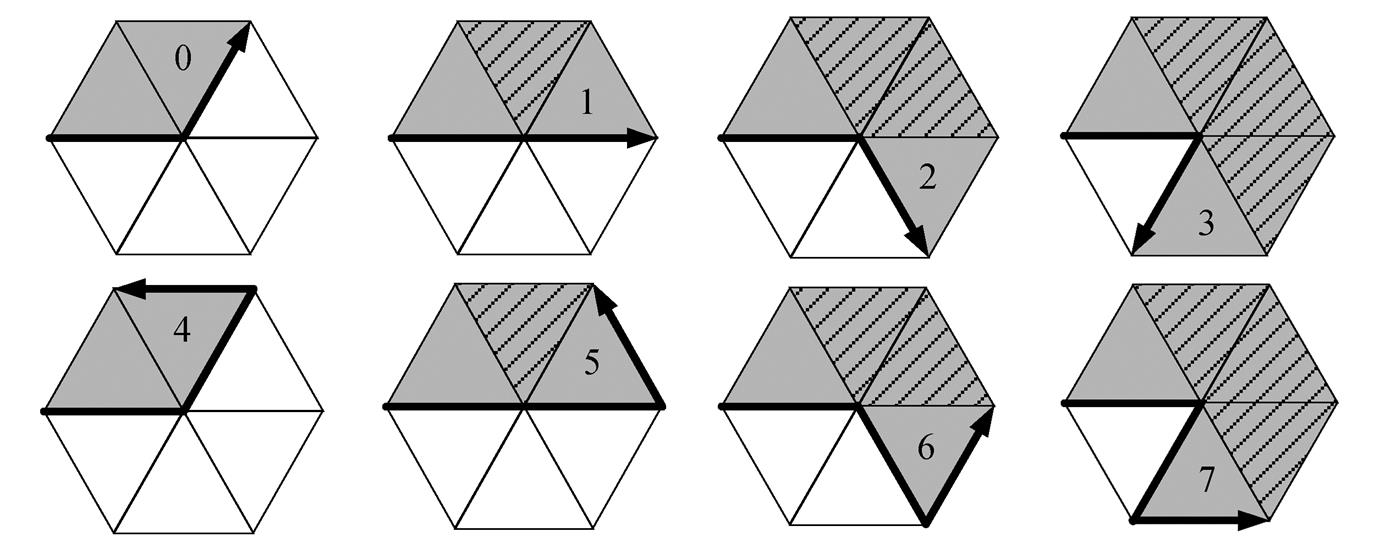
图10 边数为1和2时三角形边界网格的轮廓前进方向
Fig. 10 Contour move directions as edge number equals 1 and 2
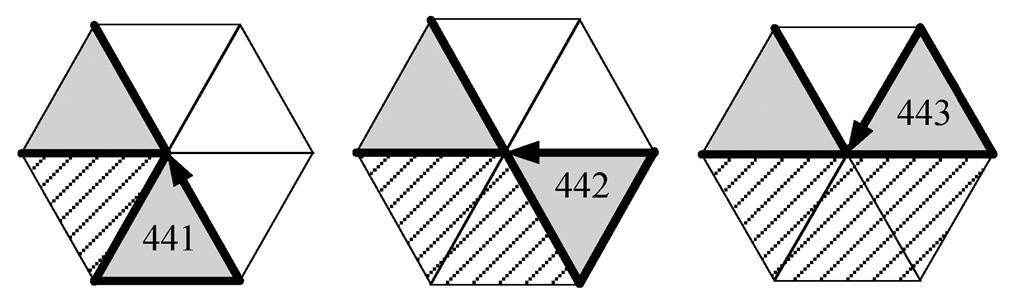
图11 边数为3时三角形边界网格的轮廓前进方向
Fig. 11 Contour move directions as edge number equals 3
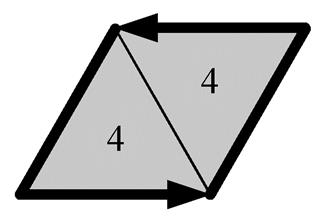
图12 组合“44”对应的三角形网格
Fig. 12 Triangular grids corresponding to “44”
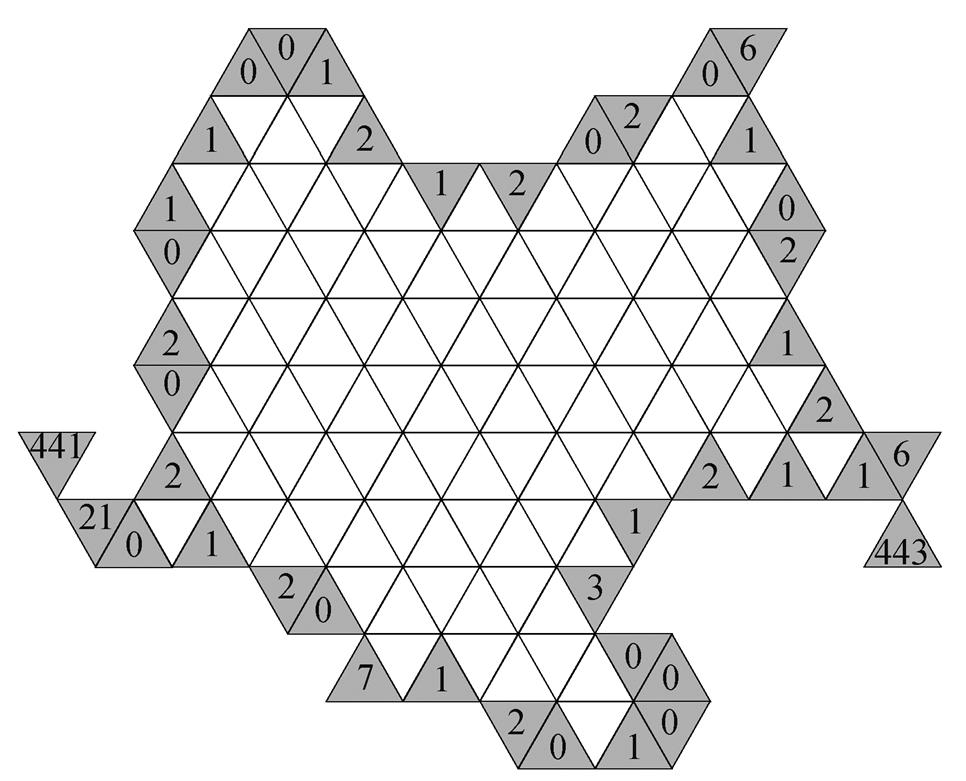
图13 边角链码示例
Fig. 13 Example of EACC
利用 F12 链码可检测不同方向的直线段, 并且编码结果与起始点选择无关。
1)F12 链码的不同码值代表边界网格中心连线的不同方向, 因此, 同一码值序列即表达边界网格在该方向上的直线段。其中, 码值序列“0404…04”表示 x 方向直线段; 正三角单元的“1717…17”和“3939…39”分别表示与 x 正方向夹角为 60°和 120°的直线段, 倒三角单元则相反; 序列“2828…28”近似地表示y方向上的直线段。
与之相比, 四边形 Freeman 链码 F8 可检测水平、垂直以及对角方向的直线段, 这个差异是由不同类型网格的邻域关系决定的。
2)将链码视为一个自然数, 将其中各个码值按某一个方向循环, 使其构成的自然数值最小, 这个过程就是归一化。图 7 中, F12 归一化后为 08479 ABB9263283246465634477828266A0B109BA0B。
由于 F12 链码表达边界中心连线的绝对方向, 因此编码结果会因旋转和翻转操作而发生变化, 即不具备旋转或翻转不变性。
RDCC 的几何特性主要包括可检测直线段、与起始点无关、旋转不变性、翻转不变性以及方便计算曼哈顿距离下的轮廓周长。
1)由于外轮廓前进的相对方向无变化即为直线段, 因此根据 RDCC 的定义, 直线段由序列“00…0”表示, 但与 F12 不同, 通过 RDCC 无法判断直线段方向。
2)RDCC同样可以通过归一化来保证链码结果与起始点无关。例如, 图 9 中 RDCC 归一化后结果为 00121222341102143021011140200433232021023121 202011。
3)经旋转或翻转等操作后, 轮廓前进的相对方向不会发生改变, 因此, RDCC 具有旋转和翻转不变性。
4)用曼哈顿距离表示的轮廓周长即为边界网格在外轮廓线上的边数之和, 这也与其顶点数相同。因此, RDCC 的总码数即为轮廓周长。
VCC 也是基于形状外轮廓各顶点的属性得到, 与轮廓前进的绝对方向无关, 因此 VCC 的几何特性与 RDCC 相同。
EACC 的几何特性包括可检测直线段、与起始点选择无关、旋转以及翻转不变性, 并能计算轮廓周长。
1)当外轮廓边数与内部网格数均为 1 时, 对应边界上的直线段, 此时码值序列为“22…2”。但是, EACC 无法检测不同方向的直线段.
2)通过归一化, 可以实现链码结果与起始点选择无关。例如, 图 12 中 EACC 的归一化编码结果为00031211443621201602021210011020224411012071201。
3)旋转与翻转操作不会改变边界网格的外轮廓边数及内部网格数, 因此 EACC 具有旋转和翻转不变性。
4)EACC 同样能够计算形状的轮廓周长。根据EACC 的定义, “0”~“3”表示边数为 1 的情况, “4”~ “7”表示边数为 2 的情况, 因此其周长可以表示为m+2×(N−m), m表示值小于 4 的码数, N 为总码数。
通过比较发现, 3 种基于边界网格外轮廓顶点或边的链码方法 RDCC, VCC 与 EACC 几何特性相似, 而 F12 的特性相对较少。
链码研究的一个重要方向是链码压缩方法。针对四边形链码, 有多种无损压缩方法[14-17]。不同链码方法在表达效率和压缩性能上存在较大的差异, 选择表达能力较强或压缩率较高的链码, 有利于进一步的压缩和优化。
链码的表达能力可以通过每个边界网格所需的平均码数 Sg 来反映。对于 F12 和 EACC, 正常情况下每个码均对应唯一一个边界网格(Sg=1)。每个三角形边界网格的顶点数且可能为 1~3 (Sg≥1), 因此RDCC 和 VCC 的表达效率低于前两种链码。
为量化地比较 F12, VCC, RDCC 和 EACC 的表达能力和压缩率, 本文选取 12 个不同类型的形状进行实验, 结果如图 14 所示。
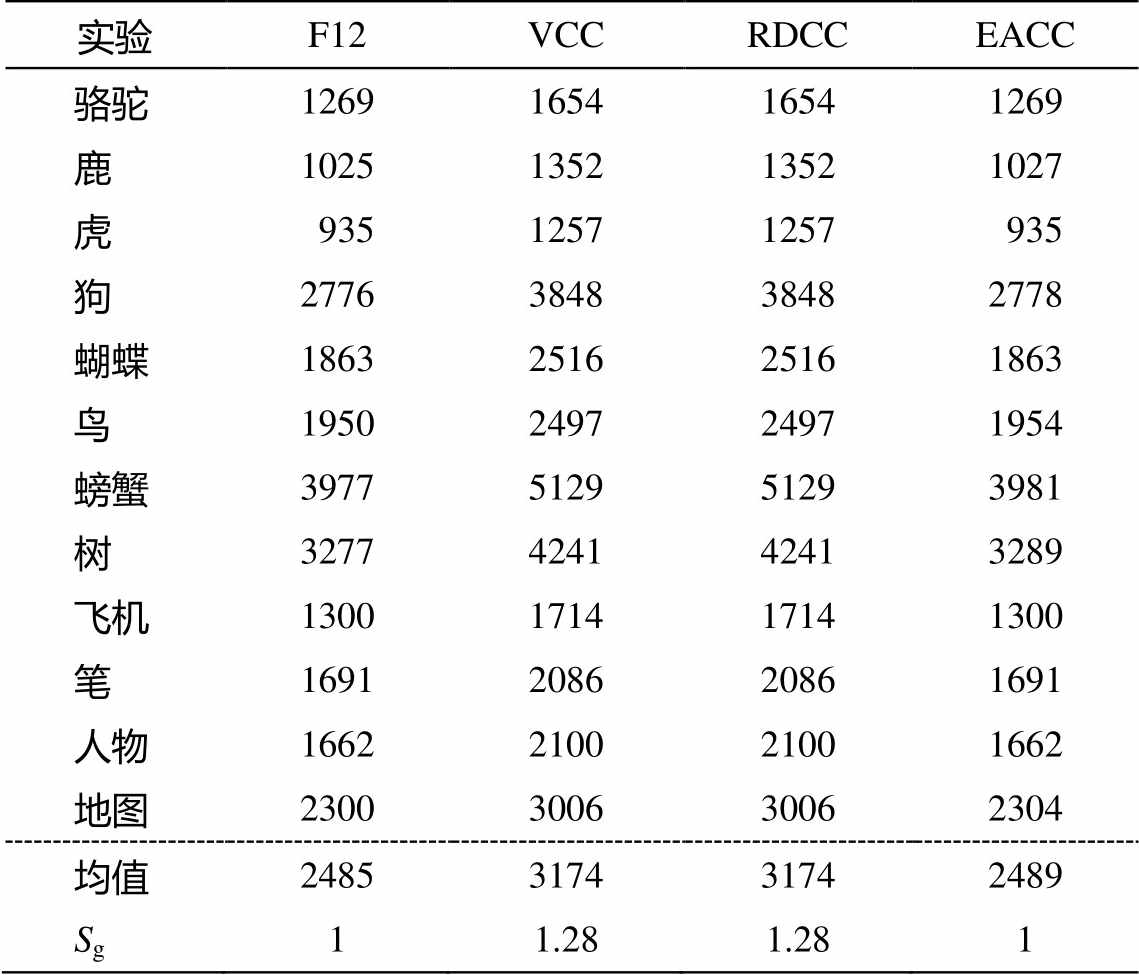
将这些形状在三角形网格中进行离散化, 分别统计 4 种方法得到的链码总码数、均值以及平均码数 Sg, 结果如表 1 所示。可以看出,EACC 和 F12 的码数最少, 部分实验中 EACC 的码数略高于 F12。这是由 EACC 进行码值组合的替换产生的, 总体上两者表达效率最高; RDCC 和 VCC 的表达效率相同, Sg=1.28, 即平均需要 1.28 个码来表达一个边界网格。实验结果验证了前面对各链码表达能力的分析结果。
图14 实验中用到的形状
Fig. 14 Shapes used in experiments
表1 不同方法得到的链码总码数
Table 1 Total code numbers of various chain codes
实验F12VCCRDCCEACC 骆驼1269165416541269 鹿1025135213521027 虎 93512571257 935 狗2776384838482778 蝴蝶1863251625161863 鸟1950249724971954 螃蟹3977512951293981 树3277424142413289 飞机1300171417141300 笔1691208620861691 人物1662210021001662 地图2300300630062304 均值2485317431742489 Sg11.281.281
四边形网格链码及其压缩方法的压缩率一般指与 F8 链码的总比特数之比。链码的压缩性能也可以通过总比特数与总边界网格数之比来衡量, 这一比值称为平均位数 Bg。对于三角形网格链码, 本文采用该指标进行对比分析。
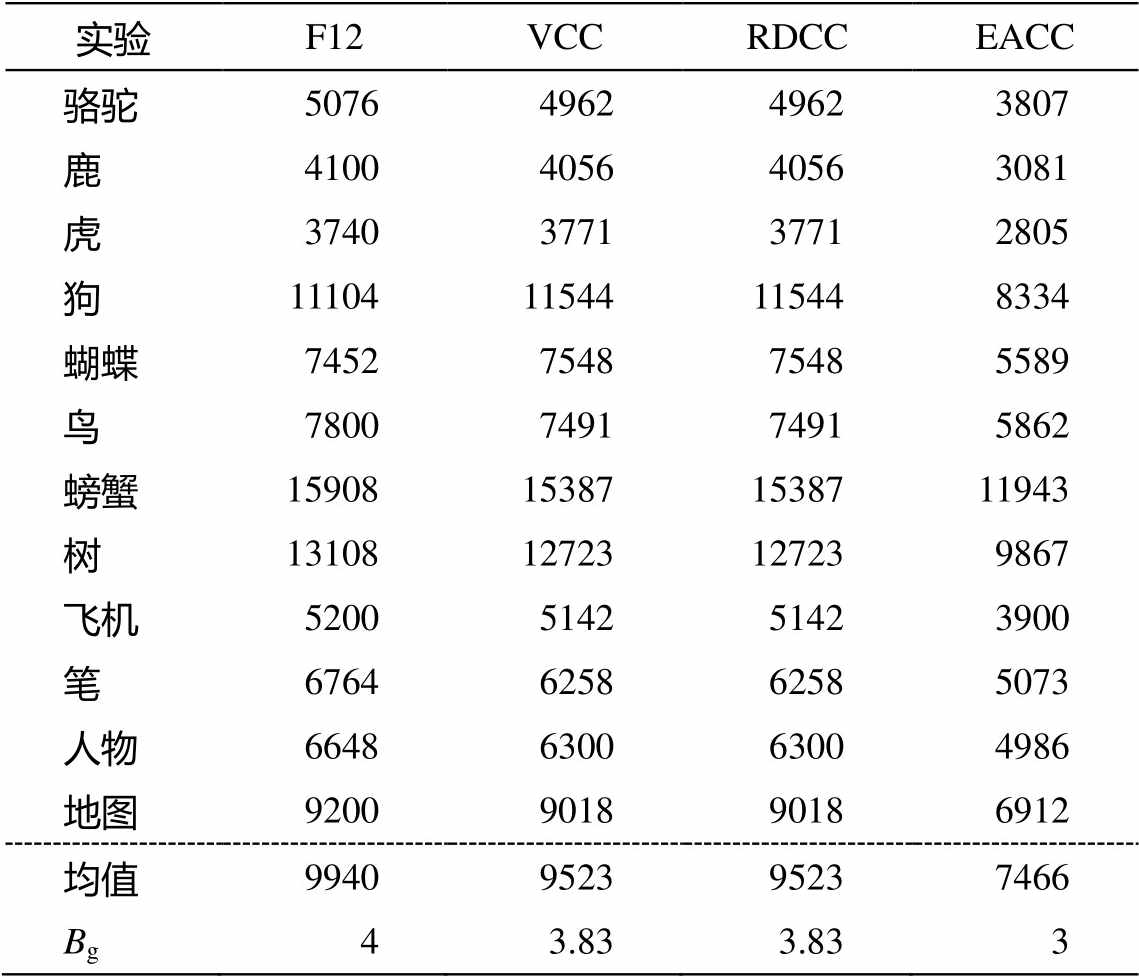
根据前面的分析, F12 链码共需要 12 个码值, 因此每个码值占 4bit 空间; RDCC 和 VCC 均有 5 个码值, 因此各需要 3 bit; EACC正好有 8 个码值, 平均位数同样为 3。根据“码数-位数”的转换关系, 由表 1 直接得到对应的以 bit 为单位的链码总长度, 并基于实验结果统计平均位数 Bg, 结果如表 2 所示。可以看出, F12 虽然表达效率高, 但由于码值过多, 平均每个码需要 4bit 表示, 压缩性能最低; RDCC和 VCC 的码数比 F12 多 28%, 但由于每个码占用位数更少, 整体压缩率略高于 F12, 为 0.955; EACC的平均码数和平均位数均最小, 与 F12 相比, 其压缩率仅为 0.75, 同时具有表达效率和压缩性能的优势。
表2 不同方法得到的链码总长度(bit)
Table 2 Total length of various chain codes (bit)
实验F12VCCRDCCEACC 骆驼5076496249623807 鹿4100405640563081 虎3740377137712805 狗1110411544115448334 蝴蝶7452754875485589 鸟7800749174915862 螃蟹15908153871538711943 树1310812723127239867 飞机5200514251423900 笔6764625862585073 人物6648630063004986 地图9200901890186912 均值9940952395237466 Bg43.833.833
对典型链码方法的分析表明, 只有 Freeman 链码能够扩展应用于三角形网格中, 但 VCC 对三角形网格形状边界角相邻的表达存在缺陷。本文提出 3 种适用于三角形网格的链码方法: 首先, 针对两种不同的三角形单元类型, 分别设计 12 方向 Free-man 链码, 使其尽量保持相对一致; 然后, 基于外轮廓前进方向的相对变化特性, 提出相对方向链码; 最后, 基于外轮廓上边界网格的边数及内部网格数, 得到三角形网格的边角链码。分析 3 种链码方法的几何特性, 并通过实验比较其表达能力和压缩率。结果表明, 3 种链码方法均能准确完备地对三角形网格形状边界进行表达, 其中边角链码的每个边界网格平均仅需要一个码值来表达, 压缩率达 0.75, 表达能力和压缩性能均最优。
参考文献
[1]Freeman H. On the encoding of arbitrary geometric configurations. IRE Transactions on Electronic Com-puters, 1961, 10(2): 260-268
[2]Bribiesca E. A new chain code. Pattern Recognition, 1999, 32: 235-251
[3]Sánchez-Cruz H, Rodríguez-Dagnino R M. Compres-sing bi-level images by means of a 3-bit chain code. SPIE Optical Eng, 2005, 44(9): 1-8
[4]Sánchez-Cruz H, Bribiesca E, Rodriguez-Diagnino M A. Efficiency of chain codes to represent binary ob-jects. Pattern Recognition, 2007, 40(6): 1660-1674
[5]Borut Ž, Mongus D, Liu Y K, et al. Unsigned man-hattan chain code. Journal of Visual Communication and Image Representation, 2016, 38: 186-194
[6]Jain J, Sahoo S K, Prasanna S M, et al. Modified chain code histogram feature for handwritten charac-ter recognition // Advances in Computer Science and Information Technology, Networks and Communica-tions, Berlin: Springer, 2012: 611-619
[7]Ema R, Supriana I, Khodra M L. Bag-of-shapes descriptor using shape association based on Freeman chain code. Journal of Theoretical and Applied Infor-mation Technology, 2017, 95(5): 1142-1153
[8]Lee D, Kim S J. Modified chain-code-based object recognition. Electronics Letters, 2015, 51(24): 1996-1997
[9]Karczmarek P, Kiersztyn A, Pedrycz W, et al. An application of chain code-based local descriptor and its extension to face recognition. Pattern Recognition, 2017, 65: 26-34
[10]Madenda Y S, Prasetyo E. Object feature extraction of songket image using chain code algorithm. Interna-tional Journal on Advanced Science, Engineering and Information Technology, 2017, 7(1): 235-241
[11]Tawfiq A. Asadi A, Joda F A. Removing spatial re-dundancy from image by using variable vertex chain code. European Academic Research, 2014, 2(1): 179-192
[12]Ren M, Karimi H A. A chain-code-based map mat-ching algorithm for wheelchair navigation. Transac-tions in GIS, 2009, 13(2): 197-214
[13]刘志坤, 夏清涛. 无线传感器网络三维覆盖策略研究. 武汉理工大学学报(交通科学与工程版), 2013, 37(3): 581-584
[14]Liu Y K, Zalik B. An efficient chain code with Huff-man coding. Pattern Recognition, 2005, 38(4): 553-557
[15]于国防, 王莉. 压缩型顶点链码的研究. 中国图象图形学报, 2010, 15(10): 1465-1470
[16]Sánchez-Cruz H. Proposing a new code by conside-ring pieces of discrete straight lines in contour shapes. Journal of Visual Communication and Image Repre-sentation, 2010, 21(4): 311-324
[17]Žalik B, Mongus D, Žalik K R, et al. Chain code compression using string transformation techniques. Digital Signal Processing, 2016, 53(6): 1-10
Study on Chain Code Methods for Triangular Grids
Abstract Only vertex chain code can be applied to triangular grids, but it has defect in angle adjacent expression. Aimed at the problem of object border representation in triangular grid, three novel chain codes were proposed and compared in character and performance. Firstly, Freeman chain code was extended to triangular grids. For two different triangular elements, the corresponding 12-direction Freeman chain code encoding rules were designed respectively. Secondly, based on the relative direction changes of the contour, the relative direction chain code was proposed. Finally, the edge chain code could be obtained by differentiating the combinations of edges number and internal grids number of the boundary grids. The geometric properties, expressive abilities and compression ratios of three novel chain codes were compared and analyzed. Experiments show that the proposed methods can accurately and completely realize the shape boundary expression of triangular grids. Among them, edge chain owns the best performance, the average code number per grid is 1, and compression ratio can reach 0.75.
Key words triangular grid; Freeman chain code; edge angle chain code; compression ratio
doi: 10.13209/j.0479-8023.2019.116
国家重点研发计划(2017YFB0503700, 2018YFB0505300)、高分辨率对地观测系统重大专项(11-Y20A02-9001-16/17, 30-Y20A01-9003-16/17)和国防科技创新特区项目(17-H863-01-ZT-005-015-02, 17-H863-01-ZT-005-022-01)资助
收稿日期: 2018-11-20;
修回日期: 2018-12-22