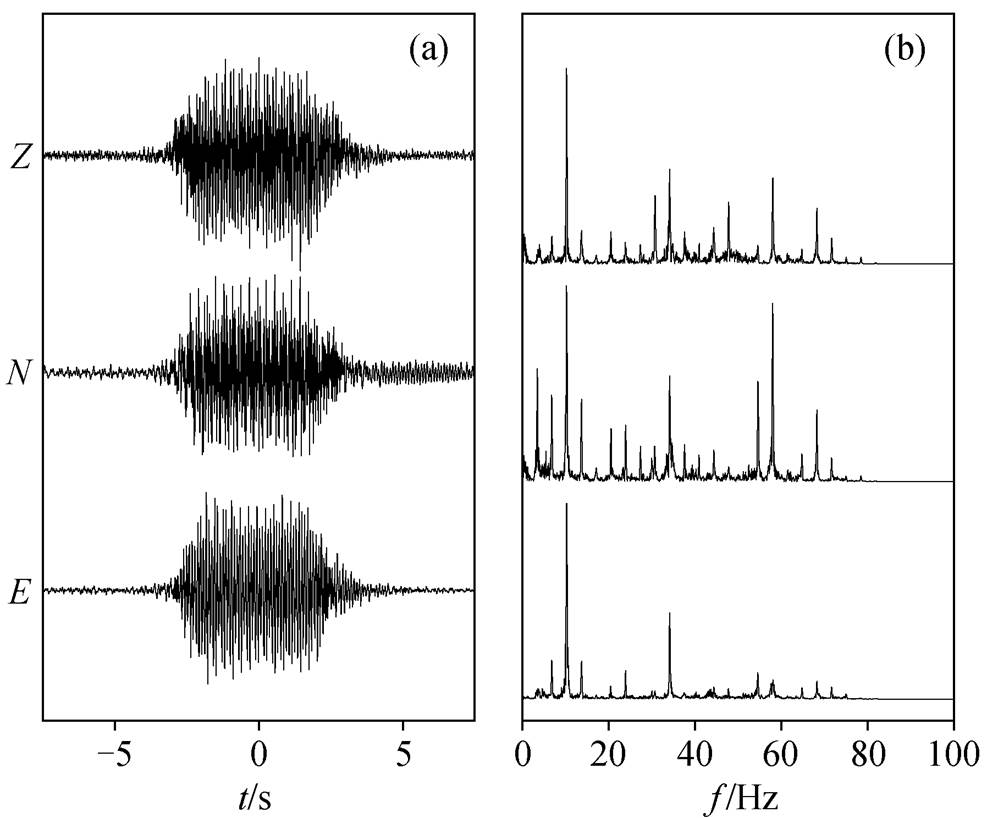
图1 高铁地震Z, N, E三分量波形(a)及其振幅谱(b)
Fig. 1 Three components (Z, N, E) waveforms (a) and their amplitude spectra (b) of a high-speed rail seismic event
摘要 使用北京大学架设的临时台阵中 11 个高铁高架桥下的短周期台站 11 天记录到的由 951 列高铁激发的共 10461 条地震记录, 利用 K-Means 聚类算法, 研究其频谱如何随列车的速度、模型、铁轨和路基变化而变化。近匀速运动的高铁所产生的高铁地震波的频谱主要由等间隔的峰组成, 其基频等于速度与车厢长度的比值。通过调整基频来降低列车速度的影响, 可使频谱模式更稳定, 便于比较。聚类结果表明, 高铁地震的频谱在相同车型、铁轨和路基条件下, 表现出稳定的模式; 这种稳定的频谱模式随车型、铁轨和路基条件的变化而显著变化。对这种稳定的频谱特征的监测, 可用于高速铁路的安全监控。
关键词 高铁; 震源; 频谱; 聚类
我国建设了大量的高铁线路, 每天有近 3 千列动车组在高铁轨道上运行。监测高铁的运行状况和保证高铁的安全运行显得愈发重要。对于动车组, 铁道运营公司主要借助整列地坑式架车机对行驶满历程的动车组进行不同等级的检修[1], 辅以在动车组上安装的感应装置对动车运行状态进行监测[2]; 对于高铁线路, 铁道运营公司主要使用综合检测列车[3]对固定设施进行监测。动车组行驶过程中, 列车与铁轨之间的挤压、摩擦和碰撞等激发的能量有一部分会以地震波的形式传播出去, 我们称之为高铁地震波。高铁运行过程中激发的地震波是良好的主动源地震波场, 蕴含动车组、铁轨和路基的结构及动力学特征。如果能提取出高铁地震(波)中蕴含的动车组、铁轨和路基信息, 将成为动态监测高铁运行状况的新工具, 同时也有助于使用高铁作为主动源探测地下结构。
2001 年就开始了针对高铁地震的研究, 近年来相关研究越来越多[4-9]。对高铁地震的早期研究使人们认识到, 高铁地震在监测高铁运行状态和探测地下结构等方面具有巨大潜力。El Kacimi 等[10]、Cai 等[11]和 Fu 等[12]基于三维有限元方法, 模拟列车运行在地面引起的振动, 并研究不同路基条件下的地面振动变化。Sussmann 等[13]提出一种通过地震面波测量路基参数的方法。这些结果表明, 高铁地震波场的激发受桥梁和路基结构的控制, 通过研究高铁地震波场可以获取桥梁和路基的相关信息。同时, 由于不同车型的动车具有不同的动力学属性, 直接影响高铁地震的波场, 因此高铁地震波场中也应包含列车车型的信息。从周围台站的地震学观测中筛选出能够反映高铁车型、铁轨和路基变化信息, 有助于实现高铁安全运行的自动监控。
2018 年以来, 本研究组在深圳和河北保定的高铁线路附近布设多期观测台站, 为研究高铁地震在监测高铁运行状态和地下介质状况提供了关键资料。曹健等[14]、刘磊等[15]、张唤兰等[16]、王晓凯等[17-18]和张固澜等[19]以此数据为基础, 从移动源的理论解、震源子波时间函数、频谱特征及聚类和地下结构成像等方面进行了系统的研究。
对于匀速运动的高铁列车, 实际观测的高铁地震信号频谱呈现等间距分立的模式。刘磊等[15]猜想这类频谱的基频 f0 与列车速度 v 和高铁车厢长度L存在如下关系:
f0 = v/L。 (1)
刘磊等[15]对频谱进行拉伸, 对齐不同车次间的基频, 消除列车速度对频谱的影响, 提取对齐后频谱的基频及其倍频的振幅作为频谱的特征, 研究这些特征随时空的变化规律。频谱特征随车次及台站空间变化的统计规律表明: 不同列车在同一台站上记录的频谱较为一致, 而同一列车在不同台站上记录的频谱特征可能具有较大的差异。同时, 基于频谱特征的聚类结果显示, 波场对于传播路径上的介质条件十分敏感, 介质条件相近的台站记录的高铁地震频谱相似, 介质条件相差较大的台站上频谱差异也较大。因此, 想要减少传播路径及其介质状况对波形的影响, 以便研究车型、路基和铁轨的信息, 必须选用近场的台站记录。
本文使用本研究组布设的台阵中高铁高架桥下方台站的高铁地震资料, 探究基频与车长、速度的关系, 提出一种更精确地获取高铁信号基频的方法, 能更加准确地估计高铁地震的基频和高铁的运行速度。根据基频伸缩频谱, 对齐不同运行速度的列车产生的频谱, 选取对齐频谱中的能量较高的频率作为特征, 并根据这些特征, 利用 K-Means 算法对频谱进行聚类分析。实际数据分析结果表明, 近场高铁的波形信息蕴含动车组速度、车型、铁轨和路基等信息: 在相同车型、铁轨和路基条件下, 高铁地震信号表现出稳定的频谱模式; 这种稳定的频谱模式随车型、铁轨和路基条件的变化而显著变化。获取具体台站上稳定的频谱特征并监测其变化, 有助于高速铁路安全状况监控。
2018 年 4 月和 5 月, 本研究组在河北省保定市高铁轨道附近布设两期流动观测台阵。台阵以短周期仪器为主, 每期有效观测时长为半个月, 共布设454 台。图 1 是一个高铁事件的三分量及其对应的频谱图, 其频谱存在明显的分立特征, 基频在 3.2 Hz 左右。刘磊等[15]以深圳高铁地震事件资料为基础进行研究, 结果表明高铁地震信号的特征主要受波场传播过程中介质条件的影响。高铁地震信号由较长时间沿轨道的移动源触发, 传播机制较为复杂。由于目前还没有能够有效地消除介质影响的方法, 导致研究其中包含的动车组、铁轨和路基等方面的信息较为困难。因此, 我们选取布设在京广高铁下方的 11 个近场台站, 以减少波场传播对高铁信号的影响。高铁轨道和台站分布如图 2 所示。

图1 高铁地震Z, N, E三分量波形(a)及其振幅谱(b)
Fig. 1 Three components (Z, N, E) waveforms (a) and their amplitude spectra (b) of a high-speed rail seismic event
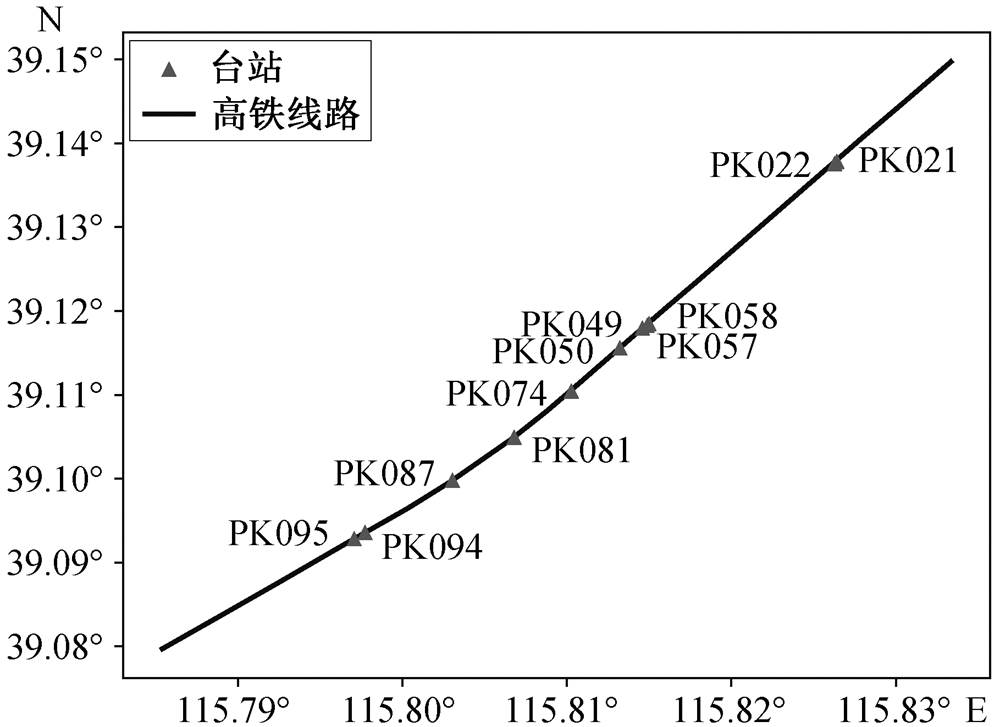
图2 台站和高铁分布
Fig. 2 Distribution of stations and the high-speed rail
为了研究方便, 我们把台站由北至南依次编号为 1~11。对高铁线路正下方的台站, 高铁地震信号的能量远大于环境噪音, 我们根据振幅挑选出每个台站上绝大多数的高铁地震信号。高铁地震信号出现的时间近似地等于高铁经过台站的时间, 根据高铁信号出现在这些台站的先后关系和到时差, 并考虑 50~100m/s 的速度区间, 我们把不同台站上属于同一列车的记录进行匹配, 并对列车的行驶方向做出判断。从这 11 个台站 11 天的记录中, 我们挑选共同记录到的 951 次列车(其中由北向南的列车 465 次, 由南向北行驶的列车 486 次)作为研究的样本。由于不同行驶方向的列车实际行驶的铁轨并不相同, 频谱可能存在差异, 所以对将由北至南和由南至北的列车分别进行研究。
对于匀速运动的列车, 假设每节车厢产生的地震波是相同的, 车厢与车厢之间仅存在时间延迟, 设单节车厢激发的高铁地震在台站处的记录为 r0(t), 则 n 节车厢一起产生的沿某一个方向的信号 r(t)可表示为
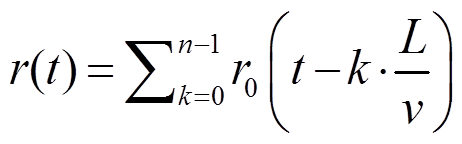 , (2)
, (2)其中, k 表示第 k 节车厢, t 表示时间。这里对问题做了简化: 不考虑复杂的激发和传播过程, 只考虑单节车厢行驶过程中在台站上产生的记录 r0(t), 研究由于不同车厢间稳定的时差对频谱的影响。
对式(2)做傅里叶变换, 得到
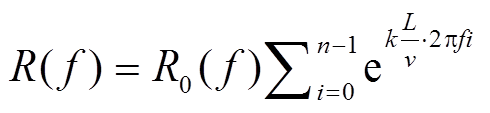 , (3)
, (3)其中, R0(f )表示单节车厢产生信号的频谱, R(f )表示总信号的频谱。式(3)可改写为
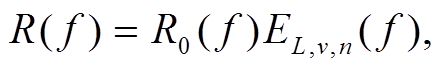 (4)
(4)
其中,
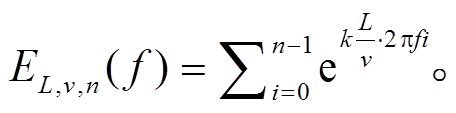 (5)
(5)对于一般的高铁信号, 可以假设L=25 m, v=80 m/s, n=8 或 16 (对应 8 和 16 节车厢的列车), EL,v,n(f )的形态(图 3)有明显的分立谱特征。当单节车厢的频谱与 EL,v,n(f )相乘之后, 其频谱也将呈现分立谱的模式。根据式(1), 当速度为 80m/s, 车厢长度为 25m 时, 高铁信号的主频为 3.2 Hz。实际观测中的大多数高铁地震信号的主频在该频点附近。
对于同一列高铁, 在速度变化不大、路基条件相近的情况下, 因传播路径短, 近场台站记录到的信号最大值出现的时间与高铁经过台站时刻的延迟时间应大致相等。所以, 可以通过不同台站间记录到的高铁地震信号最大值出现的时间差及其相对位置估计高铁运行的速度。我们以 Z 分量记录为例进行分析, 结果如图 4(a1)和(a2)所示。将记录到的高铁事件的振幅谱按速度由高到低的顺序排列, 图4(b1)和(b2)即最北的 1 号台站上高铁地震信号(分别为由北向南和由南向北列车)的振幅谱分布。
在京广高铁线路上运行的 CR400AF、CR400 AF 重联、CRH380AL、CRH380A、新 CRH380AL和 CRH380A 统型重联等动车组的中间车厢的长度都为 25m, 所以基频在这里主要受速度影响。从图 4 可以观察到, 随着速度降低, 频谱的基频也降低, 印证了我们关于频谱基频与车长和速度关系的猜想。
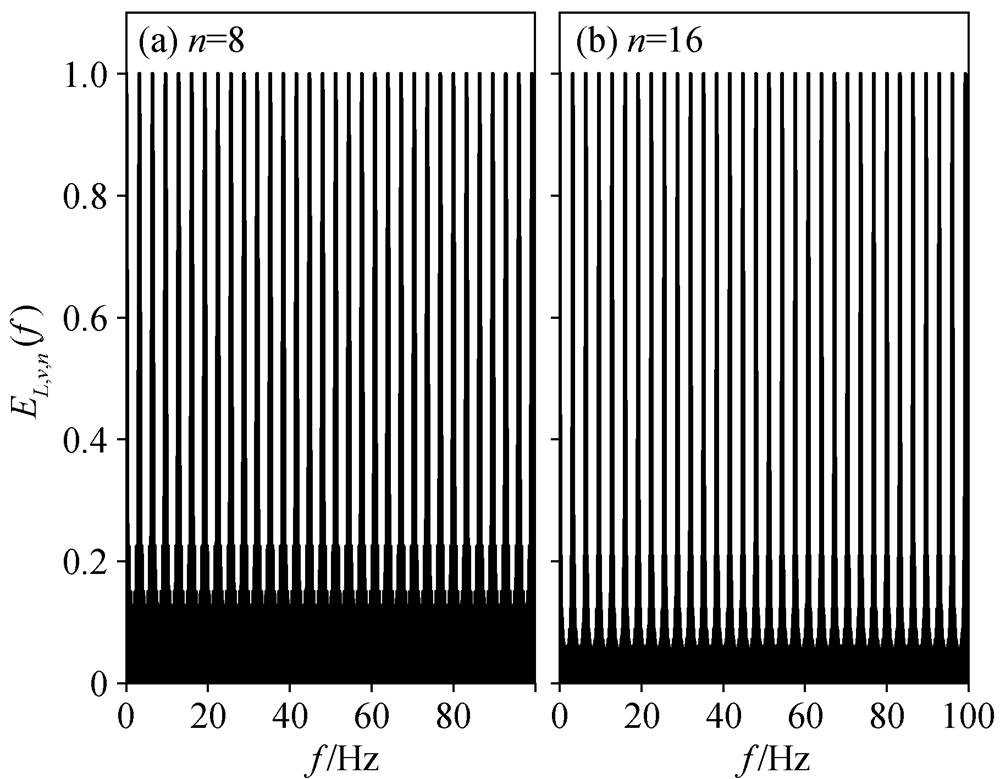
图3 函数EL,v,n(f )的形态
Fig. 3 Schematic diagram of EL,v,n(f)
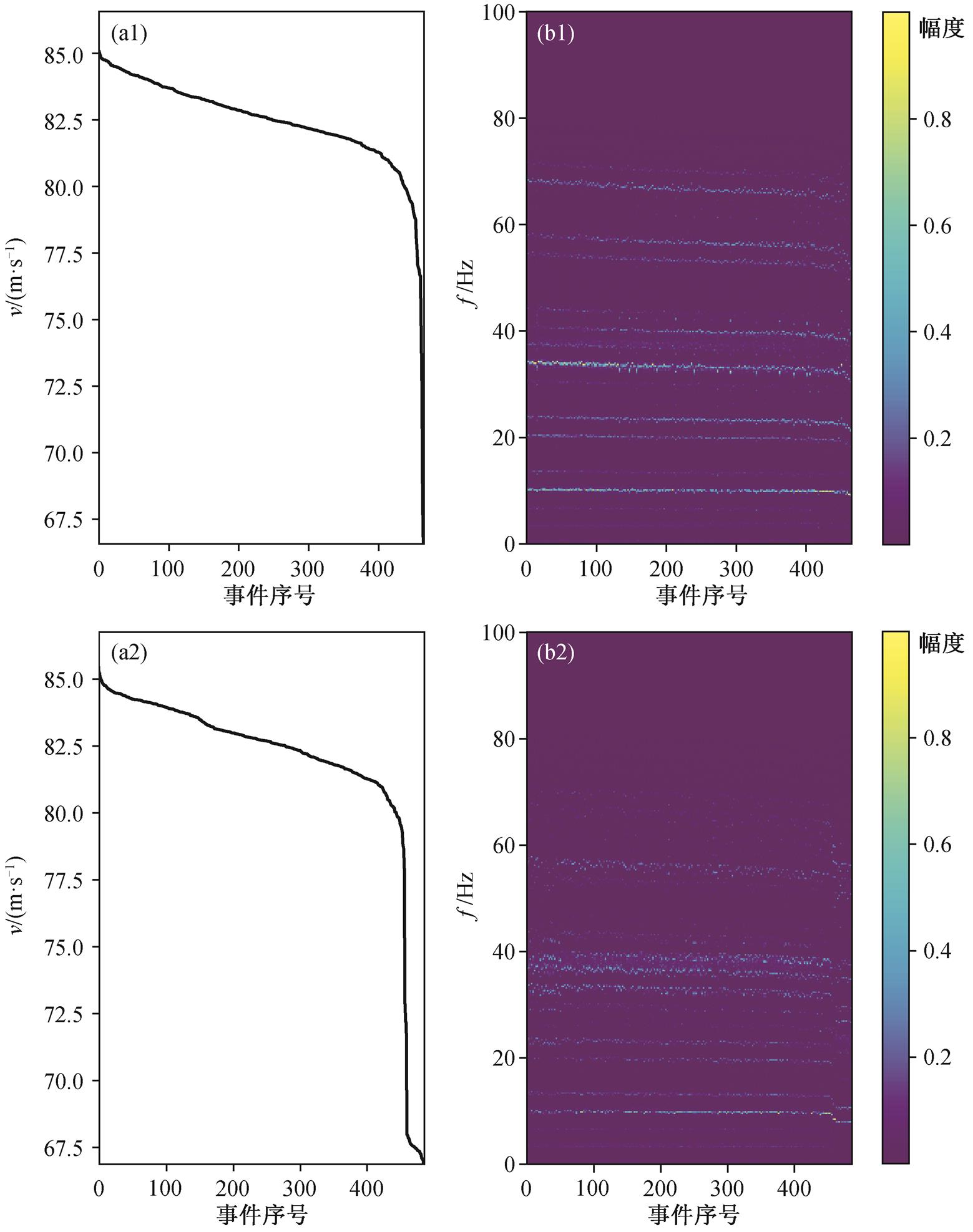
(a1)和(b1)分别为由北至南列车的速度和 Z分量振幅谱; (a2)和(b2)分别为由南至北列车的速度和 Z 分量振幅谱高铁事件按列车速度由高到低排序; 为使彩图在同一色标下尽量展示振幅谱的细节, 将幅度(除以幅度最大值)做归一化, 下同
图4 1号台站上列车速度和台站地震波Z分量的振幅谱
Fig. 4 Train velocity at station 1 and amplitude spectra of the observed Z-component seismic waves
高铁地震记录的频谱表现出分立的模式, 基频大小受速度和车长影响, 其基频和倍频处振幅则随具体的车型、铁轨和路基的变化而变化。因此, 我们通过将不同车速的频谱按基频对齐, 消除车速对频谱的影响, 从而使频谱模式与车型、铁轨和路基的关系更为清晰, 方便后续的聚类研究。
根据各个台站由最大振幅估计的到时差和台站间距离所估算的速度并不准确。如果依照此速度计算的基频来对频谱进行对齐, 高频部分的效果就会比较差。并且, 此处轨道有一个小角度的弯曲, 列车有一个近弯减速和出弯加速的运动过程, 使得对每个台站上速度的估计更为复杂。因此, 我们选择通过频谱分立的峰的位置来确定基频, 并用这个基频与频谱进行对齐。
图 5(a)展示一个 Z 分量高铁地震信号所对应的振幅谱。如果将振幅谱视为“时域”的信号, 再做傅里叶变换, 得到其“振幅谱”, 根据其峰值所处的位置, 就可以确定振幅谱中分立的峰出现的周期, 也就是基频 f0 的倒数。图 5(b)是对图 5(a)的振幅谱做傅里叶变换之后的时域结果。除零频外, 峰值最大的点位于 0.31s 处, 对应于基频 f0 = 3.22Hz。但是, 如果使用这个作为基频, 是不够准确的, 频谱在高频的部分对齐仍然不好。我们发展以下方法, 以期更精确地寻找基频。
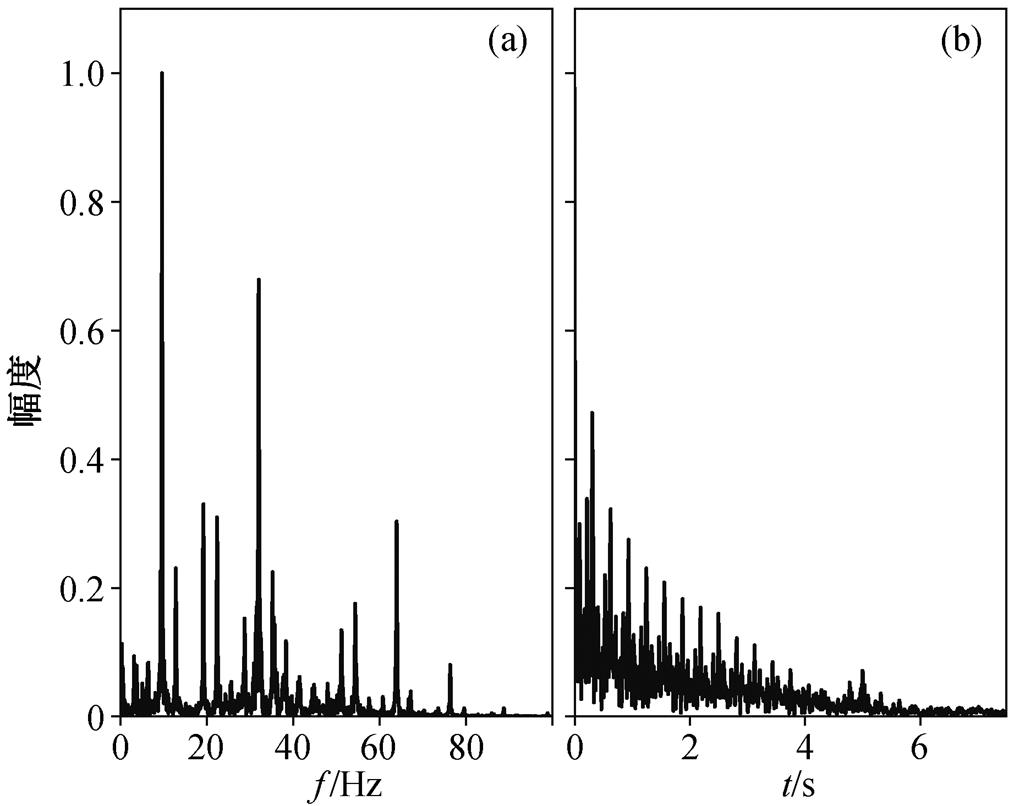
图5 高铁地震信号的振幅谱(a)及对振幅谱做傅里叶变换得到的幅度分布(b)
Fig. 5 Amplitude spectrum of high-speed rail seismic signal (a) and amplitude distribution obtained by Fourier transform on the amplitude spectrum (b)
首先, 使用上面提到的方法, 对高铁信号的振幅谱做傅里叶变换, 确定除零频外的最大峰, 以其倒数为对基频的估计值 f0'; 之后, 在 [f0'−0.2, f0'+ 0.2]范围内搜索使得下式取值最大的频率 f, 作为准确的基频f0:
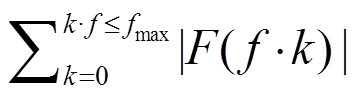 , (6)
, (6)其中, fmax 表示高铁记录的 Nyquist 频率, F 表示实际记录的高铁频谱, | |表示对复数取模。即在 f0'附近寻找一个频率, 使其本身和相应倍频的振幅和最大。当f k没有正好落在频谱的采样频率上时, 可插值或取最邻近频率的幅值。
k没有正好落在频谱的采样频率上时, 可插值或取最邻近频率的幅值。
得到较为精确的基频f0后, 利用式(1)计算列车经过每个台站的速度。为了平稳, 高速列车变速过程比较缓慢。对于高速列车的缓慢变速情况, 我们对每一列的速度进行归一化(v/vref), 由北至南的列车速度除以该列车在 1 号台站的速度(vref=v1), 由南至北的列车除以该列车在 11 号台站的速度(vref = v11)。图 6 为归一化后的速度变化曲线, 可以看出, 由北向南的列车进弯道后都先减速后加速; 由南向北的列车也可以观测到明显的由弯道带来的减速, 但由于出弯的距离不够长, 未能明显地观测到加速。由此可以间接地印证, 我们关于基频的估计是相当准确的, 能反映 5%以内的速度变化。

vref=v1或v11分别为最北边的第1号台站和最南边的第11号台站上列车的速度
图6 归一化后的速度变化
Fig. 6 Change of normalized velocity
得到对基频的估计值后, 我们将原始的频谱伸缩, 使基频变为 3.2Hz。这个频率对应的是之前假设的 25m 车长, 80m/s 运行速度的列车。图 7 是校正之后, 在 1 号台站上观测到的高铁地震信号的振幅谱。可以发现, 不同运行速度的高铁频谱的基频及其倍频已被精确地对齐。
按照基频对齐后的频谱, 不同高铁地震波记录的基频及其倍频被拉伸至同一位置, 消除了速度的影响。频谱基频和倍频的振幅随动车组、铁轨和路基的变化而变化, 是良好的反映高铁运行状态的特征。我们使用 K-Means 算法, 根据这些特征对对齐后的频谱进行聚类, 分析其中蕴含的动车组、铁轨和路基变化的信息。
我们的聚类研究主要从两方面展开: 叠加不同列车的频谱, 可以平均动车组车型对波形的影响, 从而研究铁轨和路基对波形频谱的影响; 叠加同一列车在不同台站上的波形频谱, 可以平均不同铁轨段和路基对波形频谱的影响, 从而研究不同动车组对波形频谱的影响。
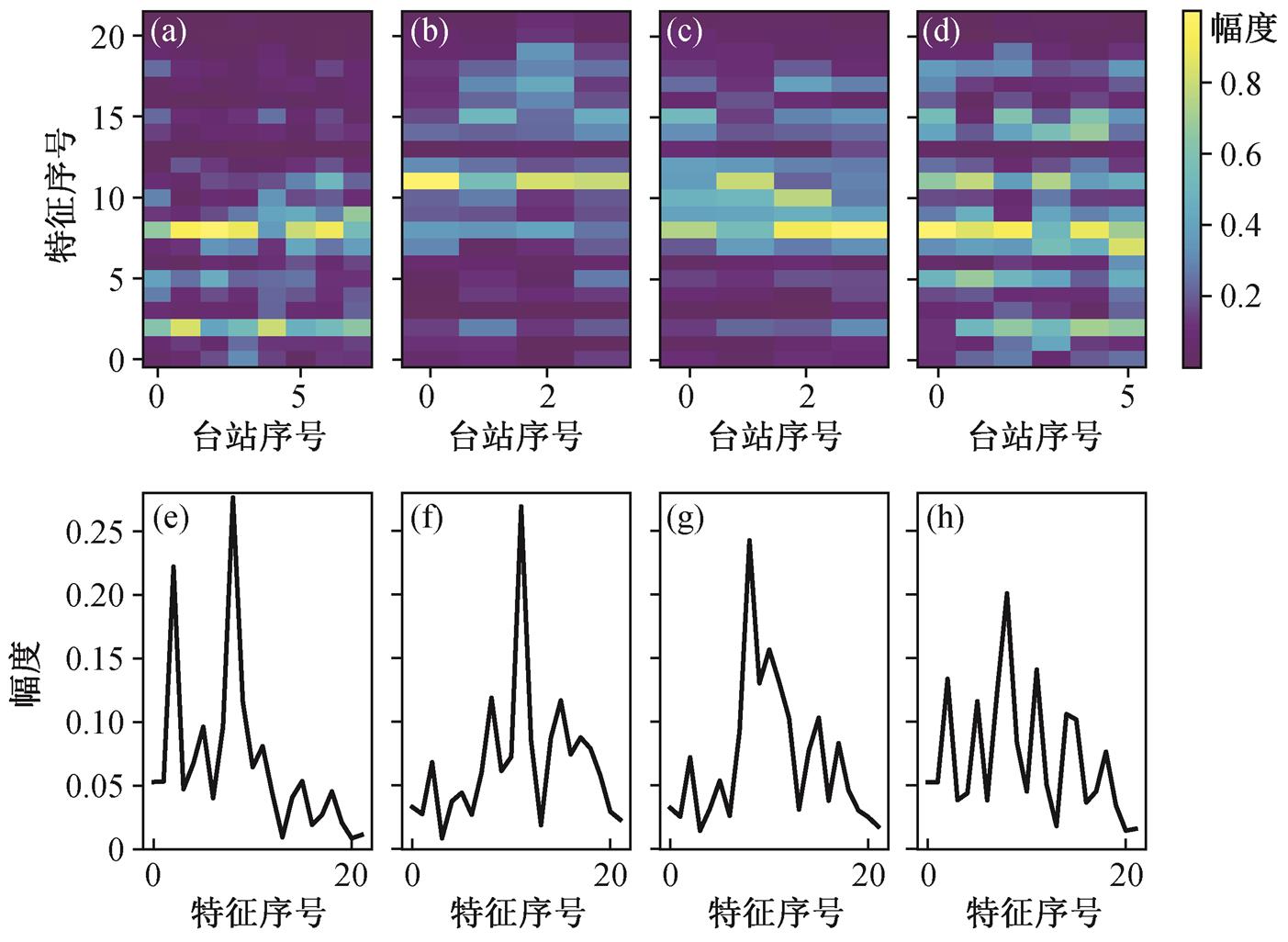
刘磊等[15]使用信号频谱中基频及基频的倍频上的能量作为聚类算法的特征。对于 200Hz 采样率的信号, 其 Nyquist 频率为 100Hz, 对于 3.2Hz 左右基频的信号, 则有 31 个左右的频率被选取为特征。考虑到实际高铁数据的频带分布范围, 我们去掉一些能量较少的频率, 从而减少特征的数量, 使得算法更加稳定。将所有台站上记录到的所有高铁时间对其后的振幅谱叠加起来, 得到如图 8(a)所示的叠加振幅谱。我们仅选取其中能量较高的 22 个峰作为特征频率(3.2, 6.4, 9.5, 12.7, 19.2, 22.4, 25.6, 28.8,32.0, 35.2, 38.3, 41.5, 44.8, 47.9, 51.1, 54.4, 57.6, 60.7, 63.9, 67.2, 70.3和73.5 Hz)。
(a)由北向南的列车; (b)由南向北的列车
图7 1号台站上经过基频校准后的振幅谱
Fig. 7 Amplitude spectra on station 1 after aligning the fundamental frequency
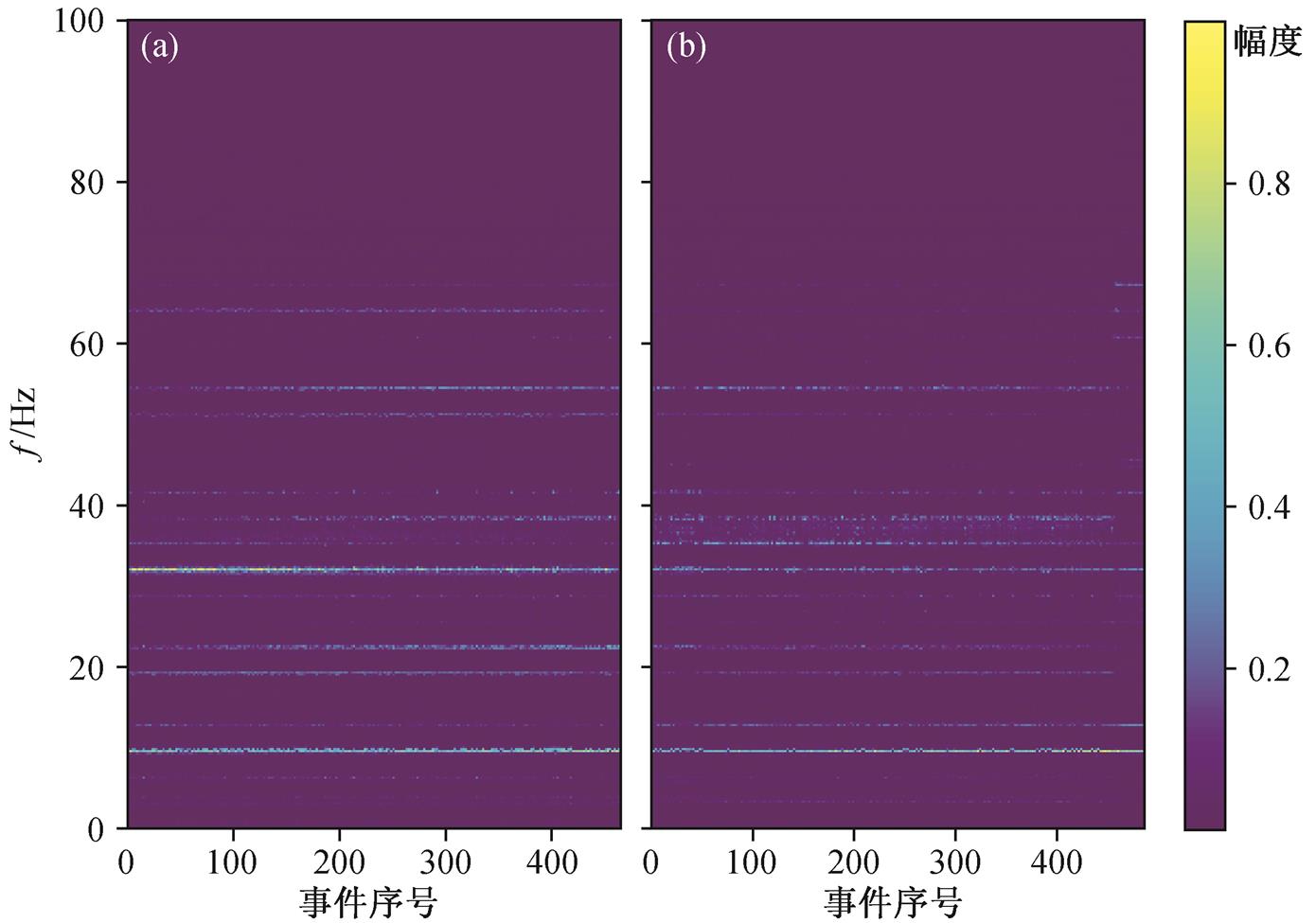
在对齐频谱之后, 我们将同一台站上记录到的高铁信号的振幅谱叠加起来。由北向南和由南向北的高铁运行在不同的铁轨上, 将其频谱分开叠加(图 8(b)和(c)), 可以明显地看出不同台站叠加后的振幅谱存在差异, 甚至对于同一台站, 由北向南和由南向北的列车叠加后的结果也不一致。由于同一台站所处的路基是一样的, 那么南北向列车的波形差异极有可能来自铁轨的差异。我们将同一台站向南向北的列车分开叠加, 共得到 22 组台站频谱, 并取其特征频率上的值进行聚类。
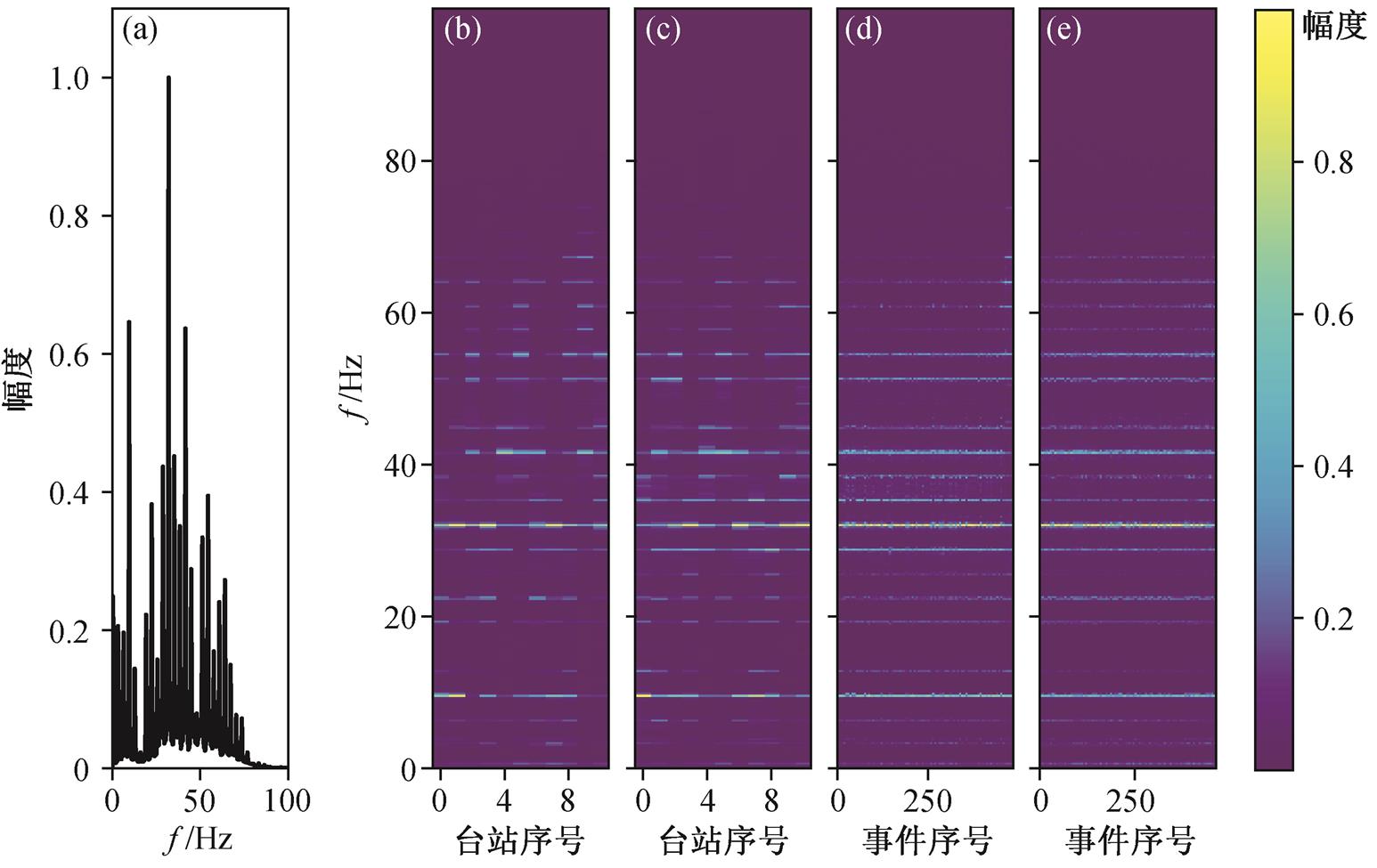
(a)所有台站上所有事件的振幅谱叠加; (b)同一台站上所有由北向南列车的振幅谱叠加, 按台站序号排列; (c)同一台站上所有由南向北列车的振幅谱叠加, 按台站序号排列; (d)对由北向南的一列车, 将其在不同台站上的振幅谱叠加起来, 按事件序号排列; (e)对由南向北的一列车, 将其在不同台站上的振幅谱叠加起来, 按事件序号排列
图8 经过基频校准后叠加的振幅谱
Fig. 8 Stacked amplitude spectra after aligning the fundamental frequency
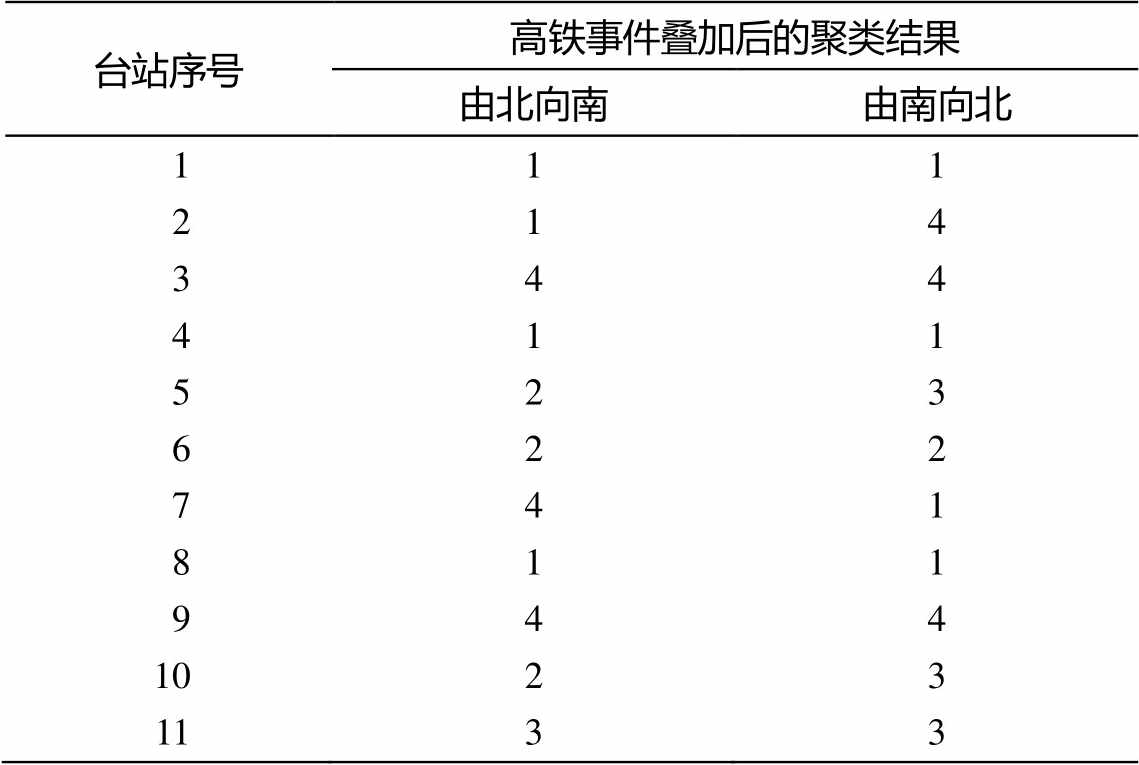
经过实验, 将这 22 组频谱聚类成 4 类, 分别用1, 2, 3 和 4 表示, 结果如表 1 所示。将同一类型的台站的特征值放在一起, 得到图 9(a)~(d), 叠加之后得到图 9(e)~(h)。特征对应的频率越低, 其编号也越小。从图 9 可以看出, 1 类台站的能量主要分布在低频部分, 且集中于两个频率上; 2 类台站的能量主要分布在比 1 类更高的部分, 且集中于一个峰上面; 3类台站的能量集中在一个峰上面, 且这个峰与 1 类台站中的一个相似; 4 类台站的能量分布则较为分散。
表 1 显示, 有 7 个台站, 不论列车运行方向如何, 其聚类结果都一致; 而 2, 5, 7 和 10 号这 4 个台站, 根据列车运行方向的不同, 其聚类结果也不同。同一台站对应的路基应该相同, 其频谱差异可能是南北向铁轨存在的差异造成的。由于缺乏对具体环境下高铁轨道的考察, 目前难以验证这个结论。但是, 不同台站和不同方向上高铁频谱存在的显著差异至少说明高铁地震对所处的铁轨和路基条件十分敏感, 其中蕴含值得进一步挖掘的铁轨和路基信息, 同时也意味着求解高铁地震波场需对铁轨和路基进行细致的建模。
表1 对台站的聚类结果
Table 1 Clustering results of stations
台站序号高铁事件叠加后的聚类结果 由北向南由南向北 111 214 344 411 523 622 741 811 944 1023 1133
将同一列车在不同台站上的振幅谱叠加起来, 得到图 8(d)和(e), 分别对应由北向南和由南向北的列车的特征值分布。可以看出, 南北走向的列车在频谱上还是存在差异的。为了避免这种差异的影响, 我们对南北方向的高铁分别聚类。经过实验, 由北向南的高铁大致可分为两类(记为 1R 和 2R 类), 如图 10 所示; 由北向南的高铁大致可分为 3 类(记为 1L, 2L 和 3L类), 如图 11 所示。
(a)~(d)展示1, 2, 3和4类台站的特征值分布; (e)~(h)为1, 2, 3和4类台站特征值叠加后的结果, 为方便比较, 折线图未做归一化处理, 下同
图9 对台站的聚类结果及其特征
Fig. 9 Clustering result of stations and their characters
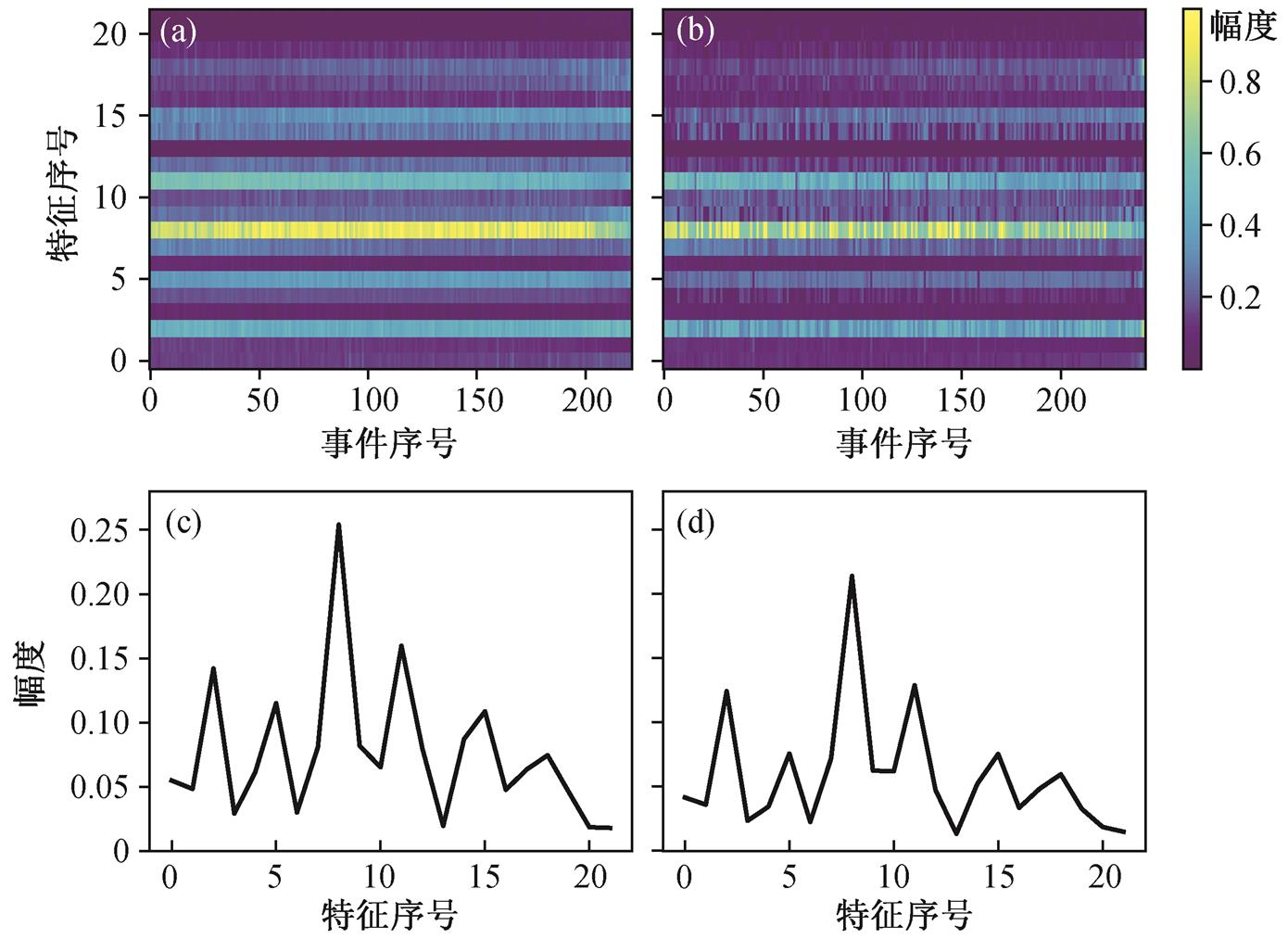
(a)和(b)分别展示1R类和2R类动车组的特征值分布; (c)和(d)分别为1R类和2R类动车组特征值叠加后的结果
图10 对由北向南的动车组的聚类结果及其特征
Fig. 10 Clustering results of trains from north to south and their characters
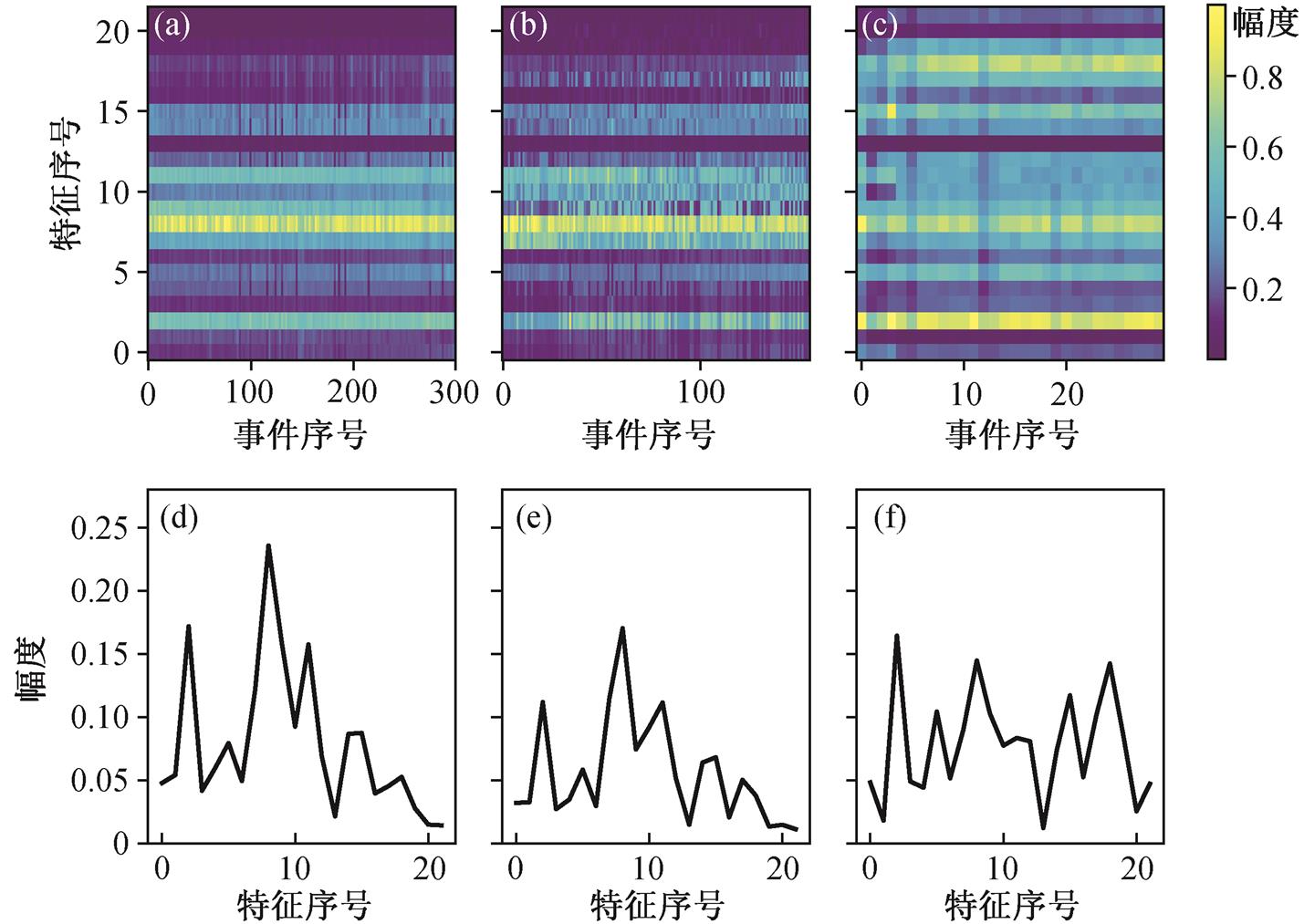
(a), (b)和(c)分别展示 1L类、2L类和3L类动车组的特征值分布; (d), (e)和(f)分别为 1L类、2L 类和 3L 类动车组特征值叠加后的结果
图11 对由南向北的动车组的聚类结果及其特征
Fig. 11 Clustering results of trains from south to north and their characters
由北向南的聚类结果中, 两类频谱的差异主要体现在低频的两个峰值大小差异, 但总体上比较相似。由南向北的聚类结果中, 1L 和 2L 的频谱特征较为接近, 其差异主要体现在能量向前两个峰的集中程度; 3L 类的频谱与前两类相差较大, 在全频率都有能量分布。
按照之前的假设, 不同台站叠加后的频谱应该反映动车组的特征。那么在不同的日期, 相同的车次应具有相同的车型, 则相应的几个高铁记录应被划分为同一类别。同一台站上, 每天同一时刻附近, 都有一辆同向的车出现, 则可以认为这些车很有可能属于同一车次, 我们据此在 11 天的高铁地震资料中将不同日期记录到的高铁和车次对应上。不同日期的同一时刻附近(2 分钟内), 至少出现 4 次同向列车, 则认为这些车属于同一车次。我们共找到 48 个由北向南的车次和 49 个由南向北的车次。
在 48 个由北向南的车次中, 相同车次的列车都被划为同一类别的有 47 个; 在 49 个由南向北的车次中, 相同车次的列车都被划为同一类别的有 41个。不同日期属于同一车次的绝大多数高铁记录都被划分为同一类, 说明同一辆动车的频谱特征较为稳定, 而这种稳定的频谱特征可能与车型相关。
为了进一步探究聚类结果与车型的关系, 需要将车次与相应的车型对应起来。对在保定东站停车的高铁, 可以查询到不同车次较为准确的出发和到达时间; 对于途径保定东站不停车的高铁, 估算到达或驶离保定东站的时刻比较困难, 本文暂不考虑。台站距保定东站约 36km, 考虑 25km 的加速或减速区间, 结合高铁通过台阵的速度, 可以估算高铁驶入或驶出保定东站的列车时刻。如果这个时刻和保定东站的列车时刻表一致, 就可以确定车次的具体名称。经筛查, 我们匹配了由北向南的 19 个车次; 由南向北的高铁中, 估计的经过保定东站的时刻常常处于时刻表上两个相近车次之间, 而估计精度不足以在两个车次之间做出判断, 有效的匹配结果较少。因此, 本文主要讨论由北向南的动车组的聚类结果与车型的关系。
确定车次后, 我们根据《中国动车组交路数据查询软件(2018.05.20 版)》(https://m.weibo.cn/2646 253421/4241845598545811)查询对应车次的车型, 结果列于表 2。除 G523 次高铁外, 1R 类对应的主要车型是 CRH380A、CRH380A 统型重联、CR400AF重联和 CRH380A 统型, 2R 类对应的主要车型是CRH380AL 和新 CRH380AL。可以看出, 聚类结果非常稳定, 在绝大多数情况下正确地区分了两大类车型, 说明这两大类车型的频谱存在稳定的差异。
由南向北的列车聚类结果中,3 L 类出现较少, 主要集中在 5:54 和 6:13 两个时间点, 我们推测应该属于动卧车型。虽然无法确定具体车次, 但动卧车型主要为 CRH2E, 以日本的新干线列车为原型研发, 而白天运行的 CRH380A 和 CR400AF 重联等车型由中国中车及其旗下企业研发, 在车身结构、动力学特点和编组上有一定的差异, 这可能是 3L 类的频谱与1L和2L类差距较大的原因。
对动车组的聚类结果表明, 相同车型的列车所激发的高铁地震波具有稳定的频谱模式; 不同车型之间, 频谱模式存在稳定的差异, 这种差异足以从频谱特征上准确地对二者加以区分。如果能借助更密集、精细的观测手段和更丰富的处理手段, 有望获得更精确的频谱模式, 并分析其中包含的动车组信息。同时, 这种稳定的与车型相关的频谱模式有助于进一步理解高铁地震激发的过程, 为我们将同一车型的频谱叠加起来以提高信噪比, 并研究其中包含的其他信息提供了支持。
考虑到中国动车组交路数据查询软件(2018.05. 20 版)并非铁道部门提供的官方软件, 今后还需要与铁道部门沟通, 争取获得更精准的信息, 不过这并不影响本文的结论。在实际应用中, 可以采用同一动车组频谱特征, 也可以采用同一方向、同一车型动车的频谱特征进行高铁安全监控。
表2 由北向南的动车组聚类结果、车次和车型
Table 2 Clustering results, train number and train type of trains from north to south
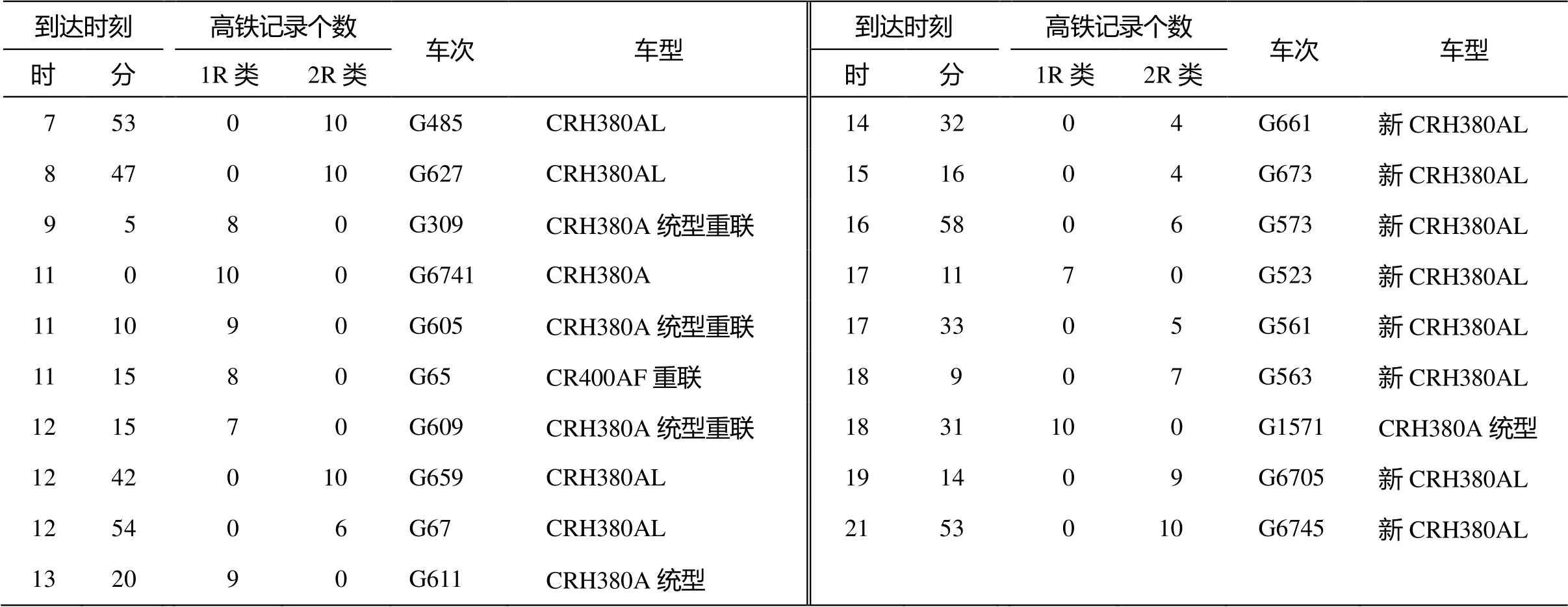
到达时刻高铁记录个数车次车型到达时刻高铁记录个数车次车型 时分1R类2R类时分1R类2R类 753010G485CRH380AL143204G661新CRH380AL 847010G627CRH380AL151604G673新CRH380AL 9580G309CRH380A统型重联165806G573新CRH380AL 110100G6741CRH380A171170G523新CRH380AL 111090G605CRH380A统型重联173305G561新CRH380AL 111580G65CR400AF重联18 907G563新CRH380AL 121570G609CRH380A统型重联1831100G1571CRH380A统型 1242010G659CRH380AL191409G6705新CRH380AL 125406G67CRH380AL2153010G6745新CRH380AL 132090G611CRH380A统型
说明: “到达时刻”是由到时和速度估算的到达保定东站的时刻。
结合前面对台阵和动车组聚类结果的分析, 我们有理由相信, 随着进一步深入研究, 将有望从中提取出更加精确的不同车型、铁轨和路基所对应的频谱模式; 当动车组状态、铁轨或路基等发生变化时, 频谱模式也会变化; 借助对频谱模式的实时监测, 可以及时发现高铁运行状态的变化, 为安排更为细致的排查和检修提供可能。
基于对高铁近场地震信号频谱的分析和聚类研究, 本文得到如下结论。
1)高铁地震信号的频谱主要由等间距分立的峰构成, 其基频与列车运行速度和车厢长度有关。
2)借助对高铁近场地震信号的频谱基频的精确测量, 可以很好地估计列车的运行速度, 并可据此对齐基频, 消除列车速度对频谱的影响。
3)以对齐基频后的频谱为基础的聚类分析结果表明, 近场台站所记录的高铁地震信号中, 当铁轨、路基和车组不同时, 频谱模式明显不同; 铁轨、路基和车组相同时, 则频谱模式具有稳定特征。
4)借助这种稳定的频谱模式, 检测其随时间的变化, 将来或有可能用于高铁运行安全监控。
致谢 感谢中国科学院地质与地球物理研究所李幼铭研究员及高铁地震学联合研究组对本研究的大力支持。感谢长安大学包乾宗教授在数据采集过程中提供的大力帮助。感谢南方科技大学陈永顺教授研究组提供部分观测仪器。
参考文献
[1]丁辉, 邢晓东. 整列地坑式架车机在我国高速列车检修中的运用. 机车电传动, 2012(2): 31-33
[2]李智敏, 苟先太, 秦娜, 等. 高速列车振动监测信号的频率特征. 仪表技术与传感器, 2015(5): 99-103
[3]何华武. 高速铁路运行安全检测监测与监控技术. 中国铁路, 2013(3): 1-7
[4]Ditzel A, Herman G C, Holscher P, et al. Elastic waves generated by high-speed trains. Journal of Computational Acoustics, 2001, 9(3): 833-840
[5]陈棋福, 李丽, 李纲, 等. 列车振动的地震记录信号特征. 地震学报, 2004(6): 651-659
[6]李丽, 彭文涛, 李纲, 等. 可作为新震源的列车振动及实验研究. 地球物理学报, 2004, 47(4): 680-684
[7]和振兴, 翟婉明. 高速列车作用下板式轨道引起的地面振动. 中国铁道科学, 2007, 28(2): 7-11
[8]翟培合, 韩忠东, 李丽, 等. 运行列车振动产生的瑞雷波特征及数据分析. 噪声与振动控制, 2008, 28(1): 18-21
[9]徐善辉, 郭建, 李培培, 等. 京津高铁列车运行引起的地表振动观测与分析. 地球物理学进展, 2017, 32(1): 421-425
[10]El Kacimi A, Woodward P K, Laghrouche O, et al. Time domain 3D finite element modelling of train-induced vibration at high speed. Computers & Stru-ctures, 2013, 118: 66-73
[11]Cai Y, Sun H, Xu C. Three-dimensional analyses of dynamic responses of track-ground system subjected to a moving train load. Computers & Structures, 2008, 86(7/8): 816-824
[12]Fu Q, Zheng C. Three-dimensional dynamic analyses of track-embankment-ground system subjected to high speed train loads. The Scientific World Journal, 2014 (4): 924592
[13]Sussmann T R, Thompson H B, Stark T D, et al. Use of seismic surface wave testing to assess track substructure condition. Construction and Building Materials, 2017, 155: 1250-1255
[14]曹健, 陈景波. 移动线源的 Green 函数求解及辐射能量分析: 高铁地震信号简化建模. 地球物理学报, 2019, 62(6): 2303-2312
[15]刘磊, 蒋一然. 大量高铁地震事件的属性体提取与特性分析. 地球物理学报, 2019, 62(6): 2313-2320
[16]张唤兰, 王保利, 宁杰远, 等. 高铁地震数据干涉成像技术初探. 地球物理学报, 2019, 62(6): 2321-2327
[17]王晓凯, 陈文超, 温景充, 等. 高铁震源地震信号的挤压时频分析应用. 地球物理学报, 2019, 62(6): 2328-2335
[18]王晓凯, 陈建友, 陈文超, 等. 高铁震源地震信号的稀疏化建模. 地球物理学报, 2019, 62(6): 2336-2343
[19]张固澜, 何承杰, 李勇, 等. 高铁地震震源子波时间函数及验证. 地球物理学报, 2019, 62(6): 2344-2354
Spectral Characteristics of High-Speed Rail Seismic Signal under Viaduct
Abstract Employing a total of 10461 seismic records induced by 951 high-speed trains recorded by 11 short-period stations of a temporary array deployed by Peking University under the high-speed railway viaduct, we observe how the spectral characteristics vary with the speed and model of the train as well as the rail and groundsill by using a clustering algorithm K-Means. For a high-speed train in uniform motion, the spectrum of the produced seismic wave is mainly composed of nearly equally spaced peaks and its fundamental frequency is equal to the ratio of the train speed to the carriage length. By aligning the fundamental frequency, the influence of the train speed is reduced to make the spectrum pattern time-independent and easy for comparison. Clustering results show that the spectra of the high-speed rail seismic events have stable patterns when the train model, rail and groundsill conditions keep the same; the stable spectrum patterns change significantly with the change of the train model, rail and groundsill conditions. The monitoring of the stable spectral characteristics might possibly be used in safety control of high-speed rail.
Key words high-speed rail; seismic source; spectrum; clustering algorithm
修回日期: 2019-08-14
收稿日期: 2019-07-17;
doi: 10.13209/j.0479-8023.2019.072
国家自然科学基金(41874071)资助