, (1)摘要 利用同步挤压小波变换方法, 对河北保定和广东深圳地区实测的高铁地震信号进行时频谱分析。结果表明, 高铁在经过高架桥时, 在其附近产生的地震信号中低频信息比通过隧道和接触地表运行产生的地震信号丰富。利用高铁地震信号的时频谱特性, 可以确定高铁运行速度的变化。
关键词 高铁地震; 时频分析; 同步挤压小波变换; 分立谱
在地震监测等传统地震学研究中, 将列车振动视为有害噪声的主要来源, 地震监测仪通常避开在铁路附近的场地布设[1]。我国规定, 如果铁路与地震监测仪位于差别很大的地质结构体上, 或中间有山脉或冲击谷地相隔, 地震台站对铁路的避让距离是 3km; 如果铁路与地震监测仪位于相同的地质结构体上, 并且中间无山脉或冲击谷地相隔, 地震台站对铁路的避让距离是 5km[2]。
以往对列车振动的研究集中在其对地震台站监测的干扰以及对铁路附近建筑物的破坏方面, 很少将列车振动视为一种震源, 用于探测地下结构的研究。当前对列车振动的研究, 目的是更好地理解列车振动的产生和短程传播机制, 主要用于解决铁道附近建筑物的安全问题。Ditzel 等[3]提出一种基于动车响应积分表示来计算动车位移的新方法, 并进行理论模型模拟, 结果与实测动车振动记录比较吻合。Wu 等[4]研究了多轮轨结构的相互作用对高频轨道振动记录的影响。Kaynia 等[5]归纳了瑞典南部高速列车引起的路基和铁路路堤振动响应的测试方案以及为预测路堤和地基响应而建立的数值预测模拟模型, 利用预测模型提出一种有效的地面振动补偿措施。Degrande 等[6]测量了运行于巴黎-布鲁塞尔-阿姆斯特丹-科隆间的国际高速列车以 223~314km/h 的速度通过铁轨时的自由振动和轨道响应。陈棋福等[7]对大秦铁路怀柔段的观测试验记录进行初步分析, 表明列车振动具有频谱较宽、重复性好和稳定性强等优点, 认为列车振动是浅层结构成像的潜在震源。Fuchs 等[8]分析了高灵敏度宽带传感器测量的列车振动, 观察到列车振动中等距谱线的显著特征, 指出以连续转向架为主导结构的准静态轴向载荷是等距谱线的主要原因。徐善辉等[9]通过对京津高铁地震信号的观测, 讨论高铁地震信号与列车车次、运行速度和观测位置之间的关系。
现有的研究结果使人们逐渐认识到, 高铁振动作为一种震源, 具备检测高铁运行安全和探测地下结构的巨大潜力。高铁地震联合研究组于 2018 年开始相应的数据观测和研究工作, 北京大学宁杰远研究组在广东深圳和河北保定地区布置多期观测任务, 为后续的研究提供重要的数据支持。曹健等[10]将高铁震源简化成一个移动的线源, 并给出在该震源作用下弹性半空间和全空间的 Green 函数。刘磊等[11]对深圳观测数据中 4500 余条高铁地震信号进行属性提取和聚类分析, 结果表明高铁震源的可重复性高, 不同观测点接收到的信号对高铁运行地质环境变化的敏感程度比较高。张唤兰等[12]对高铁地震数据干涉成像技术做了初步探索。王晓凯等[13-14]利用挤压短时傅里叶变换, 研究高铁地震信号的分立谱特征及其与列车车厢长度和运行速度之间的关系, 并利用形态成分分析方法实现地震信号的稀疏化建模。张固澜等[15]给出一种高铁地震震源子波的时间函数。
本文基于王晓凯等[13]的研究, 利用同步挤压小波变换, 对深圳和保定地区的观测数据进行挤压时频分析, 对比分析高铁列车通过隧道、高架桥梁等运行环境时地震信号的时频谱特征, 为进一步认识高铁地震信号的产生机理和后续应用提供参考。
2011 年, Daubechies 等[16]提出同步挤压小波变换。首先, 对时域信号 s(t)进行连续小波变换:
, (1)其中, 
为小波系数, a为尺度因子, b表示时移因子, 
为母小波函数的共轭。
令
。根据 Plancherel 定理, 式(1)可以写为
, (2)其中, 
表示角频率, 
和
分别是信号
和
的傅里叶变换。又因的傅里叶变换为
, (3)
将式(3)带入式(2)可得
。 (4)若
在负频率域趋于零, 且集中分布在
(为信号 s(t)的角频率)处, 则小波系数
在时间尺度平面内集中分布在尺度
附近。
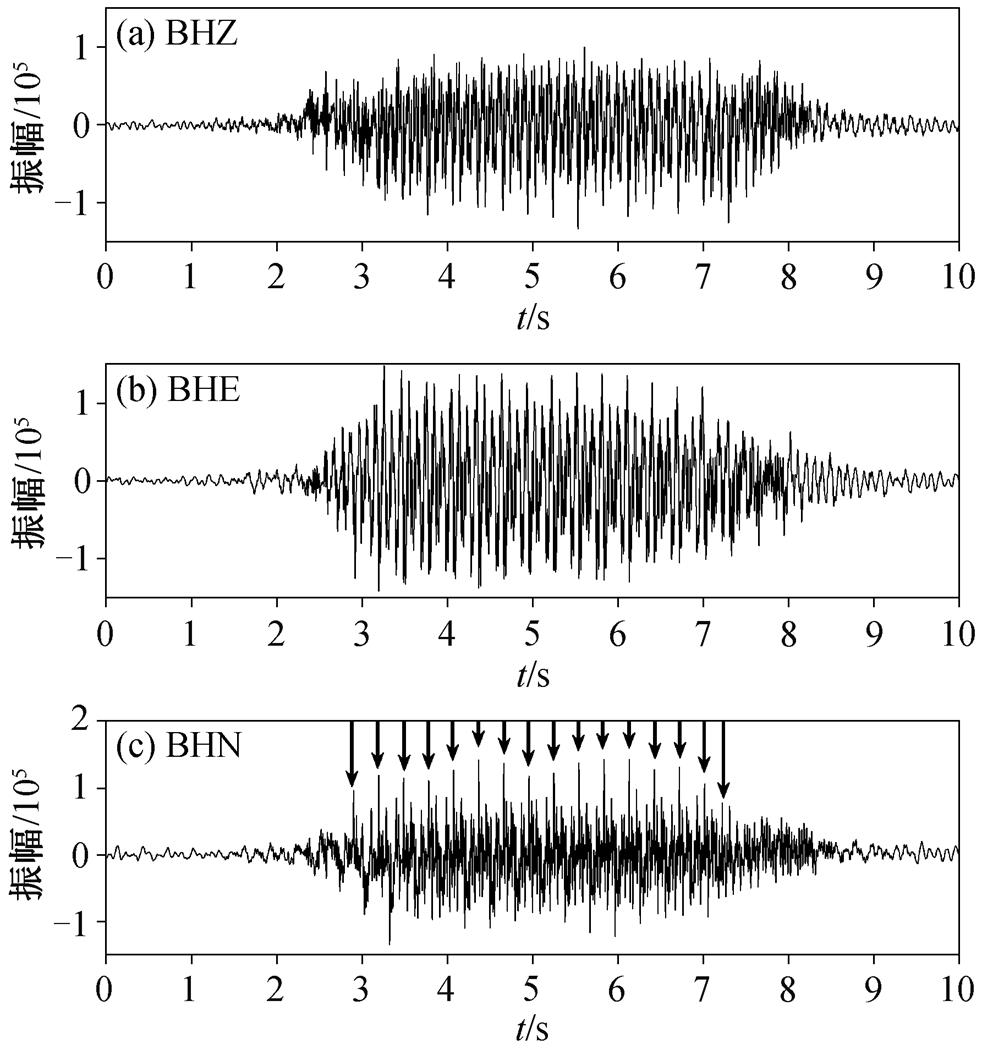
图1 列车经过时PKU21台站接收的三分量高铁地震信号
Fig. 1 Three-component high-speed train seismic signals received by PKU21 station when the train passed
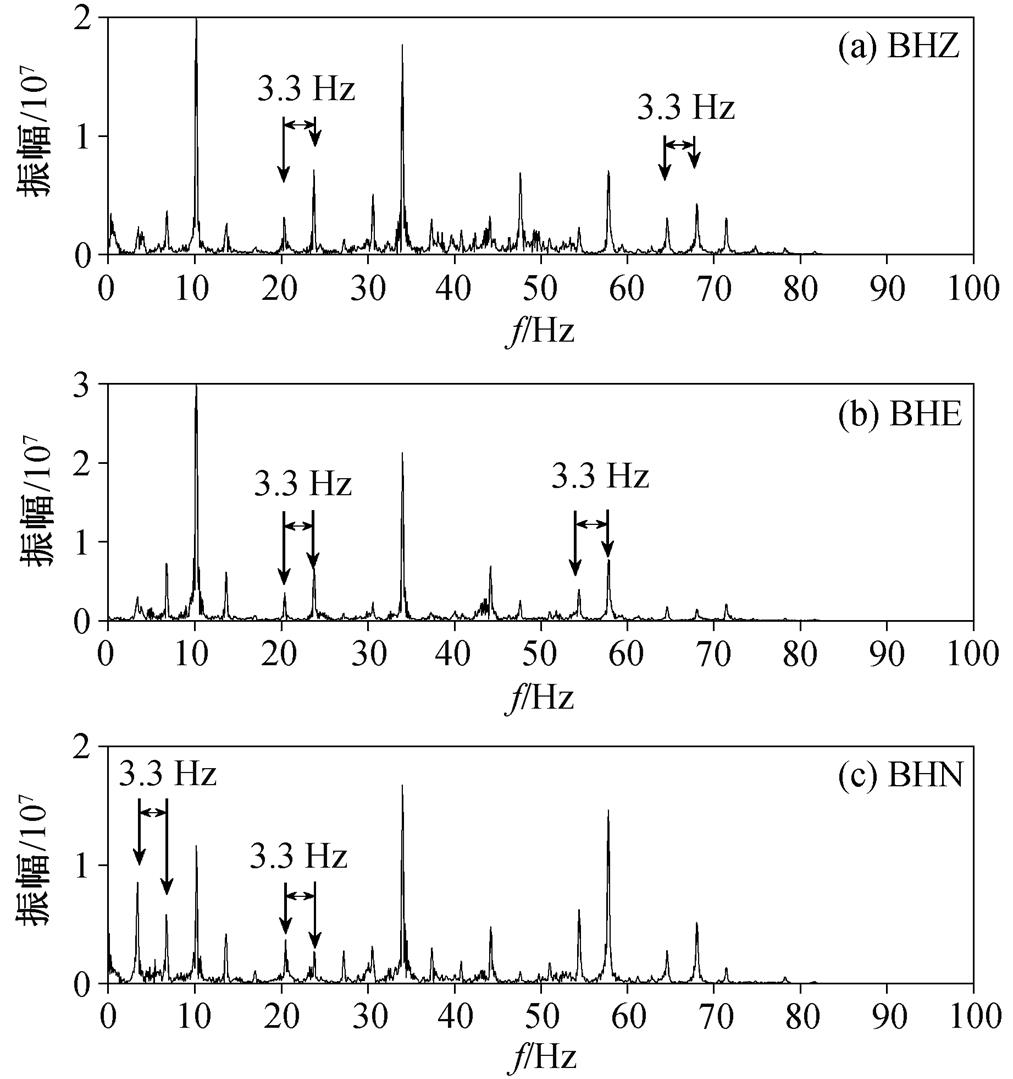
图2 图1中三分量高铁地震信号的振幅谱
Fig. 2 Amplitude spectra of three-component high-speed train seismic signals in Fig. 1
图3 图1中三分量高铁地震信号的同步挤压小波变换时频谱
Fig. 3 Synchrosqueezing wavelet transform spectra of three-component high-speed train seismic signals in Fig. 1
通过对小波系数求偏导, 可以估计瞬时频率:
(5)通过式(5), 将小波系数从时间-尺度平面
转换到时间-频率平面
, 即转变为
。小波系数的同步挤压变换量
可由挤压其中任意一个中心频率
附近区间
的值来获得(其中
)。同步挤压变换量可写成如下形式:
(6)
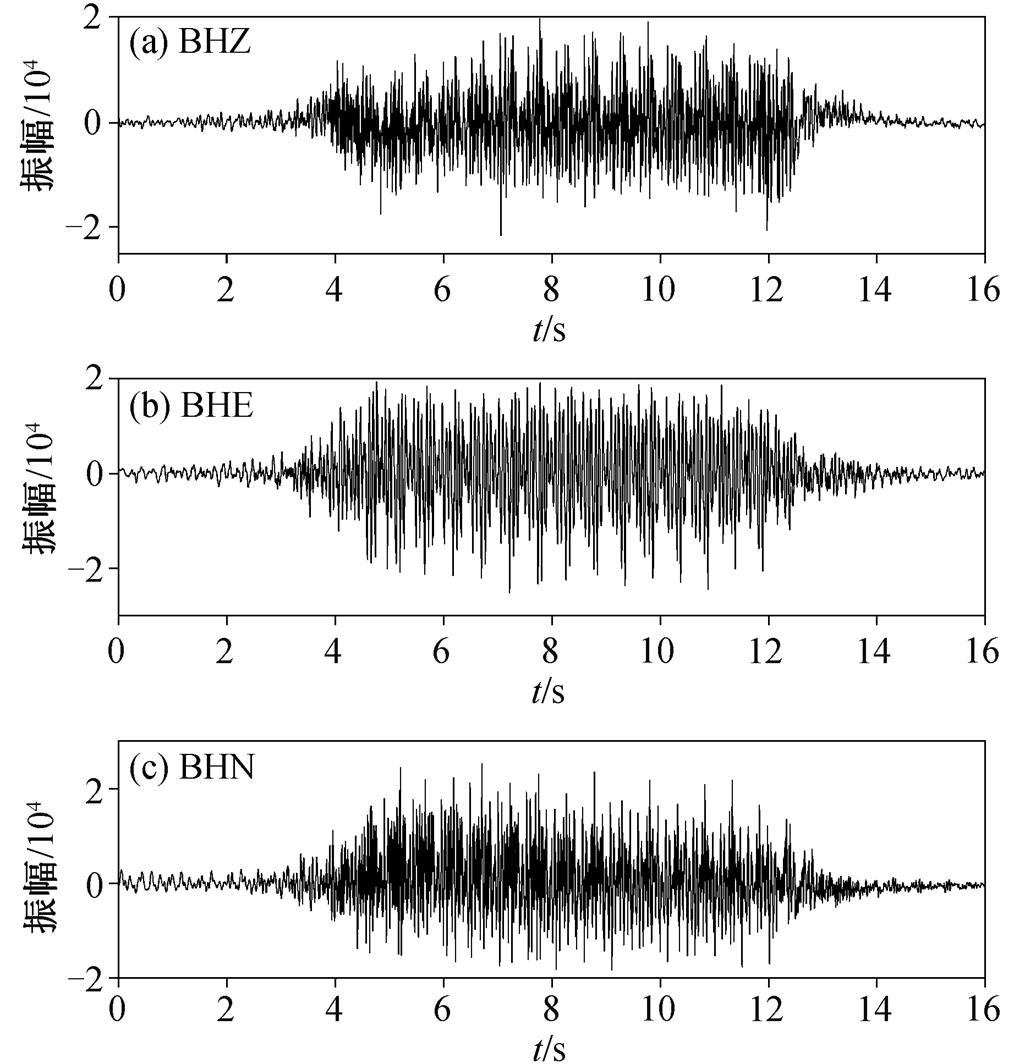
图4 列车经过时BS005台站接收的三分量高铁地震信号
Fig. 4 Three-component high-speed train seismic signals received by BS005 station when the train passed
式中, 
为离散尺度, 
, 则同步挤压小波变换的反变换式为
图5 图4中三分量高铁地震信号的振幅谱
Fig. 5 Amplitude spectra of three-component high-speed train seismic signals in Fig. 4
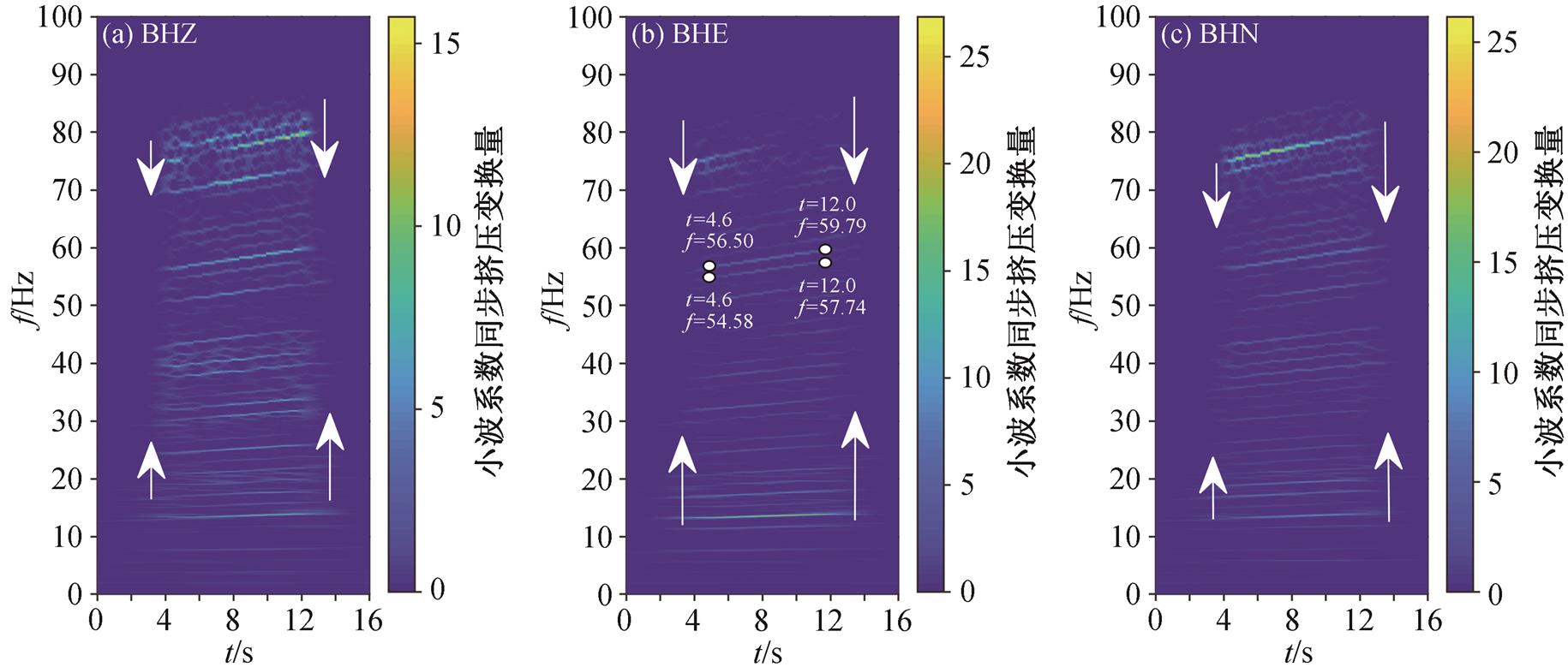
图6 图4中三分量高铁地震信号的同步挤压小波变换时频谱
Fig. 6 Synchrosqueezing wavelet transform spectra of three-component high-speed train seismic signals in Fig. 4
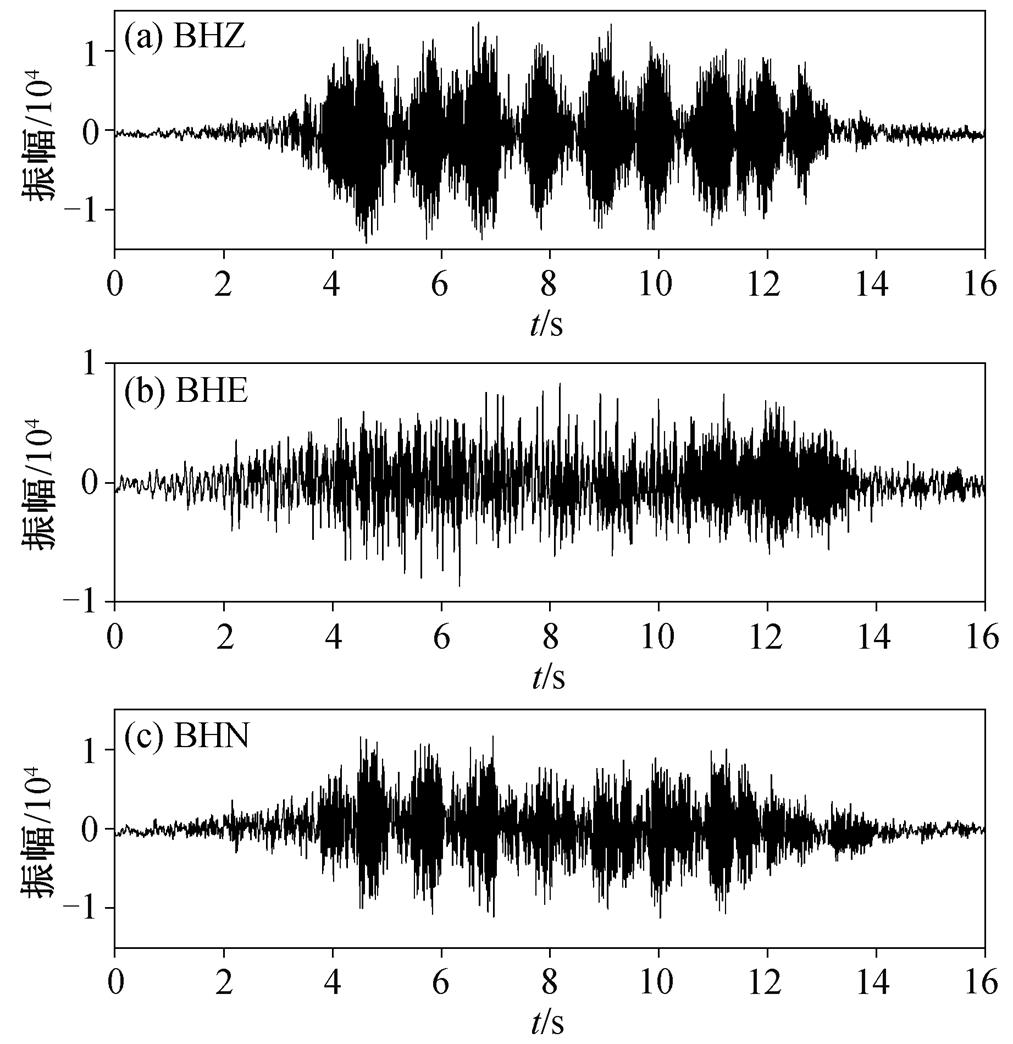
图7 列车经过时BS005台站接收的三分量高铁地震信号
Fig. 7 Three-component high-speed train seismic signals received by BS005 station when the train passed
图8 图7中三分量高铁地震信号的振幅谱
Fig. 8 Amplitude spectra of three-component high-speed train seismic signals in Fig. 7
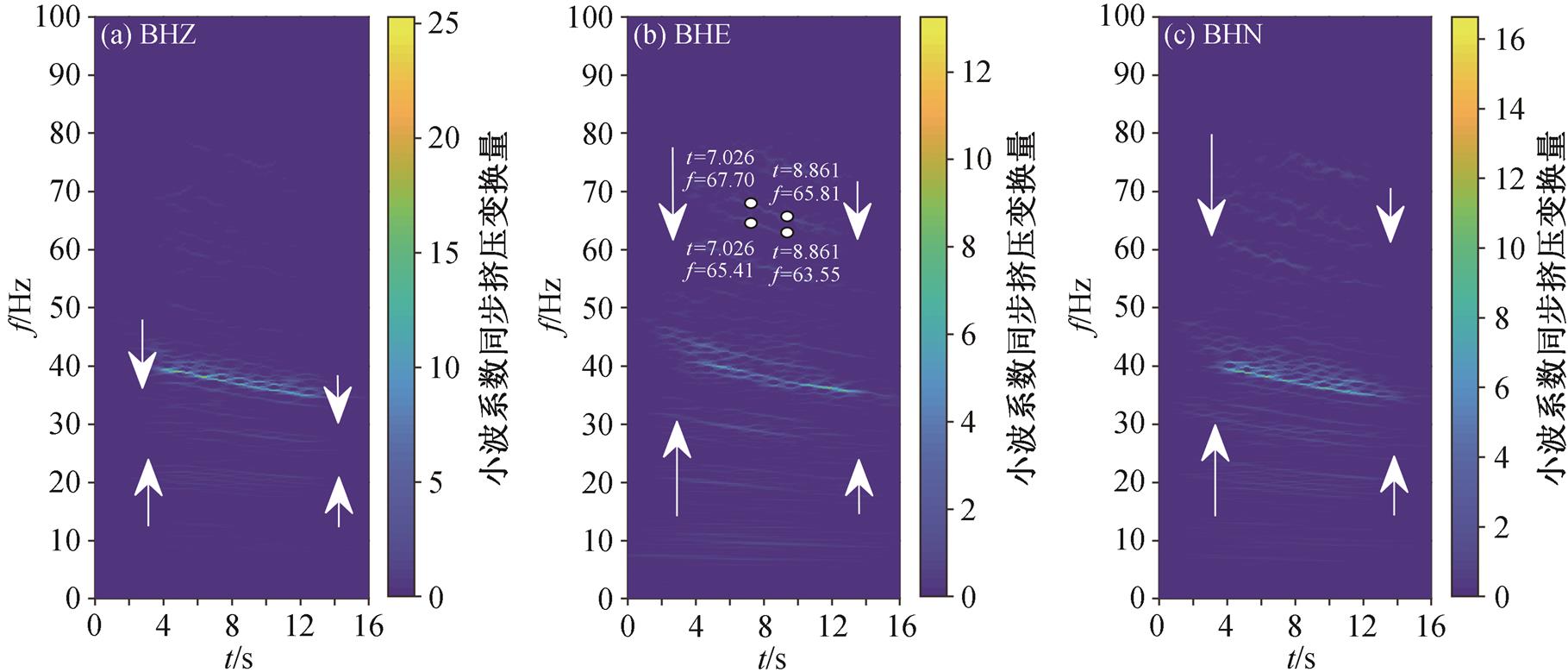
图9 图7中三分量高铁地震信号的同步挤压小波变换时频谱
Fig. 9 Synchrosqueezing wavelet transform spectra of three-component high-speed train seismic signals in Fig. 7
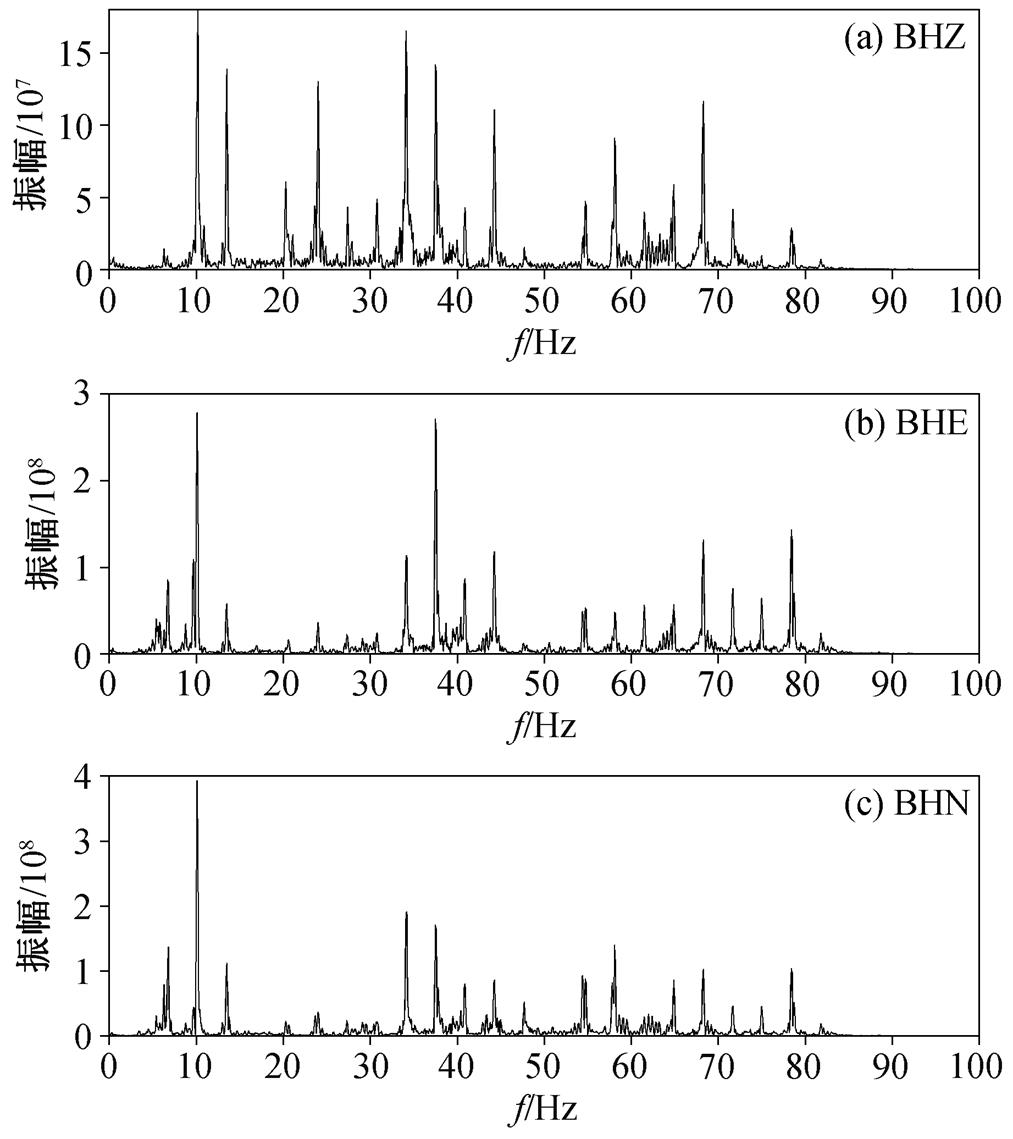
图10 G6019经过时M028台站接收的三分量高铁地震信号振幅谱
Fig. 10 Amplitude spectra of three-component high-speed train seismic signals received by M028station when G6019 passed
, (7)式中,
, 
表示取实部, 表示母小波函数的共轭傅里叶变换。
本研究选用保定地区和深圳地区短周期三分量地震监测仪的观测数据。在保定地区选择两条列车运行路段, 其中一条为高铁线路, 列车在高架桥上运行; 另一条为经过白洋淀火车站的铁路线, 因在车站附近, 列车主要在地表运行。在深圳地区选择一段高铁线路, 运行环境包括高架桥和隧道。
首先选取保定地区的高架桥桥墩附近 PKU21台站采集的高铁地震信号进行分析。图 1(a)~(c)分别为垂直分量(BHZ 分量)、东西分量(BHE 分量)和南北分量(BHN 分量)的高铁地震信号, 可以看出, 信号的 3 个分量在一定程度上具有相似性。从图 1 (c)可以看出, 相邻两个箭头处的时间间隔均约为0.3s, 反映该段波形的周期性现象。图 1(c)中指示信号周期的箭头数量为 16 个, 正好对应列车的 16节车厢数。因此可以认为, 该辆列车每 0.3 s 刚好通过一节车厢, 而我国动车组车厢的长度约为 25m, 这样可以求得速度 v = 25/0.3m/s ≈ 83.3m/s, 即约 300km/h。图 2(a)~(c)分别为图 1(a)~(c)中信号对应的振幅谱, 可以看出, 该段数据低频信息比较丰富, 主要能量分布在 3~80Hz, 分立谱的谱线之间距离几乎相等, 近似为 3.3Hz, 而 1/3.3Hz ≈ 0.3s 又正好与周期时间相对应。依据王晓凯等[13]的研究, 可知高铁列车在此区间的运行速度约为 300km/h, 与从时间域分析得到的运行速度一致。但是, 仅从时间域或频率域分析地震信号, 不能很好地反映地震信号随时间的变化情况及高铁的运行动态。为了更清晰地刻画高铁地震信号的时频特性, 本文用同步挤压小波变换对其进行计算和分析。图 3 为同步挤压小波变换时频谱, 也显示明显的分立谱特性。从图 3 (a)~(c)可以看出, 时频谱的分立谱线间距近似为3.33Hz, 且时频谱中的分立谱线与时间轴方向几乎平行, 表明高铁在此时段内运行是近似匀速状态。
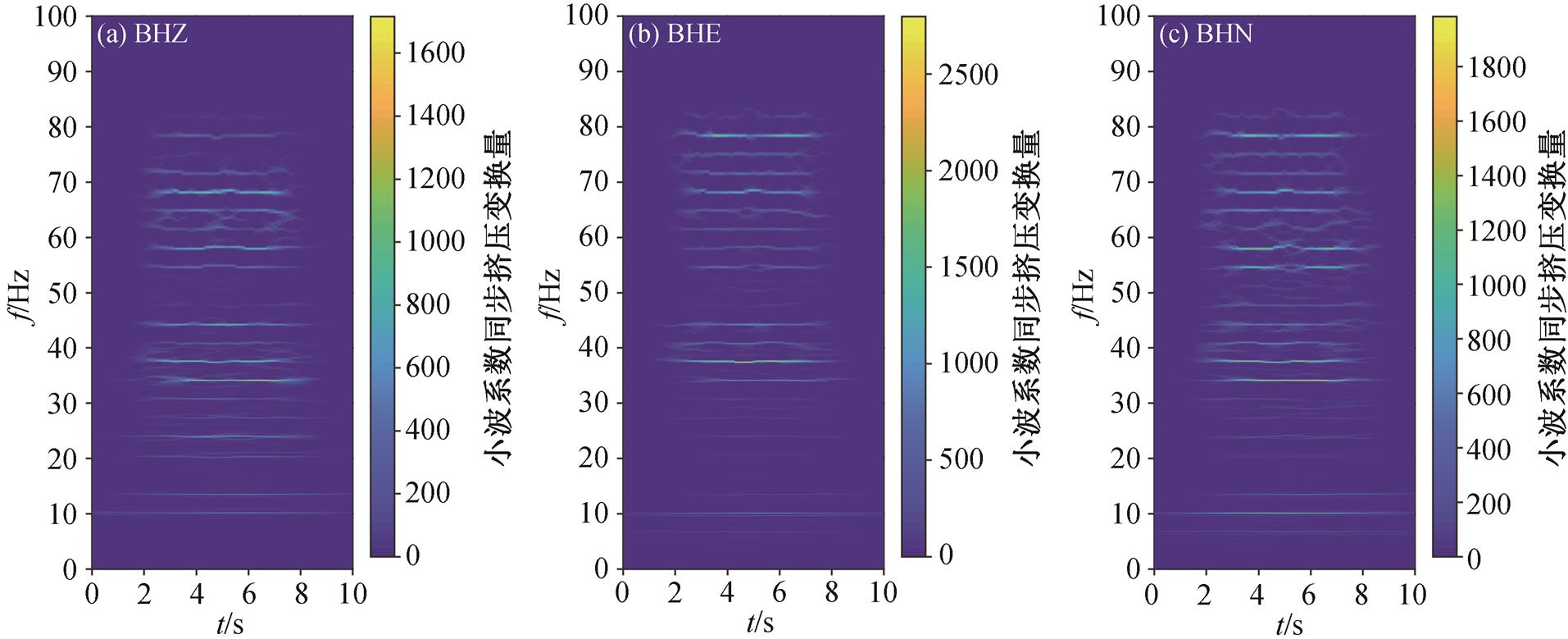
图11 G6019经过时M028台站接收的三分量高铁地震信号的同步挤压小波变换时频谱
Fig. 11 Synchrosqueezing wavelet transform spectra of three-component high-speed train seismic signals received by M028 station when G6019 passed
为了分析变速运动状态下的高铁地震信号特征, 在保定地区白洋淀火车站附近 BS005 台站选取列车加速运动时产生的地震信号, 如图 4 所示。可以看出, 信号的 3 个分量在一定程度上具有相似性。图 5(a)~(c)分别为图 4(a)~(c)中信号对应的振幅谱, 可以看出, 加速运动过程中频率谱线不完全具有匀速运动过程中所呈现的周期性。图 6(a)~(c)分别为将图 4(a)~(c)中相应的信号用同步挤压小波变换得到的时频谱, 从图 6 中白色箭头处可以看出, 在加速运行时, 沿时间轴方向, 分立谱线在频率域的分布范围加宽, 分立谱线间距变大, 高铁运行速度增大。从图 6(b)中选取的坐标点, 可以计算出加速度。图 6(b)左侧两坐标点的 t 均为 4.6s, f 分别为56.50 和 54.58Hz, 所以该时刻的谱线宽度为 1.92 Hz, 则此刻的速度为 48m/s; 右侧两坐标点的 t 均为 12.0s, f 分别为 59.79 和 57.74Hz, 所以该时刻的谱线宽度为 2.05Hz, 则此刻的速度为 51.25m/s。两坐标点的时间间隔为 12.0s−4.6s = 7.4s, 由此可计算出加速度为 0.439m/s2。
在保定地区白洋淀火车站附近 BS005 台站选取列车减速运动时产生的地震信号(图 7)做进一步分析。从图 7(a)和(c)可以看出, 信号的 BHE 和 BHN分量均具有一定的周期性。图 8(a)~(c)分别为图 7 (a)~(c)中信号对应的振幅谱, 可以看出, 减速运动时地震信号振幅谱的谱线不具有匀速运动过程中的周期性, 信号的主要能量集中在 35~40Hz 频带范围。图 9(a)~(c)分别为图 7(a)~(c)中相应的信号的同步挤压小波变换时频谱。与加速运动相比, 列车减速运动时地震信号的时频谱具有一定的规律性, 并呈现一定的变化趋势, 但无法在整个时频范围观察到清晰的分立谱线。但是, 从图 9 中箭头指示处可以看出, 高铁在减速运行时, 时频谱沿时间轴方向, 分立谱线在频率域分布范围变窄, 分立谱线间距变小, 表明高铁运行速度变小。通过从图 9(b)中选取的坐标点, 可以估算速度的变化趋势。图 9(b)左侧两个坐标点的 t 均为 7.026s, f分别为 67.70 和 65.41Hz, 因此该时刻的谱线宽度为 2.29Hz, 则此刻的速度为 57.25m/s; 右侧两个坐标点的 t 均为 8.861s, f分别为 65.81 和 63.55Hz, 因此该时刻的谱线宽度为2.26Hz, 则此刻的速度为 56.5m/s。从图 9 还可看出, 该减速运行列车的时频谱分立谱线呈曲线形态, 说明该次高铁进站前的减速不是均匀的。
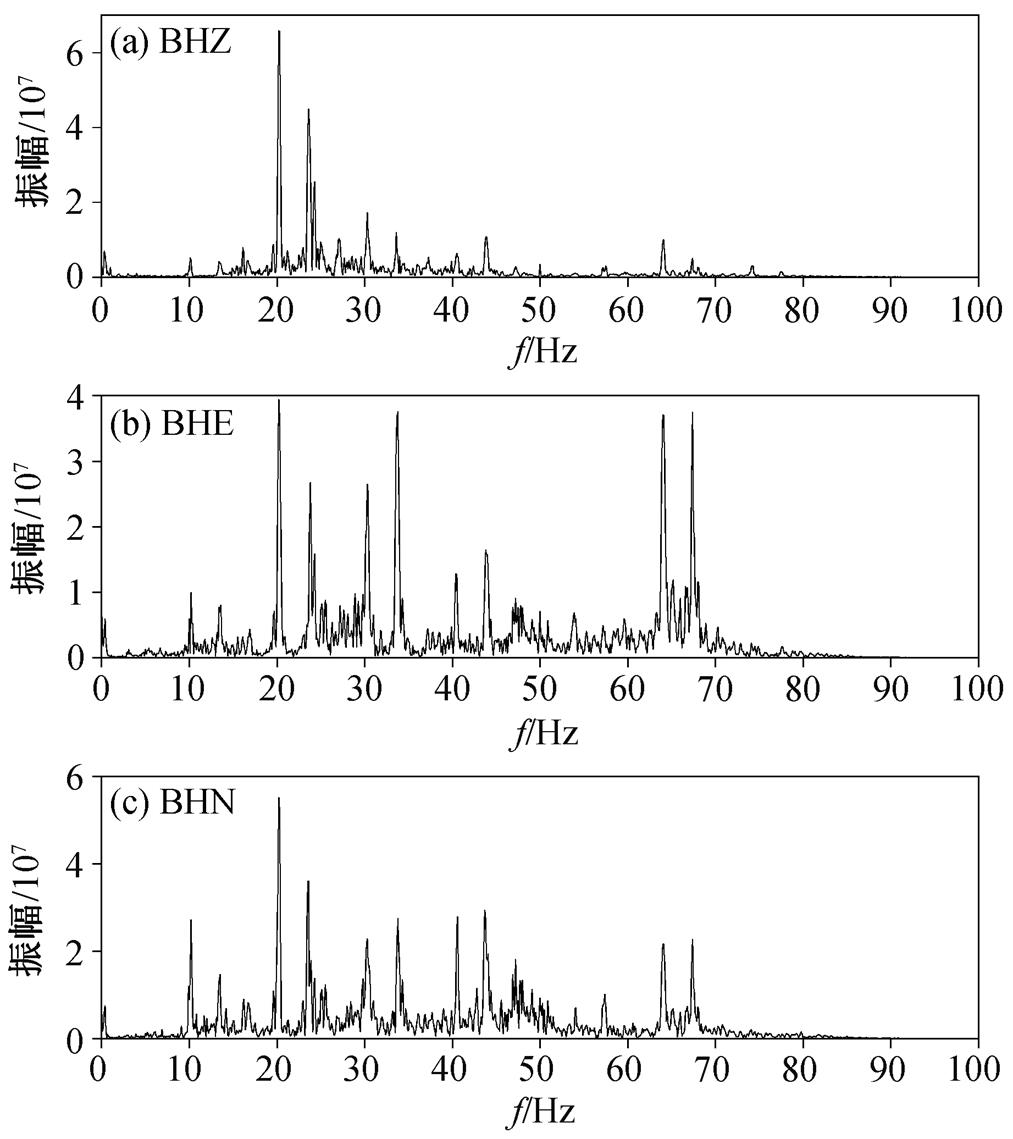
图12 G6019经过时T001台站接收的三分量高铁地震信号振幅谱
Fig. 12 Amplitude spectra of three-component high-speed train seismic signals received by T001station when G6019 passed
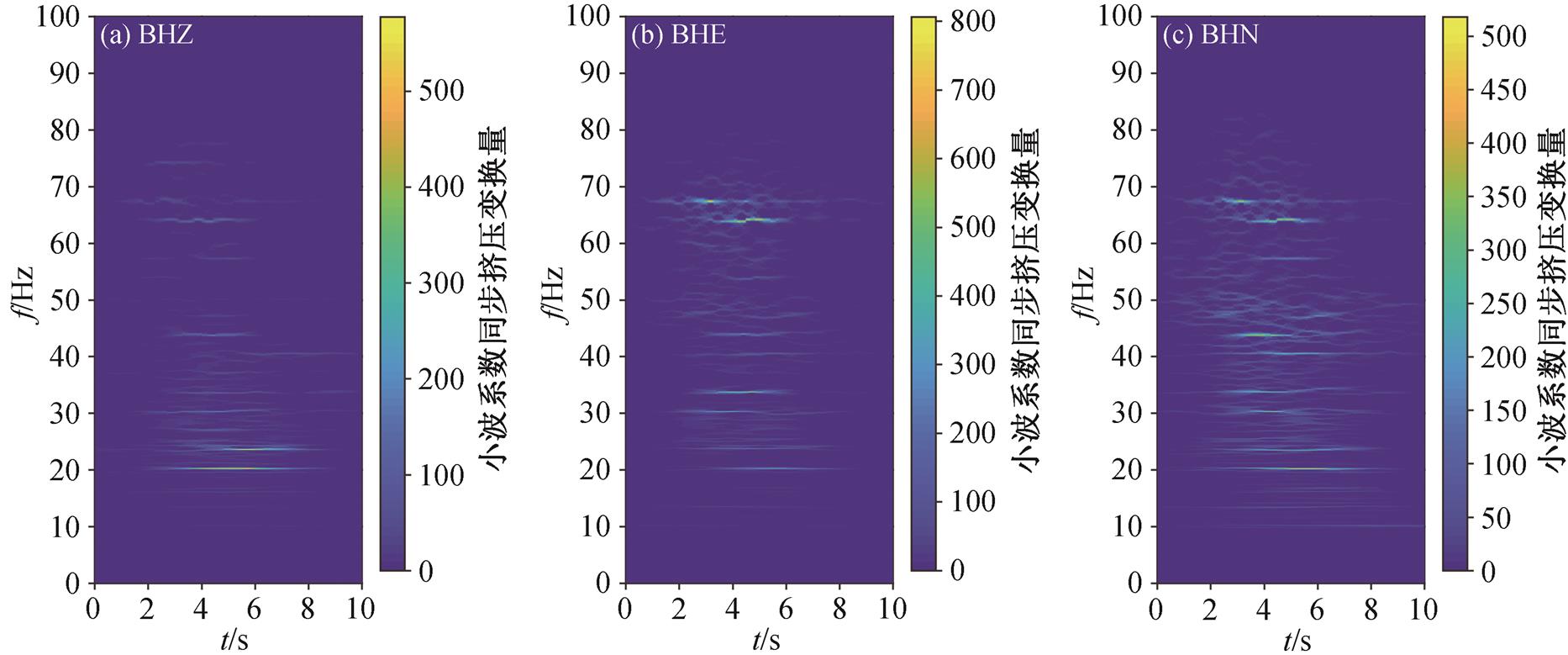
图13 G6019经过时T001台站接收的三分量高铁地震信号同步挤压小波变换时频谱
Fig. 13 Synchrosqueezing wavelet transform spectra of three-component high-speed train seismic signals received by T001 station when G6019 passed
为了分析不同运行环境下的高铁地震信号特征,我们选取深圳地区靠近高架桥附近区域的 M028 台站、远离高架桥的 T001 台站和靠近隧道区域的M009 台站同一车次高铁列车经过时采集到的高铁地震信号进行分析。从 M028 台站和 M009 台站选取的均是 2018 年 1 月 29 号由广州南开往深圳北的G6019 次高铁的地震数据, 从 T001 台站选取的是2018 年 1 月 30 号由广州南开往深圳北的 G6019 次高铁地震数据。G6019 次列车的车型均为 CRH3C重联型, 经过此观测区域的时刻为 14:00 左右。
首先, 对高架桥附近 M028 台站的数据进行傅里叶变换, 得到图 10 所示的振幅谱。可以看出, 该台站记录的高铁信号频带范围较宽, 为 3~90 Hz。M028 台站数据的同步挤压小波变换时频谱(图 11)可以更清晰地展示高铁地震信号频率随时间的变化规律, 高铁在此时段近似于匀速运行状态。
然后, 对垂直于高铁线路且远离高架桥的 T001台站数据进行频谱分析, 振幅谱如图 12 所示, 图 13为同步挤压小波变换的时频谱。从图 12 和 13 可以看出, 该台站截取的信号主要能量分布在 10~80Hz的频带范围, 与高架桥附近的 M028 台站数据相比, 该台站数据的高频部分和低频部分均有一定程度的损失。从时频谱图(图 13)中可以清晰地看出, 时频谱中的分立谱线随时间轴的变化趋于水平, 表明高铁在此时段为近似于匀速运行状态。
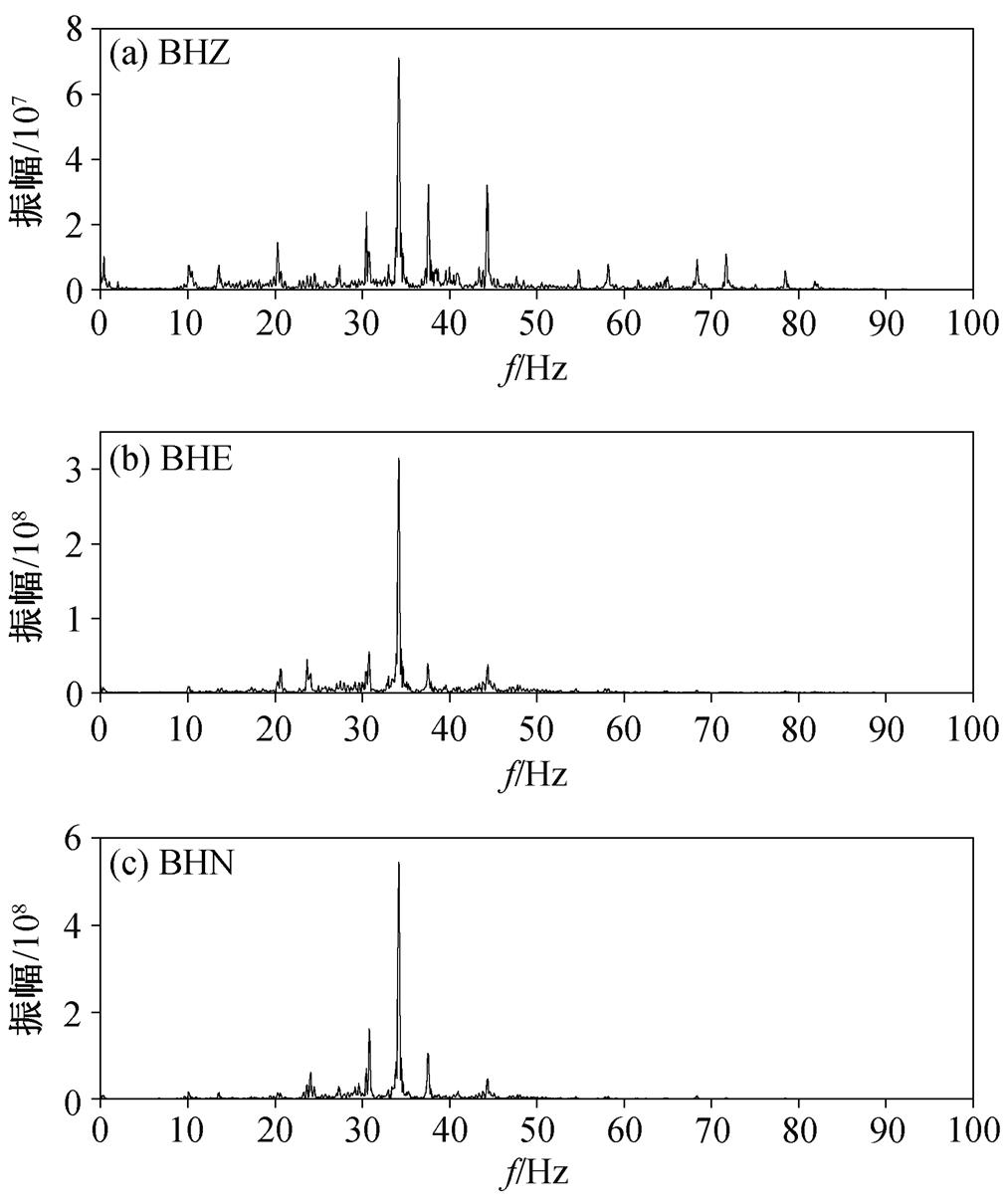
图14 G6019经过时M009台站接收的三分量高铁地震信号振幅谱
Fig. 14 Amplitude spectra of three-component high-speed train seismic signals received by M009 station when G6019 passed
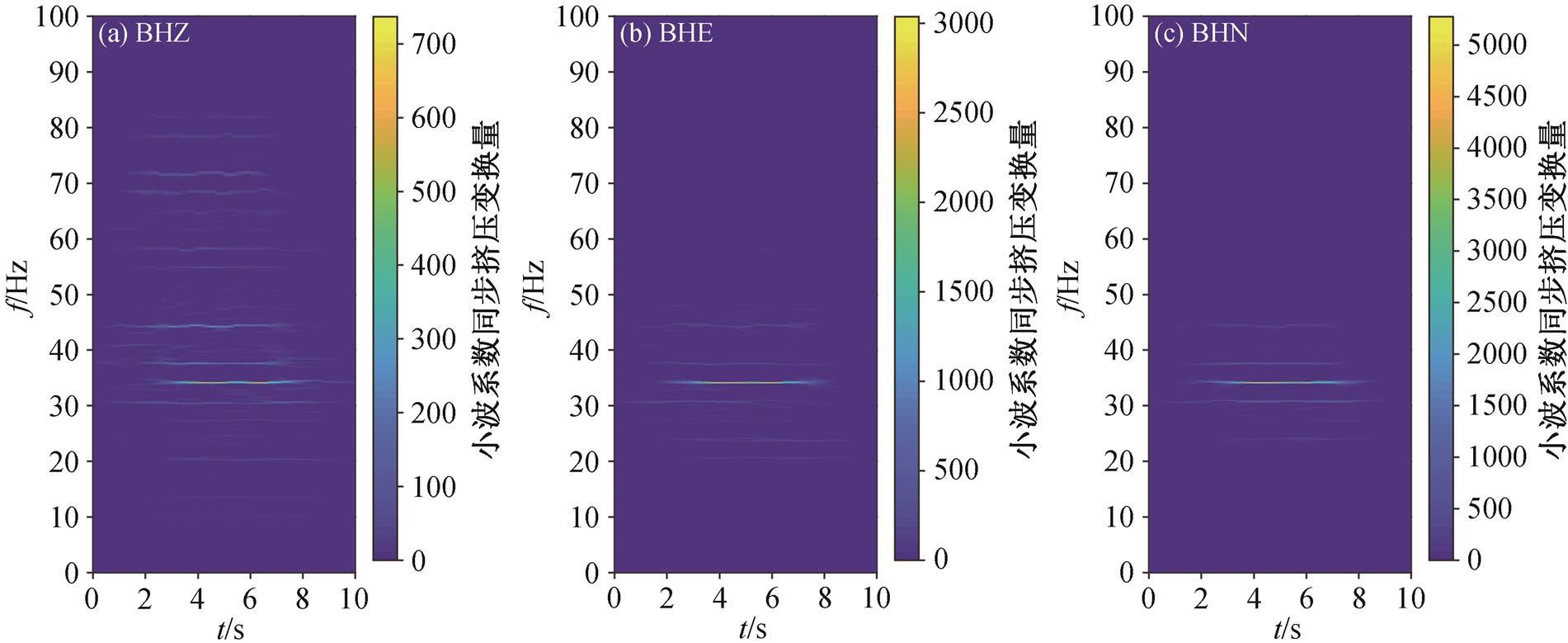
图15 G6019经过时M009台站接收的三分量高铁地震信号同步挤压小波变换时频谱
Fig. 15 Synchrosqueezing wavelet transform spectra of three-component high-speed train seismic signals received by M009 station when G6019 passed
最后, 选用靠近隧道附近 M009 台站的数据进行频谱分析和时频分析, 得到图 14 所示的振幅谱和图 15 所示的同步挤压小波时频谱。可以看出, 对同一列高铁经过隧道时产生的地震信号, BHZ 分量的能量集中在 10~80Hz 范围, 而 BHN 和 BHE 分量的能量集中在 10~60Hz 的窄带范围。时频图(图 15)可以清晰地展示高铁地震信号频率随时间的变化规律, 说明高铁在此时段近似于匀速运行状态。
从以上 3 种高铁运行环境的对比可以发现, 高铁在高架桥上运行时产生的地震信号低频信息比较明显, 并且频带较宽, 而高铁在远离高架桥区域运行时产生的地震信号中低频成分较少, 同时频带相对较窄。
本文对深圳地区和保定地区的高铁地震信号频谱特征和时频特征进行分析, 得到以下结论。
1)高铁匀速运行时产生的地震信号时频谱中的分立谱线与时间轴近于平行; 加速运行时, 沿时间轴分立谱线在频率域分布范围变宽, 分立谱线间距变大; 减速运行时, 沿时间轴分立谱线分布范围变窄, 谱线间距变小。
2)高铁通过高架桥时, 与远离高架桥区域采集的地震信号相比, 在高架桥附近采集的信号中低频成分更丰富, 频带更宽。
3)高铁通过隧道时, 与远离隧道区域采集的地震信号相比, 在隧道附近采集的信号中高频成分更少, 频带更窄。
高铁地震信号中不仅蕴含高铁运行设备结构和轨道结构的信息, 也蕴含着高铁运行区间地下结构和地质环境的信息, 因此, 在基于时频的分析方法对高铁地震信号分析处理的应用和高铁运行环境安全预警方面, 有待更深入的研究。
致谢 感谢北京大学宁杰远教授研究组提供高铁地震实测数据, 感谢中国科学院地质与地球物理研究所李幼铭研究员的支持, 感谢高铁地震联合研究组各位老师和同学的有益讨论。
参考文献
[1]Plenkers K, Husen S, Kraft T. A multi-step assessment scheme for seismic network site selection in densely populated areas. Journal of Seismology, 2015, 19: 861–879
[2]中国地震局. 地震及前兆数字观测技术规范之地震观测(试行)．北京: 地震出版社, 2001
[3]Ditzel A, Herman G C, Drijkoningen G G. Seismo-grams of moving trains: comparison of theory and measurements. Journal of Sound and Vibration, 2001, 248(4): 635–652
[4]Wu T X, Thompson D J. Vibration analysis of rail-waytrack with multiple wheels on the rail. Journal of Sound and Vibration, 2001, 239(1): 69–97
[5]Kaynia A M, Madshus C, Zackrisson P. Ground vib-ration from high-speed trains: prediction and counter-measure. Journal of Geotechnical and Geoenviron-mental Engineering, 2000, 126: 531–537
[6]Degrande G, Schillemans L. Free field vibrations during the passage of a Thalys high-speed train at variable speed. Journal of Sound and Vibration, 2001, 247(1): 131–144
[7]陈棋福, 李丽, 李纲, 等. 列车振动的地震记录信号特征. 地震学报, 2004, 26(6): 651–659
[8]Fuchs F, Bokelmann G, AlpArray Working Group (2017). Equidistant spectral lines in train vibrations. Seismological Research Letters, 2018, 89(1): 56–66
[9]徐善辉, 郭建, 李培培, 等. 京津高铁列车运行引起的地表振动观测与分析. 地球物理学进展, 2017, 32(1): 421–425
[10]曹健, 陈景波. 移动线源的 Green 函数求解及辐射能量分析: 高铁地震信号简化建模. 地球物理学报, 2019, 62(6): 2303–2312
[11]刘磊, 蒋一然. 大量高铁地震事件的属性体提取与特性分析. 地球物理学报, 2019, 62(6): 2313–2320
[12]张唤兰, 王保利, 宁杰远, 等. 高铁地震数据干涉成像技术初探. 地球物理学报, 2019, 62(6): 2321–2327
[13]王晓凯, 陈文超, 温景充, 等. 高铁震源地震信号的挤压时频分析应用. 地球物理学报, 2019, 62(6): 2328–2335
[14]王晓凯, 陈建友, 陈文超, 等. 高铁震源地震信号的稀疏化建模. 地球物理学报, 2019, 62(6): 2336–2343
[15]张固澜, 何承杰, 李勇, 等. 高铁地震震源子波时间函数及验证. 地球物理学报, 2019, 62(6): 2344–2354
[16]Daubechies I, Lu J, Wu H T. Synchrosqueezed wave-let transforms: an empirical mode decomposition-like tool. Applied Computational & Harmonic Analysis, 2010, 30(2): 243–261
Comparative Analysis of Time-Frequency Characteristics of Seismic Signal Induced by High-Speed Train
Abstract The time-frequency spectrum analysis of high-speed train (HST) seismic signals measured in Baoding, Hebei Province and Shenzhen, Guangdong Province is carried out by using synchrosqueezing wavelet transform. It is found that the seismic signals generated by HST passing through viaducts are more abundant in low-frequency information than those generated by running through tunnels and on the surface. Through the time-frequency spec-trum characteristics of the HST seismic signal, the state of change of the runing speed of HST can be determined.
Key words high-speed train seismology; time-frequency analysis; synchronous compression wavelet transform;equidistant spectral lines
doi: 10.13209/j.0479-8023.2019.076
收稿日期: 2019-08-04;
修回日期: 2019-08-15
国家自然科学基金(41074089, 41774135)和中央高校基本科研业务费专项资金(310826172002)资助