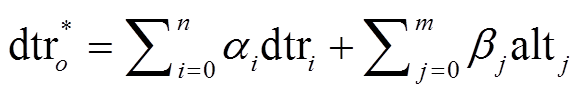, (1)摘要 基于飞行品质监控大数据, 对各机场区域低空颠簸频率进行统计。利用地形及气象观测数据, 研究低空颠簸与环境因子的相关性。结果表明, 飞机低空颠簸与地形起伏度、气温日较差以及风速有显著相关性。利用地理加权回归(GWR)模型进行拟合分析, 发现上述环境因子的影响强度存在空间差异。地形起伏度与风速的影响强度均自东北向西南逐渐增大, 气温日较差的影响强度自东南向西北再向东北逐渐增大。地理加权回归模型的调整 R2 达到 0.512, 说明模型的有效性很好。基于拟合模型对全国范围低空颠簸风险进行估计, 获得颠簸风险分级空间分布图。研究结果对机场选址和飞行安全管理具有参考价值。
关键词 低空颠簸; 地理环境因子; 地理加权回归; 相关性分析; 飞行品质监控
飞机在飞行过程中受到大气湍流的影响与冲击, 突然发生轻微抖动或摇晃, 甚至出现强烈横滚、俯仰或者偏航, 这种现象称为“飞机颠簸”。飞机颠簸轻则使乘客和飞行员稍感不适, 影响飞行品质, 重则使飞机难以操控, 损坏飞机部件结构, 甚至引发重大安全事故, 威胁飞行安全。因此, 对飞机颠簸事件的监控成为航空部门飞行品质管理(fli-ght operational quality assurance, FOQA)的重要内容。充分了解和掌握颠簸事件的分布规律以及区域环境对颠簸事件的影响, 无疑有助于提高飞行品质管理水平。
目前, 对飞机颠簸的研究集中在产生机制与预测预报等方面。飞机颠簸动力学机制的研究以大气湍流理论为基础, 通过理论分析或数值模拟等方法, 得到许多研究成果, 涉及风场、温度场和重力波等气象条件以及地形因素对飞机颠簸形成的作用。高空中水平风切变产生的湍流是引起高空飞行颠簸的重要因素, 同时风的垂直切变对引发飞机起飞和着陆时的低空飞行颠簸有重要作用[1‒3]。温度场的变化(包括垂直与水平温差梯度的改变)将促进颠簸的发生, 温度梯度越大, 颠簸越强[3‒4]。在稳定大气层结下, 浮力振荡产生重力波, 失稳的重力波破碎为湍流, 导致产生飞机颠簸[5–6]。因山脉阻挡气流而形成的山脉重力波、强烈下坡风以及转子环流、峡谷地形中的峡谷风等都是引发相应区域飞行颠簸的重要因素[7‒9]。同时, 基于对颠簸产生机制的研究, 得出一系列用于颠簸预报的指数, 包括 Ri 指数、I指数、tcr 指数以及 Ellord 指数等[10‒13]。上述研究成果对于分析和发现颠簸事件的分布规律具有理论指导意义, 但是尚不能方便地直接应用于飞行品质管理。对于飞行品质管理而言, 更需要的是对颠簸事件区域分布特征和环境影响的定量描述, 并且, 在进行区域环境影响描述时, 选择的影响因子最好是易观测、易获取的。
黄仪方等[14]基于 2006 年四川航空公司机载快速存取记录器(Quick Access Recorder, QAR)的数据, 对中国高原重要航线上飞机颠簸的分布规律做了分析。吴炎成等[15]基于 2002—2011 年的航空气象资料转发数据(aircraft meteorological data relay, AMDAR),研究了中国周边海域越洋飞行颠簸的时空分布与变化规律。申燕玲等[16]利用 2012—2015 年中国地区的飞行员报告(pilot reports, PIREPs)资料, 分析了中国冬季飞机颠簸的时空特征。虽然上述针对飞行颠簸的研究都利用了多种来源的实际飞行数据, 但研究区域限于局部, 不能反映全国范围的飞行颠簸分布特征; 对分布规律的描述限于定性, 缺乏定量表达; 并且仅涉及分布特征, 未对环境影响进行定量的分析。
飞机颠簸主要发生在起飞和降落阶段(低空颠簸)[17], 低空颠簸与高空颠簸产生的机制不完全相同[2‒3], 高空颠簸主要由风切变引起湍流而致, 低空颠簸还受地面加热作用和地形等因素的综合影响。低空颠簸的多发性与复杂性使基于实际数据的定量分析显得尤为重要。
本文基于飞行品质监控数据, 以低空颠簸事件作为研究对象, 选择地形、地面气象观测资料作为环境因子分析的基础数据, 采用最小二乘法与地理加权回归模型, 对环境因子与颠簸事件发生频率之间的相关性进行分析, 进而对全国范围内颠簸事件的发生频率进行估计, 划分低空颠簸风险等级, 为提升飞行品质管理水平提供科学依据。
飞行品质监控通过收集和分析日常的飞行数据, 提高飞行机组的操纵品质, 减少运行和维护成本, 为安全风险管理提供数据和信息支持, 是目前国际上公认的保障飞行安全的重要手段。飞行数据由数百种飞行参数构成, 这些参数包括飞行姿态位置、周围环境参数以及航空电子设备参数等[18]。当飞行参数监测内容的记录值达到或超过预先设定的标准时, 便探测到一个超限事件。航空公司和民航管理部门监控着上百种超限事件, 其中包括过载事件(或称空中垂直载荷超限)。飞机在空中飞行时, 作用在飞机上除重力之外的合力与飞机重力之比, 称为过载。过载一般指垂直方向上的过载, 又称载荷因子。载荷因子超过一定的标准时, 即被判定为出现过载事件, 可以用飞机过载代表飞机颠簸[15]。通过对飞机过载超限事件的统计, 可以获得飞机低空颠簸的发生频率。
本文使用的国内某大型航空公司 2013 年 1 月至2014 年 12 月的超限事件数据由中国民航科学技术研究院提供, 包含约 160 万条超限事件记录和超过80 万条的航段记录, 其中飞机过载事件记录超过 7万条。每条超限事件记录包含事件编码、事件发生时间、发生时所处的飞行阶段以及航段标识等字段。航段记录由航段标识(用于与同事件记录进行连接)、起飞机场、降落机场、起飞时刻和降落时刻等字段组成。
为获取地理环境因子数据, 需要数字高程模型(digital elevation model, DEM)数据和气象数据。本文使用由美国地质勘探局网站提供的 ASTER GDEM数据, 空间分辨率约为 30m, 高程误差在 10~25m范围内。下载中国及周边地区的数据, 并通过双线性插值, 根据需要分析的空间范围, 将栅格单元重采样为 500m×500m。2013—2014 年的气象日值数据由中国气象数据网提供, 包含全国 839 个国家级气象观测站的每日气象监测数据, 监测的气象要素包括气温、风速、降水量和气压等。
引起飞机低空颠簸的大气湍流包括动力湍流和热力湍流等[17,19]。动力湍流多出现在对流层的底部, 是空气流经粗糙不平的地表面或障碍物时出现的湍流, 与地形有关, 湍流强度和规模受风速影响。热力湍流由空气非均匀加热下的对流形成, 亦多出现在对流层底部。气温日较差可以表征温度场的非均匀程度, 风速和地形起伏度可以表征动力湍流的强度。本文选择气温日较差、风速和地形起伏度这 3 种环境因子, 分析其对飞机低空颠簸的影响。
在计算环境因子前, 需要设定其空间统计范围。本文主要分析起飞和降落阶段的颠簸事件, 因此将以机场为中心的覆盖起飞或降落阶段飞行距离(水平距离, 下同)的区域作为环境因子的空间统计范围。该覆盖距离并没有一个严格的标准, 且不同机场、不同飞行架次也存在差异。本文通过 800 余条航段的机载快速存取记录器 QAR 数据对该覆盖距离进行统计分析, 发现 75%以上的航段起飞和降落阶段的飞行距离小于 150km。因此, 本文将 150km 距离作为计算机场环境因子的空间范围, 并将此空间范围称为机场区域。
各统计单元(即各机场区域)内的气温日较差和风速可由地面气象观测资料计算获得。气象资料包含各观测站点的日气温最大值、最小值以及风速等观测信息, 气温日较差为日气温最大值与最小值之差。计算出统计时间范围内各站点的平均气温日较差和平均风速, 然后使用以海拔为协变量的协同克里格插值获得全国范围的气温日较差和风速分布, 进而统计出各机场区域内的平均气温日较差及平均风速。
以平均气温日较差为例, 插值得到的气温日较差为
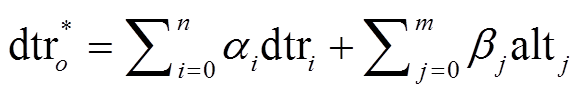, (1)式中,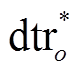 
为插值得到的 o 处的气温日较差, 
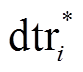和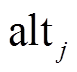
分别为对应观测站点的气温日较差及海拔, 
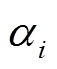和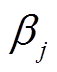
分别为需确定的协同克里金加权系数。
在插值后的气温日较差栅格中, 某机场的空间统计范围占据一片区域 S, 包含 l 个栅格, 则平均气温日较差为
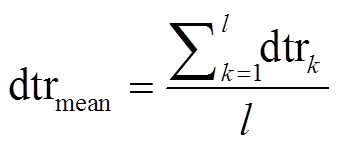, (2)式中,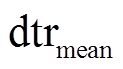 
为平均气温日较差, 
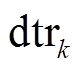为第 k 个栅格单元的气温日较差。
地形起伏度基于 DEM 数据, 通过局部高差法计算获得, 计算公式为
, (3)式中, ra 为地形起伏度,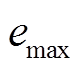 
和
分别为各机场空间统计范围内的最大和最小高程。
空间数据间往往存在自相关性, 以空间数据作为自变量时, 无法满足传统的回归模型(最小二乘估计模型)残差项独立的假设, 其参数估计将不适用。地理加权回归(geographically weighted regres-sion, GWR)模型[20]将数据空间位置引入回归系数中, 使变量间的关系可以随空间位置的改变而变化, 能够反映参数的空间非平稳性, 其结果更符合实际。因此, 本文引入 GWR 模型进行分析, 模型结构如下:
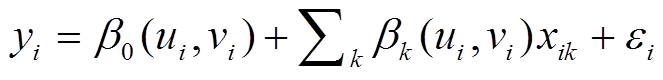, (4)式中, (ui, vi)为第 i 个样本空间单元的地理中心位置, yi 为样本 i 处的因变量, 在本研究中为各机场的颠簸频率, xik 为第 k 个自变量在样本 i 处的值, 
为第k个自变量在样本 i处的估计回归系数,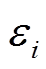
为误差项。
从某航空公司 2014 年度全年 A320 机型的航段记录中选取 68 个机场, 每个机场的航段记录数均大于 500 (512~38891, 航段记录总计 366911 条), 所有机场的颠簸频率范围为 2.22%~17.79%。在此基础上, 分别对风速、地形起伏度、气温日较差与颠簸频率的相关性进行初步分析。
对不同机场进行空间比较, 以便分析不同区域环境因子与颠簸频率的相关性。为此选择地形起伏度、年平均气温日较差和年平均风速 3 项指标, 分别进行分级, 并将每个机场对应到相应的指标等级中。在此基础上, 对应每项指标的每个等级, 分别计算落入其中的机场颠簸频率平均值, 结果如图 1所示。可以看出, 颠簸频率与年平均风速、年平均气温日较差以及地形起伏度均呈现良好的正相关关系。
风速和气温日较差是随时间变化的, 因此可以从时间维度上进一步分析风速和气温日较差两个环境因子的影响。本文以风速为例, 对风速和颠簸频率的季节变化进行趋势分析。图 2 呈现部分机场风速和颠簸频率的季节变化趋势, 为方便对比, 对数据做了归一化处理。可以看出, 二者呈现良好的一致性。
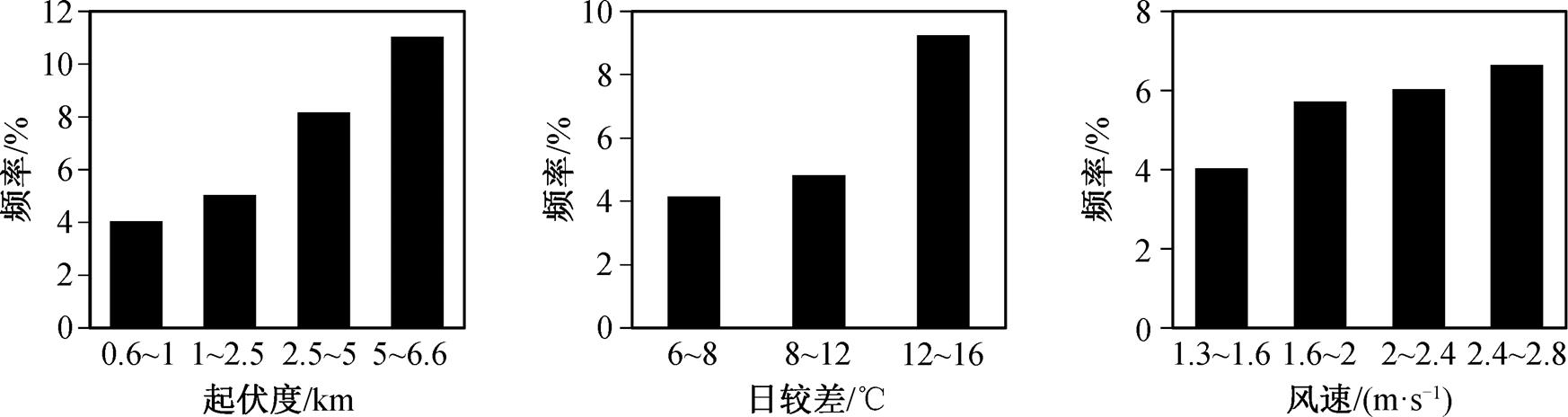
图1 颠簸频率随环境因子变化
Fig. 1 Variation of turbulence frequency in different environment factor grade
本文还利用日平均风速观测数据, 结合每日的航段记录, 分析颠簸频率与日平均风速以及气温日较差的相关性。图 3 列举部分典型机场颠簸频率与日平均风速的关系, 可以看出, 日平均风速与低空颠簸之间表现出显著的相关性。气温日较差与颠簸频率也表现出类似的相关性(图略)。
为了实现定量分析, 需要采用模型进行拟合。本文选择 2013 年度某航空公司 A320 和 B737-700 两种机型的航段记录。与单一机型相比, 这样做可以扩大样本数量, 覆盖更多的机场(84 个), 从而在更大程度上逼近真实情况。经过数据分析, 发现两种机型的颠簸频率具有很大的相似性。环境因子依然采用年平均风速、年平均气温日较差和地形起伏度3 项。图 4 展现各机场颠簸频率以及 3 个环境因子不同等级的空间分布。
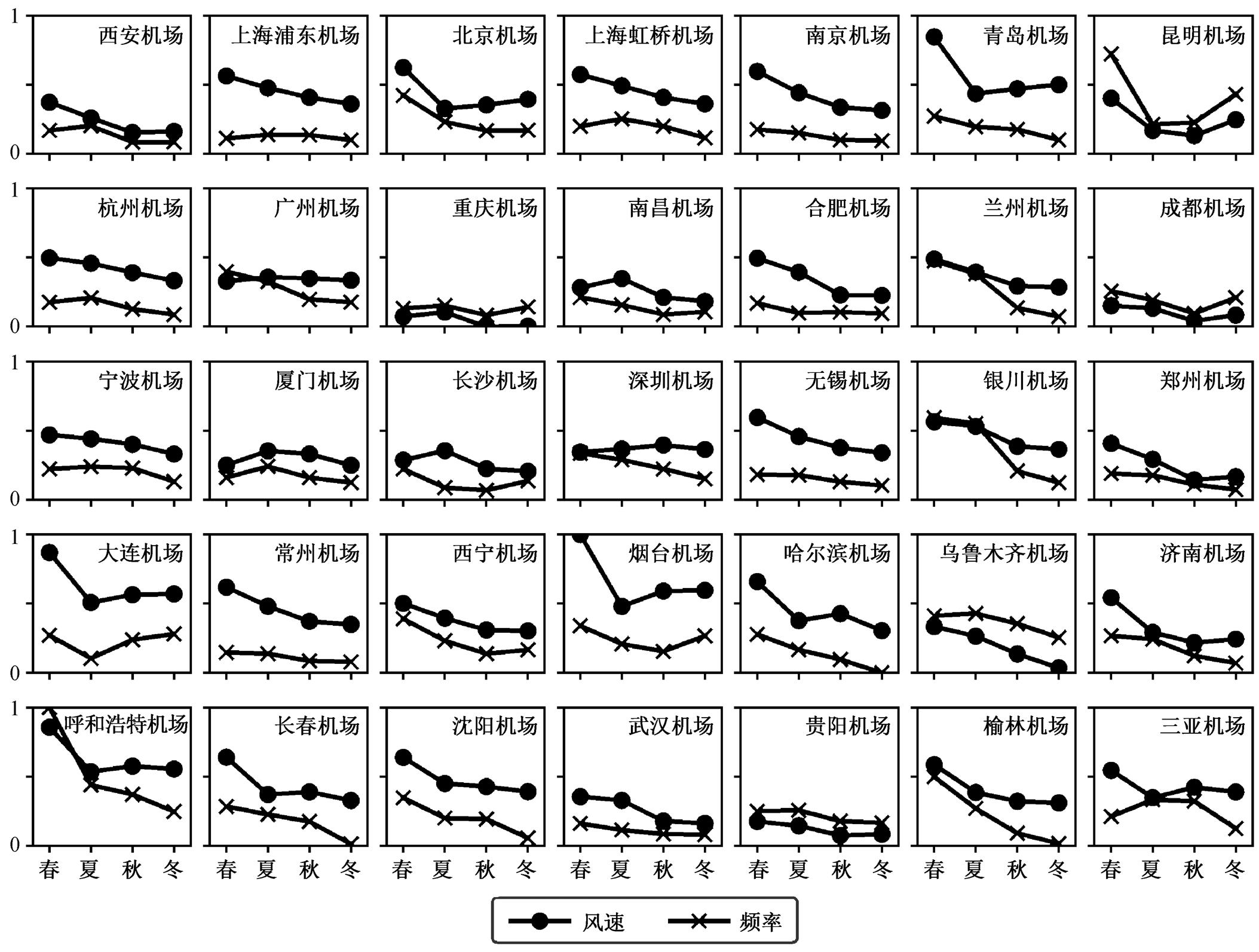
图2 颠簸频率与风速的季节变化
Fig. 2 Seasonal variation of turbulence frequency and wind speed
采用统计学中的最小二乘估计(ordinary least square, OLS)模型以及空间统计学中的地理加权回归(GWR)模型[20]进行拟合分析。模型均以机场颠簸频率为因变量, 环境因子(地形起伏度、年均气温日较差和年均风速)为自变量。下面分别对拟合结果进行分析。
OLS 模型的拟合结果见表 1。采用方差膨胀因子(variance inflation factor, VIF)对自变量进行多重共线性检验, 各自变量的方差膨胀因子均小于 10, 表明自变量间不存在多重共线性。该模型的调整R2 为0.468, 表明该模型可以解释飞机低空颠簸事件发生频率变差的46.8%。模型的显著性检验结果表明, 模型在0.01水平上显著; 自变量的显著性检验结果表明, 地形起伏度与气温日较差的回归系数在0.01水平上显著, 平均风速的回归系数在0.05 水平上显著。模型方程为
, (5)式中, f为机场的飞机年低空颠簸频率, ra 为机场的地形起伏度, dtr 为机场的年均气温日较差, ws 为机场的年均风速。
OLS 模型拟合结果表明, 地形起伏度、气温日较差和平均风速均与飞机颠簸显著正相关, 即机场区域地形起伏度越大, 气温日较差越大, 平均风速越大, 越容易发生飞机低空颠簸事件。
GWR 模型的拟合结果见表 2。与 OLS 比较, GWR 模型的调整 R2 由 0.468 提升到 0.514, 赤池信息量准则 AICc 由 831.6 下降到 802.8, 模型解释能力增强, 同时表明空间位置对飞机低空颠簸事件发生的影响。各机场区域的模型方程为
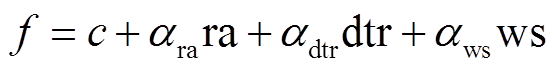, (6)式中, f为机场的飞机年低空颠簸频率, c 为常数项, 
和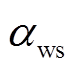
分别为地形起伏度、年均气温日较差和年均风速的系数。
不同机场区域的参数估计均不相同, 表 2 中采用中位数和四分位数表示。
图3 颠簸频率随日平均风速的变化
Fig. 3 Variation of turbulence frequency with daily mean wind speed
图4 颠簸频率及机场环境因子分级分布
Fig. 4 Spatial distribution of turbulence frequency and environment factor grade
由 GWR 模型得到各因子对飞机低空颠簸事件发生频率的影响强度空间模式, 如图 5 所示。就地形起伏度而言, 从东北向西南方向发展, 对飞机低空颠簸事件的正向影响逐渐增大。在内蒙古北部、东北三省、北京、天津及河北大部, 地形起伏度对飞机低空颠簸事件为负向影响; 在山东、山西、河南江苏北部及安徽北部为较弱的正向影响; 在浙江、福建、江西北部、湖北及宁夏等地, 表现为中等程度的正向影响; 在西北、西南、广东、广西及湖南等地, 表现为很强的正向影响。
风速对飞机低空颠簸事件发生频率影响的变化趋势与地形起伏度相似, 从东北向西南方向正向影响逐渐增大。气温日较差对飞机低空颠簸事件发生频率的正向影响则从东南向西北, 再向东北逐渐增大。在广东、福建、江西及浙江南部, 影响程度较弱; 在安徽、湖北、云南、贵州、四川、广西、海南及西藏等地, 影响程度为中等; 在山东、河南、陕西、甘肃、新疆北部等区域, 影响程度较强; 在内蒙古、山西、河北及东北三省等地, 影响程度很强。
表1 最小二乘估计(OLS)模型拟合结果
Table 1 Descriptive statistic of parameter estimates for OLS
因子系数 标准差 tSig.VIF 常数项(c)−60.36620.337−2.9680.003**− 地形起伏度(ra)0.0110.0034.1270.000**1.790 气温日较差(dtr)5.7301.3704.1830.000**1.482 平均风速(ws)19.5408.9072.1940.031*1.446 R2调整R2Sig.AICc 0.4860.4680.000**831.6
说明: **和*分别表示在0.01和0.05水平上显著, 下同。
表2 地理加权回归(GWR)拟合结果
Table 2 Descriptive statistic of parameter estimates for GWR
因子系数 25%分位数中位数75%分位数 常数项(c)−58.61−48.99−40.63 地形起伏度(ra)0.00150.00670.0131 气温日较差(dtr)3.87 4.627.58 平均风速(ws)12.3917.2123.51 R2调整R2Sig.AICc 0.5710.5140.000**802.8
最后, 采用 GWR 模型对 2014 年度各机场区域的低空颠簸频率进行预测, 并将预测结果与实际情况进行比较, 如图 6 所示, 模型的预测误差及调整R2 如表 3 所示。可以看出, 预测结果与实际情况具有较大的相似性, 平均绝对误差为 1.94%, 均方差为 2.42%, 表明该模型能够较好地拟合环境因子与颠簸频率之间的相关性。
基于上述地理加权回归模型的拟合结果, 对全国范围的低空颠簸频率进行估计。通过插值分析, 获得年平均风速、年平均气温日较差以及地形起伏度的空间栅格分布。通过 GWR 模型(式(6)), 计算每个栅格的颠簸频率估计值。对估计值进行分级, 并对同等级栅格进行合并, 得到全国范围的低空颠簸风险等级分布图(图 7)。可以看出, 东南大部及塔里木盆地低空颠簸风险级别最低, 其中东南地区地形起伏度、风速及气温日较差均较低, 塔里木盆地地形起伏度也较低; 中原地区及云南中部、青海南部、西藏北部低空颠簸风险为中等级别, 这些地区地形起伏度、风速及气温日较差均为中等级别; 东北平原到内蒙古中部及新疆北部地区低空颠簸风险级别较高, 这些地区较大的风速是引发低空颠簸事件的主导因素; 大兴安岭地区低空颠簸风险级别很高, 主要由于该地区气温日较差很大; 喜马拉雅山脉、昆仑山脉及天山山脉这些区域低空颠簸风险级别很高, 主要由很大的地形起伏度导致。
图5 各因子影响强度的空间分布
Fig. 5 Spatial distribution of environmental factors’ effect intensity
图6 模型预测值与真实值对比
Fig. 6 Comparison chart of model predicted value and the true value
表3 GWR模型预测误差
Table 3 Performance of GWR
最大负误差/%最大正误差/%平均绝对误差/%均方差/%调整 R2 −6.275.321.942.420.55
本文面向飞行品质管理, 基于飞行监控大数据以及地形和气象观测数据, 对民航飞机低空颠簸频率与环境因子的相关性进行分析, 得到以下结论。
图7 低空颠簸风险分级
Fig. 7 Grade map of risk of low-altitude turbulence
1)地理加权回归模型能够较好地拟合低空颠簸与环境因子的相关性。
2)低空颠簸发生频率与风速、气温日较差以及地形起伏度具有显著的相关性, 环境因子对低空颠簸的影响强度存在空间差异。
3)本文基于模型拟合结果制作的全国范围低空颠簸风险等级分布图对机场选址和飞行安全管理具有参考价值。
本文选取的环境因子为容易获取的地形因子以及日常观测的气象因子, 没有涵盖影响低空颠簸的所有因素, 因此拟合结果存在一定程度的偏差。今后, 随着对颠簸机理研究的深入以及观测手段的提升, 这一不足有望得到改进。另外, 由于数据量的原因, 本文仅针对特定机型进行分析, 没有对多种机型开展比较分析, 这也是今后研究中需要改进的一个重要方面。
参考文献
[1]Colson D, Panofsky H A. An index of clear air tur-bulence. Quarterly Journal of the Royal Meteorologi-cal Society, 2010, 91: 507‒513
[2]Gultepe I, Starr D O. Dynamical structure and tur-bulence in cirrus clouds: aircraft observations during FIRE. Journal of the Atmospheric Sciences, 1995, 52 (23): 4159‒4182
[3]李子良, 陈会芝. 飞机颠簸的气象条件分析. 高原山地气象研究, 1999, 19(2): 22‒23
[4]邹波. 地面加热对飞机颠簸影响的动力学初步分析. 大气科学学报, 2004, 27(4): 527‒531
[5]李子良, 黄仪方. 地形影响的飞机颠簸及其数值仿真实验. 气象, 2006, 32(11): 32‒35
[6]Guest F M, Reeder M J, Marks C J, et al. Inertial gravity waves observed in the lower stratosphere over Macquarie Island. J Atmos Sci, 2000, 57: 737‒752
[7]Nappo C J. An introduction to atmospheric gravity waves. Amsterdam: Academic Press, 2002
[8]Snyder C, Skamarock W C, Rotunno R. Frontal dy-namics near and following frontal collapse. J Atmos Sci, 1993, 50: 3194‒3211
[9]朱志愚. 高空急流区飞机颠簸的一种形成机制的探讨. 成都气象学院学报, 1997, 12(4): 298‒302
[10]Moraes O L L, Acevedo O C, Degrazia G A, et al. Surface layer turbulence parameters over a complex terrain. Atmospheric Environment, 2005, 39(17): 3103‒3112
[11]Keller J. Performance of a quantitative jet stream turbulence forecasting technique — the specific CAT risk (SCATR) index // 22nd Aerospace Sciences Mee-ting. Reno, 1984: 271‒277
[12]Dutton J A, Panofsky H A. Clear air turbulence: a mystery may be unfolding. American Association for the Advancement of Science, 1970, 167: 937‒944
[13]Oard M J. Application of a diagnostic richardson number tendency to a case study of clear air turbu-lence. Journal of Applied Meteorology, 2010, 13(7): 771‒777
[14]黄仪方, 孙智博, 肖焕权. 我国高原重要航线飞机颠簸分布规律分析. 中国民航飞行学院学报, 2011, 22(1): 5‒9
[15]吴炎成, 周林, 刘科峰, 等. 基于 AMDAR 资料应用于中国周边海域飞机低空颠簸的统计分析. 气象科学, 2014, 34(1): 17‒24
[16]申燕玲, 王东海, 巩远发. 中国冬季飞机颠簸的统计分析. 成都信息工程学院学报, 2017, 32(4): 426‒432
[17]王淑翠. 飞机颠簸产生的可能机制及其在天气预测上的应用[D]. 青岛: 中国海洋大学, 2013
[18]Mitchell K, Sholy B, Stolzer A J. General aviation aircraft flight operations quality assurance: overco-ming the obstacles. IEEE Aerospace & Electronic Systems Magazine, 2007, 22(6): 9‒15
[19]辜运燕. 我国西部干线飞机颠簸分布规律分析[D]. 广汉: 中国民用航空飞行学院, 2009
[20]Fotheringham A S, Brunsdon C, Charlton M. Geogra-phically weighted regression: the analysis of spatially varying relationships. West Sussex: John Wiley & Sons, 2003
Abstract Based on the flight quality monitoring big data, statistics were made on the frequency of low-altitude airplane turbulence in various airport areas. Besides, using topographic and meteorological data, we analyzed the correlation between low-altitude airplane turbulence and environmental factors. The results indicate a significant correlation between the low-altitude airplane turbulence and relief amplitude, wind speed, and diurnal temperature range. Also, the spatial difference of the effect intensity of these environmental factors is revealed via geographically weighted regression (GWR) model. The effect intensity of relief amplitude and wind speed increase from northeast to southwest, while the effect intensity of diurnal temperature range increases from southeast to northwest then to northeast. The adjusted R2 of the model is 0.512, which means that the model is very effective. Based on the GWR model, we estimated the risk of low-altitude airplane turbulence on the national scale, and obtained the classification map of the risk. The research results have reference value for airport location and flight safety management.
Key words low-altitude turbulence; geographical environmental factor; geographically weighted regression;correlation analysis; flight quality monitoring
doi: 10.13209/j.0479-8023.2019.036
国家自然科学基金(U1433102)资助
收稿日期: 2018‒06‒15;
修回日期: 2018‒09‒19