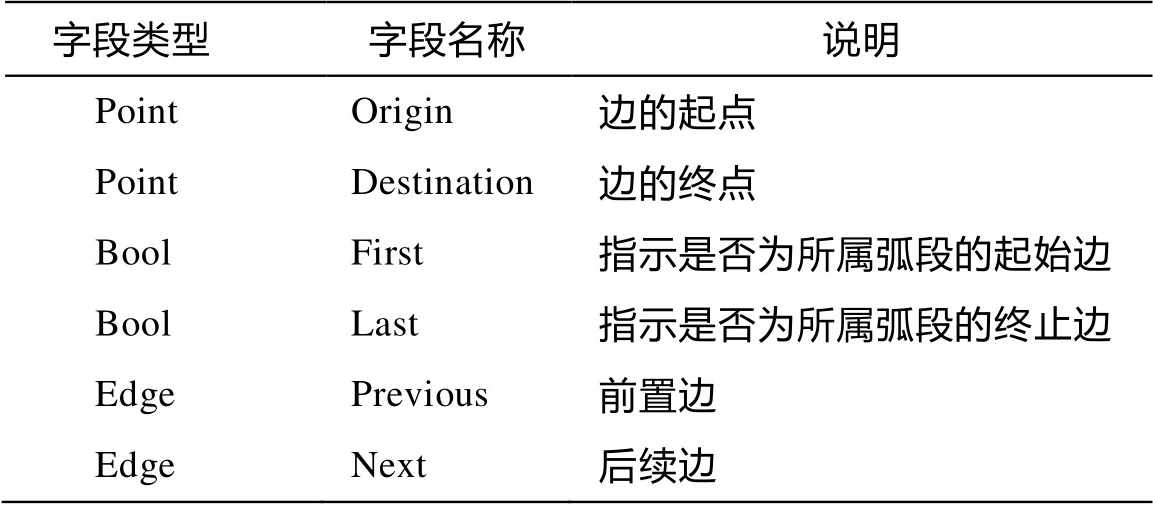
表1 边对象的数据结构
Table 1 Data structure of the edge object
字段类型字段名称说明 PointOrigin边的起点 PointDestination边的终点 BoolFirst指示是否为所属弧段的起始边 BoolLast指示是否为所属弧段的终止边 EdgePrevious前置边 EdgeNext后续边
摘要 针对多边形自动生成的传统算法在自动化和时间效率方面的不足而导致的相应商用 GIS 软件数据处理和时空分析能力的欠缺, 提出一种基于扫描思想的弧段分割和多边形自动生成算法。本算法具有以下特点: 面向从求交开始至生成多边形结束的完整任务; 充分利用求交过程中的有益信息, 以较小的算法复杂度和极小的计算量, 实现弧段分割和多边形自动构建; 避免了传统方法中多边形嵌套关系的计算, 并能有效地处理桥和悬边问题。实验结果表明, 与传统算法相比, 本算法在效率方面有明显的提升。
关键词 扫描线算法; 弧段分割; 多边形自动生成
在地理信息系统(geographical information sys-tem, GIS)中, 弧段分割及多边形自动构建在矢量数据处理和空间分析等方面被广泛应用。这个问题的描述如下: 给定平面内一个弧段集合(允许存在自相交和互相交), 输出平面内由这些弧段划分的所有闭合连通子集(即多边形集合)。
在 GIS 拓扑关系研究的早期, 研究者们关注从地图数字化到拓扑关系建立的过程[1‒2], 算法的效率不是研究的重点。随着数据的来源越来越充分, 有许多研究探讨如何从既有点线拓扑关系数据或多边形数据中建立多边形拓扑关系[3‒8], 其中包含使用网络大数据 Web-GIS 作为数据来源的思想。另外一些研究试图从图论的角度建立多边形拓扑关系, 但图的构建也需要计算方位角度并排序, 依然是一项非常耗费时间的任务[9‒10]。部分研究借鉴栅格数据的处理手段来生成拓扑关系[11‒12], 但是栅格数据的应用范围有限。也有研究采用分治策略来生成多边形的拓扑信息[13‒14], 但此类算法的实现过程比较复杂, 拼接的时候会耗费很多计算资源, 并且不一定能获得效率的提升。目前, 大多数关于多边形生成的算法都是基于方位角比较的左转多边形追踪算法[15‒23], 虽然研究者们构建了很多策略进行优化搜索方向角的选择, 但这一部分的计算仍然耗费大量的时间, 并且这些研究没有解决如何进行弧段相交断链的问题, 也没有关注一些特殊情况(比如悬边、岛等)。
归纳已有的研究成果可知, 多边形拓扑关系的自动构建一般分为 4 个阶段: 1)求弧段交点; 2)对弧段进行分割; 3)建立结点与弧段的拓扑关系; 4) 搜索多边形并建立与弧段的拓扑关系。已有的研究集中在第 3 和第 4 阶段, 不足之处在于割断了各阶段之间的有机联系, 不能充分地利用前面阶段的信息, 使得后面阶段算法的复杂度和计算量很大: 在第 3 阶段, 需要进行结点匹配(将由于计算误差导致的不完全重合的弧段端点合并为一个结点)以及结点和弧段连接关系的全局搜索; 在第 4阶段, 不仅要对构成多边形的弧段进行全局搜索, 还会形成无效多边形(如所有子区域的边界多边形), 同时要分析和计算任意两个多边形之间的包含关系, 以便实现带洞多边形的正确构建。另外, 悬边和桥也是一个不容易处理的问题。
针对上述不足, 本文提出一种基于扫描思想的弧段分割与多边形自动生成算法。该算法有以下特点: 1)从求交开始至生成多边形结束, 实现多边形自动生成的完整算法; 2)以 Benttley & Ottmann 线段求交算法[24]为基本框架进行扩展, 在求交的同时, 利用相关信息, 同步实现弧段分割和多边形自动生成, 并建立拓扑关系, 结构紧凑; 3)基于扫描思想, 避免了传统方法中的多边形嵌套关系的复杂计算, 并能有效地处理桥和悬边问题。
本算法依然使用 Bentley & Ottmann 算法中表征扫描线状态的数据结构事件点队列 Q 和状态结构 T (第 2 节将详细介绍), 并使用平衡二叉树进行组织。Bentley & Ottmann算法中的线段不包含任何属性, 为了方便弧段分割与多边形生成, 本文对普通线段添加表征方向和拓扑关系的字段, 将其扩充成一个新的数据结构—— 边(表 1)。初始化时, 边的数量等于所有弧段的边数之和。在扫描过程中, 有的边被一分为二(在交点处被分割)。
为了将边有效地组织起来, 表达边与弧段的逻辑关系, 并在弧段分割过程中实现快速更新维护, 本文设计一个数据结构: 活化边链表 E。对每个弧段的每个边建立一个边对象, 并加入 E 中, 通过设置它们的 First, Last, Previous 和 Next 属性, 建立它们之间的逻辑关系。在扫描过程中不断地更新 E, 但对 E 只有末尾插入操作, 而没有删除、中间插入和改变顺序等操作。边与弧段之间逻辑关系的更新仅仅通过对部分边的属性的更新实现, 这样可以避免更新维护过程中边的频繁移动。
图 1 是一个活化边链表 E 数据结构应用的简单例子: 两个弧段在交点 N 处被分割成 4 个弧段。分割前的两个弧段分别为 Arc(e1-e2-e3)和 Arc(e4-e5-e6), 分割后的 4 个弧段为 Arc(e1-e2)、Arc(e7-e3)、Arc (e4-e8)和 Arc(e5-e6)。而边的数量由分割前的 6 个变成分割后的 8 个。活化边链表 E 的数据结构变化见图 2。
表1 边对象的数据结构
Table 1 Data structure of the edge object
字段类型字段名称说明 PointOrigin边的起点 PointDestination边的终点 BoolFirst指示是否为所属弧段的起始边 BoolLast指示是否为所属弧段的终止边 EdgePrevious前置边 EdgeNext后续边
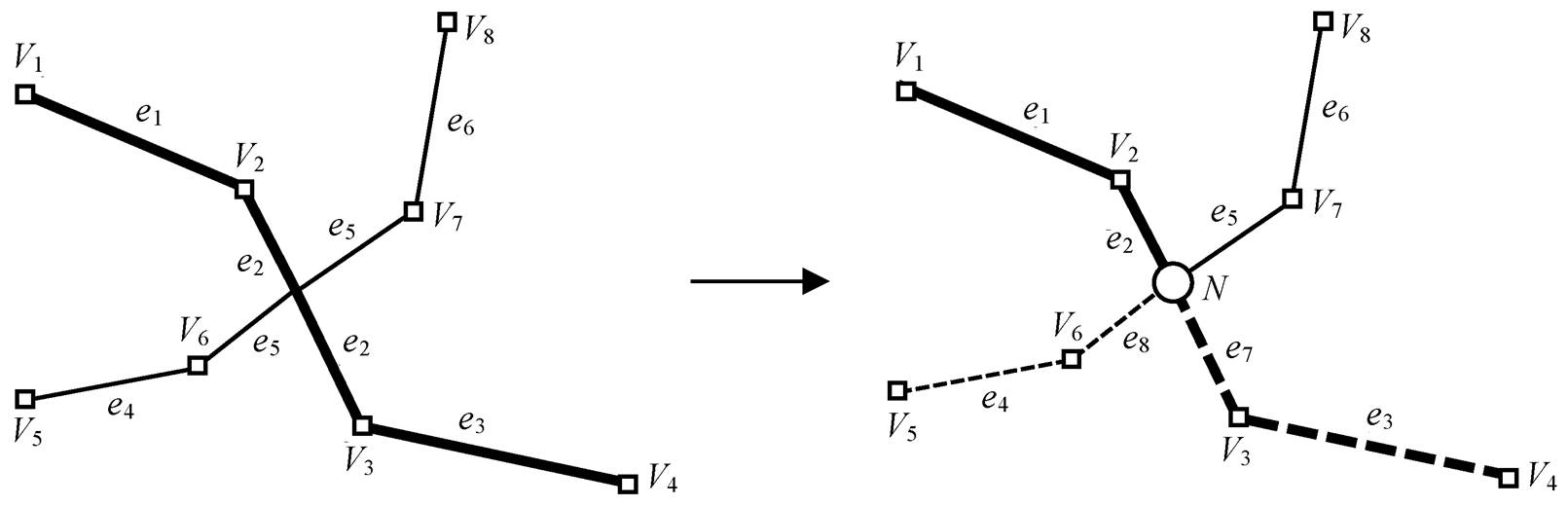
图1 两条弧段在交点处分割为 4 条弧段的示例
Fig. 1 A sample of splitting two arcs on intersection point into four arcs
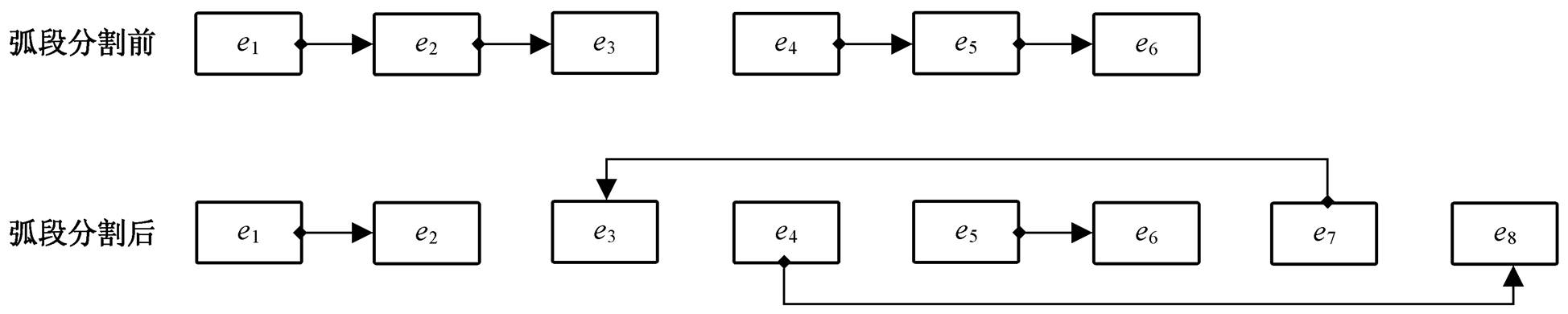
图2 活化边链表E数据结构变化
Fig. 2 Data structure change of the active edge link list E
在实际问题中, 经常出现带洞多边形。为了描述这种现象, 我们将环作为多边形的基本组成部分, 一个无洞的多边形由一个环组成, 一个带洞多边形则由一个外环和一个或多个内环组成。
在扫描过程中, 为了将所有可能形成多边形的边记录下来, 并方便提取出来作为输出结果的最终多边形, 本文设计一个数据结构: 活化多边形。一个活化多边形储存的是当前状态下可能形成此多边形的所有边的集合。随着扫描的进行, 活化多边形将不断地被更新, 包括增加边以及修改边的属性等, 直至形成一个完整有效的多边形或者被删除。在扫描开始前, 建立一个空的活化多边形集合 S, 在扫描过程中, 会有新的活化多边形加入 S, 或者已有的活化多边形被删除。由于存在删除操作, 活化多边形集合 S 采用一棵平衡二叉树进行组织。
Bentley&Ottmann 算法针对的问题是: 输入一个线段集合, 输出所有交点。此算法有两个重要概念: 事件点和扫描线状态。事件点包括线段端点以及扫描过程中逐渐发现的交点; 扫描线状态指与当前扫描线相交的所有线段构成的集合, 相对于扫描线, 这些线段是自左向右排序的。Bentley&Ottmann算法的总体思路是: 假想有一条水平线自上而下地扫过整个平面。在扫描过程中, 每遇到一个事件点, 则对状态结构 T 进行维护, 并检测新的交点。本文算法是在 Bentley & Ottmann 算法的框架下进行扩展, 重点是在处理事件点时增加弧段分割和活化多边形生成, 并在算法末尾增加最终多边形提取。本文算法流程如图 3 所示, 其中下画线部分为本文算法增加的内容。算法描述如下。
在算法开始时, 初始化一个事件队列 Q, 并将所有边的端点插入 Q 中, 以事件点为上端点的边也要和事件点一起存储。此外, 初始化一个空的状态结构 T。
初始化一个空的活化边链表 E, 将所有弧段的所有边插入 E 中。在扫描过程中进行弧段分割时, 不断地更新 E。
初始化一个活化多边形集合 S, 在扫描之前 S是空的, 随着扫描的进行, 不断有新的活化多边形加入, 也会有活化多边形被删除。
在完成上述初始化任务后, 逐一处理每个事件点。在处理事件点时, 除维护状态结构 T 和发现新的交点外, 还要进行弧段分割和活化多边形生成的操作。
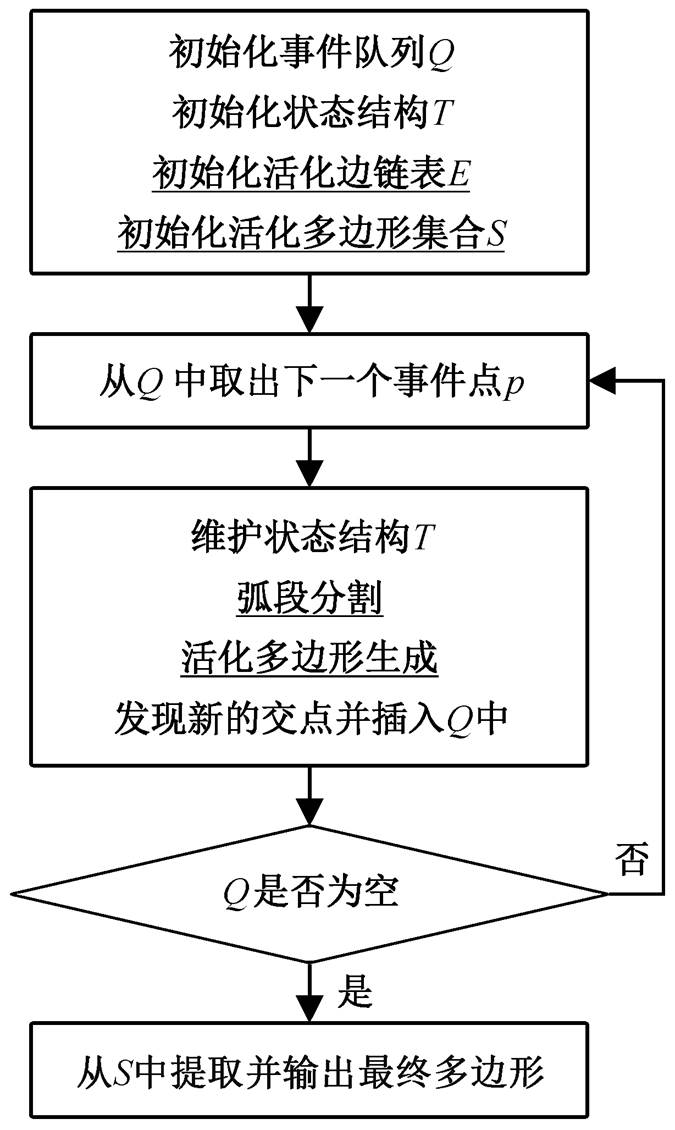
图3 本文算法流程
Fig. 3 Flow chart of the proposed algorithm
在算法的最后阶段, 从活化多边形集合 S 中提取并输出所有多边形。
本文算法的核心部分为弧段分割、活化多边形生成以及最终多边形提取, 下面分别加以描述。
设当前处理的事件点为 p, 令 U(p)为所有以 p为上端点(如是水平边则为左端点)的边构成的集合, 这些边与事件点一起存储, 且接下来将被插入状态结构 T 中。令 L(p)为 T 中以 p 为下端点的边的集合, C(p)为 T 中内部包含 p 点的边的集合。下面根据事件点的不同情况进行描述。
1)|U(p)∪L(p)∪C(p)| = 1 (即 3 个集合中的边的数量之和为 1, 下同), 此时 p 必定为某弧段的端点(end point)(图 4(a)), 不需要对 p 点所在的弧段进行分割。
2)|U(p)∪L(p)∪C(p)| = 2, 且|C(p)|=0。此时存在以下3种情况, 均无需进行弧段分割操作。
①这两条边属于同一弧段, 并且彼此为相邻边(图 4(b)), 无需进行弧段分割。
②这两条边属于同一条弧段, 并且一个为起始边, 一个为终止边 (图 4(c)), 意味着当前弧段为一条闭合弧段, 也无需进行弧段分割。
③这两条边属于不同的弧段, 并且, 或均为起始边, 或均为终止边, 或一个为起始边, 另一个为终止边(图 4(d)), 此时与 p 点相关的弧段虽然有两条, 但是 p 点作为两条弧段的端点, 仍无需进行弧段分割。
3)|U(p)∪L(p)∪C(p)| = 2, 且|C(p)|>0。如图4(e)所示, 此时必有两条弧段经过 p 点, 对这两条弧段进行分割操作。
4)|U(p)∪L(p)∪C(p)| ≥ 3。如图 4(f)所示, 此时p 点必为弧段交点, 对经过 p 点的所有弧段进行分割操作。
进行弧段分割时, 只需要对活化边链表进行维护, 算法相对简单, 不详述。
弧段分割完成后, 就可以进行活化多边形生成。此时 T 中已经没有包含 p 的边存在了, 即|C(p)|=0。如果弧段分割操作前 C(p)中有边, 则此时这些边已经被分割并分别插入 U(p)和 L(p)中了。下面根据当前事件点分割操作后 U(p)和 L(p)的不同情况, 阐述活化多边形的生成算法(为了叙述的简洁, 依然用“多边形”指代“活化多边形”这一概念)。
1)|U(p)| > 1, 且无论 L(p)中是否有边。如图 5(a)所示, 此时若 L(p)中有边, 则这些边在之前均已被处理, 因此无论 L(p)中是否有边, 只需考虑 U(p)中的边。此时 U(p)中的 N 条边可能构成 N−1 个多边形(每两个相邻边之间形成 1 个多边形), 因此新建N−1 个多边形, 然后设置 N 条边的左右多边形指针, 并将其加入相应的左右多边形中。其中, 最左侧边(图 5(a)中的 e1)的左侧多边形设置为该边左侧紧邻边(图 5(a)中的 eL)的右侧多边形, 如果不存在紧邻边, 则设置为空。最右侧边(图 5(a)中的 e3)的右侧多边形的设置方法同理, 下文中不再说明。
2)|U(p)| = 1, 且无论 L(p)中是否有边。如图5(b)所示, 设置 e1 左右的多边形, 并将 e1 加入其左右多边形中。
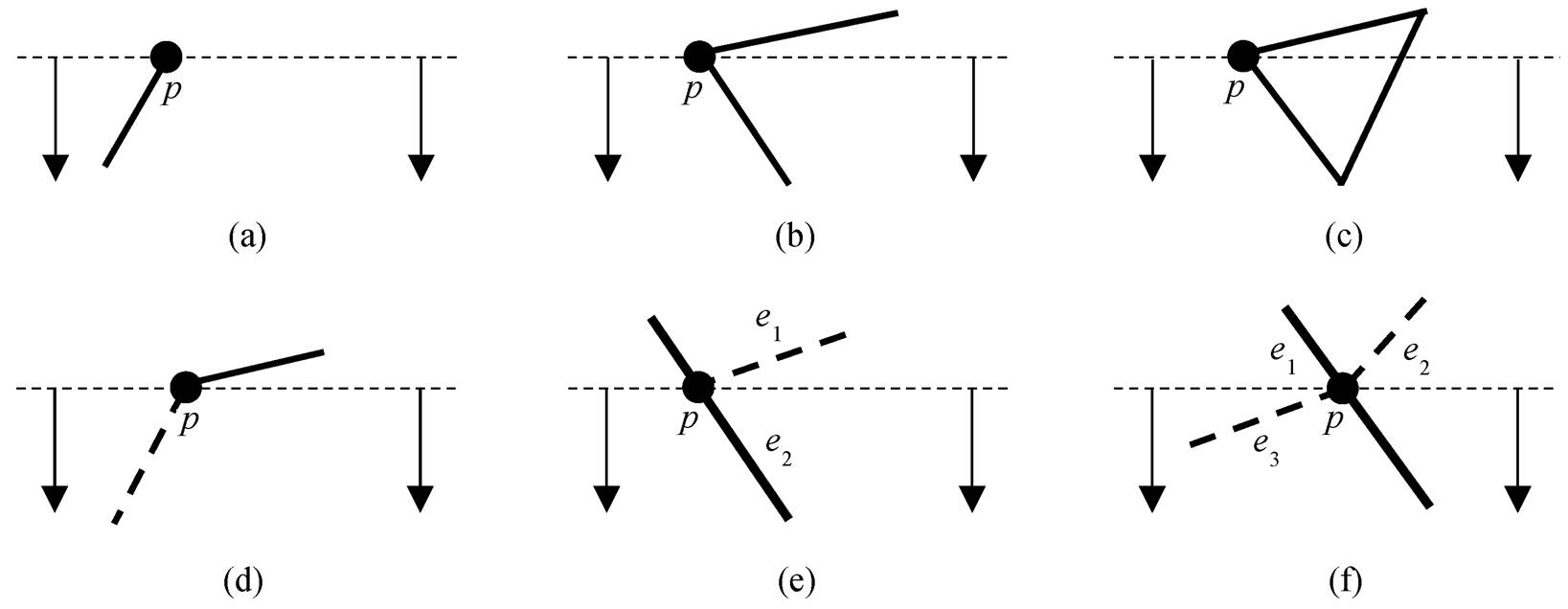
实线和虚线代表不同弧段上的边; 水平细虚线表示当前扫描线, 箭头表示扫描线移动方向。下同
图4 弧段分割前事件点类型示例
Fig. 4 Examples of event points before arc splitting
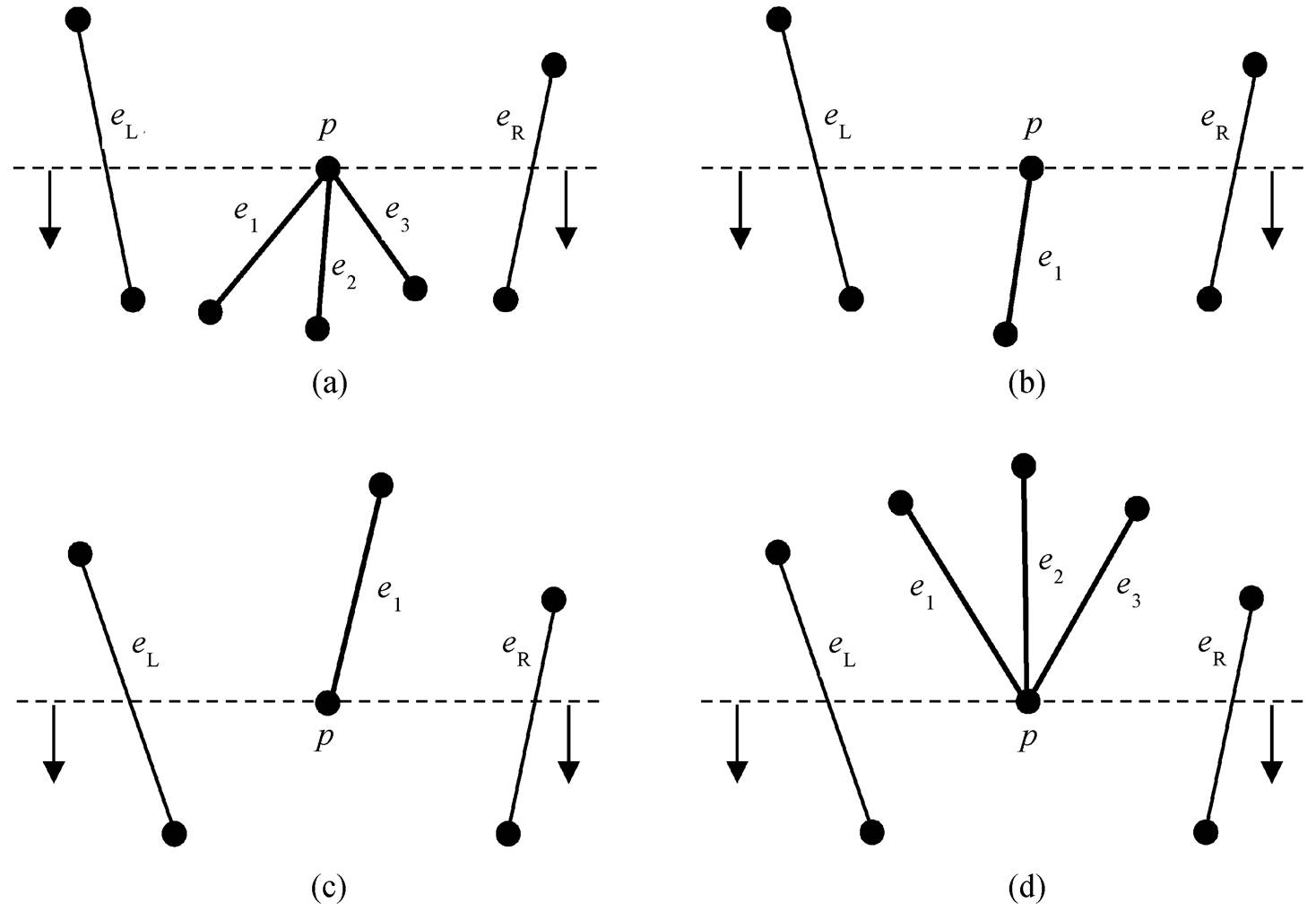
图5 活化多边形生成操作中事件点类型示例
Fig. 5 Examples of event point for active polygon creation operation
3)|U(p)| = 0, 且|L(p)| = 1。如图5(c)所示, 分以下几种情况。
①若 e1 左右侧均为空, 则不做任何操作。
②若 e1 左右仅有一侧为空, 则从活化多边形集合 S 中删除另一侧多边形, 并将被删除多边形中的所有边指向该多边形一侧的指针调整为空。
③若 e1 左右两侧均存在多边形且为同一多边形, 则不做任何操作。
④若 e1 左右两侧均存在多边形且不为同一多边形, 则将左右两侧多边形合并, 并调整相应边的多边形指针(实现方法不详述)。
4)|U(p)| = 0, 且|L(p)| > 1。如图 5(d)所示, 分以下几种情况。
①若最左侧边(图 5(d) 中的 e1)的左侧和最右侧边(图 5(d)中的 e3)的右侧均为空, 则不做任何操作。
②若最左侧边的左侧为空, 最右侧边的右侧不为空, 则从活化多边形集合 S 中删除最右侧边的右侧多边形, 并将被删除多边形中的所有边指向该多边形一侧的指针调整为空; 反之亦然。
③若最左侧边的左侧和最右侧边右侧均存在多边形且为同一多边形, 则不做任何操作。
④若最左侧边的左侧和最右侧边右侧均存在多边形且不为同一多边形, 则将最左侧边的左侧多边形和最右侧边的右侧多边形合并, 并调整相应边的多边形指针。
图6是一个活化多边形生成操作的简单示例。
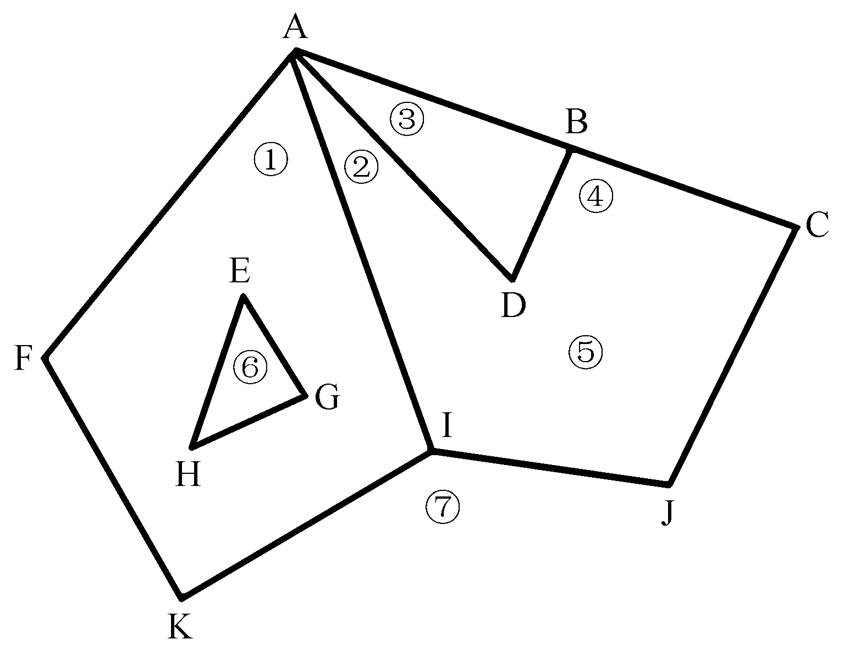
大写英文字母表示事件点, 带圈数字表示活化多边形。在各事件点进行的活化多边形生成和删除操作: A, 新建①②③; B, 新建④; D, 合并②④为⑤; E, 新建⑥; I, 新建⑦; J, 删除⑦。①③⑤⑥为最终多边形, ①为带洞多边形
图6 活化多边形生成操作示例
Fig. 6 A sample of active polygon creation operations
扫描结束后, 活化多边形的生成便全部完成。下一步, 需要从活化多边形集合中的每个活化多边形中提取出作为最终输出的多边形。对每个多边形的提取分为两步: 第一步, 通过删除活化多边形中左侧和右侧多边形相同的边, 剔除可能存在的悬链和桥; 第二步, 提取所有环, 这一步需要注意以下问题。
1)确定追踪法则。由于可能存在内环, 因此不能简单地采用顺时针或逆时针追踪法则, 而应采用右手螺旋法则, 即多边形的内部区域总是处于追踪方向的左侧。
2)可能存在多边形自身相切的情况, 即在弧段端点处可能连接了3个或3个以上的弧段。遇到这种情况, 采用最左转原则。
3)从活化多边形的边集合中第一条边所在的弧段开始搜索, 根据扫描的原理, 第一个提取的环必定为外环, 之后提取的环必定为内环。
限于篇幅, 提取算法不详述。
设输入弧段数为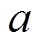
, 边数为
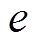, 输出的交点数为
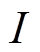, 弧段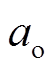数为
, 边数为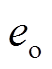
, 多边形数为
。
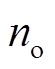时间代价方面, 线段求交与 Bentley&Ottmann算法完全相同, 时间代价为 O(e loge+ I loge )。维护活化边链表时仅需顺序插入, 分割弧段时会新建弧段, 二者耗时总和为 O(eo)+O(ao-a)。活化多边形数目不超过边数 eo, 其生成、维护、合并和删除均为线性操作, 时间代价为 O(eo)。因此, 算法总的时间代价为O(e loge + I loge ) + O(ao) + O(no) + O(eo)。
空间代价方面, 状态结构和事件队列的空间规模正如 Bentley & Ottman 算法所阐述的, 分别为O(eo)和 O(e+I), 活化的边链表的空间规模为 O(eo), 活化多边形集合与多边形集合的空间规模皆为O(no)。因此, 算法总的空间代价为 O(e+I)+O(eo) +O(no)。
为了验证本算法的有效性, 我们利用模拟数据和实际数据, 通过与左转算法和 ArcGIS 中的多边形自动生成功能(feature to polygon)进行多次对比测试, 并取平均值。实验采用的计算机配置为 2.8 GHz Intel Core i5 CPU 和 4 GB RAM, 代码用 C#语言实现。
模拟数据如图 7 所示, 实验结果如图 8 和表 2 所示。实际数据包含全国县级行政区域边界数据、全国铁路网数据和全国主要路网数据(图9, 包括高速公路、一级公路、二级公路和三级公路), 实验结果如表 3 所示。综合模拟数据和实际数据的实验结果可知, 与传统算法和 ArcGIS 相比, 本文算法在数据处理效率上明显提升。
针对传统算法的不足, 本文提出一种基于扫描思想的弧段分割和多边形自动构建算法。根据理论分析和实验验证, 得到如下结论: 1) 除求交的复杂度与传统算法相同外, 本文算法中的弧段分割以及多边形自动生成均为线性复杂度, 远远低于传统算法; 2) 除求交外, 本文算法通过设计合理的数据结构, 使得弧段分割以及多边形自动生成基本上只有比较、调整指针等运算, 很少有几何计算, 大大减少了计算量, 从而极大地提高了算法的效率; 3) 针对多边形嵌套的情况, 本文算法的效率更稳定(传统左转算法的效率对于嵌套多边形的数量非常敏感, 算法的效率不稳定); 4) 算法更优美, 结构更紧凑, 与传统算法相比, 需要处理的特殊情况极少, 对于桥或者悬链的处理更稳定、更有效; 5) 基于模拟数据和实际数据的实验结果表明, 与传统算法和ArcGIS 相比, 本文算法在数据处理效率上有明显的提升。
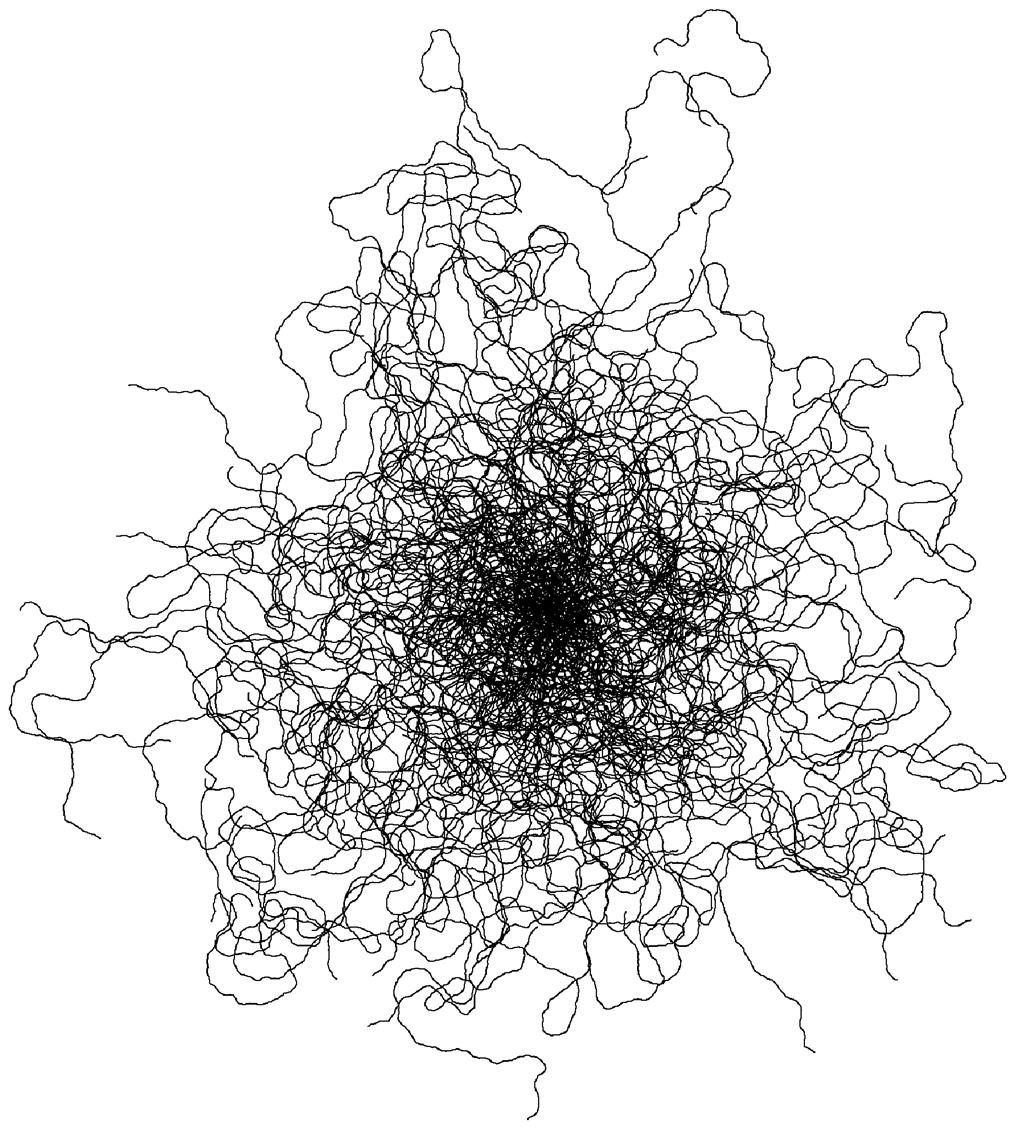
图7 模拟数据示意图
Fig. 7 Examples of artificial data
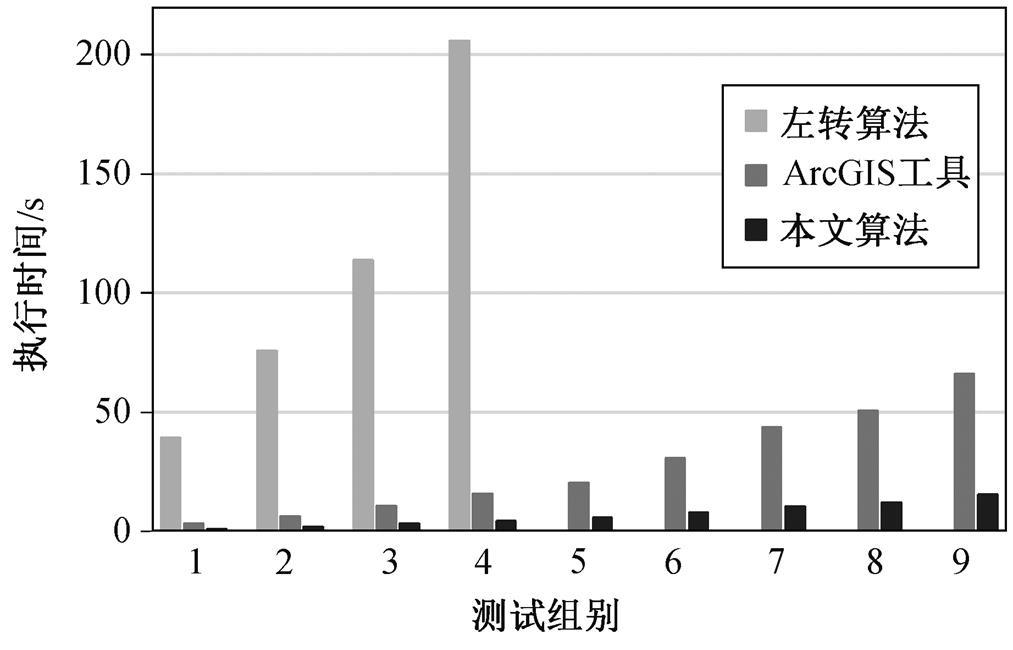
图8 模拟数据实验结果
Fig. 8 Experiment results of artificial data
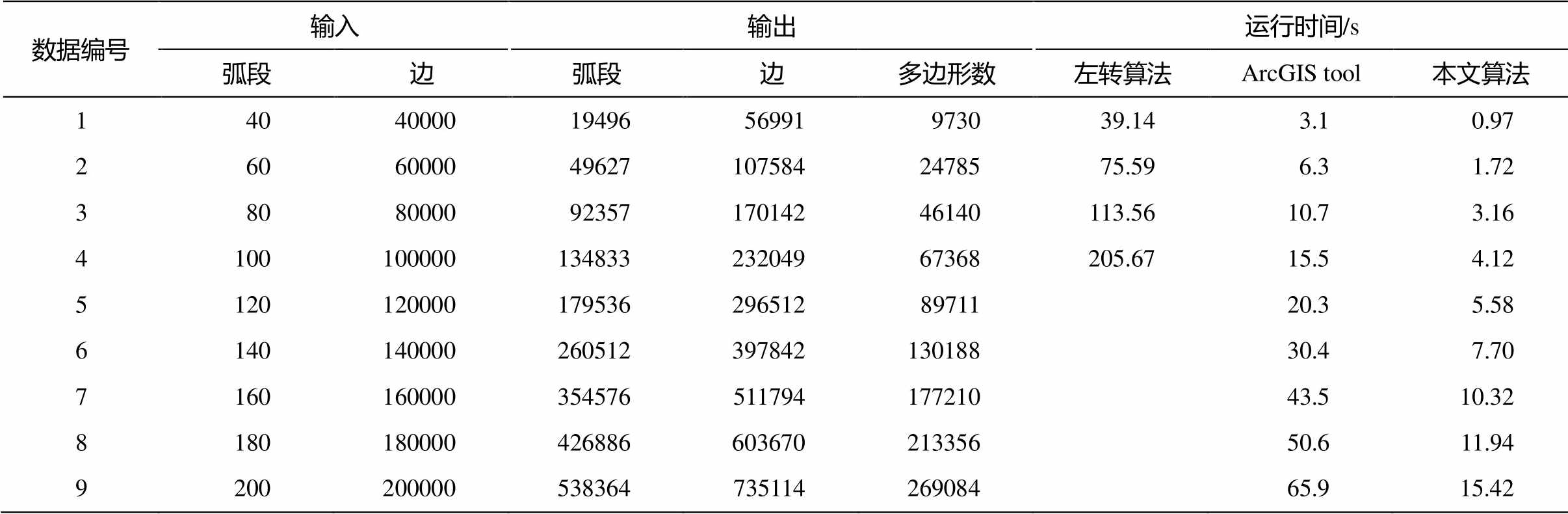
表2 模拟数据实验结果
Table 2 Experiment results of artificial data
数据编号输入输出运行时间/s 弧段边弧段边多边形数左转算法ArcGIS tool本文算法 140400001949656991973039.143.10.97 26060000496271075842478575.596.31.72 380800009235717014246140113.5610.73.16 410010000013483323204967368205.6715.54.12 51201200001795362965128971120.35.58 614014000026051239784213018830.47.70 716016000035457651179417721043.510.32 818018000042688660367021335650.611.94 920020000053836473511426908465.915.42
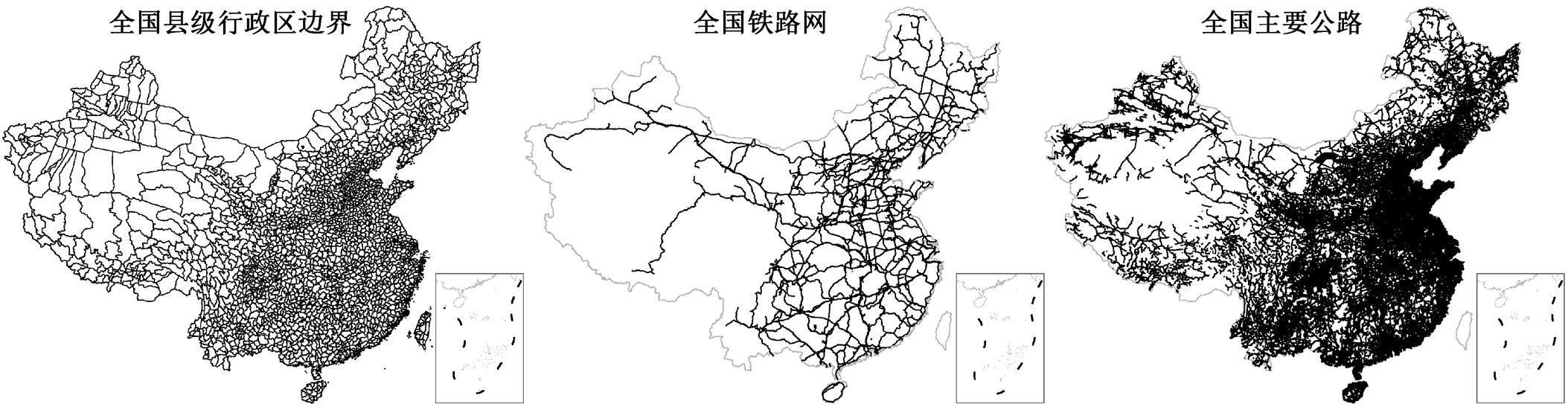
图9 实际数据示意图
Fig. 9 Samples of actual data
表3 实际数据实验结果
Table 3 Experiment results of actual data
数据集输入输出运行时间/s 弧段边总多边形带洞多边形左转算法ArcGIS tool本文算法 A1133359839934074514.8010.546.59 B509974900671585928983.207.705.47 C25853529663272490711303>2000705233
说明: A 为全国县级行政区边界线数据, B为全国铁路网数据, C为全国主要公路数据。
本文算法的另一个特点是易于扩展, 这是因为算法是以事件点的处理为核心。显然, 事件点(包括弧段端点、中间顶点和交点)是数据的骨架, 围绕数据的多种运算都可以围绕事件点展开。例如, 除实现弧段分割和多边形构建外, 通过建立合理的数据结构, 容易实现结点和弧段、多边形和弧段等拓扑关系的输出; 通过适当的扩展, 还容易实现多边形集合的布尔运算等。另外, 对于空间数据, 点是最简单的, 也最容易实现并行计算和分布式计算, 因此基于扫描的思想, 有望发展出更多的可以实现并行和分布式计算的空间数据处理算法, 从而有效地应对大数据时代对空间数据处理能力的挑战。
参考文献
[1]周心铁. 地理信息系统中由线段数字化记录重建多边形的方法. 遥感学报, 1988, 3(1): 57‒64
[2]陆守一, 韩兆云. 地理信息系统中自动获取多边形几何信息和拓扑信息算法的研究. 北京林业大学学报, 1996, 18(增刊2): 44‒47
[3]杜清运. 地图数据库中多边形数据的自动组织. 测绘学报, 1989, 18(3): 204‒212
[4]张军, 李玉祥. 地理信息系统中建立多边形拓扑关系的算法研究. 测绘科学, 1995, 20(2): 24‒28
[5]陈春, 张树文. GIS 中多边形图拓扑信息生成的数学基础. 测绘学报, 1996, 25(4): 266‒271
[6]程双伟. GIS 中拓扑关系的建立与更新[D]. 郑州: 中国人民解放军信息工程大学, 2002
[7]Yang B, Purves R, Weibel R. Efficient transmission of vector data over the internet. International Journal of Geographical Information Science, 2007, 21(2): 215‒ 237
[8]刘勖, 张镠亮, 宣国富. 基于有向弧的多边形拓扑关系生成算法. 计算机与信息技术, 2009, 17(5): 65‒67
[9]周立新, 严静, 潘云鹤. 一个基于图的多边形拓扑关系生成算法. 计算机应用, 1999, 19(10): 37‒39
[10]陈占龙, 吴亮, 刘焕焕. 基于图模型的多边形自动构建算法. 微电子学与计算机, 2011, 28(8): 143‒145
[11]王杰臣. 多边形拓扑关系构建的栅格算法. 测绘学报, 2002, 31(3): 249‒254
[12]Mineter M J. A software framework to create vector-topology in parallel GIS operations. International Journal of Geographical Information Science, 2003, 17(3): 203‒222
[13]Žalik B. A topology construction from line drawings using a uniform plane subdivision technique. Com-puter-Aided Design, 1999, 31(5): 335‒348
[14]Teng J, Huang W, Lou X. A new algorithm of cons-truction of polygon topological relationships in geo-graphic information systems // IEEE International Symposium on Geoscience and Remote Sensing. Den-ver, 2006: 2822‒2824
[15]闫浩文, 杨维芳, 陈全功, 等. 基于方位角计算的拓扑多边形自动构建快速算法. 中国图象图形学报, 2000, 5(7): 563‒567
[16]Liang X W, Liu Z Q. An algorithm of polygon auto-construction based on angle changing tendence. Jour-nal of Image & Graphics, 2005, 6(6): 785‒789
[17]李大军, 刘波, 赵宝贵, 等. 拓扑多边形自动构建的一种改进算法. 计算机工程与应用, 2005, 41(16): 80‒82
[18]付胜博, 戴冠中. GIS 中实时建立区域拓扑关系的快速算法. 信息安全与通信保密, 2006, 28(11): 66‒68
[19]Ling Y, Ouyang Y, Zhang M. Polygon auto-cons-truction algorithm based on vector external product of virtual arc // International Symposium on Intelli- gent Information Technology Application Workshops. Shanghai, 2008: 24‒27
[20]Krivograd S, Trlep M, Žalik B. A rapid algorithm for topology construction from a set of line segments // Wseas International Conference on Telecommuni-cations and Informatics. Istanbul, 2006: 133‒138
[21]卢浩, 钟耳顺, 王天宝, 等. 一种基于拓扑信息的多边形数据自动生成算法. 地理与地理信息科学, 2012, 28(4): 38‒41
[22]Vinh N N, Le B. Constructing and modeling parcel boundaries from a set of lines for querying adjacent spatial relationships // International Conference on Computational Science and Its Applications. Barce-lona, 2013: 540‒549
[23]Jia Q, Che D, Xiu C. A fast algorithm of polygon auto-construction based on left-turn algorithm in coal mine geological mapping. Science of Surveying & Mapping, 2016, 41(12): 70‒74
[24]Bentley J L, Ottmann T A. Algorithms for reporting and counting geometric intersections. IEEE Transac-tions on computers, 1979, 28(9): 643‒647
A Plane Sweep Based Arc Splitting and Polygon Auto-Construction Algorithm
Abstract Aiming at the deficiency of traditional polygon auto-construction algorithm in automation and time efficiency, which leads to the insufficiency of commercial GIS softwares’ data processing and spatial-temporal analysis ability, an arc splitting and polygon auto-construction algorithm based on plane sweep idea is proposed. Our algorithm contains three features as follows. First, it is a complete process from intersection testing until polygon construction. Next, it takes full advantage of useful information during intersection testing to realize arc splitting and polygon auto-construction at the cost of little algorithm complexity and computing resources. Finally, it avoids the calculation of nested relation and handles degenerate cases of bridge and dangling edge. The result of experiments proves the proposed algorithm improves efficiency significantly in comparison with traditional algorithms.
Key words plane sweep algorithm; arc splitting; polygon auto-construction
doi: 10.13209/j.0479-8023.2019.037
国家自然科学基金(U1433102)资助
收稿日期: 2018‒06‒15;
修回日期: 2018‒09‒19