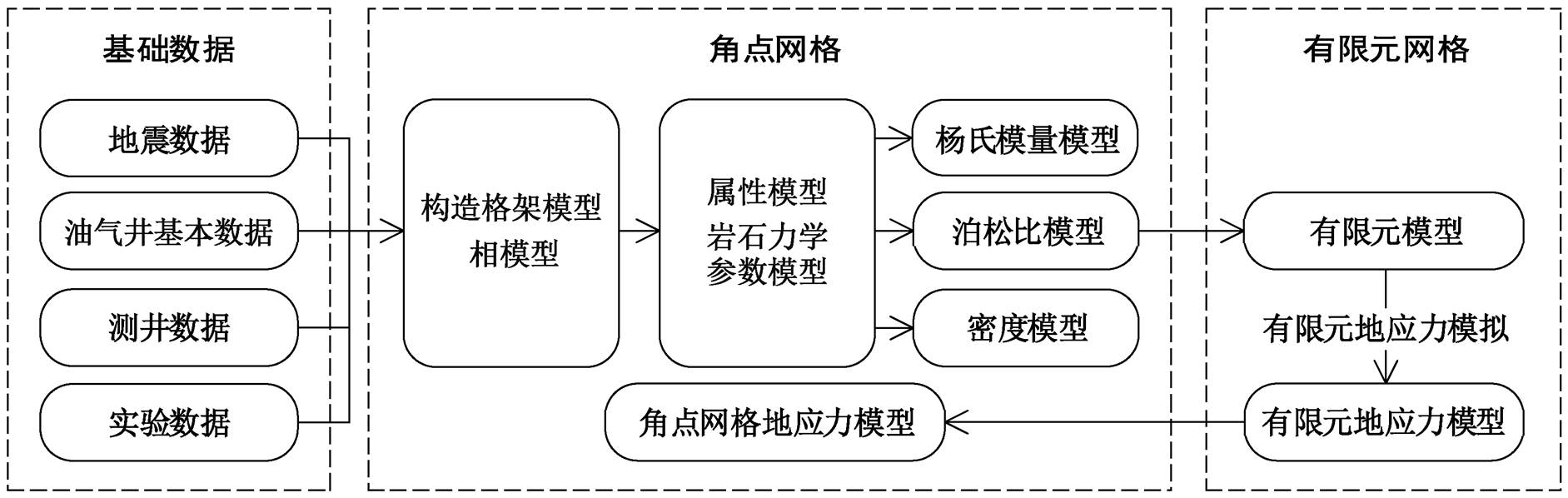
图1 基于角点网格的有限元应力模拟流程设计
Fig. 1 Design of major procedure of stress finite element simulation based on corner point grid
摘要 设计并实现三维角点网格模型的现今地应力有限元模拟方法。利用角点网格, 建立储层三维精细模型。应用网格转换算法, 将网格转换为对应的三维有限元网格模型, 采用有限元法模拟地应力场的分布。采用网格转换逆向方法, 将模型重新采样至对应的角点网格地质模型, 为后续数值模拟等流程提供数据支持, 从而保证流程的连续性和数据的一致性。通过X工区和Y工区两个油田实例数据, 模拟工区应力场分布。对比分析表明, 模拟值与实测值匹配性较好, 证明了方法的准确性和有效性。
关键词 地应力; 角点网格; 有限元网格; 网格转换
地应力又称地壳应力, 是岩体在自然状态下存在的力, 包含重力、构造应力和残余应力等。在漫长的地质演化过程中, 区域构造运动以及流体超压等各种复杂的物理化学作用导致区域地应力场不断调整, 形成具有时间和空间分布复杂性的地应力分布[1‒2]。非常规油藏的开发常常涉及大规模水力压裂, 而地应力场的大小和方向控制着油气田开发过程中人工裂缝的形成和展布[2‒4]。应力场的分布对钻井过程中井壁的稳定性等问题的研究也有十分重要的意义[5]。因此, 研究地应力场的分布对油气田的勘探开发具有重要意义[6‒7]。
角点网格由Ponting[8]提出, 并且通过ECLIPSE软件[9]实现在地质建模和油藏数值模拟的广泛应用[6,10]。随着技术的不断发展, 关于角点网格的研究逐渐完善[11‒13]。角点网格克服了传统正交性网格的不灵活性, 在表达油藏非均质性方面具有显著的优势, 可以准确地描述地层界面、断层面和尖灭等复杂地质情况[14‒15]以及储层的空间展布和属性分布特征[16‒17]。目前, 应用角点网格进行三维地应力模拟的研究较少, 通常采用有限元网格, 应用有限元方法进行三维应力场的模拟[18]。
有限元法是一种数值模拟技术, 可用于连续场问题的分析与求解, 应用领域十分广泛[19‒21]。在地应力场的数值模拟方面, 有限元法是目前应用最广泛的方法之一[22‒23]。通过建立有限元网格模型, 调整模型的边界荷载或边界位移, 可以建立较准确的基于有限元网格的三维地应力模型[24]。许多学者应用有限元方法实现复杂地质区域(如煤矿[25‒26]和隧道[27‒28]等)应力场的模拟, 但大部分研究都是直接基于有限元软件构建模型, 在油气藏这种地质结构复杂、埋藏较深的条件下, 很难建立精确的三维储层模型[24,29‒30]。
由于采用的网格剖分方法不同, 剖分后的角点网格系统中通常存在重复节点, 无法传递力、位移和能量等连续性变量, 因此基于角点网格建立的地质模型无法直接用于有限元模拟。与地质建模软件相比, 由于有限元模拟软件建模功能的局限性, 无法建立可以精细地描述储层属性特征的模型, 而地质建模软件则常常采用角点网格来实现储层的精细描述和表征。建立三维角点网格模型的现今地应力有限元模拟方法, 可以结合角点网格和有限元方法的优点, 基于角点网格建立精细的三维地质模型, 同时应用有限元方法, 进行三维应力场的模拟, 既可以有效地保留储层的特征, 也可以较准确地模拟三维应力场的分布状况。
本文建立基于角点网格的精细三维地质模型, 包含构造格架模型、相模型和属性模型。在此基础上, 设计并实现网格转换算法, 在保留储层结构和属性的情况下, 将基于角点网格的三维模型直接转换为可应用于有限元模拟的三维有限元模型。随后, 采用有限元方法, 模拟现今地应力场的分布特征, 获得三维有限元地应力场。最后, 通过网格转换后处理算法, 将地应力场重新采样至基于角点网格的三维地质精细模型, 从而实现直接基于角点网格的地应力模拟方法。
基于三维角点网格地质模型的地应力场有限元数值模拟流程(图1)主要包括以下几个步骤。首先, 利用角点网格建立较高质量的三维精细地质模型和构造模型, 即利用测井、地震和实验等基础数据, 采用三维地质构造建模方法建立三维地质网格模型, 利用属性建模插值方法建立岩石力学参数场模型。然后, 采用网格转换的方法, 将角点网格模型变换成对应的有限元网格模型, 采用有限元法模拟地应力场的分布。最后, 采用网格转换的逆方法, 将有限元地应力模型变换成对应的角点网格模型, 以便后续的分析和模拟(如甜点区域的评价、井网部署优化等)。
模拟过程中会用到角点网格和有限元网格两种不同类型的网格模型。由于角点网格与有限元网格的定义方式和数据结构不同, 使得角点网格模型与有限元网格模型的相互转换和识别存在很大问题, 对流程的连续性有较大的影响。利用网格转换算法, 将三维角点模型转换为有限元模型, 同时将岩石力学参数的属性一一对应有限元模型中有限元网格单元的材料参数, 不仅可以精确地保留地质建模软件建立的精细地质模型和属性模型的特征, 还可以克服有限元软件建模和网格剖分能力弱的缺点。

图1 基于角点网格的有限元应力模拟流程设计
Fig. 1 Design of major procedure of stress finite element simulation based on corner point grid
通过设定相应的约束条件(如位移约束和边界载荷约束等), 采用有限元方法, 可以模拟三维地应力场的分布特征, 在已知目标点多次约束反演的条件下, 获得真实分布的三维地应力场。本文设计并实现网格转换的逆向算法, 将三维有限元地应力场的应力属性重新采样至三维角点网格精细地质模型, 使得转换后的角点网格模型同时包含地应力的大小和方向, 保持了流程的连续性和数据的一致性, 可用于后期的甜点评价和井网部署等流程。
角点网格和有限元网格属于网格剖分后产生的网格模型。网格剖分主要用于数值模拟与计算, 依据不同的分类方法, 可以将网格分成多种类型: 按网格是否正交, 可分为正交网格和非正交网格; 按网格节点排列是否有序, 可分为结构化网格、非结构化网格和结构非结构混合网格; 按网格是否适应时间间歇的特点, 可分为自适应网格和非自适应网格; 等等。
结构化网格的网格区域内所有点都具有相同的毗邻单元, 横向或纵向的每一排具有相同的点数, 每个边界节点周围有两个单元, 每个内部节点周围有4个单元。角点网格属于结构化网格, 可以方便地实现储层区域边界拟合, 描述油气藏微构造形态、油藏边界、流动类型、水平井及断层, 在有限差分模拟器中实现流体的计算模拟。同时, 结构化网格还具有网格生成算法简单、生成速度快、生成质量好和数据结构简单有序等优点[31]。
角点网格属于非规则的六面体网格, 通过4条坐标线和8个网格节点(角点)坐标来描述网格块的形状, 如图2(a)和(b)所示。通过两个尺度为(i+1)× (j+1)的规则拓扑结构控制面, 控制单体结构单元。采用滑动的(k −1)条线来定义各个单元顶底界控制面和中间点的坐标, 从而在逻辑结构上形成i×j×k个子单元的规则拓扑结构模型, 如图2(c)和(d)所示。根据计算区域上下边界的笛卡尔坐标值, 采用以下公式的内插算法, 直接生成计算域内笛卡尔坐标值分布的网格:
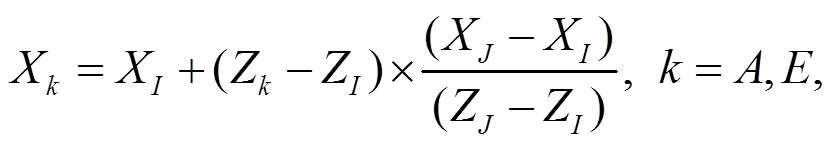
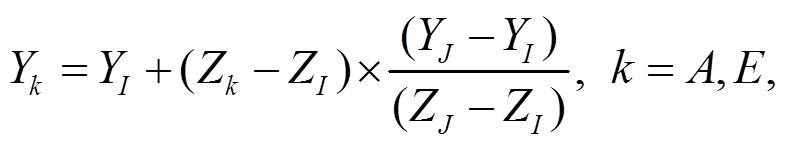
其中, A点的坐标为(XA, YA, ZA), E点的坐标为(XE, YE, ZE), I点的坐标为(XI, YI, ZI), J点的坐标为为(XJ, YJ, ZJ)。X 方向、Y 方向和Z 方向(深度)在逻辑上分别有(i+1)、(j+1)和(k+1)条坐标线, 将网格模型剖分成i, j和k个网格单元。

图2 角点网格示意图
Fig. 2 Illustration of corner-point grid
有限元法又称有限单元法, 是将求解的目标区域的方程进行离散, 使问题转化为多个有限单元(这些单元间依靠节点相互链接), 并在各个有限单元分别求解的方法。有限元网格指在应用有限元方法时通过网格剖分算法形成的结构单元, 不仅包含结构化网格, 还包含非结构化网格, 结构化网格主要为六面体网格, 非结构化网格主要为四面体网格, 应用都较广泛[32]。结构化网格(六面体网格)和非结构化网格(四面体网格)的相互转化关系如图3(a)所示, 其中包含I和II两个网格单元。网格单元I包含有限元节点1-2-4-5-7-8-10-11, 网格单元II包含有限元节点2-3-5-6-8-9-11-12。网格单元I可以转换为对应的 4 个四面体结构单元 i (节点1-10-8-7)、ii (节点1-8-5-2)、iii (节点1-5-10-4)和 iv (节点1-8-10-5)。
有限元网格由各节点连接, 与角点网格在数据结构上最主要的区别是相邻接单元间的节点处理。为了力、位移和能量等变量传递的连续性, 有限元网格的相邻网格间共用相同的网格节点。角点网格的相邻网格间节点是相对独立的, 各个网格分别拥有自己的网格节点。图3(b)表示简化后的网格系统, 其中仅包含网格单元I和II。有限元网格的网格系统包含两个网格单元(I和II)和12个节点(节点1~12), 其中节点2-5-11-8为网格I和II共用。角点网格的网格系统中仍包含两个网格单元, 但是节点数为16, 即网格单元I包含节点1-2-4-5-7-8-10-11, 网格单元II包含节点2′-3-6-5′-8′-9-12-11′, 其中网格节点2-2′, 5-5′, 8-8′和11-11′为相邻接网格中各个网格包含的节点, 虽然节点位置信息相同, 但是属于不同的网格单元。
由于网格系统的组织方式不同, 使得角点网格模型和有限元网格模型不能很好地实现转换。因此, 本文设计网格转换算法, 实现角点网格与有限元网格之间相互转换, 从而实现模拟流程的一致性和连续性。
定义两个结构体, 分别用来储存节点和网格信息。GPoint{}结构体用来储存角点网格模型中各个点的位置信息, 主要包含X, Y, Z坐标信息; GVolume {}结构体用来存储网格的相关信息, 主要包含网格的编号、网格包含的角点以及网格的属性信息(网格的有效性和密度以及岩石力学参数等)。
网格双向转换算法中主要包含以下几种函数(图4): PreProcessAlgorithm()函数用来优化输入的角点网格模型文件, 检查输入的模型文件的有效性; InputModelOperation()函数用来处理输入的角点网格模型, 并记录角点网格模型的相应信息; Gene-rateModelNode()函数用来将角点网格模型转化为有限元网格节点; GenerateFiniteGrid()函数通过处理后的有限元节点, 建立三维有限元网格模型; Gene-rateMateiralNumber()函数和GenerateMateiralAttri-bute()函数将三维有限元网格逐个进行编号, 同时针对每一个有限元网格, 通过对应角点网格的密度、岩石力学参数等属性信息, 分别设置有限元网格的材料属性参数; GenerateLoad()函数和Genera-teDisplacement()函数用来设置网格边界载荷和边界约束条件; StressOperation()函数包含模型边界载荷和边界约束在已知目标点的多次反演以及有限元模拟算法的执行, 获得三维有限元地应力场模型的两种功能; OutputCtrl()函数用来自动存储三维有限元地应力模型节点的坐标和应力应变的相关信息, 同时用来处理和存储各个有限元网格中应力的大小与方向信息; PostProcessAlgorithm()函数通过读取存储的三维有限元地应力模型, 将其转化为基于角点网格的三维地应力模型。
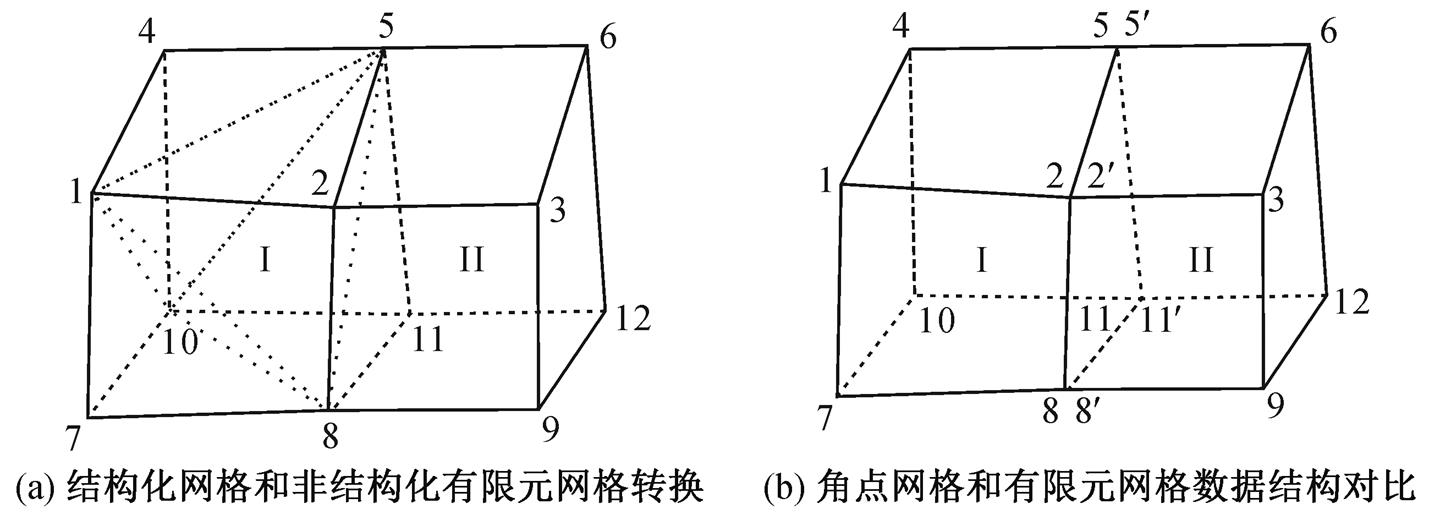
图3 有限元网格示意图
Fig. 3 Illustration of finite-element grid
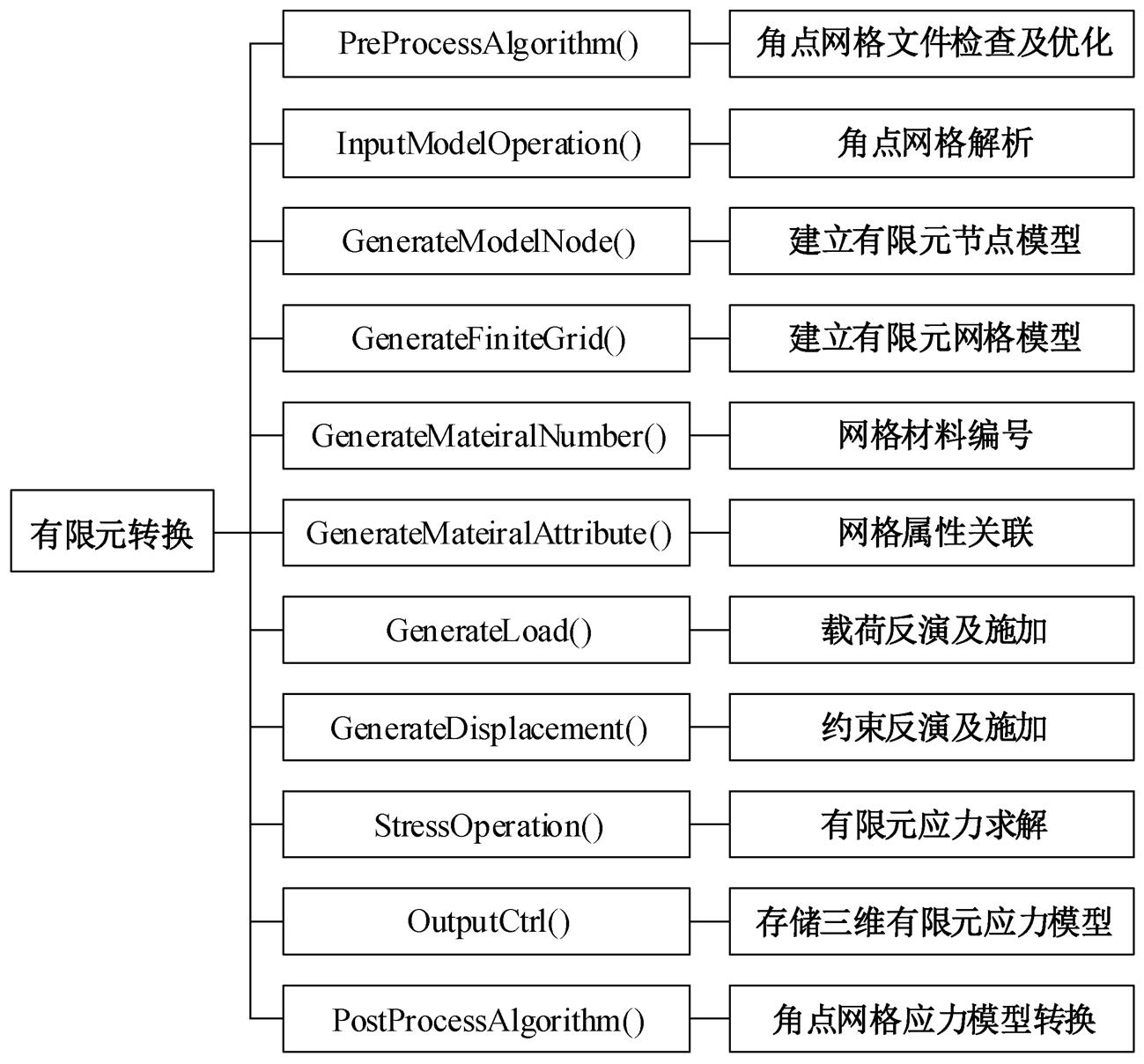
图4 算法函数及功能
Fig. 4 Function of grid coversion algorithm
首先, 利用PreProcessAlgorithm()检查输入模型的有效性, InputModelOperation()读入原始的三维角点网格模型, 记录角点网格模型中所有的节点和网格信息, 提取模型中的节点信息, GenerateModel-Node()对重复性的网格节点进行处理, 转化为对应的有限元模型的节点。然后, GenerateFiniteGrid()读取网格模型中的网格有效性信息, 将有效网格的对应节点进行关联, 从而获得三维有限元网格模型, GenerateMateiralNumber()和GenerateMateiralAttribu-te()再将网格中的属性信息与有限元网格的材料属性进行关联, 对单一网格进行网格材料的编号, 再针对每一种网格材料, 分别赋予不同的网格属性(包含杨氏模量、泊松比和密度), 从而获得完整的三维有限元模型(图5)。
利用网格转换算法分别测试不含无效网格和含无效网格的三维角点网格。分别读入角点网格模型, 对网格节点进行处理, 转换为对应的有限元节点模型。根据节点与网格的对应关系及网格的有效性, 将节点连接成有限元网格, 实现角点网格向有限元网格的转换。分别对每个网格对应的材料属性进行编号和网格属性参数的关联, 实现对每个网格分别赋予不同的网格属性(杨氏模量、泊松比和密度), 有效地保留储层或岩石内部的各向异性特征(图6)。
首先, 在已知目标点的应力或位移值的约束下, 通过算法内置的参数反演算法(集成在GenerateLoad ()和GenerateDisplacement()函数中), 自动在Gene-rateLoad()函数和GenerateDisplacement()函数中设置合理的边界载荷和边界约束的, 通过StressOpera-tion()建立有限元三维地应力场模型, 该模型可以较准确地反映地应力场的分布。Out-putCtrl()自动存储三维有限元地应力模型中的各种信息, 然后通过PostProcessAlgorithm(), 将该模型进一步转化为基于角点网格的三维地应力场模型(图7)。
基于网格前处理步骤建立的有限元网格模型, 针对已知点的应力值, 反演网格边界的约束和应力情况, 对目标储层设置相应的载荷和约束条件。采用有限元方法进行目标储层的地应力模拟, 将获得的三维有限元网格应力场模型(包含应力的大小和方向)无缝地采样至对应的角点网格模型(图8)中, 用于后续油藏数值模拟等流程, 保证分析流程的连续性。
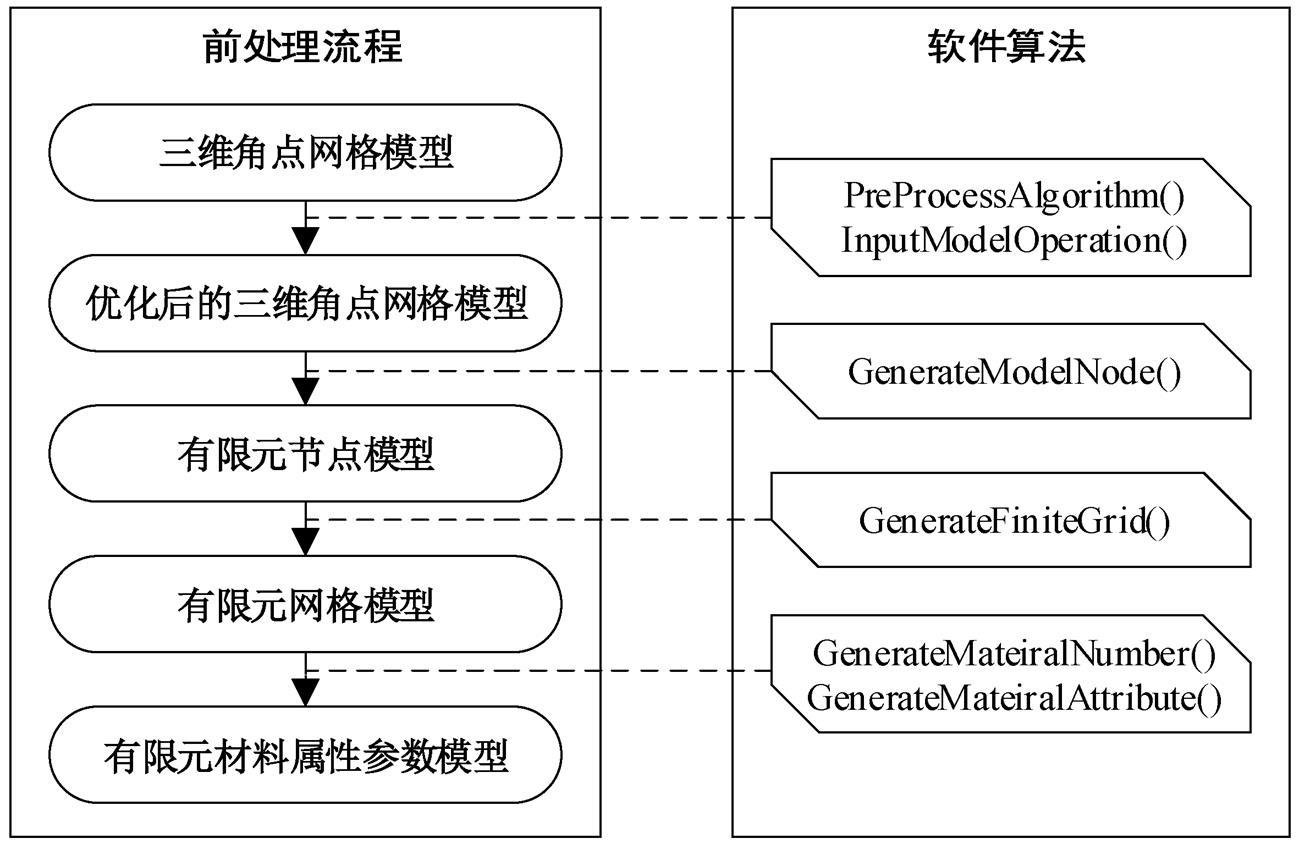
图5 前处理流程
Fig. 5 Pre-processing procedure
取两个实际工区(X工区和Y工区)的数据作为测试对象, 分别基于工区的角点网格的三维精细岩石力学参数模型进行算法测试, 对工区网格数据进行转换。在进行约束反演和有限元应力模拟后, 获得工区的三维有限元地应力场模型。将模型进行二次转换, 获得基于角点网格的应力场模型。针对该模型数据, 分别验证应力模拟值的大小和方向。结果表明, 模拟结果与实测数据的符合程度较高, 证明了算法的有效性和准确性。
X工区超低渗致密砂岩储层是中国新疆某市的一个典型超低渗岩性‒断块油气藏。该地区油藏渗透率低于0.1 mD, 储层孔隙度为8%~12.1%; 构造类型为单斜构造, 地层倾角为10°~13°; 油藏埋深为2300~3300m, 油水界面深度为2700~2750m; 含油面积为11.3km2, 地质储量23.95×106t, 可采储量为3.83×106t。X工区共有161口油水井, 截至2016年9月, 该工区累计产油1.856×106t, 采出程度约为7.72%, 地层平均压力为24.7MPa, 工区内有7口井(X1~X7)含实测地应力数据。
基于相关基础数据, 采用本文算法, 将地质工程师建立的该工区岩石力学参数模型(图9(a)和(b))进行网格转换, 模拟该工区的有限元地应力, 获得该工区最大和最小水平地应力场模型。通过逆向网格转换, 获得角点网格的三维模型。基于转换后的最大和最小主应力角点网格模型, 建立该地区水平应力差模型, 并在GSIS-Modeling软件平台实现模型的可视化, 如图9(c)所示。
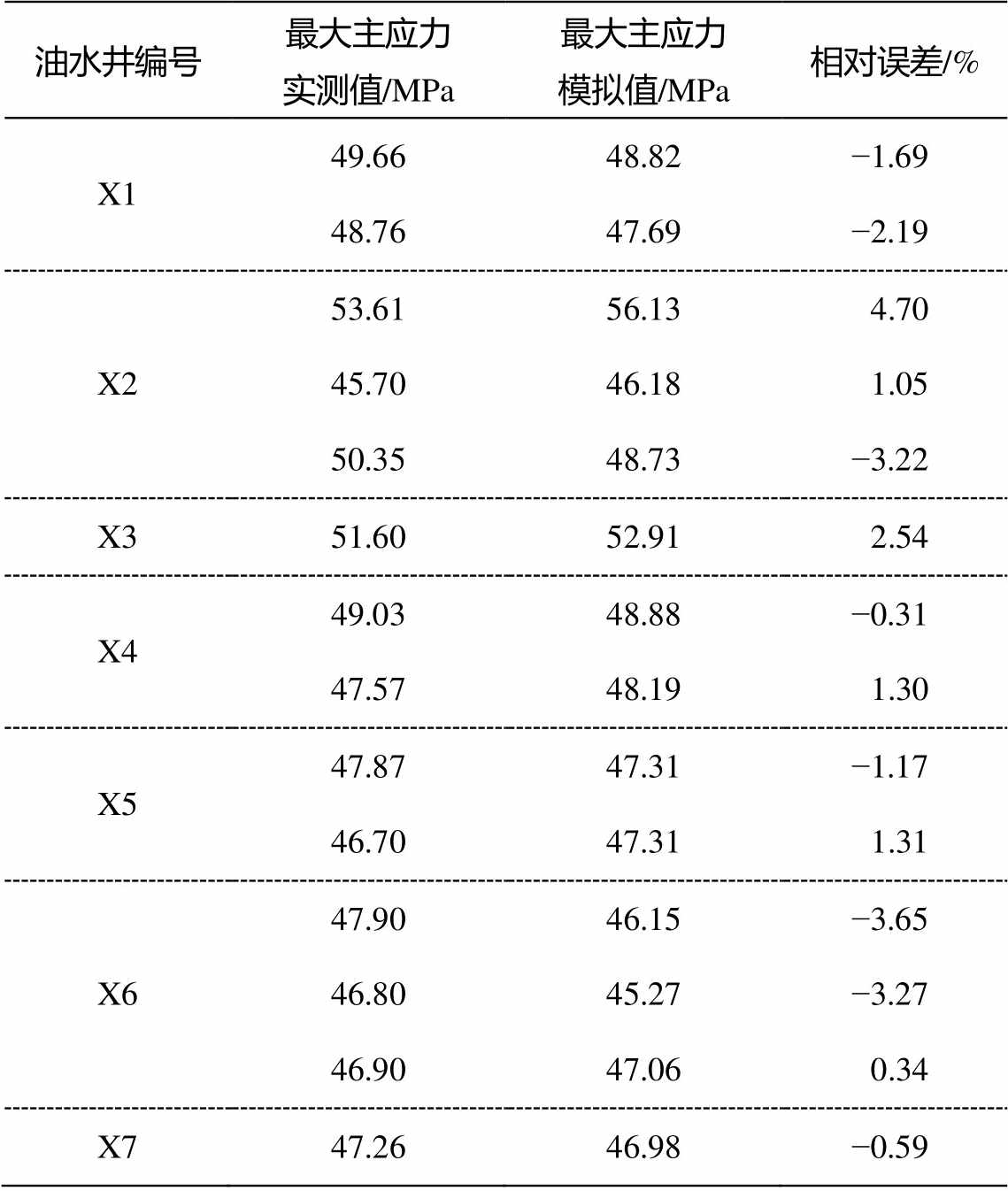
取X工区内7口井的最大主应力实测数据, 提取模拟应力场中对应的网格。通过对比模拟结果与实测结果(表1), 发现模拟值与实测值之间的相对误差较小, 正负偏差均在5%以内, 表明模拟值较准确地描绘了该工区地应力场的分布, 三维角点网格模型的现今地应力有限元模拟方法可以准确地模拟X工区的应力场分布, 方法的有效性和准确性得到很好的验证。模拟值与实测值的误差可能来自以下3个方面: 1)工区三维泊松比模型和杨氏模量模型基于测井数据、采用空间内插算法建立, 该模型的精度直接影响有限元网格模型材料参数的准确性, 进而影响模拟结果的精度; 2)实测地应力数据为该井某一特定深度处的测量值, 模拟值为该深度处对应网格的应力数据, 网格数据为该点上下一定范围内应力的均值, 因此产生相应的误差; 3)通过设定合理的边界载荷和边界约束, 可以获得该工区的三维应力场模型, 边界载荷数据的精度和边界网格约束条件的差异使模拟值与实测值产生相应的误差。
Y工区致密砂岩储层位于中国新疆某市。该地区储层孔隙度在6%~25%间, 平均约为11%, 渗透率低于0.1mD, 平均约为0.01mD; 构造类型为东高西低的西倾单斜构造, 地层倾角约为3°~5°, 断裂不发育; 储层沉积相以湖泊相为主, 也有三角洲相; 岩石类型主要包括黑色泥岩和细粉砂岩等, 为典型的致密砂岩储层。Y工区分布18口井, 其中的一口井(Y1)具有成像测井解释数据。

图6 前处理效果示意图
Fig. 6 Illustration of pre-processing procedure
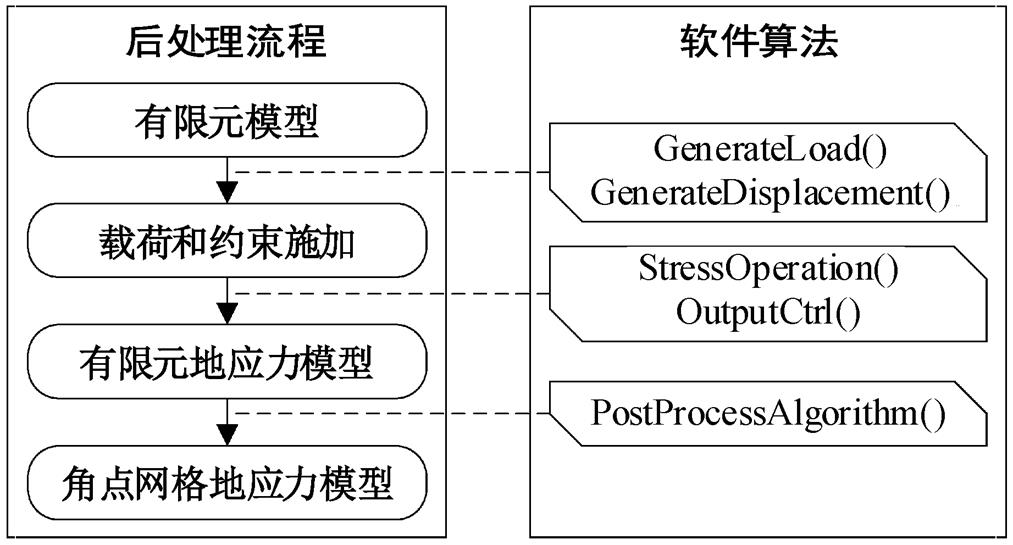
图7 后处理流程
Fig. 7 Post-processing procedure

图8 后处理流程效果图
Fig. 8 Illustration of post-processing procedure
通过GSIS-Modeling软件平台, 建立该工区的角点网格精细岩石力学参数模型(图10(a)和(b)), 采用本文方法模拟该工区的有限元地应力, 并将模拟结果转换为对应的角点网格模型。基于主应力的大小和方向, 建立该工区最大差应力模型(图10(c))和应力方向模型(图10(d)和(e))。
将 Y1 井作为验证井, 验证模拟得到的应力方向。提取该井轨迹上对应网格的应力方向模拟值, 与成像测井解释的应力方向实测结果进行对比。如图 11 所示, 应力方向的模拟结果与实测结果的符合程度较好, 较准确地反映了该工区应力的分布状况, 对工区后续甜点区域评价、井网部署和储层的大规模压裂改造具有较重要的指导意义。实测应力方向与模拟应力方向的误差可能是由于钻井过程中井壁受应力控制对称地崩落, 影响成像测井的解释结果而产生的。
本文通过分析网格结构, 设计模拟流程, 建立三维角点网格模型的地应力有限元模拟方法, 在保留三维精细地质模型的基础上, 较准确地模拟了三维应力场的分布, 并通过两个油田实例, 验证了方法的准确性和有效性。本文主要结论如下。
1)角点网格具有规则的数据结构, 可以方便地实现区域边界拟合, 同时还具有生成速度快、生成质量好以及数据结构简单等优点, 基于角点网格的精细三维地质模型可以准确地反映储层的空间展布特征。

图9 X工区三维角点网格属性模型
Fig. 9 Attribute models of oilfield X based on corner-point grid
表1 X工区最大主应力模拟值与实测值结果对比
Table 1 Value of maximum principle stress comparison and relative devation between simulation results and real data of oilfield X
油水井编号最大主应力实测值/MPa最大主应力模拟值/MPa相对误差/% X149.6648.82−1.69 48.7647.69−2.19 X253.6156.134.70 45.7046.181.05 50.3548.73−3.22 X351.6052.912.54 X449.0348.88−0.31 47.5748.191.30 X547.8747.31−1.17 46.7047.311.31 X647.9046.15−3.65 46.8045.27−3.27 46.9047.060.34 X747.2646.98−0.59
2)有限元法在求解非线性力学问题和复杂应力应变问题上具有较大优势, 基于有限元网格的有限元地应力模拟可以较准确地获取目标区域的应力分布状况。
3)基于角点网格和有限元网格数据结构的网格转换算法, 在保留网格特征的基础上, 可以实现网格之间的互相转换, 同时角点网格的属性信息也可以准确地采样至对应的有限元网格中, 自动设置对应的材料属性参数。
4)基于角点网格的有限元地应力模拟充分保留了角点网格和有限元方法的优势。通过网格转换算法, 使角点网格与有限元网格有机地融合, 既有效地保留了基于角点网格储层的结构特征, 又可以利用有限元方法对研究区进行应力模拟, 较准确地获得目标区域的地应力分布。
5)基于角点网格的有限元地应力模拟方法的实现, 可以为油田甜点区域的评价、油藏数值模拟、裂缝形态和分布的模拟以及井网的优化部署提供重要的依据, 确保油气田勘探开发过程中模型数据和流程的连续性。
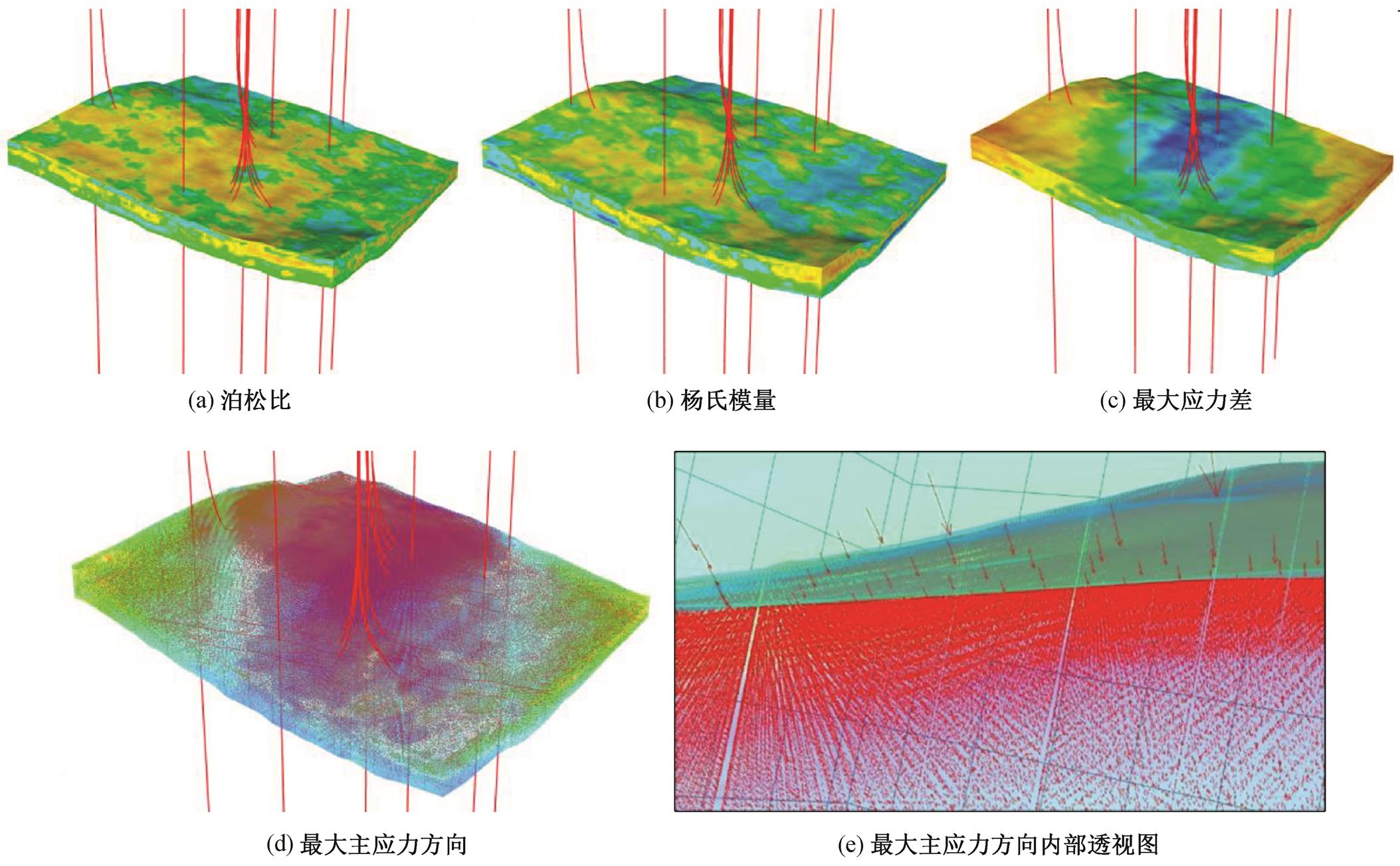
图10 Y工区三维角点网格属性模型
Fig. 10 Attribute models of oilfield Y based on corner-point grid
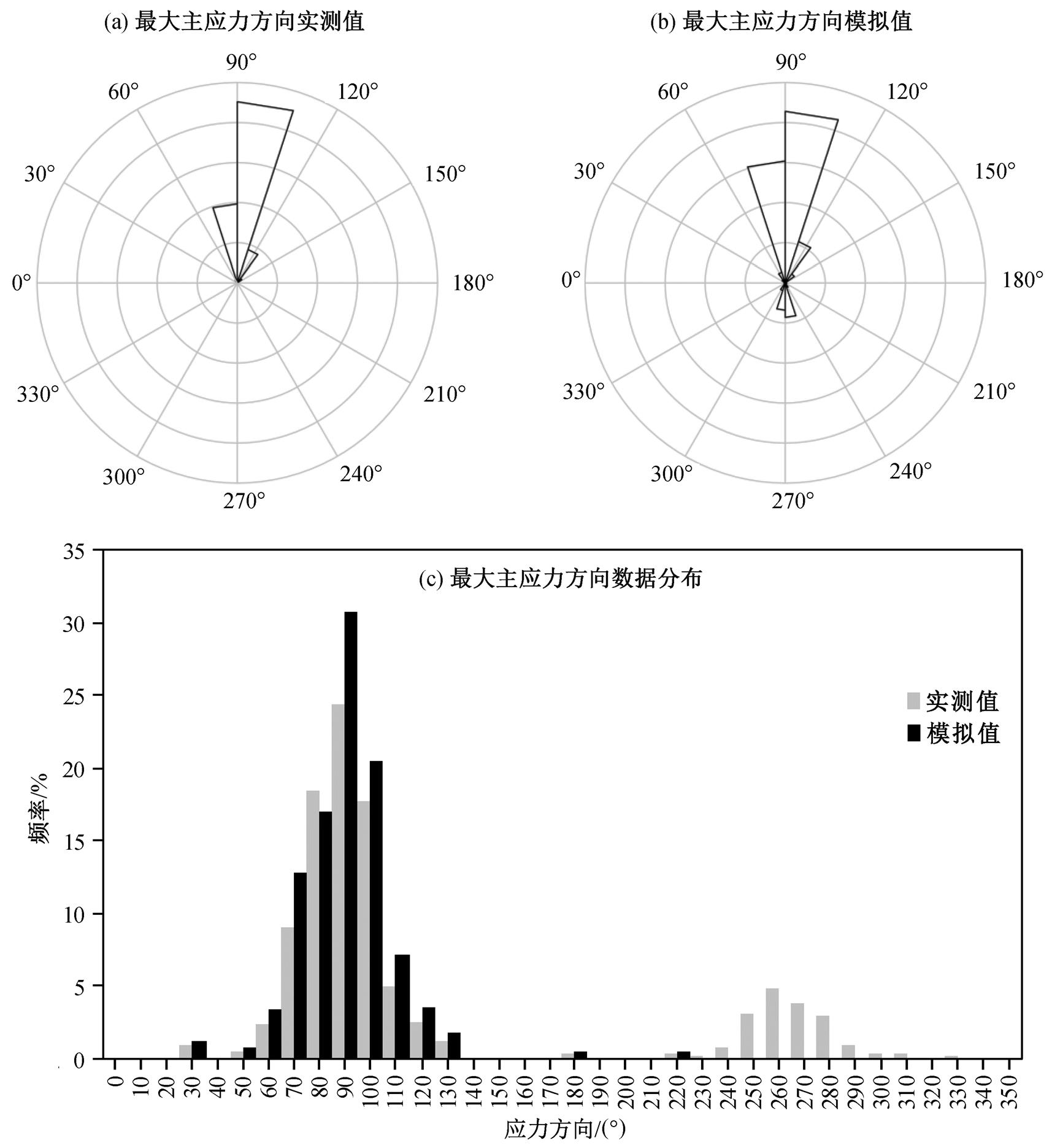
图11 Y工区最大主应力方向对比
Fig. 11 Maximum principle stress direction comparison between simulation results and real data of oilfield Y
参考文献
[1]Zang A, Stephansson O. Stress field of the earth’s crust. Dordrecht: Springer Netherlands, 2010
[2]Zang A, Stephansson O, Zimmermann G. Keynote: fatigue hydraulic fracturing. Procedia Engineering, 2017, 191(1): 1126‒1134
[3]Huang S, Liu D, Yao Y, et al. Natural fractures ini-tiation and fracture type prediction in coal reservoir under different in-situ stresses during hydraulic frac-turing. Journal of Natural Gas Science and Enginee-ring, 2017, 43(1): 69‒80
[4]Parvizi H, Rezaei-Gomari S, Nabhani F, et al. Eva-luation of heterogeneity impact on hydraulic fractu-ring performance. Journal of Petroleum Science and Engineering, 2017, 154(1): 344‒353
[5]Magnier A, Scholtes B, Niendorf T. Analysis of res-idual stress profiles in plastic materials using the hole drilling method — influence factors and practical as-pects. Polymer Testing, 2017, 59(1): 29‒37
[6]Nguyen B N, Hou Z, Bacon D H, et al. Three-dimensional modeling of the reactive transport of CO2 and its impact on geomechanical properties of reser-voir rocks and seals. International Journal of Green-house Gas Control, 2016, 46(1): 100‒115
[7]Lavrov A, Larsen I, Holt R M, et al. Hybrid FEM/ DEM simulation of hydraulic fracturing in naturally-fractured reservoirs // Proceedings of the 48th US Rock Mechanics/Geomechanics Symposium. Minnea-polis: American Rock Mechanics Association, 2014: 626‒633
[8]Ponting D K. Corner point grid geometry in reservoir simulation // Proceedings of the ECMOR I — 1st European Conference on the Mathematics of Oil Re-covery. Cambridge, 1989: 1305
[9]Schlumberger. ECLIPSE 2014 [EB/OL]. (2014‒07‒04) [2017‒03‒24]. https://www.software.slb.com/products/ eclipse/eclipse-2014
[10]Wu Q, Xu H. Three-dimensional geological modeling and its application in digital mine. Science China Earth Sciences, 2014, 57(3): 491‒502
[11]Aarnes J E, Efendiev Y. A multiscale method for modeling transport in porous media on unstructured corner-point grids. Journal of Algorithms & Compu-tational Technology, 2008, 2(2): 299‒318
[12]Han J, Shi F Z, Wu S H, et al. Generation algorithm of corner-point grids based on skeleton model. Com-puter Engineering, 2008, 34(4): 90‒92
[13]Mouton T, Borouchaki H, Bennis C. Hybrid mesh generation for reservoir flow simulation: extension to highly deformed corner point geometry grids. Finite Elements in Analysis & Design, 2010, 46(1/2): 152‒ 164
[14]Schlumberger. Petrel 2016 [EB/OL]. (2016‒06‒24) [2017‒03‒25]. https://www.software.slb.com/products/ petrel/petrel-2016
[15]Schlumberger. Petrel 2017 [EB/OL]. (2017‒06‒23) [2018‒03‒25]. https://www.software.slb.com/products/ petrel/petrel-2017
[16]Chen Q, Liu G, Li X, et al. A corner-point-grid-based voxelization method for the complex geological struc-ture model with folds. Journal of Visualization, 2017, 19(3): 1‒14
[17]Surhone L M, Timpledon M T, Marseken S F. Corner-point grid. Hong Kong: Betascript Publishing, 2010
[18]Tian Y P, Xiong L, Xing L I. Finite element method of 3-D numerical simulation on tectonic stress field. Earth Science, 2011, 36(2): 375‒380
[19]ANSYS. ANSYS 15.0 [EB/OL]. (2013‒12‒17) [2017‒ 03‒26]. http://www.ansys.com
[20]Ciarlet P G. The finite element method for elliptic problems. Paris: Université Pierre et Marie Curie, 1978
[21]Bathe K J. Finite element procedures. 2nd Edition. Watertown, MA: Klaus-Jürgen Bathe, 2014
[22]Wang H. Three dimensional tectonic stress field and migration of oil and gas in Tanhai. Acta Geosicientia Sinica, 2002, 23(2): 175‒178
[23]Li K, Zhang S, Yu W. Application of complex struc-ture modeling in tectonic stress field simulation // Proceedings of the International Geophysical Confe-rence and Exposition. Beijing, 2009: 1169
[24]Guo P, Yao L, Ren D. Simulation of three-dimensional tectonic stress fields and quantitative prediction of tectonic fracture within the Damintun Depression, Liaohe Basin, northeast China. Journal of Structural Geology, 2016, 86(1): 211‒223
[25]George J D S, Barakat M A. The change in effective stress associated with shrinkage from gas desorption in coal. International Journal of Coal Geology, 2001, 45(2/3): 105‒113
[26]Somerton W H, Söylemezoḡlu I M, Dudley R C. Effect of stress on permeability of coal. International Journal of Rock Mechanics & Mining Sciences & Geomechanics, 1975, 12(5/6): 129‒145
[27]Bhasin R, Grimstad E. The use of stress-strength rela-tionships in the assessment of tunnel stability. Tun-nelling & Underground Space Technology, 1996, 11 (1): 93‒98
[28]Eberhardt E. Numerical modelling of three-dimension stress rotation ahead of an advancing tunnel face. International Journal of Rock Mechanics & Mining Sciences, 2001, 38(4): 499‒518
[29]Lin T, Yu H, Lian Z, et al. Numerical simulation of the influence of stimulated reservoir volume on in-situ stress field. Journal of Natural Gas Science and Engineering, 2016, 36(1): 1228‒1238
[30]张志强, 师永民, 卜向前, 等. 低渗透油藏注水开发中地应力方向变化的研究分析. 北京大学学报(自然科学版), 2016, 52(5): 861‒870
[31]周为喜. 基于角点网格的煤储层三维建模研究与应用[D]. 北京: 中国矿业大学, 2015
[32]苗明. 数模网格构建与参数网格化技术研究[D]. 青岛: 中国石油大学(华东), 2008
Research of Crustal Stress Simulation Using Finite Element Analysis Based on Corner Point Grid
Abstract The development of stress finite element analysis approach based on 3D corner-point grid can establish accurate crustal stress field. Firstly, corner-point grid is employed to establish the detailed structure and attribute model of reservoir. Secondly, grid conversion algorithm is applied to convert corner-point grid to corresponding finite-element grid. Then, finite element analysis is used to get attribute model based on finite-element grid which reflects the distribution of crustal stress. Lastly, grid conversion algorithm is operated to reverse the attribute model to another format which is based on corner-point grid for subsequent analysis. Thus, the procedure continuity and data consistency has been proved by this approach. Furthermore, real data collected from oilfield X and Y are employed to simulate stress distribution and the validity and accuracy of the proposed approach can be verified by comparison between simulation results and real data.
Key words crustal stress; corner-point grid; finite-element grid; grid conversion
doi: 10.13209/j.0479-8023.2019.020
国家科技重大专项(2017ZX05013-002)和中国石油勘探开发研究院科技专项(RIPED-2016-JS-276)资助
收稿日期: 2018-05-15;
修回日期: 2018-06-12