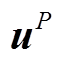可由应变核
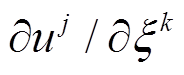引起的位移场叠加表示为摘要 根据 Okada 线弹性理论, 提出并建立海域天然气水合物开采的海底变形场模型, 对开采产生的海底变形场进行正演模拟, 并采用模拟退火方法, 对合成观测数据进行模型参数反演。结果表明, 利用测斜仪监测能够得到水合物开采区域准确的倾角、方位角和体积等信息。不同噪声水平下的测试结果表明, 所采用的模型参数反演方法具有良好的抗噪性。另外, 结合 2017 年中国南海神狐海域水合物开采试验, 分析测斜仪监测在实际应用中的可行性, 表明“产能递减型”开采方案在海底稳定性方面具有一定的优势。
关键词 天然气水合物; 海底变形监测; 测斜仪; 倾斜场; 模拟退火
天然气水合物是以甲烷为主的轻烃气体在低温高压条件下与水相互作用, 气态物质充填或被束缚在笼状水分子结构中形成的冰晶状物质, 俗称可燃冰[1‒2]。地球上的天然气水合物蕴藏量十分丰富, 主要分布于海底及陆上冻土带, 其中 90%以上的天然气水合物贮存在大陆边缘(包括沟盆体系、陆坡体系、边缘海盆陆缘等)海底的砂砾中, 集中分布在与泥火山、热液活动、盐底辟构造及大型断裂构造有关的深海盆地[3‒4]。目前, 在加拿大 Mallik 陆上冻土带[5]、美国 Ignik Sikumi 陆上冻土带[6]、日本南海海槽[7]以及中国南海神狐海域[8]等地区已相继开展天然气水合物开采试验。
在水合物开采过程中, 固体水合物分解为孔隙水和自由气体, 造成沉积物骨架软化和储层液化。随着天然气水合物生产试验的相继开展, 人们日益担心水合物开采过程中可能出现海底滑坡、滑塌和浊流等环境问题[9‒10]。当储层中以结构型水合物为主时, 高饱和度的水合物在储层中起到一定程度的支撑作用。随着水合物的分解, 储层孔隙压缩会引起海底局部区域发生变形[11‒12], 例如在加拿大Mallik 冻土带水合物生产试验中观测到试验场井口附近的轻微塌陷[13]。与冻土带环境相比, 海域水合物赋存在固结程度不高的沉积物孔隙中, 开采过程中可能引发更严重的海底塌陷甚至滑塌现象, 不但危及生产安全, 甚至可能导致甲烷气体大量泄露, 从而带来更严重的环境问题。因此, 有必要对天然气水合物开采引发的海底形变开展监测。
目前, 有关海域天然气水合物开采引发海底变形及其监测手段的研究非常匮乏。近年来, 伴随着传感器技术的发展, 使用高精度倾斜传感器(又称测斜仪)测量地表形变已经在水力压裂监测和火山研究等领域得到成功的应用[14‒15]。高精度测斜仪通过测量地层及地表微量形变产生的相对于垂直方向的角度变化来描述变形的程度及范围, 该技术的应用对象目前局限于陆地, 在海域天然气水合物开采引发海底变形监测方面未见相关研究。本文尝试性地将测斜仪监测技术应用于海底形变监测, 首先建立海域天然气水合物开采的海底变形模型, 对其产生的海底位移场及倾斜场进行正演模拟, 然后采用地球物理反演方法, 对模型参数进行反演, 并针对实际数据中可能存在的噪声对反演结果的影响进行分析。
在海域天然气水合物开采过程中, 孔隙中的水合物发生分解, 会导致地层各微观粒子间发生相对于平衡位置的错动。这种位错导致的应力应变改变以能量的形式向各个方向传播, 进而产生变形场。本文基于位错与力系的等价性, 将位错产生的位移场用拉张型力系下的点源表示, 通过对点源进行三重积分, 得到块状模型(模拟水合物开采效应)产生的变形场。
1.1.1 点源产生的位移场
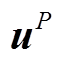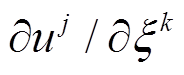在各向同性介质中, 基于位错与体力系的等价关系[16], 拉张位错可表示为 3 个向量偶极子的叠加。在对应的拉张体力系(如图 1 所示)下, 点源 P表示任一相对于平衡位置错动的天然气水合物微观粒子, 这些微观粒子共同构成天然气水合物分解的矩形变形面 Σ。在笛卡尔坐标系中, 此变形面 Σ 的中心点坐标为(0, 0, −c), 相对于水平地层的倾斜角度为 δ, 面元 dΣ 法线上的方向余弦可表示为(0, −sinδ, cosδ)。考虑天然气水合物开采产生的变形场的方向性, 半无限空间中任一点源产生的位移场可由应变核引起的位移场叠加表示为
(1)其中, M0为地震矩; F为点(ξ1, ξ2, ξ3)处的力(幅度为F); β=(λ+μ)/(λ+2μ),λ和μ为拉梅常数。
1.1.2 块状模型产生的变形场
以开采井在海底面的投影点为笛卡尔坐标系的原点, 定义 x 轴、y 轴和 z 轴的正方向分别对应正东、正北和垂直向上方向。天然气水合物开采导致的储层体积变化可用长度为 L, 宽度为 W, 高度为H, 倾角为 δ, 中心深度为 c 的三维块体等效表示(图2)。该模型的体积即为实际产出的天然气(包括固态水合物分解的天然气和可能存在的原位游离气中产出的部分)、水(包括固态水合物分解的水和储层中的自由水产出的部分)以及出砂占据的全部孔隙空间之和。这样, 整个储层因水合物开采产生的变形场可由块状模型产生的变形场等效地表示。
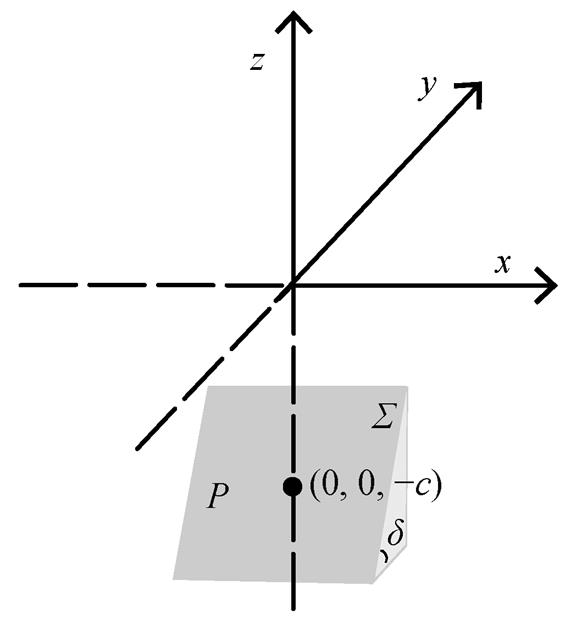
图1 点源示意图
Fig. 1 Schematic diagram of the point source
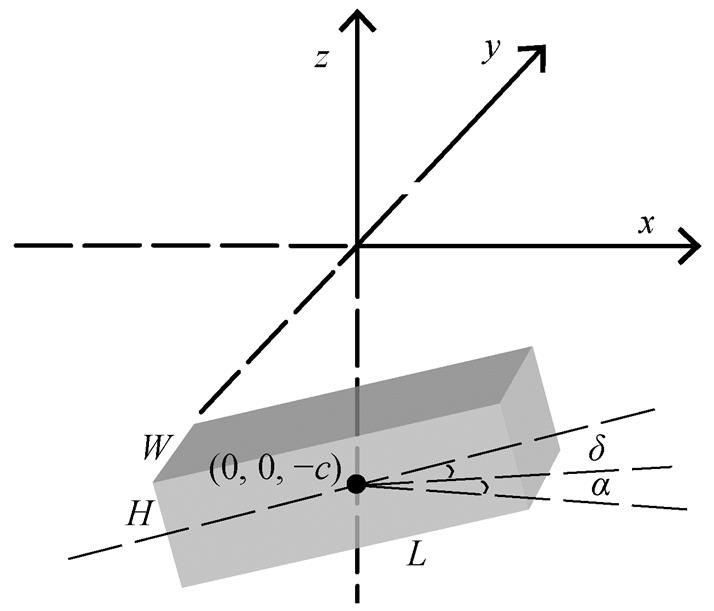
图2 块状模型示意图
Fig. 2 Schematic diagram of the block model
参考 Okada[17‒18]的方法, 根据线弹性理论, 对点源产生的位移场进行三次积分, 得到块状模型(block model, BM)产生的位移场 uBM, 接着对所得位移场求梯度, 即可得到半无限空间中任一点由上述块状模型引起的位移场对应的倾斜场。x方向的倾斜场:
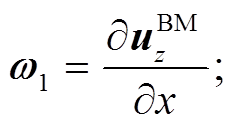(2)y方向的倾斜场:
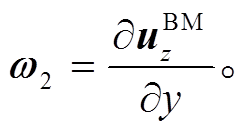(3)
反演海底变形场对应的模型参数是一类非线性优化问题。本文采用模拟退火法[19‒21]对天然气水合物分解等效模型的几何参数进行反演。目标函数的建立是地球物理反演问题的关键, 本文中目标函数定义为测斜仪所记录的观测值与模型理论值之间的相对拟合差, 计算公式为
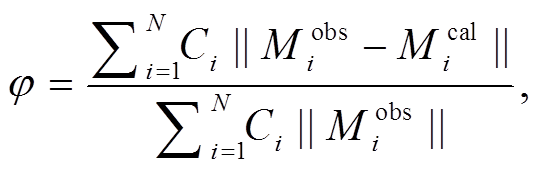(4)其中, N 为观测点个数;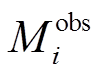
和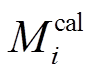
分别表示第 i 个观测点处倾斜场的实际观测值和理论计算值; Ci 为权重系数, 取值范围为 0~1, 其数值大小取决于观测数据的质量。
图 3 为海域天然气水合物开采的简化地质模型。忽略开采井附近海底的地势起伏, 假设 35 个海底测斜仪(编号依次为 1~35)以开采井为中心呈网格状均匀地布设, 网格间距 100m。在实际开采过程中, 可认为模型中心在开采井井下作业段中心点附近。定义以块状模型中心点为轴心, 倾角为模型长轴与水平面的夹角(−90°<δ<90°), 方位角为长轴的水平投影与 x 轴正向的夹角(−180°<α<180°), 正演模型的参数如表1所示。
以中国南海神狐海域 W-11 井为例, 该储层段中含水合物层的厚度约为 70m, 饱和度平均值为40%, 最高值可达 53%[22‒23]。由于结构型水合物往往存在于高饱和度、高孔隙度储层中, 因此本文取储层深度(m)范围为 195~245mbsf (meters below seafloor, 海底以下深度), 厚度 50m, 中心深度(m) 为 220mbsf, 储层饱和度为 50%, 孔隙度为 40%。2017 年中国南海天然气水合物试采的总产气量为309000m3, 标准大气压下 1m3纯水合物可大致分解出 164m3天然气, 若产出的天然气完全来自储层中固态水合物的分解, 则此次试采分解的固态水合物总体积约为 1884m3。因此, 本文取块状模型的体积为 2000m3。水合物分解过程中可能存在一个优势方向, 在该方向上分解速度更快, 产气量更高, 本文将该方向定义为方位角, 取 45°。体积沿方位角的展布定义为长度, 取 20m, 宽和高均取 10m。由于水合物储层通常呈水平产状, 坡度较平缓, 因此本文取倾角为 10°, 并根据神狐海域测井得到的纵横波速度计算出杨氏模量与泊松比。
将表 1 中的模型参数代入式(2)~(3), 计算得到各观测点处位移场和倾斜场的理论值, 对这些离散点进行全局插值, 得到整个位移场和倾斜场。从图4(a)可以看出, 垂向位移场呈向下凹陷状分布, 并存在明显的边界区域(图 4(a)中半径约为 200 m 的圆形区域), 表明水合物开采会使一定范围的区域产生形变, 此时最大垂向位移为 1.92 cm。从图 4(b)可以看出, 水平位移场明显向南东向偏移, 最大水平位移为 0.64 cm。图 4(c)中 35 个海底测斜仪监测到的倾斜场矢量(用黑色矢量箭头表示)由东‒西与南‒北两个方向的倾斜场分量合成得到, 数值单位为微弧(μR), 指该测斜仪位置处地层倾斜的角度。可以看出, 该倾斜场明显存在南东向的偏移, 与位移场的分布一致。位移场和倾斜场沿北西‒南东方向的不对称性是由倾角和方位角造成的。
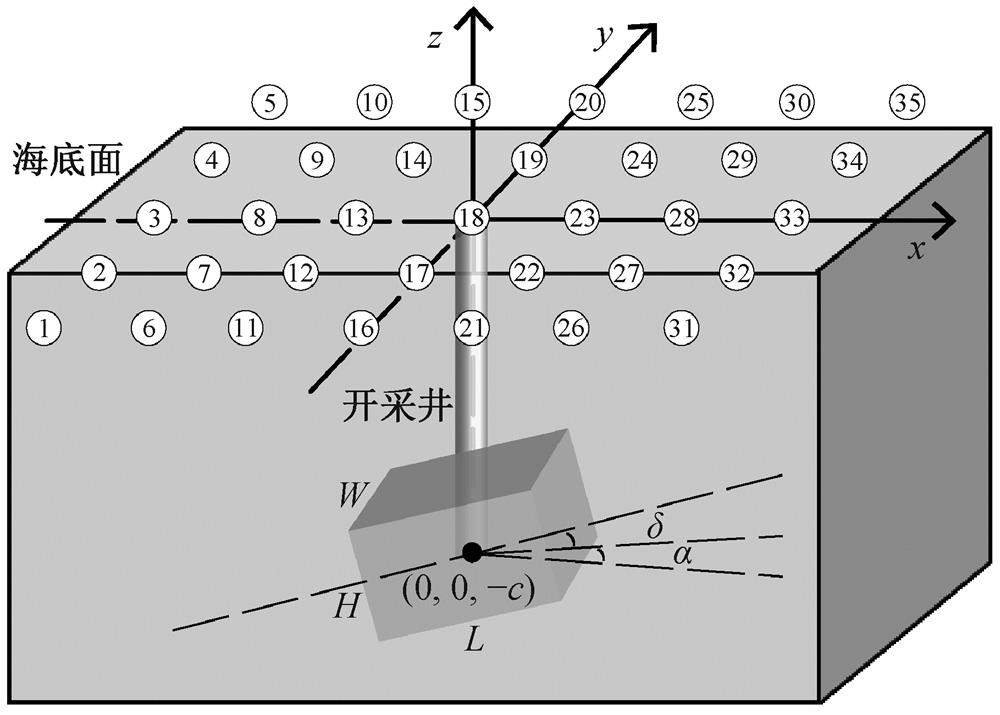
编号为 1~35 的黑色圆圈代表 35 个海底测斜仪
图3 天然气水合物开采简化地质模型
Fig. 3 Simplified geological model diagram of gas hydrate exploitation
表1 模型正演参数
Table 1 Forward modeling parameters
深度/m饱和度/%孔隙度/%中心深度/m高度/m长度/m宽度/m方位角/(°)倾角/(°)泊松比杨氏模量/GPa 195~245504022010201045100.433.20
本文对正演得到的合成倾斜场数据分别加入 3组不同程度的随机噪声(5%, 10%和 15%)来模拟实际观测值, 运用张洪亮等[24]和闫鑫等[25]提出的基于模拟退火的参数反演方法, 选择合适的初始温度及温度下降系数, 反演模型参数(包括方位角、倾角等)。图 5 和 6 分别对比无噪声条件下各个观测点处反演值与真实值对应的倾斜场矢量及位移场, 可以看到, 反演值与真实值完全重合。图 7 对比不同噪声条件下各个观测点处反演值与真实值对应的位移场值, 可以看到, 在噪声较小的条件下, 反演结果真实可信。当噪声程度增大至 15%时, 反演效果随之变差, 但所得倾斜场的理论计算值与真实值仍保持较高的吻合度, 仅在个别观测点处存在因噪声的加入而产生的较大误差, 表明测斜仪监测海底变形的方法具有良好的可行性与抗噪性。
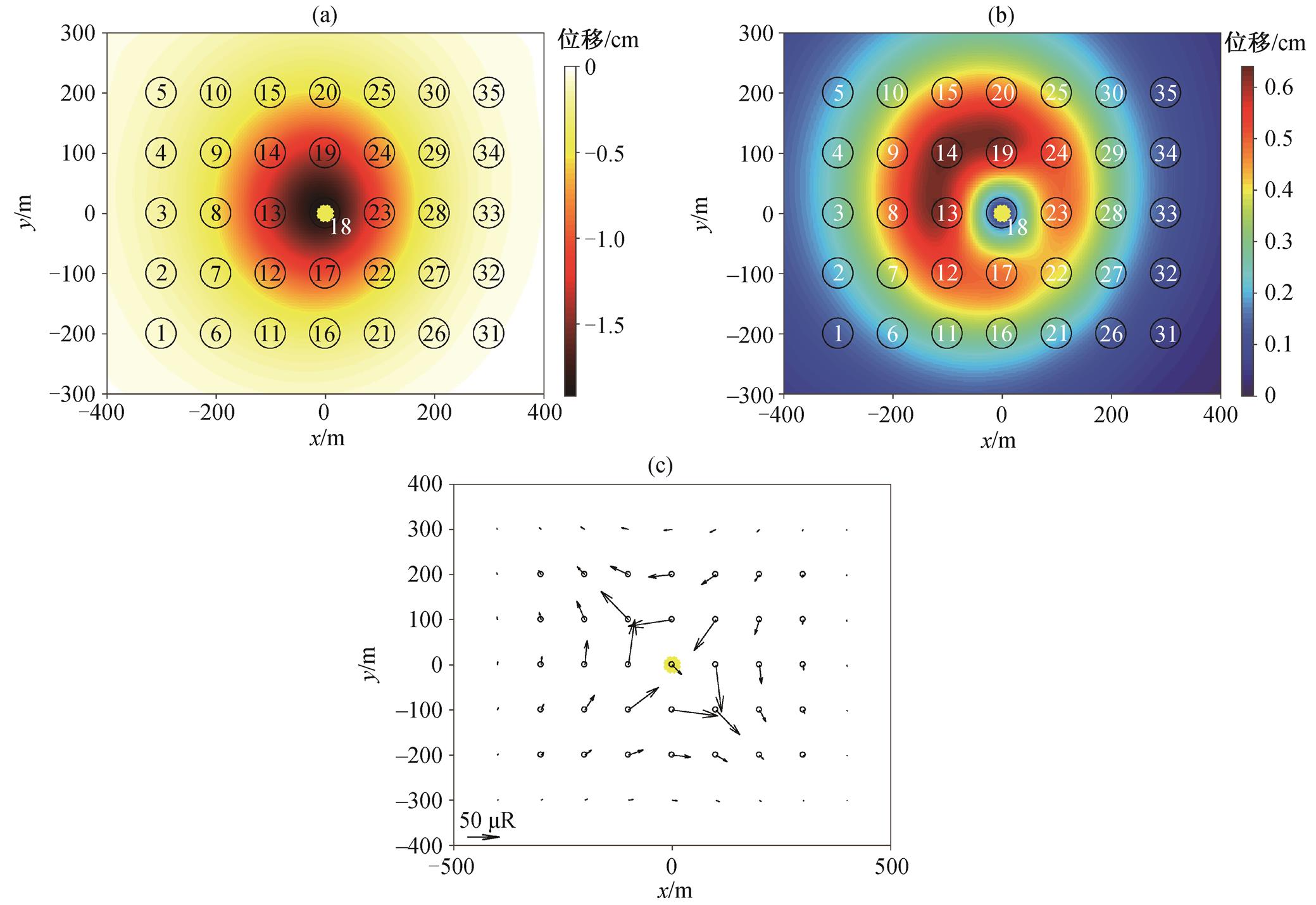
(a)垂向位移场, 最大垂向位移为1.92 cm; (b)水平位移场, 最大水平位移为0.64 cm; (c)倾斜场。黄色圆点表示开采井的井口位置
图4 变形场正演模拟结果
Fig. 4 Forward modeling of the deformation field
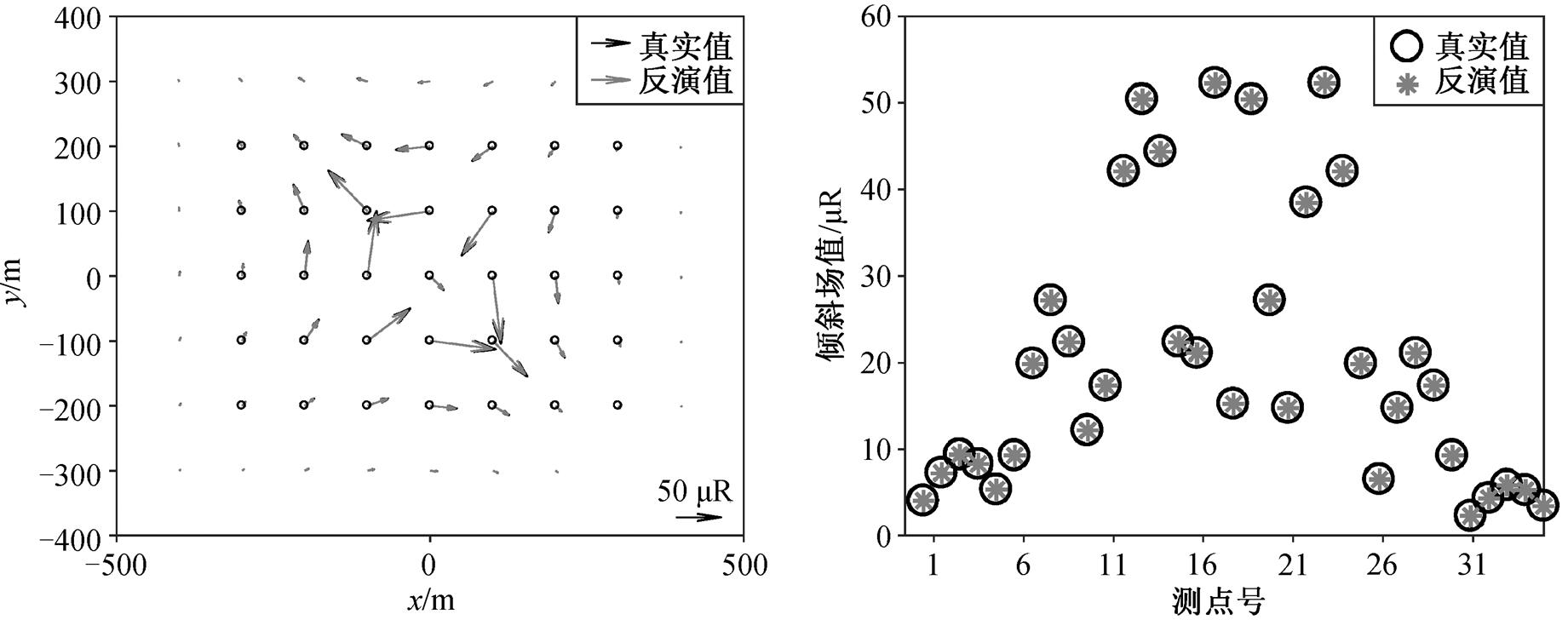
图5 无噪声条件下的倾斜场反演结果对比
Fig. 5 Comparison of inversion results of tilt field under no noise conditions
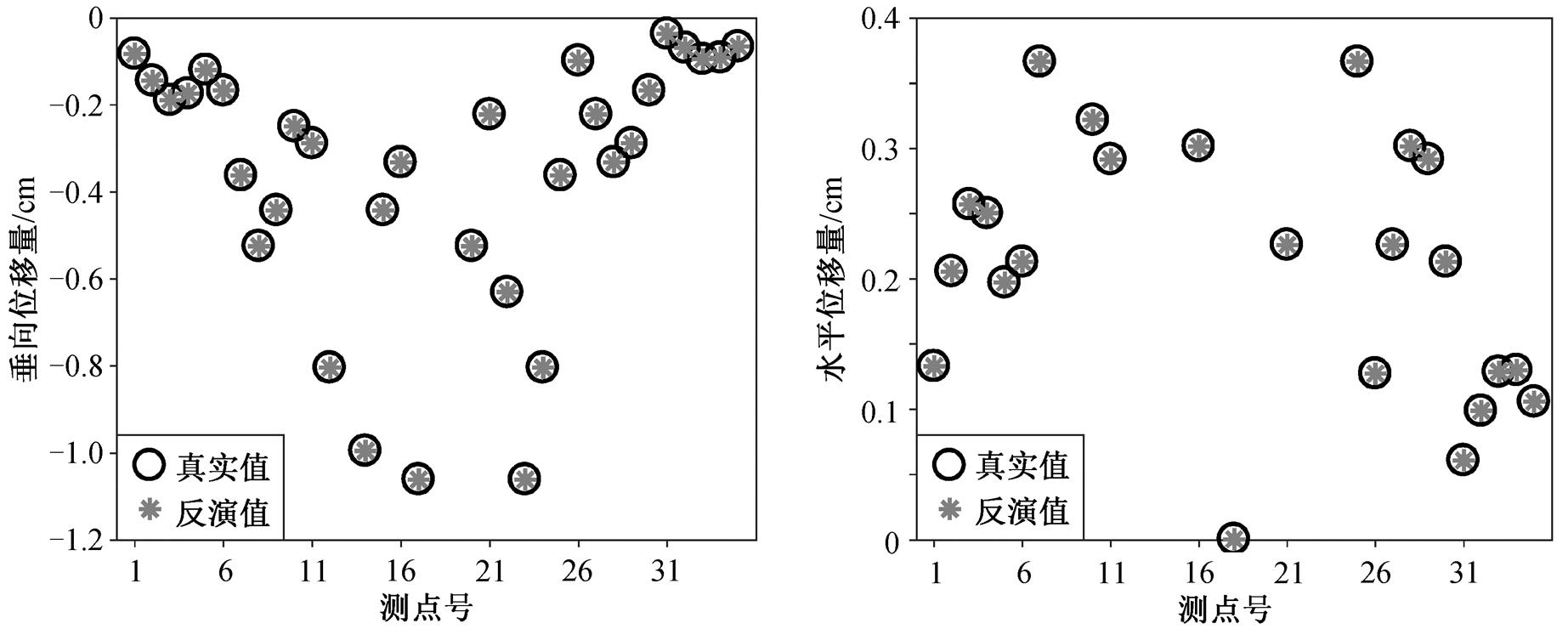
图6 无噪声条件下的位移场反演结果对比
Fig. 6 Comparison of inversion results of displacement field under no noise conditions
图7 不同噪声条件下的位移场反演结果对比
Fig. 7 Comparison of inversion results of displacement field under different noise conditions
为进一步评价实际测量数据中可能包含的测量噪声对反演结果带来的误差, 本文采用蒙特卡洛误差分析方法, 将上述试验重复进行 100 次, 每次试验加入不同程度的随机噪声, 对得到的反演结果进行统计分析, 结果见表 2。可以看出, 随着噪声增大, 方位角、倾角及体积反演结果逐渐偏离真实值, 但总体误差在可接受范围内。具体地, 在 3 组噪声条件下反演所得体积分别为 2000.4±15.8, 2008.3± 37.1 和 2011.0±46.0m3, 相应标准差分别为 0.79%, 1.85%和2.30%。由于水合物分解是相平衡条件被打破的结果, 因此储层分解范围的垂直边界相对陡直, 可以从水合物储层厚度和分解体积(天然气产量)反推得到大致的分解范围。
图 8 是不同噪声水平下位移场最大值的反演误差统计结果, 纵坐标表示反演值与真实值误差的平均值, 标准差用误差棒表示。可以看出, 随着噪声增大, 绝对误差和相对误差的均值和标准差都逐渐增大。与垂向位移相比, 水平位移最大值的绝对误差受噪声影响较小。当噪声水平达到 15%时, 垂向位移场最大值的绝对误差接近 0.01cm, 但相对误差仍低于 0.5%, 表明尽管较高水平的噪声造成反演效果变差, 但仍与真实值保持较好的吻合度。
表2 模型参数反演结果对比
Table 2 Comparison of inversion results of model parameters
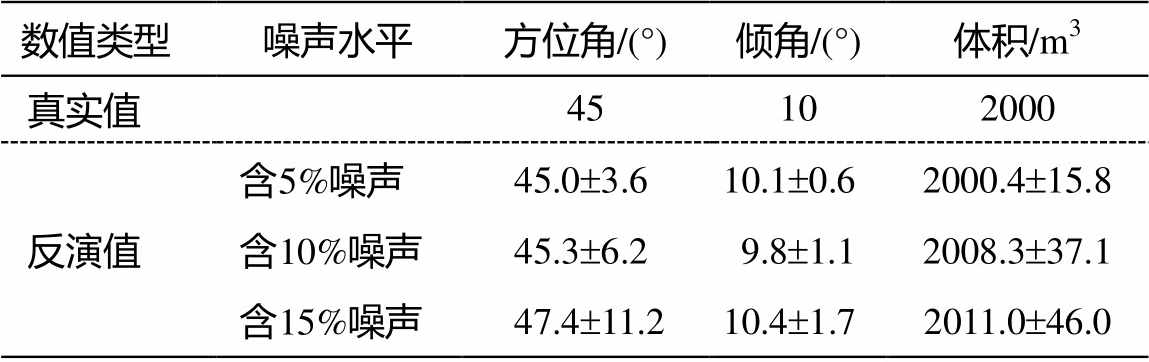
数值类型噪声水平方位角/(°)倾角/(°)体积/m3 真实值45102000 反演值含 5%噪声45.0±3.610.1±0.62000.4±15.8 含 10%噪声45.3±6.29.8±1.12008.3±37.1 含 15%噪声47.4±11.210.4±1.72011.0±46.0
2017 年中国首次南海天然气水合物试采的生产周期为 60 天, 总产气量为 309000m3, 日均产气量约为 5150m3。但是, 在试采过程中只简单地采用试采期间工程观察和生产结束后随钻测井的监测方式[26], 未开展水合物分解的海底变形监测。下面以此次天然气水合物试采为例, 从理论上分析试采过程中产生的海底变形。
试采过程中, 天然气总产量受降压开采方案、储层孔隙度、渗透率和饱和度等因素的综合影响。由于试采过程中工区的储层特性变化相对较小, 因此主要通过降压开采方案控制天然气的日均产量。这里简单地考虑两种开采模式。
第一种开采模式: 稳定井底压力。此情况下, 试采初期水合物饱和度较高, 物源充足, 产能相对较高; 随着试采的持续进行, 产能逐渐降低到一定水平。这种开采模式称为“产能递减型”。
第二种开采模式: 稳定天然气日产量。为达到稳定和安全生产的目的, 在试采过程中动态地调整井底压力, 使水合物分解速率维持恒定。这种开采模式称为“产能稳定型”。
考虑储层内固态天然气水合物完全分解产出的极限情况, 如前所述, 根据标准大气压下 1m3纯水合物大致分解为 164m3天然气, 可计算得到此次试采分解的固态水合物总体积约为1884m3, 日均分解体积约为 31.4m3。2017 年中国首次南海天然气水合物试采的目标区域 W11-17 水合物储层的深度范围为201~277 mbsf (即海平面以下 1495~1572 m), 储层总厚度为 77 m, 储层孔隙度和饱和度均为33%[26]。假设采用海底测斜仪对试采过程进行监测, 测斜仪以试采井为中心呈网格状均匀地布设, 然后模拟计算试采过程中海底变形情况。
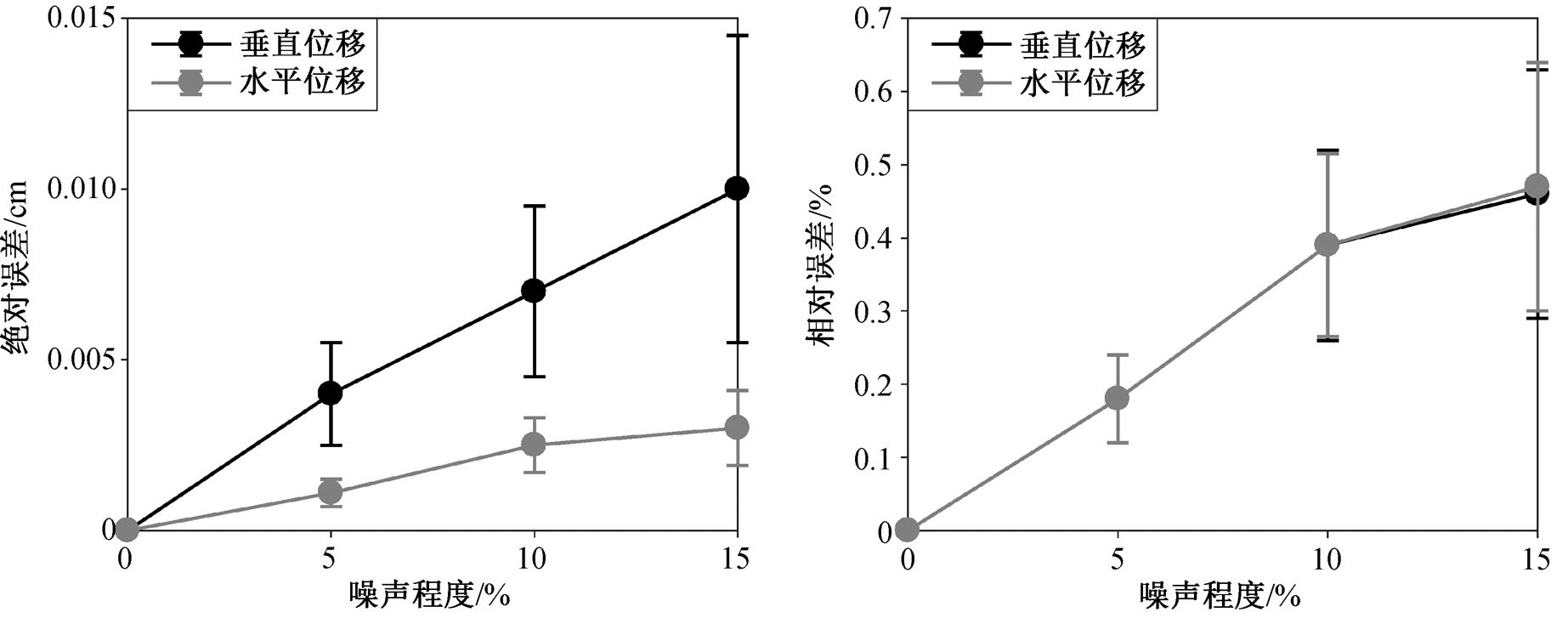
图8 不同噪声条件下位移场最大值反演误差统计
Fig. 8 Error statistics of maximum displacement field inversion under different noise conditions
图 9 反映在以上两种开采模式下, 模拟计算得到的海底变形场中最大垂向位移随试采时间的变化情况。试采开始时, 垂向位移为零; 随着试采的持续进行, 两种开采模式对应的垂向位移曲线产生明显的差别。“产能递减型”开采模式的位移曲线斜率逐渐变小, 说明垂向位移增量逐渐减小。“产能稳定型”开采模式的垂向位移随试采时间呈近似的正比关系, 且整个试采周期内垂向位移值小于“产能递减型”, 表明此种开采方案在海底稳定性方面具有一定的优势。由于总产量一致, 因此两种开采模式产生的垂向位移最大值均为 1.51cm。这一沉降量级与试采期间工程观察结果[26]相符。
需要注意的是, 由于本次试采的产气量和开采时间有限, 因此位移场变化相对较小。若进一步进行高产能、长时间的水合物生产试验, 甚至商业化开采, 海底沉降将进一步增大。利用本文方法, 通过在海底布设倾斜仪, 可实时获取海底变形场信息, 对生产过程进行反馈, 优化施工作业和降压开采方案, 保障生产的安全性。
本文提出并建立海域天然气水合物开采的海底变形物理模型, 根据变形场理论, 对海底位移场和倾斜场进行正演模拟。在对正演合成数据加入不同程度的随机噪声来模拟实际观测数据后, 利用模拟退火法, 对模型参数进行反演。反演结果表明, 在采用有限观测点的条件下, 本文方法能够对海底变形场模型的倾角、方位角和体积进行准确的反演,可为评估海域水合物开采的影响范围以及地质灾害预警提供依据。下一步工作的重点是实际资料的采集、处理和解释。
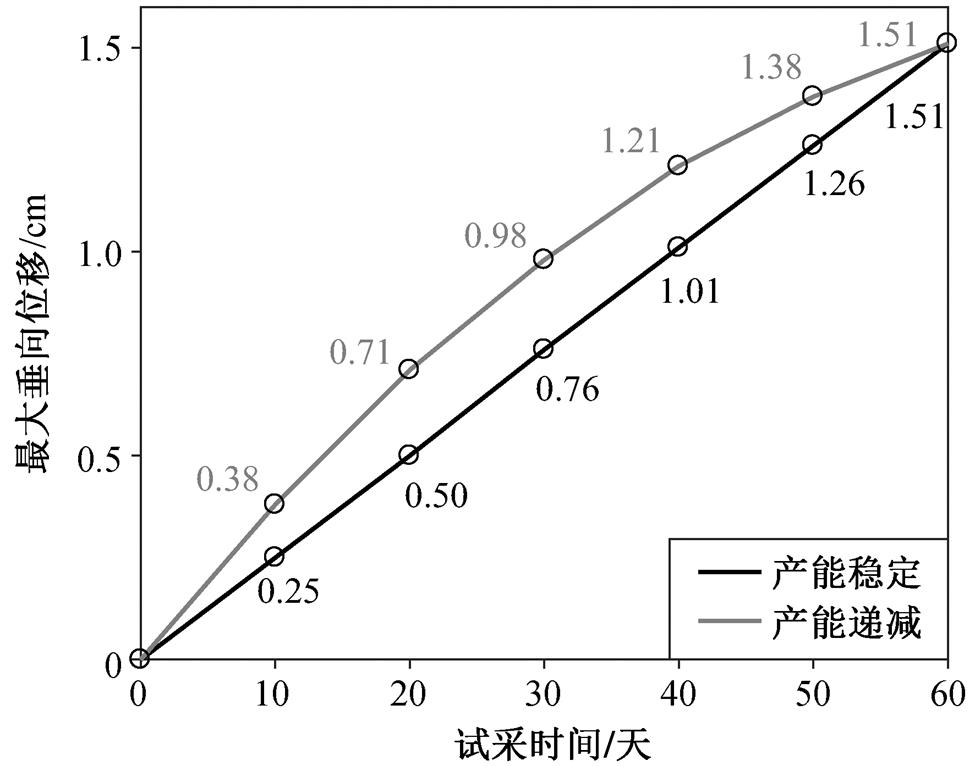
图9 不同开采模式下的最大垂向位移模拟结果
Fig. 9 Simulation results of maximum vertical displacement under different production models
参考文献
[1]Kvenvolden K A. Gas hydrates — geological perspec-tive and global change. Reviews of Geophysics, 1996, 31(2): 173‒187
[2]Sloan E D. Fundamental principles and applications of natural gas hydrates. Nature, 2003, 426: 353‒363
[3]Birchwood R, Dai J, Shelander D, et al. Develop-ments in gas hydrates. Oilfield Review, 2010, 22(1): 18‒33
[4]Jeffery B, Klauda T, Sandler S I. Global distribution of methane hydrate in ocean sediment. Energy & Fuels, 2016, 19(2): 459‒470
[5]Dallimore S R, Collett T S. Scientific results from the mallik 2002 gas hydrate production research well pro-gram, mackenzie delta, northwest territories, canada. Bulletin of the Geological Survey of Canada, 2005, 585: 1‒14
[6]张炜. 天然气水合物开采方法的应用——以 Ignik Sikumi 天然气水合物现场试验工程为例. 中外能源, 2013, 18(2): 33‒38
[7]Fujii T, Suzuki K, Takayama T, et al. Geological setting and characterization of a methane hydrate reservoir distributed at the first offshore production test site on the Daini-Atsumi Knoll in the eastern Nankai Trough, Japan. Marine and Petroleum Geo-logy, 2015, 66: 310‒322
[8]Guo Y, Yang S, Liang J, et al. Characteristics of high gas hydrate distribution in the shenhu area on the northern slope of the south china sea. Earth Science Frontiers, 2017, 24(4): 24‒31
[9]Maslin M, Owen M, Betts R, et al. Gas hydrates: past and future geohazard?. Philosophical Transactions, 2010, 368: 2369‒2393
[10]Mcconnell D R, Zhang Z, Boswell R. Review of progress in evaluating gas hydrate drilling hazards. Marine & Petroleum Geology, 2012, 34(1): 209‒223
[11]Max M D. Natural gas hydrate: in oceanic and per-mafrost environments. Boston: Kluwer Academic Pub-lishers, 2003
[12]Bünz S, Mienert J. Acoustic imaging of gas hydrate and free gas at the storegga slide. Journal of Geophy-sical Research Solid Earth, 2004, 109(B4): 380‒386
[13]Majorowicz J A, Osadetz K G. Natural gas hydrate stability in the east coast offshore-canada. Natural Resources Research, 2003, 12(2): 93‒104
[14]He Y Y, Zhang B P, Duan Y T, et al. Numerical simulation of surface and downhole deformation in-duced by hydraulic fracturing. Applied Geophysics, 2014, 11(1): 63‒72
[15]Peltier A, Beauducel F, Staudacher T, et al. Contribu-tion of tiltmeters and extensometers to monitor piton de la fournaise activity. Active Volcanoes of the Southwest Indian Ocean, 2016, 17: 287‒303
[16]Steketee J A. On volterra’s dislocations in a semi-infinite elastic medium. Canadian Journal of Physics, 1958, 36(2): 192‒205
[17]Okada Y. Surface deformation due to shear and tensile faults in a half-space. Bulletin of the Seismological Society of America, 1985, 75(4): 1135‒1154
[18]Okada Y. Internal deformation due to shear and tensile faults in a half-space. Bulletin of the Seis-mological Society of America, 1992, 82(2): 1018‒ 1040
[19]Kirkpatrick S, Jr G C, Vecchi M P. Optimization by simulated annealing. Science, 1987, 220: 606‒615
[20]Bertsimas D, Tsitsiklis J. Simulated annealing. Statis-tical Science, 1993, 8(1): 10‒15
[21]Rutenbar R A. Simulated annealing algorithms: an overview. IEEE Circuits & Devices Magazine, 2015, 5(1): 19‒26
[22]杨胜雄, 梁金强, 陆敬安, 等. 南海北部神狐海域天然气水合物成藏特征及主控因素新认识. 地学前缘, 2017, 24(4): 1‒14
[23]郭依群, 杨胜雄, 梁金强, 等. 南海北部神狐海域高饱和度天然气水合物分布特征. 地学前缘, 2017, 24 (4): 24‒31
[24]张洪亮, 何川, 谭玉阳, 等. 基于模拟退火法的水力压裂裂缝参数反演. 北京大学学报(自然科学版), 2013, 49(4): 585‒590
[25]闫鑫, 胡天跃, 何怡原. 地表测斜仪在监测复杂水力裂缝中的应用．石油地球物理勘探, 2016, 51(3): 480‒486
[26]Li J F, Ye J L, Qin X W, et al. The first offshore natural gas hydrate production test in South China Sea. China Geology, 2018, 1(1): 5‒16
Seafloor Deformation Monitoring Based on Tiltmeters for Natural Gas Hydrate Production
Abstract We present and establish a seafloor deformation model for gas hydrate exploitation in the sea area based on Okada’s linear elasticity theory. The seafloor deformation field is simulated by using high precision tiltmeters, and the model parameters are inverted by simulated annealing method. The results show that the accurate information of dip, azimuth and volume of hydrate dissociated zone can be obtained by tiltmeters. The test results at different noise levels show that the model parameter inversion method has good anti-noise performance. In addition, the feasibility of tiltmeter monitoring in practical application is analyzed according to the hydrate exploitation test in Shenhu area of South China Sea in 2017, and the results show that the type of decline in production has advantages in seabed stability.
Key words naturalgas hydrate; seafloor deformation monitoring; tiltmeter; tilt field; simulated annealing
doi: 10.13209/j.0479-8023.2019.054
国家重点研发计划项目(2017YFC0307605, 2017YFC0307702)、海洋石油工程股份有限公司“海洋平台多系统集群监测与评估技术的研究及应用”课题(Z17SJENI0053)、国家自然科学基金(41676032)和中国地质调查局国家天然气水合物专项(DD20160217)资助
收稿日期: 2018‒10‒11;
修回日期: 2018‒12‒18