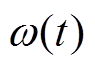, 得到新的信号序列X(t):摘要 利用集合经验模态分解算法(EEMD)和 BP 神经网络组成的混合模型, 对北京城区 PM2.5 浓度值进行短期预报。结果表明, 与单独使用 BP 神经网络模型相比, EEMD-BP 混合模型的预报准确率更高; 混合模型高频部分的预报误差是整体误差的主要方面; 混合模型的输入变量中需包含输出变量的信息; 前期污染物浓度的数值对模型的预报结果有较大的影响。
关键词 集合经验模态分解算法(EEMD); BP神经网络; PM2.5预报
近年来, 北京的高速发展引发不少环境问题, 其中的空气污染问题, 特别是大气中可吸入颗粒物危害人体健康的问题越来越受重视。李令军等[1]发现, 近期北京重污染天气的首要污染物为 PM2.5。PM2.5 指大气中直径小于或等于 2.5μm 的颗粒状悬浮物。研究发现, 环境中 PM2.5 浓度的提高增加了人类因心血管疾病引发的死亡风险[2‒4]。此外, PM2.5 可以对大气的辐射过程产生影响[5‒6], 进而对大气的能见度、降水等一系列天气现象以及气候变化造成影响[7‒9]。因此, 研究 PM2.5 的特征并对其浓度值进行预报十分必要。
目前, PM2.5 浓度值的预报方法主要有确定性方法(deterministic approaches)和统计方法(statistical approaches)[10]。Zhang 等[11‒12]对实时空气质量预报的研究历史和现状、面临的挑战和发展方向做了总结, 指出确定性方法在提高气象场预报准确率和模型输入条件准确率、模型中化学物理过程的描述、精度提高和计算有效性提升等方面仍面临着挑战。统计方法需要利用大量历史观测数据, 通过回归分析和机器学习等方法找出不同变量之间的函数关系, 再应用到未来的预报中[10]。
近年来, 机器学习方法逐渐展现出对大数据的非线性处理能力和广泛的应用前景。Wei 等[13]利用机器学习算法估算台风引起的海表温度降温, 为台风预报模式设计了台风引起海表降温的参数化方案。Jiang 等[14]利用卷积神经网络(convolutional neural network, CNN)算法, 研究台风和海洋表面反馈机制, 改进了台风数值预报模型, 2015—2016 年间 17 个台风强度的预报准确率比模型改进前提高约 20%。Li 等[15]利用人工神经网络模型重建印尼贯穿流 ITF 的多年代际长时间序列。作为一种有效的统计预报方法, 人工神经网络在空气污染预报研究中也有广泛的应用。Dutot 等[16]使用改进的多层感知机模型(multilayer perceptron, MLP), 提高了传统 MLP 模型对 O3 的预报准确率, 且优于确定性方法 CHIMERE 模型的结果。Zhou 等[17]利用集合经验模态分解(EEMD)与广义回归神经网络(generalized regression neural network, GRNN)模型相结合的方法, 对西安市的 PM2.5 浓度值进行预测, 并分别与多元线性回归模型、主成分回归模型、差分整合移动平均自回归模型以及单独使用 GRNN模型进行对比, 发现混合模型的效果均优于其他模型。Feng等[10]综合利用气团轨迹追踪模型、小波转换以及神经网络算法建立一套混合模型来预报北京市的PM2.5 浓度值, 得到较好的结果。
与多种算法融合使用的混合模型相比, 单独使用任意一种神经网络模型都不能产生最优的预测结果[15,18‒19], 因此混合模型成为一种更有效的预测方法。之前的研究中, 混合模型主要用于对模型的输入条件进行筛选和优化, 对 PM2.5 浓度值的预测仍然采用传统的 BP (back-propagation)神经网络方法, 并且未对混合模型的优势和单一模型的不足以及模型对输入变量的敏感性进行具体的分析。本文使用EEMD-BP 混合模型对北京市日均 PM2.5 浓度值进行预测, 与前人工作的不同之处在于, 我们首先将PM2.5 时间序列进行 EEMD 分解, 然后对分解后的固有模态函数(intrinsic mode function, IMF)进行神经网络建模和预测, 从而揭示 BP 神经网络对不同时间频率 PM2.5 固有模态的预测技巧, 并通过筛选和优化混合模型参数和输入条件, 为改进 PM2.5 预测模型提供新的思路。
经验模态分解(EMD)模型由 Huang 等[20]于1998 年提出。该方法能够根据信号的特点, 自适应地将信号分解为从高频到低频的一系列固有模态函数(IMF)。其基本思路是通过 3 次样条插值, 拟合出信号的极大值和极小值包络线, 进而得到数据的瞬时平衡位置。该方法直接从信号获取基函数, 因此具有自适应性。由于原始信号存在各种干扰, 且EMD 的筛选方法未必严格地从小到大单调变化, 因此可能产生尺度交叉现象, 即出现模态混叠问题。为了解决该问题, Wu 等[21]提出使用 EEMD 方法对原始序列进行模态分解, 以抑制模态混叠现象。EEMD 方法是将白噪声加入原始信号, 利用白噪声频谱的均匀分布, 当信号加在遍布整个时频空间且分布一致的白噪声背景上时, 不同时间尺度的信号会自动地分布到合适的参考尺度上, 并且由于白噪声均值为零的特性, 经多次平均后, 加入的噪声信号将相互抵消, 就可以将集成均值的结果作为最终结果。基本步骤如下。
1)给原始信号 x(t)加入一组白噪声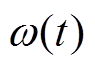, 得到新的信号序列X(t):
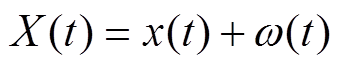。2)对 X(t)进行 EMD 分解, 得到一组 IMF 分量:
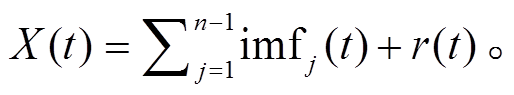
式中, imfj(t)表示第 j 个 IMF 分量, r(t)为趋势项。
3)对原始信号重复步骤 1 和 2 多次(m 次), 每次加入不同的白噪声, 每次均得到一组 IMF 分量:
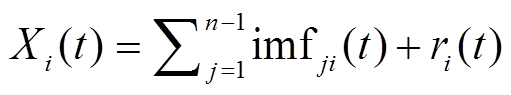。4)将每次得到的 IMF 分量集成均值, 作为最终结果:
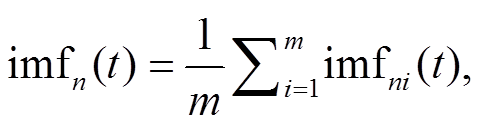
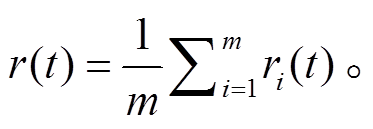
BP 神经网络是一种基于误差反向传播算法(error back-propagation)的前馈神经网络, 由一个输入层、一个或多个隐层和一个输出层构成, 其基本结构如图1所示。
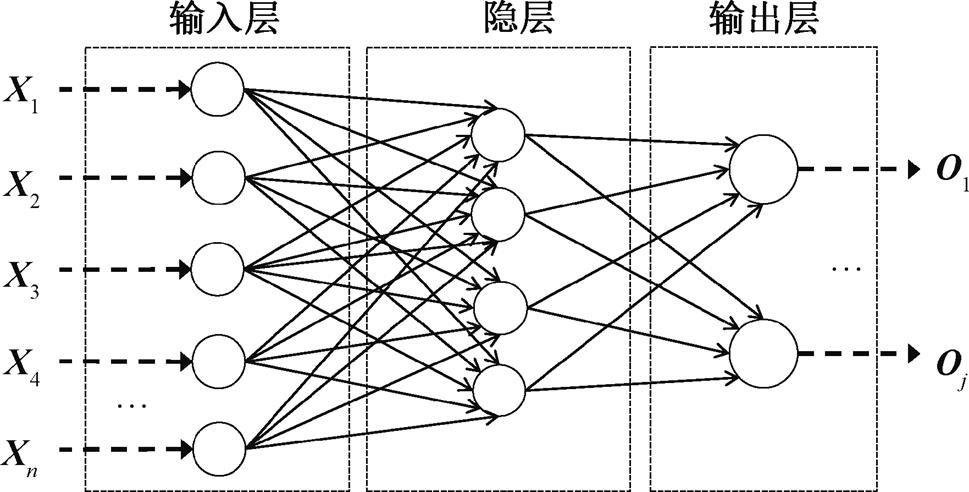
X代表输入变量, O代表输出变量
图1 BP神经网络结构
Fig. 1 BP neural network structure
BP 神经网络的算法是一种迭代算法, 每次迭代包含两个阶段, 即激励传输和权重更新。
在激励传输阶段, 输入层将接收到的归一化的输入变量传给隐层; 隐层神经元对接收到的数据进行加权求和, 再代入激活函数, 将激活后的值传给输出层; 输出层再一次加权求和并激活后得到最终结果。假设输入层、隐层和输出层分别有n, m和s个神经元, 则有
输入层: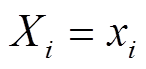 
;
隐层: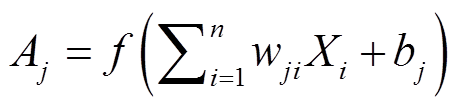 
;
输出层: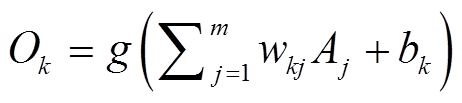 
。
式中, w为连接权重; b为偏置; f为激活函数, 常见的有sigmoid, tanh 和 Relu 等; g为线性传输函数。
在权重更新阶段, 为使误差性能函数的值最小, 利用梯度下降算法逐步修正输出层和隐层的连接权重和偏置的值。
误差性能函数: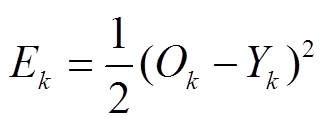 
;
输出层: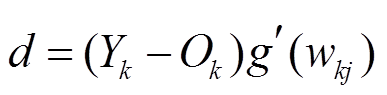 
, 
;
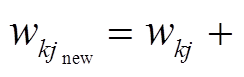
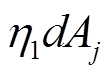隐层: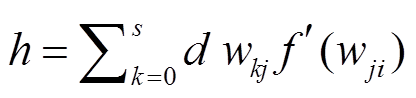 
, 
。
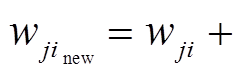
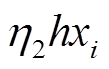式中, d和h分别表示神经元的梯度项,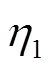
和
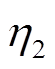为学习率。
偏置的更新步骤与权重类似。
本文采用的 PM2.5 数据来源于 http://beijingair. sinaapp.com 网站, 该网站收集全国 1497 个空气质量观测站的数据, 其中北京市的数据来自北京市环境保护检测中心网站。本文使用的北京市 PM2.5 浓度值为北京市 12 个观测站的平均值。
本文使用的气象资料来自 http://rp5.ru网站提供的北京市历史气象数据, 该网站提供未来6天的天气预报及实际天气信息。天气预报由英国 Met Office 制作, 实际天气数据由地面气象站通过气象数据国际自由交换系统提供。网站的天气预报每天05:00 和 17:00UTC 两次更新, 最新数据每天 8 次(间隔 3 小时: 00:30, 03:30, 06:30, 09:30, 12:30, 15:30, 18:30 和 21:30UTC)补充到网站数据库。该网站提供北京站(54511) 2005 年 2 月 1 日至今的历史数据。
徐敬等[22]发现, PM2.5 与气压、相对湿度和风速的相关性较好。因此, 本文选取的气象要素包括气温(℃)、露点温度(℃)、海平面气压(hPa)、10m 风向和 10m 风速(m/s)。由于所用资料缺少相对湿度这一要素, 因此使用温度和露点温度替代。
本研究使用的数据时段为 2014 年 5 月 13 日(PM2.5 数据获取网站的资料起始时间)至 2017 年 2月 1 日。获取的 PM2.5 数据为整点的小时数据, 将北京时 00:00—23:00 数据的算术平均值作为日均值使用。气象资料为每日 3 小时一次的观测数据, 分别为北京时间 02:00, 05:00, 08:00, 11:00, 14:00, 17:00, 20:00 和 23:00, 取这 8 个时次数据的算术平均值作为日均值使用。其中, 将风向风速转化为 U和 V 分量后再做平均。去除缺测数据后, 得到 979组有效数据, 将前 800 组作为训练集, 后 179 组作为测试集(图 2)。表 1 展示各要素日均值的统计信息。
本文实验分为混合模型实验(EEMD-BP)和单一模型实验(BP)。在混合模型实验中, 首先对 PM2.5浓度的原始时间序列进行 EEMD 分解, 然后对分解后的各 IMF 进行 BP 神经网络建模和预测, 最后把所有 IMF 分量之和作为对 PM2.5 浓度的预测结果。单一模型实验则直接利用 BP 神经网络对 PM2.5 浓度的原始时间序列进行建模和预测。为了比较混合模型与单一模型对 PM2.5 日均浓度值的预测效果以及不同输入变量对结果的影响, 我们设计 3 组对比实验: 将输入变量分为 3 组(仅使用气象要素、仅使用PM2.5 浓度值以及同时使用气象要素和 PM2.5 浓度值), 将这 3 组输入变量分别应用于混合模型和单一模型。
利用 EEMD 算法对各要素的时间序列进行分解, 得到 8 个 IMF 分量以及一个趋势项。本文在PM2.5浓度的原始时间序列中添加的白噪声幅值选取为 0.2, 集合数为 100。考虑到模型训练时不应该包含未来的信息, 故分别对各要素的训练集和全部时长的数据集做 EEMD 分解, 得到的结果如图 3所示。
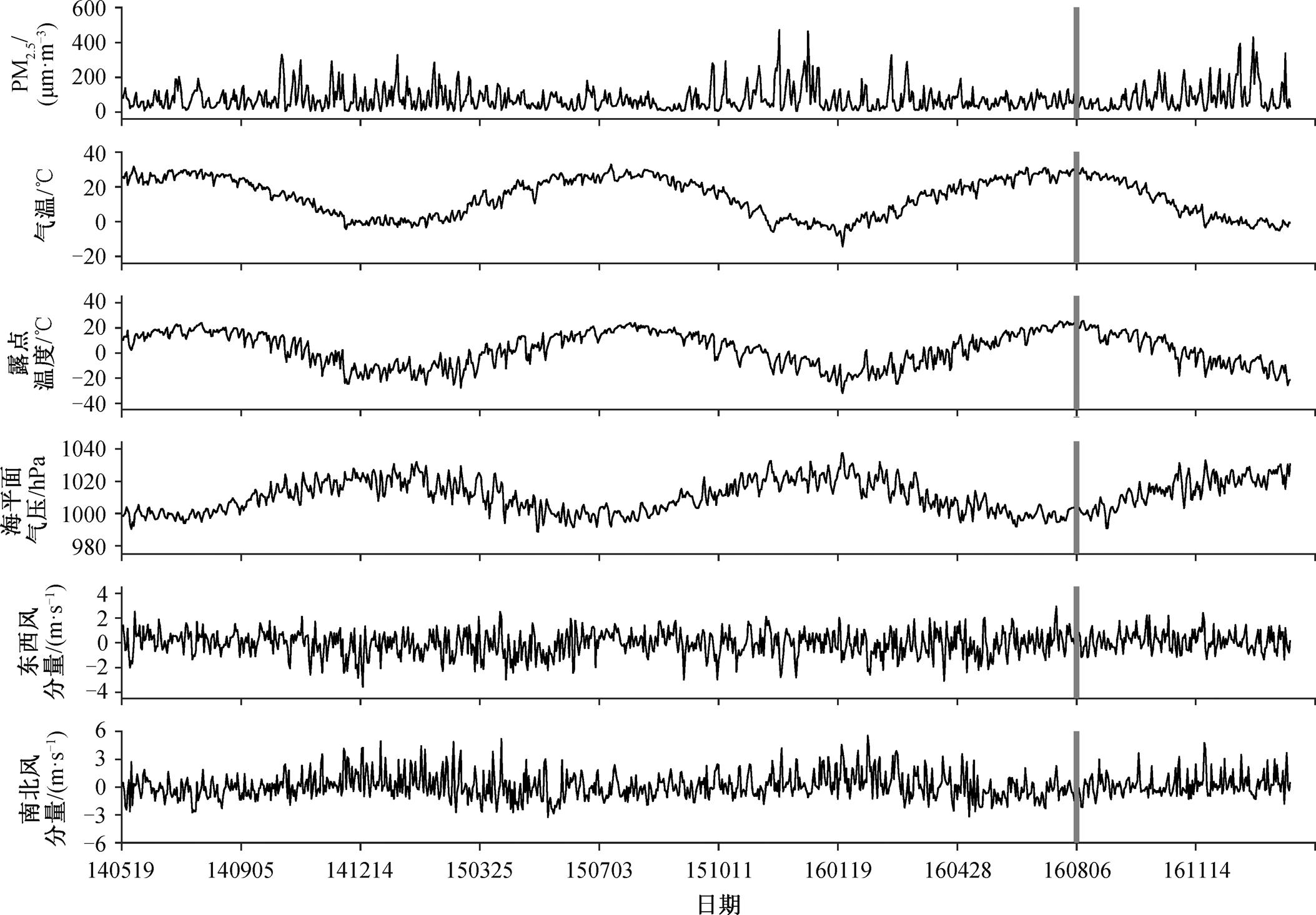
横坐标每2位数字分别表示年、月、日; 灰色竖线左侧为训练集, 右侧为测试集
图2 各要素时间序列
Fig. 2 Time series of each element
表1 各要素统计信息
Table 1 Statistics of each element
指标PM2.5/(μg·m−3)气温/℃露点温度/℃海平面气压/hPa东西风分量/ (m·s−1)南北风分量/ (m·s−1) 数值区间[5.22, 470.86][−14.25, 32.85][−31.81, 25.53][988.80, 1037.59][−3.57, 2.94][−3.23, 5.55] 平均值76.4214.173.121010.77−0.020.13 标准差67.8311.1013.3610.180.981.39
对 PM2.5 每个 IMF 分量进行频谱分析, 得到各IMF 分量对应的周期(表 2)。可以看出, IMF1 和IMF2 分别对应 4.9 和 8.6 天的周期信号, IMF3 和IMF4 是月周期信号, IMF5 和 IMF6 是季节尺度的信号, IMF7 和 IMF8 是年际尺度的周期信号。据此, 分别将 IMF3 和 IMF4, IMF5 和 IMF6, IMF7 和 IMF8以及趋势项 r 相加, 得到 3 个新的时间序列。将PM2.5 浓度的原始时间序列分为 5 组(表 2), 分别对应不同的周期, 对每组进行 BP 神经网络单一模型预测, 将各组结果相加得到最终预测值。
对 PM2.5 浓度的原始时间序列进行小波分析, 结果如图 4 所示。可以看出, 该时间段的 PM2.5 浓度值具有显著的周期性, 其中 3~14 天的周期满足95%的置信度检验, 与李梓铭等[23]的研究结果一致, 可作为选取预报输入变量的依据。
BP 神经网络输入输出: 根据对数据的分析, BP神经网络的输入变量包含 t+1 的气象要素以及当前时刻(t)到前 6 天(t−6)的 PM2.5 浓度值, 输出变量为后一天(t+1)的 PM2.5 浓度值。为了研究不同的输入变量对预报效果的影响, 将每个模型的输入变量分为 3 组进行对比。之所以选取 t+1 的气象要素, 是为了研究模型对同一时刻 PM2.5 浓度值与气象要素对应关系的学习能力, 并且, 在实际操作过程中, t+1 的气象要素可以通过数值预报得到(本文假设数值预报结果绝对准确, 因此使用观测数据代替数值预报结果)。由于无法获得预报时刻的 PM2.5 浓度值, 因此使用前期 PM2.5 浓度值替代。选用前 7 天(t−6 至 t)数据的原因是在数据预处理过程中发现3~14 天是 PM2.5 浓度值的显著周期, 因此选取具有现实意义的 7 天(一周)这一周期作为输入变量的时间范围。
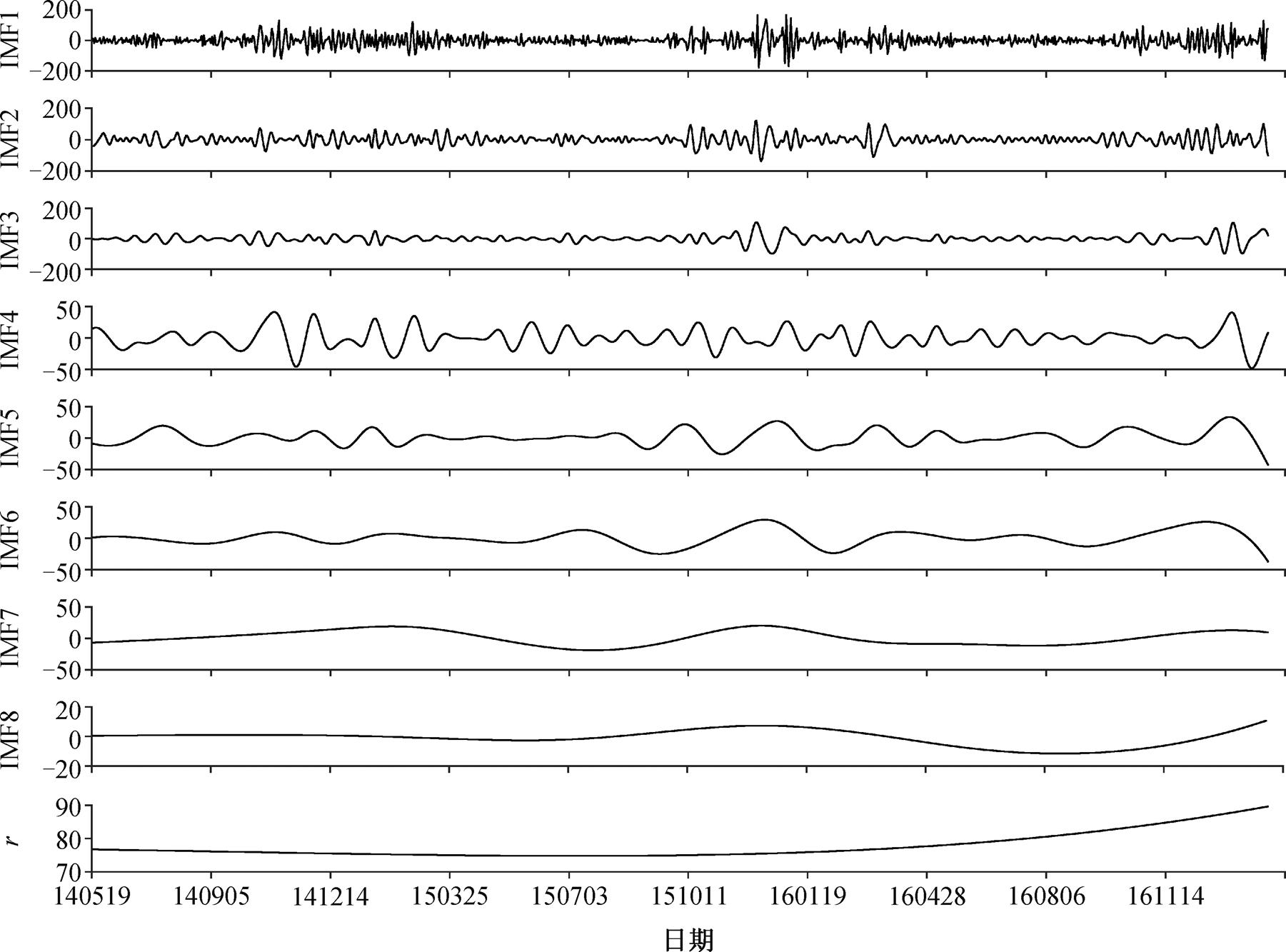
IMF1~ IMF8分别为分解得到的8个固有模态函数, 分别对应高频至低频的不同频段, r为趋势项
图3 PM2.5浓度的原始时间序列分解结果
Fig. 3 PM2.5 original sequence decomposition results
表2 PM2.5各IMF分量平均周期
Table 2 Mean cycle of each IMF component of PM2.5
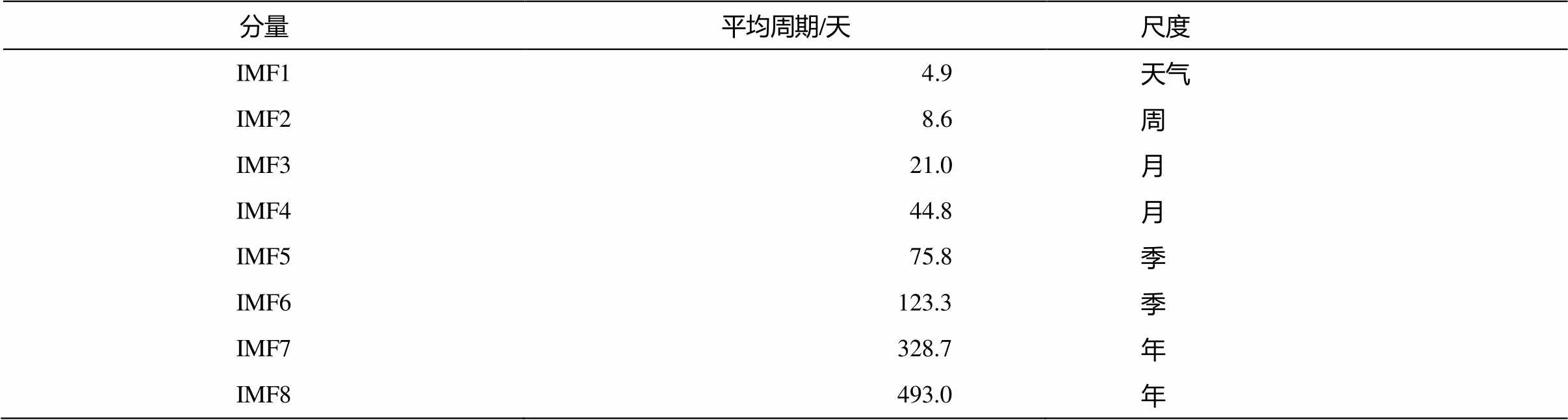
分量平均周期/天尺度 IMF14.9天气 IMF28.6周 IMF321.0月 IMF444.8月 IMF575.8季 IMF6123.3季 IMF7328.7年 IMF8493.0年
BP 神经网络隐含层设计: 隐含层数量为 1, 即单隐层结构。经过反复实验, 得知隐含层神经元个数为 8 时误差最小, 因此选取 8 个隐含层神经元。
激活函数: 隐含层选用 tanh 函数, 输出层选用purelin 线性函数。
训练算法: 选用 trainlm 作为训练函数。
其他超参数: 随机初始权重; 学习率为 0.1; 迭代次数为 1000; 训练目标为均方差达 10−11。
BP 神经网络结构如图 5 所示。
为了保证结果的客观性, 每组实验的结果均是由各个模型训练 10 次分别得到的预测结果再平均得到。选取的评价指标有绝对平均误差(MAE)、均方根误差(RMSE)、一致性指数(index of agreement,
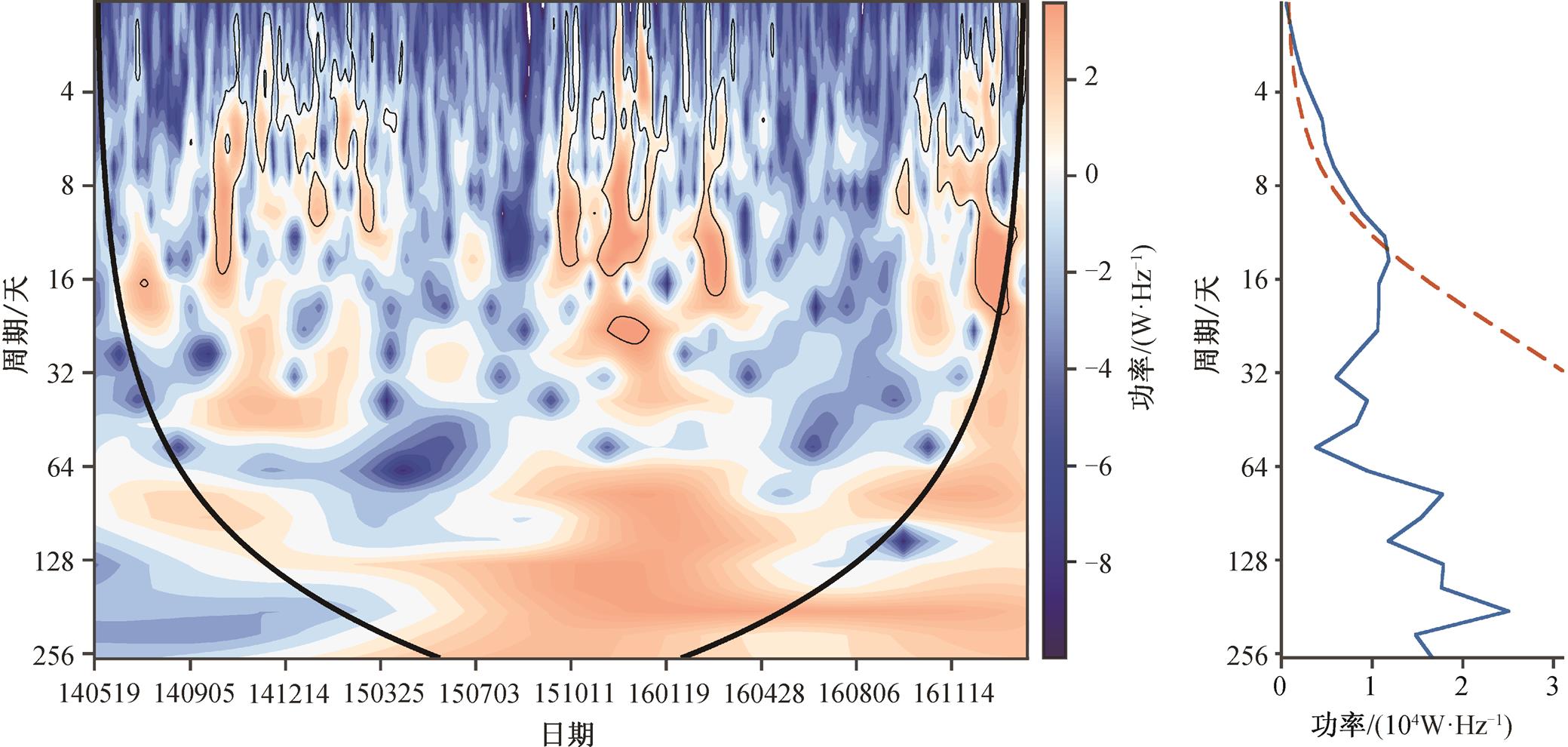
左图: 黑色U型等值线包围的区域表示通过95%显著性检验的时频部分, 黑色U型等值线外侧的部分为受边界效应影响的区域;
右图: 红色虚线为95%显著性检验曲线, 蓝色实线数值大于红色虚线的部分表示通过95%显著性检验的周期范围
图4 PM2.5日均浓度值小波功率谱和平均小波功率谱曲线
Fig. 4 Morlet wavelet power spectrum and the mean wavelet power spectrum of daily mean PM2.5
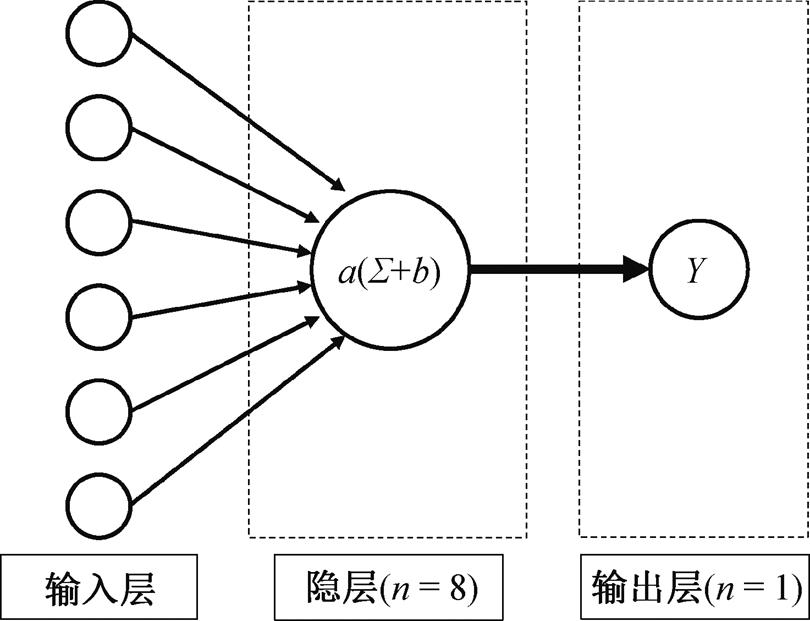
输入层变量为气象因子和PM2.5浓度值, 神经元个数与输入变量个数一致, 隐层包含8个神经元, 输出层为第二天PM2.5浓度值
图5 预拟模型的 BP 神经网络结构
Fig. 5 Structure of the BP neural network in forecasting model
IA)和决定系数(R2), 定义如下:
,
,
,
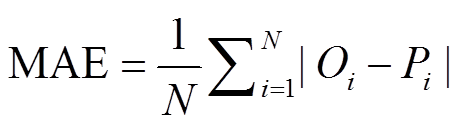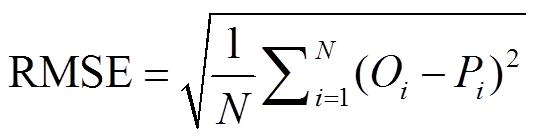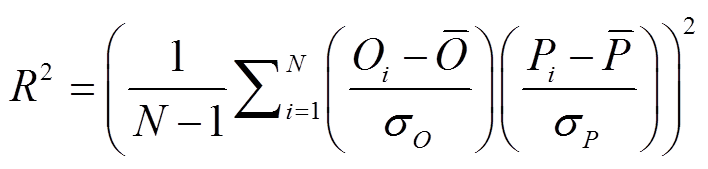,其中, N为样本个数,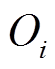 
和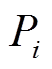
分别表示观测值和预测值, 
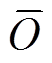和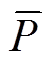
分别表示观测数据和预报数据的平均值, 
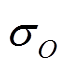和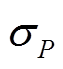
分别表示观测数据和预报数据的标准差。
表 3 显示 6 组实验结果的统计信息。可以看出, 对于相同的输入变量, 使用混合模型的预测效果基本上比使用单一模型好(仅使用气象要素作为输入变量的情况除外)。为了研究混合模型相对于单一模型优势的具体表现, 分别对实验 3 和实验 6 的结果做时频分析, 并与原始序列的小波功率谱相减, 得到图 6 所示的结果。对比发现, 与实验 3 相比, 实验 6 低频部分的时频信息与实际的时间序列更接近, 体现在低频部分(白色)的面积更大, 两者的高频部分则差别不大。从平均小波功率曲线相减的结果也可以看出, 实验 6 的结果更接近 0 值线, 表示与实际序列的曲线更接近, 说明该结果可以体现实际序列中包含的各个频段的信号; 实验 3 的曲线数值基本上小于 0, 说明此结果对实际序列中包含的各个频段信号的反映较弱。由此可得出, 与单一模型相比, 混合模型的优势体现在能够较好地学习原始序列中包含的时频信息, 但在高频部分仍存在较大的误差。
表3 实验结果统计信息
Table 3 Experimental result statistics
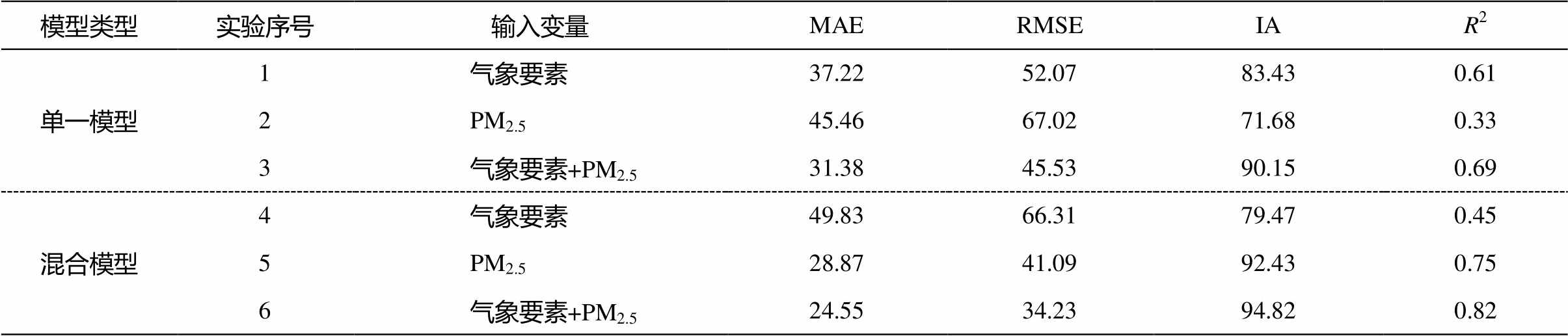
模型类型实验序号输入变量MAERMSEIAR2 单一模型1气象要素37.2252.0783.430.61 2PM2.545.4667.0271.680.33 3气象要素+PM2.531.3845.5390.150.69 混合模型4气象要素49.8366.3179.470.45 5PM2.528.8741.0992.430.75 6气象要素+PM2.524.5534.2394.820.82
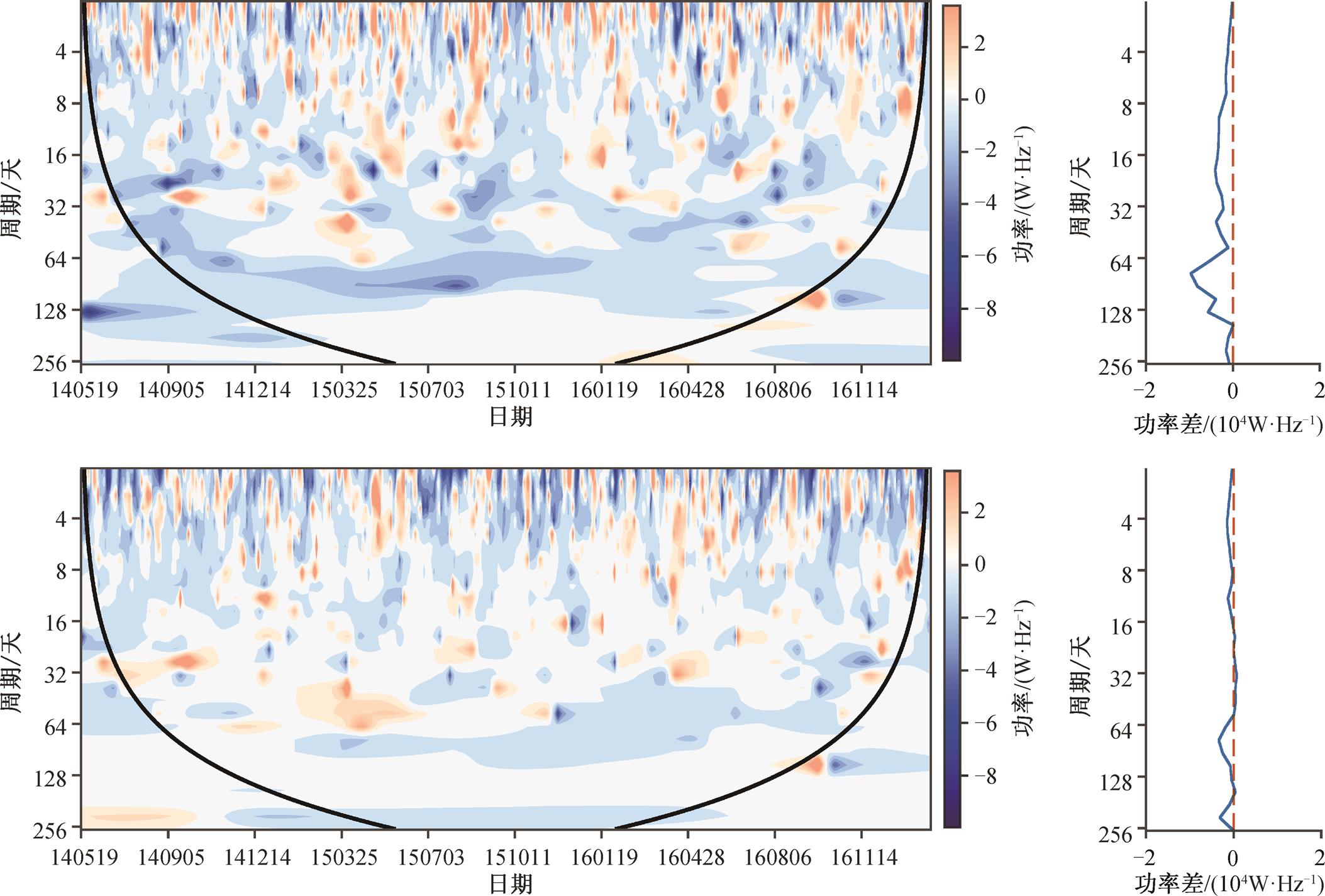
第一行: 实验 3; 第二行: 实验 6。左图: 时频信号功率谱的差值, 黑色 U 型等值线外侧的部分为受边界效应影响的区域; 右图: 蓝色实线为平均功率差值线, 红线虚线为差值的0值参考线
图6 实验3和实验6与实际序列频谱的差值
Fig. 6 The difference in frequency spectrum between the result of test 3, test 6 and the actual sequence
为了查看实验 6 相对于实验 3 的提升效果以及具体表现, 将实验 3 的结果进行 EEMD 分频, 并将最高频 IMF1 以外的其余 IMF 分量相加, 作为该结果的低频部分; 将实验 6 中 IMF1 以外的其余 IMF分量结果相加, 作为低频部分。如图 7 所示, 混合模型对低频部分的预报效果提升明显, 而对高频部分则提升不大, 说明混合模型相对于单一模型的性能提升主要体现在对低频序列的预报效果上, 对高频序列的预报效果改善不明显。对比实验 2 与实验5, 得到相同的结论。由此可知, 对于不同的输入条件, 混合模型均能有效地提升低频部分的预报性能。
从表 3 还可以看出, 在两组模型的实验中, 同时使用气象条件和前期 PM2.5 浓度值作为输入变量的预报效果均较好(实验 3 和 6), 单独使用其中一类要素作为输入变量则得到相反的结果(实验 1 和 2 对比实验 4 和 5), 说明输入条件对模型的效果有较大的影响, 且不同模型对输入变量的需求也不一样。
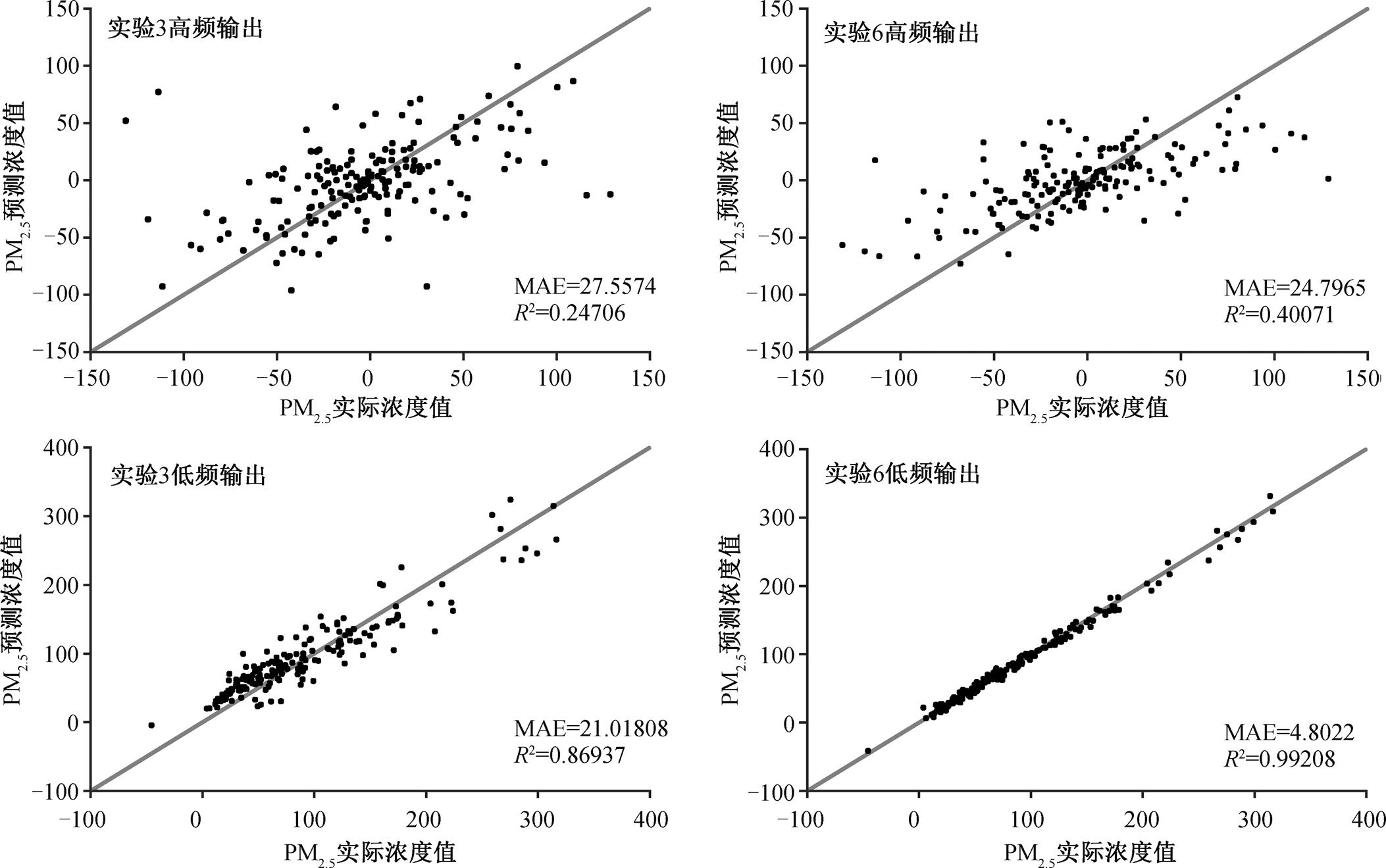
灰色实线为斜率为 1 的参考线, 选用绝对平均误差(MAE)和决定系数(R2)作为准确率的参考指标, 只选取测试集对应的时间段(2016 年 8 月 6 日至 2017 年 2 月 1 日)的数据做对比
图7 实验3与实验6高、低频预报结果
Fig. 7 High and low frequency contrast of forecast results of test 3 and test 6
实验结果中出现混合模型效果比单一模型差的情况, 下面做一简要讨论。实验 4 比实验 1 效果差, 完全失去预报能力, 分析其原因为分频以后的预测需要输入变量中含有与输出要素相对应的元素, 即输出为 PM2.5 的浓度值时需要输入变量中包含 PM2.5浓度值的信息。为此, 进行一个实验验证: 将输出变量更换为温度, 输入变量分别为其他气象要素以及 PM2.5 浓度值。这里只展示最低频段的验证结果(因为最低频段的结果体现了整体结果的下限)。结果(图 9(b))与实验 4(图 9(a))类似, 模型失去预报能力。若将温度预报实验设置成实验 5 和 6 (分别对应图 9(c)和(d))的情形, 即输入变量中包含温度序列, 则效果明显提升。由此可知, 使用混合模型做预报时, 输入条件中需要包含输出变量的信息。
为了研究排放变化(用当前时刻的 PM2.5 浓度值表示, 下同)对模型预报结果的影响, 将测试集中的数据按当前时刻(t)的污染程度分为 6 个等级: 优(0~35)、良(36~75)、轻度污染(76~115)、中度污染(116~150)、重度污染(151~250)和严重污染(>250), 代表不同的排放量。分别计算每个等级预报结果(t+1 时刻的 PM2.5 浓度值)的误差, 结果见图 10。可见, 两个模型在各个污染等级的表现与表 3 的结果基本上一致: 混合模型的效果优于单一模型, 并且在两个模型中均是将 PM2.5 和气象要素同时作为输入条件的效果较好。图 10 也显示, 前期污染浓度越大, 预测误差越大, 说明对于不同的前期污染浓度, 模型之间预报效果的对比不受影响, 但同一模型的预报效果与前期污染浓度负相关。
4 总结
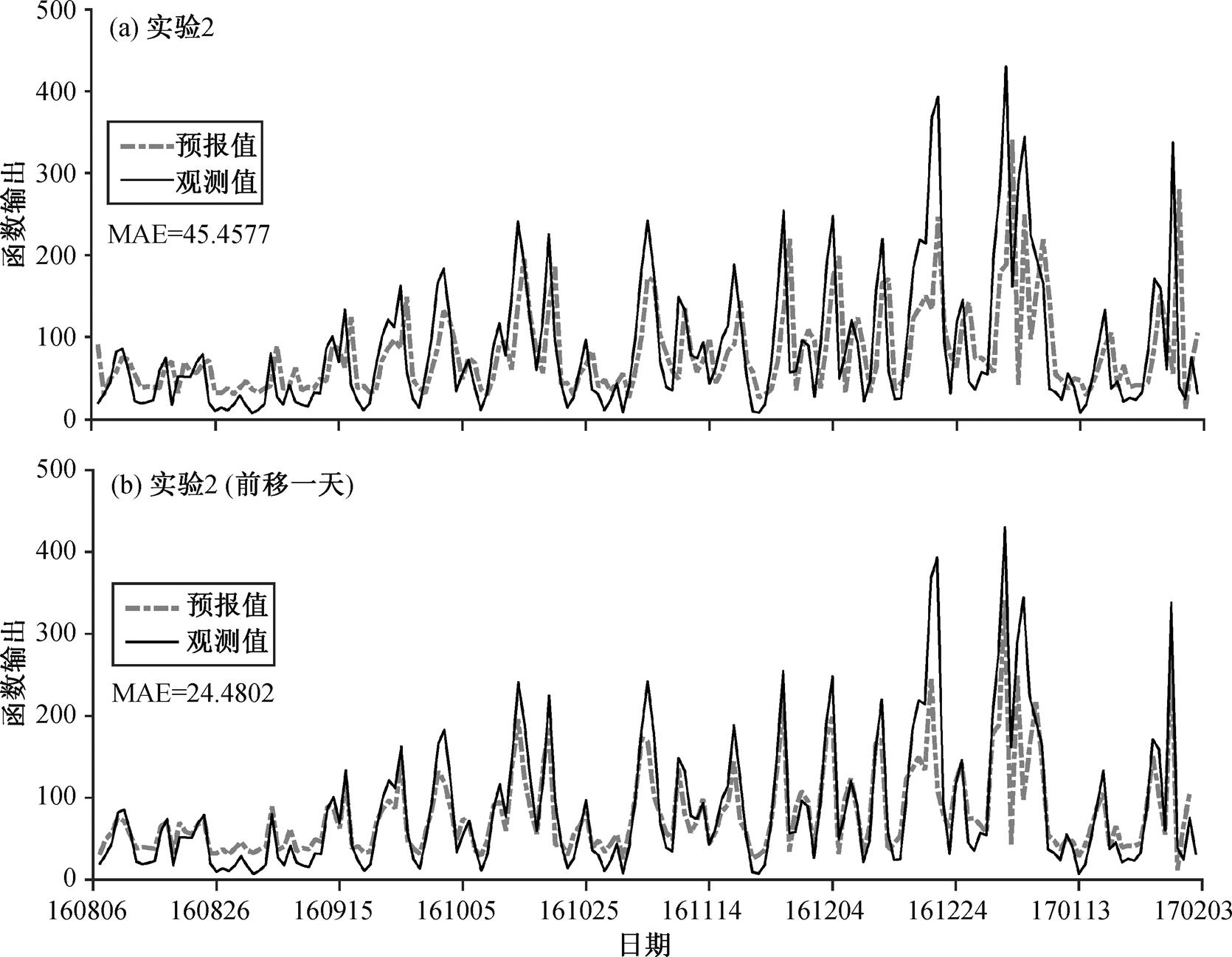
图8 实验2结果与前移一天的结果对比
Fig. 8 Test 2 results compared with the results of moving forword one day
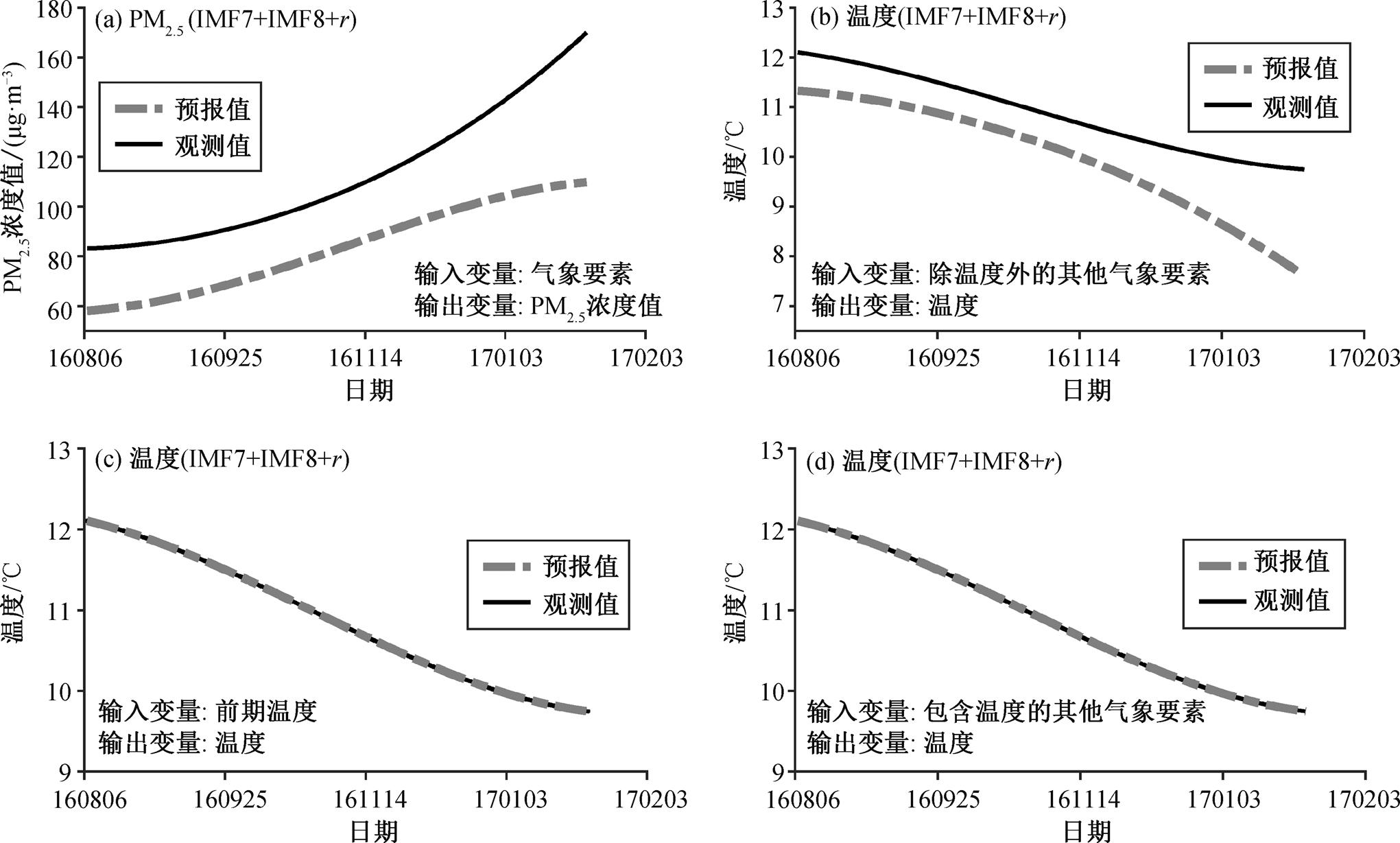
(a)为实验 4 中最长周期部分的结果; (b)~(d)为应用混合模型预报温度的最长周期的结果, 输入变量分别为不包含前期温度信息、仅使用前期温度信息和包含前期温度信息及其他要素3种情况, 分别对应实验4, 5和6的设置
图9 不同输入变量对输出结果的影响
Fig. 9 The effect of different input variables on the output
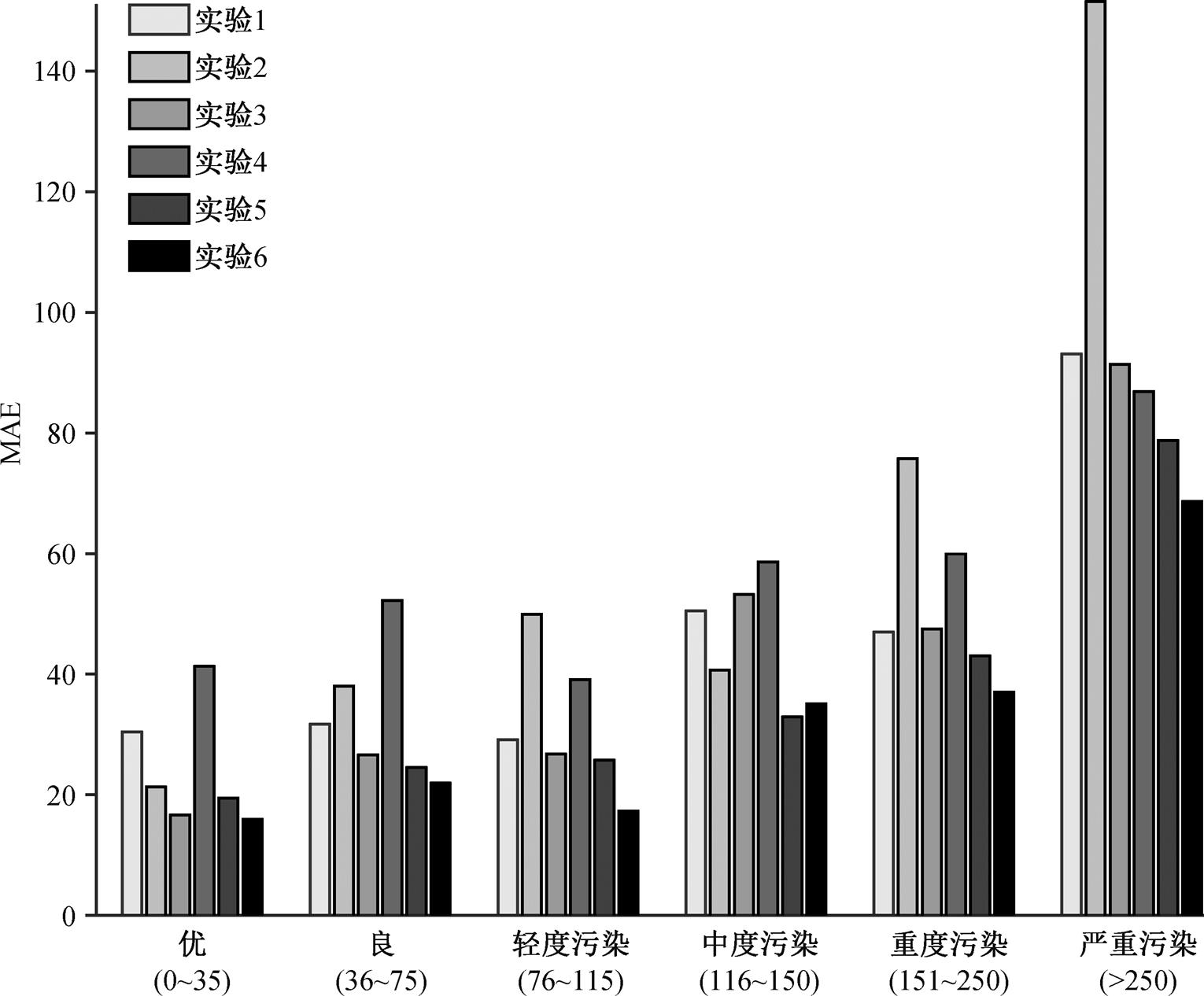
图10 不同排放量对输出结果的影响
Fig. 10 The effect of different emissions on the output
为了建立一套有效的 PM2.5 浓度预测模型, 本文首先利用 EEMD 方法提取 PM2.5 浓度值时间序列的本征模态, 分解原始序列的时频信息, 然后利用BP 神经网络, 对不同频率的 IMF 分量分别进行预测, 构建一个结构为 n-8-1(分别对应网络输入层、隐层和输出层的神经元个数, 其中输入层神经元的个数由输入变量的数量决定)的 BP 神经网络, 从而建立 EEMD-BP 混合模型对北京城区未来 24 小时的 PM2.5 浓度日均值进行预报, 得到以下结果。
1)使用混合模型时预报效果的提升体现在最高频以外的所有其他 IMF 分量上, 混合模型的误差主要出现在最高频 IMF1 上, 对其他 IMF 分量的预报可达到很高的准确率。
2)输入条件对模型的预报效果有较大的影响,不同模型对输入变量的需求也不一样。单一模型不能仅使用前期值来预报未来值, 混合模型的输入变量中必须包含前期 PM2.5 浓度信息。
3)前期污染物浓度值对模型的预报结果有较大影响, 数值越大, 模型预报准确率越低。
未来应该从以下方面对混合模型进行优化: 提升高频序列(IMF1)的预报准确率; 输入变量中必须包含需要输出的要素信息; 针对前期污染较重或排放量较大的情况进行模型优化。
参考文献
[1]李令军, 王占山, 张大伟, 等. 2013—2014 年北京大气重污染特征研究. 中国环境科学, 2016, 36(1): 27‒35
[2]Burnett R T, Rd P C, Ezzati M, et al. An integrated risk function for estimating the global burden of disease attributable to ambient fine particulate matter exposure. Environmental Health Perspectives, 2014, 122(4): 397‒403
[3]Cao J, Yang C, Li J, et al. Association between long-term exposure to outdoor air pollution and mortality in China: a cohort study. Journal of Hazardous Ma-terials, 2011, 186(2/3): 1594‒1600
[4]Yin P, Brauer M, Cohen A, et al. Ambient fine parti-culate matter exposure and cardiovascular mortality in China: a prospective cohort study. The Lancet, 2015, 386: S6
[5]Kuang Y, Zhao C S, Tao J C, et al. Impact of aerosol hygroscopic growth on the direct aerosol radiative effect in summer on North China Plain. Atmospheric Environment, 2016, 147: 224‒233
[6]Xue H, Feingold G. Large-eddy simulations of trade wind cumuli: investigation of aerosol indirect effects. Journal of the Atmospheric Sciences, 2006, 63(6): 1605‒1622
[7]陈义珍, 赵丹, 柴发合, 等. 广州市与北京市大气能见度与颗粒物质量浓度的关系. 中国环境科学, 2010, 30(7): 967‒971
[8]王志立, 郭品文, 张华. 黑碳气溶胶直接辐射强迫及其对中国夏季降水影响的模拟研究. 气候与环境研究, 2009, 14(2): 161‒171
[9]徐祥德, 王寅钧, 赵天良, 等. 中国大地形东侧霾空间分布“避风港”效应及其“气候调节”影响下的年代际变异. 科学通报, 2015, 60(12): 1132‒1143
[10]Feng X, Li Q, Zhu Y, et al. Artificial neural networks forecasting of PM2.5, pollution using air mass trajec-tory based geographic model and wavelet transforma-tion. Atmospheric Environment, 2015, 107: 118‒128
[11]Zhang Y, Bocquet M, Mallet V, et al. Real-time air quality forecasting, part I: history, techniques, and current status. Atmospheric Environment, 2012, 60 (32): 632‒655
[12]Zhang Y, Bocquet M, Mallet V, et al. Real-time air quality forecasting, part II: state of the science, cur-rent research needs, and future prospects. Atmos-pheric Environment, 2012, 60(6): 656‒676
[13]Wei J, Jiang G Q, Liu X. Parameterization of typhoon-induced ocean cooling using temperature equation and machine learning algorithms: an exam-ple of typhoon Soulik (2013). Ocean Dynamics, 2017, 67(9): 1179‒1193
[14]Jiang G Q, Xu J, Wei J. A deep learning algorithm of neural network for the parameterization of typhoon-ocean feedback in typhoon forecast models. Geophy-sical Research Letters, 2018, 45(8): 3706‒3716
[15]Li M T, Gordon A L, Wei J, et al. Multi-decadal timeseries of the Indonesian throughflow. Dynamics of Atmospheres & Oceans, 2018, 81: 84‒95
[16]Dutot A L, Rynkiewicz J, Steiner F, et al. A 24-h forecast of ozone peaks and exceedance levels using neural classifiers and weather predictions. Environ-mental Modelling & Software, 2007, 22(9): 1261‒ 1269
[17]Zhou Q, Jiang H, Wang J, et al. A hybrid model for PM2.5, forecasting based on ensemble empirical mode decomposition and a general regression neural net-work. Science of the Total Environment, 2014, 496 (2): 264‒274
[18]秦喜文, 刘媛媛, 王新民, 等. 基于整体经验模态分解和支持向量回归的北京市PM2.5预测. 吉林大学学报(地球科学版), 2016, 46(2): 563‒568
[19]Nunnari G, Dorling S, Schlink U. Modelling SO2 concentration at a point with statistical approaches. Environmental Modelling & Software, 2004, 19(10): 887‒905
[20]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings Mathematical Physical & Engineering Sciences, 1998, 454: 903‒995
[21]Wu Z, Huang N E. Ensemble empirical mode decom-position: a noise-assisted data analysis method. Ad-vances in Adaptive Data Analysis, 2009, 1(1): 1‒41
[22]徐敬, 丁国安, 颜鹏, 等. 北京地区 PM2.5 的成分特征及来源分析. 应用气象学报, 2007, 18(5): 645‒654
[23]李梓铭, 孙兆彬, 邵勰, 等. 北京城区 PM2.5 不同时间尺度周期性研究. 中国环境科学, 2017, 37(2): 407‒415
PM2.5 Forecast of Beijing Based on Ensemble Empirical Mode Decomposition and BP Neural Network
Abstract A hybrid model with ensemble empirical mode decomposition (EEMD) and BP(Back-Propagation) neural network for next-day forecasting of PM2.5 concentration in Beijing is developed. The results show that the forecast accuracy of the hybrid model is higher than single BP model. The main error comes from the highest frequency component. The input variables of the hybrid model need to contain information about the output variables. The level of pollutant concentration in the early stage has great influence on the prediction result of the models.
Key words ensemble empirical mode decomposition (EEMD); BP neural network; PM2.5 forecast
doi: 10.13209/j.0479-8023.2019.041
国家自然科学基金(41476008, 41576018)和广西壮族自治区特聘专家专项经费(2018B08)资助
收稿日期: 2018‒08‒08;
修回日期: 2018‒09‒25