满足以下微分动力学方程: 摘要 通过对三节点基因调控网络的枚举、参数空间的随机采样以及动力学模拟, 找到具有热鲁棒性(即温度补偿)的适应性基因转录调控网络, 对其进行结构分析表明, 存在 3 种最基本的结构可以实现具有热鲁棒性的适应性动力学功能, 复杂的适应性网络都以此 3 种网络为核心骨架。为了考察三节点适应性网络的适应性对网络动力学中各参数改变的敏感度, 计算了各参数相应的控制系数。对控制系数的聚类分析表明, 三节点功能网络实现热鲁棒的机制为温度隔离, 即尽管网络中所有的速率参数都依赖于温度, 但仅输出节点的生成和降解速率明显偏离 0 且具有相反的符号, 大多数热鲁棒适应性都通过输出节点的拮抗平衡调节来实现。
关键词 适应性; 功能与拓补; 转录网络; 温度补偿
细胞中的生化反应无时无刻不受环境温度的影响, 温度是影响生物生存和繁殖的重要因素之一。生物功能对环境扰动的鲁棒性, 特别是对温度变化的鲁棒性(即热鲁棒性), 对于生物系统正常功能的实现具有重要意义。目前已经有很多关于生物功能的热鲁棒性的研究, 如生物昼夜节律(即生物钟)的温度补偿[1–2]、生物网络中稳态通量的热稳定性[3–5]以及振荡网络的振荡周期温度补偿[6]。热鲁棒性的另外一个重要例子是适应性功能的温度补偿, 即当温度变化时, 适应性功能的稳态值不随温度发生变化。适应性指一个系统在外界信号作用下做出暂态响应后, 恢复到刺激之前水平的动力学行为。热鲁棒性是生物组织和细胞中普遍存在的动力学功能, 如细胞内的信号转导[7]、神经元活动的适应性[8]、稳态功能的适应性[9]以及大肠杆菌的趋化性[10]。尽管已经有一些关于适应性功能的热鲁棒性的实验研究, 例如大肠杆菌的趋化性[11]和果蝇发育过程中的信号传导[12], 但相关研究非常有限。
本文以基因调控网络为例, 研究三节点基因网络中的热鲁棒适应性。通常情况下, 网络动力学功能与网络的拓扑结构具有关联性[13–14], 寻找特定动力学功能相对应的网络拓扑结构对于了解复杂的生物学网络以及合成生物学具有重要意义[15–16]。为找出具有热鲁棒性的适应性(thermally robust adap-tation, TRA)功能网络的常见拓扑结构, 本文在对三节点基因调控网络枚举的基础上, 对基因网络动力学方程进行规模化的数值模拟研究。通过对热鲁棒适应性网络进行结构分析, 发现存在 3 种最基本的网络结构可以实现具有热鲁棒性的适应性功能, 复杂的功能网络通常以此 3 种网络为核心骨架。对控制系数的聚类分析表明, 三节点功能网络实现热鲁棒性(即温度补偿)的机制为温度隔离, 即尽管网络中所有的速率参数都依赖于温度, 但仅输出节点的生成和降解速率明显偏离 0 且具有相反的符号, 大多数热鲁棒适应性都通过输出节点的拮抗平衡调节来实现。
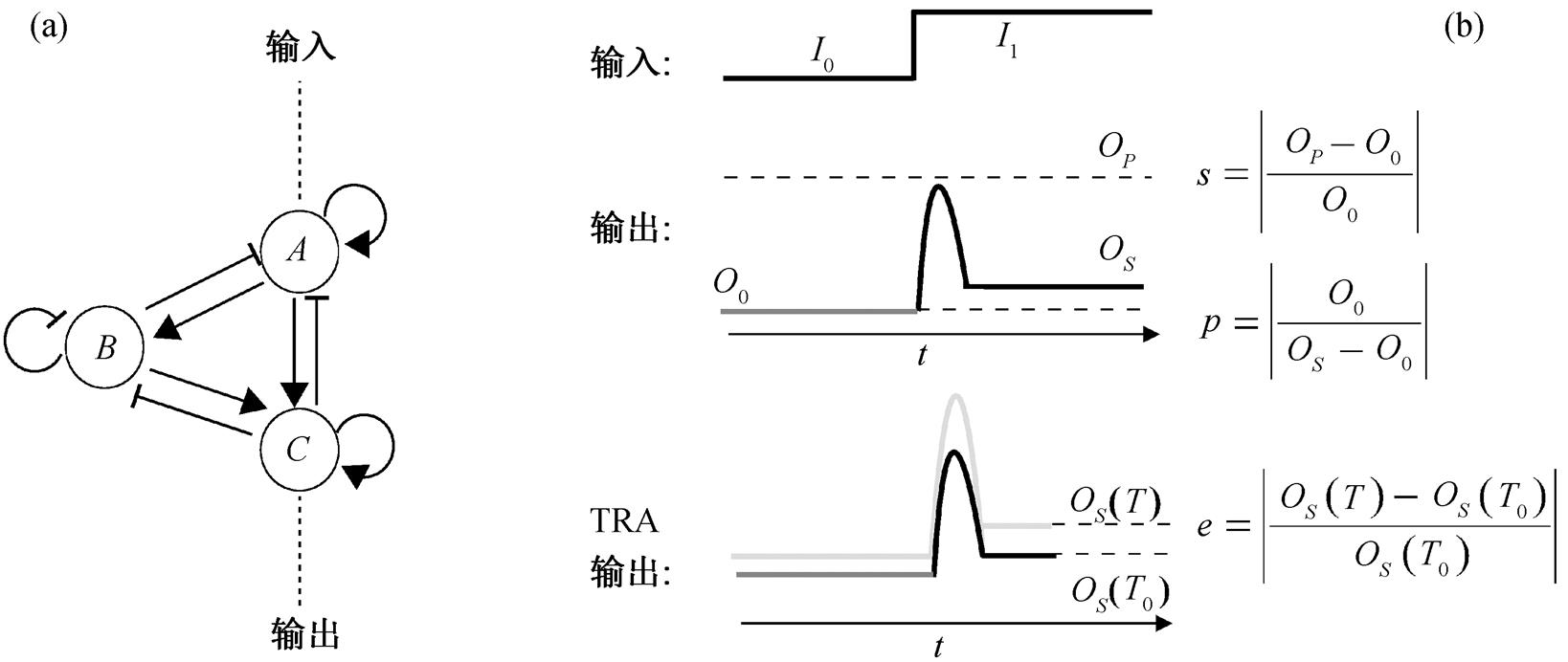
具有适应性功能的网络至少包含 3 个节点[17], 因此本文选择三节点转录调控网络作为研究对象。为了实现对所有三节点基因转录调控网络拓补结构的枚举, 我们考虑了 3 个节点之间所有 9 种可能的转录调控关系, 两两节点之间有激活、抑制或没有调控 3 种关系。如图 1(a)所示, 每个网络具有输入节点 A、中间节点 B 和输出节点 C, 节点之间的连接方式代表转录调控作用。三节点的基因调控网络共有 19683 种可能的网络拓扑。为了确保网络是连通的, 要求输入节点 A 必须直接或间接与输出节点C 相连接。因此, 可能的拓扑结构总数为 16038个。
为了描述转录调控网络的动力学行为, 采用常微分方程模型[2]。网络中每个节点代表的某基因转录翻译后, 蛋白浓度的动力学方程分为表达速率和降解速率两部分。表达速率采用Hill函数形式的输入函数, 降解速率与被降解蛋白的浓度成正比。以网络中的节点 i 为例, 若节点 j 和 k 的产物分别促进和抑制节点 i 的表达, 则节点 i 表达产物的浓度满足以下微分动力学方程:
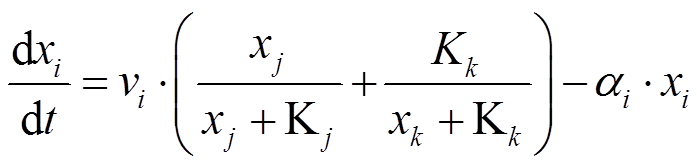, (1)其中,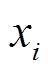 
代表节点 i 的转录翻译产物的浓度, 
为最大转录速率,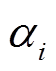 
为降解速率。
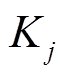和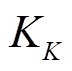
为转录因子j和k的解离常数。
特别地, 对于输入节点 A, 输入信号 I 通过直接与输入节点 A 的转录速率相乘进入节点 A 的动力学方程。当网络中有多个转录节点调控同一节点时, 选择“OR”的逻辑形式。例如, 在式(1)中, 节点 j 和 k 的产物分别对节点 i 的转录起促进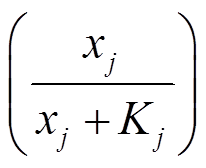作用
和抑制作用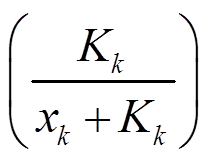
, 它们通过加和的形式调控节点i的表达。
→代表转录激活作用, 
代表转录抑制作用
图 1 网络拓扑的枚举(a)和TRA功能的定义(b)
Fig. 1 Enumeration of network topology (a) and definition of TRA function (b)
为了考虑模型中参数的影响, 我们根据文献[18–19]中对基因转录的温度依赖性的研究结果, 假定表达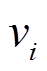速率
和降解速率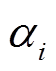均按照 Arrhenius 定律的形式随温度变化:
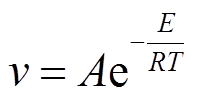, (2)其中, E是与速率v相对应的活化能。参数A, R和T 分别为指数前因子、气体普适常数和开尔文温度。本文温度变化范围为 288~308K, 在该区间内对均匀分布的 5 个温度下的动力学行为进行研究。Hill函数中的解离常数 K 为解离速率与结合速率的比值, 它们都与温度有关, 为了简化计算, 模型中阈值 K 不随温度变化。由于转录和翻译对温度的依赖关系比较复杂, 用 Arrhenius 定律描述基因表达和蛋白降解随温度的变化是一种理想化的近似。
为了通过数值计算确定一个网络结构在某组参数下是否具有适应性, 定义两个参数: 敏感度 s 和精确度 p, 如图 1(b)所示。敏感度衡量网络受到外界信号刺激后响应的敏感性, 精确度衡量系统的输出恢复到信号刺激之前的程度或适应的准确性[13]。一个系统的动力学响应如果满足敏感度大于 20％且精确度大于 100, 则从数值上可以判定为具有适应性。本文中, 如果动力学响应在[288 K, 308 K]都满足以上适应性的条件, 并且温度变化引起的输出变化的比例小于 5% (e<5%), 则判定该适应性具有热稳定性或温度补偿性, 即TRA特性。
为了较全面地了解一个网络结构在不同参数下实现适应性功能的难易程度, 用拉丁超立方抽样方法对参数空间随机采样。每个速率参数采样的范围均为 0.001~100a.u, 活化能 E 的采样范围为 50~80kJ/mol。对于每个枚举的网络拓补, 我们随机抽取10000 组参数[20]。引进 Q 值和 q 值近似地衡量一个网络结构实现适应性功能和TRA功能的鲁棒性。在 10000 组参数中, 在固定温度 288K 下可以实现适应性功能的参数组的数目, 记为 Q 值; 对于可以实现适应性的 Q 组参数, 在[288 K, 308 K]区间的不同温度下依然具有适应性的参数组的数目记为 q值, 显然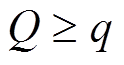
。
采用以上方法, 从 16038 个网络结构中共筛选出 122 个 TRA 功能网络, 它们在 10000 组参数中都至少在一组参数下具有 TRA 功能。图 2(a)为这些适应性网络在 Q-q 空间的分布, 图 2(b)为 TRA 网络在q 值和网络边数空间的分布。图 2(b)表明, 所有TRA 功能网络至少包含 3 条边, 并且鲁棒性比较好的网络(q>3)的边数在3~7之间。图 2(b)中下方的小圆点对应具有 3 条边的最简单的网络结构, 它们是可以实现 TRA 功能的最简单的网络, 共有 3 个(图中显示两 个点, 对应 3 个网络, 其中两 个网络由于 q 值相同而重合), 称为 TRA 模体(TRA motif)。这 3 种TRA 模体在结构上是 3 种非一致前馈网络, 其控制节点可以是比例节点或反比例节点[7]。
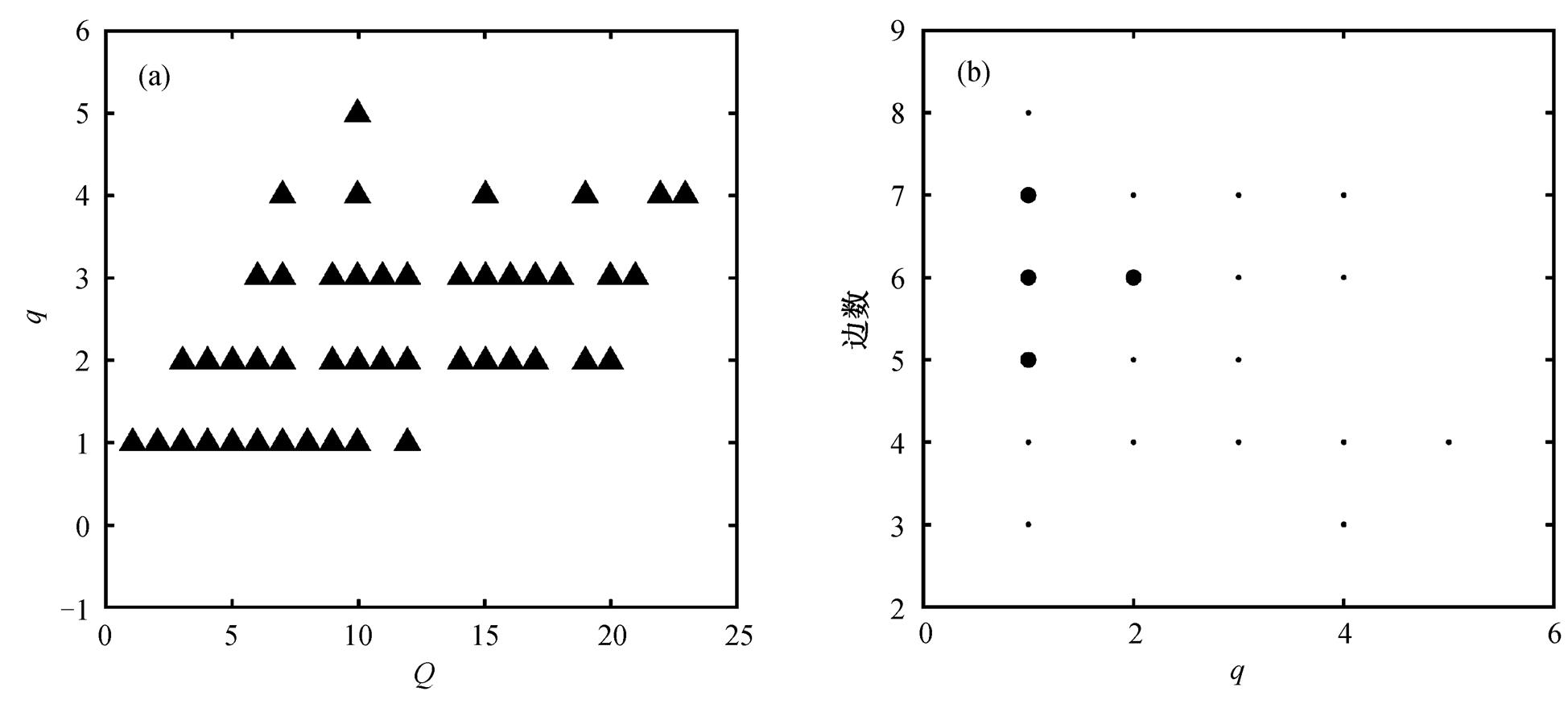
(a)黑色三角符号表示TRA网络结构所对应的Q值和q值(q>0), 灰色圆点表示具有适应性(Q>0)但不具有热鲁棒性(q=0)的网络; (b)圆点的大小表示具有相应q值和边数的网络数目的相对多少
图2 TRA功能网络在Q-q空间(a)和q-edge空间(b)的分布
Fig. 2 Distribution of TRA function networks in Q-q space (a) and q-edge space (b)
这 3 种 TRA 功能模体概括了 TRA 网络的结构特点, 结构更复杂的 TRA 功能网络基本上都以这 3种最简单的功能模体为骨架。如果一个 TRA 网络包含 a, b 和 c 这 3 种结构中的一种, 则归为对应的类, 如果不包含 3 种中的任何一种, 则归为“other”类。图 3 为 122 种 TRA 功能网络在 3 种非一致前馈TRA 功能模体中的分布, 纵轴表示对应的 motif 在TRA 功能网络中出现的频率。可以看出, 具有模体a, b, c 结构的 TRA 网络占绝大多数, 特别是模体 a和 b 所占比例很高, 而仅有小部分功能网络不包含这 3 种基本模体而具有其他结构。图 4 为模体 a 和 b在不同温度下的动力学适应性行为, 可以看出, 在不同温度下, 都具有很好的适应性功能。由于输入节点对输出节点的调控关系不同, 两个网络的输出曲线开口正好相反。
理论上, 在外界信号刺激下, 系统输出的稳态值 Os 不随温度变化, 因此实现热鲁棒的适应性需满足以下平衡条件:
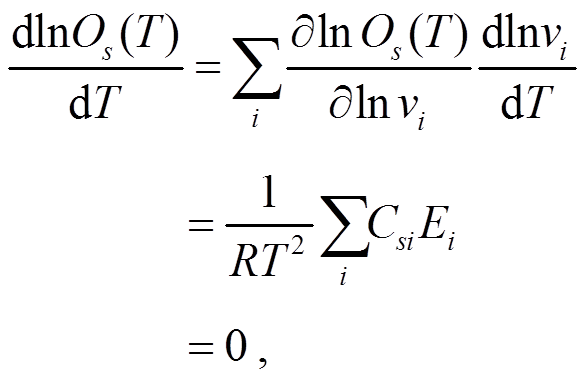(3)
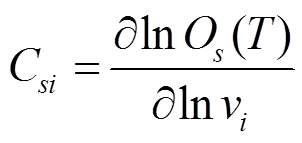为控制系数(control coefficient), 反映系统的输出 Os 对动力学参数 vi 改变的敏感程度。温度直接影响转录调控网络的反应速率, 反应速率又会对转录调控网路的功能产生影响。当网络中某个反应速率对应的控制系数大于或小于 0时, 则该速率的增加会对输出 Os 分别产生促进或抑制作用; 控制系数等于 0 时, 该速率的变化不会对Os 产生影响。
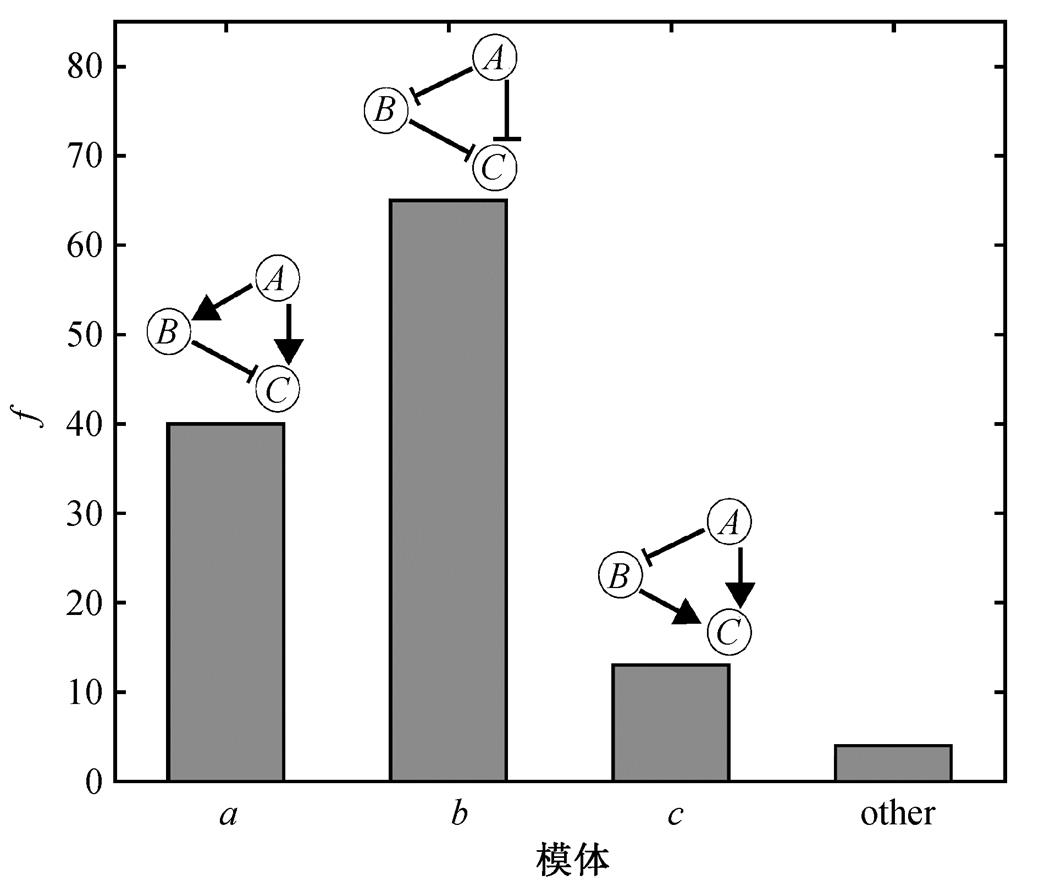
图3 TRA功能网络在3种基本TRA功能模体上的分布
Fig. 3 Distribution of TRA functional networks on the three TRA motifs
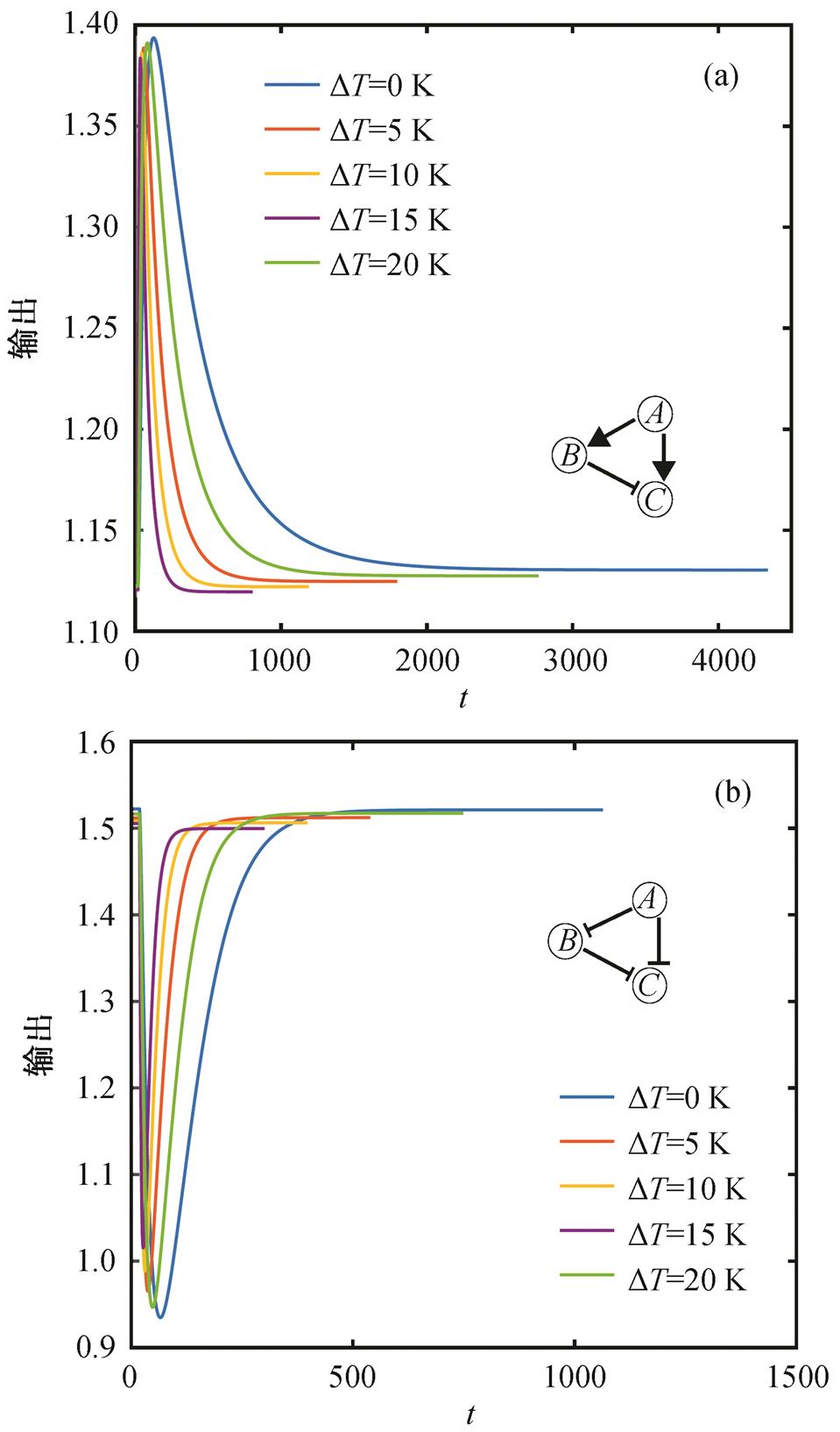
△T为相对 288 K 的偏离
图4 在不同温度下模体a和b的动态输出
Fig. 4 Dynamic output of motif a and motif b at different temperatures
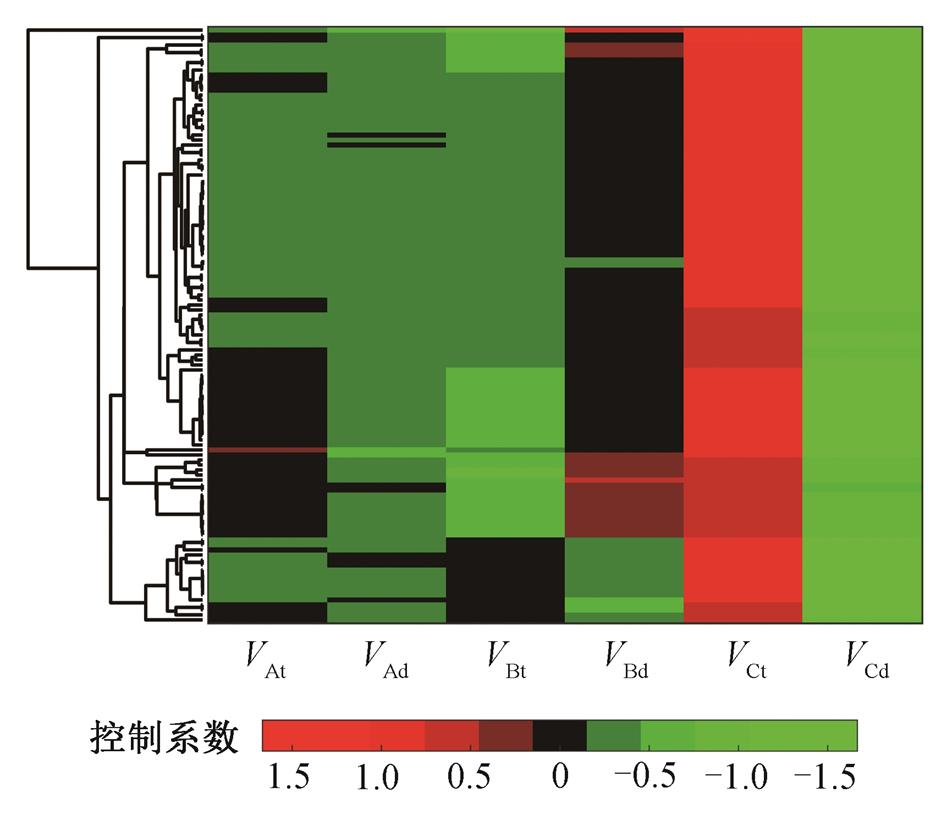
图5 TRA功能网络的控制系数的聚类分析
Fig. 5 Clustering analysis of control coefficients for the TRA functional networks
式(3)中的求和遍历动力学方程中所有的反应速率常数。式(3)表明, 温度补偿的条件在于满足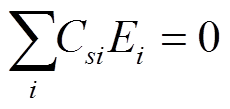
, 即每个参数的控制系数(Csi)与其活化能(Ei)的乘积的和为 0。活化能的数值都大于 0, 正是由于一个网络中不同速率对应的控制系数的数值可以为正, 也可以为负或等于 0, 才保证了温度补偿方程(式(3))的成立。根据控制系数的定义, 利用数值计算获得所有 122 个 TRA 功能网络的控制系数, 并对其进行聚类分析。
TRA 功能网络的控制系数 Csi 的聚类分析如图5 所示, 每行代表一个网络所有的控制系数。例如,图中第 1 列和第 2 列分别代表对应节点 A 的转录速率(VAt)和降解速率(VAd)的控制系数。图中的颜色条表示控制系数的大小。对于大多数网络, 聚类结果中输入节点 A 的控制系数都比较小, 控制系数基本上在 0 附近, 意味着网络的稳定输出 Os 受到节点 A参数改变的影响比较小。同样地, B 节点对应蛋白的降解速率相关的控制系数普遍接近于 0, 仅在部分网络中 B 节点的翻译生成速率常数的控制系数为负, 随温度的升高显著降低系统的输出。从图 5 可以看出, 对输出影响最大的是输出节点 C。节点 C动力学方程中的生成速率常数的控制系数为正, 且明显偏离 0, 而降解速率常数的控制系数为绝对值相对较大的负数。从控制系数的聚类来看, 这些TRA 功能网络的热鲁棒适应性主要通过输出节点调节。通过选择适当的活化能, 使得式(3)的平衡条件得到满足。
为了探究适应性功能的热鲁棒性, 本文从所有可能的拓扑结构中筛选出具有 TRA 功能的三节点转录调控网络。通过分析这些网络的拓扑结构, 我们发现 3 种 TRA 功能模体, 即 3 种非一致前馈网络 a, b 和 c。绝大多数 TRA 功能网络都以这 3 种模体为骨架构成。根据温度补偿条件, 适应性功能的温度补偿主要取决于两个因素: 活化能与控制系数。活化能取决于实际蛋白质结构, 由于不同反应速率对温度的敏感度不同, 所以在计算中对活化能随机取值。对于反应速率常数(包括翻译生成速率常数和降解速率常数), 本文假定它们随温度的变化遵循 Arrhenius 定律。控制系数的正负一般与网络拓扑结构相关。在 TRA 功能网络的控制系数的聚类中, 我们发现网络的控制系数可以为正, 也可以为负或接近 0, 这保证了只要适当地选择活化能, 就可以使得温度补偿的条件得到满足。另外, 聚类结果表明输出特征值 Os 主要取决于输出节点的反应速率, 基本上不依赖于输入节点。本文仅对“OR”逻辑调控关系做了计算, 其模型比较理想化, 但结果对于理解适应性的温度补偿机制有一定的意义, 特别是可以为实验合成热鲁棒性适应性网络提供理论基础。
参考文献
[1]Ruoff P, Loros J J, Dunlap J C. The relationship between FRQ-protein stability and temperature com-pensation in the Neurospora circadian clock. Procee-dings of the National Academy of Sciences, 2005, 102(49): 17681–17686
[2]Tseng Y Y, Hunt S M, Heintzen C, et al. Comprehen-sive modelling of the Neurospora circadian clock and its temperature compensation. PLoS Comput Biol, 2012, 8(3): 1002437–1002449
[3]Hazel J R, Prosser C L. Molecular mechanisms of temperature compensation in poikilotherms. Physiolo-gical Reviews, 1974, 54(3): 620–677
[4]Zakhartsev M V, De Wachter B, Sartoris F J, et al. Thermal physiology of the common eelpout (Zoarces viviparus). Journal of Comparative Physiology B, 2003, 173(5): 365–378
[5]Ruoff P, Zakhartsev M, Westerhoff H V. Temperature compensation through systems biology. FEBS J, 2007, 274(4): 940–950
[6]Wu L, Ouyang Q, Wang H. Robust network topologies for generating oscillations with temperature-indepen-dent periods. PLoS One, 2017, 12(2): 63–81
[7]Shi W, Ma W, Xiong L, et al. Adaptation with trans-criptional regulation. Scientific Reports, 2017, 7(1): 339–349
[8]Cao L H, Jing B Y, Yang D, et al. Distinct signaling of Drosophila chemoreceptors in olfactory sensory neu-rons. Proceedings of the National Academy of Sci-ences, 2016, 113(7): 902–911
[9]El-Samad H, Goff J P, Khammash M. Calcium homeostasis and parturient hypocalcemia: an integral feedback perspective. Journal of Theoretical Biology, 2002, 214(1): 17–29
[10]Gomez-Marin A, Duistermars B J, Frye M A, et al. Mechanisms of odor-tracking: multiple sensors for enhanced perception and behavior. Front Cell Neuro-sci, 2010, 4: Article 6
[11]Oleksiuk O, Jakovljevic V, Vladimirov N, et al. Thermal Robustness of Signaling in Bacterial Che-motaxis. Cell, 2011, 145(2): 312–321
[12]Shimizu H, Woodcock S A, Wilkin M B, et al. Compensatory flux changes within an endocytic tra-fficking network maintain thermal robustness of Notch signaling. Cell, 2014, 157(5): 1160–1174
[13]Ma W, Trusina A, El-Samad H, et al. Defining net-work topologies that can achieve biochemical adapta-tion. Cell, 2009, 138(4): 760–773
[14]Yan L, Ouyang Q, Wang H. Dose-response aligned circuits in signaling systems. PLoS One, 2012, 7(4): 34727–34736
[15]Wagner A. Circuit topology and the evolution of robustness in two-gene circadian oscillators. Procee-dings of the National Academy of Sciences, 2005, 102(33): 11775–11780
[16]Lim W A, Lee C M, Tang C. Design principles of regulatory networks: searching for the molecular algorithms of the cell. Molecular Cell, 2013, 49(2): 202–212
[17]Ma W, Lai L, Ouyang Q, et al. Robustness and modular design of the Drosophila segment polarity network. Molecular Systems Biology, 2006, 2(1): Article 70
[18]Mejia Y X, Mao H, Forde N R, et al. Thermal probing of E. coli RNA polymerase off-pathway mechanisms. J Mol Biol, 2008, 382(3): 628–637
[19]Ruoff P, Christensen M K, Wolf J, et al. Temperature dependency and temperature compensation in a model of yeast glycolytic oscillations. Biophysical Chemis-try, 2003, 106(2): 179–192
[20]Iman R L. Latin hypercube sampling. Chichester: American Cancer Society, 2014
Adaptive Functional Network with Thermal Robustness
Abstract Through the enumeration of the three-node gene regulatory network, the random sampling of the parameter space and the dynamics simulation, the adaptive gene transcriptional regulation networks with thermal robustness(namely temperature compensation) are found. The structural analysis of the thermally robust adaptive networks shows that there are three basic structures that can achieve adaptive dynamics with thermal robustness, and the complex adaptive networks with thermal robustness uses these three networks as the core skeletons. In order to investigate the sensitivity of the adaptability of the three-node adaptive network to the changes of various parameters in the network dynamics, the authors calculate the corresponding control coefficients of each parameter. The clustering analysis of the control coefficients shows that the mechanism of the three-node functional network to achieve thermal robustness is temperature isolation, that is, although all rate parameters in the network are temperature dependent, only the generation and degradation rates of the output nodes deviate significantly from zero and have opposite signs. Most thermal robustness is achieved by the antagonistic balance adjustment of the output nodes.
Key words adaptation; function and topology; gene regulation networks; temperature compensation
doi: 10.13209/j.0479-8023.2019.038
国家重大科学研究计划(2015CB910300)资助
收稿日期: 2018–08–17;
修回日期: 2018–09–23