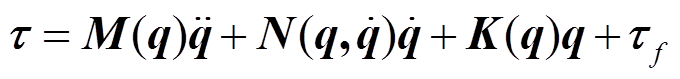, (1)摘要 为了正确地掌握空间机械臂在轨服务过程的真实动力学特性, 基于 Lagrange 方程, 获得机械臂有/无气浮装置时关节驱动力矩的差值函数, 然后利用带气浮装置的关节驱动力矩的地面实验数据减去理论差值, 预测机械臂在轨服务时的真实驱动力矩。最后采用刚性较好的小型机械臂进行实验, 验证了该方法的正确性。
关键词 空间机械臂; 动力学建模; 驱动力矩
在太空中, 空间机械臂可以比较容易地抓取并操作一个比自身大很多的大型载荷。例如, 国际空间站机械臂(SSRMS)长 17 m, 重 1800 kg, 能轻易地抓捕和操作重达 200 吨的满载航天飞机[1]。在机械臂研发过程中, 整臂级的地面物理实验是不可或缺的[2]。在地面实验时, 由于重力效应和机械臂的轻质结构, 利用气浮装置[3–7], 对空间机械臂进行平面气浮实验是机械臂最常用的实验手段。
平面气浮实验系统通常包含一个或多个移动平台, 每个移动平台借助气浮垫漂浮在固定水平面上, 从而实现机械臂的平面运动。机械臂的关节驱动力矩及其制动时的振动特征是机械臂的关键测量指标[8]。在地面气浮实验中, 对其正确测量有利于机械臂动力学、控制以及精度等研究的开展。然而, 气浮实验方法存在一个重要问题: 当机械臂或其载荷较大时, 所需气浮装置的尺寸和质量将非常可观。机械臂关节驱动力矩在驱动机械臂运动的同时, 也驱动气浮装置一起运动。地面实验测得的机械臂驱动力矩显然不同于在轨时的驱动力矩。其次, 机械臂在工作过程中, 制动是常见的操作步骤, 但是由于气浮装置的存在, 机械臂的振动特征以及制动距离会显著改变。因此, 去除气浮装置对机械臂驱动力矩和振动特征的影响, 从地面实验中获得机械臂在轨的真实驱动力矩以及制动过程中真实的振动特征, 是空间机械臂地面实验结果处理的重要环节[2]。
本文针对机械臂在轨关节驱动力矩的辨识进行理论推导, 采用 Lagrange 方程, 获得有气浮和无气浮装置时关节驱动力矩的差值函数, 然后在两种实验工况条件下, 通过实验验证理论方法的有效性。
一个自由度为 n 的空间机械臂在太空执行操作任务时, 其动力学方程可表示为如下形式[9]:
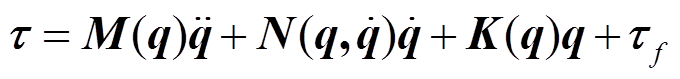, (1)其中,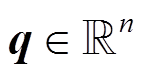 
为广义坐标, 为机械臂的关节相对转角; 
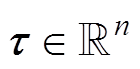是施加于机械臂关节上的广义力, 此处的广义力是机器臂在太空作业时驱动机械臂的关节控制力偶; 
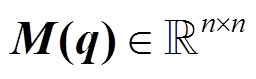是广义惯量矩阵, 是广义坐标
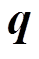的非线性函数; 
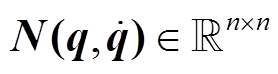是由离心力及科氏力等引起的非线性项, 为广义坐标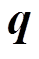和广义速度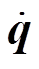
的函数;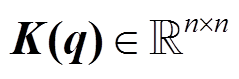 
是广义刚度矩阵, 是广义坐标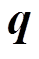的函数;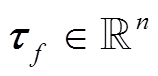 
是关节处的摩擦力矩。
由于机械臂非常重, 在地面上无法直接进行实验验证, 因此通常借助图 1 的气浮支撑设备进行实验。图 1 中的 Cj 是第 j 个气浮支撑装置与机械臂的连接位置。与机械臂相比, 支撑设备的质量和尺寸通常不能忽略。在这种实验状态下, 地面实验测量的驱动力矩并不是在轨时的真实数据, 而是机械臂和气浮装置构成的组合系统的驱动力矩。根据图1, 组合系统的动力学关系可以表示为
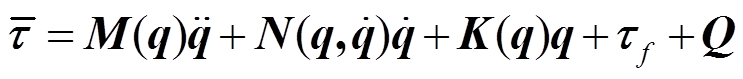, (2)其中,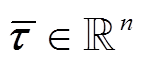 
是机械臂和气浮装置组合系统运动时的广义力(即关节控制力矩); 
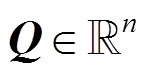是气浮支撑装备施加于机械臂支撑点的约束力和力矩的广义力。
由于在地面上只能测得与真实力矩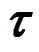
相对应的测量力矩
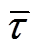, 因此需要解决如何由测量力矩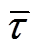获得真实力矩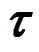。结合式(1)和(2), 当机械臂实验与在轨具有相同的运动时, 真实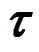力矩与测量力矩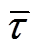之间的关系为
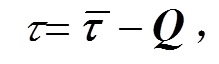(3)
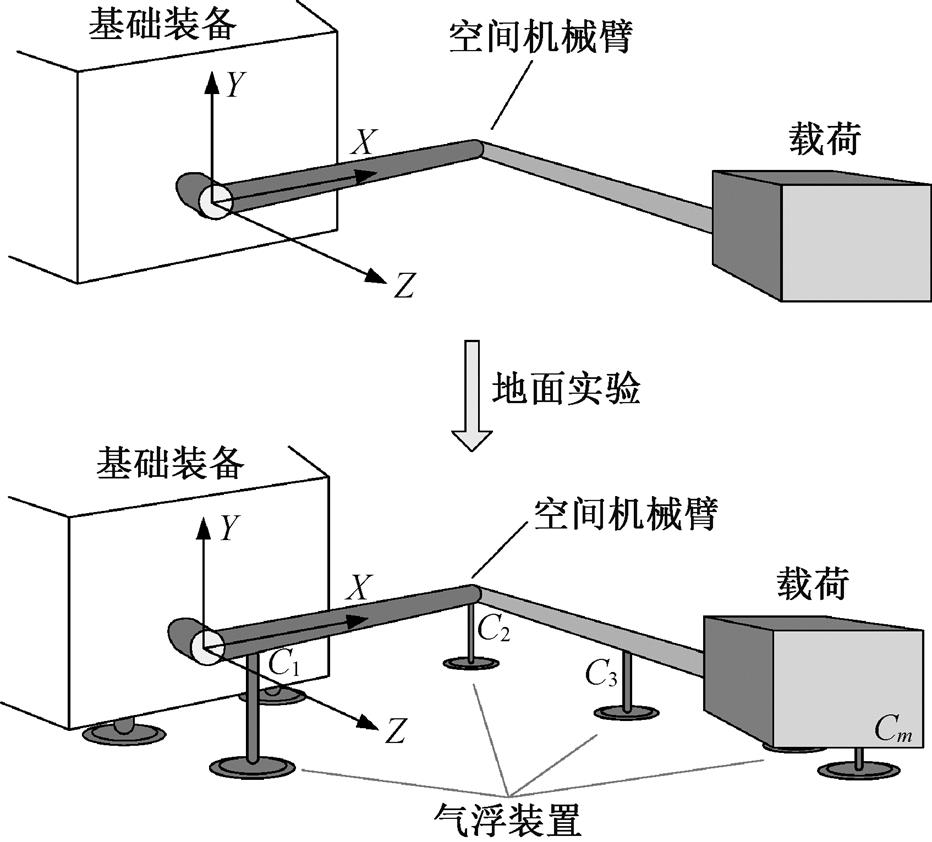
图1 空间机械臂平面气浮实验示意图
Fig. 1 Experimental sketch of space robot plane air flotation
此时, 问题转变为求解广义力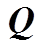
。假设共有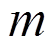
个气浮装置支撑机械臂及其载荷, 广义力为
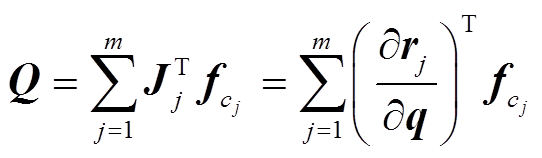。 (4) 由于对应的实验是平面的气浮实验, 因此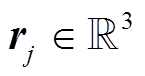
是气浮装置上固定位置 Cj 的位姿, 包括平面上的位置以及转角;
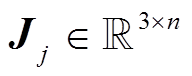是第 j个连接点的线速度和角速度的雅可比矩阵, 即
; 
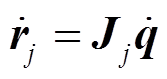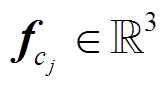是第 j 个气浮支撑设备作用于机械臂第 j 个连接点的约束力和力矩。具体受力情况如图2所示。
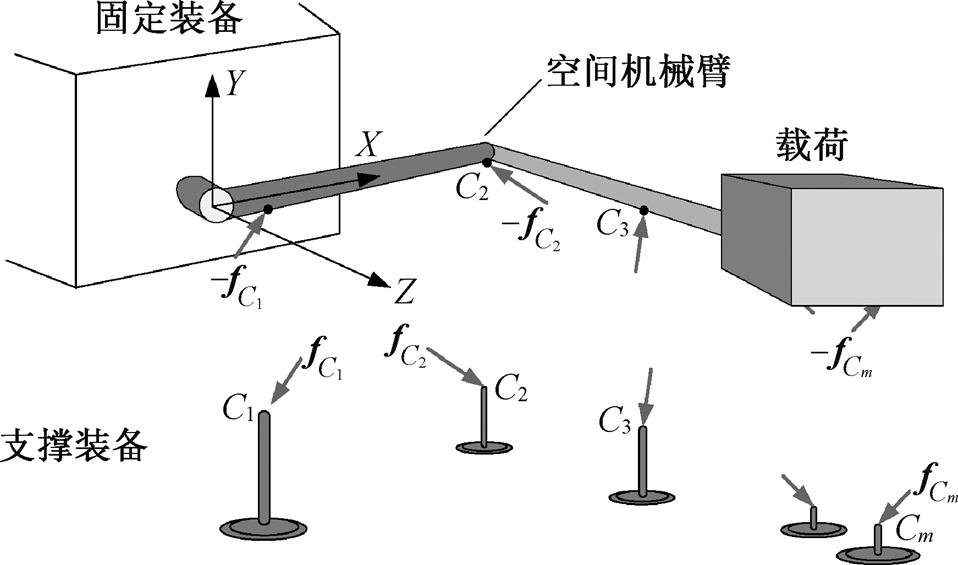
图 2 气浮支撑装置受力图
Fig. 2 Stressed sketch of air flotation support equipment
由于气浮装置直接固定在机械臂上, 所以式(4)中气浮装置的安装位置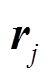
是可测的。气浮装置对机械臂产生的作用力和作用力偶
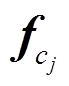可通过支撑设备的动力学模型计算。由于机械臂通常是一个主动的动力学系统, 而支撑设备是一个相对简单且被动的机械结构, 因此, 计算支撑设备的附加广义力比计算整个机械臂动力学过程简单得多。通过式(3)和地面实验数据, 来预测机械臂在轨时关节的驱动力矩, 避免了整个机械臂动力学模型的计算。实验中
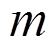个支撑设备通常相互独立, 第 j 个支撑设备的受力情况如图 3 所示, 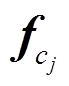可由式(5)计算得到:
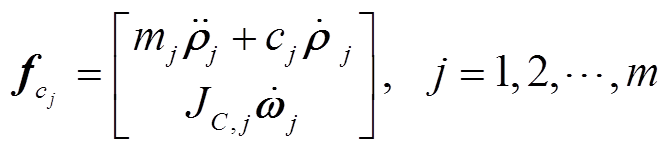, (5)其中,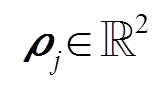 
代表第j个支撑设备的质心在平面上的位置; 
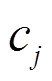是气浮实验过程中第 j 个支撑设备与地面间的摩擦系数;
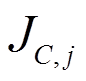是第 j 个支撑的质心转动惯量; 
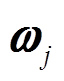是第 j 个支撑设备的角速度, 由于气浮装置与臂杆固连, 因此其角速度等于连接臂杆的角速度。在已知臂杆运动的条件下, 质心的速度、加速度和角加速度都能够得到, 因此
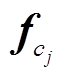也可以获得。
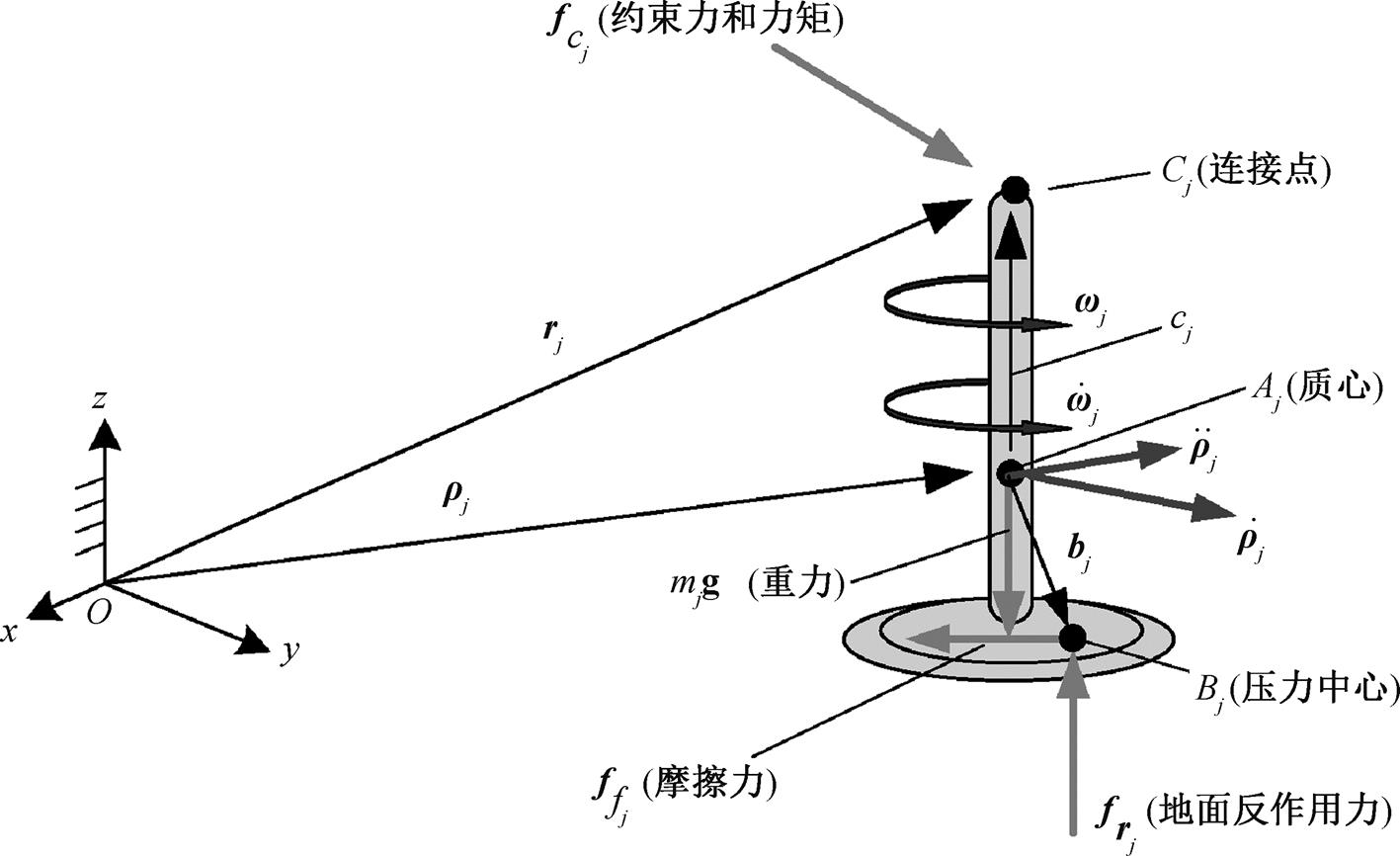
图3 第j个支撑设备的受力图
Fig. 3 Stressed schematic diagram of support equipment j
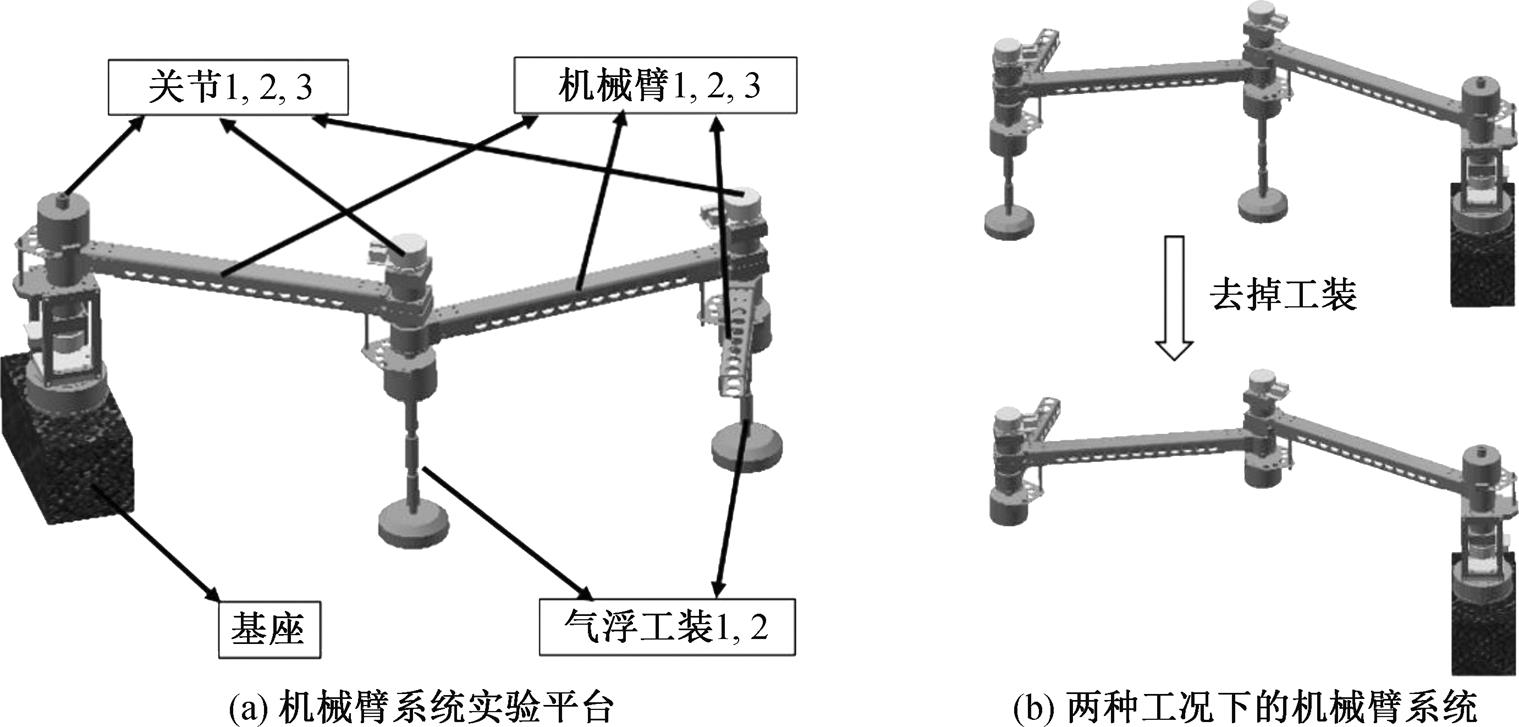
图4 实验平台示意图
Fig. 4 Schematic diagram of experiment platform
表1 小型机械臂参数
Table 1 Small robot arm parameters
编号长度/m质量/kg抗弯强度/(104N.m) 10.40.2492 20.40.2492 3 0.150.0712
表2 气浮装置参数
Table 2 Air floatation equipment parameters
编号质量/kg转动惯量/(kg·m2) 11.38020.001 21.35130.001
表3 关节参数
Table 3 Joint parameters
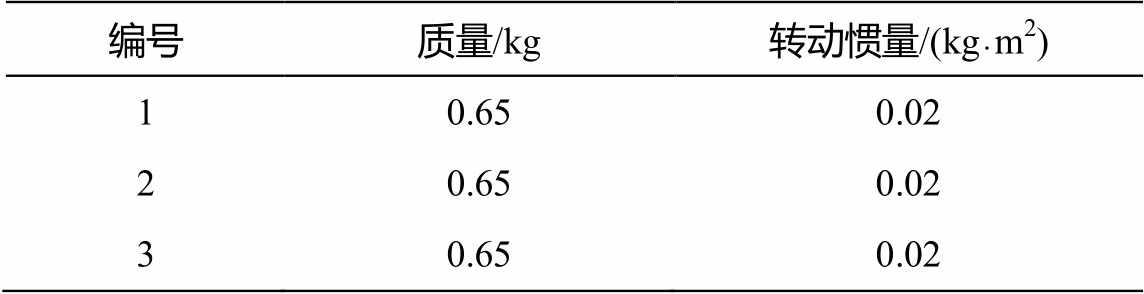
编号质量/kg转动惯量/(kg·m2) 10.650.02 20.650.02 30.650.02
为了验证理论方法的正确性, 我们制作了具有三关节三臂杆的机械臂系统, 如图 4(a)所示。气浮装置可以拆卸, 如图 4(b)所示, 系统的物理参数如表 1~3 所示。由于臂杆具有较大的刚性, 并且没有负重, 因此, 当臂杆去掉气浮装置时, 依然被认为作平面运动。本文分别在有气浮和无气浮装置的条件下, 利用基座与机械臂根部的力传感器, 测得第一个关节的驱动力矩。
我们设计两组实验。在第一组实验中, 保持 3根臂杆呈 180°状态, 机械臂的臂杆间保持不动, 只转动根部的机械臂, 在有气浮和无气浮装置两种工况条件下的相对转动角度、角速度和角加速度如图5(a)、图 6(a)和图 7(a)所示。第二组实验中, 两根机械臂的关节同时以相同的相对角速度转动, 第三个关节保持不动, 相对转动角度、角速度和角加速度如图 5(b)、图 6(b)和图 7(b)所示。其中,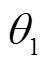 
和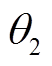
表示不含气浮装置条件下关节 1 和关节 2 的角位移, 
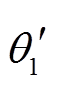和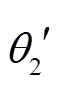
表示含气浮装置条件下关节 1 和关节 2 的角位移, 而
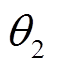和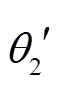表示关节的相对转角。通过不同工况下角度、角速度和角加速度的对比可以看到, 在两组不同转动条件下, 有气浮和无气浮装置机械臂的运动基本上相同。下面将验证在有无气浮装置的两种工况下, 其根部关节驱动力矩之差与式(3)预测的结果相符。
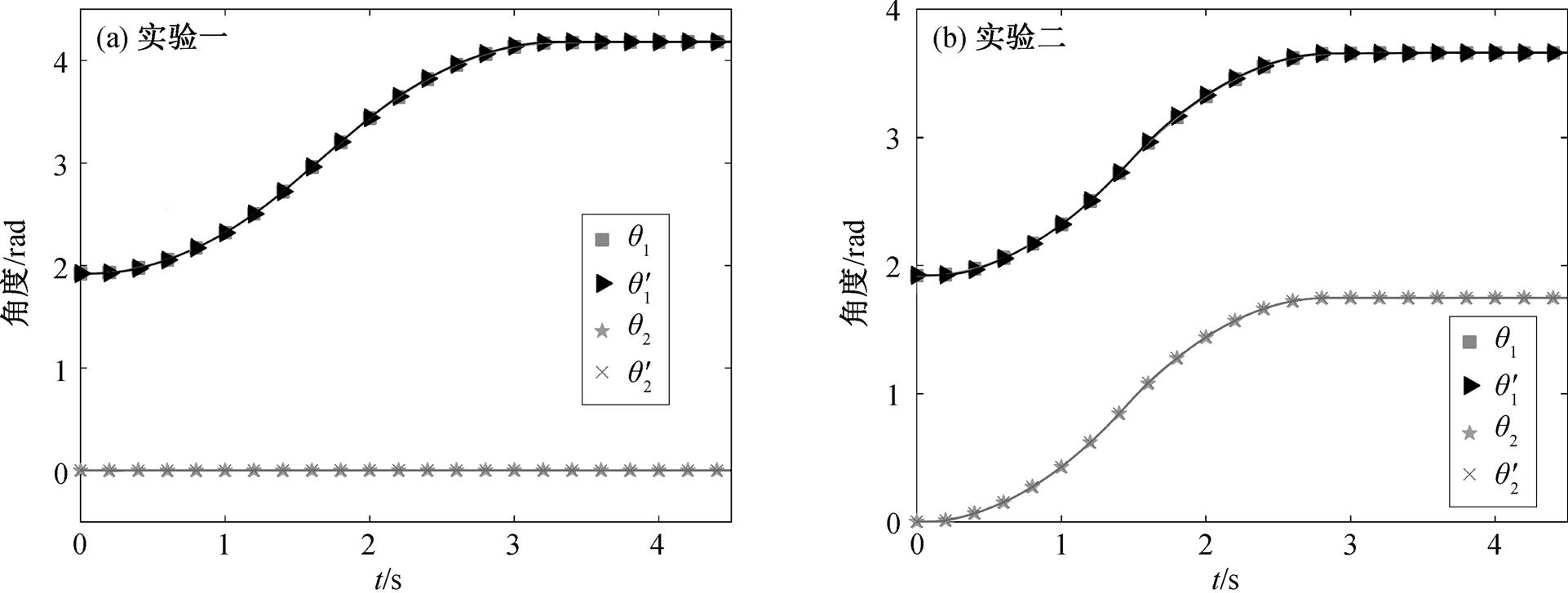
图5 关节1和2在两种工况下角位移的对比
Fig. 5 Comparison of angular displacement of joint 1 and 2 under two conditions
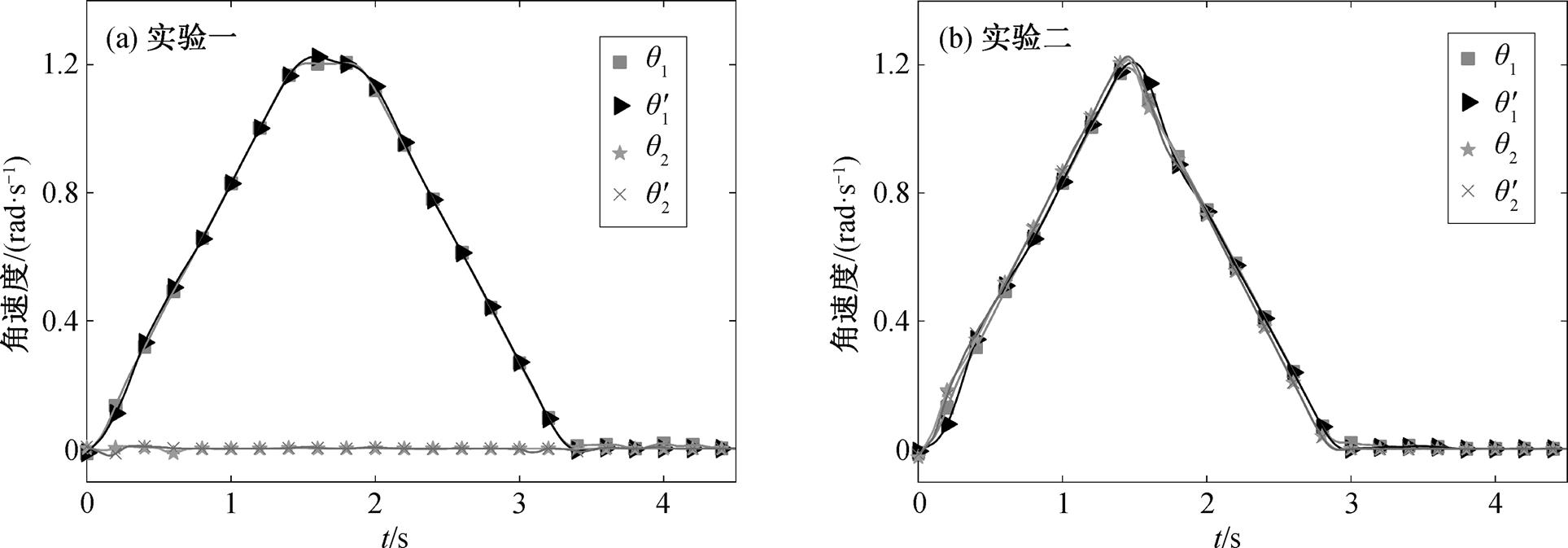
图6 关节1和2在两种工况下角速度的对比
Fig. 6 Comparison of angular speed of joint 1 and 2 under two conditions
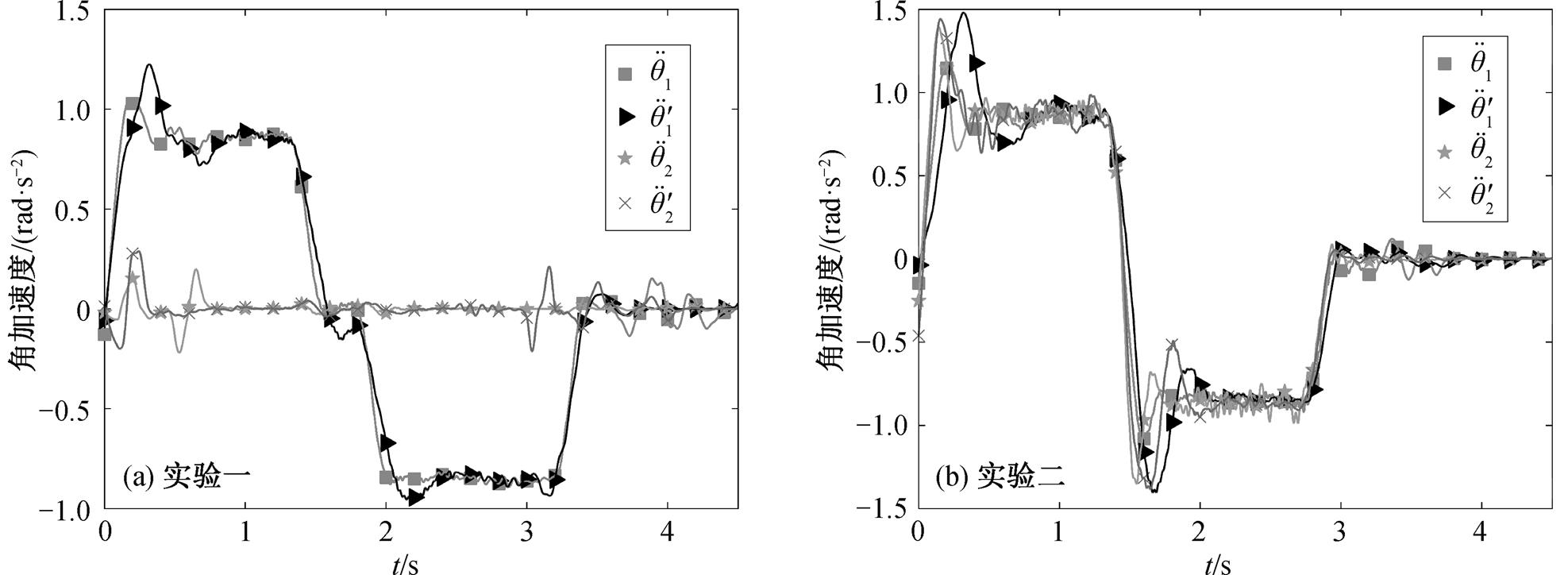
图7 关节1和2在两种工况下角加速度的对比
Fig. 7 Comparison of angular acceleration of joint 1 and 2 under two conditions
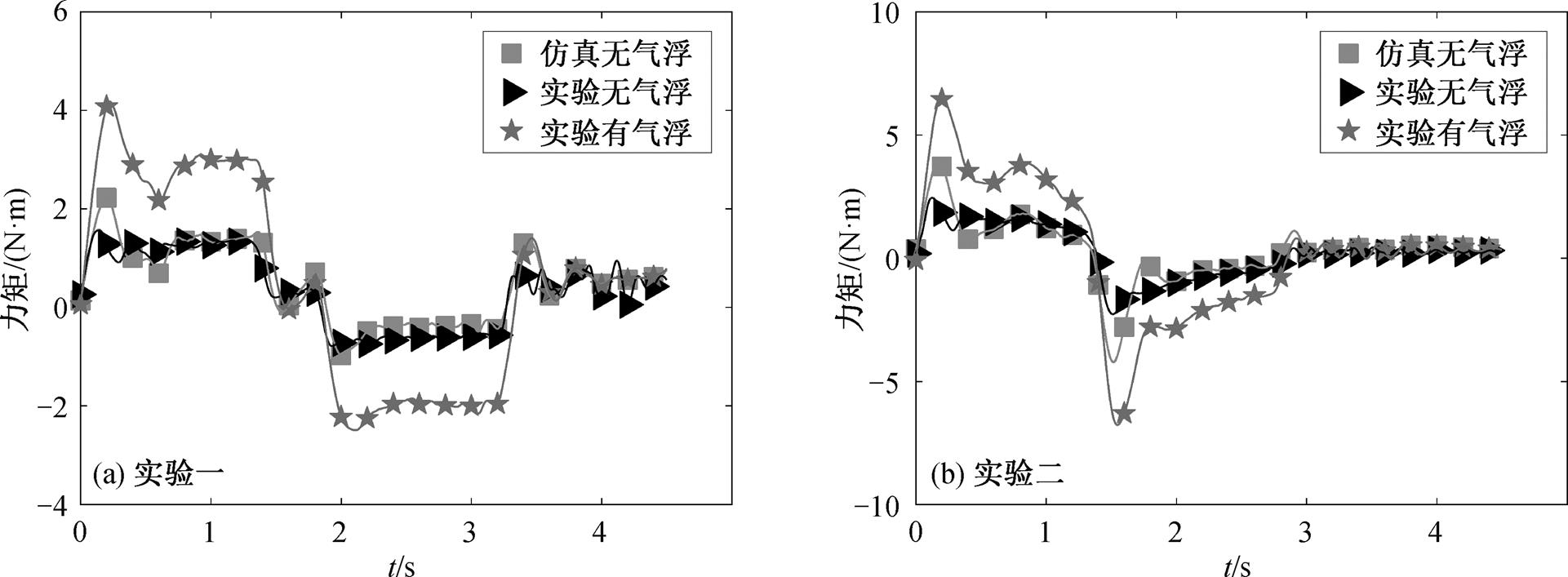
图8 数值仿真与实验测量关节1驱动力矩对比
Fig. 8 Comparison of numerical simulation and experimental measurement of joint 1’s driving torque
实验测量得到的含气浮和不含气浮装置的根部驱动力矩如图 8 所示。根据式(4)和(5), 采用表 1~ 3 中的参数, 忽略气浮装置与实验台之间的摩擦, 得到有/无气浮装置条件下的广义力差值函数 Q。利用式(3), 把有气浮装置时机械臂根部的实验驱动力矩减去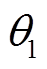
对应的广义力
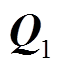, 得到图 8 中无气浮装置时的仿真驱动力矩, 此力矩曲线与无气浮装置时的实验曲线吻合。由此, 验证了式(3)的正确性。
实验与理论相符, 说明地面实验和在轨服务时机械臂关节驱动力矩可以采用刚体模型进行预测。另外, 利用式(3)预测机械臂在轨工作状态下的驱动力矩时, 可以在气浮装置和机械臂的连接处安装力传感器, 通过实验数据来辨识, 尽量避免因过多模型假设而导致的人为误差。
本文提出去除机械臂气浮实验驱动力矩中气浮装置影响的理论方法。该方法以地面机械臂与在轨机械臂的运动相同为前提, 利用 Lagrange 方程推导出两者关节驱动力矩的差值函数表达式, 此函数与气浮装置的安装位置以及物理参数有关。利用此表达式, 可以从机械臂地面实验的测量驱动力矩获得在轨服务时的真实驱动力矩, 避免了整个机械臂模型的引入及其动力学的计算。本文搭建了三臂杆三关节的机械臂气浮实验平台, 在有气浮装置和无气浮装置的条件下, 分别测得的机械臂根部的驱动力矩。然后把有气浮装置测得的实验驱动力矩减去理论预测的差值函数, 获得无气浮装置时的预测驱动力矩与无气浮装置的实验驱动力矩对比非常吻合, 从而验证了本文提出的理论方法的正确性。本文的研究结果为机械臂地面实验数据的处理提供了一条有效的途径。
参考文献
[1]Ma O, Buhariwala K, Neil R, et al. MDSF — a gene-ric development and simulation facility for flexible, complex robotic systems. Robotica, 1997, 15(1): 49–62
[2]徐文福, 梁斌, 李成, 等. 空间机器人微重力模拟实验系统研究综述. 机器人, 2009, 31(1): 88–96
[3]Ma O, Zhao Z. Understanding the true dynamics of a space manipulator from its testing with air-bearing based support equipment // AIAA SPACE 2015 Con-ference and Exposition. Pasadena, 2015: 4537
[4]Umetani Y, Yoshida K. Experimental study on two-dimensional free-flying robot satellite model // Pro-ceedings of the NASA Conference on Space Tele-robotics. Pasadena: California Institute of Techno-logy, 1989, 5: 89–87
[5]Ullman M A, Jr Cannon R H. Experiments in autonomous navigation and free-flying of a multi-manipulator, free-flying space robot // Xu Y, Kanade T. Space robotics: dynamics and control. Dordrecht: Kluwer Academic Publishers, 1993: 269–284
[6]Ballhaus W L, Alder L J, Chen V W, et al. Stanford aerospace robotics laboratory research overview // NASA Sixth Annual Workshop on Space Operations Applications and Research. Houston, 1992: 54–65
[7]Schwartz J L, Peck M A, Hall C D. Historical review of air-bearing spacecraft simulators. Journal of Gui-dance, Control, and Dynamics, 2003, 26(4): 513–522
[8]徐文福, 杜晓东, 王成疆, 等. 空间机械臂系统总体技术指标确定方法. 中国空间科学技术, 2013, 33(1): 53–60
[9]Menon C, Busolo S, Cocuzza S, et al. Issues and solutions for testing free-flying robots. Acta Astro-nautica, 2007, 60(12): 957–965
Obtaining Driving Torques of Space Manipulators Based on Ground Planar Experimental Data of the Manipulator with Air-bearing Support: Modeling and Experimental Verification
Abstract In order to extract the true dynamics of a manipulator in space from the experimental data on ground, gap functions of the joints’ driving torques are deduced by Lagrangian equations between two manipulators with and without air-bearing support. The real driving torques can be predicted by the ground data minus the gap function. Verifying experiments are designed and carried out by a small manipulator with rigid arms.
Key words space manipulator; dynamic modeling; driving torque
doi: 10.13209/j.0479-8023.2019.006
中国空间技术研究院总体部与北京航空航天大学航空学院合作项目和国家自然科学基金(11572017)资助
收稿日期: 2018–06–06;
修回日期: 2018–10–0