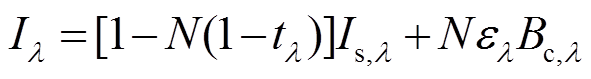, (1)摘要 针对 2016 年 4 — 9 月 90°—140°E, 15°—55°N 区域的半透明云, 使用分裂窗直方图法, 利用 Himawari-8的 AHI 观测数据进行云顶高度反演。首先使用阈值法筛选出半透明云区; 然后基于分裂窗直方图法, 利用Himawari-8 的 10.4 μm 和 12.4 μm 两个分裂窗通道数据以及 ERA-Interim 再分析资料中的温度气压层数据和位势高度气压层数据反演云顶高度, 并将反演结果与 CloudSat 的 2B-GEOPROF 产品数据进行匹配和对比, 结果表明: 1)分裂窗直方图法对 Himawari-8 数据反演半透明云云顶高度的结果与 CloudSat 的数据结果较一致, 均方根偏差为 1.45 km; 2)海陆类型对反演结果没有明显的影响。所提算法有较强的适用性, 可以应用于不同卫星的分裂窗通道数据反演, 特别是对中国新一代静止气象卫星风云四号的业务反演有理论参考价值。
关键词 分裂窗直方图法; 半透明云; Himawari-8; 云顶高度
地球表面约有 70%的区域被云覆盖, 云在天气和气候与太阳和地球辐射的强相互作用中扮演着至关重要的角色[1], 因此迫切需要对云参数的精确观测。卫星遥感可提供云参数反演的丰富信息。作为基本的云参数之一, 云顶高度对云的热辐射强迫估计、航空预警和雷暴预报以及天气和气候研究等都有十分重要的作用[2‒3]。
目前, 利用卫星遥感的辐射数据进行云顶高度反演的方法很多, 例如红外窗区通道法、线性外推法、辐射比值法和辐射余差法等[1,4]。Mouri 等[5]利用其中的 3 种方法, 对 2015 年 7 月 20 日至 8 月 2 日日本新一代静止气象卫星 Himawari-8 的云分类数据进行云顶高度反演, 其结果与 MODIS(Moderate Resolution Imaging Spectroradiometer)云顶高度的平均偏差为−541.4m, 均方根偏差为 3313.2m, 与 Ca-lipso (Cloud-Aerosol Lidar and Infrared Pathfinder Sa-tellite Observations)云顶高度的平均偏差为−1834.5m, 均方根偏差为 4457.4m, 表明将这些方法应用在 Himawari-8 数据的反演中存在一定的问题。
为了提高对 Himawari-8 数据反演云顶高度的准确度, 本文采用分裂窗直方图法, 这种方法主要有两个优点: 1) 红外分裂窗通道不受时间的影响, 在夜晚或白天都可以使用; 2) 红外分裂窗通道在卫星搭载的仪器中常见, 几乎所有的气象卫星都有分裂窗通道, 可以广泛应用于其他气象卫星数据。
分裂窗直方图法最早由 Inoue[6]提出, 用于反演半透明云的云顶温度, 他通过计算西太平洋上 4 块云的云顶温度, 发现该方法对亮温的精度比较敏感。这种方法主要依据红外分裂窗通道受大气影响较小, 两通道的亮温差主要受水汽影响, 并且在大气窗区冰粒子和水汽的辐射吸收系数随着辐射波长的增加以不同的速率增加, 得到云顶温度[7]。之后, Wu[8]采用这种方法模拟计算云顶温度, 结果表明在满足理想大气条件的情况下对云顶温度的估计较好。Parol 等[9]使用 AVHRR (Advanced Very High Re-solution Radiometer)的 11μm 和 12μm 通道亮温和亮温差数据, 对这种方法做了更深入的探究, 结果表明在不考虑散射的情况下两通道的吸收系数比是影响结果的关键参数, 并提出在多次散射的情况下, 可以引入有效吸收系数。Giraud 等[10]引入等效吸收系数, 在 100×100 的格点数据内筛选出吸收系数比值最大、等效米散射粒子半径最小的数据进行拟合, 完成大范围区域内最低云顶温度的计算。Korpela等[3]使用 AVHRR 近红外通道亮温数据, 利用分裂窗直方图法对 20°E, 60°N 附近区域的半透明云和碎块云进行云顶温度反演。Joro 等[2]将分裂窗直方图法反演的云顶高度结果与天气雷达的观测数据进行比较, 48 个例子中有 3 个结果误差小于0.5km, 30%的结果误差集中在 4.5~5.0km 范围。Cooper 等[11]研究在雷达提供云边界信息的情况下使用这种方法计算云顶温度的不确定性, 发现卷云的光学特性对反演精度的提高有重要作用。Heidinger 等[12]建立了最优估计方法对 AVHRR 数据进行云顶温度反演的框架。总而言之, 分裂窗直方图法自提出以来得到长时间的发展。本文的研究对象半透明云的云顶通常较高, 透过率较大, 反演云顶高度易受下垫面的辐射影响, 目前使用分裂窗直方图法反演半透明云的云顶高度是比较可靠的手段。
国内对半透明云云顶高度的业务反演, 目前使用的是红外窗区通道和水汽通道法反演的算法[13]。使用红外分裂窗通道进行试验研究, 可为半透明云云顶高度的获得增加一条途径。本文从云的物理特性出发, 使用Himawari-8数据, 采用分裂窗直方图法, 对 90°—140°E, 15°—55°N 区域的半透明云云顶温度进行反演。借助欧洲中长期天气预报中心提供的温度气压层和位势高度气压层再分析资料得到云顶高度, 并与 CloudSat 的雷达廓线产品数据进行对比; 选择两个个例进行具体分析, 并简单地讨论地形对反演方法精度的影响。
Himawari-8 卫星是日本最新一代的静止气象卫星, 星下点位于 140.7°E, 搭载有先进的成像仪 AHI (Advanced Himawari Imager)。AHI 有 3 个可见光通道, 3 个近红外通道, 10 个红外通道, 共计 16 个观测通道。其中, 可见光的空间分辨率是 0.5km 或 1km, 近红外通道的空间分辨率是 1km 或 2km, 红外通道的空间分辨率是 2 km。与前代静止气象卫星相比, 时间分辨率大大增加, 全圆盘图像可实现每 10 分钟一张[14]。
本研究使用的 Himawari-8 数据是国家卫星中心提供的 hdf 格式全圆盘数据, 主要利用 8.6, 10.4和 12.4μm 这 3 个红外通道数据, 数据的空间分辨率均为 2km。其中, 8.6, 10.4 和 12.4μm 通道数据用来检测半透明云的存在, 大气窗区的通道可以用来获取下垫面温度以及检测冰粒子或水、低空水汽的存在等。
CloudSat 卫星是美国 A-Train 卫星系列中的一颗极轨卫星, 上面搭载有毫米波云廓线雷达 CPR (Cloud Profile Radar), 可以探测云的内部结构, 提供云中液态水、冰水的含量等云粒子相关的信息, 每天大约可以提供 14 轨观测数据, 轨道高度为 705km。观测数据的空间分辨率沿轨道延伸方向为 1.1km, 垂直于轨道方向为 1.4km, 提供的廓线数据在垂直方向上有 125 层, 分辨率为 240m, 探测范围是距地面 30 km高度的区域[15]。
本文使用从科罗拉多州大学 CloudSat 数据处理中心获得的 R05 版本的二级产品 2B-GEOP ROF[16]。2B-GEOPROF 产品包括有探测点的经纬度信息、时间、地面高程、雷达反射率、雷达反射率因子、垂直方向上的高度信息和相应点的云掩码等数据集, 其中用来表示回波信号可靠程度的云掩码数据结果在 0~40 之间, 填充值为−9, 当有云的阈值为 20 时, 可信度为 95%, 当有云的阈值为 30 时, 可信度为98%, 当有云的阈值为 40 时可信度为99%[17]。本研究将 20 作为有云的阈值, 即从最高30km 处到地面的 125 层云掩码数据中第一个大于或等于 20 的层所在的高度视为 CloudSat 产品识别的云顶高度。
ERA-Interim 再分析资料是欧洲中长期天气预报中心提供的 NetCDF 格式的全球大气再分析资料。由于信息存储量大等原因, 再分析资料的分辨率一般较差。本研究使用的 ERA-Interim 再分析资料是 2016 年 4—9 月的温度气压层数据和位势高度气压层数据, 沿垂直方向分为 37 个气压层, 最高层的气压为 0.1hPa, 水平分辨率为 0.125°×0.125°, 每天分别在 00:00, 06:00, 12:00 和 18:00UTC 更新4 次[18‒19]。
分裂窗直方图法主要根据云粒子在大气窗区的辐射特性差异, 利用卫星探测的辐射亮度来反演云顶参数。假设云为单层云, 忽略大气在窗区通道波段的吸收和反射以及云在红外波段的散射, 并且假设云层的吸收系数为常数, 根据辐射传输方程, 卫星探测器从波长为 λ 的窗区通道感应到的辐射亮度可以表示为
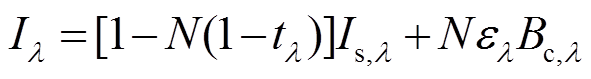, (1)其中, N 是像元中云的覆盖率(即云量), tλ 为云层在波长
通道的透过率, ελ 为云在波长为 λ 通道的发射率, Is,λ 和 Bc,λ 分别为波长为 λ 通道的地表辐射亮度和云顶辐射亮度,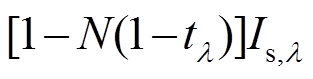 
表示晴空区的地表辐射亮度与云层透过的辐射亮度之和, 
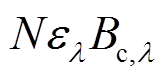表示云区的发射辐亮度。假设大气与云层处于局地热力平衡状态, 根据基尔霍夫定律有
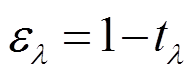, (2)
则式(1)可表示为
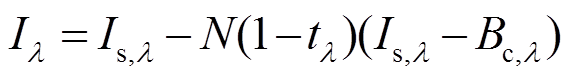。 (3)在红外长波波段, 根据普朗克定律, 辐射亮度与亮度温度近似为线性关系, 则式(3)可变化为
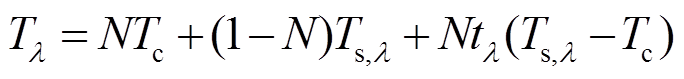。 (4)
其中, Tl, Tc 和 Ts,l分别为l通道探测的亮度温度、云顶亮度温度和对应l波段的地表亮度温度。同时, 根据比尔定律有
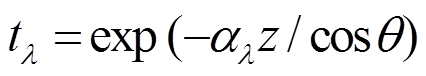, (5)其中, αλ 为云层吸收系数, θ 为路径与垂直方向的夹角。据此有
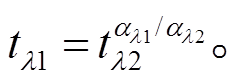(6)
对于大气窗区的两个通道, 根据式(4)和(6)可以得到
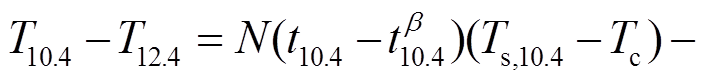
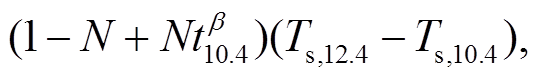(7)
其中,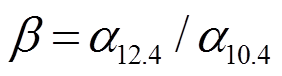
, 是两通道吸收系数的比值, 与粒子大小和相态有关。假设一个像元中的云量为 1, 此时探测器探测到的亮温可表示为
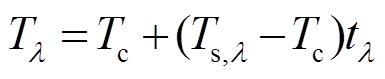, (8)大气窗区的两个通道的亮温差为
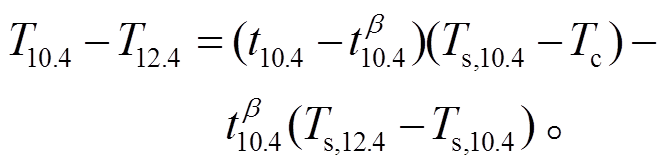(9)
式(9)表示在云顶温度和地表条件确定的情况下, 两个通道的亮温差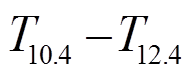
随透过率的变化关系, 而透过率从0至1的变化在卫星观测数据中表现为通道亮温
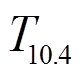的变化。
图 1 展示对云顶温度(Tc)、地表亮温(Ts,10.4)、系数(β)和地表亮温差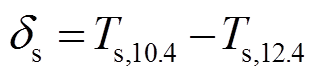
这 4 个参数取4 组不同的值时, 两个通道的亮温差随亮温的变化曲线。在晴空状态下, 
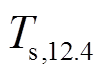, 此时透过率为 1, 通道亮温差代表在两个波长通道中感受到的地表辐射亮度的差异, 与地表发射率有关; 当云为不透明云时, 
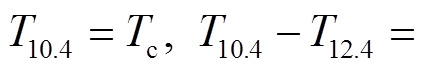0, 亮温差异消失, 两个波长通道感受到的辐射均为云顶辐射, 透过率为 0; 当云为半透明云时, 透过率介于 0~1 之间, 亮温差随着透过率的变化而变化, 当云顶温度、地表条件和透过率固定时, 亮温差随着系数 β的增大而增大, 随 T10.4的变化曲线呈拱形。
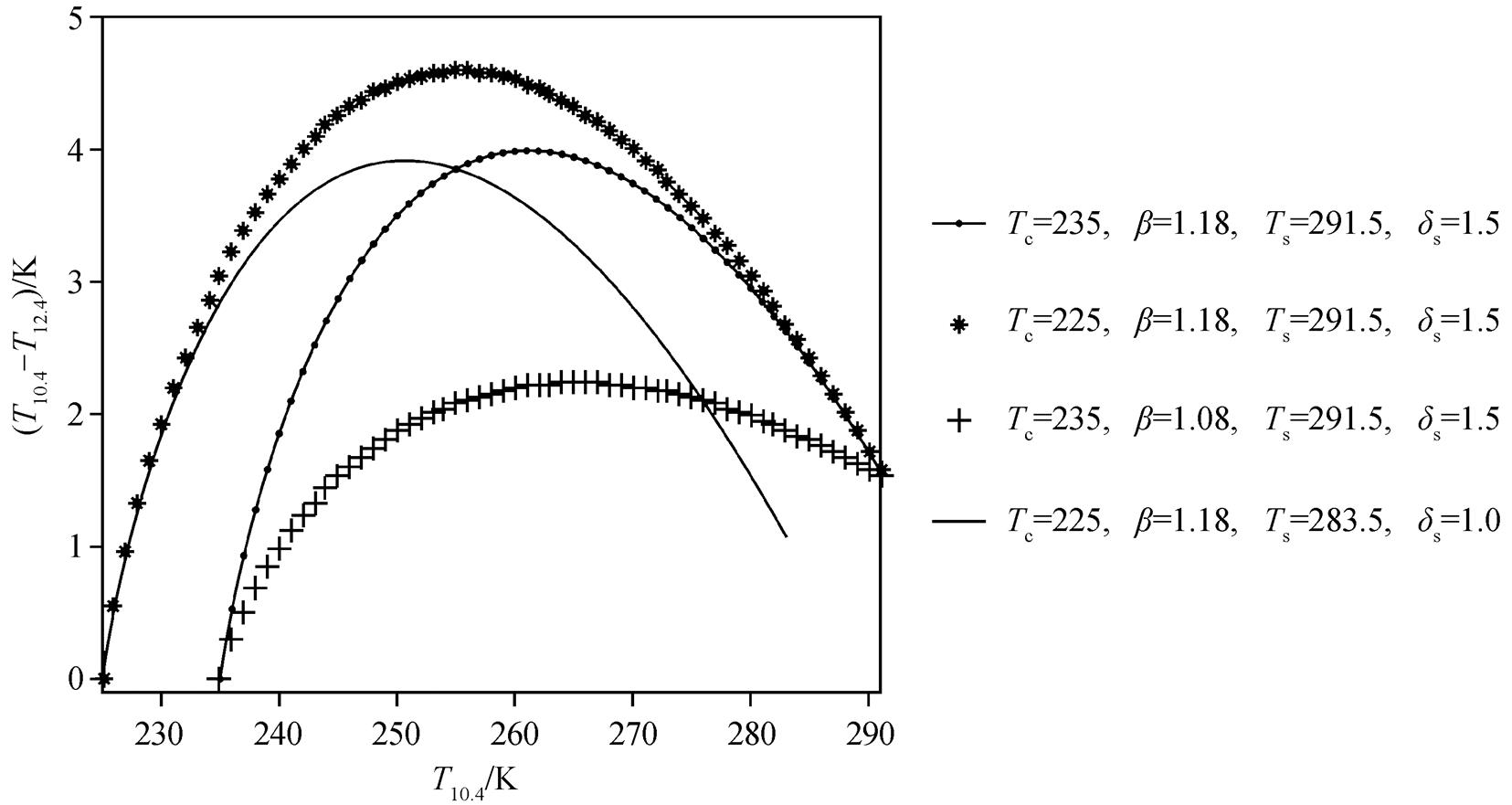
图1 不同参数条件下亮温差 T10.4-T12.4 随亮温 T10.4 的变化
Fig. 1 Variation of brightness temperature difference T10.4-T12.4with brightness temperature T10.4 for four different conditions
根据 2.1 节的原理, 假设下垫面是均一的, 可以选择一个 24×24 的像元块矩阵, 将该矩阵范围内位于不同像元的云视为具有不同的透过率, 根据每个像元对应的分裂窗亮温和亮温差, 拟合出该矩阵中 T10.4-T12.4随 T10.4 的变化关系, 拟合曲线延伸至不透明的左端时的亮温即为云顶温度。该过程中要求下垫面的温度条件接近, 因此, 当像元块矩阵对应的地表类型既有陆地又有水面时, 应该分开拟合, 得到两个拟合曲线及其分别对应的云顶温度。
本文基于分裂窗直方图法反演云顶高度的步骤如下。
1)对 Himawari-8 的观测数据进行预处理, 主要包括将 Himawari-8 数据处理成格点数据和利用阈值法进行半透明云选择。
2)筛选后的 Himawari-8 格点数据按照 24×24的像元块矩阵, 利用最小二乘法进行曲线拟合, 得到云顶温度。
3)将 Himawari-8 格点数据与 ERA-Interim 再分析资料进行时间匹配, 然后利用 ERA-Interim 再分析资料中的温度气压层数据和位势高度气压层数据, 通过云顶温度计算出云顶高度。
4)对 Himawari-8 格点数据和 CloudSat 产品 2B-GEOPROF 数据进行匹配处理, 用匹配的数据点进行对比验证。
2.2.1 数据预处理
首先将目标区域( 90°—140°E, 15°—55°N)2016年 4 月 1 日至 9 月 30 日的 Himawari-8 全圆盘数据进行格点化, 处理成分辨率为 0.02°×0.02°的等经纬度数据, 然后基于阈值法完成半透明云的筛选。研究表明, 亮温 T10.4 和亮温差是很好的区分半透明云的参数[3,20‒22]。云的温度一般较低, 用亮温作为阈值可以先去除大部分晴空像元点, 而亮温差主要受透过率、云相态、云粒子分布和其他微观物理参数的影响。例如冰云在大气窗区的发射率差异较大, 在分裂窗两个通道的亮温差较大, 因此高空的半透明云比其他类型的云和晴空状态的亮温差大。参考前人的工作[22-26], 本文选择 8 种参数, 对 2016 年 7月 1 日至 8 月 31 日的匹配数据进行计算试验, 参数条件和试验中匹配的像元点个数以及结果的均方根偏差如表 1 所示。表1 中参数条件 2, 4, 6, 7 分别对应 4 种不同的通道亮温差筛选条件, 从这 4 种筛选条件所匹配的像元点反演结果可以发现, 相对于参数条件 4, 6, 7, 参数条件 2 能得到较小的均方根偏差, 而其余的 4 种参数条件 1, 3, 5, 8是在参数条件2, 4, 6, 7 的基础上增加验证过程中对应CloudSat 产品的云顶高度筛选条件(即云顶高度大于 8km)。通过对比发现, 增加该条件可以使得筛选的像元点反演偏差结果更好, 因此最后选择半透明云对应的像元点要满足以下条件: 1) 8.6μm 和 10.4μm 的亮温差大于−0.5K; 2)10.4μm 和 12.4μm 的亮温差大于 0.2 K; 3)10.4μm 的亮温小于 288.15K; 4)验证过程中对应 CloudSat 产品的云顶高度大于 8 km。
表1 半透明云选择参数条件试验
Table 1 Semi-transparent cloud screened parameters test
编号参数条件匹配个数均方根偏差/km 1, , CTH > 8 km[24] 43061.57 2, 43651.74 3, CTH > 8 km[24] 78581.72 4100202.36 5, CTH > 8 km[24]190311.69 6241532.26 7或, 125352.36 8或, , CTH > 8 km[24] 98051.71
说明: CTH指验证过程中对应CloudSat的云顶高度, T(850 hPa)指匹配时间的ERA-Interim再分析资料中850 hPa气压层上的温度。
下面以 2016 年 4 月 1 日 18:00UTC 的 10.4μm通道数据为例, 简要地介绍预处理过程。图 2 是该时刻 10.4μm 通道全圆盘数据预处理过程的图像。Himawari-8 全圆盘数据大小为 5500×5500, 将 10.4μm 通道数据展示为灰度图(图 2(a)), 灰度越深表示亮温越高, 灰度越浅表示亮温越低, 可将白色区域视为有云区域。选择目标区域内的数据, 并将其处理成等经纬度的格点数据(图 2(b))。使用阈值法, 进行半透明云条件筛选后的图像见图2(c)。
2.2.2 最小二乘法拟合计算云顶温度
云顶温度是利用最小二乘法对 24×24 的像元块矩阵内数据进行曲线拟合得到的。已知该矩阵中所有满足半透明云筛选条件的 10.4μm 通道的亮温 xi和10.4μm 通道与12.4μm通道的亮温差yi=T10.4‒T12.4, 首先将像元对应的地表类型分为陆地或水面, 然后对两种类型的数据分别进行拟合。根据式(8)可知
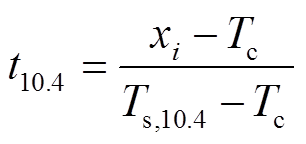, (10)设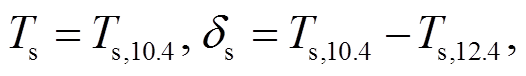
自变量为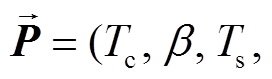
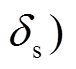, 则根据式(9)和(10)得到拟合关系式:
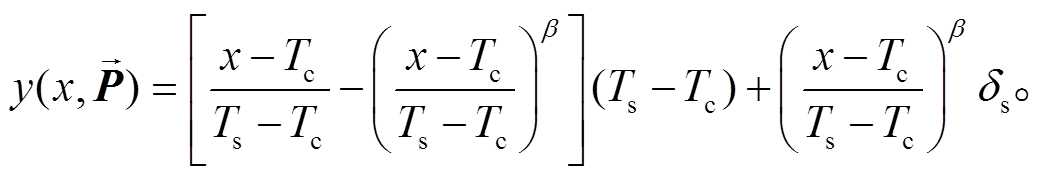(11)
从式(11)看出, 这是一个非线性曲线拟合问题, 本文使用列文伯格‒马夸尔特最小二乘法[27]。首先确定拟合参数时数据的最少数量, 当固定一种地表类型时, 设定像元块矩阵中满足条件的数据不少于25 个才可以进行拟合。然后设定拟合的初始值, 其中云顶温度 Tc 的初始值是像元块矩阵中亮温的最小值; 地表亮温 Ts 的初始值是像元块矩阵中亮温大于283.15K 数据的平均值, 如果没有相应条件的数据, 则将 Ts 设为 288.15K[27]; 地表亮温差 δs 的初始值是亮温大于 283.15K 像元的亮温差平均值, 如果没有相应条件的数据, 则将 δs 设为 2; 系数 β 为以上3 个初始值代入矩阵中拟合得出的实数, 如果该数字不大于 1, 则将 β 设为 1.1。同时, 设定拟合结果需要满足以下条件: Tc >185 K, β >1.01。
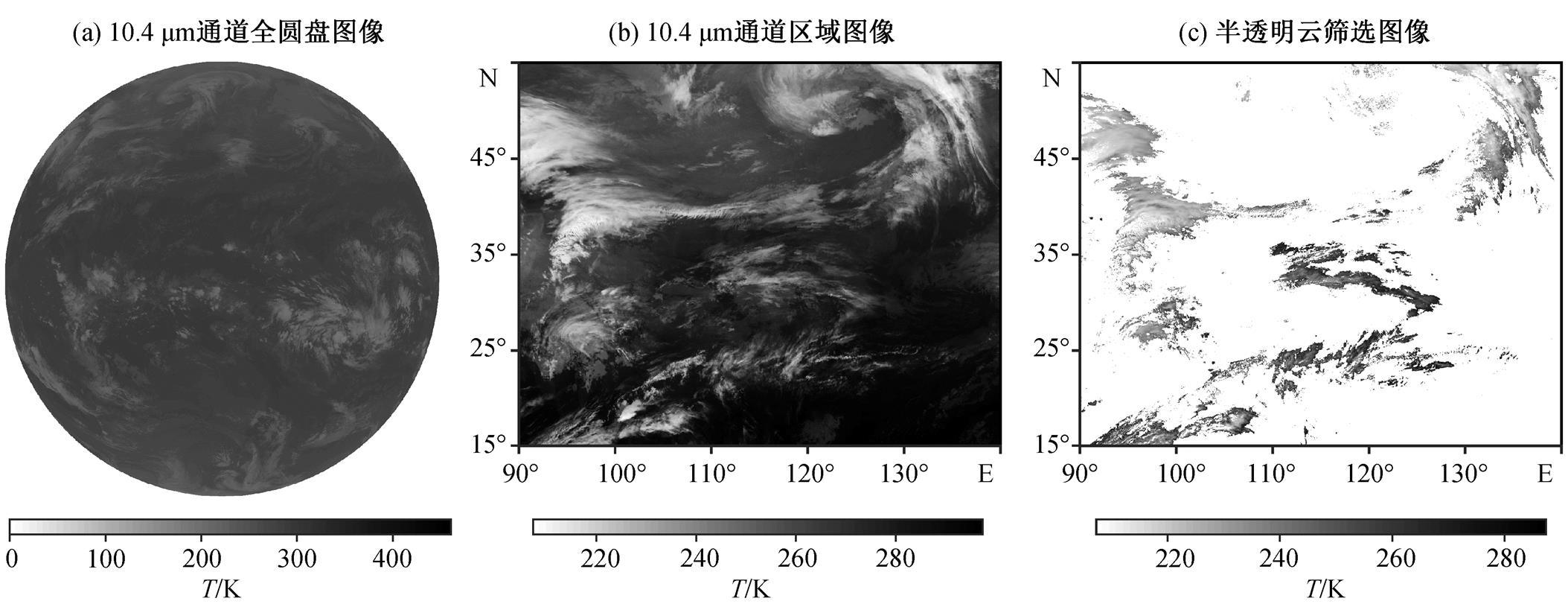
图2 2016年4月1日18:00 UTC预处理过程图像
Fig. 2 Pre-processing image at 18:00 UTC on April 1, 2016
由于固定了像元块矩阵的大小, 可能会因在某一个像元块矩阵中只存在云的边缘数据而不能满足拟合的最小数量, 使得该区域的结果缺失, 或者存在多块云, 使得拟合效果较差。为了减少这些情况的影响, 采用 Korpela 等[3]的建议, 选择 4 种不同分布形式的数据网格来获取像元块矩阵。第一种是从右下角的像元开始, 选择向上向左的固定网格来获取像元块矩阵; 第二种是从右下角的像元向左移动网格长度的一半开始, 选择向上向左的固定网格来获取像元块矩阵; 第三种是从右下角的像元向上移动网格宽度的一半开始, 选择向上向左的固定网格来获取像元块矩阵; 第四种是从右下角的像元向左移动网格长度的一半并向上移动网格宽度的一半开始, 选择向上向左的固定网格来获取像元块矩阵。最终, 每个像元的云顶温度由 4 种数据网格的拟合结果取平均得到。
2.2.3 云顶高度反演
首先, 对 Himawari-8 的格点数据和 ERA-Interim再分析资料进行时间匹配, 完成对应时间 ERA-Interim 再分析资料的格点化处理, 并规定使用的ERA-Interim 再分析资料与 Himawai-8 资料的时间差小于 1h。为了更方便地选择温度气压层和位势高度气压层数据, 通过线性插值处理, 将空间分辨率为 0.125°×0.125°的 ERA-Interim 再分析资料转换成空间分辨率为 0.02°×0.02°、高度层数仍为 37 的格点数据, 插值过程中的权重为插值点到原有数据格点的距离。
然后, 借助处理后的温度气压层和位势高度气压层数据反演云顶高度, 结果如图 3 所示, 其中虚线和粗点线表示由云顶温度得到云顶高度的过程, 圆圈处的温度为云顶温度。忽略云顶与周围大气环境的温差, 假设大气温度廓线上云顶温度对应的高度处即为云顶高度。经过处理后的每个像元点都对应一条温度气压廓线和位势高度气压廓线, 从廓线数据的最高层开始, 依次向下循环, 若云顶温度不低于该层大气温度且小于下一层大气温度, 则云在该层中间某一高度处, 并假设在这一层中温度递减率是恒定的, 计算得到云顶高度, 如图 3 中星号所示。当温度随高度的变化出现逆温时, 假设云在逆温的下层。
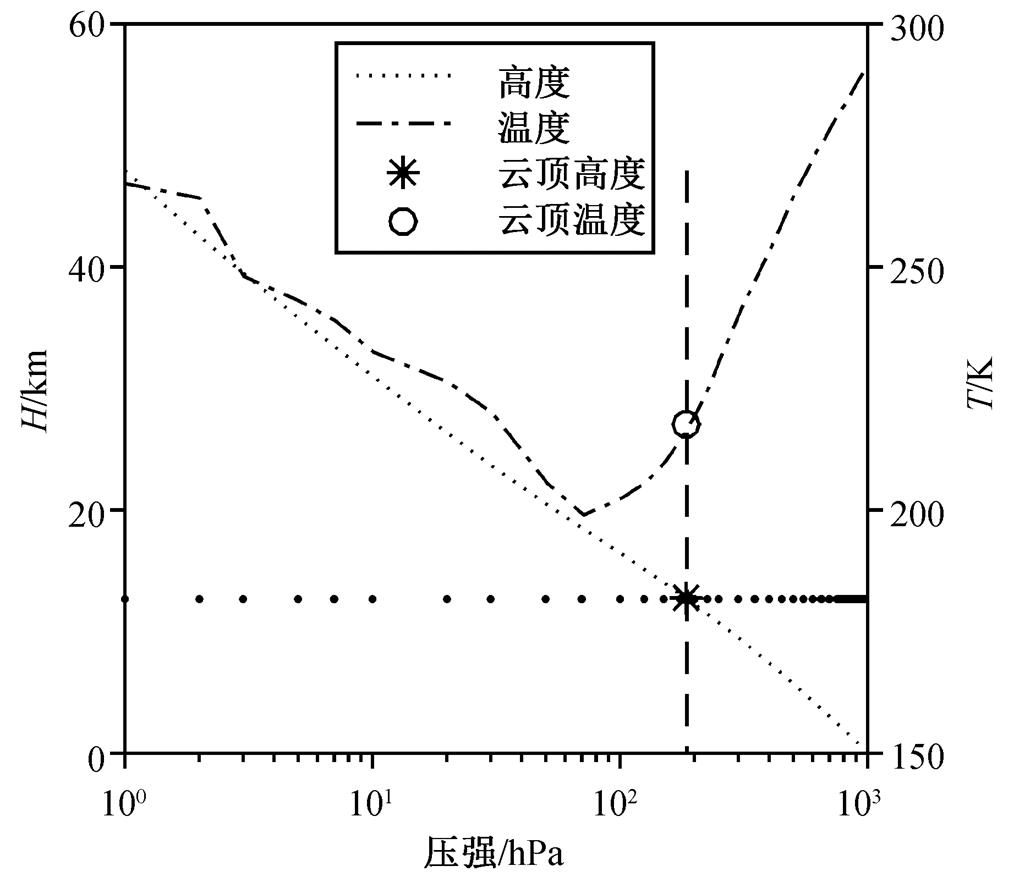
图3 云顶高度反演结果示意图
Fig. 3 Schematic diagram of cloud top height retrieval
2.2.4 结果验证
本文验证过程中使用的 CloudSat 云顶高度根据 1.2 节的方法识别得到, 验证数据要求 Himawari-8 格点数据与 CloudSat 数据的时间差在 60s 内, 空间经纬度差小于0.01°。
为了更好地查看分裂窗直方图法对一个区域半透明云的云顶高度反演结果, 本文选择 2016 年 7 月11 日05:10UTC 经纬度为 106°—122°E, 35°—47°N的区域进行分析。图 4(a)是 10.4μm 通道在该区域的云图, 图 4(b)是利用阈值法得到的半透明云图, 图 4(c)是通过分裂窗直方图法反演得到的云顶高度图。从图 4(a)和(b)可以看出, 有明显半透明云特征的区域能够通过阈值法筛选得到(例如右侧 114°—122°区域具有丝缕状特征的云), 说明阈值法能够在一定程度上完成半透明云的选择。对比图 4(b)与(c)可以发现, 有些筛选出的半透明云区并没有得到对应的云顶高度, 可能的原因如下: 1)在固定的像元块矩阵内数据量不满足研究中设定的最低拟合个数25; 2)拟合结果不满足研究中设定的拟合条件而被去掉。但是, 总体来说, 反演结果比较完整。
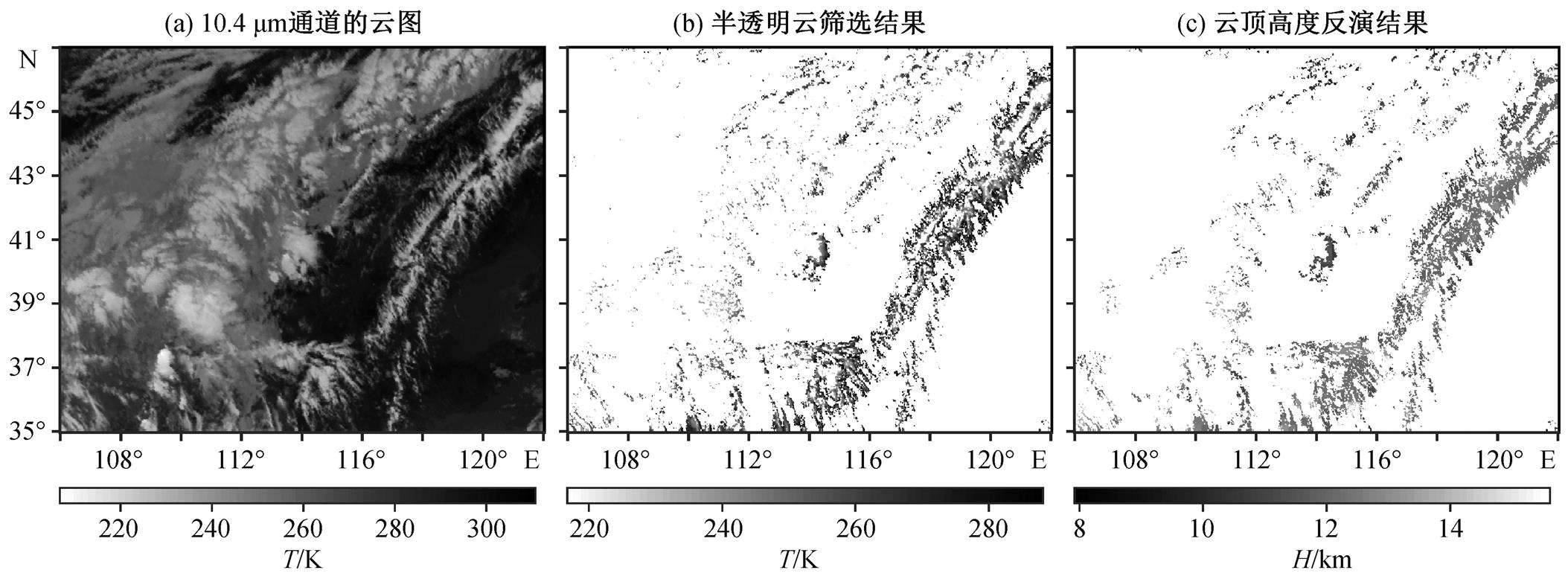
图4 2016年7月11日05:10 UTC 106°—122°E, 35°—47°N区域反演结果(实例1)
Fig. 4 Retrieval process of 106°-122°E, 35°-47°N at 05:10 UTC on July 11, 2016 (Case 1)
为了比较分裂窗直方图法反演的云顶高度与CloudSat 的 2B-GEOPROF 产品识别的云顶高度, 本文选择 2016 年 4 月 13 日 05:20UTC 的 Himawari-8与 CloudSat 的匹配区域进行比较。图 5 显示匹配区域 173 个云顶高度的结果比较, 两者之间的平均偏差(MeanE)为−0.27km, 均方根偏差(RMSE)为 0.62 km。从图 5 可以看到, 反演的云顶高度空间分辨率大约为 0.2°, 即在一定的纬度范围内有一个大致相同的云顶高度。这是由于本研究采用固定的网格分区, 从一个像元块矩阵内的数据得到一个云顶温度。若计算机能满足计算量的要求, 可以使用移动的网格分区, 进而得到分辨率更高的结果。
此外, 取此匹配轨道上两个像元点为例。一是地表类型为水面的像元(121.72°E, 28.54°N), 其云顶温度是由第二、三、四种固定网格拟合平均得到的, 拟合曲线如图 6 中黑线所示。可以看出, 3 种固定网格拟合得到的吸收系数比值 β 与云顶温度相近, 最终的平均温度为 217.32 K, 对应高度为 12.68 km, 只比匹配的 CloudSat 云顶高度 12.69km 低 0.01 km。
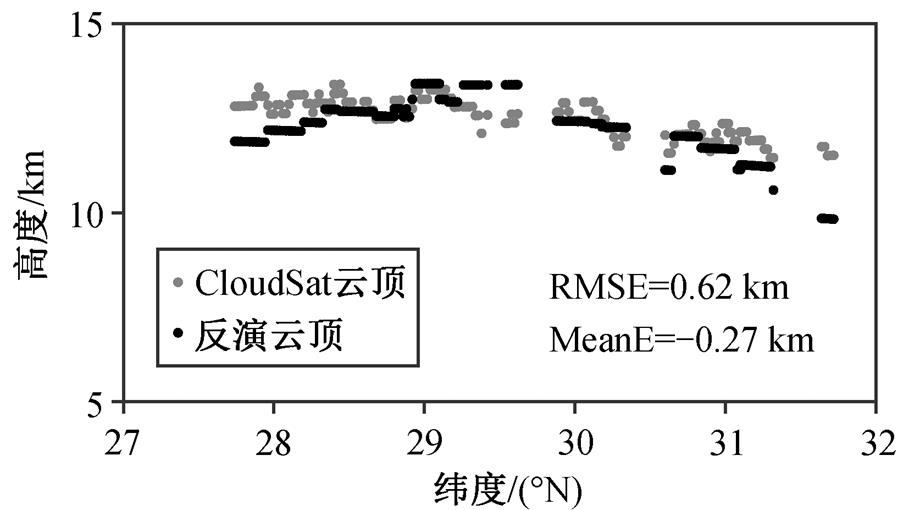
图5 2016年4月13日05:20 UTC匹配区域反演结果 (实例2)
Fig. 5 Retrieval results of the matched pixels at 05:20 UTC on April 13, 2016 (Case 2)
另一个点为地表类型为陆地的像元(120.90°E, 31.66°N), 结果由第一、二种固定网格拟合得到, 拟合曲线如图 7 所示。两者拟合的结果差异较大, 拟合的云顶温度相差近 25K, 平均后云顶温度为231.73K, 得到的云顶高度为 9.85km, 比验证结果11.75km低1.90 km。
对比上述两个像元得到结果的过程可以看出, 反演第一个像元结果的 3 个像元块矩阵数据比较相似, 亮温的变化范围和亮温差的变化范围均比较接近, 数据也比较有代表性, 从亮温的变化范围可以得出数据代表的透过率变化比较明显, 拟合结果较好。在反演第二个像元点结果的两个像元块矩阵数据中, 亮温和亮温差的变化范围有明显的区别, 第一种网格选择的像元块矩阵中亮温的变化范围为255~275K, 而图 7(b)代表的第二种网格中像元块矩阵的亮温变化范围为 265~275K, 特别是第二种网格中亮温差没有从高向低(即透过率向逐渐变小的方向)发展的代表性数据, 且数据间差异较大, 使得最后的结果差别较大。
将分裂窗直方图法反演得到的半透明云云顶高度, 跟与之匹配的 CloudSat 产品 2B-GEOPROF 识别的云顶高度进行对比, 结果如图 8 所示。从总体上看, 下垫面类型包括陆地和水面时, 9518 个数据点的对比显示, 反演结果与 CloudSat 识别的云顶高度有较好的一致性, 均方根偏差为 1.45km (图 8 (a))。其中, 地表类型为陆地的 5158 个匹配点的均方根偏差为 1.48km (图 8(b)), 地表类型为水面的4360 个匹配点的均方根偏差为 1.42km (图 8(c))。两种地表类型的结果有微小差异, 但不明显。
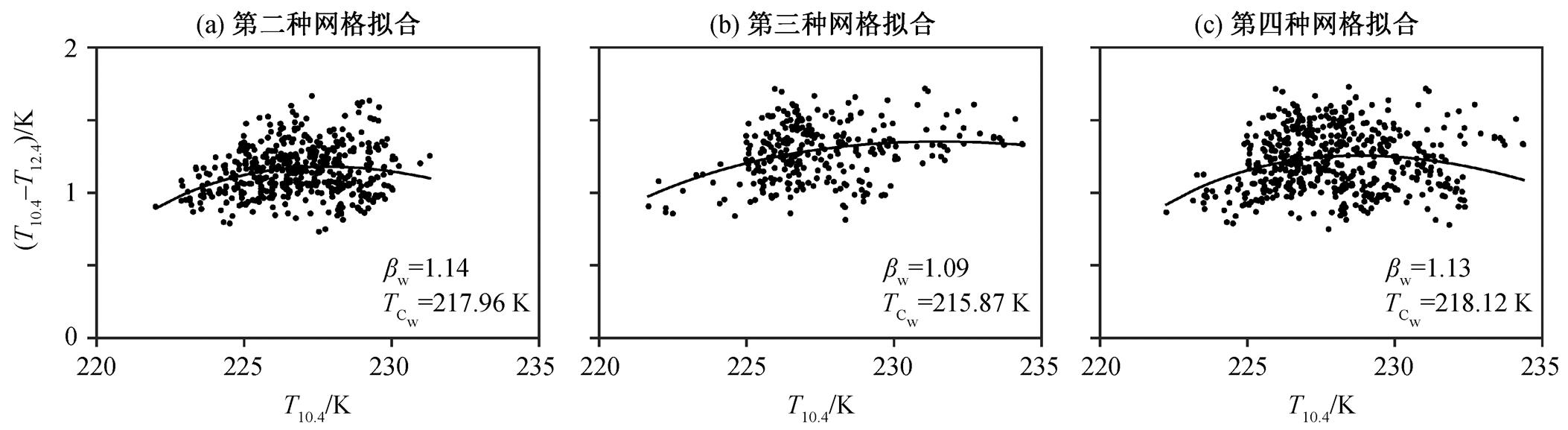
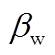为在固定网格中筛选的地表类型为水面的半透明云像元点拟合的两通道吸收系数比; TCw为拟合的水面上空云顶温度
图6 地表类型为水面的像元(121.72°E, 28.54°N)拟合结果
Fig. 6 Curve fit result of a pixel (121.72°E, 28.54°N) in the water regime
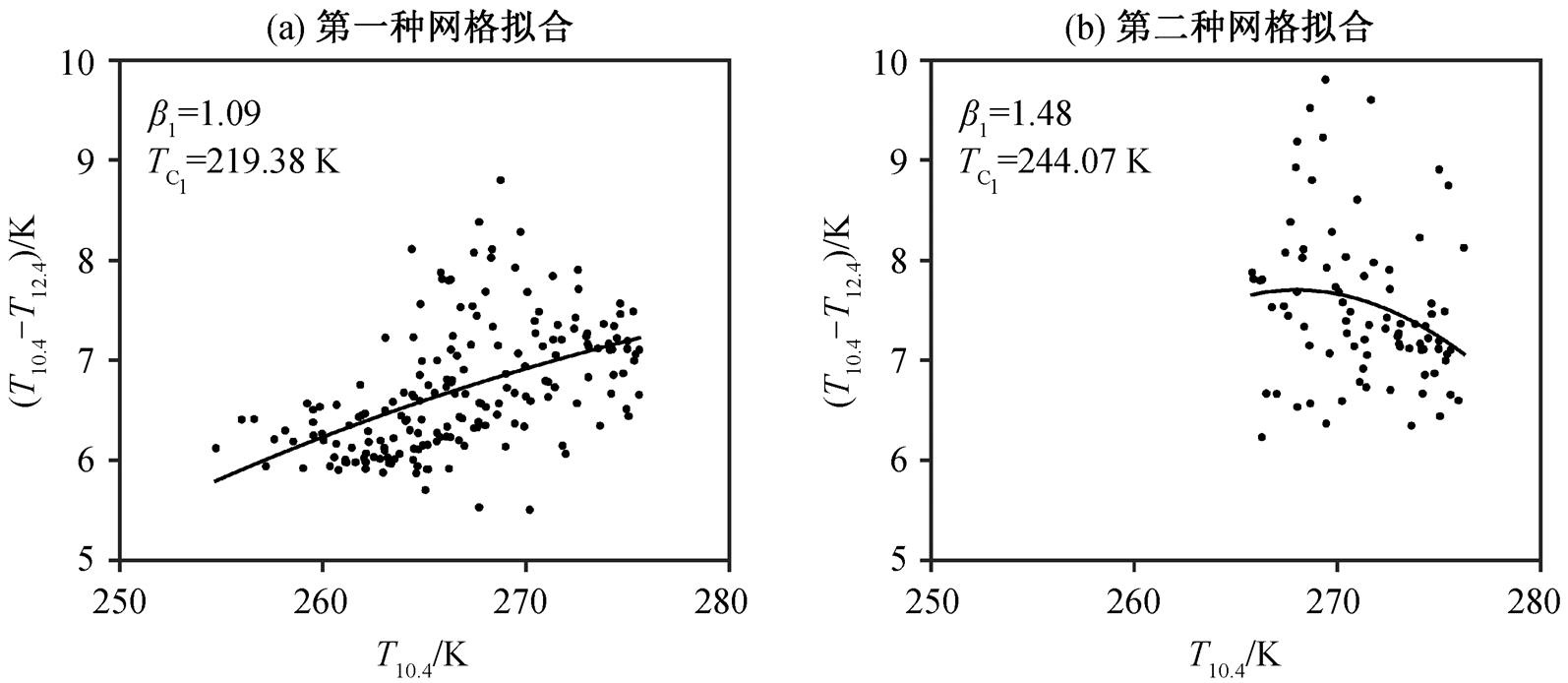
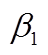为在固定网格中筛选的地表类型为陆地的半透明云像元点拟合的两通道吸收系数比; TC1为拟合的陆地上空云顶温度
图7 地表类型为陆地的像元拟合结果(120.90°E, 31.66°N)
Fig. 7 Curve fit result of a pixel (120.90°E, 31.66°N) in the land regime
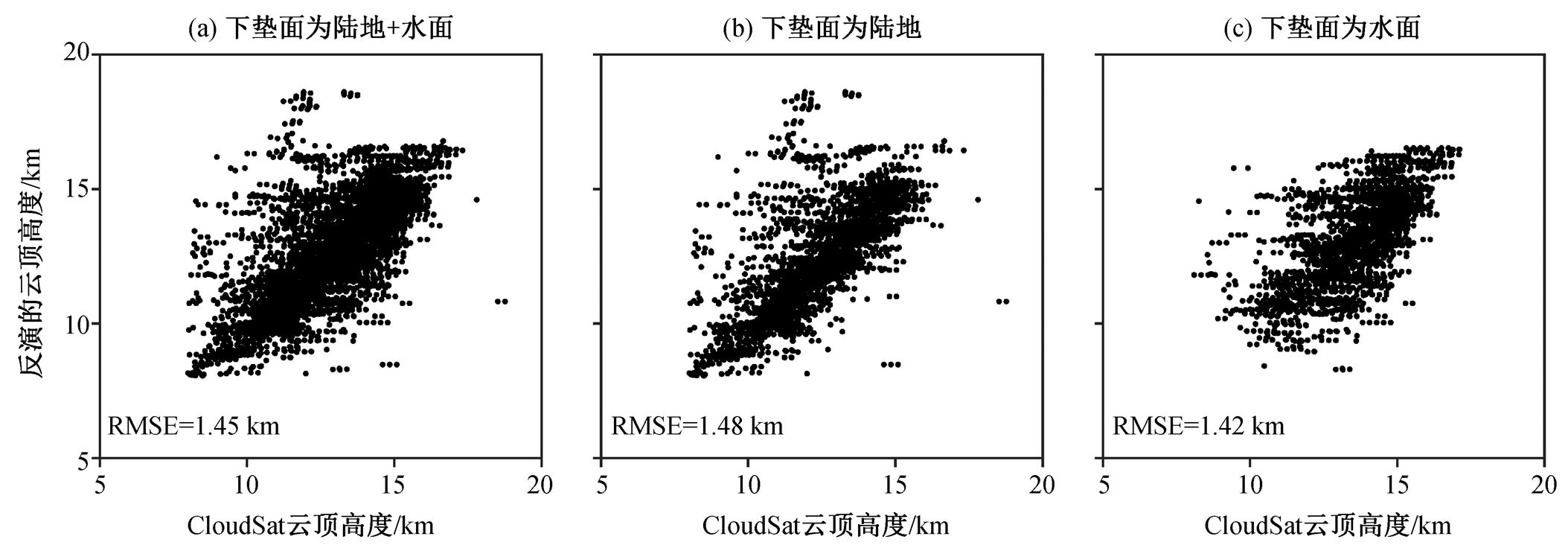
图8 半透明云反演结果
Fig. 8 Retrieval result of semi-transparent cloud
为了分析地表条件对反演结果的影响, 首先将区域分为 5°×5°的等经纬度网格, 计算每个网格中的匹配点个数 N 和均方根偏差 RMSE, 并结合 ETOP地形数据[28]进行分析, 结果如图 9 所示。对于有较多数据的经纬度网格, 在海拔 200m 以下的区域(如东北平原南部、华北平原、长江中下游地区、中国东海岸线和华南等地)以及海拔高度在 1000m 以上的呼伦贝尔高原区域反演结果的均方根偏差较小, 但对四川盆地东北部区域以及俄罗斯东南部以南日本西部以北的日本海附近区域反演结果的均方根偏差较大, 表明下垫面的海陆类型不是影响反演结果的最重要因素, 可能与区域海拔高度的差异有关。地形对反演结果的影响需要进一步的研究。
与 Mouri 等[5]利用 3 种方法对 Himawari-8 数据的反演结果相比, 本研究利用分裂窗直方图法对Himawari-8 数据的云顶高度反演结果有较大的改善, 均方根偏差明显减小。同时, 与 Joro 等[2]利用分裂窗直方图法对 AVHRR 数据的反演结果相比, 本文的反演结果有极大的提高, 特别偏差小于 0.5 km 结果的比例大大增加。以下因素对提高反演结果精度带来积极的影响: 1)设定一个像元块矩阵中对应一种地表类型的半透明云像元点的个数不少于25, 可以保证拟合结果的合理性; 2)拟合过程中采用 4 种数据网格获取像元块矩阵, 可以减少像元块矩阵选择方式带来的影响; 3)根据拟合方法的局限性设定拟合结果的条件; 4)使用 CloudSat 的云掩码数据识别云顶高度, 与 Joro 等[2]使用的验证数据(天气雷达观测数据)相比, 准确率有较大的提高。
影响本文研究结果的主要因素如下。
1)CloudSat 的 2B-GEOPROF 产品依据阈值识别云顶高度, 可能会带来一定程度的误差。
2)在 Himawari-8 的格点数据与 CloudSat 数据的匹配过程中, 时间和空间上都会存在一定程度的误差, 导致结果的误差。
3)在通过云顶温度结合 ERA-Interim 再分析资料得到云顶高度时, 两者匹配的时间差为 1h, 同时在这个过程中忽略了云顶温度与同高度层大气温度之间的差异, 并且计算云顶高度时假设在气压层之间大气温度随高度的递减率恒定, 因此会带来一定程度的误差。特别是当反演的云顶温度在逆温层附近, 或者再分析资料中两个气压层的温度接近时, 小量的温度差异反演得到的高度差异可以很大, 如图 10 中 4 个像元点的反演结果所示。图 10(a)和(b)是 2016 年 4 月 21 日 06:10UTC 的两个相近像元, 二者的大气温度廓线基本上一致, 在 150~225hPa 高度存在一个逆温层, 且反演得到的温度在逆温层附近。图 10(a)的像元反演得到的云顶温度为 212.15K, 反演的云顶高度与 CloudSat 识别的云顶高度相同, 为 12.04 km。图 10(b)的像元反演得到的云顶温度为 209.28K, 虽然与图 10(a)对应的相邻像元反演的云顶温度相差不到 3K, 但反演得到的云顶高度为 16.25km, 比 CloudSat 识别的云顶高度(11.83km)高出近 4.5km。图 10(c)和(d)分别是 2016 年 5 月 7日 06:10UTC 的另外两个相近像元, 在大气温度廓线中 125~200hPa 的高度层, 温度随高度的变化幅度较小, 与其他高度的温度变化有明显的差异。图10(c)的像元反演得到的云顶温度为 208.36K, 反演得到的云顶高度为 15.66km, CloudSat 识别的云顶高度为 12.78km, 图 10(d)的像元反演得到的云顶温度为 214.73K, 反演得到的云顶高度为 12.82km, CloudSat 识别的云顶高度为 12.78km。在两组像元的对比中都存在以下现象: 一个像元的反演结果与CloudSat 识别的云顶高度差异不大, 但相近的另一个像元反演结果偏差较大, 且每组对比像元反演的云顶温度差异都在 7K 以内。因此, 对一些区域计算云顶高度时, 利用再分析资料从云顶温度得到云顶高度的过程可能会带来较大的偏差。
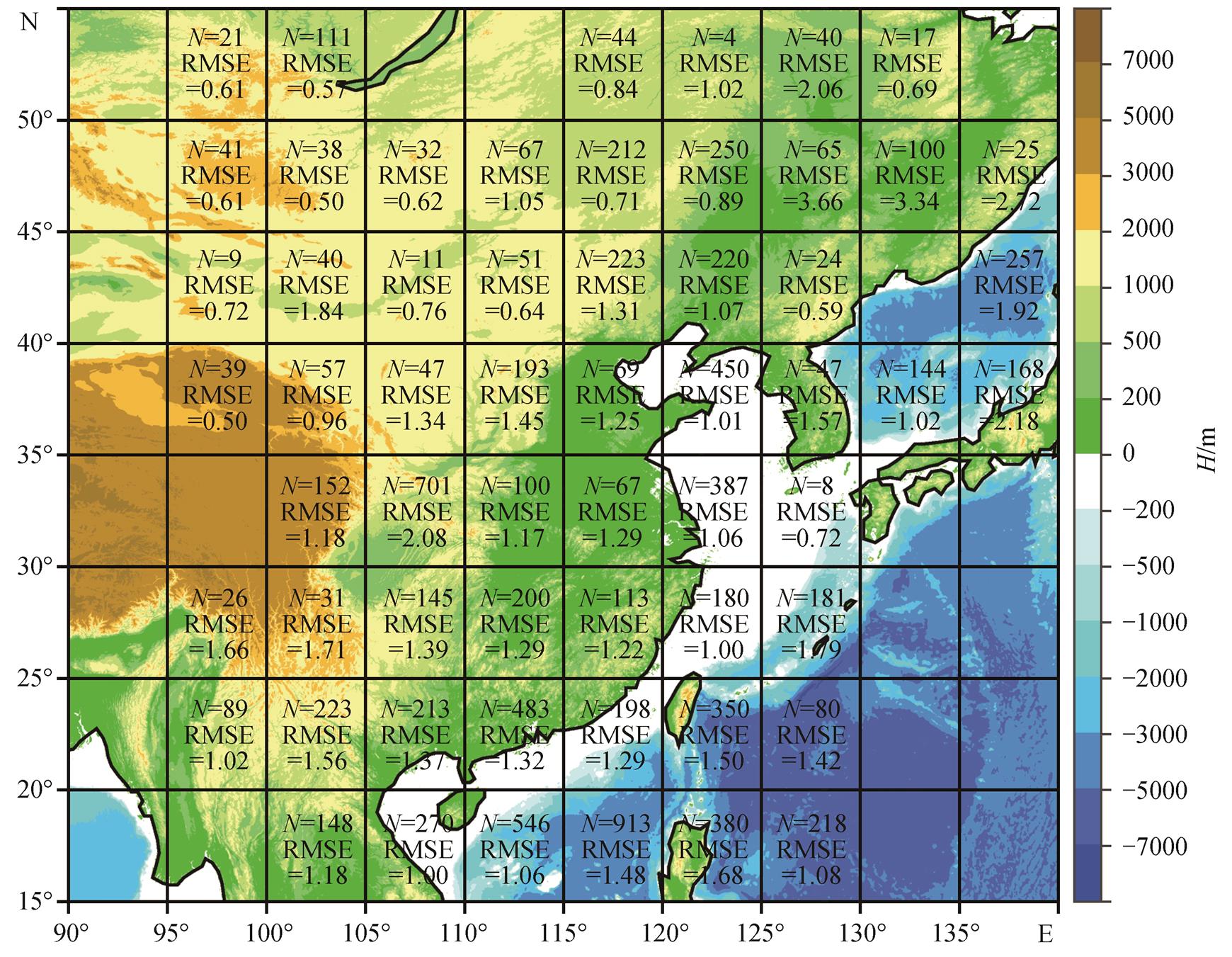
图9 均方根误差(km)在5°×5°经纬度网格的分布
Fig. 9 Root mean square error (km) in the zone 5°×5°
4)假定有云像元点的云量为 1 会带来一定程度的误差。Giraud 等[10]的研究表明, 若在一个矩阵中有较多的像元点云量不为 1, 可能使拟合得到的云顶温度偏高, 最终得到的云顶高度极有可能偏低。
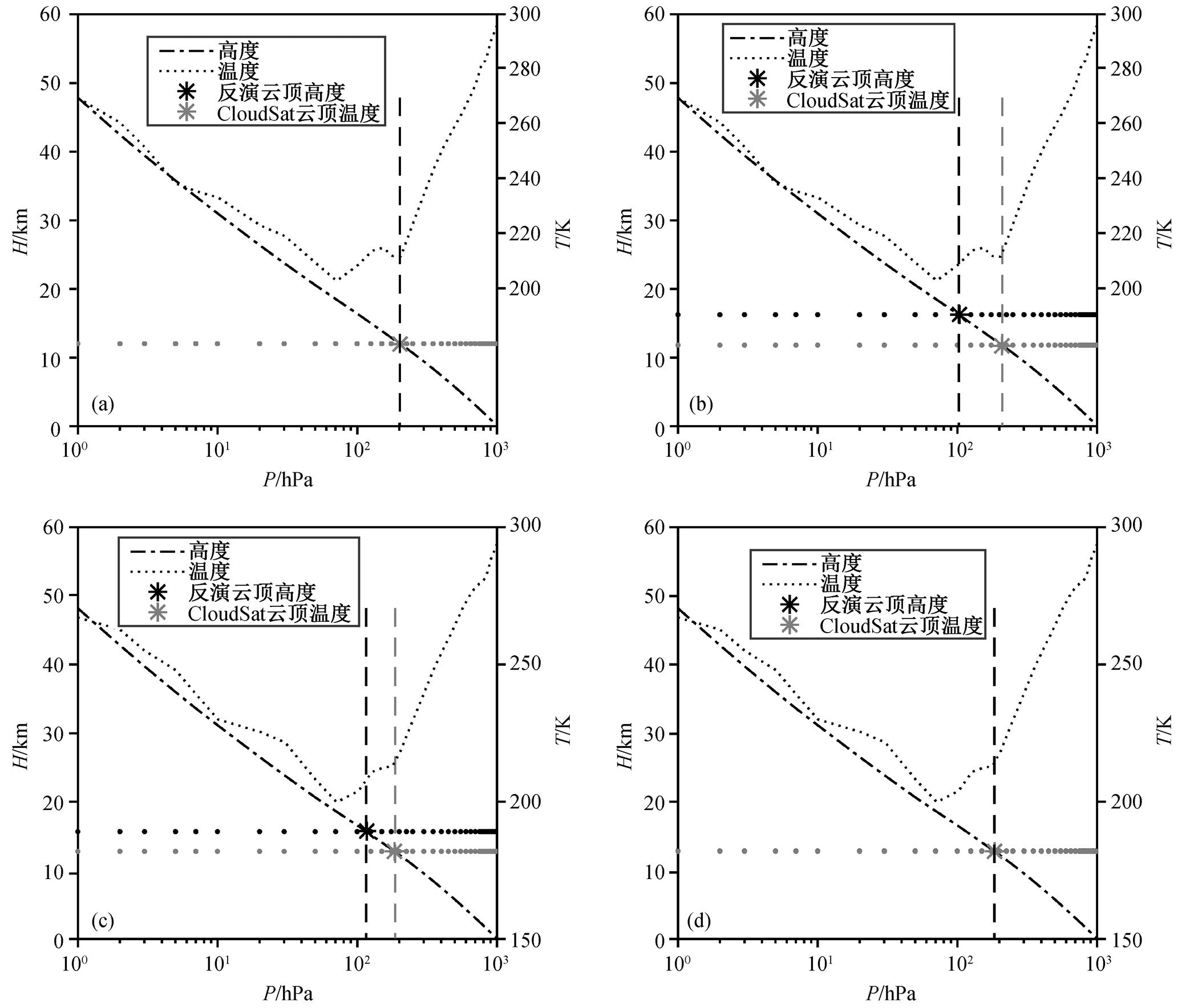
(a) 2016 年 4 月 21 日 06:10 UTC 的像元点(108.12°E, 33.14°N); (b) 2016 年 4 月 21 日 06:10 UTC 的像元点(108.10°E, 33.24°N); (c) 2016 年 5 月 7 日 06:10 UTC 的像元点(108.40°E, 32.02°N); (d) 2016 年 5 月 7 日 06:10 UTC 的像元点(108.38°E, 32.04°N)
图10 4个像元点云顶高度反演结果
Fig. 10 The retrieval cloud top height of four pixels
5)4.1 节中两种地表类型反演结果的均方根偏差比较接近, 但在海陆差异的影响不明显情况下, 反演结果的均方根偏差仍在不同区域表现出差异性, 这一现象可能与地形有关。
本研究利用 2016 年 4 月 1 日至 9 月 30 日 90°—140°E, 15°—55°N 区域 Himawari-8 的 8.6,10.4 以及12.4μm3 个通道数据, 基于阈值法筛选半透明云区, 使用分裂窗直方图法进行云顶温度反演, 结合欧洲中尺度预报中心的 ERA-Interim 再分析资料中温度气压层数据和位势高度气压层数据得到云顶高度, 并与 CloudSat 的 2B-GEOPROF 产品数据进行匹配和对比, 得到以下结论: 影响反演结果的因素较多, 但分裂窗直方图法对半透明云云顶高度的反演结果比较合理, 均方根偏差为 1.45km, 并且, 地表类型为水面或陆地反演结果均方根偏差的差异不大, 海陆差异对像元点反演结果的影响不明显。
分裂窗直方图法使用分裂窗通道数据, 从云的物理特性出发, 能得到较好的云顶高度反演结果, 并且分裂窗通道的数据不受时间和地域限制, 因此该方法有较强的适用性, 可以应用于不同卫星的分裂窗通道数据反演。特别是目前中国新一代静止气象卫星风云四号已经投入使用, 这种方法同样可以应用到风云四号卫星上, 对全国范围内半透明云的特性进行研究。在未来的工作中, 可以尝试利用CloudSat 提供的云厚度信息和云反射率因子廓线信息来识别验证半透明云区, 通过提高半透明云的筛选正确率来提高反演精度。
参考文献
[1]Hamann U, Walther A, Baum B, et al. Remote sensing of cloud top pressure/height from SEVIRI: analysis of ten current retrieval algorithms. Atmospheric Measure-ment Techniques, 2014, 7(9): 2839‒2867
[2]Joro S, Dybbroe A. Validating the AVHRR cloud top temperature and height product using weather radar data. National Institute of Water and Atmospheric Research, New Zealand & SMHI, Visiting Scientist Report [EB/OL]. (2004‒04‒15) [2018‒05‒20]. http:// www.nwcsaf.org/web/guest/vsa2
[3]Korpela A, Dybbroe A, Thoss A. Retrieving cloud top temperature and height in semi-transparent and frac-tional cloudiness using AVHRR. National Institute of Water and Atmospheric Research, New Zealand & SMHI, Visiting Scientist Report [EB/OL]. (2001‒10‒ 15) [2018‒05‒20]. http://www.nwcsaf.org/web/guest/ vsa2
[4]李万彪. 大气遥感. 北京: 北京大学出版社, 2014: 62‒67
[5]Mouri K, Suzue H, Yoshida R, et al. Algorithm theo-retical basis document of cloud top height product. Meteorological Satellite Center Technical Note, 2016, 61: 33‒42
[6]Inoue T. On the temperature and effective emissivity determination of semi-transparent cirrus clouds by bi-spectral measurements in the 10 μm window region. Journal of the Meteorological Society of Japan, 1985, 63(1): 88‒99
[7]Liou K. On the radiative properties of cirrus in the window region and their influence on remote sensing of the atmosphere. Journal of the Atmospheric Sci-ences, 1974, 31(2): 522‒532
[8]Wu M C. A Method for remote sensing the emissivity, fractional cloud cover and cloud top temperature of high-level, thin clouds. Journal of Climate and Ap-plied Meteorology, 1987, 26(2): 225‒233
[9]Parol F, Buriez J C, Brogniez G, et al. Information content of AVHRR channels 4 and 5 with respect to the effective radius of cirrus cloud particles. Journal of Applied Meteorology, 1991, 30(7): 973‒984
[10]Giraud V, Buriez J C, Fouquart Y, et al. Large-scale analysis of cirrus clouds from AVHRR data: assess-ment of both a microphysical index and the cloud-top temperature. Journal of Applied Meteorology, 2010, 36(6): 664‒675
[11]Cooper S J, L’Ecuyer T S, Stephens G L. The impact of explicit cloud boundary information on ice cloud microphysical property retrievals from infrared radi-ances. Journal of Geophysical Research Atmospheres, 2003, 108(D3): AAC8-1‒AAC8-17
[12]Heidinger A K, Pavolonis M J. Gazing at cirrus clouds for 25 years through a split window. Part I: methodo-logy. Journal of Applied Meteorology and Climato-logy, 2010, 48(6): 1100‒1116
[13]许健民, 张其松. 卫星风推导和应用综述. 应用气象学报, 2006, 17(5): 574‒582
[14]Bessho K, Date K, Hayashi M, et al. An introduction to Himawari-8/9-Japan’s new-generation geostationary meteorological satellites. Journal of the Meteorologi-cal Society of Japan, 2016, 94(2): 151‒183
[15]Im E, Durden S L, Tanelli S. CloudSat: The cloud profiling radar mission // 2006 CIE International Conference on Radar. Arlington VA, 2006: 1‒4
[16]Sassen K, Wang Z. Level 2 cloud scenario classifica-tion product process description and interface control document, version 5.0 [EB/OL]. (2007‒07‒24) [2018‒05‒20]. http://www.atmo.arizona.edu/~brunke/2B-CLDC LASS_PDICD.P_R04.20070724.pdf
[17]Marchand R, Mace G G, Ackerman T, et al. Hydrome-teor detection using cloudsat — an earth-orbiting 94-GHz cloud radar. Journal of Atmospheric and Oceanic Technology, 2008, 25(4): 519‒533
[18]Tsonevsky I, Andersson E, Persson A, et al. User guide to ECMWF forecast products, version 1.2 [EB/ OL]. (2015‒11‒23)[2018‒05‒20]. https://www.Ecmwf.int/en/elibrary/16559-ecmwf-forecast-user-guide
[19]Berrisford P, Dee D, Poli P, et al. The ERA-interim archive, version 2.0 [EB/OL]. (2011‒10‒01) [2019‒04‒01]. https://www.ecmwf.int/sites/default/files/elib rary/2011/8174-era-interim-archive-version-20.pdf
[20]Inoue T. A cloud type classification with NOAA 7 split-window measurements. Journal of Geophysical Research Atmospheres, 1987, 92(D4): 3991–4000
[21]Ackerman S A, Strabala K I, Menzel W P, et al. Discriminating clear sky from clouds with MODIS. Journal of Geophysical Research Atmospheres, 1998, 103(D24): 32141‒32157
[22]Iwabuchi H, Yamada S, Katagiri S, et al. Radiative and microphysical properties of cirrus cloud inferred from infrared measurements made by the moderate resolution imaging spectroradiometer (MODIS). Part I: retrieval method. Journal of Applied Meteorology and Climatology, 2013, 53(5): 1297‒1316
[23]Yasuhiko S, Hiroshi S, Takahito I, et al. Convective cloud information derived from Himawari-8 data [EB/OL]. (2017‒03) [2018‒06‒26]. http://www.data. jma.go.jp/mscweb/technotes/msctechrep62-2.pdf
[24]Meenu S, Rajeev K, Parameswaran K. Regional and vertical distribution of semitransparent cirrus clouds over the tropical Indian region derived from CALIPSO data. Journal of Atmospheric and Solar-Terrestrial Physics, 2011, 73(13): 1967‒1979
[25]Thoss A. Algorithm theoretical basis document for cloud top temperature, pressure and height of the NWC/PPS applicable to SAFNWC/PPS version 2014 [EB/OL]. (2014‒09‒15) [2018‒06‒26]. http://www. nwcsaf.org/AemetWebContents/ScientificDocumentation/Documentation/PPS/v2014/NWC-CDOP2-PPS-SMHI- SCI-ATBD-3_v1_0.pdf
[26]Gang H, Ping Y, Heidinger A K, et al. Detecting opa-que and nonopaque tropical upper tropospheric ice clouds: a trispectral technique based on the MODIS 8–12 μm window bands. Journal of Geophysical Re-search Atmospheres, 2010, 115(D20): 1‒11
[27]Marquardt D W. An algorithm for the least-squares estimation of nonlinear parameters. SIAM Journal of Applied Mathematics, 1963, 11(2): 431–441
[28]Amante C, Eakins B W. ETOPO1 1 —arc-minute glo-bal relief model: procedures, data sources and ana-lysis. Psychologist, 2009, 16(3): 20‒25
Retrieval of Semi-transparent Cloud Top Height Using Split Window Histograms Method
Abstract The split window histograms method was applied to retrieve the cloud top height of semi-transparent clouds in the area of 90°-140°E, 15°-55°N using the AHI data on board Himawari-8 from April 1to September 30in 2016. A threshold technique was used to screen the pixels of semi-transparent clouds. The cloud top heights of the pixels were retrieved by using the data of 10.4 mm and 12.4 mm split window channels of Himawari-8, and the data of temperature and geopotential on pressure levels from ERA-Interim reanalysis. The retrieved cloud top height was compared with the matched data of CloudSat. It is found that the split window histograms method works well, and the root mean square error of the result is 1.45 km, and the type of land or sea has no significant impact on the result. The method has strong applicability and can be used to the split window channels of different satellites, especially for the theoretical algorithm of FY-4, a new generation of geostationary meteorological satellite in China.
Key words split window histograms method; semi-transparent cloud; Himawari-8; cloud top height
doi: 10.13209/j.0479-8023.2019.032
收稿日期: 2018‒05‒24;
修回日期: 2018‒10‒29;
网络出版日期: 2019‒04‒04
国家科技支撑计划(2013CB430104)和中国科学院战略重点研究项目(XDA05040201)资助