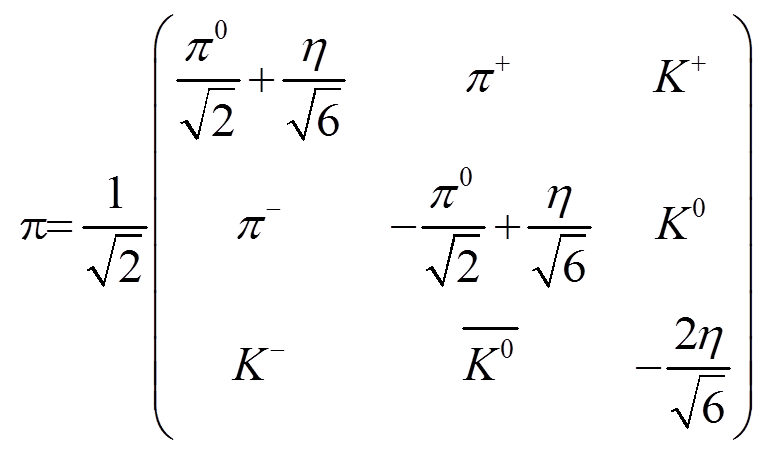 。 (1)
。 (1)摘要 采用重重子手征微扰论(HBCPT)理论, 考虑手征质量破缺效应、顶角修正、波函数重整化以及 O(p3)圈图部分, 计算重子十重态与八重态跃迁轴矢荷手征修正, 并给出理论预言。对于涉及的圈图效应, 均考虑中间态是十重态和八重态的情况。计算过程展现出合理良好的手征收敛性, 与已有实验值符合较好。
关键词 轴矢荷; 重重子手征微扰论; 十重态; 八重态
量子色动力学(quantum chromodynamics, QCD)是描述强相互作用的基本理论, 从夸克层面处理强子之间的相互作用。在高能区, QCD 的耦合常数较小, 处理强相互作用时, 按照耦合常数进行微扰展开。在低能情况下, QCD 的耦合常数很大, 用 QCD 解析求解重子和介子等束缚态强子体系非常困难。20 世纪以来, 粒子物理实验高速发展, 大量束缚态强子被发现, 学者们提出一些有效的理论方法来处理强子之间的相互作用, 如大 Nc展开、手征夸克模型、格点 QCD、QCD 求和规则以及手征微扰论等。手征微扰论是 QCD 低能区的有效理论, 夸克层次上的对称性决定强子层次上的对称性, 并反映在强子体系上。Weinberg[1]首次提出手征有效理论的基本思想和方法, Gasser等[2-3]以路径积分的形式推导手征微扰论的现代形式。纯介子体系的手征微扰论仅仅涉及赝标量介子之间的相互作用。当引入物质场时, 赝标介子作为传递相互作用的规范玻色子参与物质粒子的相互作用。Weinberg[4-5]将手征微扰论扩展到多重子体系中, 推动介子–重子体系的手征理论取得进步。Jenkins等[6]根据重夸克有效理论的思想, 发展了重重子手征微扰论。
重子的轴矢耦合是强子物理实验和理论研究的重点之一。早在 1985 年, Bijnens 等[7]用手征微扰论方法计算重子八重态的轴矢流修正, 但他们忽略了波函数重整化的贡献。1991 年, Jenkins 等[6]用重重子手征微扰论计算重子八重态的轴矢流修正, 之后, Jenkins 等[8]考虑十重态对圈图的贡献, 计算了重子八重态的轴矢流修正。Zhu 等[9]考虑反冲修正和夸克质量破缺项, 用重子手征微扰论计算重子八重态的轴矢修正, 之后, Zhu 等[10]又把中间态是重子十重态和八重态的情况都考虑, 用重重子手征微扰论计算重子八重态的轴矢修正。Ledwig 等[11]对重子八重态的轴矢耦合做进一步分析。Buchmann 等[12]用夸克模型计算核子与Δ(1232)的轴矢跃迁形状因子。Procura[13]用非相对论有效场论的方法计算核子与Δ(1232)的轴矢跃迁形状因子。Aliev 等[14]用光锥 QCD 求和规则, 计算核子与Δ(1232)的轴矢跃迁形状因子。Alexandrou 等[15]用格点 QCD 计算核子与Δ(1232)的轴矢跃迁形状因子。Kucukarslan 等[16]用光锥 QCD 求和规则, 计算重子十重态与八重态跃迁轴矢形状因子。
本文在重重子手征微扰论框架下, 系统地计算重子十重态与八重态的跃迁轴矢荷。
赝标量介子八重态的定义如下:
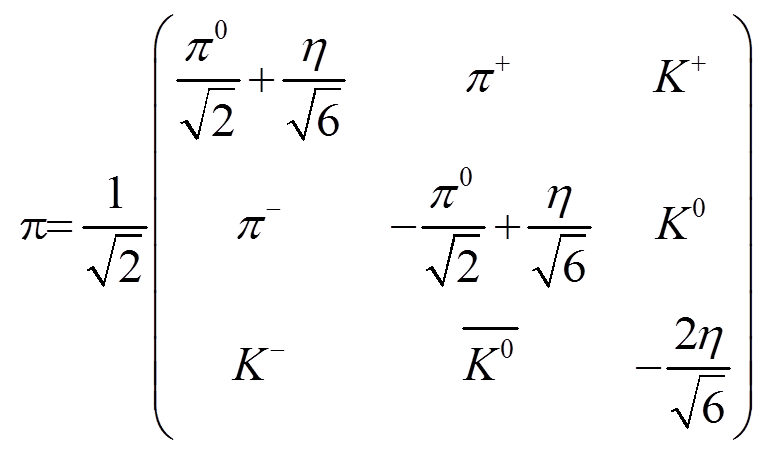 。 (1)
。 (1)重子八重态场的定义为
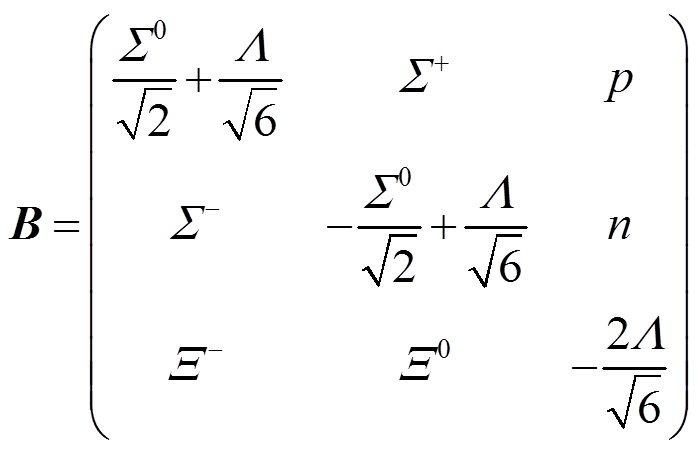 。 (2)
。 (2)
重子十重态场的定义(1, 2和3表示味道指标)为
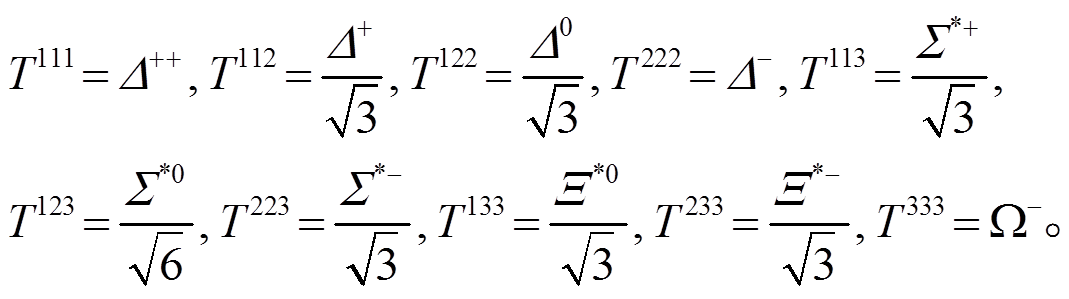
赝标量介子采用指数化:
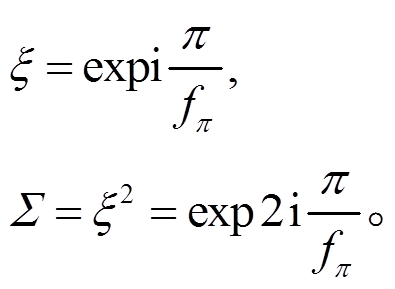 (3)
(3)
夸克质量矩阵为
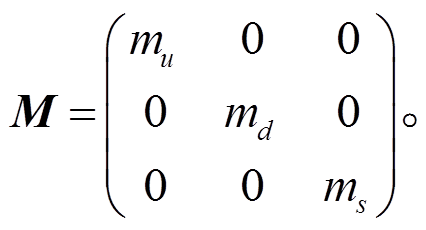
 (4)
(4)χ+ “板块”的定义为
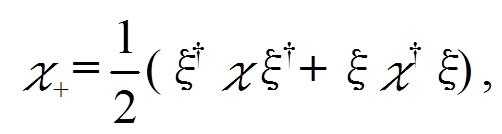
 (5)
(5)
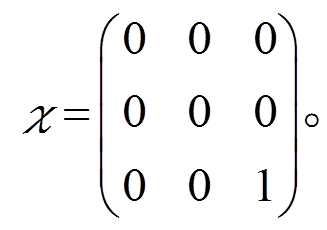
 (6)
(6)手征联络场为
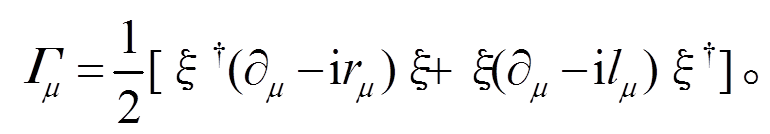 (7)
(7)
轴矢场的定义为
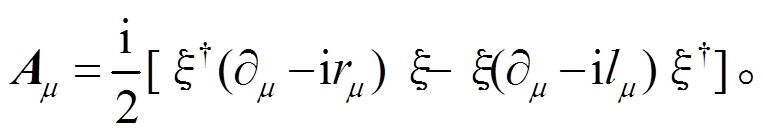 (8)
(8)重子八重态的协变微商为
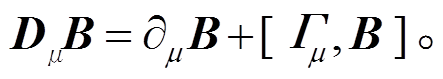
 (9)
(9)
重子十重态的协变微商(a, b, c和d为味道指标)为
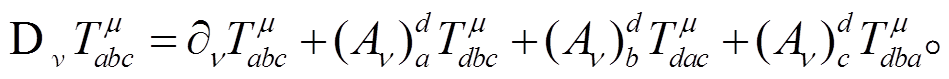 (10)
(10)在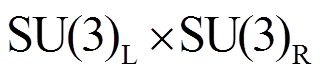 手征变换下, 介子场和重子场的变换方式为
手征变换下, 介子场和重子场的变换方式为
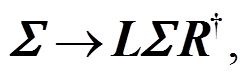 (11)
(11)
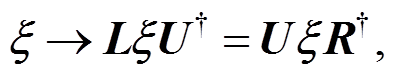 (12)
(12)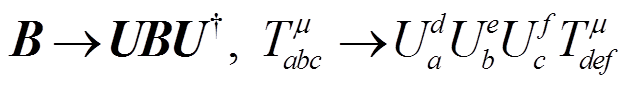 。 (13)
。 (13)
U 场的定义是式(12), 通过定义 U 场, 重子十重态和八重态场在手征变换下的方式为式(13), 比不定义 U 场情况下场的变换方式(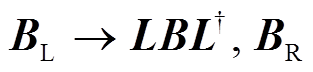
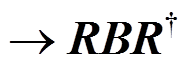 )方便。
)方便。
考虑赝标量介子场、重子十重态场和八重态场在手征变换下的变换方式以及 C, P和 T 对称性, 构造的领头阶赝标量介子–重子体系拉氏量为
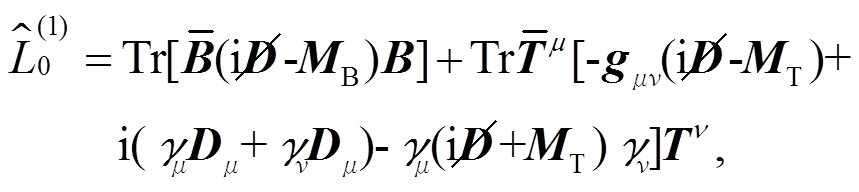
 (14)
(14)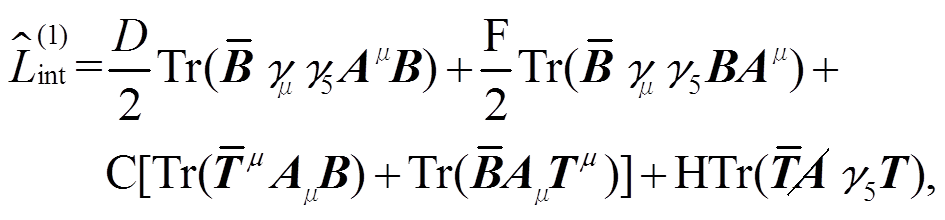 (15)
(15)
其中, MB 是重子八重态质量, MR是重子十重态质量。
物质场的质量与手征破缺能标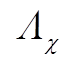 接近, 在手征极限下, 物质场的质量不为 0, 物质场的四动量不是小量, 会破坏收敛性, 通常按照动量逐阶展开方法不再适用。虽然物质场的质量较大, 但是对于低能相互作用过程, 实际的动量转移并不是全部动量, 而是离壳部分的小动量, 按照该小动量进行微扰逐阶展开, 收敛性得到保持[6,8]。
接近, 在手征极限下, 物质场的质量不为 0, 物质场的四动量不是小量, 会破坏收敛性, 通常按照动量逐阶展开方法不再适用。虽然物质场的质量较大, 但是对于低能相互作用过程, 实际的动量转移并不是全部动量, 而是离壳部分的小动量, 按照该小动量进行微扰逐阶展开, 收敛性得到保持[6,8]。
将重强子的四动量分解为
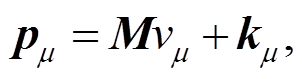 (16)
(16)其中, M 是重强子质量;vu是重强子的四速度, 满足v2=1; ku 是重强子参与低能强相互作用过程中实际发生的动量转移部分。首先从最简单的情形分析, 对于重子拉氏量:

 (17)
(17)
将ψ分解为
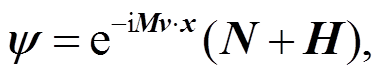
 (18)
(18)其中, N 和 H 定义为
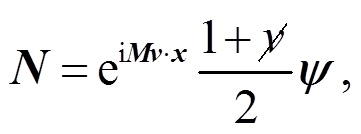
 (19)
(19)
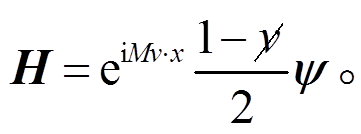
 (20)
(20) 分解之后, H和 N满足的运动方程分别相当于具有质量2M和0, H和N称为重分量场和轻分量场。
我们定义:
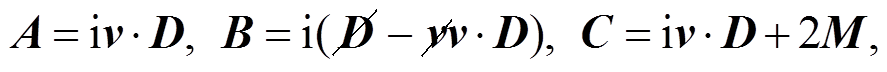

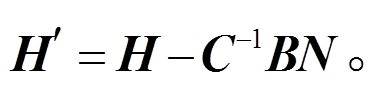
 (21)
(21)
根据上述定义, 利用γ矩阵的性质, 对拉氏量进行对角化为
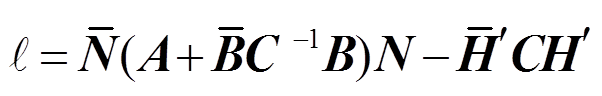 。(22)
。(22)采用路径积分方法, 从泛函积分:
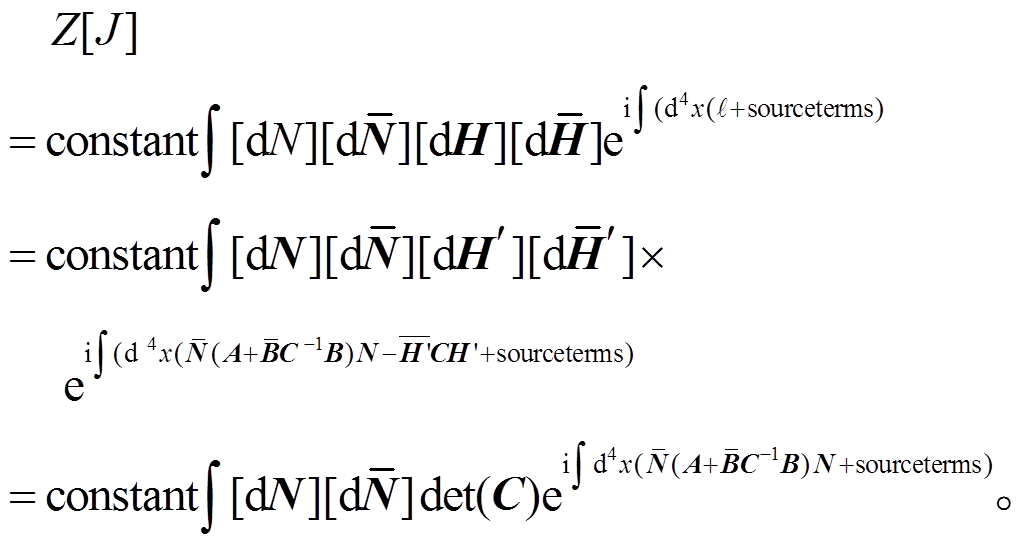
 (23)
(23)
可以看出, 重分量场被积掉, 轻分量场可以从积分中提出, 有效拉氏量最终只含有轻分量场:
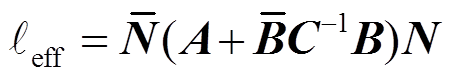 。 (24)
。 (24)由式(21)可知
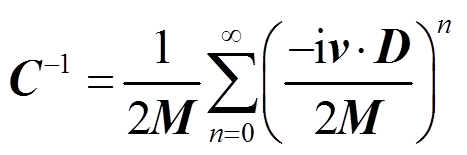 , (25)
, (25)
这样就可以按照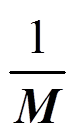 与
与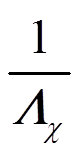 逐阶写出拉氏量, 例如:
逐阶写出拉氏量, 例如:
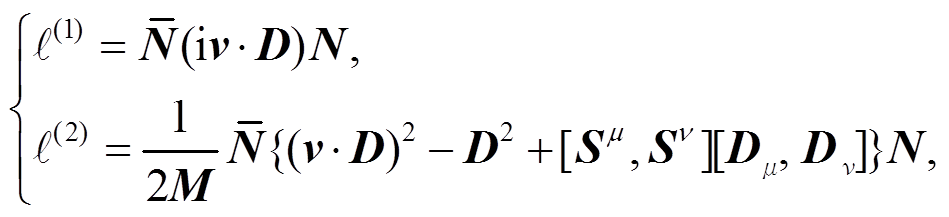 (26)
(26)其中 是定义的Pauli-Lubanski矢量。
是定义的Pauli-Lubanski矢量。
对领头阶相对论性的拉氏量(式(14)和(15)), 采用重重子约化得到

 (27)
(27)由于二阶拉氏量也可能贡献圈图中轴矢流顶点, 所以需要考虑 O(P2)阶手征拉氏量中有贡献的项。通过群结构分析得到:
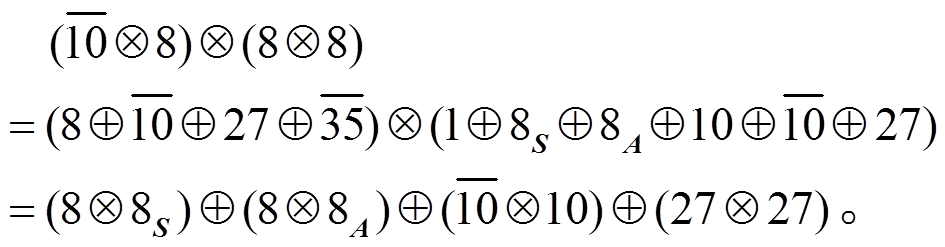 (28)
(28)
在手征变换下, 轴矢场 Aμ 和 Aν 属于伴随表示。Aμ与 Aν相乘, 得到 8S, 8A,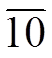 和 27 维味道表示, 由此可以写出十重态、八重态和轴矢场耦合二阶拉氏量独立的4项:
和 27 维味道表示, 由此可以写出十重态、八重态和轴矢场耦合二阶拉氏量独立的4项:
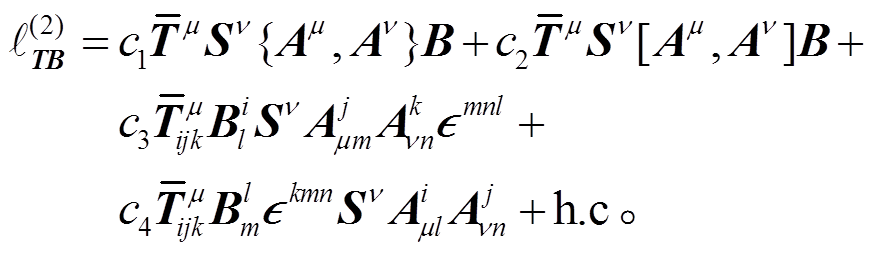
 (29)
(29)对于构造十重态与轴矢场耦合的二阶拉氏量, 由群结构分析可以得到
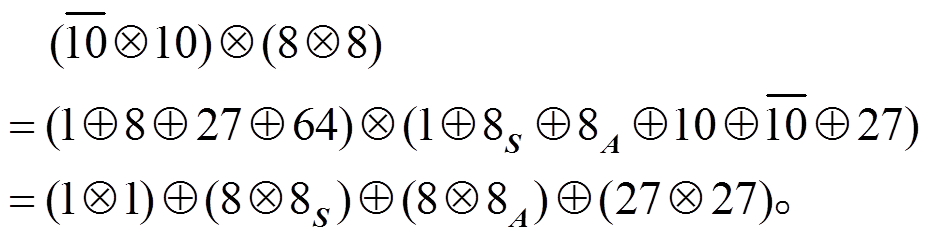 (30)
(30)
考虑所涉及场量之间洛伦兹指标的收缩方式, 可以写出十重态与轴矢场耦合的二阶拉氏量独立的9项:
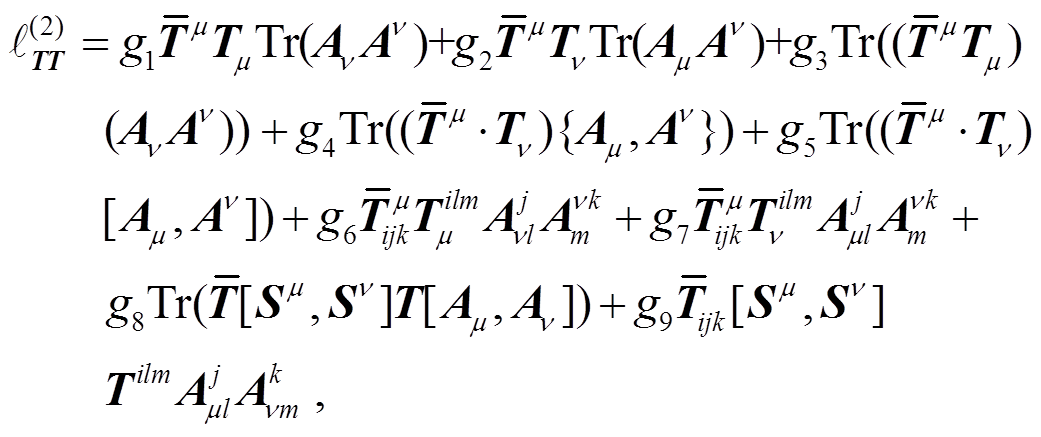 (31)
(31)同样, 也可以构造出八重态与轴矢场耦合的二阶拉氏量独立的7项:
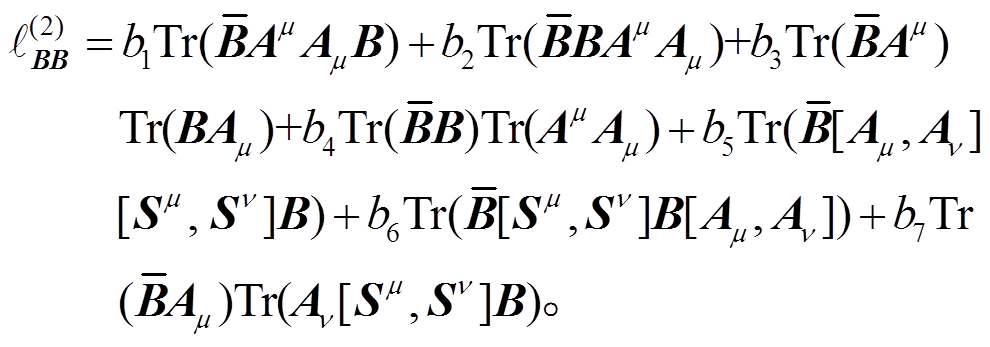 (32)
(32)
在手征变换下, χ+“板块”按照伴随表示进行变换, 群结构分析与式(28)相同。因此重子十重态、八重态和赝标量介子耦合的手征质量破缺项具有独立的4项:

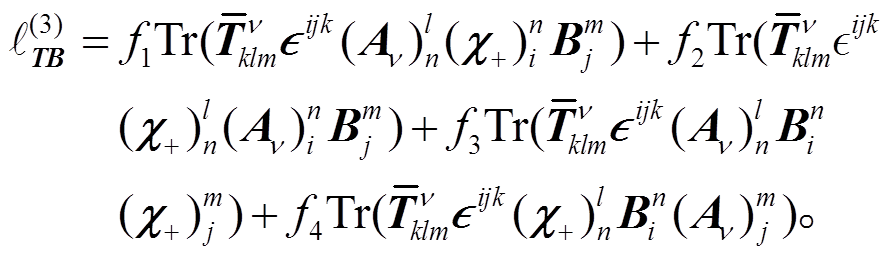 (33)
(33)将八重态手征流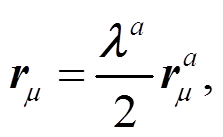
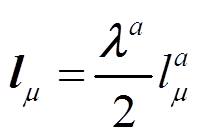 作为外源引入联络项和轴矢场中(式(7)和(8)), 轴矢流:
作为外源引入联络项和轴矢场中(式(7)和(8)), 轴矢流: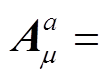
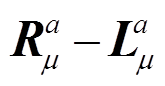 。利用诺特定理, 领头阶拉氏量(式(27))对外源求偏导数得到味道为a的轴矢流:
。利用诺特定理, 领头阶拉氏量(式(27))对外源求偏导数得到味道为a的轴矢流:
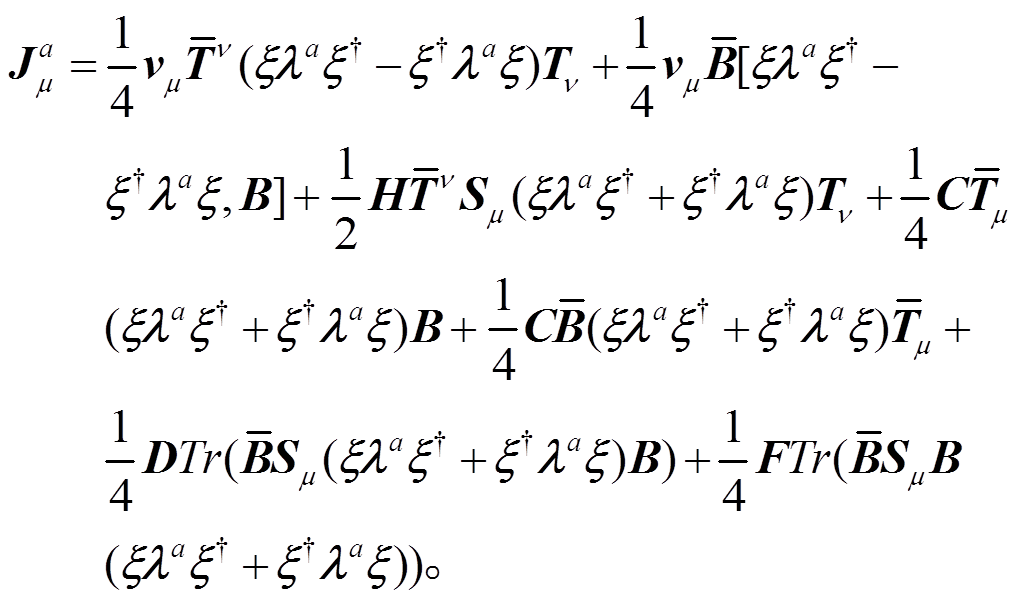 (34)
(34)下一阶的树图 O(p2)阶轴矢流来自 O(p3)阶拉氏量(式(33)):
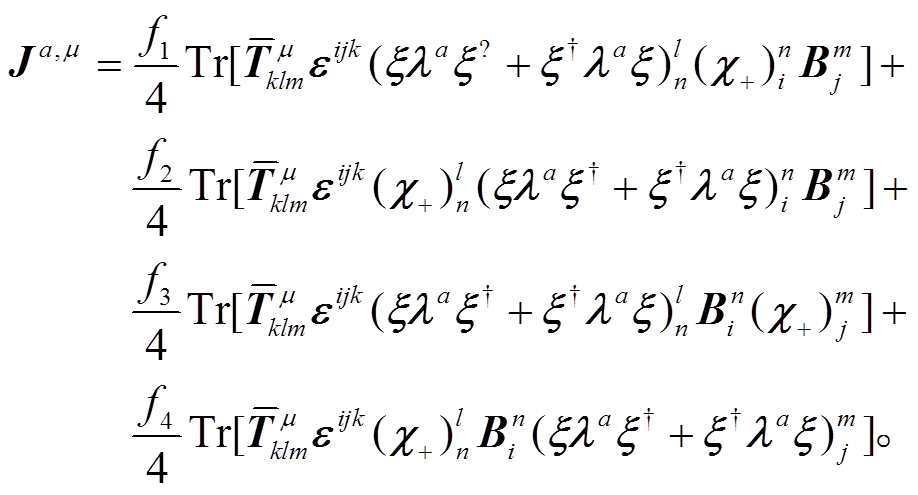 (35)
(35)
此外, 拉氏量(式(29), (31)和(32))会贡献 O(p2)阶轴矢流顶点:
 (36)
(36)式(36)会对O(p3)阶圈图(f), (g), (h), (i)图有贡献。
重子十重态与八重态之间跃迁领头阶轴矢荷(表 1), 来源于领头阶拉氏量的贡献, 可由式(34)计算得到。
重子十重态与八重态之间跃迁次领头树图阶轴矢荷(表 2), 来源于手征质量破缺项(式(33))。这里取mu=md=0, ms被吸收到低能耦合常数f1, f2, f3和f4中, 可由式(35)计算得到。
重子自能函数记为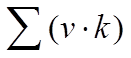 , 重整化因子:
, 重整化因子:

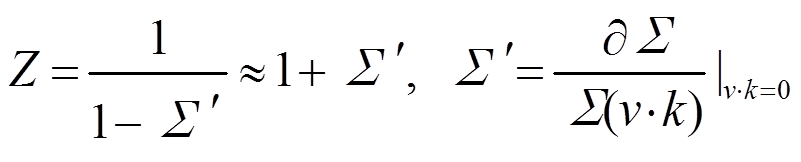 。 (37)
。 (37)
重子十重态与八重态重整化轴矢流矩阵元为:
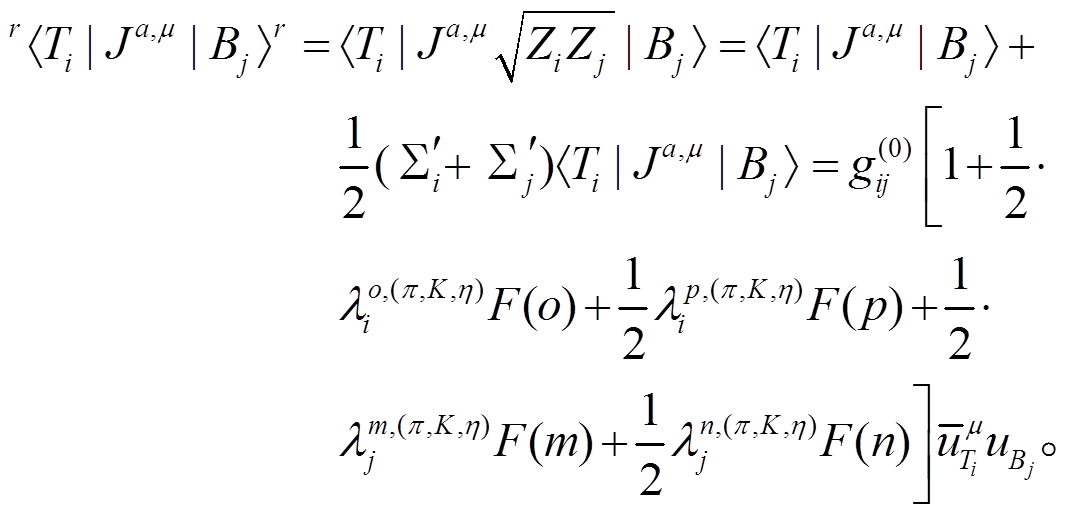 (38)
(38)由上式可知,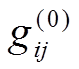 是领头阶轴矢荷, 波函数重整化的贡献来自图1(m), (n), (o)和(p), 其中重子八重态波函数重整化贡献的示意图为图 1(m)和(n), 十重态波函数重整化贡献的示意图为图(o)和(p)。
是领头阶轴矢荷, 波函数重整化的贡献来自图1(m), (n), (o)和(p), 其中重子八重态波函数重整化贡献的示意图为图 1(m)和(n), 十重态波函数重整化贡献的示意图为图(o)和(p)。
重整化的重子十重态与八重态轴矢流矩阵元为

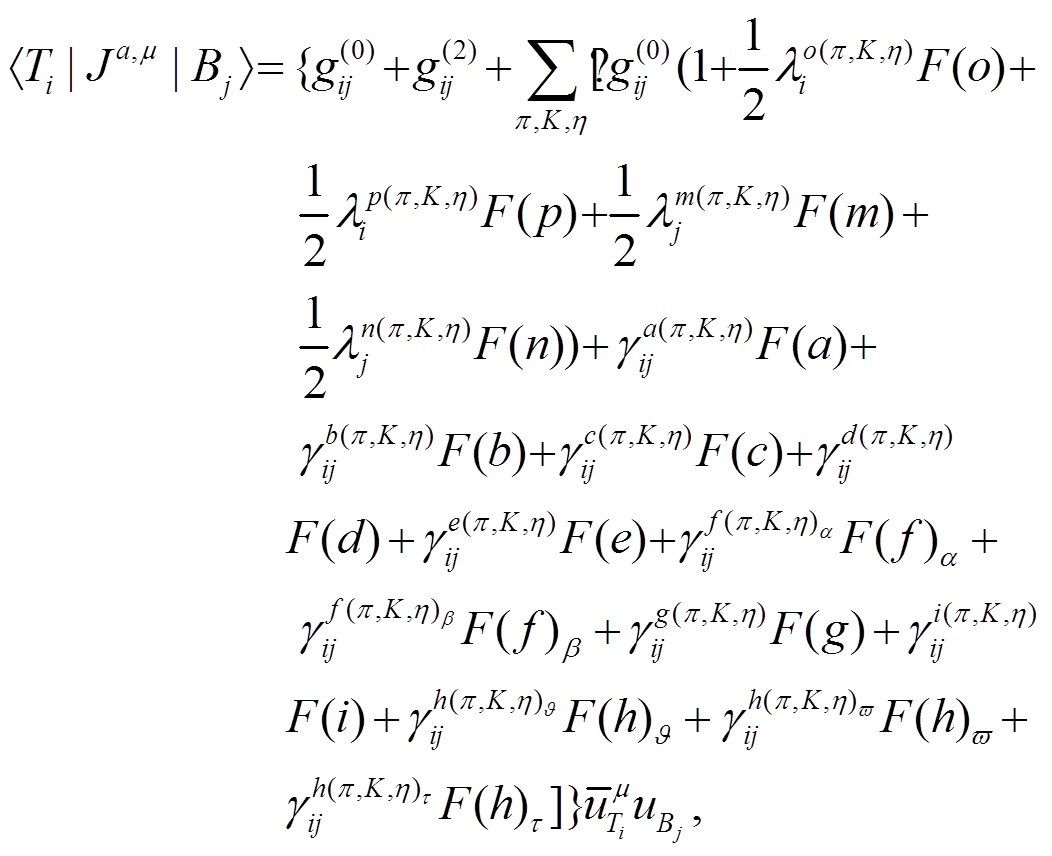 (39)
(39)其中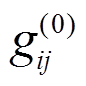 是领头阶轴矢荷, 来自领头阶拉氏量(式(27))的贡献,
是领头阶轴矢荷, 来自领头阶拉氏量(式(27))的贡献,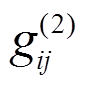 是次领头树图阶轴矢荷, 来 O(P3) 自阶拉氏量(式(33))的贡献。
是次领头树图阶轴矢荷, 来 O(P3) 自阶拉氏量(式(33))的贡献。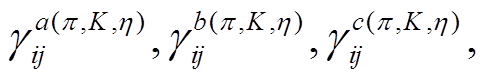
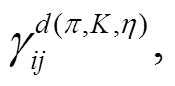
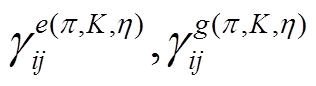 和
和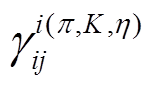 是图 1(a)~(e)和(g), (i)圈图贡献的系数,
是图 1(a)~(e)和(g), (i)圈图贡献的系数,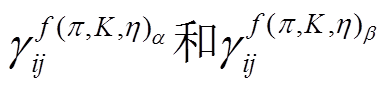 分别代表图1(f )轴矢流顶点“•”来自拉氏量(式(32))中 b1,2,3,4 项和b5,6,7 项贡献的圈图系数。
分别代表图1(f )轴矢流顶点“•”来自拉氏量(式(32))中 b1,2,3,4 项和b5,6,7 项贡献的圈图系数。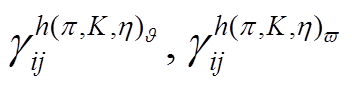 和
和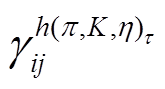 分别代表图 1(h)轴矢流顶点“•”来自拉氏量(式(31))中
分别代表图 1(h)轴矢流顶点“•”来自拉氏量(式(31))中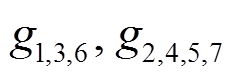 和
和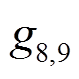 项贡献的圈图系数。
项贡献的圈图系数。
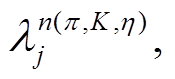
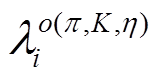 和
和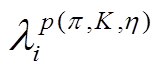 是波函数重整化系数。F(a), F(b), F(c), F(d), F(e), F(f), F(g), F(h), F(i), F(m),F(n), F(o)和 F(p)是圈图积分函数。
是波函数重整化系数。F(a), F(b), F(c), F(d), F(e), F(f), F(g), F(h), F(i), F(m),F(n), F(o)和 F(p)是圈图积分函数。
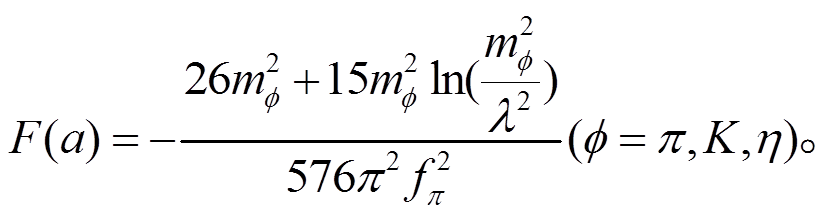 (40)
(40)
表1 重子十重态与八重态之间跃迁领头阶轴矢荷
Table 1 Leading order of decuplet-octet baryon transition axial charges

味道a=1+i2味道a=4+i5味道a=4–i5味道a =8
表2 重子十重态与八重态之间跃迁次领头树图阶轴矢荷
Table 2 Next-to-leading order tree-level of decuplet-octet baryon transition axial charges

味道a=1+i2味道a=4+i5味道 a=4–i5味道a=8
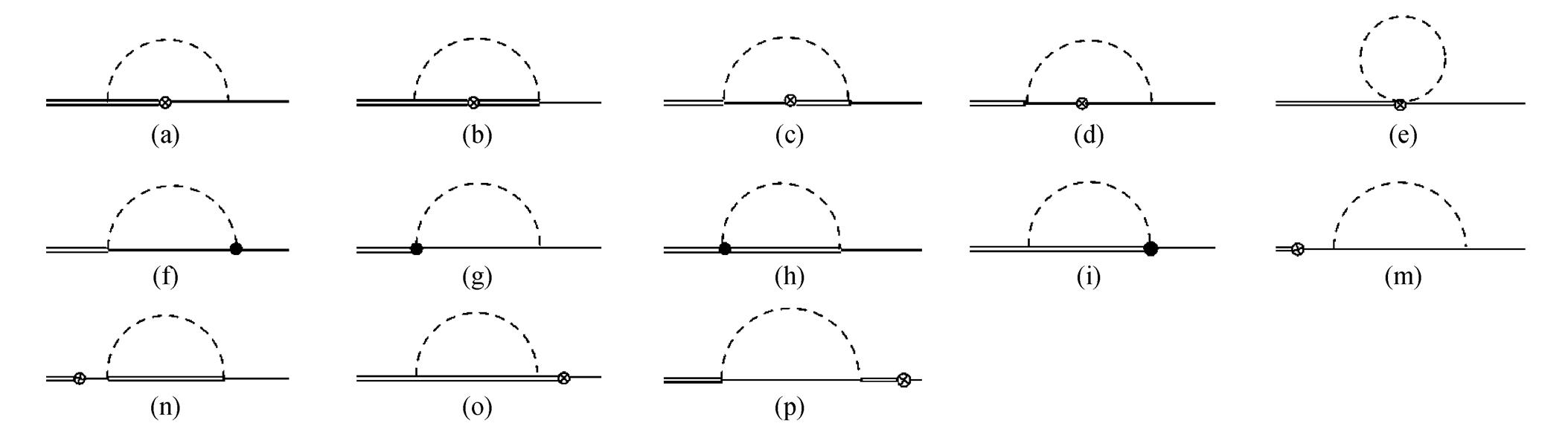
双线代表重子十重态, 单线代表八重态, 虚线代表赝标量介子。⊗代表领头阶拉氏量(式(27))贡献的轴矢流插入, •代表 O(P2)阶拉氏量(式(29), (31)和(32))贡献的轴矢流插入。(a)~(e)为 O(P2)阶顶角修正圈图, (f)~(i)为 O(P3)阶圈图, (m)~(p)为波函数重整化示意图。实际计算时分别计算重子十重态和八重态的自能修正图
图1 重子十重态与八重态跃迁轴矢荷单圈图
Fig. 1 One-loop Feynman diagram of decuplet-octet baryon transition axial charges
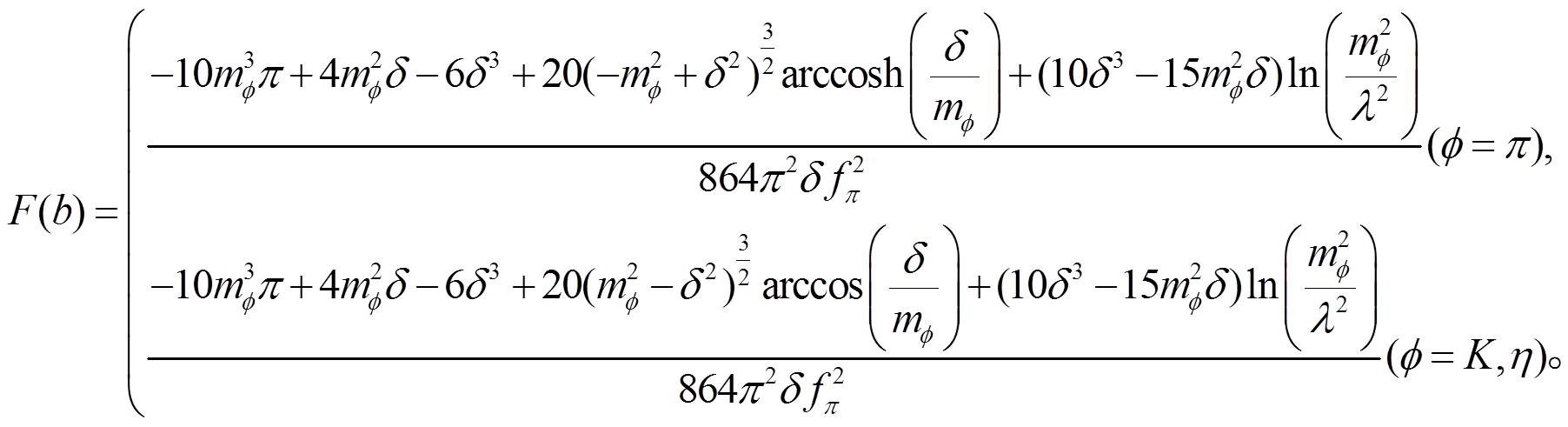
 (41)
(41)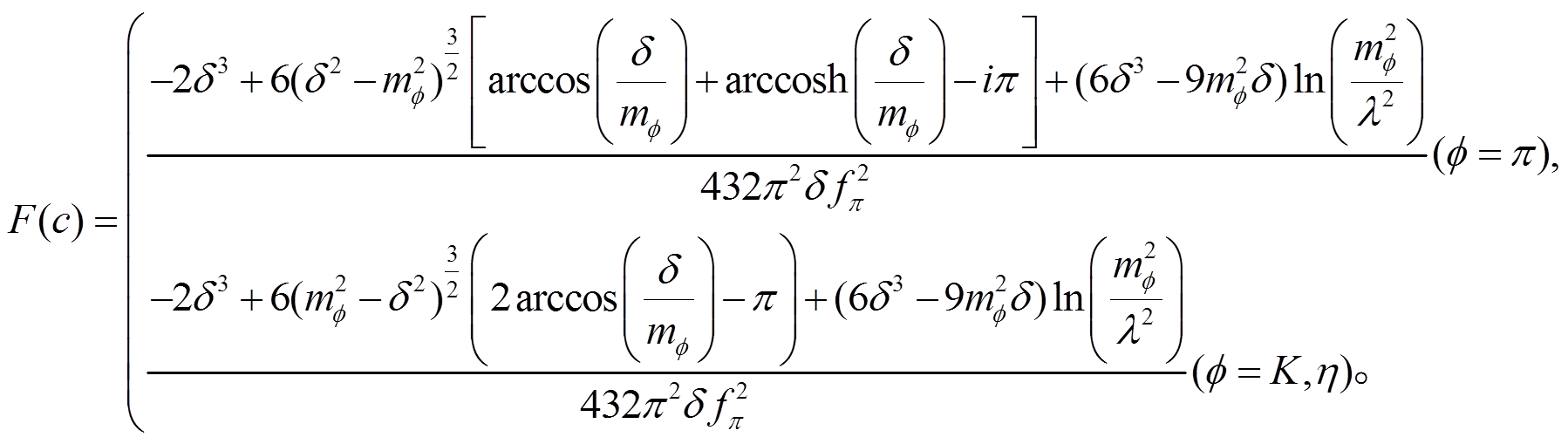 (42)
(42)
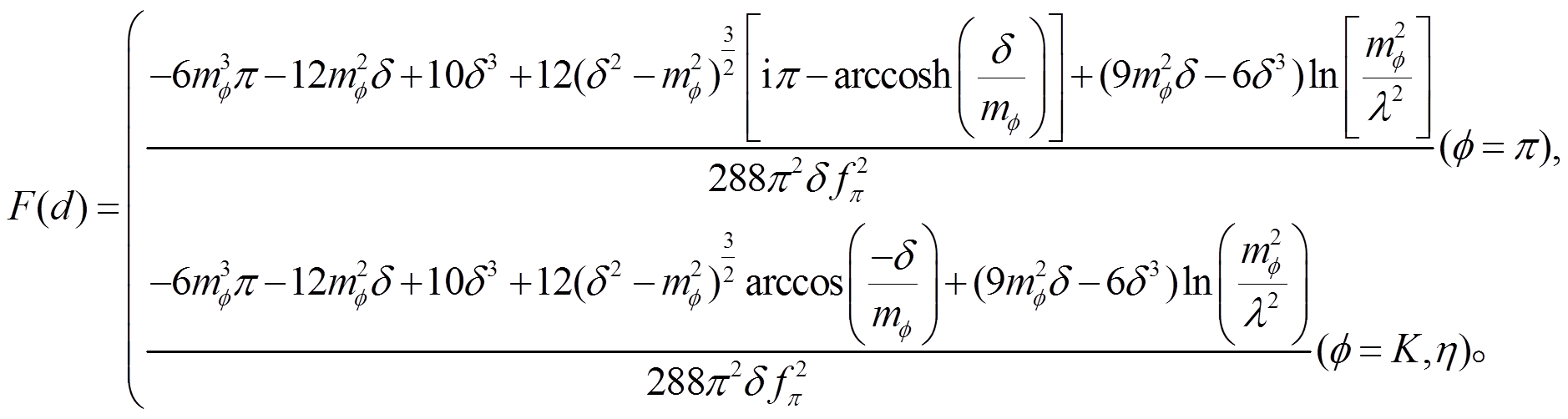 (43)
(43)
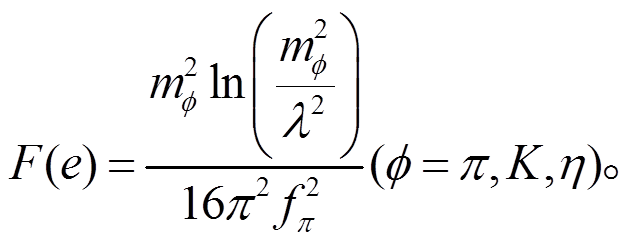 (44)
(44)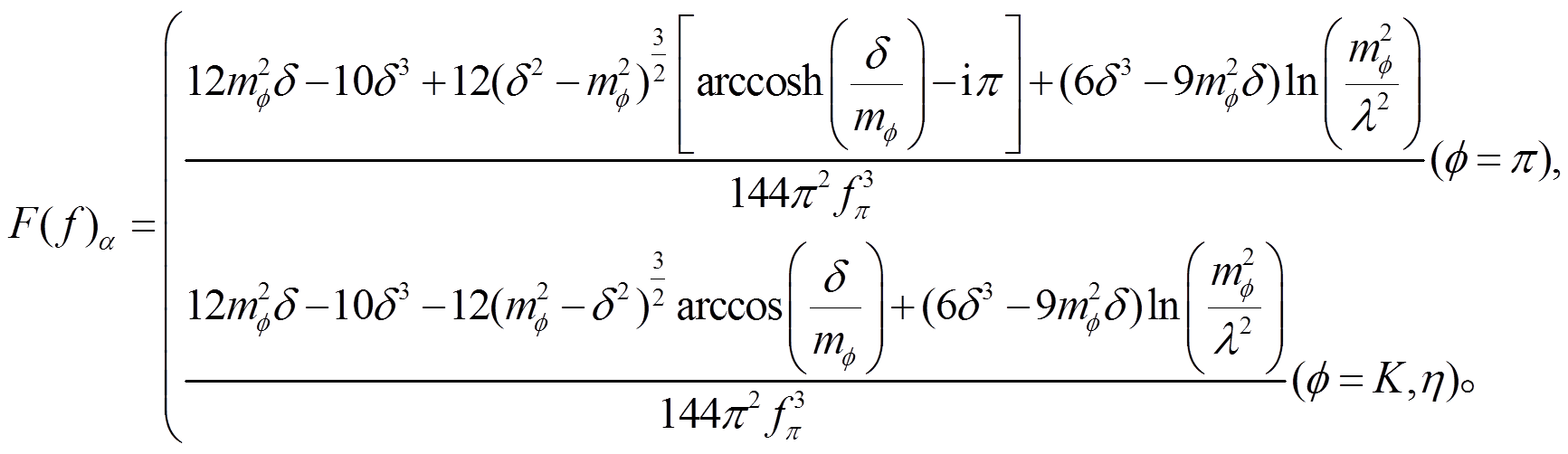 (45)
(45)
 (46)
(46)
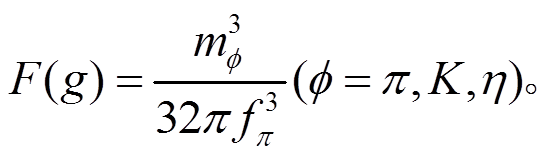 (47)
(47)
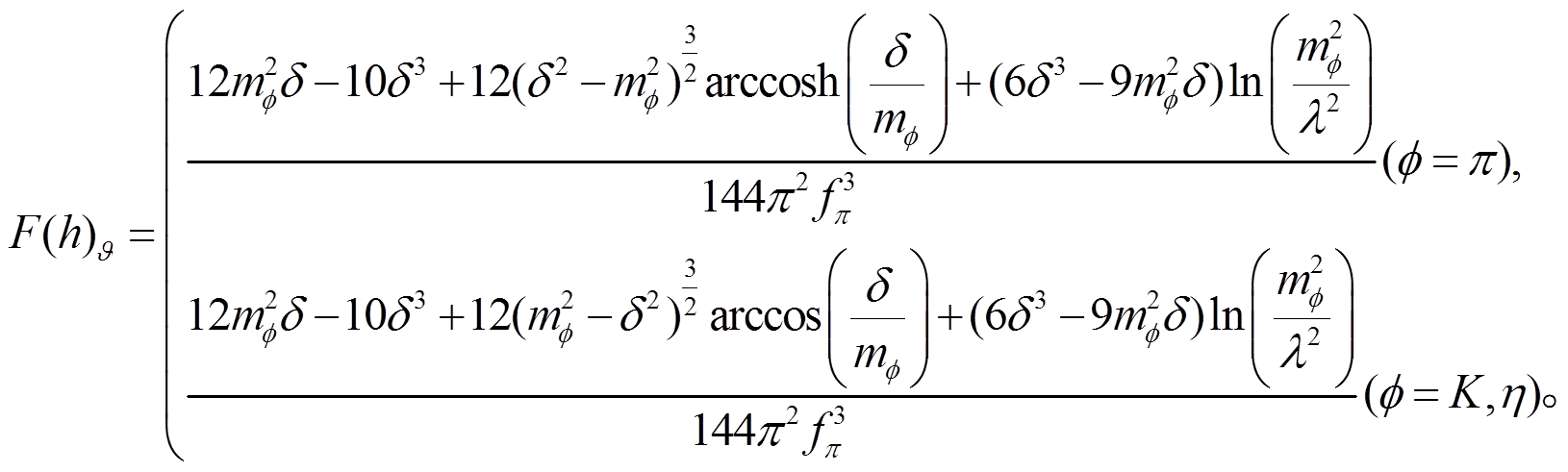 (48)
(48) (49)
(49)
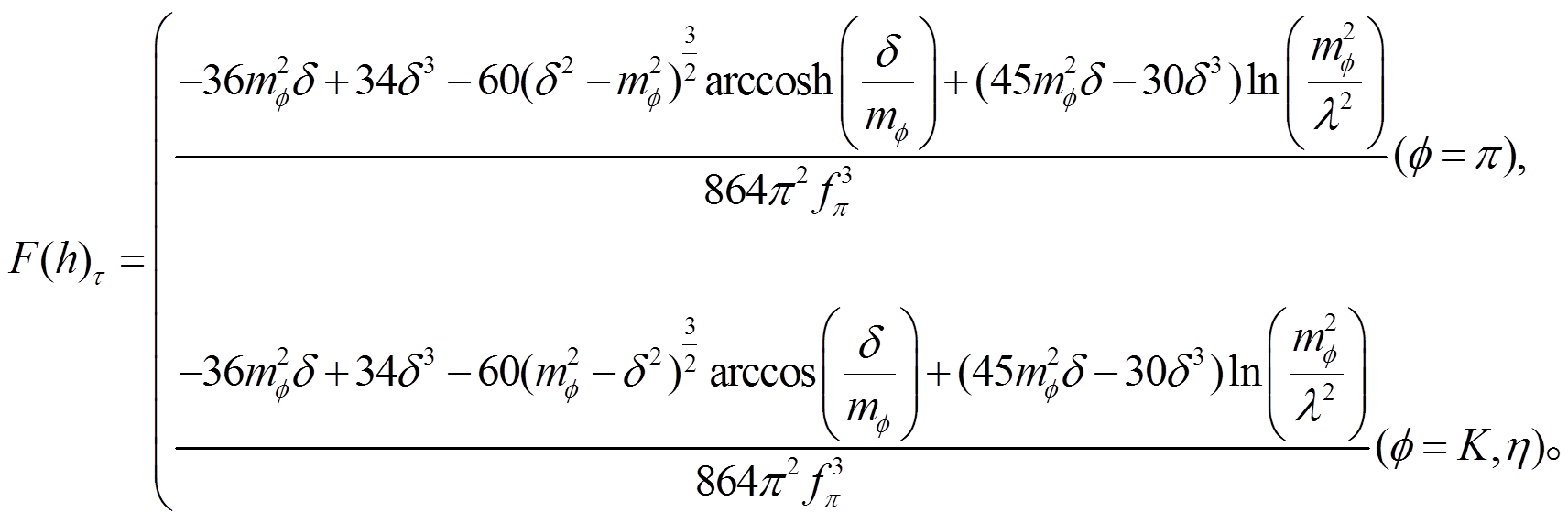 (50)
(50)
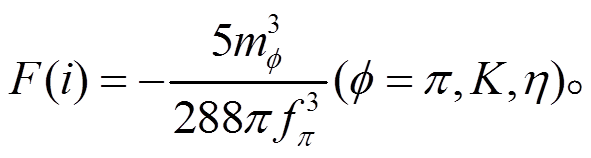
 (51)
(51)
 (52)
(52)
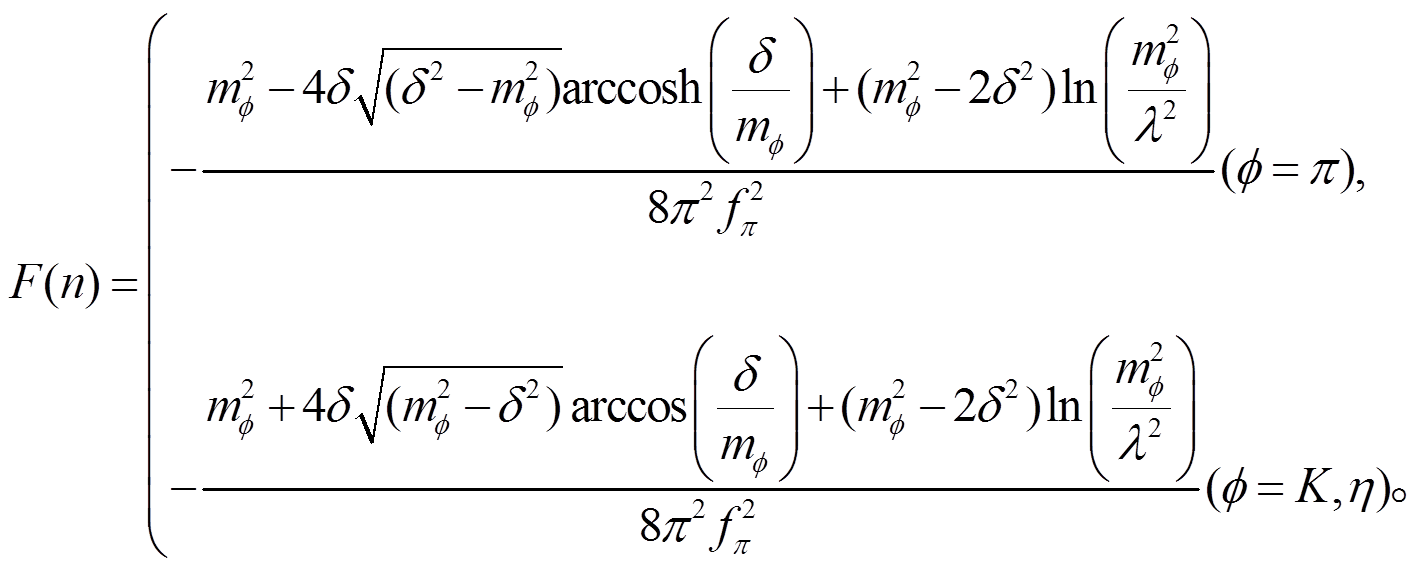 (53)
(53)
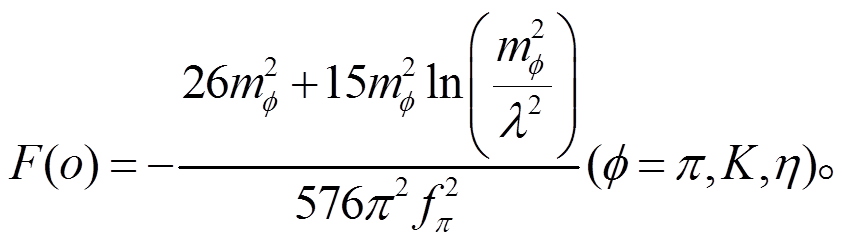 (54)
(54) (55)
(55)
实验测出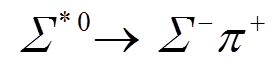 的衰变宽度约为 36 MeV,考虑到同位旋对称性, 该衰变分支比为 5.85%[17-18]。
可以计算出衰变宽度理论表达式, 从而由实验值确定未知轴矢荷
的衰变宽度约为 36 MeV,考虑到同位旋对称性, 该衰变分支比为 5.85%[17-18]。
可以计算出衰变宽度理论表达式, 从而由实验值确定未知轴矢荷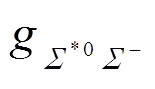 。在质心系中,
。在质心系中, 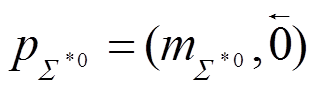 , 两体衰变公式为
, 两体衰变公式为
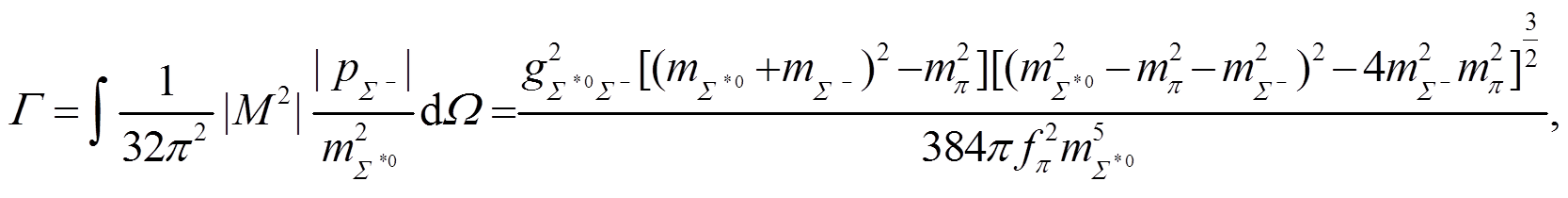 (56)
(56)可计算得到
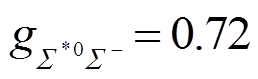 。 (57)
。 (57)
同理, 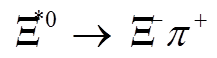 的衰变宽度约为9.1 MeV[17], 考虑到同位旋对称性, 该衰变分支比为
的衰变宽度约为9.1 MeV[17], 考虑到同位旋对称性, 该衰变分支比为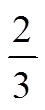 , 从而可得到
, 从而可得到
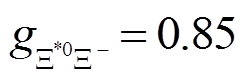 。 (58)
。 (58)在强子层次上, 质子与π耦合的费恩曼振幅为
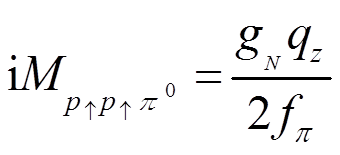 , (59)
, (59)在低能时, 在夸克层次具有
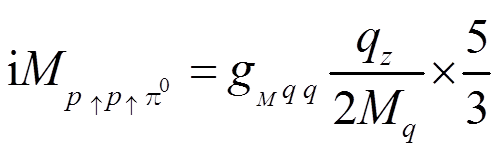 , (60)
, (60)
在强子层次,Δ+与质子的耦合的费恩曼振幅为
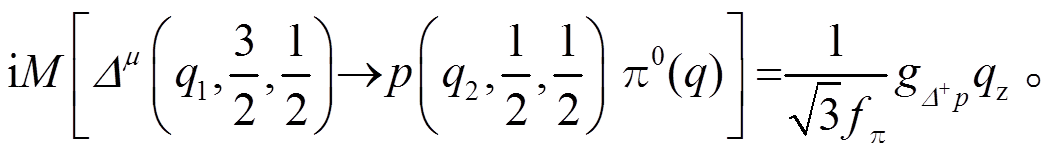 (61)
(61)在夸克层次具有
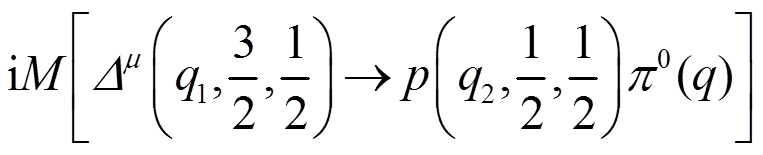
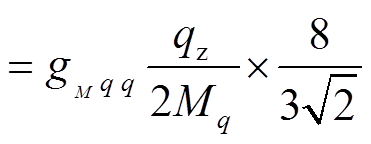 。 (62)
。 (62)对比式(59)~(62)可得
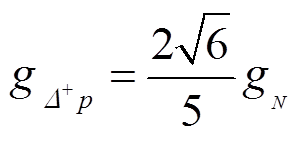 。 (63)
。 (63)
根据重子十重态与八重态耦合的领头阶拉氏量展开的C-G系数可知
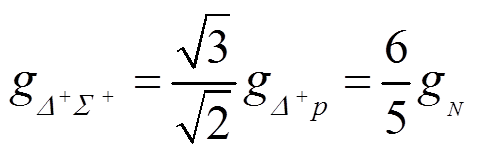 , (64)
, (64)同理可得
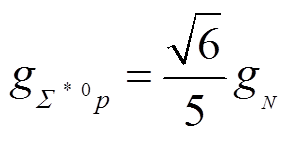 。 (65)
。 (65)
我们虽然给出跃迁轴矢荷修正到 O(p3)阶的理论表达式, 但由于 O(p3)圈图涉及耦合参数c1, c2, c3,c4; g1, g2, g3, g4, g5, g6, g7, g8, g9; b1, b2, b3, b4, b5, b6,b7, 所以估计起来非常艰难, 用共振态饱和模型等方法也只能估计出个别耦合常数。因此, 我们的数值结果只计算到O(p2)阶。
重子十重态的平均质量为 MT=1.452GeV, 重子八重态的平均质量为 MB =1.158GeV, 重子十重态与八重态的质量差为δ=0.294GeV。赝标量介子的质量为 mπ=0.140GeV, mK=0.494GeV, mη=0.55GeV。衰变常数 fπ≈0.0924GeV, 重整化能标λ=1GeV。我们采用文献[19]中的低能耦合参数(由于拉氏量(式(14))中定义的不同, 所以我们的 D, F 与文献[19]不一致):

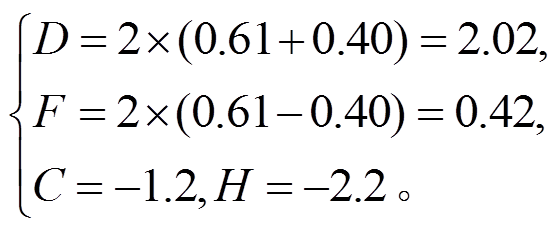 (66)
(66)由夸克模型的计算得知
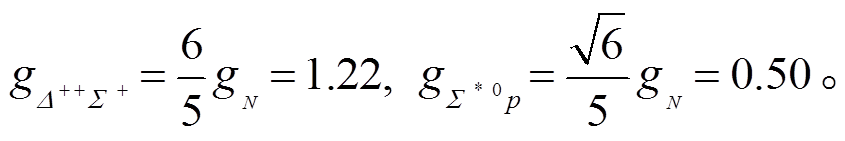 (67)
(67)
根据式(57)和(58)得到的实验值为
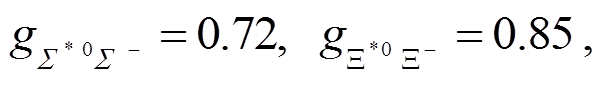 (68)
(68)D, F, C 和 H 根据式(66)取值, 原则上, 应该通过实验值来确定未知的耦合参数 f1, f2, f3 和 f4, 但在实验中, 由于重子十重态与八重态的质量差小于 K, η 的质量, 衰变到 K 和 η 的道被禁戒掉。由表 2 可知, 衰变到![]() 的实验值只能定出 f3 和 f4。于是, 我们将夸克模型估计的值(式(67))和通过实验上衰变道
的实验值只能定出 f3 和 f4。于是, 我们将夸克模型估计的值(式(67))和通过实验上衰变道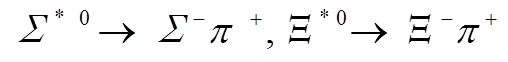 确定的值(式(68))一并作为实验值输入来确定手征质量破缺项的耦合参数 f1, f1, f3和f4:
确定的值(式(68))一并作为实验值输入来确定手征质量破缺项的耦合参数 f1, f1, f3和f4:
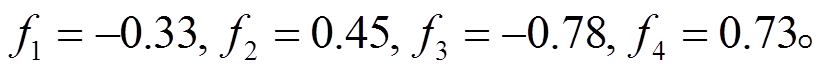 (69)
(69)
这样, 我们就得到理论表达式(41)中 O(p2)阶所需的8个低能耦合参数D, F, C, H, f1, f2, f3和f4。π+, π0和 π-是同位旋三重态,K+和K0是同位旋双重态,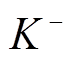 和
和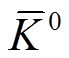 是同位旋双重态, η 是同位旋单态。这样, 只需计算味道a=1+i2, a=4+i5, a=4–i5, a=8即可, 结果见表3~6。其中, “领头阶”和“顶角修正”、“波函数重整化效应”只涉及低能耦合参数D, F, C, H, “up to O(p2)”表示领头阶、顶角修正和波函数重整化效应之和。“预言值”表示up to O(p2)与手征质量破缺项的贡献之和。“实验值”是根据粒子数据表[17]中已有的衰变道宽度确定的值。
是同位旋双重态, η 是同位旋单态。这样, 只需计算味道a=1+i2, a=4+i5, a=4–i5, a=8即可, 结果见表3~6。其中, “领头阶”和“顶角修正”、“波函数重整化效应”只涉及低能耦合参数D, F, C, H, “up to O(p2)”表示领头阶、顶角修正和波函数重整化效应之和。“预言值”表示up to O(p2)与手征质量破缺项的贡献之和。“实验值”是根据粒子数据表[17]中已有的衰变道宽度确定的值。
从表 3~6 可以看出, 手征收敛性较好, 对于味道 a=1+i2, 预言值与实验值符合较好。从表中还可以发现, 圈图中 K 圈的贡献较大。在(a), (b), (c), (d)和(e)圈图中, (e)图贡献最大; (d)图贡献比(b)图大的多, 说明圈图内线中重子八重态的贡献比重子十重态的贡献明显, 以重子八重态的贡献为主; 我们发现, (a)图贡献比(c)图大的多。
表3 味道a=1+i2重子十重态与八重态跃迁轴矢荷数值结果
Table 3 Numerical results of flavor a=1+i2 decuplet-octet baryon transition axial charges
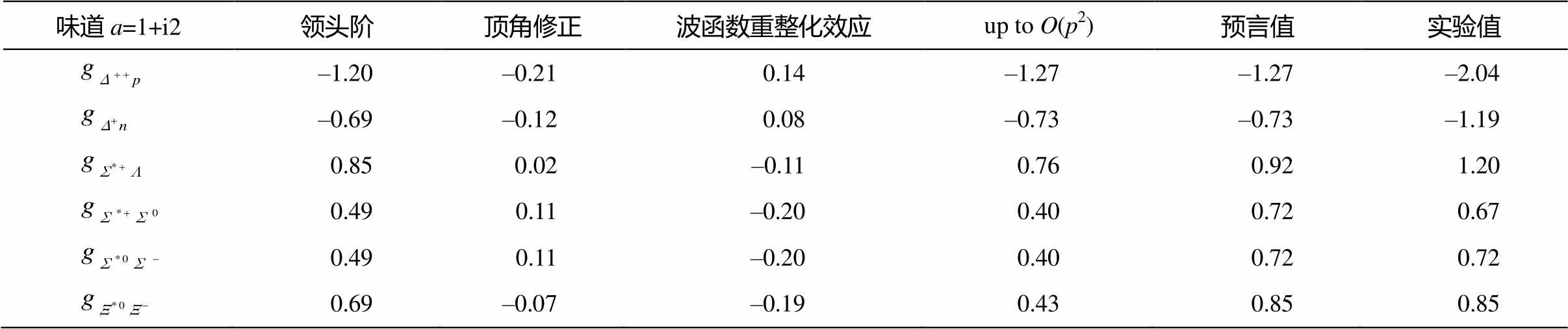
味道a=1+i2领头阶顶角修正波函数重整化效应up to O(p2)预言值实验值 –1.20–0.210.14–1.27–1.27–2.04 –0.69–0.120.08–0.73–0.73–1.19 0.850.02–0.110.760.921.20 0.490.11–0.200.400.720.67 0.490.11–0.200.400.720.72 0.69–0.07–0.190.430.850.85
表4 味道a=4+i5重子十重态与八重态跃迁轴矢荷数值结果
Table 4 Numerical results of flavor a=4+i5 decuplet-octet baryon transition axial charges

味道a=4+i5领头阶顶角修正波函数重整化效应uptoO(p2)预言值 1.200.18–0.490.891.22 –0.98–0.150.40–0.73–1.00 –0.69–0.100.28–0.51–0.70 0.69–0.0006–0.230.460.63 –0.490.00040.16–0.33–0.45
表5 味道a=4–i5重子十重态与八重态跃迁轴矢荷数值结果
Table 5 Numerical results of flavor a=4–i5 decuplet-octet baryon transition axial charges
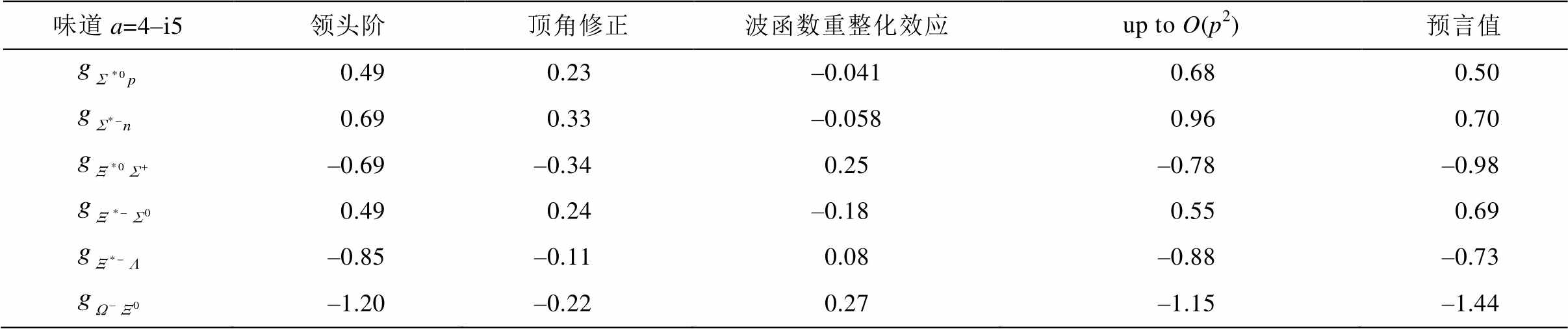
味道a=4–i5领头阶顶角修正波函数重整化效应uptoO(p2)预言值 0.490.23–0.0410.680.50 0.690.33–0.0580.960.70 –0.69–0.340.25–0.78–0.98 0.490.24–0.180.550.69 –0.85–0.110.08–0.88–0.73 –1.20–0.220.27–1.15–1.44
表6 味道a=8重子十重态与八重态跃迁轴矢荷数值结果
Table 6 Numerical results of flavor a=8 decuplet-octet baryon transition axial charges

味道a=8领头阶顶角修正波函数重整化效应up to O(p2)预言值 –0.60–0.210.23–0.58–0.68 0.600.21–0.230.580.68 0.600.21–0.230.580.68 –0.60–0.080.17–0.51–0.58 0.600.08–0.170.510.58
由同位旋对称性可知, 对于味道a=1+i2,
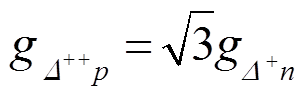 , (70)
, (70)
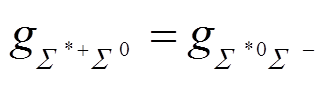 。 (71)
。 (71)
对于味道a=4+i5,
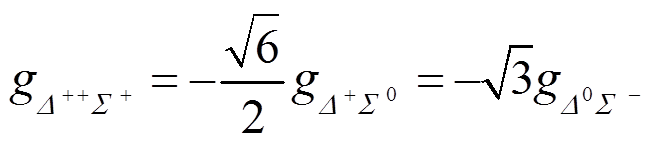 , (72)
, (72)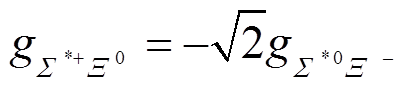 。 (73)
。 (73)
对于味道a=4–i5,
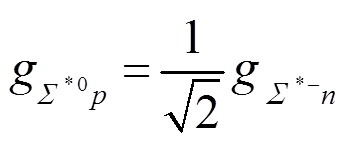 , (74)
, (74)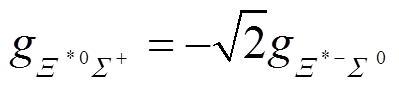 。 (75)
。 (75)
对于味道a=8,
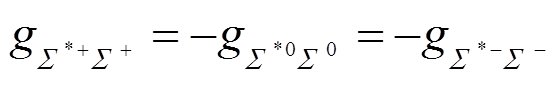 , (76)
, (76)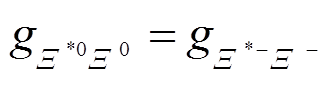 。 (77)
。 (77)
这些同位旋对称性关系在每一阶计算中都得到了验证。
本文采用重重子手征微扰论理论, 考虑手征质量破缺项、圈图顶角修正、波函数重整化效应和 O(p2)阶拉氏量贡献的轴矢流插入的圈图, 逐阶计算重子十重态与八重态跃迁轴矢流, 并给出到 O(p3)阶的理论表达式。我们尝试确定次领头阶重子十重态和八重态拉氏量涉及的低能耦合常数, 但由于低能耦合常数过多, 目前很难完全确定它们的值, 所以没有计算 O(p3)阶圈图贡献的数值部分。我们采用夸克模型和实验值确定手征质量破缺项的低能耦合常数, 数值结果计算到 O(p2)阶, 并给出理论预言, 数值结果的手征收敛性较好。计算过程中, 同位旋对称性关系得到验证。研究核子及其多重态通常需要考虑重子十重态与八重态的轴矢耦合, 本文工作或许能推动重子十重态、八重态以及原子核物理相关实验和理论的进展。
参考文献
[1]Weinberg S. Phenomenological lagrangians.Physica A, 1979, 96: 327–340
[2]Gasser J, Leutwyler H.Chiral perturbation theory to one loop. Annals of Physics, 1984, 158(1): 142–210
[3]Gasser J, Leutwyler H.Chiral perturbation theory: expansions in the mass of the strange quark. Nuclear Physics B, 1985, 250: 465–516
[4]Weinberg S.Nuclear forces from chiral Lagrangians. Physics Letters B, 1990, 251(2):288–292
[5]Weinberg S. Effective chiral lagrangians for nucleon-pion interactions and nuclear forces. Nuclear Physics B, 1991, 363(1): 3–18
[6]Jenkins E, Manohar A V. Baryon chiral perturbation theory using a heavy fermion Lagrangian. Physics Letters B, 1991, 255(4): 558–562
[7]Bijnens J, Wise M B. On the validity of chiral per-turbation theory for weak hyperon decays. Nuclear Physics B, 1985, 261: 185–198
[8]Jenkins E, Manohar A V.Chiral corrections to the baryon axial currents. Physics Letters B, 1991, 259 (3): 353–358
[9]Zhu S L, Puglia S, Ramsey-Musolf M J. Recoil order chiral corrections to baryon octet axial currents. Phys Rev D, 2001: doi: 10.1103/PhysRevD.63.034002
[10]Zhu S L, Sacco G, Ramsey-Musolf M J, et al. Recoil order chiral corrections to baryon octet axial currents and large Nc QCD. Physical Review D, 2002: doi: 10.1103/PhysRevD.66.034021
[11]Ledwig T, Martin C T, Geng L S, et al. Octet-baryon axial-vector charges and SU(3)-breaking effects in the semileptonic hyperon decays. Physical Review D, 2014: doi: 10.1103/PhysRevD.90.054502
[12]Buchmann A J, Hernandez E. Electromagnetic pro-perties of the Δ(1232). Physical Review C, 1997: doi: 10.1103/PhysRevC.55.448
[13]Procura M. Chiral symmetry and the axial nucleon to Δ(1232) transition form factors. Physical Review D, 2008: doi: 10.1103/PhysRevD.78.094021
[14]Aliev T, Azizi K, Ozpineci A. Light cone QCD sum rules analysis of the axial transition form factors. Nucl Phys A, 2008, 799: 105–126
[15]Alexandrou C, Gregory Eric B, Korzec T, et al. Δ(1232) axial charge and form factors from lattice QCD. Physical Review Letters, 2011, 107: 14–30
[16]Kucukarslan A, Ozdem U, Ozpineci A. Isovector axial vector form factors of octet–decuplet hyperon transi-tion in QCD. Journal of Physics G, 2015, 42(1): 1–21
[17]Patrignani C, Agashe K, Aielli G, et al. Review of particle physics. Chin Phys C, 2016, 40: 100001
[18]Keller D. Branching ratio of the electromagnetic de-cay of the Σ+(1385). PRD, 2012, 85(5): doi: 10.1103/ PhysRevLett.107.141601
[19]Savage M J. Strong and electromagnetic decays of the baryon decuplet. Nuclear Physics B, 1993, 399(1): 69–85
Loop Corrections to the Decuplet-Octet Baryon Transition Axial Charges
Abstract The authors calulate chiral corrections to the decuplet-octet baryon transition axial charges through O(p3) using heavy baryon chiral perturbation theory(HBCPT).Theoretical predictions are presented.Chiral symmetry breaking, vertex correctiongs, wavefunction renormalization are included.The contributions from both the intermediate decuplet and octet baryon states are taken into account in the loops. The results show reasonably good convergence of the chiral expansion and agreement with the known experimental data.
Key words axial charge; HBCPT; decuplet baryon; octet baryon
doi: 10.13209/j.0479-8023.2019.027
收稿日期: 2018–04–11;
修回日期: 2018–05–07;
网络出版日期: 2019–05–13