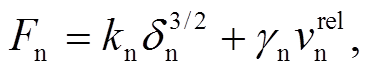
摘要 采用离散单元法(discrete element method, DEM)和实验方法, 研究用螺旋钻具钻取月壤的过程中, 月壤内部大颗粒位置和构型对钻进力载特性的影响。通过 DEM 方法和实验方法研究结果的对比分析, 明确了 DEM 方法在钻取动力学中的局限性及有效性, 发现钻进过程中碰到大颗粒时的典型力载特征及影响大颗粒有效拨开的关键因素是表面形态。
关键词 DEM 方法; 月壤; 钻取; 大颗粒; 钻进力载
目前, 国际上掀起一股深空探测热, 中国也制定了探月“三步走”计划。探月三期计划的主要任务是实现月面样品采样返回, 其中钻取采样是实现月壤样品采集的方式之一。月面钻取采样是采用中空螺旋钻具钻入月面, 实现对中心的月壤取样。月面采样对象的特性对采样任务影响很大, 特别是钻具碰到大颗粒时会产生很大的力载变化, 严重时可能导致钻进压力和扭矩超过系统驱动能力; 另外, 无法拨开的大颗粒堵住进样通道, 导致中心的月壤无法进入钻具, 从而无法取样。美国和前苏联钻取月壤的实践表明, 取样结果并不是随深度连续的[1], 钻进过程中遇到大颗粒是造成非连续效果的重要原因。
国际上对月壤钻取动力学的研究方法包括有限元法、离散单元法(discrete element method, DEM)及实验方法。庞彧等[2]采用有限元模型对钻具钻进月壤的过程进行仿真分析, 他们假设月壤为弹塑性材料, 塑性屈服准则采用土力学中的Drucker-Prager 模型, 得到钻压力以及扭矩呈周期性变化的结论。Quan 等[3–4]基于有限元, 系统地研究了钻头附近土壤的准静态应力分布。有限元方法没有描述月壤类材料钻取过程中的流变力学性质, 因此无法准确地把握月壤钻进力载的特性。Wei 等[5]、候绪研等[6]及谢宇明等[7]采用 DEM 方法对钻取过程做了仿真研究。虽然各研究团队 DEM 仿真中的颗粒接触模型不完全相同, 但得到的钻压以及扭矩均随钻进深度的增加而增加, 并深入研究了相关力载与钻杆螺距、转速的关系, 但 DEM 方法仿真结果均未与实验结果进行对比。事实上, 实验得到的力载值与DEM 仿真结果相差很大。Mellor[8]基于实验结果, 将螺旋排粉过程等效为一个质点沿粗糙斜面的运动,进而对钻杆螺旋通道内颗粒碎屑的动力学行为进行分析。Zhang 等[9]对 Mellor 模型做了修正, 在实验基础上分析螺旋排粉的力学性能参数。田野等[10]、刘飞等[11]和 Tang 等[12]在地面进行实验, 归纳分析了钻具构型对螺旋钻取性能的影响。实验方法能真实地展示月壤钻取动力学的力载规律, 但缺失内部细节, 其分析模型常建立在很多假设的基础上。综上所述, 单一的有限元法、DEM 方法及实验方法开展月壤钻取动力学分析均有较大的缺点。
月壤中存在大颗粒时比均质月壤的钻取动力学过程更复杂。目前, 仅刘天喜等[13]采用 DEM 方法对月壤中大颗粒运行轨迹及其对采样的影响做了研究, 但未进行力载特性分析及实验验证。作为月壤钻取过程中可能存在的大风险工况, 大颗粒工况对月壤钻取过程有较大的影响。
本文围绕大颗粒构型及方位等因素, 采用 DEM方法与实验方法研究钻取过程。结合两者优势, 围绕工程关注焦点, 系统地分析月壤中大颗粒对钻进力载的影响及可有效拨开的关键因素。
因 DEM 方法可以描述颗粒材料的动力学性质, 所以本文采用三维离散元软件 EDEM 对月壤钻取过程进行仿真。图 1 为模型的示意图, 整个系统包括钻具、大颗粒、均质月壤细颗粒及月壤桶。盛放颗粒的月壤桶采用底面直径为 100mm, 高为 250mm 的圆柱。均质月壤细颗粒的几何参数和材料参数如表 1 所示。
颗粒之间接触作用的描述采用如下的 Hertz-Mindlin 接触模型。在法向和切向作用中均考虑了阻尼, 同时, 切向还需考虑 Coulomb 摩擦作用。
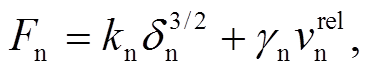
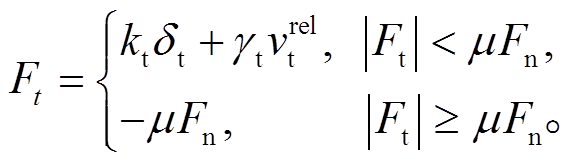
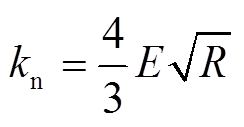 为法向刚度,
为法向刚度,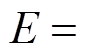
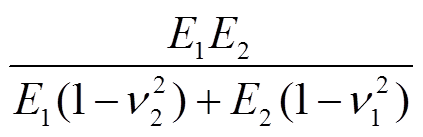 为有效杨氏模型,
为有效杨氏模型, 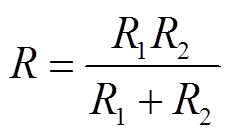 为有效半径;
为有效半径; 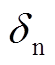 为法向嵌入量;
为法向嵌入量; 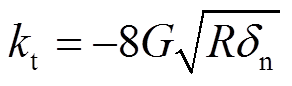 为切向刚度;
为切向刚度; 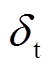 为切向位移;
为切向位移; 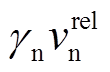 和
和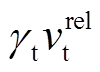 分别为法向和切向阻尼力;
分别为法向和切向阻尼力; 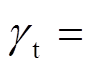
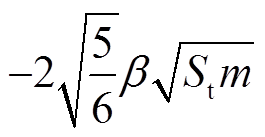 和
和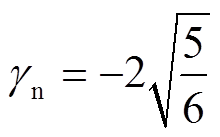
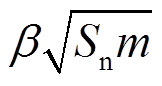 分别为法向和切向阻尼系数,
分别为法向和切向阻尼系数, 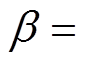
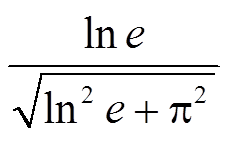 ,
, 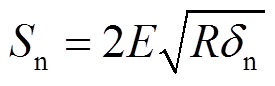 ,
, 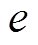 为恢复系数,
为恢复系数, 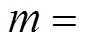
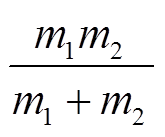 为有效质量。
为有效质量。
模型中还考虑了颗粒之间滚动摩阻的作用, 该滚动摩阻用施加在颗粒表面的力矩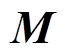 表示:
表示:
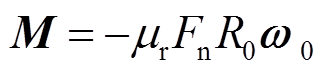 ,
,
其中,  为颗粒间滚动摩阻系数,
为颗粒间滚动摩阻系数, 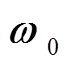 为单位相对角速度。时间步长采用半径最小颗粒瑞利时间步长的 20%, 其中瑞利时间步长
为单位相对角速度。时间步长采用半径最小颗粒瑞利时间步长的 20%, 其中瑞利时间步长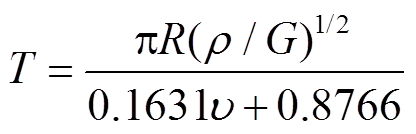 ,
, 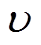 为颗粒材料的泊松比。Paulick 等[14]和 Silbert 等[15]认为, 剪切模量对散体介质行为的影响较弱。为提高计算速度, 剪切模量取值小于实际颗粒的剪切模量, 为1 MPa。
为颗粒材料的泊松比。Paulick 等[14]和 Silbert 等[15]认为, 剪切模量对散体介质行为的影响较弱。为提高计算速度, 剪切模量取值小于实际颗粒的剪切模量, 为1 MPa。
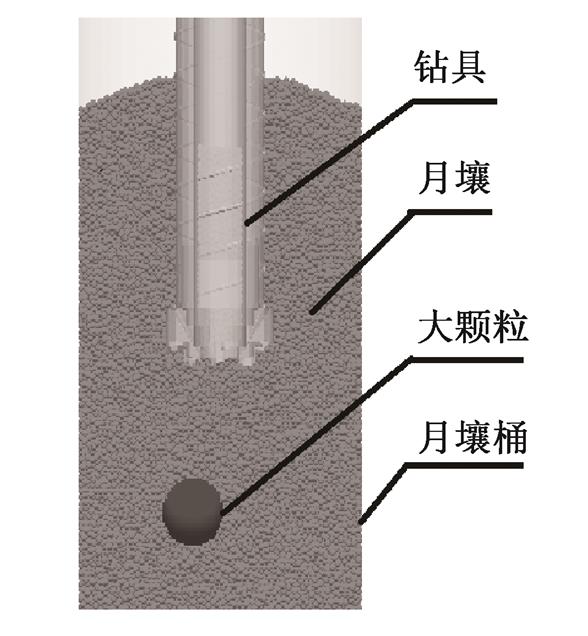
图1 钻具钻取大颗粒过程模型示意图
Fig. 1 Sketch of the model during drilling into large granular rocks
表1 DEM模型颗粒的几何参数和材料参数
Table 1 Geometric and material parameters of particles in DEM model

数量半径/mm密实度密度/(kg·m–3)泊松比剪切模量/Pa 26463010.6125000.31×106
实际月壤颗粒的粒径远小于 1mm, 单个颗粒非圆形, 颗粒之间接触过程也比较复杂。若采用实际尺度, 计算量会大大增加, 以至无法计算。所以, 本方法结果无法直接得到大颗粒对钻进力载影响的量化结果, 但相关结果可用于对钻进力载特性趋势的分析, 结合实验结果, 可以分析大颗粒状态下的力载特性。
本文仿真采用的钻头直径为 35mm, 大颗粒直径为 20mm; 设置钻具中心轴与大颗粒中心轴的距离分别为0, 7, 9, 11, 13, 15 和 19mm; 钻进参数采取回转 1000rpm–进尺 6000mm/min, 保证 DEM 仿真能正常钻进取样且快速计算参数。钻具钻取月壤的力载由钻头力载和钻杆力载两部分叠加而成。钻具受到的总的钻压力和扭矩也由两部分的钻压力和扭矩分别合成。在月壤钻取过程中, 钻头和钻杆两部分所起的作用不同, 所以分解后的钻头和钻杆力载变化规律能够反映大颗粒被拨动过程中的内在规律。
图 2 表示直径为 20mm 的大颗粒处于不同位置时的钻压力变化规律。可以看出, 钻头和钻杆上的压力变化规律存在明显的差异: 1)钻头上的压力随着深度的增加而单调增加, 钻杆上压力随着钻进深度的增加单调减小; 2)钻杆上的压力对大颗粒与钻具中心初始位置的距离不敏感, 而钻头上的压力变化曲线出现了分叉。
钻头钻压力随着钻进深度的增加越来越大, 可以解释如下: 随着钻进深度的增加, 钻头下方月壤受到的静水压力越大, 钻头需要将月壤和大颗粒挤开的力也越大, 该部分力是钻头钻压力的主要贡献部分。对钻杆来说, 随着钻进深度的增加, 钻杆受到的摩擦力越来越大, 由于螺纹的自攻效应, 回转扭矩转化为钻进力, 因此钻进深度越大, 钻杆上压力越小。钻头下方大颗粒与钻具中心轴线的距离对钻杆压力影响很小, 原因如下: 颗粒沿着钻头径向发生的偏移, 不会影响钻杆的排粉量, 因此不对钻进压力产生影响。钻头下方的大颗粒会阻碍钻头向下运动, 其位置会显著地影响钻头上的钻压力。大颗粒初始径向偏移距离≤7mm 时, 颗粒被钻头向中心拨动, 后续大颗粒一直堵在钻头下方, 钻压力上升很快; 当大颗粒初始径向偏移距离>7mm 时, 大颗粒被钻头向外挤, 很容易被拨开, 钻压力也基本上随着深度而线性增加。因此, 径向偏移 7mm 位置应为分叉点。因为钻头直径为 35mm, 所以该分叉点位于该钻头直径的 1/5 处。
图 3 表示直径为 20mm 的大颗粒处于不同位置和深度时的扭矩变化规律。钻杆上的扭矩与大颗粒的初始径向偏移距离无关, 但随着钻进深度的增加而增大。钻头上的扭矩也随着深度的增加而越来越大。由于 DEM 模型中均选择球形颗粒, 且模拟的月壤无法达到实际月壤的密实度, 因此钻头处扭矩出现较多毛刺状波动, 而钻杆扭矩不受大颗粒影响, 不同工况下重合度较好。
图 4 表示直径为 20mm 的大颗粒处于不同位置和不同深度时钻具上钻压力和扭矩的变化规律。从图 4(a)可以看出, 钻具上钻压力的变化规律基本上由钻头上钻压力的变化规律决定。从图 4(b)可以看出, 大颗粒对钻进过程的扭矩无明显的影响。
为准确地验证大颗粒对钻进力载特性的影响, 本实验在模拟月壤制备过程中定点设置大颗粒。制备完成后, 通过控制钻具位置实施定位钻取。通过验证可知, 以上方法在无大颗粒的条件下轴心位置偏差为 5mm。实验方法如下: 1)将模拟月壤巩筑至准备设置颗粒的高度, 其中模拟月壤相对密实度为100%; 2)采用模板确定设置颗粒的位置(图 5(a)); 3)在准备预设颗粒的位置挖孔, 按预定位置将颗粒放置孔内并压实(图 5(b)); 4)在上方继续装配模拟月壤桶, 并将模拟月壤制备至预设高度; 5)模拟月壤制备完成后, 转移至钻取实验台, 并采用模板确定钻孔位置及月壤桶姿态, 控制钻具按照事先确定的位置回转 120rpm, 加载 130mm/min 钻进(图 5(c)), 其中采用的钻头直径为 35mm; 为保证系统安全, 当钻进拉力超过 400N 时, 钻进加载停止, 回转不停止; 力载下降后再继续以正常钻进参数向下钻进。实验系统同时测量钻具整体受到的扭矩以及向下加载实施的拉力(对应钻具的钻压力)。
采用不同颗粒, 以不同姿态和位置放置于钻头正下方, 以验证颗粒构型和放置位置对钻进力载的影响。

图2 大颗粒在不同位置时钻头和钻杆的压力
Fig. 2 Pressure of drill bit and drill pipe with large particles at different positions
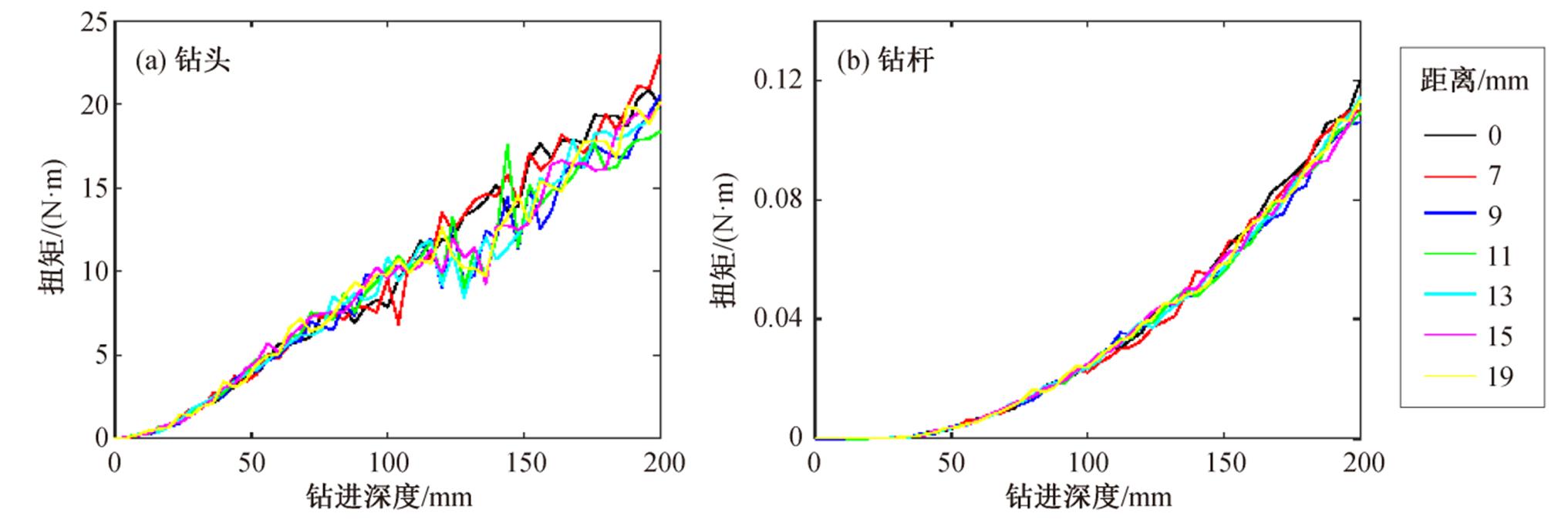
图3 大颗粒在不同位置时钻头和钻杆的扭矩
Fig. 3 Torque of drill bit and drill pipe with large particles at different positions

图4 大颗粒在不同位置时钻具的压力和扭矩
Fig. 4 Pressure and torque of the drill with large particles at different positions
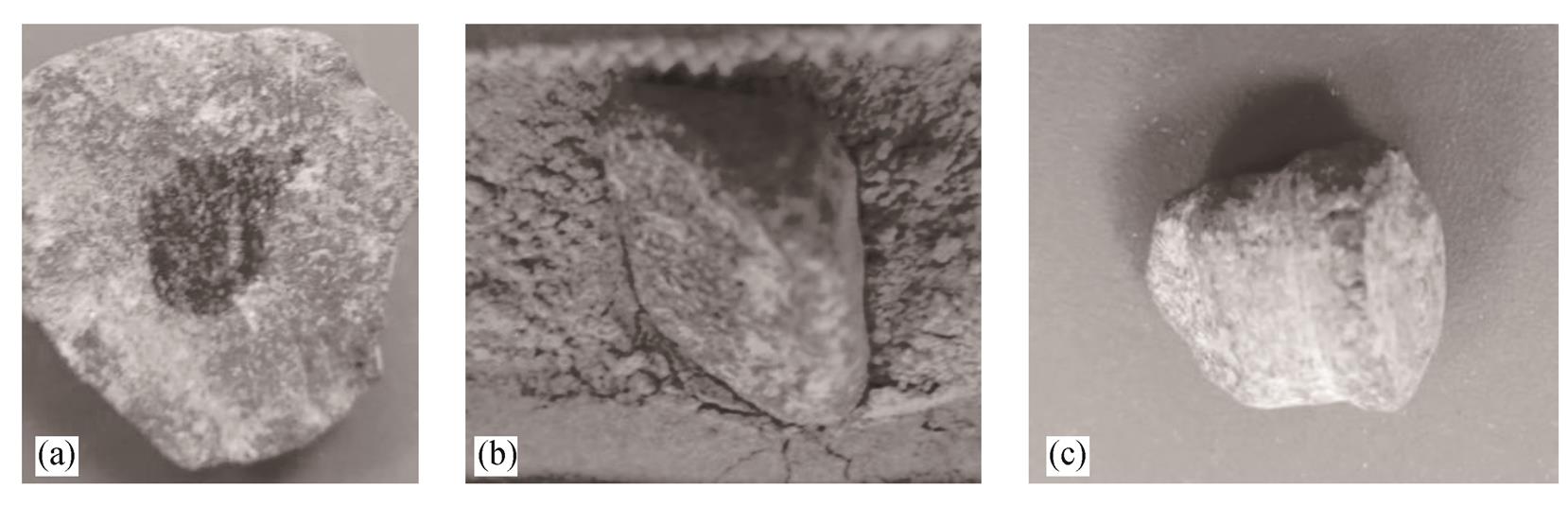
第一钻实验将 3 个颗粒放在同一钻的不同深度。颗粒均采用大块新鲜玄武岩经机械破碎得到, 表面粗糙(图 6)。第一颗尺寸为 36mm×26mm×29mm 的较圆颗粒, 放置于钻头正下方 0.88m 处; 第二颗尺寸为 42mm×42mm×30mm 的较圆颗粒, 轴心偏移 15mm 放置在 1150mm 处; 第三颗尺寸为 52mm×21mm×31mm 的大斜面颗粒, 以与水平面 75°的夹角放置在 1460mm 深度。

(a)模板与月壤桶定位; (b)颗粒定位填入; (c)钻取实验
图5 在模拟月壤制备过程中大颗粒定点设置及定点钻进实验设置
Fig. 5 Fixed-point setting and drilling experiments of large particles in the preparation of simulated lunar soil

(a)第一个颗粒; (b)第二个颗粒; (c)第三个颗粒
图6 第一钻实验中设置的颗粒
Fig. 6 Particles set in the first drilling test
图 7 为第一钻实验得到的力载曲线。可以看到, 在没有碰到大颗粒的情况下, 钻进拉力均值在 100~ 200N 之间, 回转扭矩均值在 6~10N·m。当碰到大颗粒时, 拉力和扭矩均会上升。第一个颗粒钻压升幅为 60N, 扭矩升幅为 2N·m, 该颗粒也被轻松地拨开, 钻进过程中未触发拉力保护停加载。第二和第三个颗粒均触发拉力 400N 保护, 增幅为 150N; 扭矩达到 14N·m, 增幅约为 5N·m。从图 7(a)中力载随时间变化的曲线可以看出, 扭矩的峰值超前拉力峰值 3~5s。图7(b)可以看出, 碰到大颗粒后, 力载上升的峰值区间为 30~60mm, 等于 1~2 倍的大颗粒直径。本钻实验 3 个颗粒中两颗为球形, 一颗为斜长形, 颗粒中有被放置于正中心的, 也有被放置于偏移位置的。实验结果显示, 以上颗粒均被正常拨开, 重复实验后, 颗粒同样被拨开。以上结果说明, 大颗粒被拨开的概率与颗粒姿态及位置非强相关。
第二钻实验用于验证颗粒局部形态对钻取的影响。将一颗表面较平整的颗粒置于钻具正下方, 颗粒形态如图 8 所示。本钻预设的颗粒尺寸为 36mm× 28mm×24mm, 为钝形颗粒, 放置于钻头正下方0.88m深度的位置。
图 9 为第二钻实验的力载曲线。与第一钻实验类似, 钻进拉力均值在 100~200N 之间, 回转扭矩均值在 6~10N·m 之间。碰到表面平整的大颗粒时, 扭矩均无明显上升, 但拉力迅速上升, 即使采用停加载, 再次启动后拉力仍然迅速上升。从图 8 中钻取后大颗粒的状态可以看出, 该大颗粒未被拨开, 部分被切碎进入取样区域, 部分被卡在钻头进样通道处, 阻止后续进样。从图 9 可以看出, 当大颗粒堵在钻头下方无法拨开时, 力载峰值区域对应的区间小于 30mm, 对应值为小于 1 个大颗粒直径。造成以上现象的原因如下: 面向表面平整的大颗粒, 钻具向下钻进过程中对大颗粒施加了较大的压力, 但扭矩较小, 不能产生足够大的侧向力来克服颗粒向外侧运移的阻力, 因此无法拨开。在其他实验中发生大颗粒被切碎现象时, 取出钻取后卡在钻头部位的颗粒进行分析, 发现大颗粒表面多为表面平整状态。
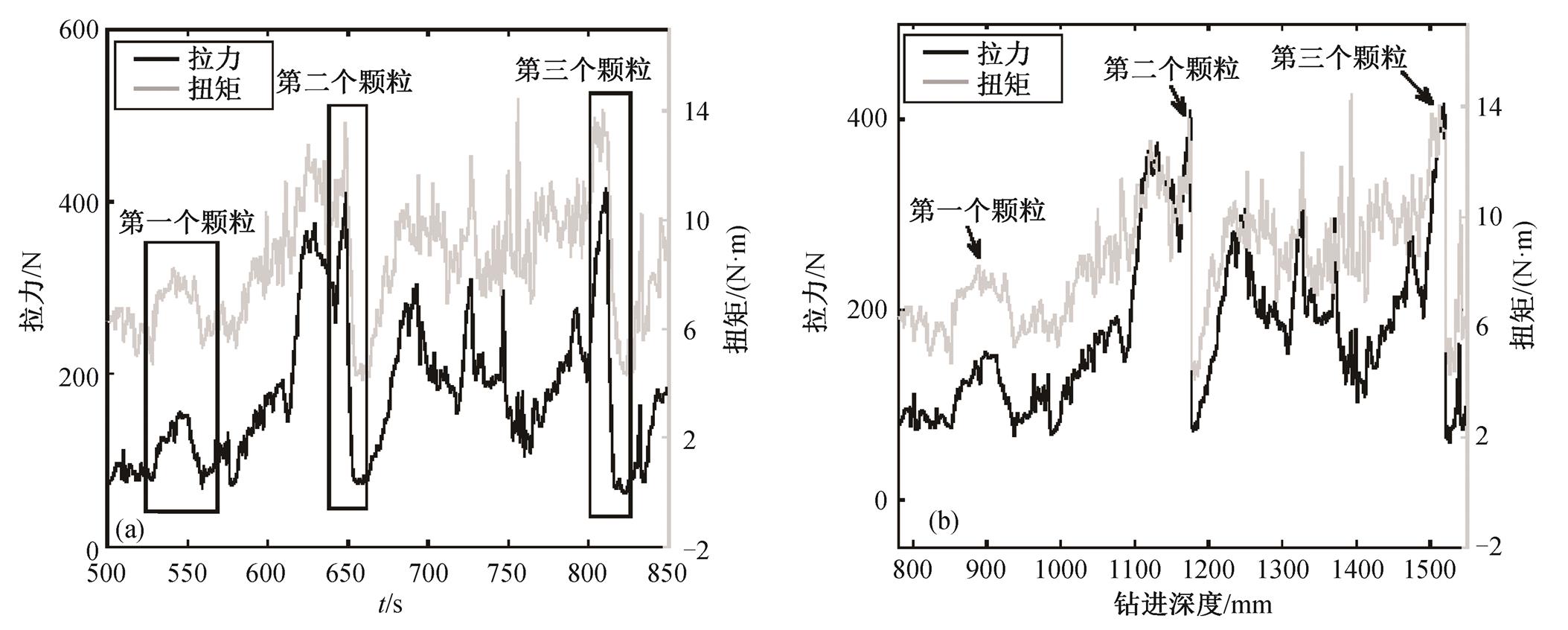
图7 第一钻实验力载随时间和钻进深度的变化
Fig. 7 Change of load with time and drilling depth in the first drilling test
(a)钻取前形态; (b)钻取后颗粒处于样品中部分; (c)钻取后颗粒卡在钻头处部分
图8 第二钻实验预设颗粒及钻取后形态
Fig. 8 Presupposed particles and post-drilling shape in the second drilling test

图9 第二钻实验力载随时间和钻进深度的变化
Fig. 9 Change of load with time and drilling depth in the second drilling test
DEM 仿真和实验得到拉力和扭矩的对比见表2。可以看到, 虽然 DEM 仿真中采用的钻进深度远比实验中大, 但 DEM 方法的计算结果明显远小于实验值。并且, 从图 4 可以看出, DEM 方法得到的扭矩随钻进深度的增加呈线性增加, 但图 7 中当钻进深度从 0.8m 变化到 1.5m 时, 平均扭矩从 6N·m 变化到9 N·m。
表2 DEM方法与实验力载的均值对比
Table 2 Comparison of mean values of DEM method and experimental load

物理量拉力/ N扭矩/(N·m) DEM仿真值2~40.1~0.35 实验值100~2006~10
造成以上差异的原因可能是: 1)DEM 仿真过程中, 虽然对颗粒采用施加预载荷方法进行压实, 但在目前允许的计算量约束下, 颗粒刚度可选择范围小, 且球形颗粒的自锁效应差, 因此无法达到实际的密实度, 导致 DEM 仿真结果相当于松散模拟月壤钻取结果; 2)受计算能力限制, 颗粒均选择半径为 1mm 的颗粒, 实际模拟月壤颗粒的粒径主要在 0.1mm 以下, 且形状复杂, 因此会造成月壤流变性质不一致。
虽然 DEM 仿真结果与实验结果差异很大, 但借用 DEM 仿真结果, 将钻具力载分解到钻头和钻杆上, 可以得到钻头切削导致的拉力约 200N, 对应钻头切削月壤导致的扭矩为 4~5 N·m。
对比图 2(a)、图 4(a)和图 7(b)可以发现, 当钻进到颗粒位置时, 拉力均出现明显波动; 当颗粒被有效地拨开后, 拉力恢复到正常值。对比图 2(a)、图 4(a)和图 7(b)和图 9(a)可以发现, 当颗粒无法拨开时, 拉力上升幅度比有效拨开时大, 上升速度也快。DEM 方法和实验均可得到以上规律。
对比图 2(b)、图 3(b)、图 4(b)和图 7~9 可以发现, DEM 仿真结果和实验结果的扭矩变化规律不一致。DEM 仿真中大颗粒对钻具扭矩没有明显影响, 而实验结果中大颗粒会导致钻具扭矩显著增加。这是由于DEM 仿真只能模拟松散月壤工况。同时, 大颗粒导致钻具扭矩显著增加, 也说明钻进过程中钻头力载是钻具力载的主要部分。
DEM 仿真结果表明, 颗粒能否被有效地拨开的分叉点位于钻头直径的 1/5 距离处, 但实验结果未观察到此现象。原因主要是 DEM 仿真中, 大颗粒均以球形表示, 钻头无法有效带动球运动, 此过程中离心力不起主要作用, 当球的位置偏离钻头直径的 1/5 时, 钻头对球的作用方向由内转向外; 但是, 实际的大颗粒表面不平整, 钻头能有效地带动颗粒转动, 大颗粒在离心力的作用下更容易被拨开; 当大颗粒表面平整, 钻头无法有效地带动时, 不容易被拨开, 从而堵住钻头。
本文采用 DEM 仿真和实验方法, 研究大颗粒对钻进力载的影响, 得到如下结论。
1)DEM 方法仿真结果与实验结果在力载量值上有较大差异, 但得到的力载在钻具内部分配关系以及大颗粒对钻进力载的影响趋势与实验结果相符合, 具有较大的借鉴作用。
2)钻具受到的拉力和扭矩主要由钻头贡献, 堵钻过程中钻具拉力和扭矩均会迅速增加。
3)表面棱角较多的大颗粒在钻具下的方位与堵钻概率的相关性不大。
4)大颗粒表面形态对堵钻有较大影响, 特别是表面平整的大颗粒, 在偏置距离较小时, 不容易被钻头拨动, 容易造成堵钻。
通过 DEM 仿真和实验方法的结果对比分析, 首次明确 DEM 方法在钻取动力学中的局限性, 但基于 DEM 方法得到的力载规律, 可在一定程度上指导人们对实验结果加深认识。同时发现, 钻进过程中碰到大颗粒时快速上升的力载特征及颗粒表面形态是影响大颗粒被有效拨开的关键因素。此研究结果可有效地支撑我国的深空探测任务。
参考文献
[1]鄢泰宁, 冉恒谦, 段新胜. 宇宙探索与钻探技术. 探矿工程(岩土钻掘工程), 2010, 37(1): 3–7
[2]庞彧, 邓湘金, 郑燕红. 面对月壤采集的自动钻取机构设计. 深空探测研究, 2011, 9(4): 22–28
[3]Quan Q, Tang J, Yuan F, et al. Drilling load modeling and validation based on the filling rate of auger flute in planetary sampling. Chinese Journal of Aeronau-tics, 2017, 30(1): 434–446
[4]Quan Q, Chen C, Deng Z, et al. Recovery rate predic-tion in lunar regolith simulant drilling. Acta Astro-nautica, 2017, 133: 121–127
[5]Wei Cheng, Wang Hongliu, Liu Tianxi. Mechanical model of hollow-external-screw drill rod for lunar soil particle vertical conveying // IEEE International Conference on Control and Automation. Hangzhou, 2013: 1240–1245
[6]侯绪研, 崔金生, 赵德明, 等. 基于离散元法的月面取样技术对月壤样品层理信息影响的分析//中国宇航学会深空探测技术专业委员会第八届学术年会. 上海, 2011: 568–577
[7]谢宇明, 卿启湘, 汤钦卿. 月壤的钻取采样离散元动态行为研究. 工程设计学报, 2013, 20(6): 476–481
[8]Mellor M. Mechanics of cutting and boring: part 7, dynamics and energetics of axial rotation machines. Hanover: US Army Cold Regions Research and Engi-neering, 1981
[9]Zhang T, Ding X. Drilling forces model for lunar regolith exploration and experimental validation. Acta Astronautica, 2017, 131: 190–203
[10]田野, 邓宗全, 唐德威, 等. 月壤钻探采样装置中的钻杆结构参数优化设计及模拟试验. 机械工程学报, 2012, 48(32): 10–15
[11]刘飞, 侯绪研, 全齐全, 等. 空心外螺旋钻杆与月壤相互作用力学模型研究. 机械制造, 2012, 49(11): 29–34
[12]Tang J, Quan Q, Jiang S, et al. A soil flowing charac-teristics monitoring method in planetary drilling and coring verification experiments. Advances in Space Research, 2016, 59(5): 1341–1352
[13]刘天喜, 魏承, 马亮, 等. 大颗粒岩块对月壤钻取过程的影响分析. 岩土工程学报, 2014, 36(11): 2118–2126
[14]Paulick M, Morgeneyer M, Kwade A. Review on the influence of elastic particle properties on DEM simulation results. Powder Technology, 2015, 283: 66–76
[15]Silbert L E, Ertaş D, Grest G S, et al. Granular flow down an inclined plane: Bagnold scaling and rheo-logy. Physical Review E, 2001, 64(5): 051302
Simulation and Experimental Study on the Effect of Large Granular Rocks in Lunar Soil on Drilling Load
Abstract The dynamics of auger drilling into lunar soil with large granular rocks was studied by discrete element method (DEM) simulation and experiment, in which the large granular rocks with different configurations were arranged at different locations. The result of simulation and experiment indicate that the surface morphology is the key factor which controls whether the granular rocks could be removed in drilling process. The result would be an important support for China’s deep space exploration mission.
Key words DEM; lunar soil; auger drilling; large granular rocks; load
doi: 10.13209/j.0479-8023.2019.008
收稿日期: 2018–04–10;
修回日期: 2018–08–08;
网络出版日期: 2019–03–12
国家自然科学基金(11502277, 51475452)资助
†E-mail: py82@163.com
† E-mail: py82@163.com