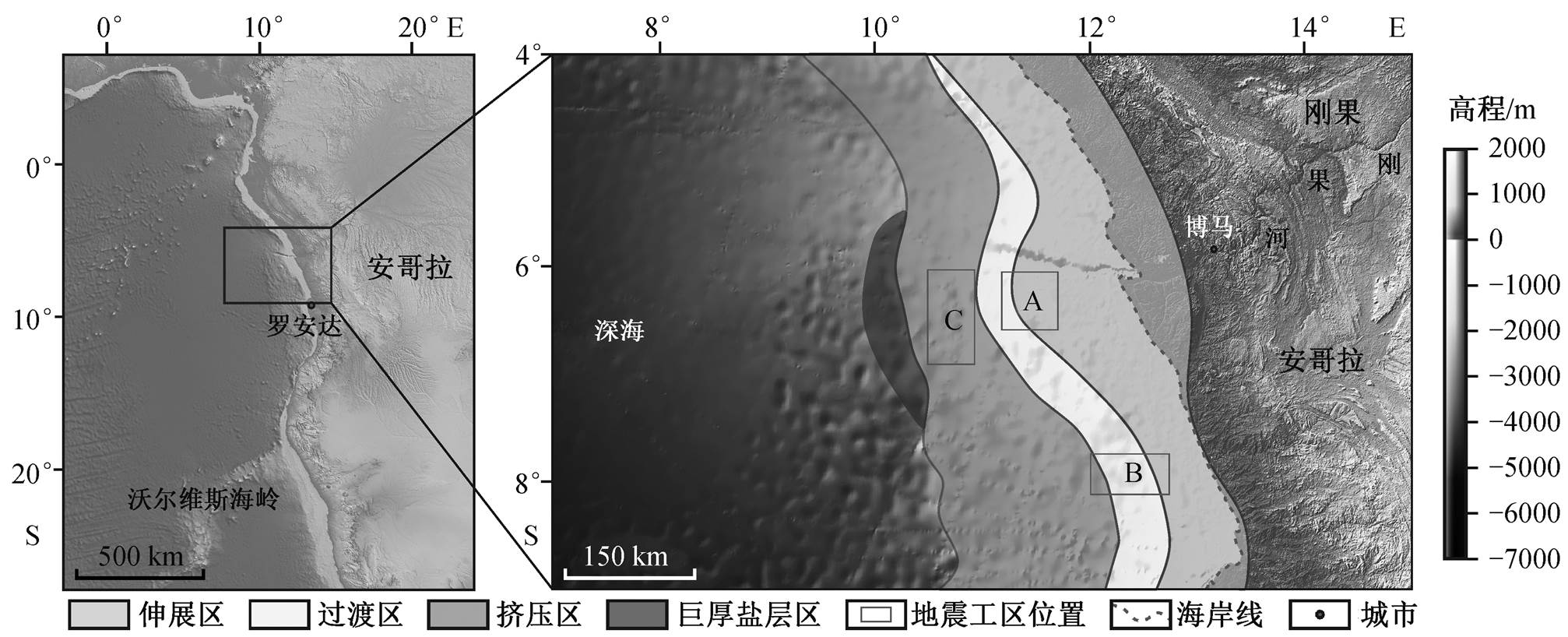
地形数据源自General Bathymetric Chart of the Oceans (https://www.gebco.net)
图1 下刚果盆地盐构造及工区位置分布
Fig. 1 Distribution map of salt structures and work area in Lower Congo Basin
摘要 基于下刚果盆地3个工区的地震数据, 总结盆地内9种典型的盐相关构造样式, 并基于离散元数值模拟方法, 以构造倾斜角度为单一控制变量建立模型, 对比分析盐岩的运动矢量演化。模拟结果表明, 随着构造倾斜角度的增加, 盐岩及其上覆岩层的流动速度逐渐增大, 后续陆源沉积物的搬运距离也越远, 更易形成盐构造; 盐岩流动主要有3种控制机制: 差异压实作用控制、差异压实作用和重力滑脱作用共同控制以及重力滑脱作用控制, 这3种控制作用均受坡度的影响, 随着坡度的改变, 3种控制作用依次出现, 控制着盐构造的形成。在上述分析结果的基础上, 建立被动陆缘盆地构造倾斜角度对盐岩流动的控制模式。
关键词 下刚果盆地; 盐构造; 离散元数值模拟; 构造倾斜角度; 控制模式
下刚果盆地位是非洲和南美洲分离后, 南大西洋开放形成的被动大陆边缘盆地[1]。20世纪70年代以来, 在西非(安哥拉)地区发现一些具有规模性储量的油气田, 其中绝大多数近海油田均与盐构造相关[2]。因此, 加深对盐构造的认识, 对于近一步开展油气勘探及油气成藏研究具有重要意义。下刚果盆地主要经历了4期构造演化: 前裂谷期、裂谷期、过渡期和漂移期[3–4], 属于过渡期(124.5~112 Ma)的阿普特阶发育厚层蒸发岩从陆向海厚度逐渐增大[5]。在大陆边缘形成的早期, 薄陆壳和年轻洋壳迅速冷却, 密度增大, 下沉, 整个大陆边缘形成向海方向的基底倾斜[6–8]。因此, 重力滑脱作用在盐构造形成过程中占据主导地位, 但对于构造坡度对盐岩流动形成盐构造的控制作用, 尚无明确的认识。本文针对下刚果盆地的3个地震工区(分别位于盆地的伸展区(A工区)、过渡区(B工区)和挤压区(C工区))(图1), 总结盆地盐构造样式。
对比南大西洋两岸盆地剖面可以发现, 位于南美板块的圣埃斯皮里图盆地和桑托斯盆地(图2(a)和(b))的大陆斜坡倾斜角度比位于非洲板块的宽扎盆地和下刚果盆地(图2(c)和(d))大, 两岸盆地的盐岩分布也有明显的差异。圣埃斯皮里图盆地和桑托斯盆地的盐构造比较单一, 在其斜坡位置, 盐岩基本上消失, 在坡下形成巨厚的盐墙。在宽扎盆地和下刚果盆地的斜坡位置有少量盐岩滞留, 靠近坡下位置多为刺穿型株状盐底辟构造, 深海部位为巨厚盐墙。可见, 盆地构造的倾斜角度影响盐构造的形成与分布。本文结合以上资料及认识, 基于离散元数值模拟方法, 针对构造倾斜角度开展盐岩的运动学对比分析, 明确其对盆地内盐岩流动的控制作用, 进而探讨盆地内形成典型盐构造样式的原因。
受盐岩流动影响, 盐岩及其上覆沉积层在不同的区带发生有规律的构造变形, 变形样式也表现出明显的构造分区特征。南大西洋被动陆缘含盐盆地从陆向海方向可划分为3个区带: 伸展区、过渡区和挤压区。从伸展区到挤压区, 盐构造的成熟度逐渐增大。前人对下刚果[9]、圣埃斯皮里图[10]、桑托斯和坎波斯[11]等盆地依此进行了区带划分。
伸展区最常见的盐构造样式为铲式生长断层、盐滚和盐筏[11–12]。由于向海方向基底斜坡的存在, 盐岩向海流动, 随着时间的推移, 坡上位置盐岩逐渐减薄, 甚至消失, 在靠近坡下位置盐岩规模性地聚集而形成这些盐构造样式。
A工区位于盆地构造倾斜的坡上位置, 剖面可见明显的地层反射界面和盐岩边界, 表现为伸展型构造特征。受盐岩流失的改造作用, 越靠近盐岩的地层, 构造变形越明显。例如, 渐新统沉积以来的地层构造变形较小, 断层少; 与阿普特阶盐岩相邻的地层, 受盐岩流动影响, 存在较大的形变以及多处断裂(图3(a2))。
过渡区(B工区)的盐株构造主要发育在盆地斜坡坡脚较平缓的部位。盐株属于后期刺穿型盐构造, 盐岩层顶界至中新统顶界表现为地堑构造, 断层呈对称型, 在靠近盐构造位置上超至盐株构造两翼。由于盐岩受到的伸展应力作用减小, 流动能力变弱, 造成深部老底辟构造的加宽早于上部年轻底辟构造, 故底辟构造呈现下宽上窄的变形样式[7](图3(b2))。
蘑菇状底辟构造由单个盐株构造发育而成, 与盐株构造相比, 蘑菇状底辟构造几乎完全刺穿整个盐上沉积层(图3(c2))。随着底辟构造的形成, 两翼围岩地层越靠近盐岩层的层位, 上倾的角度越大, 其形态受底辟构造的影响也越大[13]。
挤压区(C工区)受到强烈的构造挤压, 形成的盐构造包括盐席构造、迷你盆地和大型逆冲断层等, 均属于严重形变的构造样式。其中, 受构造环境影响, 大型的逆冲断裂在全工区, 甚至全层位(盐上层位)发育, 盐岩集中在渐新统及其上地层, 且对渐新统之上的地层造成极大的破坏(图4(a2))。
盆地的盐席构造在平面上表现为大规模侵入上覆地层, 与原盐岩层位以逆冲断层相连接, 盐席构造失去原位盐岩层的盐岩供给, 受区域构造应力影响, 呈舌状不对称地分布, 有向盆地内运动的趋势。在靠近盐席构造根部的位置, 围岩地层的形变受其影响较大(图4(b2))。
早在1933年, Barton[14]就将迷你盆地的概念应用到盐撤凹陷构造的说明中, 并对其应用准则做了解释。在下刚果盆地的地震剖面上可见渐新统的顶和底被两个大型的底辟构造截断, 两界面有明显的下凹特征(图4(c2))。
1979年, Cundall等[15]基于离散粒子间相互作用的理论提出离散元法(discrete element method, DEM)。该方法应用于脆性变形模拟和摩擦滑动的材料分析, 在断裂模拟方面也取得显著的成果, 研究者对其模拟的基本原理已有充分的认识[16-19]。

地形数据源自General Bathymetric Chart of the Oceans (https://www.gebco.net)
图1 下刚果盆地盐构造及工区位置分布
Fig. 1 Distribution map of salt structures and work area in Lower Congo Basin
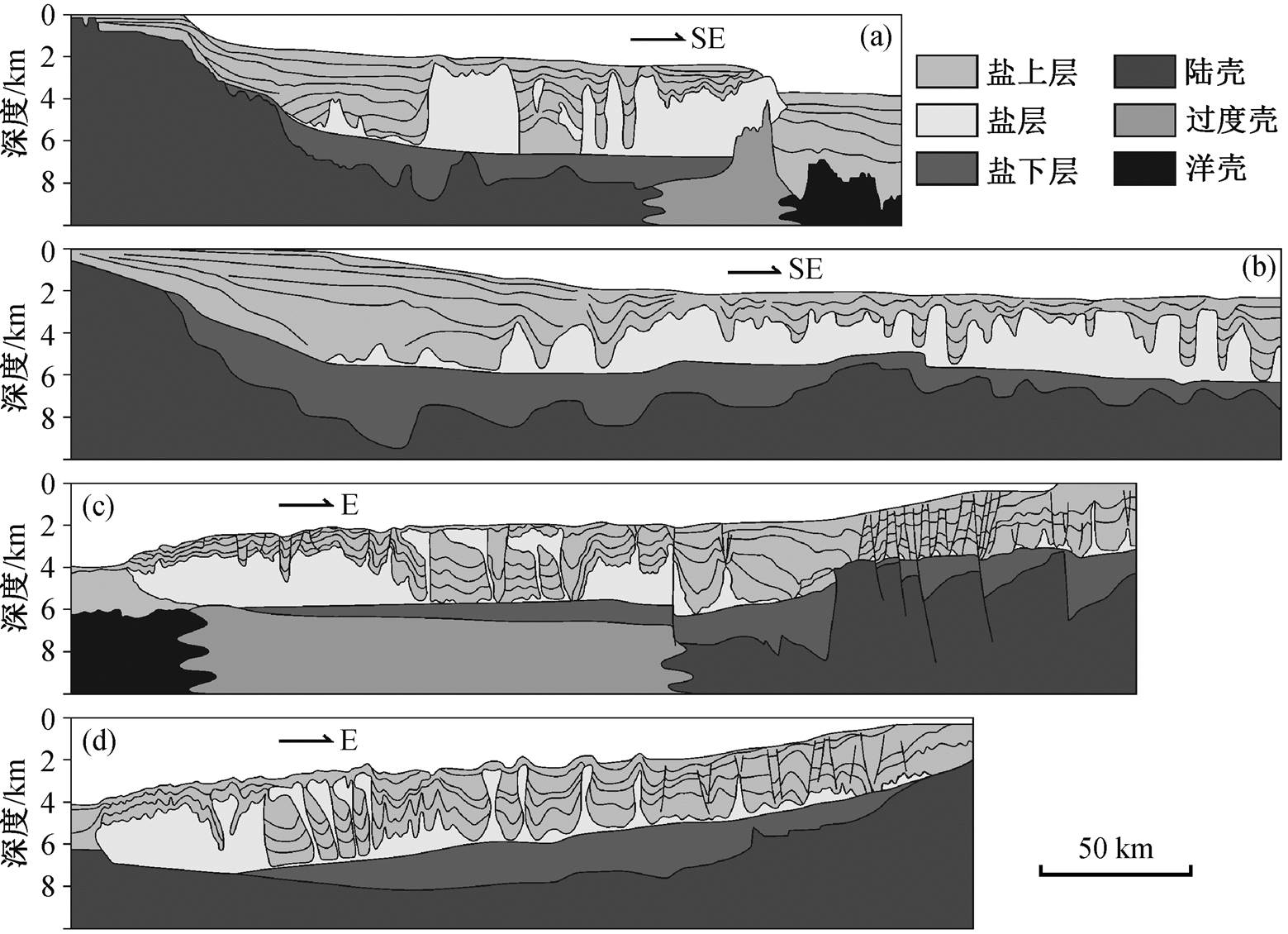
(a) 圣埃斯皮里图盆地[8]; (b) 桑托斯盆地[8]; (c) 宽扎盆地[8]; (d) 下刚果盆地[9]
图2 南大西洋两岸含盐盆地剖面解译图
Fig. 2 Seismic profiles interpretation of South Atlantic margin salt basin
DEM采用时步有限差分法求解系统中所有质点的牛顿运动方程[20]:
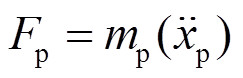 , (1)
, (1) , (2)
, (2)
其中, 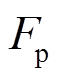 和
和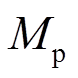 分别是作用在每个颗粒上的净力和净力矩,
分别是作用在每个颗粒上的净力和净力矩, 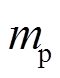 和
和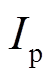 分别是质量和转动惯量,
分别是质量和转动惯量, 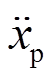 和
和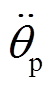 分别是离散颗粒的线性加速度和角加速度。将作用在每个颗粒上的重力、颗粒间接触力和设定的外部作用力带入式(1)和(2), 能够有效地表达颗粒的速度和位移[21]。
分别是离散颗粒的线性加速度和角加速度。将作用在每个颗粒上的重力、颗粒间接触力和设定的外部作用力带入式(1)和(2), 能够有效地表达颗粒的速度和位移[21]。
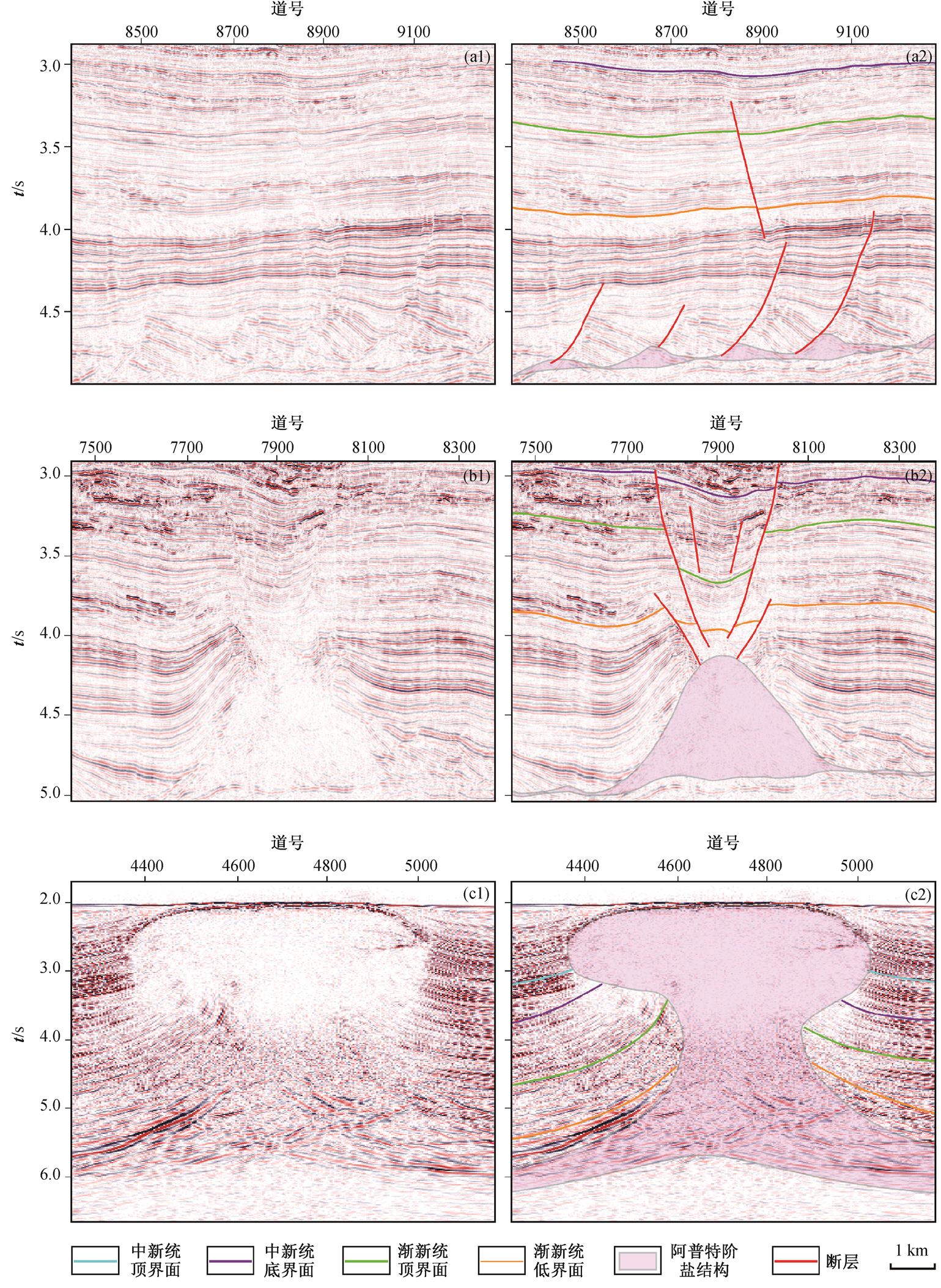
(a1)~(c1) 原始地震剖面; (a2)~(c2) 地震剖面解译。(a)位于A工区, (b)和(c)位于B工区
图3 下刚果盆地A工区和B工区盐构造地震剖面及其构造解译
Fig. 3 Seismic profiles and tectonic interpretation of the area A and B in Lower Congo Basin

(a1)~(c1) 原始地震剖面; (a2)~(c2) 地震剖面解译
图4 下刚果盆地C工区盐构造地震剖面及其构造解译
Fig. 4 Seismic profile and tectonic interpretation of the area C in Lower Congo Basin
在进行模拟时, 离散颗粒的移动造成颗粒与颗粒之间的相互作用, 颗粒接触力和位移会交替计算, 也就造成颗粒净力的不断改变, 直至计算达到平衡状态。在任意时刻, 每个小球所受的外力是此时周围小球对它作用力的矢量之和(图5(a)):
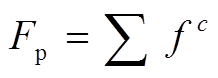 , (3)
, (3)其中, c 为周围接触小球的个数。颗粒间接触符合Hertz-Mindlin准则, 颗粒间的接触应力可转化为正应力和剪切应力(图5(b)):
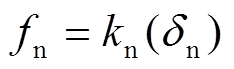 , (4)
, (4)
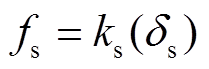 。 (5)
。 (5)其中, 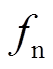 和
和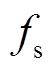 分别代表正应力和剪切应力,
分别代表正应力和剪切应力, 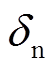 和
和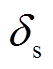 分别代表颗粒间正向上和切向上的接触量,
分别代表颗粒间正向上和切向上的接触量,  和
和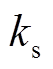 分别为颗粒间正向黏结系数和剪切黏结系数(图 5 (c))。可通过相应岩石的物理学参数, 设定球体颗粒黏结系数。剪切应力与颗粒间的摩擦系数相关, 当颗粒间的黏结强度被破坏后, 颗粒间的运动遵循滑动接触的规律, 即符合摩擦效应。
分别为颗粒间正向黏结系数和剪切黏结系数(图 5 (c))。可通过相应岩石的物理学参数, 设定球体颗粒黏结系数。剪切应力与颗粒间的摩擦系数相关, 当颗粒间的黏结强度被破坏后, 颗粒间的运动遵循滑动接触的规律, 即符合摩擦效应。
盐构造控制因素模型的建立基于离散元法。根据现有的研究结果, 南大西洋两岸被动陆缘盆地盐构造的数值模拟分析中各项重要参数值如表1所示。盐上沉积物密度为2500 kg/m3, 盐岩密度为2200 kg/m3, 水的密度为1000 kg/m3 [21–24]。盐岩层的摩擦系数为0.1, 与边界接触部位被认为是均衡流体, 摩擦系数为0, 盐上层沉积物摩擦系数为0.3。在地质年代尺度上, 盐岩被认为是黏性流体[22,25–26], 在模型中的黏度参数为1×108 Pa·s。后续陆源沉积的沉积速率为0.05 m/s[22]。
参考现有的研究结果, 建立包含3层的离散颗粒沉积模型(图6): 岩盐岩层(紫色)和盐上层(绿色), 并在盐上层设置可控的后续持续沉积层(浅蓝色)。为了对模拟结果有更直观的认识, 此模型在各层中部或接触部位还分别设定 3 个标志层: 盐岩层的白色标志层、盐上层的蓝色标志层、盐上层与后续沉积的黑色接触标志层。
为使模拟结果体现下刚果盆地不同盐构造样式的分布差异, 几何模型的宽度和深度与盆地真实情况相同: 长100 km, 高15 km。建立基于基底倾斜角度的 3 个单因素变量模型: 2.5°模型、5°模型和7.5°模型。模型中盐岩层和盐上岩层的厚度为2 km, 后续沉积的初始沉积离岸距离为20 km, 沉积速率为0.05 m/s。
3个模型的构造倾斜角度分别设为2.5°, 5°和7.5°, 在后续沉积速率和模拟时间相同的条件下, 模拟不同构造倾斜角度条件下, 下刚果盆地盐构造的样式及分布, 结果如图 7 所示。
2.5°模型中, 随着盐岩的流动, 出现多个破裂变形, 形成铲式生长正断层及盐上地堑式构造, 初步形成大规模的盐岩隆起(图 7(a))。
5°模型中, 后续陆源沉积的搬运距离比 2.5°模型增长约25%, 随着倾斜角度增大, 盐岩和上覆沉积的流动性逐渐增强。坡上盐岩厚度严重减薄, 以铲式生长断层和盐滚构造为主, 坡脚及坡下位置盐岩厚度明显增大, 盐岩层形变程度变大, 并形成多个典型的底辟构造(图7(b))。

图5 离散元数值模拟颗粒接触准则(据文献[21]修改)
Fig. 5 Criterion of particle contact in numerical simulation of discrete element (after Ref. [21])
表1 离散元模型各层岩石微观物理学参数
Table 1 Microphysical parameters of rock in each layer of discrete element model

岩层ρ/(kg·m−3)粒间摩擦系数内聚力/108 Pa黏度/(108 Pa·s)沉积速率/(m·s−1)g/(m·s−2) 盐岩22000.1119.81 盐上沉积25000.31 后续沉积25000.310.05 流体(水)1000011

图6 离散元初始模型设计图
Fig. 6 Design diagram of initial model of discrete element
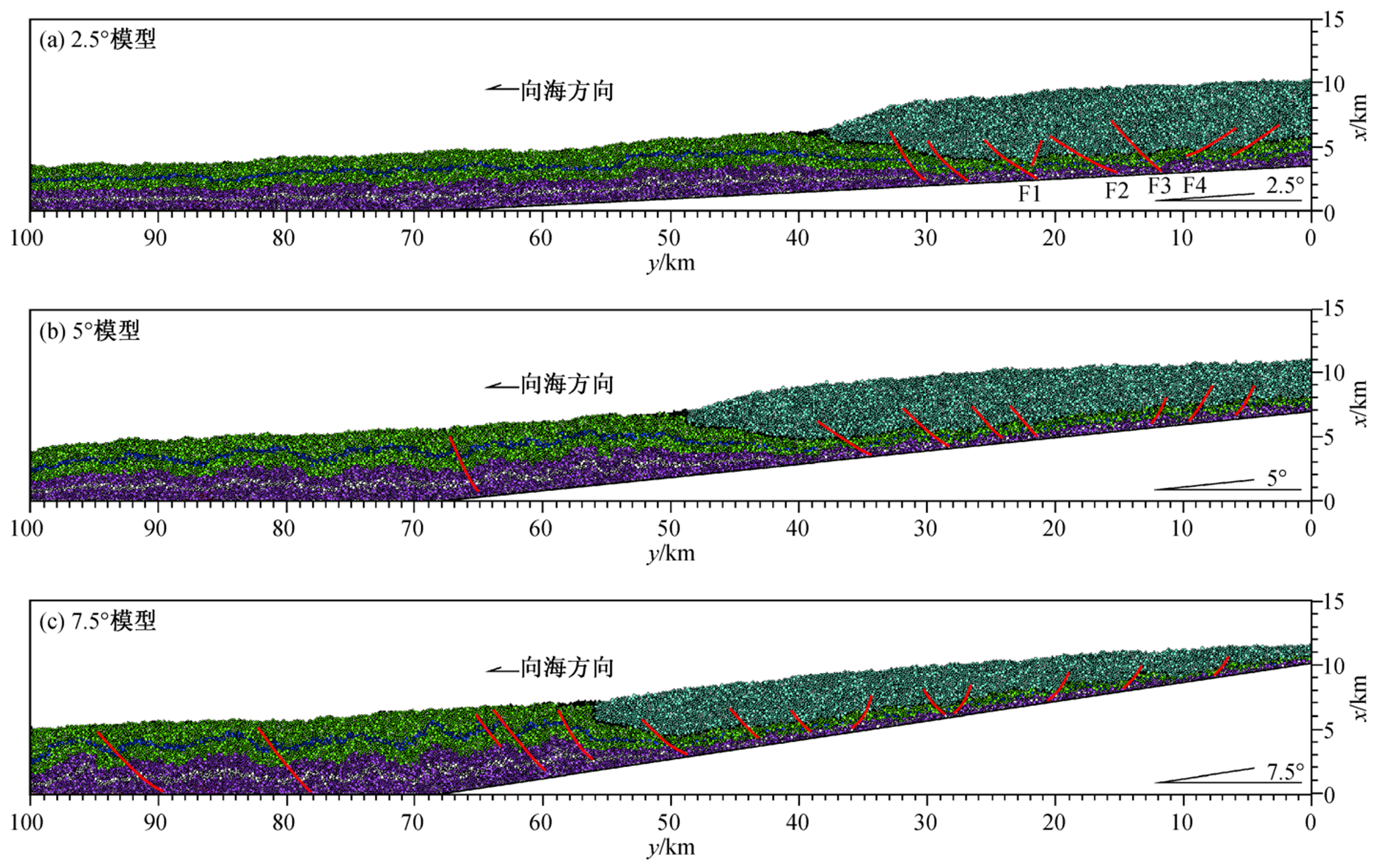
图7 构造倾斜角度模型变形模拟结果
Fig. 7 Deformation results of the base tilt angle model
7.5°模型中, 盐岩在坡脚和坡下位置集中, 坡上位置为铲式生长断层、盐滚构造和盐岩局部流失形成的盐焊接, 共 3 种主要构造样式; 坡脚位置发育多个盐底辟构造, 并在构造倾斜的最远端形成盐株构造和逆冲断层(图7(c))。
基于上述 3 个模型的运动矢量图(图 8 和 9), 探讨构造倾角对盐构造的主控作用。每个模型选取与全区域运动差异较大的 A, B 两个区域进行对比分析, 探讨下刚果盆地在不同构造倾斜角度下盐岩的流动机制。
2.5°模型中, 颗粒运动方向整体上与基底平行。虽然坡度较小, 颗粒运动速度缓慢, 但受构造倾斜的影响, 从陆向海方向, 颗粒运动速度仍呈逐渐减小的趋势。在有后续陆源沉积的部位, 颗粒运动矢量密度呈条带状低值区(图8), 这与该模型解译中的断裂F1~F4 (图7)吻合。
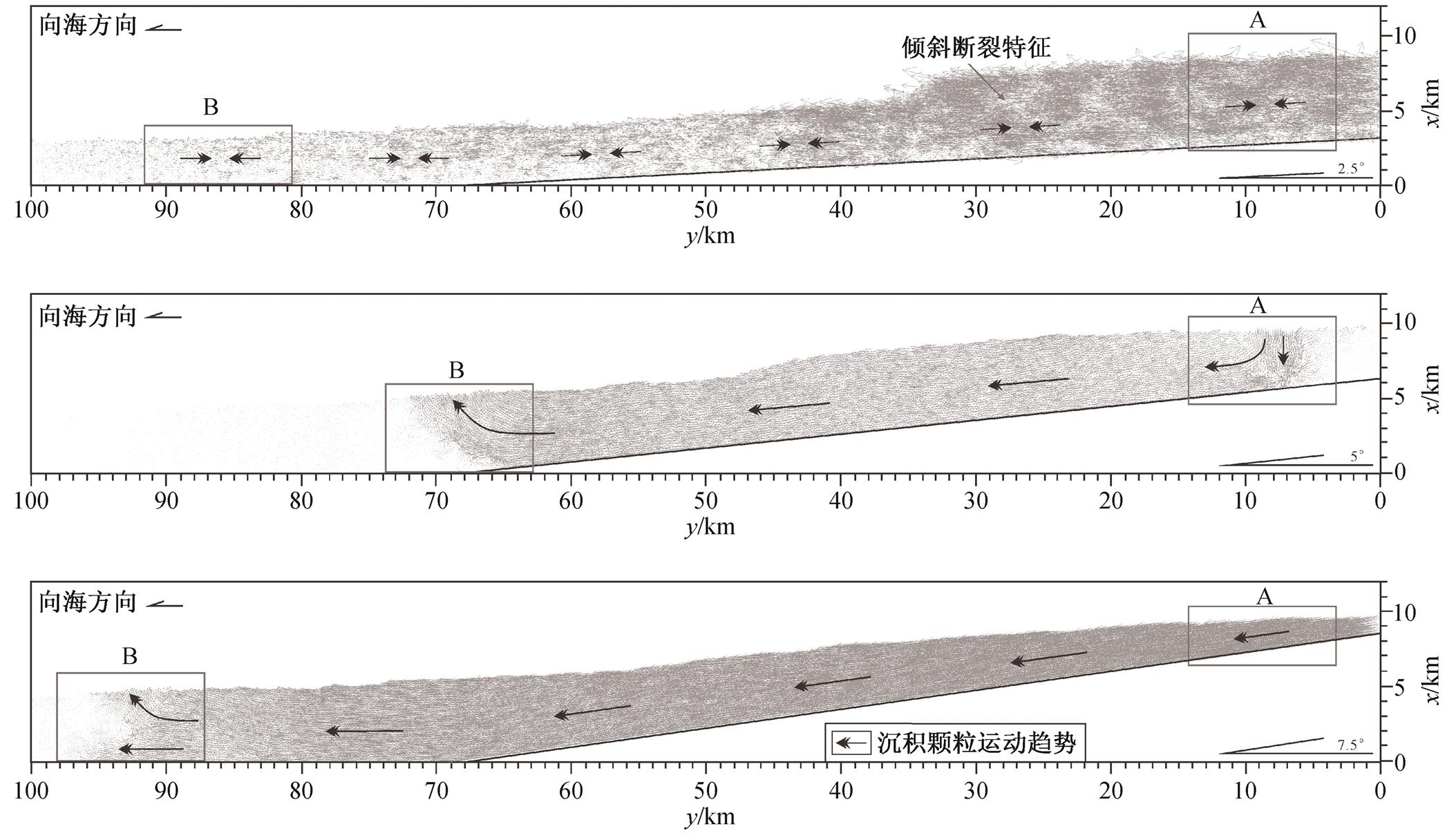
灰色箭头代表沉积颗粒的运动方向, 其长度代表运动速率, 其密度表示沉积物颗粒的活动强度, 下同; 黑色箭头指示沉积层移动方向
图8 构造倾斜角度模型颗粒运动矢量图
Fig. 8 Particle motion vector of model with basement dip angle
以2.5°模型中区域A为例, 盐岩因流动而发生小幅度的变形, 颗粒呈不规律的相向运动, 说明构造倾斜的角度对颗粒运动的影响较小。颗粒运动矢量密度低值区(图9(a1))与模型的断裂解译(图9(a2))匹配良好, 说明坡上位置盐岩的流动能力较强。盐岩的流失造成盐上沉积层存在局部颗粒运动差异, 发生破裂而形成断层, 而断层附近颗粒的运动能力较差, 断层的形成主要受其周围颗粒运动的控制。
2.5°模型中区域B远离构造斜坡, 后续陆源沉积对该处的盐岩驱动力很小, 但颗粒同样有相向运动的特征, 且有两处小幅度的构造隆起(图9(b2))。模型设定的原始沉积厚度为4 km, 而模拟结果图9(b2)中P点的地层厚度约为3.5 km, 减薄约0.5 km, 显示明显的压实作用。同时, 上覆沉积物颗粒运动矢量最密集、运动速度最大的位置(图9(b1))与盐层沉积低点(图9(b2))相吻合, 说明该区域盐岩层之上的沉积压实作用促进了盐岩的流动, 形成盐岩微隆起。
5°模型中, 盐岩及上覆沉积层颗粒运动方向基本上一致, 无相向流动现象, 在区域A和B以外, 运动矢量的大小也较均一, 说明构造倾角增大明显地促进了坡上沉积物颗粒的运动。
与2.5°模型相比, 5°模型中盐岩的运动矢量与斜坡呈平行状态, 盐上沉积物的颗粒运动矢量在坡上(近岸位置)发生明显的变化, 指示构造倾斜角度增大对促进坡上盐岩流动的两种作用: 1) 以重力作用为主的盐上沉积垂向压实作用; 2) 重力沿地层倾角的分力对盐岩的推动作用。从图9(c1)可以看出, 重力沿地层倾角分力导致的颗粒运动呈现从垂向向与斜坡平行方向的演变, 其运动矢量小于垂向的重力压实作用。两种力以下切的方式共同作用于盐岩, 极大地增强盐岩的流动能力。从模拟结果(图9(c2))也可以看出, 盐岩流动性较强, 形变明显, 且垂向压实位置的盐岩层厚度明显减薄, 表明两种作用力的差异性。
在5°模型的坡脚部位, 盐岩颗粒的运动矢量仍平行于斜坡, 而盐上层沉积物颗粒的运动矢量呈向上的趋势, 且其传播距离大于盐岩层(图9(d1)), 说明受坡度的影响, 坡上运动矢量的传播对盐上层沉积物颗粒的运动有促进作用, 使其流动性大于盐岩, 促使盐岩在坡脚部位不断积累, 形成盐构造, 且规模逐渐增大(图9(d2))。
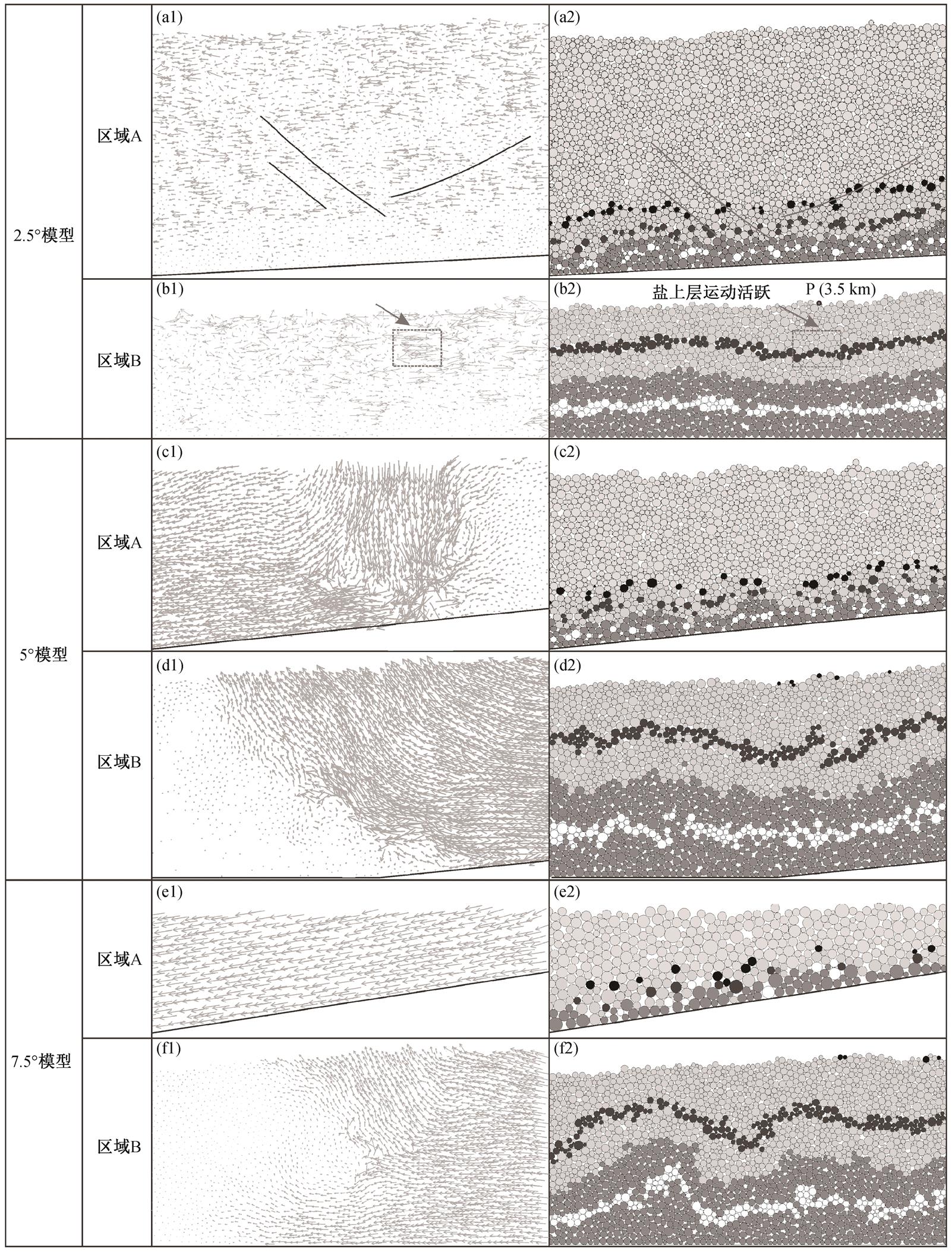
(a1)~(f1) 矢量图; (a2)~(f2) 模拟结果。黑色箭头指向盐上层颗粒运动活跃部位
图9 模型颗粒运动矢量及其模拟结果
Fig. 9 Particle motion vector of model and its modeling result
7.5°模型的运动矢量图(图9(e1)和(f1))显示, 随着构造倾斜角度进一步增大, 沉积物颗粒的流动能力均较强, 只在远离斜坡位置的模型边部相对较差, 说明较大的构造倾斜角度有利于增强盐岩及其上覆沉积层的流动性, 盐岩在坡下位置堆积形成大规模盐构造。
7.5°模型斜坡上的区域A, 沉积物颗粒的运动矢量几乎都与构造倾斜方向平行, 没有显示与5°模型相似的下切式运动方式(图9(e1))。模拟结果(图9(e2))显示, 此处地层严重减薄, 盐岩及盐上沉积层基本上消失, 以后续陆源沉积为主。与5°模型相比, 7.5°模型盐岩流动性更强, 与盆地地质情况相符。
7.5°模型区域B虽远离斜坡, 但从颗粒的运动矢量图(图9(f1))可以看到, 盐上层沉积物颗粒的运动方式与5°模型相似(运动矢量呈向上的趋势), 而盐岩层的运动矢量仍为水平方向, 虽其强度持续衰减, 但与5°模型相比, 盐岩颗粒具备持续流动的能力。沉积物颗粒的这种运动特征, 从模拟结果可以得到解释: 当构造倾斜角度较大时, 坡下位置尤其是远岸地区, 盐上沉积物颗粒的运动对盐岩流动具有促进作用; 同时, 由于盐岩层的流动性比盐上沉积层强, 使得盐岩该位置不断堆积, 形成大型的底辟构造(图9(f 2))。
基于上述模拟结果, 下刚果盆地构造倾斜角度对盐岩流动的控制模式分为以下3个类型。
1) 以盐上差异压实作用为主。当构造倾斜角度较小时, 坡度对盐岩流动的控制作用较小, 盐岩主要受上覆沉积物的差异压实作用驱动, 从差异压实部位向两侧流动。模拟结果(图10(a))显示, 盐岩及上覆沉积物相向运动, 形成构造样式主要为盐岩微隆起和局部断裂。
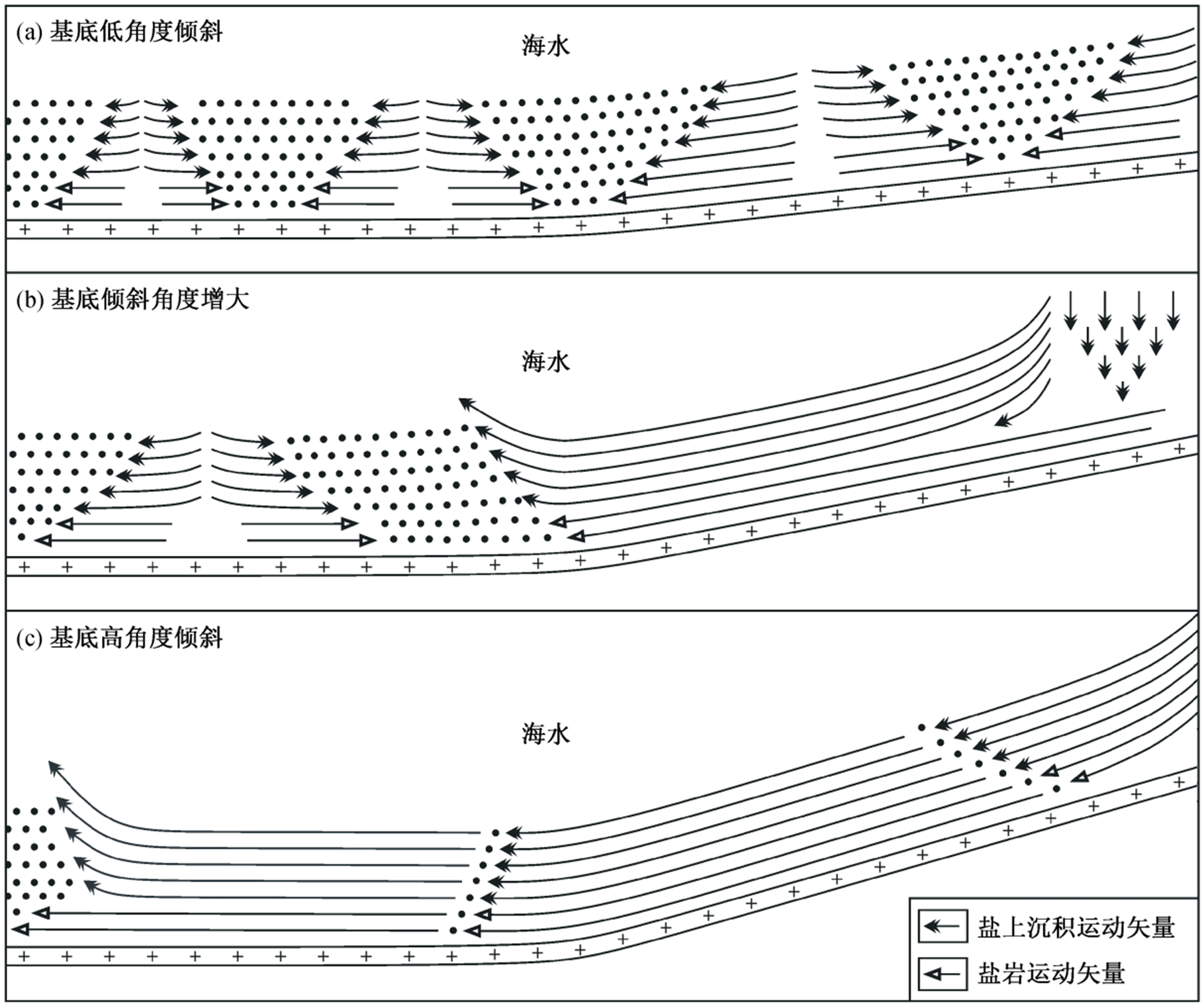
图10 构造倾斜角度的控制模式
Fig. 10 Control pattern of the structure inclination angle
2) 随着构造倾斜角度增大, 盐岩和上覆沉积物沿斜坡同向流动(向海方向), 盐上沉积物对盐岩流动的控制作用表现为: 在近岸位置, 上覆沉积物的重力垂向作用于盐岩; 在离岸稍远的位置, 上覆沉积物的重力沿构造倾斜方向以下切的方式作用于盐岩层。两种作用共同促进盐岩流动(图10(b))。坡上沉积物颗粒的运动矢量传播至坡脚后变小, 虽造成盐岩的堆积, 但没有明显地改造坡下盐岩和上覆地层。坡下位置的盐岩流动以上覆地层的差异沉积作用为主, 造成坡下和坡上的相向流动, 阻止了盐岩向深海方向的流动, 在坡脚形成底辟构造。坡上以重力的滑脱作用为主, 差异压实作用较小; 坡下受重力滑脱作用影响不大, 以差异沉积作用为主。
3) 构造倾斜角度增大至一定的程度, 促进盐岩层和上覆沉积层的流动, 差异压实作用减小, 即使在远岸位置, 盐岩仍具有较强的流动性。这也造成坡上的盐岩流失与坡下的盐岩大量堆积, 形成多个大型的底辟构造。尤其在模型边部, 出现大型的盐株构造(图10(c)), 这与南大西洋两岸盆地地质剖面的盐构造(图2)相似。此时, 差异压实作用对盐岩流动形成盐构造的控制作用比较小, 以重力滑脱作用为主。
本文基于离散元数值模拟方法, 针对构造倾斜角度对下刚果盆地盐岩流动的控制作用开展研究, 得到以下主要结论。
1) 下刚果盆地的构造倾斜是盐岩发生流动并形成盐构造的基础。盐岩在流动过程中, 改造上覆沉积地层, 导致形成的区域性压实条件不一致成为促进盐岩流动的重要因素。
2) 数值模拟结果显示, 在不同的构造倾斜角度下, 下刚果盆地的盐构造具有分区性。相对于坡下位置, 坡上位置的盐岩层以及上覆沉积层的流动性更强, 因此模拟结果中伸展型盐构造更明显, 盐岩更容易在盆地的坡脚位置积累, 形成规模较大的盐构造。
3) 当构造倾斜角度增大时, 盐岩的流动性增强。盐岩的流动主要有3种模式: 差异沉积主控、重力滑脱作用主控以及两者共同控制。在下刚果盆地的盐构造形成过程中, 构造倾斜角度是主控因素, 倾斜角度越大, 主控作用越强。
参考文献
[1]Anka Z, Séranne M, Primio R D. Evidence of a large upper-Cretaceous depocentre across the Continent-Ocean boundary of the Congo-Angola basin: impli-cations for palaeo-drainage and potential ultra-deep source rocks. Marine & Petroleum Geology, 2010, 27 (3): 601‒611
[2]Mohriak W U, Brown D E, Tari G C. Sedimentary basins in the Central And South Atlantic conjugate margins: deep structures and salt tectonics // Central Atlantic Conjugate Margins Conference. Halifax, 2008: 1‒14
[3]袁圣强, 吴时国, 马玉波, 等. 南大西洋深水盆地的构造沉积演化及含油气系统. 天然气地球科学, 2008, 19(2): 216‒221
[4]何娟, 何登发, 李顺利, 等. 南大西洋被动大陆边缘盆地大油气田形成条件与分布规律——以巴西桑托斯盆地为例. 中国石油勘探, 2011, 16(3): 57‒67
[5]Davison I. Geology and tectonics of the South At-lantic Brazilian salt basins. Geological Society Lon-don Special Publications, 2007, 272(1): 345‒359
[6]Valle P J, Gjelberg J G, Helland-Hansen W. Tectonos-tratigraphic development in the eastern Lower Congo Basin, off shore Angola, West Africa. Marine & Petro-leum Geology, 2001, 18: 909‒927
[7]Hudec M R, Jackson M P A. Terra infirma: under-standing salt tectonics. Earth Science Reviews, 2007, 82(1/2): 1‒28
[8]Kukla P A, Strozyk F, Mohriak W U. South Atlantic salt basins —witnesses of complex passive margin evolution. Gondwana Research, 2018, 53: 41‒57
[9]Marton L G, Tari G C, Lehmann C T. Evolution of the Angolan passive margin, West Africa, with emphasis on postsalt structural styles // Mohriak W U, Talwani M. Atlantic rifts and continental margins. Washington DC: American Geophysical Union, 2000, 115: 129‒149
[10]Gamboa D, Alves T M. Bi-modal deformation styles in confined mass-transport deposits: examples from a salt minibasin in SE Brazil. Marine Geology, 2016, 379: 176‒193
[11]Quirk D G, Schodt N, Lassen B, et al. Salt tectonics on passive margins: examples from Santos, Campos and Kwanza basins. Geological Society London Spe-cial Publications, 2012, 363(1): 207‒244
[12]Duval B, Cramez C, Jackson M P A. Raft tectonics in the Kwanza Basin, Angola. Marine & Petroleum Geo-logy, 1992, 9(4): 389‒404
[13]Schultz-Ela D D. Origin of drag folds bordering salt diapirs. AAPG Bulletin, 2003, 87(5): 757‒780
[14]Barton D C. Mechanics of formation of salt domes with special reference to Gulf Coast salt domes of Texas and Louisiana. AAPG Bulletin, 1933, 17(9): 1025‒1083
[15]Cundall P A, Strack O D L. The development of constitutive laws for soil using the distinct element method. Third International Conference on Numerical Methods in Geomechanics, 1979, 79(1): 289‒317
[16]Cundall P A, Hart R D. Numerical modelling of discontinua. Analysis & Design Methods, 1993, 9(2): 231‒243
[17]Morgan J K, Boettcher M S. Numerical simulations of granular shear zones using the distinct element method: 1. Shear zone kinematics and the microme-chanics of localization. Journal of Geophysical Re-search, 1999, 104(B2): 2703‒2719
[18]Cundall P A, Strack O D L. A discrete numerical mode for granular assemblies. Géotechnique, 1979, 29(1): 47‒65
[19]Burbidge D R, Braun J. Numerical models of the evolution of accretionary wedges and fold-and-thrust belts using the distinct-element method. Geophysical Journal International, 2002, 148(3): 542–561
[20]Morgan J K, Mcgovern P J. Discrete element simulations of gravitational volcanic deformation: 1. Deformation structures and geometries. Journal of Geophysical Research Atmospheres, 2005, 110(B5): 2701‒2711
[21]Dean S L, Morgan J K. Influence of mobile shale on thrust faults: Insights from discrete element simula-tions. AAPG Bulletin, 2015, 99(3): 403‒432
[22]Maxwell S A. Deformation styles of allochthonous salt sheets during differential loading conditions: insights from discrete element models [D]. Houston: Rice University, 2009
[23]Nikolinakou M A, Luo G, Hudec M R, et al. Geomechanical modeling of stresses adjacent to salt bodies: Part 2. Poroelastoplasticity and coupled over-pressures. AAPG Bulletin, 2012, 96(1): 65‒85
[24]Schultz-Ela D D. Origin of drag folds bordering salt diapirs. AAPG Bulletin, 2003, 87(5): 757‒780
[25]Morgan J K. Particle dynamics simulations of rate- and state-dependent frictional sliding of granular fault gouge. Birkhäuser Basel, 2004, 161(9/10): 1877‒1891
[26]Carter N L, Horseman S T, Russell J E, et al. Rheo-logy of rocksalt. Journal of Structural Geology, 1993, 15(9/10): 1257‒1271
Salt Structure Formation Modeling Controlled by Structure Inclination Angle: Take the Lower Congo Basin as an Example
Abstract Based on the data of three seismic work areas in the Lower Congo Basin, nine typical salt-related tectonic patterns are summarized in the basin and the distribution pattern of salt structures is confirmed. Established with the base tilt angle as a single variable based on the discrete element numerical simulation method, and evolution results of the structure and motion vectors are obtained. With the increase of the basement inclination angle, the flow velocity of salt rock and its overlying sediments gradually increases, and the subsequent terrigenous sediment transport distance is also longer. The basement inclination mainly has three kinds of control effects on the salt rock flow: differential compaction as the master control, differential compaction and gravity gliding combined, gravity gliding as master control. These three control effects are all affected by the basement inclination angle and appear in turn with the change of the angle. Based on the analysis results above, control pattern of basement inclination on salt rock flow in the passive margin basin of the South Atlantic is established.
Key words Lower Congo Basin; salt structure; numerical simulation of discrete element method; structure inclination; control pattern
doi: 10.13209/j.0479-8023.2018.095
收稿日期: 2018-03-12;
修回日期: 2018-06-19;
网络出版日期: 2018-12-18
国家科技重大专项(2016ZX05033002, 2016ZX05033001)资助