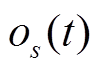 , 用
, 用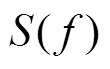 和
和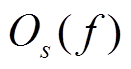 分别代表这两个振动信号的傅里叶谱, 依据场地传递函数𝐻(𝑓)的定义, 𝐻(𝑓)可写成地铁地表振动与地铁隧道振动的傅里叶谱之比:
分别代表这两个振动信号的傅里叶谱, 依据场地传递函数𝐻(𝑓)的定义, 𝐻(𝑓)可写成地铁地表振动与地铁隧道振动的傅里叶谱之比:摘要 为了在城市环境条件下获取场地振动响应特征, 提出一种互相关叠加方法, 并利用模拟数据验证方法的正确性。该方法利用地铁的地表振动记录确定场地传递函数, 能够有效地压制其他振动的干扰, 可以为获取场地传递函数提供一种新的方式。
关键词 场地传递函数; 地铁振动; 城市环境振动
场地传递函数是场地土层的地表响应振动信号与其输入振动信号的拉普拉斯变换之比, 其幅值能够反映一定条件下土层对地震动的响应特征[1]。场地传递函数的振幅谱通常称为场地响应, 或场地效应, 或场地放大因子[1–3], 在评估地震动对地面建筑、工程和设备的影响时起重要作用[2–3]。计算场地土层传递函数或场地响应特征的方法主要有两类: 经验方法和理论分析方法[3–4]。
经验方法利用地震资料直接估计场地效应, 主要有传统谱比法、广义反演法以及水平竖向谱比法。传统谱比法由Borcherdt[1]提出, 该方法将场地观测台站附近的出露基岩台站作为参考台站, 假定参考台站处的震动近似地等价于由场地下部基岩入射场地土层的震动, 则观测台与参考台震动信号的傅里叶振幅谱之比即为场地效应, 但是, 当参考台站处的场地效应不能忽略时, 谱比法计算的是相对效应[5]。该方法要求观测场地附近存在合适的参考台站和可用的地震资料, 这在很多地区难以满足。Andrews[6]在谱比法的基础上提出广义反演法, 利用台网记录进行联合反演, 同时求解震源、传播路径和场地响应。Iwata等[7]在其基础上考虑非弹性衰减, 使广义反演法更加合理。Boatwright等[8]提出参考事件法, 以一个被多数台站记录到的事件作为参考, 回避参考场地的约束。Moya等[9]以Brune震源模型为震源项, 引入遗传算法, 得到更好的反演结果。Castro等[10]提出非参数化广义反演方法, 用一个与距离有关的变量表示整个衰减, 减小不均匀性及各向异性导致的结果偏差。广义反演法在场地响应研究中得到广泛应用[11–14]。但是, 台网密度及事件记录数量可能会对广义反演法估计结果的准确性产生影响[15]。Nakamura[16]提出水平竖向谱比法(H/V谱比法, 又称噪声谱比法), 利用观测点地脉动的水平分量与垂直分量的傅里叶振幅谱之比估计场地效应。该方法被扩展应用于利用强震记录评估场地效应的研究中, 进行场地分类[17]。H/V谱比法能够得到较准确的场地基本卓越周期[5], 是估计场地响应最常用的方法之一[2,18–25]。H/V谱比法简单方便, 但它假设场地对从基岩入射的垂向地震波无放大作用, 这一点缺乏严格的理论证明。有研究显示, 当场地对垂向震动的作用不可忽略时, H/V谱比法的结果并不理想[12]。
理论分析方法以建立土体动力本构关系为核心, 通过数值模拟, 针对具体的场地模型来计算场地传递函数。根据土层非线性的特点, 可分为等效线性化方法和非线性方法。等效线性化方法最早由Idriss等[26]提出, 并得到广泛的应用。廖振鹏[27]提出地表土层地震反应的等效线性化解法, 此后又发展出考虑频率相关性的等效线性化方法[28–29]。学者们利用等效线性化方法, 给出多种场地模型的传递函数计算表达式, 并分析模型差异的影响[30–34]。等效线性化方法简单方便, 在应变较小、场地较硬的条件下, 结果比较可靠, 但在地震动较大、土层较软的条件下, 不能可靠地反映土体的真实运动过程和特征[4]。非线性方法旨在以合适的本构模型来描述土体的动应力应变关系, 能较好地反映场地的响应过程[35]。但是, 理论分析方法强烈地依赖模型和参数的准确性, 想要获得完备且可靠的场地模型及参数, 计算量很大, 难以广泛地应用于工程问题。
城市中建筑、管线密布, 给场地特征勘察带来不便, 很难获得准确的场地模型以及完备可靠的场地参数, 使得理论分析方法难以广泛应用。对经验方法来说, 城市中通常缺乏理想的参考台站和充足的地震资料, 难以满足谱比法和广义反演法的需求。同时, 大部分城市环境中, 振动源主要存在于场地表面, 不能满足噪声谱比法假定的基本应用条件。此外, 几乎24小时无间断的城市环境振动也会影响场地记录的信号质量, 不利于经验方法的应用。有学者采用爆破记录来计算浅地表的瑞利波格林函数[36–37], 但爆破源同样难以在城市环境中使用。综上所述, 在城市环境条件下, 现有各种方法的适用性及数据资料的获取均存在问题, 因此有必要寻求更易获取的震源资料和与其相适应的新方法来确定场地传递函数。
近年来, 我国城市的地铁系统发展迅猛, 地铁引起的振动也成为城市环境振动的主要成分之一。地铁振动特征相对固定, 长时间、高频次运营的地铁提供了一种新的可利用的重复振动源。对地铁的振动特征及其传播规律已有不少研究[38–43]。例如, 闫维明等[39]在地表沿与地铁隧道正交的方向布置多个测点, 测量地表垂直于地面的加速度分量, 并计算距线路轨道中心不同距离处测点与轨道中心正上方地表测点的相对传递函数。此外, 有学者在地下轨道与隧道工程实验室内, 应用自动落锤激励装置, 研究地层的传递函数[44–45]。但是, 上述研究在计算传递函数时没有考虑环境振动噪声对接收到的响应信号的干扰。
本文对利用地铁环境振动确定沿线场地响应特征的理论表达式进行推导, 提出一种计算隧道壁与地表测点间土层传递函数的方法, 并利用模拟数据对方法进行检验。
本文尝试利用地铁振动观测和地表振动观测数据来获取场地传递函数, 基本思路如下。
在一次地铁经过的过程中, 已知隧道壁上的地铁振动s(t), 假设该地铁振动经过土层传播后, 在地面场地引起的地表振动为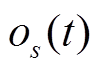 , 用
, 用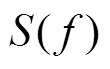 和
和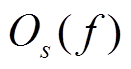 分别代表这两个振动信号的傅里叶谱, 依据场地传递函数𝐻(𝑓)的定义, 𝐻(𝑓)可写成地铁地表振动与地铁隧道振动的傅里叶谱之比:
分别代表这两个振动信号的傅里叶谱, 依据场地传递函数𝐻(𝑓)的定义, 𝐻(𝑓)可写成地铁地表振动与地铁隧道振动的傅里叶谱之比:
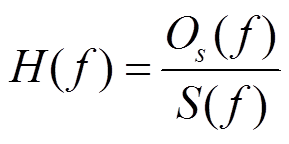 。 (1)
。 (1)在城市环境条件下, 除地铁外, 其他各类环境振动源无处不在。地面工程场地观测到的地表震动既包含地铁引起的振动, 也包含地铁以外其他振源在测点引起的振动。根据叠加原理, 观测到的地表振动可以写成
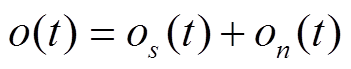 , (2)
, (2)
式中, 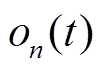 表示地铁以外的其他振动源在测点引起的振动总和。实际上, 地铁隧道壁的振动记录s(t)也包含其他振动源引起的干扰振动
表示地铁以外的其他振动源在测点引起的振动总和。实际上, 地铁隧道壁的振动记录s(t)也包含其他振动源引起的干扰振动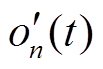 , 但在地铁经过的时间段,
, 但在地铁经过的时间段, 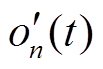 的振幅远小于地铁引起振动的振幅, 可视为噪音而被忽略, 因此可用地铁隧道壁记录s(t)近似地代表地铁振动。但是, 相对于
的振幅远小于地铁引起振动的振幅, 可视为噪音而被忽略, 因此可用地铁隧道壁记录s(t)近似地代表地铁振动。但是, 相对于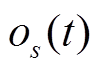 , 其他振动源在地表测点引起的振动
, 其他振动源在地表测点引起的振动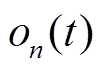 的振幅不可忽略。然而, 现有的各种方法很难区分
的振幅不可忽略。然而, 现有的各种方法很难区分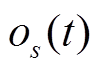 与
与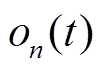 , 无法直接求取场地传递函数。
, 无法直接求取场地传递函数。
本文从地铁振动源与其他振动源的相互独立性出发, 结合其他振动源的振动特征在时间和空间上的随机性, 利用互相关叠加算法, 在理论上可以消除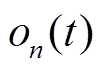 的干扰, 获得准确可靠的场地传递函数。
的干扰, 获得准确可靠的场地传递函数。
地铁振动的物理成因主要与轨道及车轮缺陷相关, 由于车速和载重的变化范围受到较大的限制, 每次地铁运行引起振动的特征非常相似。相比之下, 其他振动源(包括路面交通振动源和地面施工振动源等)及其振动特征具有多样性, 在时间和空间上具有高度的随机性。
在任意第 i 次地铁经过的时间段, 地表振动观测表示为
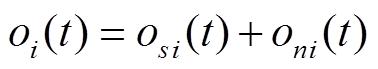 。 (3)
。 (3)考虑到地铁振动与其他振动源及其振动特征的显著差异和相互独立性, 并忽略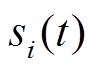 包含的干扰噪音, 则两种信号的互相关函数的期望值趋近 0, 即当下式中的 N 足够大时, 信号的平均相关性趋于零:
包含的干扰噪音, 则两种信号的互相关函数的期望值趋近 0, 即当下式中的 N 足够大时, 信号的平均相关性趋于零:
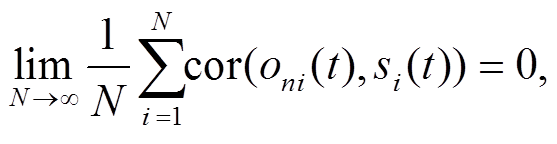 (4)
(4)
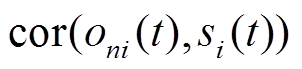 表示
表示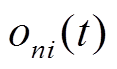 和
和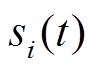 的互相关函数。为了研究场地传递函数的频率特征, 将式(4)写成相应的频域表达式:
的互相关函数。为了研究场地传递函数的频率特征, 将式(4)写成相应的频域表达式:
 。 (5)
。 (5)
令某频率函数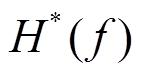 满足
满足
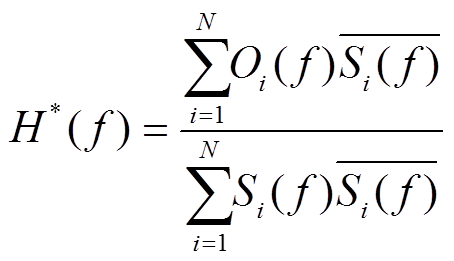 , (6)
, (6)展开可得
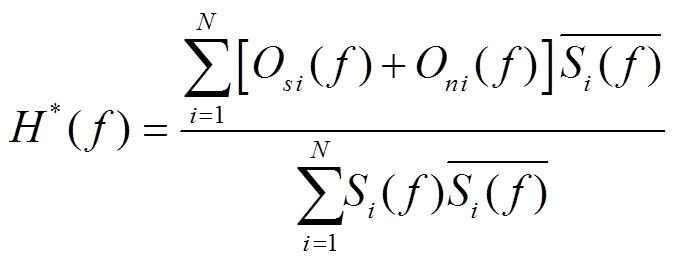
![]() 。 (7)
。 (7)
根据式(1), 可将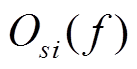 写成
写成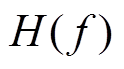 和
和 之积:
之积:
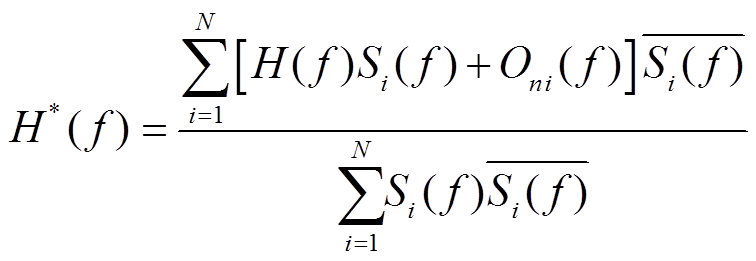
展开可得
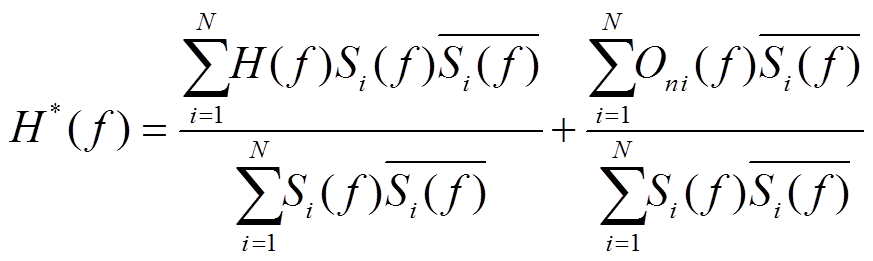
![]() , (9)
, (9)
即
 。 (10)
。 (10)令
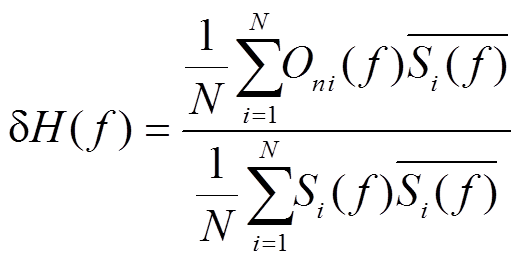
![]() , (11)
, (11)
可得
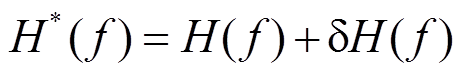 。 (12)
。 (12)根据式(5), 当叠加次数 N 足够大时, dH( f )的分子趋于零, 其分母
 , (13)
, (13)
因此, 在 N值较大的条件下, dH( f )趋于零, 从而有
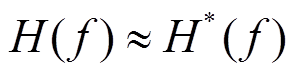 。 (14)
。 (14)因此, 可将H*( f )作为场地传递函数的估计值, 其精度依赖于样本数量N。
对于实际数据, 在较长的时间段里, 地铁隧道壁振动记录s(t)包含多次地铁经过引起的振动。可以选取合适的时窗, 对整个信号进行截断, 使得每一个时窗都包含一次地铁经过引起的振动, 然后利用式(6)来估计场地传递函数。
为了验证上述理论方法的正确性和可靠性, 本文采用模拟数据进行检验。北京大学宁杰远教授研究团队于2018年1月29—30日在深圳附近的广深港高速铁路进行了为期两天的短周期密集台阵观测, 为本文提供了可用的资料。为了最大限度地检验方法的适用性, 本文利用与地铁振动源有相似性的这批高铁资料设计地铁振动源。为了保证振幅与地铁振动的振幅量级相似, 对高铁振动的振幅进行了压制, 将高铁振动实际数据的振幅整体上缩小常数倍, 使得压制后的振幅与地铁振动的振幅量级相同(地铁振动振幅量级参照文献[46]中图2)。传递函数的合成方法如下。
首先, 主观选定两种较典型的传递函数的振幅谱形式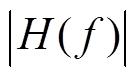 , 并分别选取不同的相位谱
, 并分别选取不同的相位谱 再利用公式
再利用公式
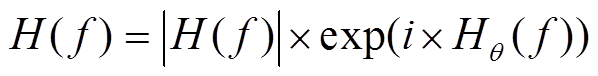
![]() 合成完整的传递函数H(f)。
合成完整的传递函数H(f)。
然后, 对H(f)做反傅里叶变化, 得到对应的时域脉冲响应函数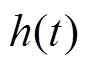 。再将实际高铁振动记录作为
。再将实际高铁振动记录作为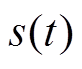 , 并根据式(1)对应的时域表达式
, 并根据式(1)对应的时域表达式
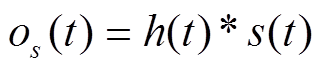 ,
,合成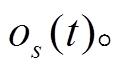 将随机噪声作为其他干扰振动
将随机噪声作为其他干扰振动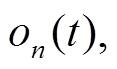 并利用式(2)合成假定的地表记录o(t)。
并利用式(2)合成假定的地表记录o(t)。
最后, 对合成信号o(t)和s(t)进行仿真验算, 利用式(6)计算传递函数的估计值H*(f), 并与设定的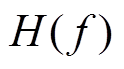 进行对比, 检验方法是否可靠。
进行对比, 检验方法是否可靠。
需要指出的是, 传递函数的相位谱反映台站间的走时差信息, 当两台站位置固定时, 走时差可近似地视为固定值, 记为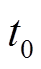 , 则传递函数的相位谱有如下形式:
, 则传递函数的相位谱有如下形式:
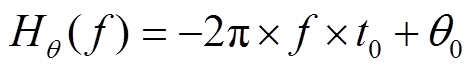 。
。此时, 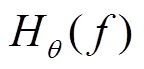 是频率
是频率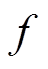 的线性函数。
的线性函数。
本文方法能够计算场地传递函数的完整信息, 包括振幅谱和相位谱两部分。此外, 场地传递函数的反傅里叶变换对应时域的脉冲响应函数, 能够反映场地接收振动信号的时间延迟和振动振幅变化等信息。图1分别展示两种振幅谱和不同相位谱对应的总计4种场地传递函数的计算结果, 叠加次数N=1000。
从图1可见, 本文方法计算得到的场地传递函数估计值的振幅谱、相位谱以及对应的时域脉冲响应函数均与设定值非常接近。图1(a2)和(b2)中相位谱在10Hz以下和40Hz以上的频段与设定值相差较多, 是因为这两个频段对应振幅谱的幅值几乎为0, 因此在计算相位谱时会有较大的误差, 但两者之积仍为0, 对结果几乎没有影响。估计值与设定值对应的时域脉冲响应函数几乎相等, 也表明此频段相位谱的误差对结果没有影响。此外, 对比图1中(a)与(b)、(c)与(d)可以看出, 在振幅谱相等的条件下, 当相位谱不同时, 时域脉冲响应函数的形状也不相同, 进一步说明相位信息会影响振动信号的波形。因此, 包含振幅谱和相位谱的场地传递函数能够更完整地反映场地对振动的响应。
从式(12)可以看出,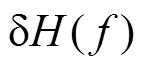 值的大小会影响本文方法计算结果的准确程度, 而
值的大小会影响本文方法计算结果的准确程度, 而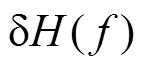 主要受叠加次数 N 的影响。从理论上讲, N越大,
主要受叠加次数 N 的影响。从理论上讲, N越大, 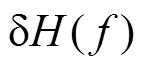 越小, 估计值越准确。考虑到实际情况下数据量有限, 因此需要考察N的取值对结果准确性的影响。为此, 本文分别计算 4 种 N 值条件下振幅相对误差的结果(图2), 并给出振幅相对误差的最大值随叠加次数变化的关系(图3)。
越小, 估计值越准确。考虑到实际情况下数据量有限, 因此需要考察N的取值对结果准确性的影响。为此, 本文分别计算 4 种 N 值条件下振幅相对误差的结果(图2), 并给出振幅相对误差的最大值随叠加次数变化的关系(图3)。
图 2 和 3 表明, 叠加次数越多, 振幅误差的整体幅值越小。当叠加次数超过 1000 时, 叠加次数的增加对振幅误差的影响就很小了。从图 2 可以看出, 对于某个固定的叠加次数, 振幅的误差在不同频段表现不同。从式(11)可以看出, 在叠加次数固定的条件下, 误差既与源信号的频谱特征有关, 又与其他干扰振动的频谱特征有关。更合理的考虑是, 相对于其他干扰振动振幅谱, 在源信号振幅谱较小的频段, 误差相对较大; 在源信号振幅谱相对较大的频段, 误差相对更小。图 4 展示叠加次数 N=1000 的情形下, 干扰振动的平均振幅谱与高铁振动的平均振幅谱之比值。对比图 2 和 4 可以看出, 干扰振动与高铁振动的振幅谱比值与误差的形状非常接近, 印证了上述考虑, 也解释了误差在1~3Hz频段相对较大的原因。
王博等[46]曾提出谱时程比方法, 尝试利用北京大学东门站附近的地铁振动, 计算地铁沿线的场地响应特征, 但他们的观测数据没有精确授时, 且未用模拟数据检验其方法。我们认为他们的方法存在以下缺陷。
1)文献[46]用场地的振幅比系数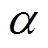 与地铁隧道壁记录
与地铁隧道壁记录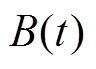 之积来表示地表测点处的地铁振动
之积来表示地表测点处的地铁振动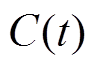 不完全合理, 因为地铁振动和场地响应振动的振幅均随时间变化, 不是固定值。场地对振动的响应并非简单地表现为振幅的改变, 还体现在振动在时间上的延迟等方面。因此, 场地对振动的响应在时域体现为卷积的形式, 并非乘积的形式, 在频率域才表现为乘积的形式。
不完全合理, 因为地铁振动和场地响应振动的振幅均随时间变化, 不是固定值。场地对振动的响应并非简单地表现为振幅的改变, 还体现在振动在时间上的延迟等方面。因此, 场地对振动的响应在时域体现为卷积的形式, 并非乘积的形式, 在频率域才表现为乘积的形式。
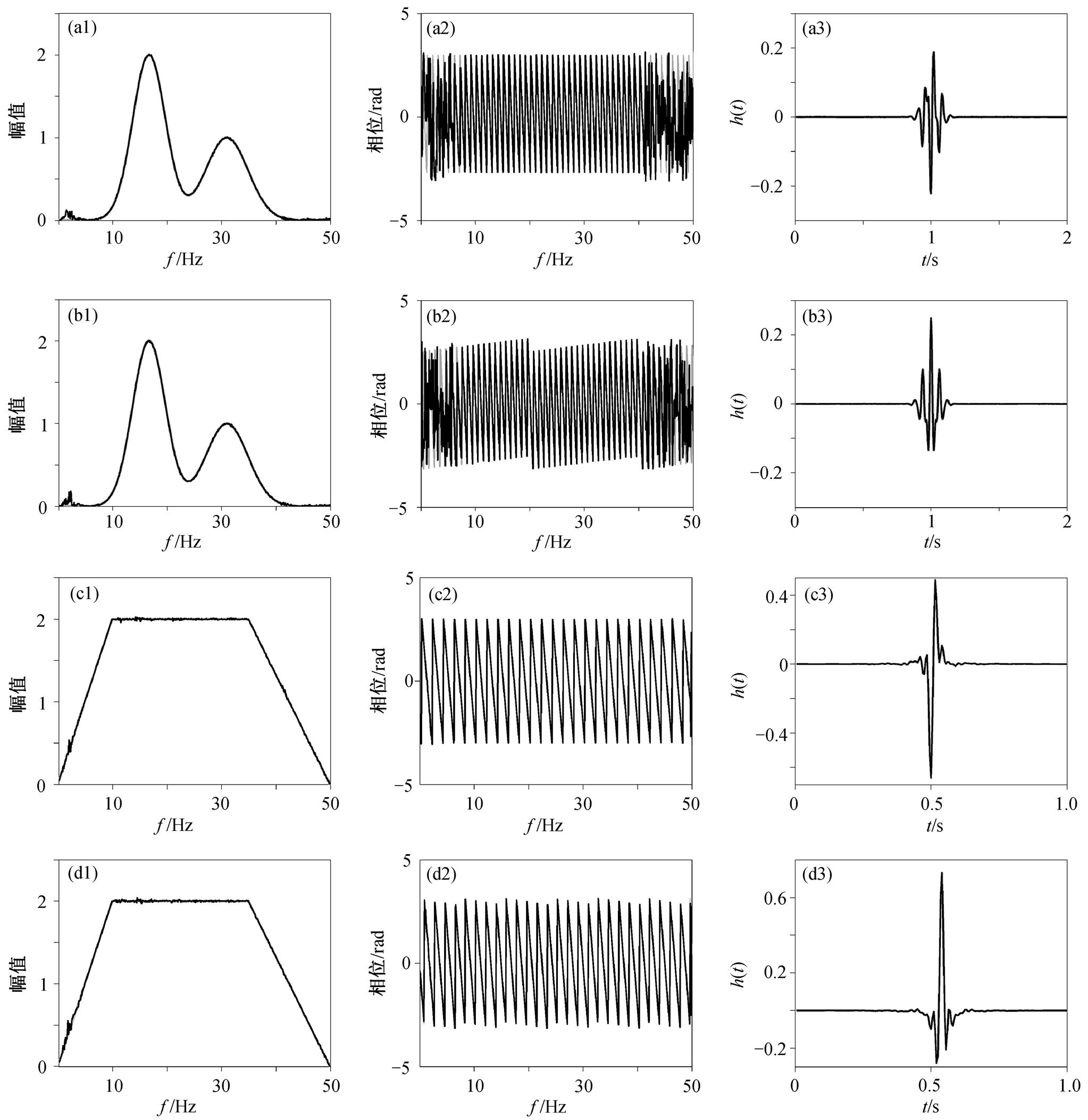
(a1)~(d1)传递函数振幅谱; (a2)~(d2)传递函数相位谱; (a3)~(d3)对应的时域脉冲响应函数。灰色曲线代表设定值, 黑色曲线代表估计值
图1 模拟数据的传递函数检验结果
Fig. 1 Transfer-function results from simulated data
2)在文献[46]的图3中, “谱时程”曲线每个点的取值是对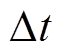 时段内振动信号平均加速度的度量, 是时域的物理量。然而, 场地传递函数是频域的概念。因此, 用加速度的度量在时间域的互相关与自相关之比得到的
时段内振动信号平均加速度的度量, 是时域的物理量。然而, 场地传递函数是频域的概念。因此, 用加速度的度量在时间域的互相关与自相关之比得到的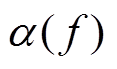 不能合适地表征场地传递函数。并且, 在中心频率越高的频段, 带宽越大, 越不能恰当地表征。
不能合适地表征场地传递函数。并且, 在中心频率越高的频段, 带宽越大, 越不能恰当地表征。
3)在实际情况中, 其他干扰振动可能小概率地与地铁振动相关, 只有足够多组信号样本的互相关函数的叠加求平均(即统计期望值)才会趋于零。文献[46]中使用1/3倍频程谱的滤波方式, 会产生较大的平滑效应, 且越高频的部分平滑效果越重。他们选用的中心频率的间隔仅为0.2Hz, 会导致从1Hz起, 相近的中心频率点的频带发生重叠, 且中心频率越高, 重叠越严重, 越发加重平滑的效果。这种平滑效果也会使地铁振动与其他干扰振动的频率混杂, 影响结果的准确性。同时, 用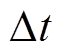 时段内的加速度方均根值作为振动的平均有效强度, 也会使地铁振动与干扰振动的振幅相互混杂, 影响结果的准确性。尤其是, 当干扰振动的振幅量级与地铁振动相似或强于地铁振动时, 振动的平均有效强度会包含较多干扰振动信息而导致结果较大的偏差。
时段内的加速度方均根值作为振动的平均有效强度, 也会使地铁振动与干扰振动的振幅相互混杂, 影响结果的准确性。尤其是, 当干扰振动的振幅量级与地铁振动相似或强于地铁振动时, 振动的平均有效强度会包含较多干扰振动信息而导致结果较大的偏差。
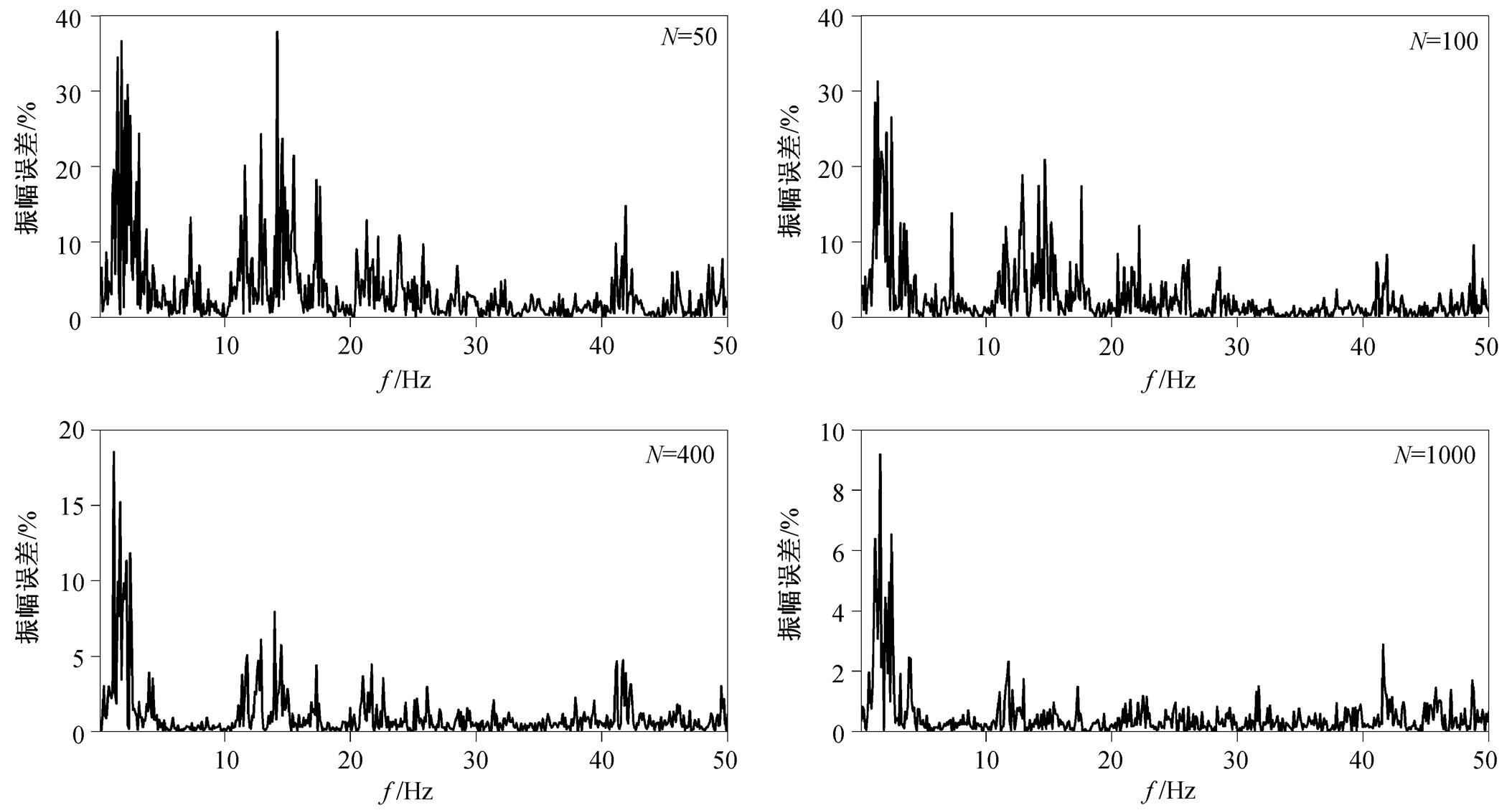
图2 不同叠加次数情况下估计值的相对误差随频率变化
Fig. 2 Relative error of estimated values for different stack times
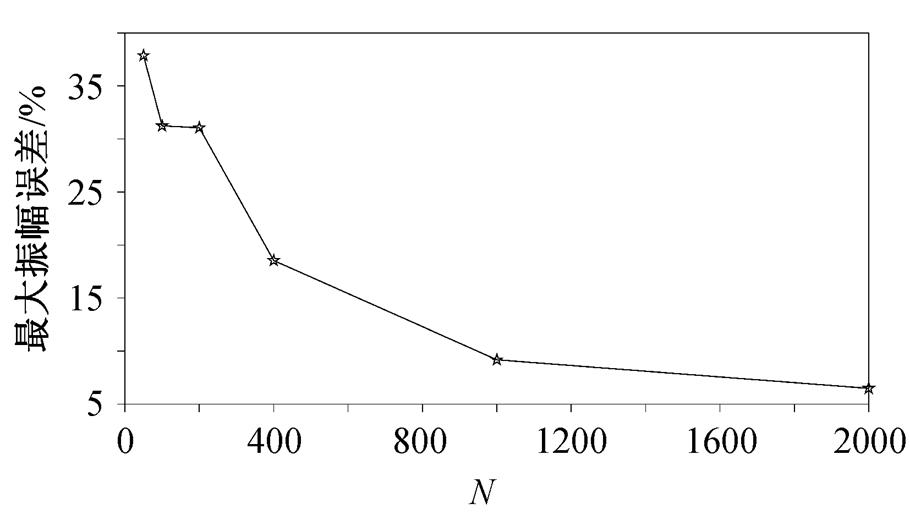
图3 最大相对振幅误差随叠加次数的变化
Fig. 3 Change of the max relative error of frequency with different stack times
4)文献[46]中求方均根谱的方式还会造成信号损失时间信息, 从而使计算结果只包含振幅信息而失去相位信息。
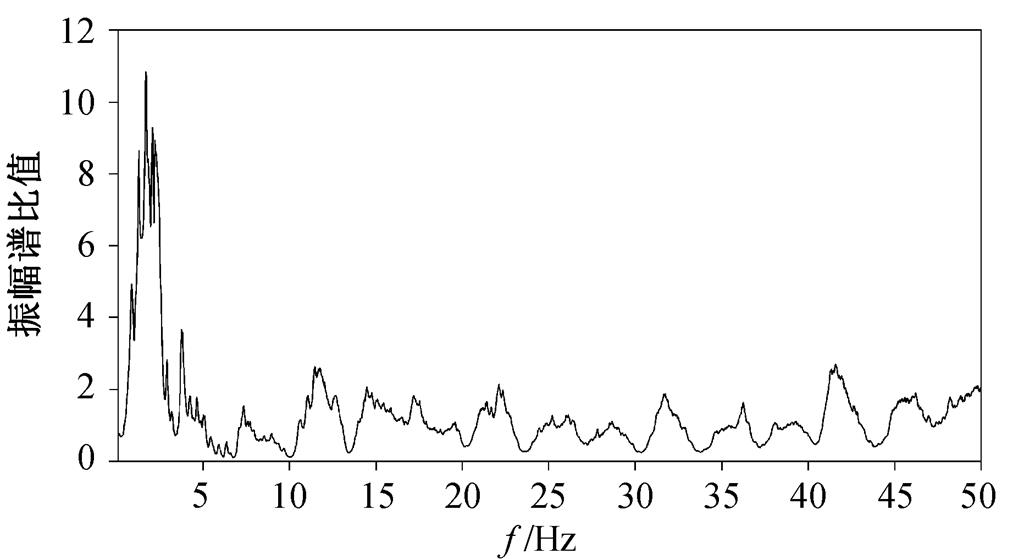
图4 干扰振动振幅谱与高铁振动振幅谱比值
Fig. 4 Spectrum ratio of noise to source
作为对比, 我们使用王博等[46]的谱时程比方法编写程序, 对上述模拟数据进行计算, 检验结果如图5所示。由于谱时程比方法只能计算传递函数的振幅, 因此图5仅对比传递函数设定值的振幅谱与使用该方法的计算结果。图5显示, 王博等[46]方法的结果存在较大的缺陷, 只在振幅较大的区域接近设定值, 而在振幅较小的频段与设定值差异很大。
其他干扰振动振幅的幅值越大, “谱时程”曲线表征的振动平均有效强度受其他干扰振动的影响越大, 可能产生结果偏差越大。图6展示将图5中干扰振动振幅扩大一倍后合成新数据的王博等[46]方法计算结果, 可以看出, 当其他干扰振动噪声的振幅扩大一倍时, 会发生更大的偏差。
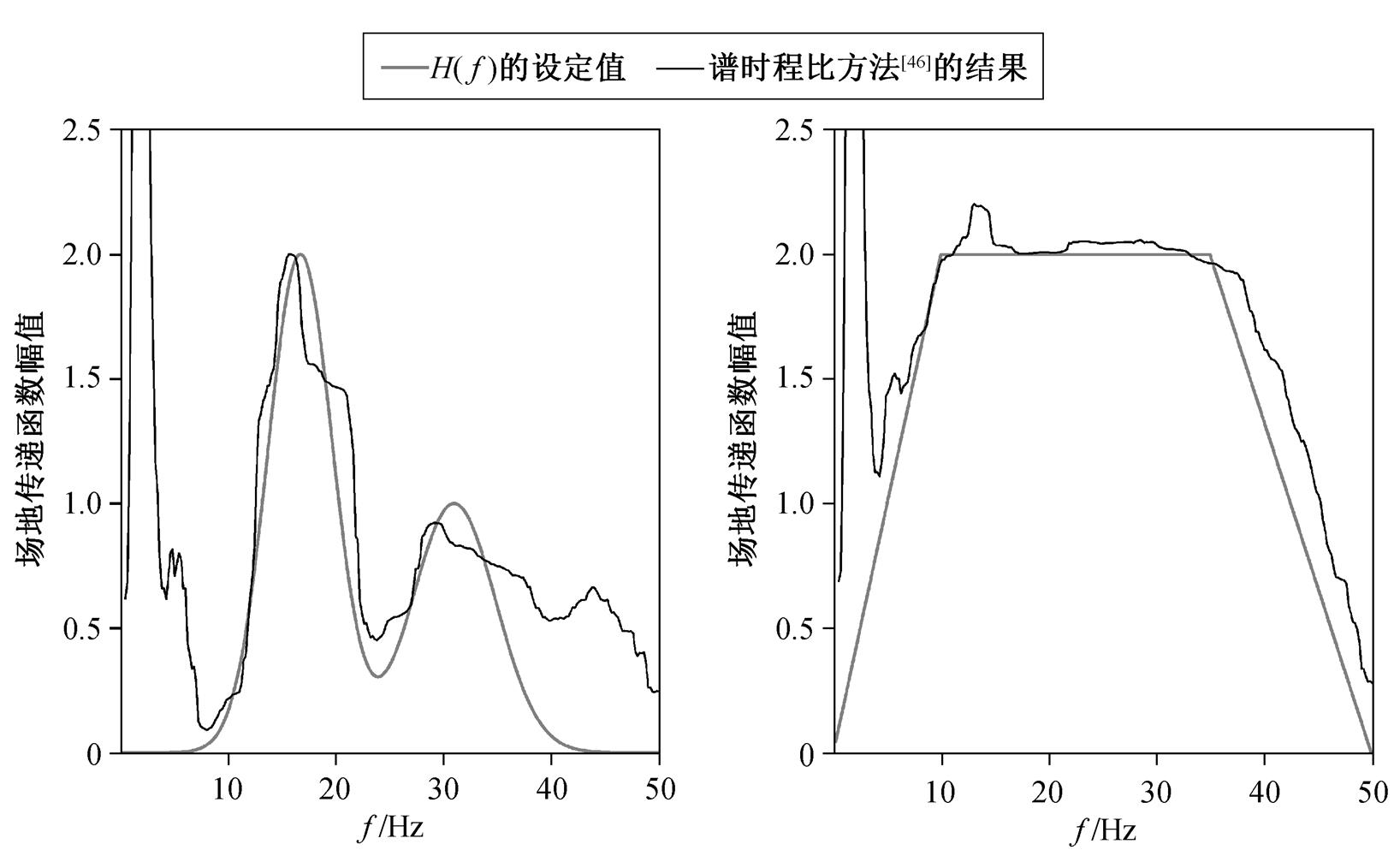
图5 模拟数据的传递函数振幅计算结果
Fig. 5 Transfer-function amplitude of simulated data
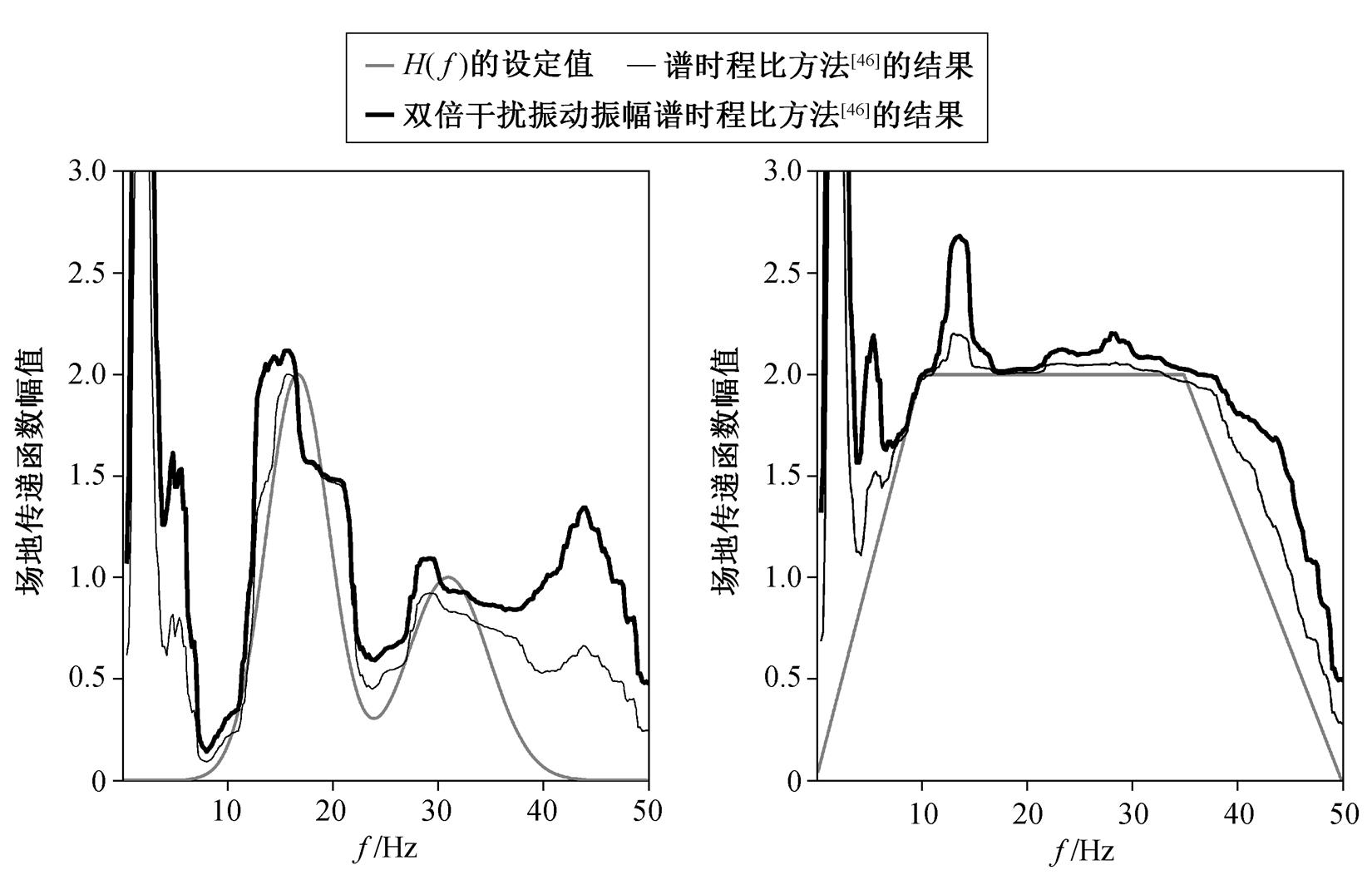
图6 不同干扰振动下的传递函数振幅计算结果对比
Fig. 6 Contrasts of transfer-function amplitude with different noise amplitude
本文提出一种利用互相关叠加计算场地传递函数的方法, 主要反映接收点与源点之间场地土层结构的振动响应。由于地铁隧道通常位于场地浅部, 因此本文方法的计算结果主要反映场地土层浅部结构的振动响应。本文仅利用模拟数据对互相关叠加的方法进行初步探究, 该方法对实际数据的计算效果有待进一步的研究和检验。
由于本文采用高铁振动数据代替地铁振动数据进行模拟, 因此主要反映高铁振动与随机噪声条件下计算结果的误差特征。对于地铁振动的结果, 还需采用地铁振动数据做进一步的分析。但是, 由于高铁和地铁引起的振动在成因上相似, 因此两种振动具有较高的相似性。并且, 从原理上讲, 本文方法要求振源振动与干扰振动相互独立, 不限制振源振动的特征。无论是高铁还是地铁, 引发的振动与其他干扰振动都是相互独立的, 满足方法的应用条件。因此, 本文的数据模拟结果足以证明本文方法的可行性。
致谢 北京大学宁杰远教授提供资料以及建设性的意见,北京大学雷军副教授、西安高新第一中学教师王博以及北京大学研究生刘天时对研究工作提供支持和帮助, 在此表示衷心感谢。
参考文献
[1]Borcherdt R D. Effects of local geology on ground motion near San Francisco Bay. Bulletin of the Seis-mological Society of America, 1970, 60(1): 29‒61
[2]Lermo J, Chavezgarcia F J. Site effect evaluation using spectral ratios with only one station. Bulletin of the Seismological Society of America, 1993, 83(5): 1574‒1594
[3]Bindi D, Parolai S, Cara F, et al. Site amplifications observed in the Gubbio Basin, Central Italy: hints for lateral propagation effects. Bulletin of the Seismolo-gical Society of America, 2009, 99(2A): 741‒761
[4]齐文浩, 薄景山. 土层地震反应等效线性化方法综述. 世界地震工程, 2007, 23(4): 221‒226
[5]Field E H, Jacob K H. A comparison and test of various site-response estimation techniques, including three that are not reference-site dependent. Bulletin of the Seismological Society of America, 1995, 85(4): 1127‒1143
[6]Andrews D J. Objective determination of source para-meters and similarity of earthquakes of different size. Geophysical Monographs Series, 1986, 37: 259‒267
[7]Iwata T, Irikura K. Source parameters of the 1983 Japan sea earthquake sequence. Journal of Physics of the Earth, 1988, 36(4): 155‒184
[8]Boatwright J, Fletcher J B, Fumal. A general inver-sion scheme for source, site, and propagation charac-teristics using multiply recorded sets of moderate-sized earthquakes. Bulletin of the Seismological So-ciety of America, 1991, 81(5): 1754‒1782
[9]Moya A, Aguirre J, Irikura K. Inversion of source parameters and site effects from strong ground motion records using genetic algorithms. Bulletin of the Seismological Society of America, 2000, 90(4): 977‒ 992
[10]Castro R P, Anderson J G, Singh S K. Site response, attenuation and source spectra of S waves along the Guerrero, Mexico, subduction zone. Bulletin of the Seismological Society of America, 1990, 80(6A): 1481‒1503
[11]Parolai S, Bindi D, Augliera P. Application of the generalized inversion technique (GIT) to a microzo-nation study: numerical simulations and comparison with different site-estimation techniques. Bulletin of the Seismological Society of America, 2000, 90(2): 286‒297
[12]Dutta U, Martirosyan A, Biswas N, et al. Estimation of S-wave site response in Anchorage, Alaska, from weak-motion data using generalized inversion method. Bulletin of the Seismological Society of America, 2001, 91(2): 335‒346
[13]章文波, 谢礼立, 郭明珠. 利用强震记录分析场地的地震反应. 地震学报, 2001, 23(6): 604‒614
[14]王宏伟, 温瑞智, 任叶飞, 等. 利用广义反演法分析芦山地震场地反应. 地震工程与工程振动, 2014, 34(4): 35‒41
[15]王宏伟, 任叶飞, 温瑞智. 地震动震源、路径及场地效应分析的广义反演方法研究进展. 地球物理学进展, 2017, 32(1): 78‒86
[16]Nakamura Y. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Railway Technical Research Institute, 1989, 30(1): 25‒31
[17]Yamazaki F, Ansary M A. Horizontal-to-vertical spectrum ratio of earthquake ground motion for site characterization. Earthquake Engineering and Struc-tural Dynamics, 1997, 26(7): 671‒689
[18]Lee C T, Cheng C T, Liao C W, et al. Site classi-fication of Taiwan free-field strong-motion stations. Bulletin of the Seismological Society of America, 2001, 91(5): 1283‒1297
[19]Zhao J X, Irikura K, Zhang J. An empirical site-classification method for strong-motion stations in Japan using H/V response ratio. Bulletin of the Seis-mological Society of America, 2006, 96(3): 914‒925
[20]陈棋福, 刘澜波, 王伟君, 等. 利用地脉动探测北京城区的地震动场地响应. 科学通报, 2008, 53(18): 2229‒2235
[21]王伟君, 刘澜波, 陈棋福, 等. 应用微动 H/V 谱比法和台阵技术探测场地响应和浅层速度结构. 地球物理学报, 2009, 52(6): 1515‒1525
[22]Konon K, Ohmachi T. Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor. Bulletin of the Seismological Society of America, 1998, 88(1): 228‒ 241
[23]任叶飞. 基于强震动记录的汶川地震场地效应研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2014
[24]温瑞智, 冀昆, 任叶飞, 等. 基于谱比法的我国强震台站场地分类. 岩石力学与工程学报, 2015, 34 (6): 1236‒1241
[25]张红才, 徐嘉隽, 陈智勇. 基于噪声谱比法的福建台网观测台站的场地响应研究. 地震学报, 2015, 37(6): 1045‒1058
[26]Idriss I M, Seed H B. Seismic response of horizontal layers. Journal of the Soil Mechanics and Foundations Division, 1968, 94: 1003‒1031
[27]廖振鹏. 地震小区划(理论与实践). 北京: 地震出版社, 1989, 141‒153
[28]蒋通, 邢海灵. 水平土层地震反应分析考虑频率相关性的等效线性化方法. 岩土工程学报, 2007, 29(2): 218‒224
[29]Yoshida N, Kobayashi S, Suetomi I, et al. Equivalent linear method considering frequency dependent cha-racteristics of stiffness and damping. Soil Dynamics and Earthquake Engineering, 2002, 22(3): 205‒222
[30]丁海平, 金星. 土层地震反应传递函数的模拟. 世界地震工程, 2000, 16(4): 36‒41
[31]丁浩. 土层结构对场地传递函数的影响[D]. 哈尔滨: 中国地震局工程力学研究所, 2007
[32]窦立军, 杨柏坡. 场地条件对传递函数的影响. 建筑科学, 2001, 17(3): 41‒46
[33]窦立军, 闫丽, 雷艳. 场地传递函数幅值谱的模拟计算. 长春工程学院学报, 2001, 2(1): 5‒10
[34]赵松戈, 胡聿贤, 廖旭. 土层参数随机性对场地传递函数的影响. 地震工程与工程振动, 2000, 20(2): 7‒12
[35]谢定义. 土动力学. 北京: 高等教育出版社, 2011
[36]高玲利, 夏江海, 潘雨迪. 高分辨线性拉东变换进行模式分离提取面波格林函数//2014 年中国地球科学联合学术年会—— 专题 24: 浅地表地球物理进展. 北京, 2014: 1452
[37]Luo Y H, Xia J H, Miller R D, et al. Rayleigh-wave mode separation by high-resolution linear Radon transform. Geophysical Journal International, 2009, 179(1): 254‒264
[38]夏禾, 曹艳梅. 轨道交通引起的环境振动问题. 铁道科学与工程学报, 2004, 1(1): 44‒51
[39]闫维明, 聂晗, 任珉, 等. 地铁交通引起地面振动的实测与分析. 铁道科学与工程学报, 2006, 3(2): 1‒5
[40]楼梦麟, 贾旭鹏, 俞洁勤. 地铁运行引起的地面振动实测及传播规律分析. 防灾减灾工程学报, 2009, 29(3): 282‒288
[41]陈建国, 夏禾, 陈树礼, 等. 运行列车引起的周围地面振动规律研究. 工程力学, 2010, 27(1): 98‒103
[42]张解东, 徐军, 雷军, 等. 地铁和城铁引起地表振动的测试分析. 现代仪器, 2008(1): 45‒48
[43]张志强, 雷军. 地铁列车运行引起的振动观测及对高精密仪器的影响. 现代仪器, 2011, 17(1): 69‒72
[44]王文斌, 刘维宁, 孙宁, 等. 隧道内脉冲激励下地层振动传递特性研究. 振动与冲击, 2013, 32(8): 162‒165
[45]刘维宁, 陈嘉梁, 吴宗臻, 等. 地铁列车振动环境影响的深孔激振实测传递函数预测方法. 土木工程学报, 2017, 50(9): 82‒89
[46]王博, 雷军. 谱时程比方法及其在确定地铁沿线地层场地响应中的应用. 地震学报, 2015, 37(1): 39‒52
A Method for Estimating the Site-Transfer-Function from Subway Vibration Data
Abstract A correlation-stack method is proposed to estimate the site effect in urban city and its accuracy is proved by simulated data. The method estimates the site-transfer-function from subway vibration data. It eliminates the disturbance of the other urban environmental vibration successfully, which offers a new approach for estima-ting the site effect.
Key words site-transfer-function; subway vibration; urban environmental vibration
doi: 10.13209/j.0479-8023.2018.027
收稿日期: 2018-03-15;
修回日期: 2018-05-11;
网络出版日期: 2018-12-25
内蒙古自治区2016年度科技重大专项“重点地区地震预测预警技术研究开发与推广示范”资助