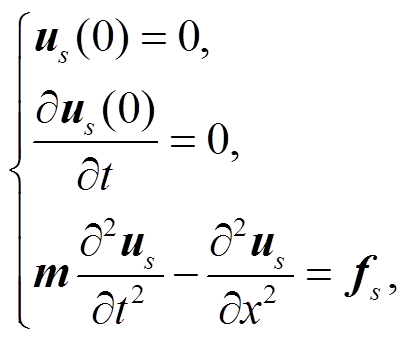 (1)
(1)摘要 为了验证地震学研究中全波形反演方法的有效性, 并研究其收敛特点, 编写基于共轭梯度法的一维地震波全波形反演程序。首先使用单个震源和台站反演出一维非均匀速度结构, 然后通过改变此过程中的各个条件, 讨论不同因素对反演结果的影响。结果显示, 全波形反演在数据较好的情况下能够得到很精确的反演结果; 震源和台站是影响反演的最主要因素; 多尺度反演以及更好的初始模型能够有效地提高反演的稳定性; 观测数据的噪声可使结果产生小尺度的波动, 但在大尺度上对结果的影响相对较小。
关键词 伴随状态法; 共轭梯度法; 全波形反演
确定地球的内部结构是地球物理领域的重要课题之一。反演问题的非线性特点给计算带来较大的难度, 因此发展出各种基于近似理论的反演方法。其中, 基于地震记录中各个震相的走时进行反演的方法被广泛应用[1], 并取得很大的成功。通过走时得到地球内部不同地震波的速度结构图像, 为地球内部的动力学研究提供了基础[2–5]。但是, 基于走时的方法有较明显的局限性: 它所依赖的射线理论只对高频地震波成立, 因此减少了可利用的信息量, 也会给识别震相带来误差, 导致结果准确性降低。
随着计算机硬件技术及算法理论的发展, 使用数值方法模拟地震波场变得越来越容易, 使得基于精确求解波动方程而非基于近似理论的反演方法成为可能。全波形反演是一种通过对合成地震图与观测地震图的差别(即目标函数)求极小值, 从而得到介质结构的反演方法。伴随状态法可以用较小的计算量求得目标函数的梯度, 然后使用共轭梯度法等非线性优化算法得到反演结果, 由于利用了完整的波形信息, 通常情况下能够得到比线性化算法分辨率更高的反演结果。Tarantola[6–8]首先提出基于最小二乘法的时间域全波形反演方法, 并建立全波形反演理论的基本框架。Tromp等[9]论证了全波形反演与有限频层析成像的关系, Chen等[10]反演了洛杉矶地区的三维地壳结构, Wang等[11]反演了比利牛斯山地区的地壳结构, Fichtner[12]反演了澳大得亚地区的壳幔速度结构, Zhu等[13]反演了欧洲地区的壳幔速度结构, Simutė等[14]反演了日本列岛地区的壳幔结构, Bozdağ等[15]开展了全球三维各向异性地壳和地幔结构的全波形反演。
尽管全波形反演已在很多区域得到应用, 并取得较好的结果, 然而该方法的局限性尚未得到很好的解决。由于初始模型、数据质量以及搜索范围等的限制, 模型的更新容易陷入错误的局部极小值, 也很难对反演结果的质量做出较准确的评价。理论测试是反演研究的重要部分, 通过理论测试, 可以对反演过程中各个因素的影响有一个定性的认识, 为实际数据的反演及评价提供基础。Kolb等[16]研究了一维速度结构反演中的多尺度以及噪声等问题。Burstedde等[17]基于一维理论测试, 研究了反演问题中的非线性优化算法、正则化和多尺度反演等问题。Aleardi等[18]研究了基于混合遗传算法的一维全波形反演的不确定性估计问题。
本文研究一维介质的速度结构反演问题。以残差平方和作为目标函数, 利用伴随状态法推导计算目标函数梯度的公式, 并使用共轭梯度法, 在不同尺度上反演模型参数, 讨论不同尺度、震源、台站、初始模型以及噪声等因素对反演结果的影响。由于反演计算与空间维数无关, 本文的结果可以为更高维数以及实际数据的反演提供有效的参考。
一维声波方程满足
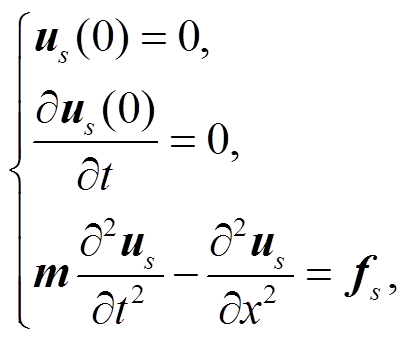 (1)
(1)其中, m为模型参数, 与速度c的关系为m=1/c2, us为震源fs引起的压力场。地震波全波形反演大致包含3 个步骤: 1)选取一个目标函数J(m), 衡量理论波形(正演计算得到的波形)us与观测波形ds的接近程度; 2)求得目标函数的导数∂J/∂m; 3)根据目标函数及其导数的值, 使用非线性优化算法求得目标函数的极小值minmJ(m)及其对应的模型参数m。
目标函数是反演过程中重要的一环, 合适的目标函数能有效地提高反演的收敛速度和结果质量。常用的目标函数有残差平方和、互相关到时差和时频波形差等。其中, 残差平方和具有计算速度快、适用范围较广的优点, 本文用其作为目标函数:
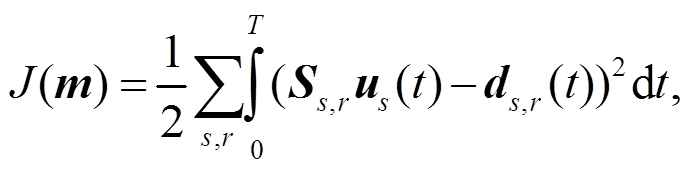 (2)
(2)其中, T 为记录总时长, t 为当前时间, 下角标 s 和 r对应震源和接收点, m为模型参数, us 为震源 s 对应的理论波形, Ss,r为将 us 投影到台站的算子, ds,r为震源 s 在台站 r 处的观测波形。
梯度类反演方法中一项重要的内容是计算目标函数对模型参数的梯度, 即∂J/∂m。由于需要大量的正演运算, 因此使用差分的方式来计算这一梯度变得不切实际。伴随法是解决这一问题的有效方法, 只需进行一次额外的正演计算, 即可求出梯度。本节使用Plessix[19]的推导结果。根据式(1)和(2), 引入函数
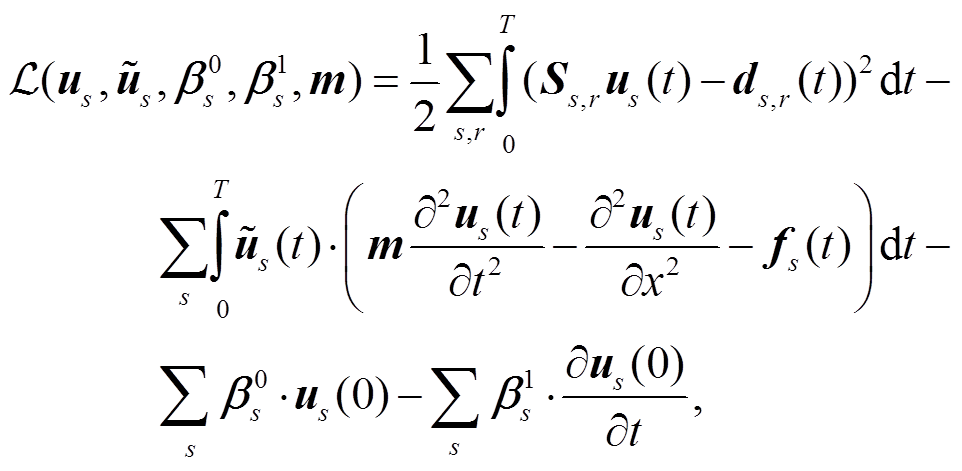 (3)
(3)其中,
 (4)
(4)
取
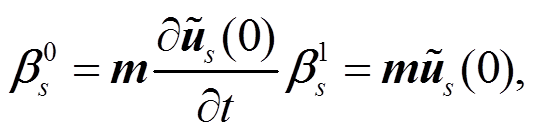 (5)
(5)对 求导可得
求导可得
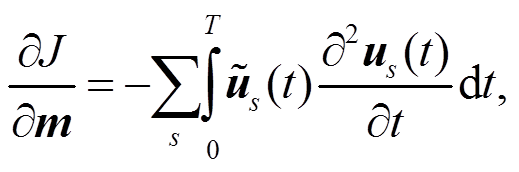 (6)
(6)
其中,  由以下方程解出:
由以下方程解出:
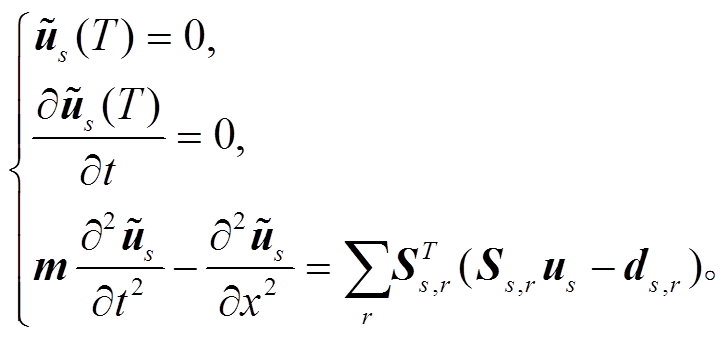 (7)
(7)式(7)的形式与式(1)完全相同, 可用与式(1)相同的方式, 一次正演计算解出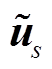 。
。
共轭梯度法是常用的非线性优化算法之一。在求得目标函数及其梯度后, 通过构造一组与梯度相关的且关于Hessian矩阵共轭的向量作为搜索方向, 在每个方向使用一维搜索法进行搜索。不同搜索方向之间互不影响, 可以取得较快的收敛速度。用二阶泰勒展开逼近J(m):
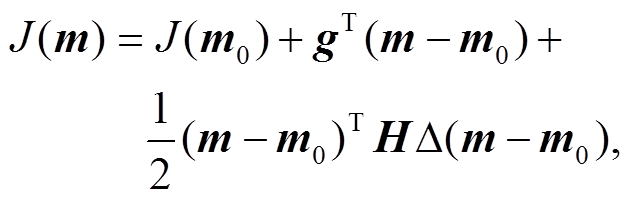 (8)
(8)其中, g为目标函数在m0点的梯度, H为Hessian矩阵。取一组关于H 共轭的向量{ρ1, ρ2, …, ρn}, 即
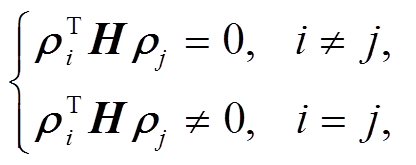
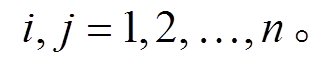 (9)
(9)
第 i 步, 给定一个起始点mi, 选取其中一个向量 ρi作为搜索方向, 通过一维搜索法确定参数ki, 使得J(mi+kiρi)=minkJ(mi+kρi), 然后取mi+1=mi+kiρi作为第i+1步的起始点, 最终得到J(m)的极小值点。采用如下方法选取共轭向量:
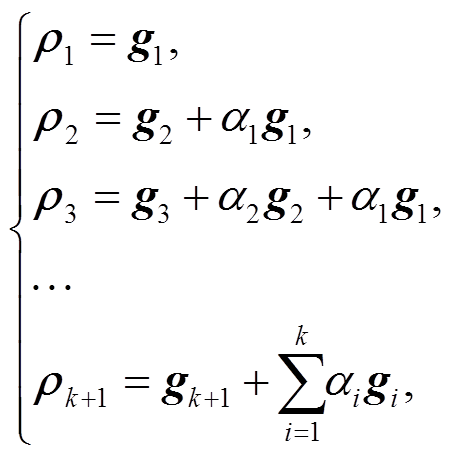 (10)
(10)其中
 (11)
(11)
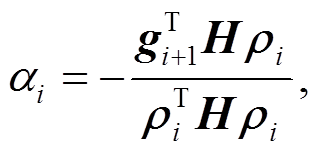 (12)
(12)由于计算H的开销很大, 通常会将式(12)改写, 以避免其出现。将
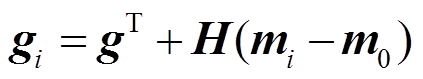 (13)
(13)
代入式(12), 即可得到Fletcher-Reeves公式:
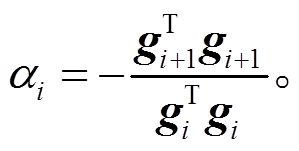 (14)
(14)反演问题的一个难点是初始模型的选取。由于求解反演问题时, 很容易陷入局部极小值, 因此初始模型的选取对反演结果的好坏有很大的影响。多尺度反演是减小局部极小值影响的有效手段, 此方法将模型离散为不同的尺度, 首先使用低频信息, 在大尺度上得到一个较粗略的结果, 然后以此结果作为初始模型, 逐渐提高使用的频率, 并进行更小尺度的反演。由于在大尺度上未知参数少, 更容易找到全局极小值, 因此在大尺度上反演的结果可作为对初始模型的一个很好的猜测。与直接在小尺度上反演相比, 多尺度反演的结果更稳定, 对初始模型的依赖相对较少, 收敛速度更快。
本文在实现多尺度反演的过程中, 没有改变正演用到的网格数, 而是直接改变模型参数的数量, 并通过插值的方法, 映射到正演所用的网格。这样做的好处是, 可以更自由地选择反演的尺度, 从而更好地避免局部极小值的影响。对于目标函数J(m)及模型参数m, 反演的步骤如下。
第一步, 取低网格数模型m′。
第二步, 选取一个合适的频率, 对观测及正演数据进行滤波。
第三步, 用共轭梯度法求得m′的最优解: 1)在正演计算中, 将m′映射到与m相同的维数; 2)计算梯度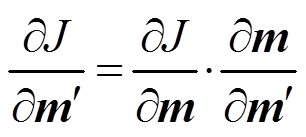 ; 3)用共轭梯度法解出m′。
; 3)用共轭梯度法解出m′。
第四步, 以m′的反演结果作为下一次反演初始模型, 提高m′的网格数及滤波频率, 重复计算直到得到m的最优解。
真实速度模型采用一维非均匀介质, 速度结构如图 1 所示。
正演计算中将模型划分为250个网格, 即Δx= 0.004km。反演的模型参数为5~100个, 并通过线性插值映射到250个网格点。总记录时长为3s, 划分为1500个时间步, 即dt=0.002s。模型顶部采用自由表面条件, 底部为吸收边界条件[20]:
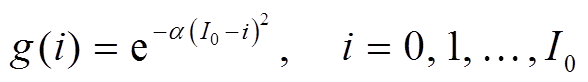 。
。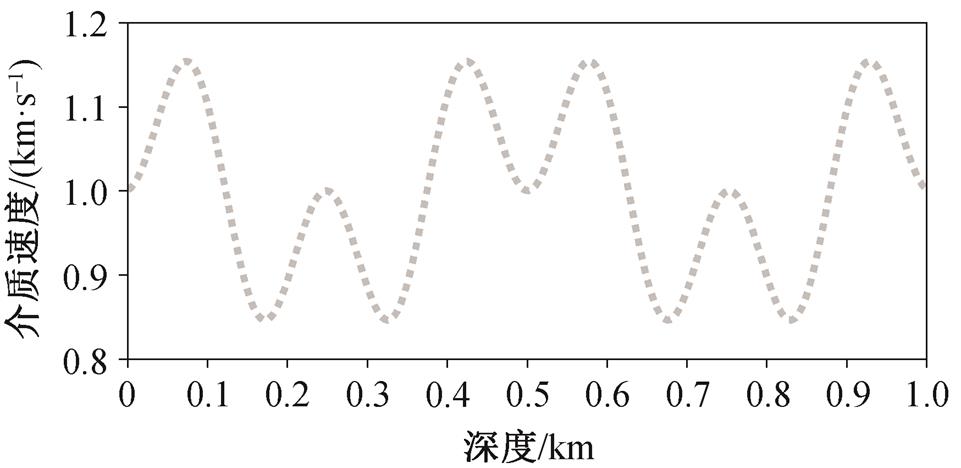
图1 介质速度结构
Fig. 1 Velocity structure of the medium
其中, α 为吸收参数, 取α=0.015; I0为吸收边界的网格数, 取I0=20。吸收边界条件不能完全消除反射波。为降低计算难度, 假设这部分反射波与实际情况相符, 而非边界条件带来的误差。
震源时间函数为Ricker子波:
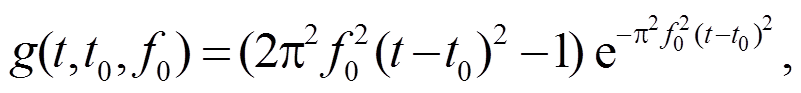
取 f0 = 25 Hz, t0 = 0.16 s。
为检验多尺度反演的有效性, 本节分别计算直接反演100个模型参数以及依次反演5, 10, 25, 50和100个模型参数的结果。对于5, 10, 25和50个模型参数的数据, 分别加入2,4,10和20Hz的低通滤波。初始速度模型为均匀速度模型v0=0.9km/s, 震源深度为0.66km, 接收点深度为0.33km。图 2 显示两种方式得到的最终结果, 可以看出, 多尺度反演显著地提升了反演质量。图 3 显示多尺度反演的中间结果, 可以看出, 多尺度反演相当于给出一个更好的初始模型。
初始速度模型是反演迭代的起点, 对反演结果有着重要的作用。全波形反演的初始速度模型通常由其他方法得到, 比如走时、有限频层析成像等。为研究初始速度模型对反演结果的影响, 本节使用6个均匀模型作为初始速度模型, 速度分别为0.5, 0.6, 0.7, 0.8, 1.0和1.1 km/s, 震源深度为0.66 km, 接收点深度为0.33 km。
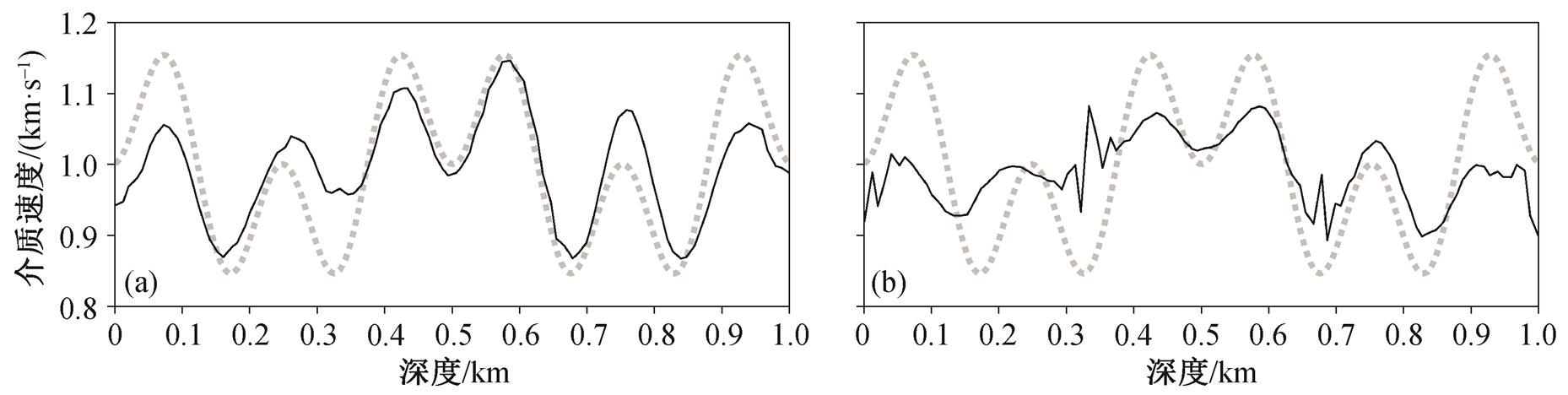
虚线代表真实模型, 实线表示反演结果, 下同
图2 使用多尺度(a)和未使用多尺度(b)反演得到的结果
Fig. 2 Inversion result with multi-scale technique (a) and without multi-scale-technique (b)
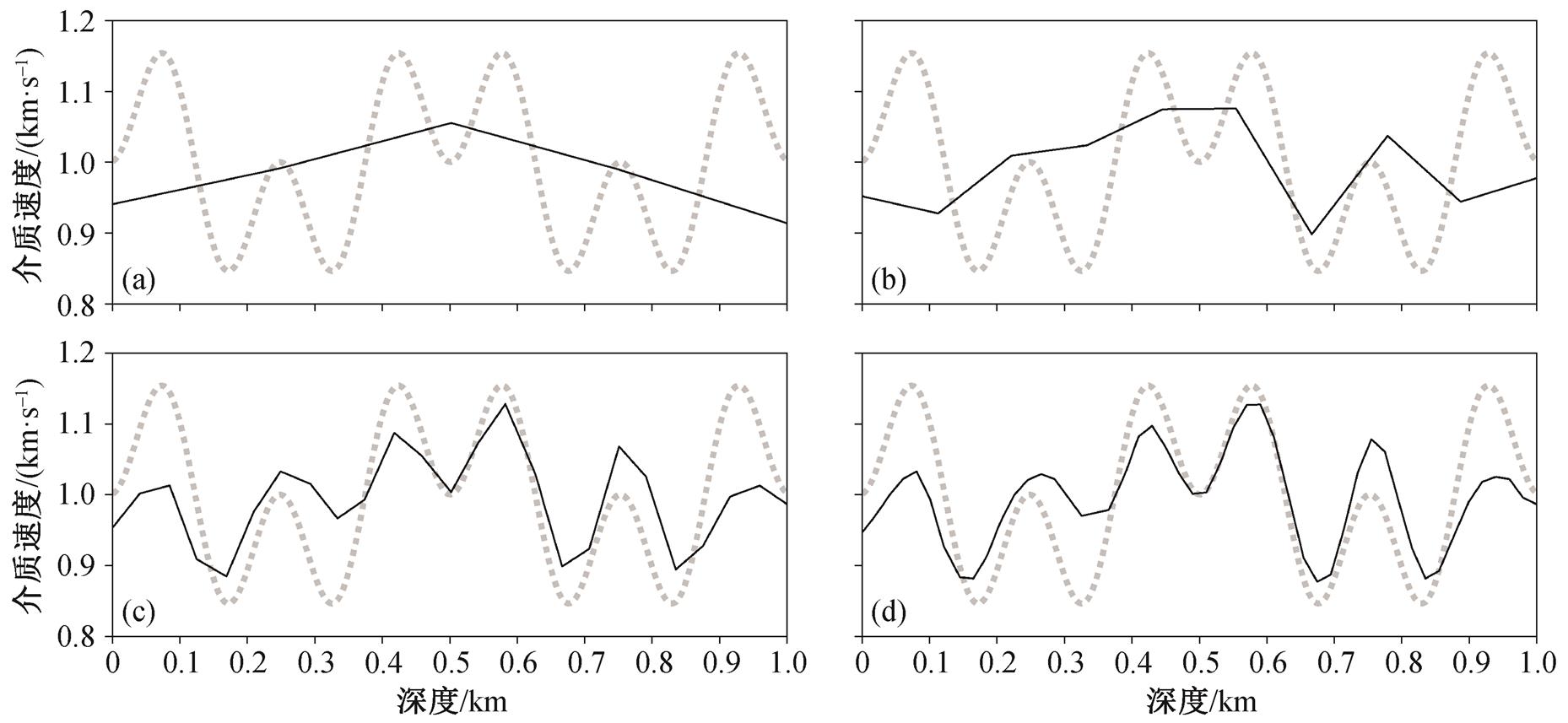
(a)模型参数为5个; (b)模型参数为10个; (c)模型参数为25个; (d)模型参数为50个
图3 不同数量模型参数的反演结果
Fig. 3 Inversion result under different number of model parameters
从图4可以看出, 反演结果强烈地依赖于初始速度模型的选取, 当初始速度模型偏离较远时, 反演收敛到的局部极小值完全无法反映真实模型的特征。因此, 一个相对准确的初始速度模型是反演成功的前提。
本文使用的模型相对简单, 仅通过走时就能估计出一个较好的一维速度作为初始模型。但是, 对于更复杂的模型, 走时给出的偏差可能大到无法收敛。为了完整地了解初始模型与收敛性的关系, 本节选择的初始模型速度范围较大, 没有考虑走时的约束。
数据量是反演可靠性的重要保证, 充足的地震记录能够有效地减少局部极小值的影响, 并提升收敛速度和反演结果质量。图 5 显示不同震源及接收点数量条件下的反演结果, 其中震源和接收点均为均匀分布, 初始模型为均匀模型。可以看出, 随着数据量的增加, 反演结果有明显变好的趋势, 说明数据量能够在一定范围内弥补初始模型的不足。对于实际模型的反演, 初始模型通常能够得到一个较好的估计值, 因此数据量通常是决定反演结果好坏的主要因素。
噪声在实际观测数据中无法避免, 如何消除噪声是反演研究的重要课题。由于噪声的复杂性, 很难在保证数据质量的前提下将其完全消除。为了更接近真实情况, 本文假设在接收点的波形中存在服从正态分布的随机扰动dp~N(μ,σ2), 均值取 μ=0, 标准差参照接收点最大震幅max(p0)的大小取不同的值, σ=k·max(p0), 初始模型v0=0.9km/s, 震源深度为 0.66km, 接收点深度为 0.33km。k依次取0.5%, 1%, 2% 和 3%。从图 6 可以看出, 反演结果在大尺度上与实际结果趋势一致, 但噪声的扰动在小尺度上导致不规则振荡, 振荡幅度随着扰动强度的增加而增加。由于噪声的存在, 反演结果在一个区间内随机分布, 因此要对噪声有一个较准确的估计, 才能根据反演结果更准确地推测实际模型。
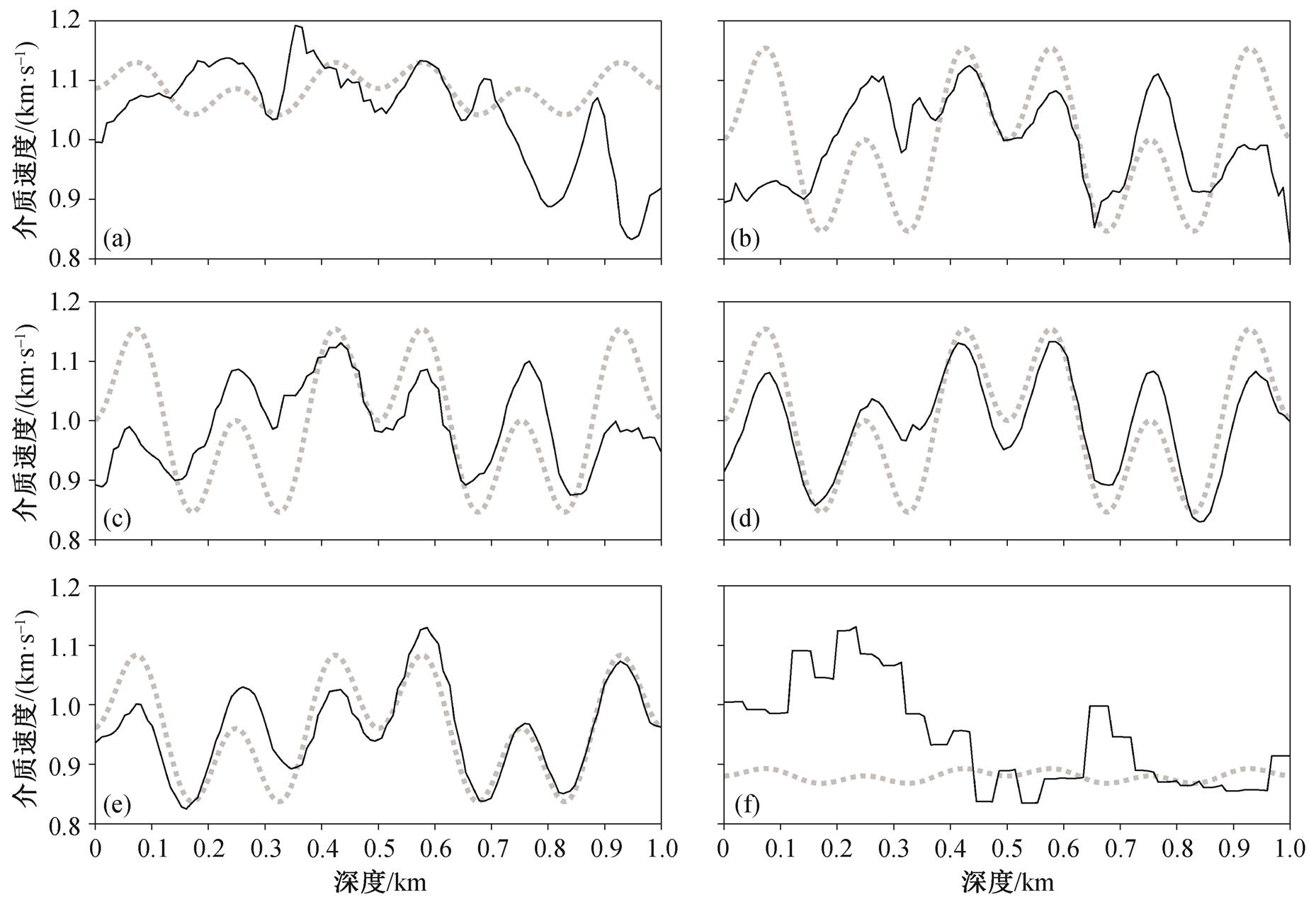
(a)~(f)的初始速度分别为0.5, 0.6, 0.7, 0.8, 1.0和1.1 km/s
图4 不同初始速度模型的反演结果
Fig. 4 Inversion result under different velocity models
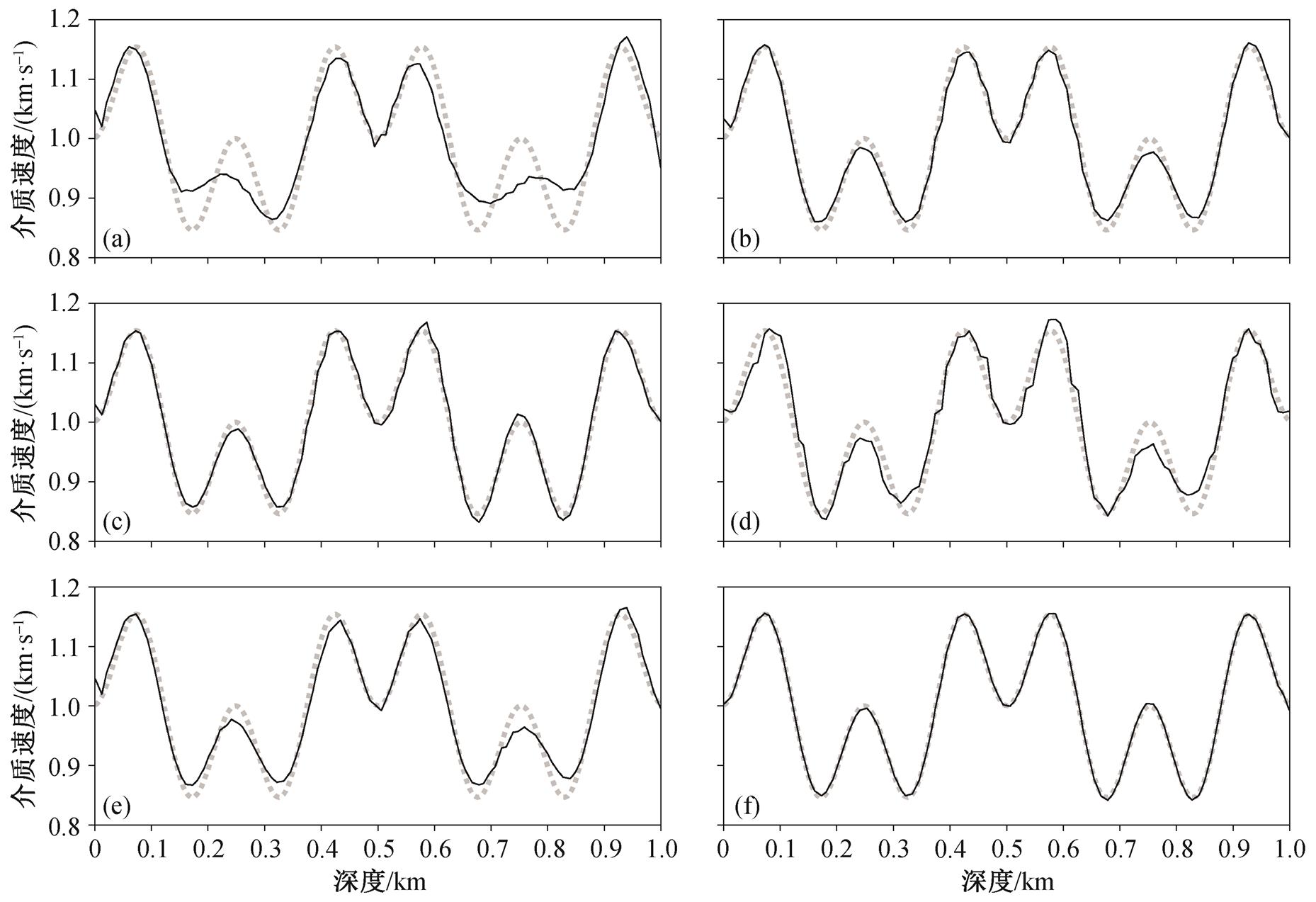
(a) v0=0.7 km/s, 1个震源, 6个接收点; (b) v0=0.7 km/s, 6个震源, 1个接收点; (c) v0=0.7km/s, 6个震源, 6个接收点; (d) v0=0.9 km/s, 1个震源, 6个接收点; (e) v0=0.9 km/s, 6个震源, 1个接收点; (f) v0=0.9 km/s, 6个震源, 6个接收点。1个震源或1个接收点的位置: 0.5 km; 6个震源或6个接收点的位置: 0.14, 0.29, 0.43, 0.57, 0.71, 0.86 km
图5 不同震源及接收点数量下的反演结果
Fig. 5 Inversion result under different number of sources and receivers
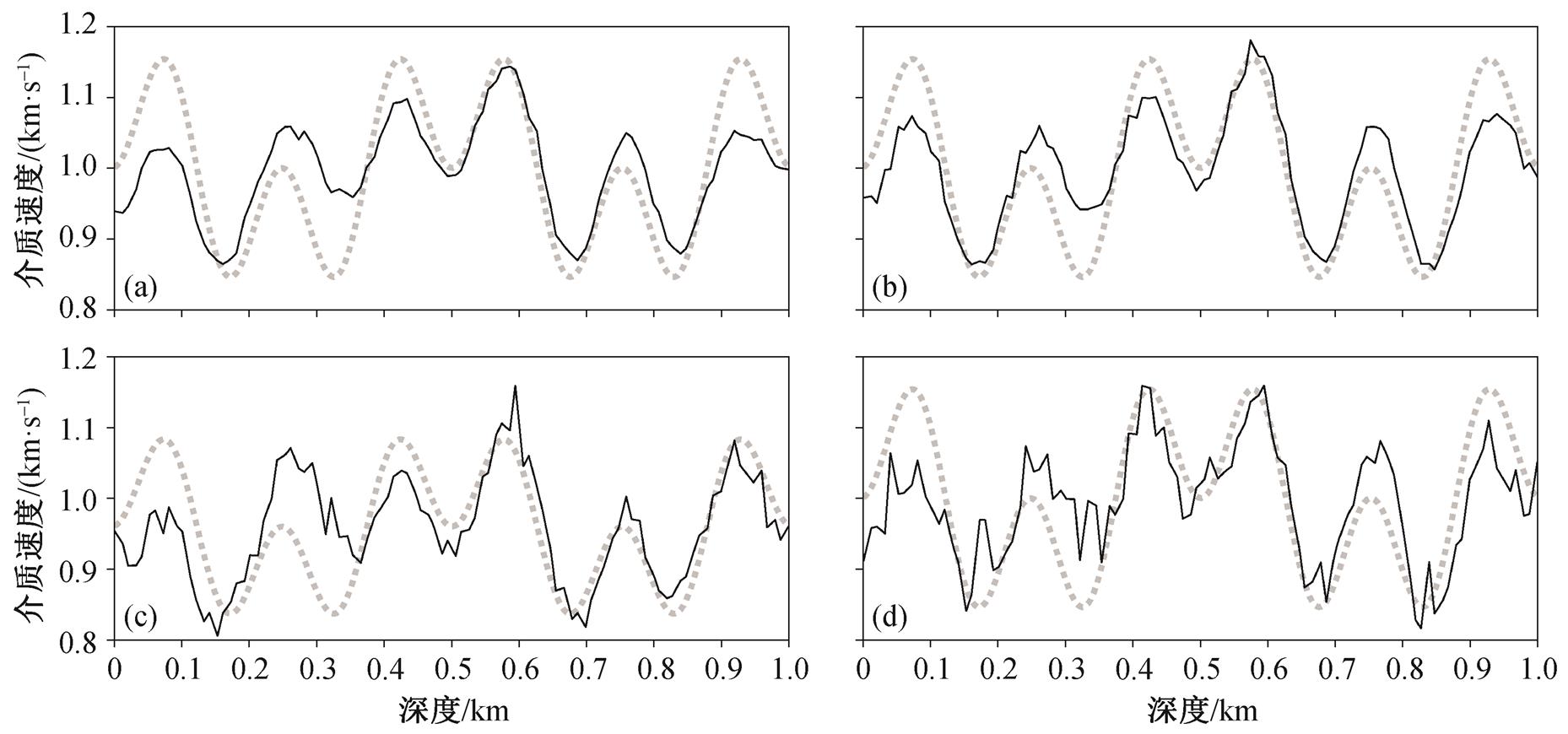
(a) k=0.5%; (b) k =1%; (c) k =2%; (d) k =4%
图6 不同噪声条件下的反演结果
Fig. 6 Inversion result under different noise conditions
本文使用伴随法和共轭梯度法进行一维全波形反演的研究, 并使用模拟介质, 在不同条件下进行反演计算, 得到与理论值比较接近的结果。计算过程中未利用一维介质的走时等性质, 反演问题的计算过程与维度无关, 比较容易推广到二维或三维。在本文研究的影响反演的因素中, 重要性从大到小依次为震源及台站的数量→初始模型的选择→多尺度反演→随机噪声。
积极布设台站, 利用尽可能多的地震数据, 依然是提升反演结果质量的最有效手段。当地震及台站数量有限时, 通过走时反演等其他方法得到更精确的初始模型, 同样能显著地改善反演结果。多尺度反演也是改进反演结果的有效方法, 但它带来的额外计算量同样不可忽视。因此, 是否使用多尺度反演, 要综合考虑现有的数据条件及先验信息。在观测波形中引入随机噪声, 通常对结果的整体趋势影响较小, 但会带来小尺度的扰动, 要求对噪声有一个大致的估计。
参考文献
[1]Fichtner A, Bunge H P, Igel H. The adjoint method in seismology, Physics of the Earth and Planetary Inte-riors, 2006, 157(1/2): 86‒104
[2]Dziewonski A M, Anderson D L. Preliminary refe-rence Earth model. Physics of the Earth & Planetary Interiors, 1981, 25(4): 297‒356
[3]Bording R P, Gersztenkorn A, Lines L R, et al. App-lications of seismic travel-time tomography. Geo-physical Journal of the Royal Astronomical Society, 2010, 90(2): 285‒303
[4]Inoue H, Fukao Y, Tanabe K, et al. Whole mantle P-wave travel time tomography. Physics of the Earth & Planetary Interiors, 1990, 59(4): 294‒328
[5]Kennett B L N, Engdahl E R, Buland R. Constraints on seismic velocities in the Earth from traveltimes. Geophysical Journal of the Royal Astronomical So-ciety, 1995, 122(1): 108‒124
[6]Tarantola A. Inversion of seismic data in acoustic approximation. Geophysics, 1984, 49(8): 1259‒1266
[7]Tarantola A. Inverse problem theory: methods for data fitting and model parameter estimation. Physics of the Earth & Planetary Interiors, 1987, 57(3): 350‒351
[8]Tarantola A. Theoretical background for the inversion of seismic waveforms including elasticity and attenu-ation. Pure & Applied Geophysics, 1988, 128(1/2): 365‒399
[9]Tromp J, Tape C, Liu Q. Seismic tomography, adjoint methods, time reversal and banana-doughnut ker-nels. Geophysical Journal of the Royal Astronomical Society, 2010, 160(1): 195‒216
[10]Chen P, Zhao L, Jordan T H. Full 3D tomography for the crustal structure of the los angeles region. Bulletin of the Seismological Society of America, 2007, 97(4): 1094‒1120
[11]Wang Y, Chevrot S, Monteiller V, et al. The deep roots of the western Pyrenees revealed by full wave-form inversion of teleseismic P waves. Geology, 2016, 44(6): G37812.1
[12]Fichtner A. Full seismic waveform inversion for structural and source parameters [D]. Munich: Lud-wig Maximilian University of Munich, 2010
[13]Zhu H, Bozdağ E, Peter D, et al. Structure of the European upper mantle revealed by adjoint tomogra-phy. Nature Geoscience, 2012, 5(7): 493‒498
[14]Simutė S, Steptoe H, Cobden L, et al. Full-waveform inversion of the Japanese Islands region. Journal of Geophysical Research Solid Earth, 2016, 121(5): 3722‒3741
[15]Bozdağ E, Peter D, Lefebvre M, et al. Global adjoint tomography: first-generation model. Geophysical Jour-nal International, 2016, 207(3) : 1739‒1766
[16]Kolb P, Collino F, Lailly P. Pre-stack inversion of a 1-D medium. Proceedings of the IEEE, 2005, 74(3): 498‒508
[17]Burstedde C, Ghattas O. Algorithmic strategies for full waveform inversion: 1D experiments. Geophysics, 2009, 26(1): WCC37
[18]Aleardi M, Mazzotti A. 1D elastic full-waveform inversion and uncertainty estimation by means of a hybrid genetic algorithm —Gibbs sampler approach. Geophysical Prospecting, 2016, 65(1): 64‒85
[19]Plessix R E. A review of the adjoint‐state method for computing the gradient of a functional with geo-physical applications. Geophysical Journal of the Ro-yal Astronomical Society, 2010, 167(2): 495‒503
[20]Cerjan C, Dan K, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equations. Geophysics, 1985, 50(4): 705‒708
A Synthetic Study on Full Seismic Waveform Inversion for One Dimensional Velocity Structure
Abstract A conjugate gradient full waveform inversion program is coded to verify the effectiveness of full seismic waveform inversion and to study its characteristics. Firstly, a one dimensional inhomogeneous model is inverted using one source and one receiver. Then, by modifying different parameters of the inversion, the factors that affect the inversion result are discussed. It is shown that full waveform inversion can produce accurate result when data is abundant. The number of sources and stations is the primary factor that affect the inversion result. Multiscale inversion and better initial model can significantly improve the stability of the inversion. Noise applied to the observed seismogram can cause small scale disturbance on the result, though large scale characteristics of the result remain more or less unaffected.
Key words adjoint method; conjugate gradient method; full waveform inversion
doi: 10.13209/j.0479-8023.2018.029
收稿日期: 2018-03-11;
修回日期: 2018-07-03;
网络出版日期: 2018-12-05
国家自然科学基金(41674052)资助