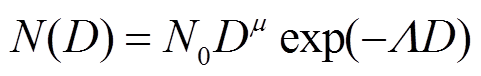 , (1)
, (1)摘要 针对GPM-CODPR观测数据反演雨滴谱算法中存在的双值问题, 提出通过匹配地面S波段天气雷达与GPM-CODPR观测数据, 为双值问题提供判断依据的方法。在建立反演查算方法的基础上, 利用雷达仿真程序Quickbeam进行算法的理论验证, 并使用观测数据进行实例验证。理论验证的结果表明, 反演结果数据和输入数据的相关系数达到0.99以上; 实例验证的结果显示, 利用此反演算法得到的雨滴谱可以反映降水过程中雨滴粒径的分布情况, 在一定程度上解决双值问题。
关键词 GPM计划; 双频降水雷达(DPR); S波段天气雷达; 雨滴谱; 反演算法; 双值问题
全球降水观测(global precipitation measure-ment, GPM)计划是美国国家航空航天局(National Aeronautics and Space Administration, NASA)和日本宇宙航空研究开发机构(Japan Aerospace Explo-ration Agency, JAXA)主导的新一代卫星观测项目, 为热带降雨观测任务(tropical rainfall measuring mission, TRMM)的升级版本, 其目标是实现对全球范围的降水观测。与TRMM相比, GPM计划的观测范围更广, 观测精度更高, 可以实现对弱降雨和降雪的观测。
作为GPM计划的核心组成部分, GPM核心观测卫星(GPM Core Observatory, 简称GPM-CO)于2014年2月27日成功发射, 3月开始返回观测数据。GPM-CO上搭载的主要探测仪器为双频降水雷达(Dual-frequency Precipitation Radar, DPR)和GPM微波成像仪(GPM Microwave Imager, GMI), 其中DPR为TRMM卫星上搭载的降水雷达(Precipitation Radar, PR)的升级版, 有两个探测波段, 分别为与PR相似的13.6GHz的Ku波段和35.5GHz的Ka波段[1]。与Ku波段相比, Ka波段的波长更短, 可以探测降水强度更小的降雨和降雪过程, 但降水造成的衰减比Ku波段严重。
除GPM-CO外, GPM计划还包括Suomi NPP, NOAA 18/19和MetOp B/C等一系列观测卫星, 这些卫星基本上采用被动遥感的探测方式。GPM计划的任务是将GPM-CO的探测数据作为标准, 为其他卫星的标定提供参考, 提高被动遥感的准确性。自GPM-CO发射入轨以来, 已获得大量的观测数据, 可为研究降水和预防洪涝灾害提供很大的帮助。
目前, 基于GPM-CODPR观测数据的雨滴谱(raindrop size distribution, RSD)反演算法仍存在一些问题。雨滴谱分布与降水观测中的很多参数(如雷达反射率因子、雨强以及降水衰减等)都紧密相关, 对研究降水的形成机制和发展演变等十分重要, 因此获取降水过程的雨滴谱分布是降水观测中的一个主要任务。在GPM项目组使用的由 Iguchi等[2]编写的DPR观测数据二级算法中, 通过建立两个波段的差分反射率因子DFR和雨滴谱的特征直径的查算表来进行雨滴谱的反演。但是, 在此查算表中存在双值问题, 即同一个差分反射率因子DFR可能对应两个特征直径。Chandrasekar等[3]、Bringi等[4]和Khajonrat等[5]提出通过补充降水过程中雨滴谱分布参数的线性约束的合理假设来规避双值问题, 但不能从根本上解决双值问题。
为解决双值问题, 本文提出通过匹配地面S波段天气雷达与GPM-CO DPR的观测数据, 实现对同一降水过程的三波段观测方法。S波段雷达的观测数据可以在反演雨滴谱函数出现双值问题时提供一个判断依据, 实现双值的筛选。选择S波段天气雷达与DPR数据进行匹配, 主要基于以下两方面的原因: 1) S波段天气雷达应用广泛, 国内已经基本上实现组网, 对陆面的覆盖率高; 2)降水对S波段雷达造成的降水衰减小, 在降水不强的情况下, 基本上可以忽略, 因此匹配之后, S波段雷达的观测数据可以为DPR观测数据的衰减订正提供参考。
Ulbrich[6]指出, Gamma分布可以充分地表现降水粒子的粒径分布特点, 其表达式为
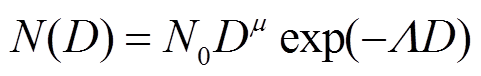 , (1)
, (1)D为雨滴直径; N0, μ和Λ分别为截距、形状因子和斜率, 三者决定谱分布函数的图像形状[7]。在实际运用中, 更多使用Gamma分布函数的变形形式:
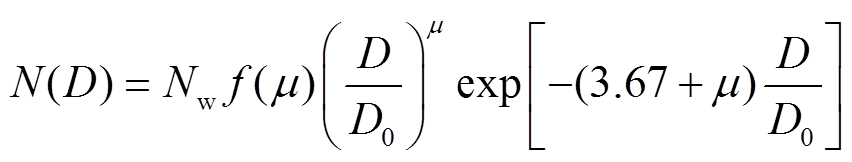 , (2)
, (2)
其中,
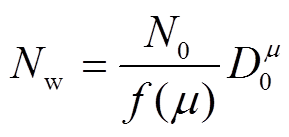 , (3)
, (3)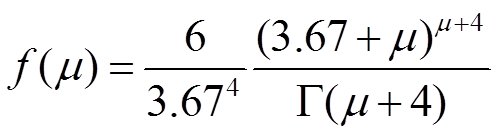 , (4)
, (4)
D0为雨滴的中值直径, 直径小于D0的雨滴含水量占总含水量的一半。D0 与μ和Λ存在以下关系[6]:
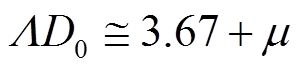 。 (5)
。 (5)雷达观测到的反射率因子为
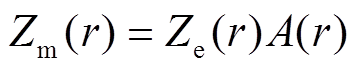 , (6)
, (6)
Ze(r)为等效反射率因子, A(r)为衰减因子, r为被测物体到雷达的距离。等效反射率因子的计算公式为
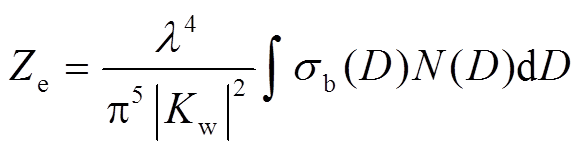 , (7)
, (7)式中, σb为粒子的后向散射截面; λ为雷达探测波段的波长; Kw的表达式为
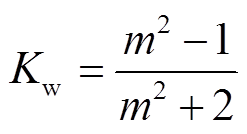 , (8)
, (8)
其中, m为复折射指数[8]。将式(2)代入式(7), 可得

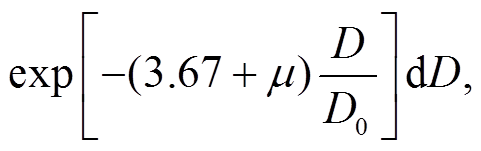 (9)
(9)
令
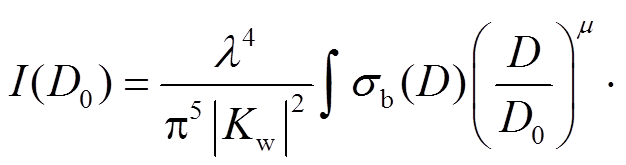
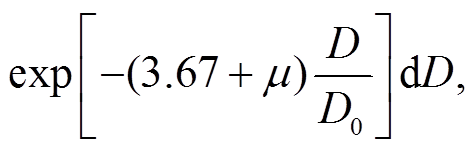 (10)
(10)
则
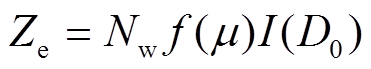 。 (11)
。 (11)对于两个不同的雷达探测波段, 可以获得相对应的等效反射率因子, 分别记为Ze1和Ze2, 此时可以计算得到差分反射率因子DFR, 其定义为
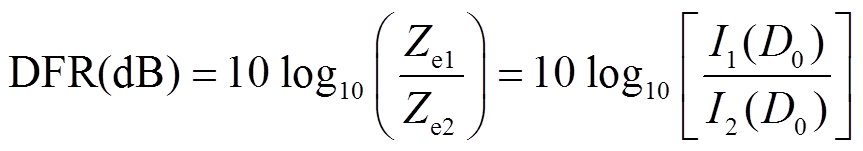 。 (12)
。 (12)
从式(12)看出, 当形状因子μ取固定值时, DFR仅与中值直径D0有关, 这样便可以建立两者的函数关系。通过观测得到的等效反射率因子获取DFR, 利用DFR与D0的函数关系获取D0值, 从式(11)可以得到Nw值, 这样便得到反演的雨滴谱分布函数。根据上述推导过程, 要建立DFR与D0的查算关系, 需要获得雨滴对3个波段的复折射指数m和单个雨滴粒子的后向散射截面σb。Segelstein[9]通过理论计算, 给出液态水对不同波长电磁波的复折射指数(表1)。在计算单个雨滴粒子的后向散射截面σb时, 则是利用Mätzler[10]开发的Matlab计算程序, 该程序可以给出单个粒子米散射理论计算的各个参数。在上述基础上利用Matlab进行编程计算, 建立DFR与D0的查算表。在本算法中, 选用Ku-Ka和S-Ku这两个差分反射率因子来进行雨滴谱的反演。
表1 3个波段的相关信息[9]
Table 1 Information of three bands[9]
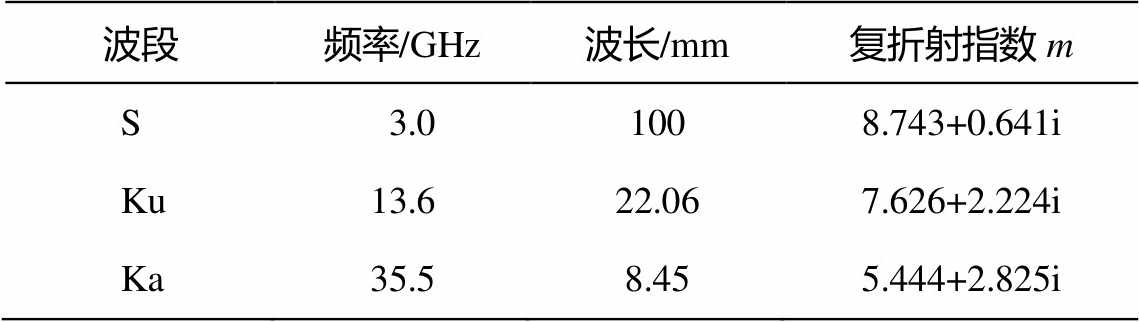
波段频率/GHz波长/mm复折射指数m S 3.01008.743+0.641i Ku13.622.067.626+2.224i Ka35.58.455.444+2.825i
对于降雨过程, Gamma分布函数的形状因子μ的取值范围为0~3, 在多数情况下的取值为3。对μ分别取值0, 1, 2和3, 计算得到图1所示的DFR与D0的函数曲线。可以看出, 若仅使用GPM-CO DPR的观测数据来进行雨滴谱反演, 当DFR(Ku-Ka)值小于0时, 便会出现双值问题, 即一个DFR(Ku-Ka)值对应两个D0值。以μ=3为例, 当D0<1.43mm时, DFR(Ku-Ka)<0, 对应的雨滴谱分布的雨滴平均直径约为0.86mm。在层状云降水中, 雨滴的平均直径一般小于0.86mm, 即双值问题在层状云降水的观测中较常见。观测数据也证实了这一结论, 在GPM-CO DPR对层状云降水和混合型降水的观测数据中, DFR(Ku-Ka)小于0的情况普遍存在。
在实现地面S波段雷达和DPR的观测数据匹配之后, 可以获得另外两组DFR值, 这里选用DFR(S-Ku)为双值问题提供判断依据。在形状因子μ取值固定的情况下, 当DFR(Ku-Ka)>0时, 从图1可以看出, 随着D0增大, DFR(Ku-Ka)呈单调递增的趋势, 则仅基于DPR的观测数据, 即可得到D0值。当DFR(Ku-Ka)<0时, 从图1中的DFR(Ku-Ka)-D0曲线可获得两个D0值, 分别记为D01和D02。若DFR(S-Ku)<0, 则对应的D0值记为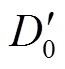 , 取D01和D02当中最接近
, 取D01和D02当中最接近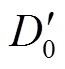 的值与D'0取平均, 作为反演所得的D0值; 若DFR(S-Ku)>0, 同样对应两个D0值, 分别记为
的值与D'0取平均, 作为反演所得的D0值; 若DFR(S-Ku)>0, 同样对应两个D0值, 分别记为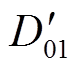 和
和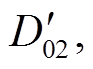 与D01和D02两两配对, 共有4组数据, 选择差值最小的一组数据的平均值作为反演所得的D0值。在获得D0值之后, 从式(10)和(11)可以得到Nw值, 这样就获得降雨过程的雨滴谱分布函数。
与D01和D02两两配对, 共有4组数据, 选择差值最小的一组数据的平均值作为反演所得的D0值。在获得D0值之后, 从式(10)和(11)可以得到Nw值, 这样就获得降雨过程的雨滴谱分布函数。
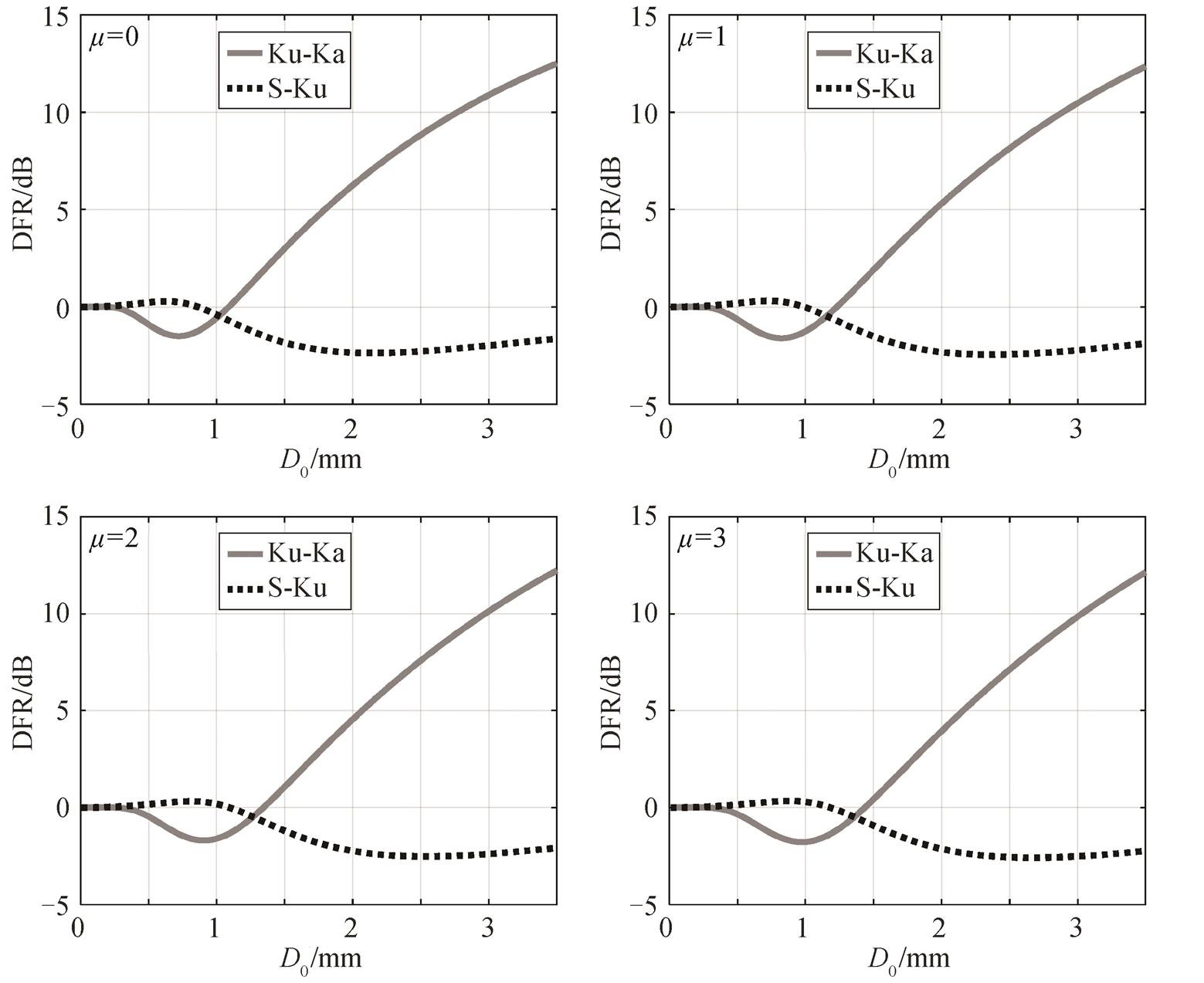
图1 不同μ值的DFR-D0曲线
Fig. 1 Curves of DFR- D0 with different μ
实现雨滴谱反演之后, 需要对算法进行检验。检验分为两部分: 利用雷达仿真程序Quickbeam进行理论验证; 利用观测数据进行实例验证。
2.1.1 Quickbeam 程序
检验雨滴谱反演算法需要有一个已知雨滴谱分布的降水过程及其对应的3个雷达探测波段的雷达反射率因子数据, 本文利用Quickbeam实现数据的获取。Quickbeam是Haynes等[11]开发的一套用于气象雷达仿真的程序, 可以实现卫星搭载和地面设置的各探测波段气象雷达的数据仿真, 工作流程如下: 输入雷达信息、水成物信息和大气环境信息; 通过米散射理论计算及大气衰减计算后, 输出雷达反射率因子及衰减量的廓线。雷达信息包括雷达位置及探测波段频率, 水成物信息包括水成物的种类、相态、谱分布模型以及混合比廓线, 大气环境信息包括气压、温度和相对湿度的廓线。
Haynes等[11]在程序中提供了一个样本数据, 其大气环境信息及水成物的混合比廓线如图2(a)~(c)所示。可以看出, 当高度在约1.6km以下时, 雨滴的混合比较均匀, 为一个稳定的降雨区域。将该样本数据作为Quickbeam的输入量, 分别对DPR的两个波段和地基S波段雷达进行仿真, 得到的反射率因子廓线如图2(d)~(f)所示。可以看出, S波段的衰减量最小, 两条曲线几乎重合; Ka波段的衰减量最大, 在降雨区域最明显; Ku波段则介于二者之间。
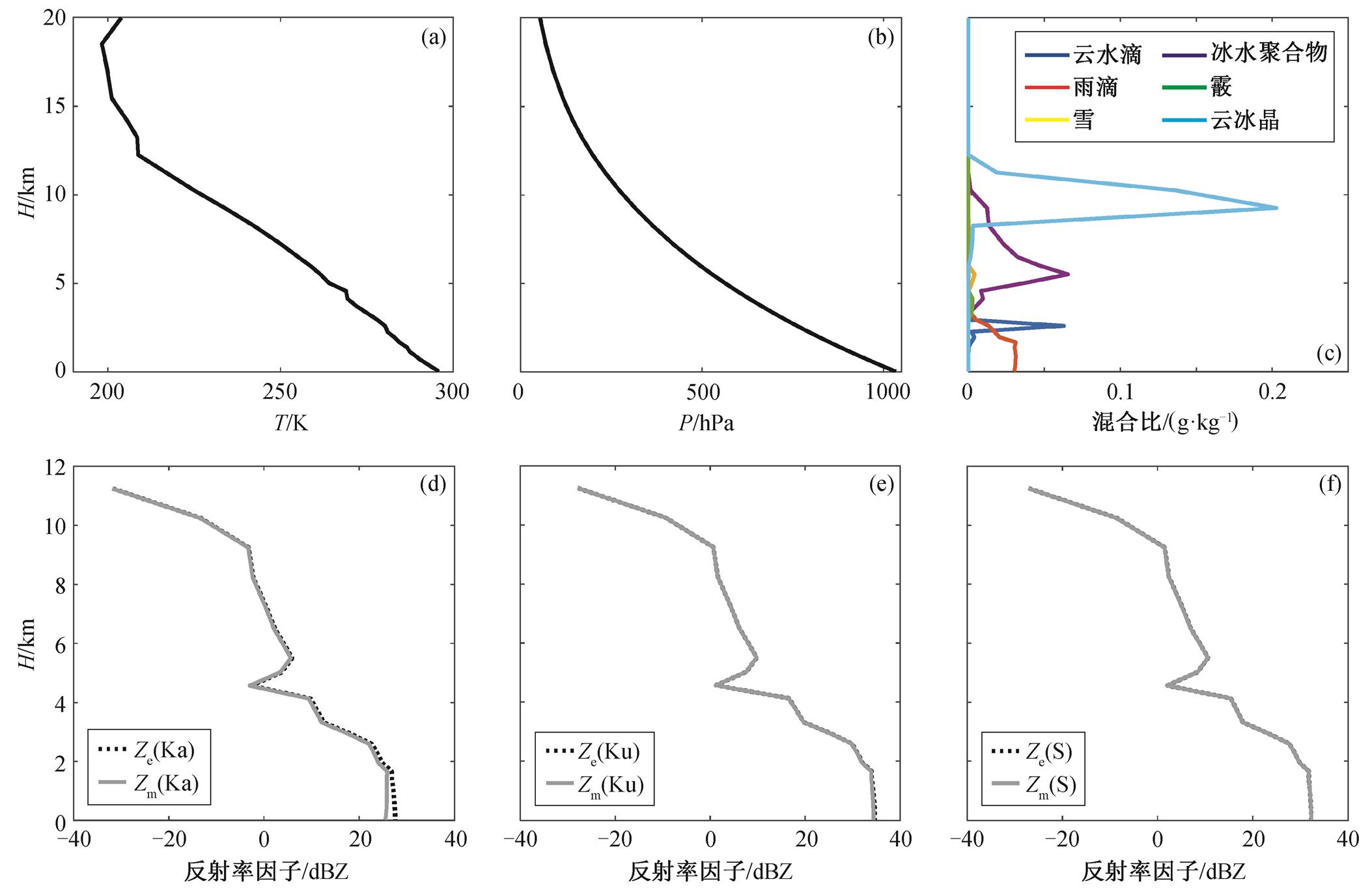
(a)~(c)中数据来自文献[11]
图2 Quickbeam程序中的样本数据及仿真结果
Fig. 2 Sample data of Quickbeam and results of simulation
在进行理论验证时, 以程序中的样本数据为基础, 通过调整其中参数获得多组新的输入数据, 这样可以比较不同参数对雨滴谱反演结果的影响。选择进行调整的参数为雨滴的混合比以及雨滴的平均直径, 这两项分别与式(2)中Nw及D0相关。在Quick-beam的初始设置中, 使用的雨滴谱分布函数模型对应的形状因子μ值为1。由于研究的对象是降雨的滴谱分布, 为了避免其他类型水成物的影响, 选择高度1km以下的样本数据。以样本数据高度最低(20m)的数据为例, 雨滴混合比为3.017×10−2g/kg, 雨滴平均直径为1000μm。得到多组样本数据后, 利用Quickbeam程序, 分别对DPR和S波段天气雷达进行仿真, 再利用仿真得到的数据进行反演验证。在反演验证的过程中, 使用未经衰减的雷达反射率因子, 对应观测数据中经过衰减订正的雷达反射率因子, 即等效反射率因子Ze。
2.1.2 利用不同雨滴混合比仿真数据进行反演验证
调整样本数据中雨滴的混合比, 其他参数保持不变, 生成一组输入数据, 使用Quickbeam进行仿真, 得到的数据如表2所示。可以看出, 随着混合比增大, 仿真结果中各波段的等效反射率因子也随之增大, 但差分反射率因子DFR基本上保持不变。
利用仿真得到的DFR数值, 通过查表的方式获取D0值, 进一步获取Nw值。根据获得的反演雨滴谱分布函数, 计算雨滴的混合比和平均直径, 结果如表3所示。可以看出, 反演得到的混合比约为输入数据中混合比的102.5%, 反演得到的雨滴平均直径则略小于输入数据的1 mm。
将反演得到的雨滴谱分布函数和输入数据中雨滴谱分布函数的曲线画在同一个坐标图上, 如图3所示。可以看到, 反演得到雨滴谱的谱型与输入数据基本上一致。若以输入数据为X 轴, 反演结果数据为Y 轴, 做线性回归分析, 各组相关系数r2达到0.9999, 但反演结果的数值略大于输入数据, 这一现象在雨滴谱的峰值位置最明显(在峰值处, 反演结果数据比输入数据大5.6%)。不同混合比的输入数据仿真结果反演得到雨滴谱的谱型基本上一致, 说明改变输入数据的混合比(即改变雨滴谱分布函数中的Nw值)不会造成雨滴谱的谱型改变。
2.1.3 利用不同雨滴平均直径仿真数据进行反演验证
程序提供的样本数据中, 雨滴的平均直径被设为1000μm。在样本数据的基础上, 将雨滴的平均直径分别设为400, 600, 800和1200 μm, 混合比保持3.017×10−2 g/kg不变, 得到包含样本数据在内的5组数据。使用Quickbeam进行仿真操作后, 得到的结果如表 4 所示。可以看出, 当雨滴平均直径为400 μm时, DFR(Ku-Ka)值为−1.52, 此时存在双值问题。另外, 随着雨滴平均直径增大, Ku波段和S波段的仿真结果数值都随之增大, Ka波段的结果则不是这样。与雨滴平均直径为1000μm时相比, 当雨滴平均直径为1200μm时, 仿真得到的等效反射率因子偏小。
表2 不同混合比输入数据的仿真结果
Table 2 Simulation results of input data with different mixing ratios

混合比/(10−2 g·kg−1)Ze(Ka)/dBZZe(Ku)/dBZZe(S)/dBZDFR(Ku-Ka)/dBDFR(S-Ku)/dB 1.01722.8029.9727.517.17−2.46 2.01725.7832.9430.487.16−2.46 3.01727.5234.6932.237.17−2.46 4.01728.7735.9333.477.16−2.46 5.01729.7336.9034.447.17−2.46
表3 雨滴谱反演结果
Table 3 Results of RSD retrieval

混合比/(10−2 g·kg−1)D0/mmNw反演混合比/(10−2 g·kg−1)反演/mm 1.0172.318 25.411.0430.993 2.0172.317 50.462.0680.992 3.0172.318 75.333.0930.993 4.0172.317100.454.1180.992 5.0172.318125.315.1450.993
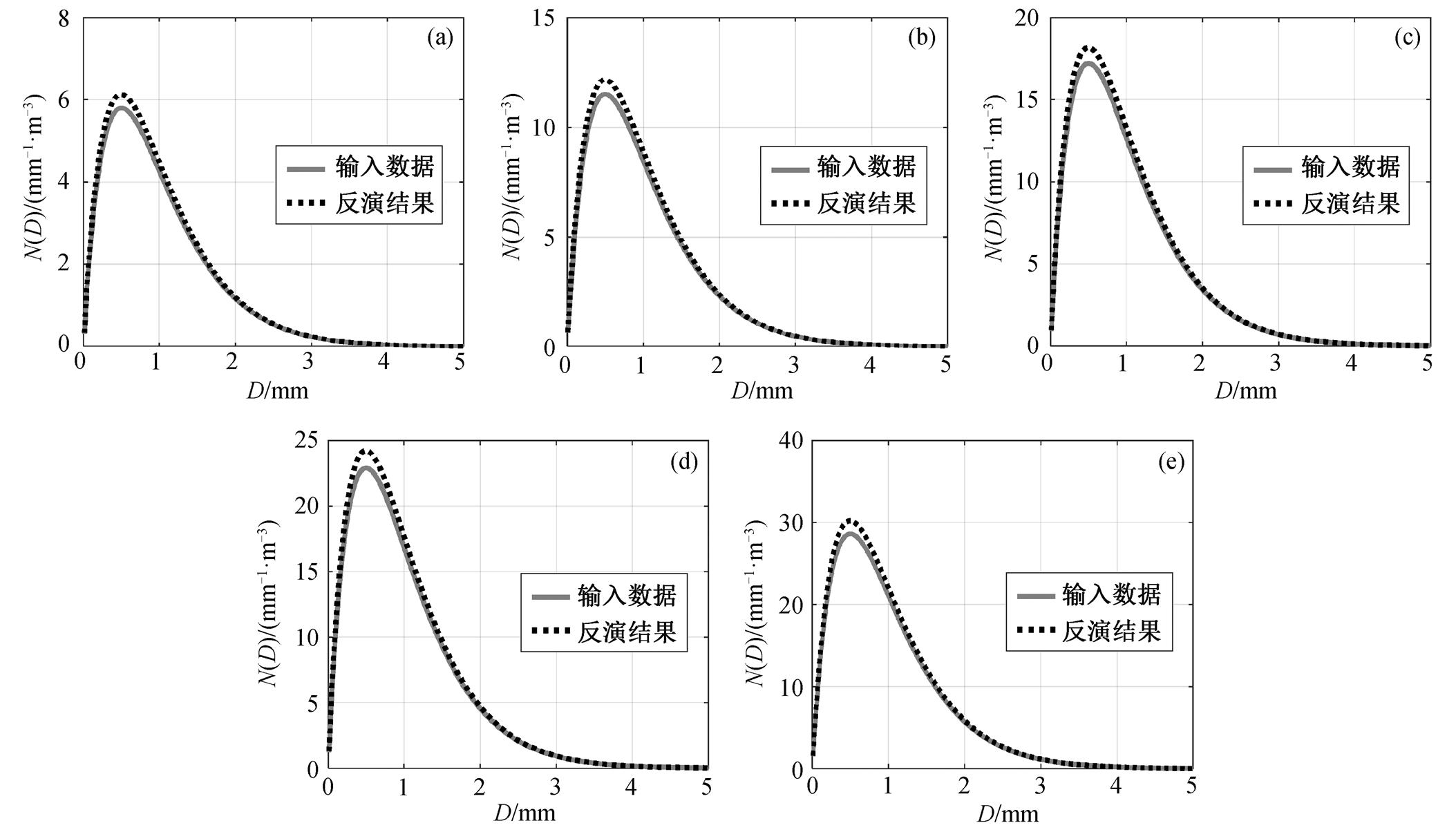
(a)~(e)中, 雨滴的混合比分依次为1.017×10−2, 2.017×10−2, 3.017×10−2, 4.017×10−2和5.017×10−2g/kg
图3 反演结果和输入数据的雨滴谱函数曲线对比
Fig. 3 Comparison of RSD function curves of retrieval results and input data
表4 不同雨滴平均直径输入数据的仿真结果
Table 4 Simulation results of input data with different average diameters of raindrop

/μmZe(Ka)/dBZZe(Ku)/dBZZe(S)/dBZDFR(Ku-Ka)/dBDFR(S-Ku)/dB 40022.1020.5820.63−1.52 0.05 60026.0327.1025.84 1.07−1.26 80027.3531.6729.48 4.32−2.19 100027.5234.6932.23 7.17−2.46 120027.1936.4234.33 9.23−2.09
采用与2.1.2节相同的方法进行雨滴谱分布函数反演, 得到的结果如表 5 所示。可以看到, 反演得到的雨滴平均直径稍小于输入数据中的平均直径; 当输入数据的平均直径为400μm时, 反演得到的雨滴混合比大于输入数据; 随着输入数据的平均直径增大, 反演得到的雨滴混合比有减小的趋势, 到输入数据的平均直径为1200μm时, 反演得到的雨滴混合比小于输入数据的雨滴混合比。
同样, 将输入数据和反演结果的雨滴谱分布函数曲线画在同一个坐标图上, 如图4所示。可以看到, 反演结果与输入数据的雨滴谱分布函数在谱型上有很大的一致性。以输入数据为X轴, 反演结果数据为Y 轴, 对数据进行线性回归分析, 结果如表6所示。可以看出, 反演结果数据与输入数据之间的相关性很强, 各组数据的相关系数r2均在0.99以上, 但反演结果数据大于输入数据。这一现象反映在线性回归得到的斜率上, 当输入数据的雨滴平均直径为400和1200 μm时更加明显。随着输入数据雨滴平均直径增大, 雨滴谱曲线的峰值位置向右偏移, 说明雨滴的平均直径对应雨滴谱分布函数中的D0, 对雨滴谱的谱型有决定性的作用。
表5 雨滴谱反演结果数据
Table 5 Results of RSD retrieval

/μmD0/mmNw反演混合比/(10−2 g·kg−1)反演/μm 4000.9103406.643.322 389.7 6001.386 601.393.147 593.2 8001.848 187.753.114 791.4 10002.318 75.333.093 992.7 12002.721 39.083.0111161.9

(a)~(e)中, 雨滴平均直径依次为400, 600, 800, 1000和1200μm
图4 反演结果和输入数据的雨滴谱函数图像对比
Fig. 4 Comparison of RSD function graphs of retrieval results and input data
首先, 我们需要将S波段天气雷达与GPM-CO DPR的观测数据进行匹配。NASA GPM项目组的Schwaller等[12]提出一套GPM计划的地面验证系统, 利用地面雷达来检验GPM计划的观测数据和反演产品, 其中包括地面雷达观测数据与GPM观测数据的匹配。与GPM-CODPR的观测模式不同, 地面雷达采用体扫模式, 在一个周期内用不同的观测仰角进行扫描观测, 而DPR因搭载在卫星上, 只能采用推扫模式。两者的观测数据分辨率也不同, 地面雷达的观测数据分辨率随被测物与雷达之间的距离而改变, DPR观测数据的水平分辨率为5km, 垂直分辨率为250m。在匹配的过程中, 需要将数据的分辨率调节成一致, 用高分辨率数据去匹配低分辨率数据, 本文采用取均值的方式来降低高分辨率数据的分辨率。这里涉及一个匹配覆盖率的问题, 即在低分辨率观测数据的一个格点内, 若高分辨率的数据不能完全覆盖这个格点, 会造成误差, 因此在进行实例验证时, 选取的数据匹配覆盖率均为1。
选择南京天气雷达站编号为Z9250的新一代天气雷达CINRAD/SA的观测数据与GPM-CODPR的观测数据进行匹配。对反演算法进行检验时, 降水过程的雨滴谱数据通过设置在距离南京天气雷达站约3km的观测场内的OTT Parsivel激光雨滴谱仪获取。在完成雷达观测数据的匹配之后, 从匹配数据中选取满足以下条件的样本进行反演验证: 1)匹配覆盖率为1; 2)高度在3500m以下; 3)距离雷达站30km以内。限制样本的高度是为了避免由温度变化引起的相态变化和亮带的影响, 限制样本与雷达站的距离是为了减小由于空间差异导致的反演结果与激光雨滴谱仪观测数据之间的差异。
表6 线性回归分析结果
Table 6 Results of linear regression analysis

平均直径/mm斜率截距r2 4001.20729−0.607800.99946 6001.08666 0.011140.99989 8001.07289 0.003820.99990 10001.05259 0.001210.99995 12001.12374−0.028270.99925
本研究选取的降雨过程是2016年5月25日21时(UTC)左右的一次降水过程。此次降水过程以层云降水和混合型降水为主, GPM-CO观测21时左右在南京上空过境, 南京站天气雷达和DPR Ku波段雷达的数据图像如图5所示。从图像可以看到, 两者观测到的信号空间分布具有很高的一致性。在实现雷达观测数据匹配后, 选取符合上述3个条件的样本, 数据如表7所示, 这里使用的DPR数据是按照目前算法进行衰减订正后的数据。对于CINRAD/SA的数据, 由降水导致的衰减可以忽略不计。从表7可以看到, 大部分样本的DFR(Ku-Ka)值小于0, 说明在层云降水和混合型降水中普遍存在双值问题。
在此次降雨过程中, 设置的激光雨滴谱仪出现一些故障, GPM-CO过境时激光雨滴谱仪的数据没有保存下来, 因此选择离卫星过境时间最近的10分钟内观测数据作为此次降雨过程的雨滴谱代表。参照何雪松等[13]对OTT Parsivel激光雨滴谱仪数据的处理方法, 对数据进行处理, 得到雨滴谱分布曲线。将由激光雨滴谱仪和样本数据反演得到的雨滴谱分布曲线画在同一坐标图上, 如图6所示。可以看出, 有的样本反演结果与雨滴谱仪观测数据在数值上相差较大, 这是由两者在时间和空间上的差异造成的, 但雨滴谱的分布仍然有相似之处, 比如反演所得雨滴谱分布曲线的峰值位置的粒子直径都比较集中, 并与激光雨滴谱仪得到的观测结果相近。
由于观测仪器条件的限制, 不能获得大范围大量的雨滴谱观测数据, 所以在进行反演算法的实例检验时仍存在很多问题。但是, 从上述尝试的实例验证结果看, 反演得到的雨滴谱在分布结构上与激光雨滴谱仪的观测结果有相近之处, 可以反映降水过程中一些雨滴谱的分布特征。
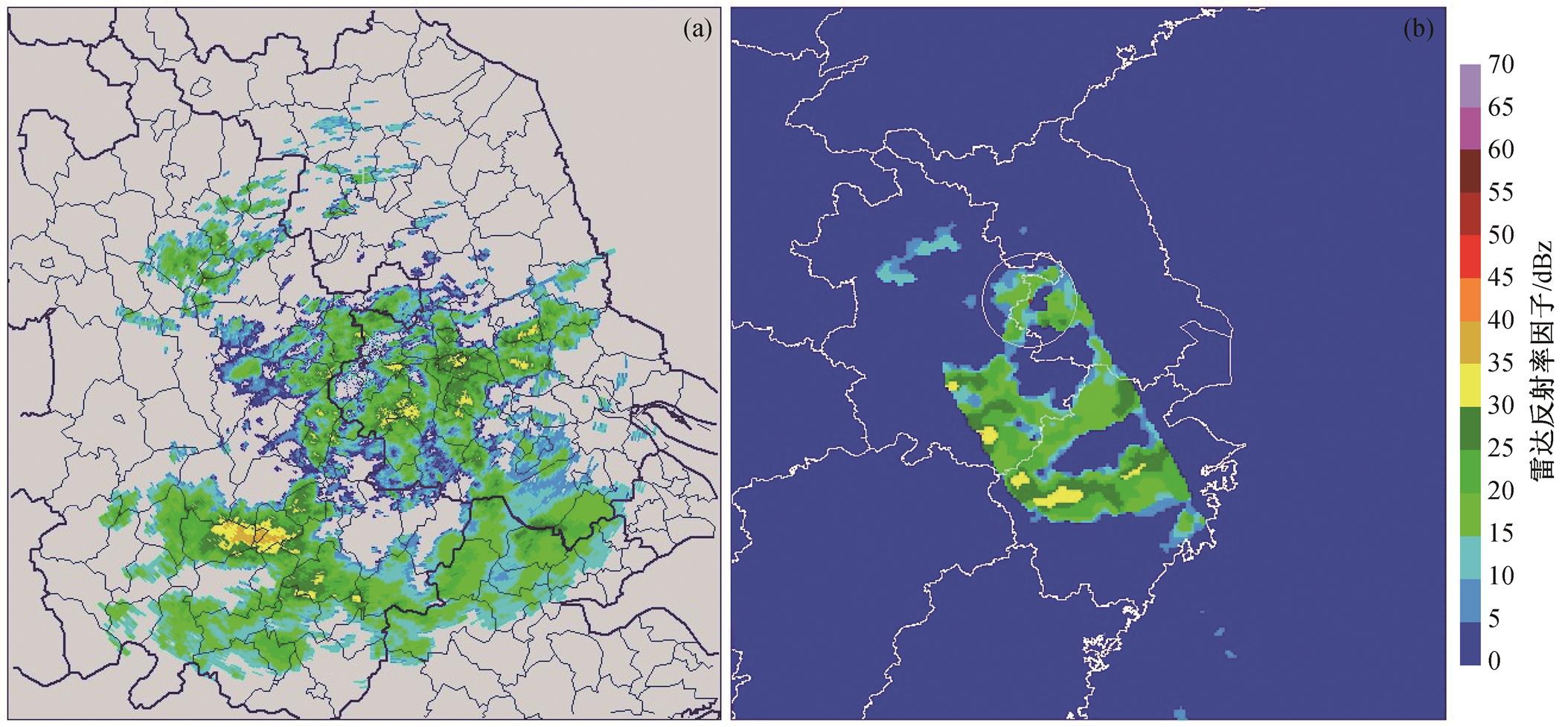
(a)南京站天气雷达Z9250号CINRAD/SA仰角为1.45°的平面显示图像; (b) GPM-CO DPR的Ku波段雷达第150个高度库(共175个高度库)的数据图像, 圆圈为南京站雷达的100 km范围
图5 地面S波段雷达和DPR Ku波段的观测图像
Fig. 5 Observation images of S-band radar and KuPR of GPM-CO DPR
表7 匹配样本数据
Table 7 The match-up sample data
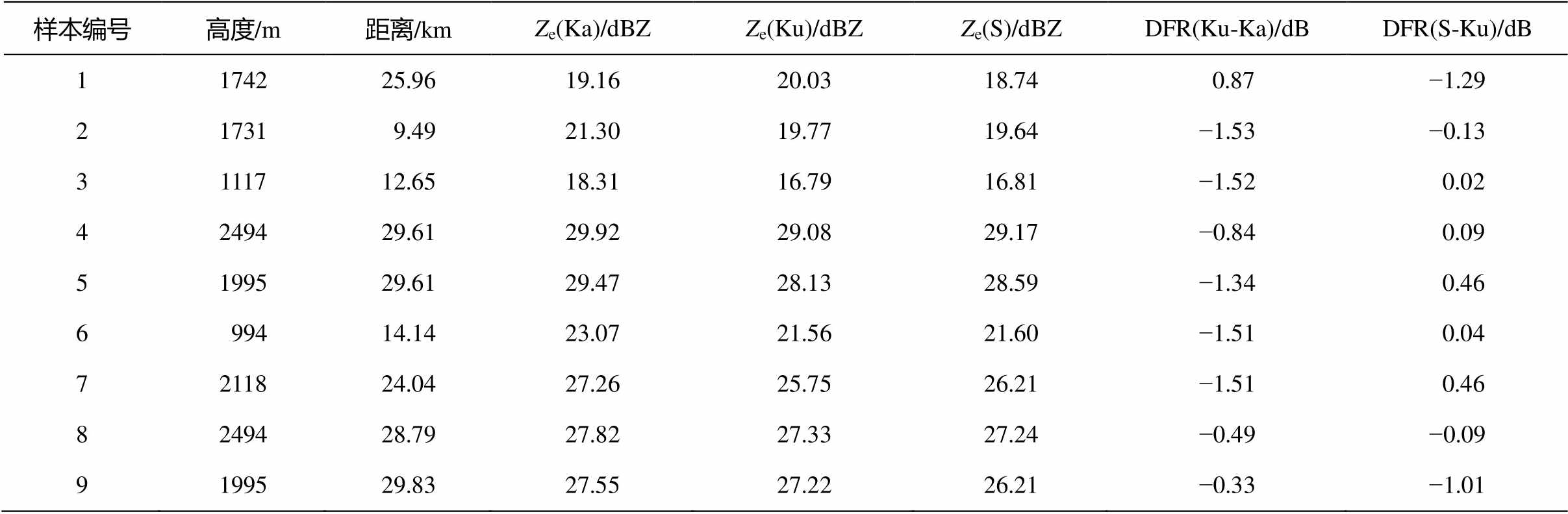
样本编号高度/m距离/kmZe(Ka)/dBZZe(Ku)/dBZZe(S)/dBZDFR(Ku-Ka)/dBDFR(S-Ku)/dB 1174225.9619.1620.0318.74 0.87−1.29 21731 9.4921.3019.7719.64−1.53−0.13 3111712.6518.3116.7916.81−1.52 0.02 4249429.6129.9229.0829.17−0.84 0.09 5199529.6129.4728.1328.59−1.34 0.46 6 99414.1423.0721.5621.60−1.51 0.04 7211824.0427.2625.7526.21−1.51 0.46 8249428.7927.8227.3327.24−0.49−0.09 9199529.8327.5527.2226.21−0.33−1.01
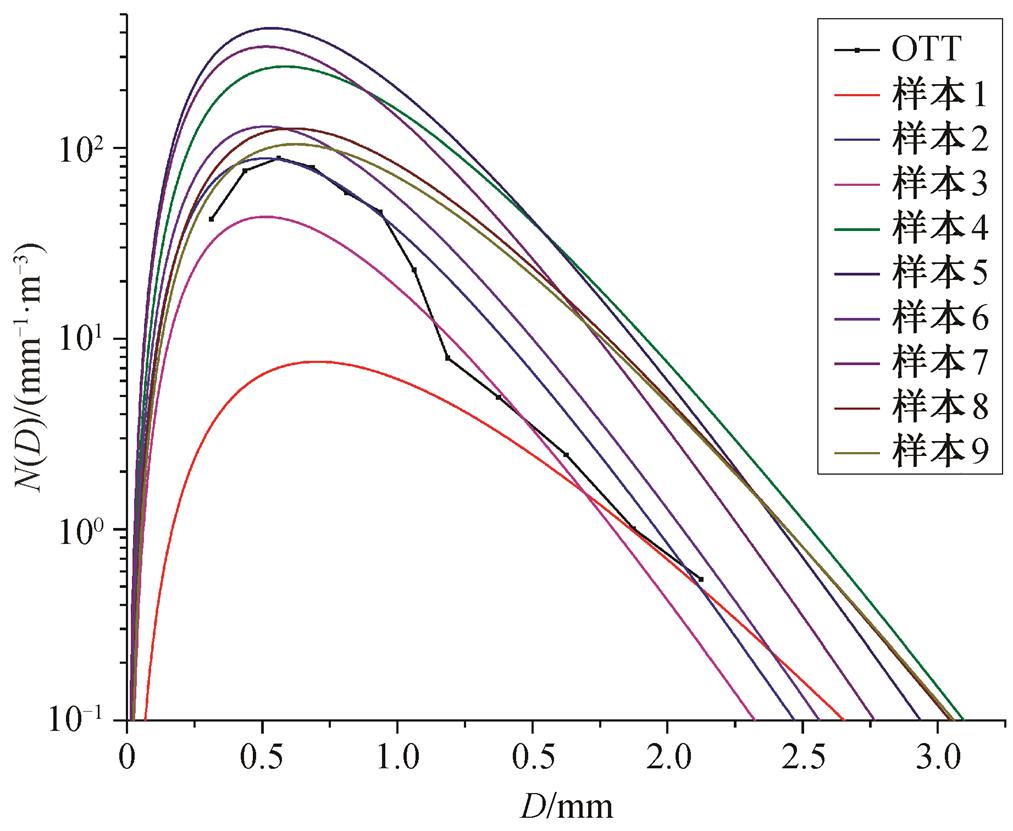
图6 样本反演结果与激光雨滴谱仪观测数据的对比
Fig. 6 Comparison of retrieval results and observation images of laser raindrop spectrometer
从前面理论验证和实例验证的结果可以看到, 本文雨滴谱反演算法的结果可以反映降雨过程中雨滴的粒径分布情况, 对于解决层云降水过程雨滴谱反演过程中经常出现的双值问题有很好的效果。但是, 该算法存在一个问题, 从图1中可以看到, 当DFR(S-Ku)>0时, S波段雷达与DPR的Ku波段观测值之间差异很小(小于观测仪器的系统误差), 如果将该数据作为双值问题的判断依据, 存在很大的不确定性。当DFR(S-Ku)>0时, 降雨过程的雨滴粒径都偏小, 对S波段和Ku波段电磁波的散射近似瑞利散射, 得到的反射率因子与探测波段波长的相关性会很小, 很难从差分反射率因子DFR中获取雨滴谱分布的相关信息。
针对上述问题, 我们提出一个改进的方法: 选用其他探测波段的雷达数据与GPM-CO DPR的观测数据进行匹配。这里讨论的几个常见雷达探测波段为X波段(10GHz)、微雨雷达MRR采用的K波段(24 GHz)和机载/星载云雷达的W波段(94 GHz), 特别是K波段和W波段, 其波长更短, 可以获取更多的小粒子的信息。计算各个波段对应的差分反射率因子DFR随中值直径D0的变化值, 得到的曲线如图7所示。由于我们的主要目的是获取解决反演雨滴谱时存在的双值问题的判断依据, 因此选定D0值的范围为0~1.5 mm。
从图7可以看到, 当D0在0~1.5的范围内变化时, DFR(X-Ku)的变化不明显, DFR(W-Ku)的变化最显著, DFR(K-Ku)则介于二者之间。如果能够获取K波段雷达或W波段雷达与GPM-CO DPR的匹配数据, 则可以为反演雨滴谱时出现的双值问题提供一个可靠性更高的判断依据。然而, 目前的观测设备尚不能提供反演雨滴谱所需要的匹配数据, 使用K波段的微雨雷达MRR和使用W波段的机载/星载云雷达, 目前只是小范围应用, 且均只能观测廓线, 观测范围十分有限, 并且, W波段在降雨过程中的衰减十分严重, 不适用于观测降雨过程。
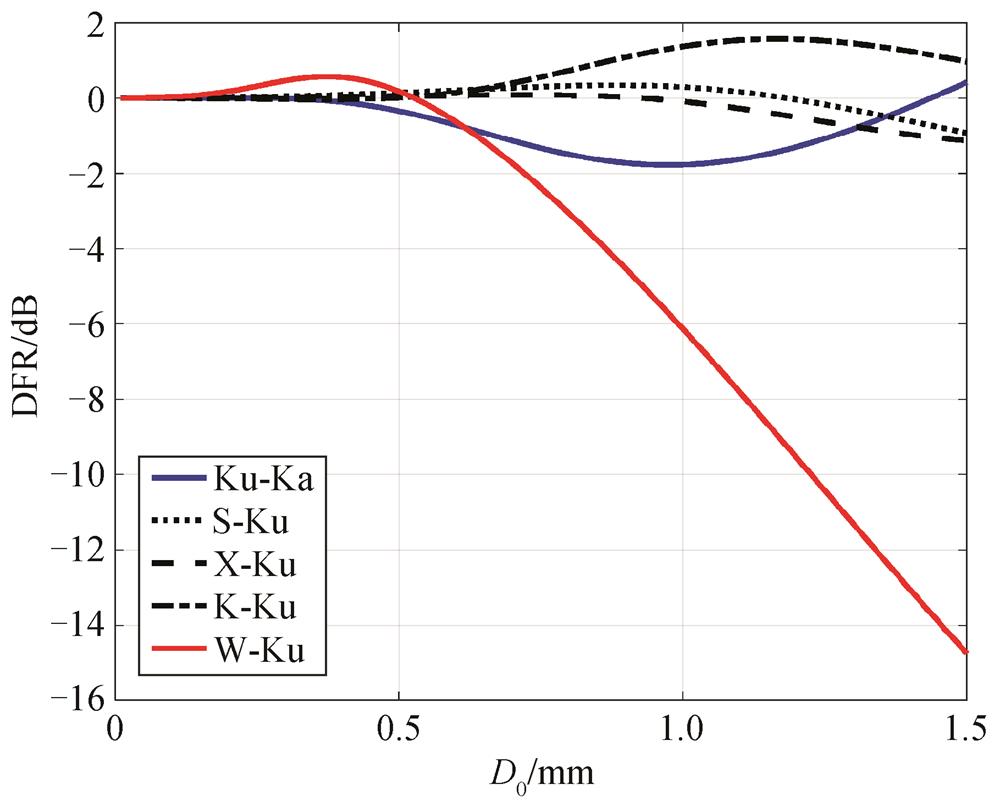
图7 各个雷达波段DFR随D0的变化
Fig. 7 Changes of DFR with D0 of different radar bands
与 K 波段雷达和 W 波段雷达相比, S 波段雷达的优势在于观测范围大, 应用广泛, 可以提供大量观测数据与 GPM-CODPR 的数据进行匹配, 并且, S 波段的降水衰减很小, 其观测值可以为 DPR 数据的衰减订正提供参考。在 GPM-CO DPR 观测数据衰减订正方面, 目前常用的方法为表面参考技术(surface reference technique, SRT), 其基本原理是, 假设地表的反射率不变, 对比有降水时与无降水时的地表回波, 认为两者之间的差异是由降水造成的衰减, 便可得到降水造成的路径积分衰减。SRT对海面观测数据的处理效果较好, 但陆面的情况远比海面复杂, 使得SRT的假设难以成立, 因此SRT在陆面的应用有很大的局限性。在实现S波段雷达与DPR观测数据的匹配后, 可由S波段数据的雷达反射率因子与雨强的关系获取雨强的信息, 为DPR数据的衰减订正提供一个可参考的数值范围, 弥补SRT在陆面应用的缺陷。
本文采用GPM-CO DPR联合地面S波段雷达反演雨滴谱, 可以在一定程度上解决原有雨滴谱反演算法中存在的双值问题。在理论验证中, 反演结果数据与输入数据表现出很高的相关性; 在实例验证中, 反演得到的雨滴谱也可以反映降水过程中雨滴粒径的分布情况。但是, 该算法在DFR(S-Ku)>0时, 使用DFR(S-Ku)作为双值问题判断依据的可靠性较差。与S波段相比, K波段和W的波段在这一方面的可靠性更好, 但在实际操作中存在数据偏少的问题。如果要兼备不同波段雷达的优势, 有待观测设备和技术的进一步发展。
参考文献
[1]Tapiador F J, Turk F J, Peterson W, et al. Global precipitation measurement: methods, datasets and applications. Atmospheric Research, 2012, 104/105: 70‒97
[2]Iguchi T, Seto S, Meneghini R, et al. GPM/DPR level-2 algorithm theoretical basis document [EB/OL]. (2017‒08‒01)[2018‒03‒21].http://www.eorc.jaxa.jp/ GPM/doc/algorithm/ATBD_DPR_201708_whole_1. pdf
[3]Chandrasekar V, Mubarak K, Lim S. Estimation of raindrop size distribution from TRMM precipitation radar observations // Proc IEEE IGARSS. Toulouse, 2003: 1712‒1714
[4]Bringi V N, Tang T, Chandrasekar V. Evaluation of a new polarimetrically based Z‒R relation. J Atmos Ocean Technol, 2004, 21(4): 612‒623
[5]Khajonrat D, Chandrasekar V. Simulation of space-borne radar observations of precipitation: application to GPM-DPR // Rroc IEEE IGARSS. Boston, MA, 2008: IV-455‒IV-458
[6]Ulbrich C W. Natural variation in the analytical form of the raindrop-size distribution. J Clim Appl Meteo-rol, 1983, 22(10): 1764‒1775
[7]Bringi V N, Chandrasekar V. Polarimetric doppler weather radar-principles and applications. Cambridge: Cambridge Univ Press, 2001
[8]张霭琛. 现代气象观测. 北京: 北京大学出版社, 2000: 352‒357
[9]Segelstein D J. The complex refractive index of water [D]. Kansas City: University of Missouri, 1981: 116‒ 146
[10]Mätzler C. MATLAB functions for mie scattering and absorption [EB/OL]. (2002‒06‒08) [2018‒03‒ 21]. https://omlc.org/software/mie/maetzlermie/Maetz ler2002.pdf
[11]Haynes J M, Marchand R T, LUO Z, et al. A multi-purpose radar simulation package: QuickBeam. Bul-letin of the American Meteorological Society, 2007, 88(11): 1723‒1727
[12]Schwaller M R, Morris K R. A ground validation network for the global precipitation measurement Mission. Journal of Atmospheric and Oceanic Tech-nology, 2011, 28(3): 301‒319
[13]何雪松, 王瑞田, 濮江平. Parsivel 雨滴谱仪数据处理方法及其应用 // 第五届苏皖两省大气探测、环境遥感与电子技术学术研讨会专辑. 北京: 中国学术期刊电子出版社, 2009: 214‒216
Combining GPM DPR with S-Band Radar to Retrieve RSD
Abstract For solving the dual-value problem of RSD raindrop size distribution retrieval algorithm using GPM-CO DPR data, a solution is put forward: combining the observation data of S-band weather radar and GPM-CO DPR to provide determinant for the dual-value problem. On the basis of completing the retrieval algorithm, the radar simulation program, Quickbeam, is utilized to validate the algorithm, and actual observation data is utilized to validate the algorithm as well. The results of theoretical validation show that the correlation coefficients between retrieved data and input data are over 0.99, and the results of validation with actual observation data show that the retrieved RSD can reflect the raindrop distribution situation of the rainfall process. The algorithm can help to solve the dual-value problem to o certain degree.
Key words GPM project; DPR; S-band weather radar; RSD; retrieval algorithm; dual-value problem
doi: 10.13209/j.0479-8023.2019.009
收稿日期: 2018-04-02;
修回日期: 2018-06-13;
网络出版时间: 2019-01-13
国家自然科学基金(41475016)和国家重点研发计划(2017YFC0209602)资助