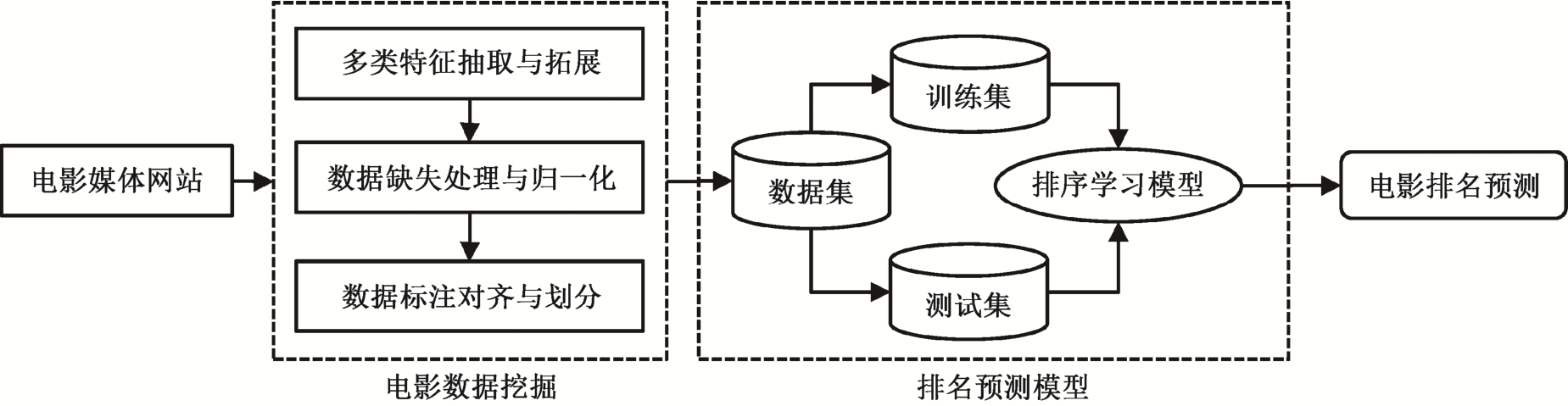
图1 面向电影排名预测的排序学习模型流程
Fig.1 Flow chart of learning to rank model for movie ranking prediction
电影是一门融合了摄影、绘画、音乐和文字等的综合艺术形式。随着现代社会的发展, 电影已深入到人类生活的方方面面, 成为人们精神娱乐不可或缺的一部分。2018年2月, 春节档电影总票房突破100亿, 创下我国单月最高票房记录, 可见电影行业的火热程度。电影票房排行是比较同期上映电影票房排名情况的指标, 不仅会影响影迷的观影选择,也对各大影视院线排场和排片具有指导作用。豆瓣电影、时光网等综合电影媒体网站不但提供电影票房排名数据, 还是众多观影者抒发观影感受、对电影进行评价的平台。还有一些平台(百度糯米电影、猫眼电影票房等)提供实时的电影票房和排名数据, 是分析实时票房波动和走势的重要数据来源。BOM (Box Office Mojo)、IMDB (Internet Movie Database)是国际上两个权威电影媒体网站, 提供丰富的电影数据和信息。
面对海量的电影数据、资讯以及评价等内容,如何从中挖掘相关信息, 进而对电影票房实现预测, 一直是研究热点。现阶段, 多数研究集中于对电影票房的预测, 或是对电影的盈亏或票房成绩进行分类任务的探索。Joshi等[1]结合电影的元数据以及抽取电影评论的文本特征, 通过线性回归模型,对首映周末票房实现初步的预测。Leung[2]通过从社交媒体网站对电影的讨论和评价中抽取特征, 构造一个多项式回归模型, 实现对电影票房的预测。Nagamma等[3]利用情感分析方法, 在电影的在线评论中挖掘相关情感特征, 结合聚类方法, 分析文本倾向性方法, 最后利用SVM模型实现电影票房预测, 具有一定的创新意义。Rhee等[4]利用单隐层的前馈神经网络, 结合电影历史信息和社交媒体数据,抽取与电影相关的特征, 定义衡量电影收益的指标,对电影是否盈利进行二分类模型的构建。
电影排名预测任务是电影票房预测的一个核心问题。电影票房指标的预测对电影投资机构的投资回报风险评估以及投资决策有重要的战略意义, 但对于影院及观影者来说, 电影票房排名指标则更有参考价值。影院可以通过增加同期排名靠前的电影的排片率来提高上座率, 让影院的收益最大化; 影迷也会青睐排名较高的热门影片。
电影排名本质上是一个排序问题, 从问题适用性和性能方面考虑, 排序学习方法[5]可为其提供理论基础。本文首次将排序学习方法引入电影排名预测任务中, 构建面向电影排名预测的排序学习模型,使电影排名预测任务的性能得到有效的提高。
本文针对电影排名预测任务, 构建面向电影排名预测的排序学习模型(movie ranking prediction,MRP)。图 1 为该模型的各部分功能及流程。
1.1.1 数据获取
本文使用的数据来自权威电影媒体网站BOM。该网站是亚马逊公司旗下一个电影票房数据统计的网站(http：//www.boxofficemojo.com), 每月平均流量高达约一百万人次, 在电影行业中被广泛地作为数据来源。该网站不仅有依据周末票房收入的电影排名情况(如图 2 所示), 还提供许多电影相关数据,如某部电影的上映周数、上映影院数和电影预算等。根据电影排名预测任务的要求, 可以将其提供的电影排名作为标注结果, 而与电影相关的数据可以通过一定的方式加工成电影的特征, 进而实现对电影排名预测模型的数据集构建。本文通过编写爬虫, 获取 2015—2017年的电影周末票房排名网页内容, 解析下载的网页文本中相关电影数据, 并通过特定结构化格式进行存储, 以便对数据进行进一步处理。
图1 面向电影排名预测的排序学习模型流程
Fig.1 Flow chart of learning to rank model for movie ranking prediction
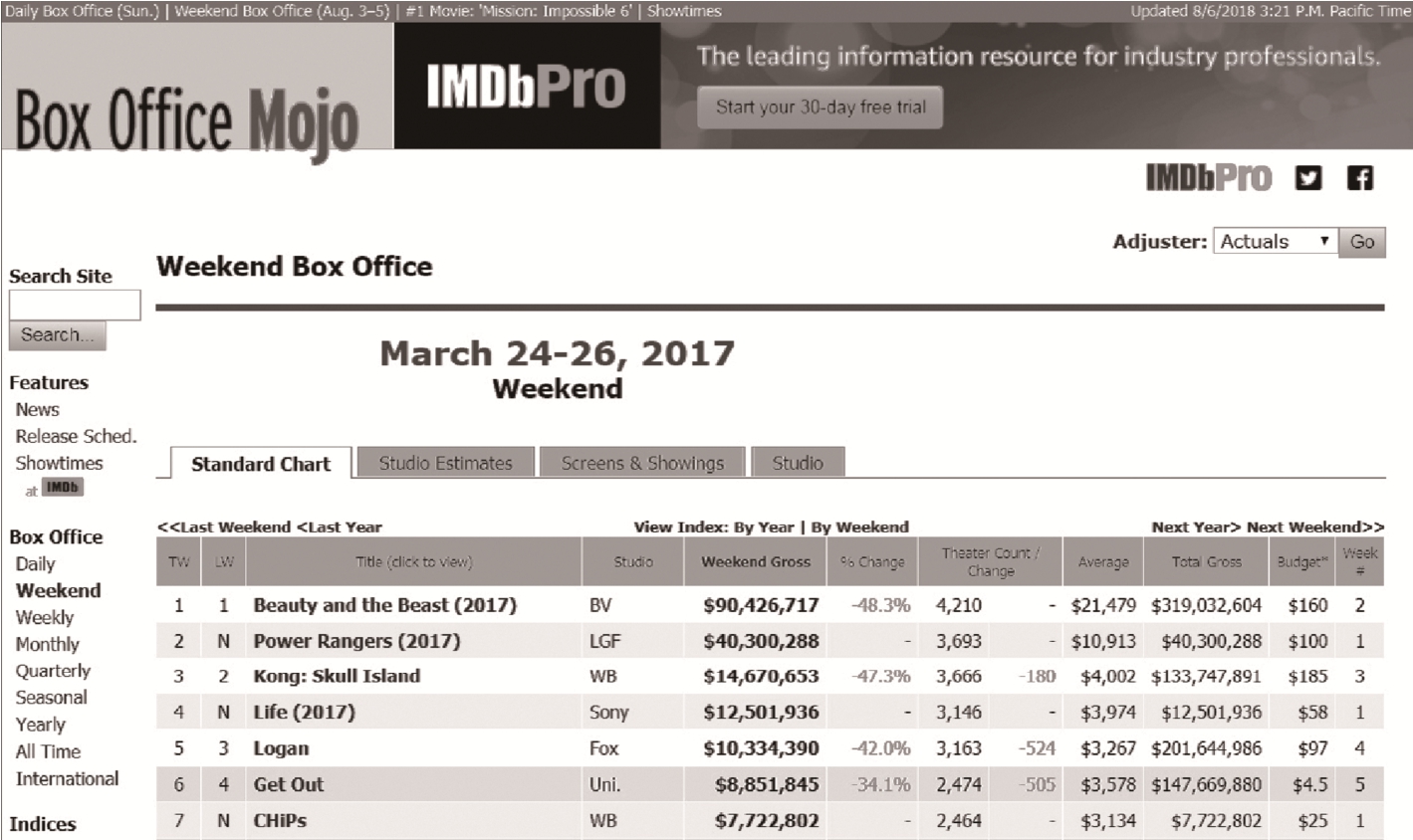
图2 BOM电影票房排名页面
Fig.2 Movies’ gross ranking page on BOM website
1.1.2 特征抽取与拓展
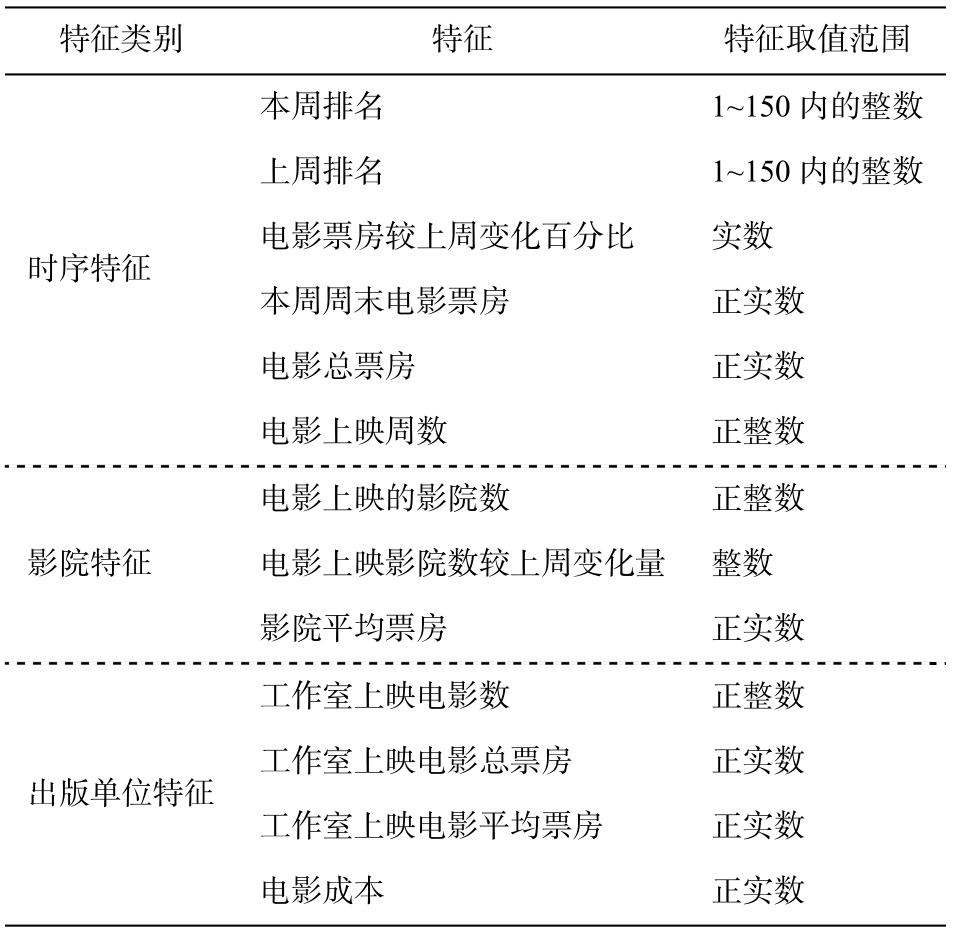
为了保证特征的有效性和完备性, 主要从 3 个方面对特征进行抽取： 时序特征、影院特征和出版单位特征, 如表 1 所示。
作为一个比较同期电影票房高低的指标, 电影排名会随着时间推移而波动, 因此, 时序在电影排名预测任务中是一个重要因素。根据隐马尔可夫模型[6]可知, 某一个状态只与上一个状态的影响有关,更早的状态带来的影响被认为融入到上一个状态中,因此关注的重点是上一个状态。受该模型启发, 在电影排序预测模型中的时序因素可以通过特征的形式体现, 也就是将上一周的电影与时序相关的数据作为预测当周排名的特征, 因此抽取“本周排名”、“上周排名”、“本周周末电影票房”、“票房较上周变化百分比”和“电影上映周数”作为时序特征。
电影票房统计常以影院为单位, 将票房数据按照一定时间间隔上报至影片发行方, 再由发行单位对票房数据进行分析、汇总和公布。如果电影在院线的上映时间长, 或总的上映影院数量多, 必然会对电影票房成绩乃至票房排名起到促进作用。因此有必要对电影的影院相关数据特征进行抽取, 故选取“电影上映的影院数”、“影院平均票房”和“电影上映影院数较上周变化量”作为影院特征。
表1 电影特征信息
Table 1 Information of movie’s features
?
许多影迷偏好选择口碑良好或著名出版单位的电影作品进行观看。排除合同的因素影响, 各影视院线在排片排场时, 也会综合电影工作室的制作水平和评价指标, 优化这些工作室出版电影的排场时段和排片比率来提高上座率, 从而增加收益。所以,电影的出版单位也是电影票房及排名的影响因素之一, 故将出版单位特征单独作为一类特征。但是,在BOM电影媒体网站提供的与出版单位相关的数据中, “工作室名称”是通过文本形式呈现的, 而数据集需要数值化特征。在特征工程中, 除可以使用词集模型对其进行拓展外, 本文考虑通过统计分析方法对“工作室名称”文本进行拓展。通过对数据集所处时间范围内的所有工作室出版的电影数量和票房进行统计分析, 拓展出“工作室上映电影数”、“工作室上映电影总票房”和“工作室上映电影平均票房”3个数值特征, 再结合“电影成本”特征, 共同构成出版单位特征。
1.1.3 数据缺失处理
处理电影特征数据的过程中存在数值缺失问题, 如果简单地舍弃这些数据, 会造成大量数据的损失, 因此须采用一定的策略来处理电影特征的缺失值。例如, 当某一部电影是首周上映时, 该电影的“上周排名”、“电影票房较上周变化百分比”以及“电影上映影院数较上周变化量”3个特征会存在数据缺失。为了充分地利用这部分数据, 并减小缺失值带来的影响, 本文将“电影票房较上周变化百分比”和“电影上映影院数较上周变化量”置零, 即默认该电影的本周票房和上映影院数与“上周”的数据持平; 同时, 将该电影的“上周排名”排名置为取值区间的中间值。还有一些电影没有提供“电影成本”数据, 因而存在缺失, 本文统一将对应的缺失值置为所有电影成本的平均值, 其他存在缺失的数据也统一使用特征平均值进行处理, 尽可能减少对数据集样本的影响。
1.1.4 数据归一化
为了避免因某些特征取值范围过大而导致其他取值范围相对较小的特征的影响被忽略, 我们通过下列线性函数, 将电影特征数据取值转换到[0, 1]的范围, 以提高排序学习模型训练的准确度和速度,归一化公式如下：
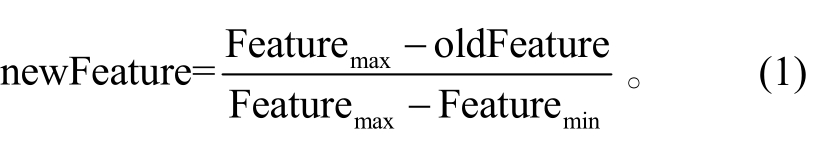
Featuremax为数据集中某个特征的最大值, Featuremin为数据集中某个特征的最小值。oldFeature为待归一化的特征数值, newFeature为归一化后的特征数值。
1.1.5 数据标注处理
可以将电影媒体网站提供的电影票房排名作为数据标注。为实现电影排名预测, 本文的标注对齐方式为, 将某部电影的下一周排名作为当前周相关特征数据的标注。
为了更好地对MRP模型进行训练和学习, 依据每周的电影周末票房排名将电影划分成4个标注档次。排名在第1位为第一档, 排在榜首电影通常是影迷的观影首选, 也是多数人关注的焦点, 标注等级为3。排名在2～3位的电影为第二档, 一般同期处于票房排名榜首竞争行列的电影数量在3部左右,标注等级为2。排名处于4～10位的电影为第三档,这个排名区间一般是小众电影, 或是早期热门电影随上映时间变长而排名下滑会占据的排名位置, 票房号召力虽然不如排在前三的电影, 但仍然有一定的保障, 故标注等级为1。排名在第10位之后的电影划分为第四档, 一般较少人关注, 因此标注等级为0。之所以选择10作为一个排名分界, 是因为通过对一些电影订票应用软件的调研, 发现为了获得利润最大化并保证影迷的观影选择, 单个影院同时上映的电影大约在10部左右, 因此这样的标注划分方式符合常识, 并具有现实意义。
1.1.6 数据格式处理
将实验数据转换为排序学习方法中常用的格式, 以方便进行模型的训练和测试。具体格式定义如下：
＜line＞ ：=＜ label ＞ qid：＜qid＞ ＜feature＞：＜value＞＜feature＞：＜value＞...＜feature＞：＜value＞ # ＜ remark ＞。
参数＜line＞表示一条数据, 每条数据占一行。结合本文提出的MRP模型, 定义中的参数说明见表 2。
通过对数据的分析、处理与整合, 最终的数据集有超过16000条的结构化数据, 图 3 展示部分格式化后的数据。
为了更好地对电影排名预测任务进行探索, 本文首次引入排序学习方法。排序学习(learning to rank)是基于机器学习提高排序结果的有效方法, 源于信息检索领域, 并有广泛的应用, 也被许多其他研究领域认同。为了让排序学习方法更好地契合电影排名预测任务的需求, 我们对相关概念进行映射, 如图4所示。
表2 数据格式参数说明
Table 2 Parameter description of data format
?
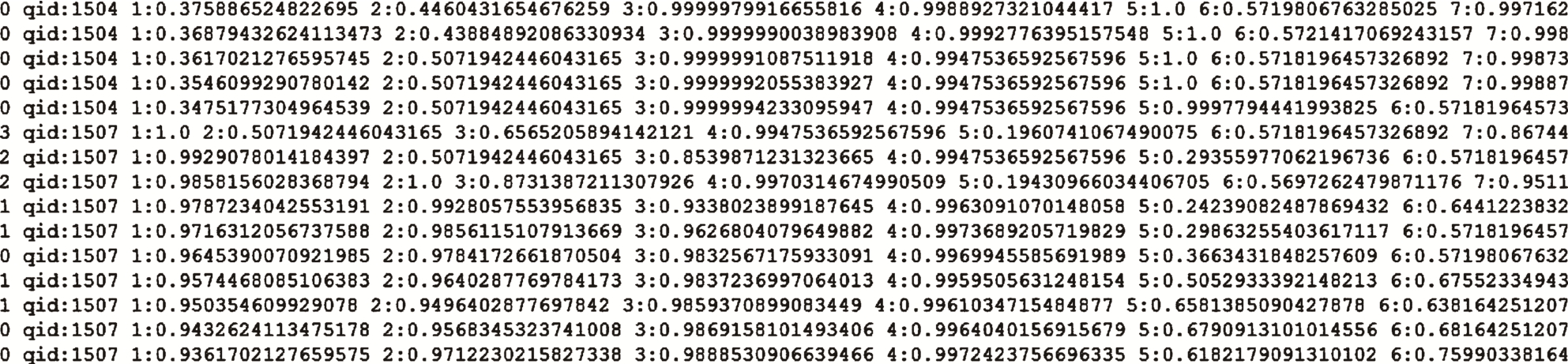
图3 格式化后部分数据示例
Fig.3 Part of data after formatting
本文以“周”作为时间切片, 收集电影票房排名数据, 将周数对应信息检索领域的查询(query), 特定周数排名榜单上的电影集合对应与查询相关的文档集合(document set), 依据每周电影排名划分的排名等级对应文档与查询的相关评级(relevance rating)。因此, 在信息检索领域通过查询词在文档集合中检索相关文档列表的问题, 就映射为在特定周数下于候选电影集合中预测电影排名列表的问题。
前面介绍了通过数据挖掘分析等方法构建数据集以及排序学习方法在电影排名预测任务上的适用性, 下面介绍几种可在MRP模型中嵌入的常用排序学习方法。
1.2.1 MART (multiple additive regression tree)
MART[7]是一种迭代的决策树算法, 每轮迭代产生一个弱分类器, 每个分类器在上一轮分类器的残差基础上进行训练。弱分类器的方差一般较小,而偏差较大。训练的过程是通过不断地降低偏差来提高分类器的精度, 弱分类器一般为CART(classification and regression tree)[8]回归树。最终训练得到的模型为
其中,M为迭代轮次,T(xi;θm)为第m轮训练的弱分类器。弱分类器的损失函数定义为
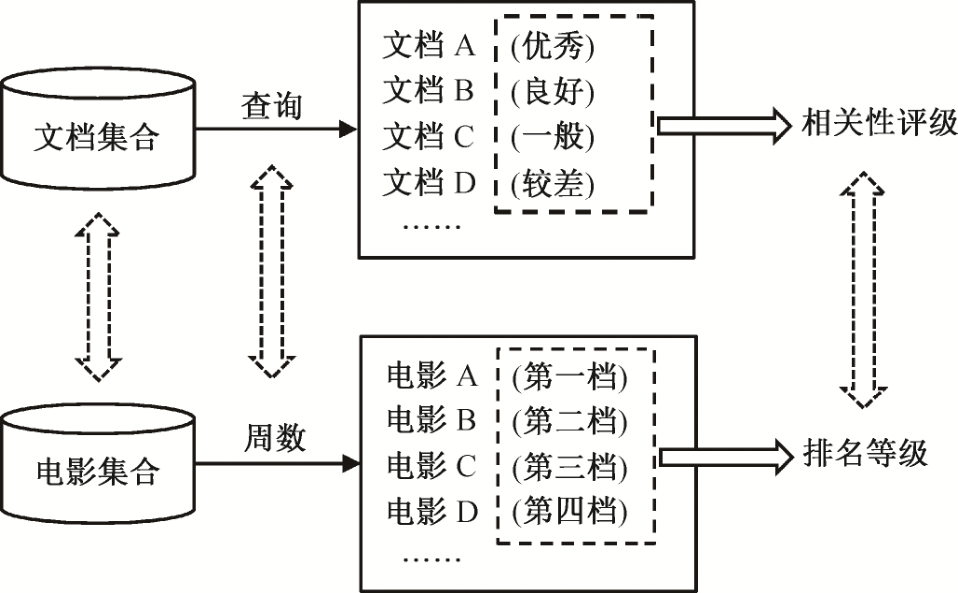
图4 电影排名预测与信息检索概念的映射关系
Fig.4 Concept mapping relation between the prediction of movie ranking and information retrieval
其中,Fm-1(xi)为第m-1 次迭代后的模型。一般选择平方损失函数, 将其梯度方向作为更新的方向,构造下一棵CART树。将每轮训练得到的弱分类器的结果累加, 得到最终的分类器。
1.2.2 RankNet
RankNet[9]是一种基于Pairwise的排序学习方法。给定查询q及与查询对应的偏序文档对集合,该模型训练的目标是得到文档的打分函数f, 进而预测文档di的相关性高于文档dj的概率Pij, 计算过程如下：
其中,oij=f(di)-f(dj)。RankNet模型利用交叉熵作为损失函数, 计算过程定义为
其中,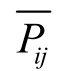
表示文档di比文档dj相关性高的置信度,即目标概率。打分函数f通常选择神经网络结构,并结合梯度下降法优化损失函数, 达到训练模型的目的。
1.2.3 LambdaMART
LambdaRank[10]在RankNet模型的基础上做了改进, 对RankNet中损失函数的梯度进行因式分解：
其中,f(di)表示文档di的得分, (i,j)∈P表示文档对(di,dj)属于训练集的偏序文档对集合P。Lambda-Rank方法将由两个文档的位置交换而引起的评价指标NDCG (normalized discounted cumulative gain)[11]的变化量
作为其中一个因子, 融入式(6)中, 避免了NDCG指标无法求导而不能直接应用的问题。
著名的LambdaMART[12-13]方法借鉴了Lambda-Rank方法中重新定义的梯度, 赋予梯度新的物理意义, 并在MART模型中使用这种新的梯度下降方法。
1.2.4 Random Forests
Random Forests[14](随机森林)是利用多棵树对样本进行训练并预测的一种排序学习方法, 由多棵CART树构成。CART决策树的划分是根据特征划分前后Gini指数的增益而进行。Gini指数是一种衡量数据不纯度的指标, 定义为
其中,Pi表示样本属于i类的概率。当Gini(A)=0时, 所有样本属于同类; 当所有类别的样本中以等概率出现时, Gini(A)取最大值。对于每棵树, 训练使用的样本子集是从总体样本采样出来的。在使用模型进行预测时, 最后的输出结果为所有树输出的平均值。
通过对数据的分析、处理与整合, 最终的数据集有超过16000条的结构化数据。在保证四档电影排名类别分布均匀的前提下, 将整个数据集划分成训练集(约12400条数据)和测试集(约3600条数据)① 测试集包括1502, 1505, 1506, 1514, 1516, 1519, 1520, 1521, 1525, 1528, 1546, 1602, 1616, 1621, 1624, 1631, 1632, 1635, 1643, 1644,1646, 1647, 1708, 1717, 1718, 1719, 1721, 1724, 1733, 1738, 1742, 1743和1744 (按照年份和周数)。。
由Joshi等[1]的研究可知, 线性回归方法是电影票房预测任务中一个最基本的预测模型, 故将线性回归作为一个对比实验。Rhee等[4]的研究结果表现良好, 因此将构造结构相似的单隐藏层前馈神经网络作为另一个对比实验。本文在MRP中分别嵌入不同的排序学习方法, 进行模型训练, 并对实验结果进行分析与评价。
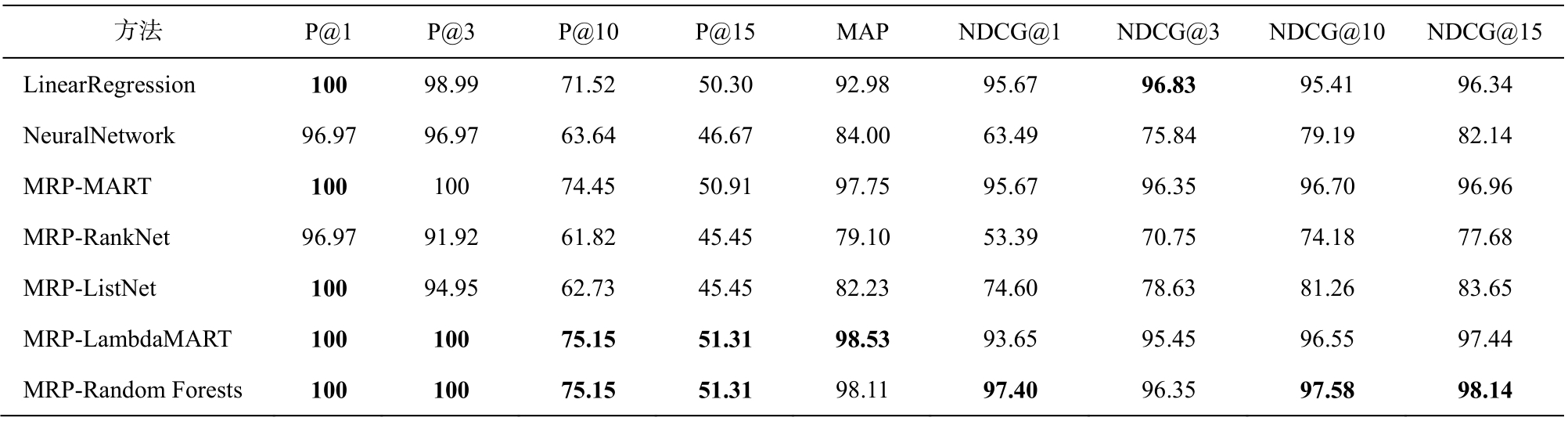
表3 是在基础实验以及在 MRP 模型中嵌入各排序学习方法在测试集上实验的P@n, MAP以及NDCG@n指标[11]结果。在信息检索领域, P@n指标用来度量排序在前n位的检索结果的准确率, 定义如下：
P@n对文档的相关性判定是二值(相关或不相关)。依据本文对电影标注划分规则可知, 排名处于前10的电影被认为是“相关“。因此, P@n迁移到电影排名预测任务中的意义可以理解为, 在预测结果中排在前n位的电影中真实排在前10 位的电影所占的比例。由于排名靠前的电影区分度较大, 各模型也容易将这些电影预测到靠前的排名, 因此部分P@1和P@3指标出现值为100%的情况。从表3还可以看出, MRP-MART, MRP-LambdaMART和MRP-Random Forests这3种排序学习方法的P@n都高于线性回归和神经网络方法, 而MRP-RankNet和MRP-ListNet方法训练的模型预测效果较差。
APq为某个查询q的平均准确率(average precision,AP)[11],I为指示函数。MAP (mean average precision)指标是所有查询的 AP 的均值。因此, MAP 指标迁移到电影排名预测任务中的意义可以理解为, 所有真实排名处于前 10 的电影在预测结果中排名靠前的平均集中程度。从表 3 数据的对比中也可以看出,在 MRP-MART, MRP-LambdaMART 和 MRP-Random Forests 模型对排名前 10 位电影的预测结果比线性回归方法提高 4～5 个百分点, 即预测排序结果中少有将真实排名在前 10 名以外的电影预测到前 10 名中, 对真实排名在前 10 位电影的排名预测结果总体上更集中, 更靠前。
图5 为 MRP 模型中嵌入 MART, LambdaMART和Random Forests以及线性回归和神经网络模型,在测试集上对电影排名预测结果的P@n曲线图。可以看出, 在n＜2时, 大部分结果的P@n都维持在100%, 即此时各模型预测排名前 2 位左右的都属于真实排于前10名的电影。在n=6 附近, 各模型的指标都出现明显下滑, 即一些真实排名在10名以外的电影被错误地预测到较靠前的排名位置。这是由于在第三档电影(标注等级1)和第四档电影(标注等级为0)边界附近, 区分度变得模糊, 因此模型在测试集上的预测结果指标下滑, 但在MRP中嵌入排序学习方法的模型P@n曲线的下降趋势明显比另外两条缓和。随着n值继续增大, 5条P@n曲线大体上都呈现下降趋势, 并在数值上趋于一致。这是由于数据预处理时, 每组电影数据标注等级非0的个数为10,所以P@n指标计算公式中分子固定, 分母则随着n逐渐增大, 导致P@n指标的下滑和趋同。
表3 P@n, MAP和NDCG@n指标实验结果(%)
Table 3 Experimental result on P@n, MAP and NDCG@n (%)
?
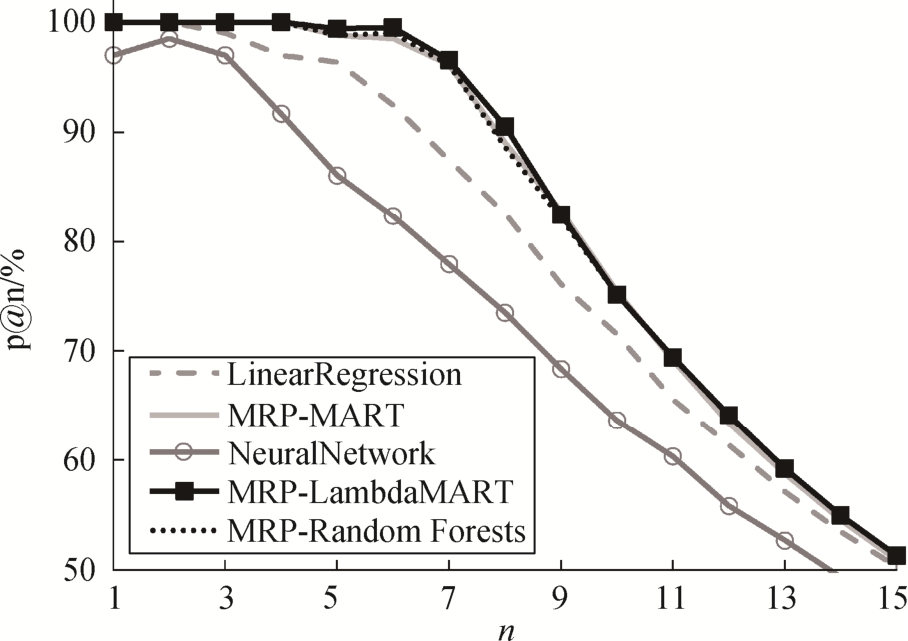
图5 P@n曲线
Fig.5 Curve graph of P@n
DCG (discounted cumulative gain)[11]是信息检索领域内一种衡量检索结果质量的指标, 计算公式如下：
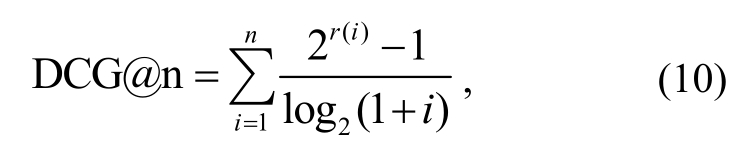
其中,r(i)表示在检索结果中排在第i位的文档的相关性等级。式中的分子与文档正相关, 分母则是根据文档排序位置的降权因子, 所以相关性越高的文档排在越靠前的位置, DCG的值会越高。IDCG(ideal discounted cumulative gain)[11]表示在理想排序状态下DCG的值。DCG指标经过正则化就变成NDCG, 计算公式为
本文将电影依据票房排名划分成4个档次, 标识不同排名区间的电影排名等级, 与信息检索领域中“相关性”的概念相对应, 结合NDCG指标的计算方式可知, 该指标能够更准确地描述模型的排名预测效果。NDCG指标迁移到电影排名预测任务中的意义可以理解为, 电影排名预测结果的质量。
从表3的NDCG@n指标可见, MRP-MART,MRP-LambdaMART和MRP-Random Forests模型对电影排名预测的整体效果优于MRP-ListNet, MRPRankNet以及神经网络模型。从NDCG@1和NDCG@10指标可以看出, MRP-Random Forests模型的排名预测效果最好, 特别是在对排名第一的电影的预测效果上。
MRP-RankNet模型排序效果较差的原因是,RankNet排序学习方法是通过定义交叉熵损失函数来回避一些信息检索评价指标不连续和不可导的问题, 所以在利用梯度下降法优化参数的过程中, 更倾向于降低造成损失的文档对数量, 而评价一个排序模型往往更关注检索结果前n个文档的相关程度,因此最终的预测效果不佳。LambdaMART方法在梯度重新定义的过程中, 通过对RankNet的梯度进行因式分解, 并将NDCG变化量作为因子融入梯度下降的表达式中, 即梯度下降过程相当于直接对NDCG指标进行优化, 所以MRP-LambdaMART模型对电影排名的预测效果优于MRP-RankNet模型。
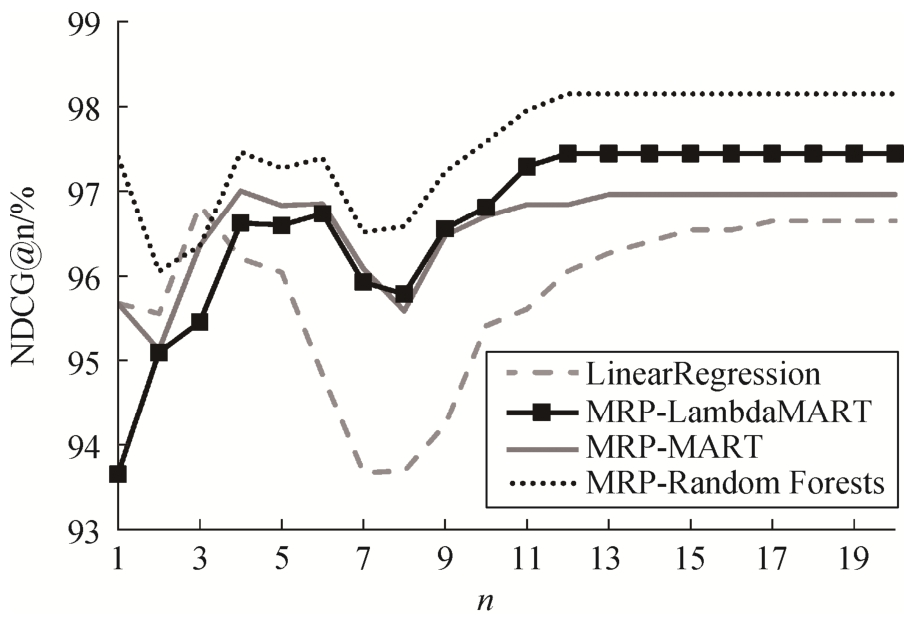
图6 NDCG@n曲线
Fig.6 Curve graph of NDCG@n
图6 为 MRP-MART, MRP-LambdaMART, MRPRandom Forests 和线性回归模型在测试集上对电影排名预测结果的 NDCG@n 曲线图。可以看出, MRPRandom Forests 模型的 NDCG@n 曲线几乎都处于最高的位置, 说明该方法对电影排名有最好的预测效果。MRP-MART 和 MRP-LambdaMART 模型的预测效果相对较差, 当n＞4时, NDCG指标才高于线性回归方法。从总体趋势来看, 每条曲线都有两处明显的局部最小值, 分别对应n为3和10附近的位置,这与本文对电影标注划分的规则是相对应的, 因为在数据集预处理时, 根据排名分界点1, 3和10将电影分成四档, 且每档标注得分按照排名递减, 分别为3, 2, 1和0分。由于在排名分界点两侧标注得分不同, 根据NDCG的计算规则可知, 此时出现预测误差会使NDCG指标的下降较为明显。从图6也容易观察到, MRP-MART, MRP-Lambda MART和MRPRandom Forests模型的NDCG@n曲线在n=13附近趋于稳定, 而线性回归的NDCG@n曲线仍处于波动的状态, 说明这些MRP模型对电影排名预测的效果更稳定, 较少出现将一些真实排名较高的电影预测到10名以外的情况。
表4是BOM网站在2017年第42周发布的电影周末票房排名结果以及各排序学习模型的预测结果。通过与官方发布数据(Official)对比可知, 线性回归模型在电影排序预测中表现不佳, 将排在第一位的电影做了错误的预测, 而且在4～10的预测结果中,将一些10名外的电影排进前10名。MRP-Random Forests模型对排名靠前的电影预测最准确, 排名在前8位的都预测正确, 9～10名的预测虽然出现偏差,不过整体效果仍然最好。MRP-MART模型的预测效果次之。MRP-LambdaMART模型对前2名都预测正确, 而对3, 4名的预测结果与真实排名相反, 第3和第 4 名属于不同的标注等级, 根据计算规则, 会导致这一周排名预测结果的NDCG指标较低。
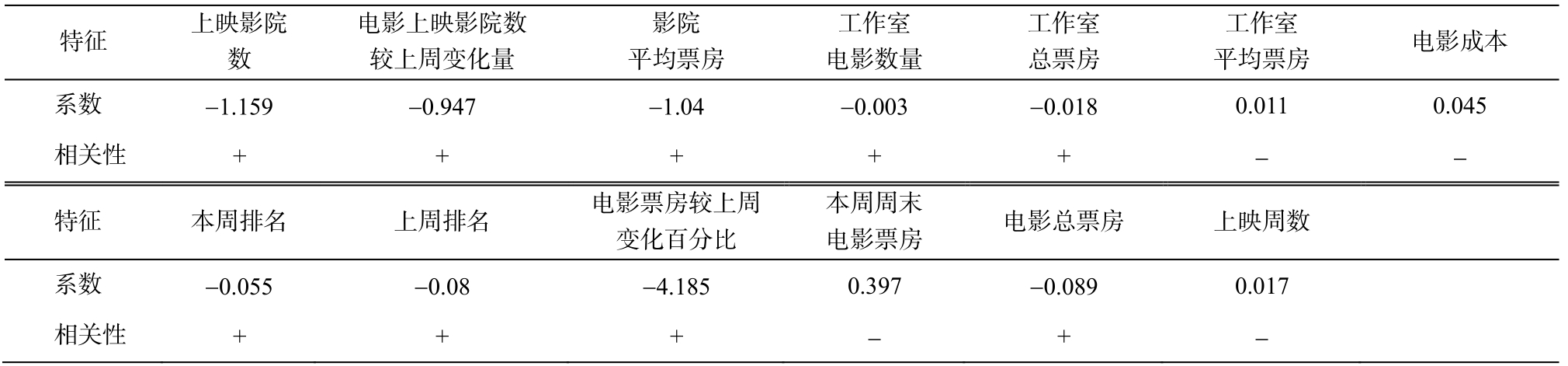
表5给出线性回归模型中各特征对应的系数值。本文的特征工程中, 利用式(1)对特征数值进行归一化。结合线性回归模型的假设函数可知, 各个特征的系数正负可以表示该特征对电影排名等级贡献的正负。由于式(1)的归一化过程中倒置了数据的大小关系, 因此系数为负的特征对电影排名等级的贡献是正向的, 反之亦然。系数的绝对值能在一定程度上体现特征的作用大小。从表5可以看出,在线性回归模型中, “电影票房较上周变化百分比”特征对电影排名等级的贡献程度最大, 这是因为良好的票房上涨趋势会对未来电影的排名有促进作用。“上映影院数”和“影院平均票房”也对电影排名等级起到较好的提升作用。电影上映的影院数量越多, 平均票房越高, 总票房必然也较高, 因此对未来电影的排名有提升作用。
表4 各预测模型对电影的排序结果
Table 4 Movie ranking prediction results using baseline and proposed models
?
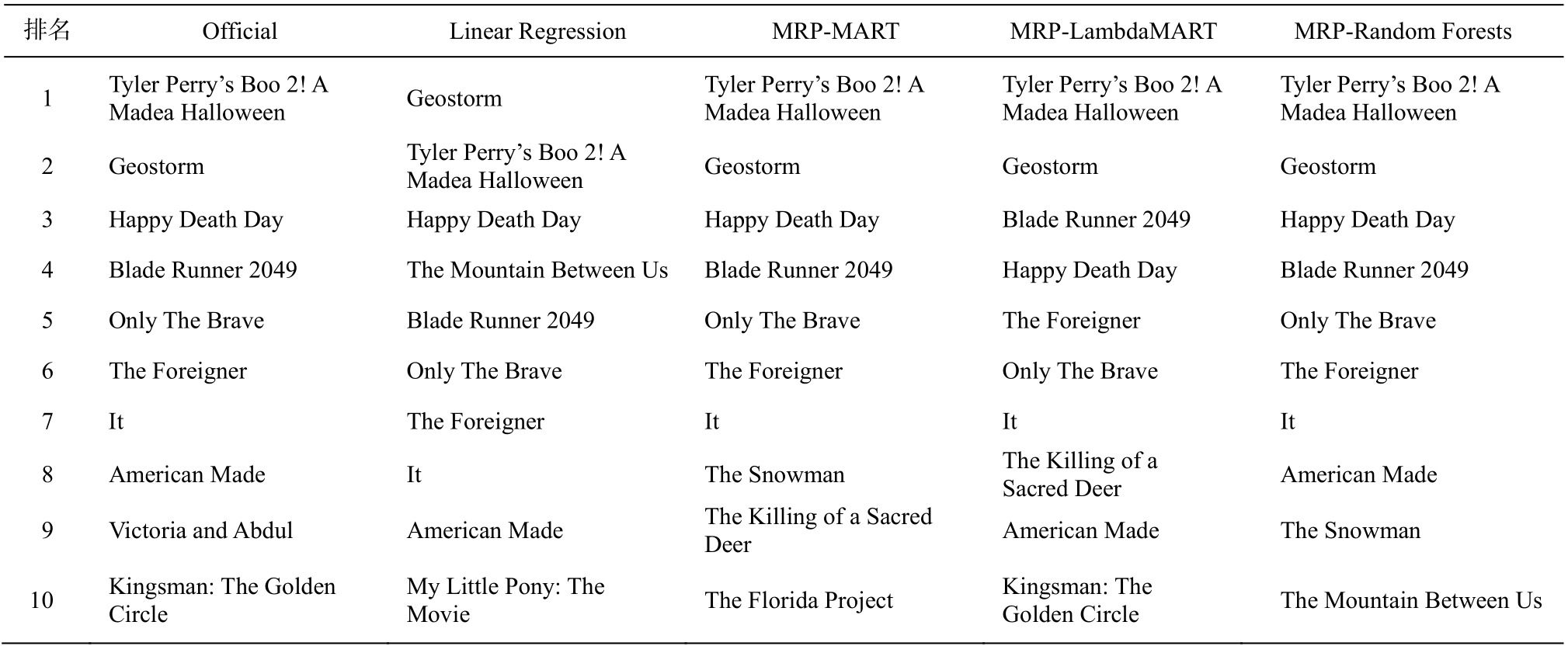
表5 线性回归模型各特征系数
Table 5 Feature coefficients of the linear regression model
?
表6 MRP-Random Forests模型特征重要程度得分
Table 6 Features’ importance score of the MRP-Random Forests model
工作室电影数量工作室总票房工作室平均票房 电影成本0.0045 0.0075 0.0061 0.0117本周周末电影票房 电影总票房 上映周数得分 0.8204 0.0055 0.0373 0.01 0.022 0.0054
表6给出MRP-Random Forests模型中各特征的重要程度得分。由随机森林模型的训练方法可知,每一棵决策树在训练时使用的数据是从整个训练集中有放回采样出来的。因此, 每棵树都对应一部分未被使用的带外数据(out of bag, OOB)。通过这些带外数据, 可以在这一棵决策树上计算带外误差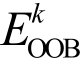
(k表示第k棵决策树)。在第k棵决策树对应的带外数据的所有样本中, 对特征x加入随机的噪声干扰后, 再次计算带外误差
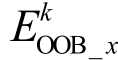, 则在整体训练集上, 特征x的重要程度得分Ix可以定义为
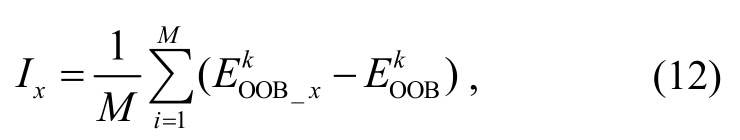
其中,M表示随机森林模型中决策树的个数。由式(12)可知,Ix值越大, 特征x的重要程度越高。
从表6可以知道, “本周排名”在MRP-Random Forests模型中最重要。本周的电影排名对未来的电影排名等级预测有很大的参考价值, 因此该特征的重要程度比较高。“电影票房较上周变化百分比”和“电影上映影院数较上周变化量”的重要程度也比较高, 这一点与线性回归模型中的特征系数的分析结论一致。“本周排名”特征在线性回归模型中对电影排名等级的贡献不大, 甚至是正相关(排名越靠前,数值越小, 电影排名等级越高, 直观上理解应该是负相关), 原因可能是训练集中大部分电影的标注等级都为0 (真实排名在10名之后的电影, 每周电影排行大约有100部左右的电影), 导致线性回归模型在该特征上整体拟合时, 为了减小全局损失, 对系数调整采取了一种折衷的方式。一些新上映的电影对电影排名的冲击较大, 导致该电影虽然在本周的排名较靠前, 标注的电影等级却比较低(下一周该电影排名下滑)。
通过对表5和6中特征重要性的分析可知, 与出版单位特征相比, 本文特征工程中提取的时序特征和影院特征在电影排名预测上能取得更好的效果。
本文提出一种面向电影排名预测的排序学习模型。该模型利用BOM网站提供的电影数据, 通过数据获取与清洗以及特征抽取与拓展等步骤, 构建数据集。在模型中嵌入多种排序学习方法, 对数据进行训练以及测试, 并与线性回归方法和神经网络方法进行对比。实验结果显示, MRP-Random Forests模型对排名的预测有比较良好稳定的结果。本文提出的电影排名预测模型MRP有效地提高了电影排名预测任务的性能, 能对各影视院线排场、排片提供参照, 也能为观影者提供热门优质的影片推荐。但是目前的模型是基于已有的电影数据对排名进行预测, 无法对新上映的电影排名进行预测。首周上映的电影, 由于前期的宣传和营销工作, 对票房的冲击力较强, 往往会占据较靠前的排名位置。未来的工作中, 将对各大电影媒体网站中即将上映电影的广告、宣传内容进行采集与分析, 解决电影的冷启动问题, 并从正上映电影的评分以及观影者对电影的评价中挖掘更多信息, 融入情感分析等方式,对特征工程以及排序模型进行拓展。
[1]Joshi M, Das D, Gimpel K, et al.Movie reviews and revenues： an experiment in text regression // Human Language Technologies： Conference of the North American Chapter of the Association of Computational Linguistics.Los Angeles, 2010： 293-296
[2]Leung C K.Social media mining： prediction of box office revenue // International Database Engineering& Applications Symposium.Bristol, 2017： 20-29
[3]Nagamma P, Pruthvi H R, Nisha K K, et al.An improved sentiment analysis of online movie reviews based on clustering for box-office prediction //International Conference on Computing, Communication & Automation.Greater Noida, 2015： 933-937
[4]Rhee T G, Zulkernine F.Predicting movie box office profitability： a neural network approach // IEEE International Conference on Machine Learning and Applications.Cancun, 2017： 665-670
[5]Li H.A short introduction to learning to rank.IEICE Transactions on Information & Systems, 2011, 94(10)： 1854-1862
[6]Rabiner L R.A tutorial on hidden Markov models and selected applications in speech recognition.Readings in Speech Recognition, 1990, 77(2)： 267-296
[7]Friedman J H.Greedy function approximation： a gradient boosting machine.Annals of Statistics, 2001,29(5)： 1189-1232
[8]Breiman L I, Friedman J H, Olshen R A, et al.Classification and regression trees (CART).Encyclopedia of Ecology, 1998, 40(3)： 582-588
[9]Burges C, Shaked T, Renshaw E, et al.Learning to rank using gradient descent // International Conference on Machine Learning.Bonn, 2005： 89-96
[10]Burges C J C, Ragno R, Le Q V.Learning to rank with nonsmooth cost functions // International Conference on Neural Information Processing Systems.Vancouver, 2006： 193-200
[11]Liu T Y.Learning to rank for information retrieval //International ACM SIGIR Conference on Research and Development in Information Retrieval.Geneva,2010： 904-904
[12]Wu Q, Burges C J C, Svore K M, et al.Adapting boosting for information retrieval measures.Information Retrieval, 2010, 13(3)： 254-270
[13]Burges C J C.From RankNet to LambdaRank to LambdaMART： an overview.Learning, 2010, 11： 1-19
[14]Breiman L.Random forests.Machine Learning, 2001,45(1)： 5-32
Research on Movie Media Website for Ranking Prediction