图1 径向基函数网络结构
Fig.1 The structure of radial basis function neural network
生态安全指一个国家或人类社会生存和发展所需的生态环境处于不受或少受破坏与威胁的状态。生态安全是构建和谐社会和实现科学发展的重要保障, 是国家安全和社会稳定的一个重要组成部分。生态压力越大, 表明该地区的生态越不安全。
目前, 最常见的生态安全评价方法是在生态足迹评价模型[1-2]基础上提出的生态压力指数法[3-4]。生态压力指数越大, 说明区域的生态压力越大。世界自然基金会(World Wide Fund for Nature, WWF)[5]根据生态足迹理论, 给出全球 147 个国家或地区的生态足迹和生态承载力数据。郭跃等[6]通过生态足迹方法和生态压力指数, 对江苏省 1999—2008年的生态安全进行动态分析, 结果显示江苏省生态压力等级处于极不安全状态, 根据线性回归预测, 江苏省未来几年的生态安全将进一步恶化。甄江红等[7]分析 1990—2010年“呼包鄂”地区生态压力指数持续攀升, 呼和浩特市处于生态较安全状态, 而包头市与鄂尔多斯市处于生态不安全状态。闵学等[8]分析了陕西省 2001—2011年生态压力指数的时序变化, 利用主成分分析方法, 得到陕西省生态安全动态变化是人口、经济、资源环境、技术和土地利用程度等多方面因素共同作用的结果, 经济发展引起的人均 GDP 增加是生态安全动态变化的主要驱动力。生态压力指数的计算方法涉及的参数较多, 难以对大范围及多区域进行生态压力评估和对比。目前我国关于生态压力的评价多为计算一个省、一个城市甚至更小区域的生态压力指数[7,9-11], 缺乏对全国范围的生态压力进行评价和对比的案例。然而,只有对全国各地区的生态压力状况进行综合评价和区域之间的比较, 才能针对不同地区制定科学合理的生态保护政策。
地区的生态压力与经济发展、人口、土地利用和资源等因素有密切的关系, 生态压力与这些因素之间具有很强的非线性关系, 且数据中有很大的噪声。MATLAB 环境下的径向基函数(RBF)神经网络能够根据学习获得的知识经验, 对复杂的问题做出合理的判断[12], 其网络结构、仿真函数和输出方法不仅能确定各评价对象所属的级别, 进行不同评价对象之间质量优劣的比较, 而且有精度较高、操作简便和实用性强的优点[13]。因此, 本文通过构建RBFN 模型, 模拟全国 31 个省级行政区(不包括香港、澳门特别行政区和台湾省)的生态压力指数,并对各地区的生态压力进行评估。
径向基函数网络(Radial Basis Function Network,RBFN)是近年被广泛应用于函数近似插值、分类研究的人工神经网络模型之一[14]。RBFN 是由一个输入层、一个隐含层和一个输出层组成的三层前向式网络, 各层有多个神经元, 相邻两层单元之间单方向连接, 通过径向基算法来获得隐层权值并确定最终输出值, 是一个多层前向监督式网络(图 1)。
图1 径向基函数网络结构
Fig.1 The structure of radial basis function neural network
图1 中,Oi(i=1, 2, …,M)表示输出层的输出;Vj(j=1, 2, …,L)表示隐含层的输出;Xk(k=1, 2, …,N)表示输入层的输入;Wij表示从隐含层单元到输出层单元的连接权;Cjk=(Cj1, …,Cjk, …,CjN)和δj分别表示隐含层单元基函数的中心和宽度;M,L和N分别表示输出单元、隐含单元和输入单元的数量。M和N与实际问题的输出和输入维数一致。L的选择则是一个复杂的问题, 至今尚无适宜的方法。通常可用构造一个人工神经网络结构或对一个网络结构进行修改, 使之与一个具体问题相适应的方法来确定隐含单元数, 或者通过模拟分析建立误差平方和与隐含单元数之间的关系, 并据此选用隐含单元数[15]。
若给定的输入为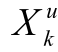
,u=1,2,...,p(p为输入模式数), 则有隐含层单元的输出
式中,
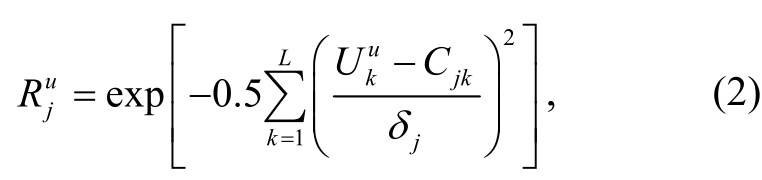
输出层单元的输出
其中,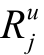
和
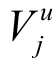都是径向对称的非线性函数, 称
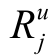为 Gauss 型径向基函数,
为归一化的径向基函数。径向基函数网络中, 需要通过学习和训练来确定隐含层单元基函数的中心Cjk、宽度δj和隐含层单元与输出层单元的联接权值Wij。
从式(1)～(3)可知, 在 RBFN 中, 隐含层执行的是一种固定不变的非线性变换, 将输入空间映射到一个新的空间, 输出层在该新的空间中实现线性组合, 可调节的参数是该线性组合的权。以上各式中的Cjk,δj和Wij需要通过学习和训练来确定。
第一步是确定基函数的中心。思路是利用一组输入模式来计算L×N个Cjk, 使Cj尽可能均匀地对输入样本数据抽样, 在数据点密集处Cj也密集。通常将基函数中心Cj的初值置为最初的L个训练样本的值。将所有样本模式按最近的基函数中心Cj分组。对每个基函数中心Cj及所有样本模式Xu=
, 满足 min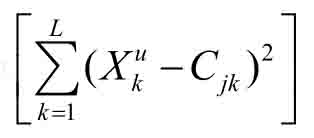
时的Xu属于Cj的子样本集θj。然后, 重新计算
, 其中Mj为子样本集θj中的样本模式数。若基函数中心Cj不再变化, 则停止训练, 其基函数中心Cj的稳定值即为所求; 否则, 重复以上步骤。
基函数中心Cj训练完毕后, 可以求出归一化参数, 即基函数的宽度δj, 表示与某个中心相联系的子样本集中样本散布的一个测度。令δj等于基函数中心与子样本集中模式之间的平均距离, 即
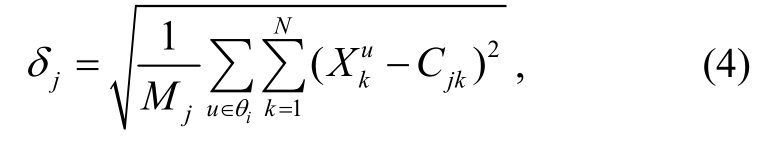
之后, 确定隐含层单元到输出层单元的连接权值。记相应于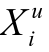
的期望输出值为
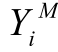, 通常的误差测度准则是平方误差最小, 即
在基函数的参数确定后, 式(5)中的 ES 是Wij的函数, 可以应用最小二乘法求解。
生态足迹模型中的生物生产面积涉及耕地、草地、林地、水域、能源和建筑用地 6 种, 因此基于生态压力指数理论模型以及有关研究中对生态压力变化驱动力因子的分析, 本文以全国 31 个省、自治区和直辖市作为研究对象, 选取人均 GDP (p1)、人均林地面积(p2)、人均草地面积(p3)、人均耕地面积(p4)、人均建设用地面积(p5)、人均化肥使用量(p6)、人均电力(p7)和人均水资源量(p8)8 个指标作为输入。这 8 个评价指标能够比较全面地反映一个地区的生态安全情况, 并且与生态压力指数计算方法所涉及的参数涵盖的方面一致。评价指标数据来自国家统计局公布的历年《中国统计年鉴》。
1.3.1 网络训练样本的构建
通过文献查阅和指标数据搜集, 最终得到 27 个训练数据样本(表 1)。具体做法是, 将参考文献[3,6,16-22]的生态压力指数研究结果作为训练目标值(target), 从《中国统计年鉴》中查找每个样本的对应年评价指标数据作为训练样本的输入值。
1.3.2 网络的训练和检验
在 MATLAB 环境下创建一个广义的回归神经元网络, 格式为
式中,P,T和 spread 分别为归一化输入矩阵、目标矩阵和径向基函数的基部宽度。spread 的取值对神经网络的仿真结果有很大的影响, 需要通过调整spread 值来改善网络训练的仿真精度。首先将训练样本的各项输入指标进行归一化处理, 然后选择训练样本中的 19 条作为训练样本集, 剩余的 7 条作为预测样本集来检验模型的预测精度, 用来训练的 19个样本包含全部 27 个训练样本涉及的各个地区。
1.3.3 结果评价
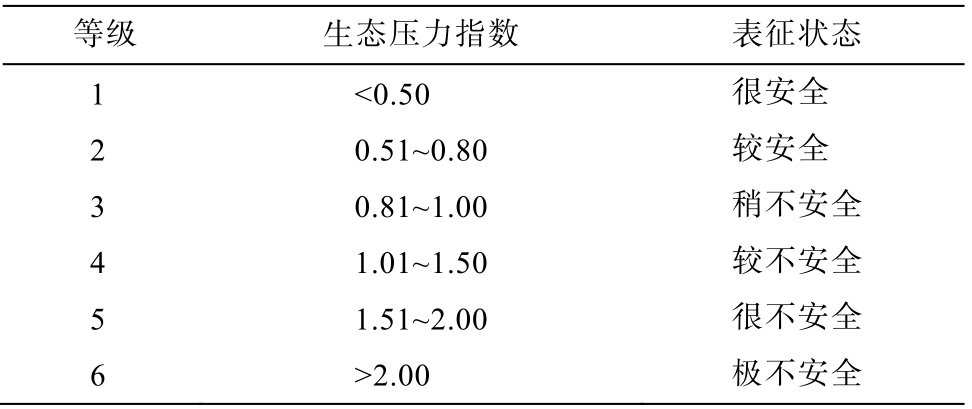
对 2008年和 2013年全国 31 个省级行政区的各项评价指标进行归一化处理, 生成输入矩阵P, 利用已训练好的网络进行仿真, 输出各地区的生态压力指数结果。赵先贵等[4]根据全球 147 个国家或地区的生态足迹和生态承载力数据, 结合各国生态环境和社会经济发展状况, 制定了生态安全评价指标和等级划分标准, 将生态压力指数划分为 6 个等级,1～6 代表生态压力依次为很安全、较安全、稍不安全、较不安全、很不安全和极不安全(表 2)。
本文依据上述标准对生态压力指数计算结果进行评价, 利用 GIS 软件对评价结果进行可视化表达。进一步, 分析 2008—2013年各地区生态压力的变化, 并按照华北(北京、天津、河北、山西和内蒙古)、东北(辽宁、吉林和黑龙江)、华东(上海、江苏、浙江、安徽、福建、江西和山东)、华南(河南、湖北、湖南、广东、广西和海南)、西南(重庆、四川、贵州、云南和西藏)以及西北(陕西、甘肃、青海、宁夏和新疆)6 大分区, 对模型得到的生态指压力指数进行比较。
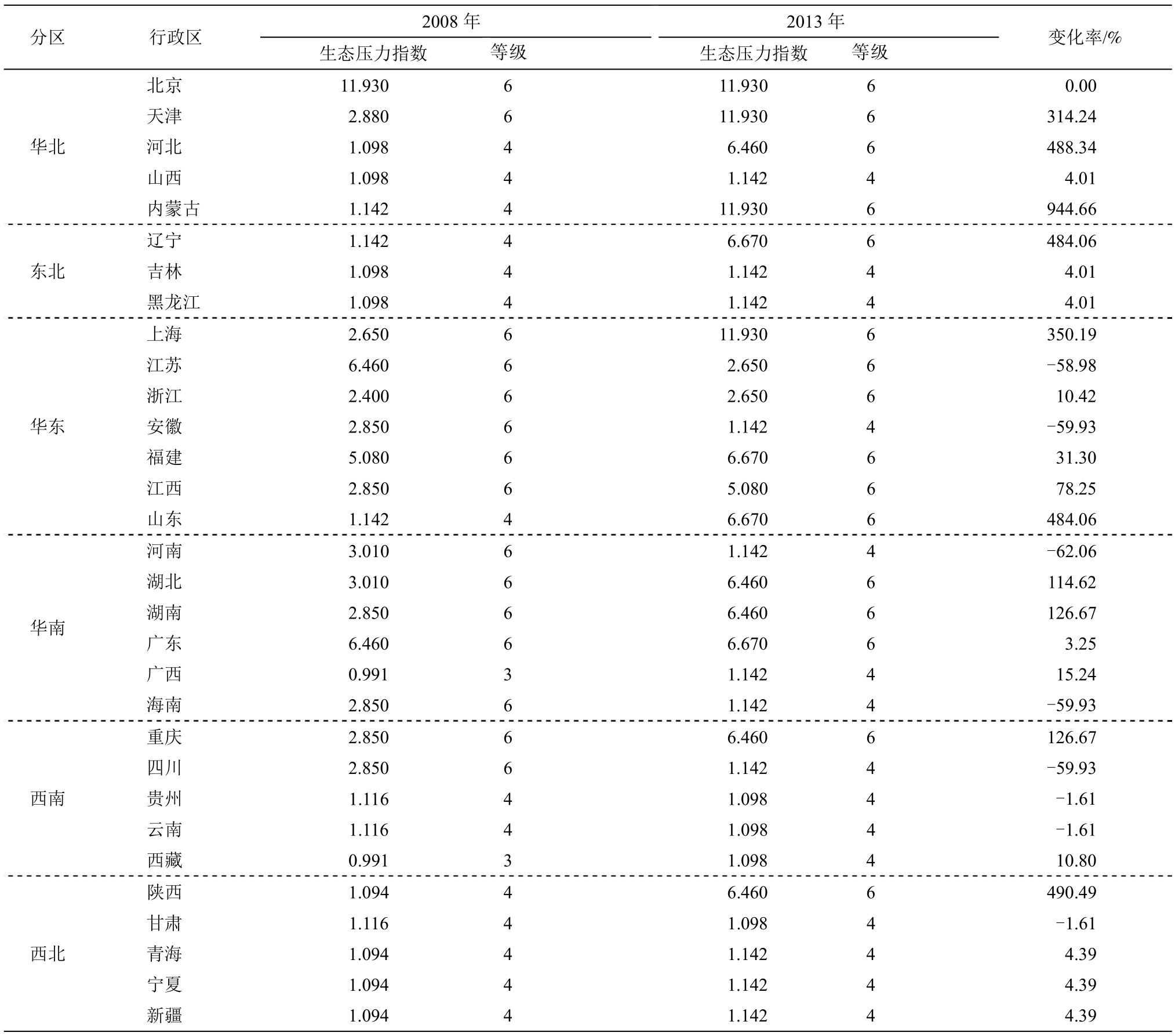
1)2008年和2013年分别输出的生态压力指数结果和两年之间的生态压力指数变化率如表 3 所示。2008年生态压力最大的地区为北京、江苏、广东、福建、河南和湖北; 2013年生态压力最大的地区为北京、天津、上海、内蒙古、广东和福建;全国大部分省级行政区的生态压力状况属于 4 级(较不安全)和 6 级(极不安全)。图 2 利用 GIS 软件形象地表达评价的结果。
2)从生态压力指数变化率上看, 2008—2013年全国 31 个省级行政区中, 生态压力恶化的有 22 个,恶化程度从高到低分别为内蒙古、陕西、河北、辽宁、山东、上海、天津、湖南、重庆和湖北; 生态压力有所减缓的省级行政区有 7 个, 减缓程度从高到低分别为河南、安徽、海南、四川、江苏、贵州、云南和甘肃; 北京的生态压力没有变化, 且一直是全国生态压力最大的地区。
表1 网络训练样本
Table 1 Training samples in the neural network
?
3)将 31 个省级行政区分为华北、东北、华东、华南、西南和西北 6 个大区, 对这 6 个区域的生态压力总体情况进行比较, 结果如图 3 所示。总体来说, 生态压力最大的是华北地区, 并且从 2008年到 2013年, 华北地区生态压力急剧恶化, 其次是华东和华南地区, 东北地区的生态压力恶化情况也很严重, 生态压力最小的是西北和西南地区, 各区域都存在不同程度的生态压力恶化现象。
表2 生态压力指数等级划分标准[4]
Table 2 Classification criteria of ecological tension index[4]
?
从生态安全评价指标体系内涵上看, 生态系统安全性指标的建立需要考虑多种因子的作用和影响, 某一区域的生态系统应该包括土地、草地、森林、水域、能源和社会环境六大系统。本文试图建立一种简单易行、科学有效的研究方法, 选取人均 GDP、人均林地面积、人均草地面积、人均耕地面积、人均建设用地面积、人均化肥使用量、人均电力和人均水资源量作为评价生态压力的 8 项输入指标, 依据生态压力指数理论和前人的研究成果建立 RBFN 模型, 对全国 31 个省级行政区的生态压力进行合理评价。
表3 生态压力指数输出结果及变化分析
Table 3 The output and variation of ecological tension index
?
评价结果表明, 全国有半数地区处于极不安全的生态压力状态, 从 2008年到 2013年, 全国 31 个省级行政区中有 22 个生态压力发生恶化。分区域来看, 北京一直是全国生态压力最大的地区。华北地区生态压力最大且恶化严重, 水资源匮乏严重,人口压力大, 华北地区各省市均为资源密集型城市,长期以来以资源为主的高能耗重工业发展较多, 如何协调统筹环境污染与经济发展的关系是华北地区面临的重要问题。生态压力恶化最明显的是东北地区。作为我国的老工业基地, 东北地区在过去发展经济的同时过度开发和利用资源, 如今生态环境的恶化限制了东北地区的发展, 因此生态环境的恢复和保护将是“振兴东北”的重要课题。西北地区虽然生态压力最小, 但是生态压力指数从 2008年到2013年倍增, 甚至超过西南地区。西部地区生态环境脆弱, 在西部大开发过程中也要关注资源和环境的保护。
通过对全国各地区的生态压力进行评价和对比, 对我国的生态安全状况有了充分认识, 这对于制定科学合理的生态保护政策, 保障生态资源的可持续利用以及协调区域生态资源, 具有一定的理论参考和实践意义。
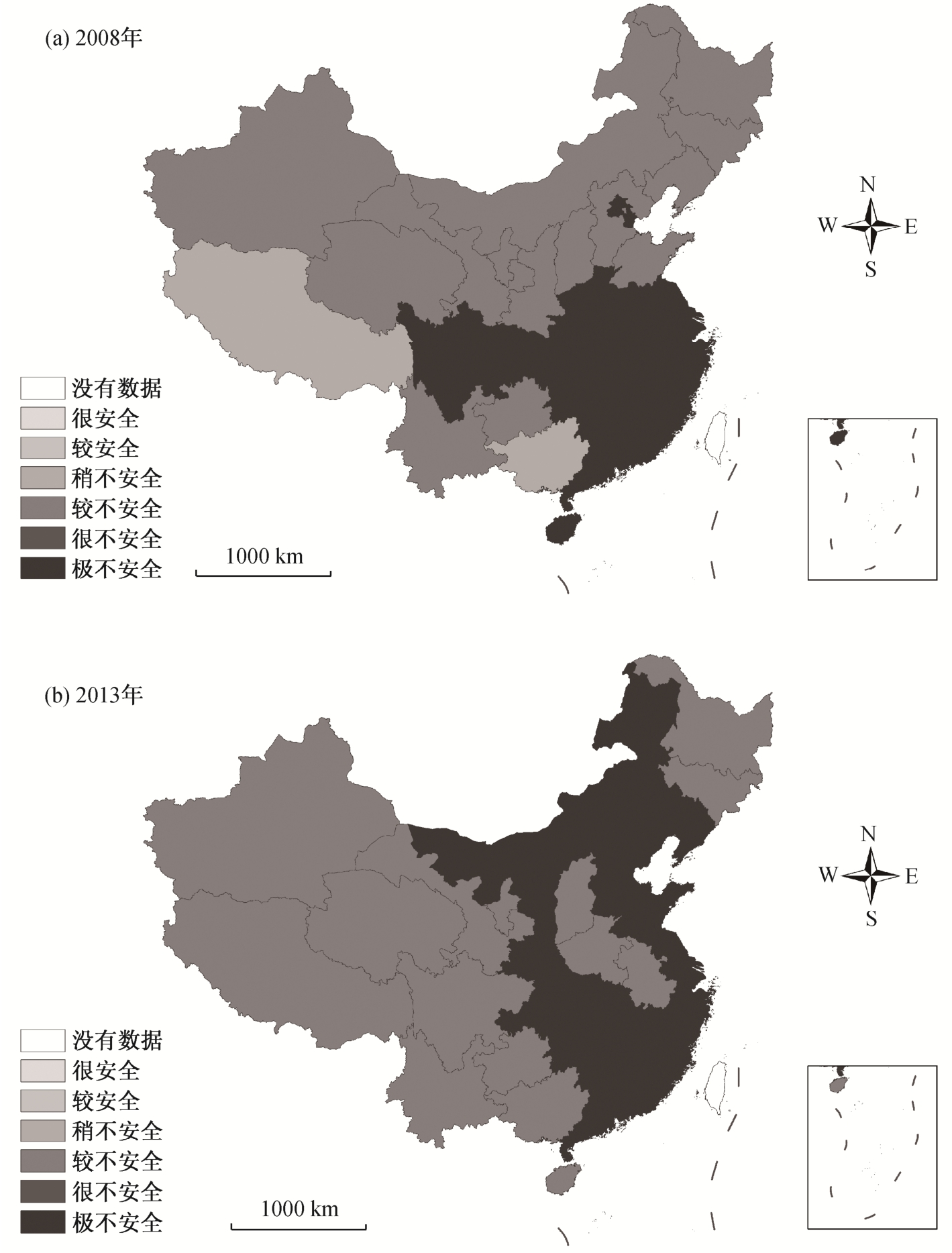
图2 2008 和 2013年全国各地区生态压力指数
Fig.2 National ecological tension map in 2008 and 2013
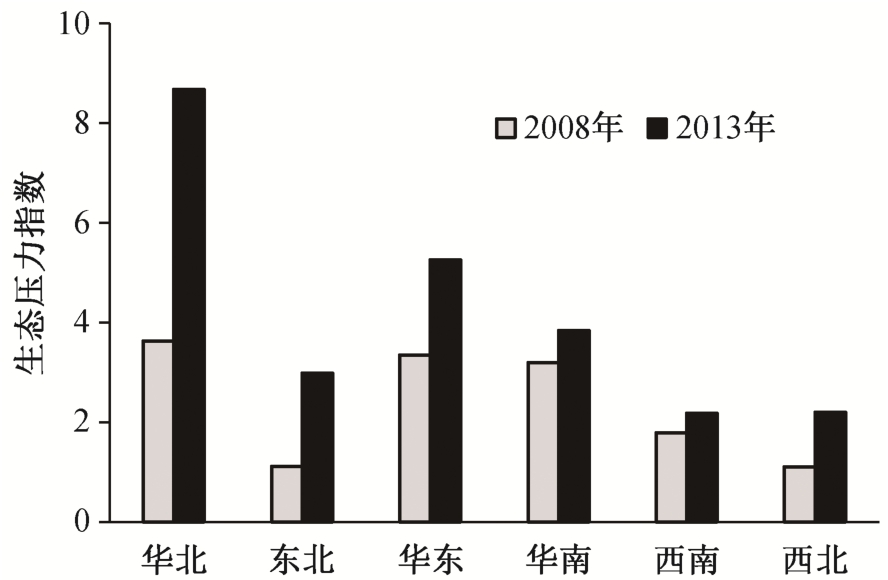
图3 2008 和 2013年全国分区域生态压力指数
Fig.3 Regional ecological tension map in 2008 and 2013
[1]Wackernagel M, Rees W E.Perceptual and structural barriers to investing in natural capital： economics from an ecological footprint perspective.Ecological Economics, 1997, 20(1)： 3-24
[2]Wackernagel M, Onisto L, Bello P, et al.National natural capital accounting with the ecological footprint concept.Ecological Economics, 1999, 29(3)： 375-390
[3]高利峰, 赵先贵.基于生态压力指数的生态安全动态分析——以上海市为例.土壤与作物, 2011, 27(3)： 273-277
[4]赵先贵, 马彩虹, 高利峰, 等.基于生态压力指数的不同尺度区域生态安全评价.中国生态农业学报,2007, 15(6)： 135-138
[5]WWF.Living Planet Report [EB/OL].(2014)[2018-05-02].http：//wwf.panda.org/about_our_earth/all_publi cations/living_planet_report_timeline/lpr_2004/index.cfm
[6]郭跃, 程晓昀, 朱芳, 等.基于生态足迹的江苏省生态安全动态研究.长江流域资源与环境, 2010(11)： 1327-1332
[7]甄江红, 罗莎莎, 何孙鹏.基于生态足迹的呼包鄂地区生态安全评价研究.内蒙古农业大学学报(自然科学版), 2015, 36(6)： 57-64
[8]闵学, 任志远.陕西省生态安全时序变化及驱动因子研究.山东农业科学, 2014, 46(11)： 104-109
[9]徐玉霞.基于生态足迹的城市生态安全评价——以宝鸡市为例.中国农学通报, 2010, 26(21)： 286-290
[10]张晶, 刘耀林, 陈新明, 等.基于生态足迹的浙江省生态安全动态研究.水土保持通报, 2008, 28(4)：185-190
[11]龚建文, 张正栋.基于生态足迹模型的区域可持续发展定量评估——以东江流域东源县为例.生态环境学报, 2009, 18(5)： 1844-1850
[12]徐建华.现代地理学中的数学方法.北京： 高等教育出版社, 1996
[13]丛爽.面向 MATLAB 工具箱的神经网络理论与应用.北京： 中国科学技术大学出版社, 1998
[14]徐秉铮.神经网络理论与应用.广州： 华南理工大学出版社, 1994
[15]黄秋昊, 蔡运龙.基于RBFN模型的贵州省石漠化危险度评价.地理学报, 2005, 60(5)： 771-778
[16]石玉琼.陕西省生态安全分析[D].西安： 长安大学,2010
[17]肖玲, 董林林, 兰叶霞, 等.基于生态压力指数的江西省生态安全评价.地域研究与开发, 2008, 27(1)： 117-120
[18]程冬鸽, 赵先贵, 张军, 等.基于生态压力指数的河南省生态安全时空差异分析.土壤与作物, 2009,25(3)： 288-293
[19]高利峰.基于生态压力指数的天津市生态安全评价.安康学院学报, 2011, 23(2)： 26-28
[20]李中才, 张杏莉.基于生态足迹的区域生态安全评价研究——以山东省为例.农业现代化研究, 2008,29(4)： 465-467
[21]蒋尊梅, 江晓波.基于 GIS 的重庆生态安全时空动态分析.人民长江, 2011, 42(15)： 81-85
[22]张静, 鲁春霞, 谢高地, 等.北京城市能源消费的生态与环境压力研究.资源科学, 2015, 37(6)： 1133-1140
Ecological Tension Index Assessment in China Based on RBFN Model