图1 交通流数据处理与预测应用总体框架
Fig. 1 Traffic flow data processing and prediction framework
李欣1,2
1.河南财经政法大学中原经济区“三化”协调发展河南省协同创新中心, 郑州 450046; 2.河南财经政法大学资源与环境学院, 郑州 450046; E-mail: lixin992319@163.com
摘要设计并实现基于 Spark 的交通流数据处理与预测分析应用框架, 可以完成交通流数据的高效清洗、统计、存储和查询。利用基于多阶空间权重矩阵的 STARIMA 模型进行交通流预测分析, 可以验证数据处理效率及对预测应用的支撑作用。对比实验结果表明: 1)交通流数据处理框架运行效率高, 适用于复杂的数据清洗和挖掘算法, 为预测模型建立数据支撑; 2)交通流预测模型对空间权重矩阵进行了多阶优化, 兼顾高效性和准确性, 预测分析结果可以为交通诱导提供参考。
关键词Spark; 数据清洗; 语义查询; 空间权重矩阵; 交通流预测
随着中国城市化进程的不断推进, 一些城市管理问题愈发突出, 其中一、二线城市的交通拥堵问题严重影响人们的生活体验, 迫切需要利用大数据技术及空间信息技术来优化交通管理水平, 对交通流进行预测, 诱导车辆出行。
目前, 国内外已经有一些相关的研究成果。在海量空间数据管理方面, Aji等[1]通过空间划分以及自定义查询引擎, 建立高性能的空间数据仓库系统Hadoop-GIS; Witayangkurn等[2]利用Java拓扑套件, 在 Post-GIS 中实现空间自定义函数运算; Abouzeid等[3]设计 HadoopDB, 在 MapReduce 框架中实现多源数据互连; Plugge 等[4]设计.MongoDB, 并通过Connector 中间件实现高效数据交换; 温馨等[5]通过自定义空间函数下推, 实现分布式空间查询。以上研究成果在一定程度上提高了空间数据管理效率, 但在框架运算能力和数据管理模式方面还有提升和优化的空间。在交通流预测分析方面, 比较成熟的研究成果有状态空间模型[6]、时间序列模型[7]、神经网络模型[8–9]和历史平均模型[10]等。一些学者基于这些模型进行了优化研究,如利用路网结构和实时时序数据构建交通状态多点预测方法[11], 利用时空自回归模型[12]模拟路网时空相关性的预测模 型[13–15], 利用路口转弯率提高城市交叉路口交通状态预测性能的网络交通状态模型[16–17], 利用路口可达性和路段连通性分析建立路网时空状态表达模型[18]等。以上研究成果建立了基本的交通流预测功能, 但应用限制较多, 对时空相关性考虑不够充分。随着数据采集技术的发展, 对交通流数据处理运算效率的需求也不断地增加。
本文基于 Spark 框架和分布式空间数据库, 设计并实现一种高效的交通流数据获取、清洗、统计和查询框架, 完成交通流预测分析的前期数据处理工作。同时, 对时空自回归移动平均模型 STARIMA的空间权重矩阵进行优化改进, 并用于交通流预测分析, 从而验证本文提出的数据处理框架的效率及其对预测应用的支撑作用, 为下一步建设城市智能交通管理平台提供理论依据。
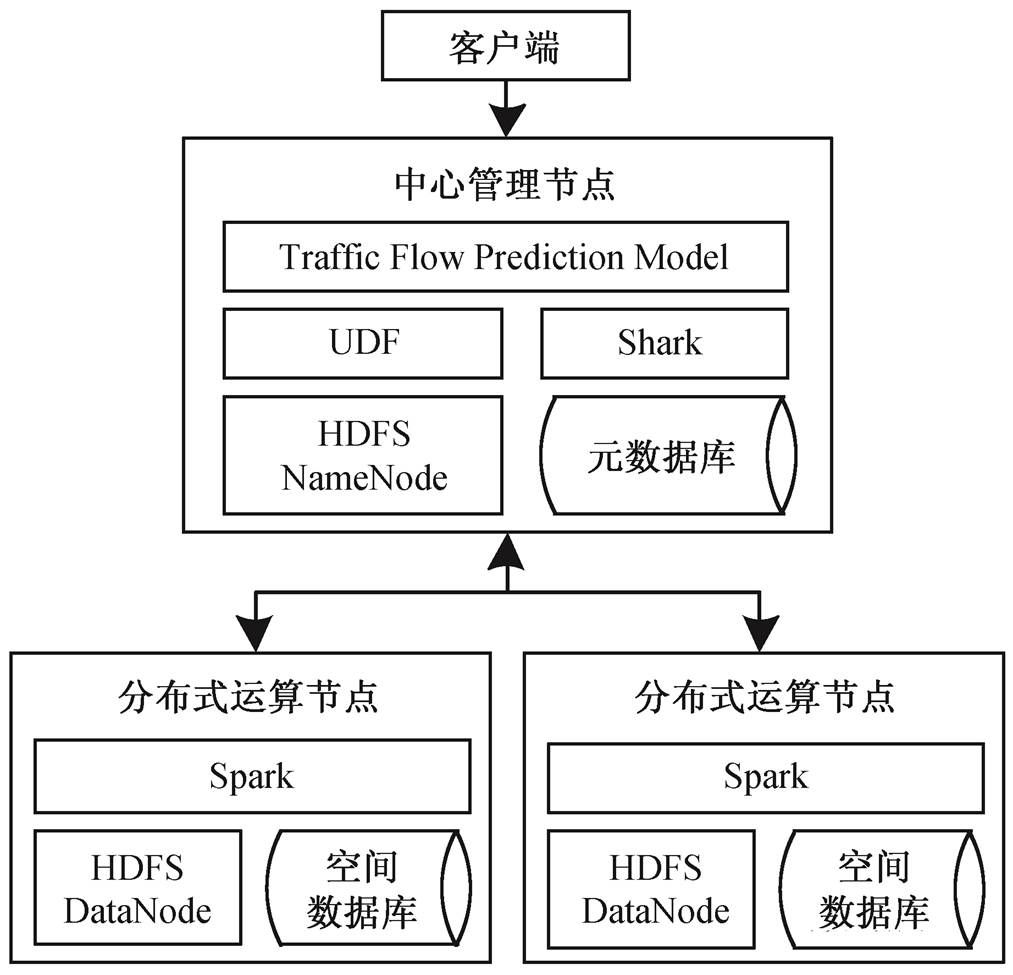
基于 Spark 的交通流数据处理与预测应用的总体框架如图 1 所示, 分为以下两个层次。

图1 交通流数据处理与预测应用总体框架
Fig. 1 Traffic flow data processing and prediction framework
1)分布式运算节点。在利用 Shark[19]完成分布式交通流数据存储的基础上, 以 Spark[20–22]作为高效计算引擎, 将交通流数据清洗和统计时的查询语句转换为弹性分布式数据集(RDD)进行操作, 完成对分布式节点的数据处理。相对于 MapReduce, 此方法的优点在于大量低速磁盘 I/O 操作被高速内存存取代替, 系统的整体运算效率得到有效的提升。
2)中心管理节点。分布式节点上经过清洗和统计的交通流中间数据集传输至中心节点后, 利用HDFS 与空间数据库相结合的方式进行管理。基于用户语义查询条件, 利用自定义空间函数 UDF 进行高效数据查询, 最终使用优化的交通流预测模型生成阶段性预测结果。
基于此框架的交通流数据处理和预测应用流程如下。
1)基于用户输入的空间范围及其他分析条件, 由中心管理节点实现语义查询语句的优化和解译, 结合元数据库中的节点信息, 完成数据处理初始化任务。
2)根据数据处理初始化需求, 在中心管理节点完成交通流数据清洗和统计工作的任务拆分, 并由相应的分布式节点执行分解后的清洗和统计任务。
3)依据分配到的数据处理任务, 使用由孤立点监测算法制定的规则, 对各个分布式节点进行数据清洗, 同时完成阶段性路网交通流数据统计, 并将其传送至中心管理节点。
4)各个分布式节点的路网交通流数据统计结果传输至中心管理节点后, 进行中间统计结果合并, 利用基于多阶空间权重矩阵的 STARIMA 模型完成交通流预测分析。
获取交通流数据的传感设备种类较多, 主要有地磁检测器、视频检测器、微波检测器和浮动车GPS 等, 通常通过有线或无限网络进行数据传输, 并在分布式节点进行处理和存储。由于设备、网络等突发性故障或系统性的原因, 采集到的数据中经常含大量错误、冗余或无效数据, 即“脏数据”[23]。为了保证后期交通流预测分析的准确性, 必须对此类数据进行纠错清洗。
王晓原等[23]设计了基于孤立点检测算法和阈值理论的交通流数据清洗方法, 可在本文设计的数据处理框架中完成分布式节点上的交通流数据清洗, 其步骤如图 2 所示。
通过实验发现, 王晓原等[23]的方法对数据的清洗效果较好, 对“脏数据”的识别率可达90%以上。经过清洗的交通流数据可以更准确地还原实际交通状态, 用其进行预测分析的结果会更准确。但是, 此方法主要对固定数据集进行运算, 且复杂度较高, 对分布式海量数据的处理效率不高。
利用本文设计的基于 Spark 的交通流数据处理框架, 可以在分布式运算节点上针对有限时段内的交通流数据集部署清洗算法, 有效地减少清洗算法在单个节点上处理的数据量。基于 Spark 的高效内存计算, 可以有效地提高系统的运行效率。
由于在数据清洗过程中需要对当前时段的数据集进行遍历, 对每一条数据记录进行孤立点检测, 因此在遍历数据的同时可以完成路网中的交通流信息统计, 将其作为中间统计数据集传输至中心节点进行预测分析。
为了提高分布式网络中交通流数据的访问效率, 需要在分布式运算节点创建并行服务, 将数据存取和清洗运算进行负载均衡配置; 还需要在中心管理节点创建数据分区元数据库, 用于存储各个分布式节点的数据信息, 以便实现数据分区索引, 提高存取效率。
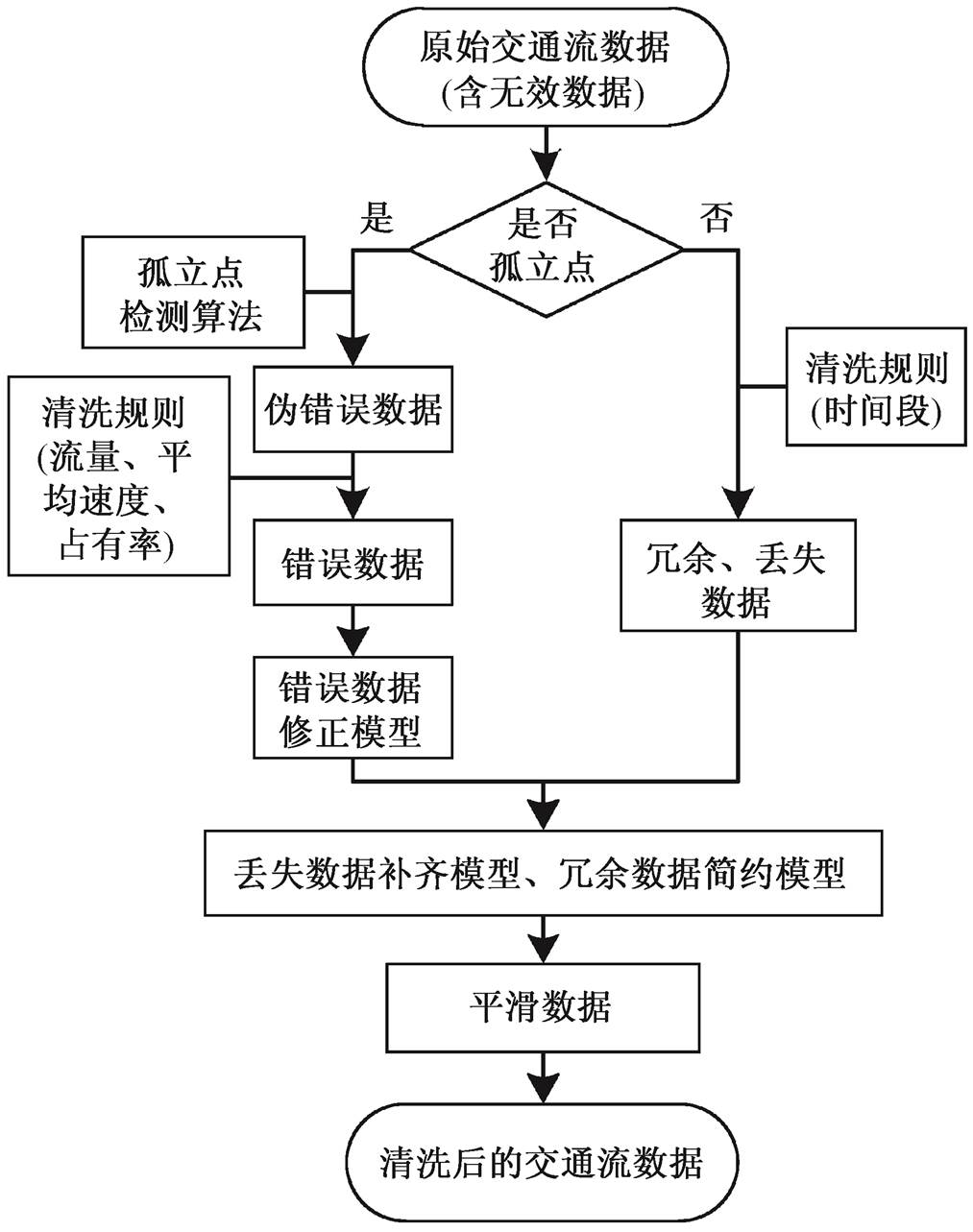
图2 交通流数据清洗步骤[23]
Fig. 2 Traffic flow data cleaning steps[23]
图 3 为并行数据存储与注册流程。首先, 按照城市路网空间分布及已有交通流量统计信息, 设置负载均衡分配规则。由传感器采集的交通流数据经过清洗后, 按负载均衡规则进行传输和存储, 同时按照交通流预测时间周期, 更新分布式节点的元数据信息(主要包括数据的时段、空间范围、数据规模和传感器类型等), 由分布式节点传送至中心节点的元数据库进行注册和存储。
为了保证系统的稳定运行, 避免节点状态异常造成的系统故障, 还需要进行数据镜像备份。本文使用较成熟的数据复制技术, 首先在分布式物理节点创建虚拟节点, 在虚拟节点存储经过负载均衡配置的不同数据集, 针对不同物理节点上的虚拟节点进行相互备份。系统运行时, 可以利用节点探测算法, 对所有虚拟节点进行扫描, 并进行节点状态实时更新。如果节点状态正常, 则提取访问数据; 一旦发现异常, 则自动切换至镜像备份数据源。交通流数据备份原理见图4。
Spark 虽然可以较大程度地提高大数据运算效率, 但其框架不支持地理信息空间查询功能, 必须通过自定义空间查询函数 UDF 来实现查询功能。由于语义查询或模糊查询为分布式查询的主要模式, 所以需要对查询语句进行语义解析, 并将查询条件分解为分布式查询任务, 分配至相应节点, 并行完成查询任务后返回结果。
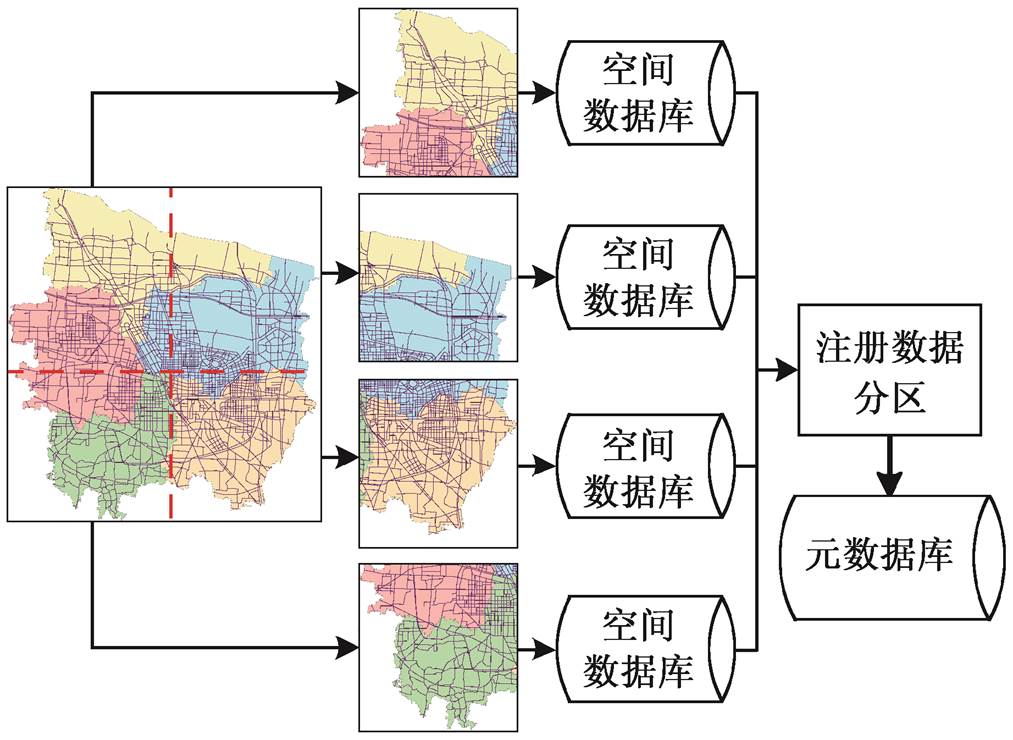
图3 并行数据存储与注册流程
Fig. 3 Parallel data storage and registration process
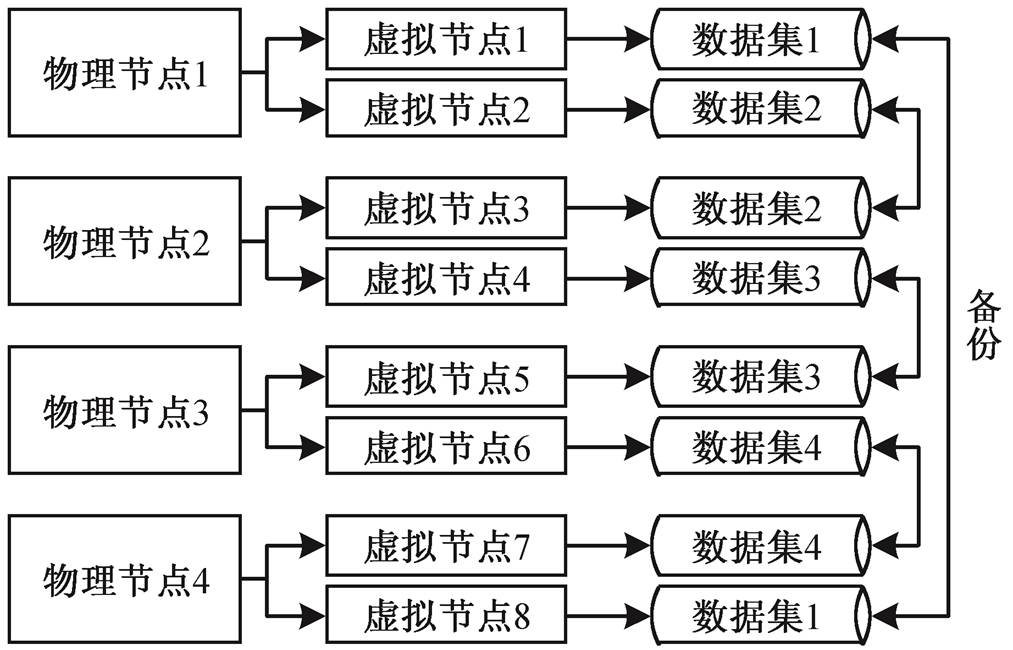
图4 交通流数据备份原理
Fig. 4 Data backup principle of traffic flow
本文实现一套空间查询 UDF 函数库, 并将其进行注册。基于语义的空间查询流程(图5)如下。
1)语义解析器: 分析用户输入的查询条件, 按照语义规则对其进行拆分, 按照查询条件的逻辑关系, 将拆分后的基本查询单元组合为查询条件树。
2)逻辑优化器: 依据查询条件树, 在已注册的自定义空间查询 UDF 函数库中搜索所需函数, 根据优化规则, 将查询逻辑顺序优化, 生成逻辑运行表, 然后进行验证与保存。
3)物理计划生成器: 读取查询条件及逻辑运行表, 参考分布式节点的元数据信息, 将查询任务转换并分解为分布式节点物理查询操作。
本文设计基于多阶空间权重矩阵的 STARIMA交通流预测模型, 对数据处理结果进行应用验证。
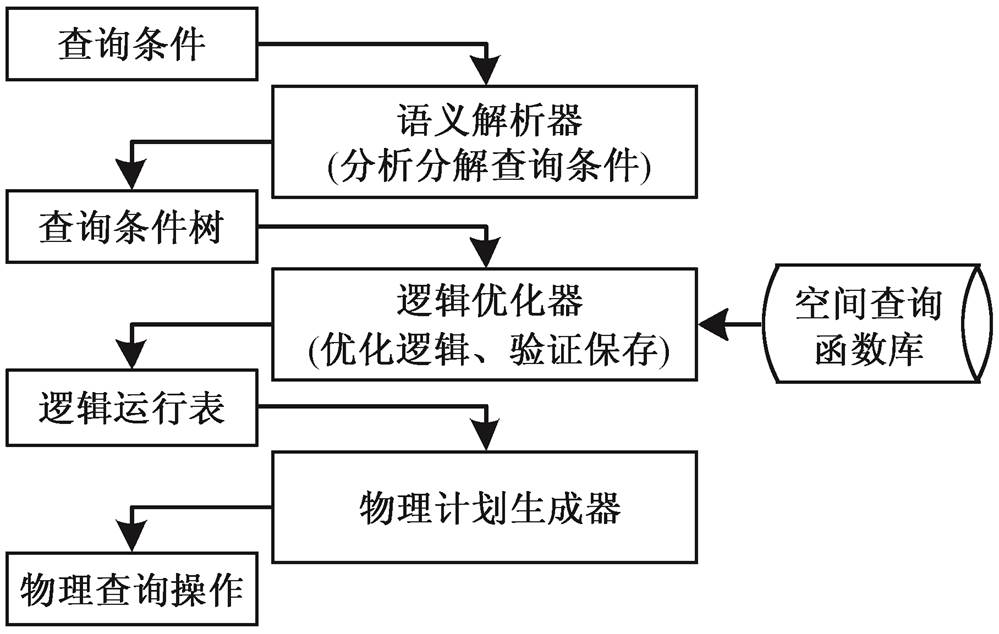
图5 基于语义的空间查询流程
Fig. 5 Spatial query process based on semantics
在城市路网拓扑关系中, 任意两路段仅存在直接邻接和经过n个其他路段间接邻接两种关系, 因此由上游路段到下游路段的交通流分配关系与路口转弯率[24]密切相关, 在仅考虑车辆选择最短路径作为最优路线的情况下, 上下游路段交通流的时空相关性即为经过n个路段的多阶路口转弯率重分配关系。结合交通流预测分析的时间周期特征, 设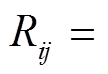
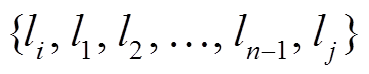 为上游路段
为上游路段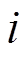 到下游路段
到下游路段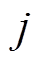 的最短路径, 第
的最短路径, 第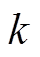 个交通流预测分析时段
个交通流预测分析时段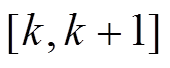 内上游路段
内上游路段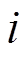 与下游路段
与下游路段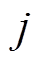 之间的时空相关性表达式为
之间的时空相关性表达式为
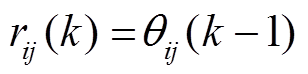 , (1)
, (1)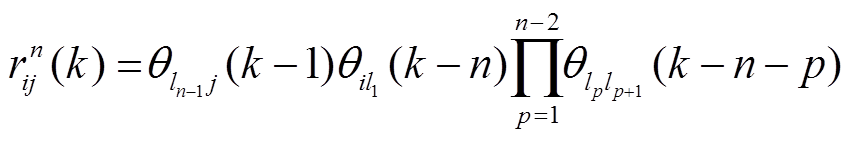 。 (2)
。 (2)式(1)中,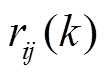 为直接邻接路段
为直接邻接路段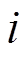 与路段
与路段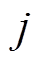 的时空相关性系数,
的时空相关性系数,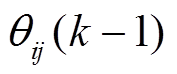 为前一统计时段内二者之间的路口转弯率。式(2)中,
为前一统计时段内二者之间的路口转弯率。式(2)中,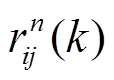 为非直接邻接路段
为非直接邻接路段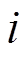 与路段
与路段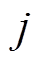 的时空相关性系数,
的时空相关性系数,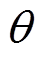 为最短路径中两个相邻路段的转弯率,
为最短路径中两个相邻路段的转弯率,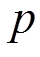 为取值范围为1至
为取值范围为1至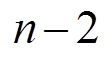 的自增变量。
的自增变量。
从式(1)和(2)可以看出, 路口转弯率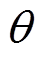 的取值范围为 0~1, 因此时空相关性系数
的取值范围为 0~1, 因此时空相关性系数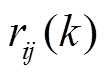 和
和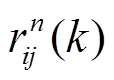 也小于 1, 且最短路径中的中间路段越多, 时空相关性系数的数值越小。经过实验发现, 2 阶以内上下游路段的交通流分配量较多, 相关性高; 3阶以上路段不仅复杂程度高, 计算量大, 而且交通流分配量少, 相关性低, 因此忽略不计。
也小于 1, 且最短路径中的中间路段越多, 时空相关性系数的数值越小。经过实验发现, 2 阶以内上下游路段的交通流分配量较多, 相关性高; 3阶以上路段不仅复杂程度高, 计算量大, 而且交通流分配量少, 相关性低, 因此忽略不计。
根据以上分析, 本文将时空自回归移动平均模型 STARIMA[25–27]的空间权重矩阵与式(1)和(2)进行组合运用, 并且将该模型用于交通流预测分析。STARIMA模型的计算公式如下:
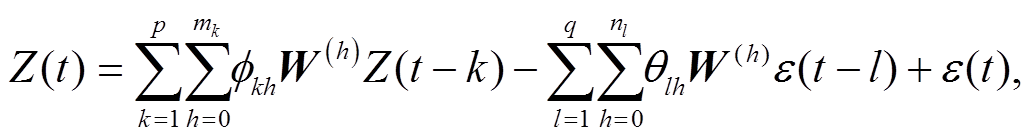 (3)
(3)其中,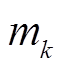 为第
为第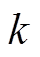 个时间自回归项的空间间隔,
个时间自回归项的空间间隔,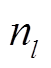 为第
为第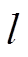 个时间移动平均项的空间间隔,
个时间移动平均项的空间间隔,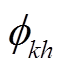 是时间延迟为
是时间延迟为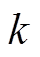 且空间间隔为
且空间间隔为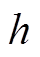 的自回归参数,
的自回归参数,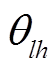 是时间延迟为
是时间延迟为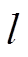 且空间间隔为
且空间间隔为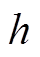 的移动平均参数,
的移动平均参数,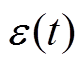 为随机误差,W(h)为
为随机误差,W(h)为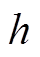 阶空间权重矩阵。
阶空间权重矩阵。
依据 Pfeifer 等[25]对权重矩阵W(h)的限制条件, 结合以上时空相关性分析, 该矩阵元素表达式为
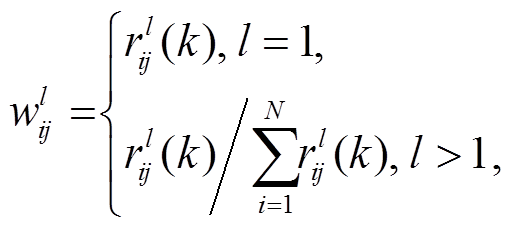 (4)
(4)其中,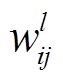 为矩阵中第
为矩阵中第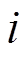 行第
行第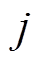 列元素值,
列元素值,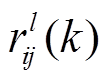 为路段i和j的l阶时空相关性系数。
为路段i和j的l阶时空相关性系数。
式(4)是在路网拓扑关系的基础上, 较充分地考虑了交通流的实际多阶重分配规律, 基于式(4)进行的交通流预测分析结果会更准确。
实验数据来自智能交通管理系统(包含车辆监控、调度指挥、交通监测和流量诱导等子系统)。在郑州市交通管理系统中, 通过视频、微波、地磁和 GPS 采集交通流数据, 系统运行日均数据增量约为 2000 万条。本文实验数据为 2016 年 12 月 5 日至 12 月 18 日(共计 14 天)的郑州市部分区域交通流数据。
实验中使用 5 台配置相同的服务器, 配置均为Intel XeonE5-2640 2.6GHz, 8核, 16GB内存。中心管理节点使用 1 台服务器, 完成分布式节点元数据管理、用户语义查询任务分配以及交通流周期预测分析等工作。分布式运算节点使用 4 台服务器, 完成交通流数据清洗、统计、存储和备份工作。
由于交通流数据是由多元传感器实时采集, 会随时间推移海量地增长, 因此必须验证本文交通流数据处理框架中的清洗、统计、存储和查询效率能否满足预测应用的需求。
根据Min 等[16]的研究结果, 交通流预测分析的时间周期以 15 分钟为宜。按系统日均采集 2000 万条数据计算, 15 分钟的平均数据量为 21 万条。考虑到高峰时段的交通流量远大于非高峰时段, 兼顾系统的可扩展性, 针对本文数据来源, 数据处理速度应达到每15分钟50~100万条。
本文除使用基于 Spark 的方法处理交通流数据外, 还使用基于 MPI 的方法和基于 MapReduce 的方法, 并对比3种方法的数据处理效率。
1)基于 MPI 的方法[28]。在 4 个分布式节点各配置 1 个从进程, 由其并行实现多源交通流数据清洗和统计, 并按照 15 分钟的时间周期将数据更新至主进程。主进程配置在中心节点, 实现中间统计信息合并汇总, 并使用预测模型进行交通流预测。
2)基于 MapReduce 的方法[13]。将交通流数据按照负载均衡规则平均分为 48 个子集, 在 4 个分布式节点设置 48 个 Map 运算和 4 个 Combine 运算, 每个 Map 运算对应 1 个数据子集进行数据清洗, Combine 运算完成本节点数据统计并将其传输至中心节点, 中心节点的 Reduce 运算对中间统计信息进行合并, 并利用预测模型进行分析。
3)基于 Spark 的方法。基于本文设计的框架, 使用 Spark 作为计算引擎, 完成交通流数据清洗, 并在 Shark 数据仓库进行存储, 在中心管理节点实现清洗后交通流统计数据的合并, 最终使用预测模型进行分析验证。
实验中整理了 6 个数据集, 数据量分别为 2万、5 万、10 万、20 万、50 万和 100 万条。针对这 6 个数据集, 使用以上 3 种方法进行效率对比(图6)。其中 50 万和 100 万条两个数据集的数据量已超过系统目前在一个预测周期内采集的最大交通流数据量。从图6得到以下结论。
1)MPI 方法在处理不同数据量的数据集时, 耗费时间与数据量成正比。由于 MPI 框架结构简单, 占用计算资源较少, 因此当数据量较小时, 数据处理时间少于其他两种方法。
2)相对于 MPI 方法, MapReduce 方法的应用框架更复杂, 数据处理耗时占比较大, 因此在数据量较小时耗时比MPI方法长, 但框架耗时基本上不受数据量影响, 随着数据量不断增加, 数据处理耗时占比不断降低, 从而使时间曲线斜率减小, 对 50 万条数据的处理时间反而少于MPI方法, 并且数据量越大, 时间优势越突出。
3)Spark 方法的时间曲线与 MapReduce 方法近似, 但总体耗时明显较少, 原因在于 MapReduce 在交通流数据清洗过程中需要进行大量 I/O 操作和资源申请, 由于磁盘存取效率远远低于内存存取, 因此 Spark 方法的内存计算模式大大提高了整体运行效率, 更适合实现复杂的数据清洗和挖掘算法。通过实验发现, Spark 方法耗时比 MapReduce 方法少60%左右。
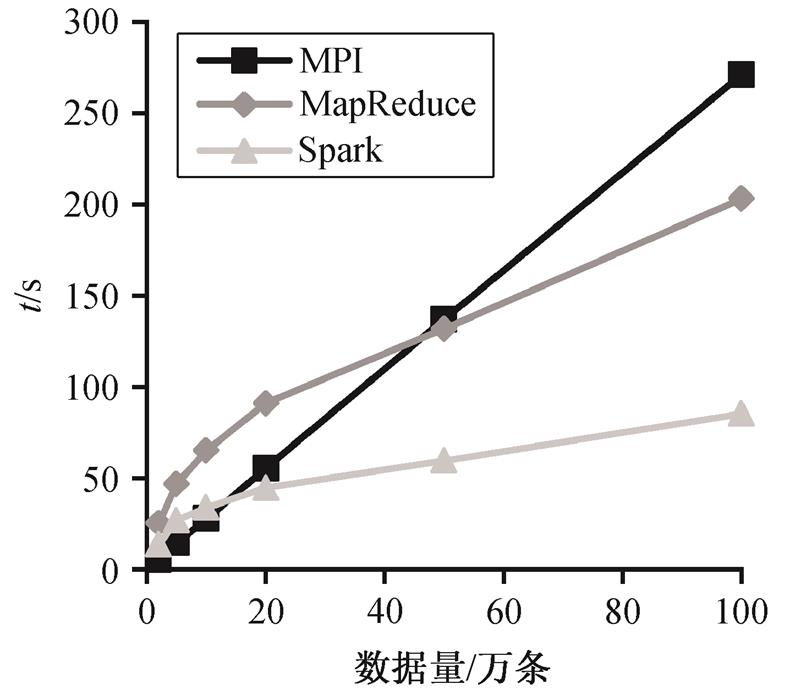
图6 3种算法不同数据量时间对比
Fig. 6 Cost of time of three algorithm for different amount of data
从总体上看, 基于 Spark 的交通流数据处理方法技术成熟, 效率较高, 适用于交通流预测应用的前期数据处理工作。
经过数据清洗和统计后, 按照预测的时间周期, 各个路段的交通流统计信息被传送至中心管理节点。基于此统计信息, 利用动态 STARIMA模型[1]和本文提出的基于多阶空间权重矩阵的 STARIMA交通流预测模型进行预测分析。首先对需要预测的区域路网进行抽象化处理。
图 7(a)为郑州市主城区及其路网, 图 7(b)为图7(a)中龙子湖高校园区路网抽象化示意图。以图7(b)中路网为例, 设定 15 分钟为预测分析的时间周期, 从实验数据集中选取前 4 天共 384 个时段作为历史数据集, 对后 10 天 960 个时段进行预测分析, 将分析结果与真实交通流数据进行对比, 计算均方误差, 定量地评价预测的准确度。
1)动态 STARIMA 模型。利用时空自回归移动平均模型STARIMA来体现交通流在时空维度上的相关性, 但此相关性仅包含一阶路段, 不能准确地反映交通流运行的真实特征, 预测结果会受到影响。
2)基于多阶空间权重矩阵的 STARIMA 模型。将空间权重矩阵扩展为多阶矩阵, 能够更准确地反映上下游交通流的时空相关性。实验结果表明, 预测分析中引入二阶空间权重矩阵可以提高分析的准确性; 三阶以上路段运算量大, 相关性弱, 为了保 证系统的高效运行, 可以忽略不计。
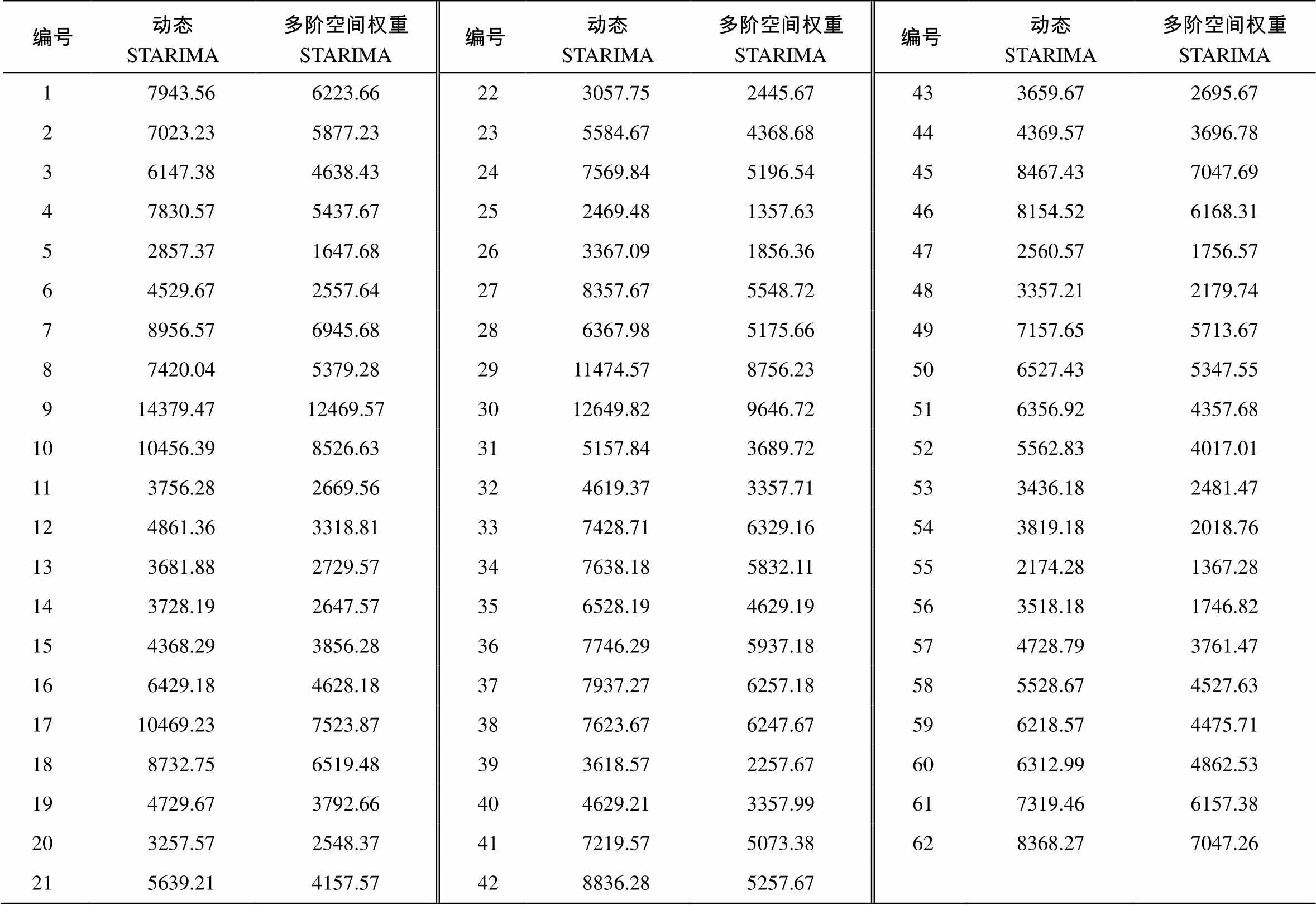
从表 1 看出, 本文预测模型比动态 STARIMA模型准确度更高, 原因在于对空间权重矩阵进行了多阶优化, 不但能够反映交通流的真实分配规律, 而且可以保证系统的运算效率, 预测结果也更准确。
在 Spark 框架下对各类传感器采集的交通流大数据进行清洗、统计、存储和查询, 可以实现交通流数据的高效处理。对交通流进行预测分析, 是解决城市拥堵问题的一种技术辅助手段。
本文设计了一种基于 Spark 的交通流数据处理与预测应用框架, 利用该框架实现交通流数据的高效清洗、统计、存储和查询。对比实验证明, 基于Spark 的数据处理方法的运算效率优于基于 MPI 和MapReduce 的方法, 可以满足交通流预测分析的应用需求。
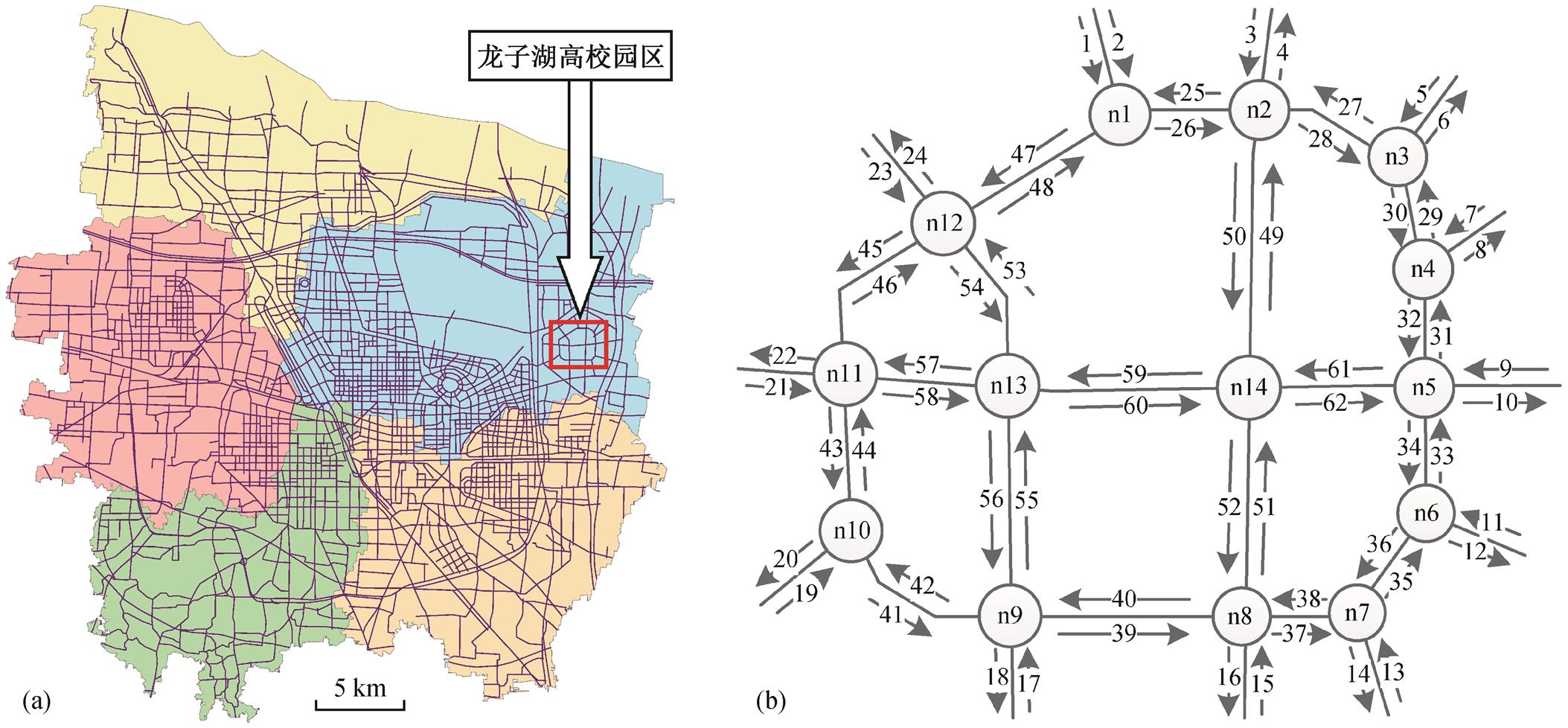
图7 郑州市城区道路交通网(a)及龙子湖高校园区路网抽象化结果示意图(b)
Fig. 7 Zhengzhou city road network (a) and abstraction of Longzi Lake college area road network (b)
表1 动态STARIMA模型和基于多阶空间权重矩阵的STARIMA模型预测结果的均方误差
Table 1 MSE comparison of dynamic STARIMA model and multi-order spatial weight matrix STARIMA model predict results
编号动态STARIMA多阶空间权重STARIMA编号动态STARIMA多阶空间权重STARIMA编号动态STARIMA多阶空间权重STARIMA 17943.566223.66223057.752445.67433659.672695.67 27023.235877.23235584.674368.68444369.573696.78 36147.384638.43247569.845196.54458467.437047.69 47830.575437.67252469.481357.63468154.526168.31 52857.371647.68263367.091856.36472560.571756.57 64529.672557.64278357.675548.72483357.212179.74 78956.576945.68286367.985175.66497157.655713.67 87420.045379.282911474.578756.23506527.435347.55 914379.4712469.573012649.829646.72516356.924357.68 1010456.398526.63315157.843689.72525562.834017.01 113756.282669.56324619.373357.71533436.182481.47 124861.363318.81337428.716329.16543819.182018.76 133681.882729.57347638.185832.11552174.281367.28 143728.192647.57356528.194629.19563518.181746.82 154368.293856.28367746.295937.18574728.793761.47 166429.184628.18377937.276257.18585528.674527.63 1710469.237523.87387623.676247.67596218.574475.71 188732.756519.48393618.572257.67606312.994862.53 194729.673792.66404629.213357.99617319.466157.38 203257.572548.37417219.575073.38628368.277047.26 215639.214157.57428836.285257.67
本文还基于交通流周期统计信息, 设计并实现了基于多阶空间权重矩阵的 STARIMA 交通流预测模型, 通过对空间权重矩阵的多阶优化, 可以定量地反映交通流在路网中的真实运行规律, 预测结果的准确性优于动态 STARIMA 模型, 可以为交通诱导提供参考信息。
本文实验中使用的数据量已具备一定的规模, 但由于硬件设备限制, 分布式节点数量较少。在未来的工作中, 需要进一步验证海量分布式节点环境下系统的运行情况。本文仅模拟了车辆移动时选择最短路径的情况, 未对更复杂的最短时间、中途点以及个人偏好等影响路径选择的因素进行分析, 需要进一步的研究和验证。
参考文献
[1]Aji A, Wang F, Vo H, et al. Hadoop-GIS: a high performance spatial data warehousing system over mapreduce // Proceedings of the 39th International Conference on VLDB Endowment. Trento, 2013: 1009‒1020
[2]Witayangkurn A, Horanont T, Shibasaki R. Perfor-mance comparisons of spatial data processing tech-niques for a large scale mobile phone dataset // Pro-ceedings of the 3rd International Conference on Com-puting for Geospatial Research and Applications. New York: ACM Press, 2012: 1‒6
[3]Abouzeid A, Bajda-Pawlikowski K, Abadi D, et al. HadoopDB: an architectural hybrid of MapReduce and DBMS technologies for analytical workloads // Proceedings of the 35th International Conference on VLDB Endowment. Lyon, 2009: 922‒933
[4]Plugge E, Hawkins T, Membrey P. The definitive guide to MongoDB: the NoSQL database for cloud and desktop computing. Berlin: Springer, 2010
[5]温馨, 罗侃, 陈荣国, 等. 基于 Shark/Spark 的分布式空间数据分析框架. 地球信息科学学报, 2015, 17(4): 401‒407
[6]Stephanedes Y J, Michalopoulos P G, Plum R A. Im-proved estimation of traffic flow for real time control. Transportation Research Record: Journal of the Tran-sportation Research Board, 1981, 795: 28‒39
[7]Ahmed M S, Cook A R. Analysis of freeway traffic time-series data by using box-jenkins techniques // Transportation Research Record 722. Washington DC: Transportation Research Board, l979: 1‒9
[8]Dougherty M S, Cobbett M R. Short-term inter-urban traffic forecasts using neural networks. International Journal of Forecasting, 2004, 13(1): 21‒31
[9]Ledoux C. An urban traffic flow model integrating neural networks. Transportation Research Part C: Emerging Technologies, 1997, 5(5): 287‒300
[10]Okutani I, Stephanedes Y J. Dynamic prediction of traffic volume through Kalman filtering theory. Tran-sportation Research Part B, 2008, 18(1): 1‒11
[11]余碧莹, 邵春福. 基于时空模型的道路网交通状态预测 // 第四届中国智能交通年会论文集. 青岛, 2008: 546‒551
[12]Martin R L, Oeppen J E. The identification of re-gional forecasting models using space-time correlation functions. Transactions of the Institute of British Geographers, 1975, 66: 95‒118
[13]Kamarianakis Y, Prastacos P. Space-time modeling of traffic flow. Computers & Geosciences, 2005, 31: 119‒133
[14]李欣, 孟德友. 基于路网相关性的分布式增量交通流大数据预测方法. 地理科学, 2017, 37(2): 209‒216
[15]Lin Shulan, Huang Hongqiang, Zhu Daqi, et al. The application of space-time ARIMA model on traffic flow forecasting // Proceedings of the 8th Interna-tional Conference on Machine Learning and Cyber-netics. Baoding, 2009: 3408‒3412
[16]Min Xinyu, Hu Jianming, Chen Qi, et al. Short-term traffic flow forecasting of urban network based on dynamic STARIMA model // Proceedings of the 12th International IEEE Conference on Intelligent Trans-portation Systems. St. Louis: Institute of Electrical and Electronics Engineers, 2009: 461‒466
[17]瞿莉. 基于动态交通流分配参数的网络交通状态建模与分析[D]. 北京: 清华大学, 2010
[18]张和生, 张毅, 胡东成, 等. 区域交通状态分析的时空分层模型. 清华大学学报(自然科学版), 2007, 47(1): 157‒160
[19]Xin R S, Rosen J, Zaharia M, et al. Shark: SQL and rich analytics at scale // Proceedings of the 2013 ACM SIGMOD International Conference on Manage-ment of Data. New York, 2013: 13‒24
[20]Zaharia M, Chowdhury M, Franklin M J, et al. Spark: cluster computing with working sets // Proceedings of the 2nd USENIX Conference on Hot Topics in Cloud Computing. Berkeley: USENIX Association, 2010: 1‒10
[21]Tabaa Y, Medouri A, Tetouan M. Towards a next generation of scientific computing in the cloud. In-ternational Journal of Computer Science, 2012, 9(6): 177‒183
[22]Zaharia M, Chowdhury M, Das T, et al. Fast and interactive analytics over Hadoop data with Spark // Proceedings of the 10th USENIX Conference on File and Storage Technologies. San Jose: USENIX Asso-ciation, 2012: 45‒51
[23]王晓原, 张敬磊, 吴芳. 交通流数据清洗规则研究. 计算机工程, 2011, 37(20): 191‒193
[24]Deng Shuo, Hu Jianming, Wang Yin, et al. Urban road network modeling and real-time prediction based on house holder transformation and adjacent vector // Advances in Neural Networks — ISNN 2009. Berlin: Springer, 2009: 899‒908
[25]Pfeifer P E, Deutsch S J. A three-stage iterative pro-cedure for space-time modeling. Technometrics, 1980, 22(1): 35‒47
[26]Pfeifer P E, Deutsch S J. Identification and interpre-tation of first-order space-time ARMA models. Tech-nometrics, 1980, 22(3): 397‒408
[27]Pfeifer P E, Deutsch S J. Variance of the sample-time autocorrelation function of contemporaneously corre-lated variables. SIAM Journal of Applied Mathema-tics, Series A, 1981, 40(1): 133‒136
[28]牛新征, 佘堃. 面向大规模数据的快速并行聚类划分算法研究. 计算机科学, 2012, 39(1): 134‒137
Efficient Traffic Flow Data Processing Method and Its Application Based on Spark Framework
LI Xin1,2
1. Collaborative Innovation Center of Three-Aspect Coordination of Central Plain Economic Region, Henan University of Economics and Law, Zhengzhou 450046; 2. College of Resource and Environment, Henan University of Economics and Law, Zhengzhou 450046; E-mail: lixin992319@163.com
AbstractA traffic flow data processing and forecasting framework based on Spark is designed, and it can complete the efficient cleaning, statistics, storage and query of traffic flow data. A multi-order spatial weight matrix STARIMA model is used to predict the traffic flow, and it can verify the efficiency of data processing and the support for the prediction. By comparative experiments, the results show that the traffic flow data processing framework is efficient, and it is suitable for realizing complex data cleaning and mining algorithms and establishing data support for the prediction model. The traffic flow prediction model optimizes the multi-order spatial weight matrix, and it takes both efficiency and accuracy into consideration. The prediction results can provide reference for traffic guidance.
Key wordsSpark; data cleaning; semantic query; spatial weighting matrix; traffic flow prediction
中图分类号P91
doi:10.13209/j.0479-8023.2018.070
国家自然科学基金(41501178, 41771445)和河南财经政法大学博士科研基金(800257)资助
收稿日期:2017–10–11;
修回日期:2017–12–01;
网络出版日期:2018–07–16