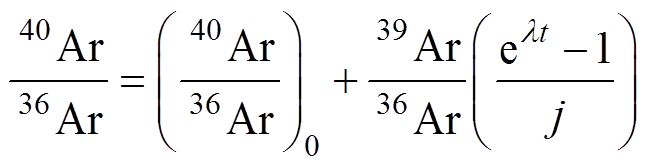(1)胡燕†季建清 周晶 涂继耀
造山带与地壳演化教育部重点实验室, 北京大学地球与空间科学学院, 北京 100871; † E-mail: yan_hu@hotmail.com
摘要激光熔蚀40Ar/39Ar 等时线法是第四纪年轻火山岩样品精细定年的新方法, 该方法处于逐步完善过程中。针对怎样判定获得的年龄结果是否可靠的问题, 通过对数据处理过程中所用参数的分析, 认为样品属性是决定年轻火山岩精细定年结果质量和可靠性的关键因素, 与样品测试数n值相关的加权均方差 MSWD (mean square weighted deviation)是判断同一样品各测试点的数据是否符合正态分布, 能否用来客观地评价测试结果, 进而评估样品是否适合进行相关测试, 结果是否可靠的重要指标。其次, 属于同一真实年龄值样品的 MSWD 在 99.7%置信区间的取值范围可通过计算加以确认, 并提出对于表面年龄和等时线年龄数据, 必须定量地考察相应的MSWD值, 判定在具有足够样品测试数(足够大的n值)的情况下, 是否符合概率统计的正态分布, 确定样品是否对应同一年龄真实值。在 MSWD 值达不到理想值 1.0 的情况下, 可以利用表面年龄概率密度曲线, 区分测试样品内部包含的非同源或非等时或封闭不好体系的数据, 再结合 MSWD 与n值关系, 适量地去除部分偏离正态分布的测试数据, 识别出可能归属多个年龄真实值的测试数据组, 并以此计算不同数据组的反等时线年龄, 获得年轻火山岩喷发的准确年龄。
关键词激光40Ar/39Ar; 等时线法; MSWD; 年轻火山岩; 数据处理
年轻火山岩的精细定年是研究火山喷发规律的基础, 也是年代学研究的前沿领域。由于火山岩成分往往富 K, 并含有放射性母体40K, 因此在火山岩定年中K-Ar法和40Ar/39Ar法运用最广泛。20世纪90年代, 随着激光、质谱和真空技术的进步, 激光40Ar/39Ar法积累了一批成功的定年结果, 成为年代学的重要方法[1]。尤其对小于 0.2Ma 的极年轻火山岩[2],40Ar/39Ar 法取得若干令人瞩目的成果[3–5], 已经可以测定人类活动历史的年龄[2,6]。
尽管激光熔蚀40Ar/39Ar 等时线法技术成熟、结果可靠, 但年轻火山岩的激光40Ar/39Ar等时线定年仍是难点。一方面, 受仪器性能和实验操作等技术环节的限制。前人在实验流程、标样研制、激光熔样和纯化系统的优化等方面进行了比较深入的讨论[2,7–10]。另一方面, 受样品属性对同位素组成的制约。例如, 样品组成的不均一性导致样品的初始40Ar/36Ar 比值不同[11–14]。事实上, 样品属性对40Ar/39Ar定年结果有重要影响[15]。
面对样品、仪器与测试过程带来的诸多不确定性, 要获得可靠的定年结果, 必须采用合理的数据处理算法, 建立数理统计和评价指标体系, 并且给出合理的地质解释。前人对40Ar/39Ar 等时线回归算法、回归质量评估以及标准偏差与不确定度的计算等方面做了探讨[16–20], 本文着重对加权均方差MSWD (mean square weighted deviation)与n值对数评估的意义进行辨析, 并依托北京大学全自动高精度激光40Ar/39Ar定年系统, 采用伯克利地质年代学中心(Berkeley Geochronology Center) Deino 博士编写的 Mass Spec 7.948 软件, 对北京大学40Ar/39Ar年代学实验室 2008—2016 年间若干第四纪火山岩样品进行(反)等时线定年数据处理, 将理论与实例相结合, 对未来的年轻火山岩精细定年工作提供 参考。
40Ar/39Ar 等时线法的原理基于 K-Ar 等时线法。假定样品中大气 Ar 为零, 初始 Ar 不为零, 考虑样品形成过程中 K-Ar 同位素体系在样品内分布的变化。对于火山岩, 这一变化过程可以分为以下 3 个阶段。
1)在岩浆中, 所有原子自由移动, 可以认为此时各元素均匀地分布在体系中。
2)随着岩浆冷却, 形成部分晶体。作为构成矿物的主要成分之一, K 在不同的矿物晶体中的含量不同, 导致放射性母体40K 在不同矿物相中含量不同。但是, 作为惰性气体, Ar 不进入矿物晶格, 因此 Ar 各同位素之间未出现分异, Ar 在岩浆体系内自由移动, 此时40Ar/39Ar 比值在岩浆体系中处处相等。
3)当温度下降到矿物对 Ar 的封闭温度以下时, Ar同位素体系封闭, Ar原子无法移动, 矿物内有了相同的初始Ar比值。同时,40K放射产生的40Ar 开始在晶体中积累。依据衰变定律, 相对于 K 含量低的晶体, 经过一段相同的时间, K 含量高的晶体具有较大的40Ar/36Ar 值。如果40Ar 仅是放射成因的, 则不同晶体的40Ar/36Ar 与40K/36Ar 的比值相同; 然而, 晶体或多或少含有初始 Ar, 因此这些40K/36Ar值与40Ar/36Ar 值拟合而成的等时线的截距等于 K-Ar 体系封闭时的初始40Ar/36Ar 值, 斜率与样品的年龄值在数学上等价。
40Ar/39Ar 法的等时线原理与 K-Ar 法相同, 激光40Ar/39Ar常用的等时线方法[21]包括正等时线
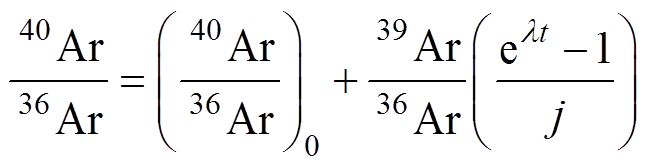(1)和反等时线
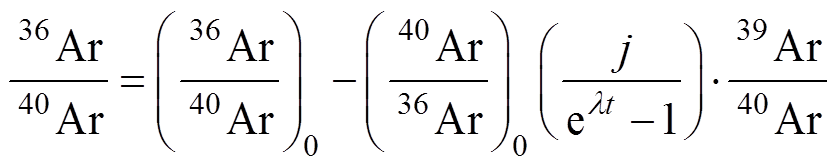。(2)
在实际应用中, 可将式(1)和(2)中的初始 Ar 比值视为直线截距, 式(1)中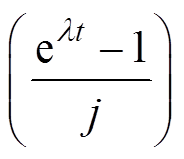
与式(2)中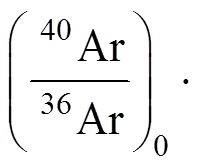
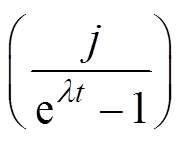为直线斜率, 是包含年龄t的表达式。测定一系列 K 含量不同、初始 Ar 比值相同的样品的Ar 同位素比值, 根据式(1)和(2)进行线性回归计算, 得到初始 Ar 比值(截距)和年龄(t), 即为等时线年龄或反等时线年龄。理论上, 由正、反等时线计算得到的年龄值应该相同[22], 但对于年轻火山岩样品, 因晶格中囚禁的36Ar 较少, 导致36Ar 测试结果的不确定度大。在正等时线表达式(式(1))中36Ar 位于分母位置, 其不确定度对计算最终年龄结果的不确定度影响很大。相比之下, 反等时线年龄更精确[23]。本文关于等时线法的讨论主要以反等时线为例。
为了获得准确的等时线年龄, 样品必须满足以下条件[24]: 1)测试点的K同位素同时进入晶格, 开始计时; 2)各测试点的初始 Ar 组成一致, 即同源; 3)K-Ar 同位素体系保持封闭。对于年轻的火山岩样品, 由于测试精度要求较高, 即便是极小的“同时、同源、封闭”的差异, 都能引起测试结果的很大偏差。例如, 就“同时”而言, 火山岩喷出地表后快速冷却, 火山岩中斑晶和基质达到 Ar 同位素封闭温度的时间可能略有差异, 相对于样品的地质年龄可忽略不计。但是, 对于年轻火山岩样品, 在样品采集和实验前处理过程中, 可以通过一些特征识别出不符合要求的样品而予以剔除, 如深部岩浆房形成的斑晶(如橄榄石)和遭受风化作用的不新鲜样品[2]。尽管如此, 样品的同源性仍是影响年龄质量的因素[25]。
MSWD 是同位素年代学中重要的数据评价指标, 可以在一定程度上帮助评估数据的准确性, 尤其是等时线年龄的数据质量。从式(1)和(2)可知, 等时线方程中的两个未知量为同位素比值, 均由测试得到, 故两个变量均具有一定的不确定度。在这种情况下对数据进行回归分析, 获得的结果比较复杂。目前, 等时线回归最好的算法是加权最小二乘法[19,26–27], 本文采用这种算法进行数据处理。MSWD的提出基于等时线回归的加权最小二乘法[16]。为了深入理解 MSWD 的含义, 下面对加权最小二乘法做简要的梳理。
根据 Mcdougall 等[1]对加权平均值计算方法的回顾, 首先以较简单的情形(即年轻火山岩激光40Ar/39Ar 表面年龄)为例。通常会计算表面年龄的加权平均值, 用此平均值来代表样品的年龄, 并根据相应的 MSWD 值来检验参加计算的数据是否符合正态分布。在实践中, 一个年轻火山岩样品通常包含 20~30 个测试点, 每个测试点的同位素比值和计算得到的表面年龄受到样品属性和仪器条件的影响, 其不确定度并不相同。根据这些数据各自的方差确定权重, 权重为方差的倒数:
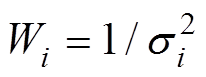。 (3)
表面年龄的加权平均值为
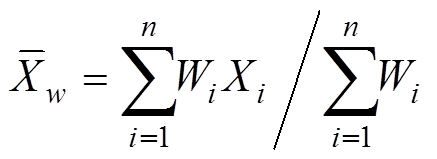, (4)其中,X代表测试点的表面年龄,n是同一个样品的测试点数。表面年龄加权平均值的方差可以由泰勒展开式近似地求得, 等于全部数据权重之和的倒数:
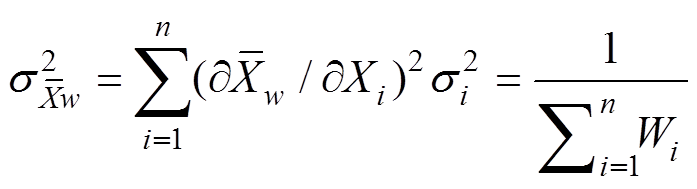。 (5)
通过单个数据方差倒数来为数据加权的好处是, 可以利用 MSWD 来检验这些数据是否属于同一个正态分布, 即同一样品的不同测试点是否对应同一个年龄真实值。换言之, 测量值彼此的差异仅由随机误差产生。如果n个相互独立的随机变量X1,X2, …,Xn均服从标准正态分布, 则这n个服从标准正态分布的随机变量的平方和构成一个新的随机变量, 其分布规律称为卡方分布。用式(6)计算加权均方差:
。 (6)如果n个测试点的表面年龄的概率统计结果服从正态分布, 则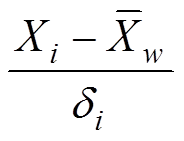
服从标准正态分布。在表面年龄计算中,n− 1 为自由度, 则 MSWD 的表达式可视为简化的卡方分布表达式。若n个测试点的表面年龄服从正态分布, 则它们对应的 MSWD 值应与一定自由度下的卡方分布值相吻合。
利用最小二乘法求取等时线时, 要求测试点距离拟合直线上对应点的残差平方和最小。定义S为残差,Xi和Yi为测试值,xi和yi为拟合值, 则有
。 (7)加权最小二乘法考虑了每个独立观测具有已知的不确定度, 两个坐标轴变量都有不确定度, 测量值和不确定度在等时线图中体现为大小不同的椭圆, 此时拟合残差表示为
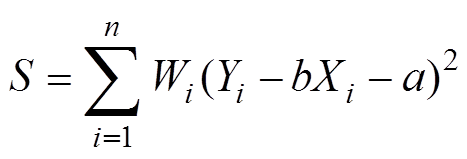, (8)
其中,
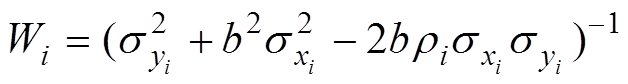。 (9)式(9)表示测量值的权重, 与测试的两个同位素比值Xi和Yi的方差有关。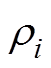
是两个变量的相关系数,a为等时线y轴截距,b为等时线斜率。这种方法可以根据两个变量的不确定度, 使残差最小化[26,28]。
利用加权最小二乘法公式, 可以进一步求取斜率和截距对应的不确定度, 以便评估数据的精确度。在获取等时线年龄时, MSWD的算法与式(6)类似。但是, 此时需要计算的不再是表面年龄与表面年龄加权平均值间的差值, 而是实际测量值与拟合值之间的差值, 即残差。另外, 等时线法的变量有两个, 自由度为n− 2, 因此等时线法的 MSWD 可以表示为
(10)其中,S为各测量值相对于等时线拟合值的残差,F为自由度。
如前所述, 等时线年龄的 MSWD 值代表残差S以n− 2为自由度的卡方分布。卡方分布公式[16]为
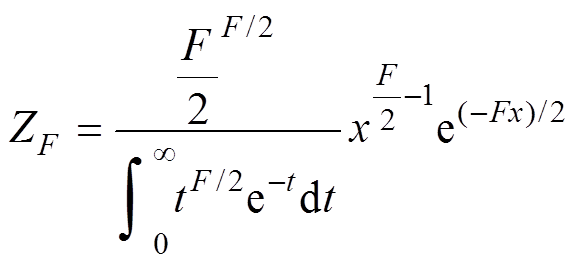。 (11)其中，ZF表示MSWD的概率密度,x为卡方分布的自变量。
正如不同标准差的正态分布曲线形态不同, 不同自由度的卡方分布形态也有差异。根据式(11), 做出不同自由度的 MSWD 概率密度曲线(图 1), 可以看出, 对应于不同自由度的曲线形态有所不同。通过计算, 可知平均值均为 1.0, 但众数各不相同, 随着自由度的增加, 曲线的不对称性逐渐降低, 众数、中位数和平均值趋于一致, 逐渐接近1.0。
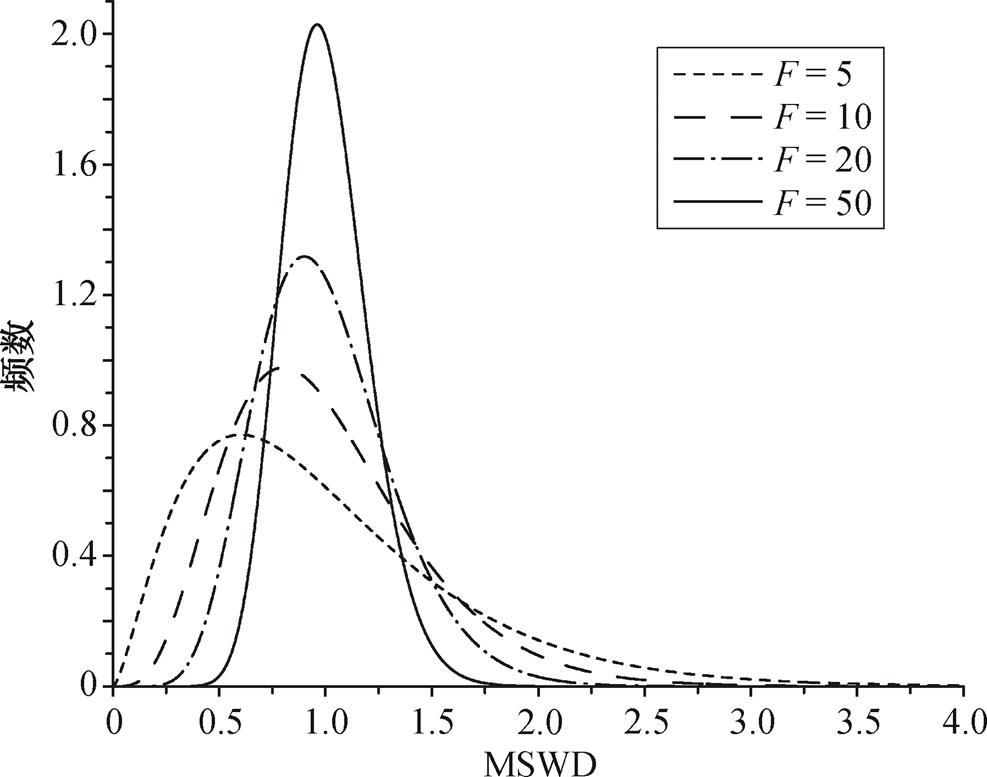
图1 不同自由度下的MSWD概率密度曲线
Fig. 1 Frequency density distributions for the MSWD with different degrees of freedom
当 MSWD 取值为相应自由度概率密度曲线的期望值(即 1.0)时, 表明考察的数据为卡方分布的概率很大。根据式(10), 对于等时线年龄数据, MSWD等于 1.0 表明各数据点残差加权后的平方和呈现很好的卡方分布, 也说明数据点的残差呈正态分布; 或者说这些数据点对应同一条等时线, 线性回归的质量很高, 等时线反映一个确定的年龄, 测试的数据点对应同一个年龄真实值。
在同位素地质年代学中, 尤其在等时线年龄的计算中, 广泛应用 MSWD 作为数据质量判别的重要参数。通常认为, MSWD=1 表明等时线拟合程度最佳, 这正是由 MSWD 的概率密度函数决定的。但是, MSWD 恰好为 1 的情况实际上不多见。进一步观察式(10), 不难发现, 表达式的分子代表测量数据偏离等时线拟合值的程度, 分母表示单次测量的不确定度。因此, 可以做出解释, 当 MSWD>1时, 说明测量值与等时线拟合值差异较大, 甚至样品并不满足等时、同源和封闭条件, 不能对应同一个真实年龄值; 当 MSWD<1 时, 说明对于数据的均匀性或良好拟合性而言, 单次测量的不确定度相对偏大, 可以认为仪器精度达不到相应的测试要 求[1,12]。
当 MSWD 等于 1 的理想条件不满足时, 测试的结果有没有意义? MSWD 的合理取值范围是什么? 如何利用 MSWD 数值判别样品质量是否满足等时线条件? 解决这一系列问题的方法是从概率密度曲线入手, 计算在一定的自由度下 MSWD 在一定置信区间的取值范围[19]。对式(11)积分可得: 当F为偶数时,
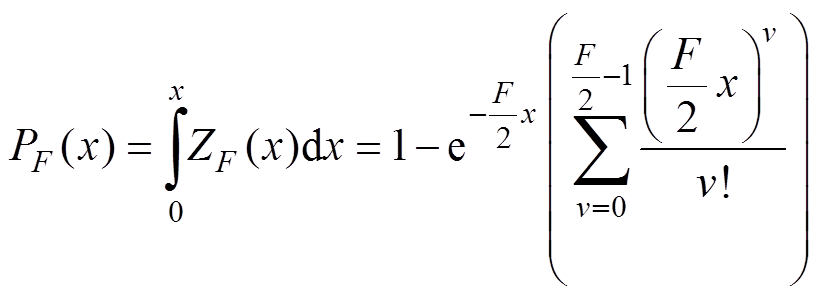; (12)当F为奇数时,
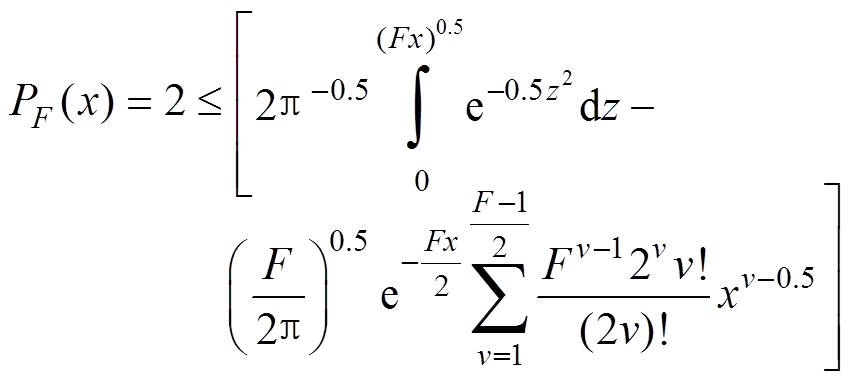。 (13)
依据式(12)和(13), 计算不同自由度下 MSWD 在95.4%和99.7%置信区间下的取值范围。
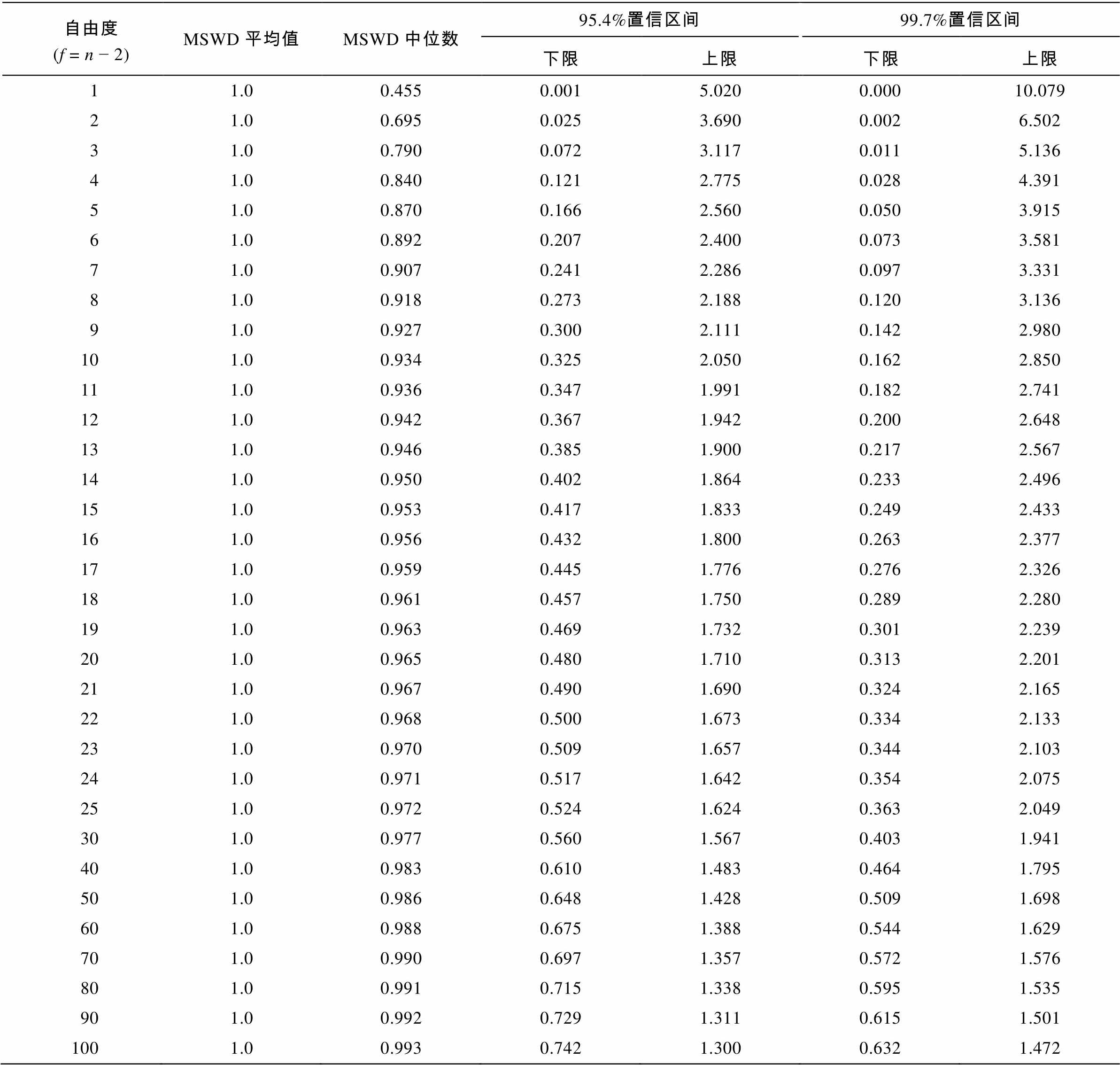
表 1 列出一系列自由度对应的 MSWD 取值。例如, 一件样品测试点数n=20, 用这 20 个数据拟合等时线, 则自由度f=n− 2=18。从表 1 可知, 如果20 个数据点对应同一个年龄真实值, 则 MSWD 值有 95.4%的可能性在 0.457~1.750 之间, 小于 0.457或大于 1.750 的概率仅为 2.3%; 有99.7%的可能性在 0.289~2.280 之间, 小于 0.289 或大于 2.280 的概率为 0.15%。Mahon[19]选取 95.4%置信区间作为划分依据。但是, 由于年轻火山岩样品测试难度大,在激光40Ar/39Ar 法定年实践中, MSWD 值偏离 1.0的情况时有发生。为了给难度较高的定年实验赋予较高的容错度, 本文计算了 MSWD 的 99.7%置信区间, 从而给质量不够理想的年龄结果提供更宽泛的 MSWD 值参考范围。因此, 依据数值的置信区间, 可将一个年龄结果的 MSWD 划分为 3 个等级: <95.4%, 95.4%~99.7%和>99.7%。如果 MSWD 溢出相应的置信区间, 可以认为等时线拟合程度不高, 测试数据的概率曲线不呈正态分布, 测量偏差不仅是测试的随机误差, 更有可能反映样品不同源或不等时, 可以认定得到的等时线年龄不可靠。
表1 自由度与MSWD数据分布
Table 1 Table of critical MSWD values versus degrees of freedom
自由度(f = n − 2)MSWD平均值MSWD中位数95.4%置信区间99.7%置信区间 下限上限下限上限 11.00.4550.0015.0200.00010.079 21.00.6950.0253.6900.0026.502 31.00.7900.0723.1170.0115.136 41.00.8400.1212.7750.0284.391 51.00.8700.1662.5600.0503.915 61.00.8920.2072.4000.0733.581 71.00.9070.2412.2860.0973.331 81.00.9180.2732.1880.1203.136 91.00.9270.3002.1110.1422.980 101.00.9340.3252.0500.1622.850 111.00.9360.3471.9910.1822.741 121.00.9420.3671.9420.2002.648 131.00.9460.3851.9000.2172.567 141.00.9500.4021.8640.2332.496 151.00.9530.4171.8330.2492.433 161.00.9560.4321.8000.2632.377 171.00.9590.4451.7760.2762.326 181.00.9610.4571.7500.2892.280 191.00.9630.4691.7320.3012.239 201.00.9650.4801.7100.3132.201 211.00.9670.4901.6900.3242.165 221.00.9680.5001.6730.3342.133 231.00.9700.5091.6570.3442.103 241.00.9710.5171.6420.3542.075 251.00.9720.5241.6240.3632.049 301.00.9770.5601.5670.4031.941 401.00.9830.6101.4830.4641.795 501.00.9860.6481.4280.5091.698 601.00.9880.6751.3880.5441.629 701.00.9900.6971.3570.5721.576 801.00.9910.7151.3380.5951.535 901.00.9920.7291.3110.6151.501 1001.00.9930.7421.3000.6321.472
在定年工作中, 经常遇到不够理想的等时线年龄, 表现为表面年龄和等时线年龄的 MSWD 值过大或过小, 甚至超出 99.7%的置信区间, 说明样品的多个测试点并不对应同一个年龄真实值。由于表面年龄的计算直接使用尼尔值代替初始 Ar 比值, 往往不适用于年轻火山岩定年, 但表面年龄的概率密度曲线可以直观地反映样品的多个测试点是否保持等时、同源和封闭。如果满足条件, 则概率密度曲线接近正态分布(图 2(a)), 正态分布的期望值为表面年龄值; 否则, 会出现不对称或多个波峰的形态(图 2(b)和(c)), 每个波峰都代表一个可能的年龄值。这种概率密度曲线形成的原因可能是不等时样品的混染, 测试点彼此之间初始 Ar 比值不均一, 等等。这些原因也可以总结为样品不符合等时线年龄的 3 个理想条件, 因此相应的等时线年龄也具有质量较差的 MSWD 值(图 3(a)和(b)), 反映样品测试质量较差。
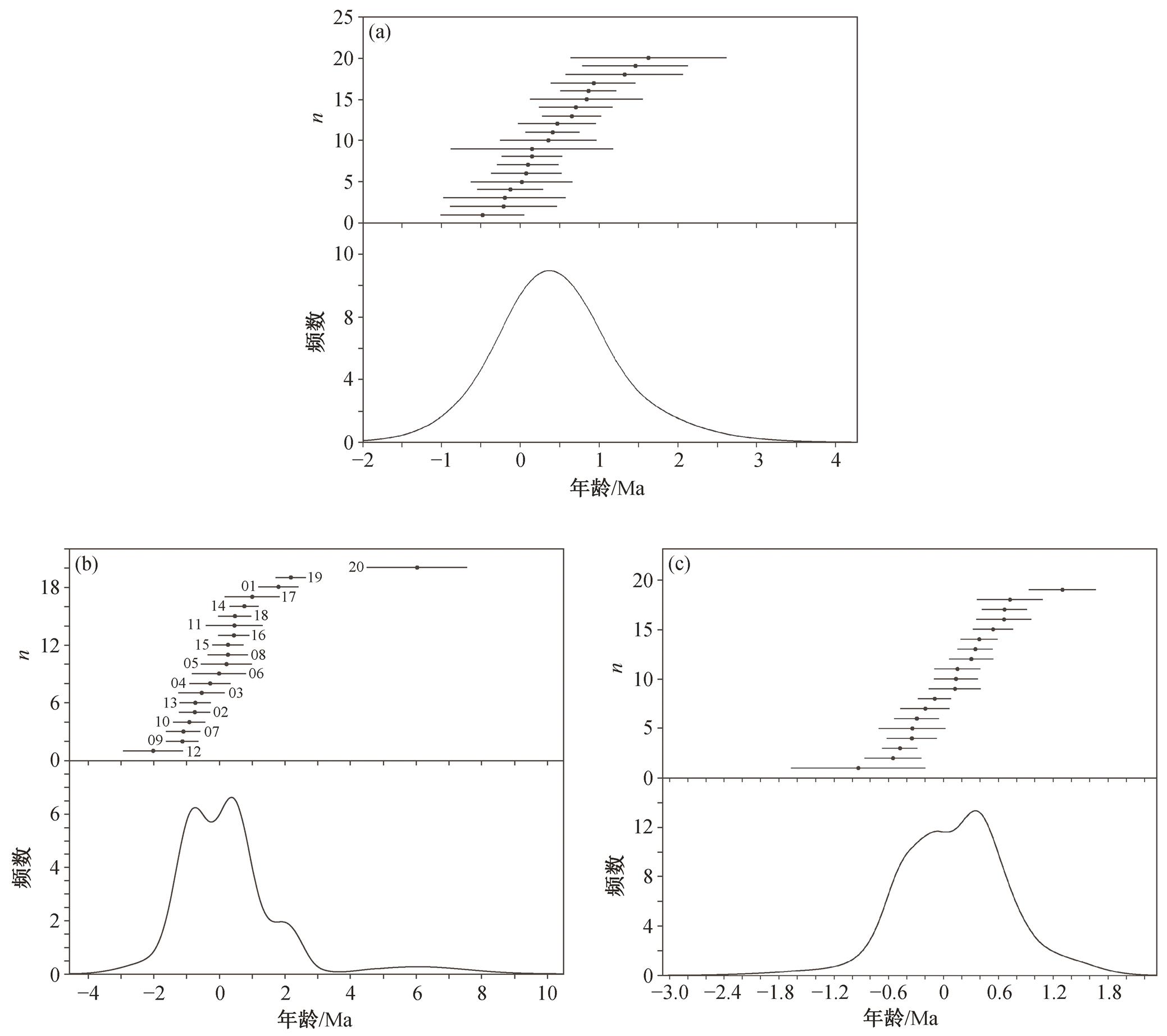
(a)样品 AS2-15 测试点的表面年龄概率密度曲线; (b)样品 AS6-8 测试点的表面年龄概率密度曲线(图中数字为测试点编号), 有多个波峰, 代表多个频率相对较高的表面年龄, MSWD=4.79,n=20, 溢出 99.7%置信区间, 说明这些表面年龄不属于同一个正态分布; (c)样品 A3-3-1 测试点的表面年龄概率密度曲线, 有 2 个波峰, 代表频率较高的表面年龄, 分别为−0.06513 Ma和0.347 Ma, MSWD=3.61,n=19, 溢出 99.7%置信区间, 说明这些表面年龄不属于同一个正态分布
图2 样品AS2-15, AS6-8和A3-3-1的表面年龄概率密度曲线
Fig. 2 Probability density curve for apparent age of sample AS2-15, AS6-8 and A3-3-1
上述实例中, MSWD值溢出其测试点数n对应的 99.7%置信区间, 反映了样品的质量问题。在40Ar/39Ar 同位素测试实践中, 通过数据处理对质量不理想的样品进行优化, 从而得到尽可能可靠的年龄结果, 是同位素年代学实验室必须做好的工作, 对获取可靠的测试结果和实验室测试信息的有效利用十分重要。
对于全部测试点表面年龄曲线具有多个波峰的样品, 推荐的数据处理方法是选取部分测试点的数据做等时线, 使 MSWD 取得可靠的数值(如 95.4%的置信区间), 即可表明所选取的数据对应于同一年龄真实值, 等时线质量良好, 年龄数据有意义。要采用这种思路, 首先必须确定数据删减原则。如果按照传统的方法直接观察等时线, 去除与当前拟合的等时线偏离较远的数据点, 这种做法主观性过强, 片面追求统计学意义上的优质, 忽略样品的地质意义, 易造成虚假年龄结果。
样品的表面年龄概率密度曲线是直观地判别样品质量的有效手段, 可以从曲线形态蕴含的信息入手, 解决去除数据点主观性过强的问题。当样品的表面年龄概率密度曲线呈现多个波峰或不对称形态、MSWD 值溢出 99.7%置信区间时, 往往会发现部分测试点的表面年龄分布比较集中, 考虑不确定度后的年龄结果大部分重合, 但个别测试点偏离众数较多。可能的原因是这些点的初始 Ar 比值与大部分测试点不同(即样品非同源), 因此选取数据时应首先考虑去除偏离最大的测试点。由于测试点都具有不确定度, 测试点数越多, 数据总体上越接近正态分布, 对样品真实年龄的代表性越强。如果去除的测试点数量过多, 年龄结果过于主观, 会削弱结果的可靠程度。根据 MSWD 判断数据是否对应同一个年龄真实值, 也是在n值越大的情况下, 结果越可信(如表 1 所示)。为避免对数据的过度筛选, 在筛选数据点的过程中, 可以将 MSWD 的数值变化作为依据。当 MSWD 取值进入 99.7%或 95.4% 置信区间后, 即停止删除数据点。本文对以 99.7%和 95.4%置信区间为标准的选点方式均做了尝试, 并对两种情况下的表面年龄加权平均值、众数以及反等时线年龄进行对比。
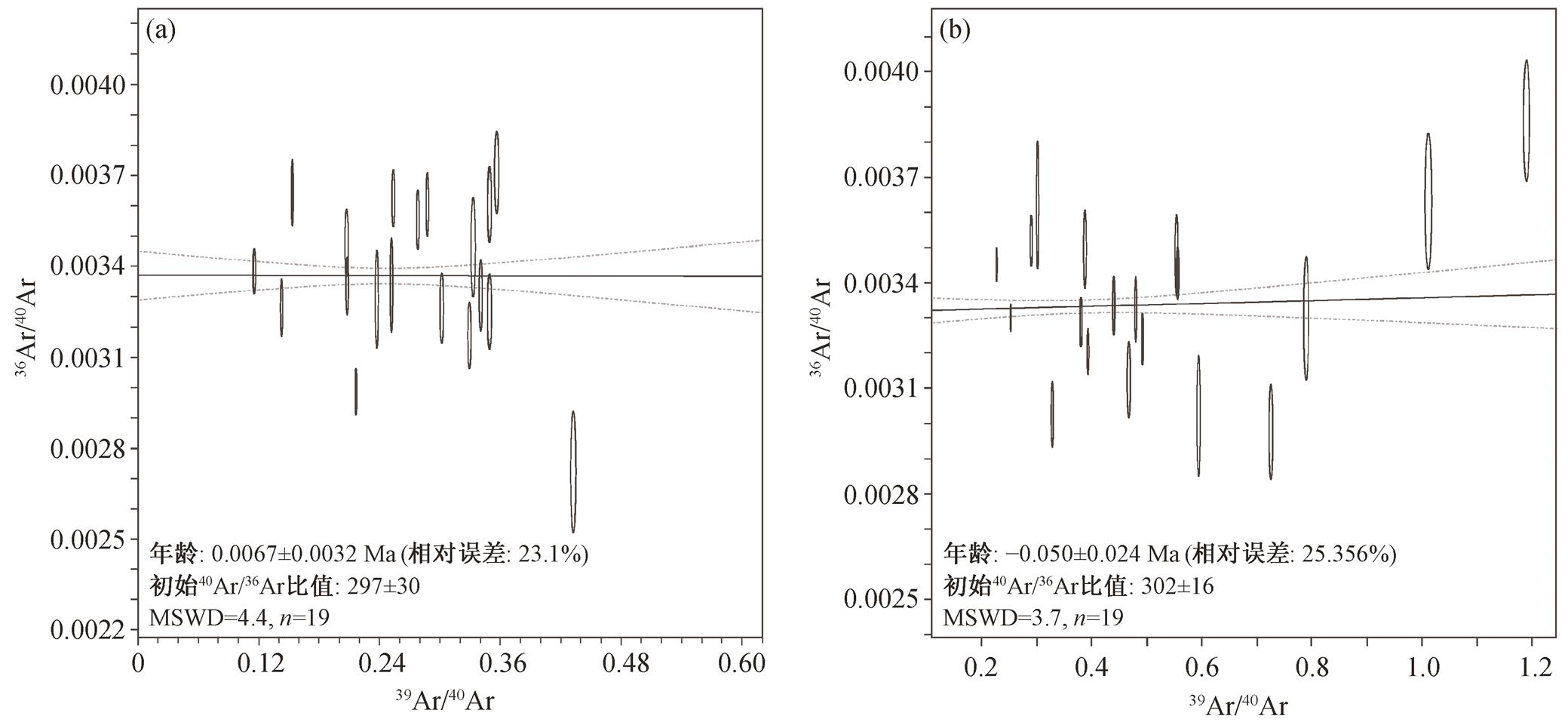
(a)样品 AS6-8 测试点的反等时线, 删除了明显偏离表面年龄中位数的 20 号数据点, 年龄为 0.0067±0.0032Ma, MSWD=4.4,n=19, 溢出 99.7%置信区间, 说明这些数据点相对于反等时线的残差不属于同一个正态分布, 即这些数据点不对应同一条反等时线, 等时线年龄不可靠; (b)样品 A3-3-1 全部测试点的反等时线, 年龄为−0.050±0.024Ma, MSWD=3.7,n=19, 溢出 99.7%置信区间, 说明这些数据点相对于反等时线的残差不属于同一个正态分布, 即这些数据点不对应同一条反等时线, 等时线年龄不可靠。黑色直线是等时线, 灰色虚线表示等时线的置信区间
图3 样品AS6-8和A3-3-1的反等时线图
Fig. 3 Inverse isochron diagram of sample AS6-8 and A3-3-1
例如, 样品 AS6-8 代表表面年龄概率密度曲线呈多个波峰的情形。观察图 2(b), 去除表面年龄为6.032Ma(点 20)和 1.895Ma(点 19)的两个明显偏离众数的数据点后, 仍能识别出大小不同的两个比较明显的年龄峰值, 一个较年轻(年龄峰值为−0.7323Ma), 一个较年老(年龄峰值为 0.3699Ma), 表明样品可能具有两组不同的初始 Ar 比值。保留较大值的年龄峰, 从图 2(b)左侧依次去除表面年龄偏离众数最远的数据点, 当去除测试点 12 和 09 时, 剩余数据的 MSWD 值位于 99.7%置信区间。继续去除测试点 07 和 10, 剩余数据的 MSWD 值进入 95.4%的置信区间。对这两组数据分别计算反等时线, 年龄结果如图 4(a)和(b)所示。保留较小值的年龄峰, 从图 2(b)右侧依次去除表面年龄偏离众数最远的数据点, 当去除测试点 01 之后, 剩余数据的 MSWD 值位于 99.7%置信区间。继续去除测试点 17 和 14, 剩余数据的 MSWD 值进入 95.4%的置信区间。对这两组数据分别计算反等时线, 年龄结果如图 4(c)和(d)所示。考虑样品 AS6-8 这一系列年龄的不确定度和 MSWD 值, 将各年龄结果投到同一坐标系中(图5), 推荐选择椭圆标示的等时线年龄结果: 0.40± 0.22Ma。采取类似的处理办法, 样品 A3-3-1 年龄综合分析结果如图 6 所示, 推荐选择椭圆标示的等时线年龄结果: 0.37±0.22 Ma。
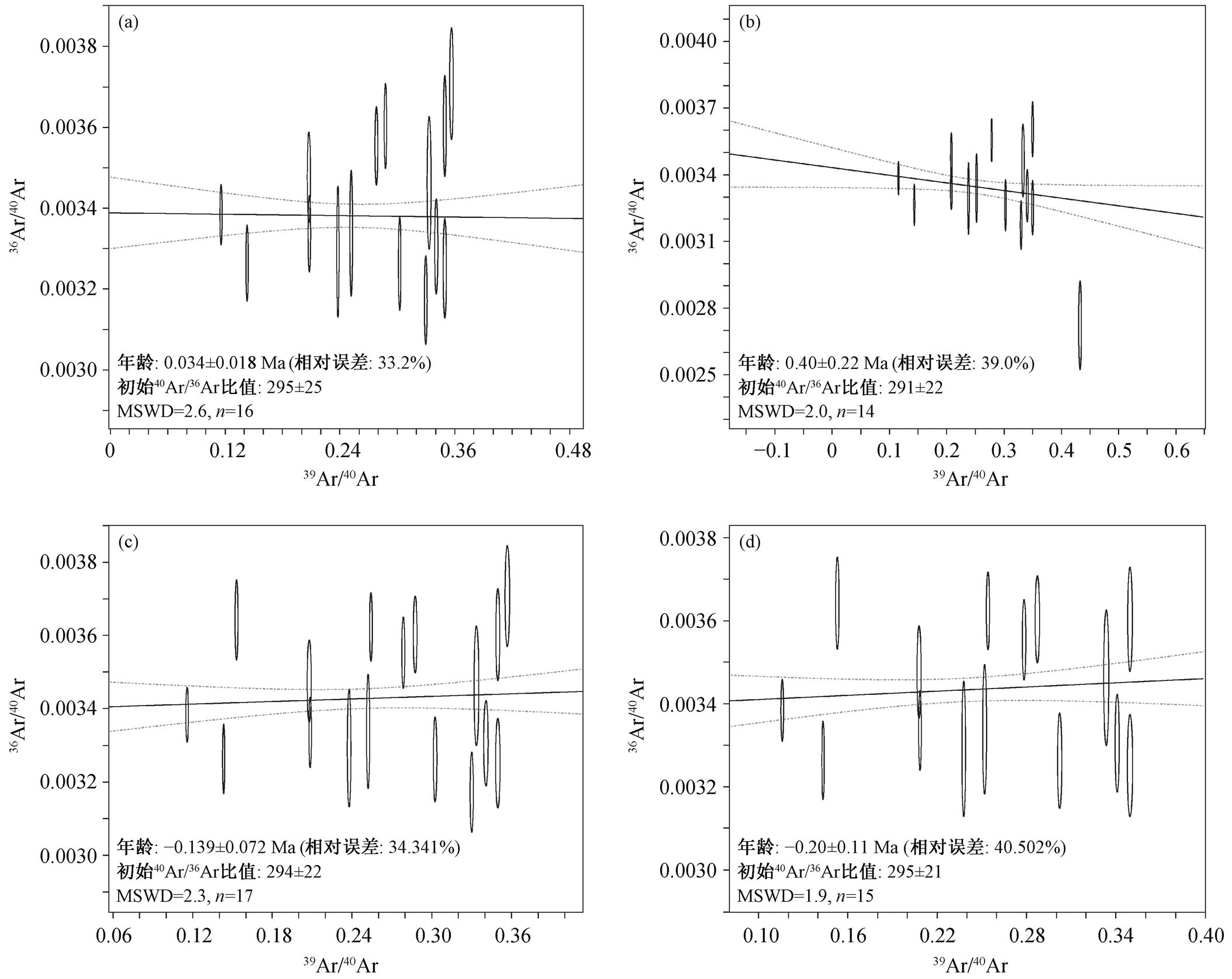
(a)保留图 2(b)中较大值年龄峰, 选取表面年龄 MSWD 在 99.7%置信区间的数据点; (b)保留图 2(b)中较大值年龄峰, 选取表面年龄 MSWD 在 95.4%置信区间的数据点; (c)保留图 2(b)中较小值年龄峰, 选取表面年龄 MSWD 在 99.7%置信区间的数据点; (d)保留图 2(b)中较小值年龄峰, 选取表面年龄MSWD在95.4%置信区间的数据点
图4 样品AS6-8经过不同选点处理后的反等时线图
Fig. 4 Inverse isochron diagram of sample AS6-8 using different data selection strategies
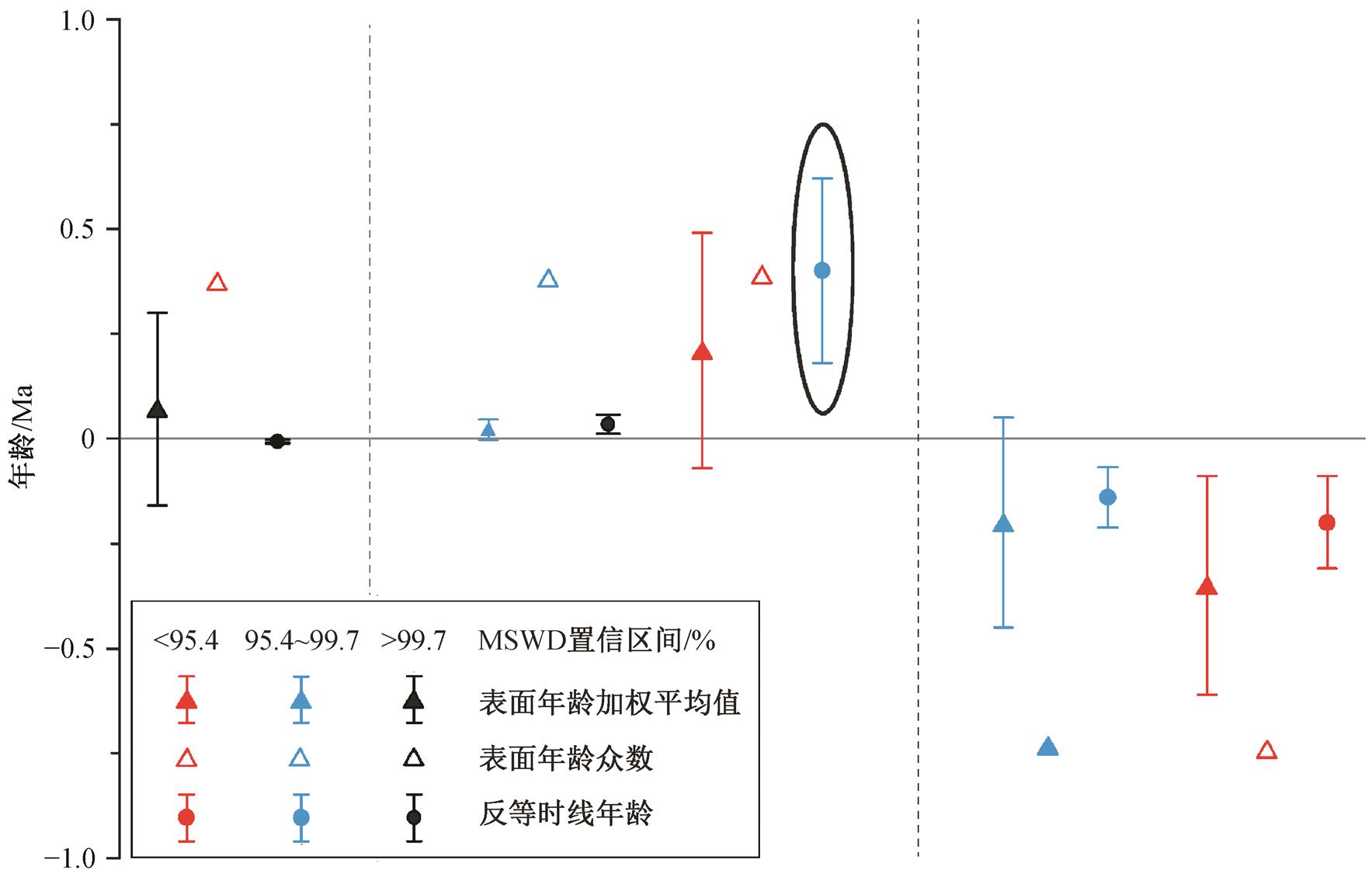
与横轴垂直的两条虚线将年龄分布分成 3 个区域, 在 3 个区域内对数据进行投影, 从左到右依次为未经选点处理的年龄结果、保留较大值年龄峰的处理结果以及保留较小值年龄峰的处理结果。空心三角形代表本组数据中表面年龄众数, 实心三角形代表表面年龄加权平均值, 圆形代表反等时线年龄。红、蓝、黑 3 种颜色用于标记数据点MSWD 的置信区间。对于表面年龄加权平均值和反等时线年龄, 数据点不同颜色代表该结果对应的 MSWD 的不同置信区间。由于表面年龄众数的计算不涉及利用 MSWD 进行评估, 因此众数数据点的颜色反映读取该众数时表面年龄加权平均值 MSWD 的置信区间, 是数据处理过程的表征。综合分析样品 AS6-8 的各类年龄数据, 推荐选择椭圆标示的等时线年龄结果: 0.40±0.22 Ma
图5 样品AS6-8表面年龄加权平均值、表面年龄众数和反等时线年龄综合分析结果
Fig. 5 Integrated chronological analysis of the mode, the weighted mean and the isochron age of sample AS6-8
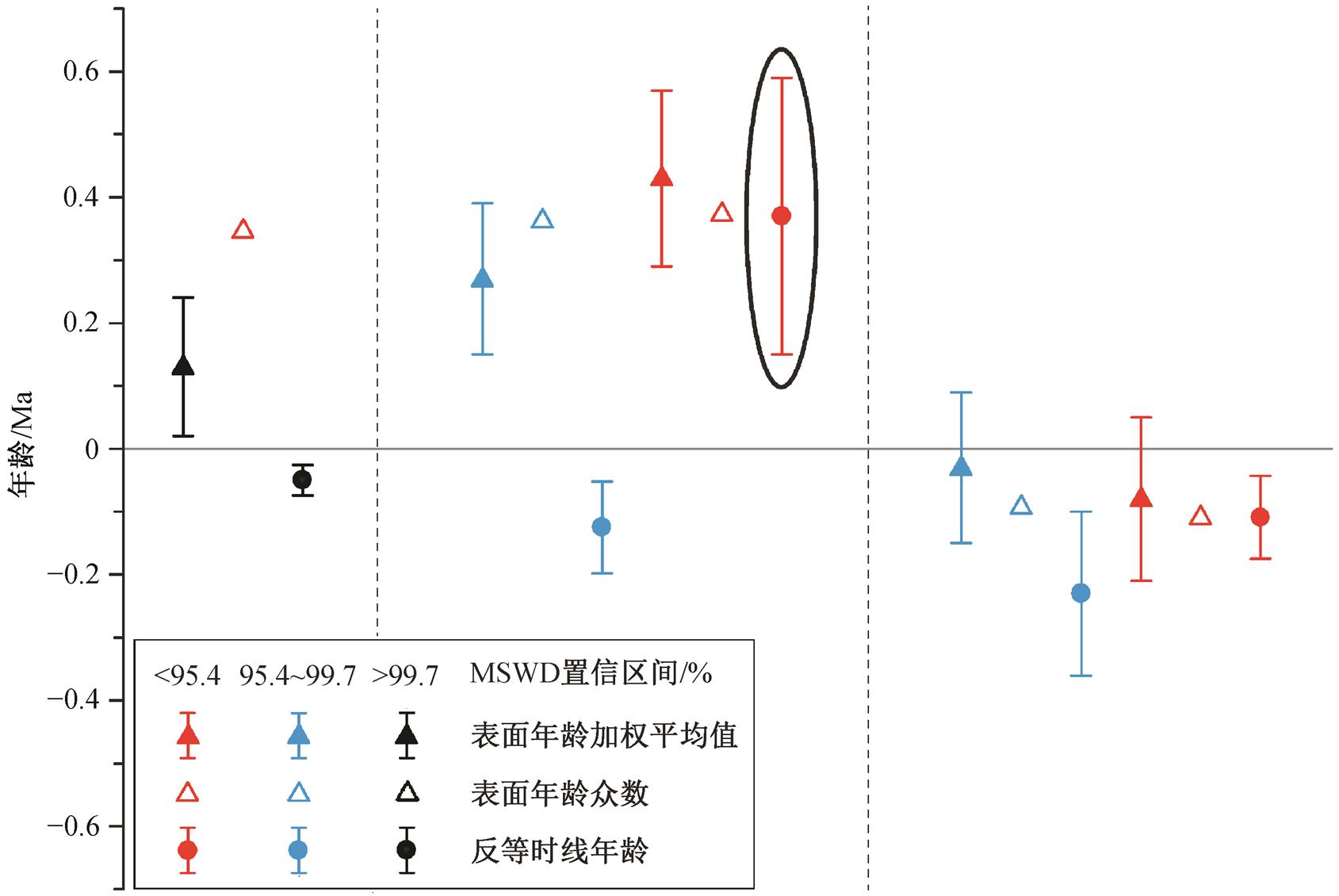
推荐选择椭圆标示的等时线年龄结果: 0.37±0.22 Ma。其余同图5
图6 样品A3-3-1表面年龄加权平均值、表面年龄众数和反等时线年龄综合分析结果
Fig. 6 Integrated chronological analysis of the mode, the weighted mean and the isochron age of sample A3-3-1
以上两个实例展示了样品年龄不属于同一个真实值时的处理方式。这种方法基于样品不同统计指标的综合运用, 试图解决样品同位素体系不均一造成的影响, 从而获得可靠的年龄结果。但是, 实例中展示的样品数据量不够理想。对于年轻火山岩, 要想获得更可靠的年龄, 需要更多的测试点, 更大的n值, 并且数据处理要结合地质信息, 才能做出最终的判断。
本文通过对年轻火山岩激光40Ar/39Ar 年龄数据质量评估参数 MSWD 和n值的辨析与计算, 结合北京大学惰性气体同位素年代学实验室对第四纪火山岩样品精细定年的实践案例, 得到结论如下。
1)MSWD 是判断测试数据是否符合正态分布, 即样品是否对应同一年龄真实值的指标, 并与测试点数n相关。属于同一真实年龄值样品的 MSWD在 99.7%置信区间的取值范围, 可通过计算加以确认。对于表面年龄和等时线年龄数据, 必须定量地考察相应的 MSWD 值, 判定在具有足够样品测试数(足够大的n值)的情况下, 是否符合概率统计的正态分布, 确定样品是否对应同一年龄真实值。
2)同一样品测试点数越多, 即n值越大, MSWD对同一置信区间的取值范围越小, 对样品质量的判别更可靠, 因此n值越大, MSWD 对年龄数据质量的评估就越可靠。因此, 在用激光40Ar/39Ar 法对年轻火山岩定年时, 尽可能增大n值(测试点数)。
3)当样品质量不理想, 即所有测试点年龄数据的 MSWD 值溢出 95.4%置信区间时, 可以尝试观察样品表面年龄是否属于正态分布, 参考 MSWD 与n值的关系。如果 MSWD 溢出一定置信区间(可根据实际需要选取 95.4%或 99.7%的置信区间作为判断标准)时去除部分数据点, 以便区分非同源样品中的不同体系。将不同体系的数据分组, 进一步计算不同组数据的(反)等时线年龄。
参考文献
[1]Mcdougall I, Harrison T M. Geochronology and ther-mochronology by the40Ar/39Ar method. New York: Oxford University Press, 1999
[2]周晶, 季建清, Deino A, 等. (极)年轻火山岩激光熔蚀40Ar/39Ar 定年. 岩石学报, 2013, 29(8): 2811‒ 2825
[3]Ton-That T, Singer B, Paterne M.40Ar/39Ar dating of latest Pleistocene (41 ka) marine tephra in the Medi-terranean Sea: implications for global climate records. Earth and Planetary Science Letters, 2001, 184(3): 645‒658
[4]Barfod D F, Fitton J G. Pleistocene volcanism on São Tomé, Gulf of Guinea, West Africa. Quaternary Geo-chronology, 2014, 21: 77‒89
[5]Yang L, Wang F, Feng H, et al.40Ar/39Ar geochrono-logy of Holocene volcanic activity at Changbaishan Tianchi volcano, Northeast China. Quaternary Geoch-ronology, 2014, 21: 106‒114
[6]Renne P R, Sharp W D, Deino A L, et al.40Ar/39Ar dating into the historical realm: calibration against pliny the younger. Science, 1997, 277: 1279‒1280
[7]Renne P R, Swisher C C, Deino A L, et al. Intercali-bration of standards, absolute ages and uncertainties in40Ar/39Ar dating. Chemical Geology, 1998, 145(1/2): 117‒152
[8]Karner D B, Renne P R, Mcdougall I, et al. The via-bility of leucite for40Ar/39Ar dating and as a Quarter- nary standard. Chemical Geology, 2001, 177 (3/4): 473‒482
[9]Layer P W, Gardner J E. Excess argon in Mount St. Helens plagioclase as a recorder of magmatic pro-cesses. Geophysical Research Letters, 2001, 28(22): 4279‒4282
[10]Nomade S, Renne P R, Vogel N, et al. Alder Creek sanidine (ACs-2): a quaternary40Ar/39Ar dating stan-dard tied to the Cobb Mountain geomagnetic event. Chemical Geology, 2005, 218(3): 315‒338
[11]Esser R P, Mcintosh W C, Heizler M T, et al. Excess argon in melt inclusions in zero-age anorthoclase feld- spar from Mt. Erebus, Antarctica, as revealed by the40Ar/39Ar method. Geochimica et Cosmochimica Acta, 1997, 61(18): 3789‒3801
[12]Jourdan F, Renne P R, Reimold W U. The problem of inherited40Ar* in dating impact glass by the40Ar/39Ar method: evidence from the Tswaing impact crater (South Africa). Geochimica et Cosmochimica Acta, 2007, 71(5): 1214‒1231
[13]Sumino H, Ikehata K, Shimizu A, et al. Magmatic processes of Unzen volcano revealed by excess argon distribution in zero-age plagioclase phenocrysts. Jour-nal of Volcanology & Geothermal Research, 2008, 175(1): 189‒207
[14]权伍勋, 季建清, 周晶. K-Ar,40Ar/39Ar定年中尼尔值和初始氩比值. 地质科学, 2015, 50(1): 213‒ 221
[15]权伍勋, 季建清, 周晶, 等. K-Ar 和40Ar/39Ar 定年数据质量评价与Q值提出. 岩石学报, 2013, 29(8): 2803‒2810
[16]Wendt I, Carl C. The statistical distribution of the mean squared weighted deviation. Chemical Geology: Isotope Geoscience Section, 1991, 86(4): 275‒285
[17]Wendt I. The statistical distribution of the mean squ-ared weighted deviation — Reply. Chemical Geology Isotope Geoscience, 1992, 94(3): 242‒243
[18]Kalsbeek F. The statistical distribution of the mean squared weighted deviation — comment: isochrons, errorchrons, and the use of MSWD-values. Chemical Geology, 1992, 94(3): 241‒242
[19]Mahon K I. The New “York” regression: application of an improved statistical method to geochemistry. International Geology Review, 1996, 38(4): 293‒303
[20]York D, Evensen N M, Martı́nez M L, et al. Unified equations for the slope, intercept, and standard errors of the best straight line. American Journal of Physics, 2004, 72(3): 367‒375
[21]Merrihue C, Turner G. Potassium-argon dating by activation with fast neutrons. Journal of Geophysical Research Atmospheres, 1966, 71(11): 2852‒2857
[22]Dalrymple G B, Lanphere M A, Pringle M S. Correla-tion diagrams in40Ar/39Ar dating: is there a correct choice?. Geophysical Research Letters, 1988, 15(6): 589‒591
[23]Kuiper Y D. The interpretation of inverse isochron diagrams in40Ar/39Ar geochronology. Earth and Pla-netary Science Letters, 2002, 203(1): 499‒506
[24]Matsumoto A, Kobayashi T. K-Ar age determination of late Quaternary volcanic rocks using the “mass fractionation correction procedure”: application to the Younger Ontake Volcano, central Japan. Chemical Geology, 1995, 125(1/2): 123‒135
[25]李蔚然. 极年轻火山岩激光40Ar/39Ar 等时线定年中的关键问题[D]. 北京: 北京大学, 2014
[26]York D. Least squares fitting of a straight line with correlated errors. Earth and Planetary Science Letters, 1968, 5: 320‒324
[27]范文博, 王文龙, 陈岳龙, 等. 最小二乘直线拟合方法及其在同位素地质年代学中的应用研究. 地质论评, 2013, 59(5): 801‒815
[28]Mcintyre G A, Brooks C. The statistical assessment of Rb-Sr isochrons. Journal of Geophysical Research Atmospheres, 1966, 71(22): 5459‒5468
MSWD andnValue in Laser Ablation40Ar/39Ar Isochron Dating for Young Volcanic Rocks
HU Yan†, JI Jianqing, ZHOU Jing, TU Jiyao
The Key Laboratory of Orogenic Belts and Crustal Evolution (MOE), School of Earth and Space Sciences, Peking University, Beijing 100871; † E-mail: yan_hu@hotmail.com
AbstractThe laser ablation40Ar/39Ar method makes it possible to date quanterary volcanic rocks precisely. So far, it lacks an assessment criterion that can be used to estimate the reliability of test data and geochronological information. The mean square weighted deviation (MSWD) and the number of measurement (nvalue) are used to be the crucial parameter to evaluate sample properties and experimental standard. When applying laser ablation40Ar/39Ar method to date young volcanic rocks, a best-fit40Ar/39Ar isochron diagram requires isotopic homogeneity of the sample and permanent closure of the isotope system at the same time. While MSWD, which is related tonvalue, is a parameter to determine whether the data are located in the same normal distribution, or in other words, whether the sample has a unified true age, it is applicable to use MSWD andnvalue to estimate the level of confidence placed on the computed mean. The critical values of MSWD for the 99.7% confidence interval using differing degrees of freedom are calculated in this paper. It is important to note that MSWD is available in evaluating dating result of both apparent and isochron ages. For the samples which tend to have heterogeneous initial40Ar/36Ar ratios or different closure times, MSWD combined with the probability density of apparent ages can be used to distinguish different groups of samples, calculate the isochron ages respectively, and interpret the result after accounting for the various parameters to evaluate the data quality.
Key wordslaser ablation40Ar/39Ar dating; isochron; MSWD; young volcanic rocks; data processing
中图分类号P597
doi:10.13209/j.0479-8023.2018.090
中国地质调查局地质调查项目(12120113013700)资助
收稿日期:2017‒06‒12;
修回日期:2018‒07‒23;
网络出版日期:2018‒09‒25