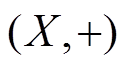 和
和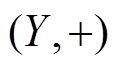 都是有限交换群,
都是有限交换群, 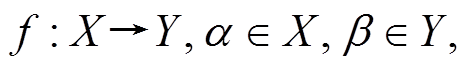 令
令殷勍1 王念平2 ,†
1.航天工程大学, 北京 101416; 2.信息工程大学密码工程学院, 郑州 450001; †通信作者, E-mail: wwnnpp@126.com
摘要 为评估 Piccolo 结构的密码性能, 对该结构抵抗差分密码分析和线性密码分析的能力进行研究。给出任意轮差分特征中活动轮函数和活动 S 盒个数的一个新的下界, 并利用 Piccolo 结构的差分线性对偶性, 给出任意轮线性逼近中活动轮函数和活动 S 盒个数的一个新的下界。同时, 证明这些下界是不可改进的。
关键词 Piccolo结构; 差分密码分析; 线性密码分析
对分组密码而言, 差分密码分析[1]和线性密码分析[2]是两种最重要的攻击方法, 评估分组密码抵抗这两种攻击的能力一直是密码学研究的热点。如果分组密码的最大差分特征概率(最大线性逼近概率)足够小, 就可以认为该密码对差分密码分析(线性密码分析)是安全的, 而差分特征概率(线性逼近概率)的上界通常可以用差分特征(线性逼近)中活动轮函数或活动 S 盒个数的下界来估计, 所以, 估计分组密码抵抗差分密码分析能力的关键在于求出活动轮函数或活动 S 盒个数的下界[3]。在研究差分特征中活动轮函数或活动 S 盒个数的下界时, 通常不考虑轮函数和 S 盒的具体结构, 而只假定轮函数和 S 盒是双射, 文献[4–7]就是按照此思路对不同的结构进行研究。
对于从 Piccolo 算法[8]中归纳出来的 Piccolo 结构[9], Shibutani等[8]利用计算机模拟的方法, 给出若干轮差分特征中活动轮函数个数的下界; 殷勍等[9]利用推导证明的方法, 给出任意轮差分特征中活动轮函数个数的下界, 但没有证明此下界不可改进。
本文将推导证明与计算机模拟相结合, 在相同条件下, 改进了殷勍等[9]的结果, 并证明所得结果是不可改进的。
定义 1[10] 设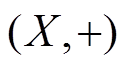 和
和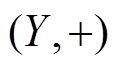 都是有限交换群,
都是有限交换群, 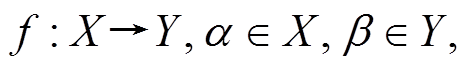 令
令
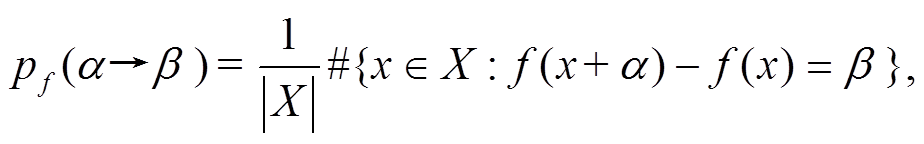
则称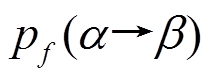 为
为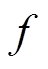 在输入差为
在输入差为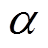 的条件下, 输出差为
的条件下, 输出差为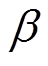 的差分概率。此外, 也称
的差分概率。此外, 也称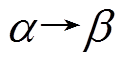 为
为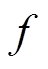 的一个差分对应, 并称
的一个差分对应, 并称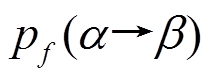 为该差分对应的概率。其中, “
为该差分对应的概率。其中, “ ”和“
”和“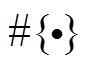 ”表示集合的元素个数。
”表示集合的元素个数。
定义 2[10] 设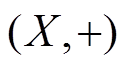 是有限交换群,
是有限交换群, 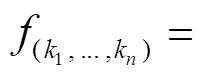
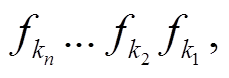
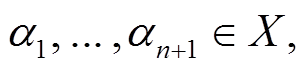 则称
则称
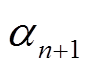 为
为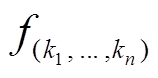 的一个起点为
的一个起点为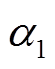 , 终点为
, 终点为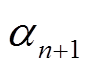 的差分传递链, 并称
的差分传递链, 并称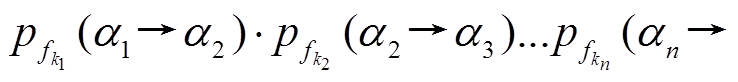
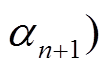 为该差分传递链的概率。
为该差分传递链的概率。
本文也称差分传递链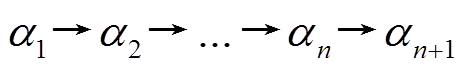 为
为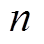 轮差分特征。
轮差分特征。
定义 3[10] 设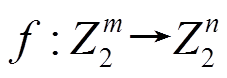 是多输出布尔函数,
是多输出布尔函数, 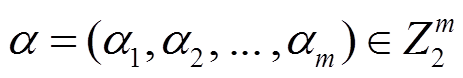 ,
, 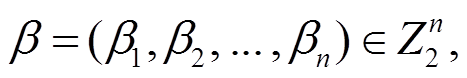 记
记
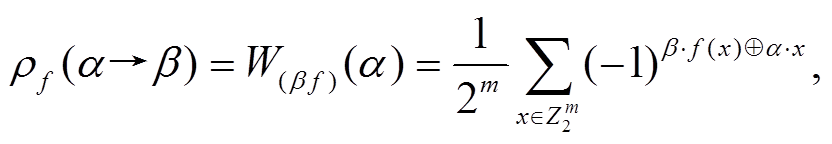
则称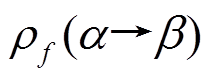 为f在输入线性组合为
为f在输入线性组合为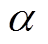 的条件下, 输出线性组合为
的条件下, 输出线性组合为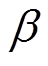 的相关系数, 称
的相关系数, 称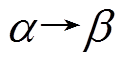 为f的一个线性逼近。其中,
为f的一个线性逼近。其中, 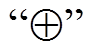 表示逐位异或,
表示逐位异或, 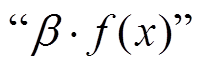 和
和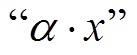 都表示点积。
都表示点积。
定义 4[10] 设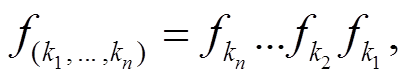 则称
则称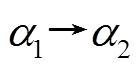
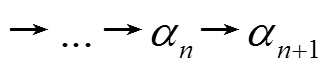 为
为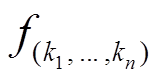 的一个起点为
的一个起点为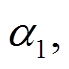 终点为
终点为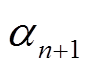 的组合传递链, 并称
的组合传递链, 并称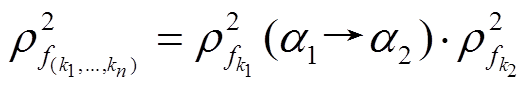
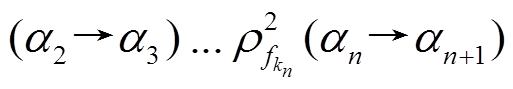 为该组合传递链的概率。
为该组合传递链的概率。
本文也称组合传递链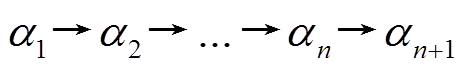 为n轮线性逼近。
为n轮线性逼近。
显然, 差分对应(线性逼近)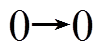 的概率恒为 1, 因此, 称
的概率恒为 1, 因此, 称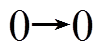 为平凡差分对应(平凡线性逼近), 否则, 称为非平凡差分对应(非平凡线性逼近)。以下考虑的都是非平凡的情形。
为平凡差分对应(平凡线性逼近), 否则, 称为非平凡差分对应(非平凡线性逼近)。以下考虑的都是非平凡的情形。
图 1 为 1 轮 Piccolo 结构, 其中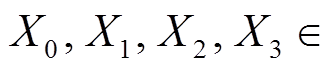
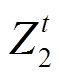 表示输入,
表示输入, 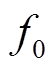 和
和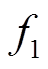 表示轮函数,
表示轮函数, 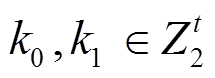 表示子密钥, 块移位变换 RP 表示将 4 个分块
表示子密钥, 块移位变换 RP 表示将 4 个分块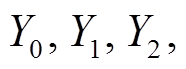
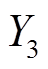 平均分成 8 个子分块后, 再对 8 个子分块进行移位变换。
平均分成 8 个子分块后, 再对 8 个子分块进行移位变换。
为了分析方便, 将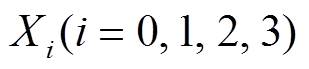 视为由左右规模相等的两部分
视为由左右规模相等的两部分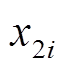 和
和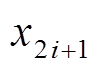 连接而成, 表示为
连接而成, 表示为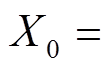
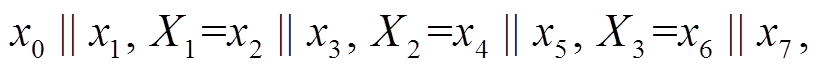 则 Piccolo结构的输入可表示为
则 Piccolo结构的输入可表示为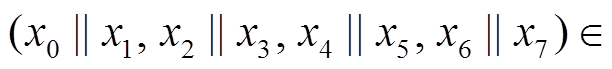
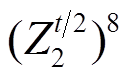 , 故 1 轮 Piccolo 结构(略去子密钥)可表示为
, 故 1 轮 Piccolo 结构(略去子密钥)可表示为
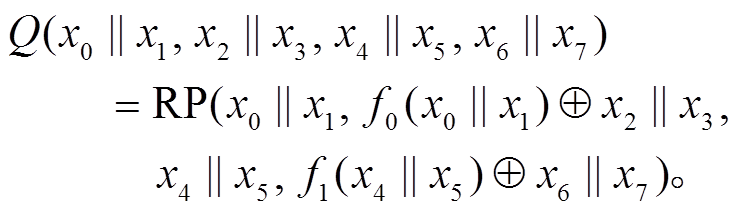
1)轮函数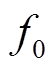 和
和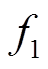 。如图 2 所示, 轮函数 f0 和f1 都采用 SPS 结构, 其中, S 表示 n 个 m 比特双射S 盒的并置(n 为偶数, nm=t, t 表示输入块
。如图 2 所示, 轮函数 f0 和f1 都采用 SPS 结构, 其中, S 表示 n 个 m 比特双射S 盒的并置(n 为偶数, nm=t, t 表示输入块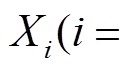
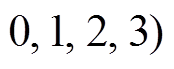 的比特位数), P 表示线性变换
的比特位数), P 表示线性变换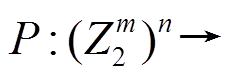
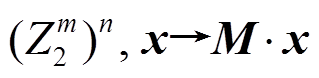 , x是列向量, M 是有限域
, x是列向量, M 是有限域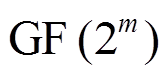 上的
上的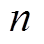 阶 MDS 矩阵。显然, P 变换的差分分支 数[10]和线性分支数[10]都为 n+1, 且轮函数f0和f1都为双射。
阶 MDS 矩阵。显然, P 变换的差分分支 数[10]和线性分支数[10]都为 n+1, 且轮函数f0和f1都为双射。
2)块移位变换 RP。如图 3 所示, 设块移位变换 RP 的输入为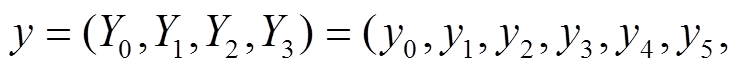
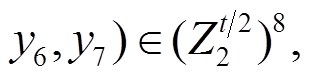 则块移位变换 RP 可表示为
则块移位变换 RP 可表示为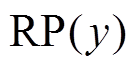
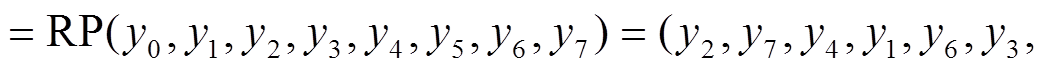
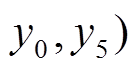 。
。
定义 5 [11] 设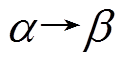 是轮函数(S盒)的一个差分对应, 若
是轮函数(S盒)的一个差分对应, 若 , 则称该轮函数(S 盒)为差分活动轮函数(S盒)。
, 则称该轮函数(S 盒)为差分活动轮函数(S盒)。
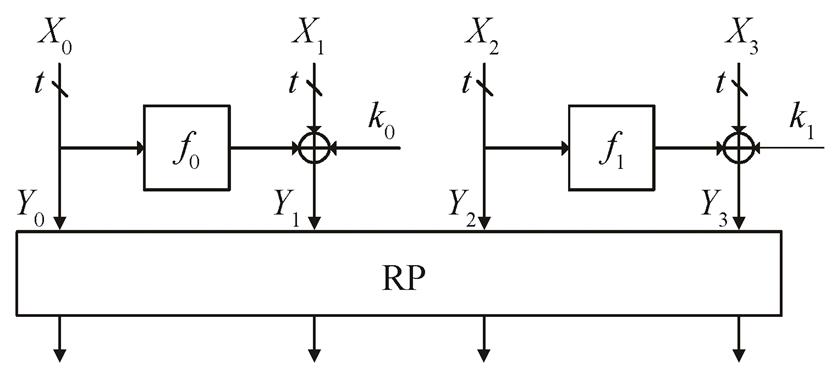
图1 Piccolo结构
Fig. 1 Piccolo structure
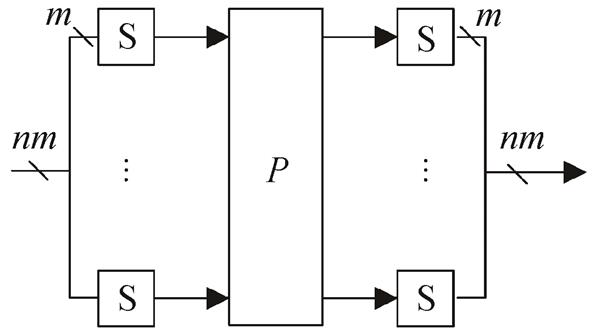
图2 轮函数
Fig. 2 Round function
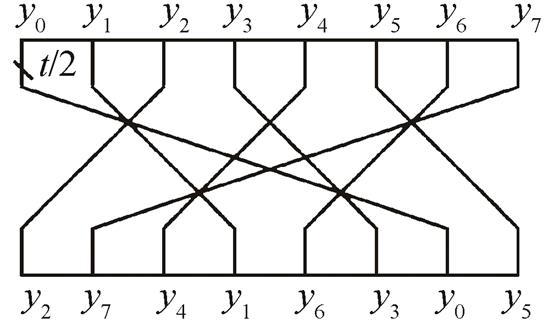
图3 块移位变换RP
Fig. 3 Block shift transformation RP
性质 1[9] 对于Piccolo结构的轮函数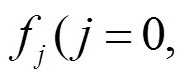
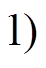 , 设
, 设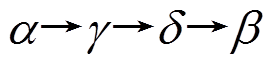 是轮函数
是轮函数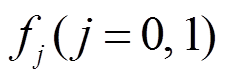 的差分对应,
的差分对应, 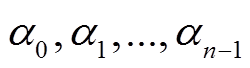 ,
,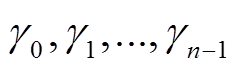 ,
,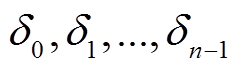 和
和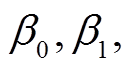
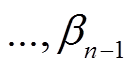 依次为
依次为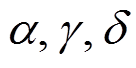 和
和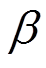 的
的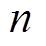 个分块, 且
个分块, 且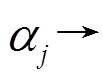
 或
或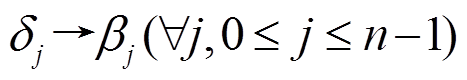 表示S变换的第
表示S变换的第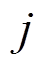 个 S 盒的差分对应,
个 S 盒的差分对应, 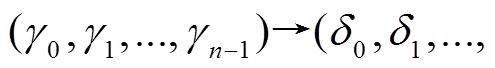
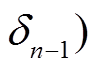 是 P 变换的差分对应。对于
是 P 变换的差分对应。对于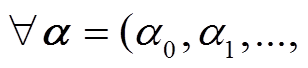
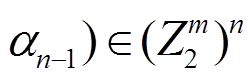 , 将
, 将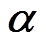 看成
看成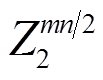 上的 2 维列向量, 即
上的 2 维列向量, 即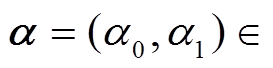
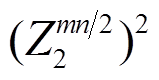 , 并将
, 并将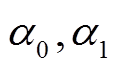 中非零元的个数记为
中非零元的个数记为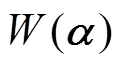 , 则对于
, 则对于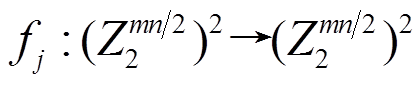 的差分对应
的差分对应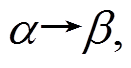 有
有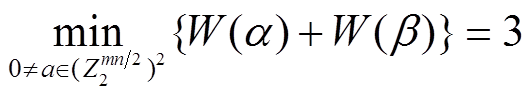 。
。
设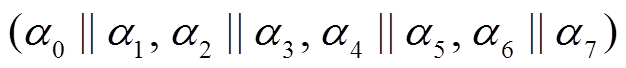 是 Piccolo 结构的输入差分, “1”代表非零差分块
是 Piccolo 结构的输入差分, “1”代表非零差分块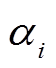 , “0”代表零差分块
, “0”代表零差分块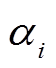
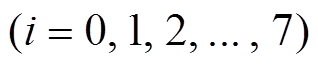 , 则 Piccolo 结构非零输入差分有且仅有 28–1=255 种表示, 即
, 则 Piccolo 结构非零输入差分有且仅有 28–1=255 种表示, 即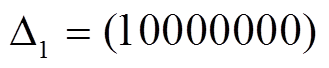
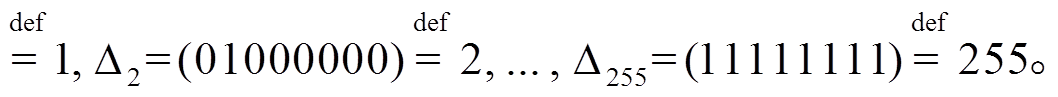 若左起第 1 和 2 位不全为零, 则
若左起第 1 和 2 位不全为零, 则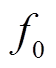 为活动轮函数; 若第 5 和 6 位不全为零, 则
为活动轮函数; 若第 5 和 6 位不全为零, 则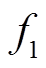 为活动轮函数。
为活动轮函数。
首先, 给出输入输出差分块“1”和“0”通过XOR运算和轮函数需要满足的约束条件。令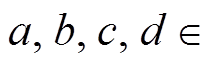
 分别代表
分别代表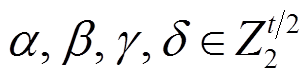 , “
, “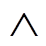 ”表示按位与, “
”表示按位与, “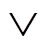 ”表示按位或。
”表示按位或。
条件 1 差分经过 XOR 运算时满足以下条件: 设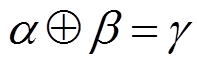 , 则
, 则

条件 1 表示, 对于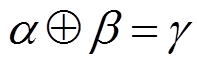 , 当
, 当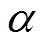 和
和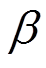 至少有一个为零时, 有 c=a+b; 当
至少有一个为零时, 有 c=a+b; 当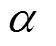 和
和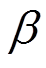 都非零时,
都非零时, 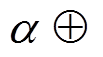
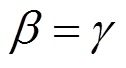 的值可能为零, 也可能不为零, 所以c=0或1。
的值可能为零, 也可能不为零, 所以c=0或1。
条件 2 差分经过轮函数时满足以下条件: 设 , 则
, 则
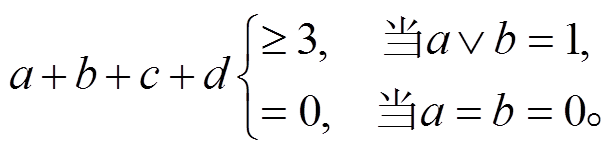
条件 2 表示, 当轮函数输入差分非零时, 因为输入差分和输出差分满足性质 1, 所以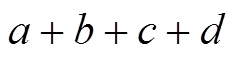
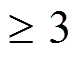 ; 当轮函数输入差分为零时, 输出差分也为零。
; 当轮函数输入差分为零时, 输出差分也为零。
以条件1和2作为约束, 对于Piccolo结构, 当给定输入差分的“0”和“1”表示和迭代轮数时, 通过计算机搜索, 容易给出输出差分的“0”和“1”表示及其所需活动轮函数个数的最小值。利用这两个约束条件可以完成以下3个实验。
实验 1 通过计算机搜索, 给出 6 轮差分特征中活动轮函数个数的最小值。
实验结果如图4所示, 其中第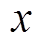 行第
行第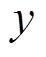 列(
列(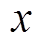 和
和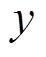 都是十六进制)交叉处的数值表示以
都是十六进制)交叉处的数值表示以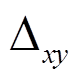 为首轮差分输入的 6 轮差分特征中活动轮函数个数的最小值。例如, 第 3 行第 e 列交叉处的数值为 7, 就表示以
为首轮差分输入的 6 轮差分特征中活动轮函数个数的最小值。例如, 第 3 行第 e 列交叉处的数值为 7, 就表示以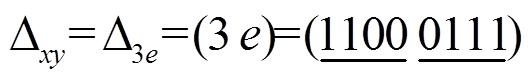 为首轮差分输入的6 轮差分特征中活动轮函数个数的最小值为 7。这里 ,
为首轮差分输入的6 轮差分特征中活动轮函数个数的最小值为 7。这里 ,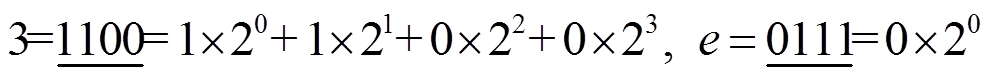
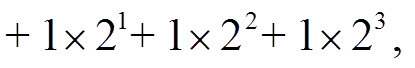 且行数和列数都从 0 开始统计。
且行数和列数都从 0 开始统计。
从图4可得以下结论。
命题 1 对于 Piccolo 结构, 任一 6 轮差分特征至少有6个活动轮函数。
实验 2 通过计算机搜索, 筛选出所有恰有 6个活动轮函数的 6 轮差分特征的尾轮输出差分(十六进制), 筛选结果记为集合 A, 表示如下(不计重复值)。

31315171923262a2b30 31323336394a4b515859 5b5e5f6263676a6b7176 7778797a7b7e7f858791 9395979ba2a4a6a7adaf b2b4b5b6b7b9bbbdbfda dbe5e7f5f7fafb
实验 3 对于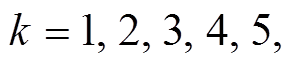 通过计算机搜索, 筛选出所有恰有
通过计算机搜索, 筛选出所有恰有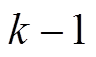 个活动轮函数的
个活动轮函数的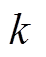 轮差分特征的首轮输入差分(十六进制), 筛选结果记为集合 B, 如下表示(不计重复值)。
轮差分特征的首轮输入差分(十六进制), 筛选结果记为集合 B, 如下表示(不计重复值)。

478bcdef4044 45484c4d54708084888a 8c8ea8b0c0c4c8ccd0d4 e0e8f0
通过观察发现, 集合 A和 B没有公共元素, 故
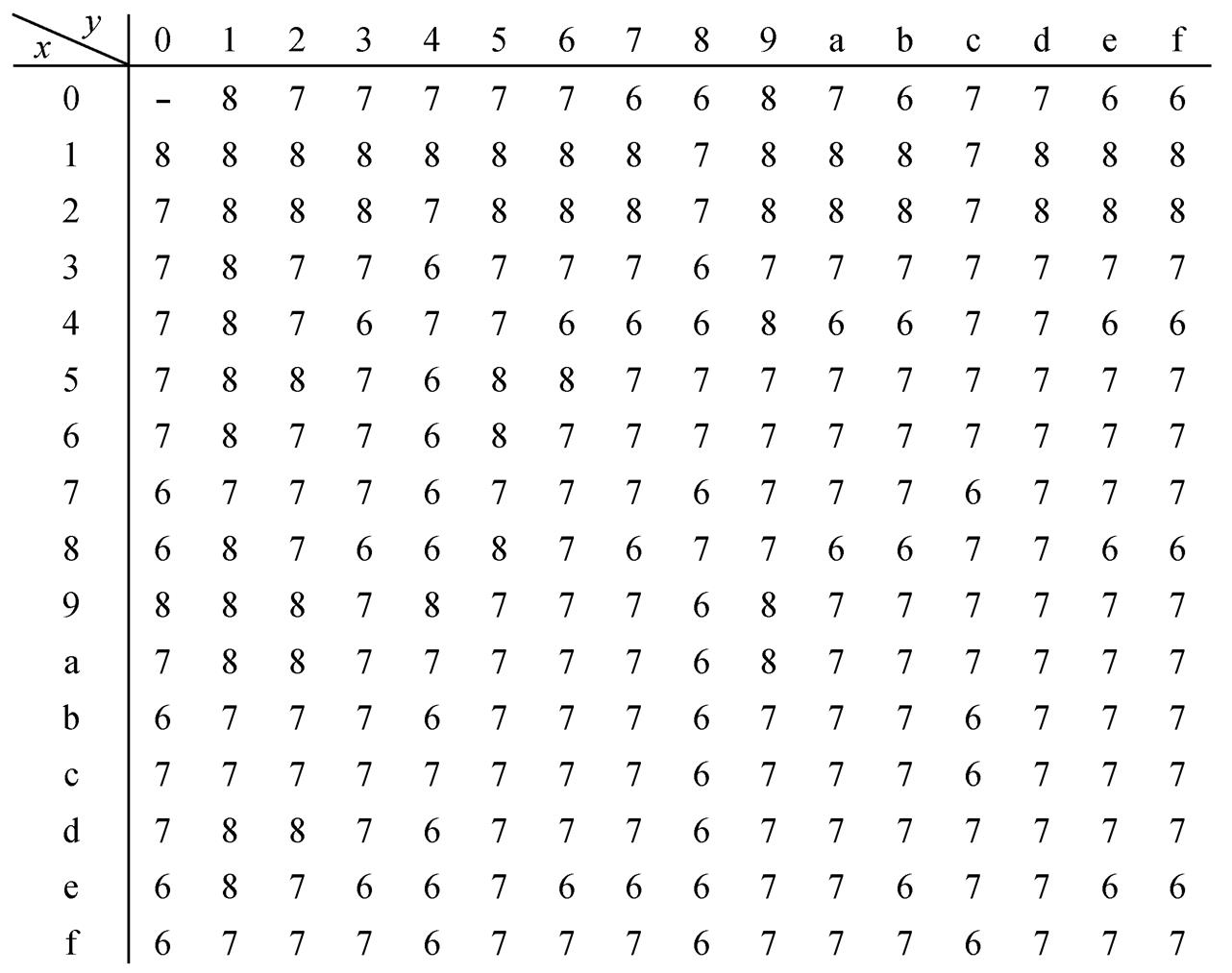
图4 6轮差分特征中活动轮函数个数的最小值
Fig. 4 Minimum of number of active round function for 6-round differential characteristics
可得以下结论。
命题 2 对于 Piccolo 结构, 任一恰有 6 个活动轮函数的6轮差分特征后面不可能“联接”一个恰有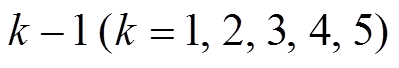 个活动轮函数的
个活动轮函数的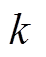 轮差分特征。
轮差分特征。
引理 1 对于 Piccolo 结构, 设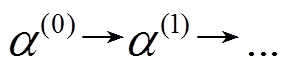
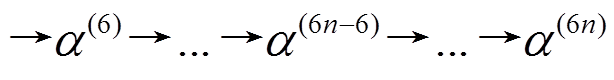 为任一恰有
为任一恰有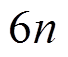 个活动轮函数的
个活动轮函数的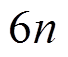 轮差分特征, 则最后 6 轮差分特征
轮差分特征, 则最后 6 轮差分特征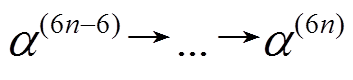 恰有6个活动轮函数。
恰有6个活动轮函数。
证明根据命题 1 可知, 6 轮差分特征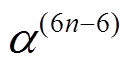
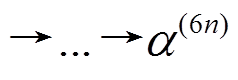 至少有 6 个活动轮函数。若
至少有 6 个活动轮函数。若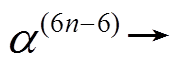
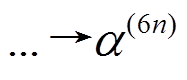 中活动轮函数的个数大于6, 则
中活动轮函数的个数大于6, 则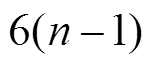 轮差分特征
轮差分特征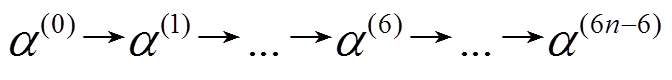 中活动轮函数的个数必小于
中活动轮函数的个数必小于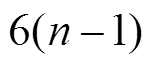 , 与命题 1 相矛盾, 故
, 与命题 1 相矛盾, 故 必含有6个活动轮函数, 所以本结论成立。
必含有6个活动轮函数, 所以本结论成立。
定理 1[9] 对于 Piccolo 结构, 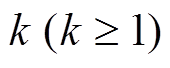 轮差分特征至少有
轮差分特征至少有 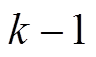 个活动轮函数。
个活动轮函数。
定理 2 对于Piccolo结构, 以下结论成立。
1)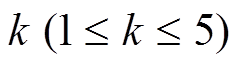 轮差分特征至少有
轮差分特征至少有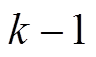 个活动轮函数。
个活动轮函数。
2)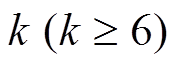 轮差分特征至少有
轮差分特征至少有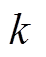 个活动轮函数。
个活动轮函数。
证明1)由定理 1, 即知。2)当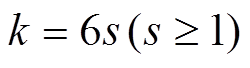 时, 由命题 1 可知, 本结论成立。当
时, 由命题 1 可知, 本结论成立。当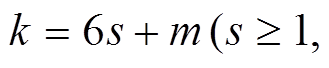
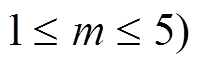 时, 分以下两种情形进行讨论。
时, 分以下两种情形进行讨论。
情形 1: 当前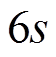 轮差分特征至少有
轮差分特征至少有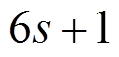 个活动轮函数时, 由定理 1 可知, 后
个活动轮函数时, 由定理 1 可知, 后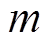 轮差分特征至少有
轮差分特征至少有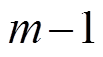 个活动轮函数, 所以
个活动轮函数, 所以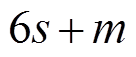 轮差分特征至少有
轮差分特征至少有 个活动轮函数。
个活动轮函数。
情形 2: 当前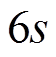 轮差分特征恰有
轮差分特征恰有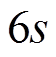 个活动轮函数时, 设
个活动轮函数时, 设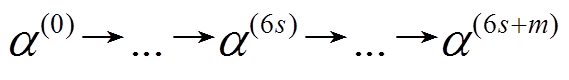 为任一
为任一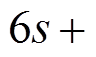
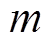 轮差分特征, 且
轮差分特征, 且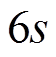 轮差分特征
轮差分特征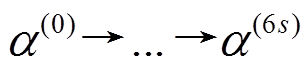 恰有
恰有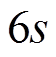 个活动轮函数。由引理 1 知,
个活动轮函数。由引理 1 知,  恰有 6 个活动轮函数, 再由命题 2 和定理 1 可 知, 后 m 轮差分特征
恰有 6 个活动轮函数, 再由命题 2 和定理 1 可 知, 后 m 轮差分特征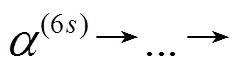
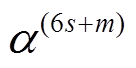 至少有
至少有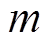 个活动轮函数, 所以
个活动轮函数, 所以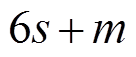 轮差分特征至少有
轮差分特征至少有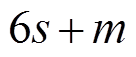 个活动轮函数。
个活动轮函数。
结合轮函数中 P 变换的差分分支数[10]为(n+1), 由定理2可得以下结论。
推论 1 对于Piccolo结构, 以下结论成立。
1)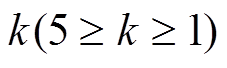 轮差分特征至少有
轮差分特征至少有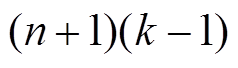 个活动S盒。
个活动S盒。
2)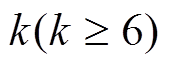 轮差分特征至少有(n+1)k 个活动 S 盒。
轮差分特征至少有(n+1)k 个活动 S 盒。
定义 6[9] 若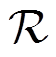 满足以下两个条件, 则称密码结构
满足以下两个条件, 则称密码结构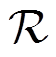 具有差分-线性对偶性。
具有差分-线性对偶性。
1)对任一活动轮函数个数为 的
的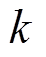 轮差分特征
轮差分特征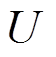 , 都存在活动轮函数个数为
, 都存在活动轮函数个数为 的
的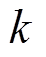 轮线性逼近
轮线性逼近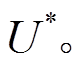
2)对任一活动轮函数个数为 的
的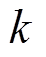 轮线性逼近
轮线性逼近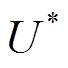 , 都存在活动轮函数个数为
, 都存在活动轮函数个数为 的
的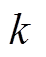 轮差分特征
轮差分特征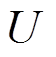 。
。
定理 3[9] Piccolo 结构具有差分–线性对偶性。
定理 4 对于 Piccolo结构, 以下结论成立。
1)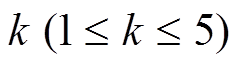 轮线性逼近至少有
轮线性逼近至少有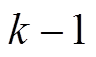 个活动轮函数;
个活动轮函数;
2)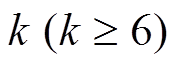 轮线性逼近至少有
轮线性逼近至少有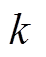 个活动轮函数。
个活动轮函数。
证明 由定理2和3易知本结论成立。
结合轮函数中 P 变换的线性分支数[10]为(n+1), 由定理4可得到以下推论。
推论 2 对于Piccolo结构, 以下结论成立。
1)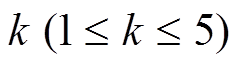 轮线性逼近至少有
轮线性逼近至少有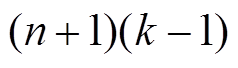 个活动S盒。
个活动S盒。
2)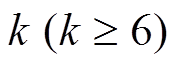 轮线性逼近至少有
轮线性逼近至少有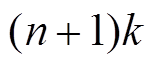 个活动S盒。
个活动S盒。
定理 5 设S盒的最大差分概率和最大线性逼近概率分别为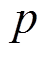 和
和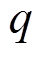 , 则以下结论成立。
, 则以下结论成立。
1)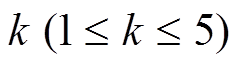 轮 Piccolo 结构的最大差分特征概率
轮 Piccolo 结构的最大差分特征概率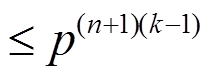 , 最大线性逼近概率
, 最大线性逼近概率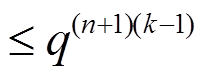 。
。
2)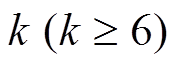 轮 Piccolo 结构的最大差分特征概率
轮 Piccolo 结构的最大差分特征概率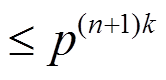 , 最大线性逼近概率
, 最大线性逼近概率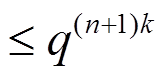 。
。
本节证明, 定理2和4给出的活动轮函数个数的下界是不可改进的, 即确实存在一类差分特征和线性逼近, 其活动轮函数的个数恰好达到给出的下界。
设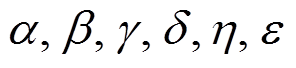 全不为零。为叙述方便, 用S1表示 2 轮差分特征
全不为零。为叙述方便, 用S1表示 2 轮差分特征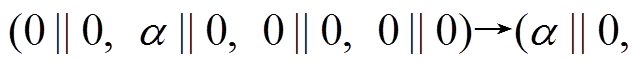
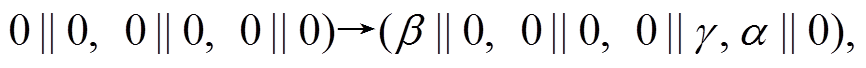 其轮函数差分对应依次为
其轮函数差分对应依次为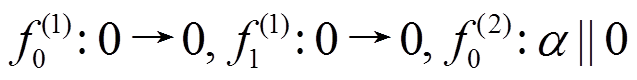
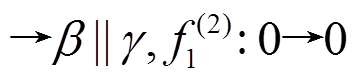 。
。
用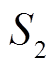 表示 3 轮差分特征
表示 3 轮差分特征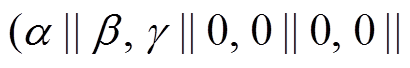
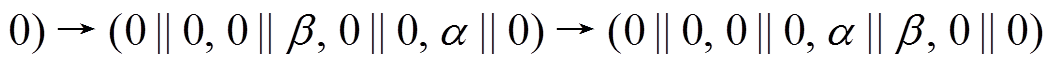
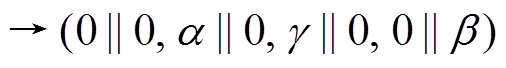 ,其轮函数差分对应依次为
,其轮函数差分对应依次为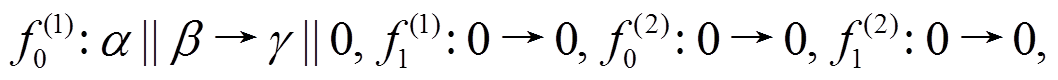
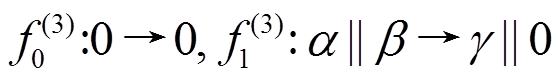 。
。
用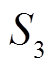 表示 4 轮差分特征
表示 4 轮差分特征
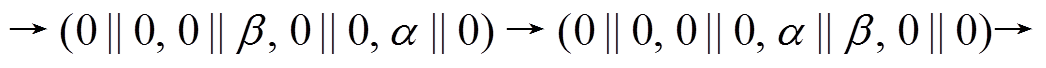
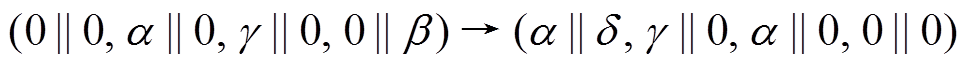 , 其轮函数差分对应依次为
, 其轮函数差分对应依次为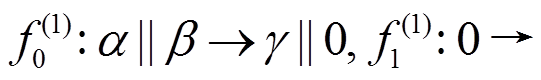
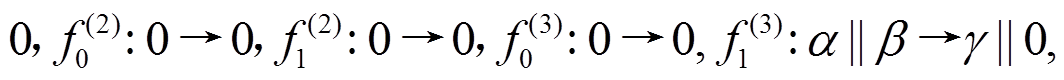
 , 其中
, 其中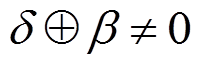 。
。
用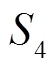 表示 5 轮差分特征
表示 5 轮差分特征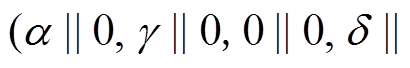
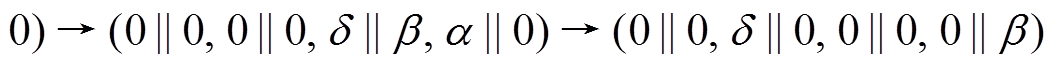
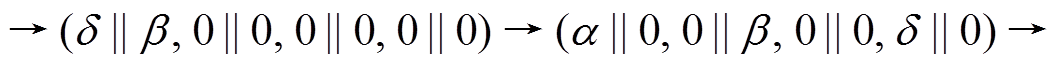
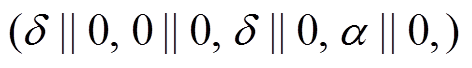 , 其轮函数差分对应依次为
, 其轮函数差分对应依次为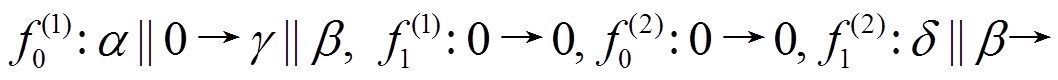

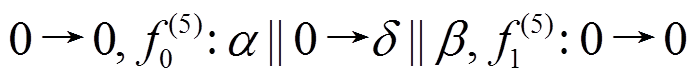 。
。
由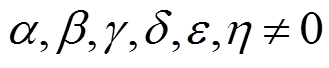 可知,
可知, 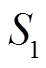 有 1 个活动轮函数,
有 1 个活动轮函数, 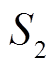 有 2 个活动轮函数,
有 2 个活动轮函数, 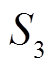 有 3 个活动轮函数,
有 3 个活动轮函数, 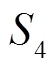 有 4 个活动轮函数。这说明, 对
有 4 个活动轮函数。这说明, 对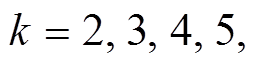 定理2第1个结论中活动轮函数个数的下界是不可改进的。又因为
定理2第1个结论中活动轮函数个数的下界是不可改进的。又因为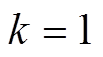 时, 显然存在恰有 0 个活动轮函数的 1 轮差分特征, 所以定理 2 第 1 个结论中的下界是不可改进的, 再由定理 3 知, 定理 4 第 1 个结论中的下界也是不可改进的。
时, 显然存在恰有 0 个活动轮函数的 1 轮差分特征, 所以定理 2 第 1 个结论中的下界是不可改进的, 再由定理 3 知, 定理 4 第 1 个结论中的下界也是不可改进的。
下面说明定理 2 第 2 个结论和定理 4 第 2 个结论中的下界是不可改进的。
S5 表示 3 轮差分特征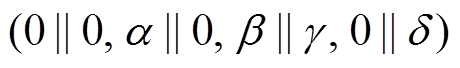
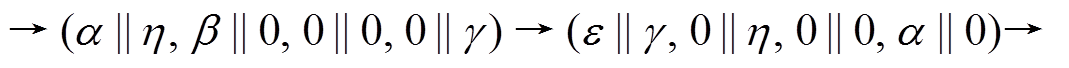
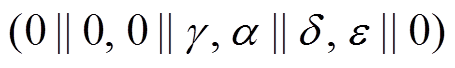 , 其轮函数差分对应依次为
, 其轮函数差分对应依次为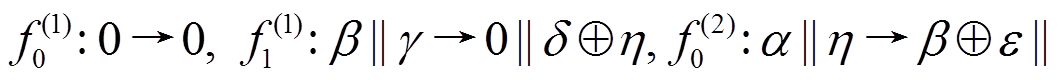
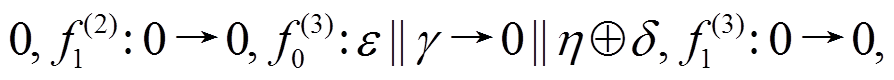 其中
其中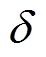
 都不为零。
都不为零。
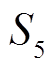 的每一轮各含有
的每一轮各含有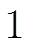 个活动轮函数。现在将两个
个活动轮函数。现在将两个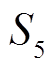 “联接”在一起得到
“联接”在一起得到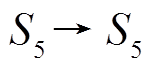 , 其中“联接”处的差分特征
, 其中“联接”处的差分特征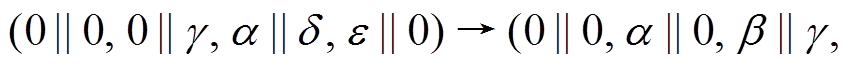
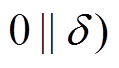 的轮函数差分对应为
的轮函数差分对应为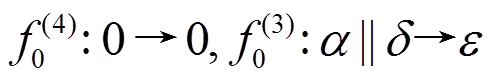
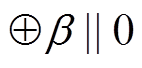 , 其中
, 其中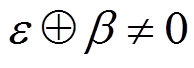 。易知,
。易知,  的每一轮各含有
的每一轮各含有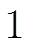 个活动轮函数。这样一来, 通过“联接”
个活动轮函数。这样一来, 通过“联接”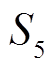 , 可以得到任意
, 可以得到任意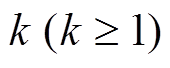 轮有
轮有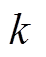 个活动轮函数的差分特征, 故定理 2 第 2 个结论中的下界是不可改进的, 再由定理 3 知, 定理 4 第 2 个结论中的下界也是不可改进的。
个活动轮函数的差分特征, 故定理 2 第 2 个结论中的下界是不可改进的, 再由定理 3 知, 定理 4 第 2 个结论中的下界也是不可改进的。
本文给出 Piccolo 结构抵抗差分密码分析和线性密码分析能力的评估结果。具体地, 给出任意轮差分特征中活动轮函数和活动 S 盒个数的一个新下界, 并利用差分线性对偶性, 给出任意轮线性逼近中活动轮函数和活动 S 盒个数的一个新下界。本研究的意义在于, 仅需要计算 S 盒的最大差分概率(最大线性逼近概率), 就可以给出差分特征(线性逼近)概率的上界, 进而估计出密码算法抵抗差分密码分析(线性密码分析)的安全性。本文的研究结果对于利用 Piccolo 结构设计新的密码算法具有重要的指导意义。下一步, 将研究 Piccolo 结构抵抗其他攻击方法的安全性。
参考文献
[1]Biham E, Shamir A. Differential cryptanalysis of DES-like cryptosystems // CRYPTO’90 Proceedings of the 10th Annual International Cryptology Confe-rence on Advances in Cryptology. Berlin, 1991: 2–21
[2]Matsui M. Linear cryptanalysis method for DES cipher // Advances in Cryptology—EUROCRYPT’93, LNCS 765. Lofthus, 1994: 386–397
[3]Knudsen L R. Practically secure Feistel ciphers // Fast Software Encryption’93, LNCS 806. Cambridge, 1994: 211–221
[4]吴文玲, 贺也平. 一类广义 Feistel 密码的安全性评估. 电子与信息学报, 2002, 24(9): 1177–1184
[5]Wang Q Y, Zhang B, Jin C H. Practical Security against differential and linear cryptanalysis for SMS4- like cipher. Journal of Networks, 2013, 8(8): 1689–1693
[6]王念平. 一类广义 Feistel 密码的安全性能分析. 大连海事大学学报, 2007, 33(3): 63–67
[7]Zhao G, Cheng L, Li C, et al. On the practical secu-rity bound of GF-NLFSR structure with SPN round function // Provable Security 2014, LNCS 8782. Hong Kong, 2014: 40–54
[8]Shibutani K, Isobe T, Hiwatari H, et al. Piccolo: an ultra-lightweight block cipher // Cryptographic Hard-ware and Embedded Systems—CHES 2011, LNCS 6917. Nara, 2011: 342–357
[9]殷勍, 王念平. Piccolo 结构抵抗差分和线性密码分析能力评估. 山东大学学报(理学版), 2016, 51(3): 132–142
[10]金晨辉, 郑浩然, 张少武, 等. 密码学. 北京: 高等教育出版社, 2009
[11]Schneier B, Kelsey J. Unbalanced Feistel networks and block cipher design // Fast Software Encryption’ 95, LNCS 3557. Cambridge, 1996: 121–144
Further Security Evaluation for Piccolo Structure against Differential and Linear Cryptanalysis
YIN Qing1, WANG Nianping2,†
1. Space Engineering University, Beijing 101416; 2. School of Cryptography Engineering, The PLA Information Engineering University, Zhengzhou 450001; † Corresponding author, E-mail: wwnnpp@126.com
Abstract To evaluate the security of Piccolo structure, the security against differential and linear cryptanalysis is investigated. A new lower bound on number of active round function and active S-boxes for arbitrary round differential characteristics is given. Using the duality between differential characteristics and linear approximations of Piccolo structure, the new lower boundon number of active round function and active S-boxes for arbitrary round linear approximationsis also given. The authors prove that these lower bounds cannot be improved.
Key words Piccolo structure; differential cryptanalysis; linear cryptanalysis
中图分类号 TN918
doi: 10.13209/j.0479-8023.2018.086
国家自然科学基金(61672031)资助
收稿日期: 2018–01–06;
修回日期: 2018–07–19;
网络出版日期: 2018–09–20