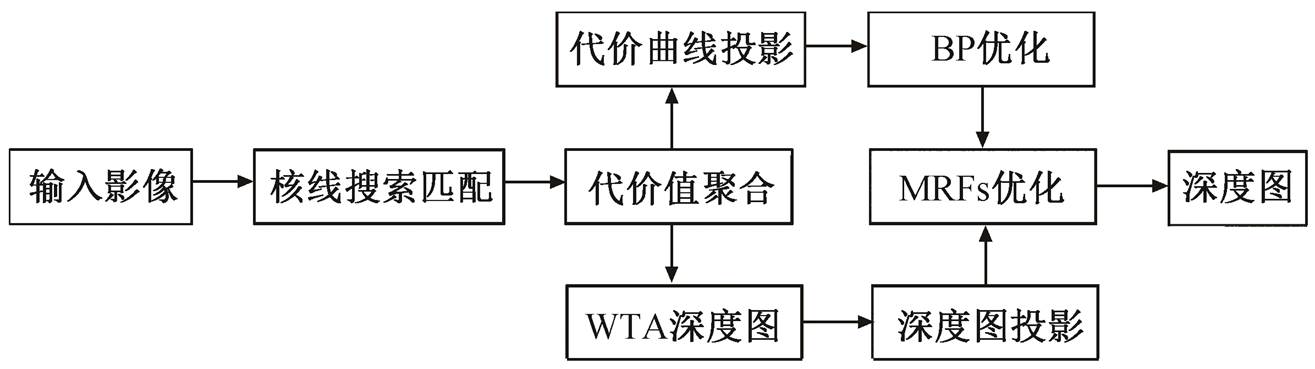
图1 深度图计算流程
Fig. 1 Depth estimation workflow
杨鹏 晏磊 赵守江 晏艺真 赵红颖†
北京大学地球与空间科学学院, 北京 100871; † 通信作者, E-mail: zhaohy@pku.edu.cn
摘要 由于微透镜影像分割了原始全光影像, 无法应用全局优化算法, 而采用WTA(winner-take-all)算法得到的深度影像虽然连续, 但包含错误估计的深度信息; 利用全局优化计算得到的深度图可以消除错误估计的深度信息, 但是受到代价计算时深度离散化的限制而不连续。基于上述情况, 提出一种直接处理微透镜阵列全光影像的代价投影策略, 在投影图像上构建代价立方体(cost volume, CV), 同时采用MRFsP(Markov Random Fields Propagation)进行优化, 结合WTA方法的优势改善离散深度图像。实验结果表明, 与现有方法对比, 利用MRFsP优化后的深度图既能消除错误匹配点, 也能保持连续。
关键词 全光影像; 深度估计; MRFsP优化
全光相机是一种深度相机, 又称为光场相机, 能够通过单次拍摄来提供场景的三维信息。随着Lytro公司和Raytrix公司研制成功手持式相机, 利用全光影像进行三维重建(深度信息)已成为研究热点[1]。虽然Lytro公司和Raytrix公司的相机结构分别属于全光1.0相机和全光2.0相机[2], 但这两款相机均有记录光线强度和方向信息的能力, 这也是利用全光相机进行三维重建的基础[3]。
对于Lytro相机, 通常进行深度估计的方式是将微透镜影像分解成图像阵列的形式[4–5], 图像阵列的行列数目等同于单个微透镜下覆盖的探测器单元数目, 而每一幅影像的分辨率等同于微透镜的总数目。为了获取深度图, 一些研究[6–10]利用传统的立体视觉特征点匹配的方式进行视差计算, 将图像阵列的中心影像作为参考影像。另外一些研究利用核线平面影像[11–15]检测同名点构成的直线斜率, 利用直线斜率与深度值一一对应的关系, 计算得到深度图[16]。这两种方式计算得到的深度影像均可以利 用图割Graph Cuts[17–18]和置信度传播BP(belief pro-pagation)[19–20]等消除误匹配。但是, 由于受光学结构的限制, 计算出的深度图与参考影像的分辨率相等(只有原始影像的1%)。
通常, Raytrix相机微透镜的数目更少, 使用上述方法进行深度计算会产生分辨率更低的深度图, 因此需要基于微透镜阵列直接进行深度计算。在基于微透镜直接计算深度的研究中, Georgiev等[21]提出一种利用归一化交叉相关算法, 沿着横向和纵向的方式, 进行同名点匹配搜索计算视差, 最终采用WTA(winner-take-all)方法得到深度图。之后, Zeller等[22-23]采用同样的思路, 但是通过强度差异计算深度, 同时改进了视差搜索方式, 主要沿着核线方向搜索同名点, 最终通过多次观测去除异常深度信息, 得到稀疏的点云信息。Fleischmann等[24]提出一种不同的利用传统视觉的方法, 首先以单个微透镜为基础, 构建代价立方体CV(cost volume), 然后采用半全局方式[25]对单个微透镜的CV进行优化, 消除误匹配。由于微透镜的边缘限定了优化的范围, 因此这种方式有待改进。
本文提出一种全局优化深度图的方法, 深度图的构建不会受到微透镜数目的限制。首先, 基于微透镜进行代价计算[22–24], CV的高度由虚拟深度的范围决定[26–28], 同时仍然保留高精度的WTA深度结果; 然后, 将CV通过获取的初步深度信息投影到像空间, 同时构建新的CV, 并利用全局BP优化产生平滑且可靠的深度图。这里获取的深度图是离散的, 因此我们会将高精度且连续的WTA深度图结果一并投影, 并利用此结果对上一步获取的离散深度图进行优化, 通过马尔科夫随机场传播(Markov Random Fields Propagation, MRFsP)[12,29]获取既连续也平滑的深度图。为验证方法的效果, 通过实验与文献[24]的方法进行对比。MRFsP优化深度图的流程如图1所示。

图1 深度图计算流程
Fig. 1 Depth estimation workflow
全光相机包含3个主要部件: 主透镜、微透镜阵列以及探测器阵列。主透镜将物方空间成像至像方空间, 并且物方景深被压缩到一个合理的像方景深, 如图2所示。可以将微透镜阵列和探测器阵列视为一个多相机阵列系统, 对像方空间进行观测, 这时就可以利用多视几何相关理论进行三维信息计算, 并获得深度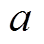 的值。探测器与微透镜之间的距离
的值。探测器与微透镜之间的距离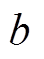 通常是一个固定值, 因此将虚拟深度
通常是一个固定值, 因此将虚拟深度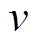 作为深度计算的最终结果[26]:
作为深度计算的最终结果[26]:
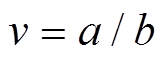 。 (1)
。 (1)在实际计算过程中, 微透镜被视为一个小孔成像模型, 因此在微透镜–探测器组成的观测系统中, 深度计算类似于双目结构, 如图3所示。
虚拟深度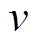 由下式计算得到:
由下式计算得到:
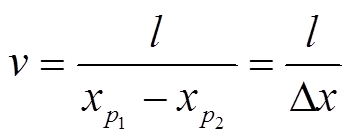 , (2)
, (2)其中, 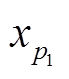 和
和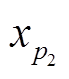 是点
是点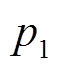 和
和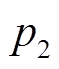 相对于微透镜的局部像点坐标, Dx 为视差。根据式(2), 可以得到虚拟深度的变化与视差变化的关系:
相对于微透镜的局部像点坐标, Dx 为视差。根据式(2), 可以得到虚拟深度的变化与视差变化的关系:
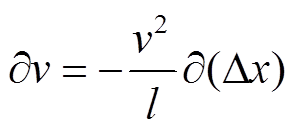 。 (3)
。 (3)
式(3)表明, 为视差计算精度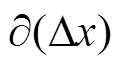 在一定的范围时,越长的基线能够保障越高的虚拟深度精度, 这时选择基线长的虚拟深度值有利于提高深度图的精度。
在一定的范围时,越长的基线能够保障越高的虚拟深度精度, 这时选择基线长的虚拟深度值有利于提高深度图的精度。
为了获得视差信息, 首先需要进行同名点的匹配来构建 CV, 匹配的具体过程如图4(a)所示, 计算时深度的离散值数目为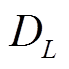 , 如图5所示。本文采用经典的SAD (sum of absolute difference)进行同名点对的强度一致性度量:
, 如图5所示。本文采用经典的SAD (sum of absolute difference)进行同名点对的强度一致性度量:

虚线部分表示不考虑微透镜和成像平面时光线的汇聚
图2 全光相机结构
Fig. 2 Structure of the plenoptic camera
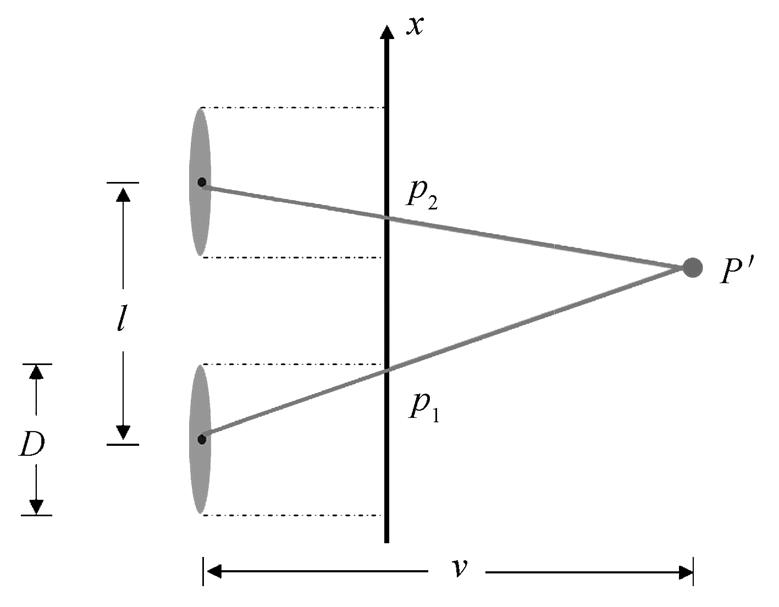
图3 微透镜–探测器系统
Fig. 3 Microlens-detector system
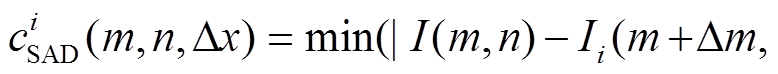
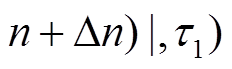 (4)
(4)
其中, 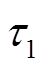 是一个限定代价大小的常数,
是一个限定代价大小的常数, 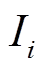 是待计算微透镜周围的第 i 个微透镜影像, 如图4(a)所示。(∆m, ∆n)是沿着基线方向的两个微透镜的偏移量。
是待计算微透镜周围的第 i 个微透镜影像, 如图4(a)所示。(∆m, ∆n)是沿着基线方向的两个微透镜的偏移量。
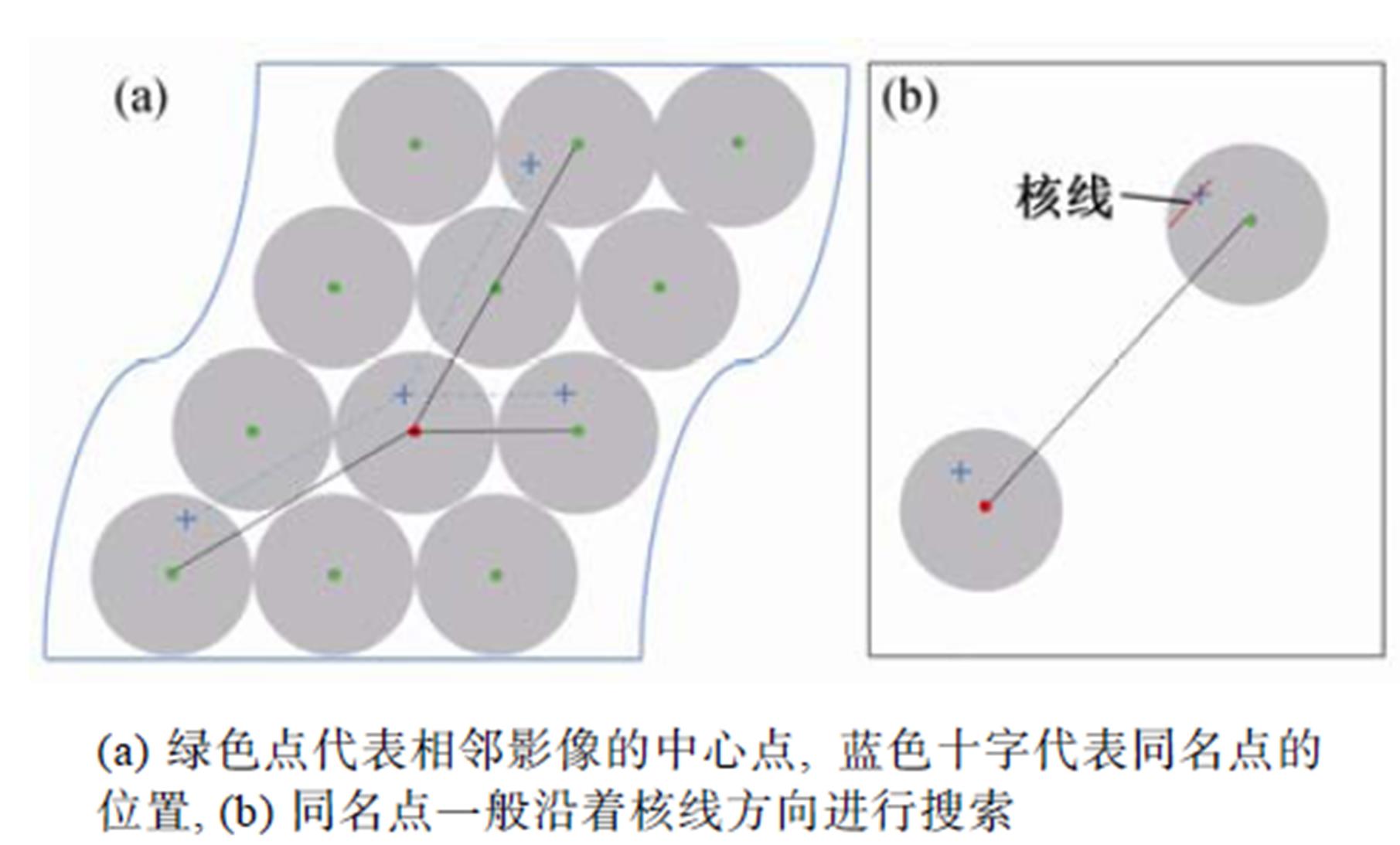
图4 多基线同名点匹配
Fig. 4 Multi-baseline corresponding points matching
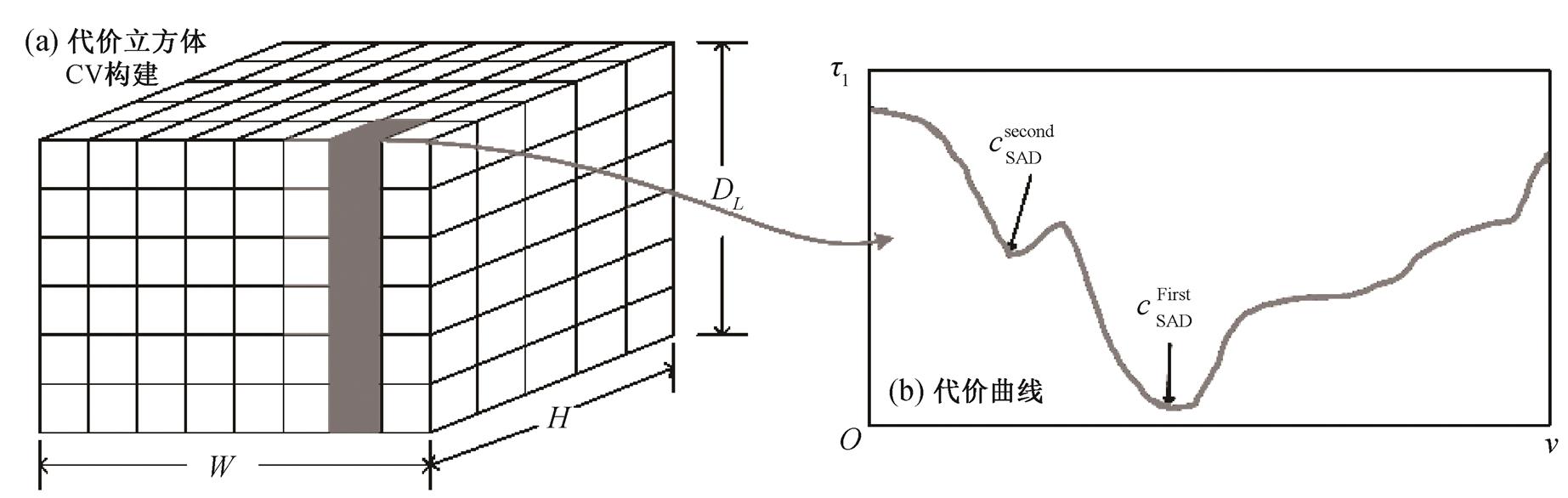
图5 深度图代价计算
Fig. 5 Cost calculation for depth map
式(2)中∆x等于偏移量的欧式距离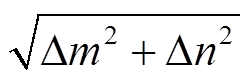 , 如图4(b)所示。此外, 考虑到鲁棒性, 视差计算采用自适应窗口[30]:
, 如图4(b)所示。此外, 考虑到鲁棒性, 视差计算采用自适应窗口[30]:
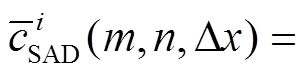
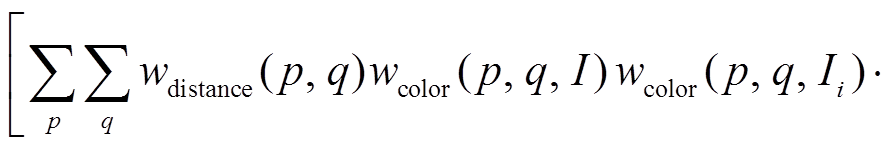
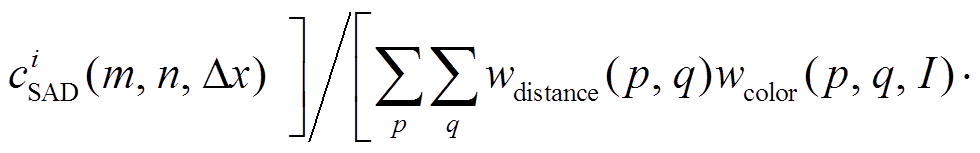
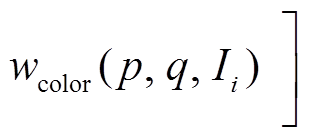 , (5)
, (5)在式(5)中, 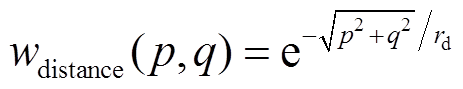 和
和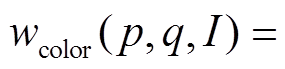
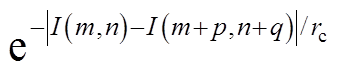 分别是基于距离信息和颜色信息的权重,
分别是基于距离信息和颜色信息的权重, 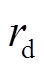 和
和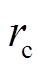 是常量。点
是常量。点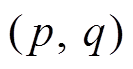 是相邻像素点的坐标。
是相邻像素点的坐标。
由于微透镜影像中的同一个点对于不同的基线会有不同的视差, 所以CV应该建立在虚拟深度上, 因此最终的代价函数应该为
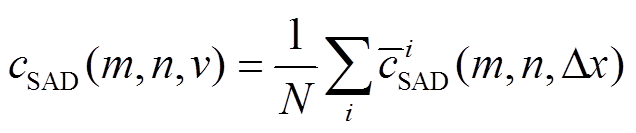 , (6)
, (6)其中, 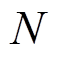 是计算中涉及的微透镜的数目,
是计算中涉及的微透镜的数目, 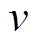 可以利用视差
可以利用视差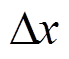 通过式(2)计算得到。
通过式(2)计算得到。
考虑到式(3)的影响, 一般利用式(6)计算代价信息会降低虚拟深度的精度。由于全光相机是一个多基线的系统, 且视差值与虚拟深度之间并不是简单的线性关系, 若要保持精度只能提高CV中的深度方向的数量。为了平衡深度信息的精度以及深度方向的数量, 我们在利用式(6)进行深度计算的同时, 保留高精度的WTA深度结果(该结果直接采用视差进行深度计算), 最后的深度图由式(2)转化至虚拟深度, 并用于后续的优化。深度计算的流程见算法1 (其中符号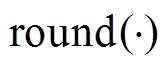 表示取整)。
表示取整)。
算法1 基于微透镜代价及WTA深度图构建算法。
1 输入: 全光数据
2 针对每一幅微透镜影像执行步骤3~5
3 对于微透镜中每一个点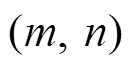 , 搜索与之最近的
, 搜索与之最近的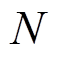 幅微透镜影像, 执行步骤4~5
幅微透镜影像, 执行步骤4~5
4 计算代价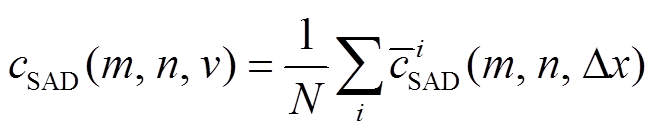 , 其中,
, 其中, 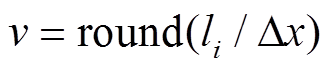
5 如果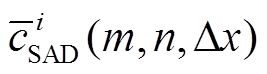 是所有可能的视差中最小的, 则将WTA赋值深度
是所有可能的视差中最小的, 则将WTA赋值深度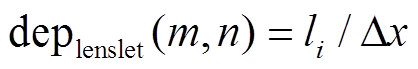
6 输出: cSAD和WTA深度图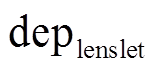
由1.2节计算得到的cSAD只能在单个微透镜影像内部进行局部优化[24], 因此本节对CV和WTA深度信息进行投影, 建立新的基于投影影像的CV和深度图。投影之前, 首先利用CV信息进行深度可靠性的估计, 建立基于微透镜影像的可信度图[20]。可信度计算公式如下:
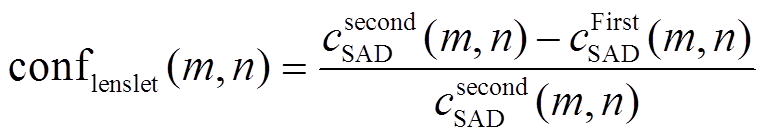 , (7)
, (7)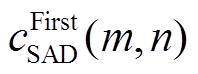 为点
为点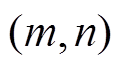 对应的最小代价值,
对应的最小代价值,  为仅次于最小代价值的代价值, 如图5(b)所示。可信度
为仅次于最小代价值的代价值, 如图5(b)所示。可信度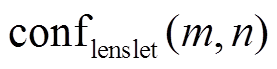 的取值范围为
的取值范围为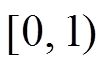 。可以利用可信度图选择合适的代价曲线进行投影。
。可以利用可信度图选择合适的代价曲线进行投影。
参考图2和3, 像方空间点 P′ 和图像点 pi (i=1, 2)以及透镜的中心满足共线条件, 因此投影到像方空间点的坐标通过下式确定:
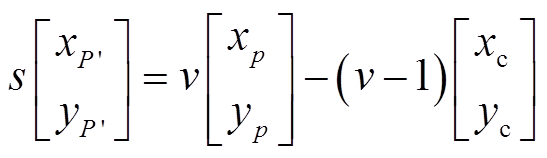 , (8)
, (8)其中, 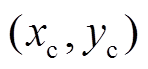 是微透镜的中心坐标,
是微透镜的中心坐标,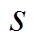 为决定投影影像的分辨率控制因子。
为决定投影影像的分辨率控制因子。
显然, 投影获得的坐标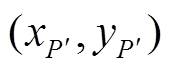 不是整数, 因此本文采用插值的手段获取投影代价曲线和投影深度图。
不是整数, 因此本文采用插值的手段获取投影代价曲线和投影深度图。
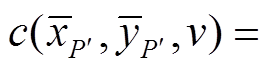
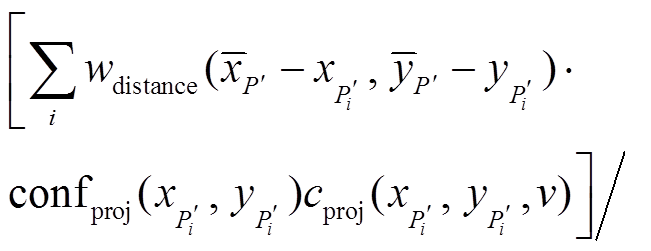
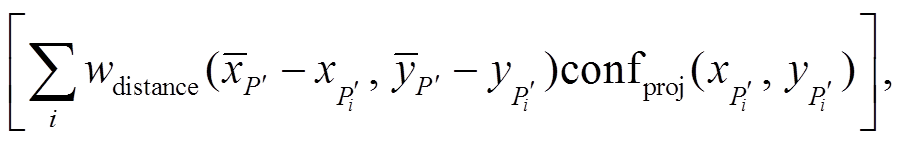 (9)
(9)
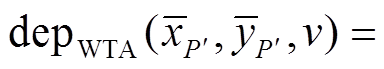
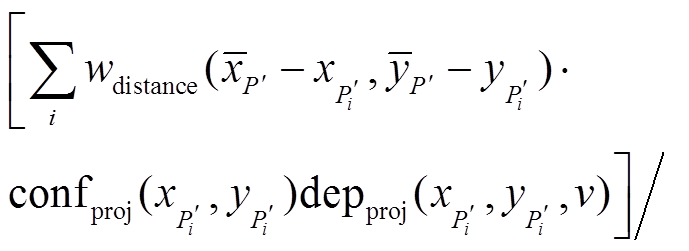
 (10)
(10)
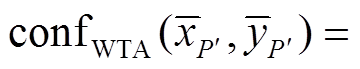
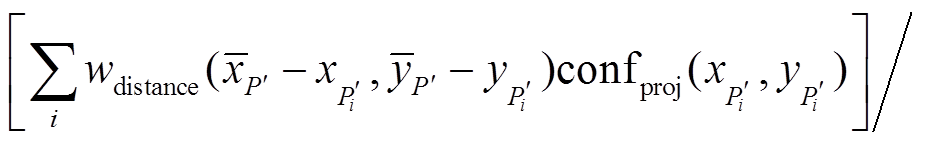
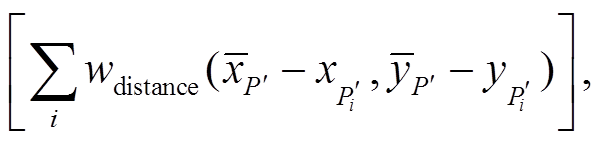 (11)
(11)
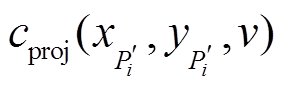 、
、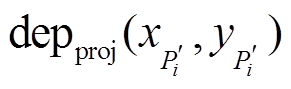 以及
以及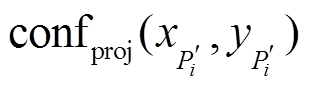 分别代表投影代价值、深度值和可信度值,
分别代表投影代价值、深度值和可信度值, 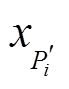 和
和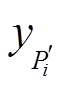 的取值在实数域连续。值得注意的是
的取值在实数域连续。值得注意的是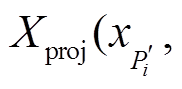

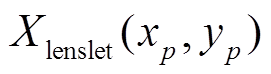 (
(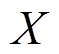 代表式(9)~(11)中
代表式(9)~(11)中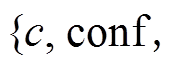
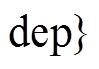 )。由于同一个点有多条代价曲线以及深度值, 因此进行插值时, 只选取可信度最大的前
)。由于同一个点有多条代价曲线以及深度值, 因此进行插值时, 只选取可信度最大的前 条代价曲线, 以此来提升鲁棒性。
条代价曲线, 以此来提升鲁棒性。
经过投影步骤, 可以得到基于投影影像的CV, 本文采用由粗到精的3层BP对其进行优化[19-20]。由于BP不能保证聚合, 故设定多次迭代得到最后的结果。代价值的每一次迭代使用式(12)和(13)。
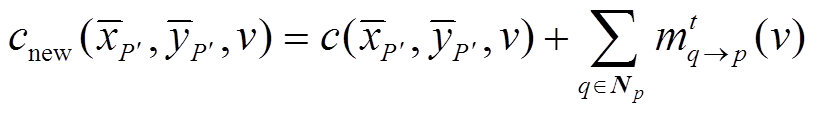 , (12)
, (12)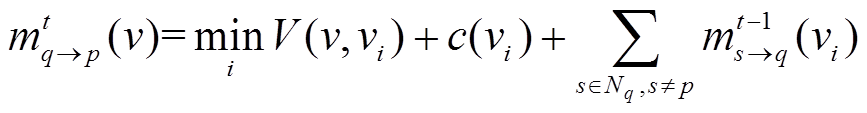 , (13)
, (13)
其中,  表示传播的信息,
表示传播的信息, 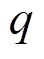 代表像点
代表像点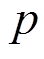 邻域的像素(本文中, 相邻像素点之间的深度约束
邻域的像素(本文中, 相邻像素点之间的深度约束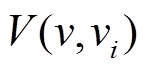 使用线性模型)。BP优化后的深度影像和可信度图计算结果如下:
使用线性模型)。BP优化后的深度影像和可信度图计算结果如下:
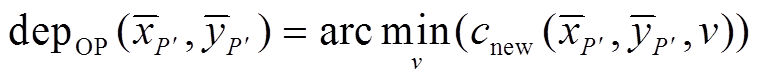 , (14)
, (14)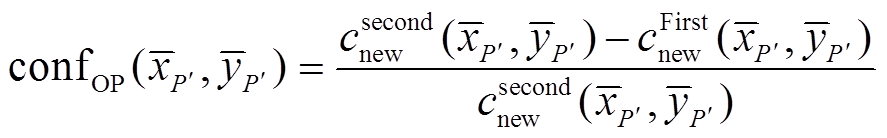 。 (15)
。 (15)
利用式(14)得到的深度图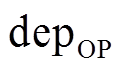 是离散的, 利用式(10)计算的深度图
是离散的, 利用式(10)计算的深度图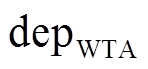 虽然包含误匹配信息但是连续的。为了结合两者的优势, 我们利用MRFsP模型[12,29]对深度图进行融合优化, 最终的深度图计算如下:
虽然包含误匹配信息但是连续的。为了结合两者的优势, 我们利用MRFsP模型[12,29]对深度图进行融合优化, 最终的深度图计算如下:
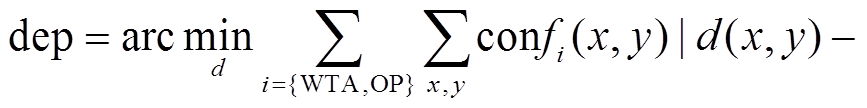
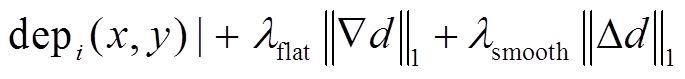 , (16)
, (16)
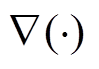 代表梯度算子,
代表梯度算子, 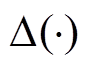 代表拉普拉斯算子。
代表拉普拉斯算子。
详细的计算过程见算法2。
算法 2 MRFsP优化深度图算法。
1 输入: 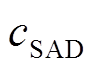 , deplenslet和conflenslet
, deplenslet和conflenslet
2 利用式(7)~(11)进行投影, 计算得到 depWTA 和confWTA
3 利用式(12)~(14)进行全局BP优化, 获得depOP和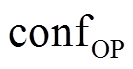
4 利用式(16)的 MRFsP获取融合两类深度图
5 输出: 优化后的深度图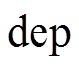
本文的数据集由Raytrix 42相机提供, 每个微透镜覆盖约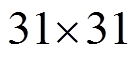 个像素单元。计算深度图前, 先用白光影像进行微透镜中心点的检测[4], 结果如图6所示。
个像素单元。计算深度图前, 先用白光影像进行微透镜中心点的检测[4], 结果如图6所示。
获取微透镜中心点信息后, 按照图1的步骤构建深度图, 计算中使用的参数如表1所示。
此外, 使用式(5)时, 自适应窗口的大小为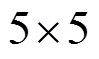 像素, 而利用式(9)~(11)进行插值计算的窗口大小为
像素, 而利用式(9)~(11)进行插值计算的窗口大小为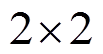 。本实验分别从深度图连续性以及深度估计的鲁棒性两个方面与现有算法的对比进行分析。
。本实验分别从深度图连续性以及深度估计的鲁棒性两个方面与现有算法的对比进行分析。
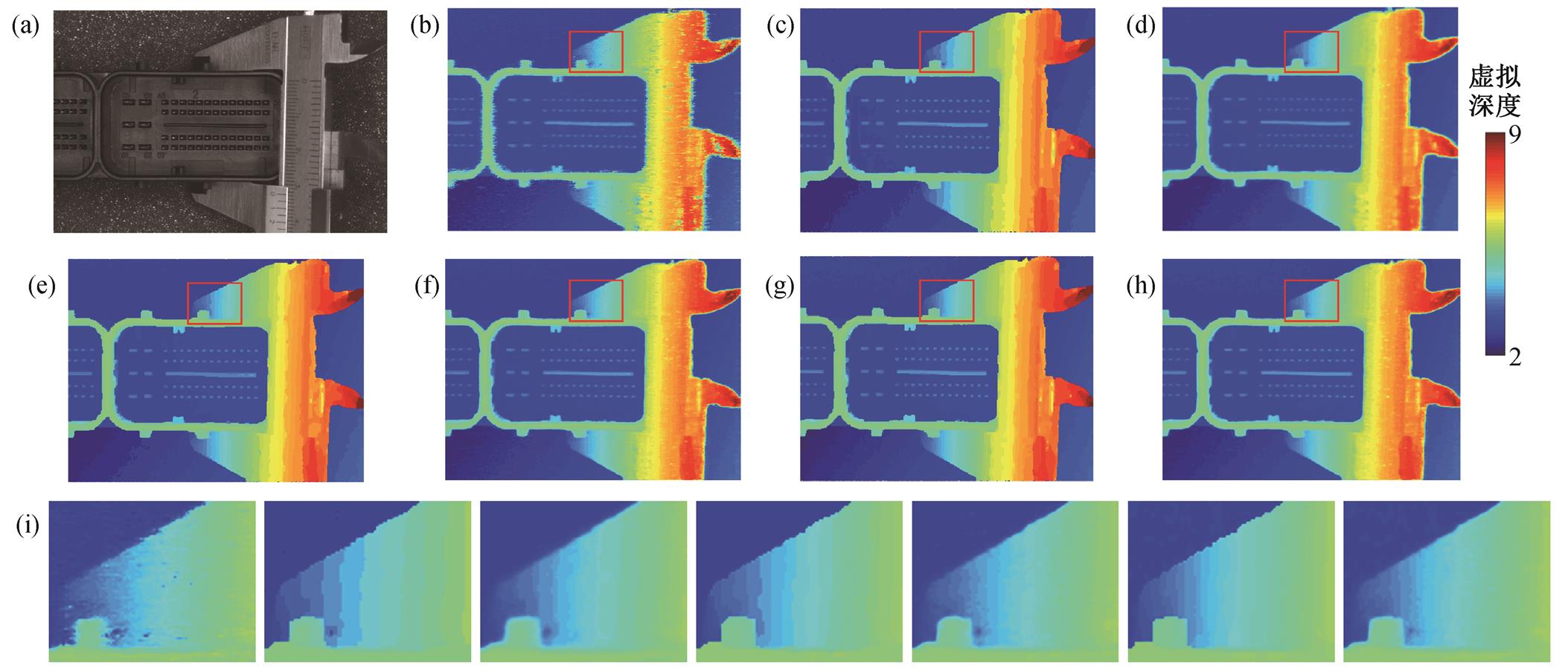
3类深度图分别建立在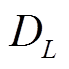 为30, 50, 70的CV上, 对比结果如图7所示。图7(b)中的结果为WTA深度图, 可以看到其中包含很多噪点, 但深度分布是连续的。用全局优化得到的深度图(图7(c), (e)和(g))可以消除这些噪点, 但是深度信息明显离散, 具有一定的阶梯性, 从放大的图像(图7(i))可以明显看到这种离散性。经过MRFsP优化后的结果(图7(d), (f)和(h))既可以消除噪点信息, 也能保持深度图的连续性。
为30, 50, 70的CV上, 对比结果如图7所示。图7(b)中的结果为WTA深度图, 可以看到其中包含很多噪点, 但深度分布是连续的。用全局优化得到的深度图(图7(c), (e)和(g))可以消除这些噪点, 但是深度信息明显离散, 具有一定的阶梯性, 从放大的图像(图7(i))可以明显看到这种离散性。经过MRFsP优化后的结果(图7(d), (f)和(h))既可以消除噪点信息, 也能保持深度图的连续性。
为了进一步对比, 本文以DL=70的深度图作为参考影像, 对图(d), (f)和(h)进行相减操作, 并将差值归一化到[0,1], 差值图像如图8所示。可以看出, 经过MRFsP优化后, 深度图的主要差异只体现在边缘地区。利用DL=50计算得到的深度图已经趋近于DL=70的深度图, 因此在深度计算中选择DL=50已经可以满足要求。
表1 本文方法的计算参数
Table 1 Parameters used in the proposed method

图6 白光影像
Fig. 6 White image
(a)彩色全聚焦影像; (b)连续的WTA投影深度图; (c)全局优化的深度图(DL=30); (d)利用(c)融合之后的深度图; (e)全局优化的深度图(DL=50); (f)利用(e)融合之后的深度图; (g)全局优化的深度图(DL=70); (h)利用(g)融合之后的深度图; (i)红色方框中放大的影像, 顺序从(b)到(h)
图7 离散深度信息优化
Fig. 7 Concrete depth value refinement
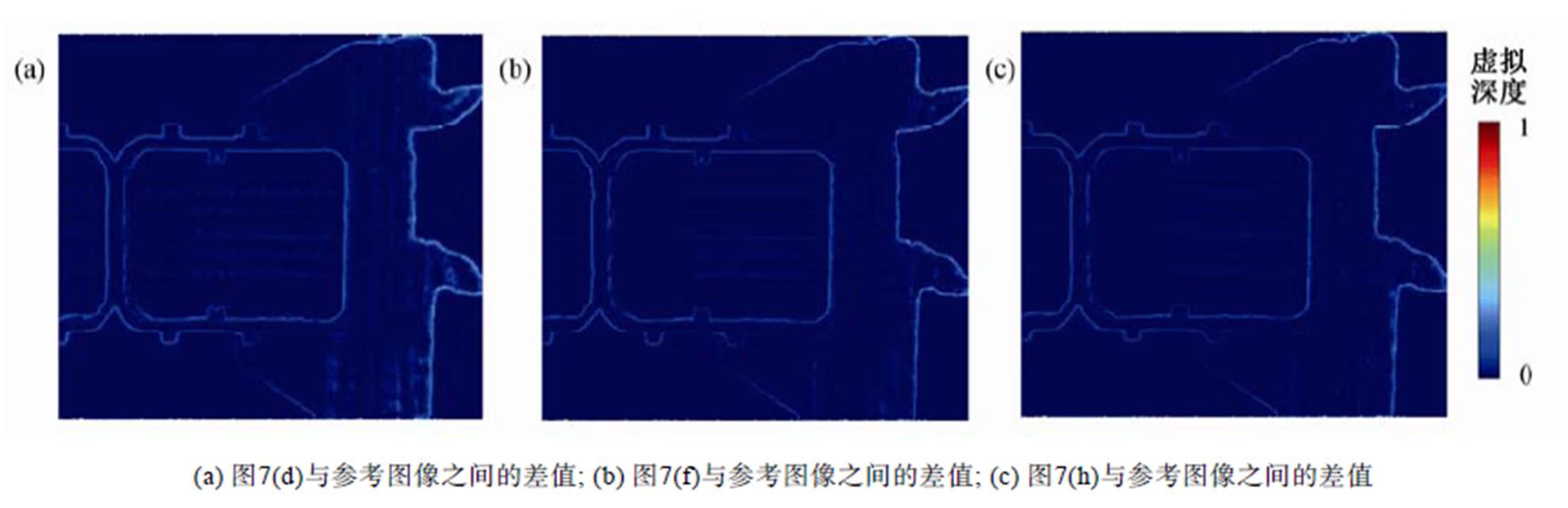
图8 深度差值图
Fig. 8 Difference map between refined depth map and the seventy-label depth map, and the difference is normalized
本节使用4组数据进行深度计算, 并与文献[24]的基于微透镜的优化方法进行对比, 结果如图9~12所示。利用基于微透镜进行局部优化的方法得到的深度图虽然比较平滑, 但是存在错误的深度信息。得益于MRFsP优化, 本文提出的方法能够增加深度图结果的鲁棒性, 且误匹配的深度信息被有效地抑制。图9(f)~12(f)中4个放大的图像中依次是WTA深度图、全局优化深度图、MRFsP优化的深度图以及利用基于微透镜半全局优化的深度图。
图9是对一个机械加工的钢结构件的三维信息提取结果, 对比图9(b)~(e), 可以明显看出, 利用WTA 方法得到的深度图(图9(b))存在较多错误估计的深度信息, 图9(c)和(e)分别利用全局算法和基于微透镜的半全局算法, 有效地减少了深度误估计的区域。从图9(f)的区域放大图可知, 利用半全局优化的深度图存在误估计的区域, 与全局优化结果(图9(c))相比效果较差。利用 MRFsP 融合全局优化以及 WTA 结果的深度图(图9(d)), 既保留了深度信息的连续性, 也能消除绝大部分的误匹配区域。
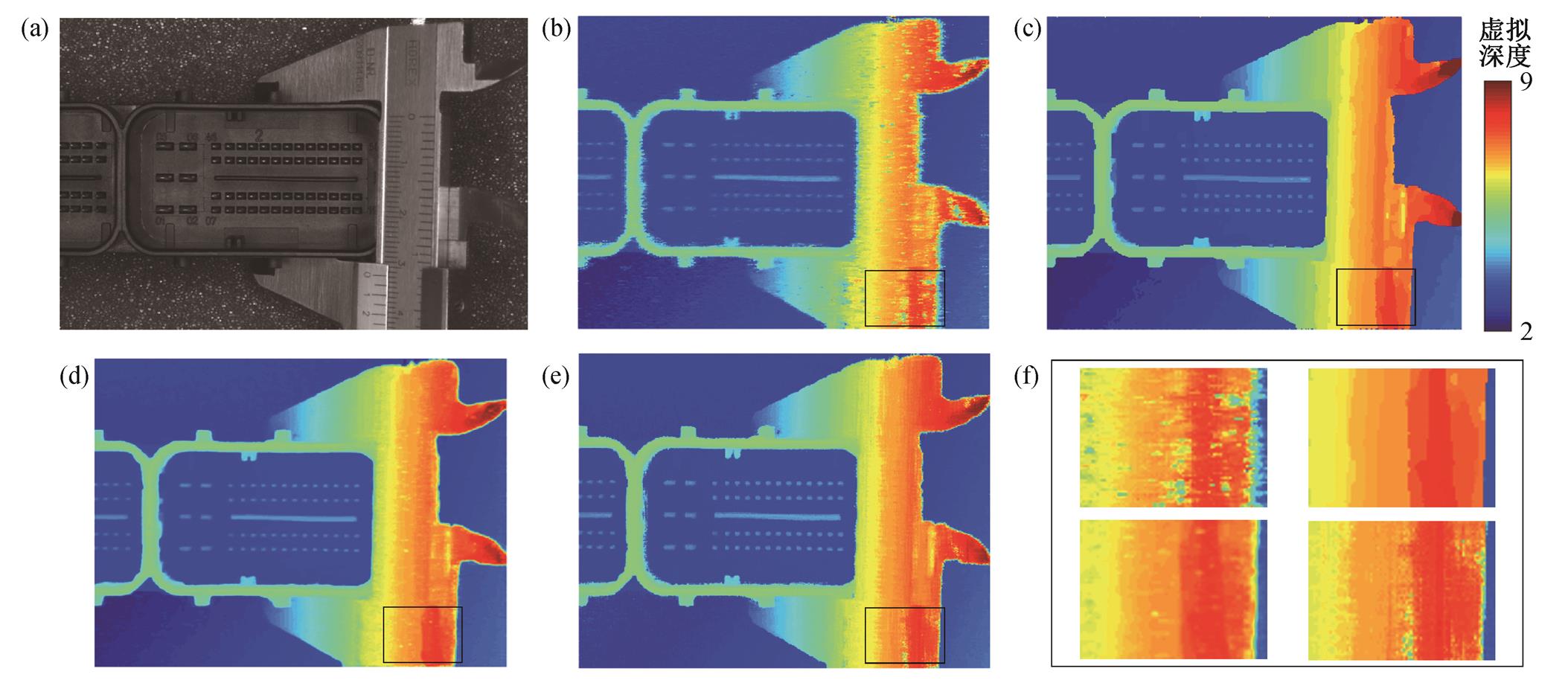
(a)彩色全聚焦影像; (b)投影的 WTA 深度图; (c) DL=50优化的深度图; (d)MRFsP 优化的深度图; (e)文献[24]得到的深度图;
(f)图(b)~(e)中黑色矩形内放大的深度图
图9 钢结构件的深度图
Fig. 9 Depth map for a workpiece
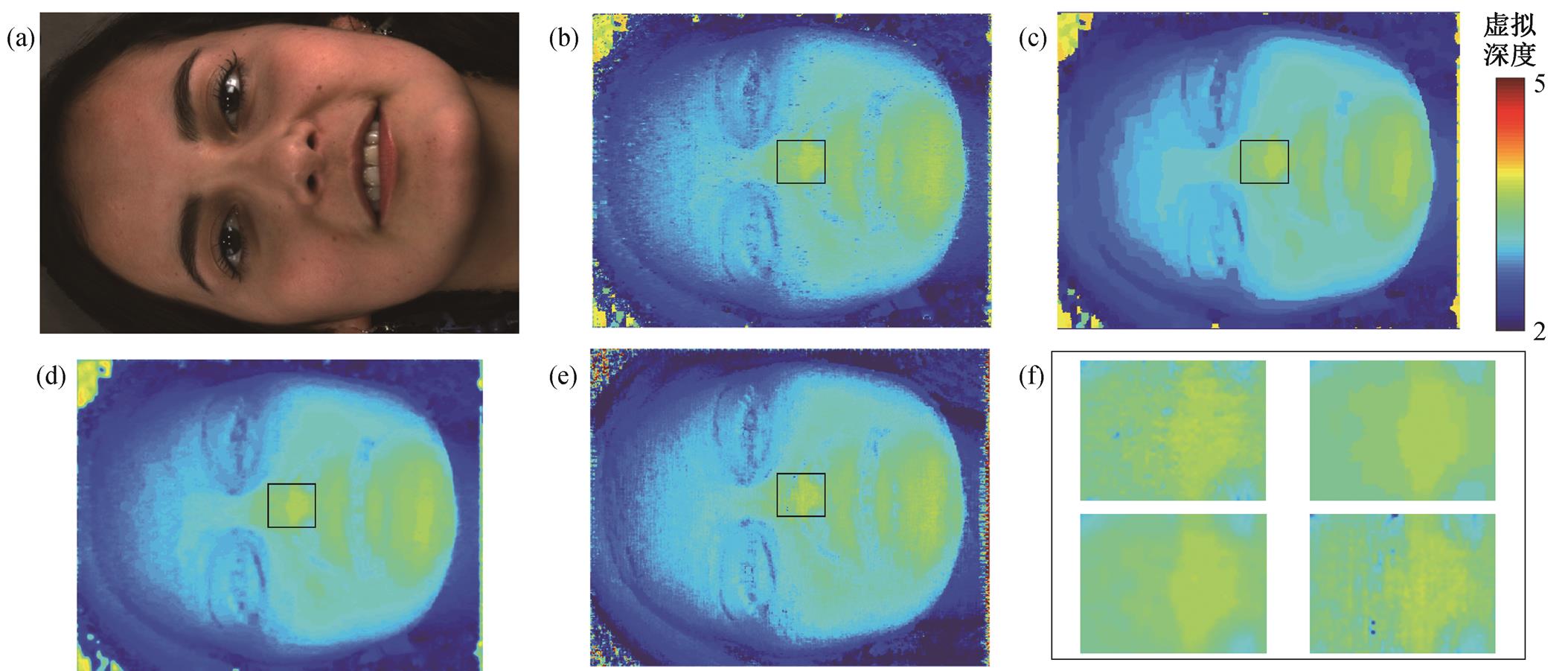
(a)彩色全聚焦影像; (b)投影的WTA深度图; (c) DL=50优化的深度图; (d)MRFsP优化的深度图; (e)文献[24]得到的深度图;
(f)图(b)~(e)中黑色矩形内放大的深度图
图10 人脸的深度图
Fig. 10 Depth map for a woman face

(a)彩色全聚焦影像; (b)投影的WTA深度图; (c) DL=50优化的深度图; (d)MRFsP优化的深度图; (e)文献[24]得到的深度图;
(f)图(b)~(e)中黑色矩形内放大的深度图
图11 水果的深度图
Fig. 11 Depth map for a fruit pile
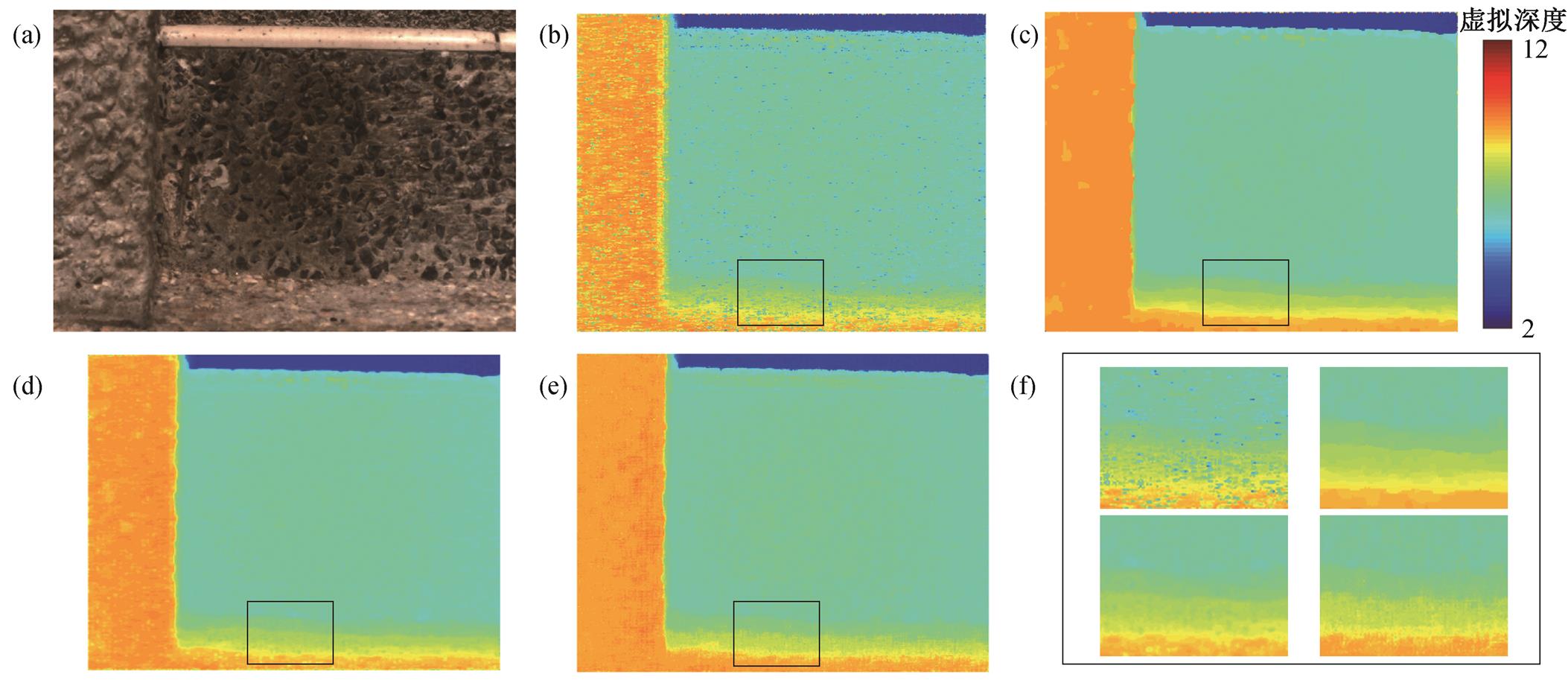
(a)彩色全聚焦影像; (b)投影的WTA深度图; (c) DL=50优化的深度图; (d) MRFsP优化的深度图; (e)文献[24]得到的深度图;
(f)图(b)~(e)中黑色矩形内放大的深度图
图12 墙角的深度图
Fig. 12 Depth map for a wall corner
图10是对人脸进行三维信息提取的结果。可以看出, 图10(b)存在大量的噪点; 图10(c)依赖全局优化可以有效地去除噪点, 但有明显的阶梯感; 利用基于微透镜的半全局优化算法得到的深度图(图10 (e))依然存在深度的误匹配点, 特别是对鼻子部位的深度估计。通过对比图10(f)的细节, 可以看出, 利用 MRFsP 方法融合得到的深度图可以保持与全局优化算法一样的效果, 且阶梯感明显降低。
图11是对水果进行三维信息提取的结果。从图11(f)可以看出, 利用基于微透镜的半句全局优化与利用 WTA 结果计算得到的深度图均包含明显的误估计点, 可知在此场景下, 基于微透镜的半全局优化不能有效地降低深度误估计, 而利用全局优化则有效地优化了误估计点。对比图11(f)的细节可知, 利用 MRFsP 方法得到的深度图继承了全局优化的优势, 同时避免了全局优化中代价的离散性。
图12是对墙角进行三维信息提取的结果。由于该场景下墙角的纹理信息丰富, 基于微透镜的半全局优化(图12(e))和利用全局优化(图12(c))均能很好地避免深度误估计, 但是WTA方法得到的深度图依然有很强的噪声。对比图12(f)的细节可知, 利用MRFsP方法融合全局优化后, 误估计区域得到极大的抑制, 同时全局优化的离散性得到改善。
本文探索了一种全局优化并获得连续深度图的方法。由于全光相机的结构与传统双目立体系统不同, 所以在进行深度计算时, 对初始的CV, 需用虚拟深度决定CV的高度离散量DL。为了提高全局优化的鲁棒性, 本文将代价信息投影到像方空间构建新的CV。此外, 为了解决全局优化只能获得离散深度图的问题, 在基于微透镜进行深度计算的同时保留WTA深度图, 并将该深度图同样投影到像方空间, 最终采用MRFsP优化获得既连续又鲁棒性好的深度图。
为了验证本文方法, 我们对不同代价离散量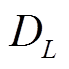 下获取的全局优化结果进行分析, 发现利用MRFsP进行优化的深度图可以用较小的
下获取的全局优化结果进行分析, 发现利用MRFsP进行优化的深度图可以用较小的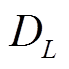 获得较好的连续性。与基于微透镜的半全局优化[24]方法对比发现, 本文提出的方法在钢结构件、人脸、水果和墙角等4种常见场景下均能取得鲁棒性较好的深度结果。在场景纹理信息较弱的情况下, 基于微透镜的半全局优化方法获得的深度图包含大量的误估计点。值得注意的是, 全光相机目前适用于近距离摄影测量, 当距离增大时, 深度信息估计的精度会降低[27], 因此本文选择的场景均属于近景摄影测量。
获得较好的连续性。与基于微透镜的半全局优化[24]方法对比发现, 本文提出的方法在钢结构件、人脸、水果和墙角等4种常见场景下均能取得鲁棒性较好的深度结果。在场景纹理信息较弱的情况下, 基于微透镜的半全局优化方法获得的深度图包含大量的误估计点。值得注意的是, 全光相机目前适用于近距离摄影测量, 当距离增大时, 深度信息估计的精度会降低[27], 因此本文选择的场景均属于近景摄影测量。
参考文献
[1]Yang P, Wang Z, Yan Y, et al. Close-range photo-grammetry with light field camera: from disparity map to absolute distance. Appl Opt, 2016, 55(27): 7477–7486
[2]Georgiev T G, Lumsdaine A. Superresolution with plenoptic 2.0 cameras // Proceedings of the Signal Recovery and Synthesis, Optical Society of America. California, 2009: STuA6
[3]Ng R. Digital light field photography [D]. Palo Alto: Stanford University, 2006
[4]Dansereau D, Pizarro O, Williams S. Decoding, cali-bration and rectification for lenselet-based plenoptic cameras. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2013, 9(4): 1027–1034
[5]Bok Y, Jeon H G, Kweon I S. Geometric calibration of micro-lens-based light-field cameras using line features. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2017, 39(2): 287–300
[6]Bishop T E, Favaro P. Full-resolution depth map esti-mation from an aliased plenoptic light field // Pro-ceedings of the 10th Asian conference on Computer vision: Volume Part II. Queenstown: 2010: 186–200
[7]Jeon H G, Park J, Choe G, et al. Accurate depth map estimation from a lenslet light field camera // Pro-ceedings of the Computer Vision and Pattern Recog-nition (CVPR). Boston, 2015: 1547–1555
[8]Navarro J, Buades A. Reliable light field multiwin-dow disparity estimation // Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP).Phoenix, 2016: 1449–1453
[9]Roberts W, Thurow B S. Correlation-based depth esti-mation with a plenoptic camera. AIAA Journal, 2017, 55(2): 1–11
[10]Yu Z, Guo X, Lin H, et al. Line assisted light field triangulation and stereo matching // Proceedings of the IEEE International Conference on Computer Vision.DarlingHarbour, 2013: 2792–2799
[11]Criminisi A, Kang S B, Swaminathan R, et al. Extrac-ting layers and analyzing their specular properties using epipolar-plane-image analysis. Computer Vision and Image Understanding, 2005, 97(1): 51–85
[12]Tao M, Hadap S, Malik J, et al. Depth from combining defocus and correspondence using light-field cameras // Proceedings of the IEEE International Conference on Computer Vision.DarlingHarbour,2013: 673–680
[13]Wang T C, Efros A A, Ramamoorthi R. Depth estimation with occlusion modeling using light-field cameras. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(1): 2170–2181
[14]Wanner S, Goldluecke B. Globally consistent depth labeling of 4D light fields. Computer Vision & Pat-tern Recognition, 2012, 23 (10): 41–48
[15]Zhang S, Sheng H, Li C, et al. Robust depth estima-tion for light field via spinning parallelogram operator. Computer Vision and Image Understanding, 2016, 145 (C): 148–159
[16]Zhang Y, Lv H, Liu Y, et al. Light-field depth esti-mation via epipolar plane image analysis and locally linear embedding. IEEE Transactions on Circuits & Systems for Video Technology, 2017, 27(4): 739–747
[17]Kolmogorov V, Zabih R. Multi-camera scene recon-struction via graph cuts // Proceedings of the 7th Eu-ropean Conference on Computer Vision: Part III. Lon-don, 2002: 82–96
[18]Kolmogorov V, Zabin R. What energy functions can be minimized via graph cuts?. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2004, 26(2): 147–59
[19]Felzenszwalb P F, Huttenlocher D P. Efficient belief propagation for early vision. International Journal of Computer Vision, 2006, 70(1): 41–54
[20]Yang Q, Wang L, Yang R. Stereo matching with color-weighted correlation, hierarchical belief propagation, and occlusion handling. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2009, 31(3): 492–504
[21]Georgiev T, Lumsdaine A. Focused plenoptic camera and rendering. Journal of Electronic Imaging, 2010, 19(2): 021106
[22]Zeller N, Quint F, Stilla U. Calibration and accuracy analysis of a focused plenoptic camera. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2014, 2(3): 205–212
[23]Zeller N, Quint F, Stilla U. Depth estimation and camera calibration of a focused plenoptic camera for visual odometry. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 118: 83–100
[24]Fleischmann O, Koch R. Lens-based depth estimation for multi-focus plenoptic cameras // Proceedings of the German Conference on Pattern Recognition. Mün-ster, 2014: 410–420
[25]Hirschm H. Accurate and efficient stereo processing by semi-global matching and mutual information. Proceedings of the Computer Vision and Pattern Recognition, 2005, 2(2): 807–814
[26]Perwass C, Wietzke L. Single lens 3D-camera with extended depth-of-field // Human Vision and Elec-tronic Imaging XVII, International Society for Optics and Photonics. San Diego, 2012: 829108
[27]Sardemann H, Maas H G. On the accuracy potential of focused plenoptic camera range determination in long distance operation. ISPRS Journal of Photogram-metry and Remote Sensing, 2016, 114: 1–9
[28]Strobl K H, Lingenauber M. Stepwise calibration of focused plenoptic cameras. Computer Vision and Image Understanding, 2016, 145(C): 140–147
[29]Janoch A, Karayev S, Jia Y, et al. A category-level 3D object dataset: putting the kinect to work // Procee-dings of the IEEE International Conference on Com-puter Vision. Washington, DC, 2011: 1168–1174
[30]Kanade T, Okutomi M. A stereo matching algorithm with an adaptive window: theory and experiment. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1994, 16(9): 920–932
Microlens-Based Continuous Depth Map Estimation with the Plenoptic Camera
YANG Peng, YAN Lei, ZHAO Shoujiang, YAN Yizhen, ZHAO Hongying†
School of Earth and Space Science, Peking University, Beijing 100871; † Corresponding author, E-mail: zhaohy@pku.edu.cn
Abstract Because the micro lenses segment the plenoptic image physically, the global optimization method is hard to be applied on the depth estimation progress and the WTA (winner-take-all) method based on the multi-baseline system will generate very coarse but continuous depth map. The global optimizations method always generate robust but concrete depth map when using multi-label technique. So cost projection strategy by directly processing the lenslet plenoptic image is proposed to build the cost volume based on the projection image for global optimization. A method based on Markov Random Fields Propagation (MRFsP) is adopted by merging the modified WTA depth result to refine the concrete depth map. For validation, the depth map built with the proposed method is compared with the microlens-based optimization result, and the result shows obvious improvement.
Key words plenoptic image; depth estimation; Markov Random Fields Propagation (MRFsP)
中图分类号 TH74
doi: 10.13209/j.0479-8023.2018.053
国家重点研发计划(2017YFB0503003)资助
收稿日期: 2017-12-01;
修回日期: 2018-01-14;
网络出版日期: 2018-08-31