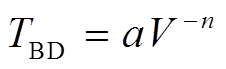, (1)
其中, V表示作用在栅氧化层两端的电压, 参数a和n是通过测试数据提取的固定常数。通过式(1), 在应力电压V0作用下, 栅氧化层对应的失效时间TBD0可以与电压V1作用下对应的失效时间TBD1相关联:
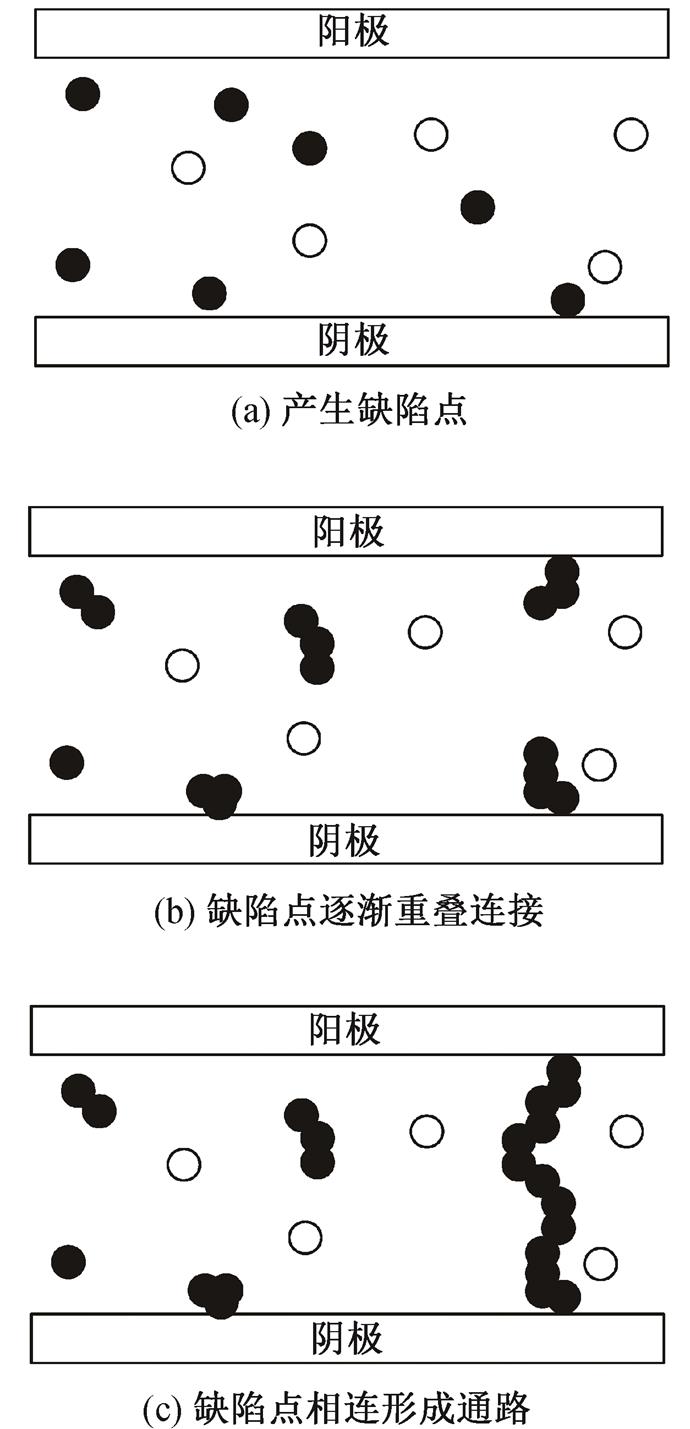
图1 栅氧化层缺陷点的产生导致渗流通路的形成
Fig. 1 Generation of the defects in the gate oxide forms the percolation path
曹鑫1 曹健1,† 王艺泽2 王源2 张兴1,2,†
1.北京大学软件与微电子学院, 北京 102600; 2.北京大学微电子学研究院, 北京 100871; † 通信作者, E-mail: caojian@ss.pku.edu.cn (曹健), zhx@pku.edu.cn (张兴)
摘要 提出一种改进的基于人体静电冲击模型(Human Body Model, HBM)应力的瞬态功率模型。利用HSPICE仿真软件, 模拟MOS管遭受的HBM应力, 得到对应的等效直流电压。HBM电路的预充电电压与MOS管对应的等效直流电压值的散点图表明, 两者保持线性关系, 并通过拉普拉斯变化得到证明。与现有的瞬态功率模型相比, 改进后的模型降低了在HBM应力作用下的计算复杂度, 可以更加简便地从统计学上预测MOS管栅氧击穿的发生, 给HBM冲击作用下MOS管栅氧化层可靠性的评估提供参考。
关键词 静电放电; 瞬态功率模型; 栅氧击穿; 人体静电冲击模型
静电放电(electrostatic discharge, ESD)指带有不同静电电势的物体发生能量转移, 直到它们具有相同的电势或者连接断开。ESD瞬态电流脉冲有1~200ns的持续时间, 并产生1A(甚至超过50A)的电流振幅[1]。如果不采取特别的保护方法, 一定的临界ESD瞬态电流脉冲会直接影响系统和器件的可靠性。半导体工业中, 芯片失效主要由ESD冲击导致[2]。芯片遭受ESD冲击后, 其功能会失效, 并且这种失效是不可逆的。随着集成电路的特征尺寸不断变小, 栅氧化层的厚度不断变薄, 导致芯片抵御ESD的能力不断降低, ESD冲击是造成栅氧化层击穿[3]的主要原因。因此, 预测芯片的失效对评估集成电路器件的可靠性和提供ESD保护方案具有非常重要的意义。
关于MOS管栅氧化层失效机制, 一般认为是在ESD应力作用下, 栅氧化层内部产生不可恢复的缺陷点, 可以将每一个缺陷点视为空位点, 这些空位点可以在栅氧化层内部捕获载流子。如图1(a)所示, 栅氧化层受到ESD应力冲击, 在内部随机产生缺陷点。随着缺陷点逐渐增多, 栅氧化层内部相邻的缺陷点逐渐重叠并连接(图1(b)), 最终在正负极之间形成一条通路, 导致栅氧化层的击穿[4–5](图1(c))。
栅氧化层的可靠性可以用ESD冲击作用下发生击穿的时间TBD表达。通过经验公式指数定律[6], 栅氧化层击穿时间与受到的电压关系如下:
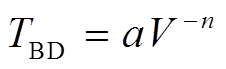, (1)
其中, V表示作用在栅氧化层两端的电压, 参数a和n是通过测试数据提取的固定常数。通过式(1), 在应力电压V0作用下, 栅氧化层对应的失效时间TBD0可以与电压V1作用下对应的失效时间TBD1相关联:
图1 栅氧化层缺陷点的产生导致渗流通路的形成
Fig. 1 Generation of the defects in the gate oxide forms the percolation path
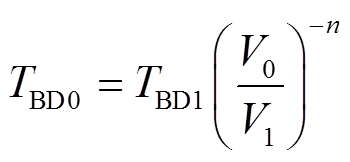。 (2)只有当 ESD 冲击作用时间小于 TBD 时, 式(2)才成立。因此, 在冲击作用时间小于 TBD 时, 由式(2)可以得出, 一种应力对氧化层的冲击可等效为另一种应力在一定时间内对氧化层的冲击。由于栅氧击穿后不可恢复, 所以可以将作用在栅氧化层的应力电压的总体效果视为每个时间段应力效果的总和。将瞬态电压划分为许多小的时间段, 将每个时间段内的电压视为常数, 则电压 Vk作用时间段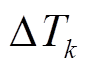
与直流电压 V0作用时间段∆Teff对氧化层造成的冲击相同:
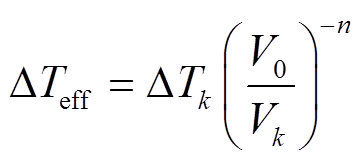。 (3)
通过对冲击作用的时间段内积分[7], 可以得到电压 V0对应的等效直流电压时间Teff:
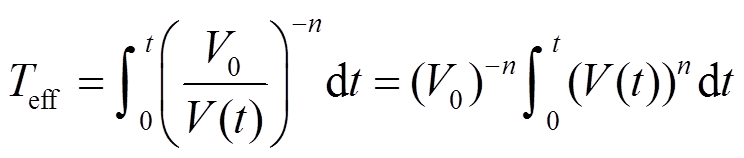。 (4)参数 n 为指数定律的常数。设定Teff等于给定的失效时间TBD0, 直流电压V0为对应的等效直流电压Veff, 则在任意瞬态电压作用时间段t内, 对应的等效直流电压为
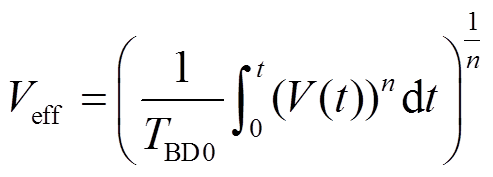。 (5)
Veff即为瞬态电压对应的等效直流电压, 当电压 Veff在时间段 TBD0内作用于氧化层时, 其对栅氧化层造成的损害与瞬态电压作用下相同。因此, 通过瞬态功率模型(式(5)), 可以从统计学上分析任意瞬态电压作用下栅氧化层的可靠性。
现有的瞬态功率模型虽然解决了评估栅氧化层击穿的问题, 但是式(5)中参数 n 在高电压下取值30, 低电压下取值44[8], 相应的等效直流电压的计算复杂度较高。
HBM可以用来模拟带静电的人体触摸芯片管脚后, 人体与芯片管脚之间发生能量转移的过程。图2为HBM电压波形发生电路及其对应的拉普拉斯变换电路。MOS管电压在1~6V之间, 其等效电容变化非常小, 因此将MOS管等效为电容。
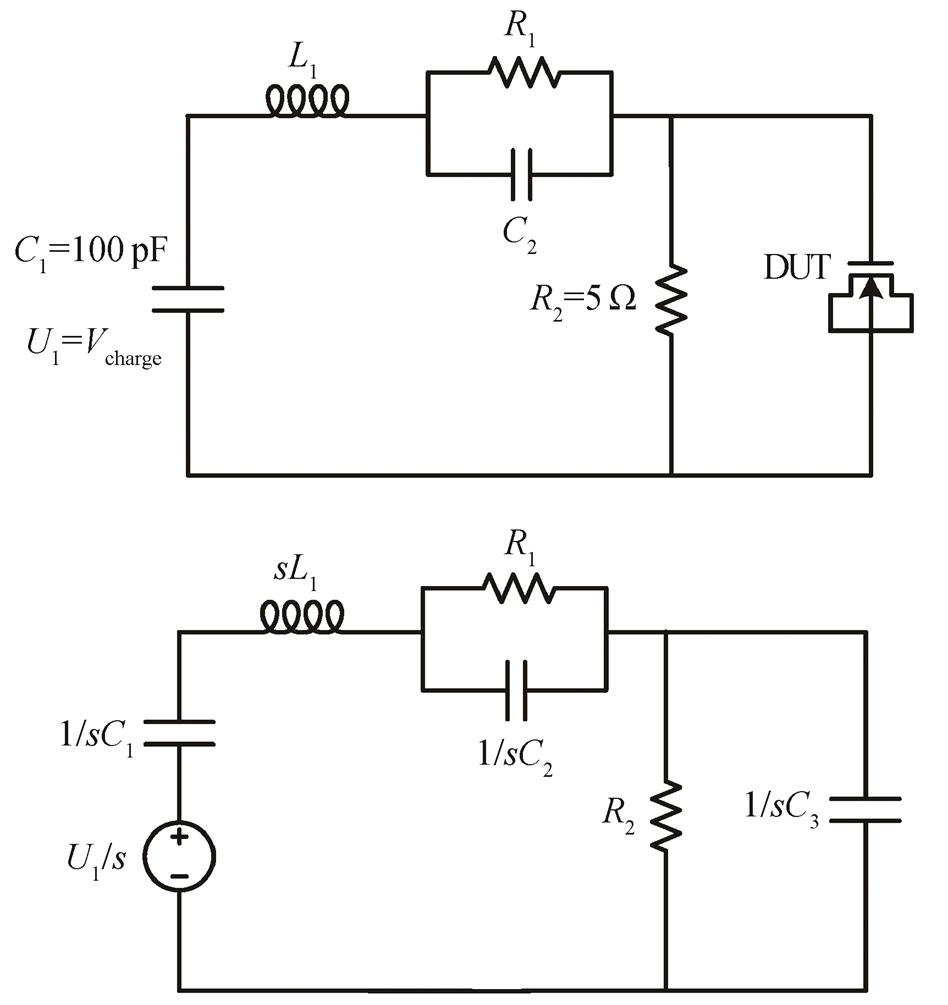
图2 传统HBM发生电路及其拉普拉斯变换
Fig. 2 Traditional circuit model generating HBM waveform and its Laplace transform
通过图2的HBM生成电路对应的拉普拉斯变换[9], 可以在频域计算得到MOS管两端对应的电压:
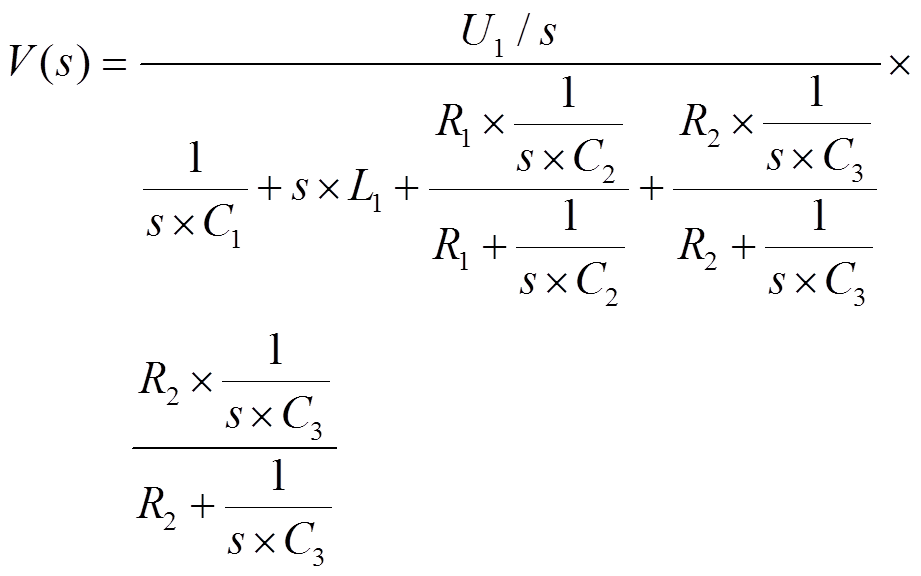
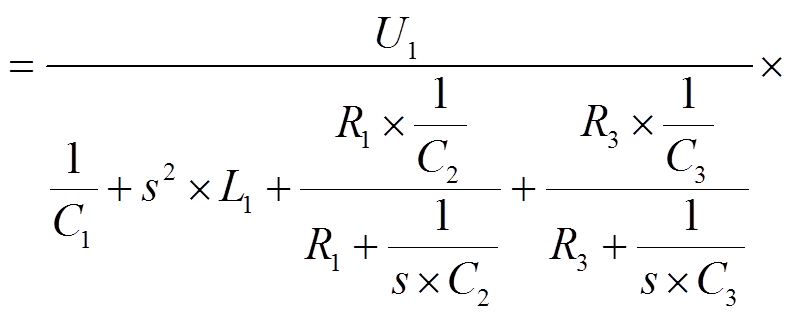
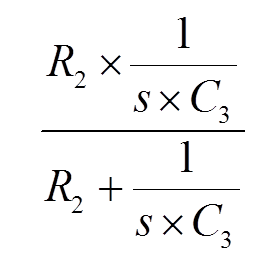
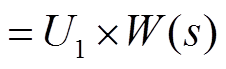。 (6)
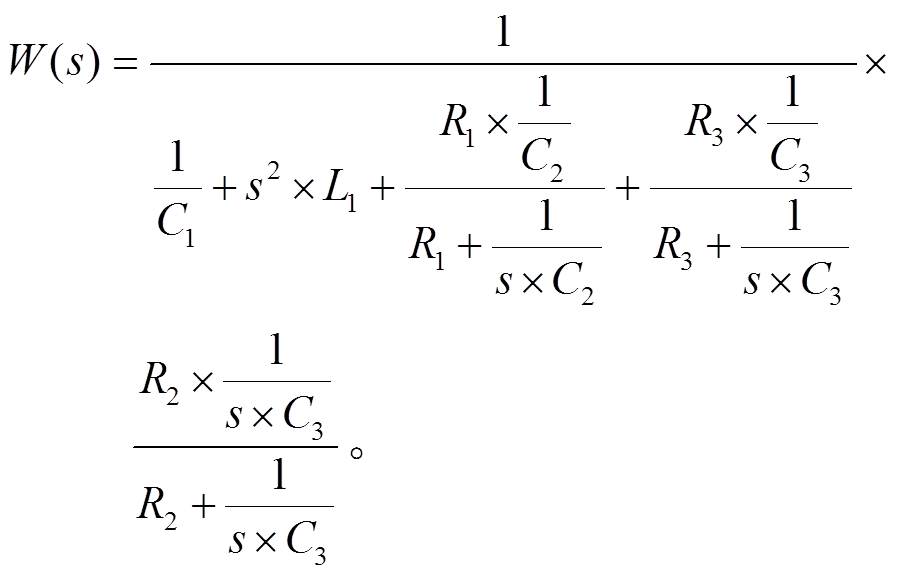(7)
由式(6)可得到MOS管时域对应的电压:
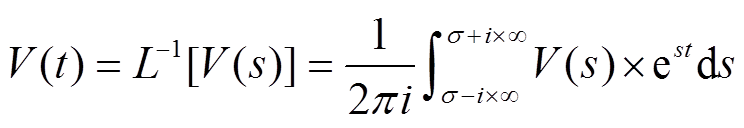
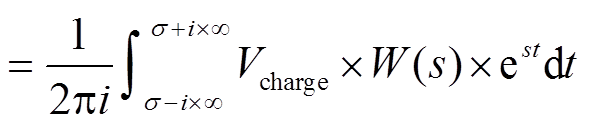
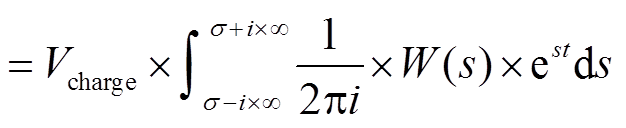
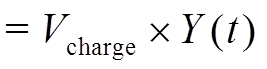, (8)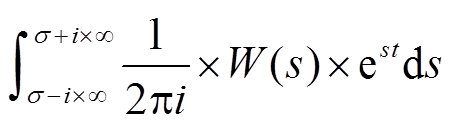
是t的函数, 因此可用Y(t)替换。根据式(5), MOS管两端对应的等效直流电压为
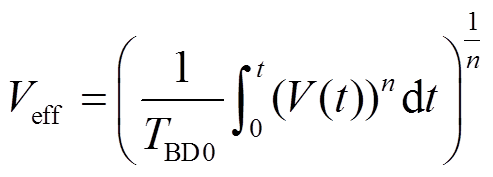
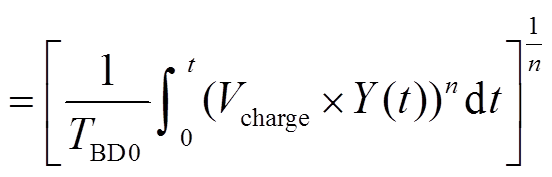
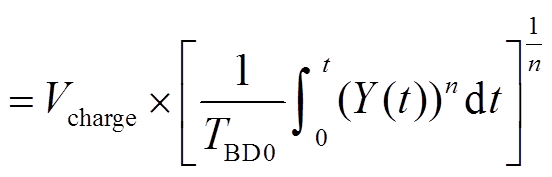, (9)
其中, t为HBM电压作用在MOS管两端的时间, Y(t)为t的函数, 参数TBD0为常数。因此, 在式(9)中, 当冲击时间一定时, 方括号中的计算结果为常数。
综上所述, 可以得出结论: 在HBM应力作用下, HBM生成电路的充电电压与MOS管两端对应的等效直流电压为线性关系。根据式(9), 在HBM应力作用下, 统计层面评估栅氧化层可靠性的复杂度大大降低。
基于65nmCMOS工艺, 利用HSPICE[10]模拟HBM应力作用下, 在HBM生成电路加载不同的充电电压Vcharge, 通过式(9)得到 MOS 管两端对应的等效直流电压。图3为不同的失效时间对应的结果。
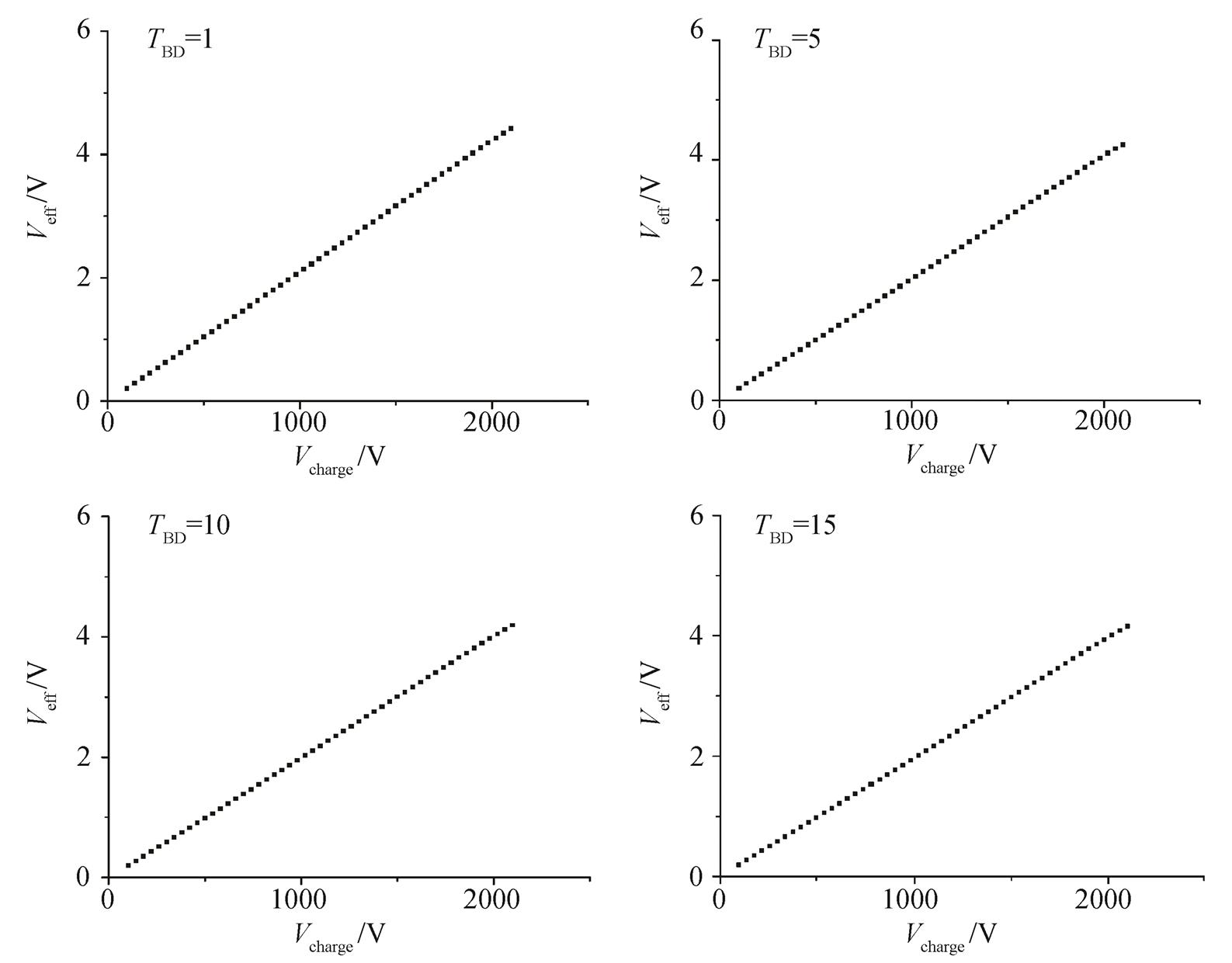
图3 HBM生成电路充电电压Vcharge与MOS管等效直流电压Veff在不同失效时间下的关系
Fig. 3 Vcharge of the HBM generating circuit and the Veff across the MOS gate oxide under different TBD
从图3可以看出, 当预充电电压 Vcharge在2kV以下时, Veff与 Vcharge基本上保持线性关系, 虽然不同栅氧化层发生失效的时间不同, 但 HBM 生成电路电压与栅氧化层的等效直流电压仍然保持一定的线性关系。在图 4 中, 当 Vcharge电压为2kV 时, MOS 管两端对应的等效直流电压为4V。模拟结果与文献[11]在同一参数下的实验结果相同。文献[11]基于瞬态功率模型, 由 MOS 管两端电压计算得到对应的等效直流电压, 在实验中, 一旦 MOS 管两端电压发生变化, 则需要重新计算其对应的等效电压, 且计算过程复杂。现有的瞬态功率模型中, MOS 管电压与等效直流电压没有建立直观的联系, 在实验中难以预判 MOS 管等效直流电压的变化。从图3和4可以看出, 建立的 HBM 充电电压 Vcharge与 MOS 等效直流电压基本上呈线性变化, 并且能够更直观地对等效直流电压的变化做预判, 更好地预测 MOS 管栅氧击穿的发生。
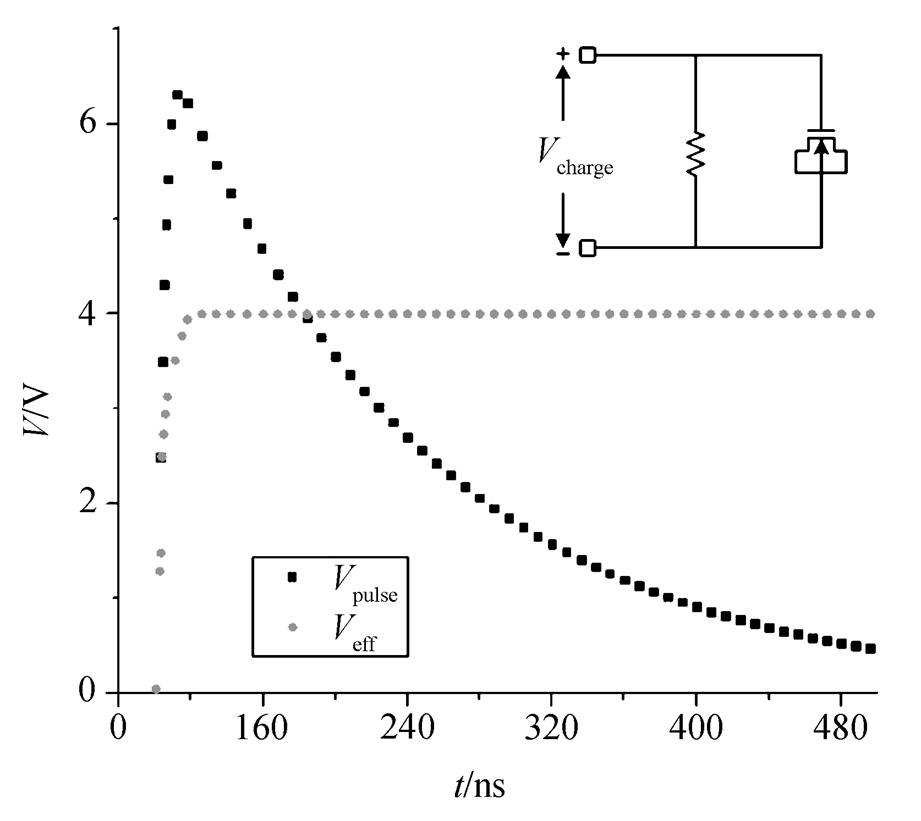
图4 HBM应力作用下MOS管两端瞬态电压Vpulse和等效直流电压Veff(V=2 kV, R=5 Ω)
Fig. 4 Vpluse and Veff across the MOS for an HBM stress (V=2 kV, R=5 Ω)
本文提出一种改进的基于人体静电冲击模型应力的瞬态功率模型。利用HSPICE仿真软件在HBM生成电路加载预充电电压, 在MOS管两端得到对应的电压。基于现有的瞬态功率模型, 计算得到MOS管两端对应的等效直流电压。通过将HBM生成电路的预充电电压值与MOS管对应的等效直流电压值做散点图, 表明两者保持线性关系。为证明其线性关系, 将HBM生成电路通过拉普拉斯变换转换到频域, 将频域内MOS管电压与预充电电压关系通过拉普拉斯反变换, 得到时间域两者之间的物理关系, 并将瞬态功率模型带入, 得到MOS管等效直流电压与预充电电压之间为线性函数关系, 推导证明了两者之间的线性关系。瞬态功率模型通过将波形形状不规则的波形转换为等效的直流电压, 将加载在MOS管两端的瞬态电压转换为直流电压, 简化了对MOS管栅氧化层击穿的评估。改进后的模型可在统计学上对ESD冲击作用下MOS管栅氧化层可靠性的评估提供参考。相对于现有的瞬态功率模型, 改进后的模型降低了在HBM应力作用下的计算复杂度, 从统计学上可以更简便地预测MOS管栅氧击穿的发生。
参考文献
[1]Semenov O, Sarbishaei H, Sachdev M. ESD protect-tion device and circuit design for advanced CMOS technologies. Waterloo: Springer, 2008
[2]Ker M D, Chen S H, Chuang C H. ESD failure mechanisms of analog I/O cells in 0.18-μm CMOS technology. IEEE Transactions on Device and Mate-rials Reliability, 2006, 6(1): 102–111
[3]Zhou Y Z, Weyl T, Hajjar J J, et al. ESD simulation using compact models: from I/O cell to full chip // IEEE Conference on Electron devices and solid-state circuits.Tainan, 2007: 53–8
[4]Degraeve R, Groeseneken G, Bellens R, et al. New insights in the relation between electron trap genera-tion and the statisticalproperties of oxide breakdown. IEEE Transactions on Electron Devices, 1998, 45(4): 904–911
[5]Stathis J H. Percolation models for gate oxide breakdown. J Appl Phys, 1999, 86(10): 5757–5766
[6]Wu E Y, Aitken J, Nowak E, et al. Voltage-dependent voltage-acceleration of oxide breakdown for ultra-thin oxides // Electron Devices Meeting. Hong Kong, 2000: 541–544
[7]Bin W, Suehle J S, Vogel E M, et al. Time-dependent breakdown of ultrathin SiO2 gate dielectrics under pulsed biased stress. Electron Dev Lett, 2001, 22(5): 224–226
[8]Wu E Y, Sune J, Vollertsen R. Comprehensive physics-based breakdown model for reliability assess-ment of oxides with thickness ranging from 1 nm up to 12 nm // IEEE International Reliability Physics Sym-posium. Montreal, 2009: 708–717
[9]Cao Jian, Wang Yize, Wang Yuan, et al. A novel SPICE circuit model of electrostatic discharge (ESD) generator. IEICE Electronics Express, 2016, 13(9): 1–8
[10]Cao Jian, Xu Jingya, Wang Yuan, et al. A compact SCR model using advanced BJT models and standard SPICE elements. Science China-Information Sciences, 59(10): 109302
[11]Miao M, Zhou Y Z, Javier A, et al.Compact failure modeling for devices subject to electrostatic discharge stresses —a review pertinent to CMOS reliability simulation. Microelectronics Reliability, 2015, 55(1): 15–23
Improvements on Transient Power Law Model under HBM Stress
CAO Xin1, CAO Jian1,†, WANG Yize2, WANG Yuan2, ZHANG Xing1,2,†
1. School of Software and Microelectronics, Peking University, Beijing 102600; 2. Key Laboratory of Microelectronic Devices and Circuits (MOE), Institute of Microelectronics, Peking University, Beijing 100871; † Corresponding authors, E-mail: caojian@ss.pku.edu.cn (CAO Jian), zhx@pku.edu.cn (ZHANG Xing)
Abstract An improved model is proposed based on the transient power law model under Human Body Model (HBM) stress. This model can predict the gate oxide breakdown statistically under HBM stress. Through HSPICE simulation tool, the corresponding DC effective voltage on the MOS can be calculated. The scatter chart of the pre-charge voltage of the HBM circuit with the effective DC voltages of the MOS shows a linear relationship. Using the Laplace transform, the linear relationship is proved. Compared with the existing transient power law model, the improved model reduces the computational complexity under the HBM stress and is easier to predict the MOS gate oxide breakdown statistically. The proposed model provides an important reference for the evaluation of the reliability of the MOS gate oxide under the impact of HBM.
Key words electrostatic discharge (ESD); transient power law model; gate oxide breakdown; human body model (HBM)
中图分类号 TP333
doi: 10.13209/j.0479-8023.2018.044
国家自然科学基金(61774005)和北京市自然科学基金(4162030)资助
收稿日期: 2017-11-09;
修回日期: 2018-03-01;
网络出版日期: 2018-09-07