曹露青 胡天跃†
北京大学地球与空间科学学院, 北京100871; † 通信作者, E-mail: tianyue@pku.edu.cn
摘要 采用基于用传统方法获取的海上单分量地震资料, 估算出同一位置速度的垂直分量(伪速度), 再与单分量压力数据联合, 达到压制鬼波的目的。将稀疏约束的反卷积方法作为鬼波压制的关键环节, 使得在浅海环境下, 由海水表面引起的检波器端上、下行波干涉产生的陷波问题得到改善, 同时低频能量得到增强, 提高了数据的分辨率。该方法可用于海上单分量压力数据的再处理, 拓宽数据的频带范围。
关键词 浅海; 伪速度; 稀疏约束; 鬼波压制
在海洋地震勘探领域, 数据采集工作的目标之一是获得较宽频带的地震数据。宽频带的地震数据中, 低频、高频成分丰富, 其中低频成分(从 1 Hz起)可以提高信号的穿透力, 增强数据分辨率, 对地球深部复杂构造的精准成像、全波形反演以及波阻抗反演的稳定性有重要作用[1–3]。宽频带数据可以提高峰值旁瓣振幅比, 为薄互层等构造的成像提供有效的原始数据。
在传统的海洋地震数据采集中, 保护数据中的低频信息, 从而得到宽频带数据是很难实现的。影响海洋地震数据频带范围、降低地震资料分辨率的一个主要原因是“鬼波”。通常, “鬼波”被视为震源激发的能量, 经海水–空气不连续界面反射后, 延迟于震源脉冲后的反射波。在震源端, 如果震源激发的能量先向上传播, 经海水表面反射后再向下传播, 称为震源鬼波; 在检波器端, 若从地下反射回来的地震波在被检波器接收之前被海水表面反射, 然后再向下传播至检波器, 则称为检波器鬼波。
经过海水表面反射的“鬼波”与上行波相互干涉,导致地震数据振幅谱上相长相消的“陷波”问题。“陷波点”的存在, 使得地震数据在特定频率处缺失。陷波频率与震源和电缆沉放深度有关, 此外地震波在海水中的传播速度以及在接收端地震波的出射角度对陷波频率也有影响。因此, 鬼波导致多种类型的陷波效应, 降低了海上数据的分辨率, 同时也限制了海上地震勘探采集数据的频带宽度。
长期以来, 压制鬼波被视为海洋地震数据处理中的一个难题。为了消除鬼波的影响, 可以从数据采集和数据处理方法两个方面来考虑。在数据采集方面, 新的技术是垂直放置上、下拖缆来记录波场, 通过对地震资料进行组合处理, 达到消除检波器鬼波的目的[4–8]。Parrack[9]最早提出上、下缆的方法来消除地震波水平传播的影响, 从而增强地震波垂直传播的能量。Brink[10]提出利用上、下缆数据采集方法, 减少海上天气恶劣时海面剧烈波浪对采集数据信噪比的影响。但是, 由于上、下缆数据在 0 Hz处均有陷波, 无法完全消除接收点鬼波的影响[11]。
上、下缆方法在鬼波压制中需要两倍的接收器覆盖同样的传播孔径, 既增加采集成本, 也降低采集效率, 因此发展出变深度拖缆采集技术。与常规的海上水平拖缆不同, 变深度拖缆采集方法是将检波器放置于深度随炮检距加大而增加的斜缆上, 可以记录到不同深度的地震数据。Soubaras[1]提出针对斜缆采集数据消除接收鬼波的处理方法, Souba-ras[12]发展了变深度斜缆叠前多道数据的鬼波压制方法, 并且保留了数据的 AVO (Amplitude variation with offset, 振幅随偏移距的变化)信息。在利用 海上单条拖缆采集拓宽频带压制鬼波方面, 刘春成等[13]提出“犁式”电缆采集技术: 电缆前端接收器的深度随炮检距增加而线性地变大, 到达一定的深度后, 电缆的沉放深度不再发生变化。因此, 该采集装置可以在水下不同深度处记录到地震波场信息, 实现压制鬼波和拓宽地震数据频带的目的。
与传统的海上拖缆采集方法相比, 双检采集技术的不同之处在于增加了记录地震波垂直速度的检波器。利用压力与速度记录数据鬼波极性相反这一特征, 通过对压力与速度数据进行校正、匹配与合并, 达到消除检波器鬼波的目的。双检接收采集技术由Barr等[14]提出, 并应用于海底电缆数据, 用来消除水柱混响。Loewenthal[15]和 Tenghamn 等[16]将双检采集技术应用于拖缆采集中。Carlson 等[17]通过对双检数据进行上、下行波场分离, 达到拓宽频带、提高数据分辨率的效果。Day等[18]针对双检接收采集的实际数据与理想条件下无噪音、无限孔径数据的差异, 通过对速度、检波器深度和空间假频等的误差分析, 提出相应的减弱误差影响的波场分离处理方法。
双检接收采集装备需在同一位置放置速度传感器和压力传感器, 并同时记录两个传感器的数据。与常规的拖缆采集相比, 增加了成本。Teigen 等[19]分析了不同模式的噪音源对拖缆采集的影响, 并指出由于海水流动引起的拖缆机械振动是主要的噪音源, 与压力检波器相比, 记录粒子运动的传感器对拖缆的振动更敏感, 因此降低了采集数据整体的信噪比和可信度。
本文通过对现有的浅海单分量压力数据进行再处理[20–21], 模拟双检采集中的速度垂直分量(简称伪速度)数据, 进而分离出上行波场, 并与原始压力数据进行合并, 得到鬼波压制后的结果, 达到拓宽地震数据频带范围和增强低频信号能量的效果。
考虑图 1 所示的震源在接受面以下的情况, 即接受面与自由表面没有震源。根据格林函数互易定理, 可以将x0处的压力波场表示为
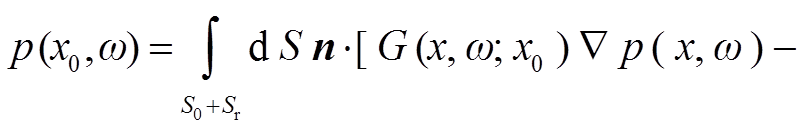
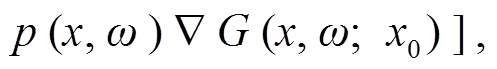 (1)
(1)
p 是用角频率 ω表示的压力波场, n 为边界曲面指向外的单位法向量, G 表示在均匀介质中从接收面Sr的 x 点到 x0 处的格林函数, S0 和 Sr 均为无限延伸的自由表面和接收面, 区域内为无源声波介质。
速度的垂直分量 Vn 与压力场的梯度满足以下运动方程:
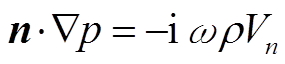 , (2)
, (2)其中, ρ为波传播介质的密度。
我们假设 S0 为空气与海水的水平分界面(即在S0 上没有压力), 在该界面的反射系数为−1, 且接受面 Sr 同样为水平面。将式(1)转换到水平波数域求解, 可以得到速度的垂直分量Vz:
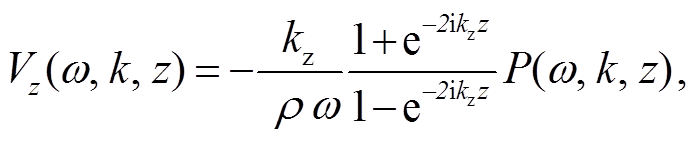 (3)
(3)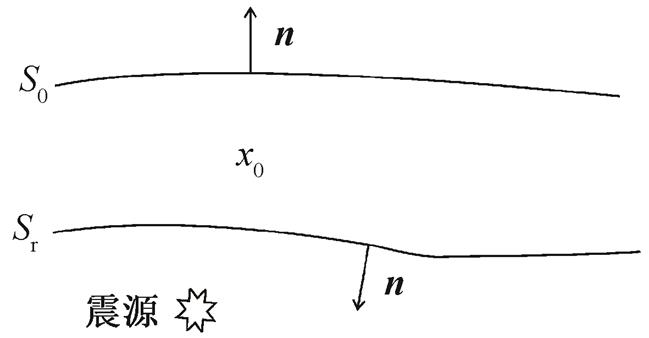
图1 格林函数互易定理应用模型
Fig. 1 Application model for Green’s reciprocal theorem
其中, k = | k |, 是波数矢量k的模; kz是k的垂直分量; ω是角频率; ρ是海水密度; z为接收器深度。式(3)即为伪速度的计算公式, 分母代表理想状态下的压力鬼波算子, 分子代表理想状态下粒子运动的鬼波方程。用GP和GV分别代表压力和速度垂直分量鬼波算子, 可以得到以下方程:
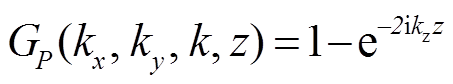 , (3a)
, (3a)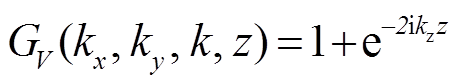 , (3b)
, (3b)
其中, 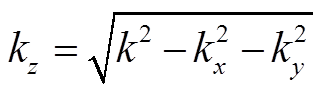 为垂直波数,
为垂直波数, 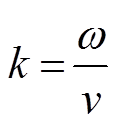 为波数, ω=2πf, kx 和 ky 分别是 x 和 y 方向水平波数的两个分量。对于垂直传播的平面波, kx=ky=0, 鬼波子波在频率慢度域内的表达方程式为
为波数, ω=2πf, kx 和 ky 分别是 x 和 y 方向水平波数的两个分量。对于垂直传播的平面波, kx=ky=0, 鬼波子波在频率慢度域内的表达方程式为
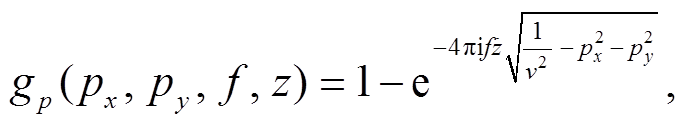 (4a)
(4a)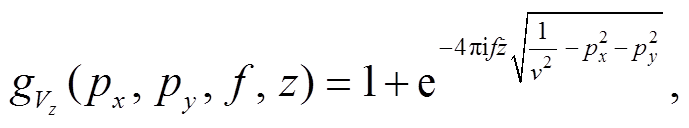 (4b)
(4b)
其中, px和py为水平慢度, f代表频率, v是声波在水中的传播速度。考虑二维情况, 假设py=0。
然而, 我们不能通过式(3)直接求取同位置处的速度垂直分量 Vz, 因为在式(3)的求解过程中需要 将压力鬼波算子从记录的压力数据中反卷积掉, 而在实际数值计算中, 反卷积的过程在频率域引入除数为零的问题。由此, 本文采用稀疏约束的联合L1−L2 范数反卷积方法, 可以得到更精确并稳定的结果。
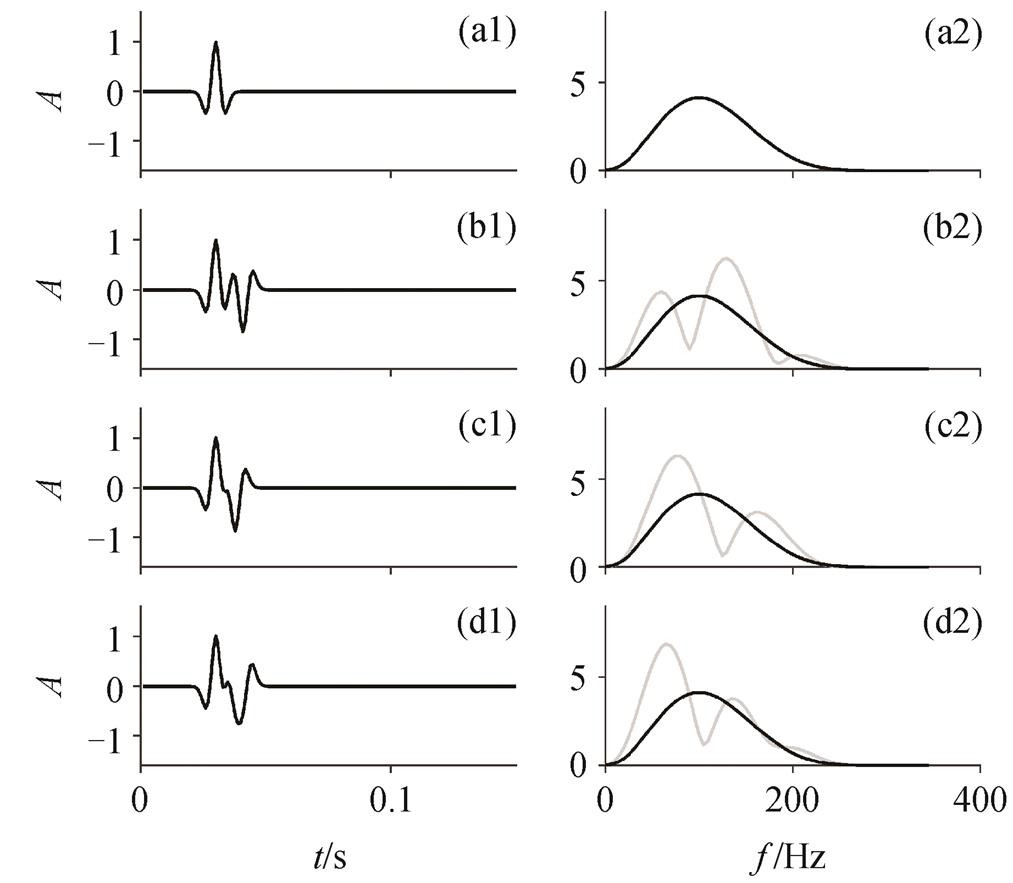
(a1)海底一次反射波波形; (b1)只含检波器鬼波的波形; (c1)只含震源鬼波的波形; (d1)含震源检波器鬼波的波形; (a2)~(d2)分别为(a1)~(d1)的频率响应。黑色曲线为一次反射波频谱图, 灰色曲线为含不同鬼波地震记录的频谱图, A表示振幅, t表示时间, f表示频率
图2 海底一次反射波与鬼波波形及频率响应特征
Fig. 2 Waveform and frequency spectrum of water bottom primary and ghost reflections
反射地震勘探中, 通常将地震图视为地下反射序列与地震子波卷积的结果。假设震源子波为w(t), 地下的反射系数序列用 r(t)表示, n(t)为噪音, 地震记录道s(t)可表示为
s(t) = w(t) * r(t) + n(t)。 (5)
从上述公式看出, 实际地震记录中存在震源子波的影响, 与相邻同相轴相互干扰, 降低了地震记录的分辨率。采用地震反卷积方法, 可以将子波从地震道中排除, 得到真实的地震反射率序列。由于子波在频率域是带限信号, 反卷积实际上是一个欠定问题, 得到稳定解的关键是针对不同的物理问题进行正则化处理。针对本文讨论的问题, 我们假设反卷积的结果在时间域是稀疏的, 因此可以将解决此类问题的方法归结为稀疏脉冲反卷积。稀疏约束的表征形式很多, 有的是通过建立范数的最优化问题使得解稀疏[22–23], 有的是应用随机方法, 在非线性最优化结构中确认稀疏解的位置与振幅[24]。其中, 建立目标函数范数的最优化模型最便捷高效。
本文讨论的问题是求取消除鬼波子波影响后的上行波场, 因此建立的目标函数的范数模型为
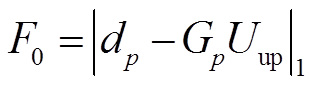 , (6)
, (6)其中, F0 为目标函数, 假设上行波场 Uup 是稀疏的, 由此建立稀疏约束的反卷积问题。方程(6)不是处处连续可导的, 因此需要对其进行变换, 得到稳定的近似L1范数解, 其目标函数为
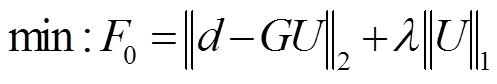 , (7)
, (7)
其中, λ为正则化参数, 可以通过凸函数优化的方法[25]对式(7)求解, 得到理想的稳定结果。从鬼波压制效果来看, 使用凸函数优化算法优于快速迭代阈值收缩算法[26]。
在浅海环境下, 一方面, 记录的近偏移距海底反射数据很少; 另一方面, 由于海水深度浅, 导致鬼波与海底反射一次波的到时非常接近, 混叠在一起产生干涉效应, 使得地震数据在特定频率处能量缺失(也称陷波点), 严重地降低了地震数据的信噪比。压力数据中陷波频率fn的计算公式如下:
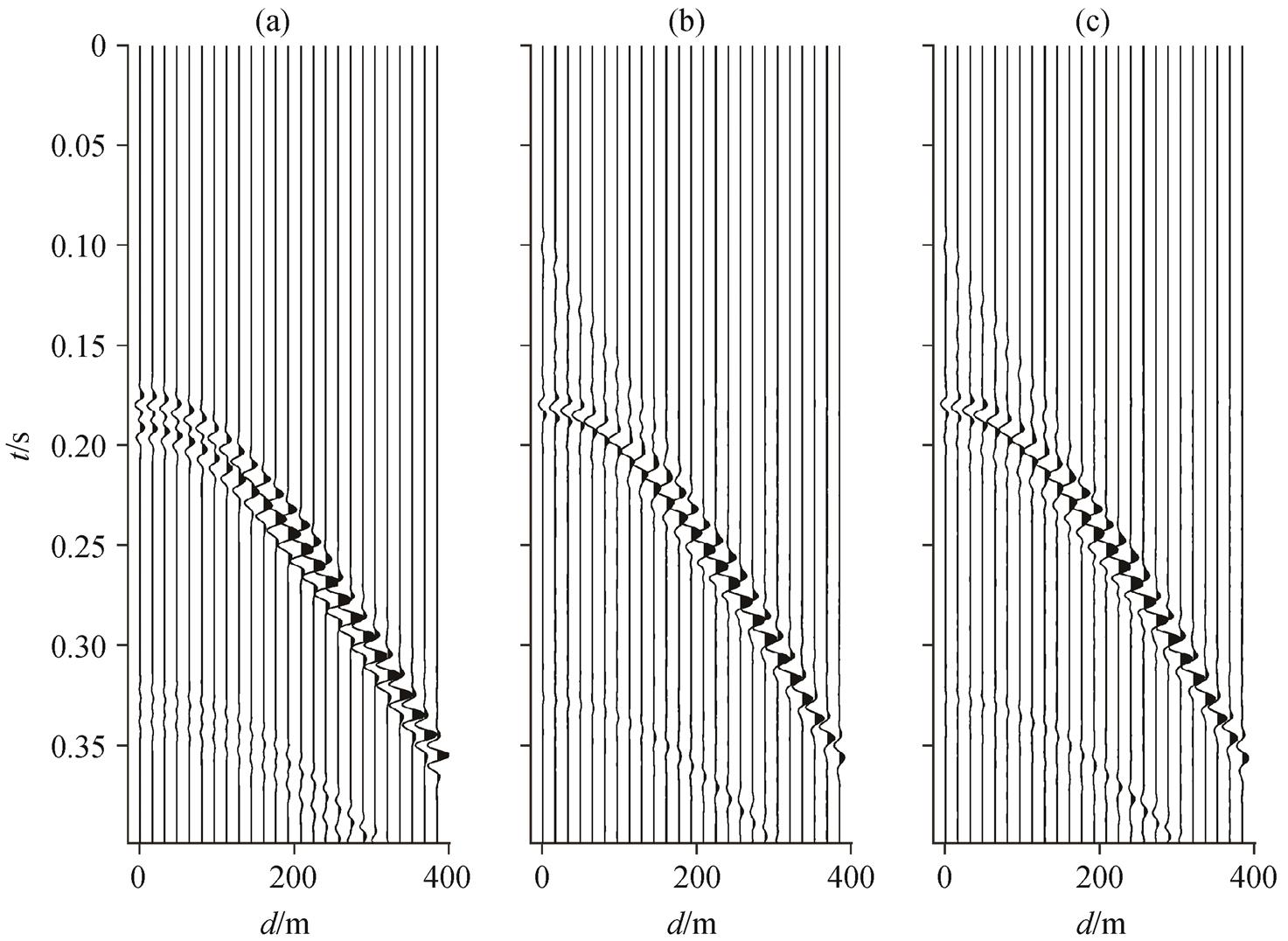
(a)模拟的含鬼波的地震道集; (b)通过稀疏反演求得的上行波地震道集; (c)数据合并后的压制鬼波后的地震道集
图3 简单模型数据鬼波压制前后数据对比
Fig. 3 Comparison of simple model data before and after deghosting results
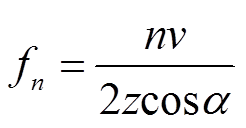 , (8)
, (8)其中, n代表陷波点的阶数, v为地震波在海水中传播的速度, z为检波器深度, α为地震波传播方向与检波器的夹角。
选取一个地震波垂直入射的零偏移距道, 海水深度为30 m, 震源深度为 6 m, 检波器深度为 8 m, 观察上行反射波与震源鬼波及检波器鬼波干涉的地震记录及其频率响应(图 2), 通过比较, 可以看出不同类型的鬼波对地震信号频谱的影响是有差异的。
首先考虑一个简单的二维模型。地震波正演模型为水平层状结构, 第一层为海水层, 水深 100m, 假设地震波在海水中的传播速度为 1500m/s; 第二层为海底地层, 地震波在地层中的传播速度为 2500 m/s。采取单边放炮的方式, 共计201道, 道间距为2m。只考虑存在检波器鬼波的情况, 震源深度设为1 m, 检波器深度为水下8 m。
鬼波消除结果如图 3 所示, 可以看出, 图 3(b)和(c)中, 由检波器鬼波引起的虚假同相轴已被压制掉。图 4 为鬼波去除前后的频谱对比, 可见陷波点频率处能量得到补偿, 且低频段能量得到增强。
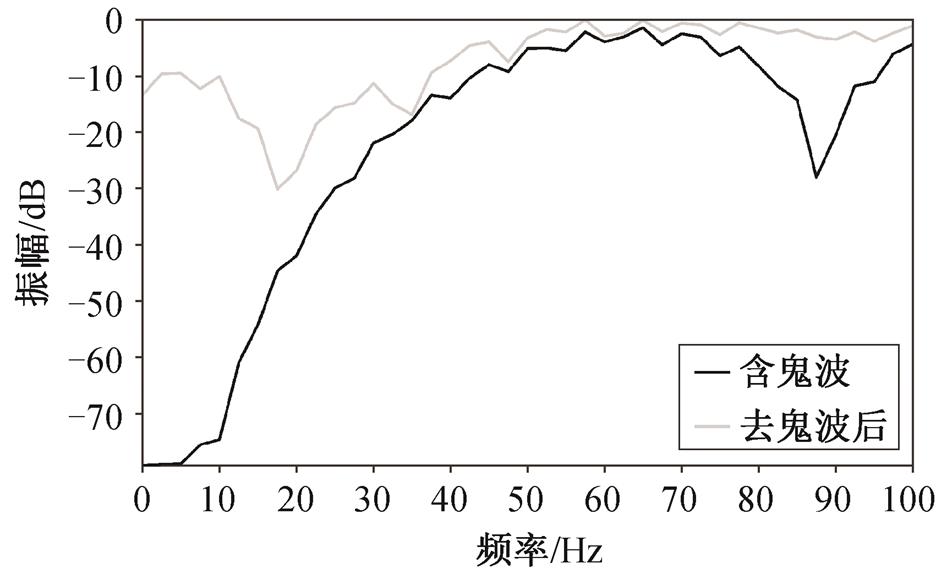
图4 简单模型数据去鬼波前后频谱对比
Fig. 4 Frequency spectrum comparison of simple model data before and after deghosting
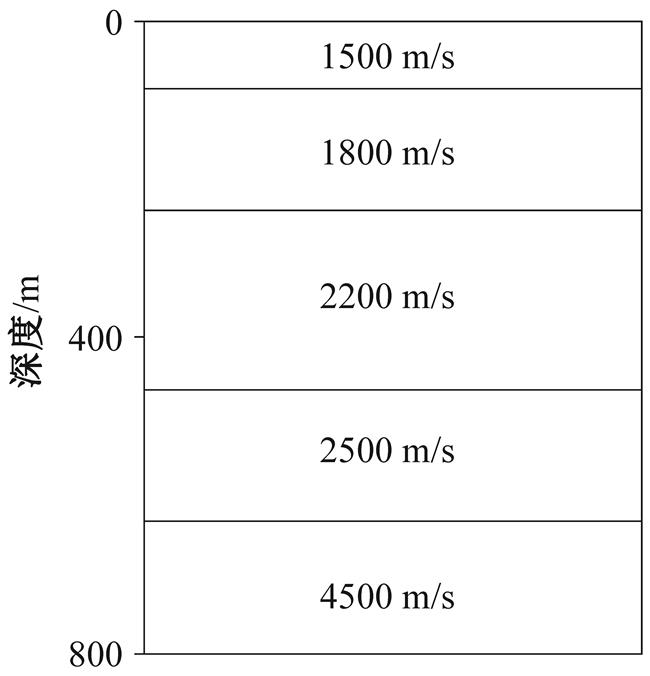
图5 浅海速度模型
Fig. 5 Velocity model of shallow sea
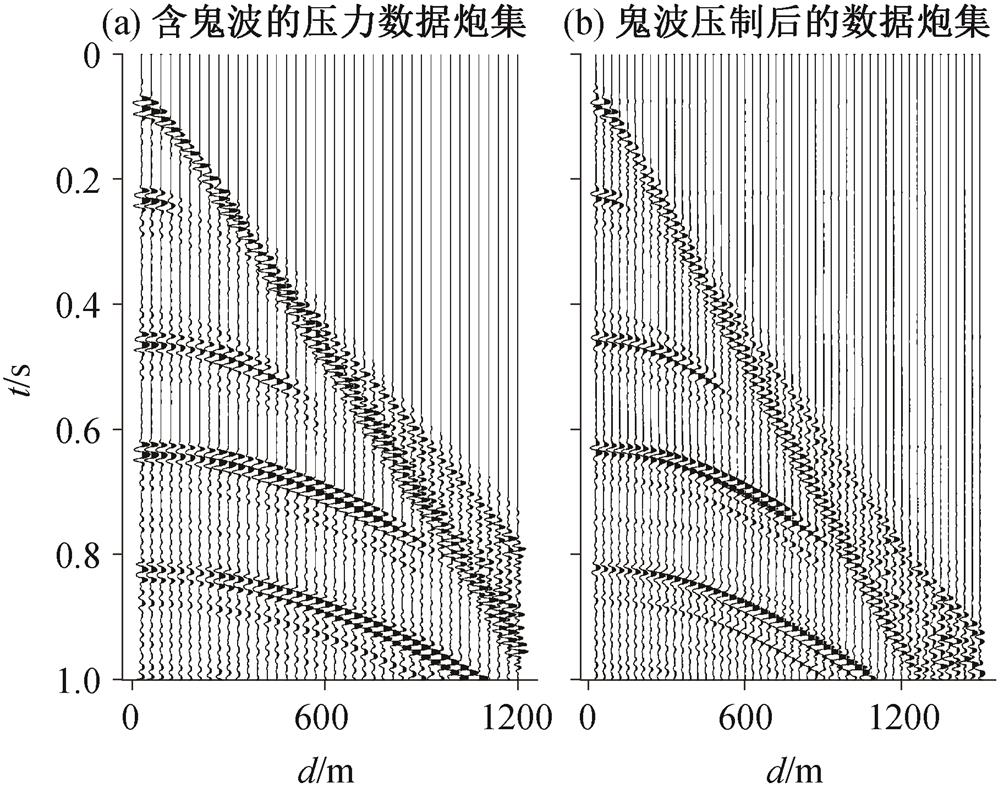
图6 时间–空间域鬼波压制前后单炮地震道集对比
Fig. 6 Comparison of single shot gather in t-x domain before and after deghosting
以上只考虑一般水深的情况, 海底一次反射波与鬼波的干涉现象不明显。下面考虑一个海水深度较浅的 5 层二维模型。如图 5 所示, 速度模型的第一层为海水层, 水深 30m, 地震波在海水中的传播速度为 1500m/s。采取单边放炮的方式, 共计 125道, 道间距为 12m, 最大偏移距为 1500m, 震源深度为 6m, 检波器深度为水下 8m, 采样间隔为 1 ms, 记录时长为 1s。该方法是在时间–慢度(t - p) 域进行计算。
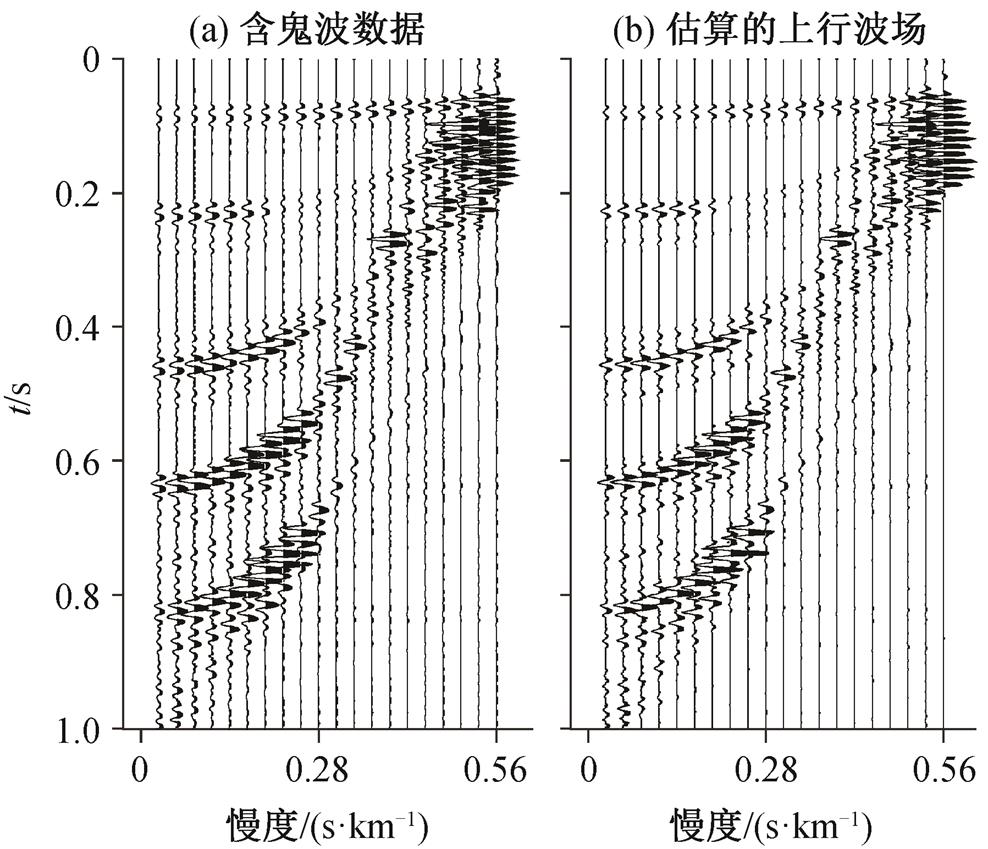
图7 时间–慢度域含鬼波数据与估算的上行波场数据对比
Fig. 7 Comparison of data with ghosts and estimated up-going wavefield data in tau-pdomain
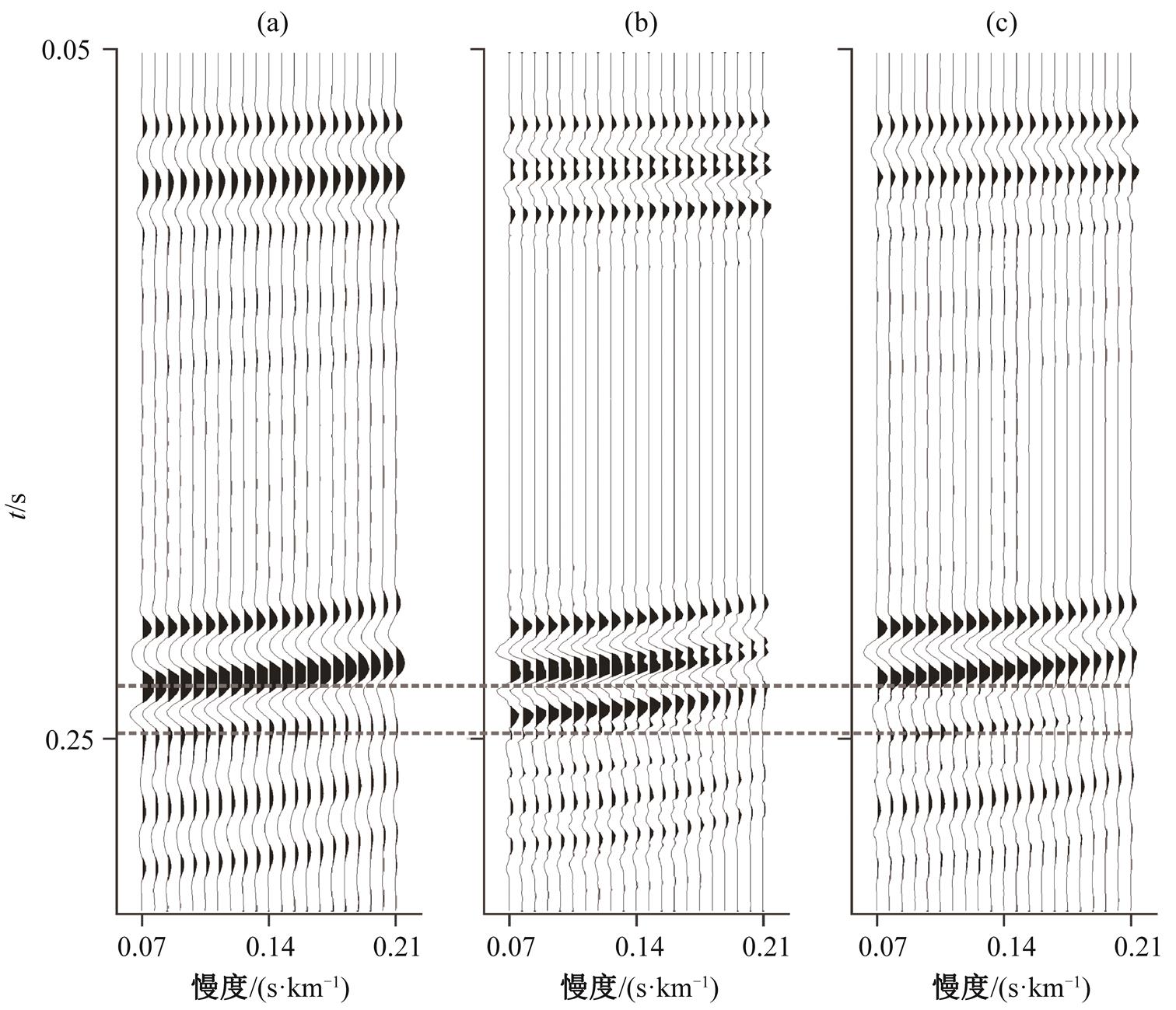
(a)含鬼波压力数据; (b)模拟的伪垂直速度; (c)压制鬼波后的压力数据。两虚线间为鬼波压制前后近偏移距道集的结果对比
图8 时间–慢度域近偏移距波形对比
Fig. 8 Waveform display of near-offset t-pdomain results
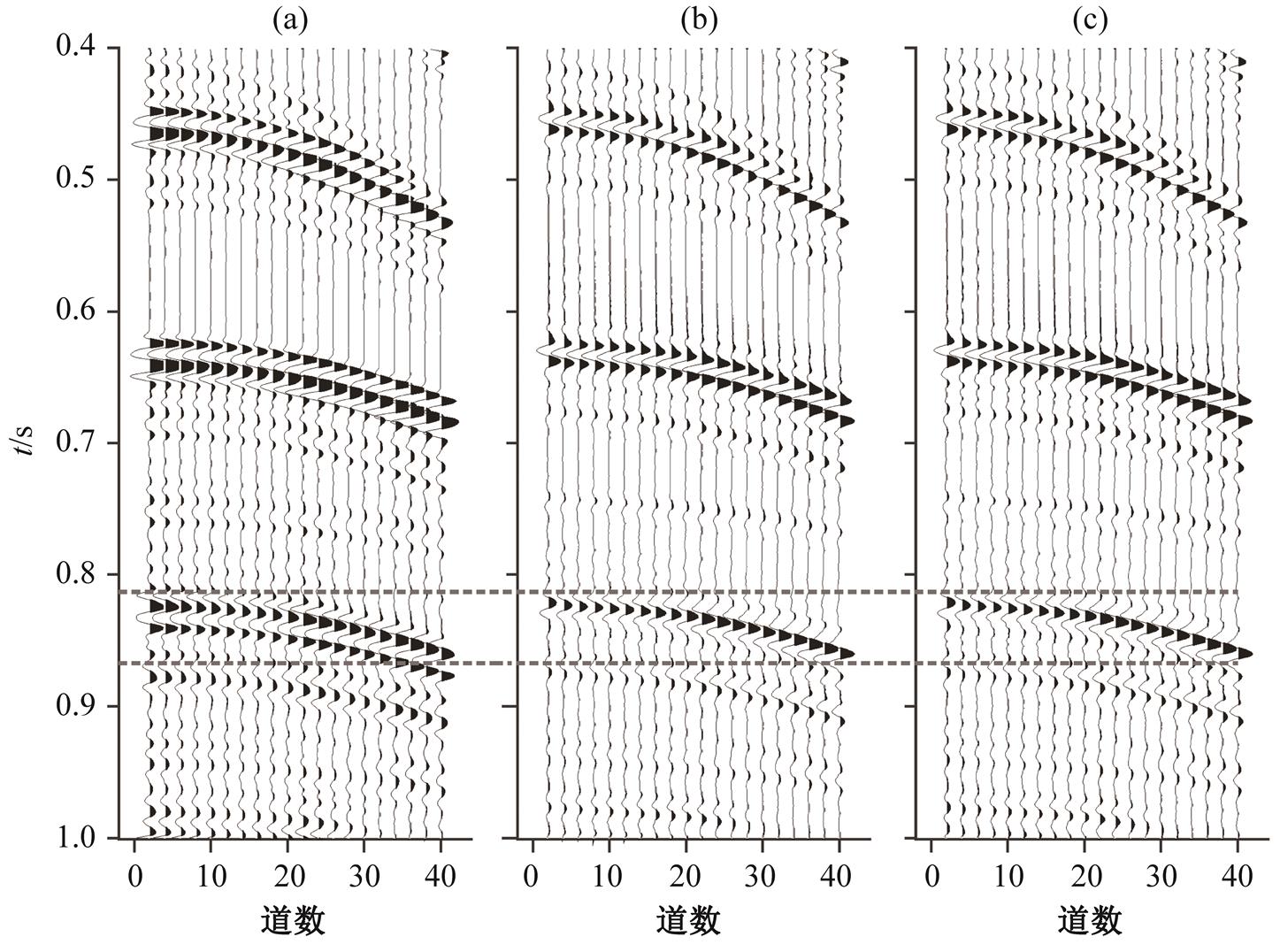
(a)含鬼波压力数据; (b)估算的上行波场数据; (c)压制鬼波后的压力数据。两虚线间为鬼波压制前后近偏移距道集结果对比
图9 时间–空间域近偏移距去除鬼波波形对比
Fig. 9 Waveform comparison of near-offset t-x domain deghosted resu lts
图 6 显示浅海模型数据在时间–空间(t-x)域鬼波压制前后单炮地震道集的对比, 可以看到图 6(b)中鬼波虚假同相轴已得到压制。图 7 对比 t - p 域含鬼波数据(图 7(a))与通过稀疏约束的反卷积方法估算的上行波场数据(图 7(b)), 在消除了鬼波算子的影响之后, 估算的上行波场数据不含鬼波。
将上行波场数据与速度鬼波算子进行褶积, 得到同一位置的伪垂直速度数据(图 8(b))。将伪垂直速度数据与原始记录的含鬼波压力数据(图 8 (a))进行合并, 得到压制鬼波后的最终结果(图 8(c))。通过对比图 8 两条虚线之间的结果可以发现, 含鬼波的压力数据与伪垂直速度数据在波形的极性上是相反的, 这也是鬼波得到压制的原理。
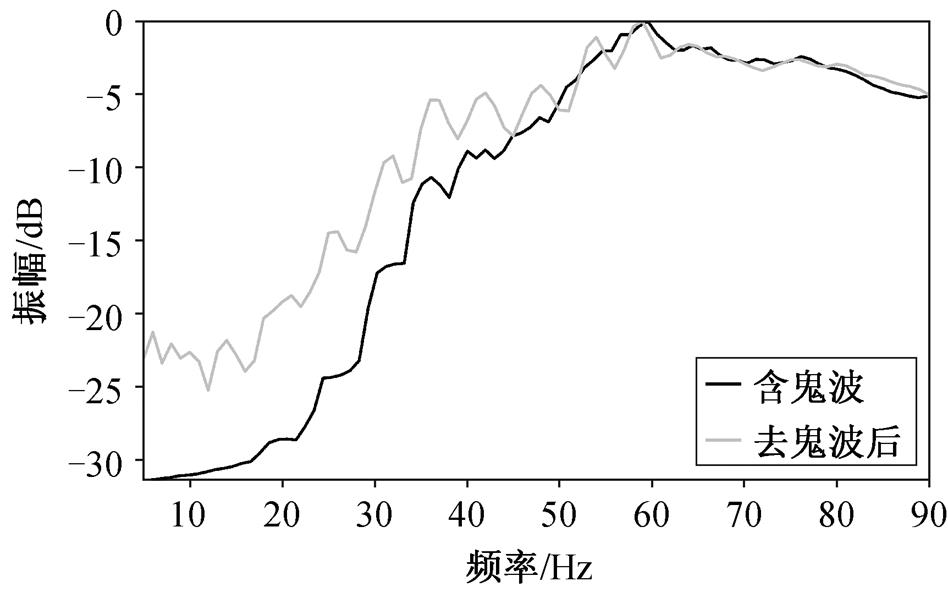
图10 浅海模型数据去鬼波前后频谱对比
Fig. 10 Frequency spectrum comparison of shallow- sea model data before and after deghosting
图 9 对比近偏移距时间域上行波场与压制鬼波前后的数据。对比图 3 与图 9 可知, 估算的上行波场与鬼波压制后的结果相似。但是, 我们不将上行波场作为鬼波压制的最终结果, 而是计算出伪速度的垂直分量, 以此模拟双检波器的接收数据, 通过合并伪垂直速度和压力数据的方法, 达到压制鬼波的目的。这样做的原因在于, 采取稀疏约束的反卷积方法得到的上行波场会在一定程度上压制有效弱信号。若将计算的上行波场数据(图 3(b)和图 9(b))与原始含鬼波的地震数据(图 3(a)和图 9 (a))合并处理, 得到的压制鬼波后的结果(图 3(c)和图 9(c))则能在压制鬼波的同时, 更好地保存地震数据中的有效弱信号。
图 10 为鬼波压制前后的频谱对比, 可以看出, 伪速度压制鬼波的方法可以有效地提高数据的低频能量, 特别是在 0~20Hz 低频范围内, 低频能量得到明显的补偿。
本文通过对海上单分量压力数据进行处理, 得到垂直分量的伪速度数据, 以此模拟双检波器采集的速度垂直分量地震数据, 并将稀疏反卷积的方法应用于上行波场的反演中, 有效地压制鬼波, 提高了数据的分辨率, 同时增强了海上单分量地震数据的低频能量, 实现对传统的单分量地震数据的充分利用, 并对地震数据的后续处理(如地震成像、波形反演)效果起到积极作用。
参考文献
[1]Soubaras R. Deghosting by joint deconvolution of a migration and a mirror migration // SEG Technical Program Expanded Abstracts. Denver, 2010: 3406‒ 3410
[2]Ten Kroode F, Bergler S, Corsten C, et al. Broadband seismic data — the importance of low frequencies. Geophysics, 2013, 78(2): WA3‒WA14
[3]Robertsson J O A, Ronen S, Singh S, et al. Broad-band seismology in oil and gas exploration and production — introduction. Geophysics, 2013, 78(2): WA1‒WA2
[4]Sonneland L, Berg L E, Eidsvig P, et al. 2-D deg-hosting using vertical receiver arrays // SEG Tech-nical Program Expanded Abstracts. Houston, 1986: 516–519
[5]Posthumus B J. Deghosting of twin streamer configu-ration. Geophysical Prospecting, 1993, 41(3): 267‒ 286
[6]Singh S C. Broadband receiver response from dual-streamer data and applications in deep reflection seismology. Geophysics, 1996, 61(1): 232‒243
[7]Hill D, Combee L, Bacon J. Over/under acquisition and data processing: the next quantum leap in seis-mic technology?. First Break, 2006, 24(6): 81‒95
[8]Xuan Y, Li H, Zhang Z, et al. An adaptive over/under streamers strategy for marine seismic acquisition // SEG Technical Program Expanded Abstracts. New Orleans, 2015: 90‒94
[9]Parrack A L. Method of marine reflection-type seis-mic exploration. US 3979713 A [P/OL]. 1976: https:// patents.google.com/patent/US3979713
[10]Brink M. Application of vertical receiver arrays in 3-D seismic exploration // SEG Technical Program Expanded Abstracts. Tulsa, 1988: 460‒463
[11]Kragh E, Muyzert E, Curtis T, et al. Efficient broadband marine acquisition and processing for improved resolution and deep imaging. The Leading Edge, 2010, 29(4): 464‒469
[12]Soubaras R. Pre-stack deghosting for variable-depth streamer data [C/OL] // SEG Technical Program Expanded Abstracts. Las Vegas, 2012: https://dx.doi. org/10.1190/segam2012-1083.1
[13]刘春成, 焦振华, 管西竹, 等. 海洋“犁式”电缆地震资料采集与处理方法. 中国海上油气, 2016, 28(5): 1‒7
[14]Barr F J, Sanders J I. Attenuation of water column reverberations using pressure and velocity detectors in a water-bottom cable // SEG Technical Program Expanded Abstracts. Dallas, 1989: 653‒656
[15]Loewenthal D. On dual field measurements using geo-hydrophones // SEG Technical Program Expanded Abstracts. Los Angeles, 1994: 861‒864
[16]Tenghamn R, Vaage S, Borresen C. A dual-sensor towed marine streamer: Its viable implementation and initial results // SEG Technical Program Expanded Abstracts. Houston, 2007: 989‒993
[17]Carlson D H, Long A, Söllner W, et al. Increased resolution and penetration from a towed dual-sensor streamer. First Break, 2007, 25(12): 71‒77
[18]Day A, Klüver T, Söllner W, et al. Wavefield-separation methods for dual-sensor towed-streamer data. Geophysics, 2013, 78(2): WA55‒WA70
[19]Teigen Ø, Özdemir A K, Kjellesvig B, et al. Charac-terization of noise modes in multicomponent (4C) towed streamers [C/OL] // SEG Technical Program Expanded Abstracts. Las Vegas, 2012: https://dx.doi. org/10.1190/segam2012-0792.1
[20]Ferber R, Caprioli P, West L. L1 pseudo-estimation and deghosting of single-component marine towed-streamer data. Geophysics, 2013, 78(2): WA21‒WA26
[21]Momoh E, Halliday D F, Ferber R, et al. Pseudo-Vzdeghosting of deep-tow seismic data and implications for low-frequency signal estimation // SEG Technical Program Expanded Abstract. New Orleans, 2015: 4525‒4529
[22]Debeye H W J, Riel P V. Lp-norm deconvolution. Geophysical Prospecting, 1990, 38(4): 381–403
[23]Wang Y. Seismic impedance inversion using L1-norm regularization and gradient descent methods. Journal of Inverse and Ill-posed Problems, 2011, 18(7): 823‒838
[24]Velis D R. Stochastic sparse-spike deconvolution. Geophysics, 2007, 73(1): R1‒R9
[25]Boyd S, Vandenberghe L. Convex optimization. IEEE Transactions on Automatic Control, 2006, 51(11): 1859
[26]Beck A, Teboulle M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Transactions on Image Processing, 2009, 18(11): 2419‒2434
Shallow Sea Deghosting with Pseudo VelocityMethod
CAO Luqing, HU Tianyue†
School of Earth and Space Sciences, Peking University, Beijing 100871; † Corresponding author, E-mail: tianyue@pku.edu.cn
Abstract Based on marine single-componentseismic data acquired by conventional acquisition method, the vertical component of velocity (pseudo-Vz) at the same position is estimated. The pseudo-Vz is then combined with the single component of pressure data to get the aim of deghosting. By applying the sparsity constraint de-convolution method as an intermediate procedure, improvements of shallow sea single-component seismic data in resolution as well as in filling the frequency notches, which are caused by the interference of the up- and down-going waves at the receivers are achieved. In addition, the energy of low-frequency signal is enhanced. The proposed method can be used for re-processing the existing single-component data through which can broaden the frequency bandwidth.
Key words shallow sea; pseudo velocity; sparsity constraint; deghosting
中图分类号 P315
doi: 10.13209/j.0479-8023.2018.028
国家自然科学基金(41674122)和国家科技重大专项(2016ZX05004-003)资助
收稿日期: 2017-09-09;
修回日期: 2017-10-15;
网络出版日期: 2018-05-15