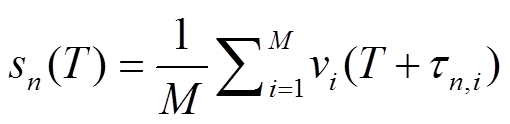, (1) 刘志鹏 宋超 盖增喜 †
北京大学地球与空间科学学院, 北京 100871
摘要 基于三维地球模型, 分别使用南美洲和亚洲的远场P波数据资料, 对2016年11月13日Mw 7.8级新西兰地震的破裂过程进行反投影成像分析。结果显示, 该地震是破裂方向为东北的单边破裂, 破裂长度约为140km, 延伸至海中, 破裂速度约为 1.65km/s。该地震的高频能量释放有两个阶段, 分别为 20~40s 和 60~ 80 s, 其中第二阶段为能量释放的主要阶段, 该阶段的低频能量聚束分布与该地震的矩心位置较为一致。从南美洲数据得到的高频破裂分布与地面峰值加速度的结果较为一致。通过对比分析南美洲和亚洲数据的结果, 指出在反投影分析中, 为了获取更精确的高频破裂细节, 应尽量选取位于三维不均匀性较弱区域的台阵数据, 以增强高频信号的相关性。
关键词 2016年新西兰地震; 破裂过程; 三维地球模型; 反投影方法
2016 年 11 月 13 日 11:02(UTC), 新西兰南岛东北端发生一起 Mw 7.8 级大地震, 造成数十人受伤, 两人死亡, 并摧毁当地十余座建筑。地震还引发多起山体滑坡等次生灾害, 造成很大的经济损失。根据美国地震学联合研究会(Incorporated Research In-stitutions for Seismology, IRIS)给出的结果, 震中位置为 42.7245°S, 173.0647°E, 震源深度为 22 km。该地震发生的位置处于 Puysegu 俯冲带与 Hikurangi俯冲带之间的 Alpine 断层系 [1] 。这两个俯冲带的俯冲方向完全相反, Alpine 断层系中的断层以转换断层为主, 断层性质的多样性导致该地区地质背景结构极为复杂。因此, 有必要对该地震的破裂过程进行深入研究。
在地震学研究中, 理解大地震的破裂过程可以帮助我们研究破裂机制, 并为震后救援提供快速响应。2005 年, 反投影方法被首次使用, 从此广泛地应用于研究大地震的动态破裂过程 [2 - 7] 。之前的反投影方法研究中, 通常采用一维层状地球结构模型来计算射线走时, 例如利用 PREM [8] 、IASP91 [9] 和AK135 [10] 来计算 P 波的走时。一维模型的反投影方法仅在下列两种情况下适用: 1)破裂的区域较小; 2)射线穿过部分的速度结构与一维模型的结构极其相似。因此, 当破裂范围大至成百上千公里或射线路径穿过部分的速度结构与一维模型相差较大时, 这样的假设就会失效。
近年来, 得益于宽频带数字地震台站的布置和反演技术的进步, 地震学家得到越来越精确的全球三维速度结构模型。与传统的一维模型相比, 这些模型可以更精确地计算走时。因此我们或许可以将三维模型结合到反投影分析中来研究大地震, 从而获得比使用一维模型分辨率更高的结果。本文采用一个全球三维速度结构模型—— LLNL-G3Dv3 模 型 [11] , 作为参考模型来进行三维射线追踪, 得到走时, 从而实现反投影分析。本文分别使用来自南美洲和亚洲的台站数据, 对 2016 年新西兰地震破裂过程进行反投影成像和分析。
与地震勘探中经常使用的逆时偏移方法类似, 传统波形聚束反投影方法的核心思想是将格林函数简化为一个时间域内的只与从震中到台站的走时相关、与振幅无关的时移函数 [2,12] 。为了得到地震源区能量释放的时空过程, 将地震台站记录到的波形反向传播到源区, 并根据聚束能量(normalized po-wer)进行成像。具体过程为, 首先将震源区域网格化为格点, 作为备选的子事件源。然后, 为了找到某一时刻子源所在的位置, 将所有台站记录到的波形在时间轴上根据走时进行移动, 序号为 n 的备选子事件源上叠加的波形可以表示成
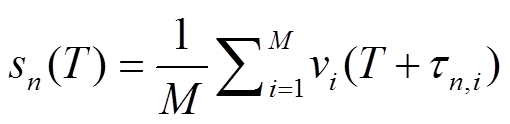, (1) 其中, M 是台站的总数, v i 是归一化后台站 i 记录的原始波形, T 是破裂时间, τ n , i 代表从格点 n 到台站 i 的绝对走时。实际应用中, 经常使用 P 波初至开始很短一段时间内的波形来进行多道互相关 [13] , 从而对齐同一台阵的数据。这样做类似于主事件定位法的思想, 可以减少三维不均匀性在震中位置的影响, 将初始破裂点成像在震源位置, 并确定其余子源相对于震源点的位置。最后, 对齐后的数据可以写成
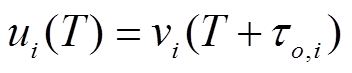, (2)
τ o , i 是从震中到台站 i 的绝对走时, 实际应用中可以写成基于一个参考速度结构模型的理论走时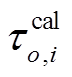 
和走时误差项 δτ o , i , 其中误差项代表地球实际结构与参考模型的差异对走时的影响。因此, 式(2)可以分解为
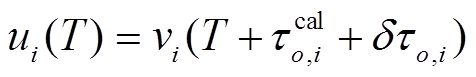。 (3) 当进行实际反投影成像时, 误差项 δτ o , I 可以通过互相关估计。值得注意的是, 直接通过互相关得到的时移 ξ τ o , i 只是一个相对值。所以有
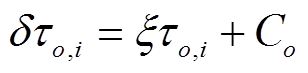, (4)
这里 C o 是一个常数, 用来代表 δτ o , i 与 x τ o , i 的差异。虽然无法得到 C o 的具体值, 但是不会影响反投影的结果。因此, 对齐后的波形可以写成
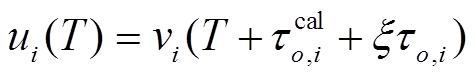。 (5) 基于对齐的波形和主事件定位法的概念, 将式(1)变形为
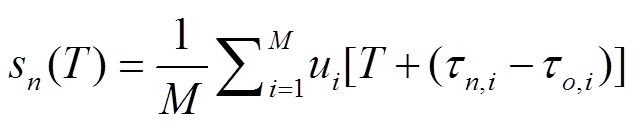。 (6)
与式(2)同理, 式(6)可以分解为
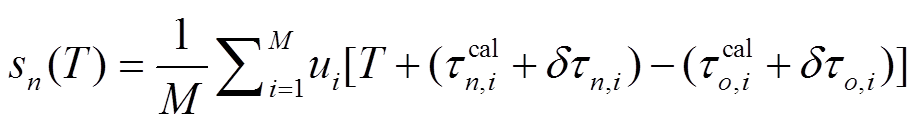, (7) δτ n , i 是从格点 n 到台站 i 的理论走时与绝对走时的差值。如果根据式(7)中各项的物理意义进行重新分组, 则有
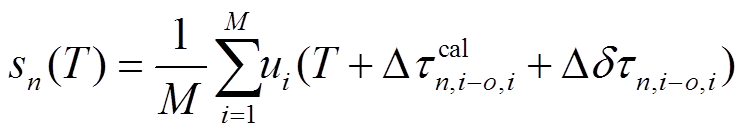, (8)
其中,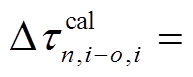 
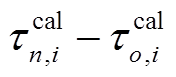是一阶项(理论走时差别项); 
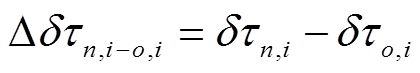是二阶项(误差差别项)。虽然式(8)在形式上比式(1)复杂, 但是更容易实现。
在传统反投影方法中, 一阶项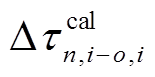 
是基于一维各向同性层状地球模型计算的, 二阶项 
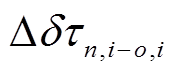经常被忽略, 因此, 震中所在的格点到各个台站的走时误差被用于所有格点。但是, 这样的假设只对震中附近的格点有效。随着可能的子源位置向远离震中的方向移动, 假设就会逐渐失效。尤其是使用不那么精确的模型时, 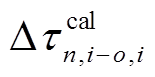的误差将会累积至 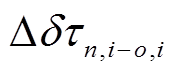, 对反投影结果会有负面影响。很多借助余震信息进行改进的反投影方法被引入地震学研究中 [14 - 16] 。与传统的反投影方法相比, 在这些研究中地震的破裂过程得到校正, 并展现了更高的空间分辨率。这些依赖于余震的方法将对余震数据进行互相关得到的时移等相关信息用在余震震中所在的格点上, 然后通过不同的插值方法得到所有离散化的源区格点二阶项的值。但是, 这种校正方法有两个局限性: 1)通过互相关得到的时移并不是绝对值, 而是一个相对值, 所以根据式(4), 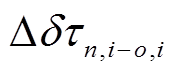中会有一个位置的常数, 这个常数对每个格点是不同的; 2)由于余震的定位精度可能较低, 因此会导致插值的结果有偏差, 从而引起二次误差, 影响反投影的结果。以上两点导致这些依赖余震的反投影校正方法在实际应用中并不稳定。
使用更多的余震信息来校正反投影结果的初衷是, 可以借助余震信息得到一个更精确的走时表, 用于反投影的实现。如果使用余震信息, 这个走时表可以将每一个子源到台站的射线路径上三维不均匀性考虑进去, 从而得到更精确的走时。实际上, 三维地球速度结构模型就是一个基于大量的全球地震数据和观测的综合的结果。这让我们想到, 或许可以采用三维地球模型直接计算走时。当然, 这种方法等效于使用前震信息, 而不是某个地震的余震信息。这种方法的优点是, 如果三维模型是更可信的, 那么一阶项 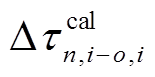将会更精确, 所以二阶项 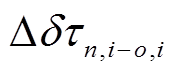会被最小化, 并且不会引入由于使用余震信息而导致的误差。除此之外, 由于无需等到余震发生, 因此可以更快地得到结果。
本研究使用的三维全球P波速度结构模型——LLNL-G3Dv3 模型, 是由 Simmons 等 [11] 反演得到的。这个模型基于一个非球面的地球结构, 并以层状镶嵌的格点为框架, 包含地壳和上地幔的多层起伏界面。为了得到这个模型, 共使用全球 7000 个台站来自1万个地震事件的总计约280万条的直达P波记录。所有的地震事件都通过名为Bayesloc的多事件定位算法 [17 - 18] 重新精确定位, 并作为得到模型的输入参数, 这显然提高了地震定位的精度。由于使用了大量的质量较好的数据, 因此我们使用这个模型来进行射线追踪, 从而计算三维模型下 P 波的走时, 进行反投影分析。我们利用一个专门支持提取该模型信息的电脑程序 LLNL-Earth3D ① 来提高后续计算过程的效率。
为了使用三维模型反投影方法对 2016 年 7.8级新西兰地震的同震破裂过程进行高频成像, 我们从IRIS 的数据中心(http://ds.iris.edu/wilber3/find_stations/ 5197722)获取来自南美洲和亚洲的两个台阵数据, 分别进行计算。这些台阵位于震中位置的不同方位(图 1)。首先, 所有的地震记录都经过 0.5~2Hz 的带通滤波, 并且进行归一化处理。然后, 所有的波形都通过多道互相关, 并且根据理论到时进行对齐(图 2)。我们采用的震中位置为 42.73°S, 173.07°E, 深度为 22 km。震源区(42.23°—44.73°S, 172.57°—175.07°E)被分隔为 0.1°×0.1°的格点, 这表示源区被分隔为 25×25 个格点。由于相对走时差对深度的变化不敏感 [19] , 整个破裂过程是在震源深度为 22km的水平面上进行成像的。为了得到此次地震的时空破裂过程, 我们采用一个长为 10s 的滑动窗, 滑动步长为1s, 对数据进行分段化处理。考虑到数据量充足且台站分布较好, 我们使用线性叠加的聚束成像方法, 从而避免对原始波形的改动。
基于三维模型, 分别得到使用南美洲数据和亚洲数据发震后 90s 的反投影破裂过程(图 3)。选择截取至 90s的原因是, 90s之后的聚焦结果较差, 无法观测到稳定聚焦的破裂点。两组数据的结果有共同的特征, 同时也有一些差异。首先, 两组结果都证明, 本次地震的破裂从震中处开始, 向东北方向传播, 这与该地区Alpine断层系中断层的走向基本上一致。此外, 在高频能量辐射的过程中, 两组数据的结果均表明出破裂过程中存在两个能量释放的峰值, 如图 4 所示。第一个峰值发生在初始破裂后20~40s, 第二个峰值发生在初始破裂后 60~80 s。从两组结果的差异来看, 南美洲数据的结果破裂尺度较大, 约为 140km, 并且一直传播到海岸线; 亚洲数据的结果破裂尺度较小, 约为 100 km。分别将两组结果的高频辐射源位置投影在通过最小二乘法拟合的各自的破裂方向上, 利用得到的投影距离来研究破裂速度(图 5)。南美洲数据得到的破裂速度较大, 为 1.65 km/s; 亚洲数据得到的破裂速度较小, 为 1.28 km/s。
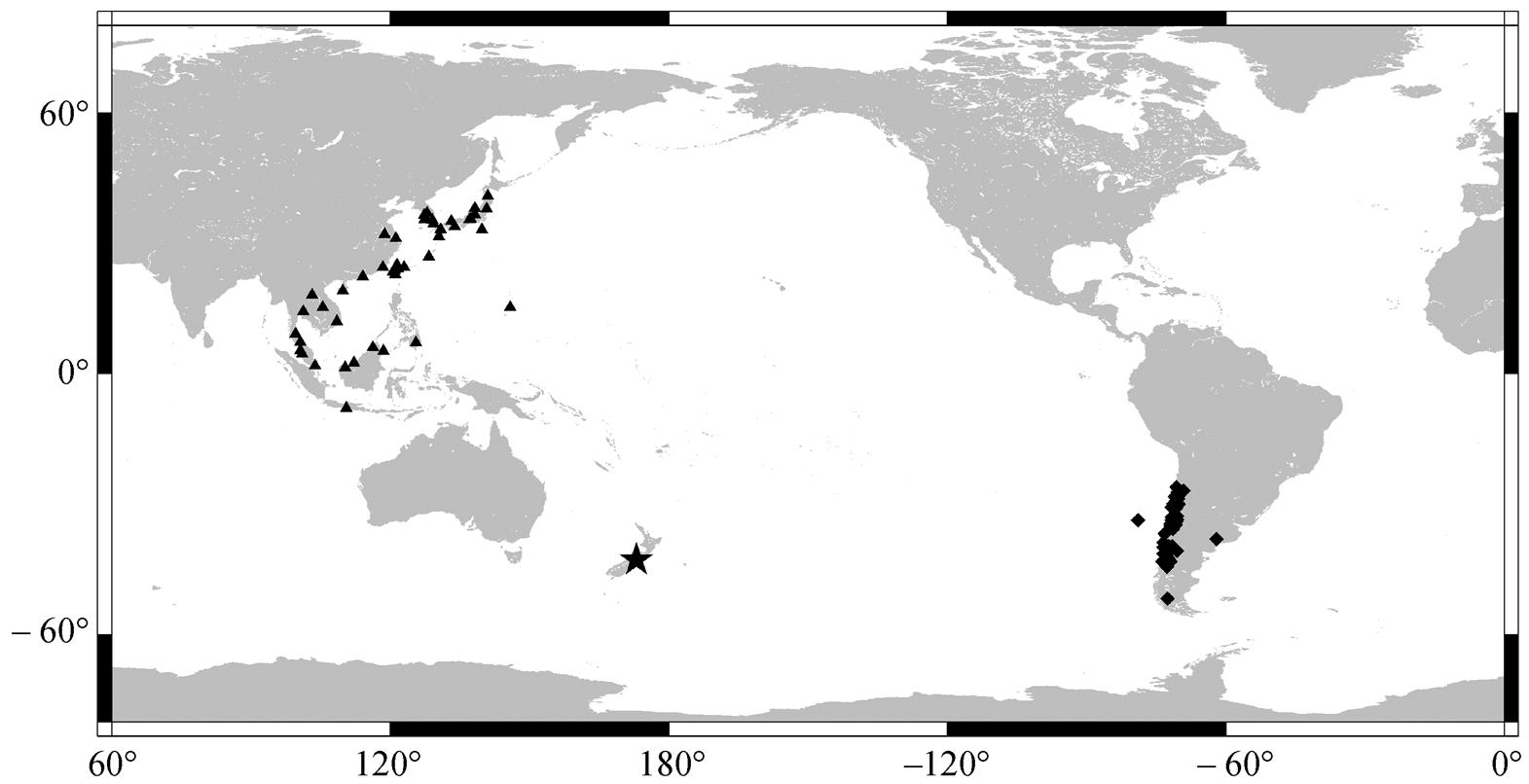
五角星代表震中位置, 菱形代表南美洲台站, 三角形代表亚洲台站
图1 亚洲和南美洲台站分布
Fig. 1 Distribution of South American array and Asian array
图2 反投影成像中使用的南美洲数据(a)和亚洲数据(b)
Fig. 2 Data of South American array (a) and Asian array (b) for back projection analysis
区别于前人的方法, 本文使用三维地球模型, 因此有必要对该三维模型对于本次事件的分辨率进行检测。检测的方法为, 选取本次地震的一个余震(http://ds.iris.edu/spud/eventplot/13298018), 将其波形视为主震事件后的连续波形, 对其相对于主震震中的矩心位置分别使用一维模型和三维模型进行反投影(图 6)。需要注意的是, 由于余震的绝对位置定位存在误差, 因此目录位置仅作为参考, 而不作为判断反投影位置是否准确的依据。这里使用的判断依据为: 使用不同台阵数据得到的反投影余震位置基于哪个模型更为一致。可以看到, 使用一维模型时, 不同数据成像的位置相差较大。当使用三维模型后, 南美洲和亚洲数据所确定的矩心位置明显靠拢, 展现出更高的分辨率。因此证明, 使用三维模型可以提升该区域的反投影成像精度。但是, 由于该余震距震中位置较近, 而远离震中的区域(如图 3 中破裂尾端区域)没有适用震级的余震发生, 因此, 我们无法对远离震中区域成像的分辨率进行测试。
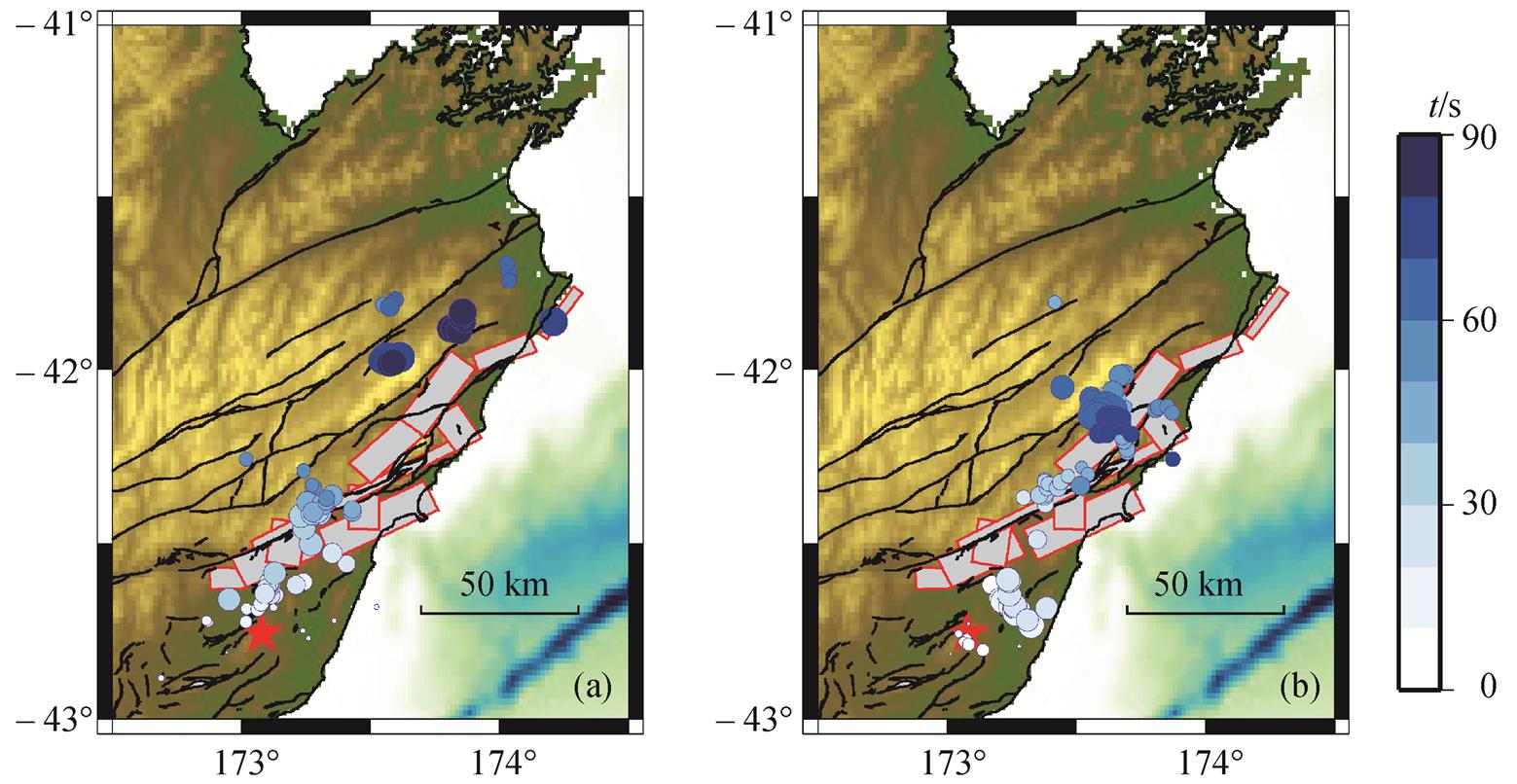
(a)南美洲数据的结果, (b)亚洲数据的结果; 蓝色圆圈代表反投影高频辐射源位置, 红色五角星代表震中位置, 黑线代表断层(来源: http://data.gns.cri.nz/af/), 红线圈住部分为通过地表观测推断可能发生破裂的断层面在地表的投影
图3 新西兰地震反投影结果
Fig. 3 Back projection results of Asian (a) and South American (b) data
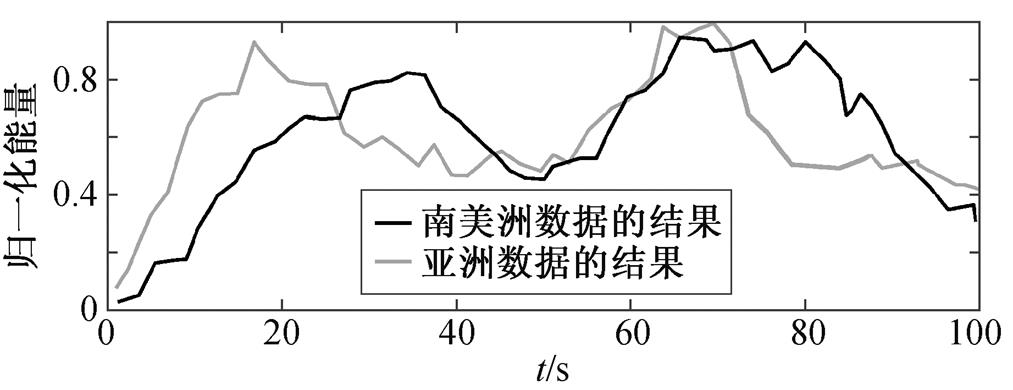
图4 破裂释放的能量随破裂时间变化曲线
Fig. 4 Power radiation during the rupture process
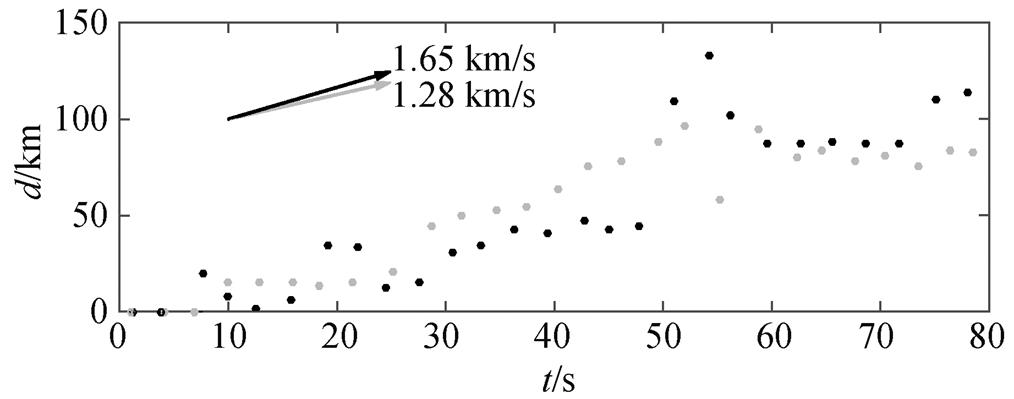
黑色圆点为南美洲数据的结果, 灰色圆点为亚洲数据的结果; 箭头的斜率代表最小二乘拟合后求出的破裂速度
图5 破裂前沿传播位置与震中在破裂方向上的投影距离随破裂时间的变化
Fig. 5 Rupture speeds estimated by the projected distance and rupture time
为了探究两组台阵数据得到的结果在破裂的后半段有差异的原因, 分别使用低频数据(0.05~1Hz)对 50s 之后的破裂(即第二个能量释放峰值的时间段), 使用40 s的时间窗进行聚束能量分析(图 7)。
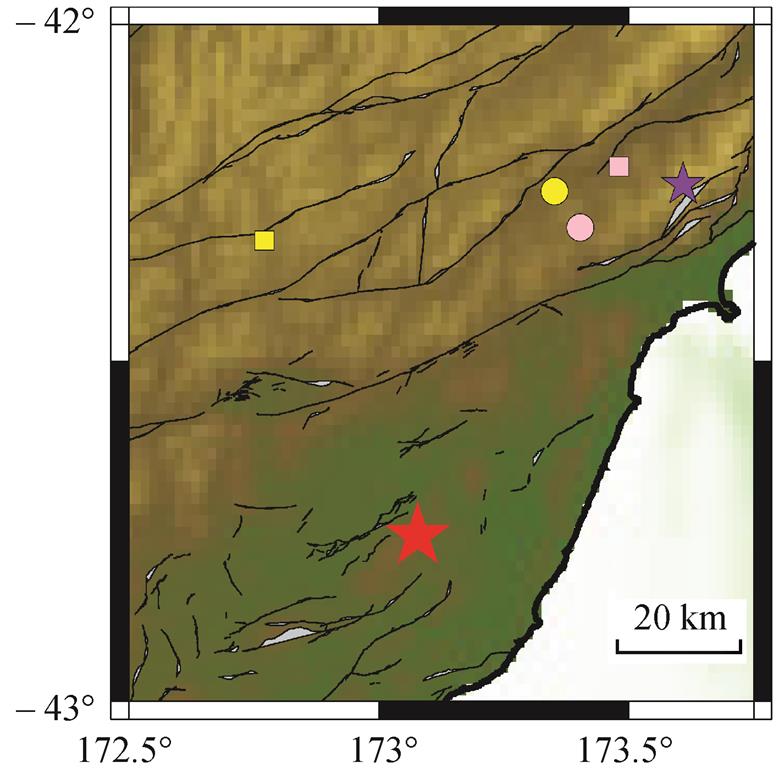
黄色和粉色图标分别代表使用一维模型(PREM)和三维模型的反投影结果, 正方形和圆圈分别代表使用南美洲数据和亚洲数据的反投影结果, 红色和紫色五角星分别代表主震震中和余震的目录位置
图6 分别使用一维模型和三维模型对余震进行定位的位置分布
Fig. 6 Aftershock relative localization via back projection with 1-D and 3-D earth model
可以发现, 两组数据低频能量的峰值基本上与该地震的矩心位置一致(图 8)。由于矩心位置也是使用低频数据进行矩张量反演得到的, 且低频部分 60s前的能量极低 [20] , 因此低频反投影方法与矩张量反演方法得到的矩心位置一致, 说明这两组台阵中台站位置的设定均可以对低频数据进行相对准确的成像。一般来讲, 由于数据相关程度较高, 低频数据的能量较为集中, 受三维非均匀性影响较小, 因此比高频数据更容易成像, 但分辨率较低。两组台阵均能对低频能量位置进行成像, 说明台阵中台站的位置分布情况较好。但是, 对于破裂末期, 南美洲的高频数据反投影仍然可以成像, 而亚洲数据的高频结果则停滞在矩心位置附近。这可能是由于亚洲台站大多位于海岛, 台站下方三维不均匀性较强, 虽通过三维模型有一定程度的修正, 但其影响仍然无法消除, 所以对破裂末期的高频部分聚焦效果较差, 其结果中破裂前沿停滞在极大能量释放区域。相反, 南美洲台站位于相对稳定的南美洲大陆, 三维非均匀性相对较弱, 因此通过三维模型修正后, 高频部分更容易相干聚焦, 对于破裂末期的成像分辨率也更高。此外, 图 3 中, 南美洲数据的结果与通过地表观测得到的可能破裂的断层分布也更为一致 [21] 。因此, 由南美洲数据得到的结果能更好地展示本次地震的破裂细节特征。
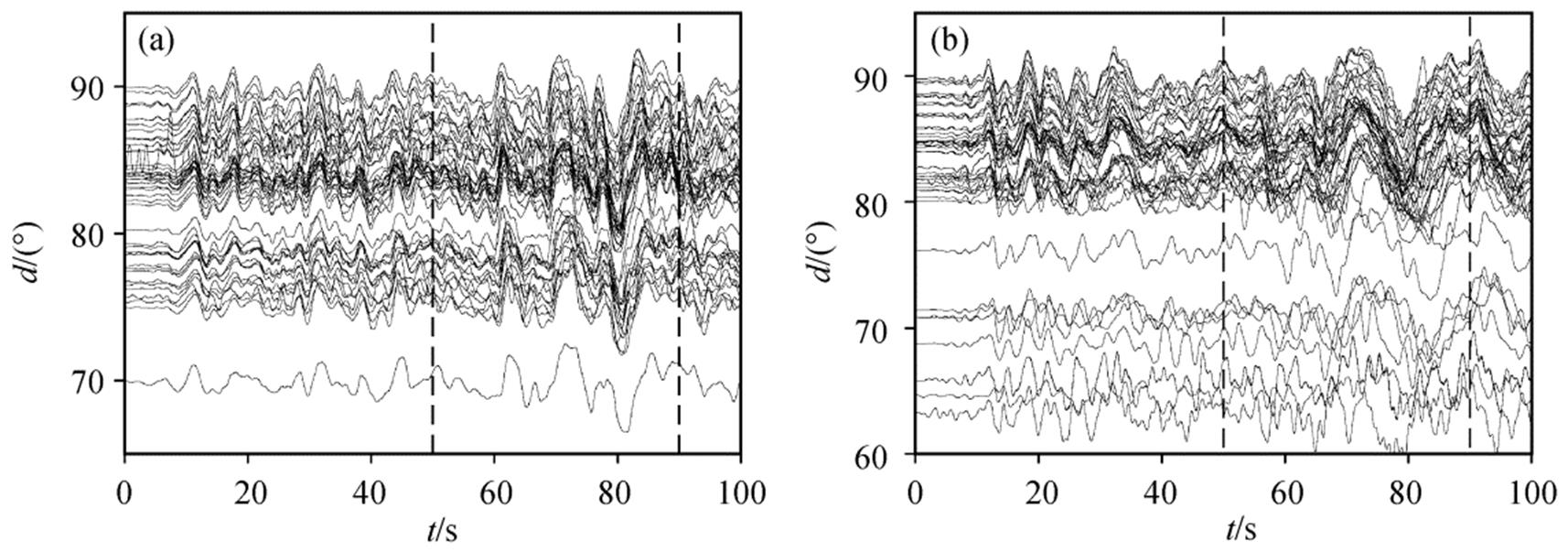
(a)南美洲数据结果, (b)亚洲数据结果; 两条竖直的黑色虚线之间为对低频部分成像使用的数据
图7 使用低频数据的波形
Fig. 7 Data used for low frequency back projection
为了更好地理解高频源分布的意义, 将反投影得到的位置与地面峰值加速度(peak ground accele-ration, PGA)进行对比(图 9)。可以发现, 南美洲数据的结果与 PGA 的分布更为一致, 破裂均传播到东北端海中的断层。由于 PGA 是与加速度相关的物理量, 因此能更好地展示高频部分的信息, 所以从理论上讲, PGA 与高频反投影结果应该更为耦合。这表明, 我们可以通过PGA的结果, 对反投影分析的结果进行一些有效性分析。同时, PGA 与 高频反投影结果互相补充, 可以对地震高频特征分析提供帮助。
前面的分析说明, 与亚洲数据相比, 南美洲数据给出的结果能更完整地展示本次地震的高频破裂特征。因此, 我们认为南美洲数据给出的1.65 km/s的破裂速度更为准确。亚洲数据给出的破裂速度较小, 是因为末期的破裂停滞在距离震中约 100km处, 破裂前沿未向远处移动。1.65 km/s的破裂速度与 Hollinsworth 等 [20] 基于澳洲数据给出的 1.5~2.0 km/s 的速度值区间较为一致, 略为大于 Zhang 等 [22] 使用多台阵联合反投影给出的 1.4~1.6km/s 的破裂 速度。
与传统一维模型反投影方法相比, 本文使用的三维模型反投影方法的最大改进是对走时的估计更为准确, 并依此得到空间分辨率更高的地震破裂过程反投影结果。为了更直观地展示使用三维模型后对走时估计准确性的提升, 我们在地震图上分别标出使用三维模型和一维模型得到的理论走时(图10)。可以看到, 对于南美洲数据, 一维模型估计的走时明显地系统性偏小, 三维模型的估计更为准确; 对于亚洲数据, 一维模型计算的走时比三维模型稍大, 但由于亚洲数据信噪比较低, 很难直观地分辨P 波初至, 因此无法准确地判断哪个模型估计得更准确。值得注意的是, 根据式(4), 由走时预测的系统性偏差所得到的常数并不会影响反投影的结果, 因此我们分别计算基于三维模型和一维模型的理论走时与实际走时的差值, 并进行去平均处理以消除系统性偏差, 得到理论走时与实际走时的相对误差(图 11)。可以观察到, 使用三维模型的结果明显更为集中, 走时相对误差值接近 0, 而一维模型的结果涨落较大, 特别是对于亚洲数据, 走时计算结果更为离散。
本文分别使用南美洲和亚洲的数据, 用三维地球模型对 2016 年 Mw 7.8 级新西兰地震进行反投影分析。结果显示, 本次事件为东北方向的单边破裂, 破裂长度约为 140km, 延伸至海中, 破裂速度约为 1.65km/s。该地震的高频能量释放有两个阶段, 分别为 20~40s 和 60~80s, 其中, 第二个阶段为能量释放的主要阶段。该阶段的低频能量聚束分布与该地震的矩心位置较为一致。本文讨论了亚洲数据成像结果不如南美洲数据理想的原因, 认为使用三维模型可以在一定程度上减弱地球介质横向不均匀性对反投影结果的影响, 但是受限于三维模型的分辨率, 该影响无法完全修正, 特别是在台站分布区域的结构差异较大、区域性非均匀性较强的情况下, 修正幅度有限。这对选择用于反投影分析的数据提出了要求, 即尽可能选取位于稳定的横向不均匀性较弱区域的台阵。此外, 本文对比了使用不同模型时理论走时与实际走时的差别, 发现使用三维模型可以明显地提升走时估计的精确度。
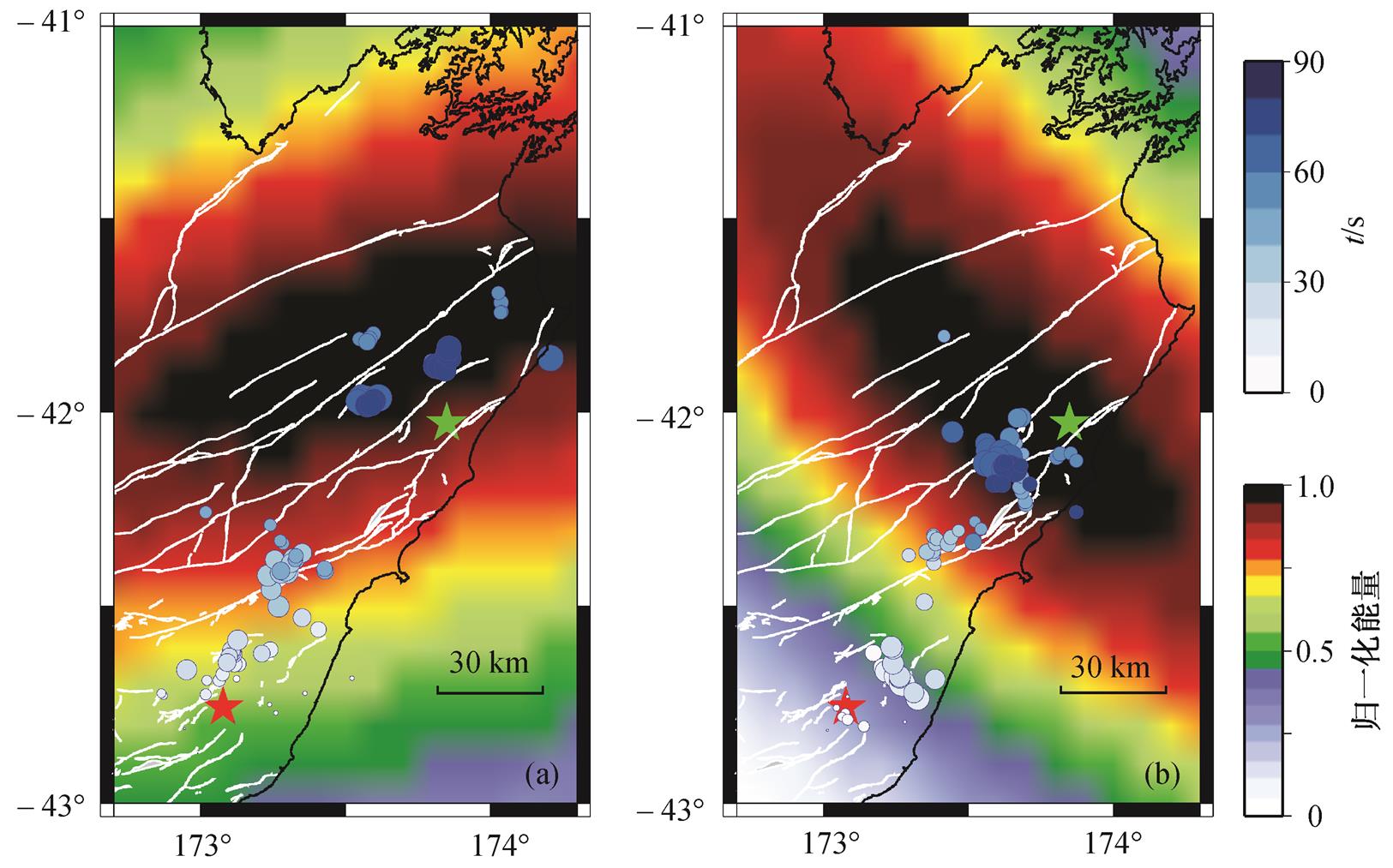
(a) 南美洲数据结果, (b) 亚洲数据结果; 蓝色圆圈代表反投影高频辐射源位置, 白色实线代表当地断层分布, 红色五角星代表震中位置, 绿色五角星表示本次地震矩心位置(来源: http://ds.iris.edu/spud/momenttensor/13456320), 背景颜色代表低频部分的归一化聚束能量分布
图8 高频辐射源位置与50~90 s低频能量分布
Fig. 8 Distribution of accumulated low frequency power during 50‒90 s and high frequency radiators
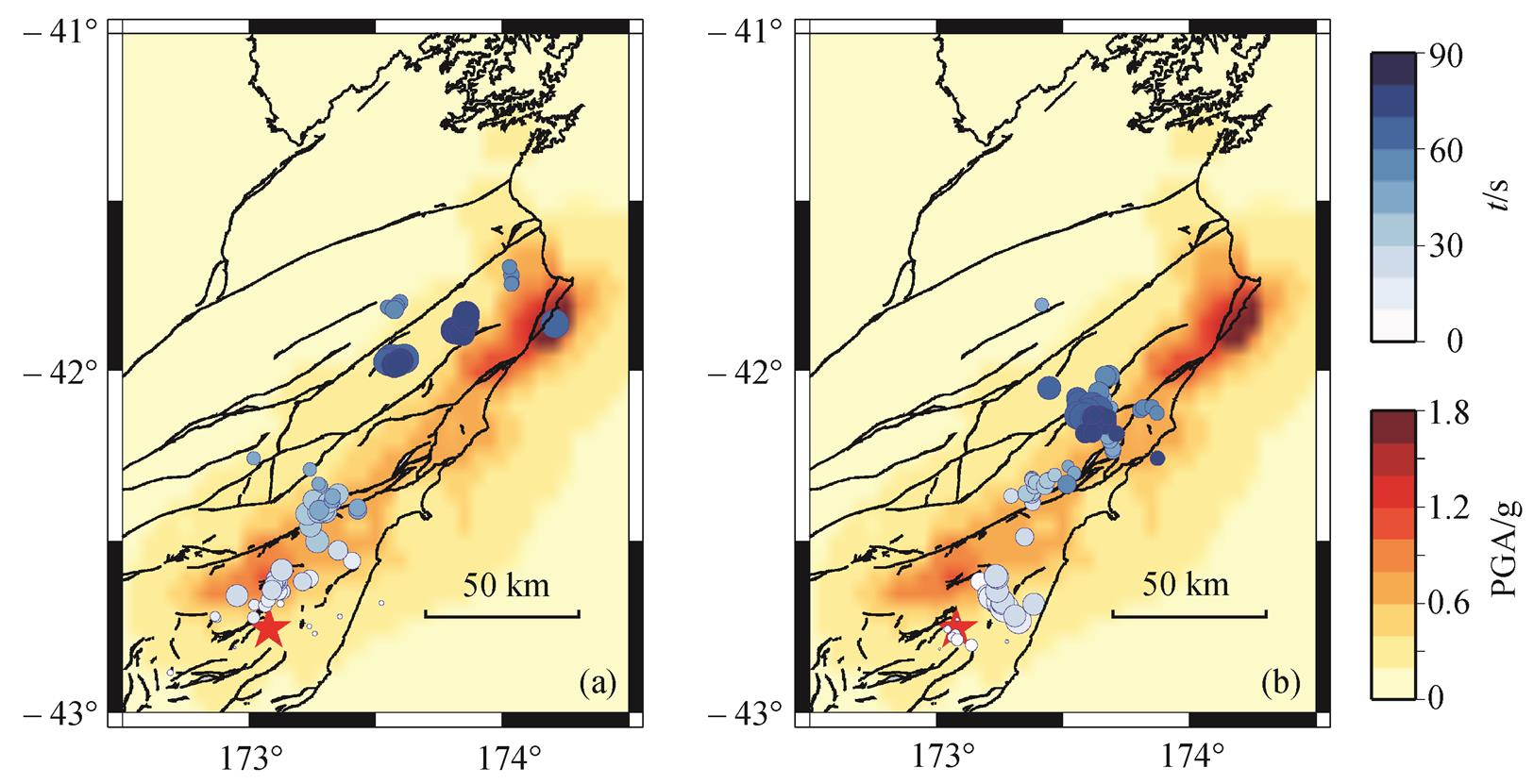
(a)南美洲数据结果, (b)亚洲数据结果; 蓝色圆圈代表反投影高频辐射源位置, 红色五角星代表震中位置, 黑色实线代表当地断层分布, 背景颜色代表PGA分布(来源:https://earthquake.usgs.gov/earthquakes/eventpage/us1000778i#shakemap)
图9 高频辐射源位置与地面峰值加速度分布
Fig. 9 Distribution of peak ground acceleration and high frequency radiators
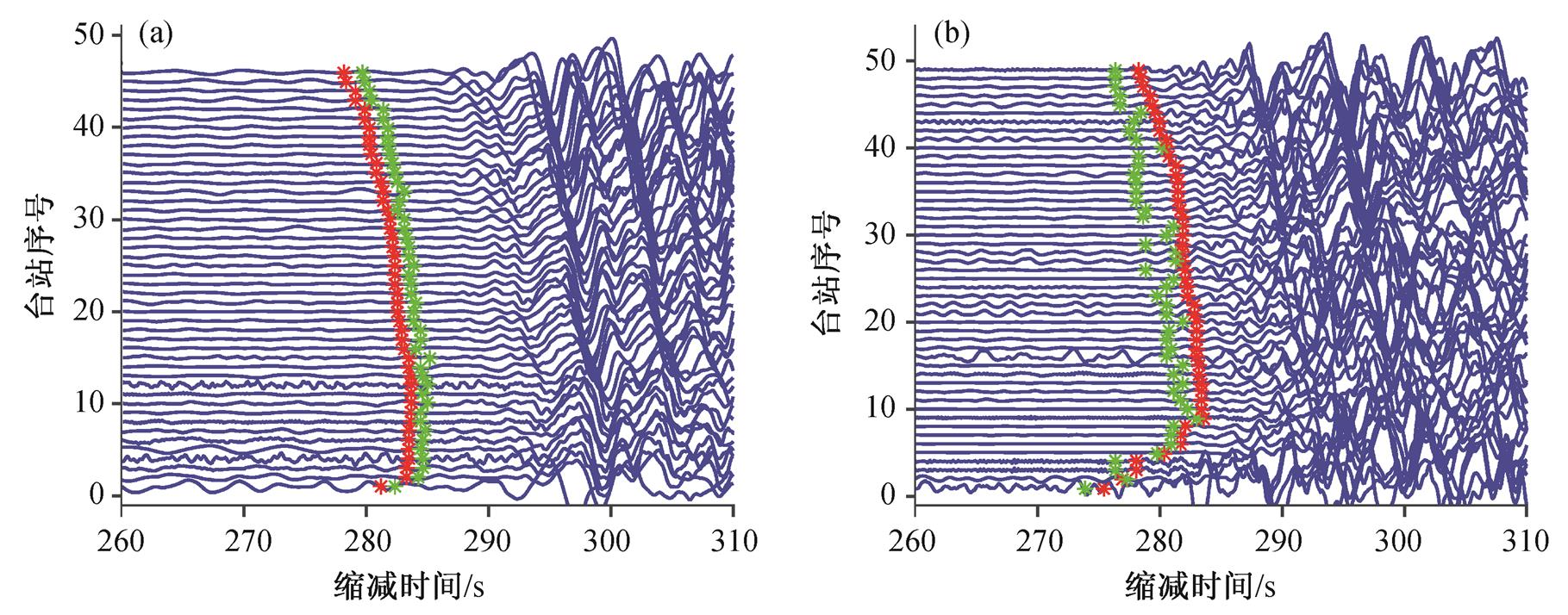
(a)南美洲数据的波形, (b)亚洲数据的波形; 红色星号为基于一维模型的理论走时, 绿色星号为基于三维模型的理论走时; 缩减时间为实际时间减去震中距与参考速度(此处为20 km/s)的比值
图10 一维模型与三维模型理论走时对比
Fig. 10 Predicted travel times based on 3-D and 1-D model
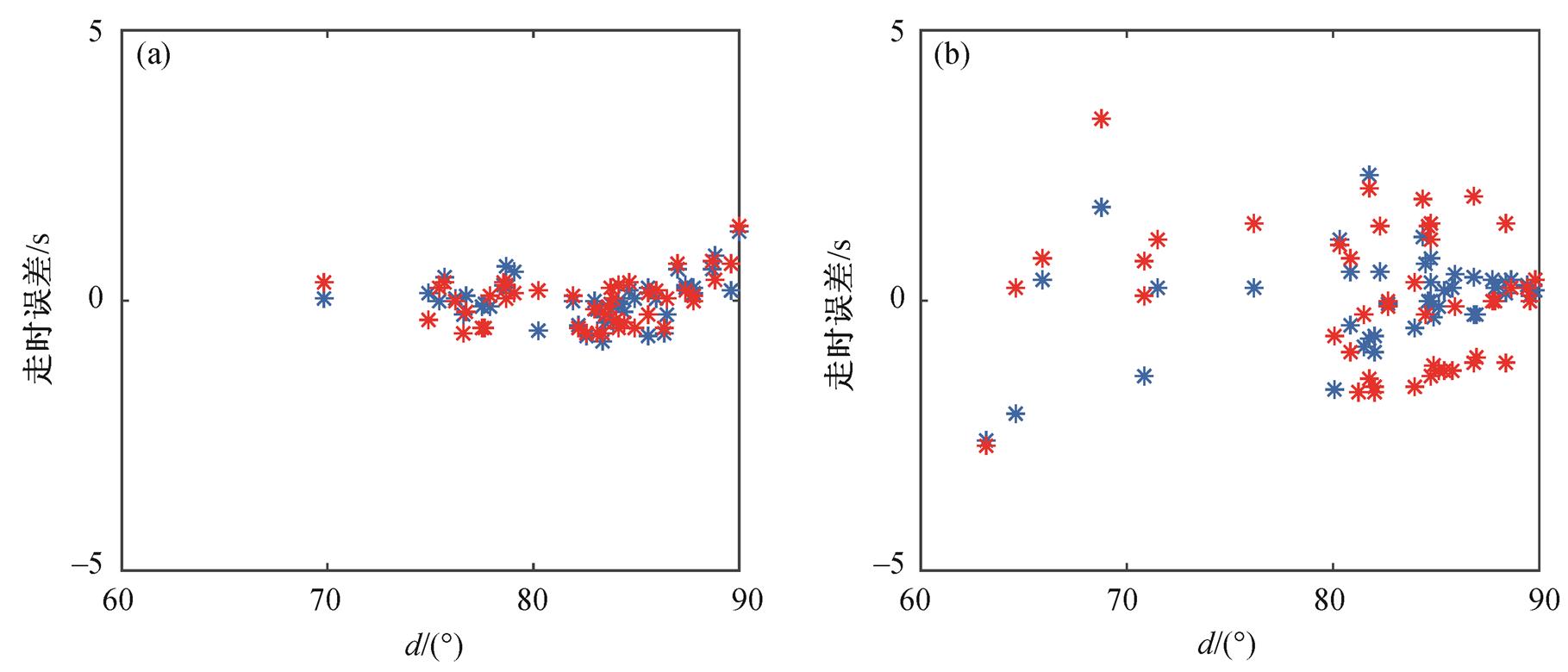
(a)和(b)分别为南美洲数据和亚洲数据基于三维模型(蓝色星号)和一维模型(红色星号)计算出的理论走时与实际走时的去平均差值
图11 南美洲台阵与亚洲台阵走时误差对比
Fig. 11 Travel time error of the South American and Asian array
对余震位置的反投影成像测试说明, 与一维模型相比, 三维模型的使用可以有效地提高空间分辨率。同时, 与使用余震信息对不均匀性进行修正的方法相比, 三维模型反投影无需等待足够数量的用于校正的余震的发生(数天甚至数周), 并且可以避免因余震定位不准而引入的二次误差, 因此可在震后第一时间给出更准确的反投影结果, 达到快速响应的目的, 为震后救灾提供帮助。随着观测数据的不断累积, 三维模型不断的迭代升级, 分辨率也会获得提升。因此, 三维地球模型可以在今后的应用中为反投影分析提供更多帮助。
参考文献
[1]Shi X H, Wang Y, Liu J, et al. How complex is the 2016 Mw 7.8 Kaikoura earthquake, South Island, New Zealand?. Science Bulletin, 2017, 62(5): 309‒311
[2]Ishii M, Shearer P M, Houston H, et al. Extent, duration and speed of the 2004 Sumatra-Andaman earthquake imaged by the Hi-Net array. Nature, 2005, 435: 933‒936
[3]Meng L, Inbal A, Ampuero J P. A window into the complexity of the dynamic rupture of the 2011 Mw 9 Tohoku‐Oki earthquake. Geophysical Research Let-ters, 2011, 38(7): L00G07
[4]Zhang H, Ge Z. Tracking the rupture of the 2008 Wenchuan earthquake by using the relative back-projection method. Bulletin of the Seismological Society of America, 2010, 100(5B): 2551‒2560
[5]Krüger F, Ohrnberger M. Tracking the rupture of the Mw = 9.3 Sumatra earthquake over 1,150 km at tele-seismic distance. Nature, 2005, 435: 937‒939
[6]Walker K T, Shearer P M. Illuminating the near‐sonic rupture velocities of the intracontinental Kokoxili Mw 7.8 and Denali fault Mw 7.9 strike‐slip earthquakes with global P wave back projection ima-ging. Journal of Geophysical Research Solid Earth, 2009, 114(2): 1205‒1222
[7]Satriano C, Kiraly E, Bernard P, et al. The 2012 Mw 8.6 Sumatra earthquake: Evidence of westward sequ-ential seismic ruptures associated to the reactivation of a N-S ocean fabric. Geophysical Research Letters, 2012, 39(15): L15302
[8]Dziewonski A M, Anderson D L. preliminary refer-ence earth model. Physics of the Earth & Planetary Interiors, 1981, 25(4): 297‒356
[9]Kennett B L N. Traveltimes for global earthquake location and phase identific. Geophysical Journal International, 1991, 105(2): 429‒465
[10]Kennett B L N, Engdahl E R, Buland R. Constraints on seismic velocities in the Earth from traveltimes. Geophysical Journal International, 1995, 122(1): 108‒ 124
[11]Simmons N A, Myers S C, Johannesson G, et al. LLNL-G3Dv3: global P wave tomography model for improved regional and teleseismic travel time pre-diction. Journal of Geophysical Research Atmos-pheres, 2012, 117(B10): 189‒200
[12]Yao H, Shearer P M, Gerstoft P. Subevent location and rupture imaging using iterative backprojection for the 2011 Tohoku Mw 9.0 earthquake. Geophysical Journal International, 2012, 190(2): 1152‒1168
[13]VanDecar J, Crosson R. Determination of teleseismic relative phase arrival times using multi-channel cross-correlation and least squares. Bulletin of the Seismo-logical Society of America, 1990, 80(1): 150‒169
[14]Meng L, Zhang A, Yagi Y. Improving back projection imaging with a novel physics‐based aftershock cali-bration approach: a case study of the 2015 Gorkha earthquake. Geophysical Research Letters, 2016, 43 (2): 628‒636
[15]Ishii M, Shearer P M, Houston H, et al. Teleseismic P wave imaging of the 26 December 2004 Sumatra‐ Andaman and 28 March 2005 Sumatra earthquake ruptures using the Hi‐net array. Journal of Geophys-ical Research Atmospheres, 2007, 112(B11): 429‒430
[16]Palo M, Tilmann F, Krüger F, et al. High-frequency seismic radiation from Maule earthquake (Mw 8.8, 2010 February 27) inferred from high-resolution back projection analysis. Geophysical Journal Interna-tional, 2014, 199(2): 1058‒1077
[17]Myers S C, Johannesson G, Hanley W. Incorporation of probabilistic seismic phase labels into a Bayesian multiple-event seismic locator. Geophysical Journal International, 2009, 177(1): 193–204
[18]Myers S C, Johannesson G, Hanley W. A Bayesian hierarchical method for multiple‐event seismic loca-tion. Geophysical Journal International, 2007, 171: 1049‒1063
[19]Xu Y, Koper K D, Sufri O, et al. Rupture imaging of the Mw 7.9 12 May 2008 Wenchuan earthquake from back projection of teleseismic P waves. Geochemistry, Geophysics, Geosystems, 2009, 10(4): Q04006
[20]Hollinsworth J, Ye L, Avouac J P. Dynamically triggered slip on a splay fault in the Mw 7.8, 2016 Kaikoura (New Zealand) earthquake. Geophysical Research Letters, 2017, 44(8): 3517–3525
[21]Bradley B A, Razafindrakoto H N, Polak V. Ground-motion observations from the 14 November 2016 Mw 7.8 Kaikoura, New Zealand, earthquake and insights from broadband simulations. Seismological Research Letters, 2017, 88(3): 740‒756
[22]Zhang H, Koper K D, Pankow K, et al. Imaging the 2016 Mw 7.8 Kaikoura, New Zealand earthquake with teleseismic P waves: a cascading rupture across mul-tiple faults. Geophysical Research Letters, 2017, 44: doi: 10.1002/2017GL073461
Utilizing Back-Projection Method Based on 3-D Global Tomography Model to Investigate Mw 7.8 New Zealand South Island Earthquake
LIU Zhipeng, SONG Chao, GE Zengxi †
School of Earth and Space Sciences, Peking University, Beijing 100871
Abstract Based on a 3-D global velocity structure model, the authors used teleseismic P wave data from Asian and South American array to image the rupture process of 2016 Mw 7.8 New Zealand earthquake via back-projection analysis. The results show that the rupture is a unilateral one with northeast direction, extending to the ocean. The rupture speed is about 1.65 km/s. There are two phases dominated by high frequency power radiation, occurring during 20 - 40 s and 60 - 80 s, respectively. The second phase is the major one, whose distribution of low frequency power radiation is consistent with the centroid location of the event. The high frequency back projection result of the South American data is better correlated with the peak ground acceleration result. According to the comparison and analysis of the Asian and South American results, it could be inferred that in order to obtain more detailed rupture information of high frequency, the data of array deployed in the region with lower 3-D heterogeneity should be adopted in back projection analysis to enhance the coherency of waveforms.
Key words 2016 New Zealand earthquake; rupture process; 3-D earth model; back projection method
† Corresponding author , E-mail: zge@pku.edu.cn
doi: 10.13209/j.0479-8023.2017.105
中图分类号 P315
收稿日期: 2017-04-24;
修回日期: 2017-05-31;
网络出版日期: 2017-06-04
†通信作者 , E-mail: zge@pku.edu.cn
国家自然科学基金(41374045, 41774047)资助
①https://www-gs.llnl.gov/nuclear-threat-reduction/nuclear-explosion-monitoring/global-3d-seismic-tomography